Hydrothermal Carbonization Kinetics of Lignocellulosic Agro-Wastes: Experimental Data and Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. HTC Tests
2.2. Analytical Determinations
2.3. HTC Reactor Heat-Up Transient Phase
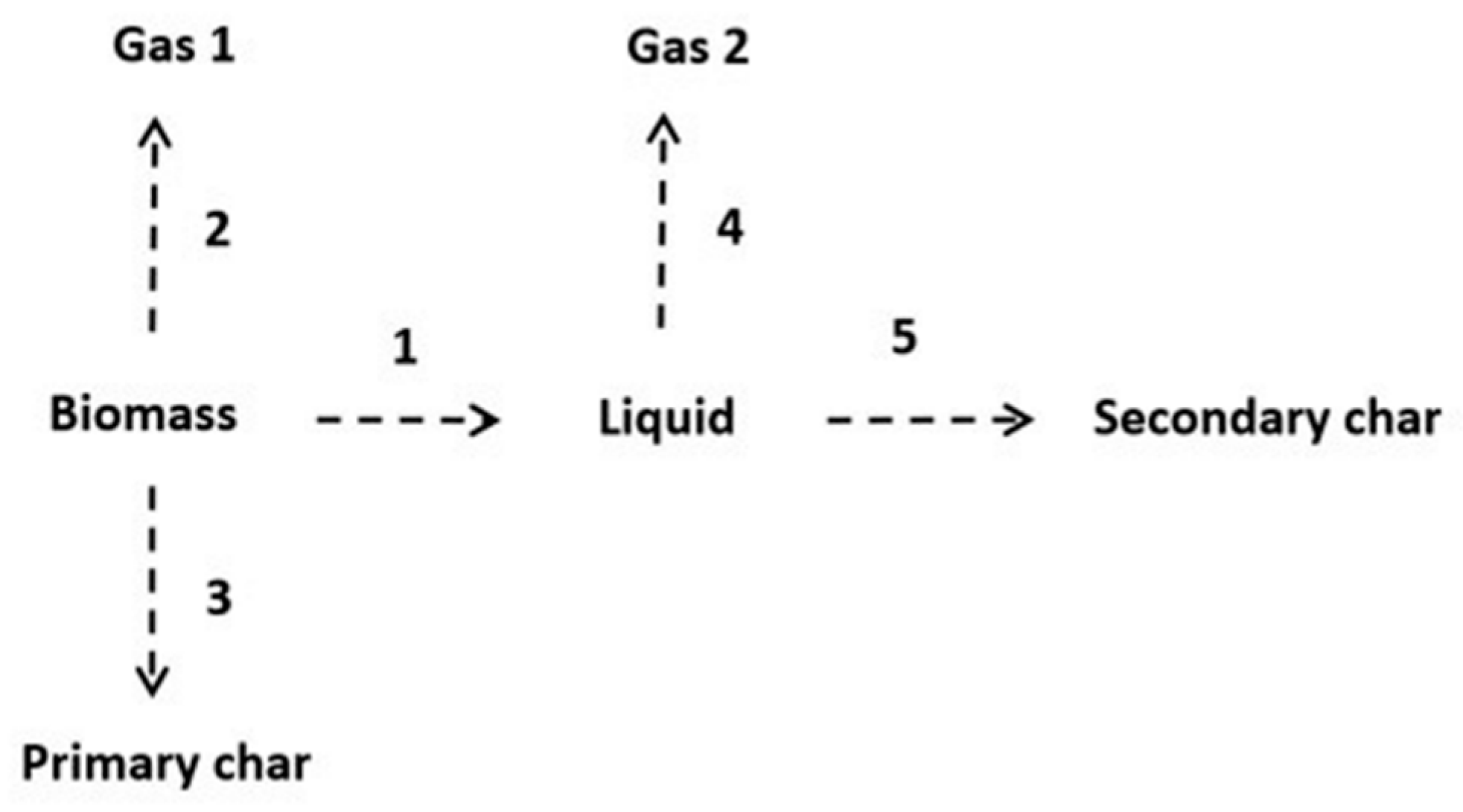
2.4. Kinetics Model
3. Results and Discussion
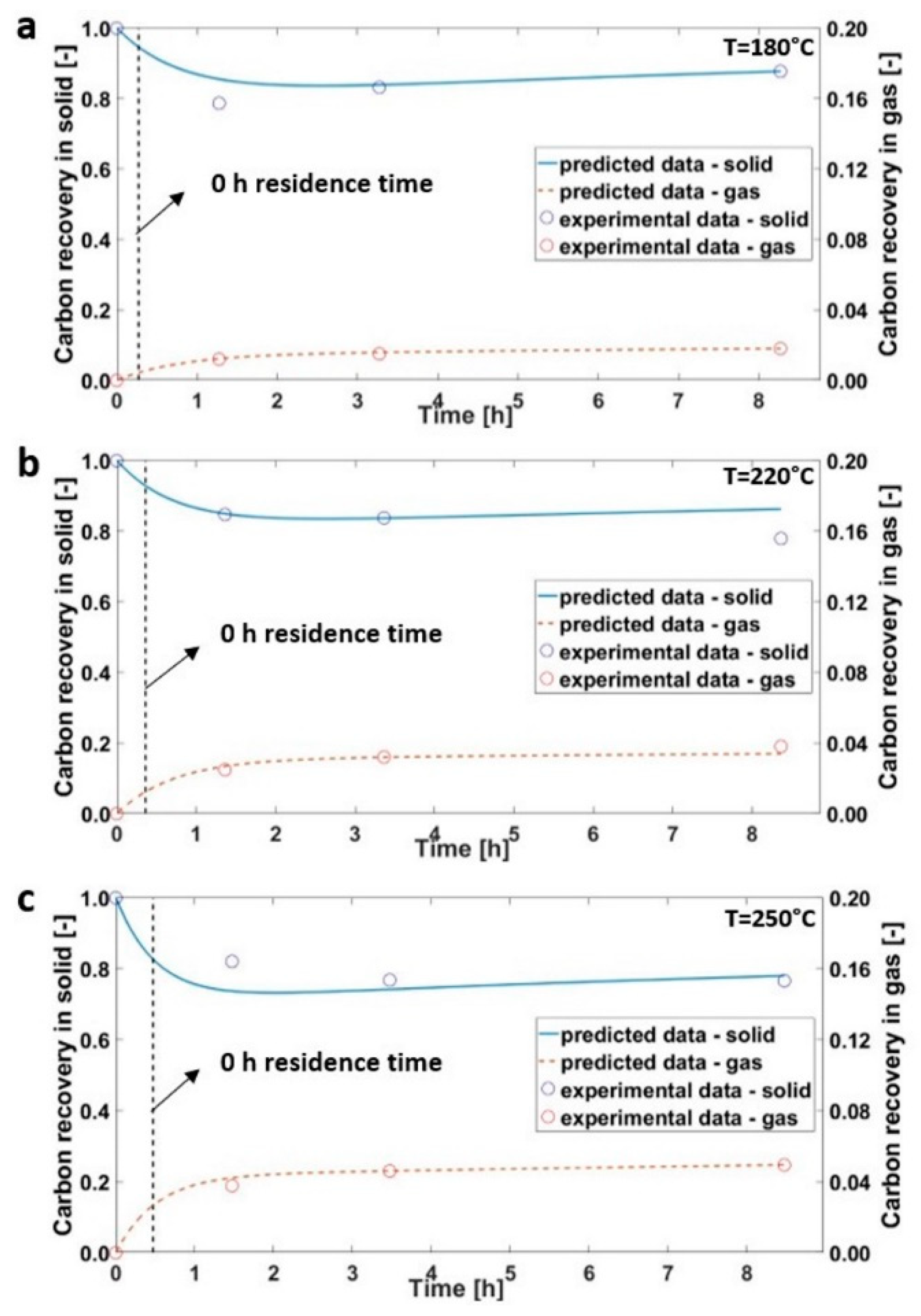
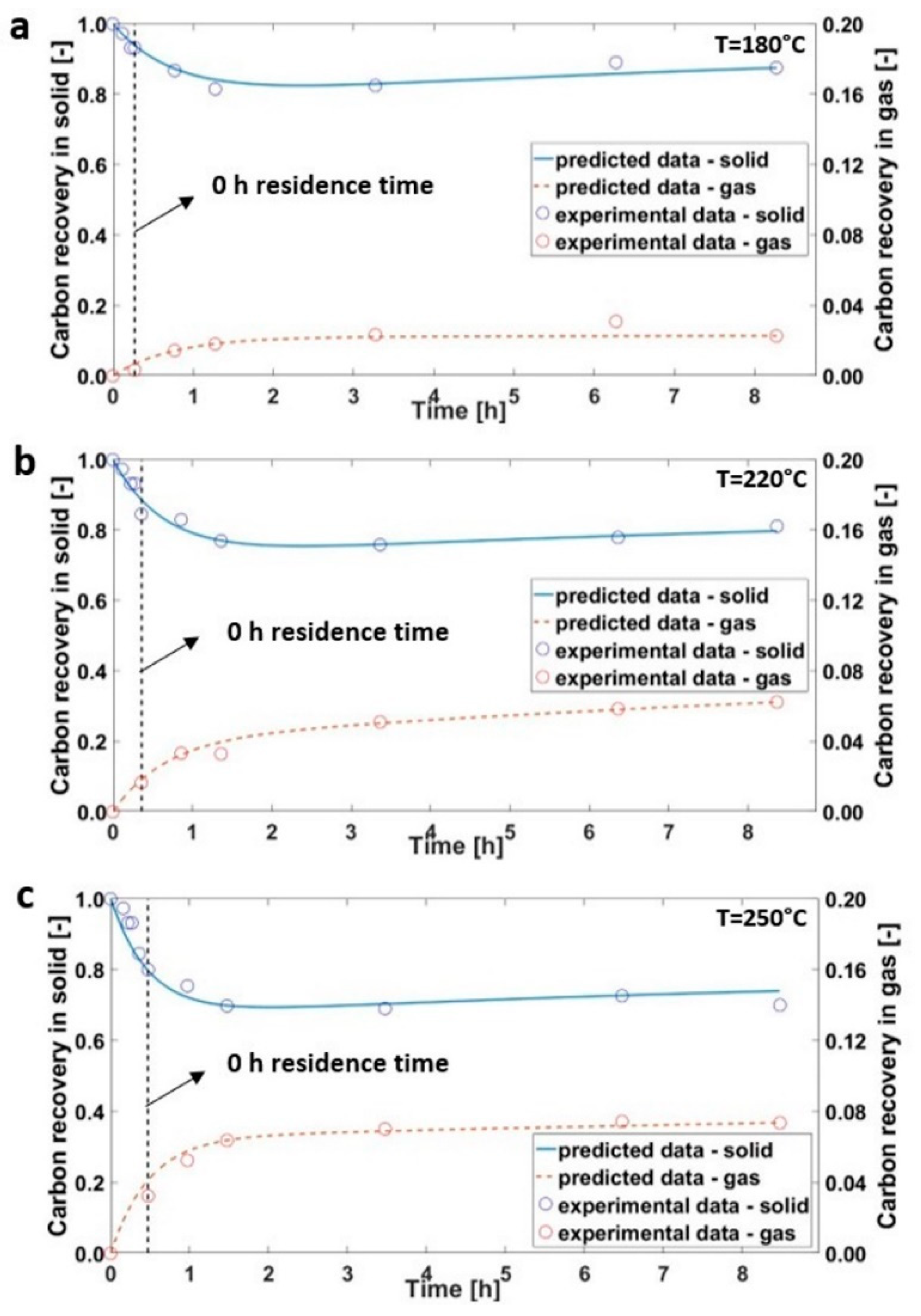
3.1. Hydrothermal Carbonization of Olive Trimmings
3.2. Hydrothermal Carbonization during Transient Time
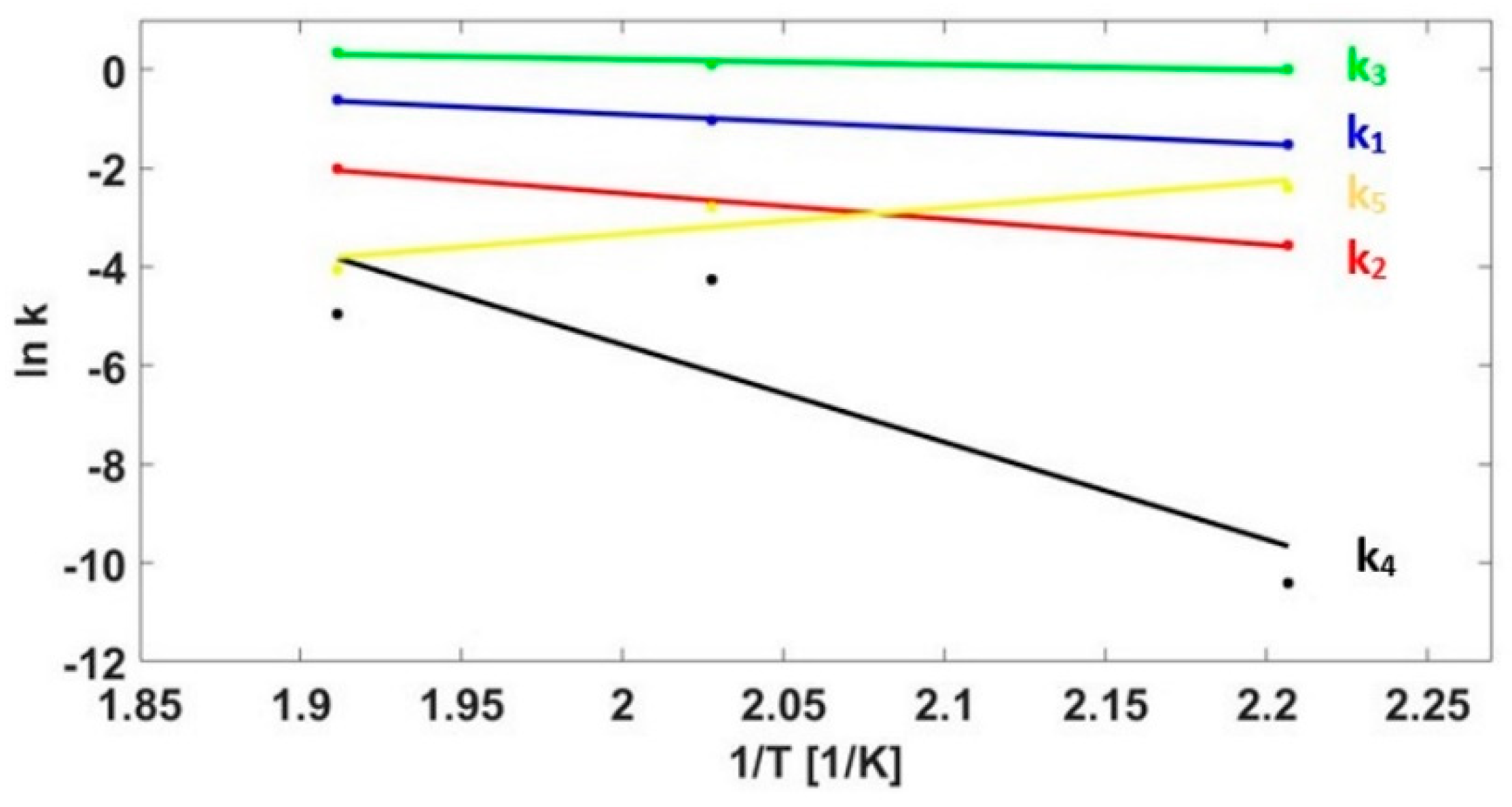
3.3. Kinetics Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

| Process Conditions | Error (%) | ||
|---|---|---|---|
| Olive Trimmings | Grape Marc | Opuntia Ficus Indica | |
| 120 °C, 0 h | 0.32 | - | - |
| 150 °C, 0 h | 1.15 | - | - |
| 180 °C, 0 h | 0.71 | - | - |
| 180 °C, 0.5 h | 0.62 | - | 11.17 |
| 180 °C, 1 h | 3.37 | 8.63 | 3.02 |
| 180 °C, 3 h | 0.55 | 0.95 | 1.32 |
| 180 °C, 6 h | 3.62 | - | - |
| 180 °C, 8 h | 0.02 | 0.00 | - |
| Avg. 180 °C | 1.30 | 3.19 | 5.17 |
| 120 °C, 0 h | 1.35 | - | - |
| 150 °C, 0 h | 0.72 | - | - |
| 180 °C, 0 h | 2.12 | - | - |
| 220 °C, 0 h | 4.87 | - | - |
| 220 °C, 0.5 h | 2.94 | - | 10.23 |
| 220 °C, 1 h | 0.14 | 0.30 | 1.08 |
| 220 °C, 3 h | 0.24 | 0.03 | 0.66 |
| 220 °C, 6 h | 0.56 | - | - |
| 220 °C, 8 h | 1.67 | 10.58 | - |
| Avg. 220 °C | 1.62 | 3.64 | 3.99 |
| 120 °C, 0 h | 4.2 | - | - |
| 150 °C, 0 h | 4.21 | - | - |
| 180 °C, 0 h | 4.14 | - | - |
| 220 °C, 0 h | 2.74 | - | - |
| 250 °C, 0 h | 0.25 | - | - |
| 250 °C, 0.5 h | 4.22 | - | 5.05 |
| 250 °C, 1 h | 0.14 | 10.19 | 4.03 |
| 250 °C, 3 h | 1.89 | 3.27 | 0.23 |
| 250 °C, 6 h | 0.00 | - | - |
| 250 °C, 8 h | 5.69 | 1.72 | - |
| Avg. 250 °C | 2.75 | 5.06 | 3.10 |

| Parameters | Olive Trimmings (n = 1) | ||
|---|---|---|---|
| T (°C) | 180 | 220 | 250 |
| k1 (s−1) | 0.22 | 0.35 | 0.54 |
| k2 (s−1) | 0.03 | 0.07 | 0.13 |
| k3 (s−1) | 1.01 | 1.11 | 1.41 |
| k4 (s−1) | 0.00 | 0.01 | 0.007 |
| k5 (s−1) | 0.09 | 0.06 | 0.02 |
| n (-) | 1.00 | 1.00 | 1.00 |
| Parameters | Olive Trimmings (n = 1) |
|---|---|
| k0,1 (s−1) | 163.18 |
| k0,2 (s−1) | 2.75 × 103 |
| k0,3 (s−1) | 10.97 |
| k0,4 (s−1) | n.a. |
| k0,5 (s−1) | n.a. |
| Ea,1 (kJ/mol) | 24.95 |
| Ea,2(kJ/mol) | 43.33 |
| Ea,3 (kJ/mol) | 9.09 |
| Ea,4 (kJ/mol) | n.a. |
| Ea,5 (kJ/mol) | n.a. |
References
- Dinc, G.; Yel, E. Self-catalyzing pyrolysis of olive pomace. J. Anal. Appl. Pyrolysis 2018, 134, 641–646. [Google Scholar] [CrossRef]
- Volpe, M.; D’Anna, C.; Messineo, S.; Volpe, R.; Messineo, A. Sustainable Production of Bio-Combustibles from Pyrolysis of Agro-Industrial Wastes. Sustainability 2014, 6, 7866–7882. [Google Scholar] [CrossRef]
- Volpe, M.; Panno, D.; Volpe, R.; Messineo, A. Upgrade of citrus waste as a biofuel via slow pyrolysis. J. Anal. Appl. Pyrolysis 2015, 115, 66–76. [Google Scholar] [CrossRef]
- Borel, L.D.M.S.; Lira, T.S.; Ribeiro, J.A.; Ataíde, C.H.; Barrozo, M.A.S. Pyrolysis of brewer’s spent grain: Kinetic study and products identification. Ind. Crops Prod. 2018, 121, 388–395. [Google Scholar] [CrossRef]
- Sánchez, J.D.; Ramírez, G.E.; Barajas, M.J. Comparative kinetic study of the pyrolysis of mandarin and pineapple peel. J. Anal. Appl. Pyrolysis 2016, 118, 192–201. [Google Scholar] [CrossRef]
- Luz, C.; Cordiner, S.; Manni, A.; Mulone, V. Biomass fast pyrolysis in a shaftless screw reactor: A 1-D numerical model. Energy 2018, 157, 792–805. [Google Scholar] [CrossRef]
- Volpe, M.; Goldfarb, J.L.; Fiori, L. Hydrothermal carbonization of Opuntia ficus indica cladodes: Role of process parameters on hydrochar properties. Bioresour. Technol. 2018, 247, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Kruse, A.; Funke, A.; Titirici, M.-M. Hydrothermal conversion of biomass to fuels and energetic materials. Curr. Opin. Chem. Biol. 2013, 17, 515–521. [Google Scholar] [CrossRef] [PubMed]
- Kambo, H.S.; Dutta, A. A comparative review of biochar and hydrochar in terms of production, physico-chemical properties and applications. Renew. Sustain. Energy Rev. 2015, 45, 359–378. [Google Scholar] [CrossRef]
- Saha, N.; Saba, A.; Reza, M.T. Effect of hydrothermal carbonization temperature on pH, dissociation constants, and acidic functional groups on hydrochar from cellulose and wood. J. Anal. Appl. Pyrolysis 2018. [Google Scholar] [CrossRef]
- Benavente, V.; Calabuig, E.; Fullana, A. Upgrading of moist agro-industrial wastes by hydrothermal carbonization. J. Anal. Appl. Pyrolysis 2015, 113, 89–98. [Google Scholar] [CrossRef]
- Düdder, H.; Wütscher, A.; Vorobiev, N.; Schiemann, M.; Scherer, V.; Muhler, M. Oxidation characteristics of a cellulose-derived hydrochar in thermogravimetric and laminar flow burner experiments. Fuel Process. Technol. 2016, 148, 85–90. [Google Scholar] [CrossRef]
- Sabio, E.; Álvarez-Murillo, A.; Román, S.; Ledesma, B. Conversion of tomato-peel waste into solid fuel by hydrothermal carbonization: Influence of the processing variables. Waste Manag. 2016, 47, 122–132. [Google Scholar] [CrossRef] [PubMed]
- Volpe, M.; Wüst, D.; Merzari, F.; Lucian, M.; Andreottola, G.; Kruse, A.; Fiori, L. One stage olive mill waste streams valorisation via hydrothermal carbonisation. Waste Manag. 2018, 80, 224–234. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, E.; Atila, B.; Mumme, J.; Reza, M.T.; Toptas, A.; Elibol, M.; Yanik, J. Characterization of products from hydrothermal carbonization of orange pomace including anaerobic digestibility of process liquor. Bioresour. Technol. 2015, 196, 35–42. [Google Scholar] [CrossRef]
- Volpe, M.; Fiori, L. From olive waste to solid biofuel through hydrothermal carbonisation: The role of temperature and solid load on secondary char formation and hydrochar energy properties. J. Anal. Appl. Pyrolysis 2017, 124, 63–72. [Google Scholar] [CrossRef]
- Lucian, M.; Volpe, M.; Gao, L.; Piro, G.; Goldfarb, J.L.; Fiori, L. Impact of hydrothermal carbonization conditions on the formation of hydrochars and secondary chars from the organic fraction of municipal solid waste. Fuel 2018, 233, 257–268. [Google Scholar] [CrossRef]
- Arauzo, P.J.; Olszewski, M.P.; Kruse, A. Hydrothermal Carbonization Brewer’s Spent Grains with the Focus on Improving the Degradation of the Feedstock. Energies 2018, 3226. [Google Scholar] [CrossRef]
- Mäkelä, M.; Volpe, M.; Volpe, R.; Fiori, L.; Dahl, O. Spatially resolved spectral determination of polysaccharides in hydrothermally carbonized biomass. Green Chem. 2018, 20, 1114–1120. [Google Scholar] [CrossRef]
- Gao, L.; Volpe, M.; Lucian, M.; Fiori, L.; Goldfarb, J.L. Does Hydrothermal Carbonization as a Biomass Pretreatment Reduce Fuel Segregatuion of Coal-Biomass Blends During Oxidation? Energy Convers. Manag. 2019, 181, 93–104. [Google Scholar] [CrossRef]
- Mäkelä, M.; Fullana, A.; Yoshikawa, K. Ash behavior during hydrothermal treatment for solid fuel applications. Part 1: Overview of different feedstock. Energy Convers. Manag. 2016, 121, 402–408. [Google Scholar] [CrossRef]
- Codignole Luz, F.; Volpe, M.; Fiori, L.; Manni, A.; Cordiner, S.; Mulone, V.; Rocco, V. Spent coffee enhanced biomethane potential via an integrated hydrothermal carbonization-anaerobic digestion process. Bioresour. Technol. 2018, 256, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Breulmann, M.; Van Afferden, M.; Müller, R.A.; Schulz, E.; Fühner, C. Process conditions of pyrolysis and hydrothermal carbonization affect the potential of sewage sludge for soil carbon sequestration and amelioration. J. Anal. Appl. Pyrolysis 2017, 124, 256–265. [Google Scholar] [CrossRef]
- Duman, G.; Toptas, A.; Ucar, S.; Yanik, J. Comparative evaluation of dry and wet carbonization of agro industrial wastes for the production of soil improver. J. Environ. Chem. Eng. 2018, 6, 3366–3375. [Google Scholar] [CrossRef]
- Titirici, M.M. Hydrothermal Carbons: Synthesis, Characterization, and Applications. In Novel Carbon Adsorbents; Tascón, J.M.D., Ed.; Elsevier Ltd.: Oxford, UK, 2012; pp. 351–399. [Google Scholar]
- Benstoem, F.; Becker, G.; Firk, J.; Kaless, M.; Wuest, D.; Pinnekamp, J.; Kruse, A. Elimination of micropollutants by activated carbon produced from fibers taken from wastewater screenings using hydrothermal carbonization. J. Environ. Manag. 2018, 211, 278–286. [Google Scholar] [CrossRef] [PubMed]
- Lucian, M.; Fiori, L. Hydrothermal Carbonization of Waste Biomass: Process Design, Modeling, Energy Efficiency and Cost Analysis. Energies 2017, 10. [Google Scholar] [CrossRef]
- Hitzl, M.; Corma, A.; Pomares, F.; Renz, M. The hydrothermal carbonization (HTC) plant as a decentral biorefinery for wet biomass. Catal. Today 2015, 257, 154–159. [Google Scholar] [CrossRef]
- Missaoui, A.; Bostyn, S.; Belandria, V.; Cagnon, B.; Sarh, B. Hydrothermal carbonization of dried olive pomace: Energy potential and process performances. J. Anal. Appl. Pyrolysis 2017, 128, 281–290. [Google Scholar] [CrossRef]
- Christoforou, E.; Fokaides, P.A. A review of olive mill solid wastes to energy utilization techniques. Waste Manag. 2016, 49, 346–363. [Google Scholar] [CrossRef]
- Poerschmann, J.; Baskyr, I.; Weiner, B.; Koehler, R.; Wedwitschka, H.; Kopinke, F.-D. Hydrothermal carbonization of olive mill wastewater. Bioresour. Technol. 2013, 133, 581–588. [Google Scholar] [CrossRef]
- Volpe, M.; Fiori, L.; Volpe, R.; Messineo, A. Upgrading of Olive Tree Trimmings Residue as Biofuel by Hydrothermal Carbonization and Torrefaction: a Comparative Study. Chem. Eng. Trans. 2016, 50, 13–18. [Google Scholar] [CrossRef]
- Jatzwauck, M.; Schumpe, A. Kinetics of hydrothermal carbonization (HTC) of soft rush. Biomass Bioenergy 2015, 75, 94–100. [Google Scholar] [CrossRef]
- Jung, D.; Kruse, A. Evaluation of Arrhenius-type Overall Kinetic Equations for Hydrothermal Carbonization. J. Anal. Appl. Pyrolysis 2017, 127, 286–291. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhan, H.; Song, Y.; He, C.; Huang, Y.; Yin, X. Insights into the evolution of chemical structures in lignocellulose and non lignocellulose biowastes during hydrothermal carbonization (HTC). Fuel 2019, 236, 960–974. [Google Scholar] [CrossRef]
- Funke, A.; Ziegler, F. Hydrothermal carbonization of biomass: A summary and discussion of chemical mechanisms for process engineering. Biofuels Bioproduct Biorefinery 2010, 160–177. [Google Scholar] [CrossRef]
- Liu, Z.; Balasubramanian, R. Hydrothermal Carbonization of Waste Biomass for Energy Generation. Procedia Environ. Sci. 2012, 16, 159–166. [Google Scholar] [CrossRef]
- Reza, M.T.; Yan, W.; Uddin, M.H.; Lynam, J.G.; Hoekman, S.K.; Coronella, C.J.; Vásquez, V.R. Reaction kinetics of hydrothermal carbonization of loblolly pine. Bioresour. Technol. 2013, 139, 161–169. [Google Scholar] [CrossRef]
- Borrero-lópez, A.M.; Masson, E.; Celzard, A.; Fierro, V. Modelling the reactions of cellulose, hemicellulose and lignin submitted to hydrothermal treatment. Ind. Crops Products 2018, 124, 919–930. [Google Scholar] [CrossRef]
- Álvarez-Murillo, A.; Sabio, E.; Ledesma, B.; Rom, S. Generation of biofuel from hydrothermal carbonization of cellulose. Kinetics modelling. Energy 2016, 94, 600–608. [Google Scholar] [CrossRef]
- Baratieri, M.; Basso, D.; Patuzzi, F.; Castello, D.; Fiori, L. Kinetic and Thermal Modeling of Hydrothermal Carbonization Applied to Grape Marc. Chem. Eng. Trans. 2015, 43, 505–510. [Google Scholar] [CrossRef]
- Karayildirim, T.; Sinaǧ, A.; Kruse, A. Char and coke formation as unwanted side reaction of the hydrothermal biomass gasification. Chem. Eng. Technol. 2008, 31, 1561–1568. [Google Scholar] [CrossRef]
- Knezevic, D.; Van Swaaij, W.; Kersten, S. Hydrothermal Conversion Of Biomass. II. Conversion Of Wood, Pyrolysis Oil, And Glucose In Hot Compressed Water. Ind. Eng. Chem. Res. 2010, 49, 104–112. [Google Scholar] [CrossRef]
- Basso, D.; Patuzzi, F.; Castello, D.; Baratieri, M.; Rada, C.E.; Weiss-Hortala, E.; Fiori, L. Agro-industrial waste to solid biofuel through hydrothermal carbonization. Waste Manag. 2016, 47, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Fiori, L.; Basso, D.; Castello, D.; Baratieri, M. Hydrothermal Carbonization of Biomass: Design of a Batch Reactor and Preliminary Experimental Results. Chem. Eng. Trans. 2014, 37, 55–60. [Google Scholar] [CrossRef]
- Basso, D.; Weiss-Hortala, E.; Patuzzi, F.; Castello, D.; Baratieri, M.; Fiori, L. Hydrothermal carbonization of off-specification compost: A byproduct of the organic municipal solid waste treatment. Bioresour. Technol. 2015, 182, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Berge, N.D.; Ro, K.S.; Mao, J.; Flora, J.R.V.; Chappell, M.A.; Bae, S. Hydrothermal Carbonization of Municipal Waste Streams. Environ. Sci. Technol 2011, 45, 5696–5703. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Jordan, B.; Berge, N.D. Thermal conversion of municipal solid waste via hydrothermal carbonization: Comparison of carbonization products to products from current waste management techniques. Waste Manag. 2012, 32, 1353–1365. [Google Scholar] [CrossRef]
- Romàn, S.; Libra, J.; Berge, N.; Sabio, E.; Ro, K.; Li, L.; Ledesma, B.; Bae, S. Hydrothermal Carbonization: Modeling, Final Properties Design and Applications: A Review. Energies 2018, 11, 216. [Google Scholar] [CrossRef]
- Lucian, M.; Piro, G.; Fiori, L. A Novel Reaction Kinetics Model for Estimating the Carbon Content into Hydrothermal Carbonization Products. Chem. Eng. Trans. 2018, 65, 379–384. [Google Scholar] [CrossRef]
- Libra, J.A.; Ro, K.S.; Kammann, C.; Funke, A.; Berge, N.D.; Neubauer, Y.; Titirici, M.-M.; Fühner, C.; Bens, O.; Kern, J.; et al. Hydrothermal carbonization of biomass residuals: a comparative review of the chemistry, processes and applications of wet and dry pyrolysis. Biofuels 2011, 2, 71–106. [Google Scholar] [CrossRef]
- Lei, Y.-Q.; Su, Q.-H.; Tian, R. Morphology evolution, formation mechanism and adsorption properties of hydrochars prepared by hydrothermal carbonization of corn stalk. RSC Adv. 2016, 109. [Google Scholar] [CrossRef]
- Ulbrich, M.; Preßl, D.; Fendt, S.; Gaderer, M.; Splietho, H. Impact of HTC reaction conditions on the hydrochar properties and CO2 gasification properties of spent grains. Fuel Process. Technol. 2017, 167, 663–669. [Google Scholar] [CrossRef]
- Titirici, M.M. Sustainable Carbon Materials from Hydrothermal Processes, 1st ed.; Titirici, M.-M., Ed.; John Wiley & Sons, Ltd.: London, UK, 2013; ISBN 9781118622179. [Google Scholar]
- Kruse, A.; Badoux, F.; Grandl, R.; Wüst, D. Hydrothermale Karbonisierung: 2. Kinetik der Biertreber-Umwandlung. Chemie-Ingenieur-Technik 2012, 84, 509–512. [Google Scholar] [CrossRef]
- Almagrbi, A.M.; Hatami, T.; Glisic, S.B.; Orlovi, A.M. Determination of kinetic parameters for complex transesterification reaction by standard optimisation methods. Hemijska Industrija 2014, 68, 149–159. [Google Scholar] [CrossRef]
- Urych, B. Determination of kinetic parameters of coal pyrolysis to simulate the process of underground coal gasification (UCG). J. Sustain. Mining 2014, 13, 3–9. [Google Scholar] [CrossRef]
- Hwang, I.; Aoyama, H.; Matsuto, T.; Nakagishi, T.; Matsuo, T. Recovery of solid fuel from municipal solid waste by hydrothermal treatment using subcritical water. Waste Manag. 2012, 32, 410–416. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Wang, B.; Fan, W. Kinetic Compensation Effect in the Thermal Decomposition of Biomass in Air Atmosphere. Fire Saf. Sci. 2003, 7, 581–592. [Google Scholar] [CrossRef]
- Fiori, L.; Valbusa, M.; Lorenzi, D.; Fambri, L. Modeling of the devolatilization kinetics during pyrolysis of grape residues. Bioresour. Technol. 2012, 103, 389–397. [Google Scholar] [CrossRef]


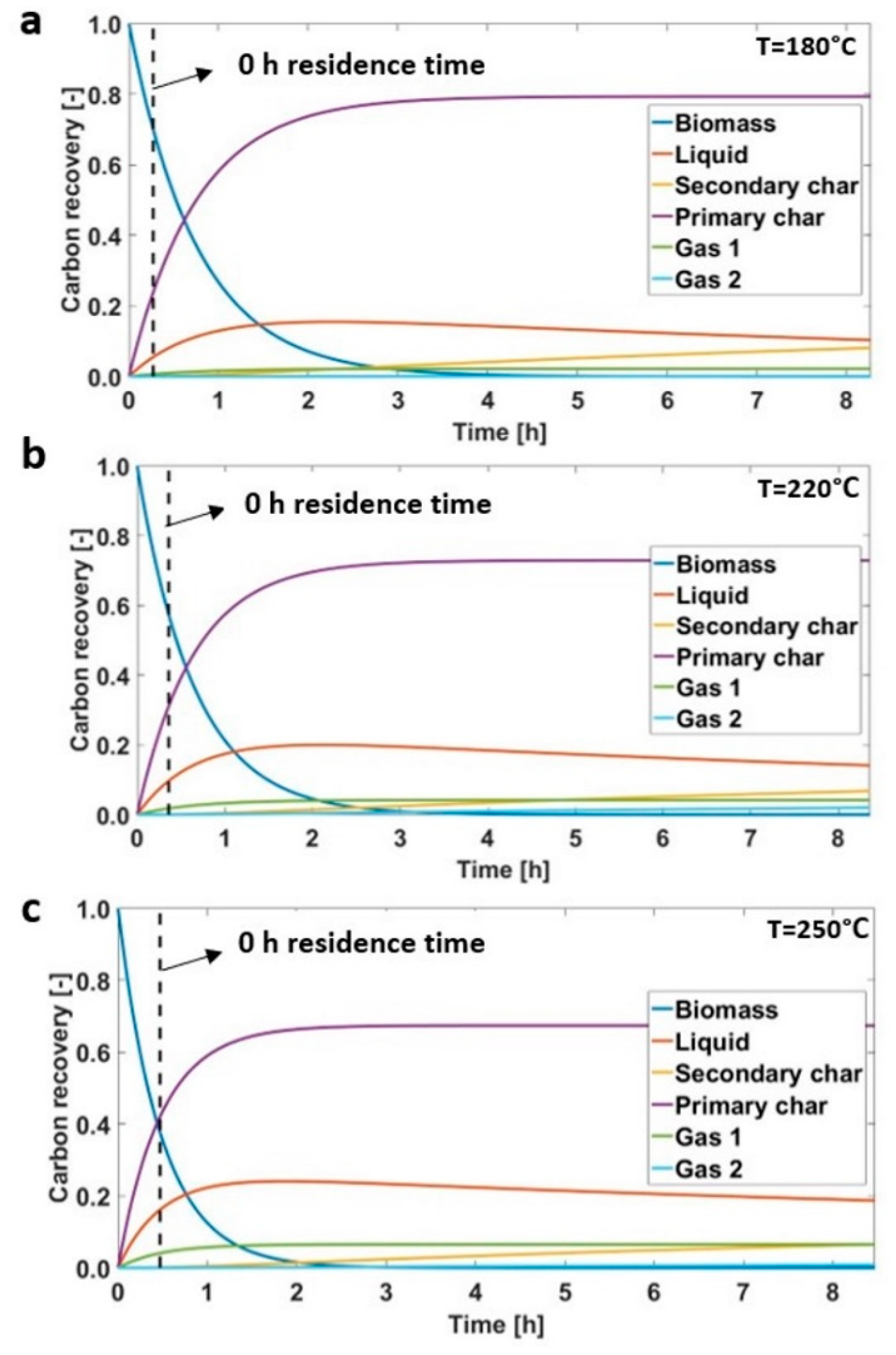
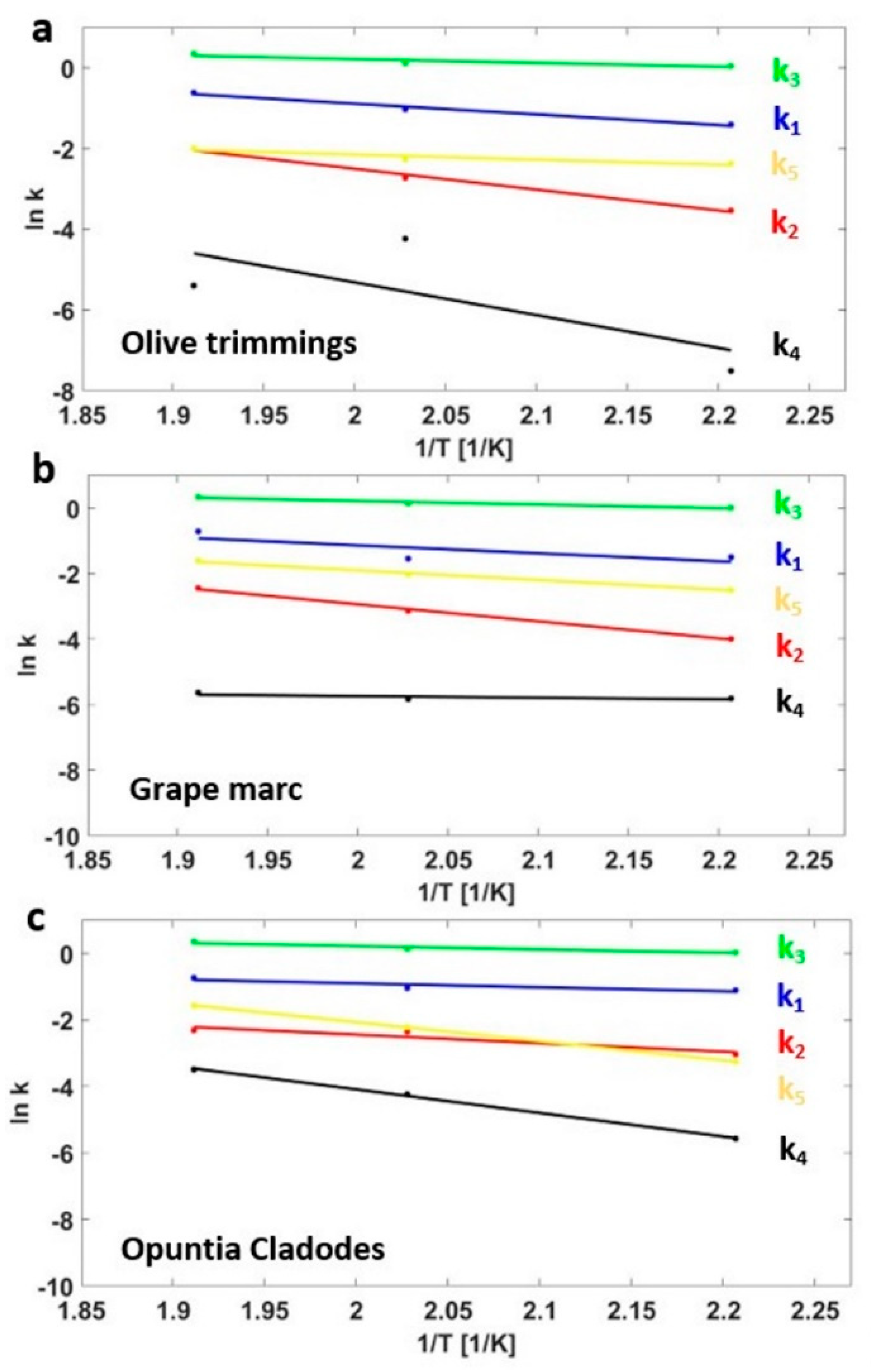
| Sample | Mass Yields (-) | Proximate Analysis (wt % on a d.b.) | Ultimate Analysis (wt % on a d.b.) | HHV (MJ/kg) | EY (-) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Solid | Liquid | Gas | VM | FC | Ash | C | H | N | O 2 | |||
| OT raw | - | - | - | 78.4 | 17.6 | 4.0 | 48.3 | 6.1 | 1.5 | 40.0 | 19.8 | - |
| 120 °C, 0 h | 0.93 | 0.07 | 0.00 | 81.3 | 15.0 | 3.7 | 50.6 | 5.9 | 1.6 | 38.1 | 20.1 | 0.94 |
| 150 °C, 0 h | 0.91 | 0.09 | 0.00 | 82.2 | 14.0 | 3.8 | 49.6 | 6.0 | 1.8 | 38.8 | 20.2 | 0.92 |
| 180 °C, 0 h | 0.88 | 0.11 | 0.01 | 81.2 | 15.7 | 3.1 | 51.3 | 5.9 | 1.6 | 38.1 | 20.5 | 0.91 |
| 180 °C, 0.5 h 1 | 0.78 | 0.20 | 0.02 | 77.3 | 19.9 | 2.8 | 53.7 | 6.2 | 1.5 | 35.7 | 21.8 | 0.86 |
| 180 °C, 1 h | 0.72 | 0.25 | 0.03 | 76.1 | 20.3 | 3.5 | 54.3 | 6.1 | 1.8 | 34.3 | 22.6 | 0.82 |
| 180 °C, 3 h | 0.70 | 0.26 | 0.04 | 72.9 | 23.2 | 3.9 | 56.7 | 6.2 | 1.8 | 31.4 | 23.4 | 0.83 |
| 180 °C, 6 h | 0.73 | 0.22 | 0.05 | 73.8 | 21.9 | 4.3 | 58.9 | 5.9 | 1.6 | 29.2 | 24.1 | 0.89 |
| 180 °C, 8 h | 0.73 | 0.23 | 0.04 | 76.8 | 18.0 | 4.0 | 57.8 | 5.3 | 1.6 | 31.3 | 23.7 | 0.88 |
| 220 °C, 0 h | 0.74 | 0.23 | 0.03 | 76.3 | 20.3 | 3.5 | 55.3 | 5.9 | 1.5 | 33.7 | 22.3 | 0.83 |
| 220 °C, 0.5 h 1 | 0.71 | 0.23 | 0.06 | 72.9 | 23.0 | 4.1 | 56.3 | 6.2 | 1.6 | 31.7 | 23.9 | 0.86 |
| 220 °C, 1 h | 0.63 | 0.31 | 0.06 | 70.6 | 25.1 | 4.3 | 59.4 | 6.2 | 1.9 | 28.3 | 24.7 | 0.78 |
| 220 °C, 3 h | 0.58 | 0.33 | 0.09 | 64.4 | 31.4 | 4.2 | 63.0 | 6.3 | 2.2 | 24.4 | 26.4 | 0.77 |
| 220 °C, 6 h | 0.57 | 0.33 | 0.10 | 66.9 | 28.4 | 4.6 | 65.5 | 6.0 | 2.0 | 21.8 | 26.7 | 0.77 |
| 220 °C, 8 h | 0.61 | 0.28 | 0.11 | 70.1 | 23.6 | 4.4 | 64.1 | 5.5 | 1.9 | 24.1 | 26.7 | 0.82 |
| 250 °C, 0 h | 0.66 | 0.28 | 0.06 | 72.3 | 23.7 | 4.0 | 58.1 | 6.2 | 1.6 | 30.0 | 23.9 | 0.80 |
| 250 °C, 0.5 h 1 | 0.58 | 0.33 | 0.09 | 66.3 | 30.3 | 3.4 | 63.2 | 6.3 | 1.8 | 25.3 | 27.3 | 0.79 |
| 250 °C, 1 h | 0.52 | 0.37 | 0.11 | 66.8 | 29.2 | 4.0 | 65.3 | 6.2 | 2.3 | 22.2 | 27.8 | 0.72 |
| 250 °C, 3 h | 0.48 | 0.39 | 0.12 | 59.6 | 35.7 | 4.7 | 68.9 | 6.3 | 2.5 | 17.6 | 29.0 | 0.71 |
| 250 °C, 6 h | 0.50 | 0.37 | 0.13 | 56.3 | 39.9 | 3.8 | 70.6 | 5.9 | 2.2 | 17.5 | 29.6 | 0.74 |
| 250 °C, 8 h | 0.49 | 0.38 | 0.13 | 61.8 | 32.0 | 4.1 | 69.0 | 5.5 | 2.1 | 19.3 | 28.9 | 0.72 |
| Parameters | Olive Trimmings | Grape Marc | Opuntia Ficus Indica | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T (°C) | 180 | 220 | 250 | 180 | 220 | 250 | 180 | 220 | 250 |
| k1 (s−1) | 0.24 | 0.35 | 0.54 | 0.22 | 0.21 | 0.49 | 0.33 | 0.35 | 0.48 |
| k2 (s−1) | 0.03 | 0.07 | 0.14 | 0.02 | 0.04 | 0.09 | 0.05 | 0.09 | 0.10 |
| k3 (s−1) | 1.05 | 1.13 | 1.40 | 1.00 | 1.14 | 1.41 | 1.04 | 1.14 | 1.41 |
| k4 (s−1) | 0.001 | 0.014 | 0.005 | 0.003 | 0.003 | 0.004 | 0.004 | 0.015 | 0.030 |
| k5 (s−1) | 0.09 | 0.10 | 0.14 | 0.08 | 0.13 | 0.20 | 0.04 | 0.11 | 0.21 |
| n (-) | 1.10 | 1.51 | 2.01 | 1.10 | 1.51 | 2.00 | 1.11 | 1.51 | 2.00 |
| Parameters | Olive Trimmings | Grape Marc | Opuntia Ficus Indica |
|---|---|---|---|
| k0,1 (s−1) | 82.32 | 41.55 | 4.31 |
| k0,2 (s−1) | 2.51 × 103 | 1.69 × 103 | 14.71 |
| k0,3 (s−1) | 7.99 | 11.28 | 9.37 |
| k0,4 (s−1) | 5.38 × 104 | 0.0086 | 2.40 × 104 |
| k0,5 (s−1) | 1.41 | 52.78 | 1.14 × 104 |
| Ea,1 (kJ/mol) | 22.03 | 20.23 | 9.82 |
| Ea,2(kJ/mol) | 42.93 | 43.14 | 21.33 |
| Ea,3 (kJ/mol) | 7.75 | 9.18 | 8.39 |
| Ea,4 (kJ/mol) | 67.35 | 4.11 | 58.92 |
| Ea,5 (kJ/mol) | 10.37 | 24.41 | 7.44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucian, M.; Volpe, M.; Fiori, L. Hydrothermal Carbonization Kinetics of Lignocellulosic Agro-Wastes: Experimental Data and Modeling. Energies 2019, 12, 516. https://doi.org/10.3390/en12030516
Lucian M, Volpe M, Fiori L. Hydrothermal Carbonization Kinetics of Lignocellulosic Agro-Wastes: Experimental Data and Modeling. Energies. 2019; 12(3):516. https://doi.org/10.3390/en12030516
Chicago/Turabian StyleLucian, Michela, Maurizio Volpe, and Luca Fiori. 2019. "Hydrothermal Carbonization Kinetics of Lignocellulosic Agro-Wastes: Experimental Data and Modeling" Energies 12, no. 3: 516. https://doi.org/10.3390/en12030516
APA StyleLucian, M., Volpe, M., & Fiori, L. (2019). Hydrothermal Carbonization Kinetics of Lignocellulosic Agro-Wastes: Experimental Data and Modeling. Energies, 12(3), 516. https://doi.org/10.3390/en12030516







