Feature Selection Algorithms for Wind Turbine Failure Prediction
Abstract
:1. Introduction
2. Automatic Feature Selection Algorithms
Compilation of Used Criteria
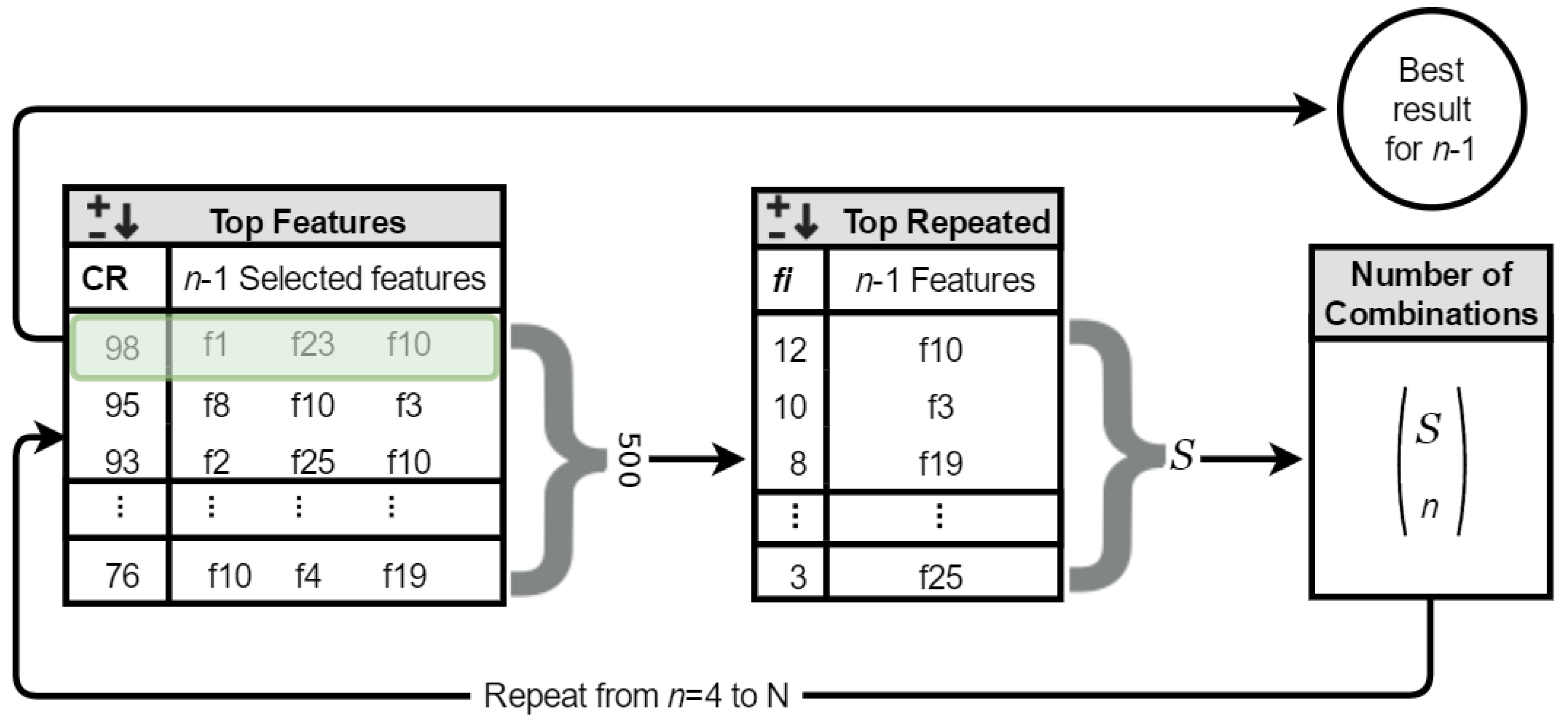
3. Exhaustive-Search-Based Quasi-Optimal Algorithm
- Calculate the frequency of selection of the characteristics for the case n-1 using the best 500 results.
- Sort the features according to its frequency.
- Select the subset of S features with highest frequency.
- Calculate all possible combinations of these S features taking n at a time (without repetition).
- Select the best combination based on the classification rate obtained with the k-NN classifier.
4. Study Case and Methodology
4.1. Data-Set Description
4.2. Classification System
5. Experimental Results and Discussion
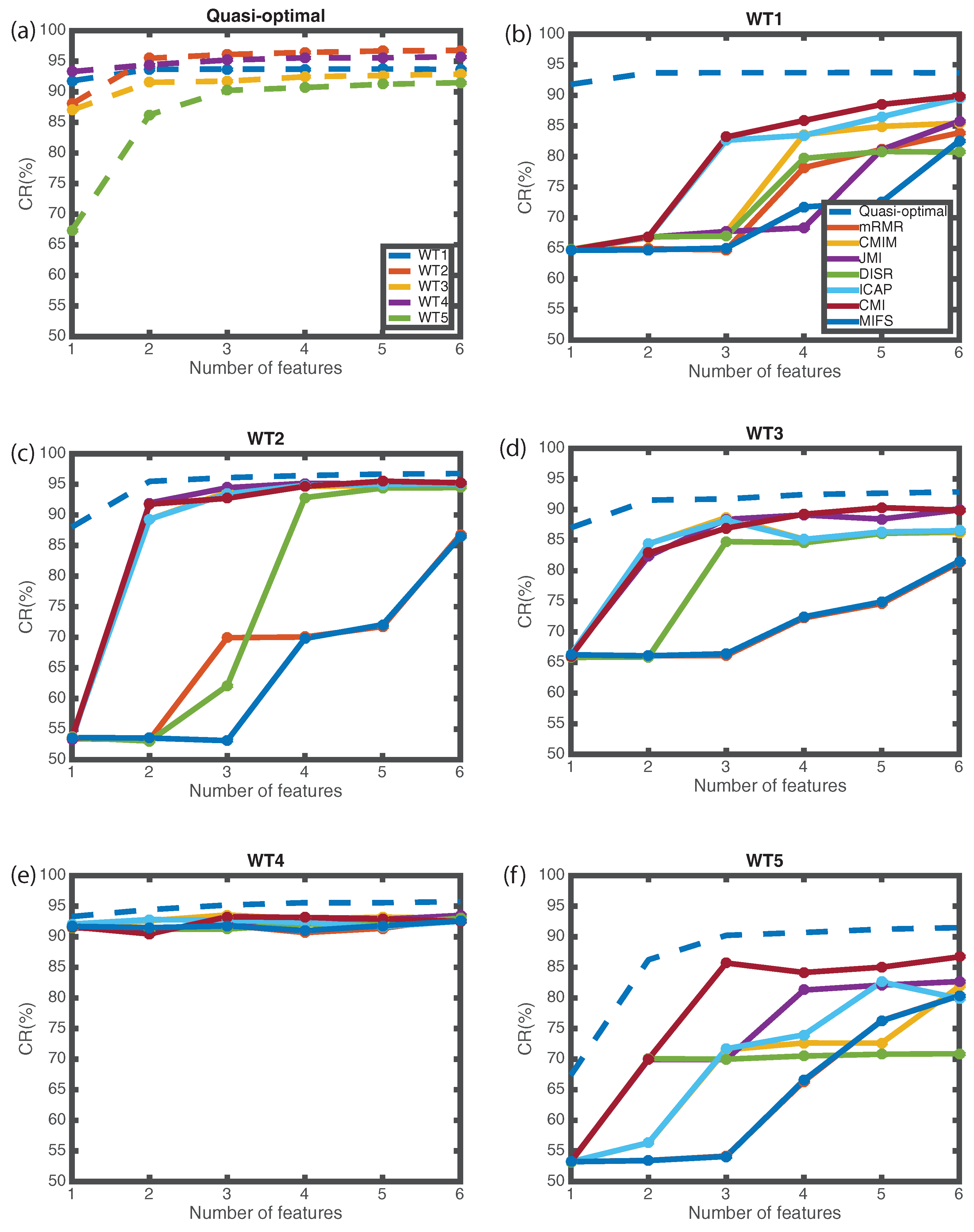
5.1. Quasi-Optimal vs. Automatic Feature Selection
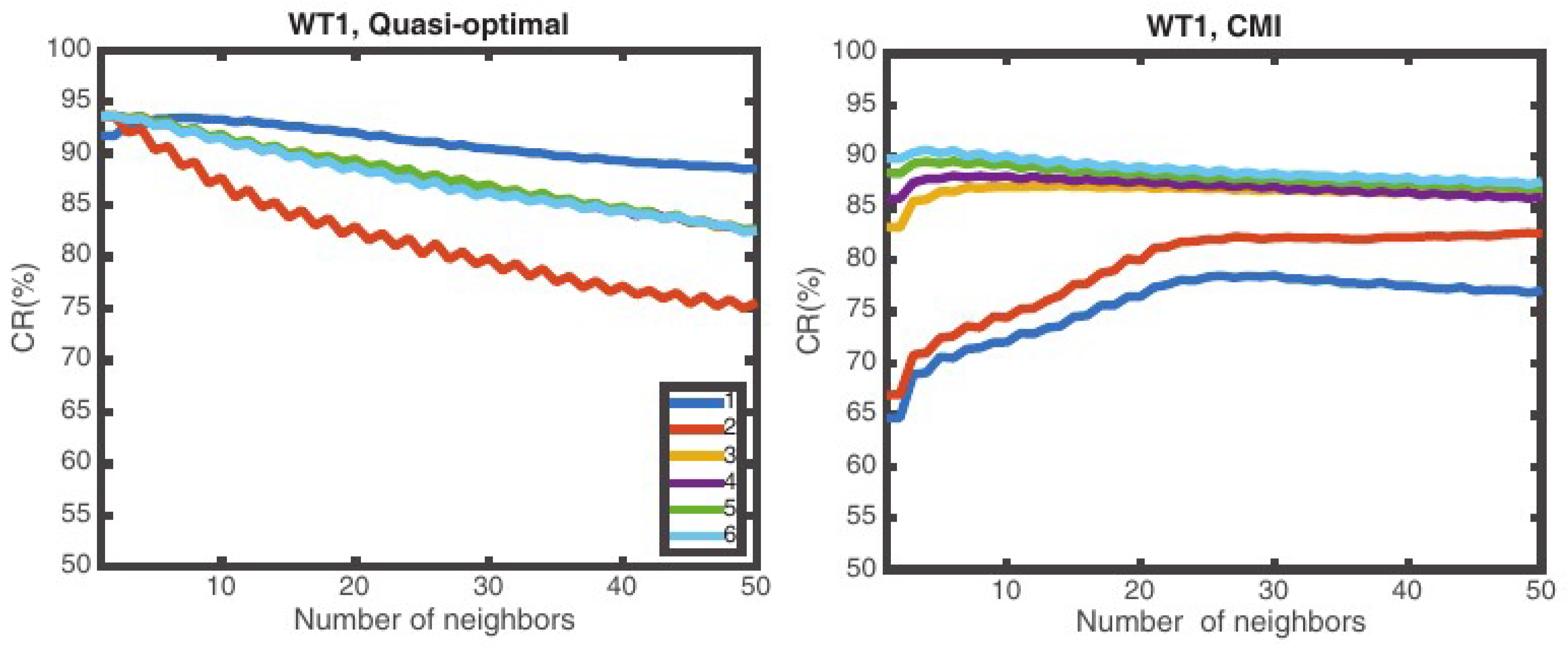
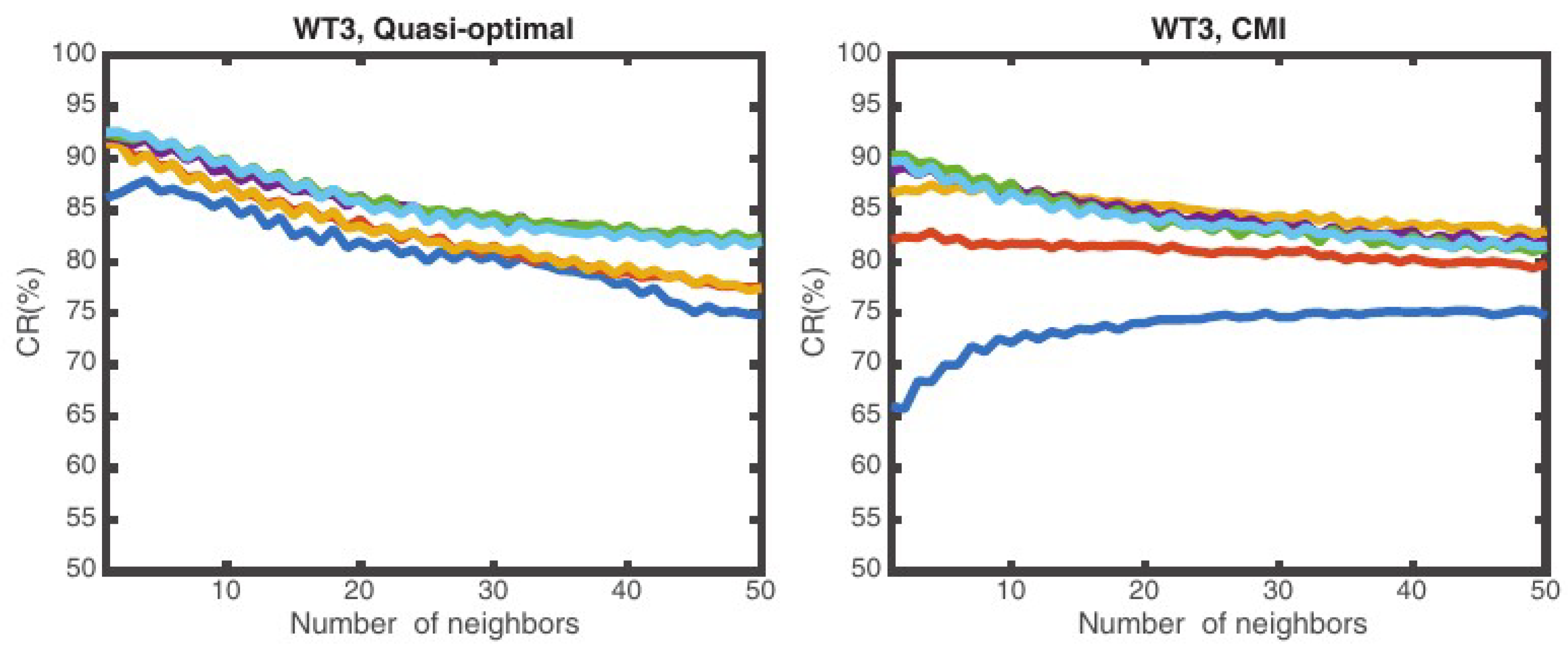
5.2. Effect of the Number of Neighbors Considered
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. European Commission Guidance for the Design of Renewables Support Schemes; Official Journal of the European Union: Brussels, Belgium, 2013; p. 439. [Google Scholar]
- The European parliament and the council of the European Union. Guidelines on State Aid for Environmental Protection and Energy 2014–2020; Official Journal of the European Union: Brussels, Belgium, 2014; pp. 1–55. [Google Scholar]
- David Bailey, E.W. Practical SCADA for Industry; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- IEC. International Standard IEC 61400-25-1; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2006. [Google Scholar]
- García Márquez, F.P.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy 2012, 46, 169–178. [Google Scholar] [CrossRef]
- Romero, A.; Lage, Y.; Soua, S.; Wang, B.; Gan, T.-H. Vestas V90-3MW Wind Turbine Gearbox Health Assessment Using a Vibration-Based Condition Monitoring System. Shock Vib. 2016, 2016, 18. [Google Scholar] [CrossRef]
- Weijtjens, W.; Devriendt, C. High frequent SCADA-based thrust load modeling of wind turbines. Wind Energy Sci. 2017. [Google Scholar] [CrossRef]
- Wilkinson, M. Use of Higher Frequency SCADA Data for Turbine Performance Optimisation; Technical Report; DNV GL, EWEA: Brussels, Belgium, 2016. [Google Scholar]
- Vestas R&D Department. General Specification VESTAS V90 3.0MW; Technical Report; Vestas Wind Systems: Ringkobing, Denmark, 2004. [Google Scholar]
- Tyagi, P. The Case for an Industrial Big Data Platform; Technical Report; General Electric (GE): Boston, MA, USA, 2013. [Google Scholar]
- Henry Louie, A.M. Lossless Compression of Wind Plant Data. IEEE Trans. Sustain. Energy 2012, 2012, 598–606. [Google Scholar] [CrossRef]
- Vestas&IBM. Turning Climate into Capital with Big Data; Technical Report; International Business Machines Corporation (IBM): Armonk, NY, USA, 2011. [Google Scholar]
- Shafiee, M.; Patriksson, M.; Strömberg, A.B.; Tjernberg, L.B. Optimal redundancy and maintenance strategy decisions for offshore wind power converters. Int. J. Reliab. Qual. Saf. Eng. 2015, 22, 1550015. [Google Scholar] [CrossRef]
- Hameed, Z.; Hong, Y.; Cho, Y.; Ahn, S.; Song, C. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Scappaticci, L.; Terzi, L. Diagnosis of Wind Turbine Misalignment through SCADA Data. Diagnostyka 2017, 18, 17–24. [Google Scholar]
- Astolfi, D.; Castellani, F.; Garinei, A.; Terzi, L. Data mining techniques for performance analysis of onshore wind farms. Appl. Energy 2015, 148, 220–233. [Google Scholar] [CrossRef]
- Qiu, Y.; Feng, Y.; Tavner, P.; Richardson, P.; Erdos, G.; Chen, B. Wind turbine SCADA alarm analysis for improving reliability. Wind Energy 2012, 15, 951–966. [Google Scholar] [CrossRef]
- Gray, C.S.; Watson, S.J. Physics of failure approach to wind turbine condition based maintenance. Wind Energy 2010, 13, 395–405. [Google Scholar] [CrossRef]
- Bartolini, N.; Scappaticci, L.; Garinei, A.; Becchetti, M.; Terzi, L. Analysing wind turbine states and scada data for fault diagnosis. Int. J. Renew. Energy Res. 2017, 7, 323–329. [Google Scholar]
- Garcia, M.C.; Sanz-Bobi, M.A.; del Pico, J. SIMAP: Intelligent System for Predictive Maintenance: Application to the health condition monitoring of a windturbine gearbox. Comput. Ind. 2006, 57, 552–568. [Google Scholar] [CrossRef]
- Singh, S.; Bhatti, T.; Kothari, D. Wind power estimation using artificial neural network. J. Energy Eng. 2007, 133, 46–52. [Google Scholar] [CrossRef]
- Zaher, A.; McArthur, S.; Infield, D.; Patel, Y. Online wind turbine fault detection through automated SCADA data analysis. Wind Energy 2009, 12, 574–593. [Google Scholar] [CrossRef]
- Marvuglia, A.; Messineo, A. Monitoring of wind farms’ power curves using machine learning techniques. Appl. Energy 2012, 98, 574–583. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Bangalore, P.; Tjernberg, L.B. Self evolving neural network based algorithm for fault prognosis in wind turbines: A case study. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; pp. 1–6. [Google Scholar]
- Cui, Y.; Bangalore, P.; Tjernberg, L.B. An Anomaly Detection Approach Based on Machine Learning and SCADA Data for Condition Monitoring of Wind Turbines. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Bangalore, P.; Tjernberg, L.B. An artificial neural network approach for early fault detection of gearbox bearings. IEEE Trans. Smart Grid 2015, 6, 980–987. [Google Scholar] [CrossRef]
- Mazidi, P.; Bertling Tjernberg, L.; Sanz-Bobi, M.A. Performance Analysis and Anomaly Detection in Wind Turbines based on Neural Networks and Principal Component Analysis. In Proceedings of the 12th Workshop on Industrial Systems and Energy Technologies, Madrid, Spain, 23–24 September 2015. [Google Scholar]
- Mazidi, P.; Tjernberg, L.B.; Bobi, M.A.S. Wind turbine prognostics and maintenance management based on a hybrid approach of neural networks and a proportional hazards model. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2017, 231, 121–129. [Google Scholar] [CrossRef]
- Mazidi, P. From Condition Monitoring to Maintenance Management in Electric Power System Generation with focus on Wind Turbines. Ph.D. Thesis, Universidad Pontificia Comillas, Madrid, Spain, 2018. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F.; Achiche, S. Wind turbine condition monitoring based on SCADA data using normal behavior models. Part 1: System description. Appl. Soft Comput. 2013, 13, 259–270. [Google Scholar] [CrossRef]
- Astolfi, D.; Scappaticci, L.; Terzi, L. Fault diagnosis of wind turbine gearboxes through temperature and vibration data. Int. J. Renew. Energy Res. 2017, 7, 965–976. [Google Scholar]
- Vidal, Y.; Pozo, F.; Tutivén, C. Wind turbine multi-fault detection and classification based on SCADA data. Energies 2018, 11, 3018. [Google Scholar] [CrossRef]
- NREL. NWTC Information Portal (FAST). 2018. Available online: https://nwtc.nrel.gov/FAST (accessed on 10 January 2019).
- Leahy, K.; Hu, R.L.; Konstantakopoulos, I.C.; Spanos, C.J.; Agogino, A.M.; O’Sullivan, D.T.J. Diagnosing and predicting wind turbine faults from SCADA data using support vector machines. Int. J. Progn. Health Manag. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Kusiak, A.; Li, W. The prediction and diagnosis of wind turbine faults. Renew. Energy 2011, 36, 16–23. [Google Scholar] [CrossRef]
- Leahy, K.; Gallagher, C.; O’Donovan, P.; Bruton, K.; O’Sullivan, D.T.J. A Robust Prescriptive Framework and Performance Metric for Diagnosing and Predicting Wind Turbine Faults Based on SCADA and Alarms Data with Case Study. Energies 2018, 11, 1738. [Google Scholar] [CrossRef]
- Du, M.; Tjernberg, L.B.; Ma, S.; He, Q.; Cheng, L.; Guo, J. A SOM based Anomaly Detection Method for Wind Turbines Health Management through SCADA Data. Int. J. Progn. Health Manag. 2016, 7, 1–13. [Google Scholar]
- Blanco-M, A.; Gibert, K.; Marti-Puig, P.; Cusidó, J.; Solé-Casals, J. Identifying Health Status of Wind Turbines by Using Self Organizing Maps and Interpretation-Oriented Post-Processing Tools. Energies 2018, 11, 723. [Google Scholar] [CrossRef]
- Leahy, K.; Gallagher, C.; O’Donovan, P.; O’Sullivan, D.T.J. Cluster analysis of wind turbine alarms for characterising and classifying stoppages. IET Renew. Power Gener. 2018, 12, 1146–1154. [Google Scholar] [CrossRef]
- Gonzalez, E.; Stephen, B.; Infield, D.; Melero, J. On the Use of High-Frequency SCADA Data for Improved Wind Turbine Performance Monitoring; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 926, p. 012009. [Google Scholar]
- Zhao, Y.; Li, D.; Dong, A.; Kang, D.; Lv, Q.; Shang, L. Fault Prediction and Diagnosis of Wind Turbine Generators Using SCADA Data. Energies 2017, 10, 1210. [Google Scholar] [CrossRef]
- Wang, K.S.; Sharma, V.S.; Zhang, Z.Y. SCADA data based condition monitoring of wind turbines. Adv. Manuf. 2014, 2, 61–69. [Google Scholar] [CrossRef] [Green Version]
- Lewis, D.D. Feature selection and feature extraction for text categorization. In Proceedings of the Workshop on Speech and Natural Language; Association for Computational Linguistics: Stroudsburg, PA, USA, 1992; pp. 212–217. [Google Scholar]
- Brown, G.; Pocock, A.; Zhao, M.J.; Luján, M. Conditional likelihood maximisation: a unifying framework for information theoretic feature selection. J. Mach. Learn. Res. 2012, 13, 27–66. [Google Scholar]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.H.; Moody, J.E. Data Visualization and Feature Selection: New Algorithms for Nongaussian Data; Advances in Neural Information Processing Systems (NIPS); MIT Press: Boston, MA, USA, 1999; Volume 99, pp. 687–693. [Google Scholar]
- Meyer, P.E.; Bontempi, G. On the use of variable complementarity for feature selection in cancer classification. In Applications of Evolutionary Computing; Springer: Berlin, Germany, 2006; pp. 91–102. [Google Scholar]
- Cheng, H.; Qin, Z.; Feng, C.; Wang, Y.; Li, F. Conditional mutual information-based feature selection analyzing for synergy and redundancy. ETRI J. 2011, 33, 210–218. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleuret, F. Fast binary feature selection with conditional mutual information. J. Mach. Learn. Res. 2004, 5, 1531–1555. [Google Scholar]
- Jakulin, A. Machine Learning Based on Attribute Interactions. Ph.D. Thesis, Fakulteta za racunalništvo in informatiko, Univerza v Ljubljani, Liubliana, Slovenia, June 2005. [Google Scholar]
- Thomas, J.A.; Cover, T. Elements of Information Theory; Wiley: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef] [Green Version]
- Domeniconi, C.; Yan, B. Nearest neighbor ensemble. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 1, pp. 228–231. [Google Scholar]
- Zhou, Z.H.; Yu, Y. Adapt bagging to nearest neighbor classifiers. J. Comput. Sci. Technol. 2005, 20, 48–54. [Google Scholar] [CrossRef]
- Hall, P.; Samworth, R.J. Properties of bagged nearest neighbour classifiers. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 363–379. [Google Scholar] [CrossRef] [Green Version]
- Samworth, R.J. Optimal weighted nearest neighbour classifiers. Ann. Stat. 2012, 40, 2733–2763. [Google Scholar] [CrossRef]

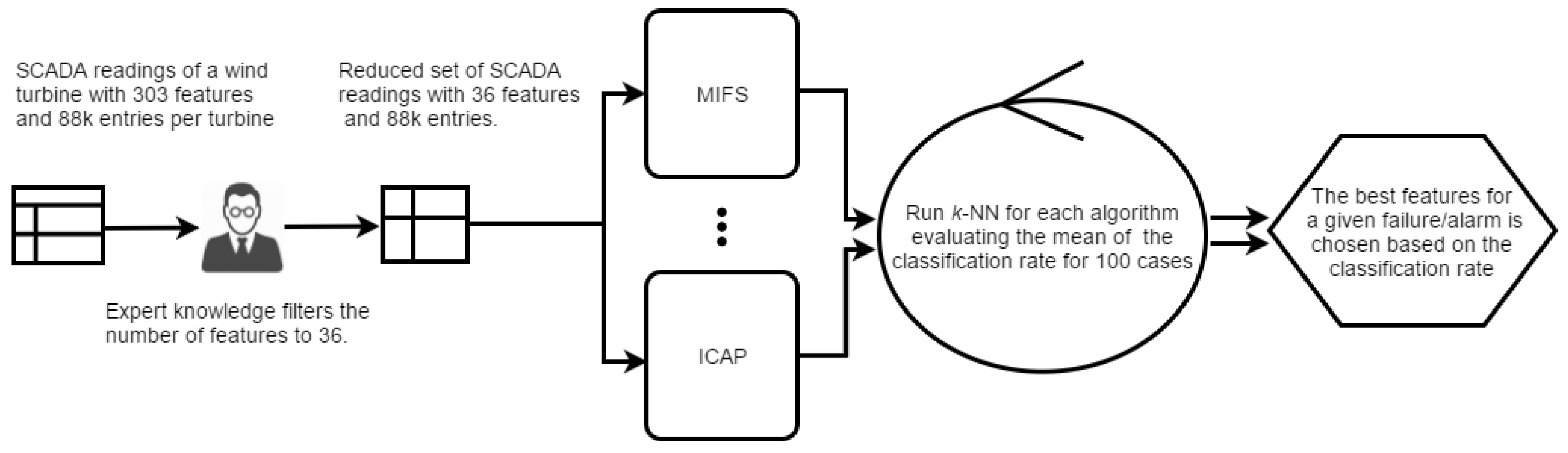
| Criterion | Full Name | Authors | Relevance/Redundance |
|---|---|---|---|
| MIFS | Mutual Information Feature Selection | [46] | no |
| CMI | Conditional Mutual Information | [49] | yes |
| JMI | Joint Mutual Information | [47] | yes |
| mRMR | Min-Redundancy Max-Relevance | [50] | no |
| DISR | Double Input Symmetrical Relevance | [48] | yes |
| CMIM | Conditional Mutual Info Maximisation | [51] | yes |
| ICAP | Interaction Capping | [52] | yes |
| Group | Variable Code | Variable Name | Description |
|---|---|---|---|
| A | 1 | WGDC.TrfGri.PwrAt.cVal.avgVal | Active power |
| 2 | WGDC.TrfGri.PwrAt.cVal.minVal | ||
| 3 | WGDC.TrfGri.PwrAt.cVal.maxVal | ||
| 4 | WGDC.TrfGri.PwrAt.cVal.sdvVal | ||
| B | 1 | WTRM.TrmTmp.Brg1.avgVal | Main bearing 1 Temperature |
| 2 | WTRM.TrmTmp.Brg1.minVal | ||
| 3 | WTRM.TrmTmp.Brg1.maxVal | ||
| 4 | WTRM.TrmTmp.Brg1.sdvVal | ||
| C | 1 | WTRM.TrmTmp.Brg2.avgVal | Main bearing 2 Temperature |
| 2 | WTRM.TrmTmp.Brg2.minVal | ||
| 3 | WTRM.TrmTmp.Brg2.maxVal | ||
| 4 | WTRM.TrmTmp.Brg2.sdvVal | ||
| D | 1 | WTRM.Brg.OilPres.avgVal | Main bearing oil pressure (inside bearing) |
| 2 | WTRM.Brg.OilPres.minVal | ||
| 3 | WTRM.Brg.OilPres.maxVal | ||
| 4 | WTRM.Brg.OilPres.sdvVal | ||
| E | 1 | WTRM.Gbx.OilPres.avgVal | Gearbox oil pressure |
| 2 | WTRM.Gbx.OilPres.minVal | ||
| 3 | WTRM.Gbx.OilPres.maxVal | ||
| 4 | WTRM.Gbx.OilPres.sdvVal | ||
| F | 1 | WTRM.Brg.OilPresIn.avgVal | Main bearing oil pressure (inlet hose) |
| 2 | WTRM.Brg.OilPresIn.minVal | ||
| 3 | WTRM.Brg.OilPresIn.maxVal | ||
| 4 | WTRM.Brg.OilPresIn.sdvVal | ||
| G | 1 | WNAC.WSpd1.avgVal | Wind Speed sensor 1 |
| 2 | WNAC.WSpd1.minVal | ||
| 3 | WNAC.WSpd1.maxVal | ||
| 4 | WNAC.WSpd1.sdvVal | ||
| H | 1 | WNAC.Wdir1.avgVal | Wind direction sensor 1 |
| 2 | WNAC.Wdir1.minVal | ||
| 3 | WNAC.Wdir1.maxVal | ||
| 4 | WNAC.Wdir1.sdvVal | ||
| I | 1 | WNAC.Wdir2.avgVal | Wind director sensor 2 |
| 2 | WNAC.Wdir2.minVal | ||
| 3 | WNAC.Wdir2.maxVal | ||
| 4 | WNAC.Wdir2.sdvVal |
| CR(%) | 1F | CR(%) | 2F | CR(%) | 3F | CR(%) | 4F | CR(%) | 5F | CR(%) | 6F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT1 | 91.79 | A1 | 93.67 | A2 E3 | 93.71 | A2 B2 B3 | 93.71 | A1 B1 B2 B3 | 93.73 | A3 A4 B1 B3 B4 | 93.66 | A1 A2 A3 B1 B2 B3 |
| 91.78 | A3 | 93.66 | A1 E3 | 93.70 | A3 B4 E2 | 93.70 | A1 A3 B4 E3 | 93.69 | A1 A2 A3 B4 E3 | 93.64 | A1 A4 B1 B2 B3 B4 | |
| 91.71 | A2 | 93.65 | A3 B1 | 93.70 | A2 B1 B3 | 93.68 | A1 A2 A3 E3 | 93.68 | A1 A3 A4 B4 E3 | 93.61 | A1 A2 A3 A4 B4 E2 | |
| 81.70 | B3 | 93.64 | A3 E3 | 93.69 | A1 A3 E3 | 93.68 | A3 A4 B2 B3 | 93.67 | A1 A4 B1 B3 B4 | 93.61 | A1 A3 A4 B1 B2 B3 | |
| 81.63 | B2 | 93.62 | A2 B3 | 93.69 | A1 B1 B2 | 93.67 | A2 A4 B2 B3 | 93.65 | A3 B1 B2 B3 B4 | 93.60 | A1 A2 A3 A4 B1 B2 | |
| WT2 | 88.01 | B3 | 95.48 | A3 C2 | 96.10 | A2 C2 D1 | 96.43 | B1 C2 D1 G3 | 96.67 | A3 B1 C2 D2 G3 | 96.77 | A2 A3 B3 C2 D2 H1 |
| 87.87 | B1 | 95.46 | A1 C2 | 96.05 | A3 C2 D1 | 96.42 | A3 C2 D1 G3 | 96.62 | A2 B2 C2 D1 G3 | 96.74 | A1 A3 B1 C2 D2 H1 | |
| 87.85 | B2 | 95.31 | A2 C2 | 95.99 | A3 C2 D2 | 96.38 | A2 C2 D1 H1 | 96.56 | A1 A3 C2 D2 H1 | 96.73 | A1 A2 B3 C2 D1 G3 | |
| 85.83 | C2 | 95.20 | B2 C2 | 95.89 | A1 C2 D1 | 96.38 | B1 C2 D2 G3 | 96.55 | A2 A3 C2 D1 H1 | 96.73 | A2 A3 B1 C2 D2 G3 | |
| 85.60 | E1 | 94.99 | B3 C2 | 95.77 | A2 C2 D2 | 96.38 | A1 C2 D2 G3 | 96.55 | A3 B3 C2 D1 G1 | 96.73 | A1 A2 B1 C2 D1 H1 | |
| WT3 | 87.02 | C3 | 91.54 | A2 E3 | 91.74 | A3 B1 E3 | 92.45 | A3 C1 D3 E3 | 92.67 | B3 C1 C3 D2 E3 | 92.89 | B3 C1 C3 D2 E1 E3 |
| 86.90 | C2 | 91.44 | A1 E3 | 91.73 | B1 C3 E3 | 92.36 | A1 C1 D3 E3 | 92.66 | B3 C1 C3 D2 E1 | 92.85 | B1 C1 C3 D2 E1 E3 | |
| 79.33 | B1 | 91.37 | A3 E3 | 91.67 | A2 B3 E3 | 92.23 | B1 C1 D1 E3 | 92.61 | A3 C1 D2 E1 E3 | 92.82 | A2 C1 C3 D2 E1 E3 | |
| 78.95 | B2 | 91.10 | B2 E3 | 91.65 | A3 A4 E3 | 92.18 | B3 C1 D3 E3 | 92.58 | B1 C1 C3 D2 E3 | 92.80 | A3 C1 C3 D2 E1 E3 | |
| 78.79 | B3 | 91.01 | B1 E3 | 91.62 | B3 C3 E3 | 92.17 | B2 C1 D2 E3 | 92.58 | B2 C1 C3 D2 E1 | 92.78 | B1 B4 C1 C3 D2 E3 | |
| WT4 | 93.30 | C2 | 94.44 | C2 D2 | 95.18 | B1 C2 D2 | 95.56 | B1 C2 D2 E2 | 95.56 | B1 B2 C2 D2 H3 | 95.74 | B1 C2 D2 D3 E2 H3 |
| 92.27 | C3 | 94.32 | D1 E2 | 95.14 | C2 D2 H3 | 95.47 | B1 C2 D2 H3 | 95.54 | B3 C2 D2 E2 H3 | 95.59 | A4 B1 C2 D2 D3 H3 | |
| 91.46 | C1 | 94.32 | D2 E2 | 94.97 | B3 C2 D2 | 95.37 | B1 B4 C2 D2 | 95.42 | B1 B3 C2 D2 D3 | 95.55 | B2 B3 B4 C2 D2 E2 | |
| 91.29 | D2 | 94.22 | C2 D1 | 94.94 | C2 D1 H3 | 95.30 | B1 B3 C2 D2 | 95.42 | B1 B4 C2 D2 E2 | 95.55 | B1 B2 C2 D1 D2 E2 | |
| 90.98 | D3 | 93.74 | B3 C2 | 94.92 | D1 E2 H3 | 95.29 | B2 C2 D2 H3 | 95.40 | B1 C2 D2 D3 H3 | 95.47 | A4 B3 C2 D2 E2 H3 | |
| WT5 | 67.37 | A2 | 86.25 | A1 E2 | 90.23 | A3 C3 E2 | 90.70 | A2 C3 E2 E3 | 91.23 | A1 B2 C3 E2 E3 | 91.49 | A1 B3 C1 C3 E3 G1 |
| 67.28 | A3 | 86.08 | A3 E2 | 90.12 | A2 C3 E2 | 90.64 | A3 C3 E2 E3 | 91.22 | A3 B2 C3 E2 E3 | 91.47 | A2 B3 C1 C3 E3 G1 | |
| 67.21 | A1 | 86.05 | A2 E2 | 90.12 | A1 C3 E2 | 90.63 | A1 C3 E2 E3 | 91.22 | A2 B3 C3 E2 E3 | 91.46 | A2 B1 C1 E2 E3 G1 | |
| 66.31 | B3 | 85.96 | A3 E3 | 90.01 | A2 C2 E3 | 90.62 | A1 B1 C3 E2 | 91.22 | A1 B1 C3 E2 E3 | 91.42 | A3 B3 C1 C3 E3 G1 | |
| 66.27 | B2 | 85.92 | A3 E1 | 89.98 | A2 C3 E3 | 90.59 | A1 B3 C3 E2 | 91.22 | A1 B3 C3 E2 E3 | 91.42 | A2 B2 C1 C3 E2 E3 |
| F1-Score | 1F | F1-Score | 2F | F1-Score | 3F | F1-Score | 4F | F1-Score | 5F | F1-Score | 6F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT1 | 0.9238 | A1 | 0.9397 | A2 E3 | 0.9403 | A2 B2 B3 | 0.9403 | A1 B1 B2 B3 | 0.9404 | A3 A4 B1 B3 B4 | 0.9398 | A1 A2 A3 B1 B2 B3 |
| 0.9237 | A3 | 0.9396 | A1 E3 | 0.9398 | A3 B4 E2 | 0.9399 | A1 A3 B4 E3 | 0.9399 | A1 A2 A3 B4 E3 | 0.9395 | A1 A4 B1 B2 B3 B4 | |
| 0.9231 | A2 | 0.9397 | A3 B1 | 0.9402 | A2 B1 B3 | 0.9398 | A1 A2 A3 E3 | 0.9397 | A1 A3 A4 B4 E3 | 0.9398 | A1 A2 A3 A4 B4 E2 | |
| 0.8448 | B3 | 0.9394 | A3 E3 | 0.9399 | A1 A3 E3 | 0.9400 | A3 A4 B2 B3 | 0.9398 | A1 A4 B1 B3 B4 | 0.9393 | A1 A3 A4 B1 B2 B3 | |
| 0.8442 | B2 | 0.9395 | A2 B3 | 0.9401 | A1 B1 B2 | 0.9399 | A2 A4 B2 B3 | 0.9397 | A3 B1 B2 B3 B4 | 0.9392 | A1 A2 A3 A4 B1 B2 | |
| WT2 | 0.8875 | B3 | 0.9557 | A3 C2 | 0.9616 | A2 C2 D1 | 0.9646 | B1 C2 D1 G3 | 0.9671 | A3 B1 C2 D2 G3 | 0.9680 | A2 A3 B3 C2 D2 H1 |
| 0.8862 | B1 | 0.9553 | A1 C2 | 0.9612 | A3 C2 D1 | 0.9646 | A3 C2 D1 G3 | 0.9666 | A2 B2 C2 D1 G3 | 0.9677 | A1 A3 B1 C2 D2 H1 | |
| 0.8858 | B2 | 0.9539 | A2 C2 | 0.9606 | A3 C2 D2 | 0.9642 | A2 C2 D1 H1 | 0.9659 | A1 A3 C2 D2 H1 | 0.9677 | A1 A2 B3 C2 D1 G3 | |
| 0.8730 | C2 | 0.9526 | B2 C2 | 0.9596 | A1 C2 D1 | 0.9642 | B1 C2 D2 G3 | 0.9659 | A2 A3 C2 D1 H1 | 0.9677 | A2 A3 B1 C2 D2 G3 | |
| 0.8555 | E1 | 0.9505 | B3 C2 | 0.9584 | A2 C2 D2 | 0.9642 | A1 C2 D2 G3 | 0.9658 | A3 B3 C2 D1 G1 | 0.9676 | A1 A2 B1 C2 D1 H1 | |
| WT3 | 0.8825 | C3 | 0.9198 | A2 E3 | 0.9205 | A3 B1 E3 | 0.9264 | A3 C1 D3 E3 | 0.9289 | B3 C1 C3 D2 E3 | 0.9309 | B3 C1 C3 D2 E1 E3 |
| 0.8827 | C2 | 0.9190 | A1 E3 | 0.9194 | B1 C3 E3 | 0.9255 | A1 C1 D3 E3 | 0.9288 | B3 C1 C3 D2 E1 | 0.9306 | B1 C1 C3 D2 E1 E3 | |
| 0.8229 | B1 | 0.9182 | A3 E3 | 0.9196 | A2 B3 E3 | 0.9244 | B1 C1 D1 E3 | 0.9285 | A3 C1 D2 E1 E3 | 0.9301 | A2 C1 C3 D2 E1 E3 | |
| 0.8197 | B2 | 0.9158 | B2 E3 | 0.9207 | A3 A4 E3 | 0.9239 | B3 C1 D3 E3 | 0.9281 | B1 C1 C3 D2 E3 | 0.9299 | A3 C1 C3 D2 E1 E3 | |
| 0.8189 | B3 | 0.9150 | B1 E3 | 0.9185 | B3 C3 E3 | 0.9242 | B2 C1 D2 E3 | 0.9279 | B2 C1 C3 D2 E1 | 0.9300 | B1 B4 C1 C3 D2 E3 | |
| WT4 | 0.9369 | C2 | 0.9453 | C2 D2 | 0.9521 | B1 C2 D2 | 0.9559 | B1 C2 D2 E2 | 0.9562 | B1 B2 C2 D2 H3 | 0.9578 | B1 C2 D2 D3 E2 H3 |
| 0.9261 | C3 | 0.9442 | D1 E2 | 0.9518 | C2 D2 H3 | 0.9551 | B1 C2 D2 H3 | 0.9556 | B3 C2 D2 E2 H3 | 0.9562 | A4 B1 C2 D2 D3 H3 | |
| 0.9179 | C1 | 0.9441 | D2 E2 | 0.9499 | B3 C2 D2 | 0.9541 | B1 B4 C2 D2 | 0.9544 | B1 B3 C2 D2 D3 | 0.9560 | B2 B3 B4 C2 D2 E2 | |
| 0.9157 | D2 | 0.9431 | C2 D1 | 0.9499 | C2 D1 H3 | 0.9533 | B1 B3 C2 D2 | 0.9546 | B1 B4 C2 D2 E2 | 0.9557 | B1 B2 C2 D1 D2 E2 | |
| 0.9124 | D3 | 0.9383 | B3 C2 | 0.9500 | D1 E2 H3 | 0.9534 | B2 C2 D2 H3 | 0.9543 | B1 C2 D2 D3 H3 | 0.9551 | A4 B3 C2 D2 E2 H3 | |
| WT5 | 0.7532 | A2 | 0.8767 | A1 E2 | 0.9072 | A3 C3 E2 | 0.9115 | A2 C3 E2 E3 | 0.9159 | A1 B2 C3 E2 E3 | 0.9165 | A1 B3 C1 C3 E3 G1 |
| 0.7526 | A3 | 0.8755 | A3 E2 | 0.9062 | A2 C3 E2 | 0.9109 | A3 C3 E2 E3 | 0.9160 | A3 B2 C3 E2 E3 | 0.9163 | A2 B3 C1 C3 E3 G1 | |
| 0.7522 | A1 | 0.8752 | A2 E2 | 0.9063 | A1 C3 E2 | 0.9108 | A1 C3 E2 E3 | 0.9158 | A2 B3 C3 E2 E3 | 0.9163 | A2 B1 C1 E2 E3 G1 | |
| 0.7472 | B3 | 0.8742 | A3 E3 | 0.9053 | A2 C2 E3 | 0.9104 | A1 B1 C3 E2 | 0.9159 | A1 B1 C3 E2 E3 | 0.9159 | A3 B3 C1 C3 E3 G1 | |
| 0.7469 | B2 | 0.8680 | A3 E1 | 0.9050 | A2 C3 E3 | 0.9100 | A1 B3 C3 E2 | 0.9159 | A1 B3 C3 E2 E3 | 0.9177 | A2 B2 C1 C3 E2 E3 |
| CR(%) | 1F | CR(%) | 2F | CR(%) | 3F | CR(%) | 4F | CR(%) | 5F | CR(%) | 6F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CMI | 64.73 | E1 | 66.93 | E1 E4 | 83.19 | E1 E4 F1 | 85.89 | E1 E4 F1 H1 | 88.52 | A1 E1 E4 F1 H1 | 89.9 | A1 C4 E1 E4 F1 H1 |
| 53.58 | E4 | 91.76 | C2 E4 | 92.72 | C2 E4 H1 | 94.68 | A2 C2 E4 H1 | 95.51 | A2 C2 D3 E4 H1 | 95.26 | A2 C2 D3 E2 E4 H1 | |
| 66.03 | D3 | 82.92 | B1 D3 | 86.97 | B1 C2 D3 | 89.24 | B1 C2 D3 G3 | 90.31 | B1 C2 D3 E3 G3 | 89.90 | B1 C2 D3 E3 F4 G3 | |
| 91.62 | D2 | 90.45 | D2 F3 | 93.27 | D2 E2 F3 | 93.15 | D2 E2 E3 F3 | 92.95 | A1 D2 E2 E3 F3 | 92.50 | A1 D2 E2 E3 F3 H4 | |
| 53.24 | E2 | 70.03 | C3 E2 | 85.71 | C3 E2 H3 | 84.16 | C3 E2 F4 H3 | 85.03 | C3 E2 F4 H1 H3 | 86.72 | A1 C3 E2 F4 H1 H3 | |
| CMIM | 64.68 | E1 | 66.74 | E1 E4 | 67.66 | E1 E2 E4 | 83.59 | C1 E1 E2 E4 | 84.94 | C1 C2 E1 E2 E4 | 85.46 | C1 C2 E1 E2 E3 E4 |
| 53.68 | E4 | 89.29 | D1 E4 | 93.73 | A1 D1 E4 | 94.64 | A1 D1 E2 E4 | 94.78 | A1 D1 E2 E3 E4 | 95.14 | A1 D1 E1 E2 E3 E4 | |
| 66.02 | D3 | 84.37 | C3 D3 | 88.71 | B1 C3 D3 | 85.15 | B1 C3 D3 H3 | 86.13 | B1 C3 D3 F1 H3 | 86.25 | A1 B1 C3 D3 F1 H3 | |
| 91.60 | D2 | 92.63 | D2 E3 | 93.55 | D2 E2 E3 | 92.91 | A1 D2 E2 E3 | 93.21 | A1 D2 E2 E3 F4 | 93.03 | A1 D2 E2 E3 F3 F4 | |
| 53.24 | E2 | 56.31 | E2 E3 | 71.53 | E2 E3 F4 | 72.64 | E1 E2 E3 F4 | 72.62 | E1 E2 E3 E4 F4 | 81.87 | C1 E1 E2 E3 E4 F4 | |
| DISR | 64.84 | E1 | 66.9 | E1 E4 | 66.98 | B4 E1 E4 | 79.69 | B4 C4 E1 E4 | 80.83 | B4 C4 E1 E2 E4 | 80.72 | A4 B4 C4 E1 E2 E4 |
| 53.62 | E4 | 53.05 | A4 E4 | 62.10 | A4 C4 E4 | 92.83 | A4 C2 C4 E4 | 94.40 | A1 A4 C2 C4 E4 | 94.46 | A1 A4 C1 C2 C4 E4 | |
| 65.84 | D3 | 65.91 | A4 D3 | 84.76 | A4 C3 D3 | 84.57 | A4 C3 D1 D3 | 86.08 | A4 C1 C3 D1 D3 | 86.43 | A4 C1 C3 D1 D2 D3 | |
| 91.52 | D2 | 91.19 | A4 D2 | 91.25 | A4 D1 D2 | 92.07 | A4 D1 D2 D3 | 91.96 | A4 B4 D1 D2 D3 | 93.05 | A4 B4 D1 D2 D3 E3 | |
| 53.19 | E2 | 70.07 | C3 E2 | 69.99 | C3 E1 E2 | 70.51 | C3 E1 E2 E3 | 70.80 | C2 C3 E1 E2 E3 | 70.89 | C2 C3 C4 E1 E2 E3 | |
| ICAP | 64.64 | E1 | 66.84 | E1 E4 | 82.66 | C1 E1 E4 | 83.48 | C1 E1 E3 E4 | 86.50 | C1 E1 E3 E4 G1 | 89.53 | A1 C1 E1 E3 E4 G1 |
| 53.65 | E4 | 89.30 | D1 E4 | 93.45 | A1 D1 E4 | 94.84 | A1 D1 E2 E4 | 95.02 | A1 D1 E1 E2 E4 | 95.08 | A1 D1 E1 E2 E3 E4 | |
| 66.28 | D3 | 84.43 | C3 D3 | 88.25 | B1 C3 D3 | 85.13 | B1 C3 D3 H3 | 86.34 | B1 C3 D3 F1 H3 | 86.55 | A1 B1 C3 D3 F1 H3 | |
| 92.08 | D2 | 92.80 | D2 E3 | 92.71 | A1 D2 E3 | 92.31 | A1 D2 E3 F4 | 91.65 | A1 D2 E3 F3 F4 | 92.54 | A1 D2 E3 F3 F4 H1 | |
| 53.23 | E2 | 56.35 | E2 E3 | 71.69 | E2 E3 F4 | 73.97 | C4 E2 E3 F4 | 82.60 | C1 C4 E2 E3 F4 | 79.92 | C1 C4 E2 E3 F2 F4 | |
| JMI | 64.67 | E1 | 66.82 | E1 E4 | 67.75 | E1 E2 E4 | 68.35 | E1 E2 E3 E4 | 81.13 | C4 E1 E2 E3 E4 | 85.78 | C2 C4 E1 E2 E3 E4 |
| 53.30 | E4 | 91.96 | C2 E4 | 94.45 | A1 C2 E4 | 95.17 | A1 C2 D1 E4 | 95.07 | A1 A2 C2 D1 E4 | 94.99 | A1 A2 C2 D1 E2 E4 | |
| 66.26 | D3 | 82.39 | B1 D3 | 88.40 | B1 C3 D3 | 89.12 | B1 C3 D2 D3 | 88.44 | B1 C3 D1 D2 D3 | 89.94 | B1 C1 C3 D1 D2 D3 | |
| 91.43 | D2 | 91.30 | D2 F3 | 92.02 | D2 D3 F3 | 92.73 | D2 D3 E3 F3 | 92.84 | D1 D2 D3 E3 F3 | 93.49 | D1 D2 D3 E2 E3 F3 | |
| 53.28 | E2 | 69.95 | C3 E2 | 69.96 | C3 E1 E2 | 81.29 | C3 E1 E2 F4 | 82.09 | C3 E1 E2 E3 F4 | 82.68 | C2 C3 E1 E2 E3 F4 | |
| MIFS | 64.68 | E1 | 64.76 | B4 E1 | 65.05 | A4 B4 E1 | 71.76 | A4 B4 D4 E1 | 72.57 | A4 B4 D4 E1 G4 | 82.56 | A4 B4 C4 D4 E1 G4 |
| 53.62 | E4 | 53.54 | A4 E4 | 53.11 | A4 B4 E4 | 69.82 | A4 B4 E4 G4 | 72.06 | A4 B4 E4 F4 G4 | 86.47 | A4 B4 D4 E4 F4 G4 | |
| 66.27 | D3 | 66.10 | B4 D3 | 66.43 | A4 B4 D3 | 72.47 | A4 B4 C4 D3 | 74.91 | A4 B4 C4 D3 G4 | 81.55 | A4 B4 C4 D3 G1 G4 | |
| 91.71 | D2 | 91.48 | A4 D2 | 91.77 | A4 B4 D2 | 91 | A4 B4 D2 G4 | 91.81 | A4 B4 C4 D2 G4 | 92.56 | A4 B4 C4 D2 G3 G4 | |
| 53.23 | E2 | 53.42 | A4 E2 | 54.09 | A4 B4 E2 | 66.56 | A4 B4 E2 G4 | 76.26 | A4 B4 E2 G4 H2 | 80.36 | A4 B4 C4 E2 G4 H2 | |
| mRMR | 64.83 | E1 | 64.94 | B4 E1 | 64.74 | A4 B4 E1 | 78.19 | A4 B4 C4 E1 | 81.16 | A4 B4 C4 D4 E1 | 83.89 | A4 B4 C4 D4 E1 H1 |
| 53.44 | E4 | 53.26 | A4 E4 | 69.94 | A4 E4 G4 | 70.05 | A4 B4 E4 G4 | 71.76 | A4 B4 E4 F4 G4 | 86.77 | A4 B4 D4 E4 F4 G4 | |
| 65.81 | D3 | 66.14 | B4 D3 | 66.14 | A4 B4 D3 | 72.29 | A4 B4 C4 D3 | 74.63 | A4 B4 C4 D3 G4 | 81.33 | A4 B4 C4 D3 G1 G4 | |
| 91.45 | D2 | 91.32 | A4 D2 | 91.88 | A4 B4 D2 | 90.68 | A4 B4 D2 G4 | 91.37 | A4 B4 C4 D2 G4 | 93.12 | A4 B4 C4 D2 G3 G4 | |
| 53.24 | E2 | 53.44 | A4 E2 | 54.16 | A4 B4 E2 | 66.37 | A4 B4 E2 G4 | 76.29 | A4 B4 E2 G4 H2 | 80.40 | A4 B4 C4 E2 G4 H2 |
| F1-Score | 1F | F1-Score | 2F | F1-Score | 3F | F1-Score | 4F | F1-Score | 5F | F1-Score | 6F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CMI | 0.7015 | E1 | 0.7198 | E1 E4 | 0.8326 | E1 E4 F1 | 0.8608 | E1 E4 F1 H1 | 0.8874 | A1 E1 E4 F1 H1 | 0.9010 | A1 C4 E1 E4 F1 H1 |
| 0.6630 | E4 | 0.9195 | C2 E4 | 0.9279 | C2 E4 H1 | 0.9477 | A2 C2 E4 H1 | 0.9555 | A2 C2 D3 E4 H1 | 0.9528 | A2 C2 D3 E2 E4 H1 | |
| 0.7341 | D3 | 0.8359 | B1 D3 | 0.8731 | B1 C2 D3 | 0.8966 | B1 C2 D3 G3 | 0.9072 | B1 C2 D3 E3 G3 | 0.9040 | B1 C2 D3 E3 F4 G3 | |
| 0.9178 | D2 | 0.9051 | D2 F3 | 0.9333 | D2 E2 F3 | 0.9322 | D2 E2 E3 F3 | 0.9298 | A1 D2 E2 E3 F3 | 0.9252 | A1 D2 E2 E3 F3 H4 | |
| 0.6812 | E2 | 0.7618 | C3 E2 | 0.8597 | C3 E2 H3 | 0.8436 | C3 E2 F4 H3 | 0.8522 | C3 E2 F4 H1 H3 | 0.8695 | A1 C3 E2 F4 H1 H3 | |
| CMIM | 0.7015 | E1 | 0.7185 | E1 E4 | 0.7262 | E1 E2 E4 | 0.8403 | C1 E1 E2 E4 | 0.8537 | C1 C2 E1 E2 E4 | 0.8592 | C1 C2 E1 E2 E3 E4 |
| 0.6633 | E4 | 0.8953 | D1 E4 | 0.9385 | A1 D1 E4 | 0.9472 | A1 D1 E2 E4 | 0.9484 | A1 D1 E2 E3 E4 | 0.9520 | A1 D1 E1 E2 E3 E4 | |
| 0.7338 | D3 | 0.8480 | C3 D3 | 0.8901 | B1 C3 D3 | 0.8567 | B1 C3 D3 H3 | 0.8637 | B1 C3 D3 F1 H3 | 0.8683 | A1 B1 C3 D3 F1 H3 | |
| 0.9188 | D2 | 0.9273 | D2 E3 | 0.9363 | D2 E2 E3 | 0.9295 | A1 D2 E2 E3 | 0.9325 | A1 D2 E2 E3 F4 | 0.9314 | A1 D2 E2 E3 F3 F4 | |
| 0.6812 | E2 | 0.6933 | E2 E3 | 0.7382 | E2 E3 F4 | 0.7489 | E1 E2 E3 F4 | 0.7490 | E1 E2 E3 E4 F4 | 0.8302 | C1 E1 E2 E3 E4 F4 | |
| DISR | 0.7022 | E1 | 0.7194 | E1 E4 | 0.7194 | B4 E1 E4 | 0.8088 | B4 C4 E1 E4 | 0.8201 | B4 C4 E1 E2 E4 | 0.8188 | A4 B4 C4 E1 E2 E4 |
| 0.6638 | E4 | 0.6584 | A4 E4 | 0.7063 | A4 C4 E4 | 0.9302 | A4 C2 C4 E4 | 0.9449 | A1 A4 C2 C4 E4 | 0.9455 | A1 A4 C1 C2 C4 E4 | |
| 0.7330 | D3 | 0.7319 | A4 D3 | 0.8515 | A4 C3 D3 | 0.8484 | A4 C3 D1 D3 | 0.8637 | A4 C1 C3 D1 D3 | 0.8681 | A4 C1 C3 D1 D2 D3 | |
| 0.9179 | D2 | 0.9146 | A4 D2 | 0.9140 | A4 D1 D2 | 0.9223 | A4 D1 D2 D3 | 0.9210 | A4 B4 D1 D2 D3 | 0.9313 | A4 B4 D1 D2 D3 E3 | |
| 0.6810 | E2 | 0.7620 | C3 E2 | 0.7572 | C3 E1 E2 | 0.7612 | C3 E1 E2 E3 | 0.7623 | C2 C3 E1 E2 E3 | 0.7629 | C2 C3 C4 E1 E2 E3 | |
| ICAP | 0.7009 | E1 | 0.7188 | E1 E4 | 0.8310 | C1 E1 E4 | 0.8389 | C1 E1 E3 E4 | 0.8666 | C1 E1 E3 E4 G1 | 0.8970 | A1 C1 E1 E3 E4 G1 |
| 0.6627 | E4 | 0.8949 | D1 E4 | 0.9358 | A1 D1 E4 | 0.9490 | A1 D1 E2 E4 | 0.9508 | A1 D1 E1 E2 E4 | 0.9514 | A1 D1 E1 E2 E3 E4 | |
| 0.7358 | D3 | 0.8480 | C3 D3 | 0.8858 | B1 C3 D3 | 0.8562 | B1 C3 D3 H3 | 0.8696 | B1 C3 D3 F1 H3 | 0.8715 | A1 B1 C3 D3 F1 H3 | |
| 0.9226 | D2 | 0.9291 | D2 E3 | 0.9275 | A1 D2 E3 | 0.9234 | A1 D2 E3 F4 | 0.9174 | A1 D2 E3 F3 F4 | 0.9252 | A1 D2 E3 F3 F4 H1 | |
| 0.6811 | E2 | 0.6935 | E2 E3 | 0.7394 | E2 E3 F4 | 0.7617 | C4 E2 E3 F4 | 0.8371 | C1 C4 E2 E3 F4 | 0.8129 | C1 C4 E2 E3 F2 F4 | |
| JMI | 0.7006 | E1 | 0.7186 | E1 E4 | 0.7272 | E1 E2 E4 | 0.7324 | E1 E2 E3 E4 | 0.8229 | C4 E1 E2 E3 E4 | 0.8623 | C2 C4 E1 E2 E3 E4 |
| 0.6613 | E4 | 0.9212 | C2 E4 | 0.9454 | A1 C2 E4 | 0.9523 | A1 C2 D1 E4 | 0.9514 | A1 A2 C2 D1 E4 | 0.9505 | A1 A2 C2 D1 E2 E4 | |
| 0.7350 | D3 | 0.8307 | B1 D3 | 0.8872 | B1 C3 D3 | 0.8950 | B1 C3 D2 D3 | 0.8883 | B1 C3 D1 D2 D3 | 0.9024 | B1 C1 C3 D1 D2 D3 | |
| 0.9167 | D2 | 0.9133 | D2 F3 | 0.9204 | D2 D3 F3 | 0.9276 | D2 D3 E3 F3 | 0.9285 | D1 D2 D3 E3 F3 | 0.9354 | D1 D2 D3 E2 E3 F3 | |
| 0.6814 | E2 | 0.7613 | C3 E2 | 0.7568 | C3 E1 E2 | 0.8242 | C3 E1 E2 F4 | 0.8319 | C3 E1 E2 E3 F4 | 0.8377 | C2 C3 E1 E2 E3 F4 | |
| MIFS | 0.7013 | E1 | 0.7014 | B4 E1 | 0.7035 | A4 B4 E1 | 0.7238 | A4 B4 D4 E1 | 0.7259 | A4 B4 D4 E1 G4 | 0.8275 | A4 B4 C4 D4 E1 G4 |
| 0.6635 | E4 | 0.6610 | A4 E4 | 0.6579 | A4 B4 E4 | 0.6979 | A4 B4 E4 G4 | 0.7203 | A4 B4 E4 F4 G4 | 0.8659 | A4 B4 D4 E4 F4 G4 | |
| 0.7351 | D3 | 0.7329 | B4 D3 | 0.7335 | A4 B4 D3 | 0.7326 | A4 B4 C4 D3 | 0.7528 | A4 B4 C4 D3 G4 | 0.8213 | A4 B4 C4 D3 G1 G4 | |
| 0.9195 | D2 | 0.9172 | A4 D2 | 0.9199 | A4 B4 D2 | 0.9103 | A4 B4 D2 G4 | 0.9180 | A4 B4 C4 D2 G4 | 0.9258 | A4 B4 C4 D2 G3 G4 | |
| 0.6812 | E2 | 0.6815 | A4 E2 | 0.6841 | A4 B4 E2 | 0.6888 | A4 B4 E2 G4 | 0.7639 | A4 B4 E2 G4 H2 | 0.8058 | A4 B4 C4 E2 G4 H2 | |
| mRMR | 0.7025 | E1 | 0.7027 | B4 E1 | 0.7004 | A4 B4 E1 | 0.7948 | A4 B4 C4 E1 | 0.8169 | A4 B4 C4 D4 E1 | 0.8414 | A4 B4 C4 D4 E1 H1 |
| 0.6618 | E4 | 0.6594 | A4 E4 | 0.6994 | A4 E4 G4 | 0.6988 | A4 B4 E4 G4 | 0.7182 | A4 B4 E4 F4 G4 | 0.8689 | A4 B4 D4 E4 F4 G4 | |
| 0.7322 | D3 | 0.7331 | B4 D3 | 0.7315 | A4 B4 D3 | 0.7301 | A4 B4 C4 D3 | 0.7507 | A4 B4 C4 D3 G4 | 0.8199 | A4 B4 C4 D3 G1 G4 | |
| 0.9168 | D2 | 0.9159 | A4 D2 | 0.9212 | A4 B4 D2 | 0.9071 | A4 B4 D2 G4 | 0.9137 | A4 B4 C4 D2 G4 | 0.9316 | A4 B4 C4 D2 G3 G4 | |
| 0.6812 | E2 | 0.6816 | A4 E2 | 0.6843 | A4 B4 E2 | 0.6869 | A4 B4 E2 G4 | 0.7646 | A4 B4 E2 G4 H2 | 0.8063 | A4 B4 C4 E2 G4 H2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marti-Puig, P.; Blanco-M, A.; Cárdenas, J.J.; Cusidó, J.; Solé-Casals, J. Feature Selection Algorithms for Wind Turbine Failure Prediction. Energies 2019, 12, 453. https://doi.org/10.3390/en12030453
Marti-Puig P, Blanco-M A, Cárdenas JJ, Cusidó J, Solé-Casals J. Feature Selection Algorithms for Wind Turbine Failure Prediction. Energies. 2019; 12(3):453. https://doi.org/10.3390/en12030453
Chicago/Turabian StyleMarti-Puig, Pere, Alejandro Blanco-M, Juan José Cárdenas, Jordi Cusidó, and Jordi Solé-Casals. 2019. "Feature Selection Algorithms for Wind Turbine Failure Prediction" Energies 12, no. 3: 453. https://doi.org/10.3390/en12030453
APA StyleMarti-Puig, P., Blanco-M, A., Cárdenas, J. J., Cusidó, J., & Solé-Casals, J. (2019). Feature Selection Algorithms for Wind Turbine Failure Prediction. Energies, 12(3), 453. https://doi.org/10.3390/en12030453









