A Non-Uniform Transmission Line Model of the ±1100 kV UHV Tower
Abstract
:1. Introduction
- (1)
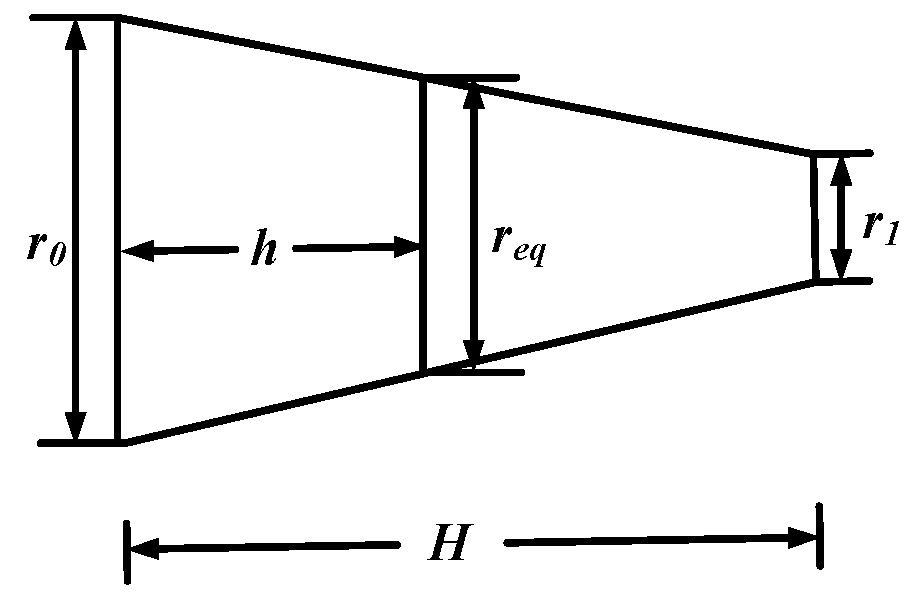
- An approach to simplify the non-uniform transmission line model is proposed in this paper. The vertical parts of the tower are equalized to a single conductor system and its non-uniform distributed parameters are derived based on the theory of the biconical antenna; and the horizontal cross-arms are modeled as surge impedances since they are parallel to the ground.
- (2)
- The influence of the tower’s spatial structure changes on its electromagnetic transient response is studied. It is concluded that the more accurately the nominal height of the tower is modeled, the more accurately its electromagnetic transient response is reflected.
- (3)
- The applicability of the non-uniform transmission line model in lightning transient analysis is studied. Through comparing the lightning electromagnetic transient responses with the non-uniform transmission line model and with the multi-segment multi-surge impedance model, the applicability of the non-uniform transmission line model is verified.
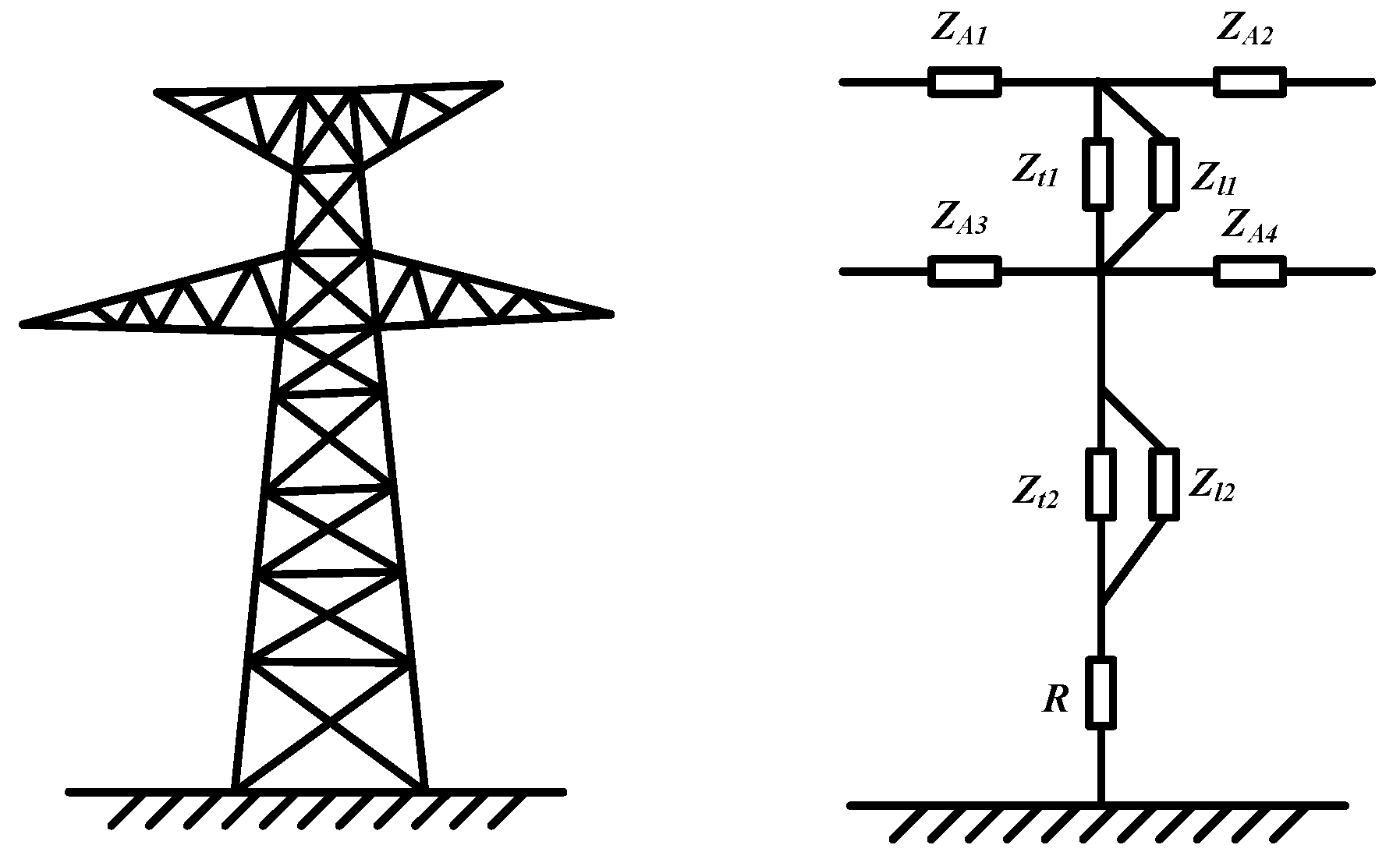
2. The Multi-Surge Impedance Model of the Tower
3. Non-Uniform Transmission Line Model of the Tower
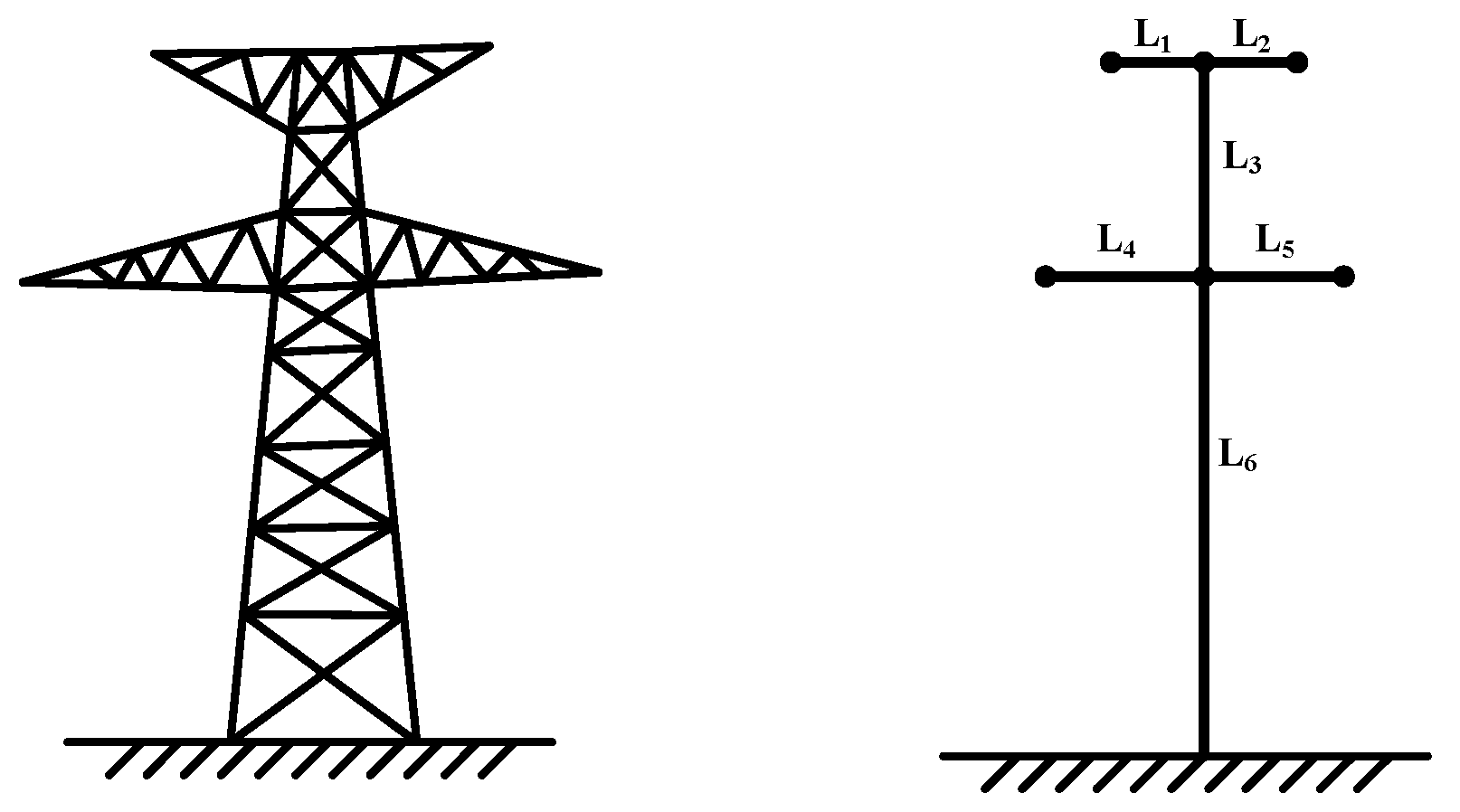
3.1. Modeling of the Horizontal Cross Arms
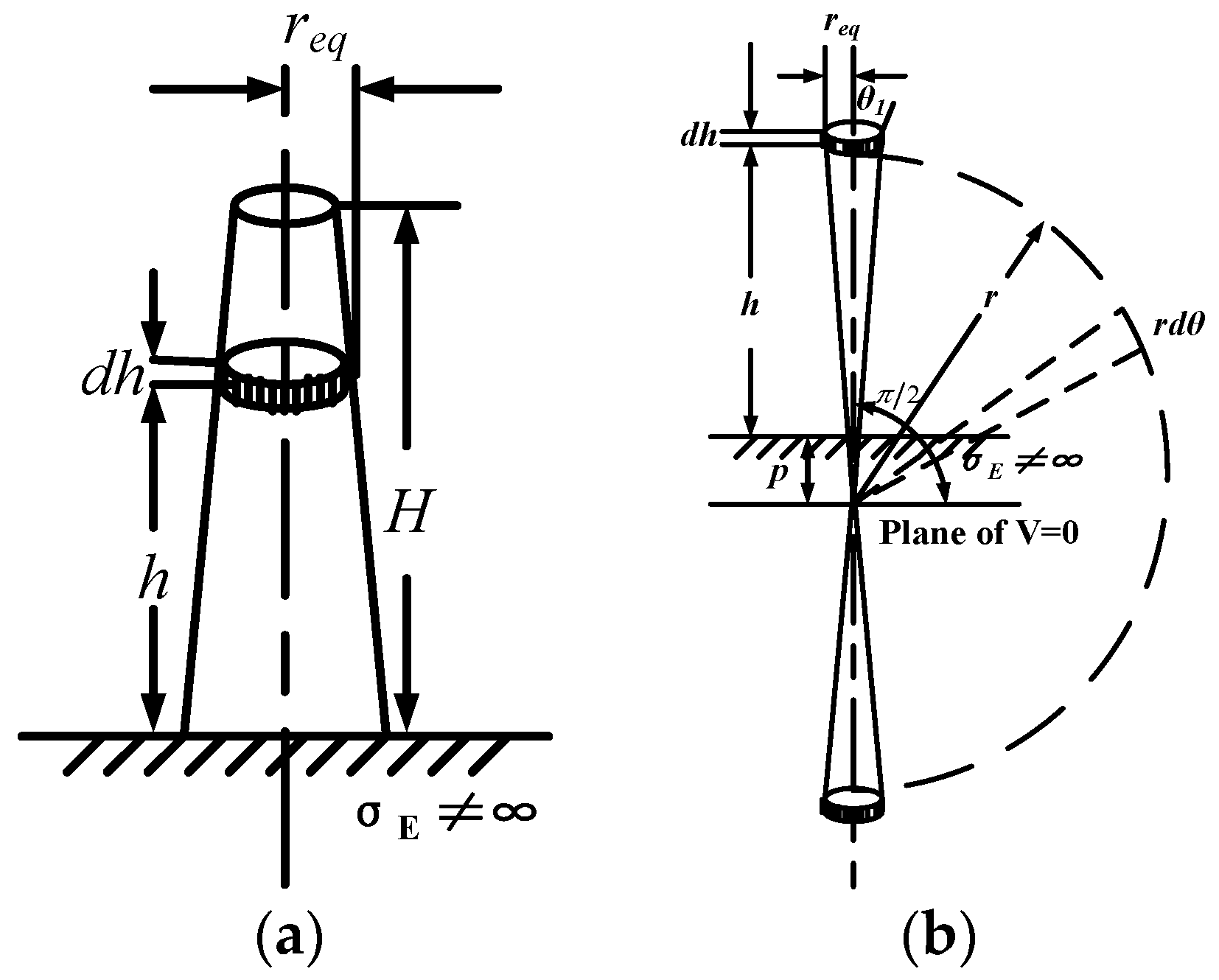
3.2. Modeling of the Vertical Main Body
4. Simulation Analysis
4.1. Simulation Model and Parameters
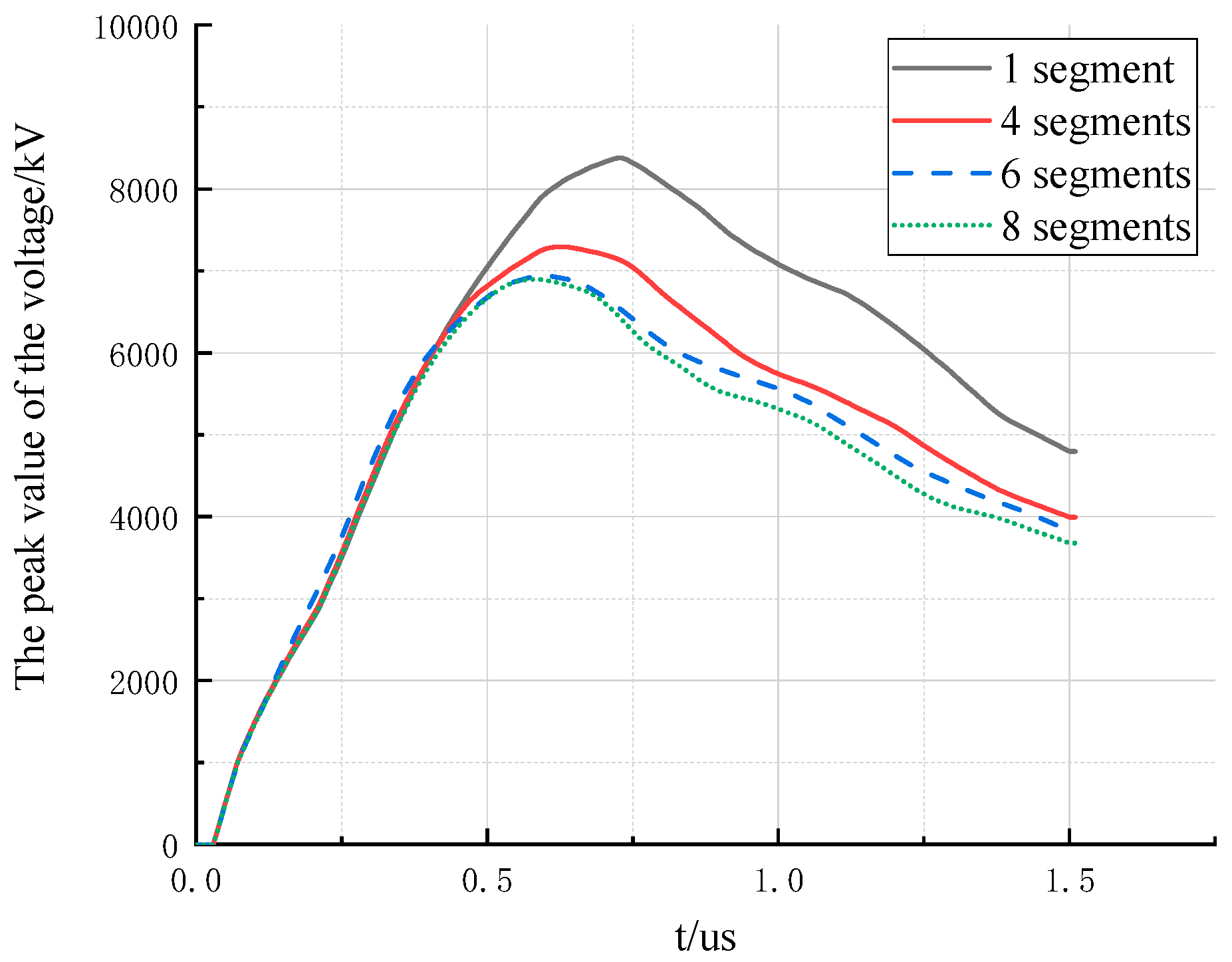
4.2. Simulation Results of the Multi-Segment Multi-Surge Impedance Model
- (1)
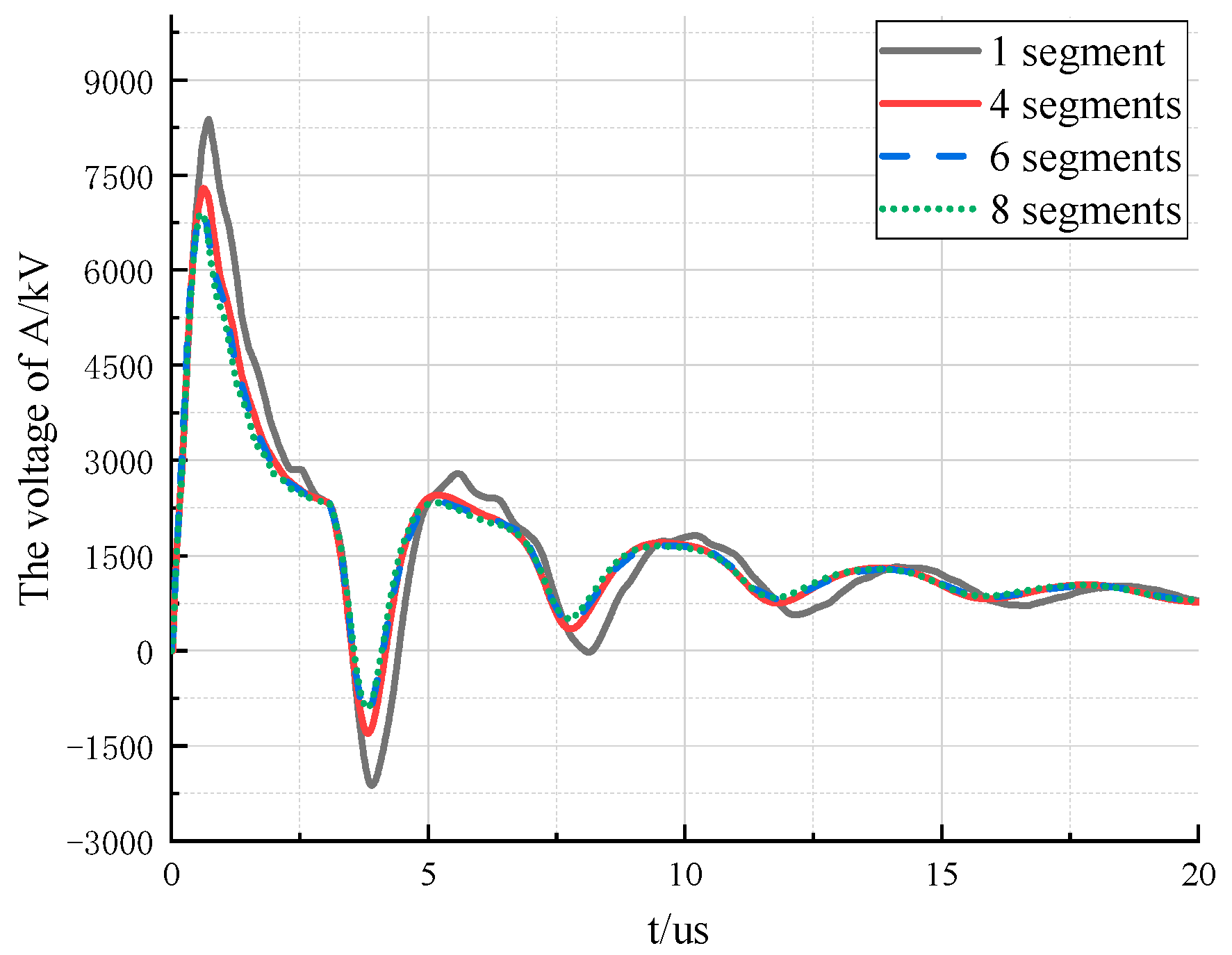
- As the number of segments in the nominal height increases, the amplitude of the voltage gradually decreases. Compared with the one segment model, the overvoltage amplitude of the 8 segments model decreased by about 15.6%. This is because as the number of the divided segments increases, the geometric spatial structure of the nominal height is modeled by more surge impedances; and the impedance values of the respective parts are sequentially reduced, so that the peak value of the voltage is correspondingly reduced.
- (2)
- When the nominal height is segmented differently, the overall fluctuation trend of the voltage is almost the same.
- (3)
- As the number of segments of the nominal height increases, the peak of the voltage appears earlier and earlier. Compared with the one segment model, the time the peak appears is about 0.15 μs ahead of time when the nominal height is divided into 8 segments. This is because the more the number of segments of the nominal height is, the smaller the height and the larger the equivalent radius is. Therefore, the surge impedance of the portion closer to the ground is smaller. That is, when the lightning wave has not transmitted to the bottom of the tower, some of the reflected waves have returned to the top of the tower. This reflected wave slows down the rise of the peak voltage and decreases the peak value.
- (4)
- When the number of segments of the nominal height increases, the gradient of the voltage peak reduction is getting smaller and smaller. For example, when 6 segments or 8 segments are used to represent the nominal height of the tower, the peak value and fluctuation of the voltage waveform at the top of the tower are not much different. It indicates that as the number of segments for modelling the nominal height reaches a certain level, the peak value will change little and reach its saturation value. Then, further subdivision will have little effect on the electromagnetic transient response of the tower.
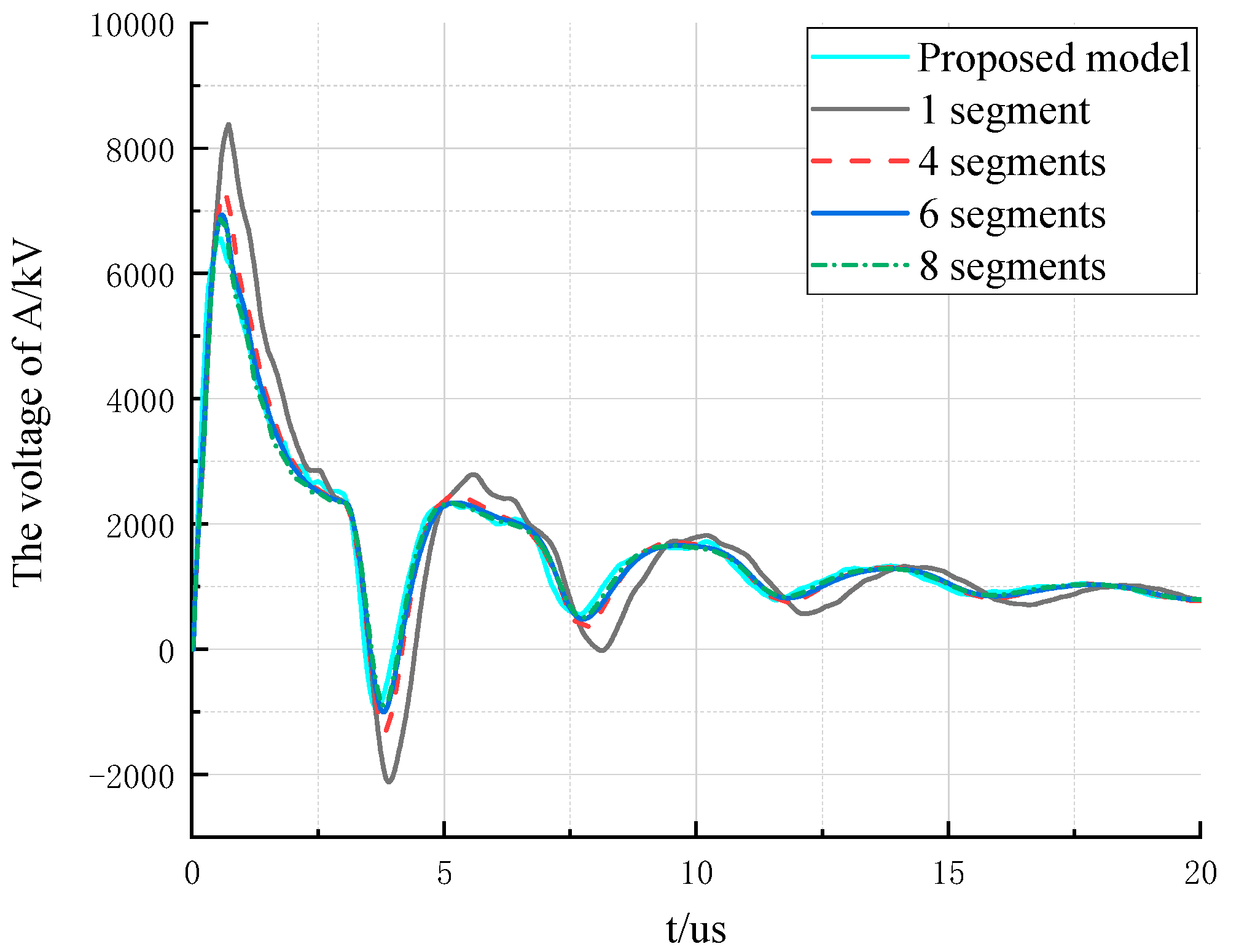
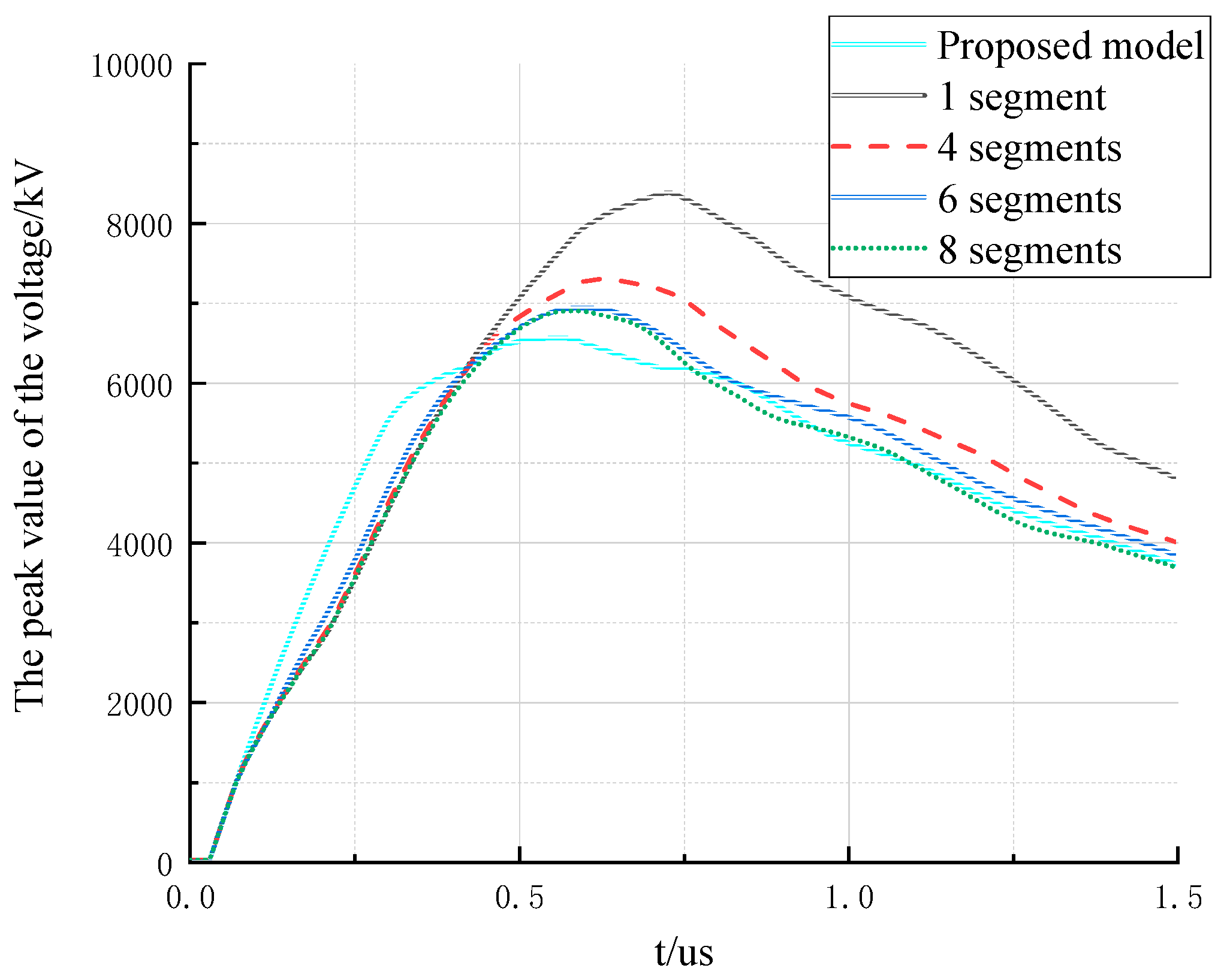
4.3. Simulation Results of the Non-Uniform Transmission Line Model
- (1)
- The peak of the voltage with the non-uniform transmission line model is lower.
- (2)
- The voltage waveform with the non-uniform transmission line model fluctuates more, but the basic fluctuation trend is consistent.
5. Conclusions
- (1)
- As the number of segments of the nominal height increases, the peak value of the voltage at the top of the tower is gradually reduced, and the peak time is gradually decreased. When the number of segments reaches a certain level, the transient response waveform of the tower will change little.
- (2)
- The transient response of the tower with the non-uniform transmission line model is very close to the saturated response of the multi-segment multi-surge impedance model. It indicates that the results with the non-uniform transmission line model in lightning protection analysis are more reliable. So the non-uniform transmission line model should be selected.
- (3)
- It can be seen that the non-uniform transmission line model built in this paper is consistent with the electromagnetic transient response of the multi-segment multi-surge impedance model. It shows that the proposed model can reflect the changes of the spatial structure of the tower more realistically, and is more suitable for the lightning transient analysis of ±1100kV UHV tower than the multi-surge impedance model.
- (4)
- The accuracy of the tower model determines the reliability of the lightning protection analysis. As the structure of the tower becomes more and more complicated, the ordinary multi-surge impedance model is no longer applicable, and a more accurate tower model must be built. The future modeling of the tower should focus on the physical characteristics. The model of the tower should be able to better reflect the electric and magnetic field generated by the lightning current and the tower’s own structure.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.J.; Zhu, L.Y.; Ji, S.C.; Zhang, Q. Present and development of lightning protection for HV transmission lines and substations. Insul. Surge Arresters 2010, 3, 35–46. [Google Scholar]
- IEEE Working Group on Estimating Lightning Performance of Transmission Lines. A Simplified Method for Estimating Lightning Performance of Transmission Line. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 919–932. [Google Scholar]
- Li, P.G. A new viewpoint about lightning trip-out of UHV transmission lines. Power Syst. Technol. 2000, 24, 63–65. [Google Scholar]
- Xu, Z.H. Lighting Transient Study of Transmission Tower and Analysis of Invaded Wave to Substation; North China Electric Power University (Hebei): Beijing, China, 2006. [Google Scholar]
- Hara, T.; Yamamoto, O. Modeling of a transmission tower for lightning-surge analysis. IEE Proc. Gener. Transm. Distrib. 1996, 143, 283–289. [Google Scholar] [CrossRef]
- Wang, D.J.; Zhou, H.; Chen, J.M.; Lao, J.; Zhu, T.; Bao, J.; Zhang, L.; Wang, J. Design of Multi-Surge Impedance Model for Ultra-High Transmission Tower and Analysis on Its Transient Characteristic Caused by Lightning Stroke. Power Syst. Technol. 2007, 31, 11–16. [Google Scholar]
- Du, L.; Mi, X.; Xiao, N.Z.; Yu, S.; Yang, Y.; Yang, Q. Equivalent Model of Cross Arm and Inclined Holder of Transmission Tower. High Volt. Eng. 2012, 38, 3025–3032. [Google Scholar]
- Gutierrez R, J.A.; Moreno, P.; Naredo, J.L.; Bermudez, J.L.; Paolone, M.; Nucci, C.A.; Rachidi, F. Nonuniform transmission tower model for lightning transient studies. IEEE Trans. Power Deliv. 2004, 19, 490–496. [Google Scholar] [CrossRef]
- Huangfu, Y.; Wang, S.; Wang, G.; Xu, W.; Zhang, H. Modeling and Insulation Performance Analysis of Composite Transmission Line Tower under Lightning Overvoltage. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Mo, F.J.; Chen, Y.P.; Ruan, J.J. Study on transmission tower models and their lightning performance calculation. Power Syst. Technol. 2004, 28, 80–84. [Google Scholar]
- Liang, Y.M.; Ge, D. Tower model in calculation of lightning protection on multi-circuit transmission line with same tower. High Volt. Eng. 2006, 31, 76–77. [Google Scholar]
- Zhang, Y.; Gao, Y.D.; Du, B.; Shi, W. New tower model in calculation of lightning protection on transmission line. J. Xi’an Jiaotong Univ. 2004, 38, 365–368. [Google Scholar]
- Yang, Q.; Zhao, J.; Sima, W.X.; Feng, J.; Yuan, T. Lightning back-flashover performance of the Yun-Guang UHV DC transmission lines. High Vol. Eng. 2008, 34, 1330–1335. [Google Scholar]
- Zhang, Y.J.; Sima, W.X.; Zhang, Z.J. Summary of the study of tower models for lightning protection analysis. High Vol. Eng. 2006, 32, 93–97. [Google Scholar]
- Ishii, M.; Baba, Y. Numerical electromagnetic field analysis of tower surge response. IEEE Trans. Power Deliv. 1997, 12, 483–488. [Google Scholar] [CrossRef]
- Naredo, J.L.; Moreno, P.; Soudack, A.C.; Marti, J.R. Frequency Independent Representation of Transmission Lines for Transient Analysis through the Method of Characteristics. In Proceedings of the Joint International Power Conference Athens Power Tech, Athens, Greece, 5–8 September 1993. [Google Scholar]
- Ishii, M.; Kawamura, T.; Kouno, T.; Ohsaki, E.; Shiokawa, K.; Murotani, K.; Higuchi, T. Multistory transmission tower model for lightning surge analysis. IEEE Trans. Power Deliv. 1991, 6, 1327–1335. [Google Scholar] [CrossRef]
- Jordan, E.C.; Andrews, C.L. Electromagnetic Waves and Radiating Systems. Am. J. Phys. 1968, 19, 477–478. [Google Scholar] [CrossRef]
- Du, L.; Mi, X.; Yang, Y.; Yang, Q. The equivalent model of transmission tower under lightning striking. High Volt. Eng. 2011, 37, 28–33. [Google Scholar]
- Imece, A.F.; Durbak, D.W.; Elahi, H.; Kolluri, S.; Lux, A.; Mader, D.; McDermott, T.E.; Morched, A.; Mousa, A.M.; Natarajan, R.; et al. Modeling guidelines for fast front transients. IEEE Trans. Power Deliv. 2002, 11, 493–506. [Google Scholar]
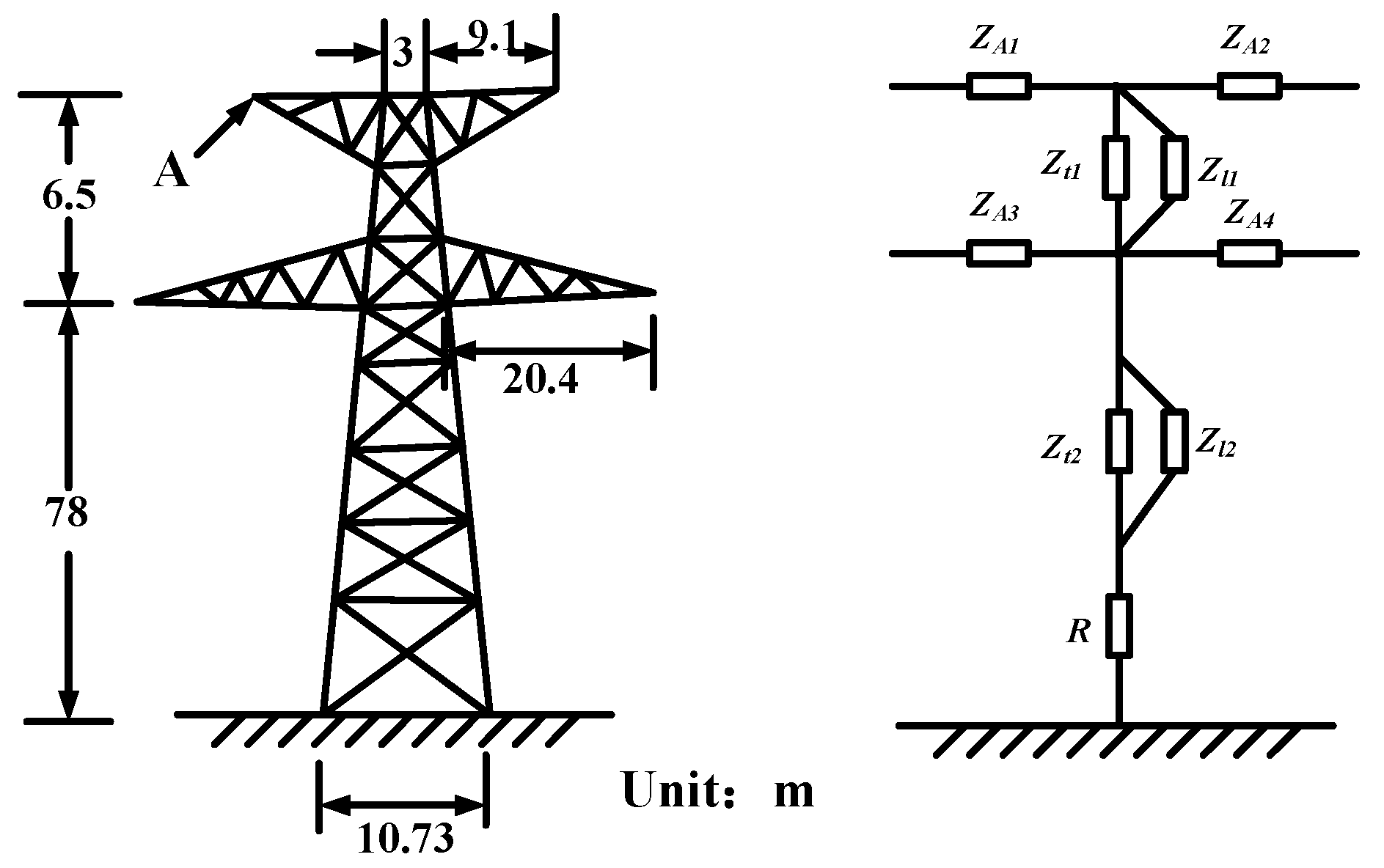

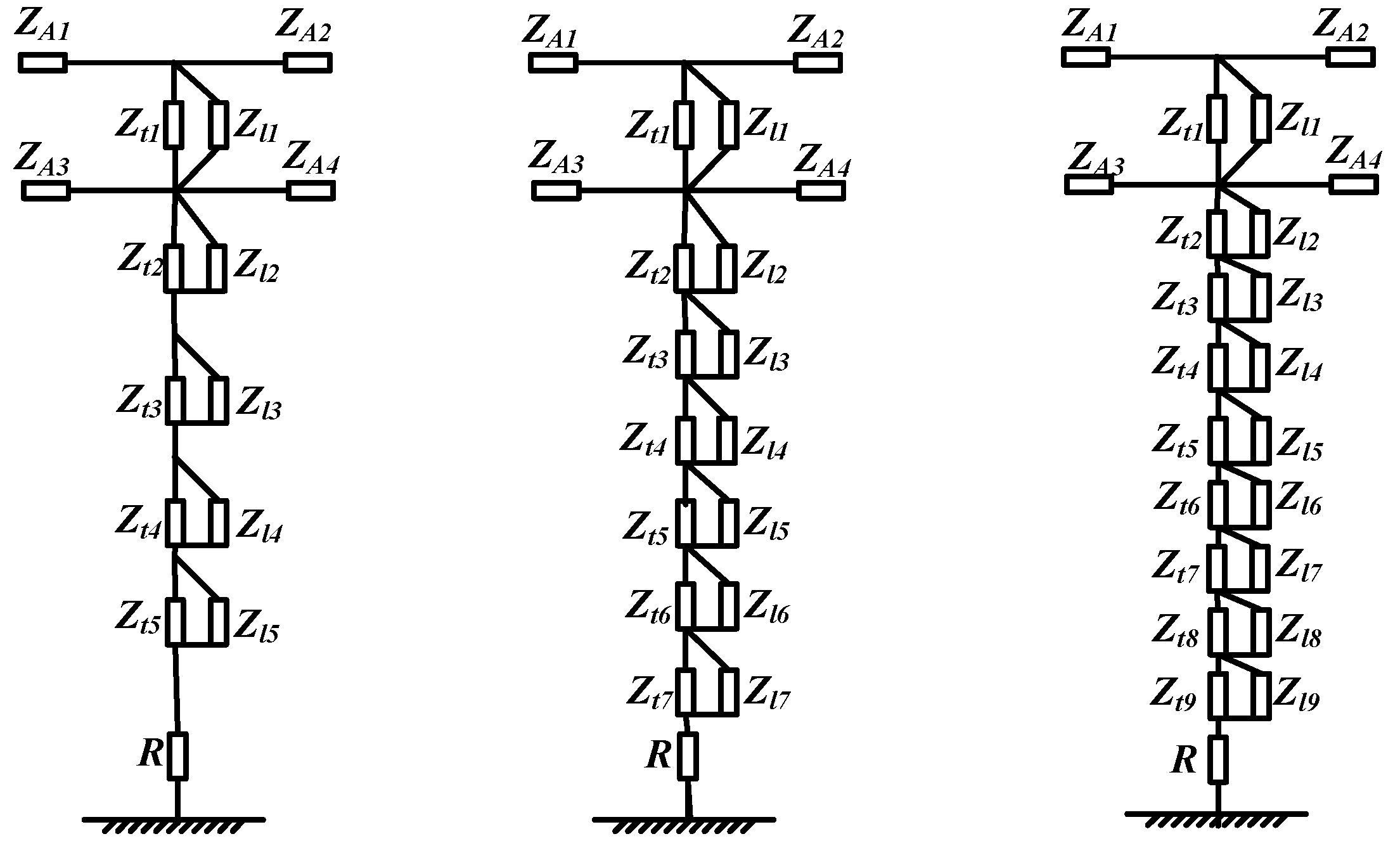
| Tower Parameters | Parameters of the Main Body | ||
|---|---|---|---|
| Tower material | Iron | Number of columns | 4 |
| Tower resistivity | 9.09 × 10−7 Ω/m | Column equivalent radius | 0.1 m |
| Tower magnetic permeability | 4π × 10−4 H/m | Maximum distance between columns | 10.73 m |
| Ground resistivity | 30 Ω·m | Minimum distance between columns | 3.0 m |
| Parameter Name | Surge Impedance/Ω | Parameter Name | Surge Impedance/Ω |
|---|---|---|---|
| ZA1 | 288 | ZA2 | 288 |
| ZA3 | 270 | ZA4 | 270 |
| Zt1 | 180 | Zl1 | 1620 |
| Zt2 | 141 | Zl2 | 1269 |
| Parameter Name | Surge Impedance/Ω | Parameter Name | Surge Impedance/Ω |
|---|---|---|---|
| ZA1 | 288 | ZA2 | 288 |
| ZA3 | 270 | ZA4 | 270 |
| Zt1 | 180 | Zl1 | 1620 |
| Zt2 | 160 | Zl2 | 1440 |
| Zt3 | 130 | Zl3 | 1170 |
| Zt4 | 96 | Zl4 | 864 |
| Zt5 | 46 | Zl5 | 414 |
| Parameter Name | Surge Impedance/Ω | Parameter Name | Surge Impedance/Ω |
|---|---|---|---|
| ZA1 | 288 | ZA2 | 288 |
| ZA3 | 270 | ZA4 | 270 |
| Zt1 | 180 | Zl1 | 1620 |
| Zt2 | 163 | Zl2 | 1467 |
| Zt3 | 143 | Zl3 | 1287 |
| Zt4 | 121 | Zl4 | 1089 |
| Zt5 | 97 | Zl5 | 873 |
| Zt6 | 67 | Zl6 | 603 |
| Zt7 | 20 | Zl7 | 180 |
| Parameter Name | Surge Impedance/Ω | Parameter Name | Surge Impedance/Ω |
|---|---|---|---|
| ZA1 | 288 | ZA2 | 288 |
| ZA3 | 270 | ZA4 | 270 |
| Zt1 | 180 | Zl1 | 1620 |
| Zt2 | 165 | Zl2 | 1485 |
| Zt3 | 149 | Zl3 | 1341 |
| Zt4 | 134 | Zl4 | 1206 |
| Zt5 | 117 | Zl5 | 1053 |
| Zt6 | 98 | Zl6 | 882 |
| Zt7 | 77 | Zl7 | 693 |
| Zt8 | 48 | Zl8 | 432 |
| Zt9 | 3 | Zl9 | 27 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Fu, Y.; Yu, J.; Xu, Z. A Non-Uniform Transmission Line Model of the ±1100 kV UHV Tower. Energies 2019, 12, 445. https://doi.org/10.3390/en12030445
Guo X, Fu Y, Yu J, Xu Z. A Non-Uniform Transmission Line Model of the ±1100 kV UHV Tower. Energies. 2019; 12(3):445. https://doi.org/10.3390/en12030445
Chicago/Turabian StyleGuo, Xianshan, Ying Fu, Jingqiu Yu, and Zheng Xu. 2019. "A Non-Uniform Transmission Line Model of the ±1100 kV UHV Tower" Energies 12, no. 3: 445. https://doi.org/10.3390/en12030445
APA StyleGuo, X., Fu, Y., Yu, J., & Xu, Z. (2019). A Non-Uniform Transmission Line Model of the ±1100 kV UHV Tower. Energies, 12(3), 445. https://doi.org/10.3390/en12030445






