Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview
Abstract
1. Introduction
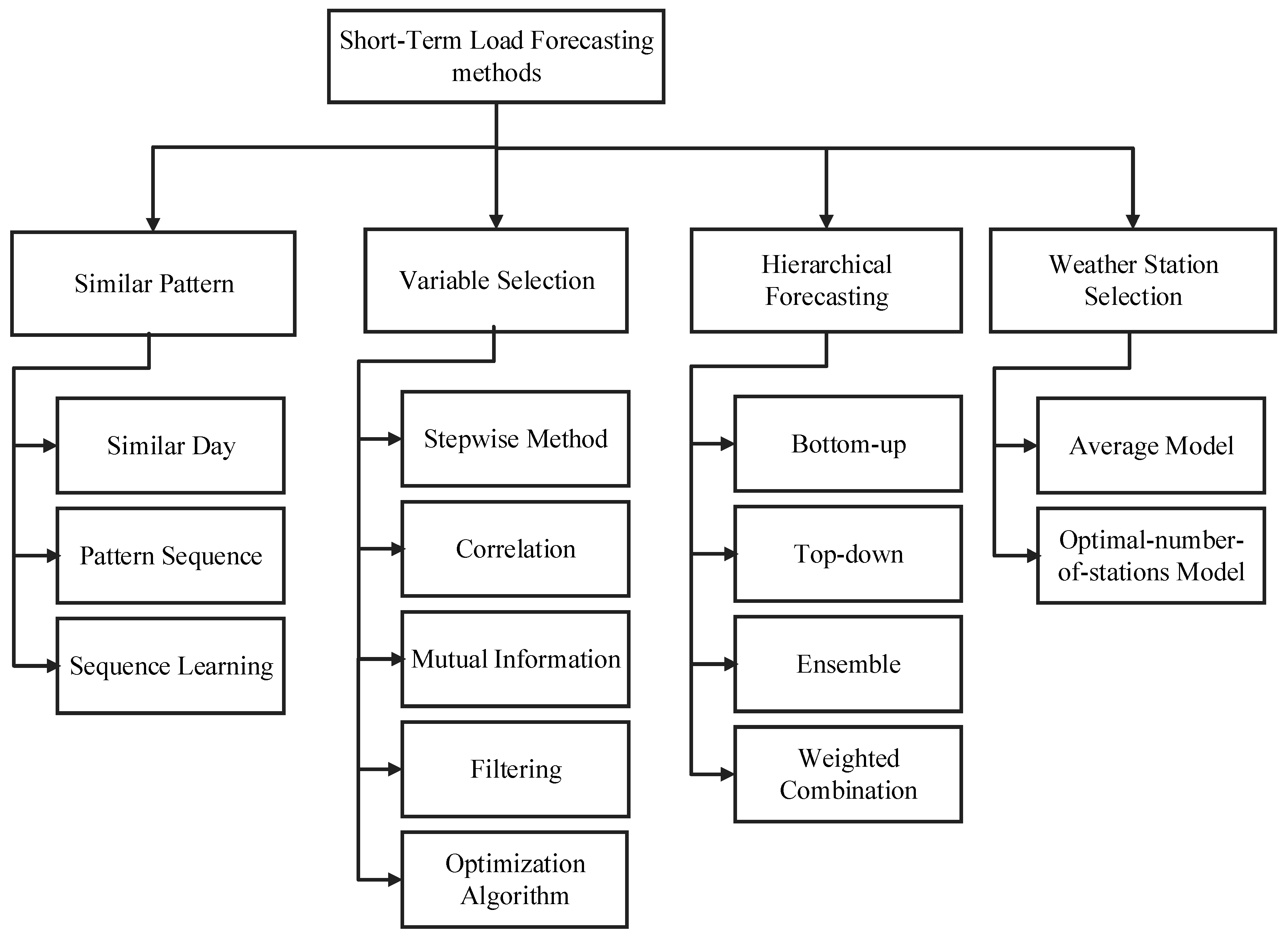
2. STLF Methodologies
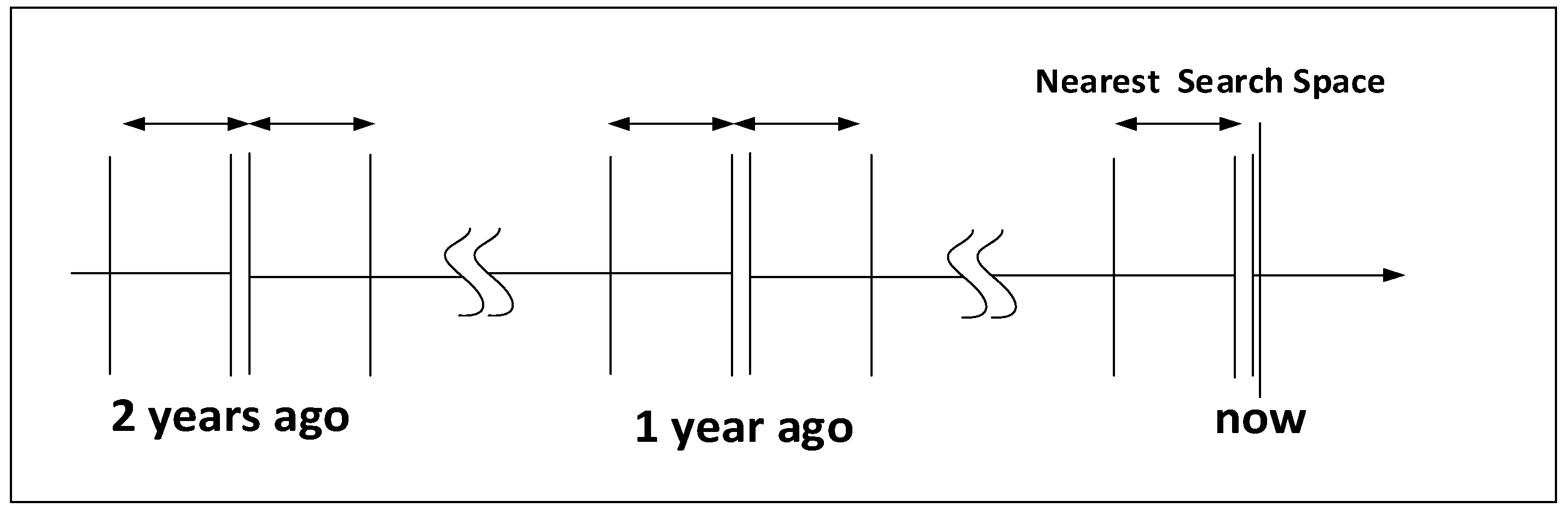
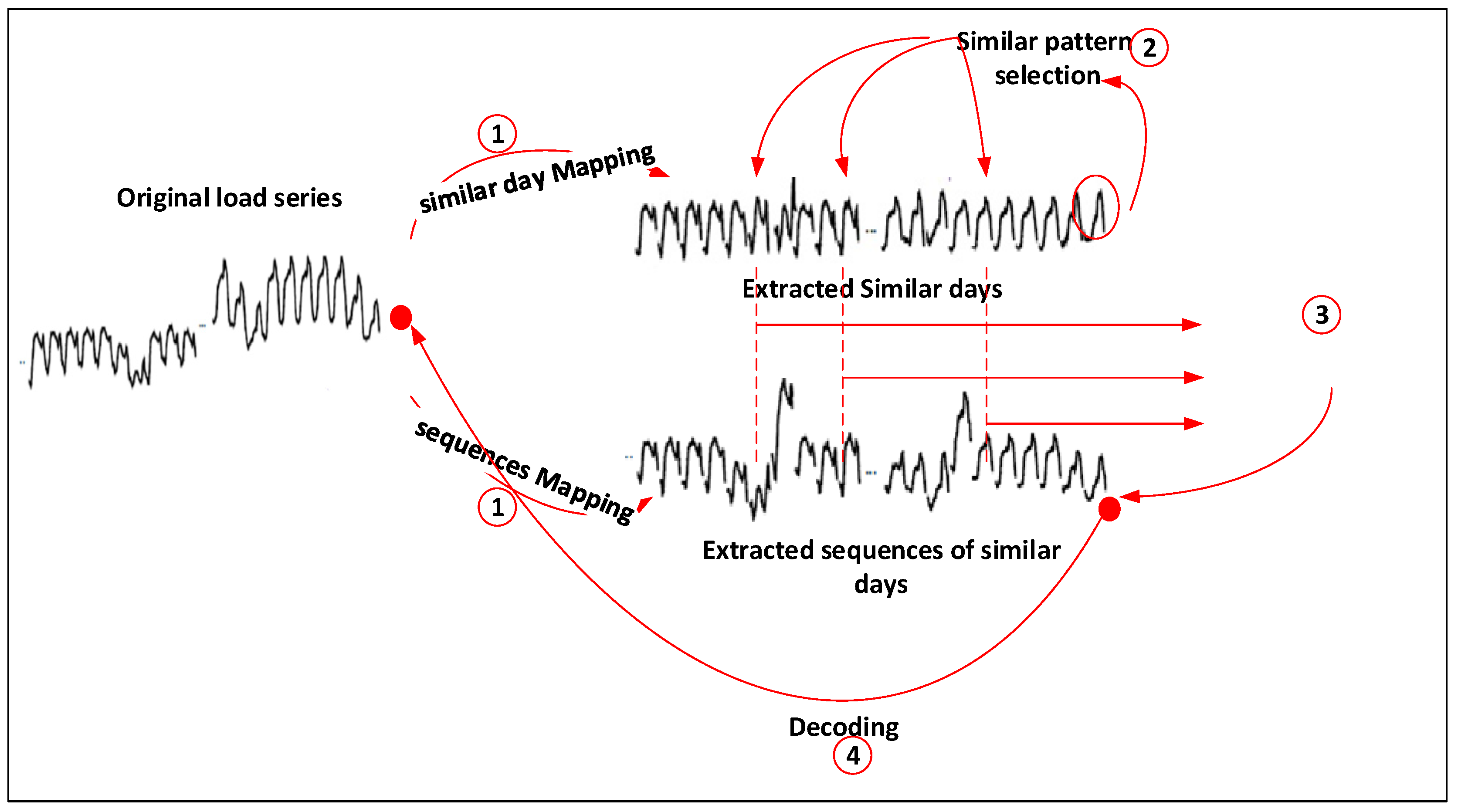
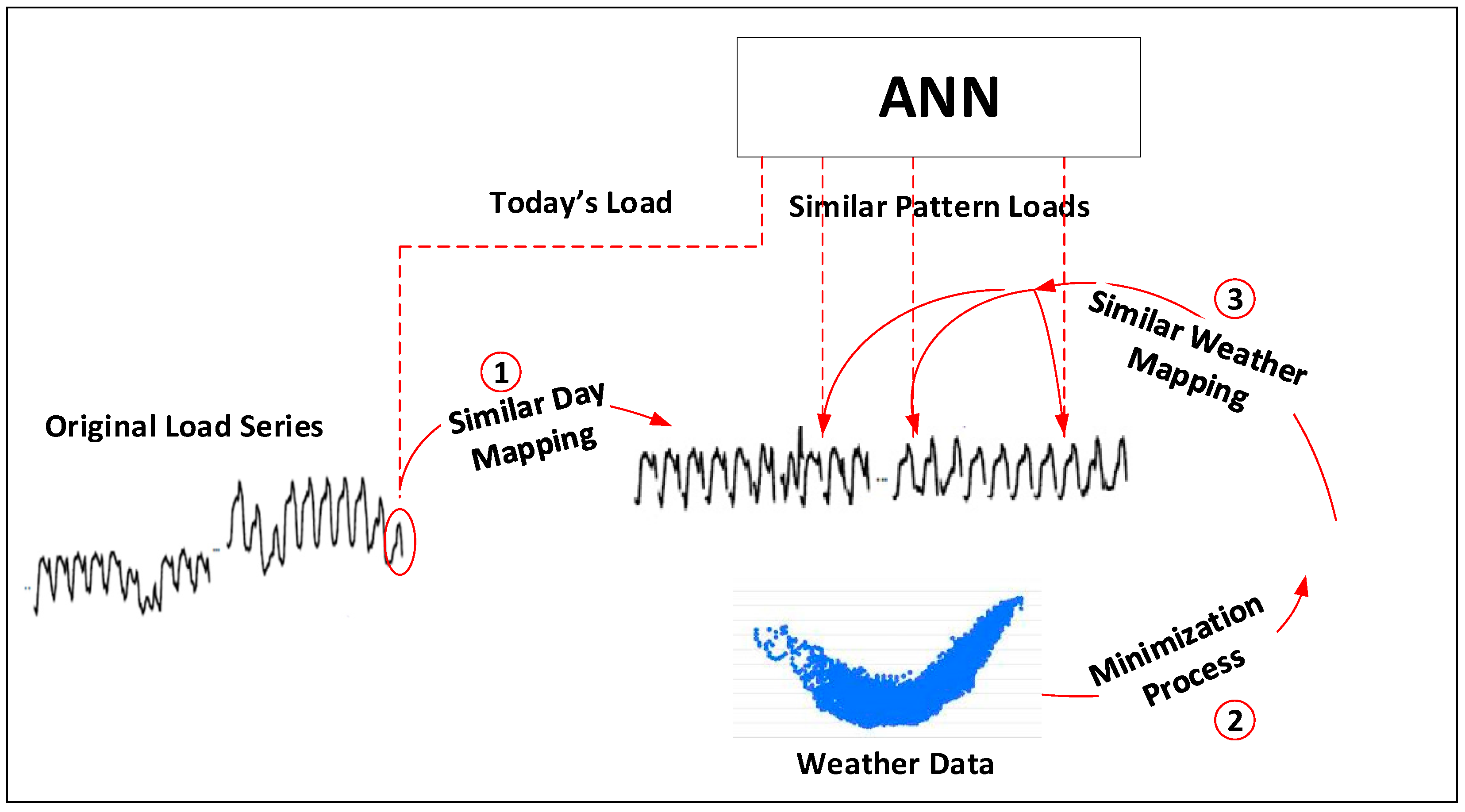
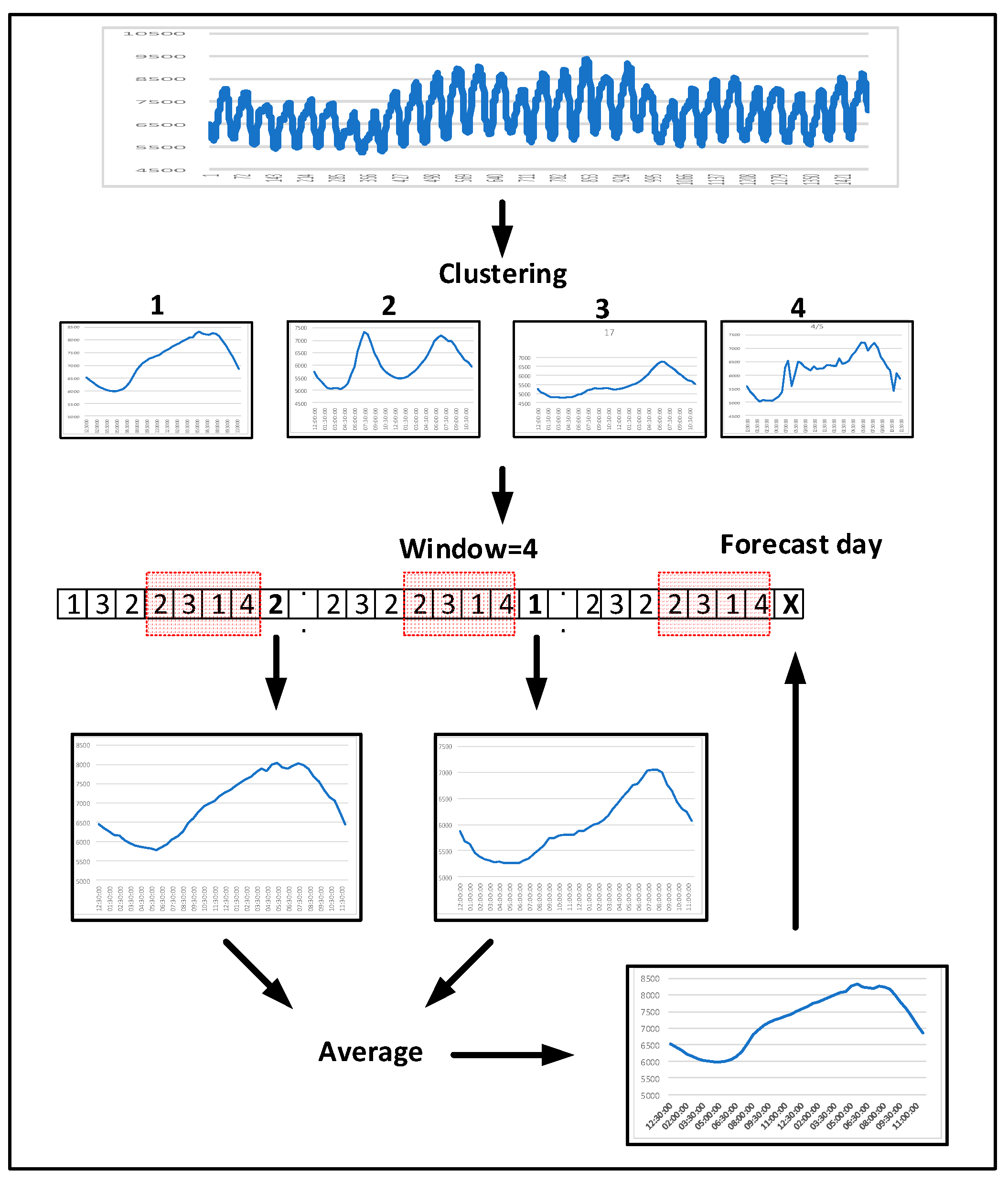
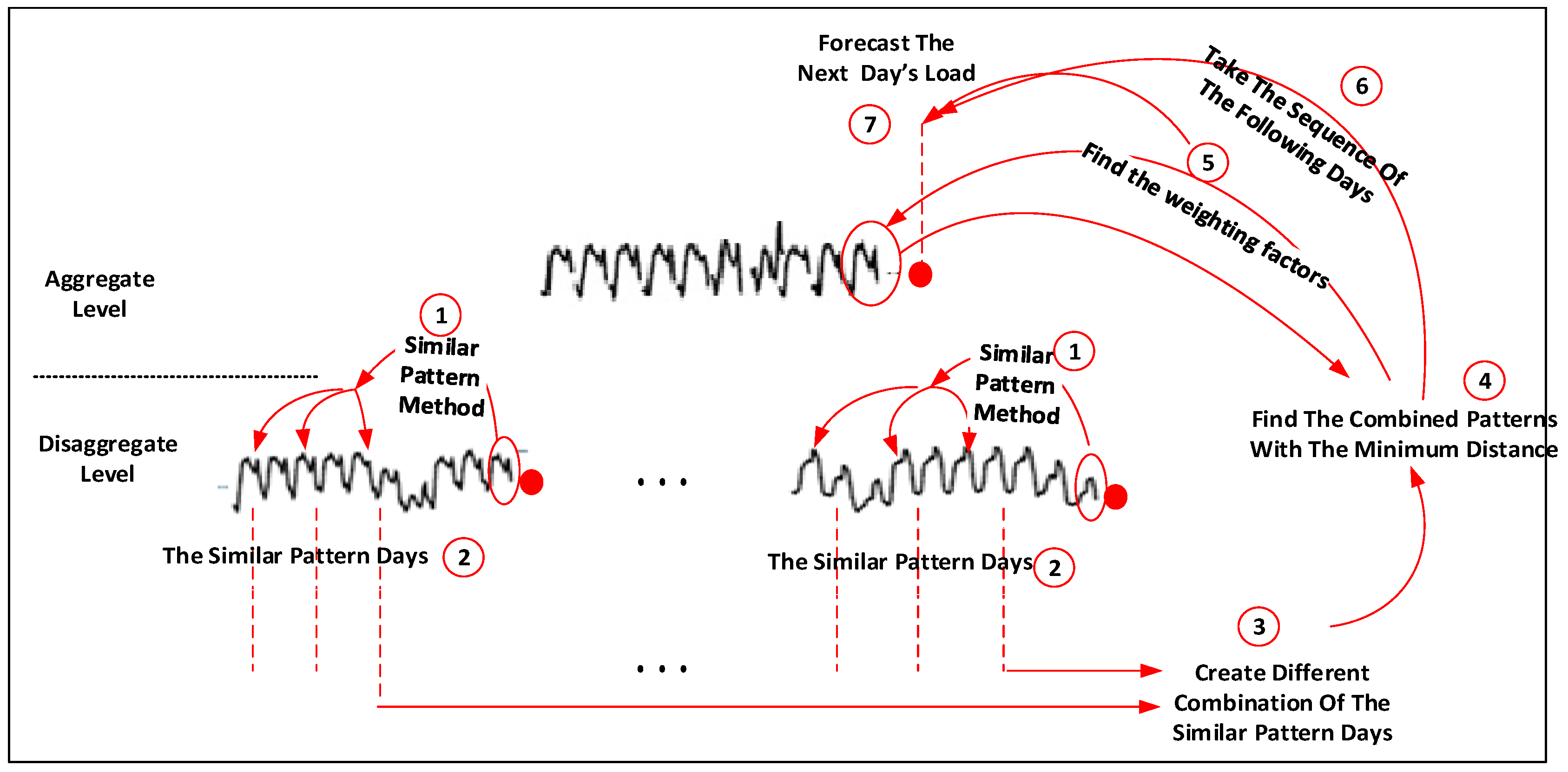
2.1. Similar-Pattern Method
2.2. Variable Selection Method
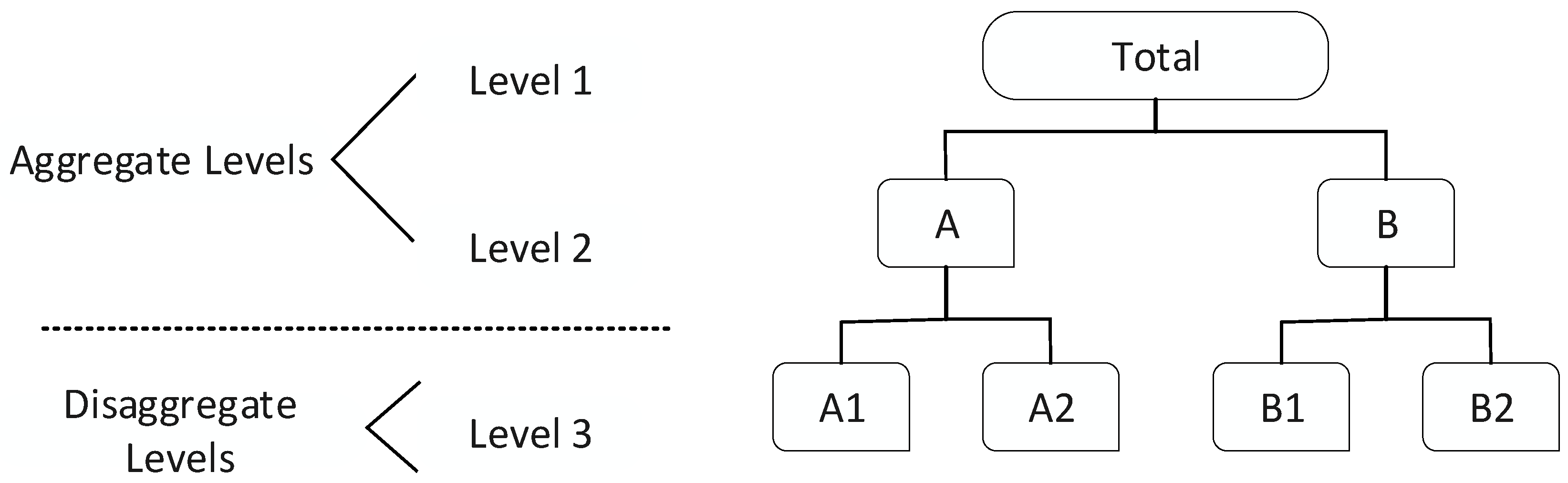
2.3. Hierarchical Forecasting
2.4. Weather Station Selection
3. Method Evaluation and Future Work
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ANN | Artificial Neural Network |
| ARIMA | Auto-Regressive Integrated Moving Average |
| ARMA | Auto-Regressive Moving Average |
| CI | Computational Intelligence |
| DTW | Dynamic Time Warping |
| GEFC | Global Energy Forecasting Competition |
| HSTLF | Hierarchical Short-Term Load Forecasting |
| STLF | Short-Term Load Forecasting |
| MI | Mutual Information |
| RNN | Recurrent Neural Network |
| SARIMA | Seasonal Auto-Regressive Integrated Moving Average |
| SVM | Support Vector Machine |
References
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power Systems: Forecasting, Scheduling, and Risk Management; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 498–505. [Google Scholar] [CrossRef]
- Khotanzad, A.; Afkhami-Rohani, R.; Lu, T.-L.; Abaye, A.; Davis, M.; Maratukulam, D.J. ANNSTLF-a neural-network-based electric load forecasting system. IEEE Trans. Neural Netw. 1997, 8, 835–846. [Google Scholar] [CrossRef]
- Huang, S.-J.; Shih, K.-R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations. IEEE Trans. Power Syst. 2003, 18, 673–679. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karamousantas, D.C.; Chatzarakis, G.; Katsikas, S.; Liatsis, P. Electricity demand loads modeling using AutoRegressive Moving Average (ARMA) models. Energy 2008, 33, 1353–1360. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Tong, L.-I. Forecasting time series using a methodology based on autoregressive integrated moving average and genetic programming. Knowl.-Based Syst. 2011, 24, 66–72. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Panciatici, P.; Mili, L. Electric load forecasting based on statistical robust methods. IEEE Trans. Power Syst. 2011, 26, 982–991. [Google Scholar] [CrossRef]
- Chen, B.-J.; Chang, M.-W. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Srinivasan, D. Interval type-2 fuzzy logic systems for load forecasting: A comparative study. IEEE Trans. Power Syst. 2012, 27, 1274–1282. [Google Scholar] [CrossRef]
- Fan, S.; Hyndman, R.J. Short-term load forecasting based on a semi-parametric additive model. IEEE Trans. Power Syst. 2012, 27, 134–141. [Google Scholar] [CrossRef]
- Mandal, P.; Senjyu, T.; Urasaki, N.; Funabashi, T. A neural network based several-hour-ahead electric load forecasting using similar days approach. Int. J. Electr. Power Energy Syst. 2006, 28, 367–373. [Google Scholar] [CrossRef]
- Moghram, I.; Rahman, S. Analysis and evaluation of five short-term load forecasting techniques. IEEE Trans. Power Syst. 1989, 4, 1484–1491. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Fallah, S.; Deo, R.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational intelligence approaches for energy load forecasting in smart energy management grids: state of the art, future challenges, and research directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Feinberg, E.A.; Genethliou, D. Load forecasting. In Applied Mathematics for Restructured Electric Power Systems; Springer: New York, NY, USA, 2005; pp. 269–285. [Google Scholar]
- Hong, T.; Wang, P.; White, L. Weather station selection for electric load forecasting. Int. J. Forecast. 2015, 31, 286–295. [Google Scholar] [CrossRef]
- Mu, Q.; Wu, Y.; Pan, X.; Huang, L.; Li, X. Short-term load forecasting using improved similar days method. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Dudek, G. Pattern similarity-based methods for short-term load forecasting–Part 1: Principles. Appl. Soft Comput. 2015, 37, 277–287. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-term load forecasting: similar day-based wavelet neural networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Senjyu, T.; Takara, H.; Uezato, K.; Funabashi, T. One-hour-ahead load forecasting using neural network. IEEE Trans. Power Syst. 2002, 17, 113–118. [Google Scholar] [CrossRef]
- Teeraratkul, T.; O’Neill, D.; Lall, S. Shape-based approach to household electric load curve clustering and prediction. IEEE Trans. Smart Grid 2018, 9, 5196–5206. [Google Scholar] [CrossRef]
- Iglesias, F.; Kastner, W. Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies 2013, 6, 579–597. [Google Scholar] [CrossRef]
- Seem, J.E. Pattern recognition algorithm for determining days of the week with similar energy consumption profiles. Energy Build. 2005, 37, 127–139. [Google Scholar] [CrossRef]
- Alvarez, F.M.; Troncoso, A.; Riquelme, J.C.; Ruiz, J.S.A. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using Smart Meter Data to Improve the Accuracy of Intraday Load Forecasting Considering Customer Behavior Similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Liu, C.; Jin, Z.; Gu, J.; Qiu, C. Short-term load forecasting using a long short-term memory network. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-term residential load forecasting based on resident behaviour learning. IEEE Trans. Power Syst. 2018, 33, 1087–1088. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting–a novel pooling deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Advances in Neural Information Processing Systems; 2014; pp. 3104–3112. [Google Scholar]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 7046–7051. [Google Scholar]
- Satish, B.; Swarup, K.; Srinivas, S.; Rao, A.H. Effect of temperature on short term load forecasting using an integrated ANN. Electr. Power Syst. Res. 2004, 72, 95–101. [Google Scholar] [CrossRef]
- Barman, M.; Choudhury, N.D.; Sutradhar, S. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India. Energy 2018, 145, 710–720. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Jin, C.H.; Pok, G.; Lee, Y.; Park, H.-W.; Kim, K.D.; Yun, U.; Ryu, K.H. A SOM clustering pattern sequence-based next symbol prediction method for day-ahead direct electricity load and price forecasting. Energy Convers. Manag. 2015, 90, 84–92. [Google Scholar] [CrossRef]
- Panapakidis, I.P. Clustering based day-ahead and hour-ahead bus load forecasting models. Int. J. Electr. Power Energy Syst. 2016, 80, 171–178. [Google Scholar] [CrossRef]
- Goia, A.; May, C.; Fusai, G. Functional clustering and linear regression for peak load forecasting. Int. J. Forecast. 2010, 26, 700–711. [Google Scholar] [CrossRef]
- Mori, H.; Itagaki, T. A precondition technique with reconstruction of data similarity based classification for short-term load forecasting. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 280–285. [Google Scholar]
- Verdú, S.V.; Garcia, M.O.; Senabre, C.; Marín, A.G.; Franco, F.G. Classification, filtering, and identification of electrical customer load patterns through the use of self-organizing maps. IEEE Trans. Power Syst. 2006, 21, 1672–1682. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice. 2018. Available online: https://otexts.org/fpp2/ (accessed on 28 November 2018).
- Lusis, P.; Khalilpour, K.R.; Andrew, L.; Liebman, A. Short-term residential load forecasting: Impact of calendar effects and forecast granularity. Appl. Energy 2017, 205, 654–669. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A strategy for short-term load forecasting by support vector regression machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Espinoza, M.; Joye, C.; Belmans, R.; De Moor, B. Short-term load forecasting, profile identification, and customer segmentation: a methodology based on periodic time series. IEEE Trans. Power Syst. 2005, 20, 1622–1630. [Google Scholar] [CrossRef]
- May, R.; Dandy, G.; Maier, H. Review of input variable selection methods for artificial neural networks. Artificial Neural Networks-Methodological Advances and Biomedical Applications. 2011. Available online: https://www.intechopen.com/ (accessed on 28 November 2018).
- Koprinska, I.; Rana, M.; Agelidis, V.G. Correlation and instance based feature selection for electricity load forecasting. Knowl.-Based Syst. 2015, 82, 29–40. [Google Scholar] [CrossRef]
- Nedellec, R.; Cugliari, J.; Goude, Y. GEFCom2012: Electric load forecasting and backcasting with semi-parametric models. Int. J. Forecast. 2014, 30, 375–381. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Y.; Xie, L.; Liu, D.; Huang, J. A hybrid model based on selective ensemble for energy consumption forecasting in China. Energy 2018, 159, 534–546. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based feature selection of discrete and numeric class machine learning. In Proceedings of the Seventeenth International Conference on Machine Learning, San Francisco, CA, USA, 29 June–2 July 2000. [Google Scholar]
- Kouhi, S.; Keynia, F.; Ravadanegh, S.N. A new short-term load forecast method based on neuro-evolutionary algorithm and chaotic feature selection. Int. J. Electr. Power Energy Syst. 2014, 62, 862–867. [Google Scholar] [CrossRef]
- Estévez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized mutual information feature selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Cao, Y. Mutual information and non-fixed ANNs for daily peak load forecasting. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1523–1527. [Google Scholar]
- Elattar, E.E.; Goulermas, J.; Wu, Q.H. Electric load forecasting based on locally weighted support vector regression. IEEE Trans. Syst. Man Cybern. Part C 2010, 40, 438–447. [Google Scholar] [CrossRef]
- Wi, Y.-M.; Joo, S.-K.; Song, K.-B. Holiday load forecasting using fuzzy polynomial regression with weather feature selection and adjustment. IEEE Trans. Power Syst. 2012, 27, 596. [Google Scholar] [CrossRef]
- Schaffernicht, E.; Gross, H.-M. Weighted mutual information for feature selection. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 181–188. [Google Scholar]
- Reis, A.R.; Da Silva, A.A. Feature extraction via multiresolution analysis for short-term load forecasting. IEEE Trans. Power Syst. 2005, 20, 189–198. [Google Scholar]
- Amjady, N.; Keynia, F. Short-term load forecasting of power systems by combination of wavelet transform and neuro-evolutionary algorithm. Energy 2009, 34, 46–57. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T.; Chiong, R. Hybrid filter–wrapper feature selection for short-term load forecasting. Eng. Appl. Artif. Intell. 2015, 40, 17–27. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Lin, S.-W.; Ying, K.-C.; Chen, S.-C.; Lee, Z.-J. Particle swarm optimization for parameter determination and feature selection of support vector machines. Expert Syst. Appl. 2008, 35, 1817–1824. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Xiong, T. Comprehensive learning particle swarm optimization based memetic algorithm for model selection in short-term load forecasting using support vector regression. Appl. Soft Comput. 2014, 25, 15–25. [Google Scholar] [CrossRef]
- Amjady, N.; Keynia, F.; Zareipour, H. Short-term load forecast of microgrids by a new bilevel prediction strategy. IEEE Trans. Smart Grid 2010, 1, 286–294. [Google Scholar] [CrossRef]
- Sheikhan, M.; Mohammadi, N. Neural-based electricity load forecasting using hybrid of GA and ACO for feature selection. Neural Comput. Appl. 2012, 21, 1961–1970. [Google Scholar] [CrossRef]
- Liang, Y.; Niu, D.; Hong, W.-C. Short term load forecasting based on feature extraction and improved general regression neural network model. Energy 2019, 166, 653–663. [Google Scholar] [CrossRef]
- Santos, P.; Martins, A.; Pires, A. Designing the input vector to ANN-based models for short-term load forecast in electricity distribution systems. Int. J. Electr. Power Energy Syst. 2007, 29, 338–347. [Google Scholar] [CrossRef]
- Ghadimi, N.; Akbarimajd, A.; Shayeghi, H.; Abedinia, O. Two stage forecast engine with feature selection technique and improved meta-heuristic algorithm for electricity load forecasting. Energy 2018, 161, 130–142. [Google Scholar] [CrossRef]
- Hong, W.-C.; Dong, Y.; Lai, C.-Y.; Chen, L.-Y.; Wei, S.-Y. SVR with hybrid chaotic immune algorithm for seasonal load demand forecasting. Energies 2011, 4, 960–977. [Google Scholar] [CrossRef]
- Hu, Z.; Bao, Y.; Chiong, R.; Xiong, T. Mid-term interval load forecasting using multi-output support vector regression with a memetic algorithm for feature selection. Energy 2015, 84, 419–431. [Google Scholar] [CrossRef]
- Swarup, K.S.; Satish, B. Integrated ANN approach to forecast load. IEEE Comput. Appl. Power 2002, 15, 46–51. [Google Scholar] [CrossRef]
- Khotanzad, A.; Afkhami-Rohani, R.; Maratukulam, D. ANNSTLF-artificial neural network short-term load forecaster-generation three. IEEE Trans. Power Syst. 1998, 13, 1413–1422. [Google Scholar] [CrossRef]
- Kalaitzakis, K.; Stavrakakis, G.; Anagnostakis, E. Short-term load forecasting based on artificial neural networks parallel implementation. Electr. Power Syst. Res. 2002, 63, 185–196. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Zhao, T. Using Quadratic Programming to Optimally Adjust Hierarchical Load Forecasting. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Sun, X.; Luh, P.B.; Cheung, K.W.; Guan, W.; Michel, L.D.; Venkata, S.; Miller, M.T. An efficient approach to short-term load forecasting at the distribution level. IEEE Trans. Power Syst. 2016, 31, 2526–2537. [Google Scholar] [CrossRef]
- Hong, T.; Shahidehpour, M. Load Forecasting Case Study; EISPC, US Department of Energy: Washington, DC, USA, 2015.
- Capasso, A.; Grattieri, W.; Lamedica, R.; Prudenzi, A. A bottom-up approach to residential load modeling. IEEE Trans. Power Syst. 1994, 9, 957–964. [Google Scholar] [CrossRef]
- Stephen, B.; Tang, X.; Harvey, P.R.; Galloway, S.; Jennett, K.I. Incorporating practice theory in sub-profile models for short term aggregated residential load forecasting. IEEE Trans. Smart Grid 2017, 8, 1591–1598. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Ahmed, R.A.; Athanasopoulos, G.; Shang, H.L. Optimal combination forecasts for hierarchical time series. Comput. Stat. Data Anal. 2011, 55, 2579–2589. [Google Scholar] [CrossRef]
- Gamakumara, P.; Panagiotelis, A.; Athanasopoulos, G.; Hyndman, R.J. Probabilistic Forecasts in Hierarchical Time Series; Monash University: Melbourne, Australia, 2018. [Google Scholar]
- Nose-Filho, K.; Lotufo, A.D.P.; Minussi, C.R. Short-term multinodal load forecasting using a modified general regression neural network. IEEE Trans. Power Deliv. 2011, 26, 2862–2869. [Google Scholar] [CrossRef]
- Fan, S.; Methaprayoon, K.; Lee, W.-J. Multiregion load forecasting for system with large geographical area. IEEE Trans. Ind. Appl. 2009, 45, 1452–1459. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Sun, M.; Kang, C.; Xia, Q. An ensemble forecasting method for the aggregated load with sub profiles. IEEE Trans. Smart Grid 2018, 9, 3906–3908. [Google Scholar] [CrossRef]
- Yang, Y. Combining forecasting procedures: some theoretical results. Econ. Theory 2004, 20, 176–222. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S. Global energy forecasting competition 2012. Int. J. Forecast. 2014, 30, 357–363. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y.; Hong, T.; Laing, T.D. Relative humidity for load forecasting models. IEEE Trans. Smart Grid 2018, 9, 191–198. [Google Scholar] [CrossRef]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging on sister forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Charlton, N.; Singleton, C. A refined parametric model for short term load forecasting. Int. J. Forecast. 2014, 30, 364–368. [Google Scholar] [CrossRef]
- Lloyd, J.R. GEFCom2012 hierarchical load forecasting: Gradient boosting machines and Gaussian processes. Int. J. Forecast. 2014, 30, 369–374. [Google Scholar] [CrossRef]
- Taieb, S.B.; Hyndman, R.J. A gradient boosting approach to the Kaggle load forecasting competition. Int. J. Forecast. 2014, 30, 382–394. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Kikusato, H.; Yoshizawa, S.; Kawano, S.; Yoshida, A.; Wakao, S.; Murata, N.; Amano, Y.; Tanabe, S.-i.; Hayashi, Y. Distributed energy management for comprehensive utilization of residential photovoltaic outputs. IEEE Trans. Smart Grid 2018, 9, 1216–1227. [Google Scholar] [CrossRef]
| Paper | Method | Formulae | Parameters |
|---|---|---|---|
| [21] | Euclidean distance minimization | (1) | θ: historical days f: forecast day i: historical day in θ : weather factor under consideration |
| [12,22] | Weighted Euclidean distance minimization | (2) | : deviation of load of forecast day and historical day : deviation of slope between load on forecast day and load of historical day : deviation of temperature between forecast day and historical day : Weight factor |
| Method | Publications | Technique |
|---|---|---|
| Similar-Pattern Method | ||
| [12,20,21,22,23,35,36] | similar day | |
| [24,25,26,27,37,38,39,40,41] | pattern-sequence | |
| [28,29,30,31,32,33,34] | sequence learning |
| Publication | Technique |
|---|---|
| [11,48,49] | Stepwise |
| [57,58] | Filter |
| [3,9,47,51,65,66] | Correlation |
| [47,53,54,55,67] | Mutual Information |
| [60,61,62,63,64,68,69] | Optimization Algorithms |
| Combination Method | Formulae | Parameters |
|---|---|---|
| Linear Programming | : base forecast : adjusted forecast : weight factor | |
| Quadratic Programming | : base forecast : adjusted forecast : load of the aggregated level : Load of the disaggregated level : participation factor |
| Method | Advantages | Disadvantages |
|---|---|---|
| Similar-Pattern Method |
|
|
| Variable Selection Method |
|
|
| Hierarchical Method |
|
|
| Weather Station Selection |
|
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K.-w. Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies 2019, 12, 393. https://doi.org/10.3390/en12030393
Fallah SN, Ganjkhani M, Shamshirband S, Chau K-w. Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies. 2019; 12(3):393. https://doi.org/10.3390/en12030393
Chicago/Turabian StyleFallah, Seyedeh Narjes, Mehdi Ganjkhani, Shahaboddin Shamshirband, and Kwok-wing Chau. 2019. "Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview" Energies 12, no. 3: 393. https://doi.org/10.3390/en12030393
APA StyleFallah, S. N., Ganjkhani, M., Shamshirband, S., & Chau, K.-w. (2019). Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies, 12(3), 393. https://doi.org/10.3390/en12030393






