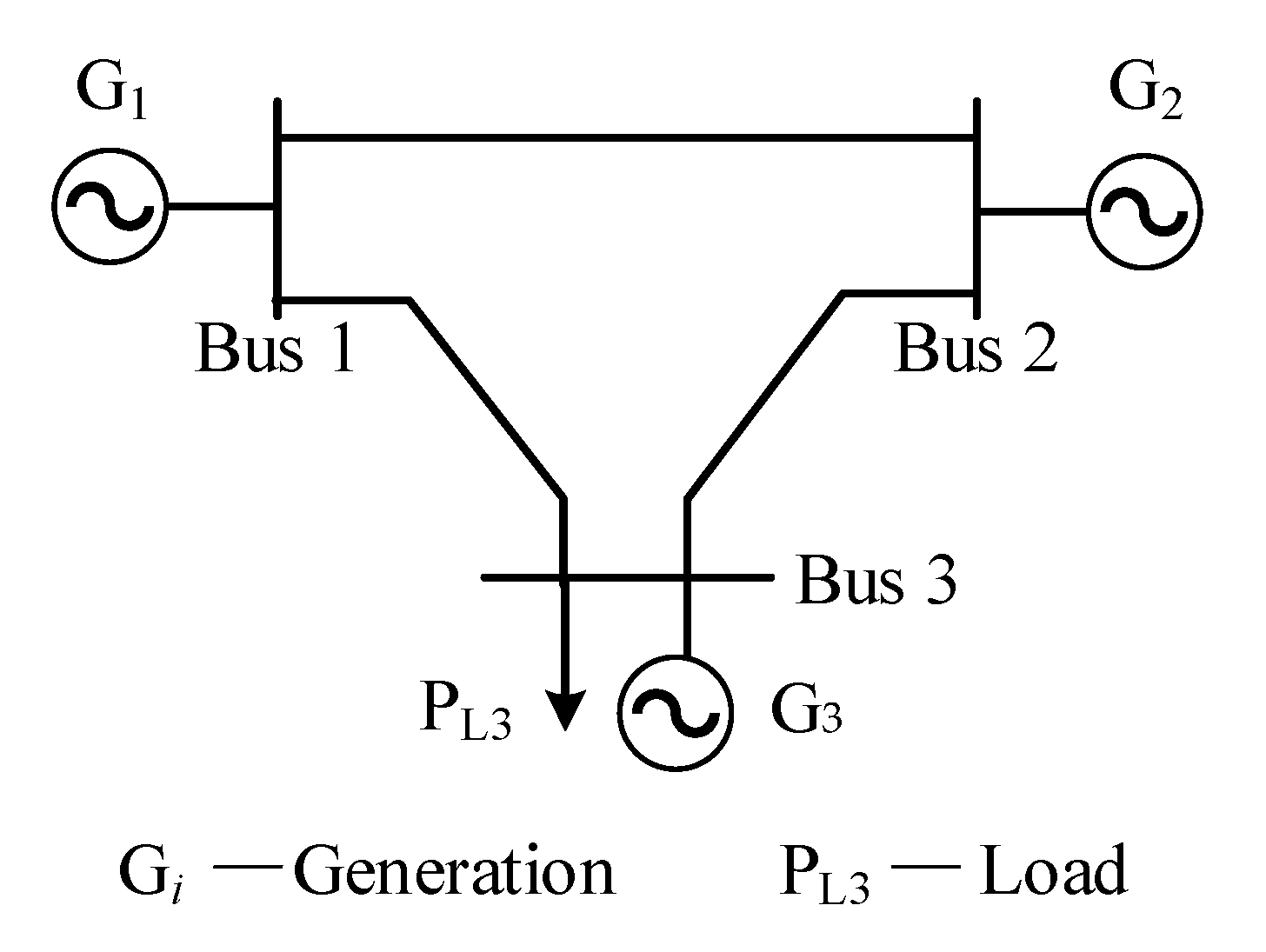
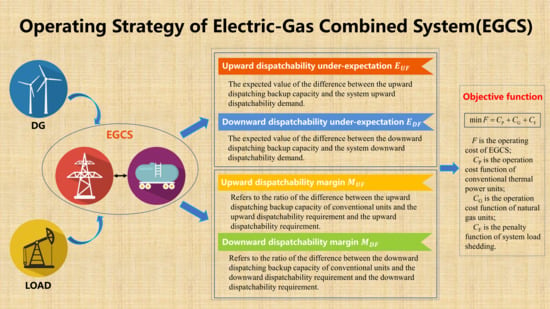
3.3. Evaluation Index of Dispatchability on EGCS
The dispatchability indexes of the traditional power system usually include parameters such as adjustable power range, output, or load regulation rate. For EGCS, the concept of dispatchability can be analogized, and the supply and demand of dispatchability of power side, network side, and load side can be quantitatively analyzed.
(1) Dispatchability analysis of conventional power
The conventional power included in the EGCS studied in this paper include thermal power units and gas units, which are the main dispatching supply resources in the system. The upward/downward dispatchability is respectively
FG+ and
FG−, as shown in Equations (7) and (8):
where
PG is the real-time output of the unit.
PGmax and
PGmin are, respectively, the maximum and minimum output of the unit.
The sum of Equations (7) and (8) can obtain the total amount of dispatching resources
FG that can be provided by conventional units, as shown in Equation (9):
(2) ispatchability analysis of distributed energy
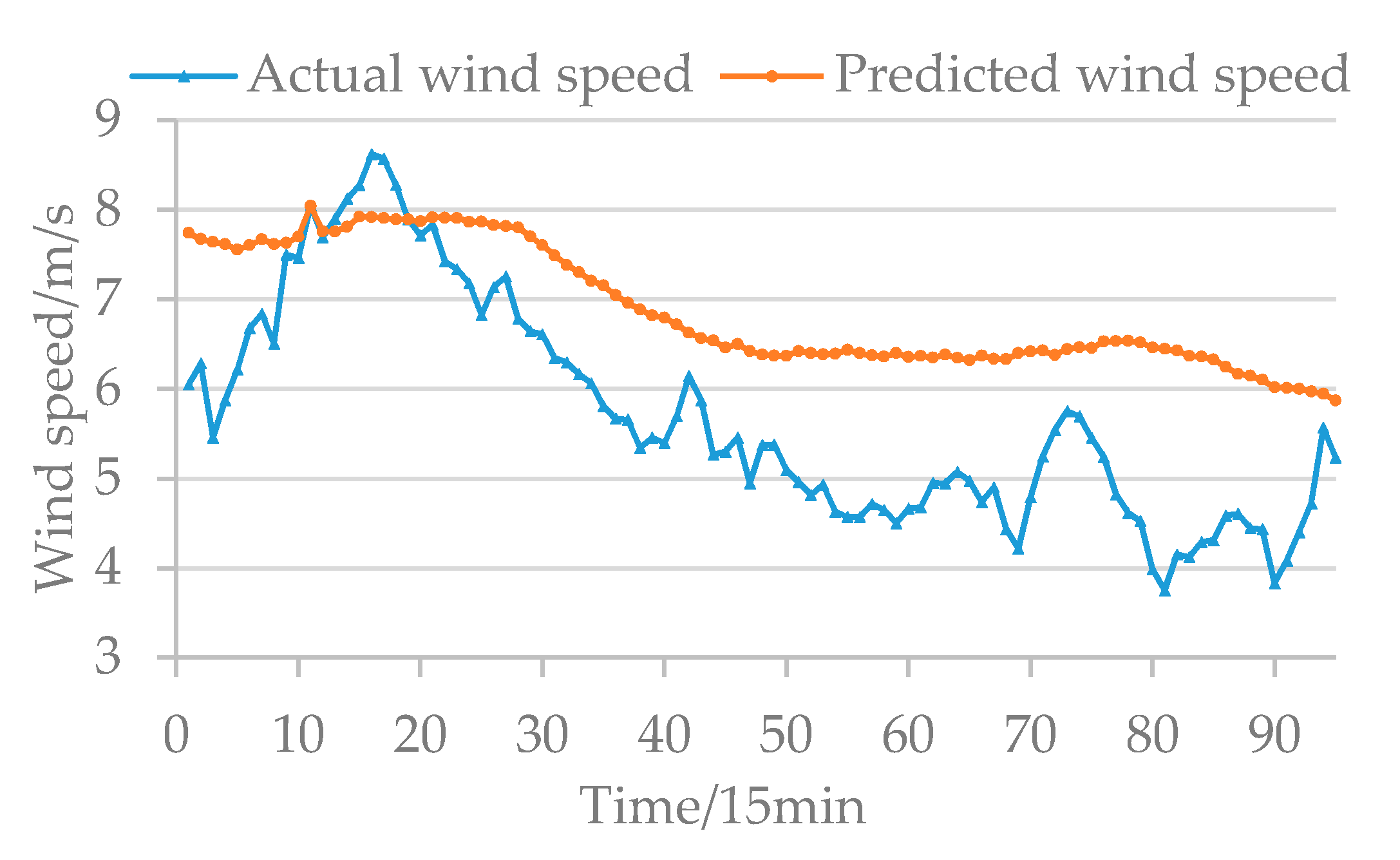
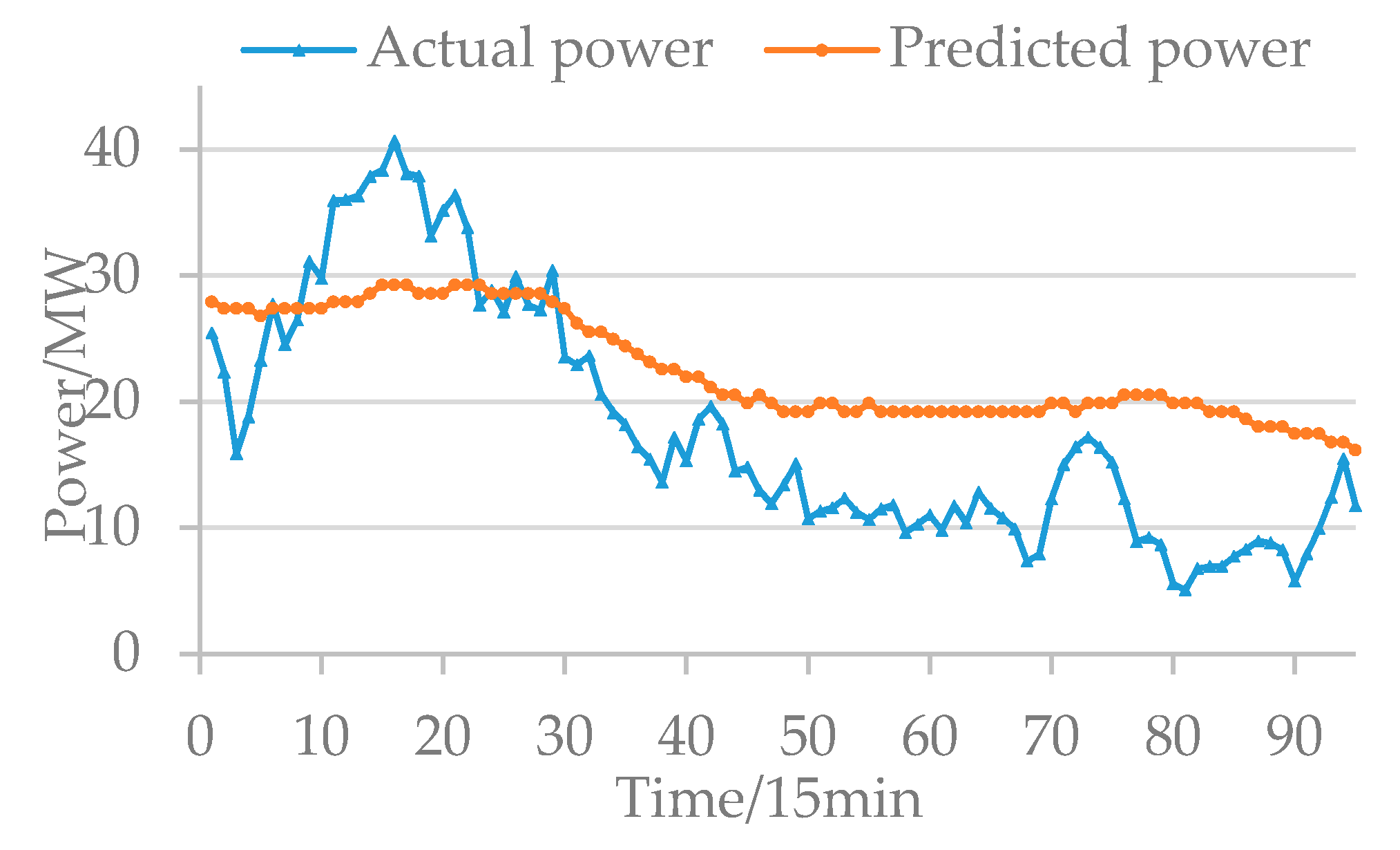
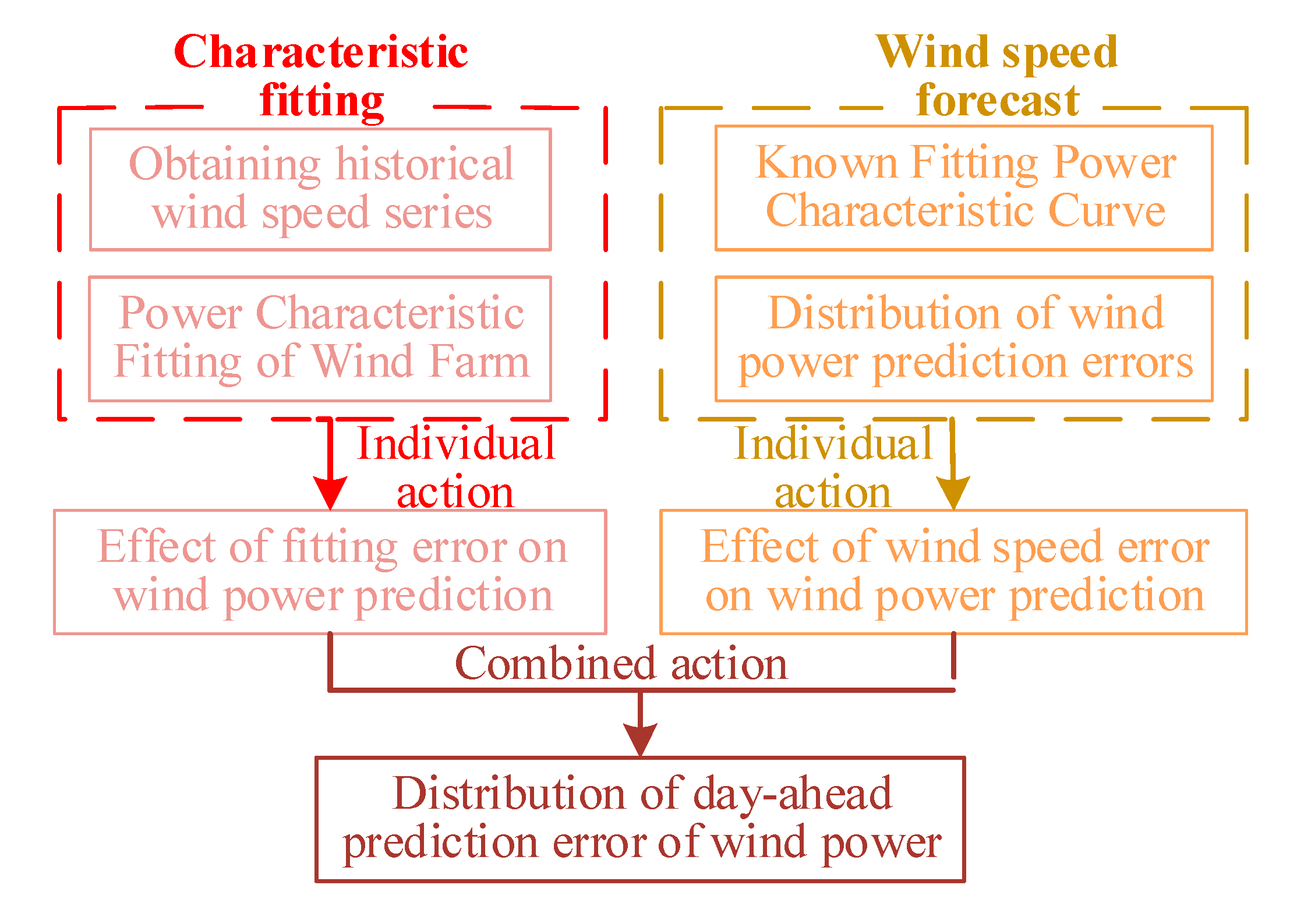
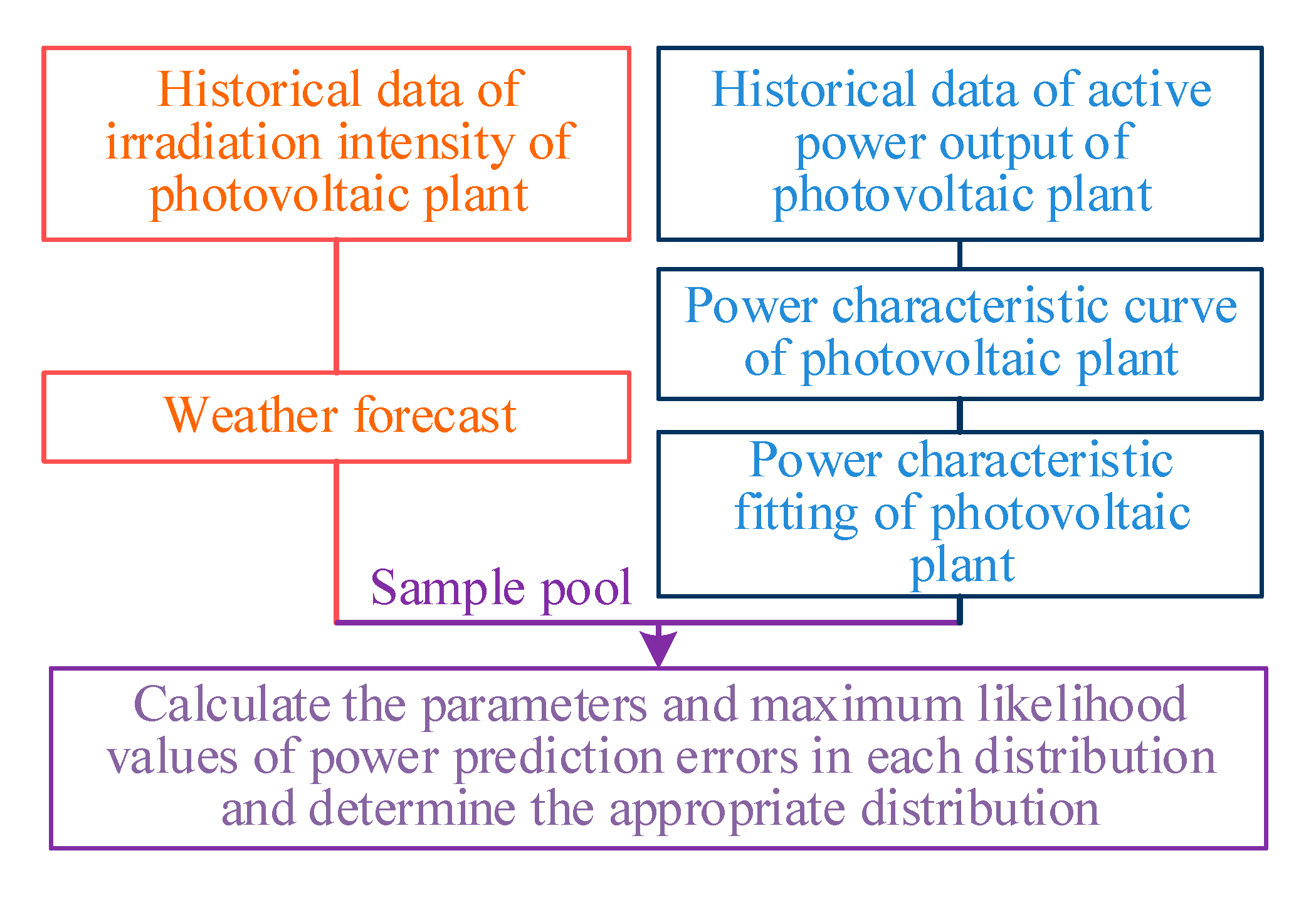
Distributed energy such as wind and photovoltaic cannot be as stable and controllable as conventional power. Therefore, in the process of power balance, the output of the distributed energy is equivalent to the conventional power according to the given confidence capacity, while the remaining part is the un confidence capacity caused by the prediction error, which consumes the dispatchable resources. Therefore, the dispatching resources that are provided and consumed are as shown Equations (10) and (11):
where
Fres,t is the dispatchability that renewable energy can provide in
tth period.
Pcl,t is the confidence capacity. in
tth period.
Dres,t is the dispatchability of renewable energy consumption in
tth period.
Pres,t is the output power of renewable energy in
tth period.
(3) Dispatchability analysis of controllable load
The controllable load can be regarded as a “conventional power” on the load side because of the load’s ability to be artificially adjusted. The dispatchability provided can be calculated according to Equation (9).
(4) Dispatchability analysis of uncontrollable load
The uncontrollable load is a resource that consumes dispatchability. Usually, the system will reserve a part of the backup capacity according to the historical maximum load when setting up the start-up mode, and the backup coefficient will be expressed as
µ. The load’s demand for dispatching resources is shown in Equation (12):
where
Dload is the dispatchability of uncontrollable load consumption.
Pload,max and
Pload,min are, respectively, peak and valley values of day-ahead load forecasting.
(5) Dispatchability analysis of network side energy conversion
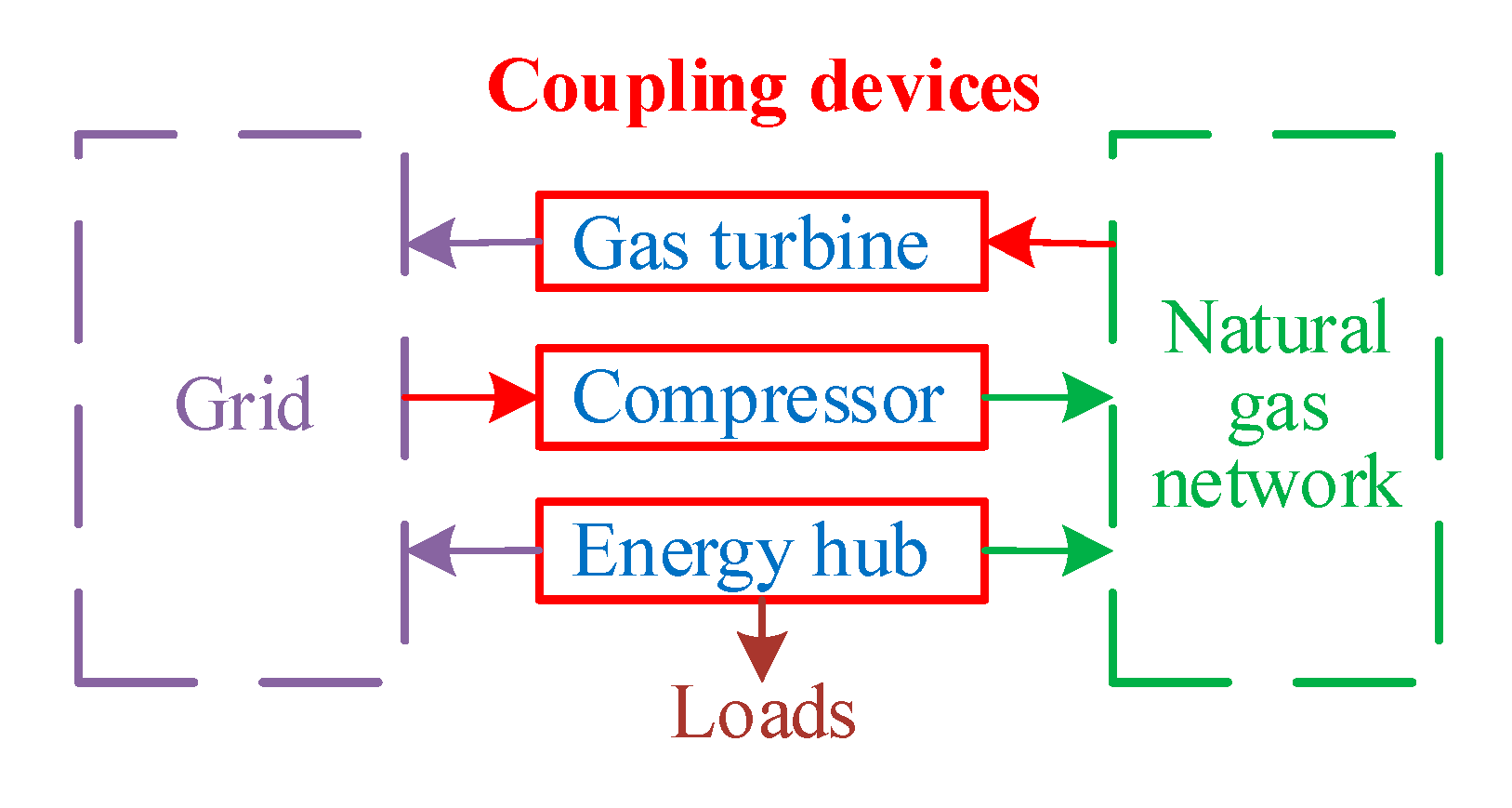
There are different types of energy conversion on the network side of EGCS. Take P2G as an example. When the natural gas capacity in the network is insufficient and the electricity is surplus, the energy can be converted to natural gas through the energy conversion device. At this time, power can be regarded as the source side energy. The power’s dispatchability analysis is similar to the conventional power dispatchability analysis, there is a problem of energy conversion efficiency because the network side energy conversion is a conversion between different energy sources. Therefore, the dispatchability calculation of network side energy conversion in the link of P2G is shown in Equation (13).
where
FP2G is the dispatchability of P2G devices.
ηP2G is the energy conversion efficiency of P2G devices.
PP2G is the electric power input to P2G devices.
CP2G is the natural gas power output by P2G devices.
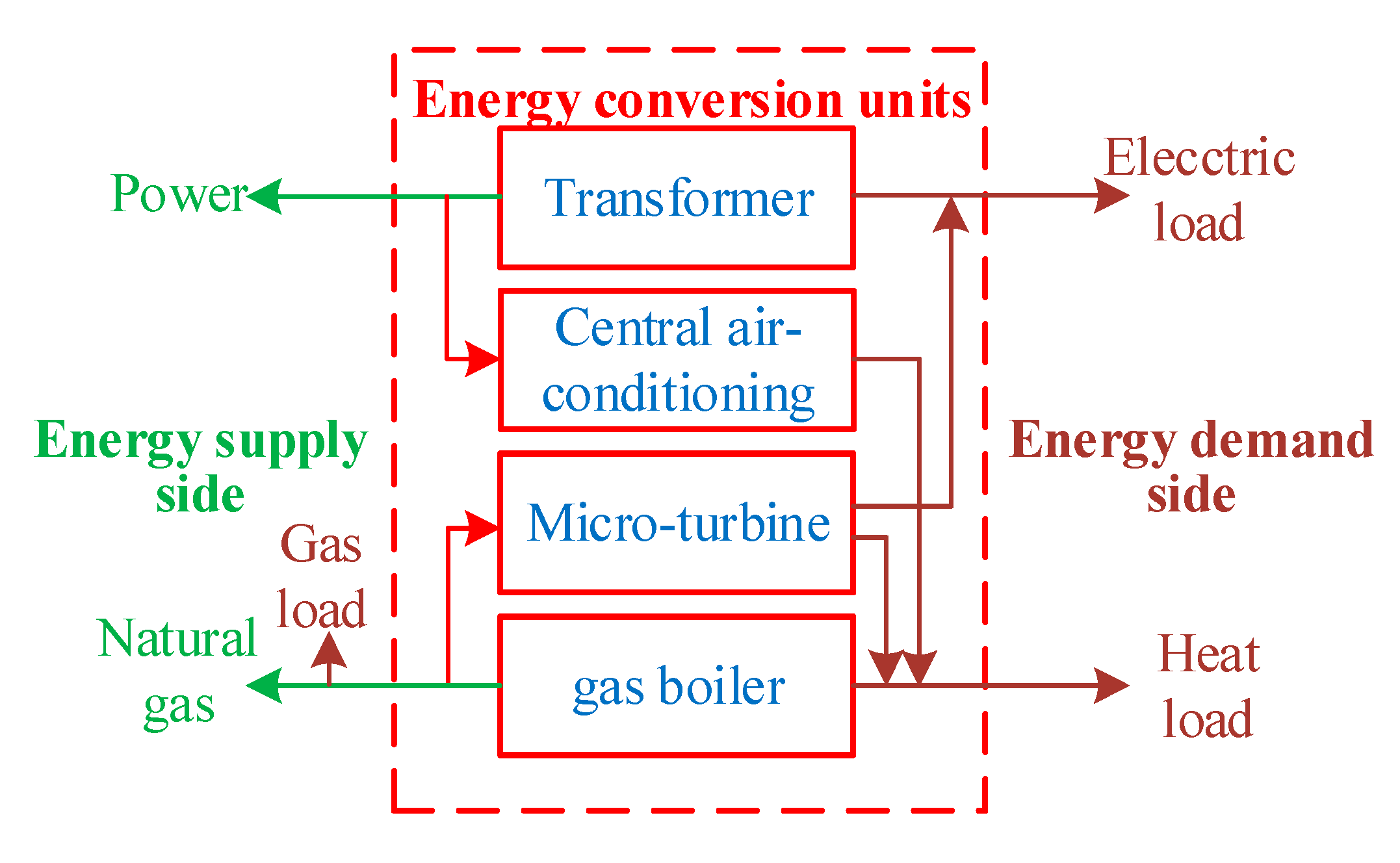
The controllable load and uncontrollable load mentioned in this paper include electric load, gas load, and heat load. Since the studied network is a grid and natural gas network, the heat load is equivalent to electric load and gas load.
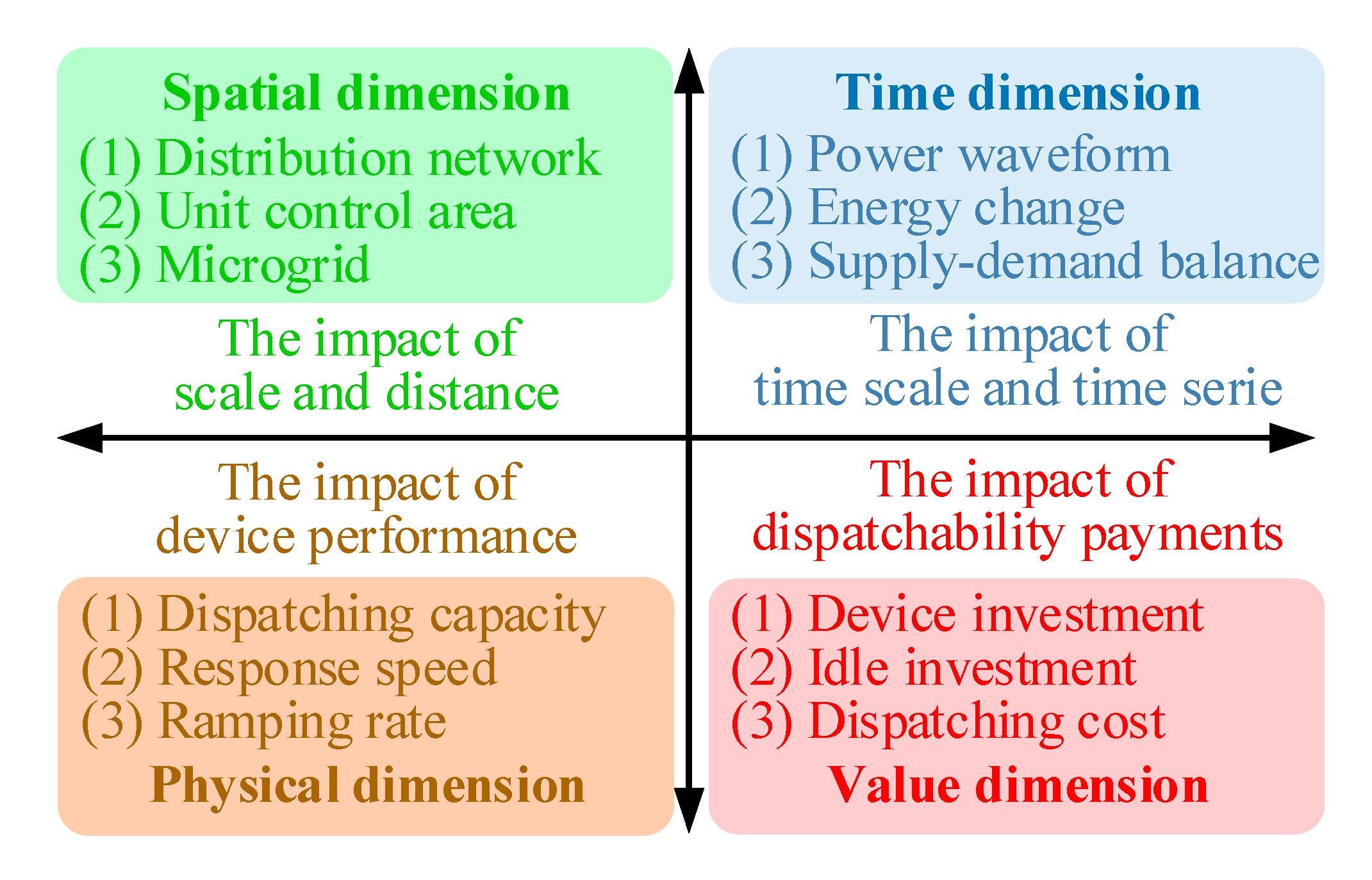
According to the multi-dimensional attributes of dispatchability and the quantitative analysis of dispatchability of different types of resources, various factors that need to be considered in establishing the EGCS dispatchability indexes can be obtained as shown in
Table 1.
As shown in
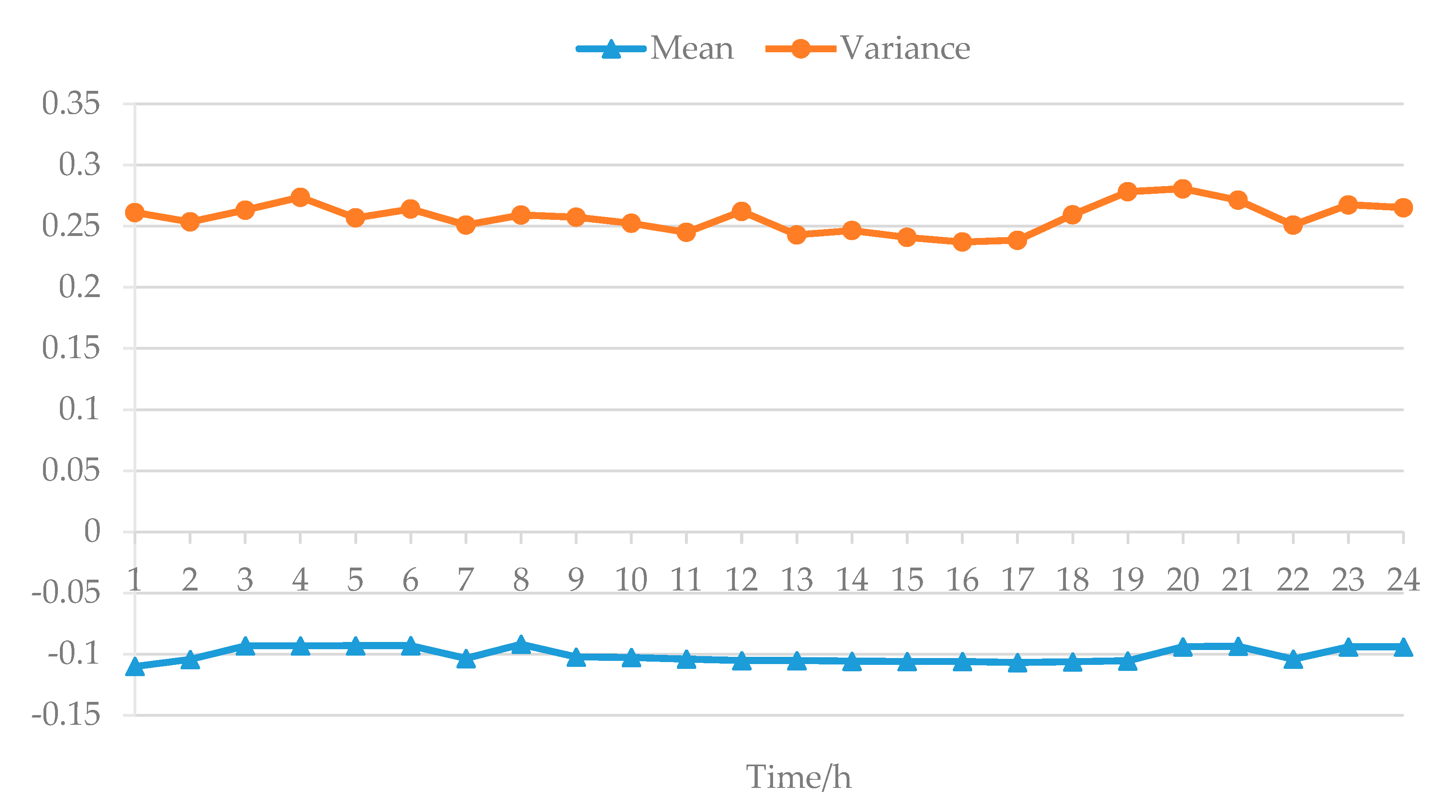
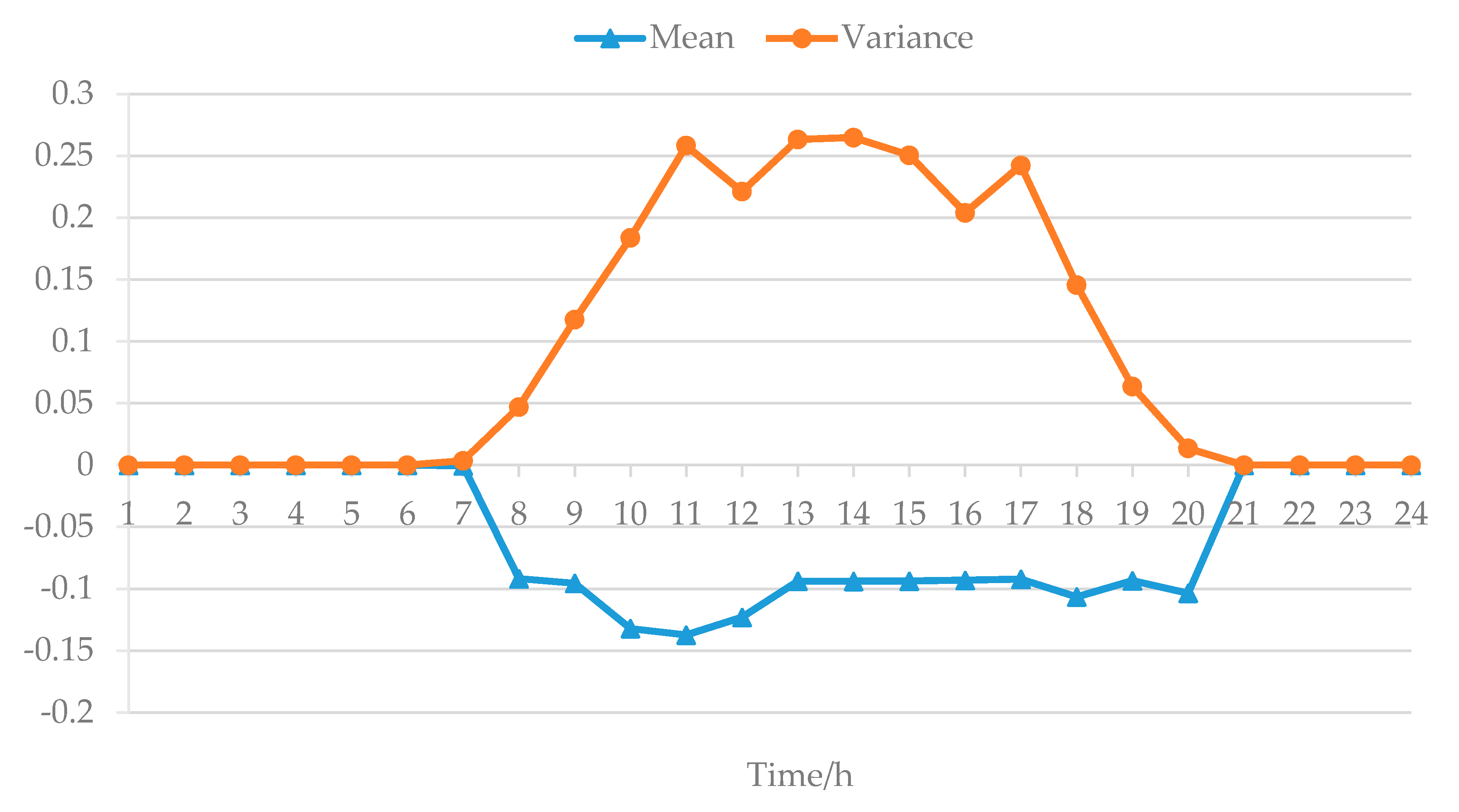
Table 1, electricity balance and flow balance are the prerequisites for the secure and stable operation of the grid and natural gas network, and they must be met. Therefore, they are regarded as constraint conditions of dispatching model. The ramping rate and energy conversion efficiency of units are inherent characteristics of EGCS dispatchability, which cannot be changed after being put into operation. Therefore, they exist as general parameters in the calculation of dispatchability index or constraints. The value dimension parameters can be used as the objective function of the dispatching model to evaluate the dispatchability of the system from the economic point of view. Most importantly, due to the influence of natural factors and prediction errors, the output of wind turbines and photovoltaic units will be uncertain in time scale. At the same time, the available regulating capacity of conventional units will fluctuate with the switching state on time scale. These factors will directly affect the system’s upward and downward ability in the dispatching stage; that is, the factors have a great impact on the system’s dispatchability. Moreover, the natural gas network is an inertial system, while the grid is a real-time system. Therefore, this paper uses natural gas system to regulate the power system. Considering the capacity of coordinated dispatching of conventional thermal power units, gas generating units, distributed wind, and photovoltaic units in the 24-h operation phase of EGCS, the random variation of load is also considered. Four dispatchability evaluation indexes are proposed.
Index 1: Upward dispatchability under-expectation
EUF, is the expected value of the difference between the upward dispatching backup capacity and the system upward dispatchability demand in the system during the operation cycle.
EUF reflects the average value of the system’s failure to replenish resources when the consumption of dispatching resources increases, and the smaller the value, the better.
where
RUF,t is the upward dispatching backup capacity available for the system in
tth period.
PL.net,t and
PL,net,t+1 are, respectively, the net load in
tth and (
t+1)th period.
NG is the total amount of natural gas units in the system.
is the upper limit of the active power output of the
ith conventional unit in
tth period.
is the actual active output of the
ith conventional unit in
tth period.
is the upward ramping rate of the
ith conventional unit.
is the dispatching interval.
Index 2: Downward dispatchability under-expectation
EDF, is the expected value of the difference between the downward dispatching backup capacity and the system downward dispatchability demand in the system during the operation cycle.
EDF is reflected that when the resource that consumes dispatchability is reduced, the system cannot cut out the average value of supplied resources due to inertia and other problems, and the smaller the value, the better.
where
RDF,t is the downward dispatching backup capacity available for the system in
tth period.
is the lower limit of the active power output of the
ith conventional unit in
tth period.
is the downward ramping rate of the
ith conventional unit.
Index 3: Upward dispatchability margin,
MUF, refers to the ratio of the difference between the upward dispatching backup capacity of conventional units and the upward dispatchability requirement of the system and the upward dispatchability requirement of the system during the operation period.
MUF reflects the adequacy level of dispatching resources that the system can provide when the increase in resources that consume dispatchability; the greater the value, the better.
where
FUF,t is the system’s upward dispatchability requirement in
tth period.
is the predicted output power of the
wth DG unit W in
tth period.
NDG is the total amount of DG units.
is the actual output power of the
wth DG unit W in
tth period.
Index 4: Downward dispatchability margin
MDF, refers to the ratio of the difference between the downward dispatching backup capacity of conventional units and the downward dispatchability requirement of the system and the downward dispatchability requirement of the system during the operation period.
MDF reflects the adequacy level of dispatching resources that the system can cut when the decrease in resources that consume dispatchability; the greater the value, the better.
where
FDF,t is the system’s downward dispatchability requirement in
tth period.
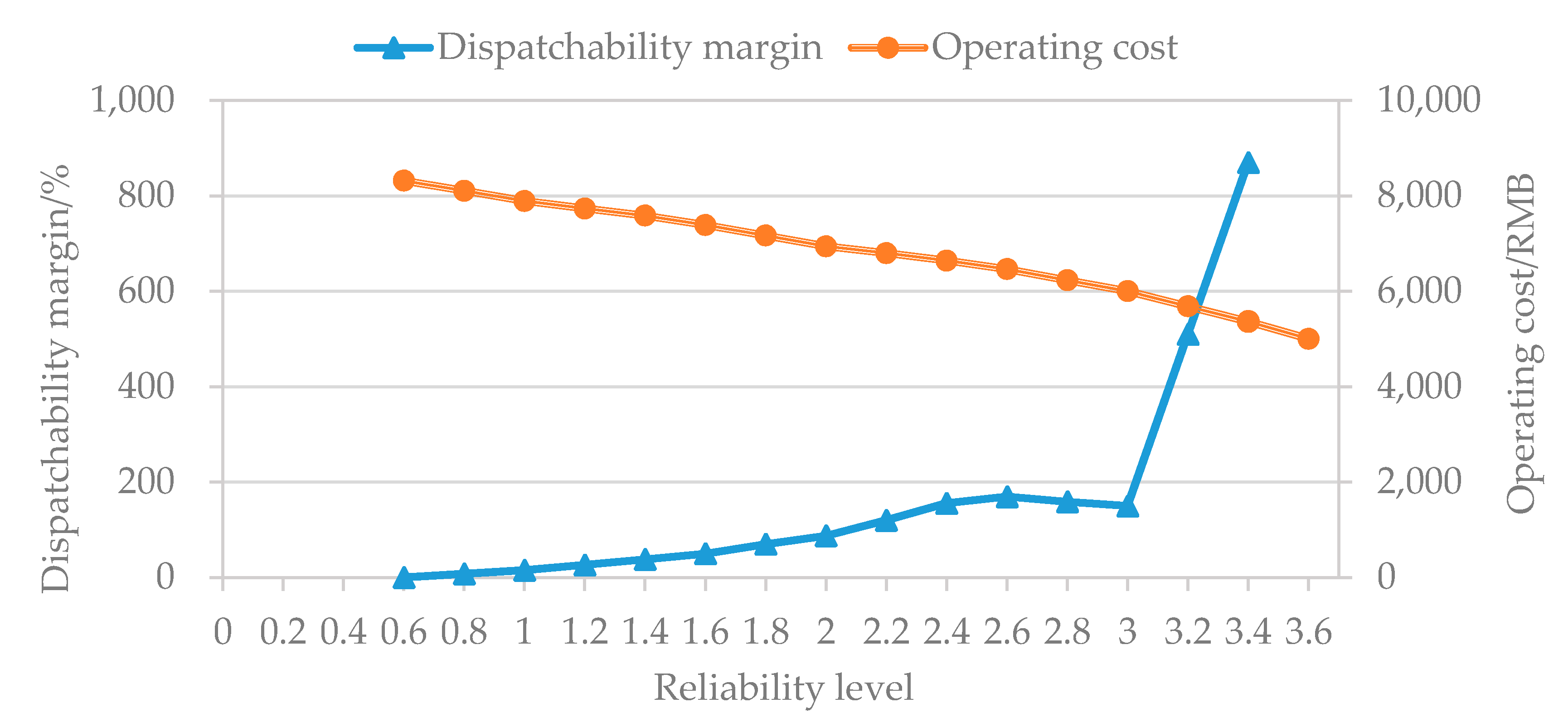
The system operation must satisfy certain reliability. The above indexes 3 and 4 can indicate the reliability level of the system. However, due to the uncertain factors in the system, the current EGCS should try to achieve the optimal economy under the premise of ensuring the reliability of the system operation.