An Adiabatic Coaxial Line for Microcalorimeter Power Measurements in Wireless Communication for Smart Grid †
Abstract
1. Introduction
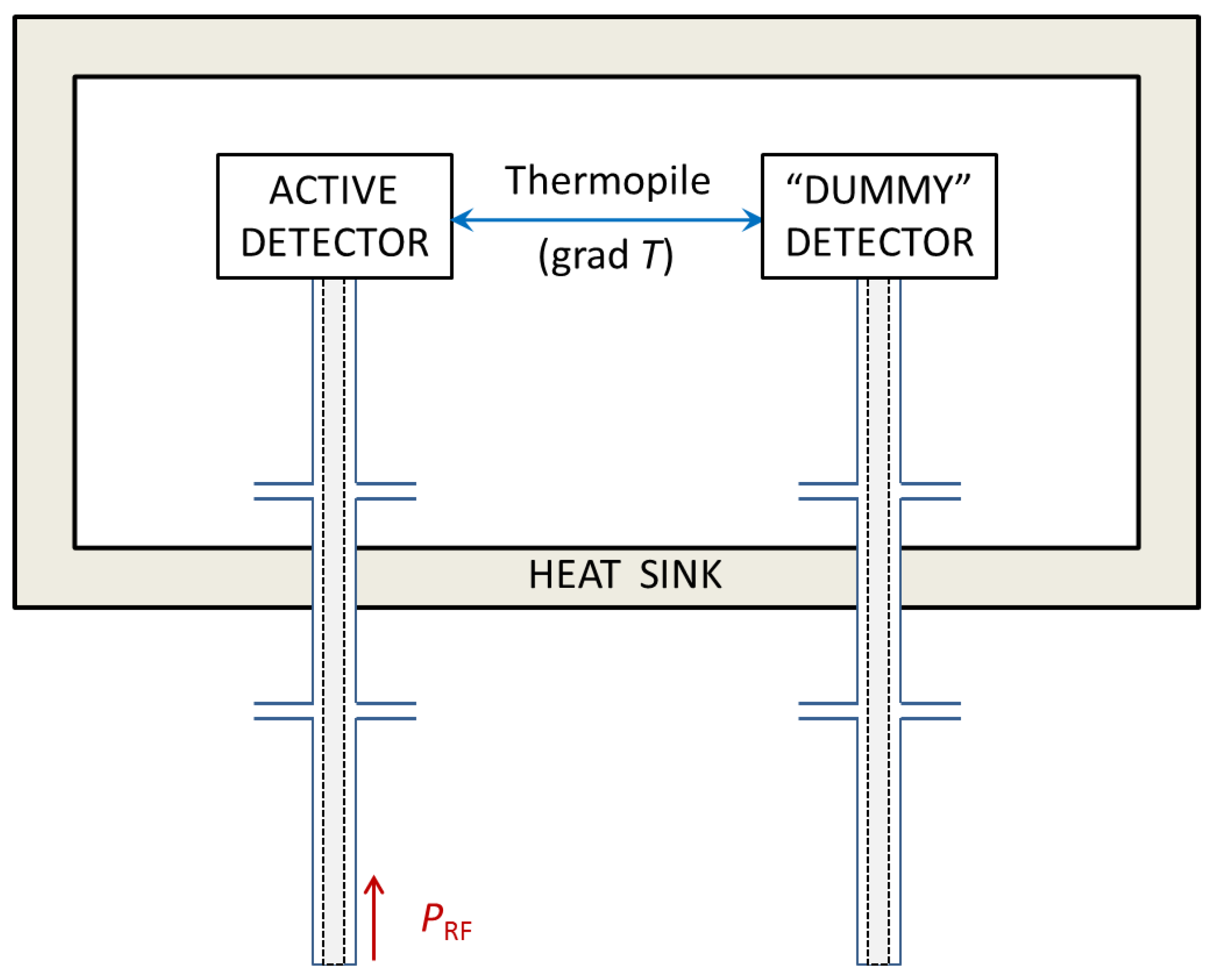
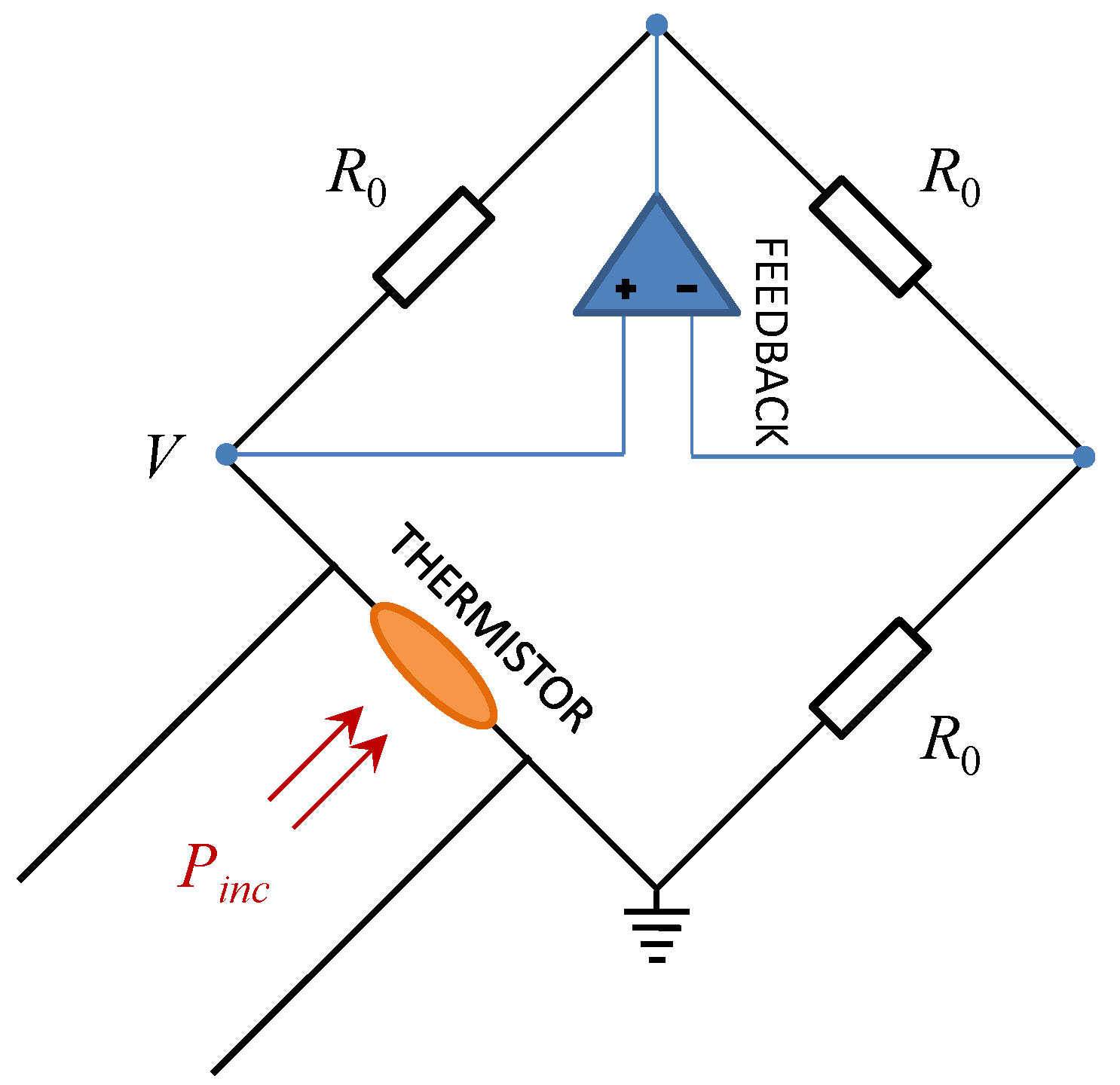
2. The Microcalorimeter Power Measurement
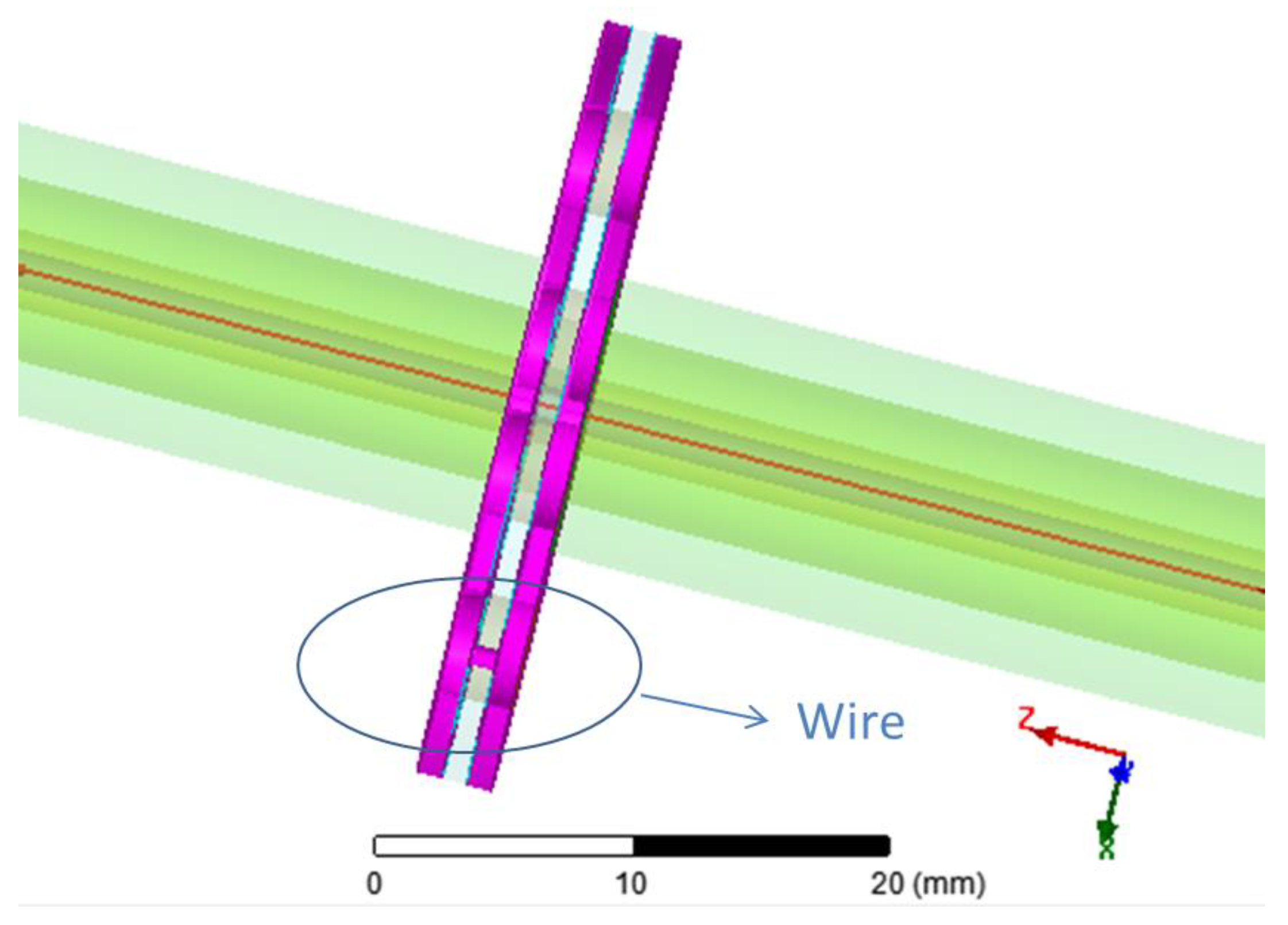
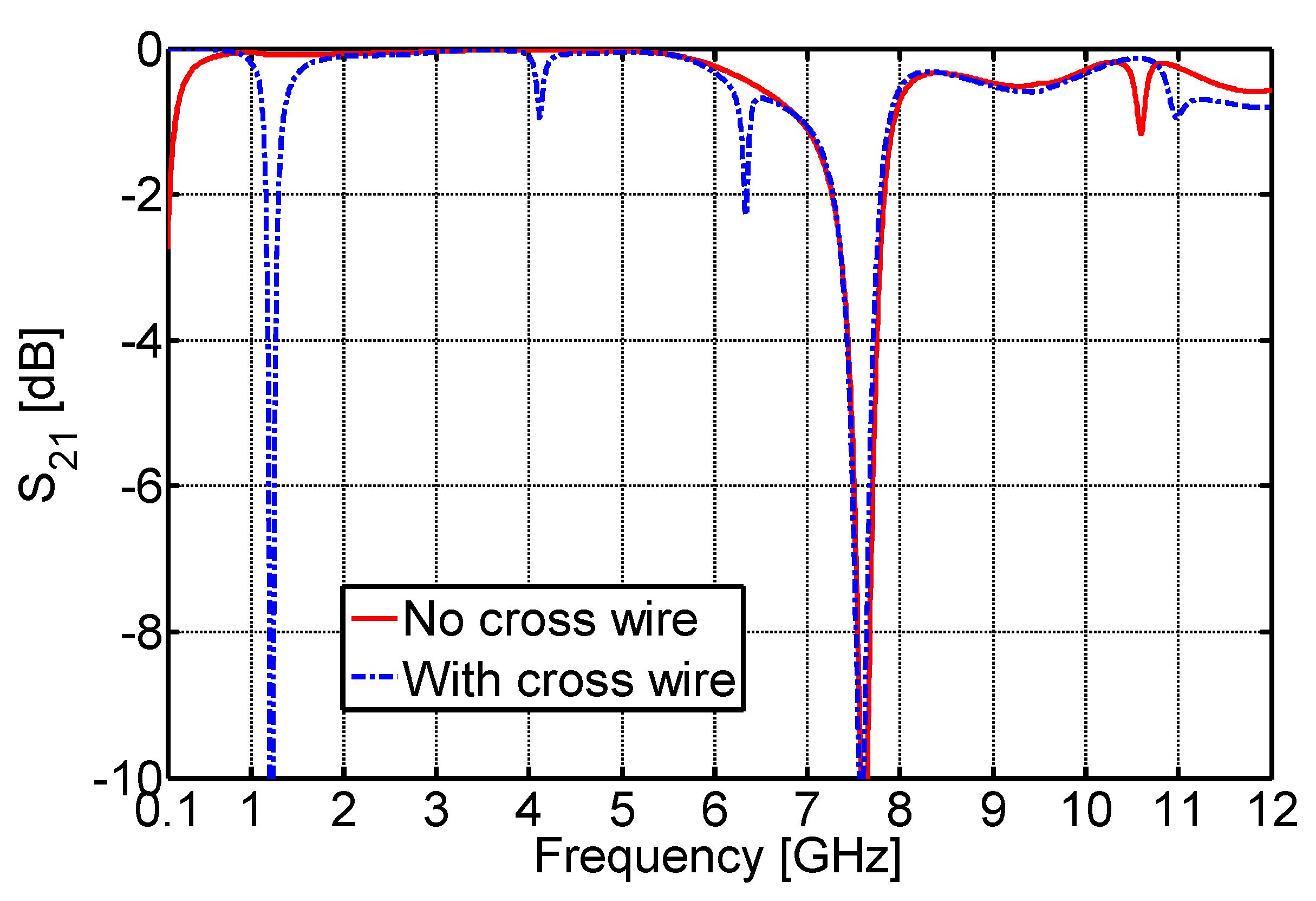
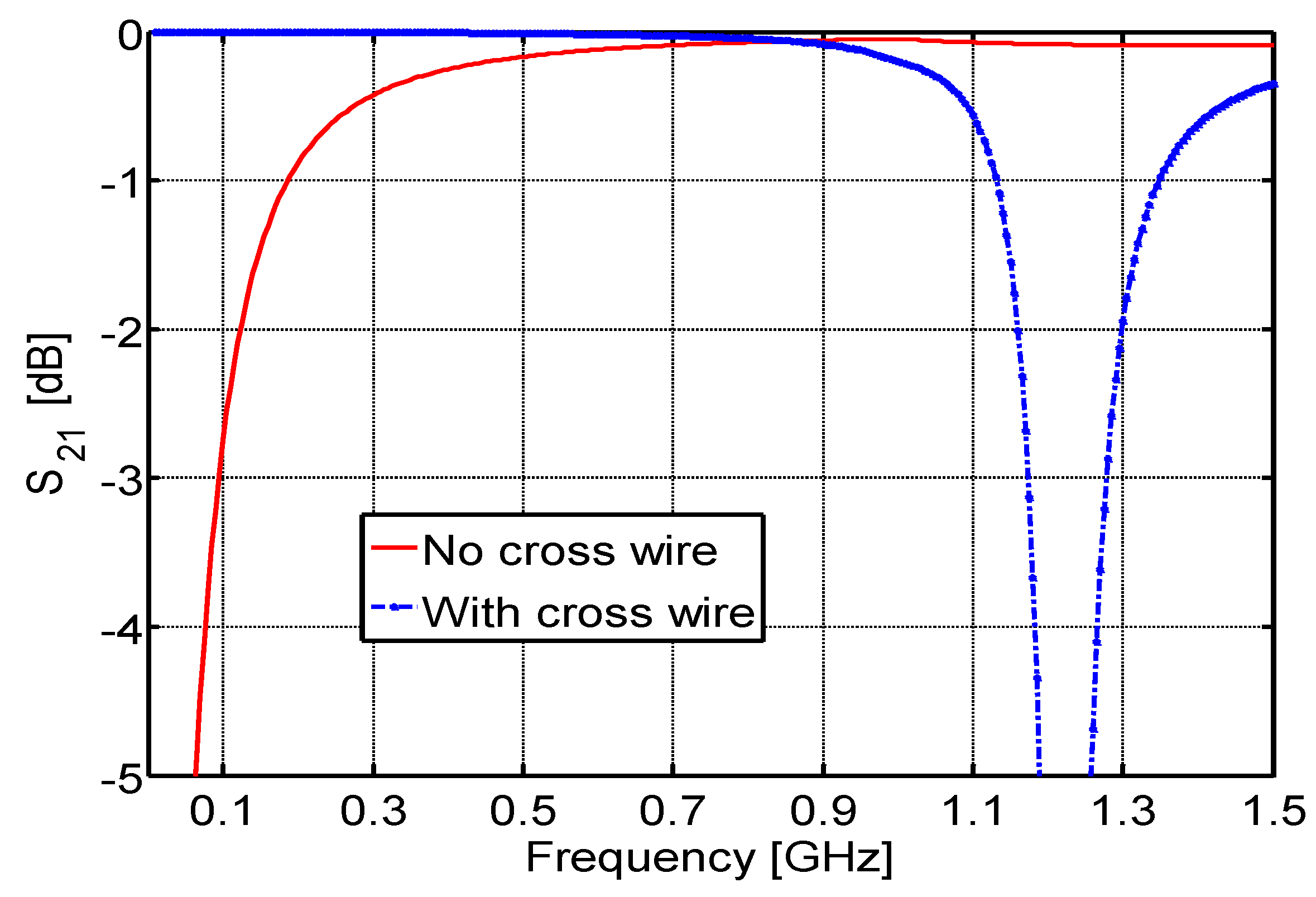
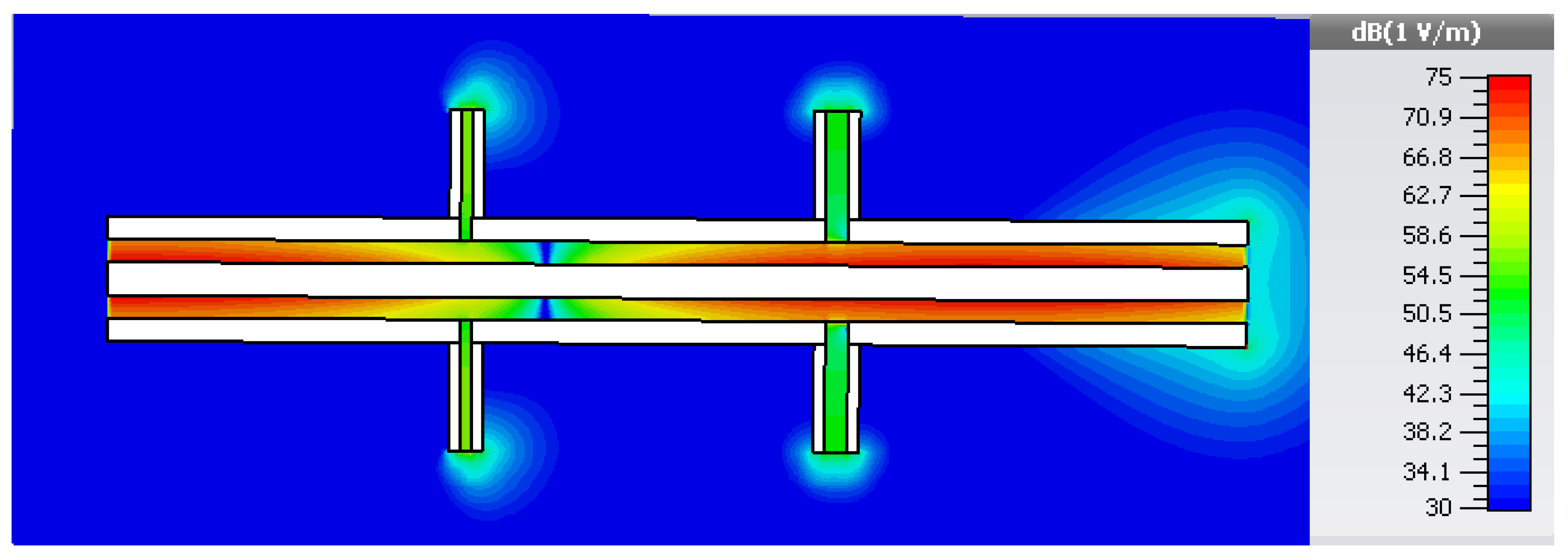
3. Flange-Type Gaps Design in Coaxial Line
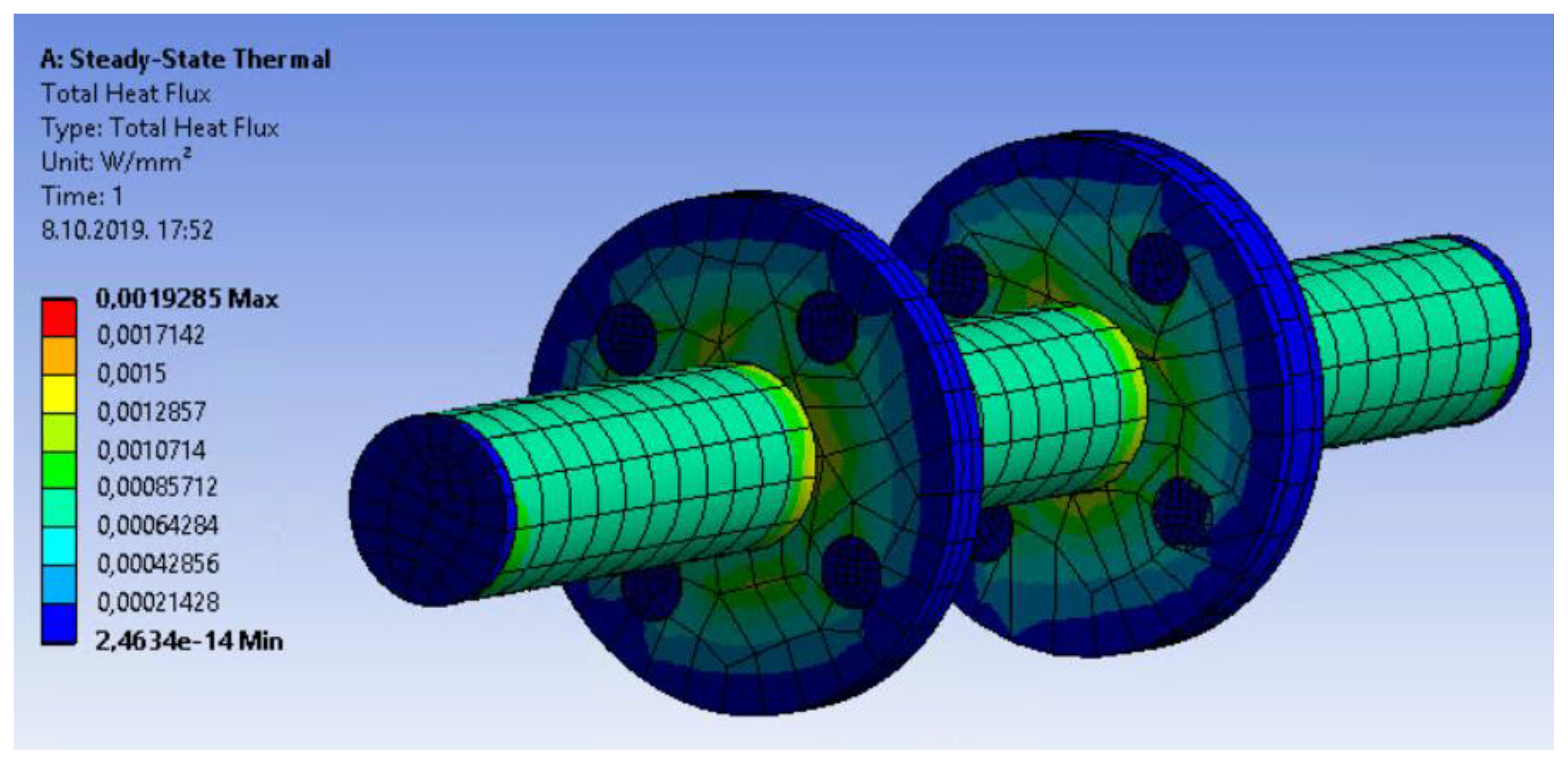
4. Thermal Considerations on the Adiabatic Line
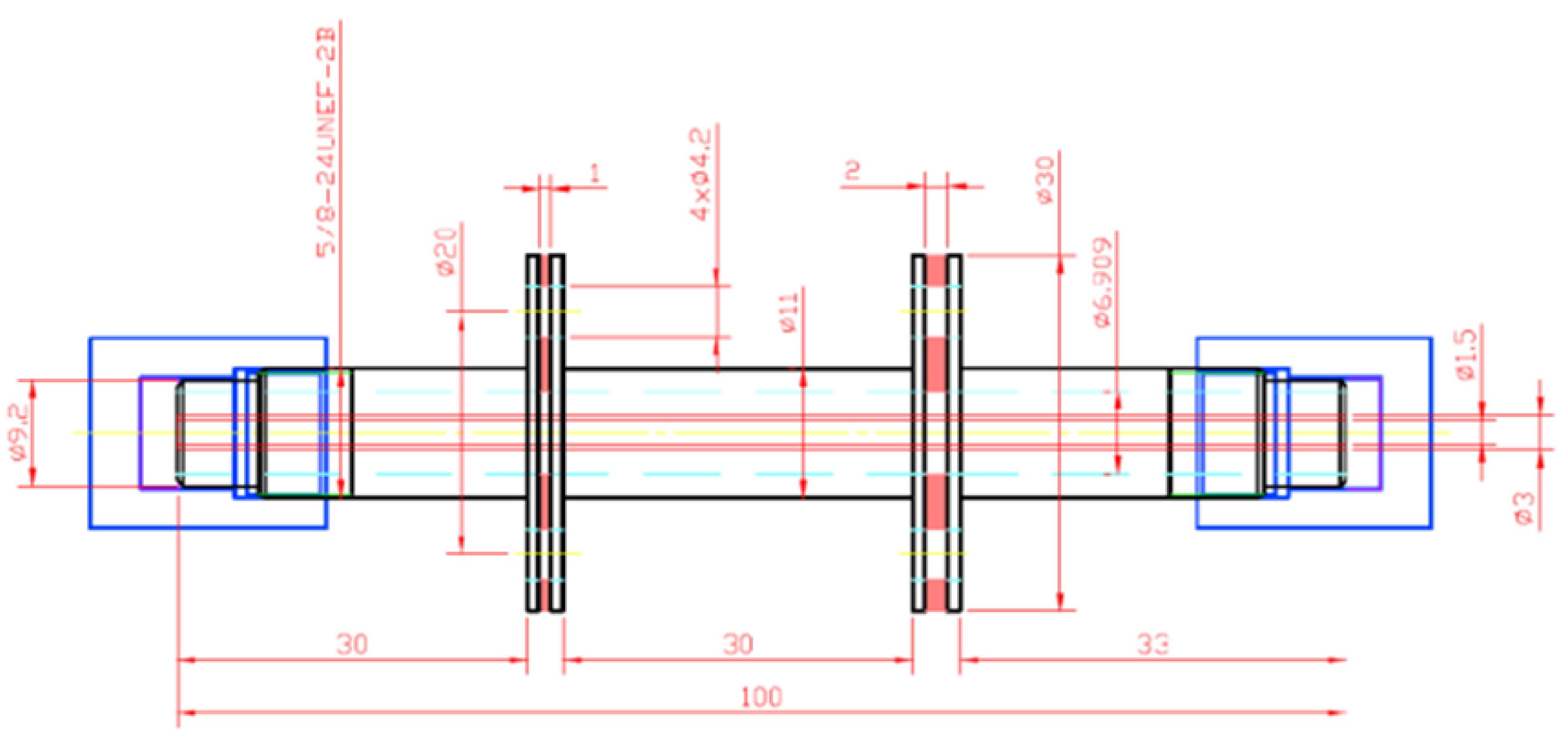
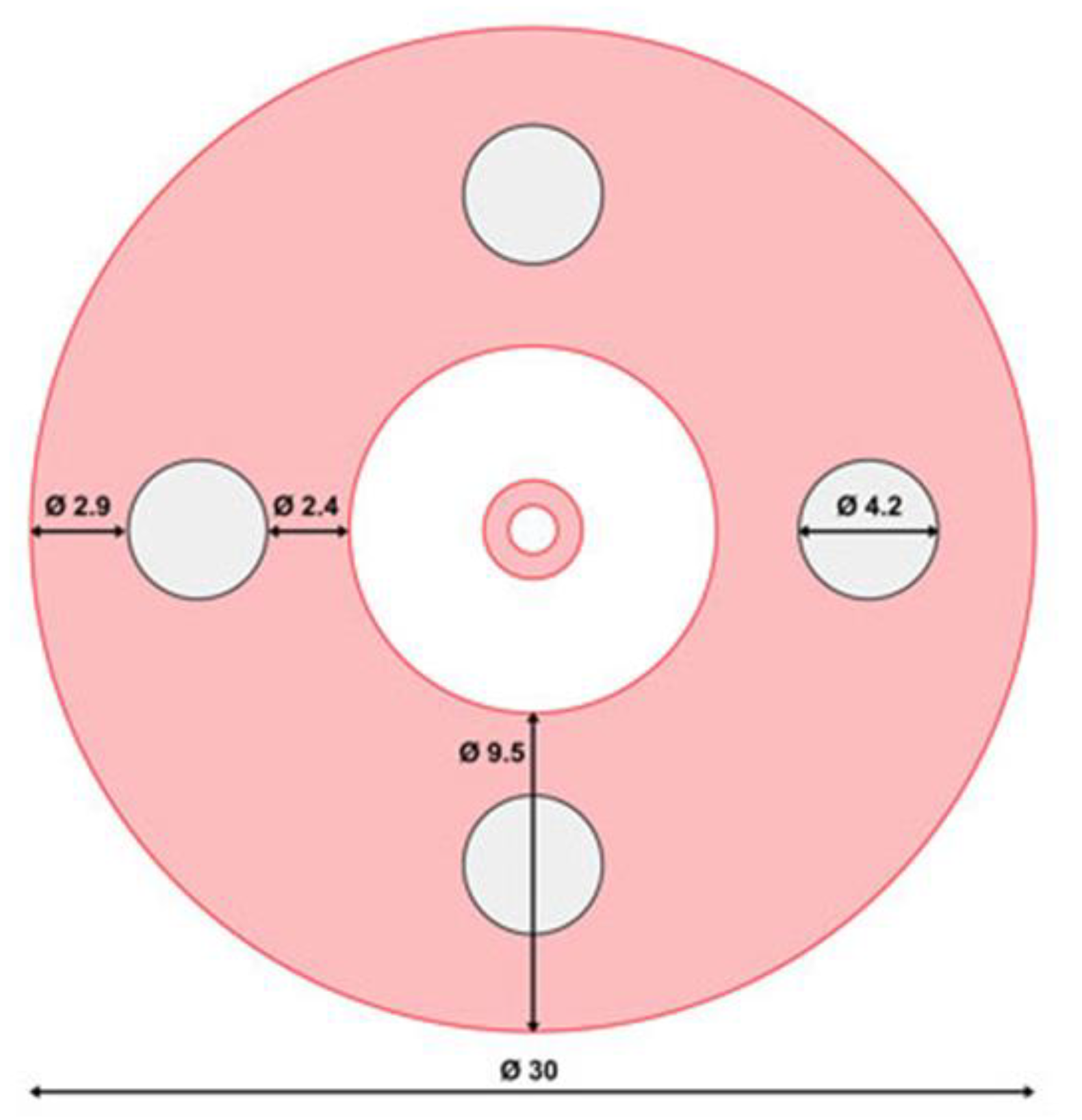
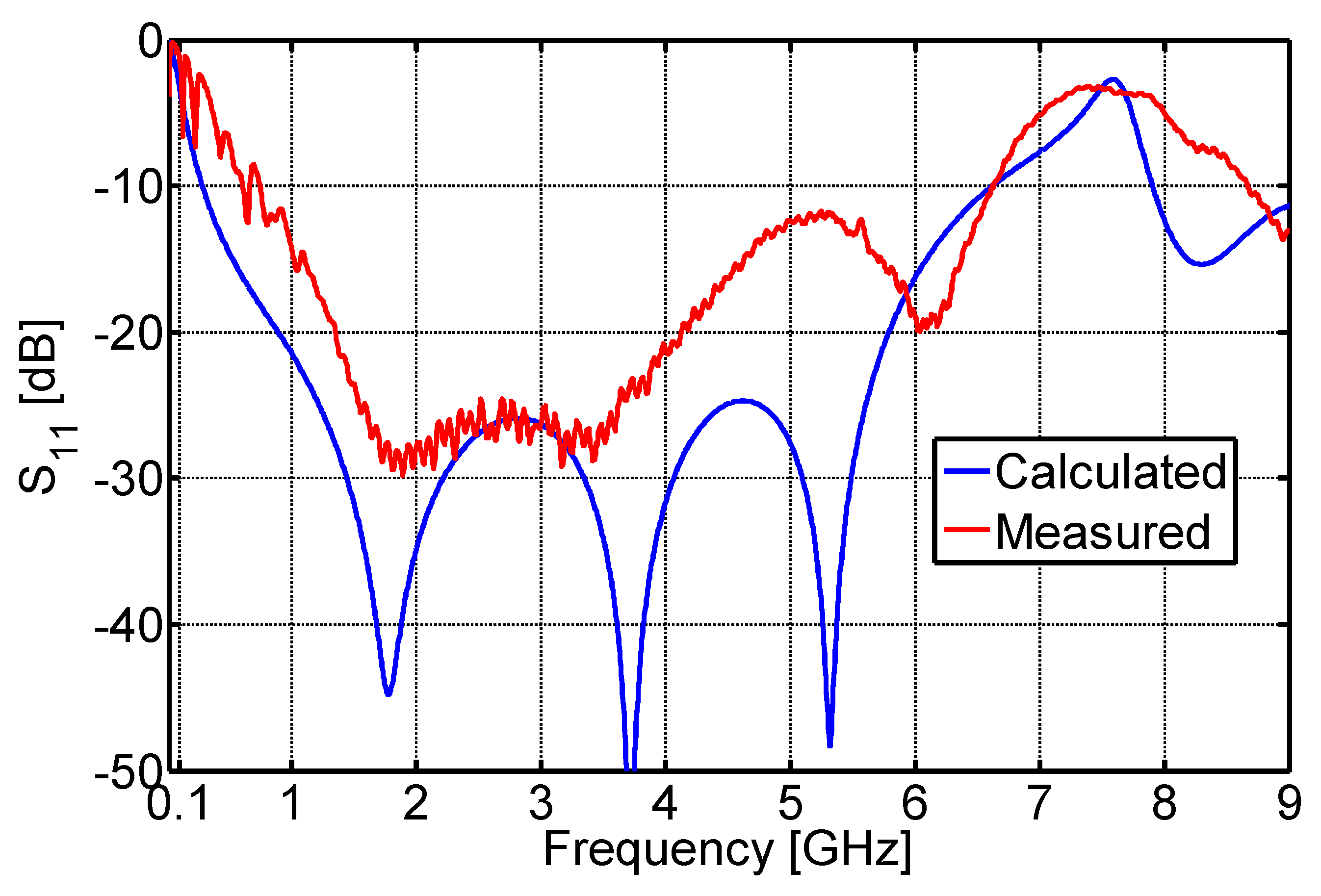
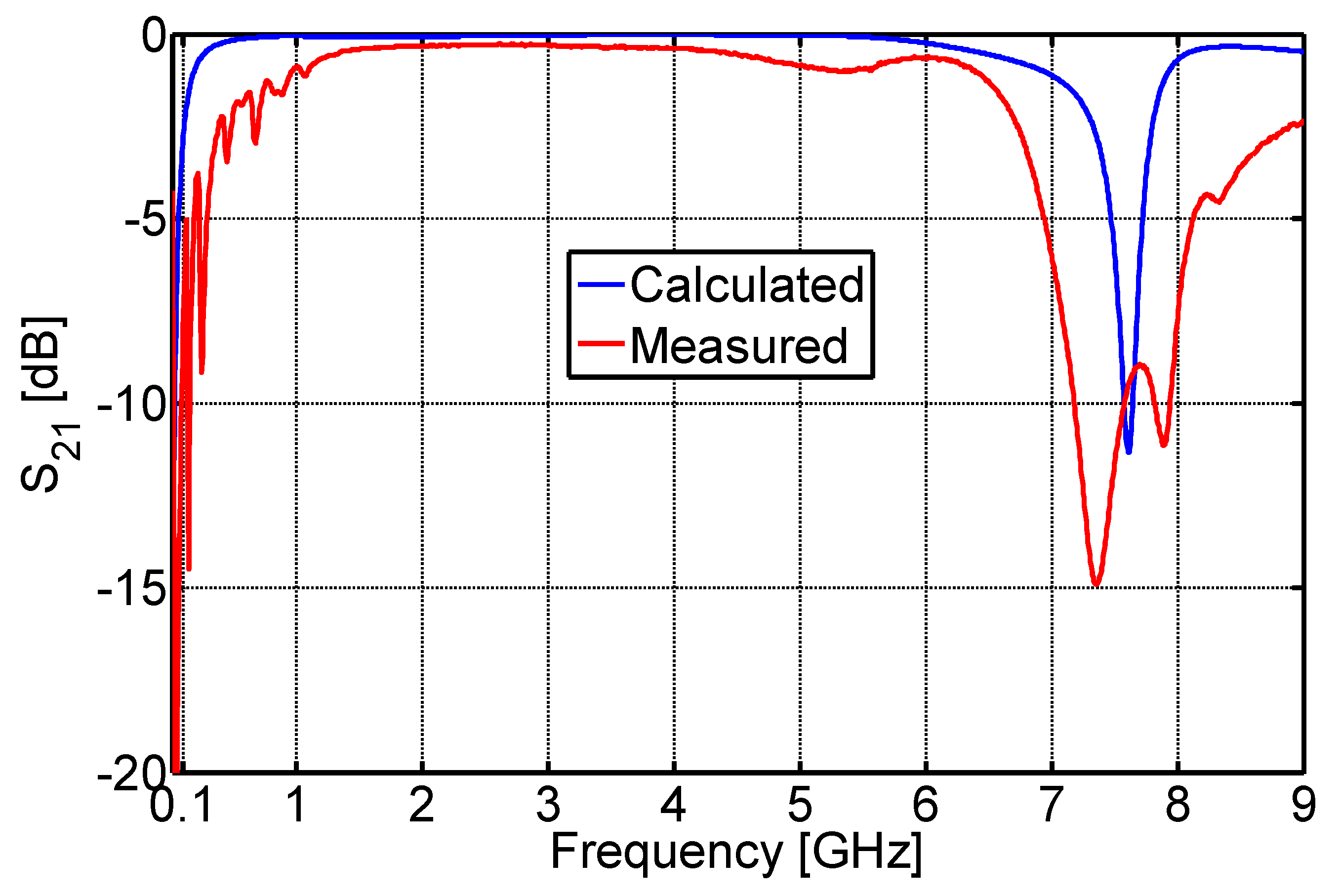
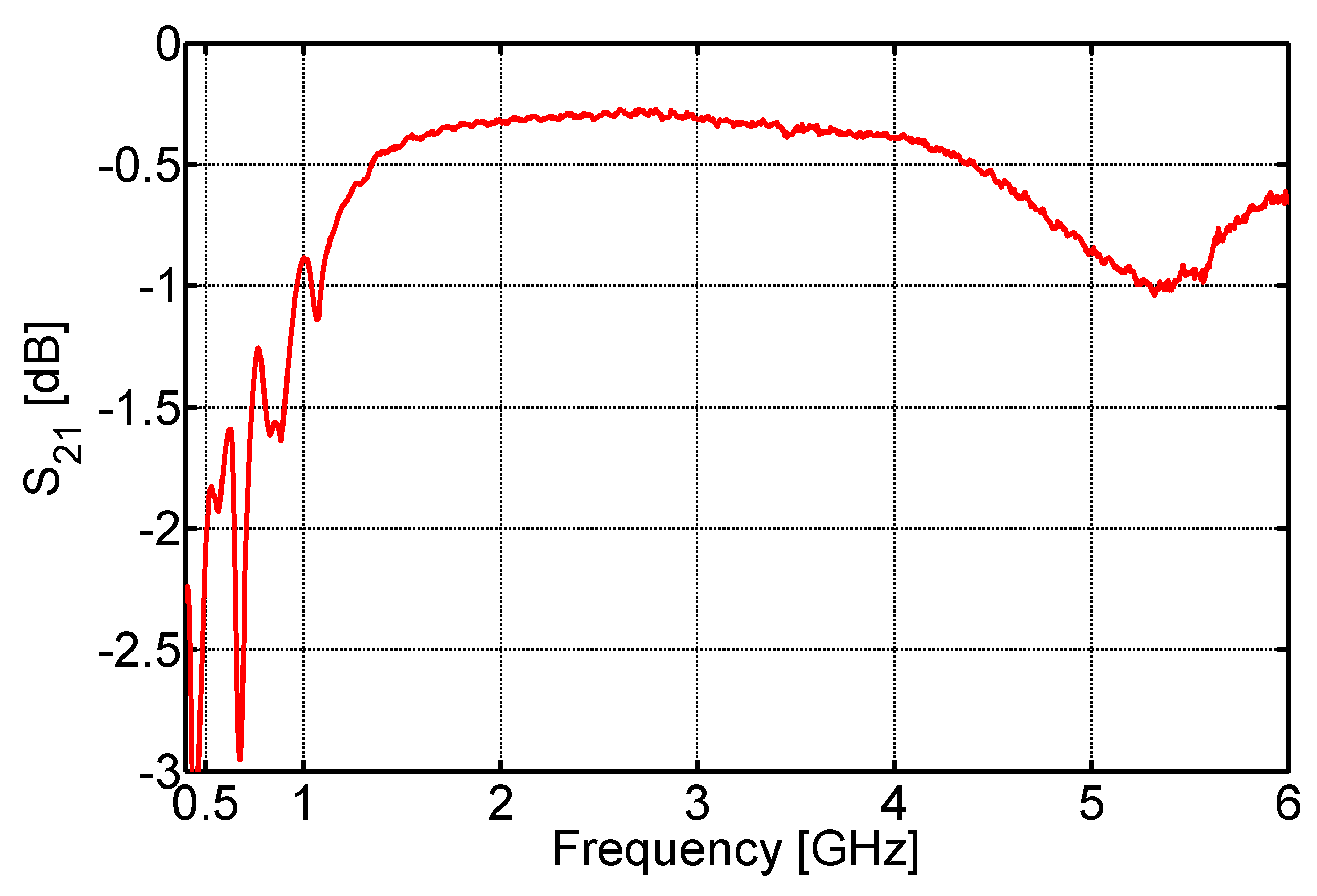
5. Manufactured Adiabatic Line Prototype
6. Conclusion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Heat Flow (W)—One Gap | Heat Flow Reduction—One Gap | Heat Flow (W)—One Gap + Wire | Heat Flow Reduction—One Gap + Wire |
|---|---|---|---|
| 0.0992 | 56.86% | 0.1244 | 45.91% |
References
- Lai, H.W.; Tsui, C.M.; Li, H.W.; Ma, C.K.; Chan, K.Y. Provision of Traceable Calibration Services at SCL to Underpin Development of Smart City Initiatives. In Proceedings of the 2018 IEEE Symposium on Product Compliance Engineering—Asia (ISPCE-CN), Shenzhen, China, 5–7 December 2018; 4p. [Google Scholar]
- Tepati, V.; Ferrero, A.; Sayed, M. (Eds.) Modern RF and Microwave Measurement Techniques; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Rohde&Schwarz. RF Voltage and Power Measurements Brochure [Online]. 2018. Available online: https://cdn.rohde-schwarz.com/pws/dl_downloads/dl_common_library/dl_brochures_and_datasheets/pdf_1/SLMESS_E.PDF (accessed on 3 April 2019).
- Clark, R.F. The Microcalorimeter as a National Microwave Power Standard. Proc. IEEE 1986, 74, 102–104. [Google Scholar] [CrossRef]
- Ivsic, B.; Dadic, M.; Malaric, R.; Martinovic, Z. Thermal Considerations on Adiabatic Coaxial Line for Microcalorimeter Measurements. In Proceedings of the 2019 2nd International Colloquium on Smart Grid Metrology (SMAGRIMET), Split, Croatia, 9–12 April 2019; pp. 131–134. [Google Scholar]
- Huang, Y.; Yuan, W.; Cui, X.; Meng, Y.S.; Li, Y. WR-42 Waveguide Microcalorimeter for Thermistor Mount Calibration. In Proceedings of the 2018 Conference on Precision Electromagnetic Measurements (CPEM 2018), Paris, France, 8–13 July 2018. [Google Scholar]
- Ahmad, S.; Rustagi, V.K.; Govil, A.K.; Aggarwal, R.; Pal, B.; Kothari, P.C. Automation of Direct Comparison Technique and Study of long term Performance on the Calibration factor of the Thermistor Mounts in N-type Coaxial line up to 18 GHz. In Proceedings of the 2007 Asia-Pacific Microwave Conference, Bangkok, Thailand, 11–14 December 2007. [Google Scholar]
- Allen, J.W.; Clague, F.R.; Larsen, N.T.; Weidman, M.P. NIST Microwave Power Standards in Waveguide; U.S. Department of Commerce, National Institute of Standard and Technology: Boulder, CO, USA, 1999; Volume 1511, pp. 1–56.
- Chung, N.S.; Shin, J.; Bayer, H.; Honigbaum, R. Coaxial and Waveguide Microcalorimeters for RF and Microwave Power Standards. IEEE Trans. Instrum. Meas. 1989, 38, 460–464. [Google Scholar] [CrossRef]
- Kwon, J.Y.; Kang, T.W.; Kim, H.J. A design and implementation of 3.5 mm coaxial microcalorimeter for RF and microwave power standards at KRISS. In Proceedings of the 2008 Conference on Precision Electromagnetic Measurements Digest, Broomfield, CO, USA, 8–13 June 2008; pp. 422–423. [Google Scholar]
- Kwon, J.Y.; Lee, D.J. Adiabatic Design for a Coaxial Transmission Line. IEEE Trans. Instrum. Meas. 2014, 63, 1760–1768. [Google Scholar] [CrossRef]
- Botello-Perez, M.; Crowley, T.P.; Garcia-Ruiz, I.; Jardon-Aguilar, H. CENAM's primary standard for microwave power up to 18 GHz. In Proceedings of the 2016 Conference on Precision Electromagnetic Measurements (CPEM 2016), Ottawa, ON, Canada, 10–15 July 2016. [Google Scholar]
- Botello-Perez, M.; Crowley, T.P.; Garcia-Ruiz, I.; Jardon-Aguilar, H. Characterization of a Type-N Coaxial Microcalorimeter for Use as Microwave Power Standard at CENAM. IEEE Trans. Instrum. Meas. 2019, 68, 558–565. [Google Scholar] [CrossRef]
- Yuan, W.; Cui, X.; Li, Y.; Ma, C.; Meng, Y.S. Uncertainty analysis and evaluation of a WR-28 (26.5 to 40 GHz) millimeter-wave power standard. In Proceedings of the 2016 Conference on Precision Electromagnetic Measurements (CPEM 2016), Ottawa, ON, Canada, 10–15 July 2016. [Google Scholar]
- Cox, M.; Harris, P.; Iuculano, G.; Pellegrini, G. The evaluation of the uncertainty associated with comparison loss in microwave power meter calibration. In Proceedings of the 2006 IEEE International Workshop on Advanced Methods for Uncertainty Estimation in Measurement (AMUEM 2006), Sardagna, Italy, 20–21 April 2006; pp. 34–39. [Google Scholar]
- Martinovic, Z.; Dadic, M.; Malaric, R.; Martinovic, Z. Electromagnetic analysis of adiabatic coaxial line with applied air gap. In Proceedings of the 25th International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 21–23 September 2017; pp. 101–105. [Google Scholar]
- López, G.; Moura, P.; Moreno, J.I.; Camacho, J.M. Multi-Faceted Assessment of a Wireless Communications Infrastructure for the Green Neighborhoods of the Smart Grid. Energies 2014, 7, 3453–3483. [Google Scholar] [CrossRef]
- Reka, S.; Dragicevic, T.; Siano, P.; Prabaharan, S.R.S. Future Generation 5G Wireless Networks for Smart Grid: A Comprehensive Review. Energies 2019, 12, 2140–2157. [Google Scholar]
- Dadić, M.; Sandelić, M.; Hegeduš, H.; Petrović, G. A circular loop time constant standard. J. Energy Energ. 2018, 67, 103–107. [Google Scholar]
- Konjevod, J.; Malarić, R.; Dadić, M.; Mostarac, P.; Hegeduš, H. Measurement of DC properties and relative humidity (RH) dependence of wideband AC current shunts. Measurement 2019, 131, 1–6. [Google Scholar] [CrossRef]
- Chung, N.S.; Shin, J.; Bayer, H.; Honigbaum, R. Precision Coaxial and Waveguide Microcalorimeters for RF and Microwave Power Standards. In Proceedings of the 1988 Conference on Precision Electromagnetic Measurements, Ibaraki, Japan, 7–10 June 1988; pp. 182–183. [Google Scholar]
- Rosenberger Technical Data Sheet [Online]. 2018. Available online: https://catalog.rosenberger.com/images/documents/db/05CK001-150_DB.pdf (accessed on 14 March 2019).
- Riddle, B.; Baker-Jarvis, J.; Krupka, J. Complex permittivity measurements of common plastics over variable temperatures. IEEE Trans Microw. Theory Tech. 2003, 51, 727–733. [Google Scholar] [CrossRef]
- Ansys HFSS Website 2018. Available online: https://www.ansys.com/products/electronics/ansys-hfss (accessed on 12 February 2019).
- Holman, J.P. Heat Transfer, 10th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Ansys Mechanical Website 2018. Available online: https://www.ansys.com/products/structures/ansys-mechanical-enterprise (accessed on 3 February 2018).
- Čatić, I. Knowledge of Thermal Properties, a Key to the Successful Polymer processing. Polimeri 1983, 4, 67–79. [Google Scholar]
- Pauling, L. General Chemistry, 2nd ed.; Freeman: San Francisco, CA, USA, 1953. [Google Scholar]

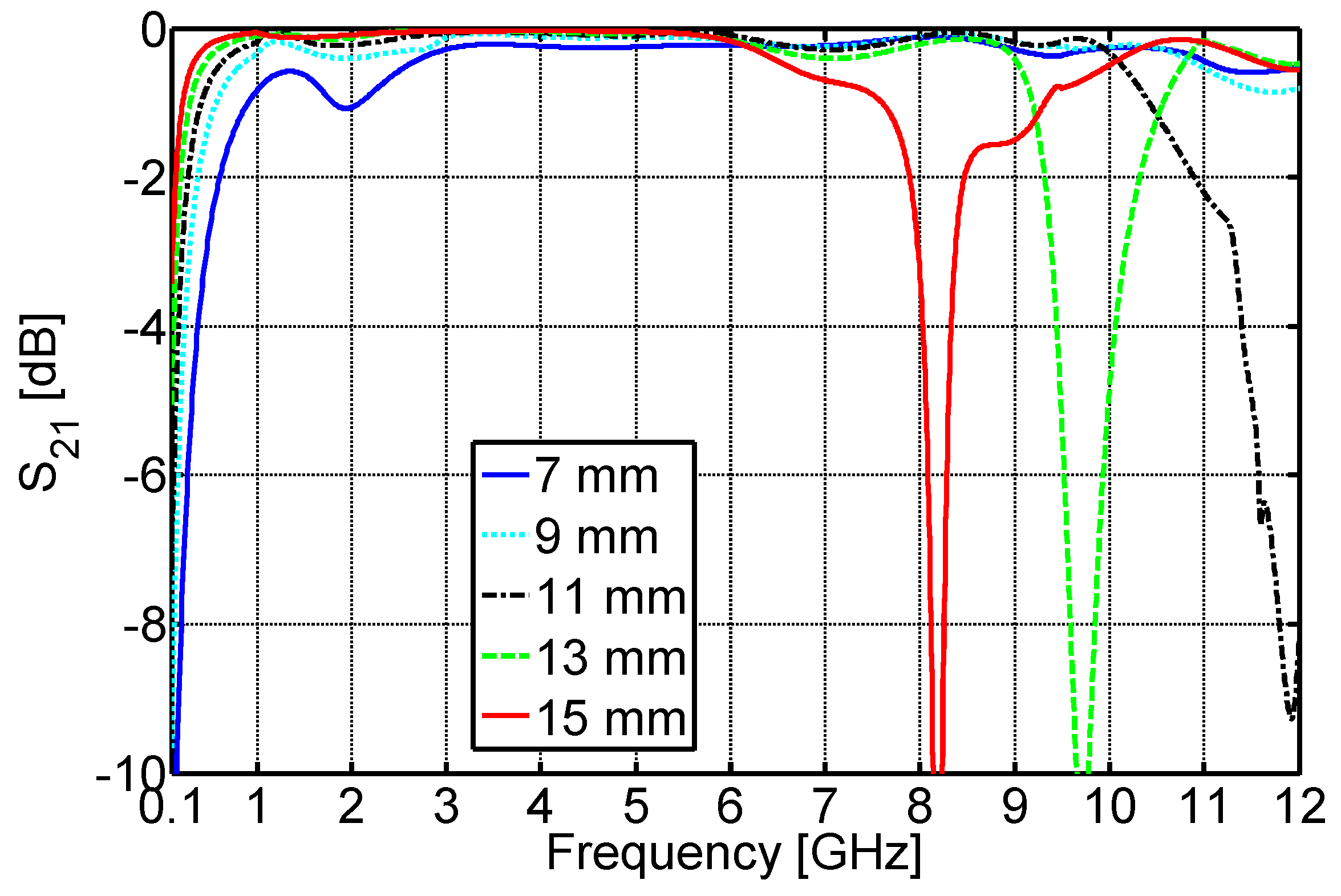
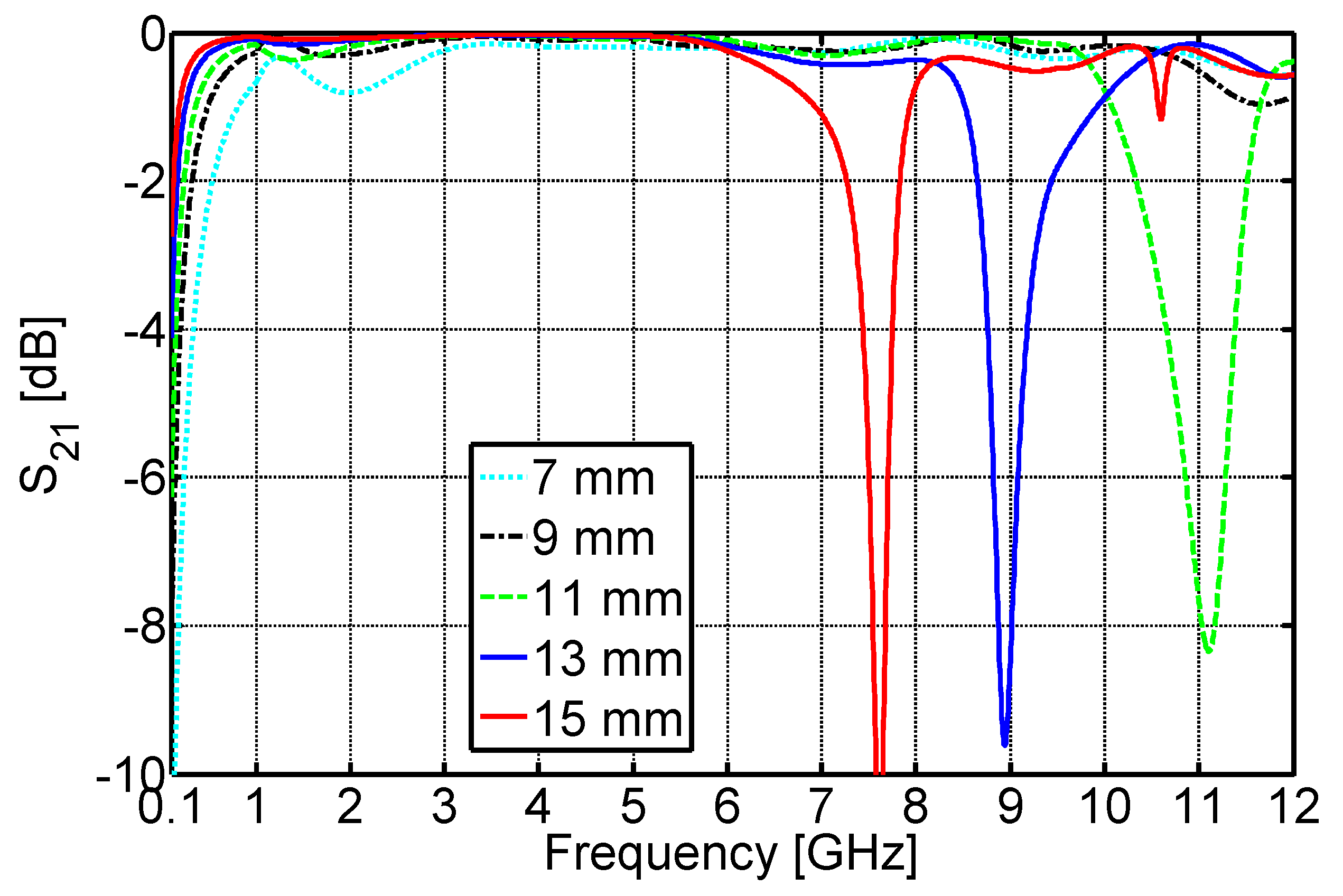
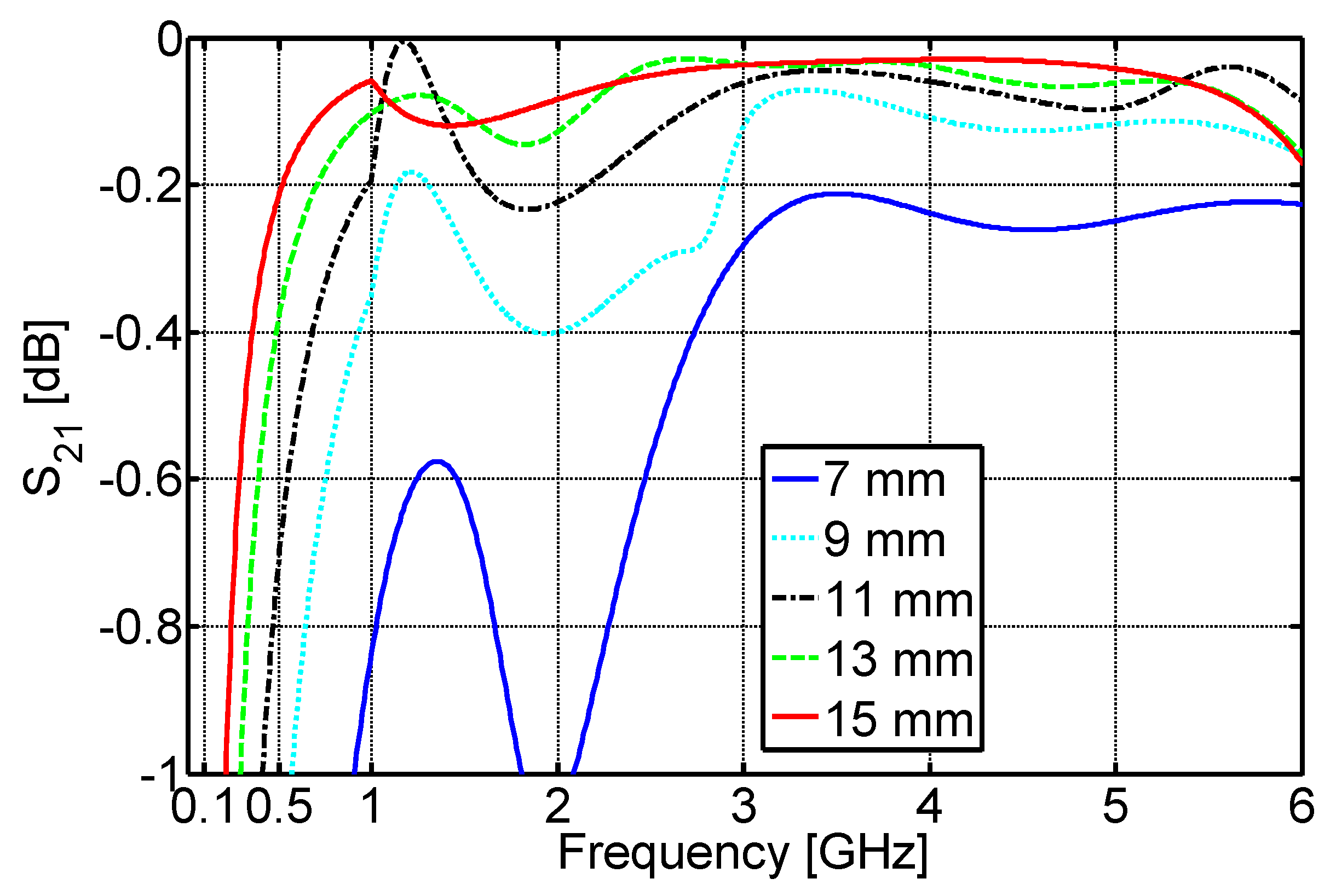







| Plastic Material | Flange Radius (mm) | Heat Flow (W)—One Gap | Heat Flow Reduction—One Gap | Heat Flow (W)—Two Gaps | Heat Flow Reduction—Two Gaps |
|---|---|---|---|---|---|
| Polyethylene | 11 | 0.0820 | 64.33% | 0.0361 | 84.27% |
| 13 | 0.1063 | 53.78% | 0.0482 | 79.03% | |
| 15 | 0.1164 | 49.36% | 0.0622 | 72.95% | |
| 17 | 0.1296 | 43.64% | 0.0715 | 68.87% | |
| Acetal homopolymer | 11 | 0.0662 | 71.21% | 0.0275 | 88.04% |
| 13 | 0.0835 | 63.69% | 0.0373 | 83.78% | |
| 15 | 0.0992 | 56.86% | 0.0475 | 79.34% | |
| 17 | 0.1131 | 50.86% | 0.0576 | 74.96% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinovic, Z.; Dadic, M.; Ivsic, B.; Malaric, R. An Adiabatic Coaxial Line for Microcalorimeter Power Measurements in Wireless Communication for Smart Grid. Energies 2019, 12, 4194. https://doi.org/10.3390/en12214194
Martinovic Z, Dadic M, Ivsic B, Malaric R. An Adiabatic Coaxial Line for Microcalorimeter Power Measurements in Wireless Communication for Smart Grid. Energies. 2019; 12(21):4194. https://doi.org/10.3390/en12214194
Chicago/Turabian StyleMartinovic, Zeljko, Martin Dadic, Branimir Ivsic, and Roman Malaric. 2019. "An Adiabatic Coaxial Line for Microcalorimeter Power Measurements in Wireless Communication for Smart Grid" Energies 12, no. 21: 4194. https://doi.org/10.3390/en12214194
APA StyleMartinovic, Z., Dadic, M., Ivsic, B., & Malaric, R. (2019). An Adiabatic Coaxial Line for Microcalorimeter Power Measurements in Wireless Communication for Smart Grid. Energies, 12(21), 4194. https://doi.org/10.3390/en12214194






