Probabilistic Methodology for Calculating PV Hosting Capacity in LV Networks Using Actual Building Roof Data
Abstract
1. Introduction
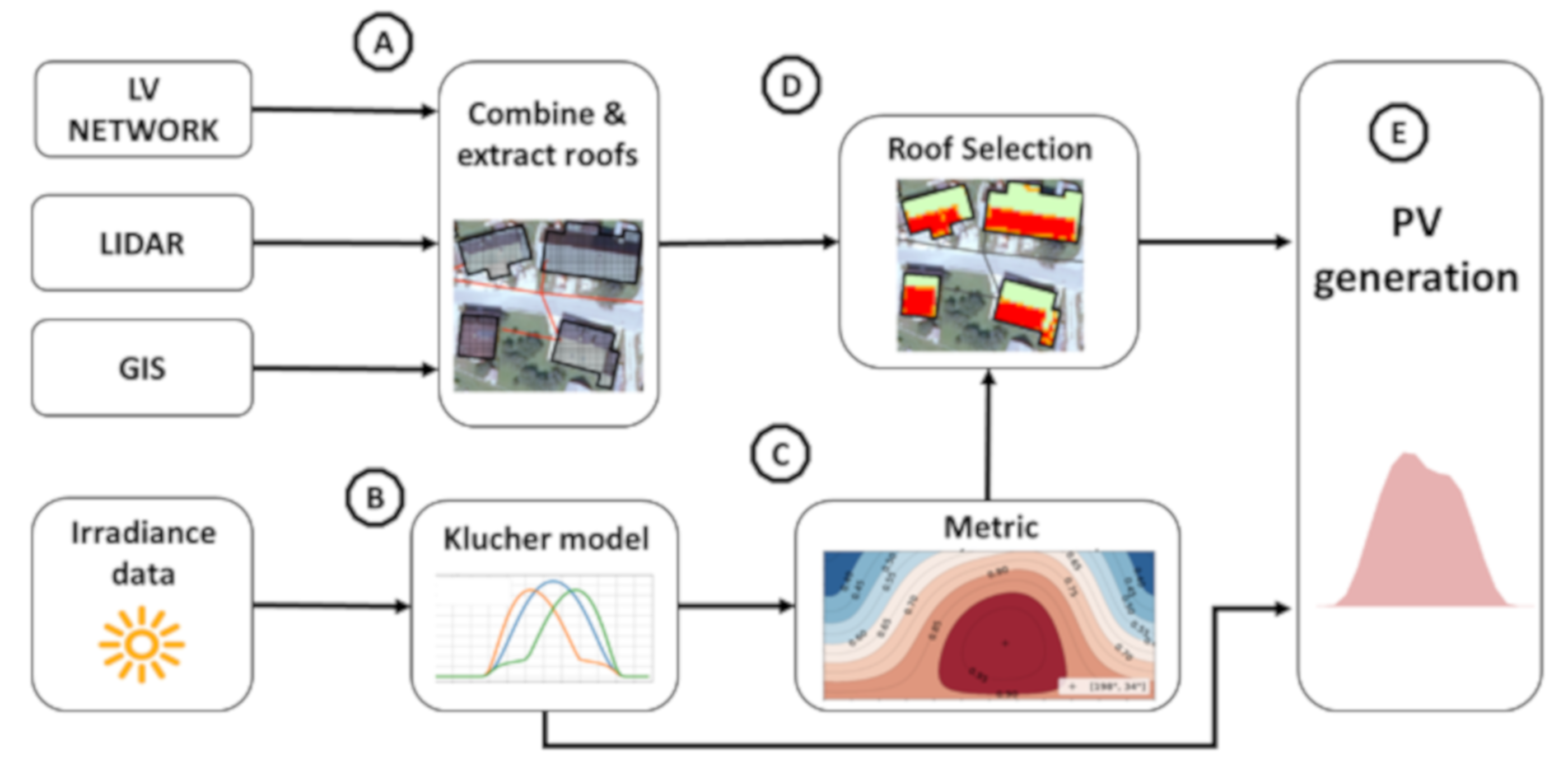
2. Methodology
2.1. Input Data Preparation
- electrical network data;
- measurements from smart meters (not essential);
- LIDAR;
- GIS (land register); and
- solar irradiance data.
- represents the GHI measurements; and
- represents the DHI measurements, for the last few years and with an hourly resolution.
2.2. Consumption and PV Generation Modeling
- selecting roofs with high PV potential; and
- accurate modeling of stochastic PV generation on different roof surfaces.
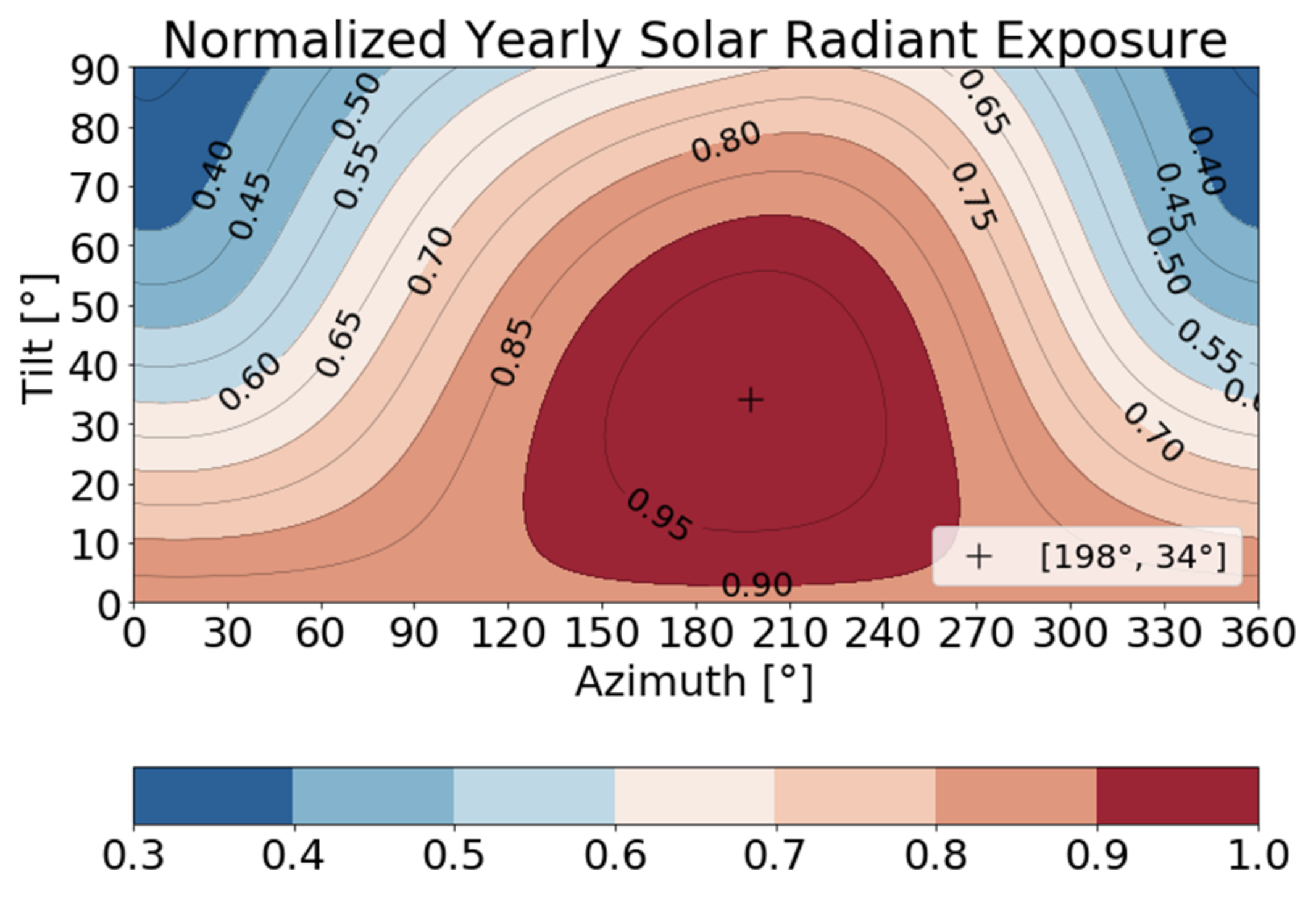
2.2.1. Solar Irradiance on Tilted and Oriented Surfaces
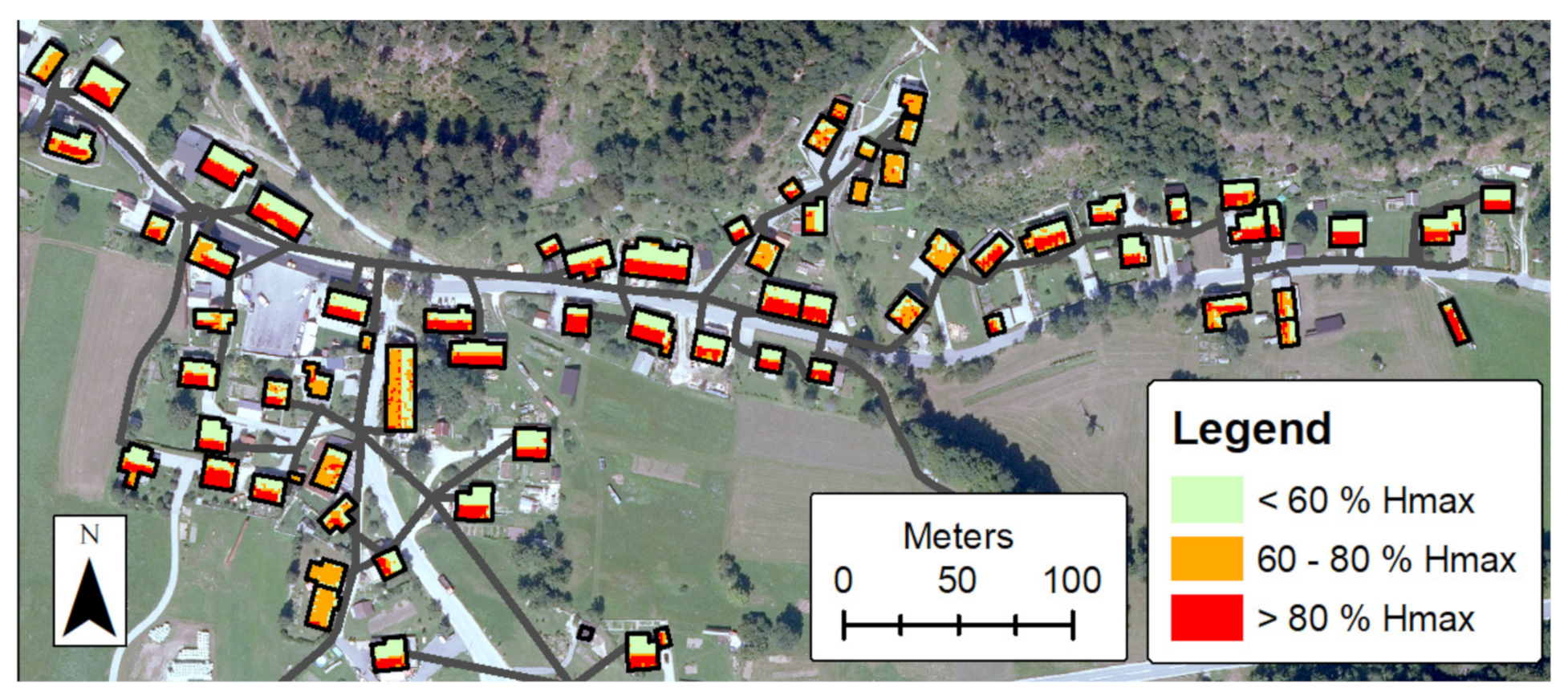
2.2.2. Selecting Roofs with High PV Potential
2.2.3. Stochastic PV Generation Modeling using Actual Roofs Surfaces
- Randomly choose one column for a previously chosen hour from matrix I. Here we utilize random sampling with replacement from a finite population, which means that one column can be selected more than once. The result is a vector holding irradiance for every tilt-orientation combination on a particular day and represents one weather scenario.
- Select roofs with high PV potential using Hmetric and utilize PV systems (μPV) and inverter efficiency (μinverter) to derive PV generation for all tilt-orientation combinations from vector D (Pg has unit [W/m2])PV systems’ and inverters’ efficiencies of 15% and 95% are utilized in the calculations to obtain actual PV generations.
- Let matrix B represent a subset of matrix A, where B holds only the selected columns (randomly chosen roofs during PV hosting capacity calculations) and the total number of chosen roofs is denoted as i. For every column j in a matrix B (every selected roof), we calculate
- Which means that PV generation is summarized for all surfaces in a particular roof to create PV generation on a particular day.After calculating PV generation for every roof in step 3, the results are stacked vertically to create a PV generation vector.
- Output of the procedure in step 4 is PV generated power for every chosen roof on a particular day, which is further used in load flow calculations.
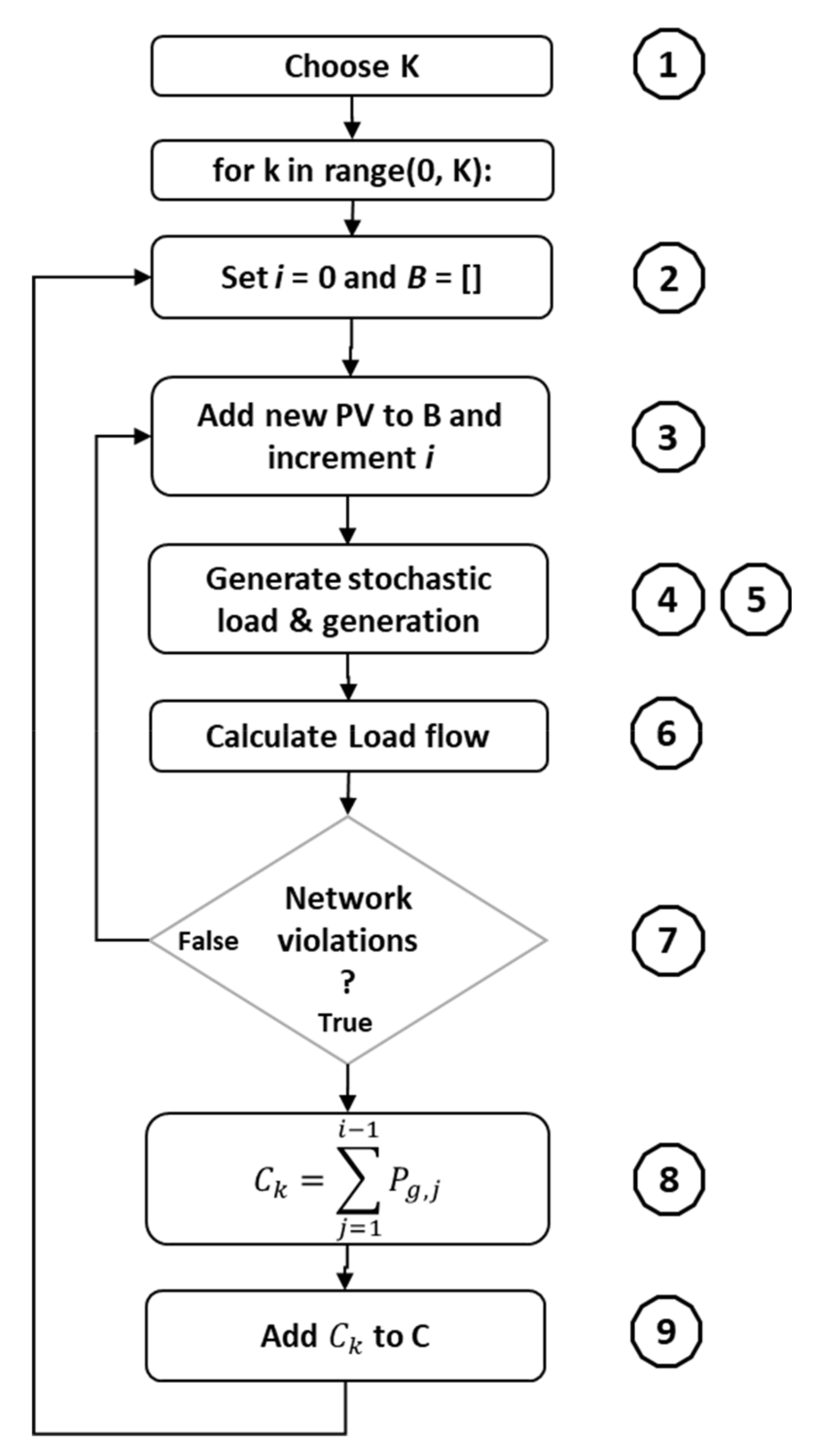
2.3. Calculating PV Hosting Capacity Using the Monte Carlo Method
- Choose real number K which denotes the number of iterations and equals to a size of a final set C.
- Set i = 0, where i denotes the total number of chosen roofs and create empty matrix B, which later holds the information about the roof data.
- Randomly select one column from a matrix A holding roofs data and add a selected column to B. Here, we utilize random sampling without replacement, which means that every roof (location) has the same chance of being chosen and that every roof is chosen only once (until the network violation occur and all the locations are reset).
- Generate stochastic load (described in Section 2.2) for all consumers and form a load matrix Pl of size r (number of roofs and consumers).
- Generate stochastic PV generation (described in Section 2.2.3) for all chosen roofs and form a PV generation matrix Pg,PV using roof matrix B from step 3.
- Calculate load flow. Here, we solve the following equations:where PGk is active power generation, PDk is active power demand, QGk is reactive power generation, QDk is reactive power demand, Vk is voltage, and δk is voltage angle for a particular node k in a network. Vj is voltage and δj is voltage angle for a node j which is close to the node k. In our case, PGk, PDk, QGk, and QDk are random variables representing consumer demand and PV generation. PDk equals to Pl (calculated in step 7), QDk = 0.33 Pl, PGk for every bus equals to Pg,PV (calculated in step 8) and QGk = 0.
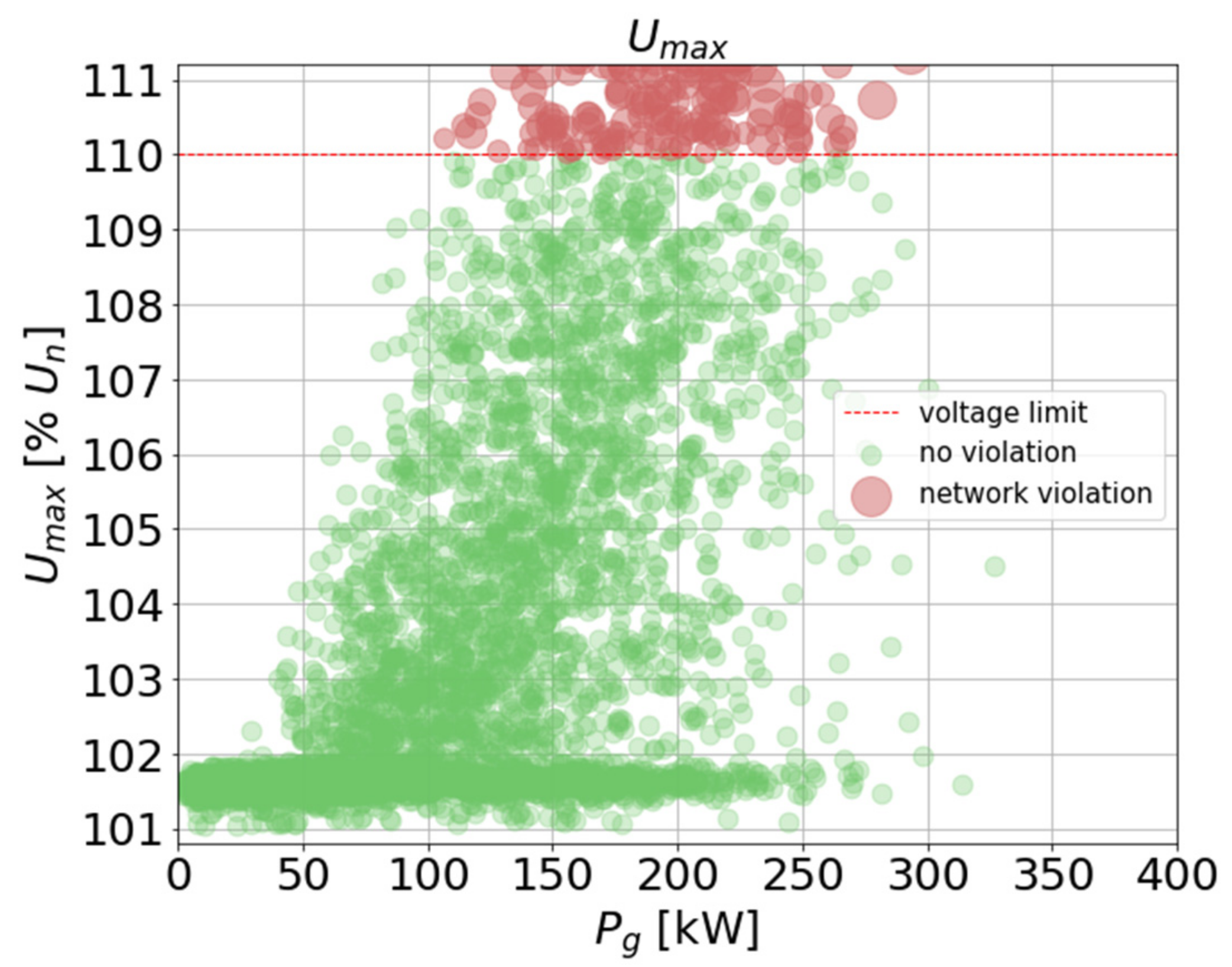
- Check network violations (voltage limits and element loadings). If there are no violations, return to a step 3. If there is at least one violation, go to the next step.
- Aggregate the nominal power of all PVs in the network without the last one (there were no violations until the last PV was added). If Pg,j denotes installed power of j-th added PV system in the network and Ck is one value in a set C of PV hosting capacity values then Ck is calculated as follows:
- Add Ck to a set C which holds PV hosting capacities.
3. Case Study
3.1. Data Preparation
3.2. Solar Potential Results for an Analyzed Village
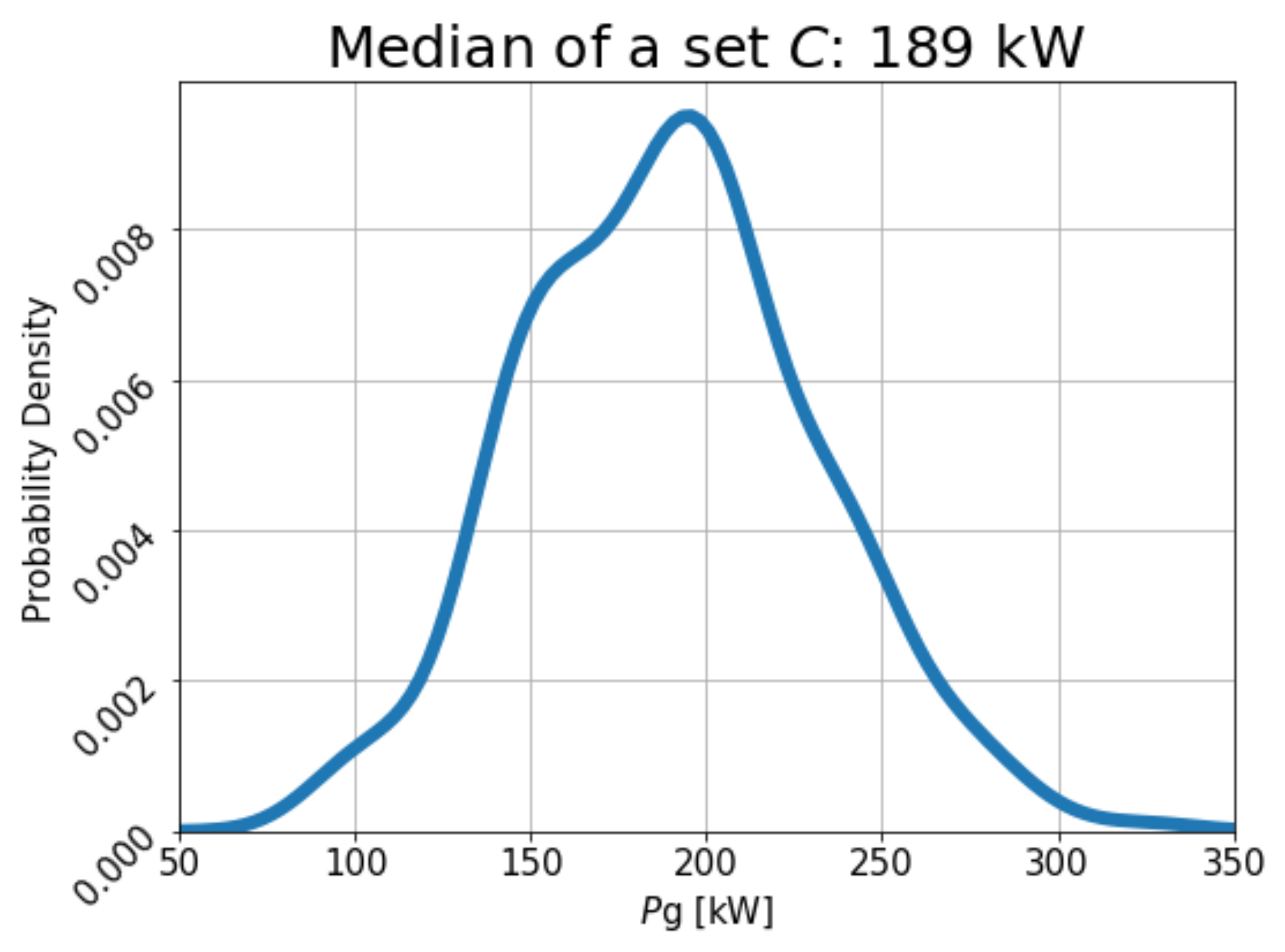
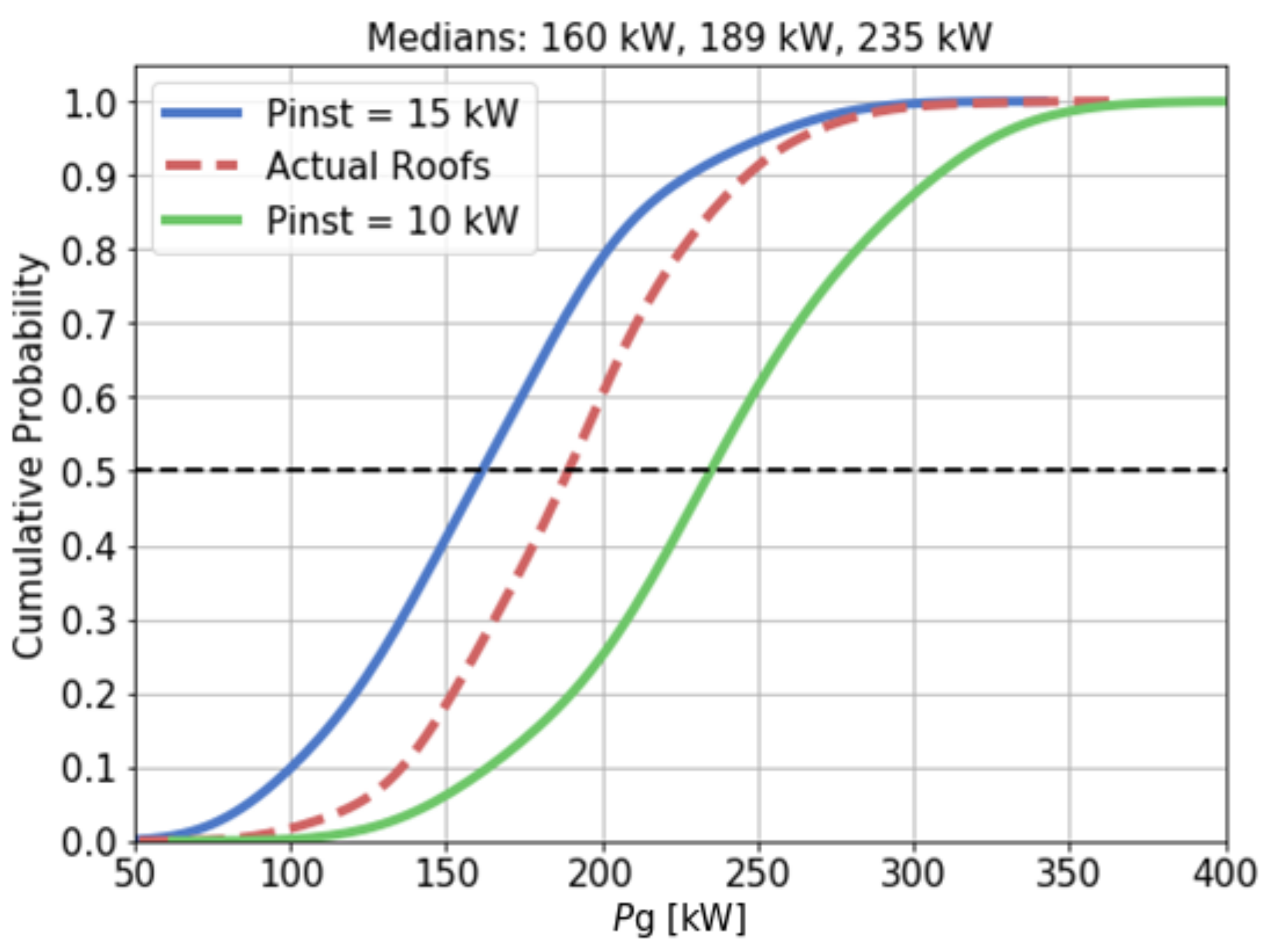
3.3. PV Hosting Capacity Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bletterie, B.; Kadam, S.; Renner, H. On the classification of low voltage feeders for network planning and hosting capacity studies. Energies 2018, 11, 651. [Google Scholar] [CrossRef]
- Georgilakis, P.S.; Hatziargyriou, N.D. A review of power distribution planning in the modern power systems era: Models, methods and future research. Electr. Power Syst. Res. 2015, 121, 89–100. [Google Scholar] [CrossRef]
- Chen, P.; Chen, Z.; Bak-Jensen, B. Probabilistic load flow: A review. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 1586–1591. [Google Scholar]
- Sakar, S.; Balci, M.E.; Abdel Aleem, S.H.E.; Zobaa, A.F. Increasing PV hosting capacity in distorted distribution systems using passive harmonic filtering. Electr. Power Syst. Res. 2017, 148, 74–86. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S.; Ge, L.; Wu, L. Distributed Generation Hosting Capacity Evaluation for Distribution Systems Considering the Robust Optimal Operation of OLTC and SVC. IEEE Trans. Sustain. Energy 2016, 7, 1111–1123. [Google Scholar]
- Bollen, M.H.; Hassan, F. Integration of Distributed Generation in the Power System; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 80. [Google Scholar]
- Kolenc, M.; Papič, I.; Blažič, B. Assessment of maximum distributed generation penetration levels in low voltage networks using a probabilistic approach. Int. J. Electr. Power Energy Syst. 2015, 64, 505–515. [Google Scholar] [CrossRef]
- Ballanti, A.; Pilo, F.; Navarro-Espinosa, A.; Ochoa, L.F. Assessing the benefits of PV var absorption on the hosting capacity of LV feeders. In Proceedings of the IEEE PES ISGT Europe 2013, Copenhagen, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Smith, J.; Rylander, M. Stochastic analysis to determine feeder hosting capacity for distributed solar PV. Electr. Power Res. Inst. Palo Alto CA Tech. Rep. 2012, 1026640, 0885–8950. [Google Scholar]
- Navarro, A.; Ochoa, L.F.; Randles, D. Monte Carlo-based assessment of PV impacts on real UK low voltage networks. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Navarro-Espinosa, A.; Ochoa, L.F. Probabilistic impact assessment of low carbon technologies in LV distribution systems. IEEE Trans. Power Syst. 2015, 31, 2192–2203. [Google Scholar] [CrossRef]
- Divshali, P.H.; Soder, L. Improving Hosting Capacity of Rooftop PVs by Quadratic Control of an LV-Central BSS. IEEE Trans. Smart Grid 2019, 10, 919–927. [Google Scholar] [CrossRef]
- Schultis, D.-L. Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies 2019, 12, 1560. [Google Scholar] [CrossRef]
- Saad, S.N.M.; van der Weijde, A.H. Evaluating the Potential of Hosting Capacity Enhancement Using Integrated Grid Planning modeling Methods. Energies 2019, 12, 3610. [Google Scholar] [CrossRef]
- Abad, M.S.S.; Ma, J.; Zhang, D.; Ahmadyar, A.S.; Marzooghi, H. Probabilistic Assessment of Hosting Capacity in Radial Distribution Systems. IEEE Trans. Sustain. Energy 2018, 9, 1935–1947. [Google Scholar] [CrossRef]
- Torquato, R.; Salles, D.; Pereira, C.O.; Meira, P.C.M.; Freitas, W. A Comprehensive Assessment of PV Hosting Capacity on Low-Voltage Distribution Systems. IEEE Trans. Power Deliv. 2018, 33, 1002–1012. [Google Scholar] [CrossRef]
- Oliveira, T.; Carvalho, P.; Ribeiro, P.; Bonatto, B. PV Hosting Capacity Dependence on Harmonic Voltage Distortion in Low-Voltage Grids: Model Validation with Experimental Data. Energies 2018, 11, 465. [Google Scholar] [CrossRef]
- Arshad, A.; Püvi, V.; Lehtonen, M. Monte Carlo-Based Comprehensive Assessment of PV Hosting Capacity and Energy Storage Impact in Realistic Finnish Low-Voltage Networks. Energies 2018, 11, 1467. [Google Scholar] [CrossRef]
- Ding, F.; Mather, B. On Distributed PV Hosting Capacity Estimation, Sensitivity Study, and Improvement. IEEE Trans. Sustain. Energy 2017, 8, 1010–1020. [Google Scholar] [CrossRef]
- Al-Saadi, H.; Zivanovic, R.; Al-Sarawi, S.F. Probabilistic Hosting Capacity for Active Distribution Networks. IEEE Trans. Ind. Inf. 2017, 13, 2519–2532. [Google Scholar] [CrossRef]
- Palacios-Garcia, E.; Moreno-Muñoz, A.; Santiago, I.; Moreno-Garcia, I.; Milanés-Montero, M. PV Hosting Capacity Analysis and Enhancement Using High Resolution Stochastic Modeling. Energies 2017, 10, 1488. [Google Scholar] [CrossRef]
- Ding, F.; Mather, B.; Gotseff, P. Technologies to increase PV hosting capacity in distribution feeders. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; 2016; pp. 1–5. [Google Scholar]
- Dubey, A.; Santoso, S.; Maitra, A. Understanding photovoltaic hosting capacity of distribution circuits. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Mulenga, E.; Bollen, M.H.J.; Etherden, N. A review of hosting capacity quantification methods for photovoltaics in low-voltage distribution grids. Int. J. Electr. Power Energy Syst. 2020, 115, 105445. [Google Scholar] [CrossRef]
- Ismael, S.M.; Aleem, S.H.A.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Freitas, S.; Catita, C.; Redweik, P.; Brito, M.C. Modelling solar potential in the urban environment: State-of-the-art review. Renew. Sustain. Energy Rev. 2015, 41, 915–931. [Google Scholar] [CrossRef]
- Conti, S.; Raiti, S. Probabilistic load flow using Monte Carlo techniques for distribution networks with photovoltaic generators. Sol. Energy 2007, 81, 1473–1481. [Google Scholar] [CrossRef]
- Navarro-Espinosa, A.; Ochoa, L.F. Increasing the PV hosting capacity of LV networks: OLTC-fitted transformers vs. reinforcements. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2015; pp. 1–5. [Google Scholar]
- Klucher, T.M. Evaluation of models to predict insolation on tilted surfaces. Sol. Energy 1979, 23, 111–114. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Manz, H.; Felsmann, C.; Strachan, P.A.; Frank, T.; Maxwell, G.M. Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation. Sol. Energy 2007, 81, 254–267. [Google Scholar] [CrossRef]
- El-Khattam, W.; Hegazy, Y.; Salama, M. Investigating distributed generation systems performance using Monte Carlo simulation. IEEE Trans. Power Syst. 2006, 21, 524–532. [Google Scholar] [CrossRef]
- Torquato, R.; Shi, Q.; Xu, W.; Freitas, W. A Monte Carlo simulation platform for studying low voltage residential networks. IEEE Trans. Smart Grid 2014, 5, 2766–2776. [Google Scholar] [CrossRef]
- Vallée, F.; Klonari, V.; Lisiecki, T.; Durieux, O.; Moiny, F.; Lobry, J. Development of a probabilistic tool using Monte Carlo simulation and smart meters measurements for the long term analysis of low voltage distribution grids with photovoltaic generation. Int. J. Electr. Power Energy Syst. 2013, 53, 468–477. [Google Scholar] [CrossRef]
- Ruiz-Rodriguez, F.; Hernandez, J.; Jurado, F. Probabilistic load flow for radial distribution networks with photovoltaic generators. IET Renew. Power Gener. 2012, 6, 110–121. [Google Scholar] [CrossRef]
- Widén, J.; Wäckelgård, E.; Paatero, J.; Lund, P. Impacts of distributed photovoltaics on network voltages: Stochastic simulations of three Swedish low-voltage distribution grids. Electr. Power Syst. Res. 2010, 80, 1562–1571. [Google Scholar] [CrossRef]
- Grabner, M.; Bregar, Z.; Ivanjko, Š.; Valenčič, L. Improved model for the spatial load forecasting of the Slovenian distribution network. CIRED Open Access Proc. J. 2017, 2017, 2354–2357. [Google Scholar] [CrossRef]
- Kastelec, D.; Rakovec, J.; Zakšek, K.; Medved, S. Sončna Energija v Sloveniji; Založba ZRC, ZRC SAZU: Ljubljana, Slovenia, 2007. [Google Scholar]
- Thurner, L.; Scheidler, A.; Schäfer, F.; Menke, J.-H.; Dollichon, J.; Meier, F.; Minecke, S.; Braun, M. Pandapower—An open-source python tool for convenient modeling, analysis, and optimization of electric power systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
| Variable Name | Unit | Explanation |
|---|---|---|
| Irradiance | radiant flux received by a surface per unit area; | |
| Radiant exposure | radiant energy received by a surface per unit area. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grabner, M.; Souvent, A.; Suljanović, N.; Košir, A.; Blažič, B. Probabilistic Methodology for Calculating PV Hosting Capacity in LV Networks Using Actual Building Roof Data. Energies 2019, 12, 4086. https://doi.org/10.3390/en12214086
Grabner M, Souvent A, Suljanović N, Košir A, Blažič B. Probabilistic Methodology for Calculating PV Hosting Capacity in LV Networks Using Actual Building Roof Data. Energies. 2019; 12(21):4086. https://doi.org/10.3390/en12214086
Chicago/Turabian StyleGrabner, Miha, Andrej Souvent, Nermin Suljanović, Andrej Košir, and Boštjan Blažič. 2019. "Probabilistic Methodology for Calculating PV Hosting Capacity in LV Networks Using Actual Building Roof Data" Energies 12, no. 21: 4086. https://doi.org/10.3390/en12214086
APA StyleGrabner, M., Souvent, A., Suljanović, N., Košir, A., & Blažič, B. (2019). Probabilistic Methodology for Calculating PV Hosting Capacity in LV Networks Using Actual Building Roof Data. Energies, 12(21), 4086. https://doi.org/10.3390/en12214086








