Behaviour of Distribution Grids with the Highest PV Share Using the Volt/Var Control Chain Strategy
Abstract
1. Introduction
2. Materials and Methods
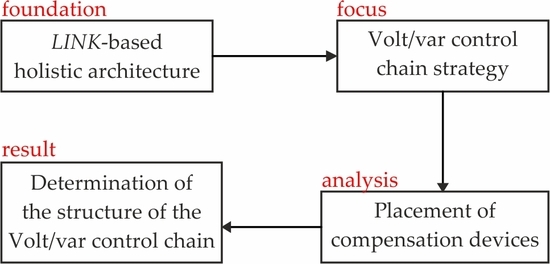
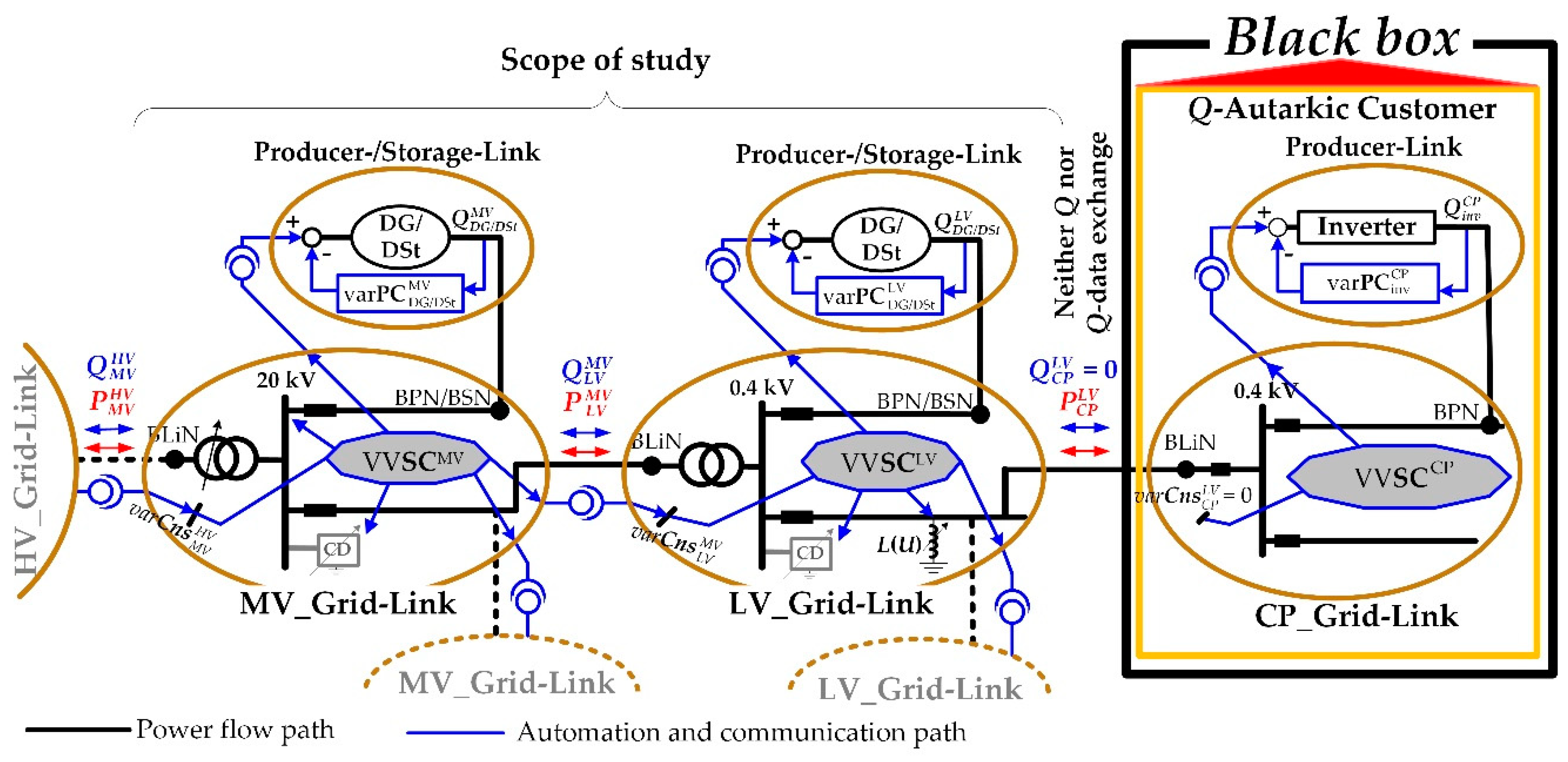
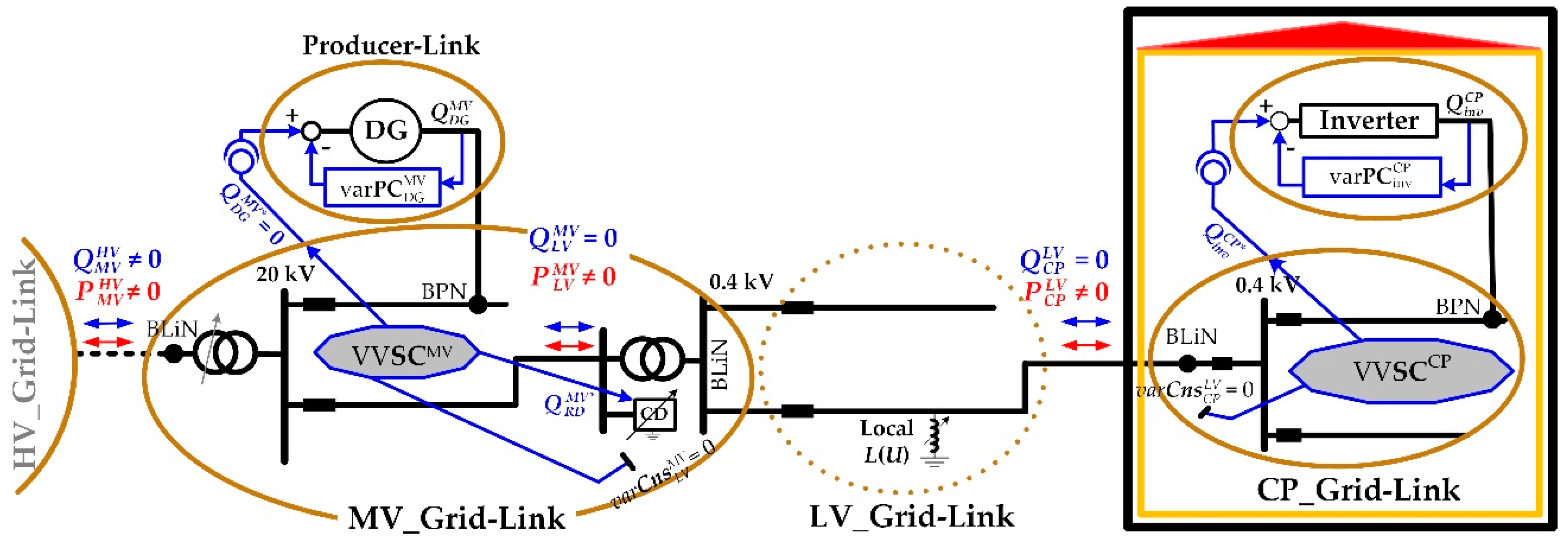
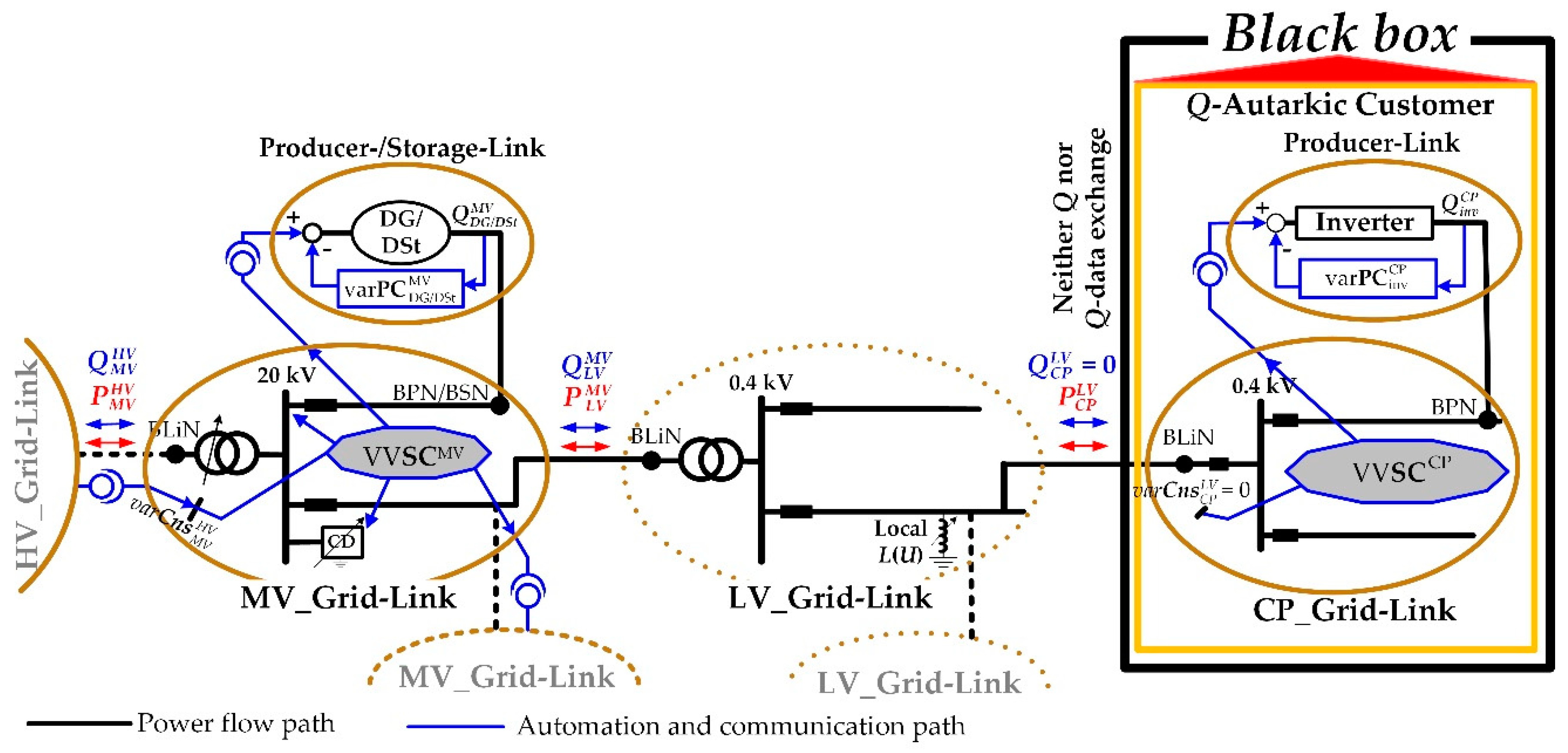
2.1. Fundamentals of Volt/Var Control Chain Strategy
- (a)
- the voltage set-point for the primary control of the supplying transformer and other transformers included in the MV_link-grid (e.g., 34.5 kV/11 kV, etc.) that have On-Load-Tap-Changer (OLTC);
- (b)
- the var set-points for the primary controls of all RDs included in the MV_link-grid;
- (c)
- the var set-points for the primary controls of all DGs and Distributed Storages (DSt) connected to the MV_link-grid;
- (d)
- the var set-points for the Volt/var secondary controls of all neighbour MV_ or LV_grid-links, while respecting the var constraint at the border to the HV_link-grid.
- (a)
- the voltage and var set-points for the primary controls of all RDs included in the LV_link-grid;
- (b)
- the var set-points for the primary controls of all DGs and DSts connected to the LV_link-grid;
- (c)
- the var set-points for the Volt/var secondary controls of all neighbour LV_ or CP_grid-links, while respecting the var constraint at the border to the MV_link-grid.
- (d)
- calculates in real time
- (e)
- the var set-point for the primary control of the PV-inverter connected to CP_link-grid; while respecting the var constraint at the border to the LV_link-grid.
2.2. Model Description
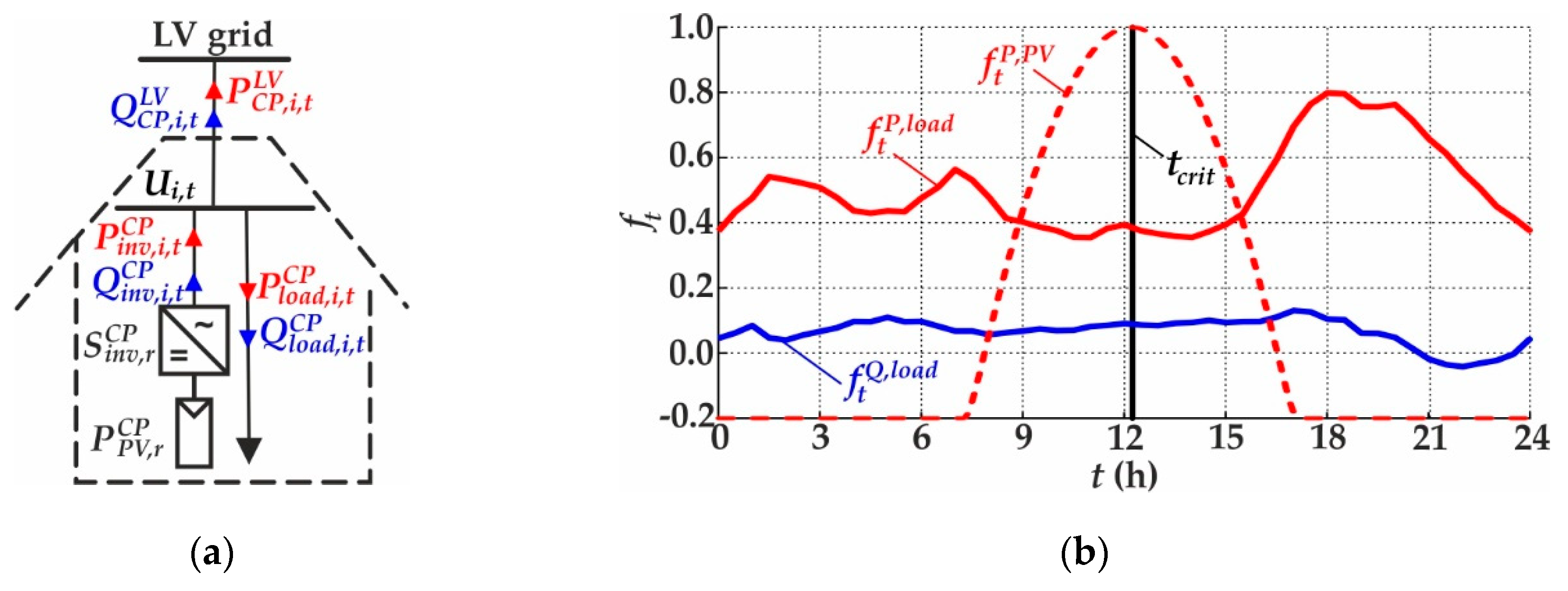
2.2.1. Customer Plant Model
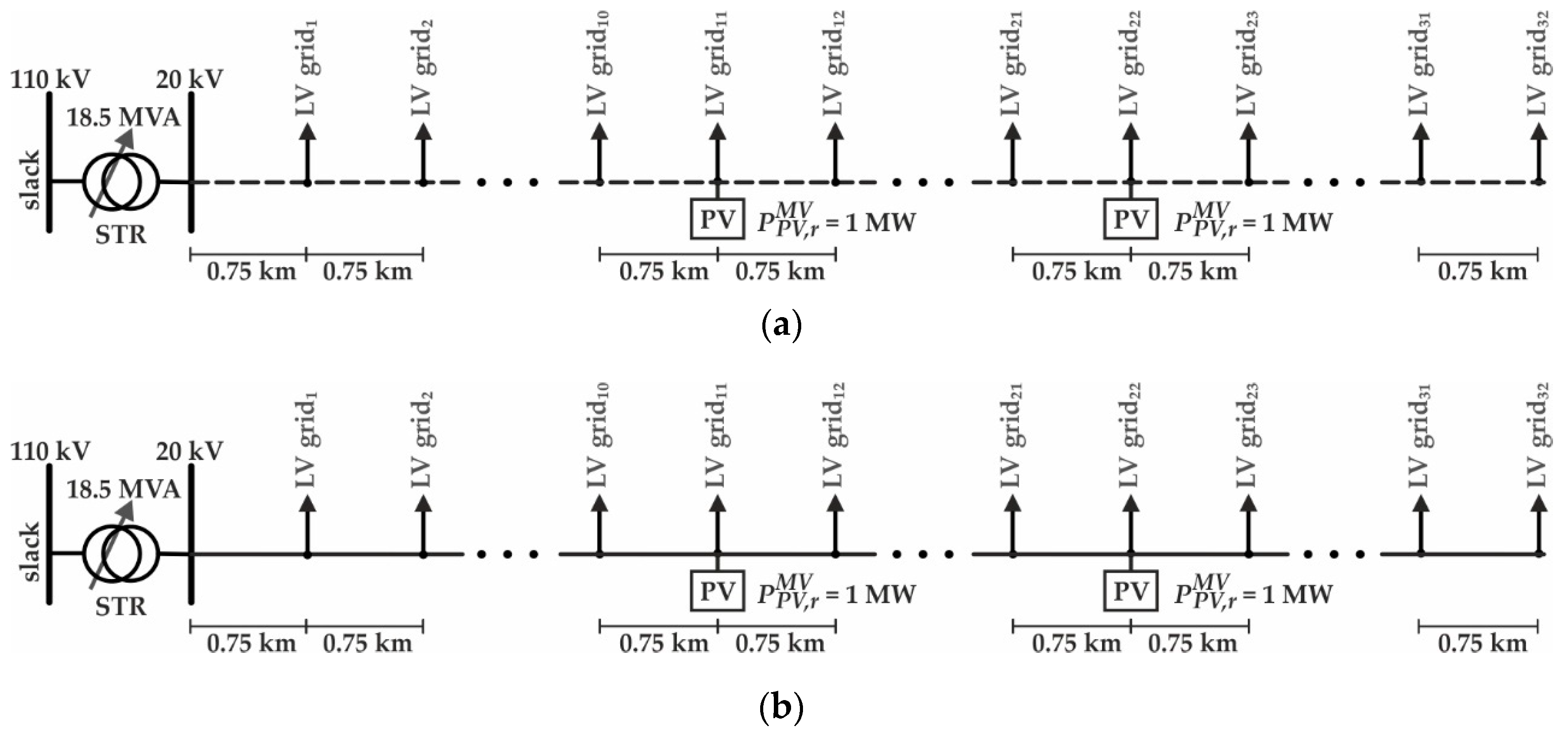
2.2.2. Distribution Grid Models
2.3. Simulated Control Setups
3. Results and Discussion
3.1. Behaviour of Distribution Grids
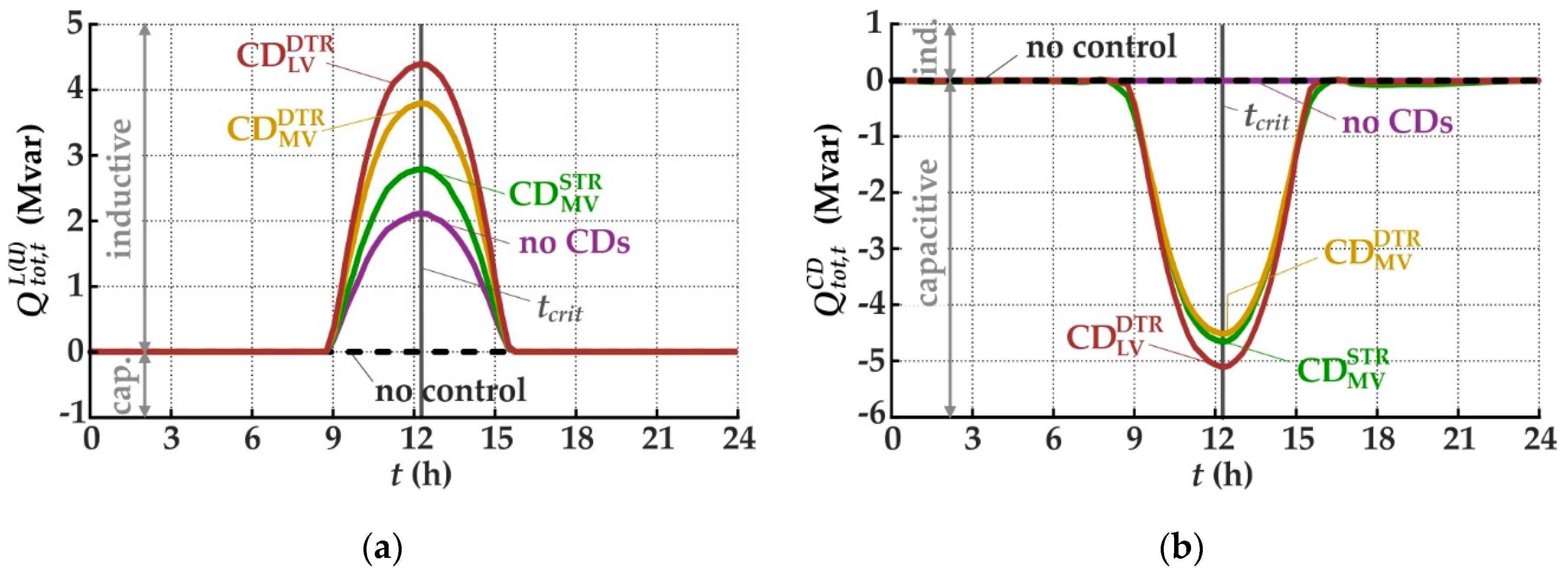
- (a)
- the total reactive power consumption of all L(U)s included in the LV_link-grids, ;
- (b)
- the total reactive power contribution of all CDs included in MV_ or LV_link-grids, ;
- (c)
- the reactive power exchange between HV_ and MV_link-grid, , at the STR primary side;
- (d)
- the active power losses of the distribution grid, , including losses of transformers, cables and overhead lines;
- (e)
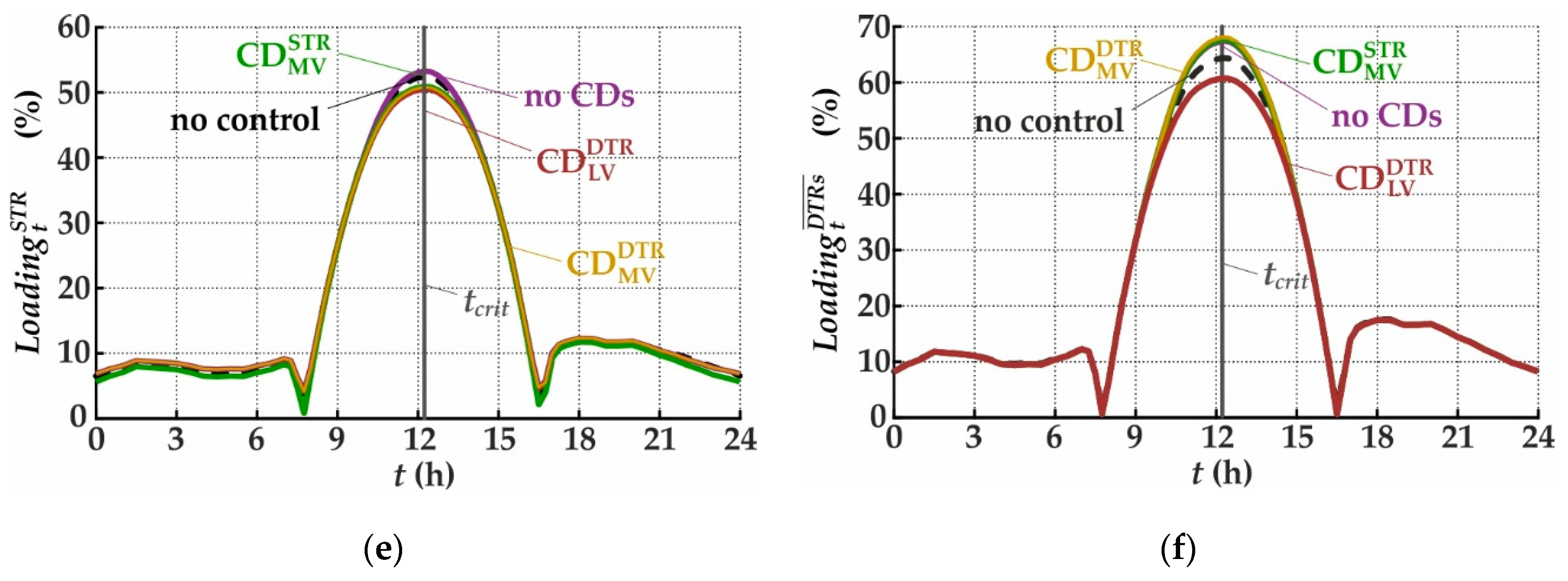
- the STR loading, ;
- (f)
- the mean loading of all DTRs, , which is calculated as inwhere is the loading of the DTR k at time-point t, and 32 is the number of DTRs;
- (g)
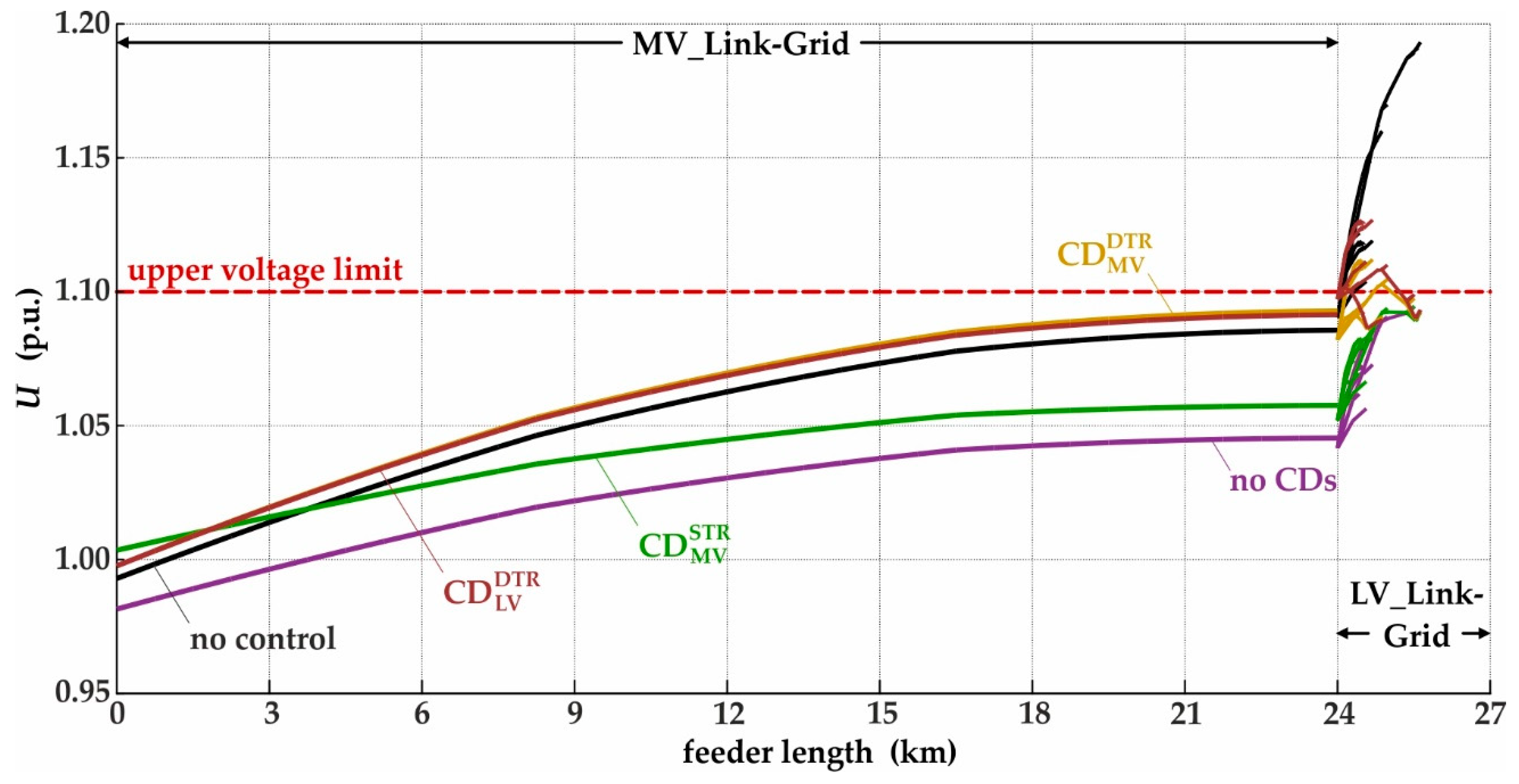
- the voltage limit violation index, , which is calculated as inwhere is the number of LV_link-grid nodes that violate the upper voltage limit at time-point t; is the number of LV_link-grid nodes that violate the lower voltage limit at time-point t; is the voltage of the LV_link-grid node u with upper voltage limit violation at time-point t; is the voltage of the LV_link-grid node v with lower voltage limit violation at time-point t; is the upper voltage limit; and is the lower voltage limit. Only LV_link-grid nodes are considered because the simulations show that no voltage limit violations appear in the MV_link-grid.
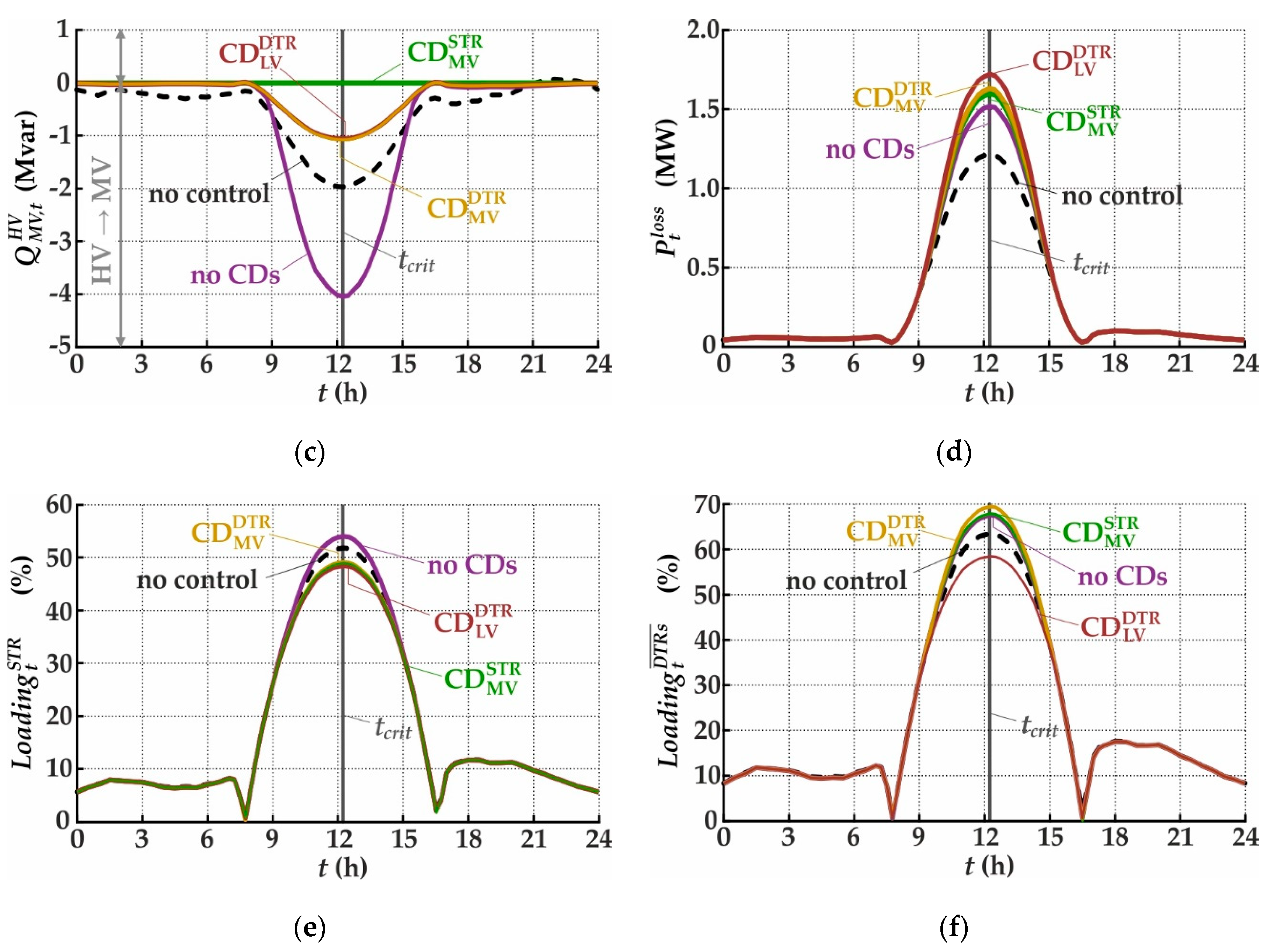
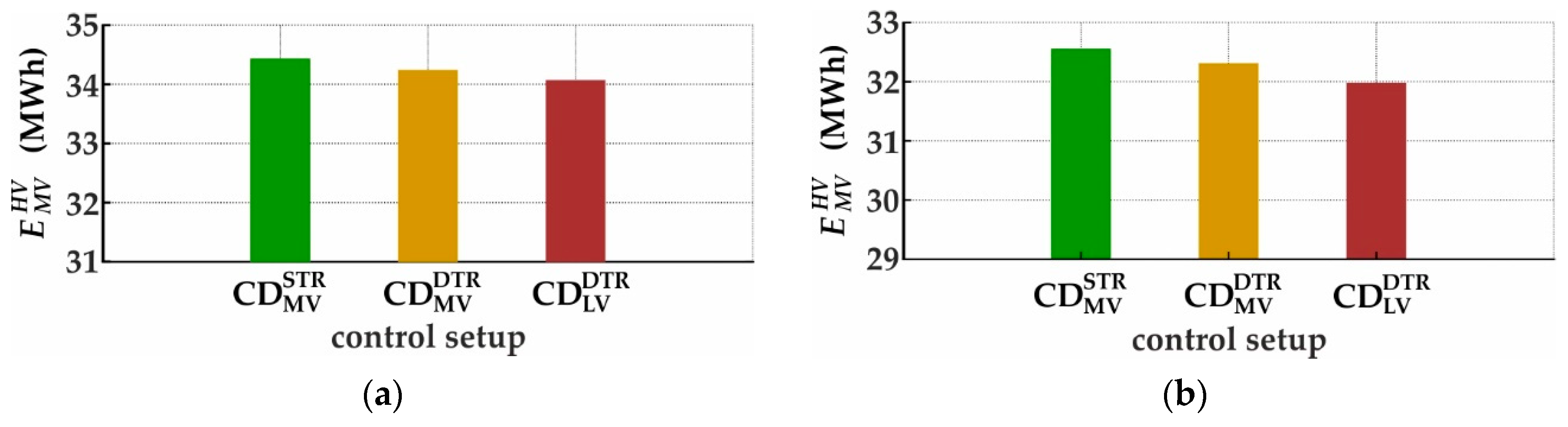
3.1.1. Distribution Grid with Cable Conductors in MV Level
3.1.2. Distribution Grid with Overhead Conductors in MV Level
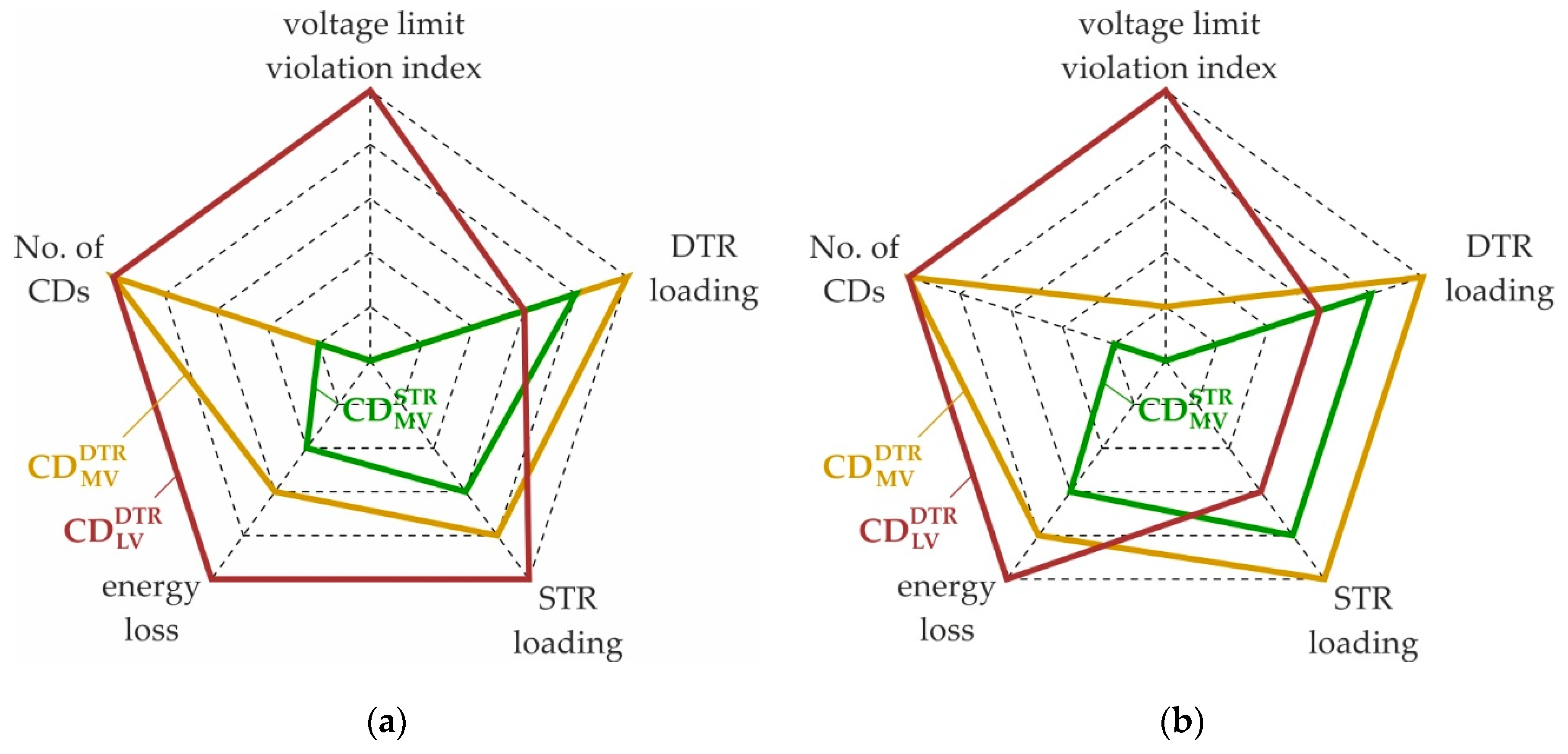
3.1.3. Effect of CD Placement
3.2. Discussion
- (a)
- MV_ and LV_link-grids have the same operator and as a result they do not have external interfaces between each other [16];
- (b)
- No reactive power is exchanged between LV_link-grids and CPs because of the Q-autarky of the latter;
- (c)
- No distributed energy resources are foreseen to deliver reactive power to the LV_link-grids;
- (d)
- At each LV feeder with voltage limit violation potential is installed one locally controlled L(U).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| BLiN | Boundary link node | MV | Medium voltage |
| BPN | Boundary producer node | OLTC | On load tap changer |
| BSN | Boundary storage node | OpEx | Operational expenditures |
| CapEx | Capital expenditures | PC | Primary control |
| CD | Compensation device | PV | Photovoltaic |
| CP | Customer plant | RD | Reactive device |
| DG | Distributed generation | RPM | Reactive power margin |
| DSO | Distribution system operator | SC | Secondary control |
| DSt | Distributed storage | STR | Supplying transformer |
| DTR | Distribution transformer | TSO | Transmission system operator |
| HV | High voltage | VCRD | Voltage control reactive device |
| ICT | Information and communications technology | VVC | Volt/var control |
| LC | Local control | VVSC | Volt/var secondary control |
| LV | Low voltage | ||
| constraint at the border to the HV_link-grid | Primary controls of DGs and DSts connected to the LV_link-grids | ||
| Var constraint at the border to the HV_link-grid | Primary controls of RDs included in the LV_link-grids | ||
| Var constraint at the border to the MV_link-grid | Primary controls of PV-inverters connected to CP_link-grids | ||
| Var constraint at the border to the LV_link-grid | Primary controls of the STR or other transformers with OLTC included in the MV_link-grid | ||
| Local controls of L(U)s included in the LV_link-grids | VVSC of MV_grid-link | ||
| Primary controls of CDs included in the MV_link-grid | VVSC of LV_grid-link | ||
| Primary controls of DGs and DSts connected to the MV_link-grid | VVSC of CP_grid-link | ||
| Primary controls of RDs included in the MV_link-grid | VVSC of neighbour MV_ or LV_grid-links | ||
| Primary controls of CDs included in the LV_link-grids | VVSC of neighbour LV_ or CP_grid-links |
| , , | Active power ZIP coefficients for time-point t. |
| , , | Reactive power ZIP coefficients for time-point t. |
| Active energy exchange between MV_ and HV_link-grid over the all-time horizon. | |
| Active energy loss over the all-time horizon. | |
| Active power load profile factor at time-point t. | |
| Reactive power load profile factor at time-point t. | |
| Active power production profile factor at time-point t. | |
| Loading of the DTR k at time-point t. | |
| Mean loading of all DTRs at time-point t. | |
| The average DTRs’ loading over the all-time horizon. | |
| The STR loading at time-point t. | |
| The average STR loading over the all-time horizon. | |
| Number of LV_link-grid nodes that violate the upper voltage limit at time-point t. | |
| Number of LV_link-grid nodes that violate the lower voltage limit at time-point t. | |
| N | Number of conducted load-flow simulations per control setup and distribution grid model. |
| Active power production of the PV-system of the CP i at time-point t. | |
| Active power consumption of the loads of the CP i at time-point t. | |
| Module-rating of the PV-system of each CP. | |
| Active power flow from the CP i to LV_link-grid at time-point t. | |
| Active power consumption of each CP’s load for nominal grid voltage at time-point t. | |
| Peak active power demand of each CP’s load. | |
| Active power production of each PV-system connected to the MV_link-grid at time-point t. | |
| Module-rating of each PV-system connected to the MV_link-grid. | |
| Active power losses of the distribution grid at time-point t. | |
| Active power flow from the MV_ to HV_link-grid at time-point t. | |
| Reactive power production of the PV-system of the CP i at time-point t. | |
| Reactive power consumption of the loads of the CP i at time-point t. | |
| Reactive power flow from the CP i to LV_link-grid at time-point t. | |
| Reactive power consumption of each CP’s load for nominal grid voltage at time-point t. | |
| Total reactive power consumption of all L(U)s included in the LV_link-grids at time-point t. | |
| Total reactive power contribution of all CDs included in MV_ or LV_link-grids at time-point t. | |
| Reactive power flow from the MV_ to HV_link-grid at time-point t. | |
| Inverter-rating of the PV-system of each CP. | |
| Inverter-rating of each PV-system connected to the MV_link-grid. | |
| Actual voltage at the BLiN of the CP i at time-point t. | |
| Nominal voltage of LV_link-grids. | |
| Voltage of the LV_link-grid node u with upper voltage limit violation at time-point t. | |
| Voltage of the LV_link-grid node v with lower voltage limit violation at time-point t. | |
| Upper voltage limit. | |
| Lower voltage limit. | |
| Voltage limit violation index at time-point t. | |
| Average voltage limit violation index over the all-time horizon. | |
| Critical time-point, where the maximal PV production occurs. | |
| Time-step used to sample the load and production profiles. |
References
- Guterres, A. Secretary-General’s Remarks at High-Level Meeting on Climate and Sustainable Development, 28 March 2019; United Nations: New York, NY, USA, 2019; Available online: https://www.un.org/sg/en/content/sg/statement/2019-03-28/secretary-generals-remarks-high-level-meeting-climate-and-sustainable-development-delivered (accessed on 4 October 2019).
- Environmental Protection Agency. Distributed Generation of Electricity and Its Environmental Impacts. Available online: https://www.epa.gov/energy/distributed-generation-electricity-and-its-environmental-impacts (accessed on 4 October 2019).
- Eurelectric. Power Distribution in Europe: Facts and Figures. 2013. Available online: https://www3.eurelectric.org/media/113155/dso_report-web_final-2013-030-0764-01-e.pdf (accessed on 4 October 2019).
- Bollen, M.H.J.; Sannino, A. Voltage control with inverter-based distributed generation. IEEE Trans. Power Deliv. 2005, 20, 519–520. [Google Scholar]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovolt. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Bae, Y.; Vu, T.; Kim, R. Implemental Control Strategy for Grid Stabilization of Grid-Connected PV System Based on German Grid Code in Symmetrical Low-to-Medium Voltage Network. IEEE Trans. Energy Convers. 2013, 28, 619–631. [Google Scholar] [CrossRef]
- Esslinger, P.; Witzmann, R. Improving grid transmission capacity and voltage equality in low-voltage grids with a high proportion of distributed power plants. In Proceedings of the International Conference Smart Grid Clean Energy Technologies, Chengdu, China, 27–30 September 2011. [Google Scholar]
- Malekpour, A.R.; Pahwa, A. Reactive power and voltage control in distribution systems with photovoltaic generation. In Proceedings of the North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012. [Google Scholar]
- Ciocia, A.; Boicea, V.A.; Chicco, G.; Leo, P.D.; Mazza, A.; Pons, E.; Spertino, F.; Hadj-Said, N. Voltage Control in Low-Voltage Grids Using Distributed Photovoltaic Converters and Centralized Devices. IEEE Trans. Ind. Appl. 2019, 55, 225–237. [Google Scholar] [CrossRef]
- NERC. Reliability Guideline: Reactive Power Planning. December 2016. Available online: https://www.nerc.com/comm/PC_Reliability_Guidelines_DL/Reliability%20Guideline%20-%20Reactive%20Power%20Planning.pdf (accessed on 4 October 2019).
- Chiang, H.D.; Wang, J.C.; Tong, J.; Darling, G. Optimal capacitor placement, replacement and control in large-scale unbalanced distribution systems: Modeling and a new formulation. IEEE Trans. Power Syst. 1995, 10, 356–362. [Google Scholar] [CrossRef]
- Lund, P. The Danish cell project—Part 1: Background and general approach. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, Fl, USA, 24–28 June 2007. [Google Scholar]
- ETIP SNET. Holistic Architectures for Future Power Systems. 8 March 2019. Available online: https://www.etip-snet.eu/white-paper-holistic-architectures-future-power-systems/ (accessed on 4 October 2019).
- Ilo, A. The Energy Supply Chain Net. Energy Power Eng. 2013, 5, 384–390. [Google Scholar] [CrossRef][Green Version]
- Ilo, A. Effects of the Reactive Power Injection on the Grid—The Rise of the Volt/var Interaction Chain. Smart Grid Renew. Energy 2016, 7, 217–232. [Google Scholar] [CrossRef]
- Ilo, A. Link—The Smart Grid Paradigm for a Secure Decentralized Operation Architecture. Electr. Power Syst. Res. 2016, 131, 116–125. [Google Scholar] [CrossRef]
- Ilo, A.; Schultis, D.-L. Low-voltage grid behaviour in the presence of concentrated var-sinks and var-compensated customers. Electr. Power Syst. Res. 2019, 171, 54–65. [Google Scholar] [CrossRef]
- Schultis, D.-L.; Ilo, A. A new Volt/var local control strategy in low-voltage grids in the context of the LINK-based holistic architecture. In Proceedings of the IEWT, Vienna, Austria, 13–15 February 2019. [Google Scholar]
- Schultis, D.-L.; Ilo, A.; Schirmer, C. Overall performance evaluation of reactive power control strategies in low voltage grids with high prosumer share. Electr. Power Syst. Res. 2019, 168, 336–349. [Google Scholar] [CrossRef]
- Schultis, D.-L. Comparison of Local Volt/var Control Strategies for PV Hosting Capacity Enhancement of Low Voltage Feeders. Energies 2019, 12, 1560. [Google Scholar] [CrossRef]
- Schirmer, C.; Ilo, A. The impact of the uncoordinated local control of decentralized generation on the reactive power margin. In System Operation and Control, Proceedings of the CIGRE Session 47, Paris, France, 26–31 August 2018; Cigre: Paris, France, 2018. [Google Scholar]
- Ilo, A.; Schultis, D.-L.; Schirmer, C. Effectiveness of Distributed vs. Concentrated Volt/Var Local Control Strategies in Low-Voltage Grids. Appl. Sci. 2018, 8, 1382. [Google Scholar] [CrossRef]
- Schultis, D.-L. Volt/Var Behaviour of Low Voltage Grid-Link in European Grid Type. Master’s Thesis, TU Wien, Viena, Austria, November 2017. [Google Scholar]
- E-Control, Technische und organisatorische Regeln für Betreiber und Benutzer von Netzen. TOR Erzeuger: Anschluss und Parallelbetrieb von Stromerzeugungsanlagen des Typs A und von Kleinsterzeugungsanlagen. Version 1.0. 2019. Available online: https://www.e-control.at/documents/1785851/1811582/TOR+Erzeuger+Typ+A+V1.0.pdf/6342d021-a5ce-3809-2ae5-28b78e26f04d?t=1562757767659 (accessed on 4 October 2019).
- Schultis, D.-L.; Ilo, A. Adaption of the Current Load Model to Consider Residential Customers Having Turned to LED Lighting. In Proceedings of the IEEE APPEEC, Macao, China, 1–4 December 2019. Accepted for Publication. [Google Scholar]
- Schultis, D.-L. Daily Load Profiles and ZIP Models of Current and New Residential Customers; Mendeley Data; Elsevier: Amsterdam, The Netherlands, 2019; Volume 1. [Google Scholar] [CrossRef]
- Schultis, D.-L.; Ilo, A. TUWien_LV_TestGrids; Mendeley Data; Elsevier: Amsterdam, The Netherlands, 2018; Volume 1. [Google Scholar] [CrossRef]
- ZUQDE-Project, Final Report. 2012. Available online: https://www.energieforschung.at/assets/project/final-report/ZUQDE.pdf (accessed on 4 October 2019).
- Ilo, A.; Schaffer, W.; Rieder, T.; Dzafic, I. Dynamische Optimierung der Verteilnetze—Closed loop Betriebergebnisse. In Proceedings of the VDE Kongress, Stuttgart, Germany, 5–6 November 2012. [Google Scholar]
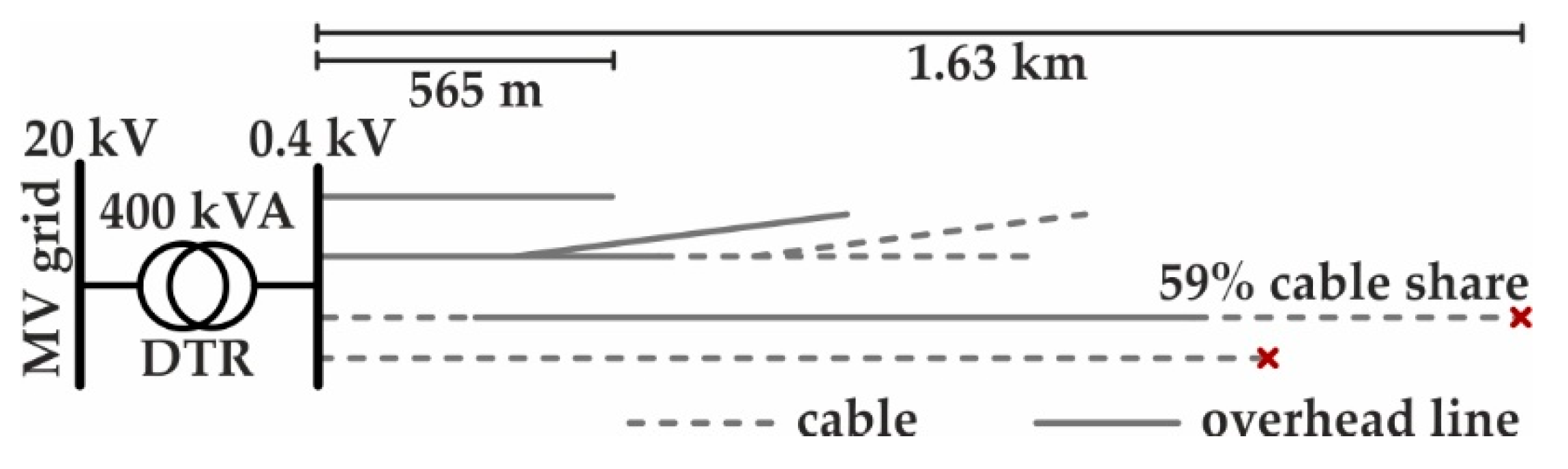
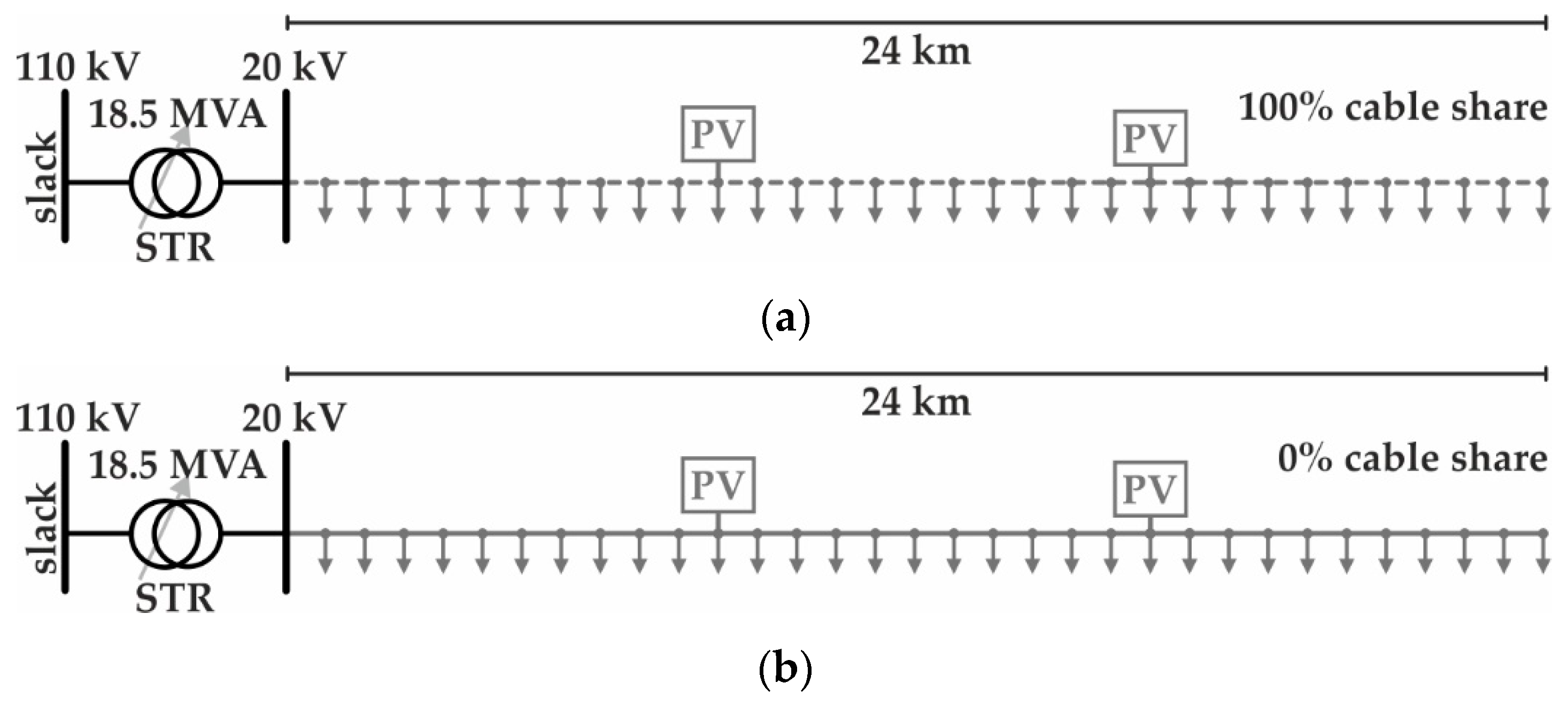
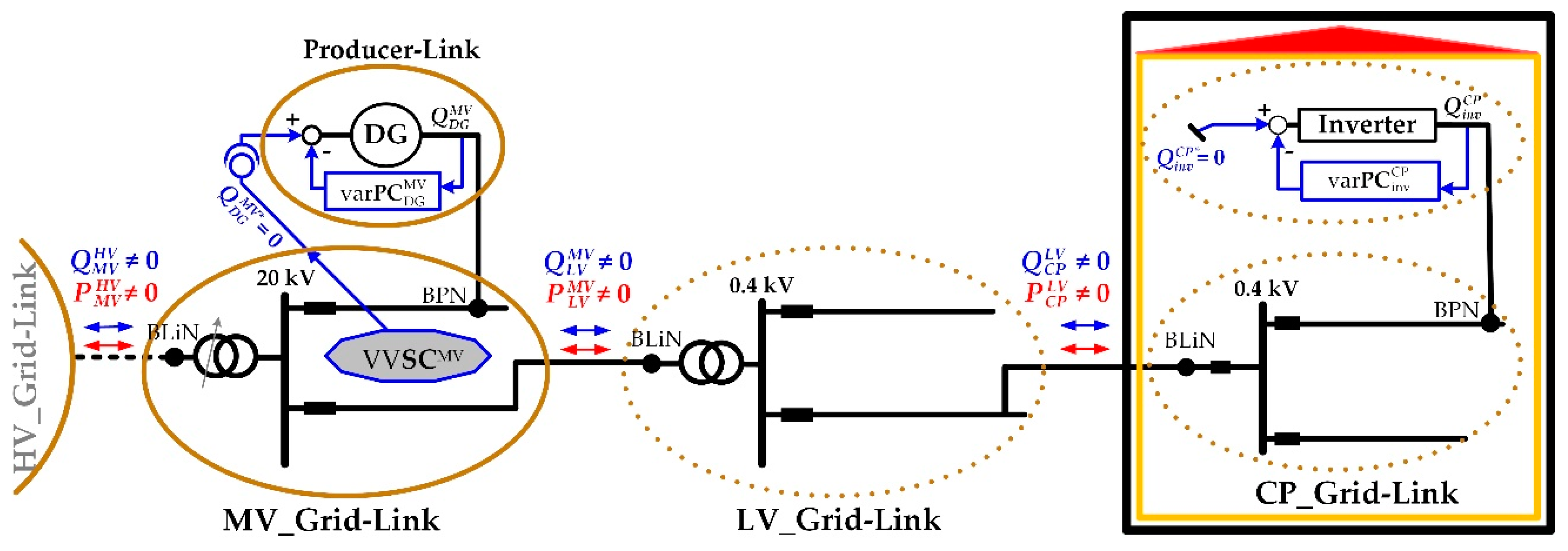
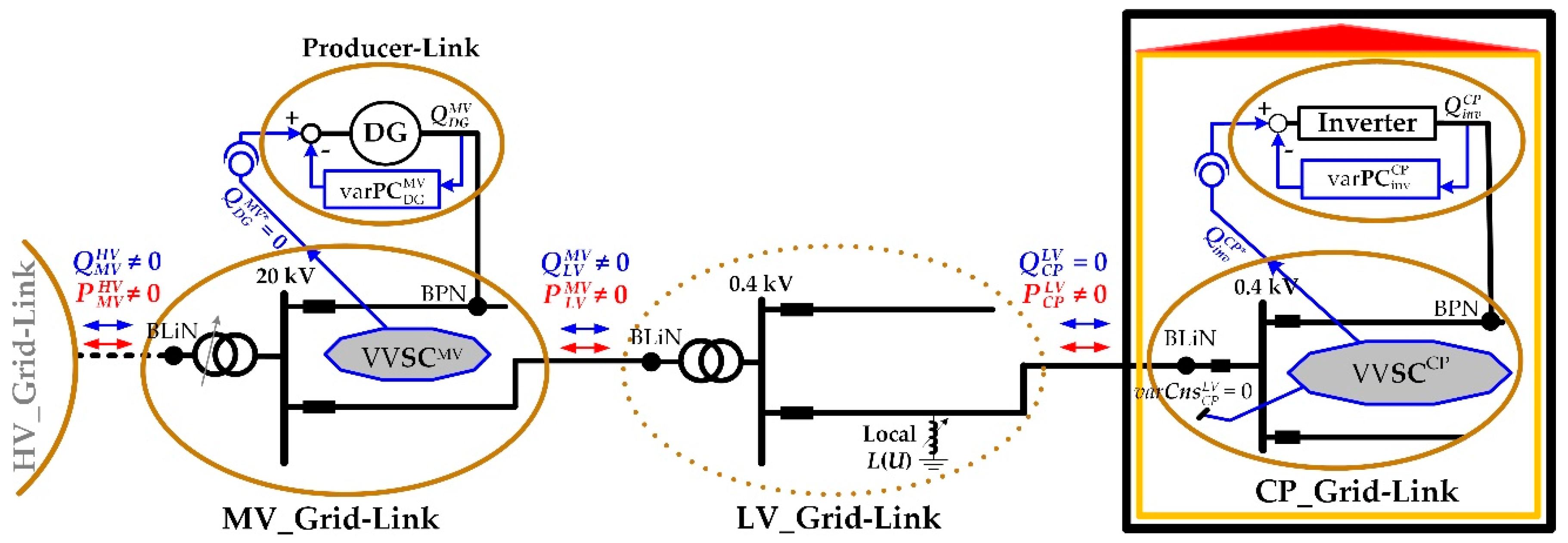




| Device | Purpose | Set-Point for varPC | |
|---|---|---|---|
| RD | VCRD | Voltage control | U* |
| CD | Var compensation | Q* | |
| Control Setup | (Mvar) | (Mvar) | (Mvar) | (MW) | (%) | (%) |
|---|---|---|---|---|---|---|
| No control | 0.00 | 0.00 | −0.70 | 0.94 | 52.44 | 64.40 |
| No CDs | 2.07 | 0.00 | −2.65 | 1.17 | 53.28 | 67.47 |
| 2.63 | −3.17 | 0.00 | 1.23 | 50.95 | 67.74 | |
| 3.03 | −3.67 | 0.11 | 1.25 | 50.81 | 68.11 | |
| 3.60 | −4.24 | 0.11 | 1.33 | 50.35 | 60.74 |
| Control Setup | (Mvar) | (Mvar) | (Mvar) | (MW) | (%) | (%) |
|---|---|---|---|---|---|---|
| No control | 0.00 | 0.00 | −1.97 | 1.22 | 51.85 | 63.53 |
| No CDs | 2.11 | 0.00 | −4.04 | 1.52 | 54.03 | 67.61 |
| 2.79 | −4.66 | 0.00 | 1.60 | 48.93 | 67.90 | |
| 3.80 | −4.52 | −1.08 | 1.63 | 49.04 | 69.42 | |
| 4.40 | −5.11 | −1.06 | 1.72 | 48.50 | 58.49 |
| Conductor Type in MV Level | Control Setup | (-) | (MWh) | (MWh) | (%) | (%) | No. of CDs (-) |
|---|---|---|---|---|---|---|---|
| Cable | 0.0000 | 6.5051 | 34.4286 | 17.9049 | 23.9071 | 1 | |
| 0.0000 | 6.6000 | 34.0946 | 18.5570 | 23.9116 | 32 | ||
| 0.0016 | 7.2863 | 33.8003 | 19.0885 | 23.5122 | 32 | ||
| Overhead | 0.0000 | 8.3320 | 32.5502 | 17.4605 | 23.9019 | 1 | |
| 0.1484 | 8.4739 | 32.3078 | 17.4682 | 24.1743 | 32 | ||
| 0.8307 | 8.8536 | 31.9763 | 17.3888 | 22.3732 | 32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultis, D.-L.; Ilo, A. Behaviour of Distribution Grids with the Highest PV Share Using the Volt/Var Control Chain Strategy. Energies 2019, 12, 3865. https://doi.org/10.3390/en12203865
Schultis D-L, Ilo A. Behaviour of Distribution Grids with the Highest PV Share Using the Volt/Var Control Chain Strategy. Energies. 2019; 12(20):3865. https://doi.org/10.3390/en12203865
Chicago/Turabian StyleSchultis, Daniel-Leon, and Albana Ilo. 2019. "Behaviour of Distribution Grids with the Highest PV Share Using the Volt/Var Control Chain Strategy" Energies 12, no. 20: 3865. https://doi.org/10.3390/en12203865
APA StyleSchultis, D.-L., & Ilo, A. (2019). Behaviour of Distribution Grids with the Highest PV Share Using the Volt/Var Control Chain Strategy. Energies, 12(20), 3865. https://doi.org/10.3390/en12203865