Optimization Strategy of SVC for Eliminating Electromagnetic Oscillation in Weak Networking Power Systems
Abstract
:1. Introduction
- (1)
- A quantitative method is provided for evaluating the influence of SVC on electromagnetic oscillation modes.
- (2)
- The contradiction between reactive power regulation ability and electromagnetic oscillation suppression ability of the SVC is revealed, which provides a basis for the definition of a comprehensive optimization objective function.
- (3)
- The performance criteria considering the damping characteristic and reactive performance of the SVC provides a new way to optimize PI parameters aiming at minimizing the negative effects of the SVC.
- (4)
- The process of SVC parameter optimization and the steps of multi-SVC parameter optimization in large power grid are proposed.
2. Problem Formulation
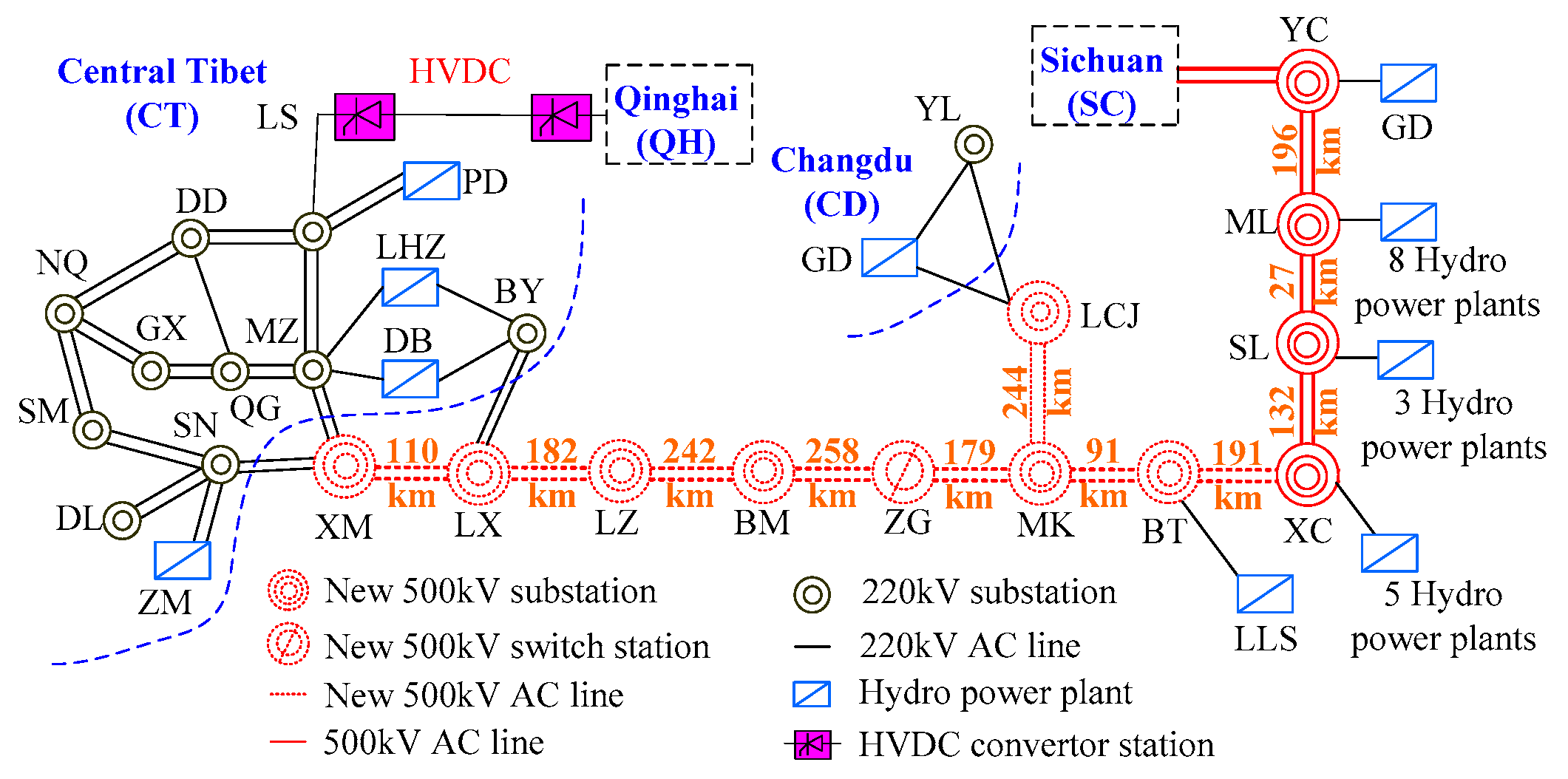
2.1. A Brief Introduction of CTAIP
- (1)
- The length of the tie-line reaches 1497 km, and there is no power supply on the transmission lines.
- (2)
- The maximum short circuit current of 500 kV bus is only 5 kA. In substation LZ, it is only 3–4 kA.
2.2. Electromagnetic Oscillation of CTAIP
3. Characteristics of Electromagnetic Oscillation Induced by SVCs
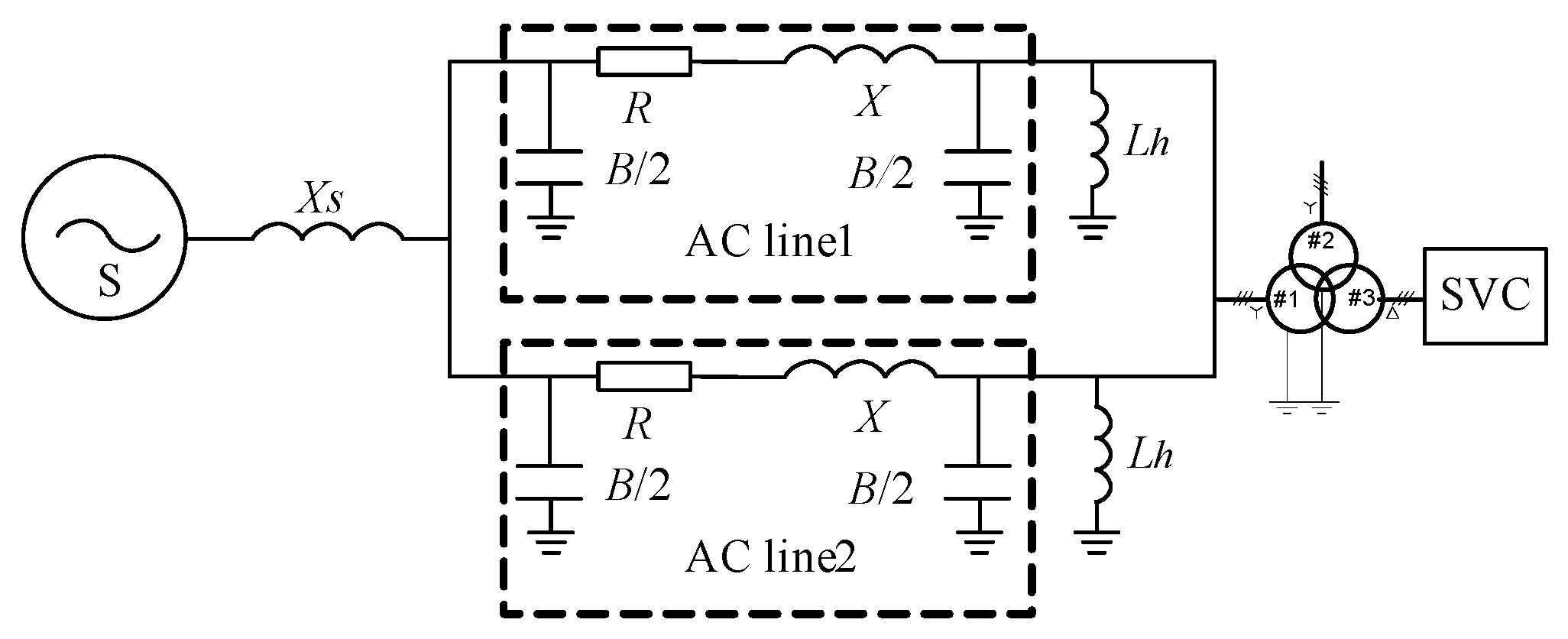
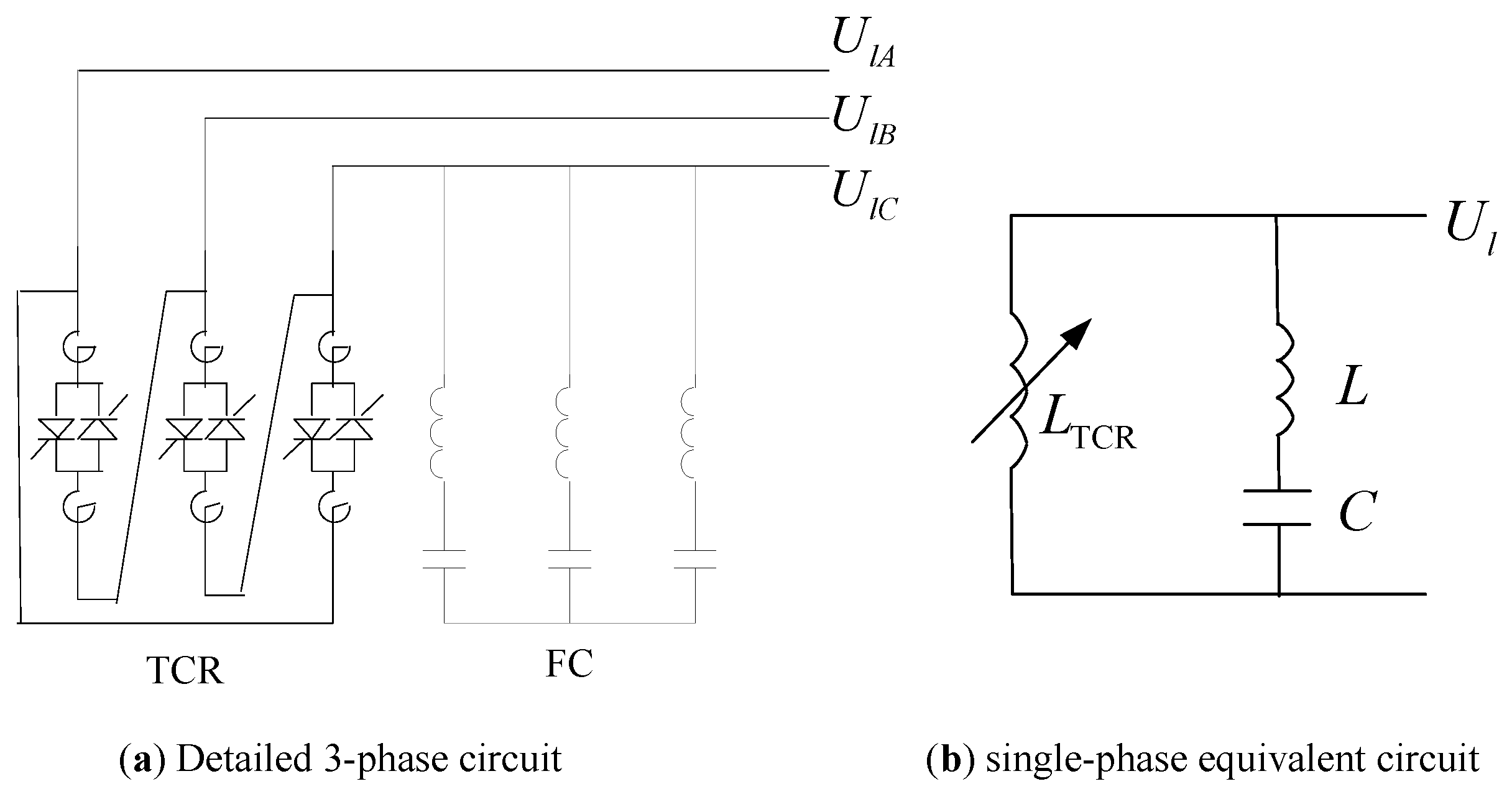
3.1. Simplified Model
3.2. Electromagnetic Oscillation Mode Calculation
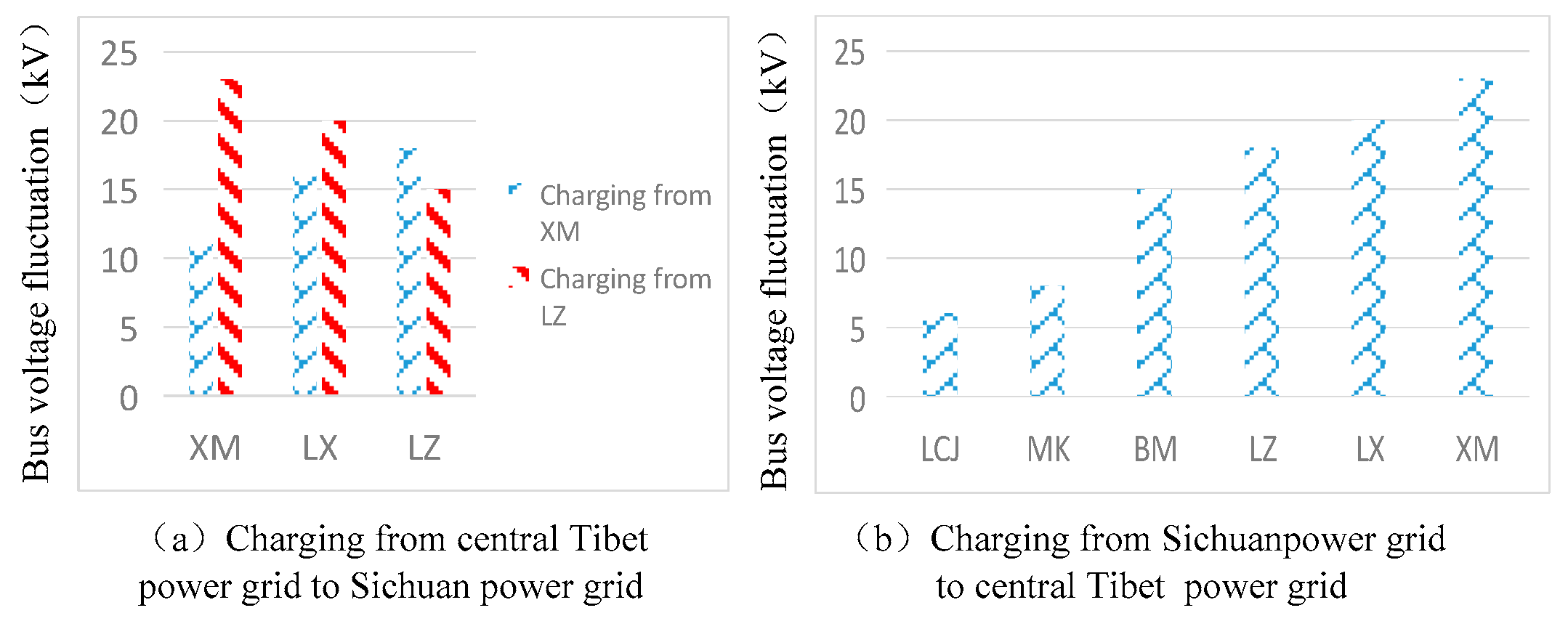
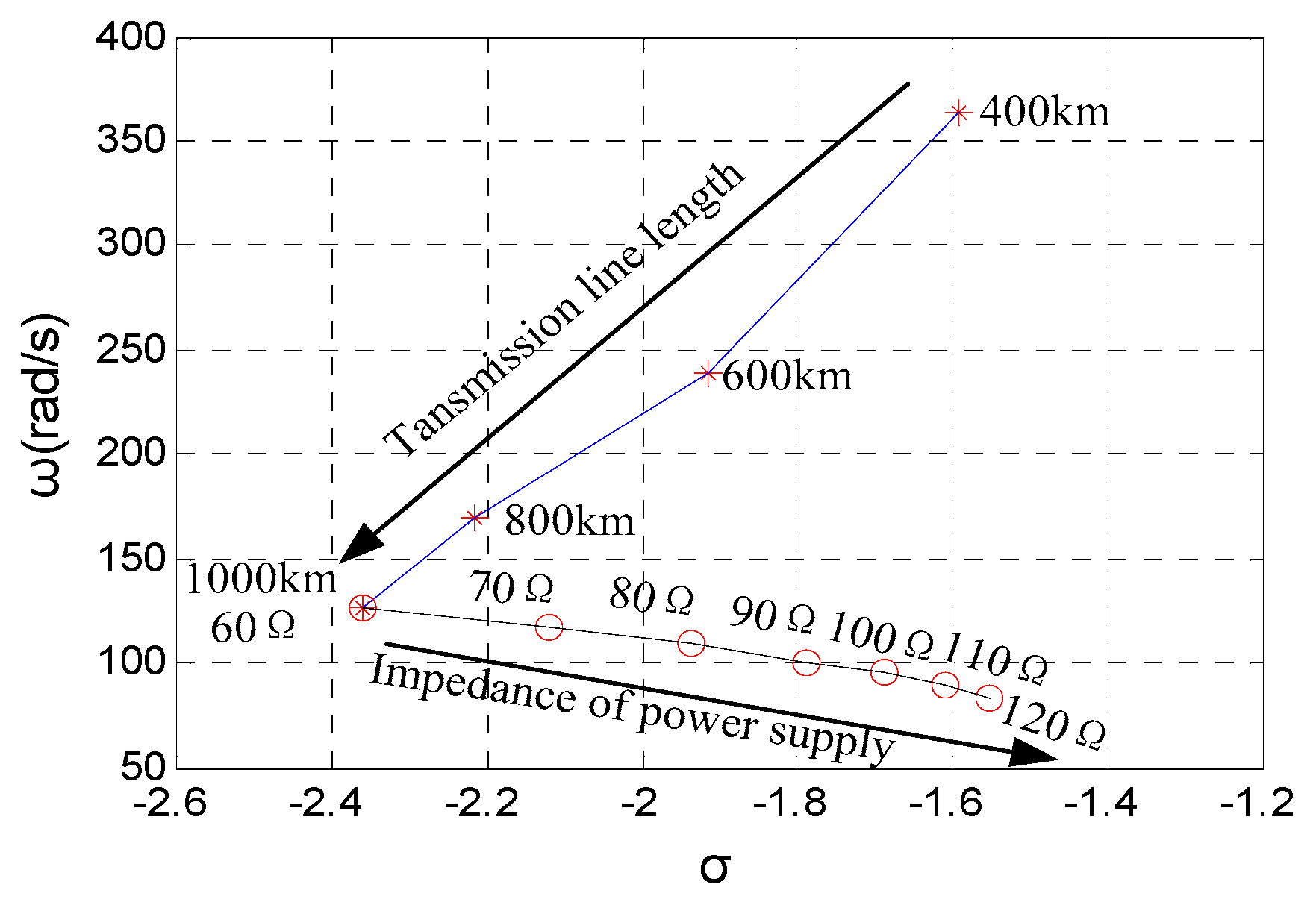
3.3. Key Influence Factors of the Electromagnetic Oscillation
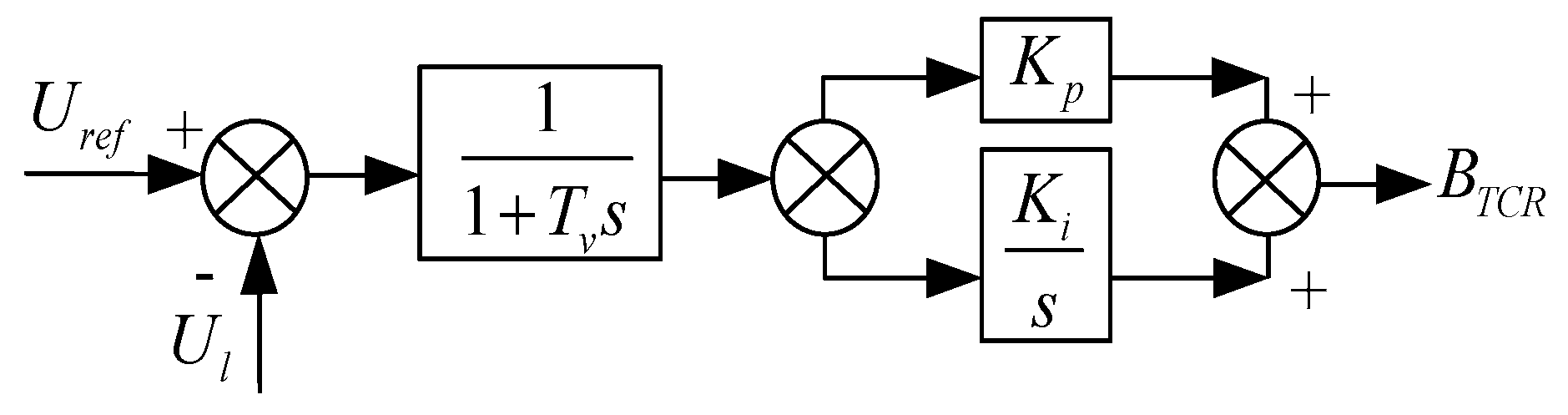
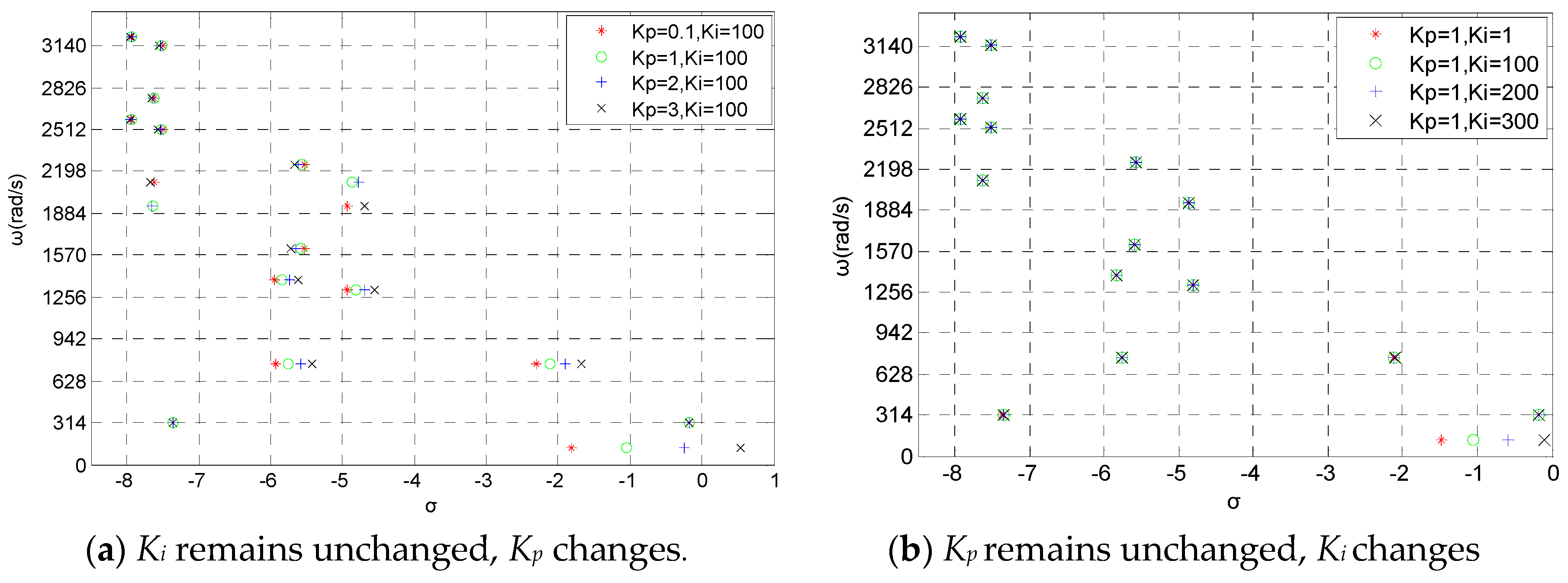
3.4. Sensitivity of SVC Control Parameters to Electromagnetic Oscillation
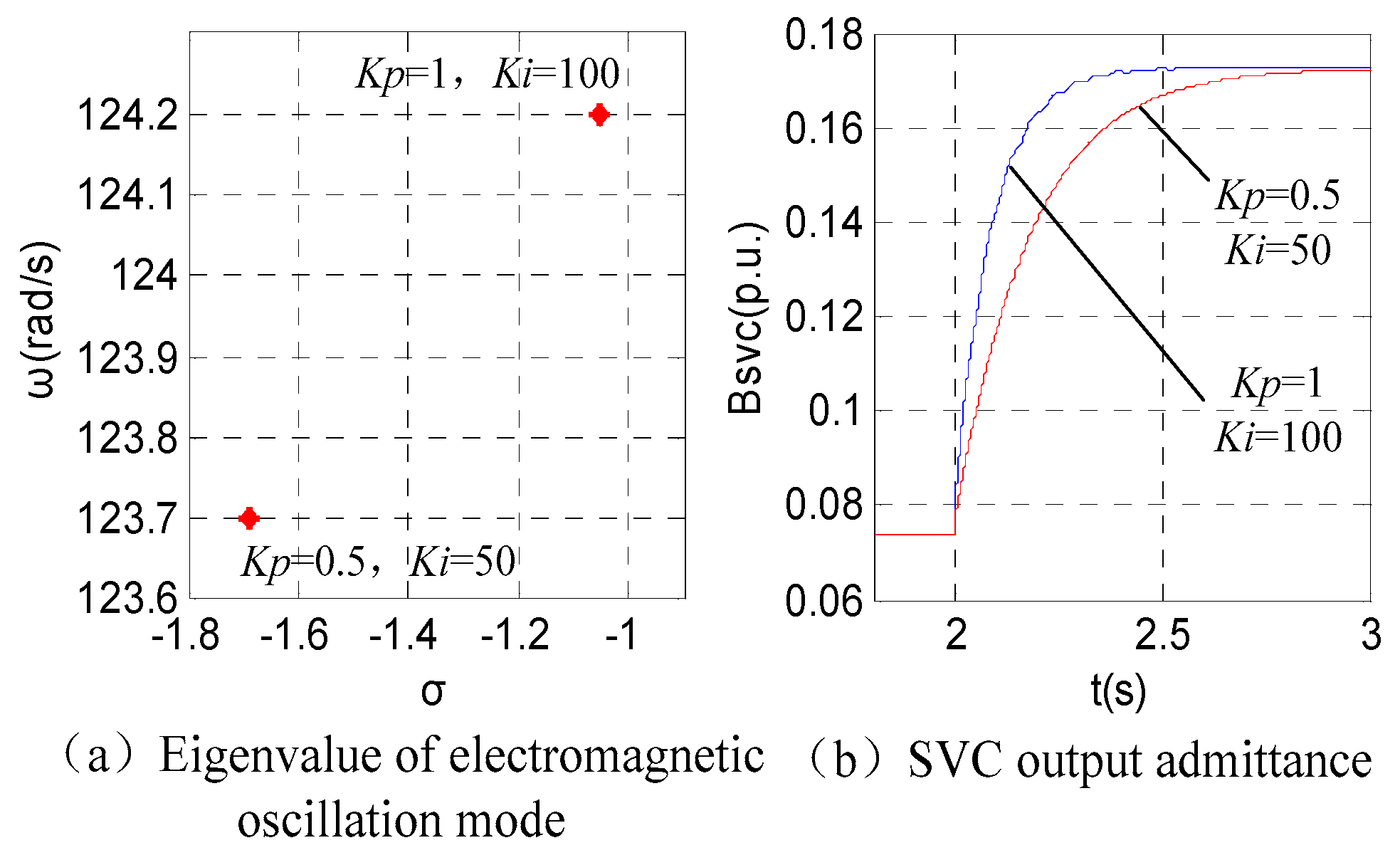
3.5. Effect of SVC Control Parameters on Reactive Power Regulation Performance
4. Parameter Optimization Strategy
4.1. Reactive Power Regulation Performance index
4.2. Electromagnetic Oscillation Suppression Capability Index
4.3. Optimization Objective Function
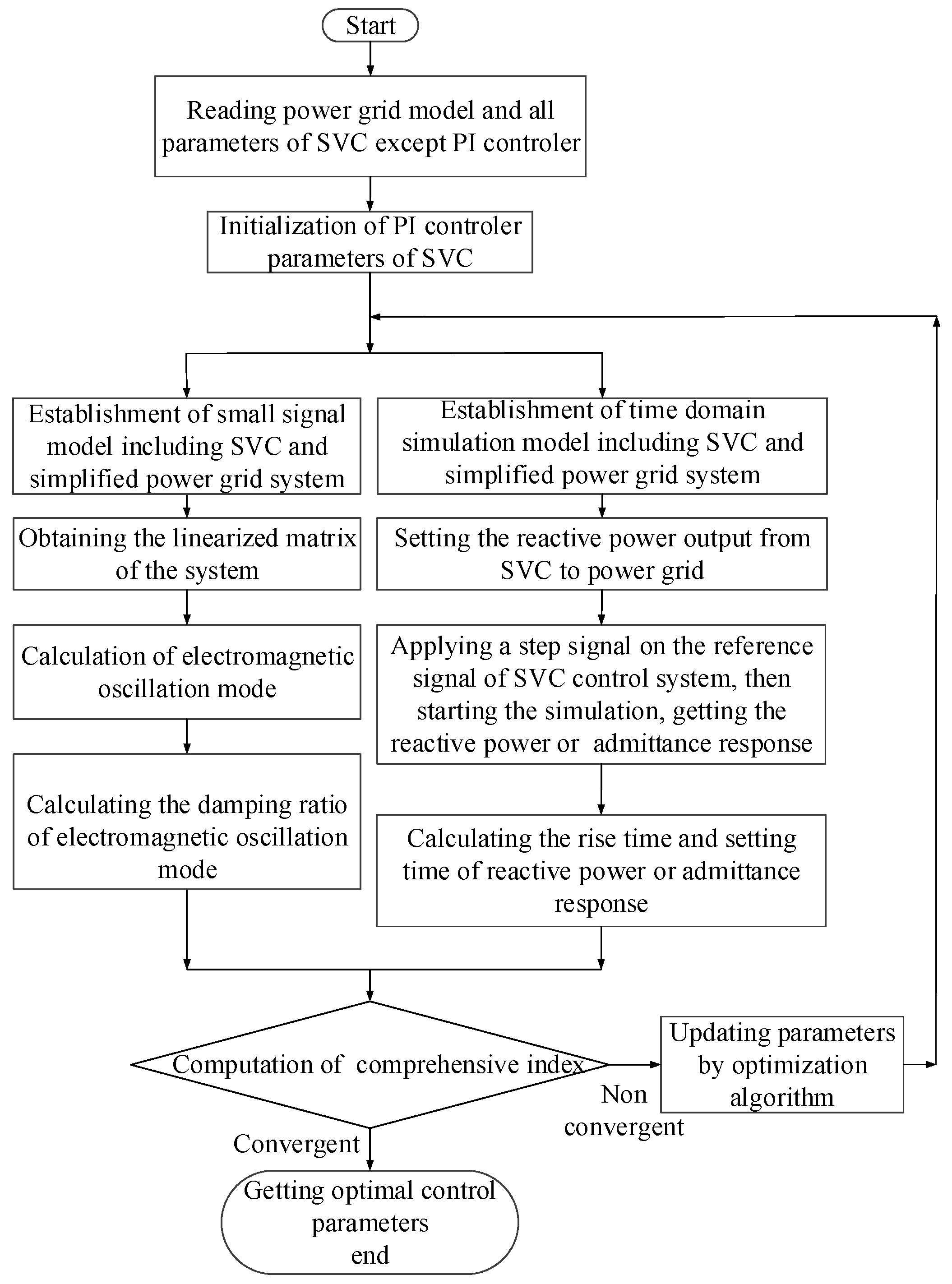
Optimization Process
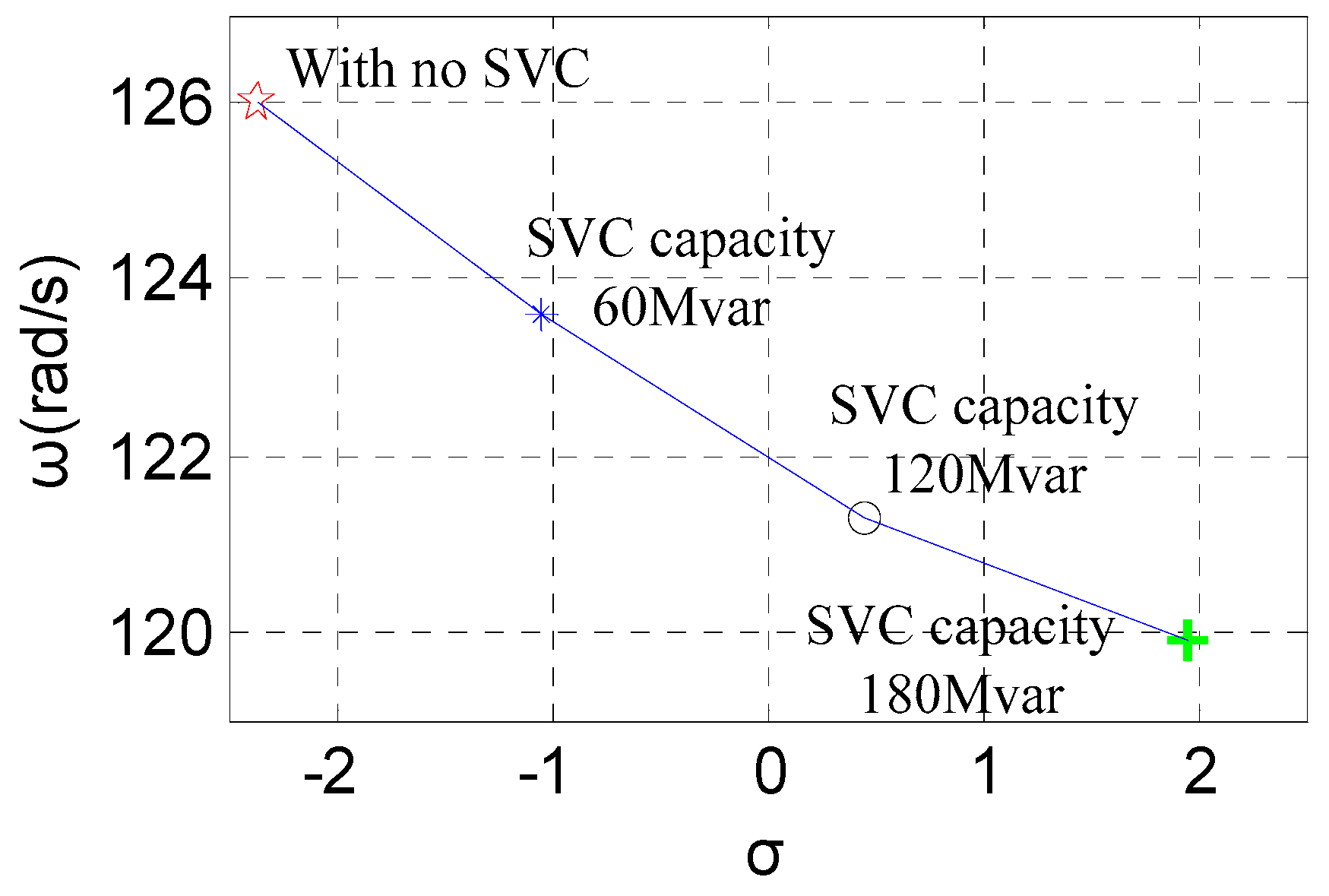
5. Case Study
6. Application in CTAIP
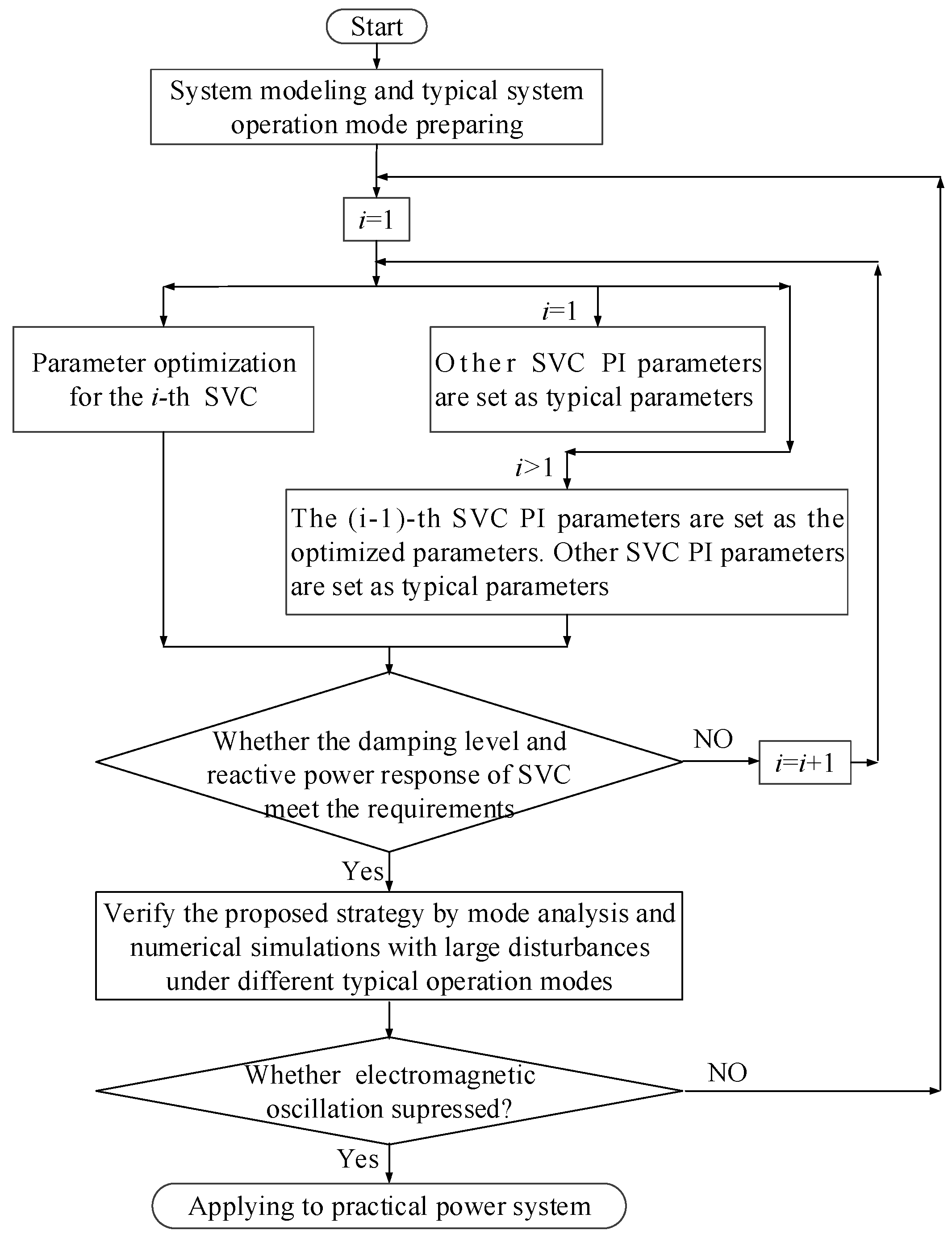
6.1. Parameter Optimization of CTAIP
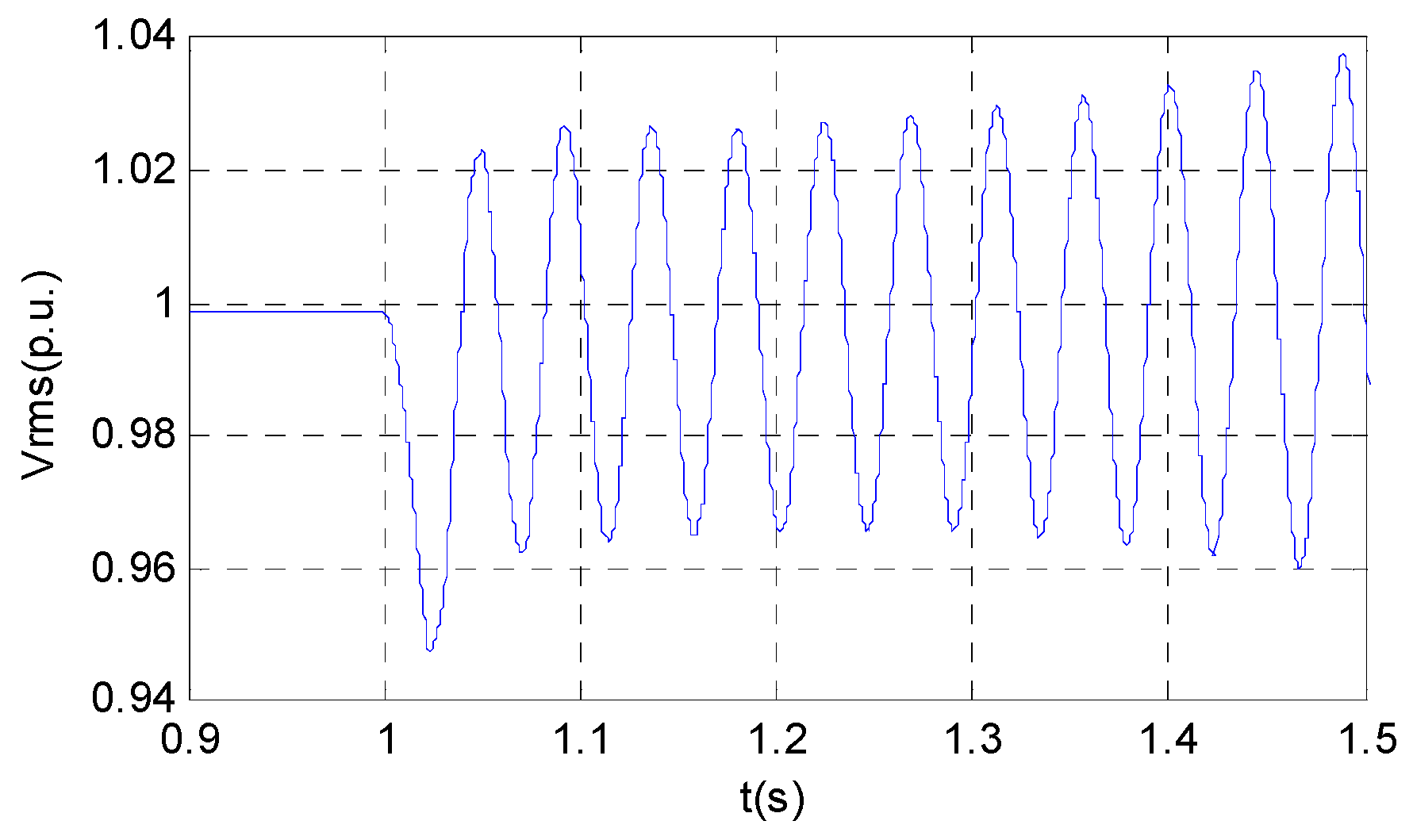
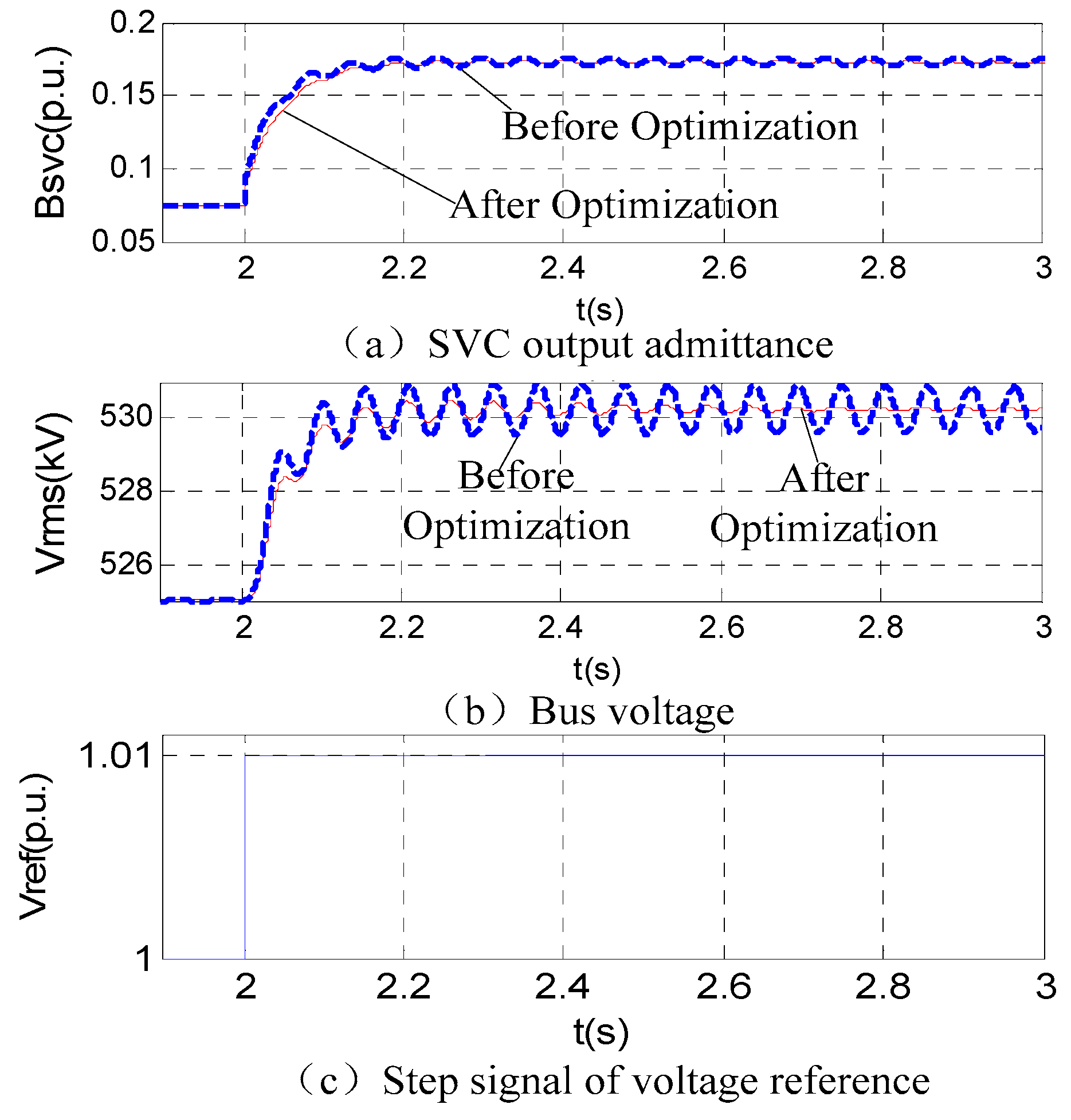
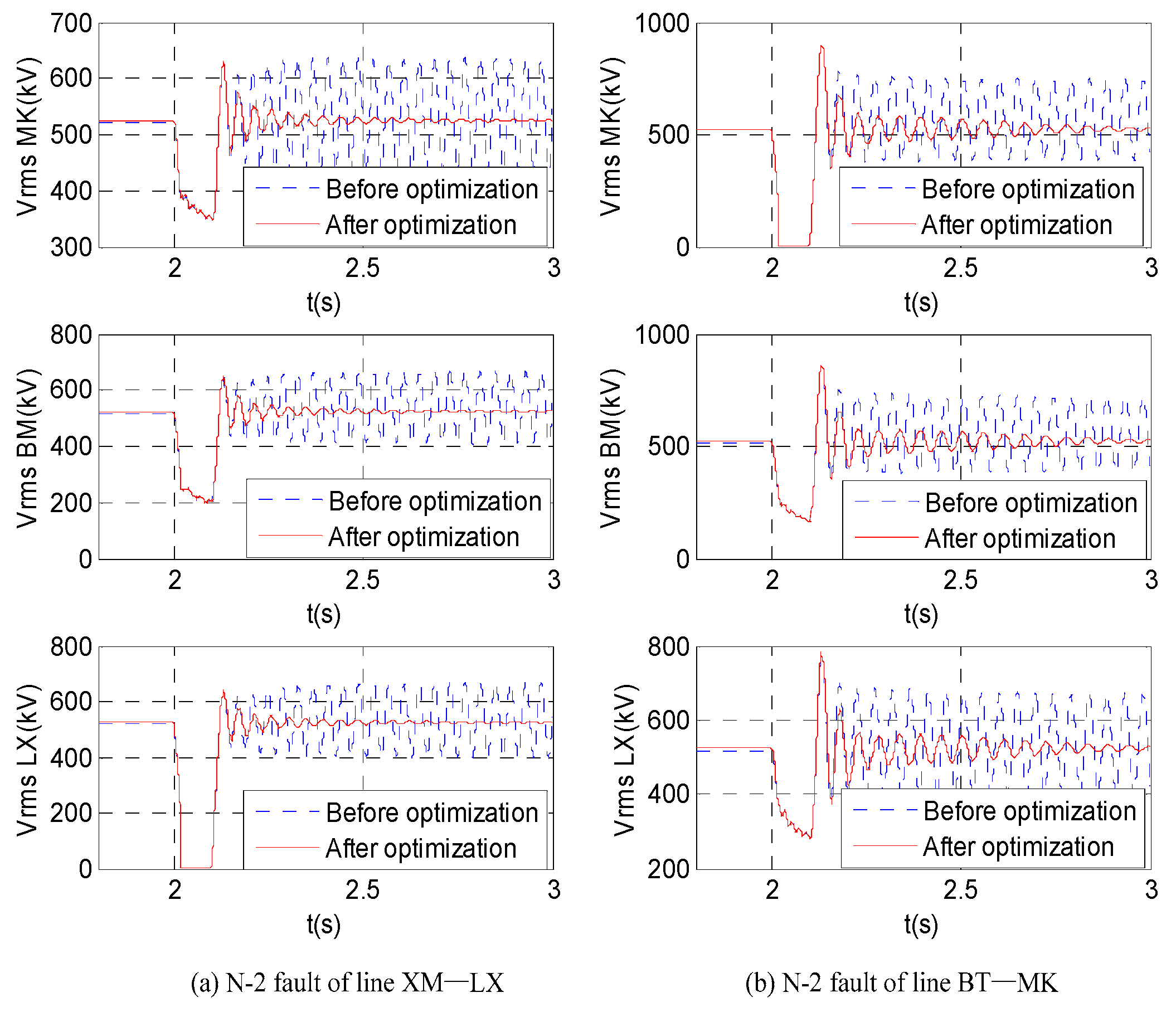
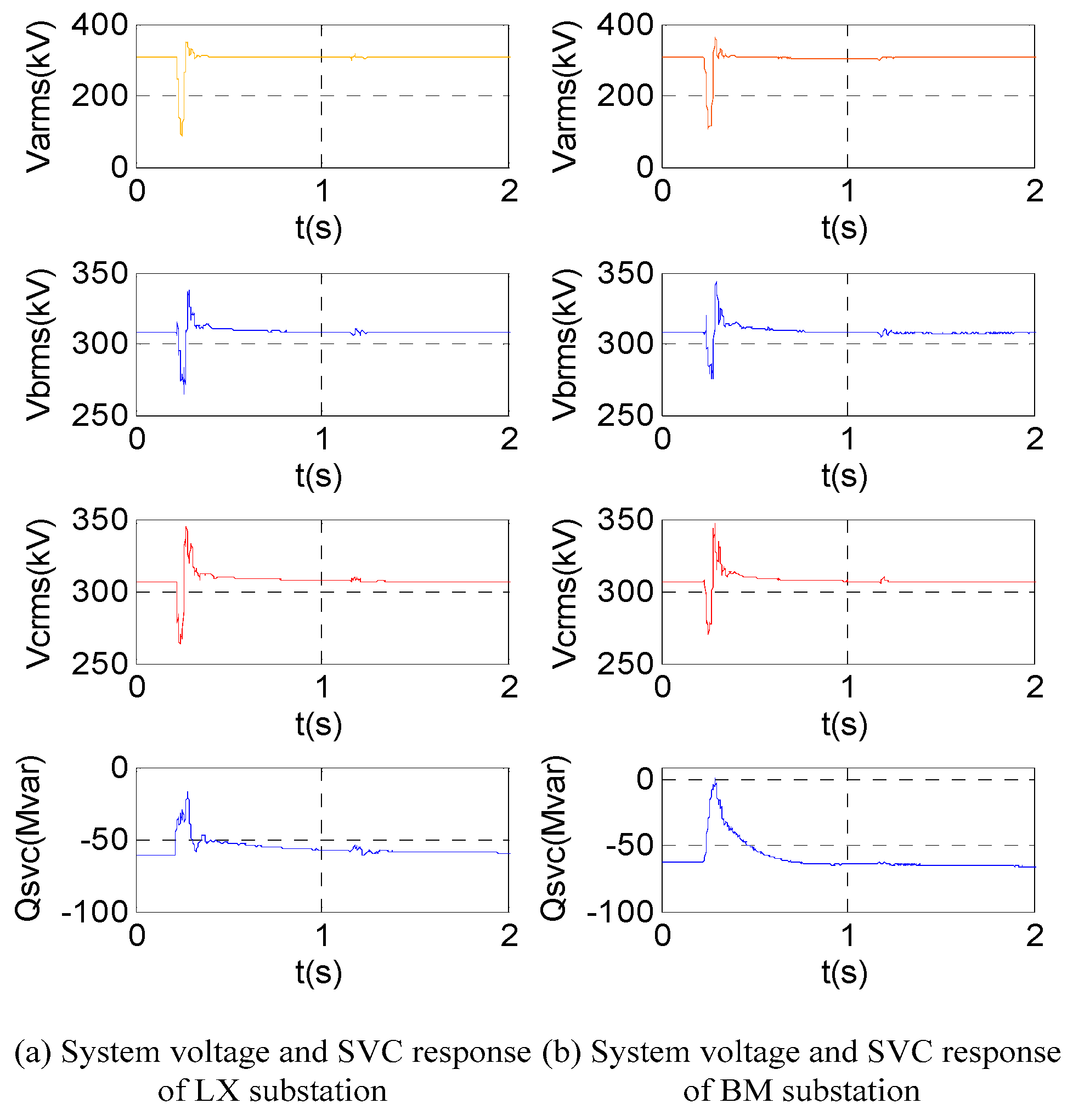
6.2. Validation of Control Strategy
6.2.1. Simulation with PSCAD/EMTDC
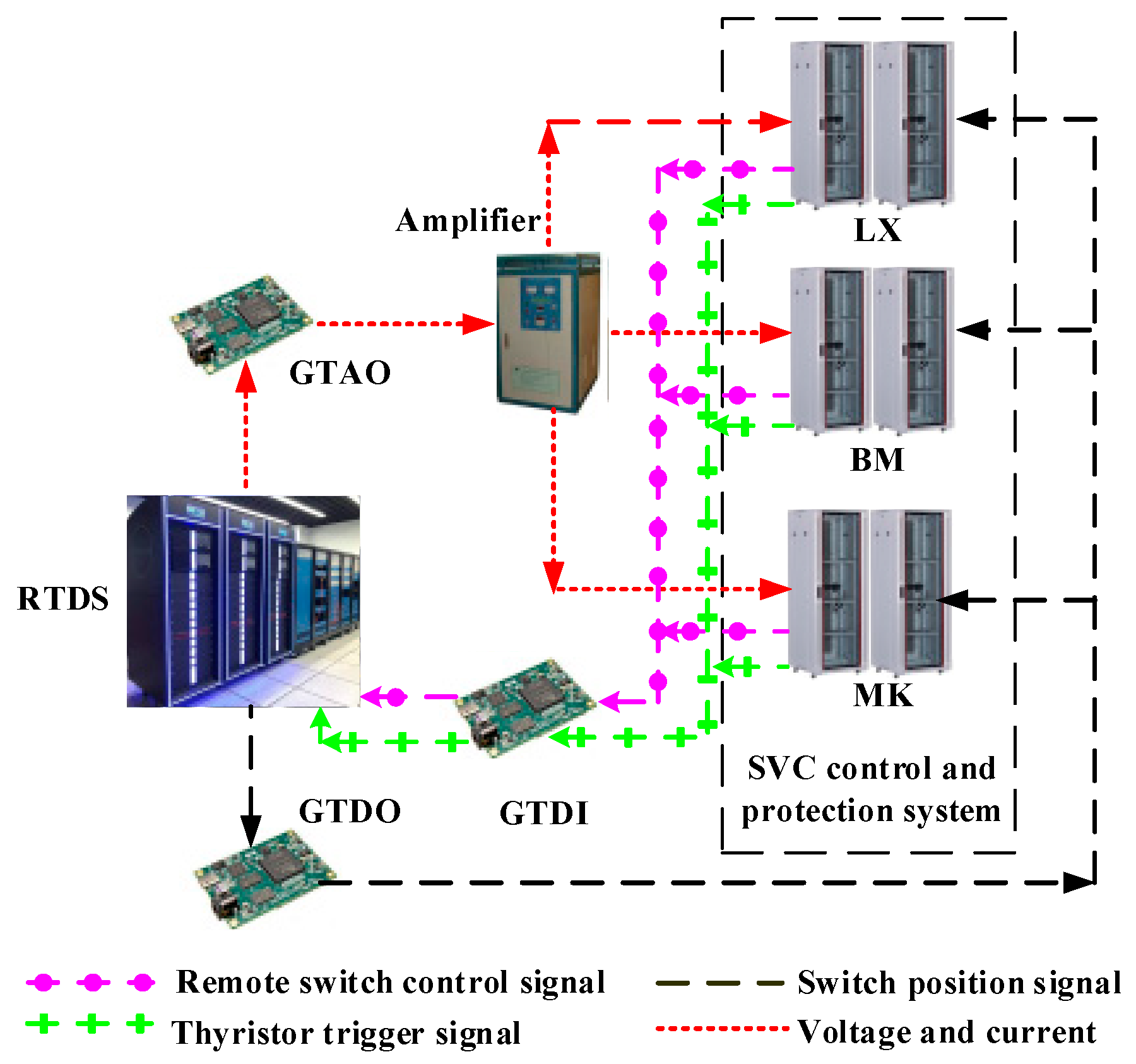
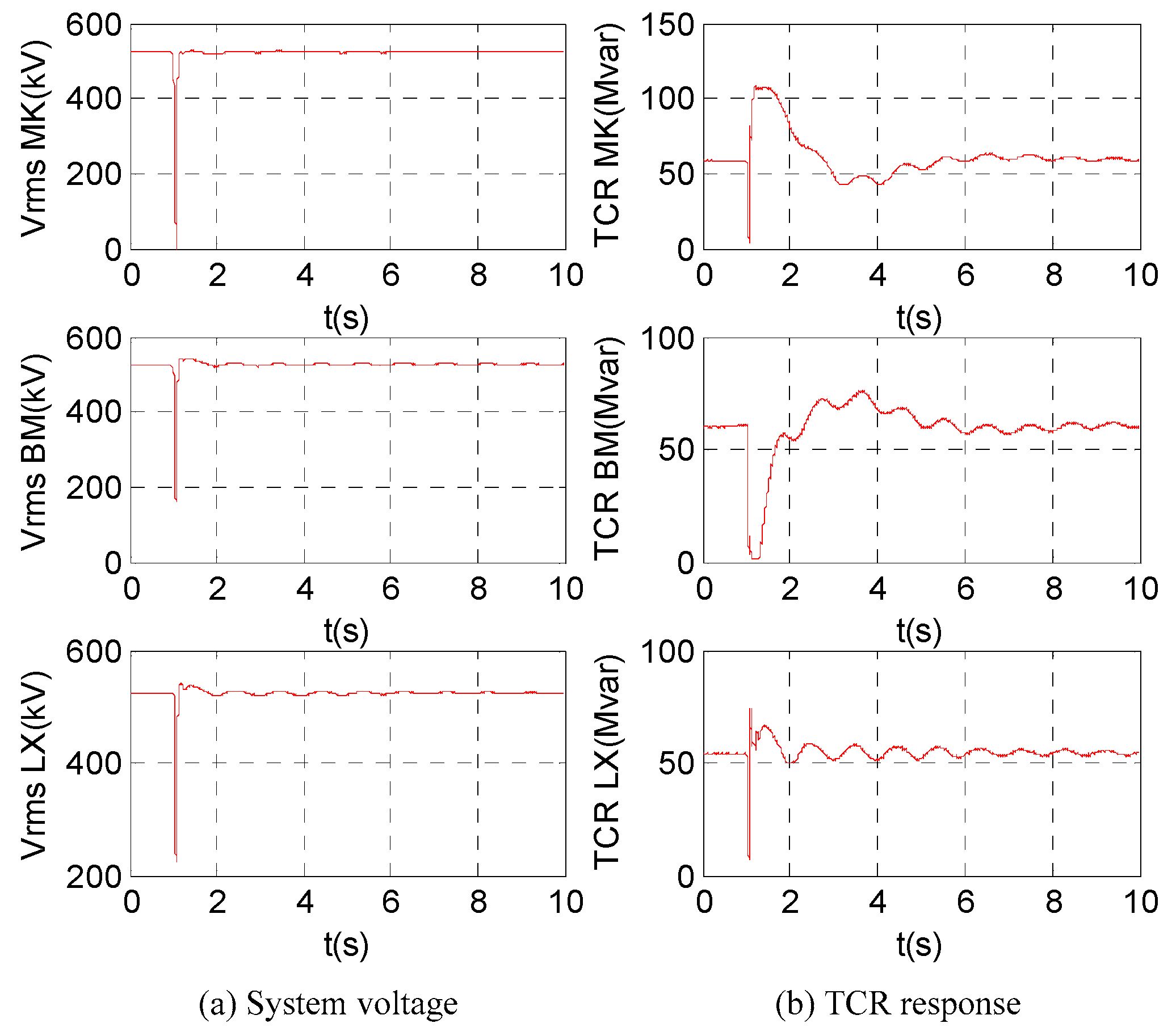
6.2.2. Simulation with RTDS
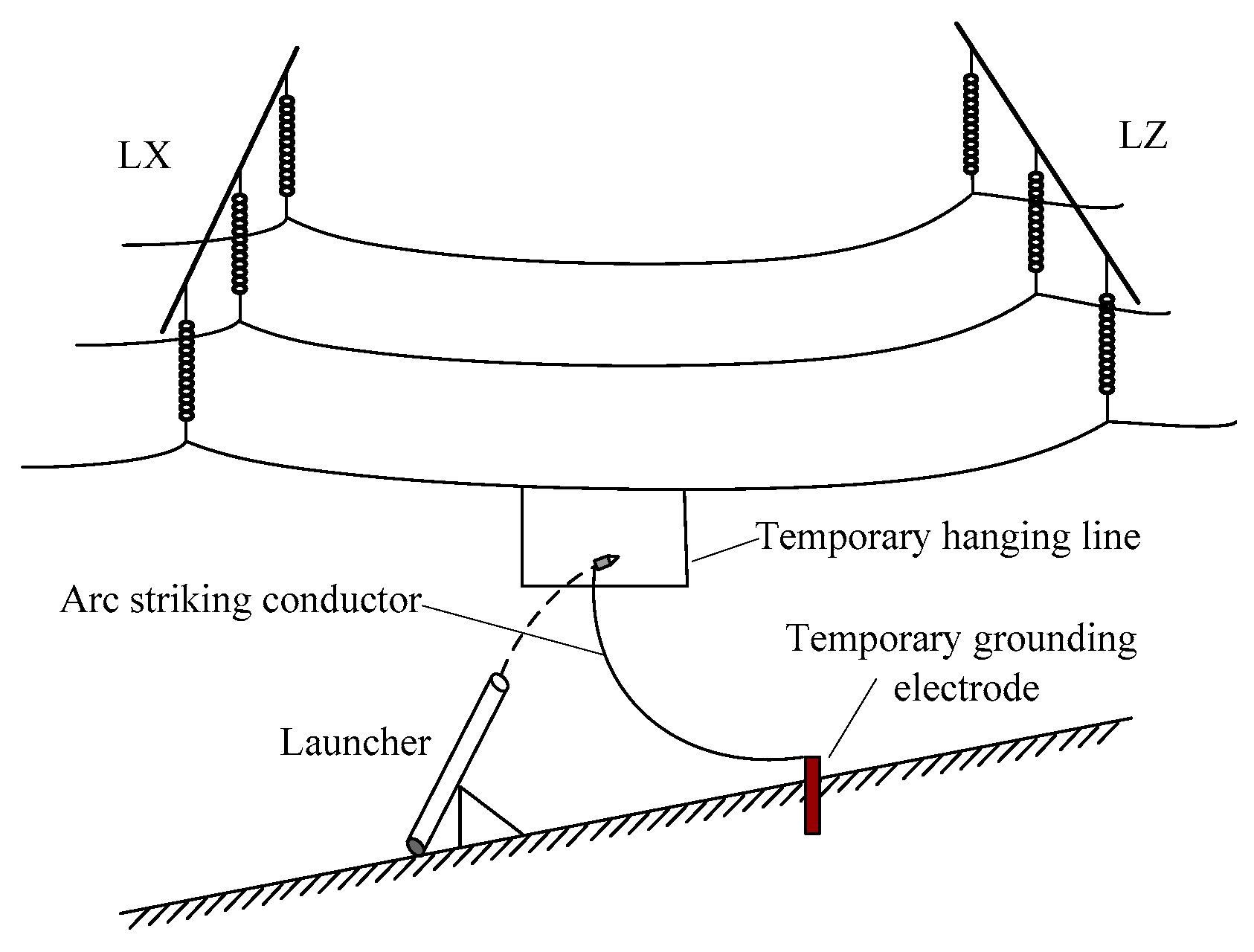
6.3. Engineering Verification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peng, Q.; Yang, H.Y.; Wang, H.; Blaabjerg, F. On Power Electronized Power Systems: Challenges and Solutions. In Proceedings of the IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018. [Google Scholar]
- Hu, B.J.; Yuan, H.; Yuan, M.X. Modeling of DFIG-Based WTs for Small-Signal Stability Analysis in DVC Timescale in Power Electronized Power Systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.R.; Jiang, Q.R.; Liu, X.D. Centralised solution for subsynchronous control interaction of doubly fed induction generators using voltage-sourced converter. IET Gener. Trans. Distrib. 2015, 9, 2751–2759. [Google Scholar] [CrossRef]
- Chowdhury, M.; Mahmud, M.; Shen, W.; Pota, H. Nonlinear controller design for series-compensated DFIG-based wind farms to mitigate subsynchronous control interaction. IEEE Trans. Energy Convers. 2017, 32, 707–719. [Google Scholar] [CrossRef]
- Watson, W.; Coultes, M.E. Static exciter stabilizing signals on large generators-mechanical problems. IEEE Trans. Power Appar. 1973, 92, 204–211. [Google Scholar] [CrossRef]
- Bahrman, M.; Larsen, E.V.; Piwko, R.J.; Patel, H.S. Experience with HVDC- turbine-generator torsional interaction at Square Butte. IEEE Trans. Power Appar. 1980, 99, 966–975. [Google Scholar] [CrossRef]
- Prabhu, N.; Padiyar, K.R. Investigation of subsynchronous resonance with VSC-based HVDC transmission system. IEEE Trans. Power Deliv. 2009, 24, 433–440. [Google Scholar] [CrossRef]
- Harnefors, L. Analysis of subsynchronous torsional interaction with power electronic converters. IEEE Trans. Power Syst. 2007, 22, 305–313. [Google Scholar] [CrossRef]
- Emadi, A.; Khaligh, A.; Rivetta, C.H.; Williamson, G.A. Constant power loads and negative impedance instability in automotive systems: Definition modeling stability and control of power electronic converters and motor drives. IEEE Trans. Veh. Technol. 2006, 55, 1112–1125. [Google Scholar] [CrossRef]
- Bi, T.S.; Li, J.Y.; Zhang, P.; Mitchell-Colgan, E. Study on response characteristics of grid side converter controller of PMSG to sub-synchronous frequency component. IET Renew. Power Gener. 2017, 11, 966–972. [Google Scholar] [CrossRef]
- Huang, P.H.; EI Moursi, M.; Xiao, S.W.; Kirtley, J.L. Subsynchronous resonance mitigation for series-compensated DFIG-based wind farm by using two-degree-of-freedom control strategy. IEEE Trans. Power Syst. 2015, 30, 1442–1454. [Google Scholar] [CrossRef]
- Chen, Y.H.; Huang, B.Y.; Sun, H.S.; Wang, L. Analysis of control interaction between D-PMSGs-based wind farm and SVC. J. Eng. 2019, 16, 1266–1270. [Google Scholar] [CrossRef]
- Tao, H.; Chong, L.; Ban, L.G.; Zhu, Y.Y.; Wei, C.X.; Li, L.F.; Jiang, W.P.; Dong, P.; Zhao, B.; Liu, W.L. Real-time simulation and parameter optimization of SVC control strategy for central-Tibet power grid. Power Syst. Technol. 2014, 38, 1001–1007. [Google Scholar]
- Chen, G.; Tang, F.; Shi, H.B.; Yu, R.; Wang, G.H.; Ding, L.J.; Liu, B.S.; Lu, X.N. Optimization strategy of hydro-governors for eliminating ultra low frequency oscillations in hydro-dominant power systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1086–1094. [Google Scholar] [CrossRef]
- Bian, X.Y.; Geng, Y.; Lo, K.L.; Fu, Y.; Zhou, Q.B. Coordination of PSSs and SVC damping controller to improve probabilistic small-signal stability of power system with wind farm integration. IEEE Trans. Power Syst. 2016, 31, 2371–2382. [Google Scholar] [CrossRef]
- Abdulrahman, I.; Radman, G. Wide-area-based adaptive neuro-fuzzy SVC cntroller for damping interarea oscillations. Can. J. Electr. Comput. Eng. 2018, 41, 133–144. [Google Scholar]
- Asghari, R.; Mozafari, B.; Naderi, M.S.; Amraee, T.; Nurmanova, V.; Bagheri, M. A novel method to design delay-sheduled controllers for damping inter-area oscillations. IEEE Access 2018, 6, 71932–71946. [Google Scholar] [CrossRef]
- Alimuddin; Nurhalim, G.; Arafiyah, R. Optimization placement static var compensator (SVC) using artificial bee colony (ABC) method on PT PLN (Persero) Jawa-Bali, Indonesia. In Proceedings of the 2018 1st International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 4–6 April 2018. [Google Scholar]
- Pandya, M.C.; Jamnani, J.G. Coordinated control of SVC and TCSC for voltage profile improvement employing particle swarm optimization. In Proceedings of the 2017 International Conference on Smart Technologies for Smart Nation (SmartTechCon) 2017 International Conference on Smart Technologies for Smart Nation (SmartTechCon), Bangalore, India, 17–19 August 2017. [Google Scholar]
- Zhang, K.S.; Shi, Z.D.; Huang, Y.H.; Qiu, C.J.; Yang, S. SVC damping controller design based on novel modified fruit fly optimization algorithm. IET Renew. Power Gener. 2018, 12, 90–97. [Google Scholar] [CrossRef]
| Xs (Ω) | R (Ω/km) | X (Ω/km) | B (Siem/km) | Transformer (750 MVA) | ||
|---|---|---|---|---|---|---|
| 60 | 0.0166 | 0.2968 | 4.24 × 10−6 | X12 (%) | X13 (%) | X23 (%) |
| 12 | 44 | 30 | ||||
| Parameter Source | LX | BM | MK | |||
|---|---|---|---|---|---|---|
| kp | Ki | kp | Ki | kp | Ki | |
| Before optimization | 4 | 100 | 4 | 100 | 4 | 100 |
| After optimization | 1.1237 | 94.8621 | 1.9826 | 152.2815 | 2.0596 | 197.2081 |
| Parameter Source | LX | BM | MK | |||
|---|---|---|---|---|---|---|
| T0.9 (s) | Ts (s) | T0.9 (s) | Ts (s) | T0.9 (s) | Ts (s) | |
| Before optimization | 0.20 | 0.49 | 0.16 | 0.43 | 0.14 | 0.41 |
| Parameters optimization | 0.27 | 0.62 | 0.19 | 0.54 | 0.16 | 0.49 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, H.; Sun, X.; Chen, G.; Zhang, H.; Tang, Y.; Xu, L.; Ding, L.; Fan, C.; Xu, Y. Optimization Strategy of SVC for Eliminating Electromagnetic Oscillation in Weak Networking Power Systems. Energies 2019, 12, 3489. https://doi.org/10.3390/en12183489
Shi H, Sun X, Chen G, Zhang H, Tang Y, Xu L, Ding L, Fan C, Xu Y. Optimization Strategy of SVC for Eliminating Electromagnetic Oscillation in Weak Networking Power Systems. Energies. 2019; 12(18):3489. https://doi.org/10.3390/en12183489
Chicago/Turabian StyleShi, Huabo, Xinwei Sun, Gang Chen, Hua Zhang, Yonghong Tang, Lin Xu, Lijie Ding, Chengwei Fan, and Yin Xu. 2019. "Optimization Strategy of SVC for Eliminating Electromagnetic Oscillation in Weak Networking Power Systems" Energies 12, no. 18: 3489. https://doi.org/10.3390/en12183489
APA StyleShi, H., Sun, X., Chen, G., Zhang, H., Tang, Y., Xu, L., Ding, L., Fan, C., & Xu, Y. (2019). Optimization Strategy of SVC for Eliminating Electromagnetic Oscillation in Weak Networking Power Systems. Energies, 12(18), 3489. https://doi.org/10.3390/en12183489





