1. Introduction
In engineering, an ideal solution or project must be established due to economic, technical, practical, and environmental limitations. In the design and construction of power transmission or distribution lines, two types of cable can be used, namely overhead or underground cables [
1]. High-voltage underground cables have been widely used as electrical conductors in different applications such as medium-voltage industrial facilities, underground and submarine transmission connections, renewable energy plants [
1], the feeding of residential buildings and urban centers, as well as in facilities where environmental and visual aspects require the use of underground cables. However, the installation of underground cables represents a significant financial expenditure when compared with the application of overhead cables [
1,
2].
In addition, the complex manufacturing process of underground cables and the diversity of products and manufacturers can lead to the commercialization of low-performance cables. The use of good performance cables is essential for underground applications, since the cables are subjected to several stresses during their lifetime, such as electrical (due to operation voltages, overvoltage surges, and others), thermal (since the cables are subjected to abnormal temperature rises, thermal expansion, and contraction), mechanical (such as external damages, lateral impact, and pressure abnormalities), and environmental (due to humidity, oxidation, solar radiation, and other phenomena) [
1].
Therefore, in order to ensure operation under the aforementioned stresses and improve the power supply reliability and continuity, cables must be exposed to routine and type electrical tests to guarantee, essentially, the dielectric performance of the insulation material and reduce, consequently, the financial losses for power utilities and industries. One of the most widely used materials is cross-linked polyethylene (XLPE) [
2,
3,
4,
5].
Although most failures in a power cable occur at its junctions and terminations, the evaluation of the cable insulation material is extremely necessary. One of the tests required for this evaluation is the cable breakdown voltage determination. International standards IEC 60229 and IEC 60520-2 [
6,
7] establish the test requirements for high-voltage cables. In Brazil, the standards NBR 10299 and NBR 16132 [
8,
9] provide the specifications in regard to the tests for the statistical distribution of puncture electric field strength in cables for systems with a voltage above 15 kV. NBR 10299 aims to set the minimum failure rate based on the installed cable length. A generally accepted value is 6.7 × 10
−4 failure/(year × km) [
8].
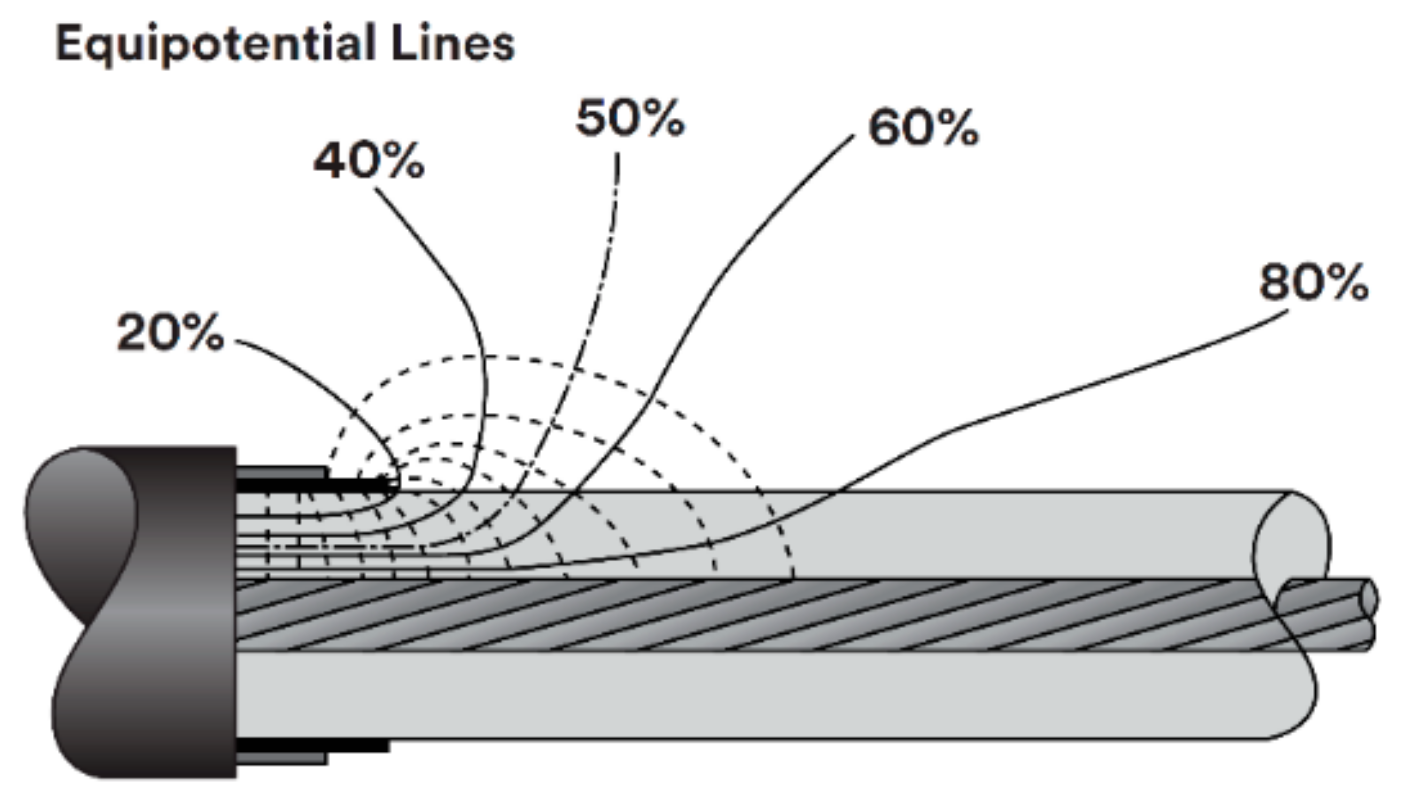
The prescribed tests should be performed using a sample of at least 3 m effective length, that is, without considering the terminations on both sides. The external shielding is grounded and a rising AC voltage is applied over the cable until the internal breakdown is reached. The experimental setup should ensure the breakdown occurrence on the effective length cable. Considering that the tests can subject the cable to overvoltages with values of 5 to 10 times greater than the normal operation voltage, the main problem faced during the tests is the electric field distortion at the cable ends, which causes external rupture and prevents the evaluation of the inner insulating material.
To carry out the installation in field or breakdown voltage tests in insulated cables, it is necessary to remove a part of the cable insulation. While the electric field inside the effective length has a predictable distribution, with a radial direction and logarithmical behavior [
1,
2,
10], there is a great field intensification at the cable ends. The electric field in the vicinity of the shield end is illustrated in
Figure 1. Thus, such a predictable distribution should be guaranteed to allow successful tests.
The cable end consists of a conductor, semiconductor layers, insulating layer, and conductive tape for the shielding, in addition to air. The diversity of materials with different electrical characteristics, dielectric strength, and relative permittivity provides highly non-uniform electric fields with both axial and tangential field components. The tangential electric field is one of the main reasons for failures in terminals [
12,
13]. The field enhancement at the cable end produces surface and external discharges in the air, which can be prevented by using properly designed terminations [
1,
9,
10,
14]. In this sense, arrangements with different characteristics were studied by [
12,
13,
14,
15,
16,
17,
18,
19].
Most of the studies that have dealt with the electric field distribution in high-voltage cable terminations apply commercial software based on the finite element method (FEM) for the purpose of analysis and/or design of terminations, joints, or stress relief cones. In [
12,
15,
16], simulations were used to assist in the design of stress cones based on high-temperature superconductors (HTS). The authors of [
16] proposed the use of an epoxy/ZnO conductive layer to improve the electric field distribution. Other studies compared different materials and field grading options for cables. In [
13], for example, different types of field grading options for 36 kV paper-insulated lead cables (PILC) and cross-linked polyethylene (XLPE) cables were compared. In [
17], the impact of defects on cable joints was analyzed, and [
18] studied the electric field in a cable termination undergoing transient stresses. During the project stage of a termination, another possible objective is to estimate areas more susceptible to defects and thus improve prototypes. In this regard, [
19] calculated the electric field in a sleeve for a 110 kV cable using FEM, in order to estimate zones more susceptible to dielectric breakdown and thus improve a sleeve prototype.
Some of the aforementioned studies presented termination projects based on the stress cone concept, and analyzed electric field distribution or the influence of different materials. However, there is a lack of studies related to termination performance during overvoltage tests or breakdown voltage tests. In addition, some proposed prototypes require expensive materials.
Therefore, a methodology for the conception, drawing, and electrostatic simulation of a feasible termination is reported in this paper. The termination must be able to ensure the completion of overvoltage tests on cables. The proposed procedure can also be used for the design of optimized cable terminations. Such terminations are usually responsible, for example, for the linking between different transmission lines, functioning as connectors. For the analyses of the electrical stresses at the termination, computational simulations were performed using a commercial software based on the finite element method and a single-phase 35 kV cable model, which was used as a sample. Conventional materials were considered in the project, which represents a potential cost reduction.
2. Materials and Methods
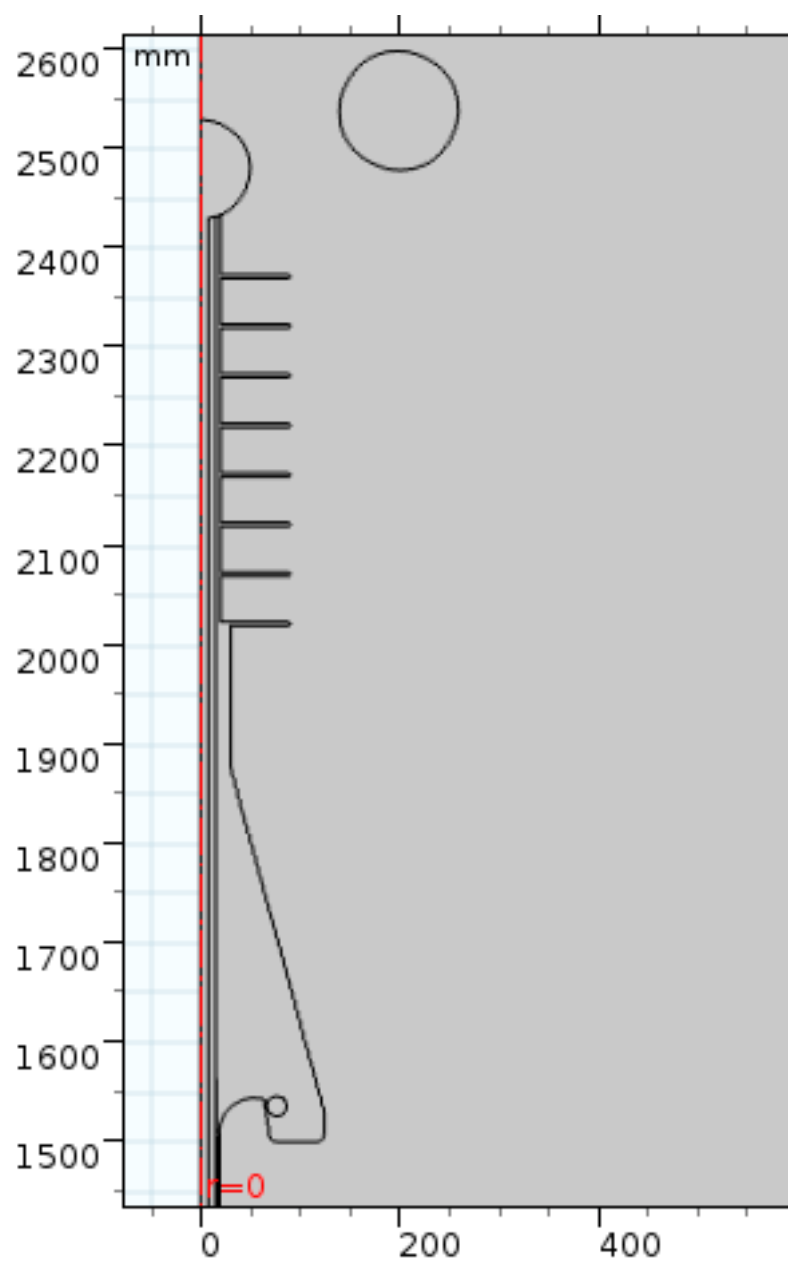
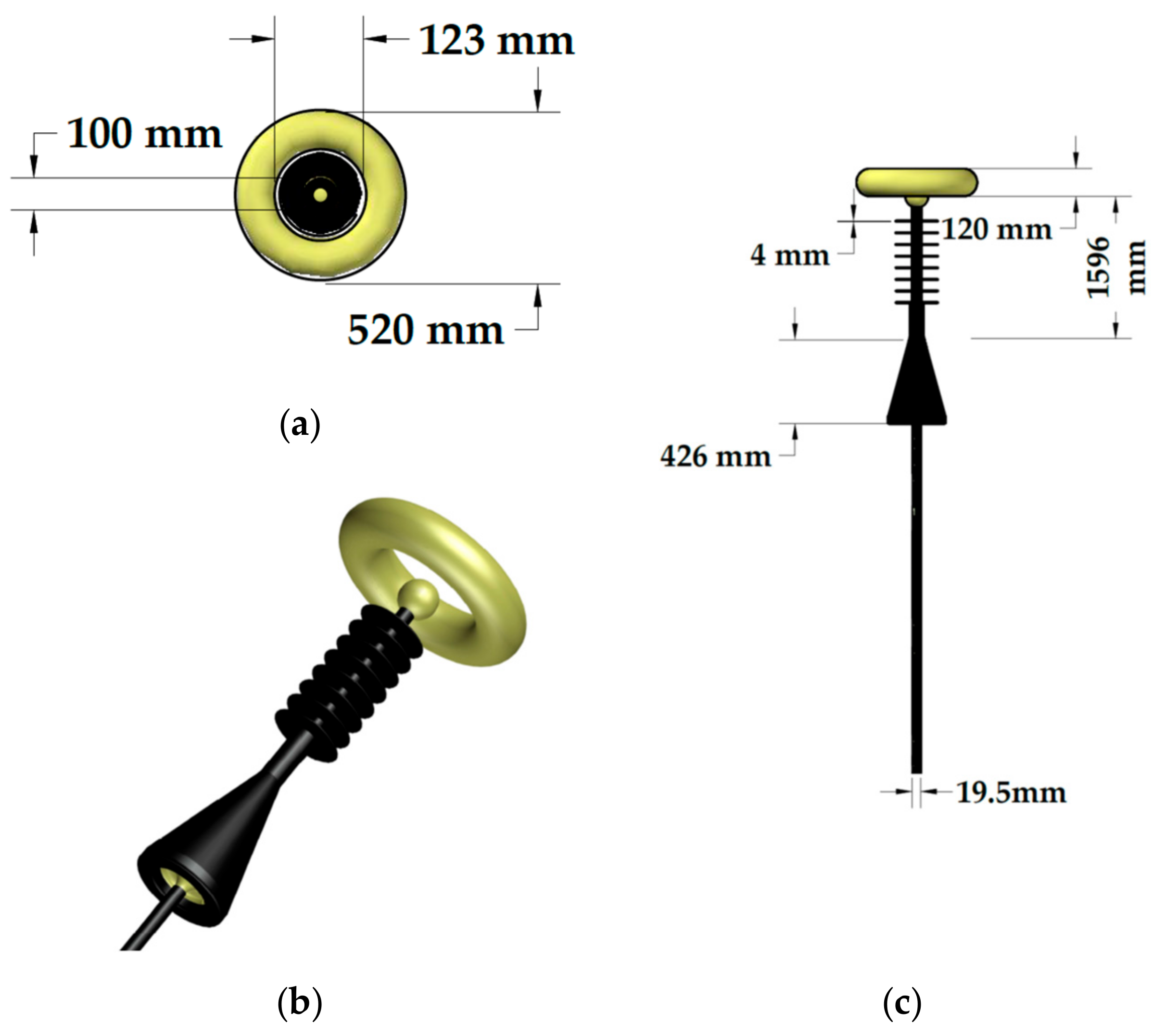
Sections of an XLPE 35 kV insulated cable designed for application in underground and underwater environments were used as design samples. As can be seen in
Figure 2, the cable consists of a copper conductor suitable for the electric current conduction; a thin semiconductor layer for the reduction of electric field distortions; a thick layer of insulation material, the XLPE being used for electrical insulation; another semiconductor layer; a conductive layer applied for the shielding or uniformization of the electric field inside the cable; and, finally, a layer of insulating rubber for mechanical protection. The layers can be seen from the (right) outermost to the (left) innermost part.
Initially, 5 m wide cable sections were used as samples in the laboratory tests. The samples were composed of 3 m of intact cable and two bare ends on both sides. An AC voltage of 300 kV was applied to the high-voltage cable to perform a dielectric withstand test on the internal insulation material. Although several termination configurations were implemented, the breakdown occurred externally to the cable before it was possible to puncture the test portion, resulting in an incorrect application of the insulation material evaluation test.
In order to identify the cable termination points most susceptible to discharges and to design an optimized termination in which the electric field intensity in those points is minimal, the COMSOL Multiphysics
® software (version 5.4, COMSOL AB, Stockholm, Sweden) was used to perform 2D axis-symmetric simulations of the cable terminations. This software implements FEM to solve electrostatic problems [
20] through three main steps—geometry modeling, assignment of material properties to each part of the modeled geometry, and choice of a mathematical model to describe the phenomenon.
For the studies presented in this paper, the electrostatic physics module was used. Using this model, it is possible to solve an electrostatic problem using Gauss’s Law:
associated with the definition:
and the constitutive equation:
In Equations (1)–(3), the electric displacement field (
D) symbolizes the way in which the electric field (
E) will affect the organization of electric charges in the surroundings.
D (C/m
2) and the electric field itself (V/m) represent the interaction between charged objects. In Equation (1),
represents the free electric charge density [
20]. The operator nabla (
) represents the vector differential operator.
By definition, ε
0 is the permittivity of free space and its value is 8.8542 × 10
−12 F/m. ε
r represents the relative permittivity of the material. The relative permittivity values of the materials used in the simulations can be seen in
Table 1.
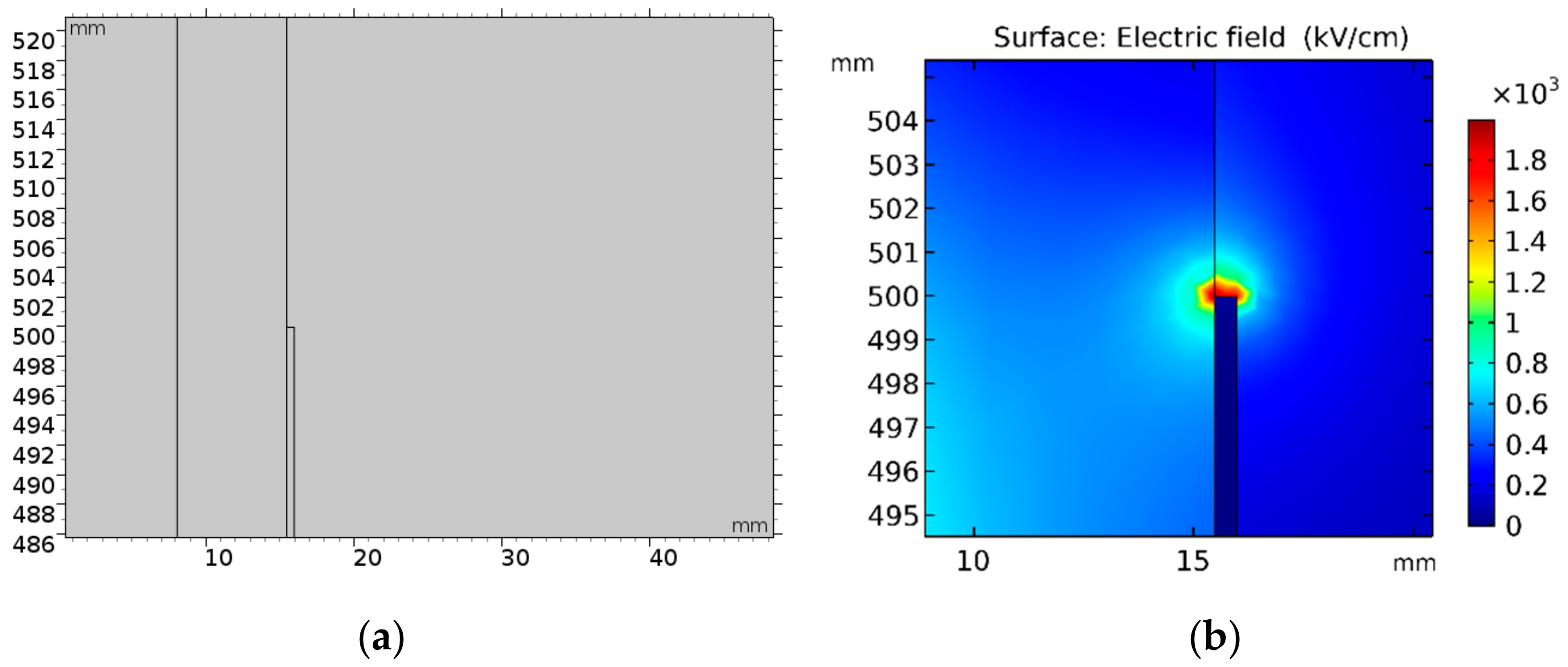
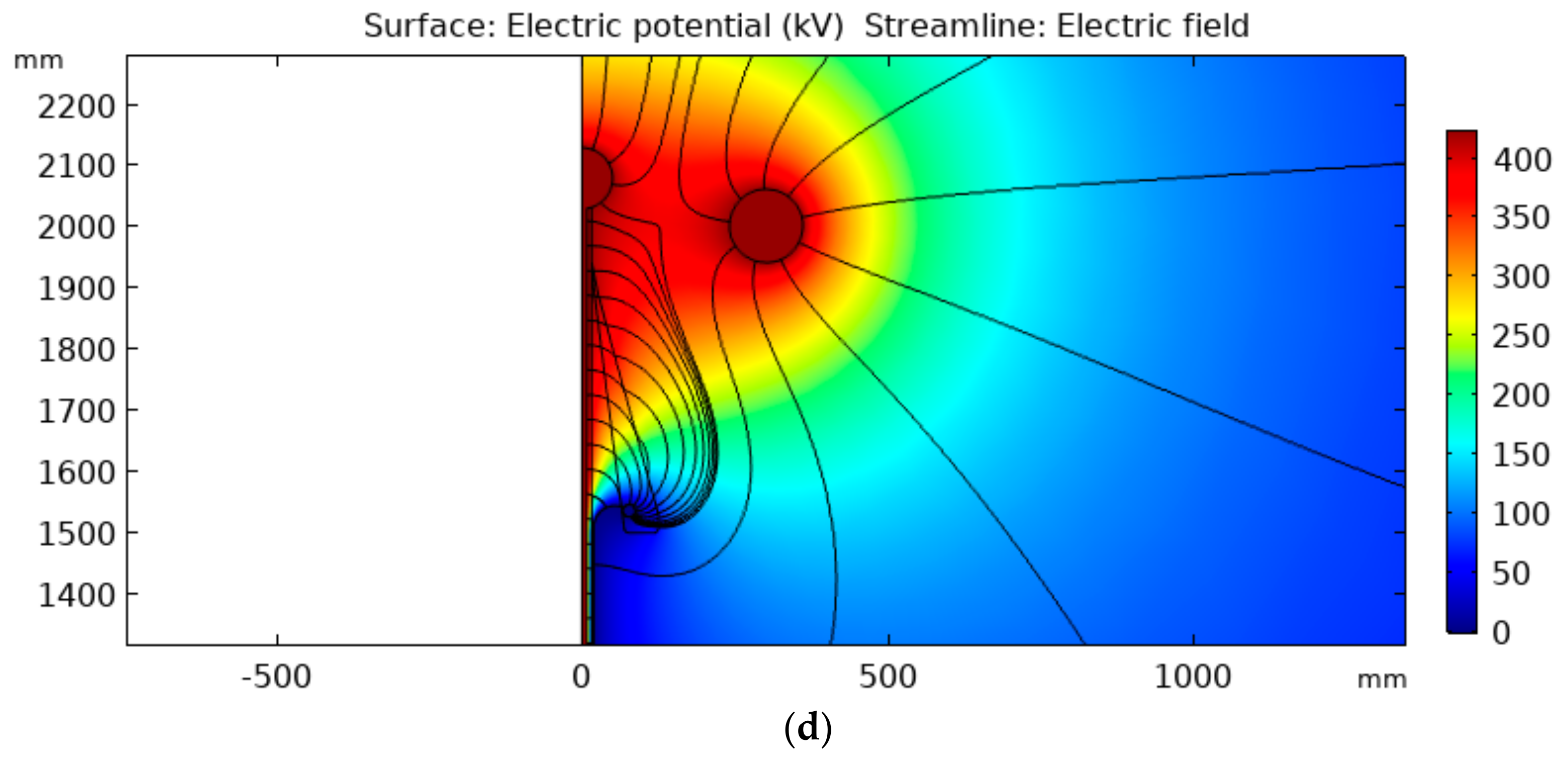
With the selected physics and material properties, the initial geometry of the cable termination that presented external discharges was modeled and simulated in order to identify the points where the electric field exceeded the breakdown’s stipulated limits for the air.
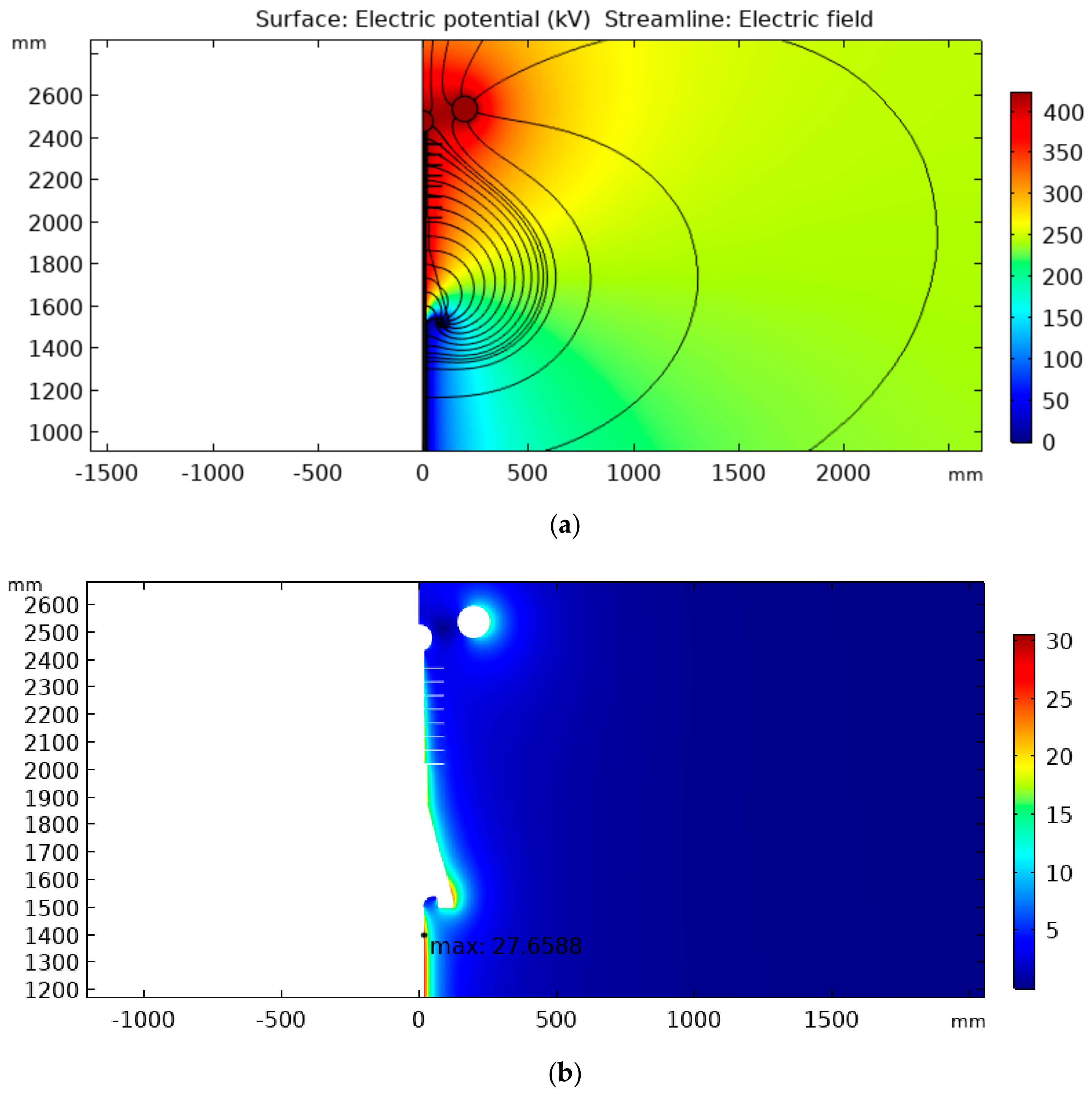
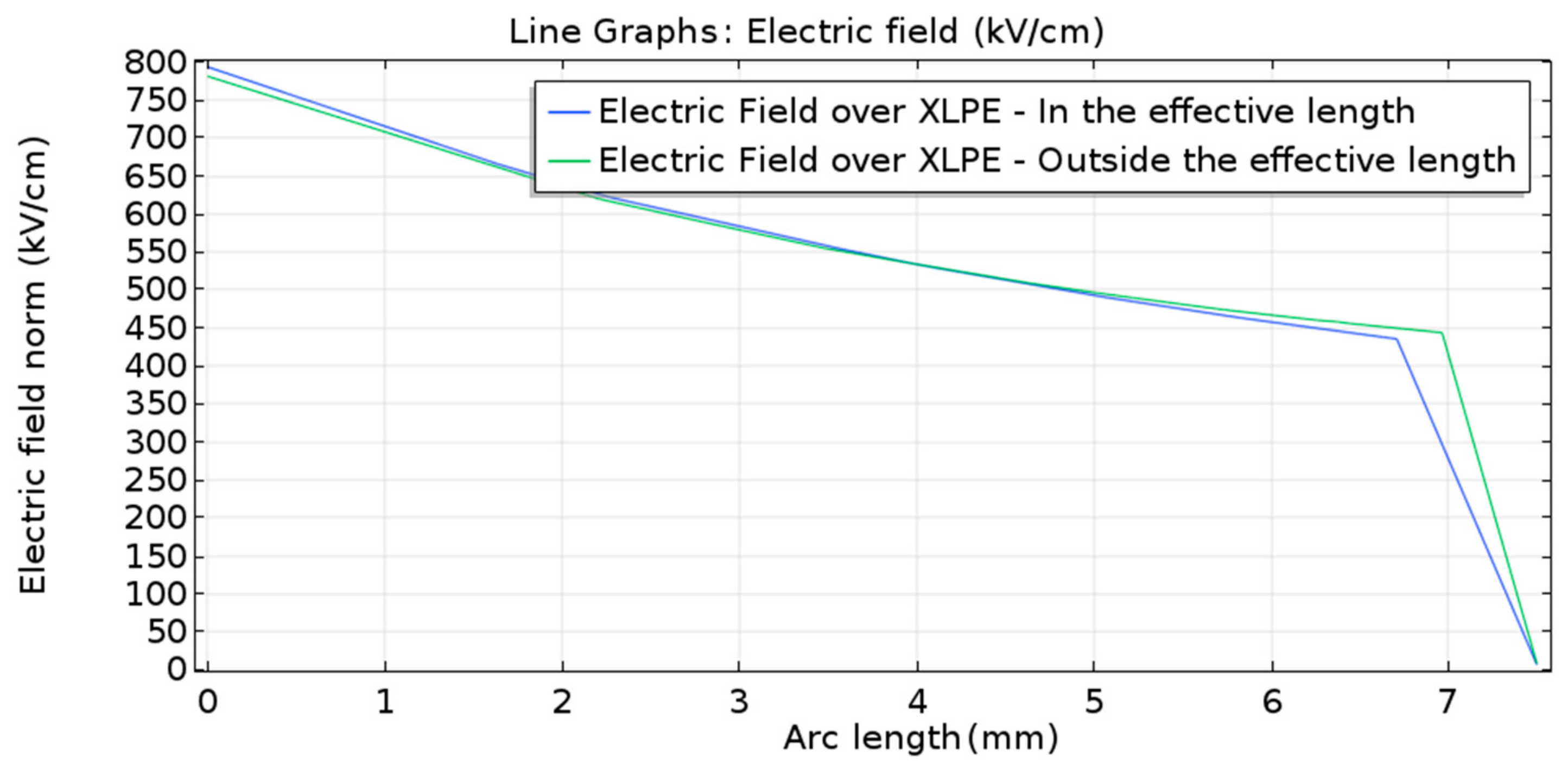
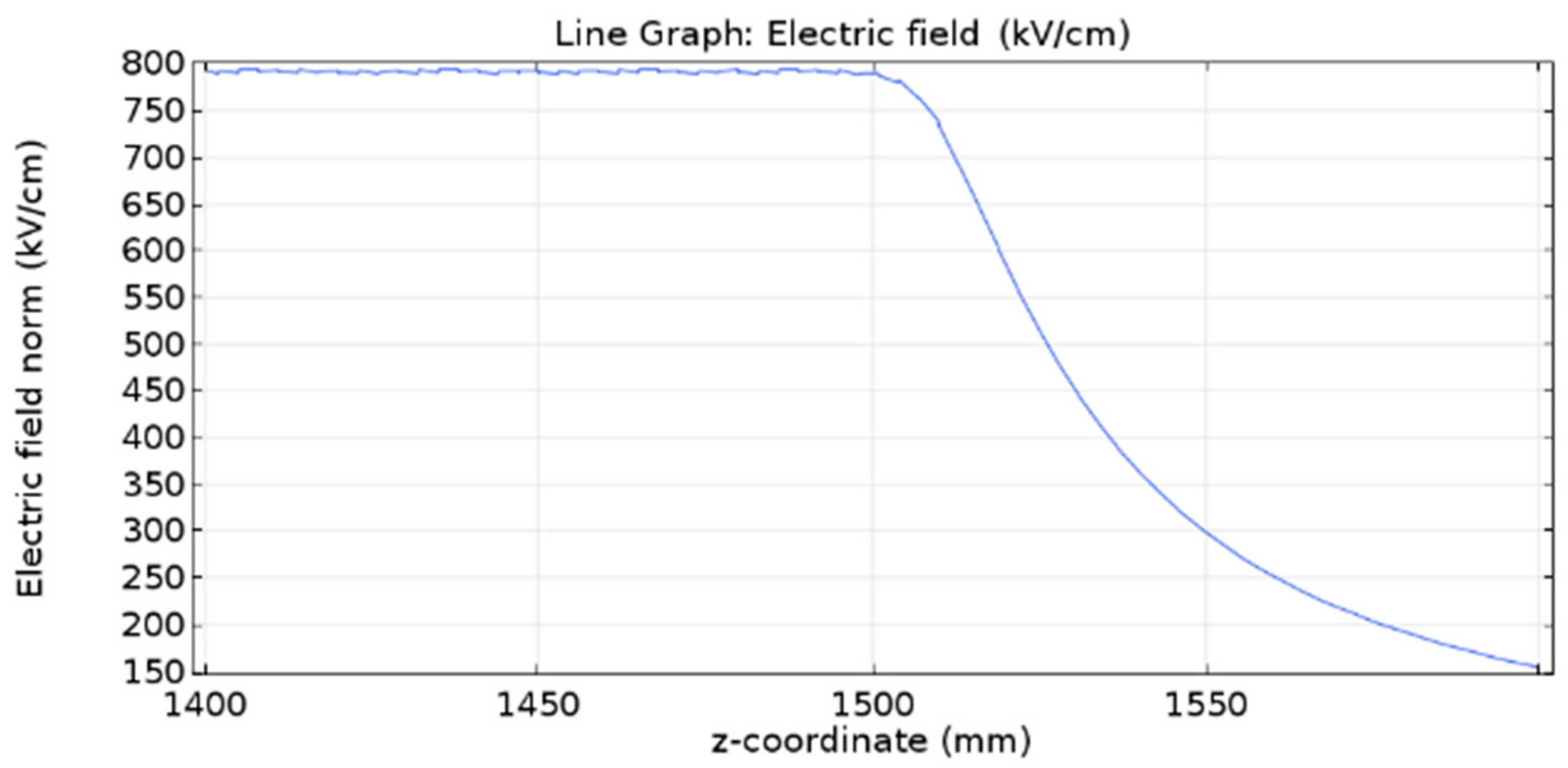
Figure 3 shows that the intensification of the electric field occurred at the cable termination. Due to the high-intensity electric field at the external shielding end, it was necessary to build a termination model for the cable to accomplish successful overvoltage tests.
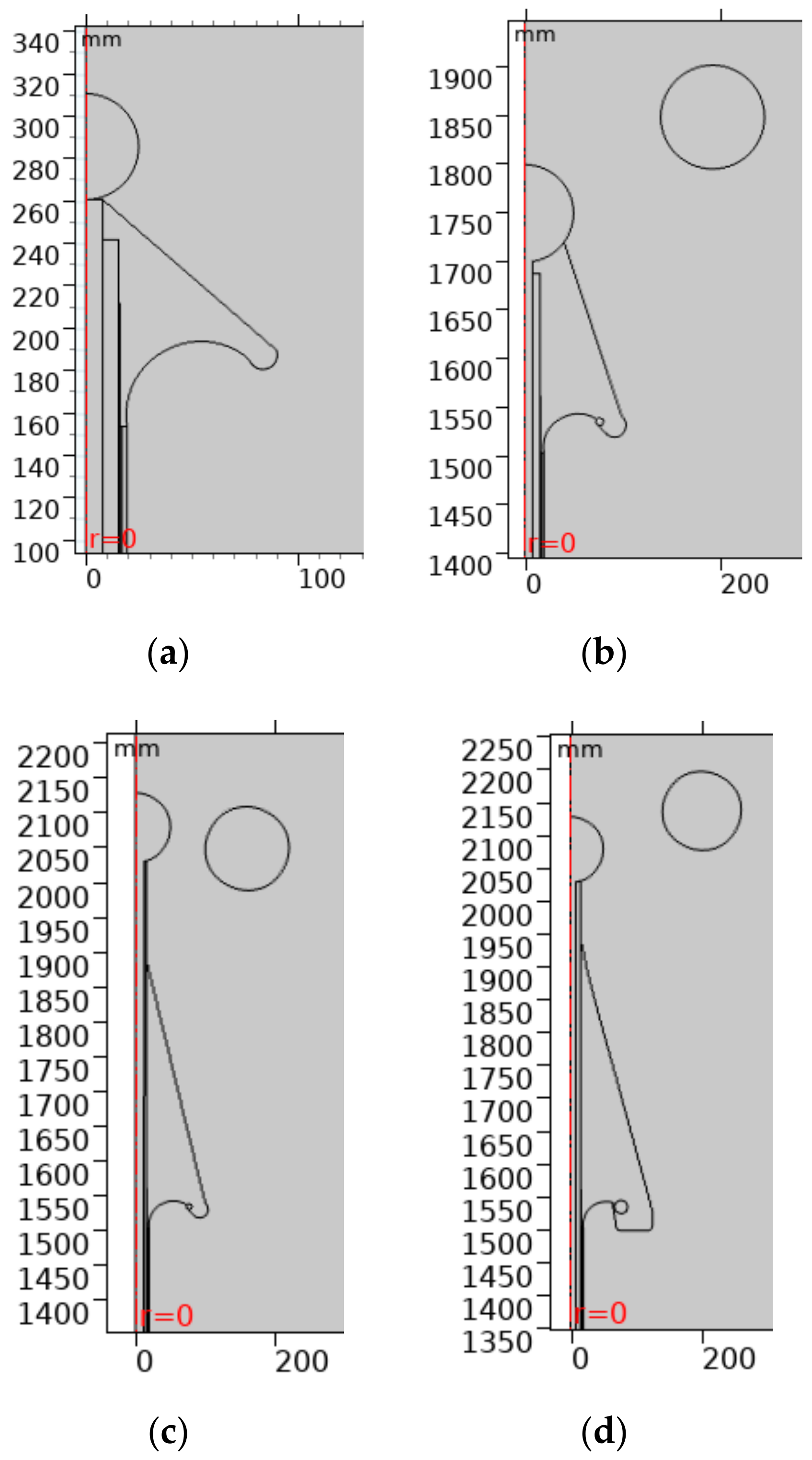
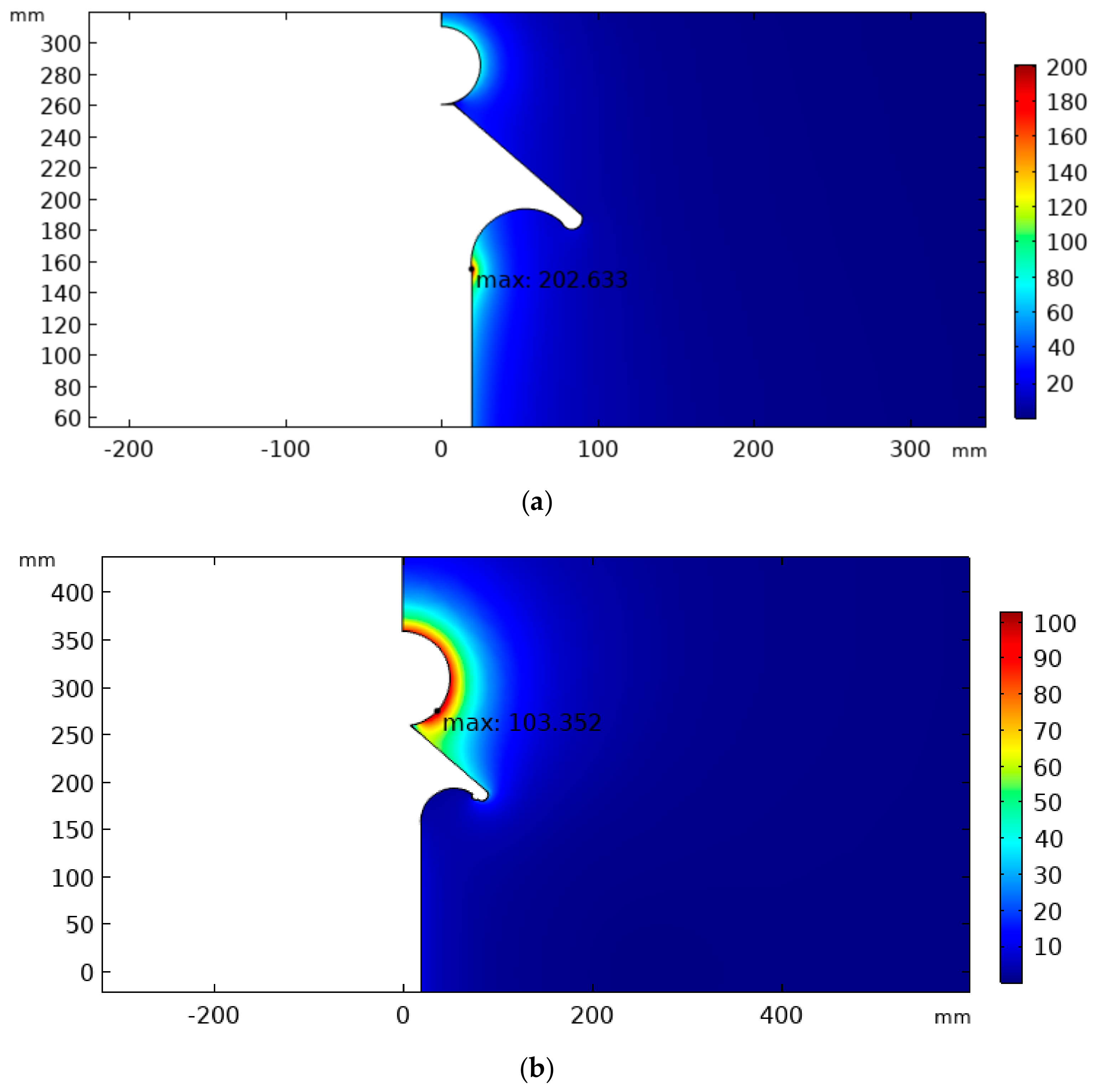
By applying the steps presented for preparing the simulation environment, we simulated successive cable termination geometries from the concept of the stress relief cone. Several models were created and tested until a final configuration was established. The main objectives of the simulations were to minimize the electric field near the cutting region of the semiconductor layer and in the air region between the termination and the high-voltage electrode, in order to minimize corona and reduce the possibility of discharges between the high-voltage electrode and the external grounded shield. Thus, in an overvoltage test, the insulation evaluated was guaranteed to be the internal one, since it was subjected to greater electrical stresses.
The simulation tests consisted of evaluating internal and external maximum electric field strength, as well the average electric field strength between the conductor terminal and the grounding end. In order to make a conservative estimation of the termination performance, a value of 424 kV was used as boundary condition for the applied potential on the simulations. This value corresponds to the peak value for a 300 kV RMS voltage. Due to the axisymmetric geometry, only a half longitudinal sectional view of the model was used in the analysis.
4. Summary and Conclusions
The main contribution of this work is the proposition of a methodology that allows the design of adequate terminations that can withstand voltage tests and breakdown voltage tests in cables. Therefore, it was necessary to develop a termination that guaranteed that the greater electrical stress was applied to the internal insulation.
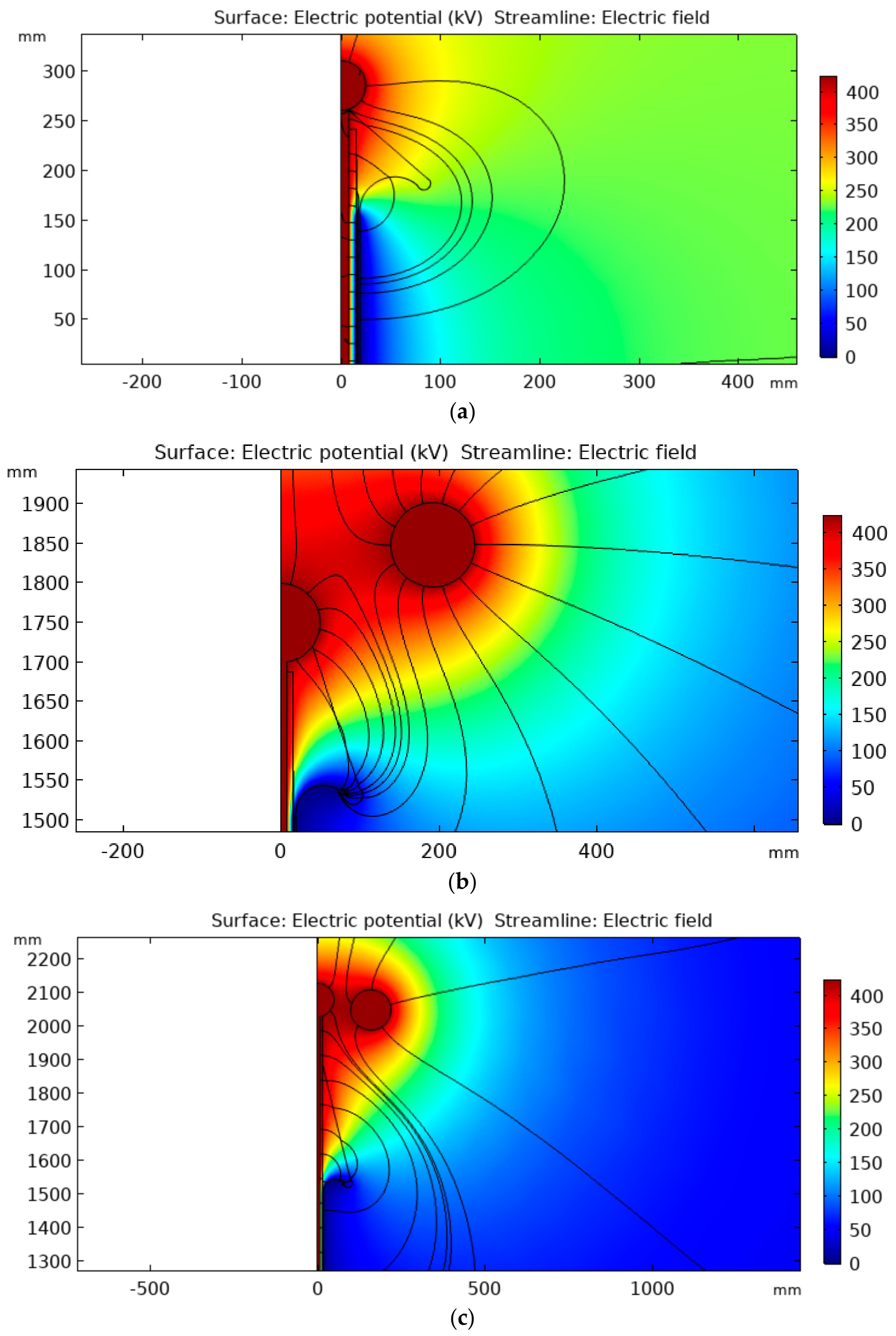
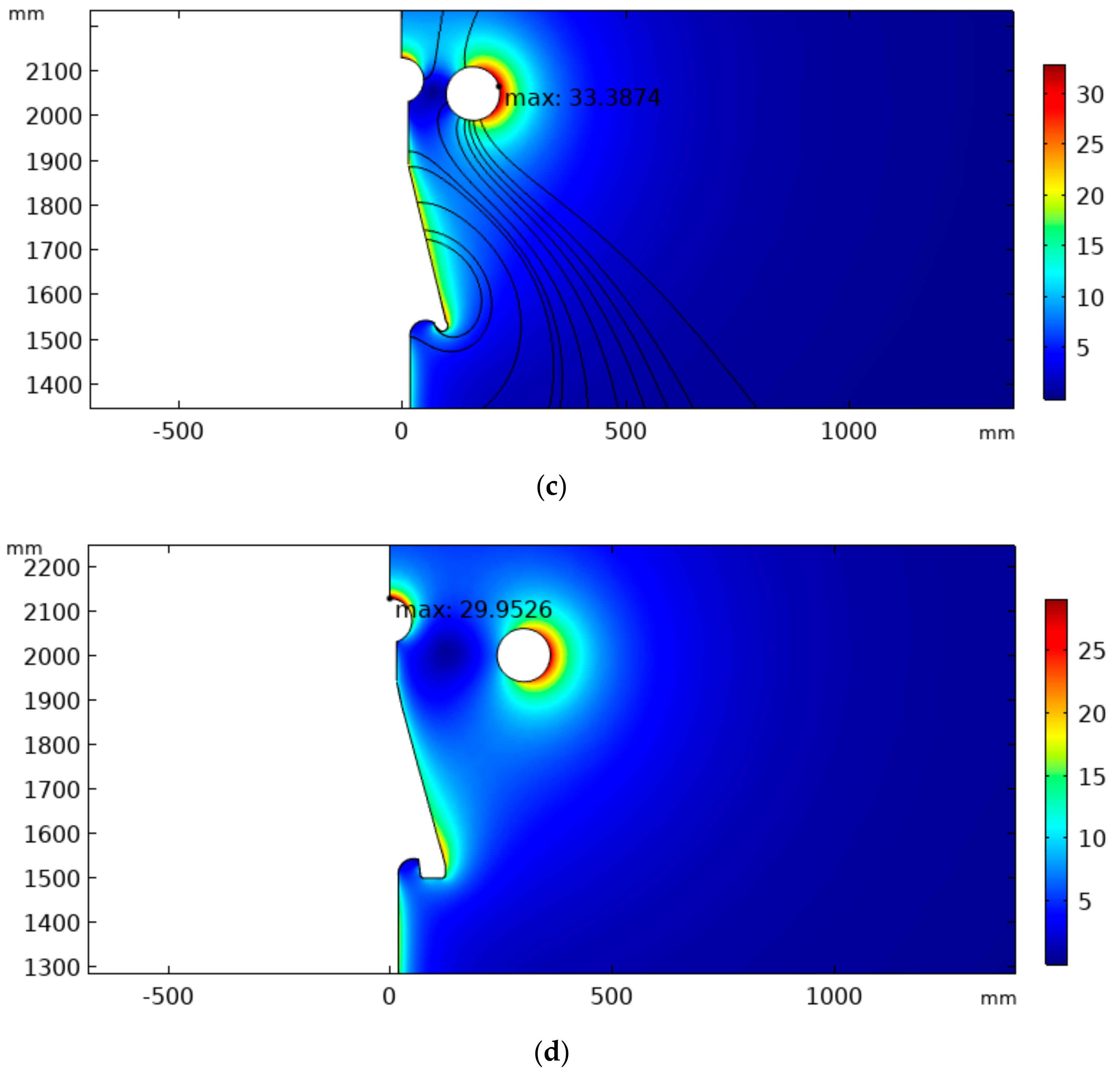
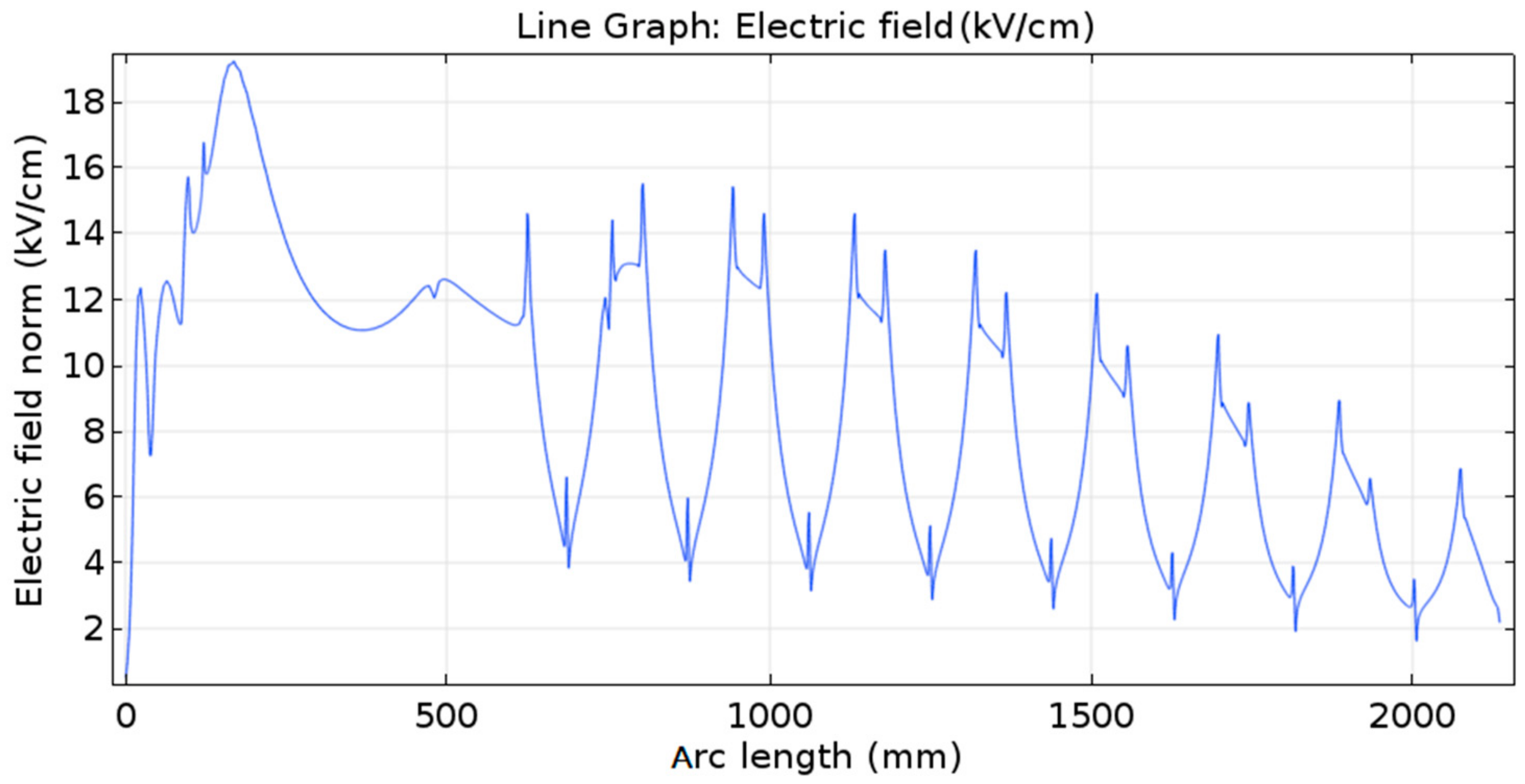
The optimized cable termination ensured that the electric field presented a greater probability of electrical breakdown inside the cable, in the cable part represented by the 3 m effective length. The achieved termination model minimized the probability of surface discharges and electrical breakdown between the high-voltage electrode and the external ground. In this context, the electric field distribution in the air and termination surface was also analyzed. As shown in
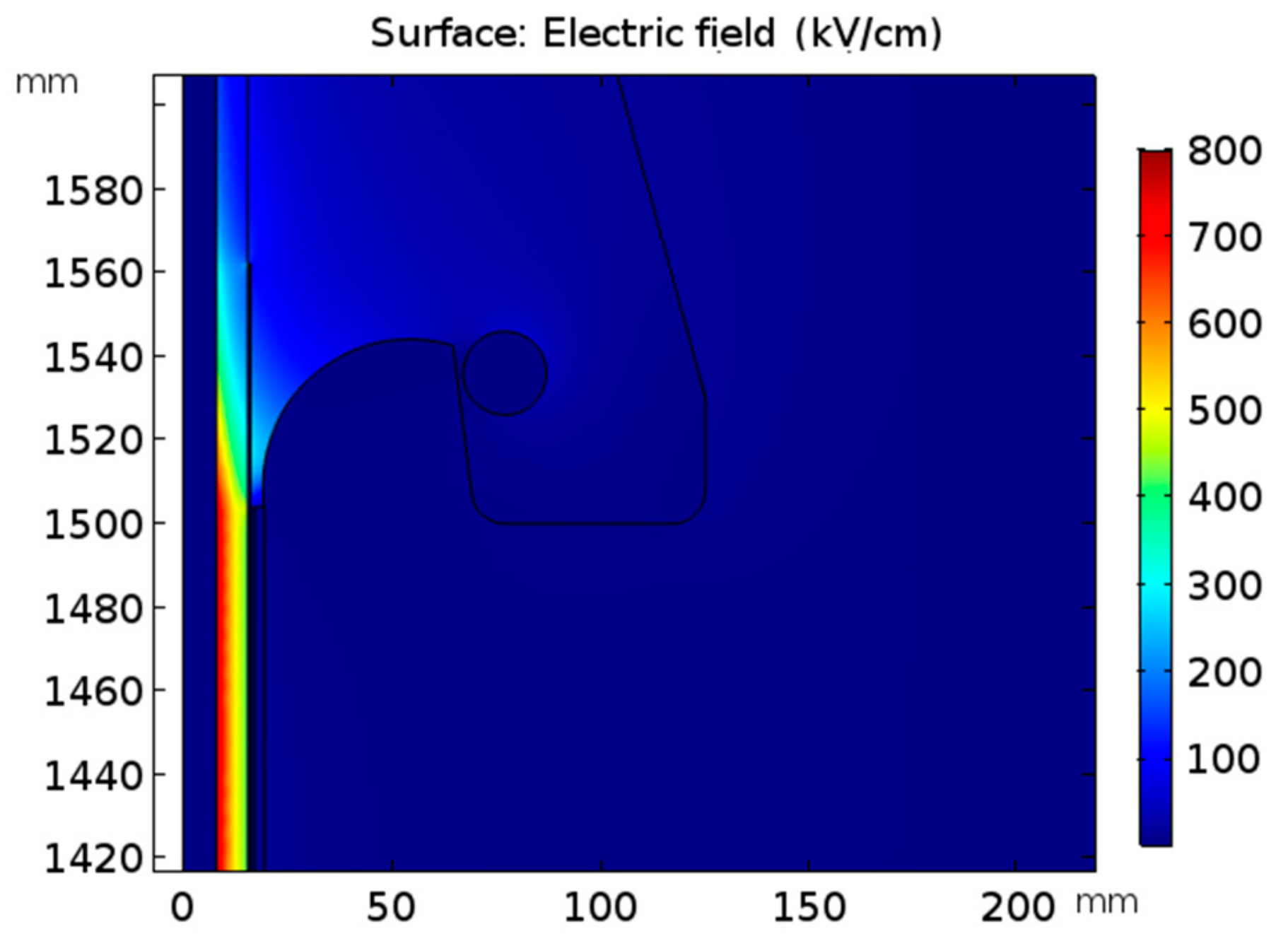
Figure 15, the proposed termination allows the control of the surface electric field.
The proposed methodology was tested using a 35 kV XLPE cable model. The designed termination model contained an additional insulator to avoid tangential discharges and increase creepage distance, a metal sphere at the end of the structure, and a ring-shaped electrode to improve the electric field distribution in the surrounding air. As a result, the average electric field throughout the superficial path was about 8.8 kV/cm, and the maximum electric field strength was about 19 kV/cm, near the stress relief cone surface.
From the analysis of the results obtained in the simulations, it was observed that the objective was reached, given that, when applying the termination created, dielectric breakdown is more likely to occur in the effective length (inner part) of the cable. The performed simulations showed that a termination with the proposed dimensions and materials decreased the probability of electrical discharge at the terminations of the cable to be tested. The proposed termination eliminated the field intensification at the termination of the cable.
The proposed methodology benefits from advanced simulations to perform initial tests and to avoid wasting resources with unsatisfactory termination models. A termination was effectively developed for the cable considered so that overvoltage tests could be performed. Furthermore, conventional materials were considered in the proposed design, which represents a potential cost reduction. Future research may be carried out by developing new models in search of an improved result. The proposed termination should be built to carry out experimental tests in relation to its functionality. This study may also contribute as a basis for future studies in the HVDC area, especially the ones related to cable terminations.