Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations †
Abstract
1. Introduction
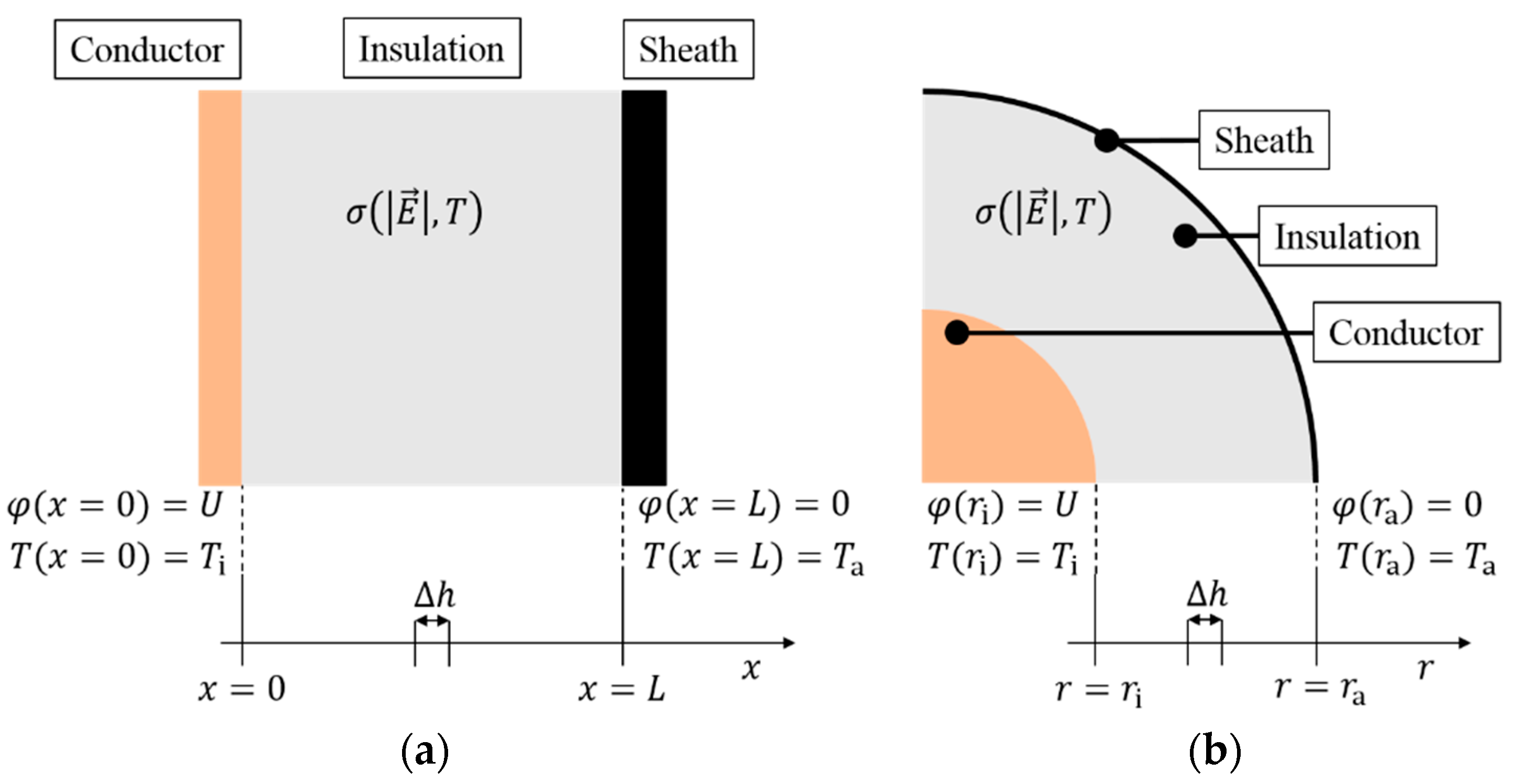
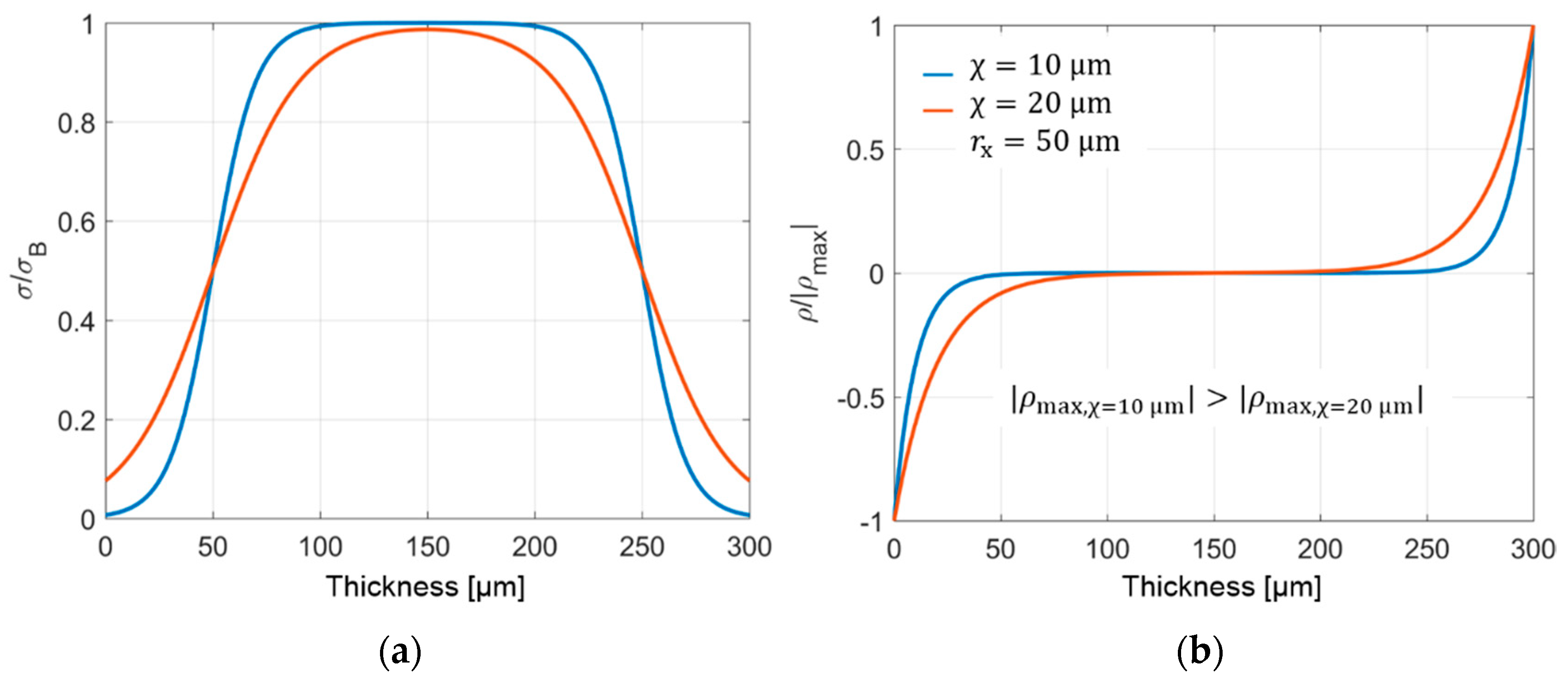
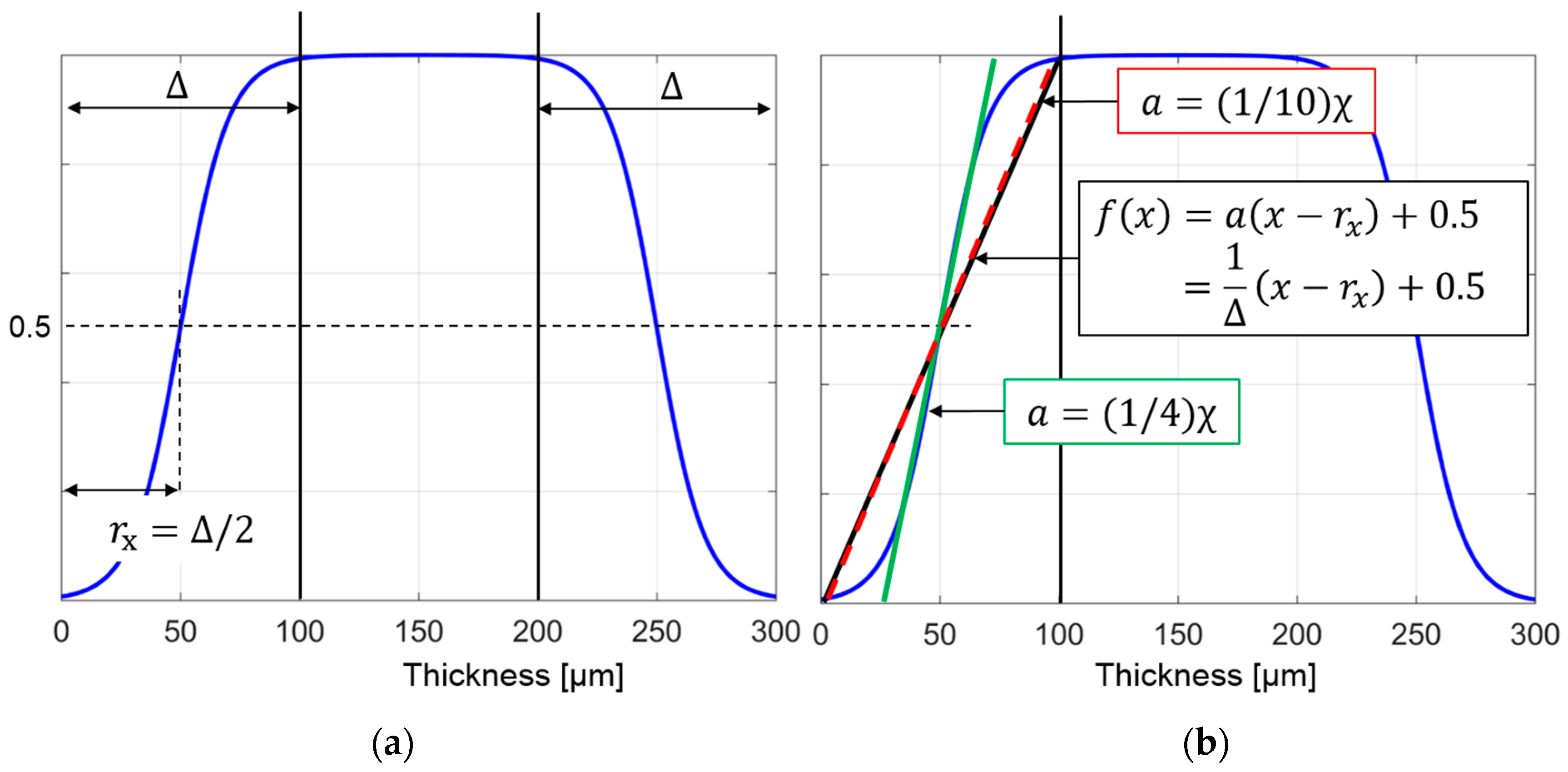
2. Empirical Conductivity Model Equation for the Simulation of the Stationary Charge Distribution
3. Comparison between Simulated and Measured Space Charge Distribution
3.1. Measurements of XLPE Insulation
3.2. Measurements of LDPE Insulation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Electric field [V/m] | |
| Ea | Constant for the temperature dependency of the bulk electric conductivity [eV] |
| Current density [A/m2] | |
| Constant for the bulk electric conductivity [A/m2] | |
| k = 1.38 × 10−23 | Boltzmann constant [J/K] |
| K1 | Conductivity variations at the conductor |
| K2 | Conductivity variations at the sheath |
| L | Thickness of planplanar insulation [m] |
| N | Number of grid points |
| r | Coordinate for the cylindrical insulation [m] |
| ra | Radius of the conductor in cylindrical coordinates [m] |
| ri | Radius of the conductor in cylindrical coordinates [m] |
| rx | Distance between the conductor (sheath) and the position of the highest gradient of K1 (K2) [m] |
| T | Temperature [°C] |
| Ta | Sheath temperature [°C] |
| Ti | Conductor temperature [°C] |
| U | Applied voltage [V] |
| x | Coordinate for the planplanar insulation [m] |
| γ | Constant for electric field dependency of the bulk electric conductivity [m/V] |
| Δ | Gradient region at the conductor and the sheath [m] |
| Δh | Distance between two grid points [m] |
| δ+ | Positive surface charges at the conductor [C/m2] |
| δ− | Negative surface charges at the sheath [C/m2] |
| ε0 = 8.854 × 10−12 | Dielectric constant [As/(Vm)] |
| εr | Relative permittivity |
| η | Sum of the difference between ρs and ρM |
| ρ | Space charge density [C/m3] |
| ρM | Measured space charge density [C/m3] |
| ρs | Simulated and filtered space charge density [C/m3] |
| σ | Total electric conductivity with hetero charges [S/m] |
| σB | Bulk electric conductivity without hetero charges [S/m] |
| φ | Electric potential [V] |
| χ | Distance constant to define the conductivity gradient in the vicinity of both electrodes [m] |
References
- Hanley, T.L.; Burford, R.P.; Fleming, R.J.; Barber, K.W. A general review of polymeric insulation for use in HVDC cables. IEEE Electr. Insul. Mag. 2003, 19, 14–24. [Google Scholar] [CrossRef]
- Dissado, L.A. The origin and nature of ‘charge packets’: A short review. In Proceedings of the International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Fleming, R.J. Space Charge in Polymers, Particularly Polyethylene. Braz. J. Phys. 1999, 29, 280–294. [Google Scholar] [CrossRef]
- Küchler, A. High Voltage Engineering–Fundamentals, Technology, Applications, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 583–590, 503–507. [Google Scholar] [CrossRef]
- Fabiani, D.; Montanari, G.C.; Dissado, L.A.; Laurent, C.; Teyssedre, G. Fast and Slow Charge Packets in Polymeric Materials under DC Stress. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 241–250. [Google Scholar] [CrossRef]
- Wang, X.; Yoshimura, N.; Murata, K.; Tanaka, Y.; Takada, T. Space-charge characteristics in polyethylene. J. Phys. D Appl. Phys. 1998, 84, 1546–1550. [Google Scholar] [CrossRef]
- Takeda, T.; Hozumi, N.; Suzuki, H.; Okamoto, T. Factors of Hetero Space Charge Generation in XLPE under dc Electric Field of 20 kV/mm. Electr. Eng. Jpn. 1999, 129, 13–21. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Modeling the Field in Polymeric Insulation Including Nonlinear Effects due to Temperature and Space Charge Distributions. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Fort Worth, TX, USA, 22–25 October 2017; pp. 10–13. [Google Scholar] [CrossRef]
- Hjerrild, J.; Holboll, J.; Henriksen, M.; Boggs, S. Effect of Semicon-Dielectric Interface on Conductivity and Electric Field Distribution. IEEE Trans. Electr. Insul. 2002, 9, 596–603. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Empirical Conductivity Equation for the Simulation of Space Charges in Polymeric HVDC Cable Insulations. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athene, Greece, 10–13 September 2018. [Google Scholar] [CrossRef]
- LeRoy, S.; Segur, P.; Teyssedre, G.; Laurent, C. Description of bipolar charge transport in polyethylene using a fluid model with constant mobility: Model predictions. J. Phys. D Appl. Phys. 2003, 37, 298–305. [Google Scholar]
- Wintle, H.J. Charge Motion and Trapping in Insulators–Surface and Bulk Effects. IEEE Trans. Electr. Insul. 1999, 6, 1–10. [Google Scholar] [CrossRef]
- Bodega, R. Space Charge Accumulation in Polymeric High Voltage DC Cable Systems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006; pp. 78–88. [Google Scholar]
- Kumara, J.R.S.S.; Serdyuk, Y.V.; Gubanski, S.M. Surface Potential Decay on LDPE and LDPE/Al2O3 Nano-Composites: Measurements and Modeling. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3466–3475. [Google Scholar] [CrossRef]
- Boudou, L.; Guastavino, J. Influence of temperature on low-density polyethylene films through conduction measurement. J. Phys. D Appl. Phys. 2002, 35, 1555–1561. [Google Scholar] [CrossRef]
- Bambery, K.R.; Fleming, R.J.; Holboll, J.T. Space charge profiles in low density polyethylene samples containing a permittivity/conductivity gradient. J. Phys. D Appl. Phys. 2001, 34, 3071–3077. [Google Scholar] [CrossRef]
- Fleming, R.J.; Henriksen, M.; Holboll, J.T. The Influence of Electrodes and Conditioning on Space Charge Accumulation in XLPE. IEEE Trans. Electr. Insul. 2000, 7, 561–571. [Google Scholar] [CrossRef]
- Lv, Z.; Cao, J.; Wang, X.; Wang, H.; Wu, K.; Dissado, L.A. Mechanism of Space Charge Formation in Cross Linked Polyethylene (XLPE) under Temperature Gradient. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3186–3196. [Google Scholar] [CrossRef]
- Bodega, R.; Morshuis, P.H.F.; Straathof, E.J.D.; Nilsson, U.H.; Perego, G. Characterization of XLPE MV-size DC Cables by Means of Space Charge Measurements. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Kansas City, MO, USA, 15–18 October 2006; pp. 11–14. [Google Scholar] [CrossRef]
- Mizutani, T. Space Charge Measurement Techniques and Space Charge in Polyethylene. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 923–933. [Google Scholar] [CrossRef]
- Wu, J.; Lan, L.; Li, Z.; Yin, Y. Simulation of Space Charge Behavior in LDPE with a Modified of Bipolar Charge Transport Model. In Proceedings of the International Symposium on Electrical Insulating Materials, Niigata, Japan, 1–5 June 2014; pp. 65–68. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Conductivity-based model for the simulation of homocharges and heterocharges in XLPE high-voltage direct current cable insulation. IET-SMT 2019. [Google Scholar] [CrossRef]
- Fu, M.; Dissado, L.A.; Chen, G.; Fothergill, J.C. Space Charge Formation and its Modified Electric Field under Applied Voltage Reversal and Temperature Gradient in XLPE Cable. IEEE Trans. Electr. Insul. 2008, 15, 851–860. [Google Scholar] [CrossRef]
- Bambery, K.R.; Fleming, R.J. Space Charge Accumulation in Two Power Cables Grades of XLPE. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 103–109. [Google Scholar] [CrossRef]
- Lim, F.N.; Fleming, R.J.; Naybour, R.D. Space Charge Accumulation in Power Cable XLPE Insulation. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 273–281. [Google Scholar] [CrossRef]
- Imburgia, A.; Miceli, R.; Sanseverino, E.R.; Romano, P.; Viola, F. Review of Space Charge Measurement Systems: Acoustic, Thermal and Optical Methods. IEEE Trans. Dielectr. Electr. Insul. 2015, 23, 3126–3142. [Google Scholar] [CrossRef]
- Karlsson, M.; Xu, X.; Gaska, K.; Hillborg, H.; Gubanski, S.M.; Gedde, U.W. DC Conductivity Measurements of LDPE: Influence of Specimen Preparation Method and Polymer Morphology. In Proceedings of the 25th Nordic Insulation Symposium, Västerås, Sweden, 19–21 June 2017. [Google Scholar] [CrossRef][Green Version]
- Xu, X.; Gaska, K.; Karlsson, M.; Hillborg, H.; Gedde, U.W. Precision electric characterization of LDPE specimens made by different manufacturing processes. In Proceedings of the 2018 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Athene, Greece, 10–13 September 2018. [Google Scholar] [CrossRef]
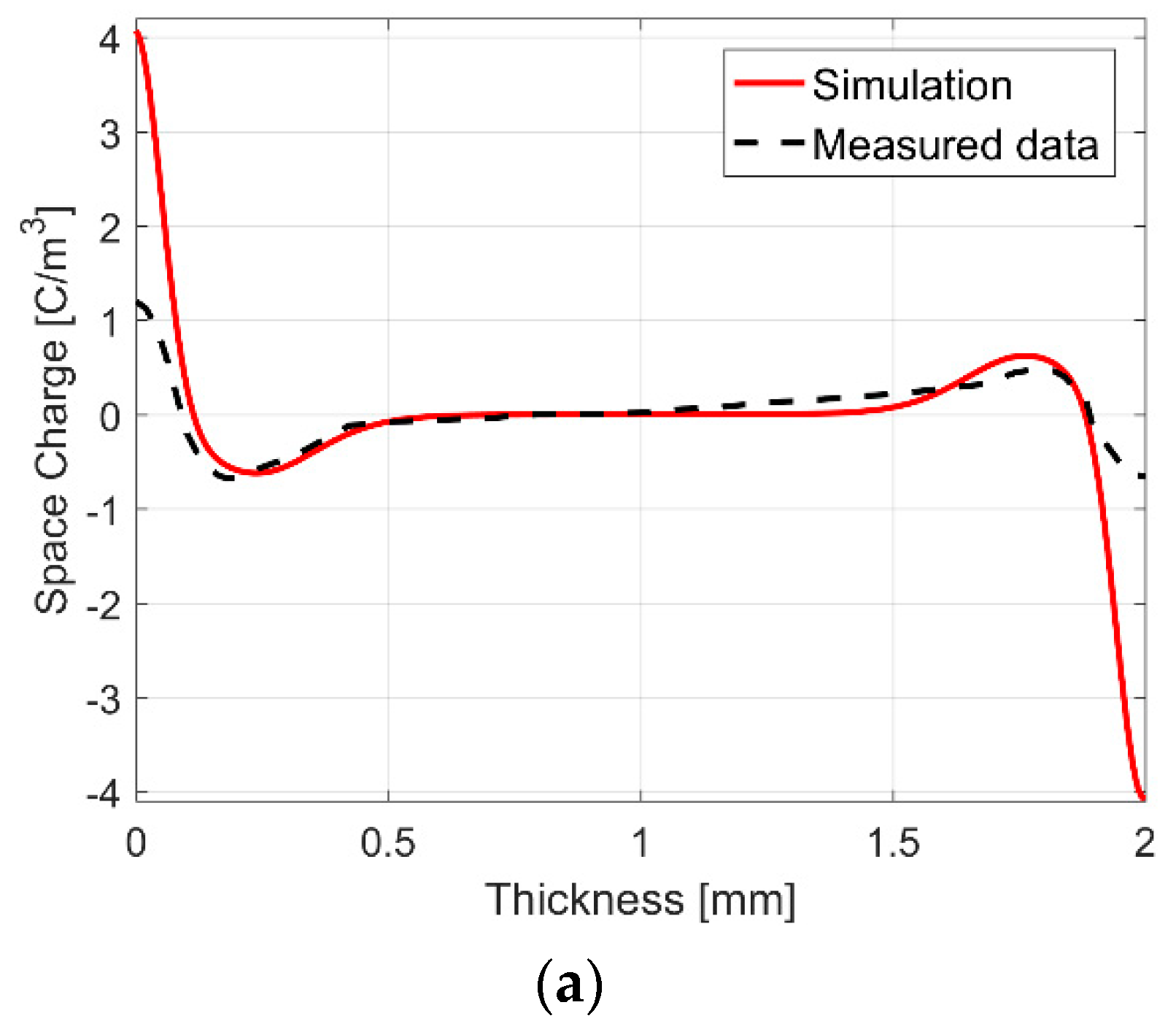

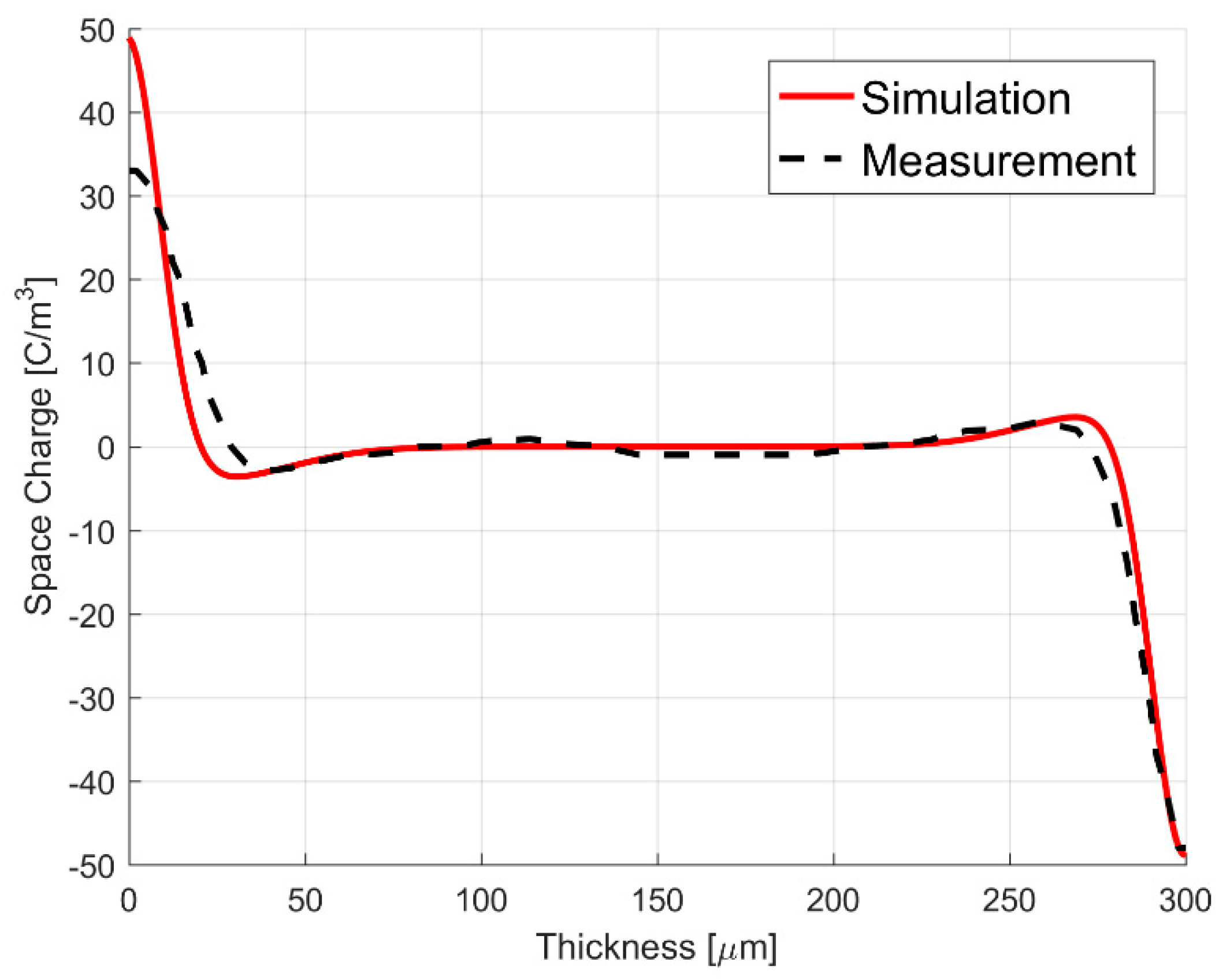
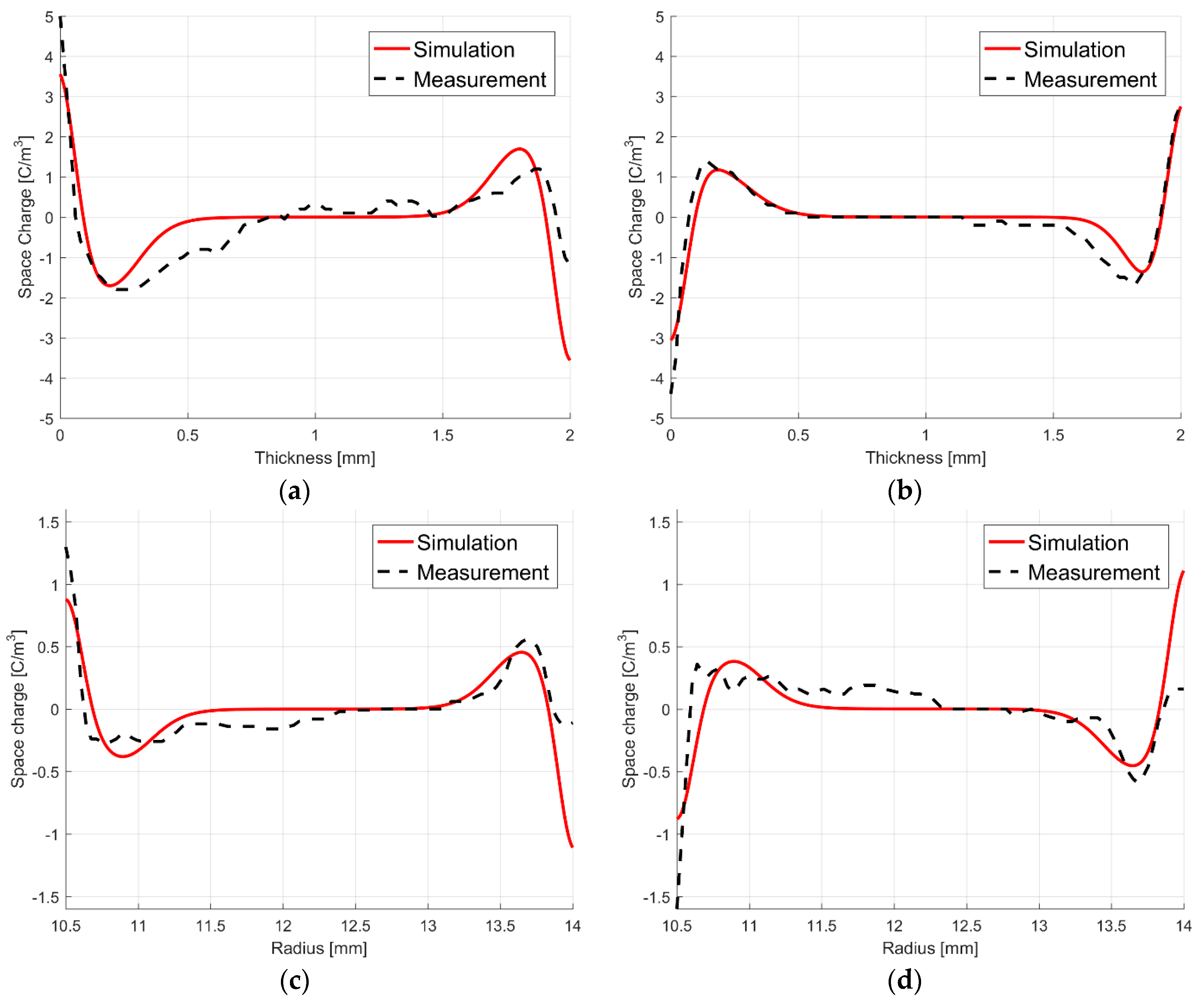
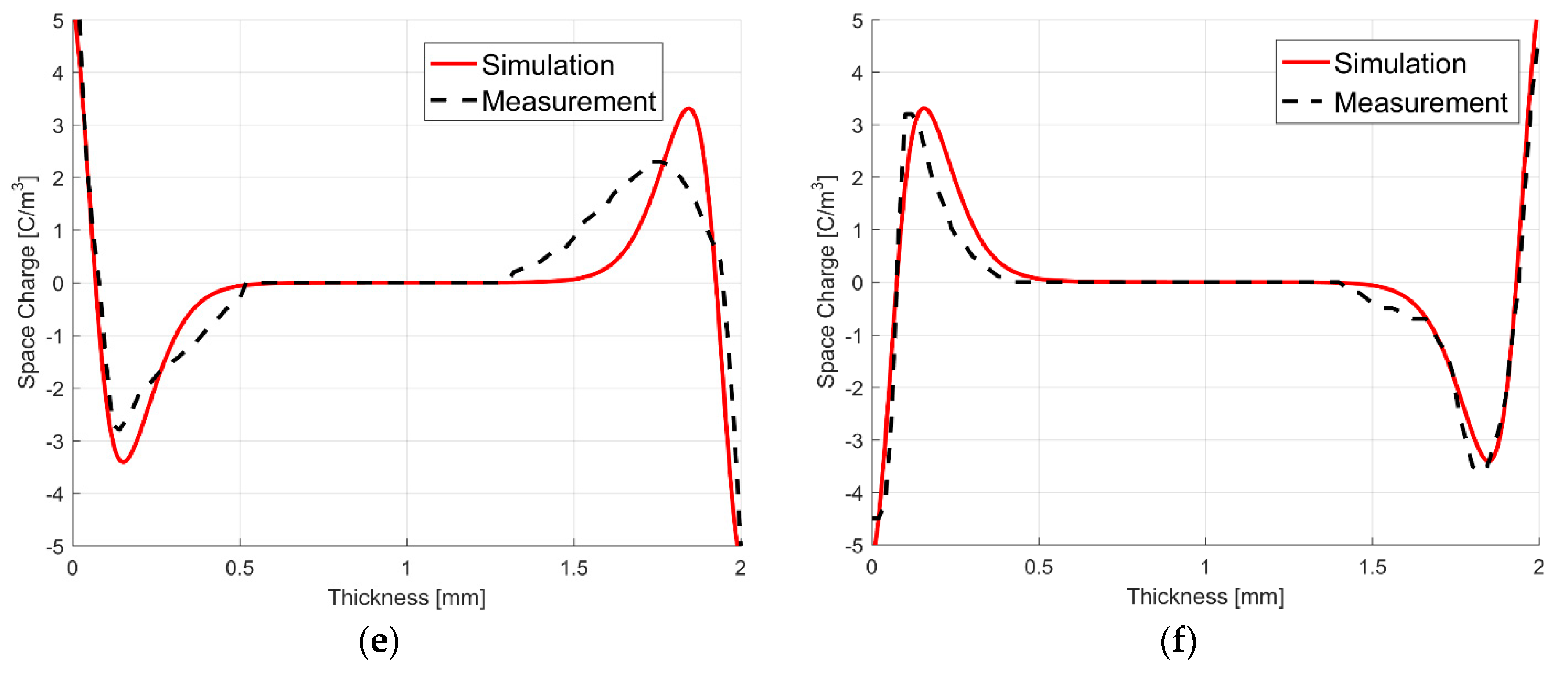

| Figure 4a | Figure 4b | Figure 5 |
|---|---|---|
| U = 40 kV | U = 90 kV | U = 15 kV |
| L = 2 mm | ri = 5 mm ra = 9.5 mm | L = 0.3 mm |
| T = 27 °C = const. | Ti = 65 °C Ta = 50 °C | T = 27 °C = const. |
| = 1 × 1014 A/m2 | = 1 × 1014 A/m2 | = 0.04224 A/m2 |
| Ea = 1.40 eV | Ea = 1.48 eV | Ea = 0.84 eV |
| γ = 2 × 10−7 m/V | γ = 2 × 10−7 m/V | γ = 4.251 × 10−7 m/V |
| χ = 65.3 μm | χ = 0.15 mm | χ = 10 μm |
| rx = 0.3 mm | rx = 0.68 mm | rx = 45 μm |
| Ref. | χ | rx | Insulation Thickness | Width of Charge Region Δ |
|---|---|---|---|---|
| [20], Figure 4a | 0.052 mm | 0.25 mm | 2 mm | 0.26·L |
| [19], Figure 4b | 0.12 mm | 0.60 mm | 4.5 mm | 0.22 × (ra − ri) |
| [6], XLPE, planplanar, +U | 0.052 mm | 0.25 mm | 2 mm | 0.26·L |
| [6], XLPE, planplanar, −U | 0.052 mm | 0.25 mm | 2 mm | 0.26·L |
| [6], XLPE, cylindrical, +U | 0.0875 mm | 0.44 mm | 3.5 mm | 0.28 × (ra − ri) |
| [6], XLPE, cylindrical, −U | 0.0875 mm | 0.44 mm | 3.5 mm | 0.28 × (ra − ri) |
| [6], LDPE, planplanar, +U | 0.052 mm | 0.25 mm | 2 mm | 0.26·L |
| [6], LDPE, planplanar, −U | 0.052 mm | 0.25 mm | 2 mm | 0.26·L |
| [21], Figure 5 | 8 μm | 40 μm | 300 μm | 0.267·L |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jörgens, C.; Clemens, M. Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations. Energies 2019, 12, 3018. https://doi.org/10.3390/en12153018
Jörgens C, Clemens M. Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations. Energies. 2019; 12(15):3018. https://doi.org/10.3390/en12153018
Chicago/Turabian StyleJörgens, Christoph, and Markus Clemens. 2019. "Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations" Energies 12, no. 15: 3018. https://doi.org/10.3390/en12153018
APA StyleJörgens, C., & Clemens, M. (2019). Empirical Conductivity Equation for the Simulation of the Stationary Space Charge Distribution in Polymeric HVDC Cable Insulations. Energies, 12(15), 3018. https://doi.org/10.3390/en12153018





