1. Introduction
Photovoltaic (PV) generation is one of the most widely applied forms of renewable energy generation (REG), which converts universally available solar energy into electricity through the photovoltaic effect [
1]. The whole generation process is nearly independent of fossil fuels, and the rapidly growing usage of PV technologies is in line with sustainable goals and renewable targets proposed worldwide. Moreover, recent price drops in solar panels since 2010 have boosted PV installations globally, and the cumulative installed capacity of PV panels worldwide reached 385 GW in 2017 [
2]. Supported by various incentive plans and more large-scale development contracts, the overall PV industry is expected to follow the current exponential trend of development in the coming ten years. According to the World Bank, electric power consumption per capita in the United Arab Emirates (UAE) is more than three times higher than the world average [
3]. Hence, massive PV projects are a promising solution to compensate the high energy budget, especially suitable for countries like the UAE, which is abundant in solar energy.
Unlike fossil fuels, the intermittent and non-dispatchable nature of REG poses new threats to power systems, and potential impacts include voltage fluctuations, harmonics, reverse power flows and malfunction of protection devices [
4]. Specifically, the voltage problem under high PV penetration is studied in [
5]. Using practical UK distribution network data, voltage rise at midday and voltage dip during occasional clouds are observed and assessed, and the influence on network management relies on case-by-case network status. Meanwhile, excessive harmonic voltage and current induce extra losses, like core losses in transformers and generators, as well as increase transmission losses in the conductor, which further causes overheating and affects lifecycles of power equipment, and potentially causes maloperation of protective devices [
6]. Furthermore, the PV generation can be either connected to transmission or distribution network, and the severity of corresponding problems also vary. For instance, from statistics in the Greek power system, 97.8% of PV systems are connected at the voltage levels of 20 kV and 0.4 kV, and the lack of control schemes like active power curtailment indicates PV generation is more problematic in the distribution network [
7]. Research work in this paper focuses on the distribution network with a maximum of 1000 kW of PV installation capacity. This range is classified as medium to small scale, based on classifications made in [
8].
Energy storage is a promising technology for work with renewables to mitigate intermittency and enhance controllability of REG, especially under the trend of decreasing manufacturer costs. Its basic functions include load shifting and grid balancing during unavailability of renewable energy, as well as smoothing REG outputs [
9]. For example, a combined PV-battery storage system using appropriate control strategies based on voltage measurement is capable of regulating bus voltage [
10]. The authors in [
11] developed the battery control strategy using State of Charge (SoC) information, which can reduce short-term fluctuations from PV caused by weather conditions and maximize the usage of battery capacity. However, the frequent usage of a battery can possibly reduce its lifecycle. To accommodate more PV generation and mitigate fluctuations of power balancing, authors in [
12] evaluated optimal battery capacity to achieve a flat power profile.
The direct benefits of using a hybrid PV and storage system are power balancing and voltage regulations. Batteries are more frequently used due to their robustness and relatively low cost. Proper scheduling and sizing of a battery system are major obstacles in relevant applications. In this paper, a hybrid PV battery system is built to investigate and improve the whole process.
Furthermore, cost is another constraint in limiting storage applications, and many researchers have endeavored to prove profitability of using energy storage. Under eight possible scenarios of a German residential PV system, the profitability of battery storage was assessed using a techno-economic model developed in [
13], with net present value (NPV) as the objective function. Electricity market information plays a significant role in profitability. Authors in [
14] predicted that feed-in tariffs are phasing out in coming years and the evaluated economic viability of PV storage system. Results show that a small-scale PV-battery system with enough self-sufficiency is profitable even without feed-in tariffs. Thus, economic feasibility of applying storage with PV system depends on factors such as costs, incentives like feed-in-tariffs (FIT) and electricity prices; therefore, the associated economic analysis of the PV-battery system is also performed in this paper.
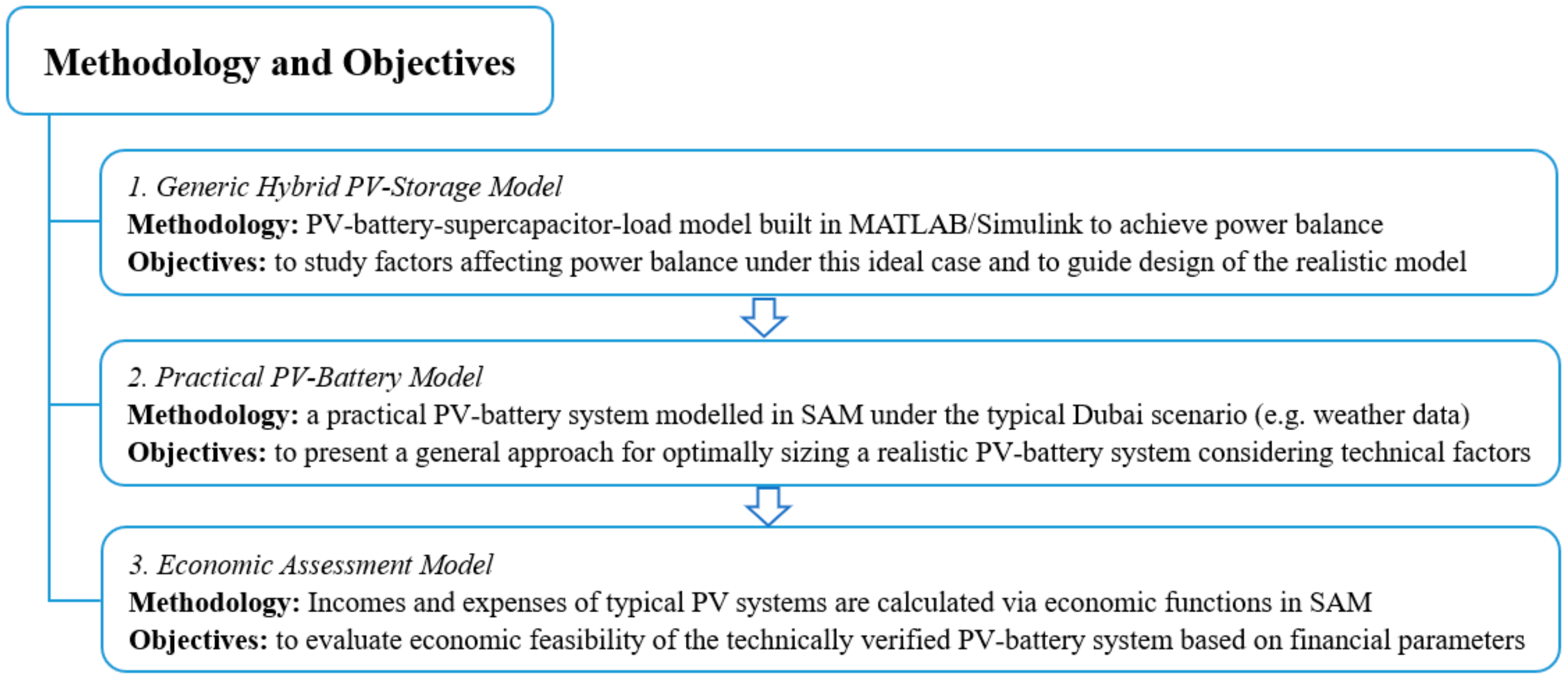
The aim of this paper is to evaluate the role of energy storage to maximize PV pervasiveness based on realistic test scenarios. Both technical and economic aspects are investigated and evaluated using a generic hybrid PV storage model which is designed and built using MATLAB/Simulink for a residential power network. To appreciate the optimal dispatch, sizing process and economic feasibility, a practical PV-Battery is modeled and investigated using the System Advisor Model (SAM).
2. System Modeling
To understand interactions between a PV system, distribution network and energy storage system, as well as assess economic values, three test models were proposed, simulated and analyzed. A block diagram is presented in
Figure 1 to explain the logic sequence of developing three test models in this paper. Specific methodologies are explained separately in this section.
2.1. Generic Hybrid PV-Storage Model
The intermittency of PV generation can be either short-term caused by cloud cover, or long-term due to unavailability of solar at night. Like in [
15] and [
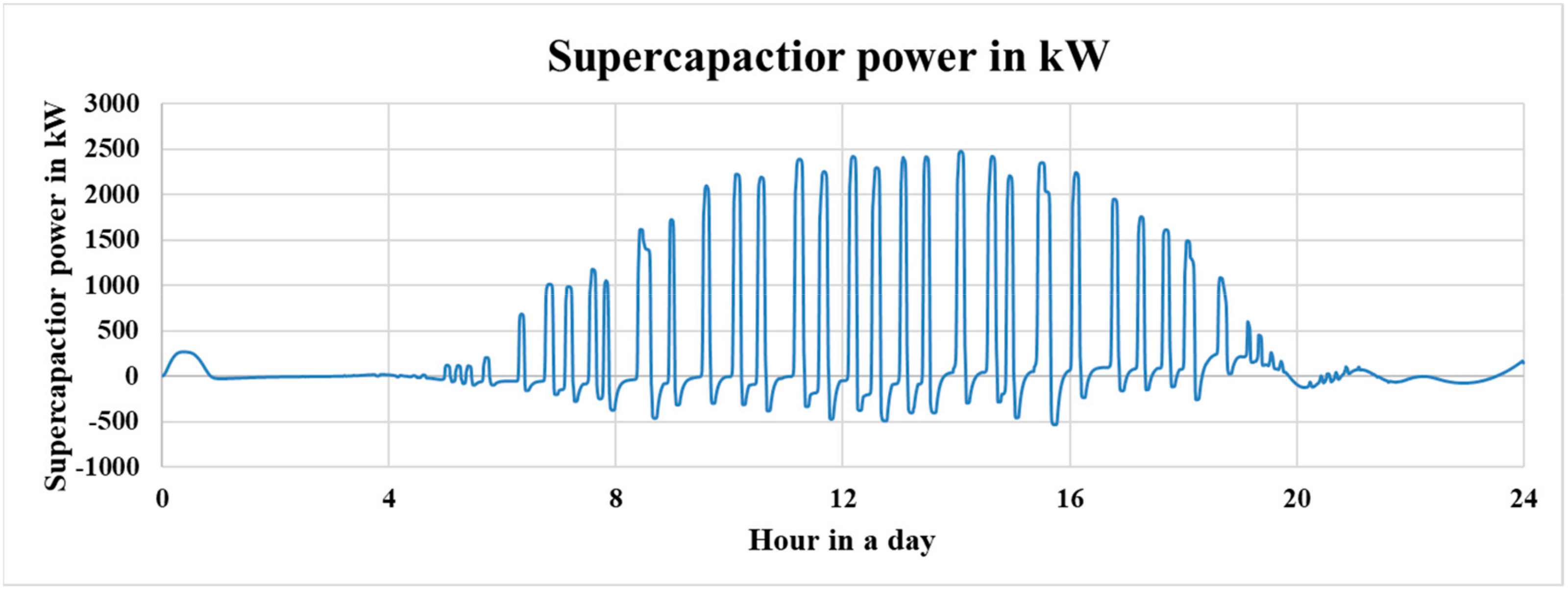
16], many researchers are investigating the hybrid PV storage system using a battery-supercapacitor to optimize the overall performance, which utilizes the high power density of a supercapacitor (SC), and the high energy density of battery.
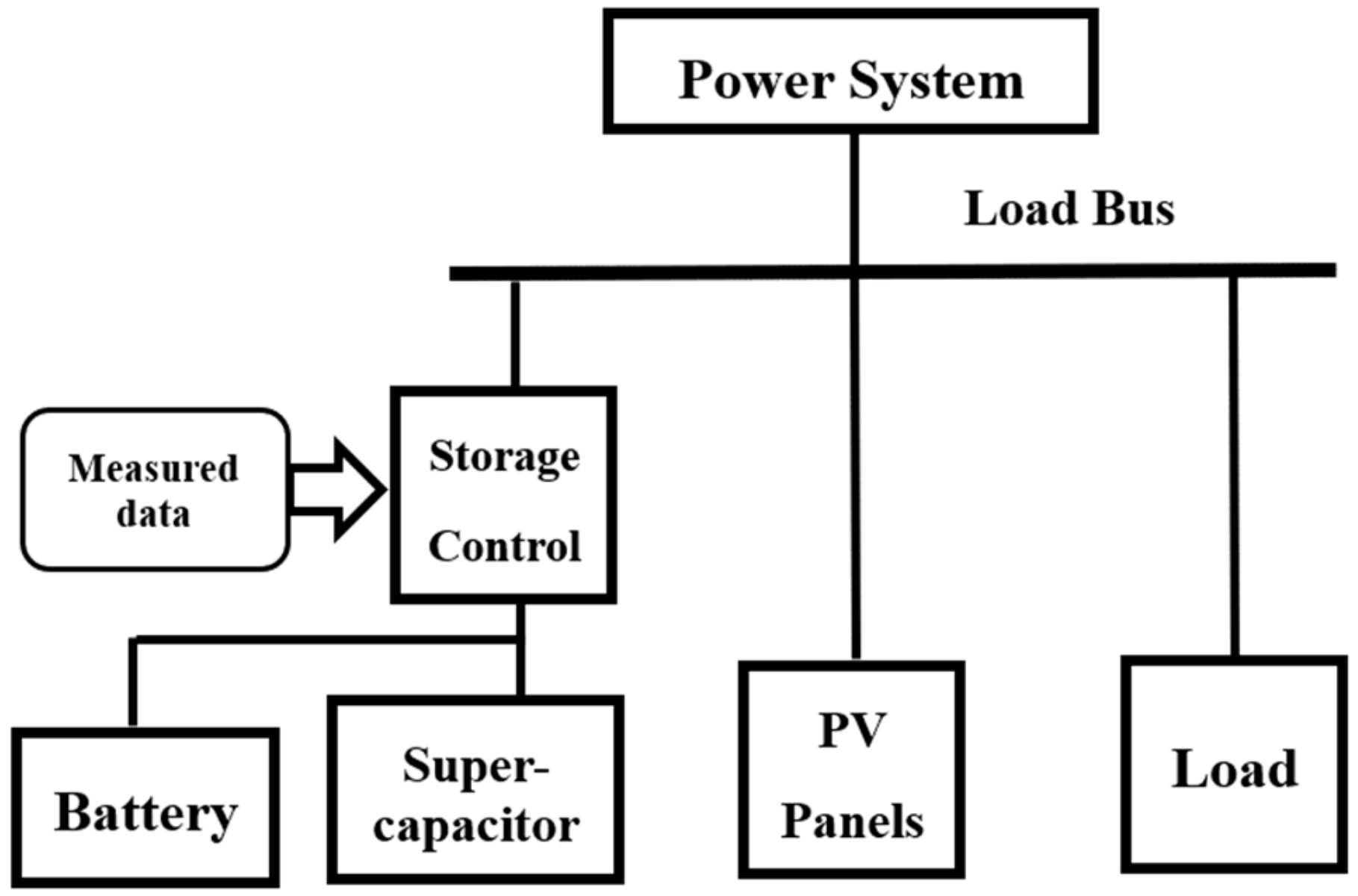
The microgrid model studied in this paper was implemented in MATLAB/Simulink [
17]. Instead of achieving zero energy balance, the objective was to obtain a constant load profile through the hybrid system design. Its generic schematic is presented in
Figure 2.
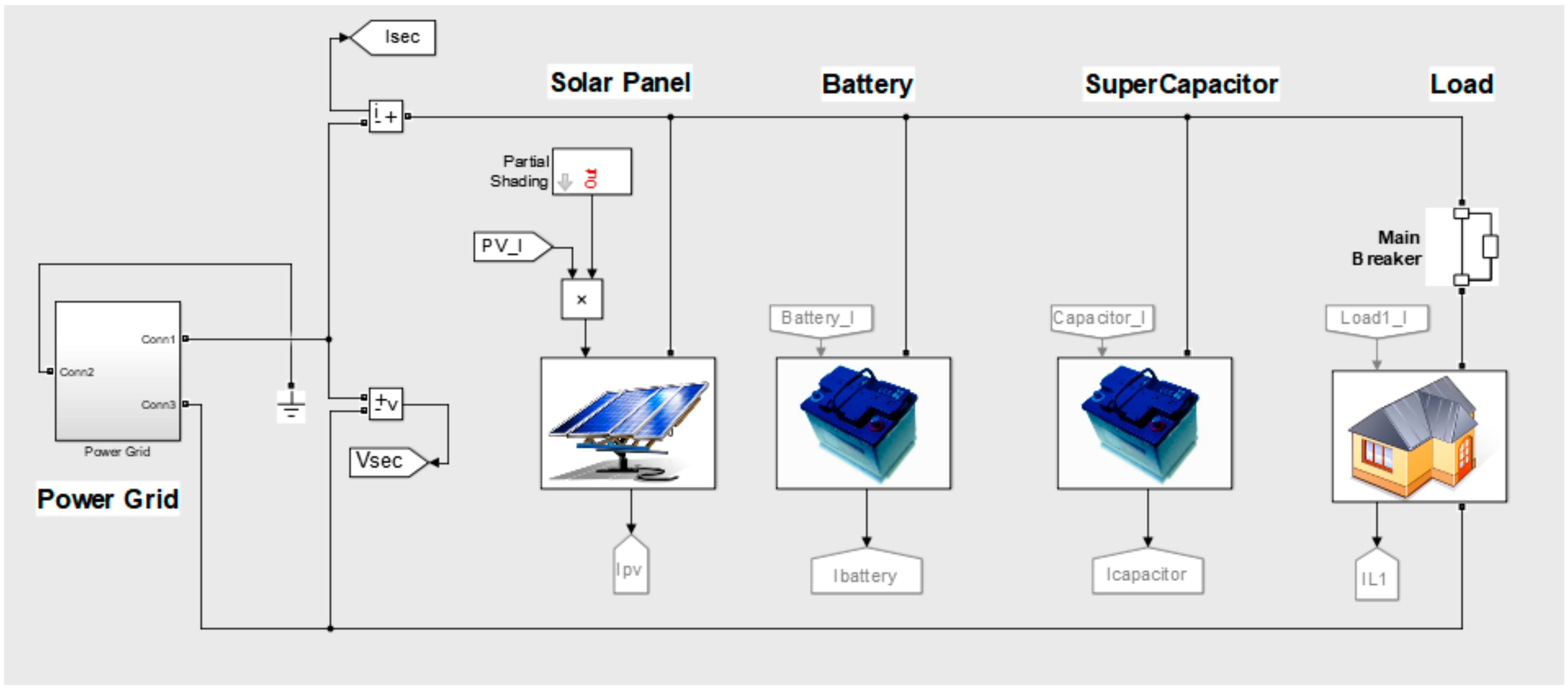
The corresponding Simulink model is presented in
Figure 3, which is adapted based on the microgrid model in [
17]. To simplify analysis, in this generic model, all components, like solar panel, battery, supercapacitor and load are modelled as controlled current sources, where input current works as control signals. The model’s objective is to maintain constant load current via hybrid storage system.
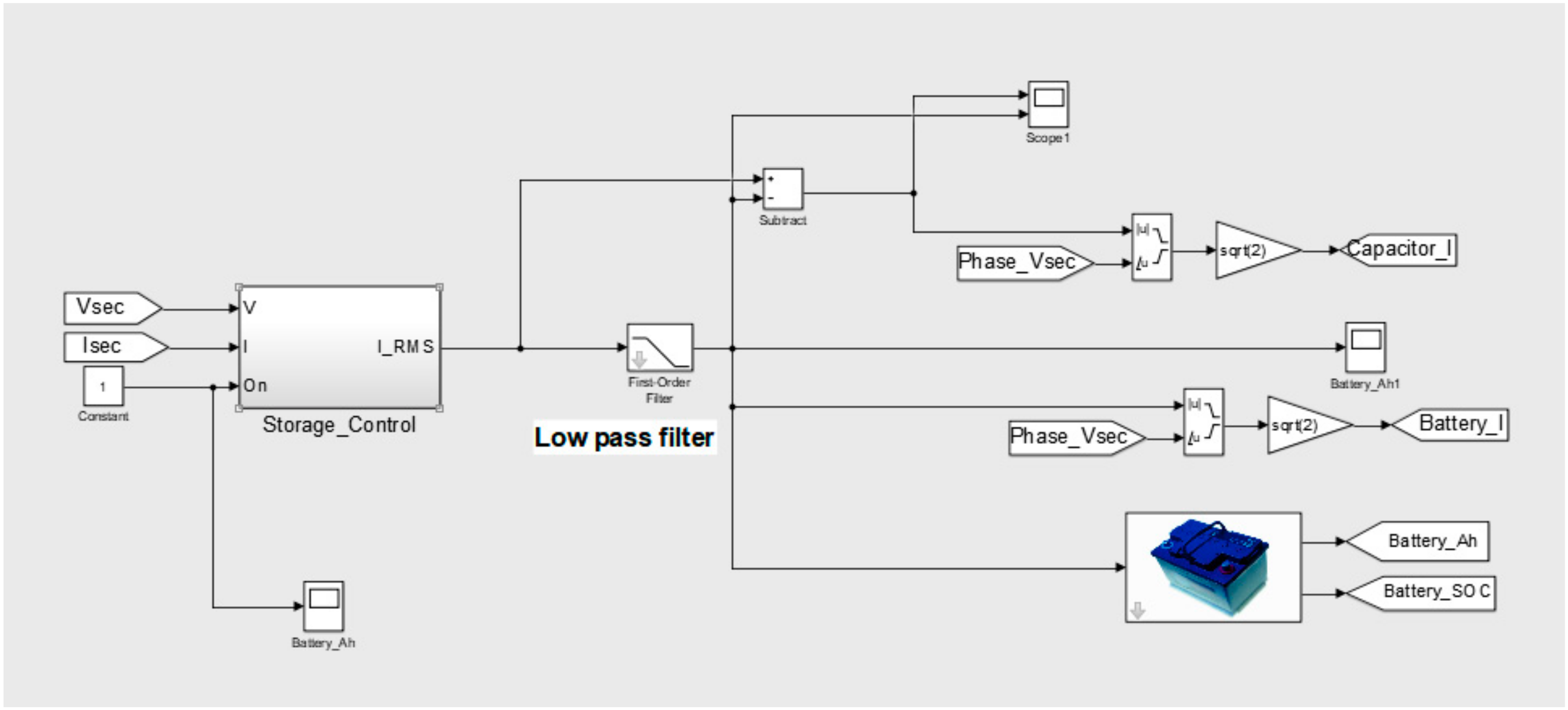
The implementation of a storage control block is shown in
Figure 4. Based on the moving average algorithm [
18], the power dispatch between the battery and the supercapacitor is implemented using a low-pass filter, which separates out high frequency signals. Batteries only react to long-term power gaps, whilst supercapacitors react to mitigate short and instant fluctuations. The processed signals are fed back into
Figure 3 to achieve power balance after fluctuations from the load side.
The effective application of this hybrid system depends on the optimal sizing of storage system because of high component costs. The whole system then had to be simulated, and basic sizing criteria are discussed using residential data.
2.2. Practical PV-Battery Model
A typical residential PV system is modelled in the System Advisor Model to understand interactions between the PV system and battery. SAM is excellent at evaluating system performance and expenses for grid-connected renewable projects. It is used to simulate practical scenarios using local weather inputs and equipment data from manufacturers [
19]. Model parameters are based on the typical Dubai scenario, which can be adapted to any scenario.
2.2.1. Weather Data
Typical meteorological year (TMY) weather data for Dubai was used with 8760 hourly samples [
20].
2.2.2. PV Modules and Inverter
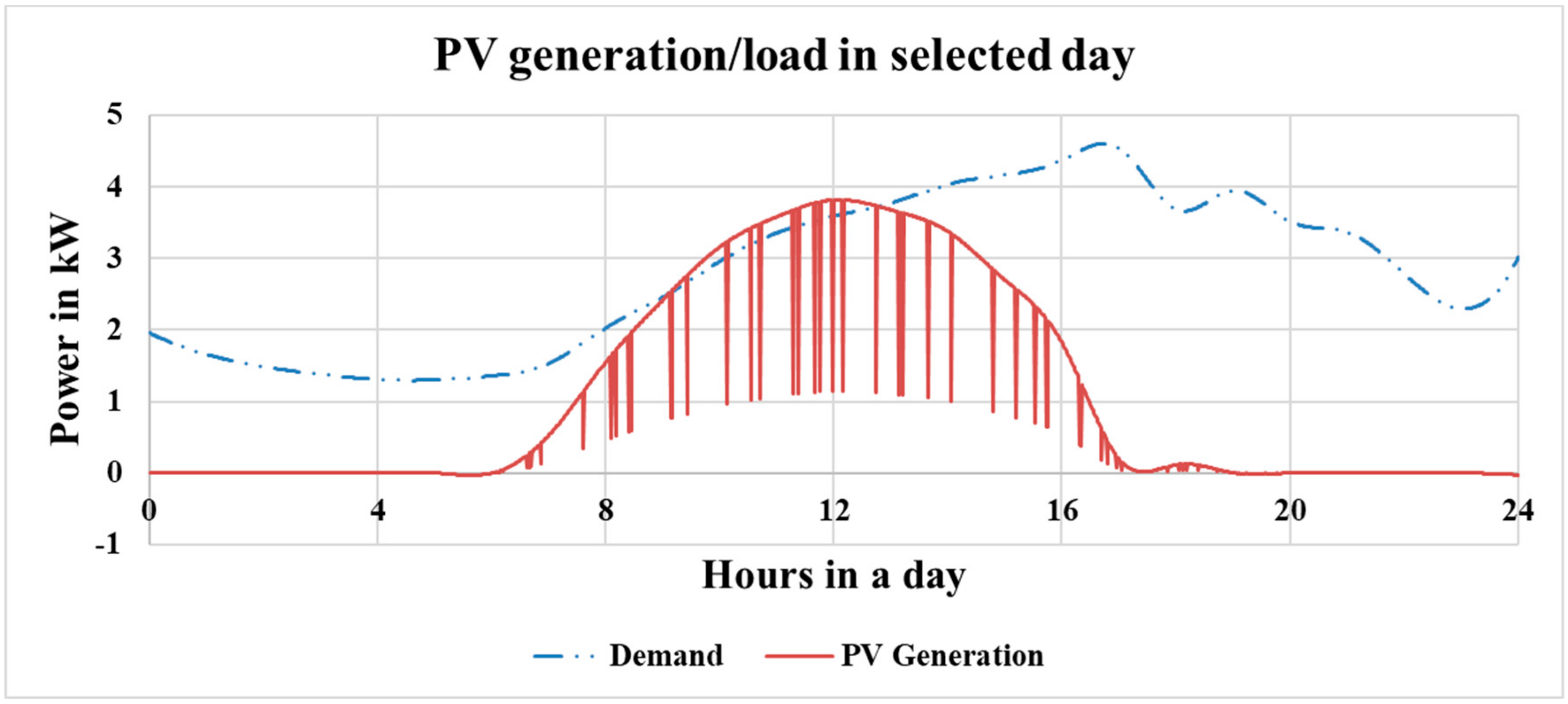
The module type was LG320N1C-G4, manufactured by LG with the DC capacity of 320 W [
21]. The total capacity of PV array was 5.12 kW with 16 modules. A compatible inverter of 5 kW manufactured by Schneider Electric. Annual PV generation is about 9000 kWh.
2.2.3. Load Model
Load profile estimator is an embedded function in SAM. The typical load profile of Dubai was modelled [
22]. The annual peak load was 4.8 kW and the annual demand was 18,000 kWh.
2.2.4. Battery Model and Controller
Lead-acid batteries were used because of their low capital costs in kWh and mature technologies [
23]. It is stated in [
13], that lead-acid is the most commonly applied battery technology in the distributed PV system. Technical parameters of battery bank are computed by default in SAM. Meanwhile, battery controllers are available in SAM for optimizing battery usage and two modes are mainly studied in this paper [
24]:
One-day look ahead mode: The 24-h prediction of PV and load is performed at the start of each day during annual simulation. A target power from the grid is calculated, and the battery is dispatched to meet this hourly target.
One-day look behind mode: This mode is like look-ahead mode. Rather than predictions for 24-h ahead though, the previous 24-h data are used in this mode.
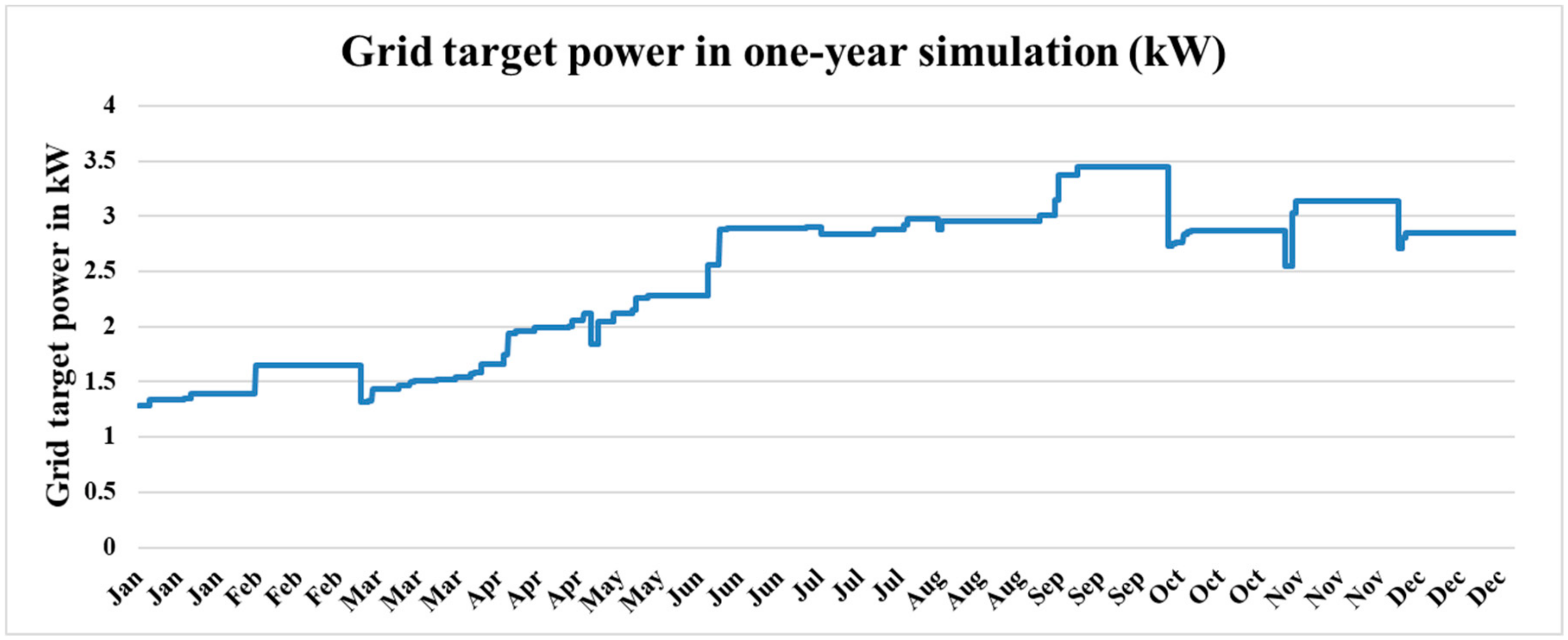
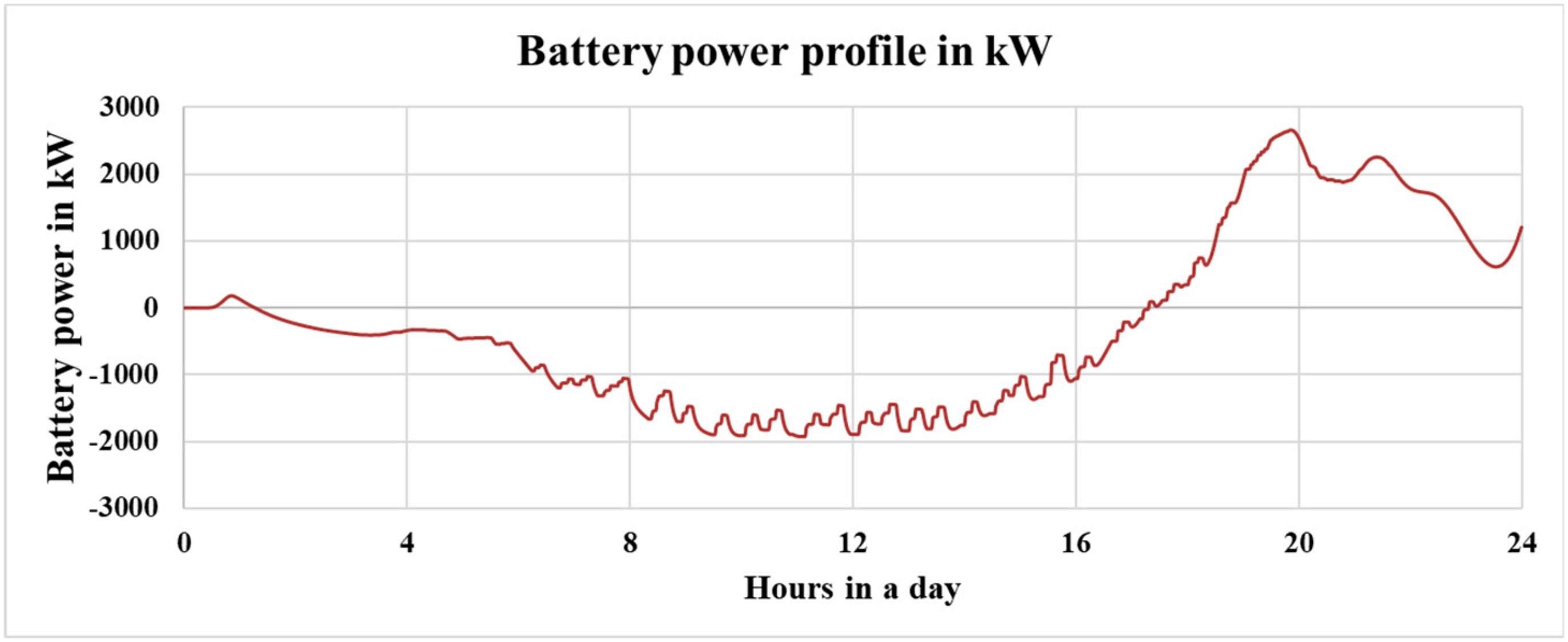
Figure 5 shows the hourly grid target power plotted on a yearly scale. The power profile is updated daily, and the required power is higher in summer months, like September, than winter months in January.
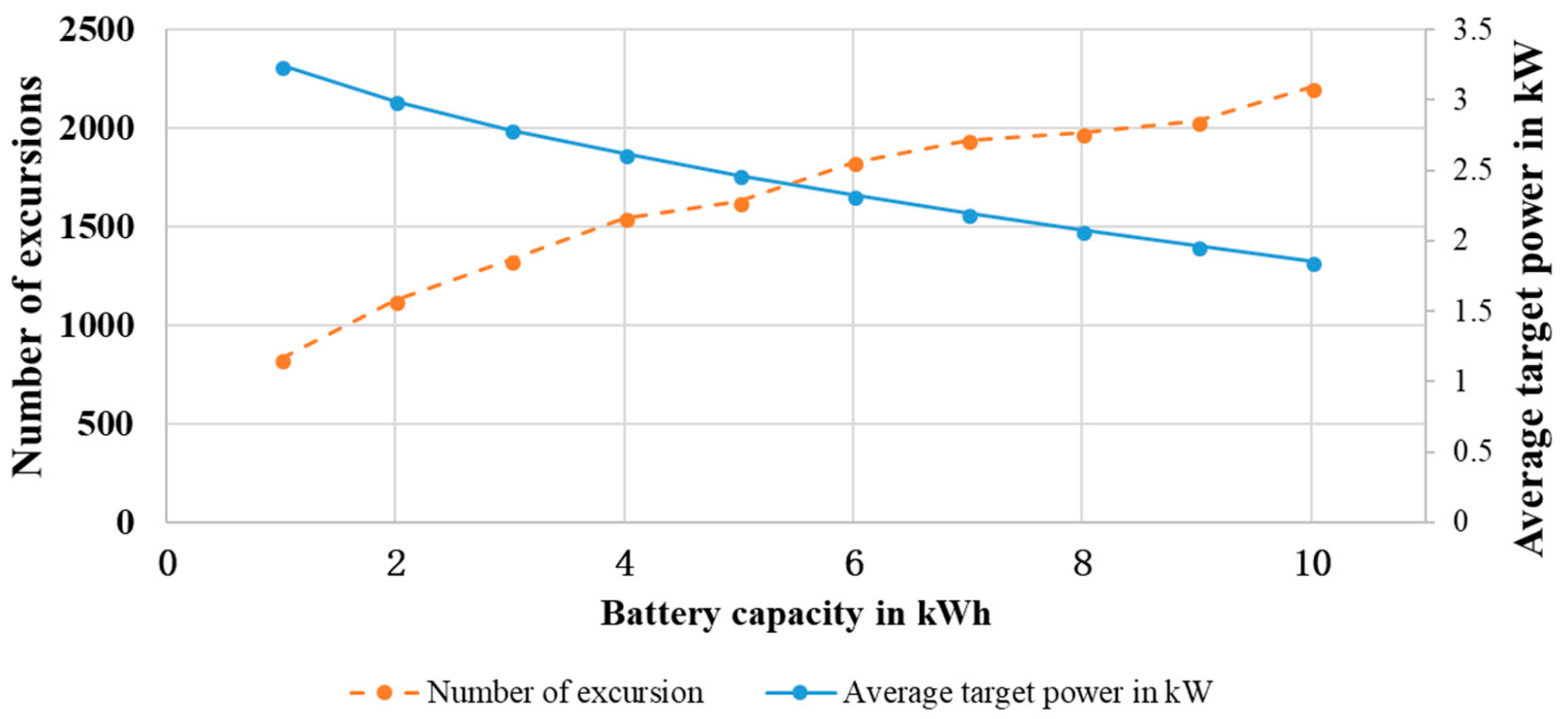
Excluding economic factors, two technical criteria are proposed to identify optimal battery capacity in kWh and kW regarding this residential PV system:
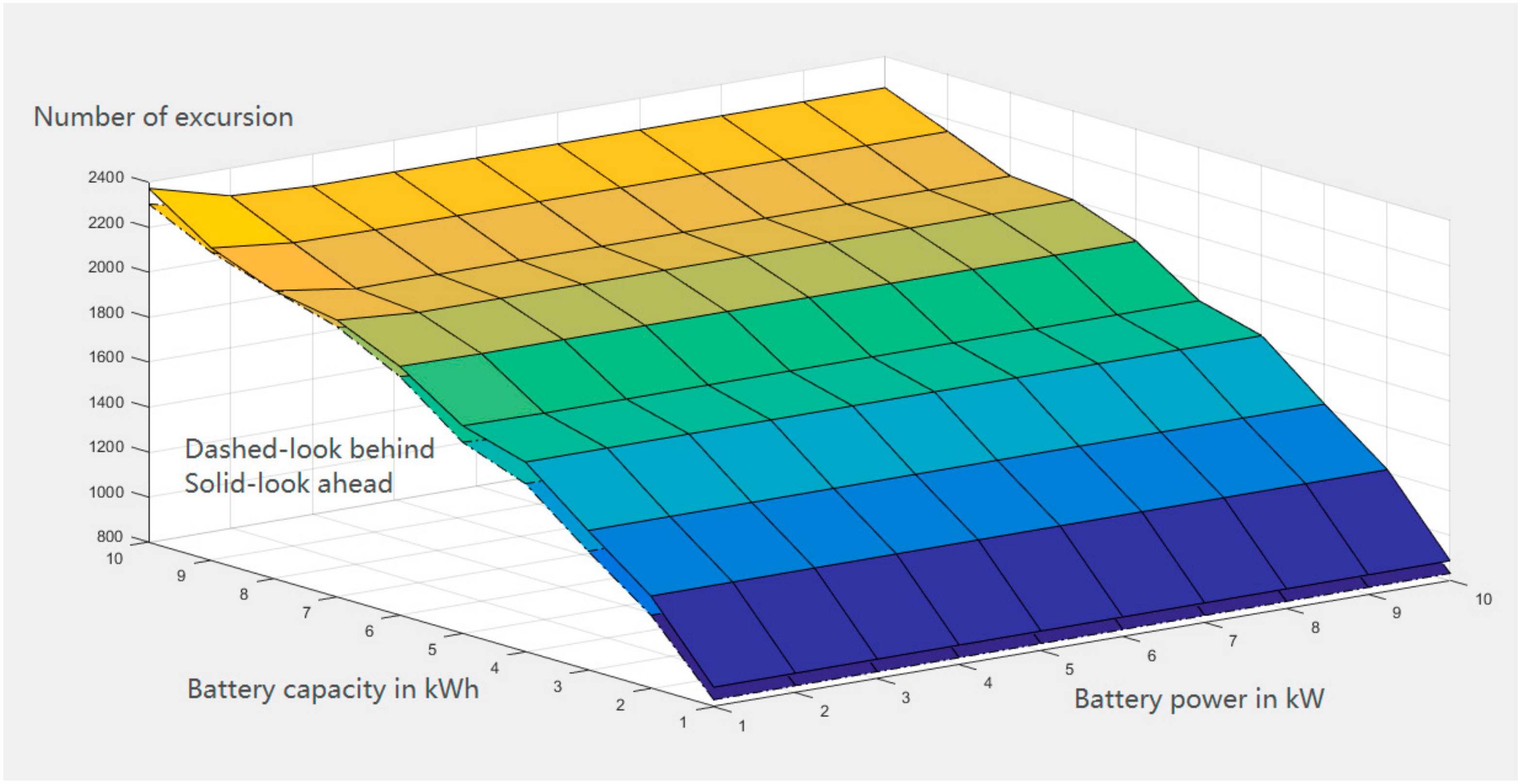
• Number of Excursions
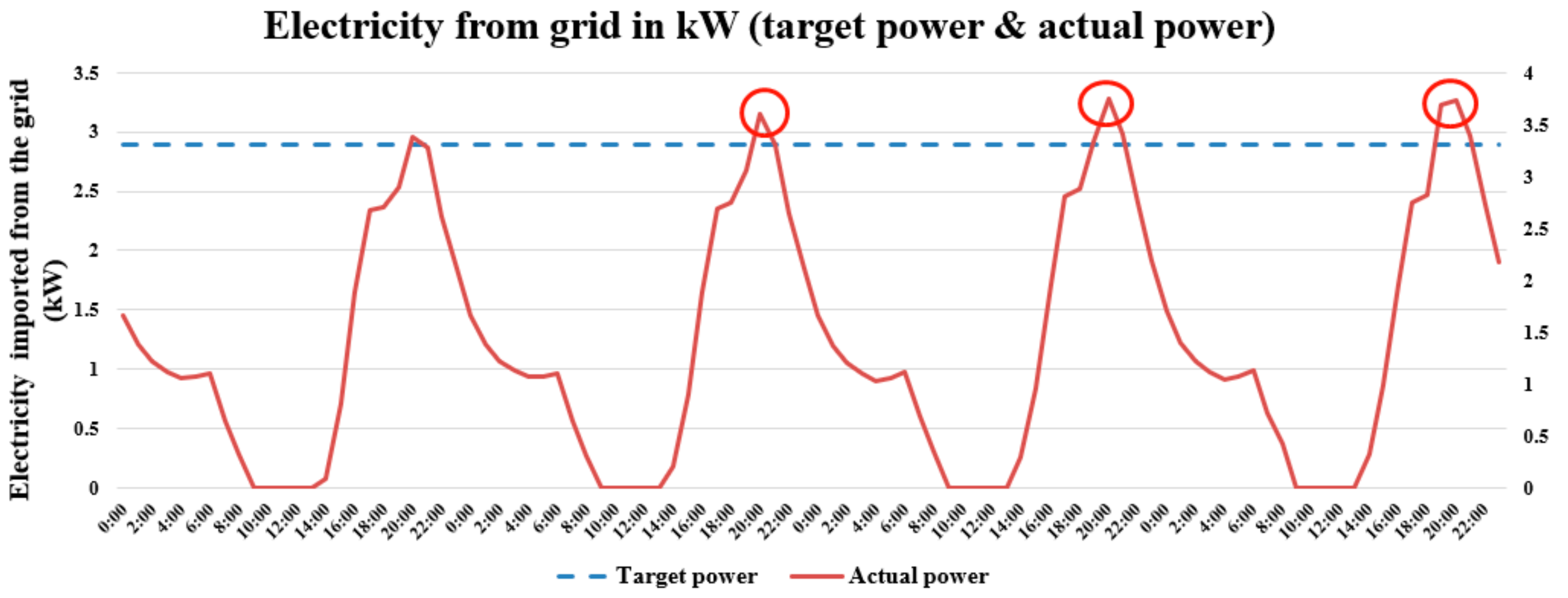
In this paper, the excursion is defined as the case when actual electricity required from the grid is higher than 1.05 times the targeted grid power, which indicates the failure of the dispatch controller. As explained in the previous section, the targeted grid power is calculated in SAM as the energy schedule updated in the timeframe of 24 h. Since there are 8760 samples in a one-year simulation, the number of excursions is the number of hourly samples having the abovementioned case.
Figure 6 shows an example of excursion, where red circles indicate samples when actual power is greater than the target.
The corresponding math definition for annual excursion number is given by.
where
Pactual is actual active power drawn from the grid in kW, and
Ptarget is the targeted power from the grid set by dispatch controller in kW.
Obviously, a smaller number of excursions indicates better controller performance.
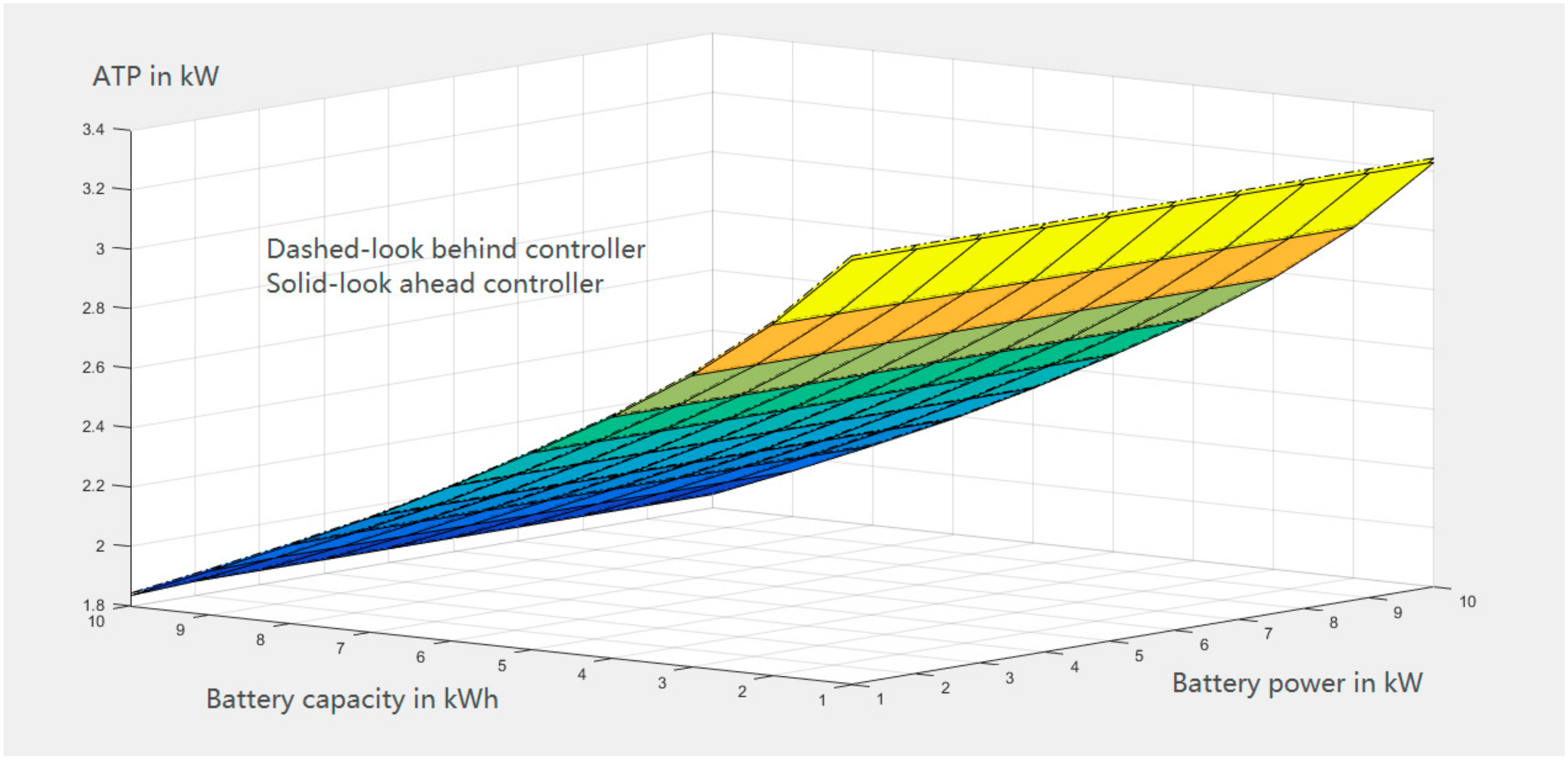
• Average target power (ATP)
ATP is derived by averaging all hourly target samples in kW, as presented in
Figure 5. Its mathematical expression is presented as:
For this specific model, a net import from the grid is around 9000 kWh annually. Ideally, the target power from the grid should meet this gap with a flat profile, hence the ideal ATP is evaluated as:
where
Pload is the consumed power from the grid in kW, and
PPV are the PV outputs in kW. However, due to factors like daily and seasonal differences between generation and load, actual ATP is much greater than the ideal ATP value. A well-designed controller can make this value close to the ideal case, which means enhanced controllability from a network planning point of view.
Both criteria are applied to identify a suitable battery size for the PV-battery combination from the technical side.
2.3. Economic Assessment
A basic financial model was set up to investigate the feasibility of PV system from the economic side.
Table 1 summarizes the equipment costs relevant to the PV system based on state-of-the-art resources.
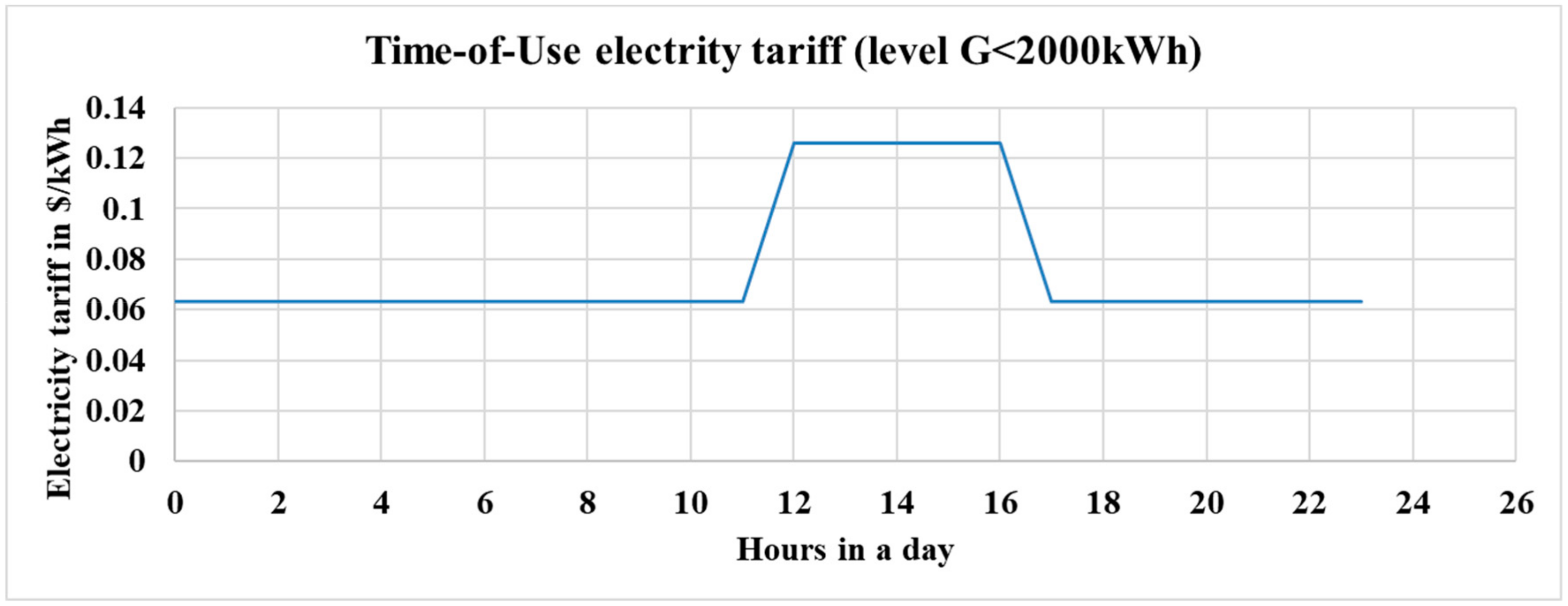
Meanwhile, electricity tariffs for residential customers in Dubai shown in
Table 2 were used for analysis [
30]. Local currency was converted to US dollars to facilitate analysis.
Level G stands for green; level Y stands for yellow; level O stands for orange; level R stands for red; slab tariff is regulated by Dubai Electricity and Water authority (DEWA) which is adjustable in real-time to promote energy efficiency.
Three financial indicators were used to evaluate the economic feasibility:
The economic assessment ran for different cases, and those indicators were used to judge the financial viability and effectiveness.
4. Discussion
Energy storage is frequently used in off-grid PV systems to obtain power balance. Driven by economic incentives, more grid-connected PV systems are adopting storage devices. The combined battery–supercapacitor storage model demonstrates the technical value of the hybrid PV-storage system in mitigating PV intermittency and non-linear load. However, the high equipment cost of supercapacitor stops this application at the demonstration stage. The design of a dispatch controller is the key element in practical PV-battery system models. However, the specified power target cannot be met throughout the year, due to factors like unpredictable weather and battery malfunction. Optimal sizing for a battery system in the residential levels to follow the power target is shown by assessing two contradictory criteria—the number of excursions and ATP, which demonstrates the performance of the proposed hybrid system. Statistical results show that the PV-battery system can attenuate fluctuations, as well as reduce the maximum power exchange with the grid. Statistical indicators like standard deviation and mean are used for better illustration.
Economic feasibility of the PV-battery system was also investigated. Recent market data shows the competitiveness of battery applications in grid-connected systems, where no significant difference is observed regarding project costs between only PV and a PV-battery system (shown in
Table 4). Based on the existing tariff structure in Dubai, feed-in-tariffs are recommended to encourage more applications of PV and a battery, which further reduces network stress under high-loading afternoons, as well as ancillary reserves. Meanwhile, these benefits can be generalized to other parts of the world by customizing incentive packages.
Furthermore, the impact of an inverter should not be ignored in realistic applications. Authors in [
32] capture the clipping effects when inverters reach the limit of converting DC power based on fuzzy logic. More harmonic components are generated in line with clipping effects, which further diminishes the performance overall of a PV system. This reason drives more researchers to identify optimal sizes of inverters. For instance, a genetic algorithm is employed in [
33] to assess the NPV of PV arrays under various inverter capacities to achieve maximum economic benefits. Cloud enhancement is used as another criterion in the process of inverter sizing in [
34].
Therefore, inverter sizing procedures will be studied in the future research work. A possible correlation between inverter sizing and battery sizing can be further investigated. Meanwhile, harmonic generation is a common problem in practical PV systems, which could possibly be another decisive parameter for designing PV-storage systems.
Finally, under the present decreasing trend of costs for PV related renewable projects, more technical and financial value from energy storage will be appreciated in the near future, even without incentives.
5. Conclusions
To mitigate intermittency and fluctuations brought on by PV installations, and further improve maximum PV popularity, energy storage is identified as one promising solution. In this paper, three different models were developed in sequence to assess the effectiveness of introducing energy storage into residential PV systems from different perspectives.
Firstly, a generic PV-battery-supercapacitor model was built in Simulink, and a flat load profile was proven achievable. Power density, power capacity and dispatch controllers are three key factors to reduce power fluctuations. However, in practical implementation, the functionality of dispatch controller and the high material cost of supercapacitor limits the practical implementation of this ideal model.
Inspired by outcomes from the generic model, a practical PV-battery model was built in SAM, which was based on residential household data in Dubai. Optimal sizing of the battery system was achieved by evaluating technical parameters which can effectively mitigate network variations.
In the third model, economic assessment results showed that grid-connected PV system with the optimized battery size can be profitable with reasonable incentives.
To summarize, a generalized approach for optimizing battery size in PV systems is proven to be both technically and economically feasible. Future work will focus on inverter sizing and minimization of harmonics in PV system design.