Modelling the EU Internal Electricity Market: The PRIMES-IEM Model
Abstract
1. Introduction
- Unnecessary restrictions of the use of interconnections (due to the setting of Net Transfer Capacity limits from a national, rather than a multi-country, perspective) hampering the optimal utilisation of interconnectors, thus limiting the volume of cross-border trade.
- Illiquid and uncoupled intra-day and balancing markets causing sub-optimal market prices and reducing the cross-border sharing of balancing resources, thus entailing unnecessary costs.
- Priority dispatch privileges granted to a significant part of generation and load, thus undermining the liquidity of the wholesale markets and the cost-effectiveness of costs and plant dispatching in the day-ahead.
- Lack of market liquidity combined with cross-border restrictions implying frequent market splitting in the market coupling and driving non-optimal re-dispatching and unnecessary costs.
- Lack of market participation by renewables and other power resources operating as “must-take”, which otherwise would optimise their operation and would have incentives to forecast the weather accurately to minimise exposure to balancing costs.
- Lack of close coordination in the management of control areas between the transmission system operators in the EU internal market of electricity, implying an increase in reserve and ancillary services costs due to the non-optimal definition of reserve requirements when defined from a national rather than multi-system perspective.
2. Modelling the European Electricity Markets
2.1. Existing Literature
2.2. Overview of the PRIMES-IEM Modelling Approach
2.3. Detailed Model Description
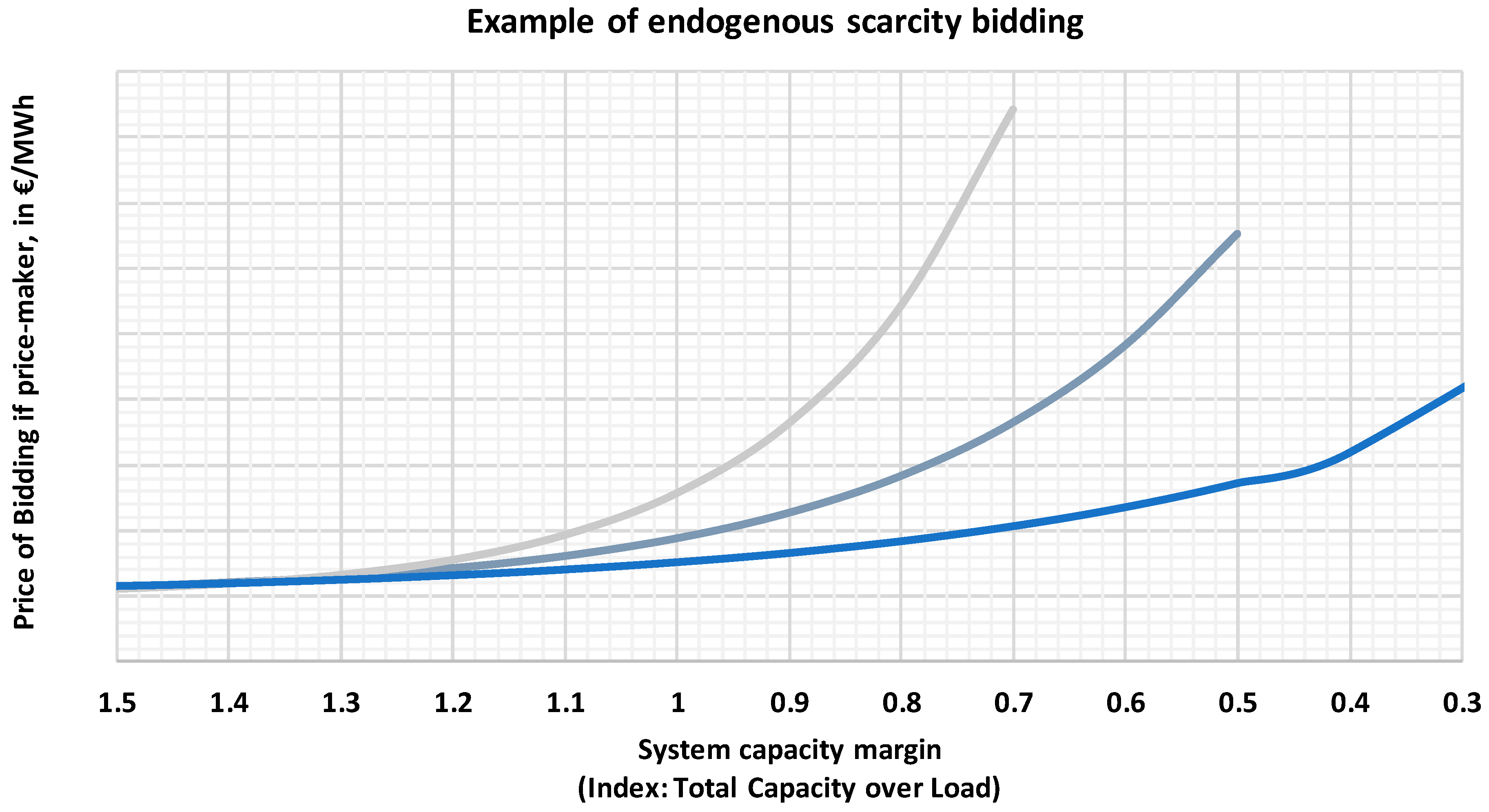
2.3.1. Bidding by Generators
2.3.2. Nomenclature
2.3.3. Modelling of the Day-Ahead Market
2.3.3.1. Modelling a Pure Energy Market for the Day-Ahead
2.3.3.2. Modelling of Co-Optimisation of Energy with Ancillary Services
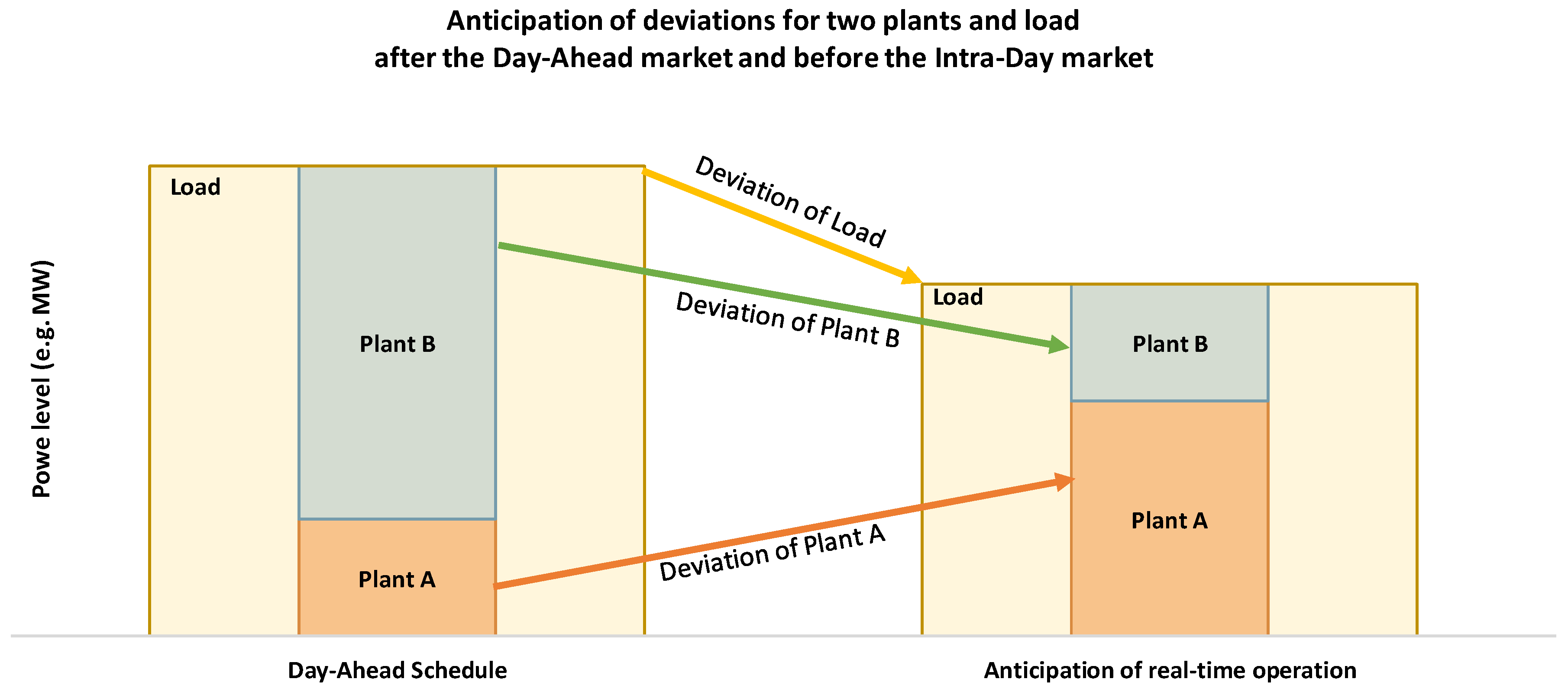
2.3.4. Generation of Random Events after the Day-Ahead Market
2.3.5. Simulation of the Intra-Day Market
2.3.6. Simulation of the Balancing/Reserves Market
2.3.7. The Final Stage of Simulation to Represent System Operation
2.4. Modelling Market Distortions and Policy Remedies
- Nominations: Nomination is a practice of declaring a block of generation and load to the TSO for respecting in the dispatching schedule. The declaration in an out-of-the-market action and may concern one or more than one control areas, and in this case, may also declare the use of interconnection capacities. The model represents nominations via user-defined parameters. The nominated plant resources operate as must-take in the modelling of the DAM and the nominated load as must-serve. Generation nominated cross-border implies a reduction in the available transfer capacity of interconnectors.
- Priority dispatch: The model represents priority dispatch of power plants via user-defined parameters. They operate in the modelling of DAM as must-take. The model includes the possibility of generation curtailment for technical reasons, albeit by applying a high penalty when the resource is in priority dispatch.
- Consideration of balancing and ancillary services: The model allows optionally for optimising the offering of both energy and reserves in the day-ahead market simulation simultaneously. This option can be used to reflect that energy markets have reached a high level of maturity and generators anticipate and minimise their exposure to the balancing markets.
- Demand response: The model represents demand response as an endogenous shifting of demand quantities from peak hours to off-peak hours. User-defined parameters control whether demand-response is eligible in the various markets. Consumers offer pairs of quantities and prices as bids for demand response, and total amounts are subject to limitation by potential.
- RES in intra-day and balancing: User-defined parameters may control whether variable RES can participate in the intra-day market, in which case they can bid for a downward adjustment. The eventual exposure of RES to balancing costs incentivises them to improve the weather forecasting error, which is part of the random event generation modelled between the DAM and the Intra-Day markets. When RES plants participate in the intra-day market, they cannot be under priority dispatch.
- Price caps: Price caps for the bids in the various markets are exogenous parameters of the model. Low levels of price caps may limit the revenues of generation resources. However, the model does not capture the eventual adverse effects on generation investment, as capacity expansion is outside the scope of the model.
- Net transfer capacity (NTC) restrictions: The NTC values are exogenous parameters and can apply on all stages of the markets. Increasing the NTC values up to making physical capacities as the binding constraints is a way of modelling full integration of the grid and system operation. In this case, the Kirchhoff laws restrictions do apply.
- Market liquidity: The model allows for the consideration of illiquid or regulated markets, in particular for the intra-day and balancing markets, by applying administratively (exogenously) defined prices for the settlement of deviations and ancillary services, instead of a market-clearing price derivation.
- Participation of cross-border flows: User-defined parameter can represent whether or not cross border flows are allowed to participate in the intra-day market for covering deviations and in balancing for covering the ancillary services. Re-dispatching and market split prices are endogenous in the model for the DAM and the intra-day market.
- Reserve requirements: Reserve requirements are exogenous parameters and are specified in detail for each type of ancillary service and separately for each control area. Representing the eventual strong coordination of the system operators or the establishment of regional system operator bodies is included in the model via a reduction of reserve requirements when coordination applies. However, the reduction is also exogenous.
3. Model Application for the Electricity Market Reform to the Horizon of 2030
3.1. Context of the Model Application
3.2. Results of the Model Application
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Clean Energy for All Europeans; Publications Office of the European Union: Luxembourg, 2019; ISBN 978-92-79-99843-0. [Google Scholar]
- European Commission. Communication for the Commission to the European Parliament: A Clean Planet for All. A European Strategic Long-Term Vision for a Prosperous, Modern, Competitive and Climate Neutral Economy. COM(2018) 773 Final. Available online: https://ec.europa.eu/clima/sites/clima/files/docs/pages/com_2018_733_en.pdf (accessed on 30 November 2018).
- Capros, P.; Kannavou, M.; Evangelopoulou, S.; Petropoulos, A.; Siskos, P.; Tasios, N.; Zazias, G.; DeVita, A. Outlook of the EU energy system up to 2050: The case of scenarios prepared for European Commission’s “clean energy for all Europeans” package using the PRIMES model. Energy Strategy Rev. 2018, 22, 255–263. [Google Scholar] [CrossRef]
- E3MLab. Primes Model Version 2018, Detailed Model Description. Available online: http://www.e3mlab.eu/e3mlab/PRIMES%20Manual/The%20PRIMES%20MODEL%202018.pdf (accessed on 4 June 2019).
- Lannoye, E.; Flynn, D.; O’Malley, M. Evaluation of Power System Flexibility. IEEE Trans. Power Syst. 2012, 27, 922–931. [Google Scholar] [CrossRef]
- Nosair, H.; Bouffard, F. Reconstructing Operating Reserve: Flexibility for sustainable power systems. IEEE Trans. Sustain. Energy 2015, 6, 1624–1637. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Smeers, Y. Remuneration of Flexibility using Operating Reserve Demand Curves: A Case Study of Belgium. Energy J. 2017, 38, 105–135. [Google Scholar] [CrossRef]
- Neuhoff, K.; Barquin, J.; Bialek, J.W.; Boyd, R.; Dent, C.J.; Echavarren, F.; Grau, T.; Von Hirschhausen, C.; Hobbs, B.F.; Kunz, F.; et al. Renewable electric energy integration: Quantifying the value of design of markets for international transmission capacity. Energy Econ. 2013, 40, 760–772. [Google Scholar] [CrossRef]
- Newbery, D.; Strbac, G.; Viehoff, I. The benefits of integrating European electricity markets. Energy Policy 2016, 94, 253–263. [Google Scholar] [CrossRef]
- ACER/CEER ACER/CEER—Annual Report on the Results of Monitoring the Internal Electricity and Natural Gas Markets in 2017—Electricity Wholesale Markets Volume. Available online: https://www.acer.europa.eu/Official_documents/Acts_of_the_Agency/Publication/MMR%202017%20-%20ELECTRICITY.pdf (accessed on 4 June 2019).
- Tennbakk, B.; Von Schemde, A.; Daan, S.; Capros, P. Electricity Market Functioning: Current Distortions, and How to Model Their Removal; Brussels, Belgium. 2016. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/electricity_market_functioning_-_current_distortions_and_how_to_model_t.pdf (accessed on 9 June 2019).
- European Commission. Proposal for a Directive of the European Parliament and of the Council on Common Rules for the Internal Market in Electricity (Recast). COM/2016/0864 final/2—2016/0380 (COD). Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A52016PC0864R%2801%29 (accessed on 4 June 2019).
- European Commission. Proposal for a Regulation of the European Parliament and of the Council on the Internal Market for Electricity (Recast) COM/2016/0861 Final—2016/0379 (COD). Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:d7108c4c-b7b8-11e6-9e3c-01aa75ed71a1.0001.02/DOC_1&format=PDF (accessed on 4 June 2019).
- European Commission. Commission Staff Working Document: Impact Assessment of the Market Design Initiative SWD(2016) 410 Final. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/mdi_impact_assessment_main_report_for_publication.pdf (accessed on 4 June 2019).
- Ventosa, M.; Baíllo, Á.; Ramos, A.; Rivier, M. Electricity market modeling trends. Energy Policy 2005, 33, 897–913. [Google Scholar] [CrossRef]
- Garcia, A. Modeling electricity markets: A brief introduction. In Economic Market Design and Planning for Electric Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 21–44. ISBN 978-0-470-52916-4. [Google Scholar]
- González, P.; Villar, J.; Díaz, C.A.; Campos, F.A. Joint energy and reserve markets: Current implementations and modeling trends. Electr. Power Syst. Res. 2014, 109, 101–111. [Google Scholar] [CrossRef]
- Vijay, A.; Fouquet, N.; Staffell, I.; Hawkes, A. The value of electricity and reserve services in low carbon electricity systems. Appl. Energy 2017, 201, 111–123. [Google Scholar] [CrossRef]
- Oggioni, G.; Murphy, F.H.; Smeers, Y. Evaluating the impacts of priority dispatch in the European electricity market. Energy Econ. 2014, 42, 183–200. [Google Scholar] [CrossRef]
- Supponen, M. Factors that Influence the Targets and Criteria for Electricity Interconnector Investments. Available online: http://fsr.eui.eu/publications/factors-that-influence-the-targets-and-criteria-for-electricity-interconnector-investments/ (accessed on 4 June 2019).
- ENTSO-E. Ten-Year Network Development Plan 2014. Available online: https://www.entsoe.eu/publications/tyndp/tyndp-2014/ (accessed on 4 June 2019).
- Van den, B.K.; Delarue, E.; D’haeseller, W. DC Power Flow in Unit Commitment Models; KU Leuven Energy Institute: Leuven, Belgium, 2014. [Google Scholar]
- Christopher, A.; Maxime, C.; Laurent, F.; Von Schemde, A. METIS Technical Note T3—Market Module Configuration for Study S12: Focus on Day-Ahead, Intra-Day and Balancing Markets; Brussels, Belgium. 2016. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/metis_t3_-_market_model_configuration_for_s12.pdf (accessed on 9 June 2019).
- COWI; AF Mercados EMI; ECOFYS; THEMA; VITO. Impact Assessment Study on down Stream Flexibility, Price Flexibility, Demand Response & Smart Metering; Brussels, Belgium. 2016. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/demand_response_ia_study_final_report_12-08-2016.pdf (accessed on 9 June 2019).
- Klemperer, P.D.; Meyer, M.A. Supply function equilibria in oligopoly under uncertainty. Econometrica 1989, 57, 1243–1277. [Google Scholar] [CrossRef]
- Rudkevich, A. On the Supply Function Equilibrium and Its Applications in Electricity Markets. Decis. Support. Syst. 2005, 40, 409–425. [Google Scholar] [CrossRef]
- Sioshansi, R.; Oren, S. How good are supply function equilibrium models: An empirical analysis of the ERCOT balancing market. J. Regul. Econ. 2007, 31, 1–35. [Google Scholar] [CrossRef]
- Day, C.J.; Hobbs, B.F.; Jong-Shi, P. Oligopolistic competition in power networks: A conjectured supply function approach. IEEE Trans. Power Syst. 2002, 17, 597–607. [Google Scholar] [CrossRef]
- Willems, B.; Rumiantseva, I.; Weigt, H. Cournot versus Supply Functions: What does the data tell us? Energy Econ. 2009, 31, 38–47. [Google Scholar] [CrossRef]
- Eager, D.; Bialek, J.; Johnson, T. Validation of a dynamic control model to simulate investment cycles in electricity generating capacity. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Eager, D.; Hobbs, B.F.; Bialek, J.W. Dynamic modeling of thermal generation capacity investment: application to markets with high wind penetration. IEEE Trans. Power Syst. 2012, 27, 2127–2137. [Google Scholar] [CrossRef]
- NEMO COMMITTEE. Euphemia Public Description. Available online: https://www.epexspot.com/document/40503/Euphemia%20Public%20Description (accessed on 4 June 2019).
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 3. [Google Scholar]
- European Parliament. Legislative Resolution of 26 March 2019 on the Proposal for a Regulation of the European Parliament and of the Council on the Internal Market for Electricity (Recast). Available online: http://www.europarl.europa.eu/doceo/document/TA-8-2019-0227_EN.html (accessed on 4 June 2019).
- European Council. European Council (23 and 24 October 2014)—Conclusions. Available online: https://www.consilium.europa.eu/media/24561/145397.pdf (accessed on 4 June 2019).
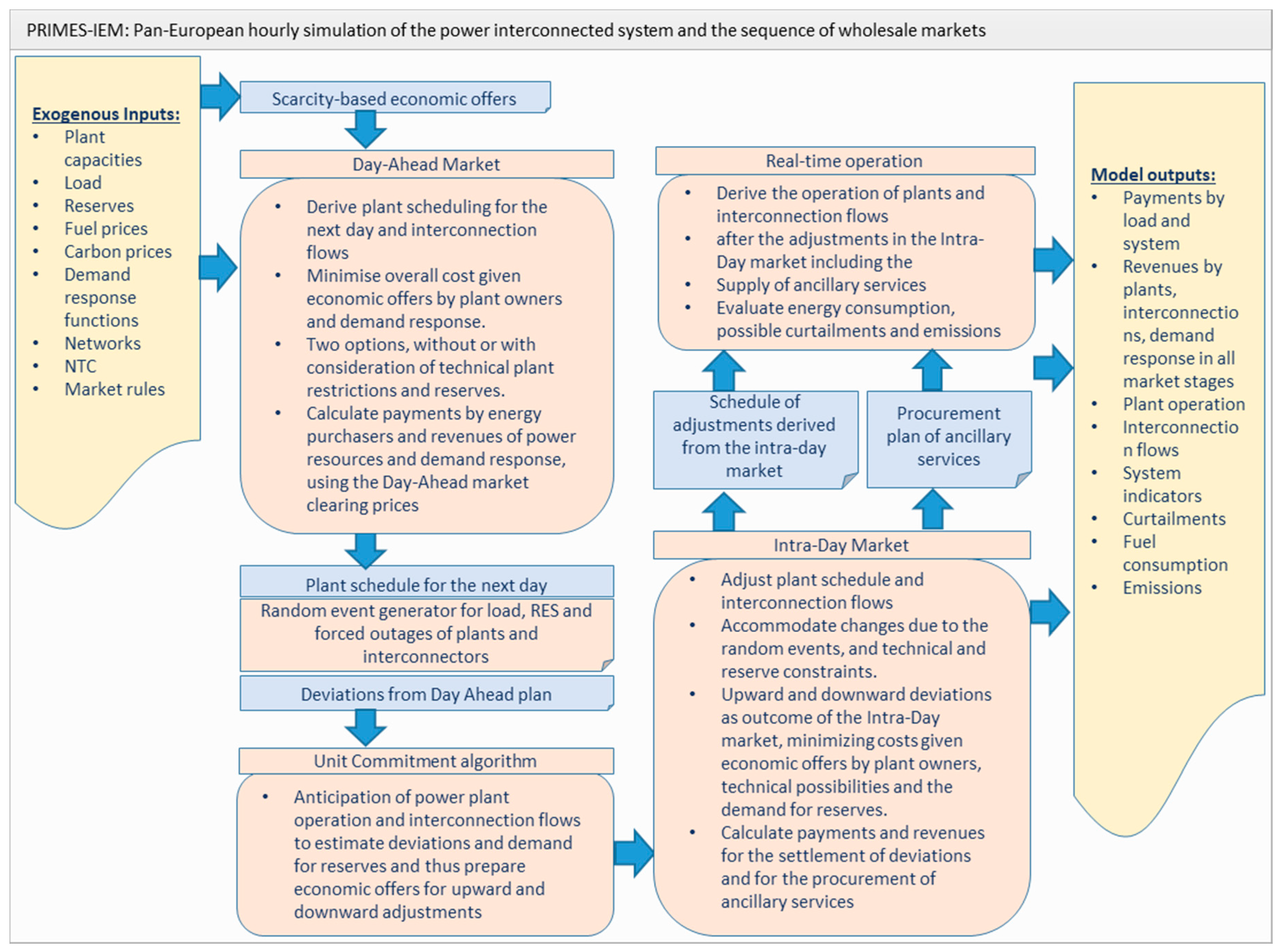
| Starting Point: Basic Projection, Including ETS Prices, Gas Prices, Variable RES Developments, Capacity Expansion, Electricity Demand, Reserve Requirements | |
|---|---|
| 1 | Simulation of the day-ahead market |
| 2 | Generation of random events between day-ahead and intra-day |
| 3 | Simulation of unit commitment to determine deviations from real-time operation |
| 4 | Simulation of the intra-day market for upward and downward deviations |
| 5 | Simulation of the reserves market or procurement |
| 6 | Final simulation of the system operation (real-time) |
| 7 | Calculation of payments by consumers, revenues of power plants, interconnections and demand response, as well as energy consumption and emissions |
| Nomenclature | |
|---|---|
| Sets | |
| or | system nodes |
| or | hourly time slices in a year |
| power plants | |
| or | interconnectors |
| types of ancillary services | |
| reference or swing node | |
| Parameters | |
| non-increasing demand function depending on prices | |
| power plant’s capacity | |
| power plant’s hourly availability factor in the day-ahead schedule | |
| interconnectors’ thermal capacity | |
| incidence matrix, describing the network’s topology | |
| inverse incidence matrix | |
| net transfer capacity limitations, which apply on pairs of nodes | |
| a matrix includes the susceptance of each interconnector in the elements of the main diagonal | |
| power plant’s technical minimum generation level | |
| power plant’s ramping capability | |
| power plant’s minimum up time | |
| power plant’s minimum down time | |
| demand for upward ancillary services | |
| demand for downward ancillary services | |
| unexpected variation of the hourly demand | |
| forecast errors of the availability of variable renewables sources or forced outages of large power plants | |
| unplanned loss of transmission lines | |
| demand for upward deviation in the intra-day market | |
| demand for downward deviation in the intra-day market | |
| start-up cost only for the plants performing start-up specifically in the intra-day | |
| shut-down cost only for the plants performing shut-down specifically in the intra-day | |
| hourly generation by each power plant in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| hourly plant’s contribution to upward ancillary services in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| hourly plant’s contribution to downward ancillary services in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| power plant’s operating status in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| flows over interconnections in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| hourly net position of a node in the day-ahead schedule (variable of DAM simulation fed as a parameter to the intra-day simulation) | |
| upward limit of cross-border contribution to ancillary services | |
| power plant’s operating level in the intra-day schedule (variable of intra-day simulation fed as a parameter to the reserves simulation) | |
| flows over interconnections in the intra-day schedule (variable of intra-day simulation fed as a parameter to the reserves simulation) | |
| hourly net position of a node in the intra-day schedule (variable of intra-day simulation fed as a parameter to the reserves simulation) | |
| Positive Variables | |
| hourly demand for electricity in the day-ahead schedule | |
| hourly generation by each power plant in the day-ahead schedule | |
| power plant’s bids for electricity expressed as non-decreasing functions | |
| hourly generation by power plants with priority dispatch | |
| hourly plant’s contribution to upward ancillary services | |
| hourly plant’s contribution to downward ancillary services | |
| power plant’s bids for contribution to upward ancillary services | |
| power plant’s bids for contribution to downward ancillary services | |
| upward adjustment of the plant scheduling committed in the DAM-derived schedule | |
| upward adjustment of the plant scheduling committed in the DAM-derived schedule | |
| upward adjustment provided by the possible start-up of an offline, in the DAM schedule, plant | |
| downward adjustment provided by the possible shut-down of a committed, in the DAM schedule, plant | |
| power plants’ bids for an upward adjustment in the intra-day market | |
| power plants’ bids for a downward adjustment in the intra-day market | |
| Free Variables | |
| flows over interconnections | |
| hourly net position (sum of energy inflows and outflows in a node) | |
| phase angles for nodes | |
| marginal electricity price of the system | |
| adjustment of flows over interconnections in the intra-day market | |
| adjustment of the net position of a node in the intra-day market | |
| cross-border contribution to ancillary services | |
| Binary Variables | |
| power plant’s operating status (1 if committed, 0 else) in the day-ahead schedule | |
| start-up of a power plant in the day-ahead schedule | |
| shut-down of a power plant in the day-ahead schedule | |
| power plant’s operating status (1 if committed, 0 else) in the intra-day market | |
| start-up of a power plant in the intra-day market | |
| shut-down of a power plant in the intra-day market | |
| deviation of power plant’s operating status between the day-ahead and intra-day schedule (1 if committed in the intra-day, while offline in the DAM) | |
| deviation of power plant’s operating status between the day-ahead and intra-day schedule (1 if committed in the DAM, while offline in the intra-day) | |
| start-up of a power plant in the intra-day, which was offline in the DAM | |
| shut-down of a power plant in the intra-day, which was committed in the DAM | |
| EU in 2030 | Optimal Case | Current Practices | Cost Savings Due to Market Reform | ||
|---|---|---|---|---|---|
| - | Bn € | Bn € | Bn € | % Difference | Shares by Market Stage |
| Day-ahead market | 317.6 | 326.2 | 8.5 | 2.6% | 34.3% |
| Intra-day market | 11.6 | 22.1 | 10.5 | 47.3% | 42.1% |
| Ancillary services | 1.9 | 7.7 | 5.9 | 75.9% | 23.6% |
| Total | 331.2 | 356.0 | 24.9 | 7.0% | 100.0% |
| EU in 2030 | Optimal Case | Current Practices | Cost Savings Due to Market Reform | |
|---|---|---|---|---|
| Total all market stages | Bn € | Bn € | Bn € | % difference |
| North Europe | 30.8 | 31.8 | 1.0 | 3.3% |
| British Isles | 41.3 | 47.3 | 6.0 | 12.8% |
| Central Western Europe | 178.6 | 181.7 | 3.0 | 1.7% |
| Central Eastern Europe | 44.4 | 46.6 | 2.2 | 4.7% |
| Iberian Peninsula | 26.9 | 38.3 | 11.4 | 29.8% |
| South Eastern Europe | 9.2 | 10.4 | 1.2 | 11.4% |
| Day-Ahead Markets | Bn € | Bn € | Bn € | % difference |
| North Europe | 29.7 | 29.7 | 0.0 | 0.1% |
| British Isles | 39.3 | 43.7 | 4.4 | 10.0% |
| Central Western Europe | 171.9 | 168.3 | −3.6 | −2.1% |
| Central Eastern Europe | 42.3 | 40.7 | −1.6 | −3.9% |
| Iberian Peninsula | 25.8 | 34.4 | 8.6 | 25.0% |
| South Eastern Europe | 8.6 | 9.4 | 0.8 | 8.1% |
| Intra Day Markets | Bn € | Bn € | Bn € | % difference |
| North Europe | 0.6 | 1.3 | 0.7 | 52.5% |
| British Isles | 1.9 | 2.2 | 0.3 | 15.4% |
| Central Western Europe | 6.1 | 11.0 | 5.0 | 45.1% |
| Central Eastern Europe | 1.7 | 4.0 | 2.3 | 58.1% |
| Iberian Peninsula | 0.9 | 2.6 | 1.7 | 65.2% |
| South Eastern Europe | 0.5 | 0.9 | 0.4 | 45.9% |
| Ancillary Services | Bn € | Bn € | Bn € | % difference |
| North Europe | 0.5 | 0.8 | 0.3 | 40.3% |
| British Isles | 0.1 | 1.4 | 1.3 | 95.3% |
| Central Western Europe | 0.7 | 2.4 | 1.7 | 70.7% |
| Central Eastern Europe | 0.4 | 1.8 | 1.4 | 79.2% |
| Iberian Peninsula | 0.1 | 1.2 | 1.1 | 88.4% |
| South Eastern Europe | 0.1 | 0.1 | 0.0 | 6.7% |
| EU in 2030 [Bn €] | Total | Day-Ahead Markets | Intra-Day Markets | Ancillary Services |
|---|---|---|---|---|
| Coordinated management of reserves and broad market participation | 5.0 | - | - | 5.0 |
| Coupled Intra-Day markets and broad participation of resources | 4.7 | - | 4.7 | - |
| Liquid and coupled Day-Ahead Markets co-optimizing energy and reserves | 4.8 | 2.2 | 2.6 | - |
| Removal of priority dispatch and nominations in all market stages | 4.6 | 1.3 | 2.4 | 0.9 |
| Removal of NTCs in all market stages and flow-based allocation of interconnection capacities | 5.8 | 5.0 | 0.8 | - |
| Total cost savings | 24.9 | 8.5 | 10.5 | 5.9 |
| EU in 2030 | Optimal Case | Current Practices | Difference | % Difference |
|---|---|---|---|---|
| Cross-border flows in the Day-Ahead market (TWh) | 312 | 213 | 100 | 46.8% |
| Cross-border flows in the intra-day market (TWh) | 182 | 76 | 106 | 140.7% |
| Annual contribution of cross-border to reserves market in GW | 3433 | 313 | 3120 | 996.8% |
| EU in 2030 | Optimal Case | Current Practices | Difference | % Difference |
|---|---|---|---|---|
| - | TWh | TWh | TWh | % |
| Electricity demand | 3339 | 3339 | 0 | 0.0% |
| Demand Response | 0 | 3 | −3 | −100.0% |
| Net Imports | −1 | −1 | 0 | 0.0% |
| Total electricity generation | 3340 | 3340 | 0 | 0.0% |
| By plant type: | - | - | - | - |
| Nuclear | 698 | 682 | 15 | 2.3% |
| Solids | 342 | 424 | −81 | −19.2% |
| Gas | 607 | 640 | −33 | −5.2% |
| RES | 1556 | 1458 | 99 | 6.8% |
| small CHP | 137 | 136 | 0 | 0.4% |
| EU in 2030 | Optimal Case | Current Practices | Difference | % Difference |
|---|---|---|---|---|
| - | TWh | TWh | TWh | % |
| Upward and downward re-dispatching needs | 473 | 543 | −70 | −13.0% |
| Participation by plant type: | - | - | - | - |
| Nuclear | 22 | 40 | −18 | −44.9% |
| Solids | 82 | 145 | −62 | −43.1% |
| Gas | 180 | 235 | −55 | −23.4% |
| RES | 189 | 125 | 65 | 52.0% |
| EU in 2030 | Optimal Case | Current Practices | Difference | % Difference |
|---|---|---|---|---|
| DAM scheduled quantities for RES generation (TWh) | 1160 | 1160 | 0 | 0.0% |
| Curtailment of RES generation in real-time schedule (TWh) | 7.5 | 19.0 | −11.5 | −60.6% |
| Curtailment of RES generation, as percentage of the DAM scheduled quantities (%) | 0.6% | 1.6% | −1.0% | −60.6% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kannavou, M.; Zampara, M.; Capros, P. Modelling the EU Internal Electricity Market: The PRIMES-IEM Model. Energies 2019, 12, 2887. https://doi.org/10.3390/en12152887
Kannavou M, Zampara M, Capros P. Modelling the EU Internal Electricity Market: The PRIMES-IEM Model. Energies. 2019; 12(15):2887. https://doi.org/10.3390/en12152887
Chicago/Turabian StyleKannavou, Maria, Marilena Zampara, and Pantelis Capros. 2019. "Modelling the EU Internal Electricity Market: The PRIMES-IEM Model" Energies 12, no. 15: 2887. https://doi.org/10.3390/en12152887
APA StyleKannavou, M., Zampara, M., & Capros, P. (2019). Modelling the EU Internal Electricity Market: The PRIMES-IEM Model. Energies, 12(15), 2887. https://doi.org/10.3390/en12152887




