Thermal Decomposition of a Single AdBlue® Droplet Including Wall–Film Formation in Turbulent Cross-Flow in an SCR System
Abstract
1. Introduction
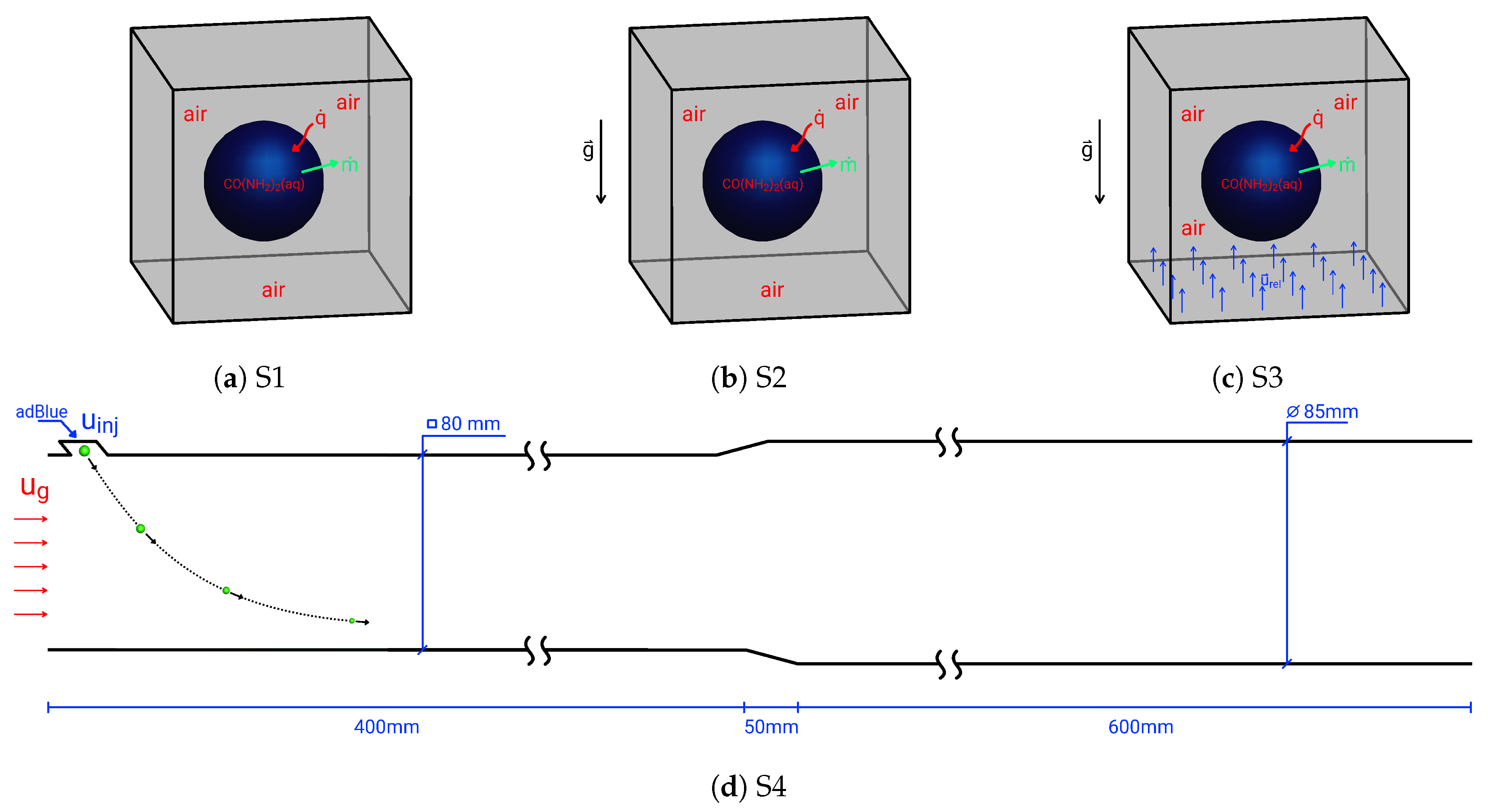
2. Droplet Configurations under Study
3. Model Formulation
3.1. LES-Based Eulerian–Lagrangian Numerical Module
3.1.1. Description of Carrier Phase and LES Model
3.1.2. Lagrange Particle Tracking
3.1.3. Thermal Decomposition
3.1.4. Liquid Wall Film and Deposit Formation
3.1.5. Numerical Procedure
3.2. Detailed Mathematical Modelling
3.2.1. Governing Equations
3.2.2. Numerical Solution
3.2.3. Interface
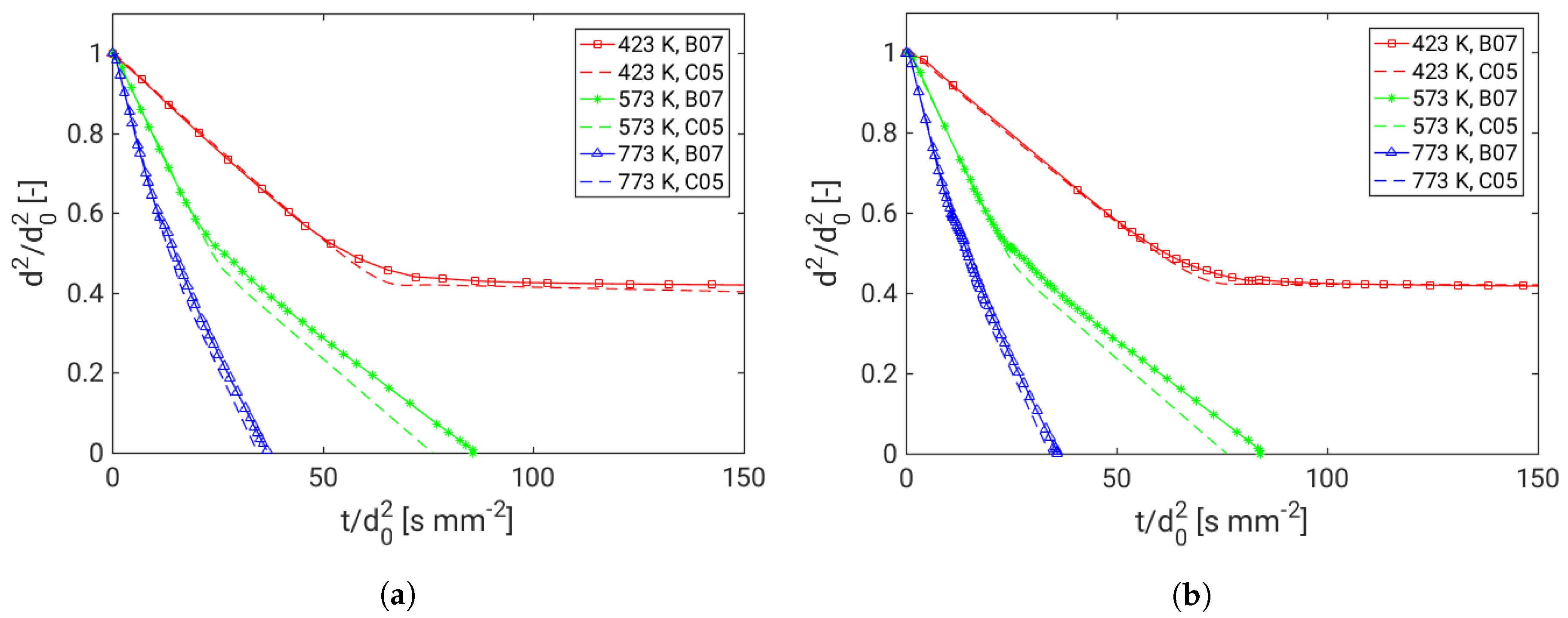
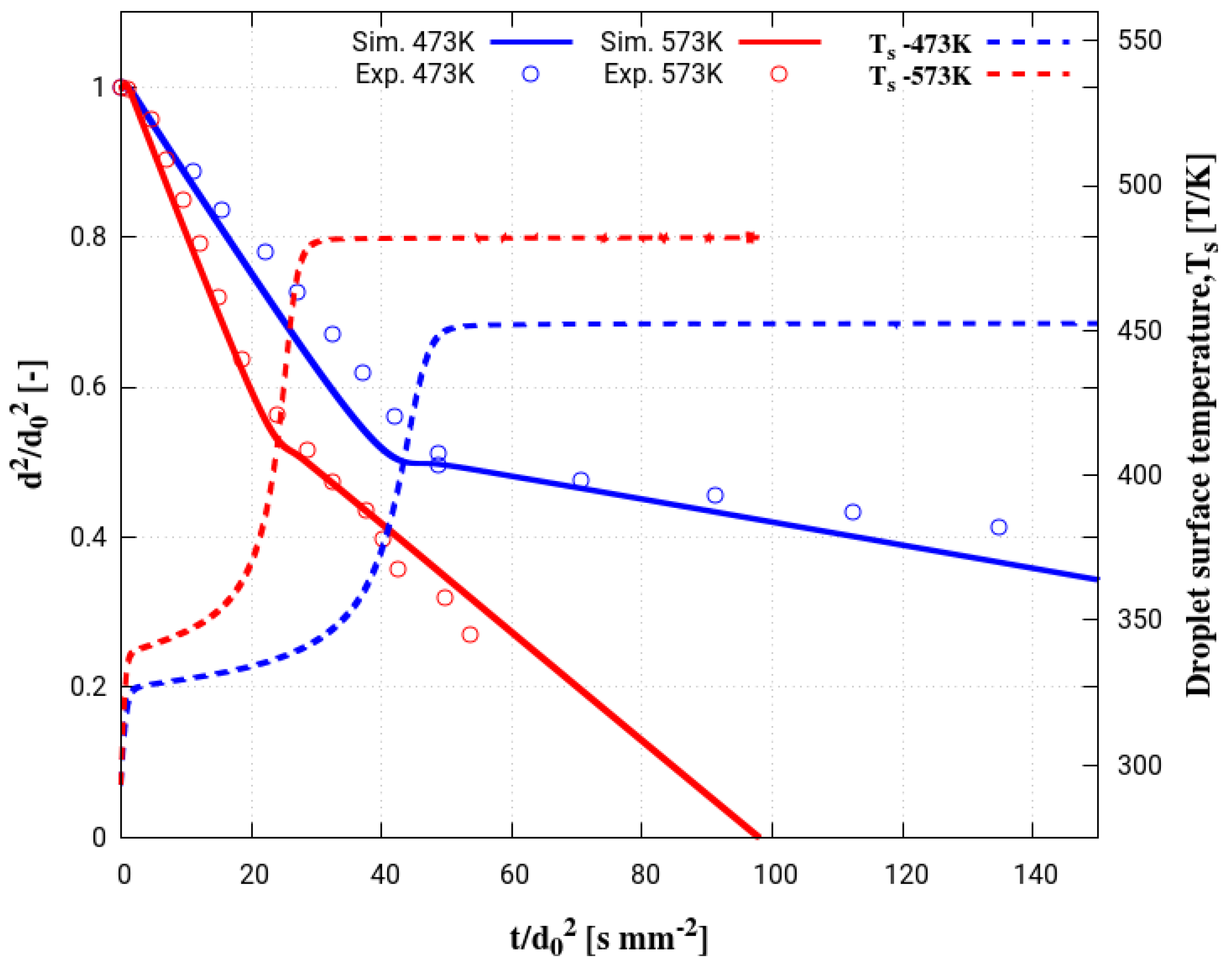
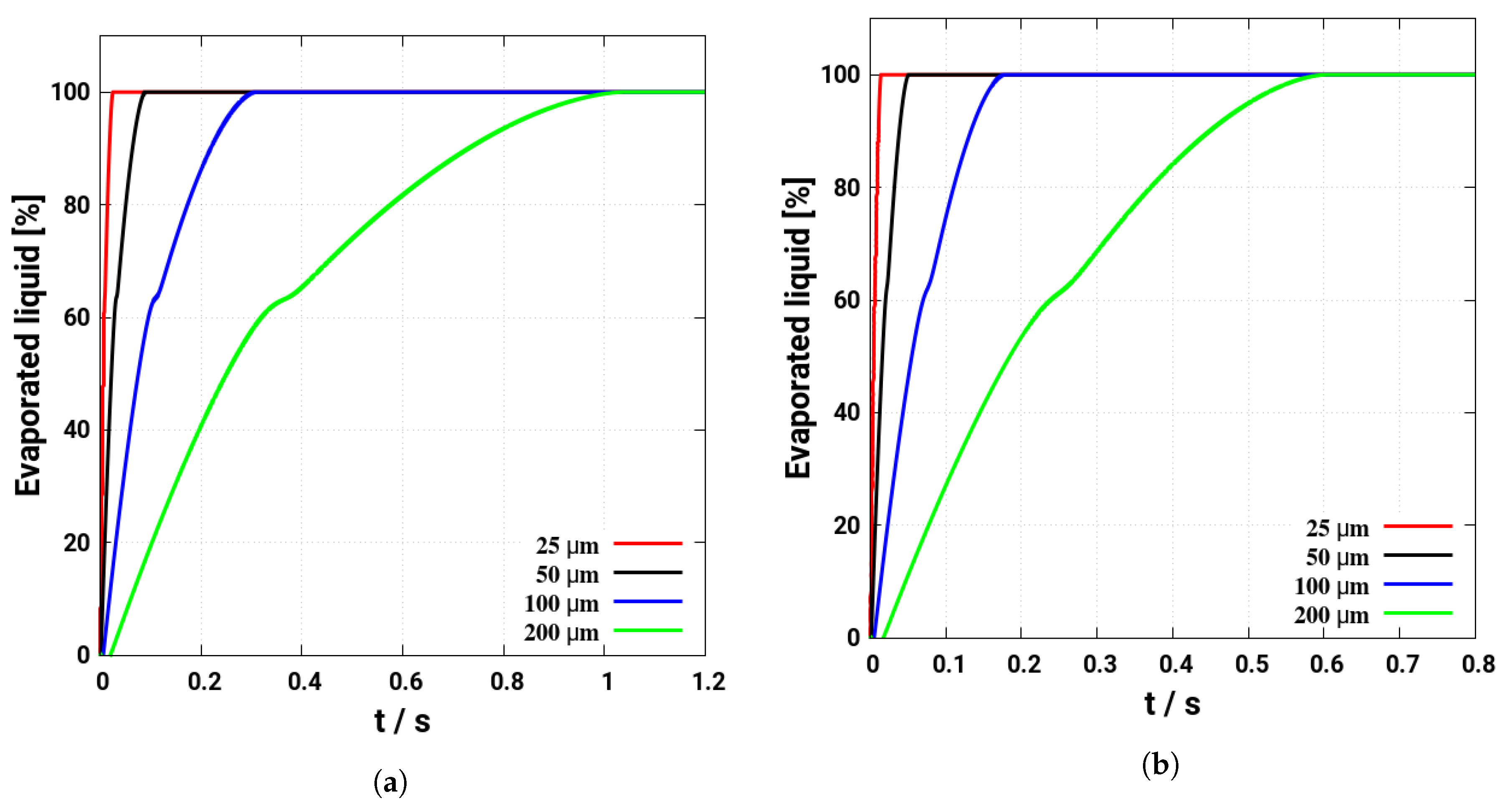
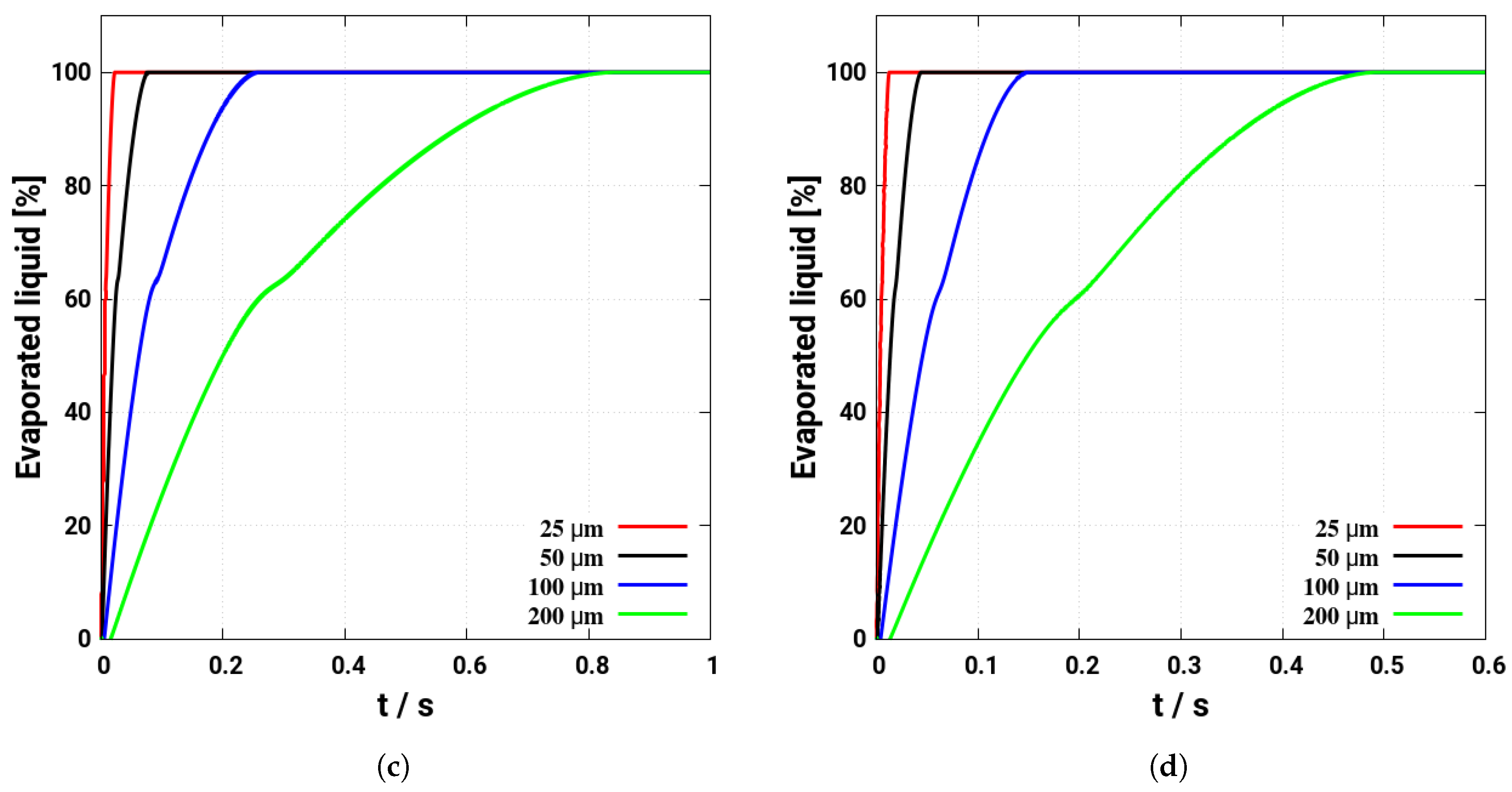
4. Assessment of the Multicomponent Evaporation Model: Evaporation Characteristics
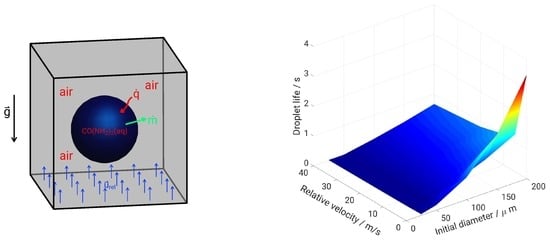
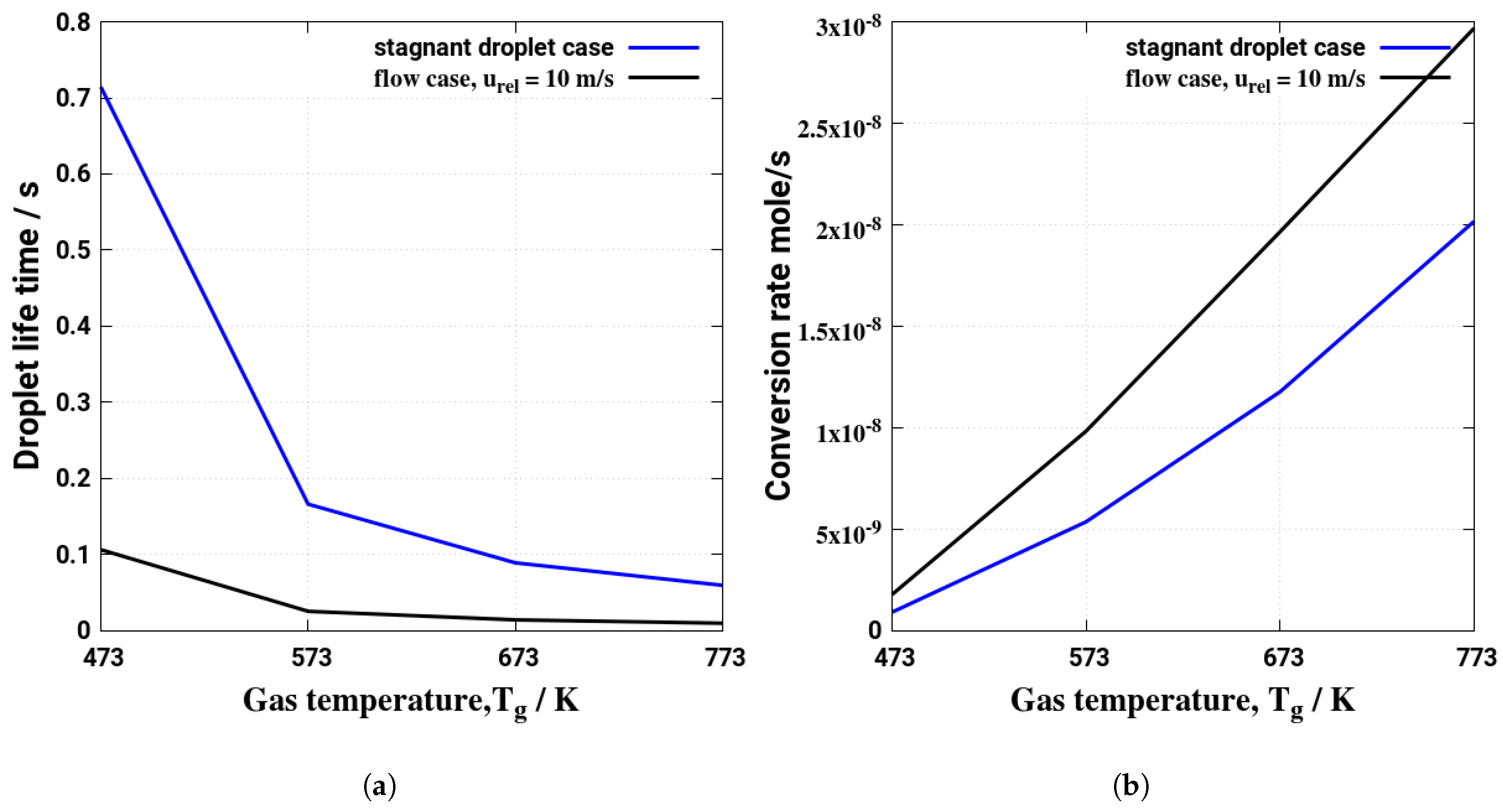
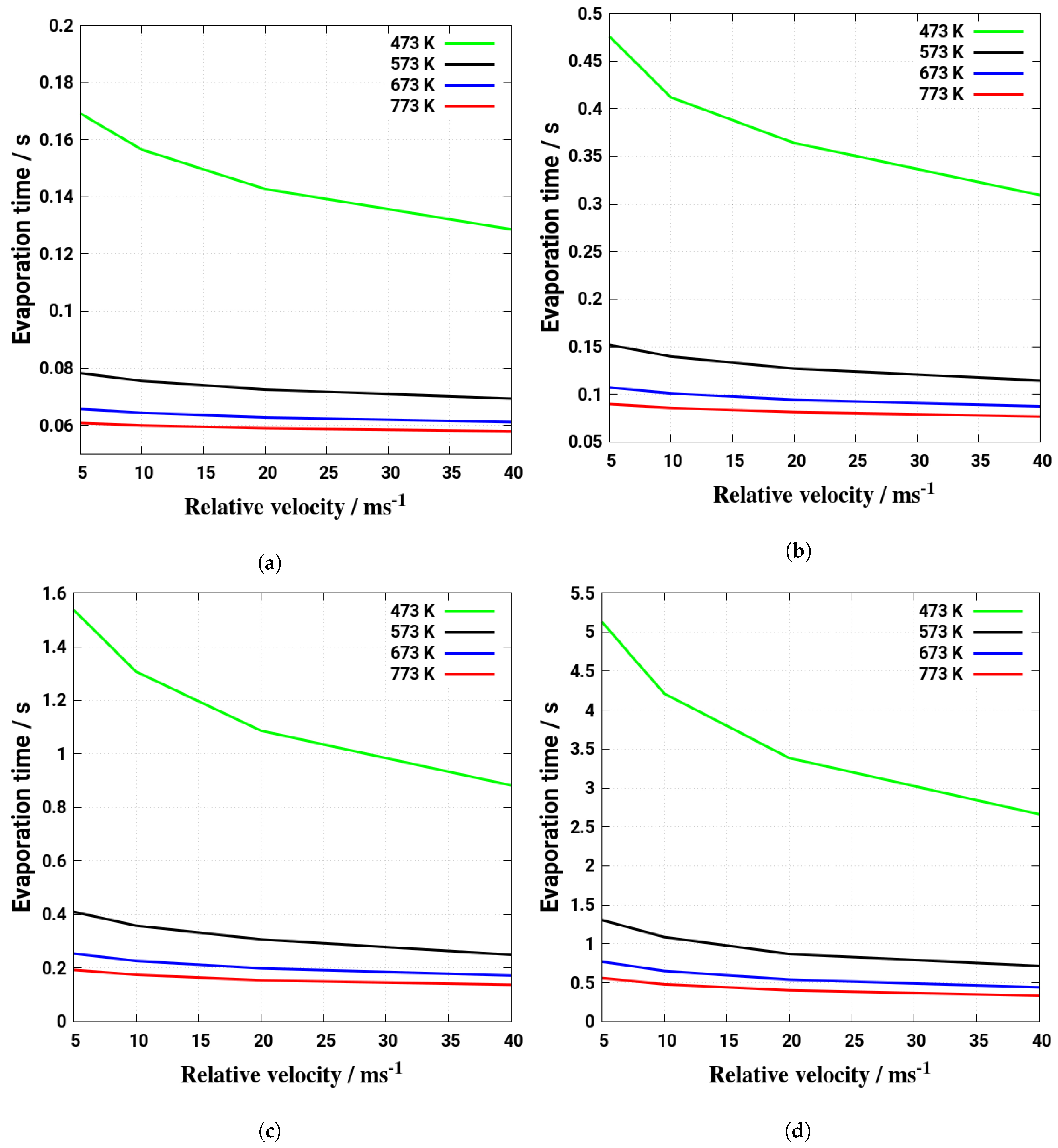
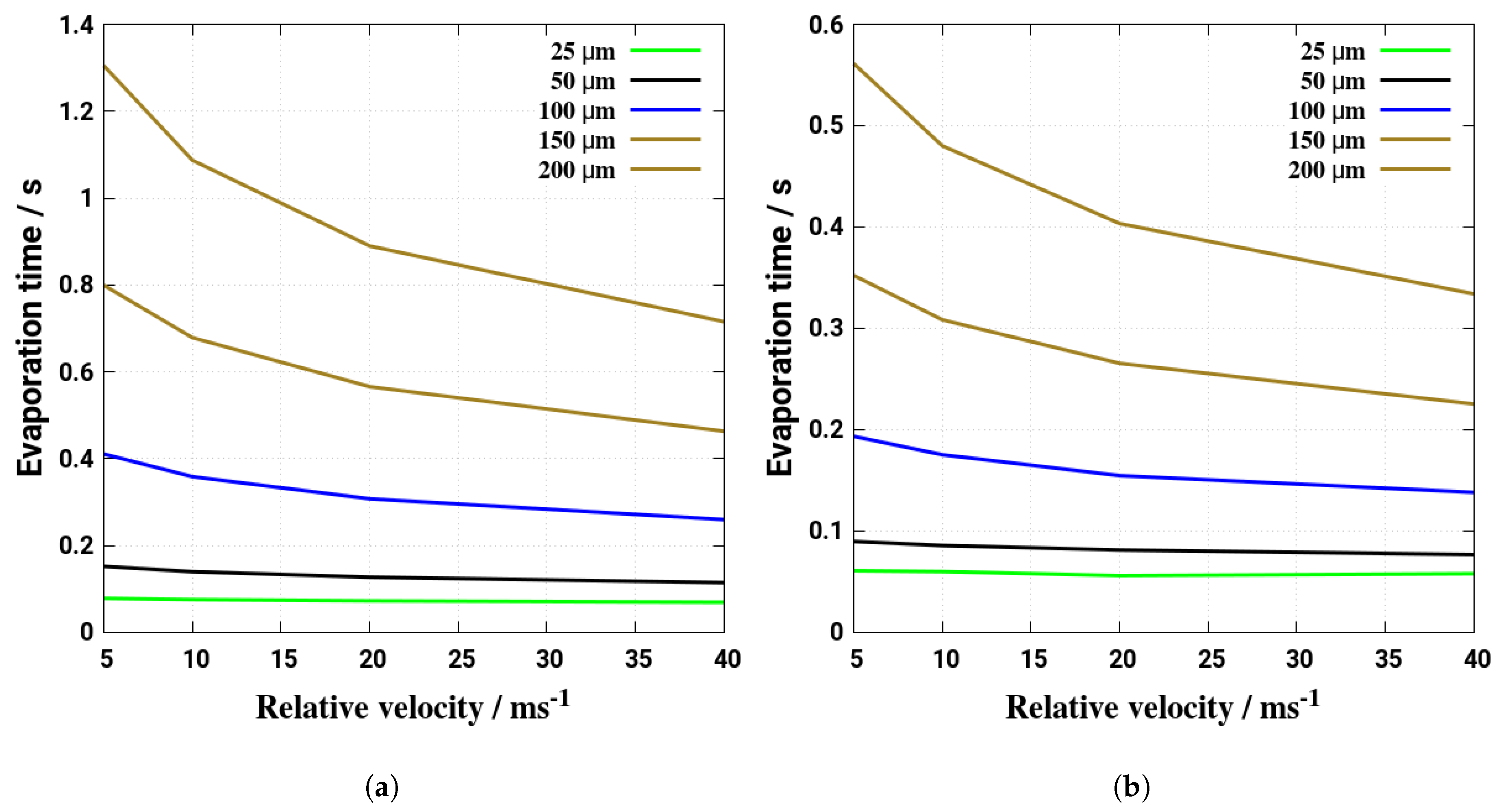
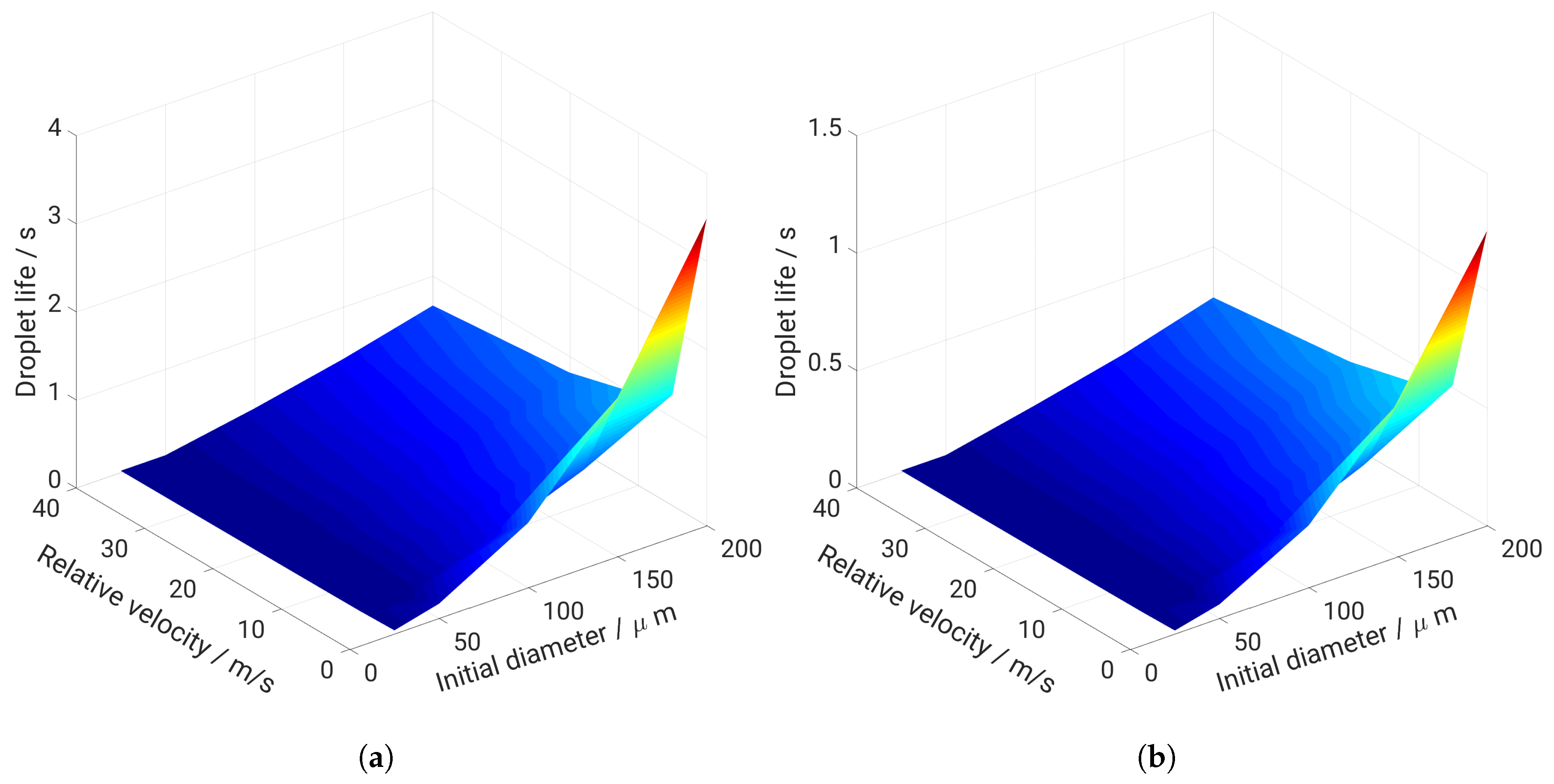
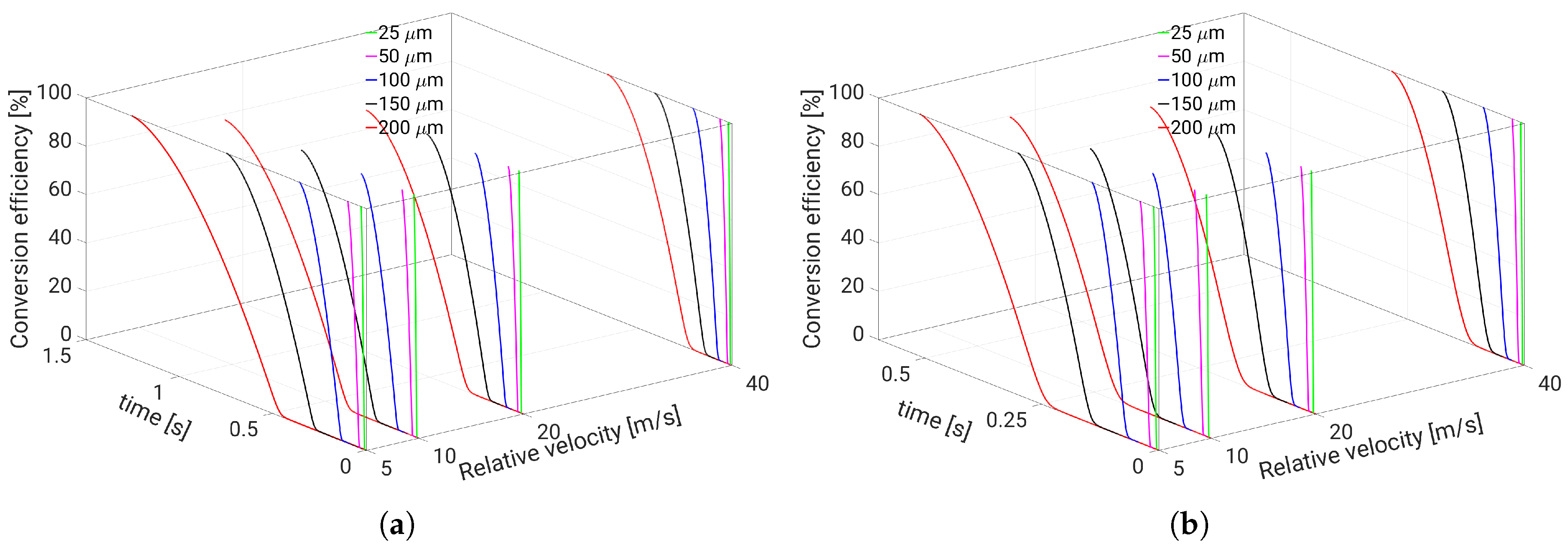
5. Evaporation and Thermal Decomposition Characteristics: Influence of Droplet Relative Velocity
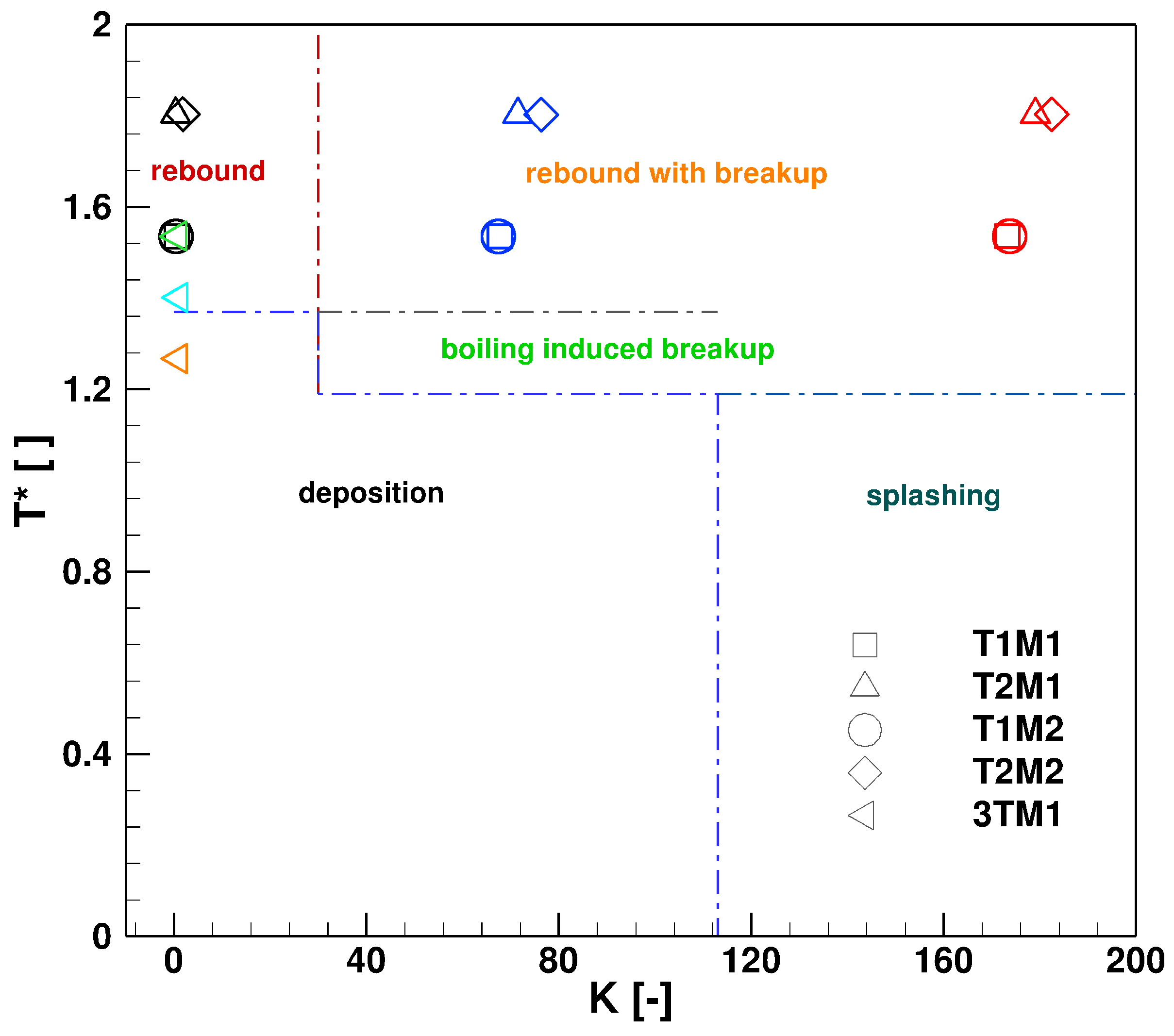
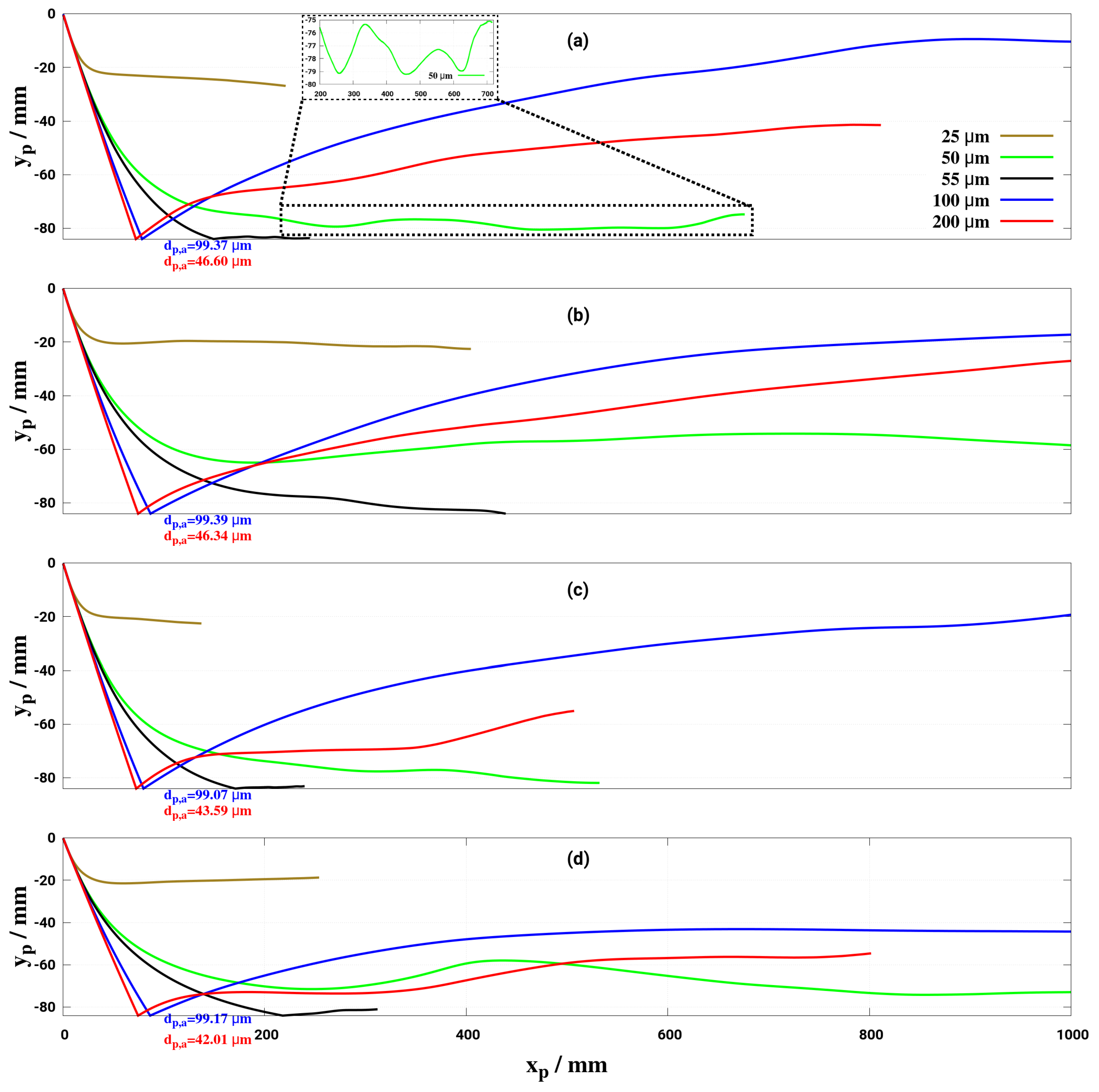
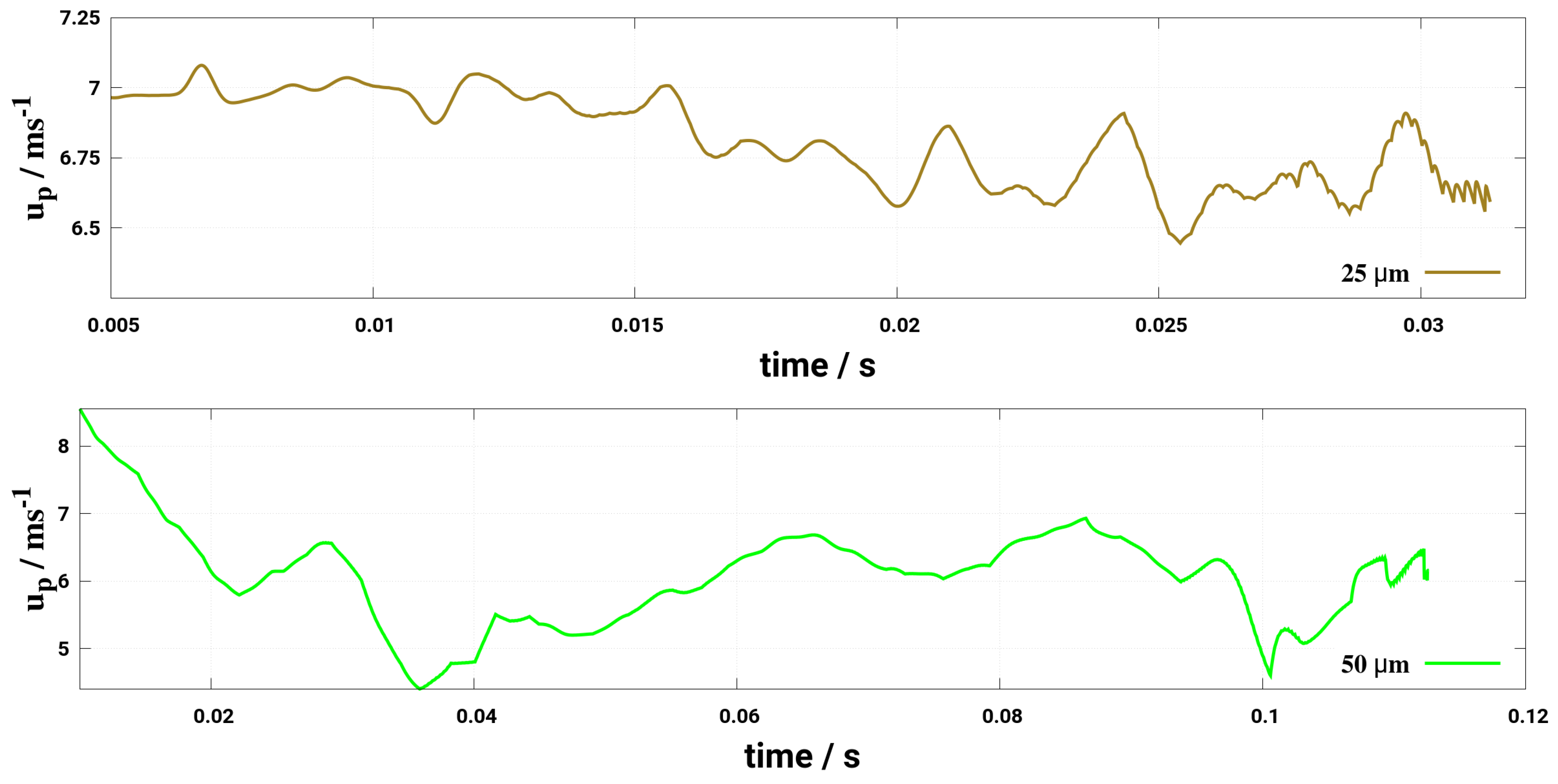
6. Effect of Turbulent Cross-Flowing on Droplet Dynamics Characteristics
7. Conclusions
- As the evaporation characteristics obviously depend on the AdBlue® droplet diameter, gas phase temperature and droplet relative velocity, it turns out that a smaller droplet diameter, higher temperature and relative velocity lead to shorter droplet life time as the droplet evaporates faster. Under such conditions, possible droplet/wall interaction processes on the pipe wall or/and at the entrance front of the monolith are avoided.
- Since the gaseous NH3 generated by urea decomposition is intended to reduce NOX emission in the SCR system, it is apparent for the prediction of high NOX removal performance that UWS injector system which allows to realize such operating conditions (droplet with smaller diameter, higher relative velocity and gas temperature) will support high conversion efficiency of urea into NH3.
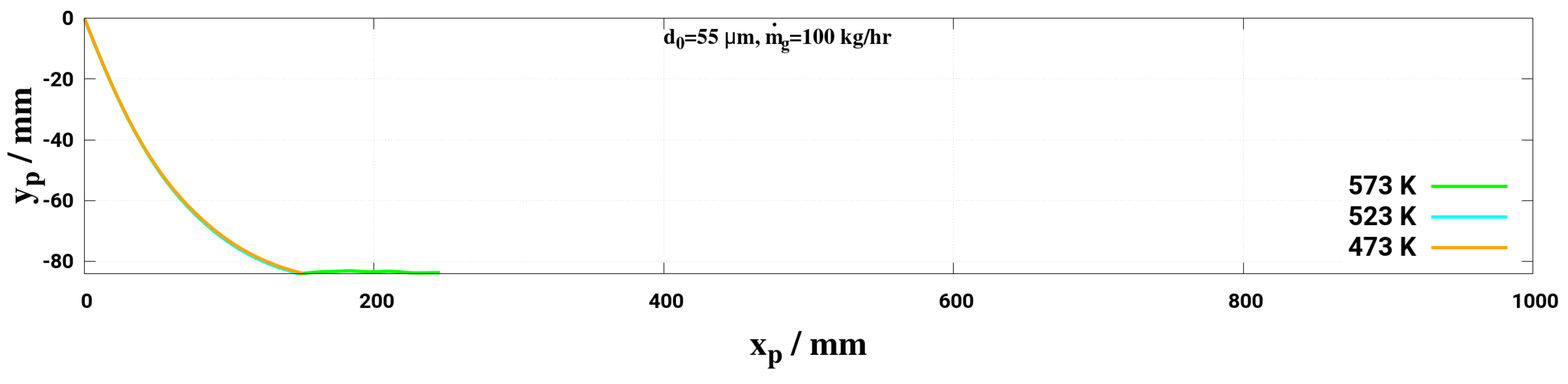
- Lower mass flow rate and higher gas temperature reduce considerably the droplet trajectory allowing a droplet to fully decompose before interacting with the entrance section of the monolith. This may help to avoid impinging and deposition on the pipe wall for small droplet (d < 50 m) for the investigated conditions.
- The wall deposition consists essentially of two main processes: first, droplet impingement on the wall for which, based on K and T* values, the droplet can undergo various physical processes such as deposition, splashing rebound, breakup. Second, only deposited droplet may form solid deposition based on chemical kinetics and phase thermodynamics. In the present study only phase thermodynamics are considered to define the solid deposition, while chemical kinetics for solid deposit formation is scope of our ongoing research activities. On this basis, it has been clearly shown that the droplet wall impingement can be favorable scenario as it can be responsible for breakup into smaller droplets and subsequently cause faster evaporation and conversion.
- Considering the two-way coupling between the gas phase and droplet, it turns out that the turbulent dispersion is adequately captured by LES for a case of a Stoke’s number that is larger than one as it appears in this study without accounting for a subgrid scale dispersion model. Note that for RANS (URANS) additional dispersion model must be included which may require more numerical care with respect to the phase coupling procedure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Regulation (EC) No 715/2007 of the European Parliament and of the Council of 20 June 2007 on Type Approval of Motor Vehicles with Respect to Emissions from Light Passenger and Commercial Vehicles (Euro 5 and Euro 6) and on Access to Vehicle Repair and Maintenance Information; Technical Report; Official Journal of the European Union: Brussels, Belgium, 2007.
- Nova, I.; Tronconi, E. (Eds.) Urea-SCR Technology for deNOx After Treatment of Diesel Exhausts; Springer Press: Singapore, 2014. [Google Scholar]
- Tripathi, G.; Dhar, A.; Sadiki, A. Recent Advancements in After-Treatment Technology for Internal Combustion Engines—An Overview. In Advances in Internal Combustion Engine Research. Energy, Environment, and Sustainability; Srivastava, D., Agarwal, A., Datta, A., Maurya, R., Eds.; Springer Press: Singapore, 2018; pp. 159–179. [Google Scholar]
- Nishad, K.; Sadiki, A.; janicka, J. Numerical Modeling of adBlue Droplet Evaporation in the Context of SCR-DeNOx. In Proceedings of the 18th Annual Conference of Liquid Atomization and Spray Systems-Asia (ILASS-Asia), Chennai, India, 6–10 November 2016. [Google Scholar]
- Birkhold, F.; Meingast, U.; Wassermann, P.; Deutschmann, O. Modeling and simulation of the injection of urea-water-solution for automotive SCR DeNOx-systems. Appl. Catal. B Environ. 2007, 70, 119–127. [Google Scholar] [CrossRef]
- Praveena, V.; Martin, M.L.J. A review on various after treatment techniques to reduce NOx emissions in a CI engine. J. Energy Inst. 2017. [Google Scholar] [CrossRef]
- Nishad, K.; Sadiki, A.; Janicka, J. Numerical investigation of adBlue droplet evaporation and thermal decomposition in the context of NOx-SCR using a multi-component evaporation model. Energies 2018, 11, 222. [Google Scholar] [CrossRef]
- Ebrahimian, V.; Nicolle, A.; Habchi, C. Detailed modeling of the evaporation and thermal decomposition of urea-water solution in SCR systems. AIChE J. 2012, 58, 1998–2009. [Google Scholar] [CrossRef]
- Ström, H.; Sasic, S.; Andersson, B. Effects of the Turbulent-to-Laminar Transition in Monolithic Reactors for Automotive Pollution Control. Ind. Eng. Chem. Res. 2011, 50, 3194–3205. [Google Scholar] [CrossRef]
- Spiteri, A. Experimental Investigation of the Injection Process in Urea-SCR deNOx Exhaust Gas After-Treatment Systems. Ph.D. Thesis, Department of Mechanical and Process Engineering, ETH Zürich, Switzerland, 2016. [Google Scholar]
- Stein, M.; Bykov, V.; Mass, U. The Effect of Evaporation Models on Urea Decomposition from Urea-Water-Solution Droplets in SCR Conditions. Emiss. Control Sci. Technol. 2018, 3, 263–274. [Google Scholar] [CrossRef]
- Abramzon, B.; Sirignano, W. Droplet vaporization model for spray combustion calculations. Int. J. Heat Mass Transf. 1989, 32, 1605–1618. [Google Scholar] [CrossRef]
- Sazhin, S.S.; Elwardany, A.E.; Heikal, M.R. New approaches to the modelling of multi-component fuel droplet heating and evaporation. J. Phys. Conf. Ser. 2015, 585, 012014. [Google Scholar] [CrossRef]
- Sadiki, A.; Chrigui, M.; Janicka, J.; Maneshkarimi, M. Modeling and Simulation of Effects of Turbulence on Vaporization, Mixing and Combustion of Liquid-Fuel Sprays. Flow Turbul. Combust. 2005, 75, 105–130. [Google Scholar] [CrossRef]
- Miller, R.S.; Harstad, K.; Bellan, J. Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations. Int. J. Multiph. Flow 1998, 24, 1025–1055. [Google Scholar] [CrossRef]
- Gan, X.; Yao, D.; Wu, F.; Dai, J.; Wei, L.; Li, X. Modeling and simulation of urea-water-solution droplet evaporation and thermolysis processes for SCR systems. Chin. J. Chem. Eng. 2016, 24, 1065–1073. [Google Scholar] [CrossRef]
- Olsson, L.; Sjövall, H.; Blint, R.J. A kinetic model for ammonia selective catalytic reduction over Cu-ZSM-5. Appl. Catal. B Environ. 2008, 81, 203–217. [Google Scholar] [CrossRef]
- Wurzenberger, J.C.; Wanker, R. Multi-Scale SCR Modeling, 1D Kinetic Analysis and 3D System Simulation; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Kaario, O.T.; Vuorinen, V.; Zhu, L.; Larmi, M.; Liu, R. Mixing and evaporation analysis of a high-pressure SCR system using a hybrid LES-RANS approach. Energy 2017, 120, 827–841. [Google Scholar] [CrossRef]
- Ström, H.; Lundström, A.; Andersson, B. Choice of urea-spray models in CFD simulations of urea-SCR systems. Chem. Eng. J. 2009, 150, 69–82. [Google Scholar] [CrossRef]
- Gökalp, I.; Chauveau, C.; Simon, O.; Chesneau, X. Mass transfer from liquid fuel droplets in turbulent flow. Combust. Flame 1992, 89, 286–298. [Google Scholar] [CrossRef]
- Sornek, R.; Dobashi, R.; Hirano, T. Effect of turbulence on vaporization, mixing, and combustion of liquid fuel soray. Combust. Flame 2000, 120, 479–491. [Google Scholar] [CrossRef]
- Nishad, K.; Ries, F.; Janicka, J.; Sadiki, S. Analysis of spray dynamics of urea-water-solution jets in a SCR-DeNOx system: An LES based study. Int. J. Heat Fluid Flow 2018, 70, 247–258. [Google Scholar] [CrossRef]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1964. [Google Scholar]
- Ranz, W.; Marshall, W. Evaporation from drops: Part 2. Chem. Eng. Prog. 1952, 18, 173–180. [Google Scholar] [CrossRef]
- Wang, T.J.; Baek, S.W.; Lee, S.Y.; Kang, D.H.; Yeo, G.K. Experimental Investigation on Evaporation of Urea-Water-Solution Droplet for SCR Applications. AIChE J. 2009, 55, 3267–3276. [Google Scholar] [CrossRef]
- Wu, P.K.; Kirkendall, K.A.; Fuller, R.P.; Nejad, A.S. Spray Structures of Liquid Jets Atomized in Subsonic Cross-Flows. J. Propuls. Power 1998, 14, 173–182. [Google Scholar] [CrossRef]
- Prakash, R.S.; Sinha, A.; Raghunandan, B.; Tomar, G.; Ravikrishna, R. Breakup of Volatile Liquid Jet in Hot Cross Flow. Procedia IUTAM 2015, 15, 18–25. [Google Scholar] [CrossRef]
- Chrigui, M.; Sadiki, A.; Ahmadi, G. Study of interaction in spray between evaporating droplets and turbulence using second order turbulence RANS modelling and a Lagrangian approach. Prog. Comput. Fluid Dyn. 2004, 4, 162–174. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Montorfano, A.; Piscaglia, F.; Onorati, A. Wall-adapting subgrid-scale models to apply to large eddy simulation of internal combustion engines. Int. J. Comput. Math. 2014, 91, 62–70. [Google Scholar] [CrossRef]
- Ries, F.; Nishad, K.; Dressler, L.; Janicka, J.; Sadiki, A. Evaluating large eddy simulation results based on error analysis. Theor. Comput. Fluid Dyn. 2018, 1–20. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulence Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Chrigui, M.; Masri, A.R.; Sadiki, A.; Janicka, J. Large Eddy Simulation of a Polydisperse Ethanol Spray Flame. Flow Turbul. Combust. 2013, 90, 813–832. [Google Scholar] [CrossRef]
- Torres, D.J.; O’rourke, P.J.; Amsden, A.A. Efficient multicomponent fuel algorithm. Combust. Theory Model. 2003, 7, 66–86. [Google Scholar] [CrossRef]
- Munnannur, A.; Chiruta, M.; Liu, Z.G. Thermal and Fluid Dynamic Considerations in Aftertreatment System Design for SCR Solid Deposit Mitigation. In Proceedings of the SAE 2012 World Congress & Exhibition, Detroit, MI, USA, 24–26 April 2012; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Börnhorst, M.; Deutschmann, O. Single droplet impingement of urea water solution on a heated substrate. Int. J. Heat Fluid Flow 2018, 69, 55–61. [Google Scholar] [CrossRef]
- Kuhnke, D. Spray Wall Interaction Modelling by Dimensionless Data Analysis. Ph.D. Thesis, Department of Mathematics, Darmstadt University of Technology, Darmstadt, Germany, 2004. [Google Scholar]
- O’Rourke, P.J.; Amsden, A.A. A Spray/Wall Interaction Submodel for the KIVA-3 Wall Film Model. In Proceedings of the SAE 2000 World Congress, Detroit, MI, USA, 6–9 March 2000; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Nishad, K. Modeling and Unsteady Simulation of Turbulent Multi-Phase Flow Including Fuel Injection in IC-Engines. Ph.D. Thesis, Department of Mechanical Engineering, Technische Universität Darmstadt, Darmstadt, Germany, 2013. [Google Scholar]
- Nishad, K.; Pischke, P.; Goryntsev, D.; Sadiki, A.; Kneer, R. LES Based Modeling and Simulation of Spray Dynamics including Gasoline Direct Injection (GDI) Processes using KIVA-4 Code. In Proceedings of the SAE 2012 World Congress & Exhibition, Detroit, MI, USA, 24–26 April 2012; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Goryntsev, D.; Nishad, K.; Sadiki, A.; Janicka, J. Application of LES for Analysis of Unsteady Effects on Combustion Processes and Misfires in DISI Engine. Oil Gas Sci. Technol. Rev. IFP Energies Nouvelles 2014, 69, 129–140. [Google Scholar] [CrossRef][Green Version]
- Stauch, R.; Lipp, S.; Maas, U. Detailed numerical simulations of the autoignition of single n-heptane droplets in air. Combust. Flame 2006, 145, 533–542. [Google Scholar] [CrossRef]
- Maas, U. Mathematische Modellierung instationärer Verbrennungsprozesse unter verwendung detaillierter chemischer Reaktionsmechanismen. Ph.D. Thesis, Universität Heidelberg, Heidelberg, Germany, 1988. [Google Scholar]
- Smith, L.J.; Berendsen, H.J.C.; van Gunsteren, W.F. Computer simulation of urea-water mixtures: A test of force field parameters for use in biomolecular simulation. J. Phys. Chem. B 2004, 108, 1065–1071. [Google Scholar] [CrossRef]
- Kontin, S.; Höfler, A.; Koch, R.; Bauer, H.J. Heat and Mass Transfer accompanied by Crystallisation of single Particles containing Urea-water-solution. In Proceedings of the 23rd Annual Conference on Liquid Atomization and Spray Systems, Brno, Czech Republic, 12–14 September 2010. [Google Scholar]
- Ryddner, D.T.; Trujillo, M.F. Modeling Urea-Water Solution Droplet Evaporation. Emiss. Control Sci. Technol. 2015, 1, 80–97. [Google Scholar] [CrossRef]
- Wei, L.; Youtong, Z.; Asif, M. Investigation on UWS Evaporation for Vehicle SCR Applications. AIChE J. 2016, 62, 880–890. [Google Scholar] [CrossRef]
- Yaws, C.L. Chemical Properties Handbook; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Reid, R.; Prausnitz, J.; Poling, B. The Properties of Gases and Liquids, 4th ed.; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Maas, U.; Warnatz, J. Ignition processes in hydrogen-oxygen mixtures. Combust. Flame 1988, 74, 53–69. [Google Scholar] [CrossRef]
- Stauch, R. Detaillierte Simulation von Verbrennungsprozessen in Mehrphasensystemen. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 2007. [Google Scholar]
- Deuflhard, P.; Hairer, E.; Zugck, J. One-step and Extrapolation Methods for Differential-Algebraic systems. Numer. Math. 2004, 51, 501–516. [Google Scholar] [CrossRef]
- Fede, P.; Simonin, O.; Villedieu, P.; Squires, K. Stochastic Modeling of the Turbulent Subgrid Fluid Velocity Along Inertial Particle Trajectories. In Proceedings of the Summer Program Center for Turbulence Research Stanford University, Stanford, CA, USA, 4–9 July 2006. [Google Scholar]
- Ahmadi, W.; Mehdizadeh, A.; Chrigui, M.; Sadiki, A. Numerical Evaluation of Unsteadiness in Particle Dispersion Modeling. J. Fluids Eng. 2014, 137, 034502. [Google Scholar] [CrossRef]
| Variables | |||||
|---|---|---|---|---|---|
| mass | 0 | 0 | 0 | ||
| momentum | |||||
| species mass fraction | 0 | ||||
| enthalpy |
| Properties | Detailed Simulation [B07] | Reduced Model [C05] |
|---|---|---|
| Droplet phase | Resolved 1D | Resolved 1D |
| Gas phase close to droplet | Resolved 1D | Not resolved, 0D (Film model) |
| Ambient conditions | Given as boundary condition of gas-phase | Taken from LES |
| Interface | Local evaporation balance | Film model connects ambient |
| Connects gas-phases and droplet | onditions and droplet | |
| Values at interface | Vapor pressure and partial | Weighted average of droplet |
| pressure | data and ambient conditions | |
| Gradients at interface | Local gradients (first element | Interface value to ambient |
| of gas phase) | condition | |
| Diffusion | Mixture average | Only evaporating species |
| Initial Diameter, (m) | T, (K) | Relative Velocity, urel (m/s) |
|---|---|---|
| 25 | 473 | 0, 5, 10, 20, 40 |
| 573 | 0, 5, 10, 20, 40 | |
| 673 | 0, 5, 10, 20, 40 | |
| 773 | 0, 5, 10, 20, 40 | |
| 50 | 473 | 0, 5, 10, 20, 40 |
| 573 | 0, 5, 10, 20, 40 | |
| 673 | 0, 5, 10, 20, 40 | |
| 773 | 0, 5, 10, 20, 40 | |
| 100 | 473 | 0, 5, 10, 20, 40 |
| 573 | 0, 5, 10, 20, 40 | |
| 673 | 0, 5, 10, 20, 40 | |
| 773 | 0, 5, 10, 20, 40 | |
| 150 | 473 | 0, 5, 10, 20, 40 |
| 573 | 0, 5, 10, 20, 40 | |
| 673 | 0, 5, 10, 20, 40 | |
| 773 | 0, 5, 10, 20, 40 | |
| 200 | 473 | 0, 5, 10, 20, 40 |
| 573 | 0, 5, 10, 20, 40 | |
| 673 | 0, 5, 10, 20, 40 | |
| 773 | 0, 5, 10, 20, 40 |
| Case | Gas Temperature, (K) | Gas Flow Rate, (kg/h) | Droplet Diameter (m) |
|---|---|---|---|
| T1M1 | 573 | 100 | 25, 50, 55, 100, 200 |
| T1M2 | 573 | 200 | 25, 50, 55, 100, 200 |
| T2M1 | 673 | 100 | 25, 50, 55, 100, 200 |
| T2M2 | 673 | 200 | 25, 50, 55, 100, 200 |
| 3TM1 | 573, 523, 473 | 100 | 55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishad, K.; Stein, M.; Ries, F.; Bykov, V.; Maas, U.; Deutschmann, O.; Janicka, J.; Sadiki, A. Thermal Decomposition of a Single AdBlue® Droplet Including Wall–Film Formation in Turbulent Cross-Flow in an SCR System. Energies 2019, 12, 2600. https://doi.org/10.3390/en12132600
Nishad K, Stein M, Ries F, Bykov V, Maas U, Deutschmann O, Janicka J, Sadiki A. Thermal Decomposition of a Single AdBlue® Droplet Including Wall–Film Formation in Turbulent Cross-Flow in an SCR System. Energies. 2019; 12(13):2600. https://doi.org/10.3390/en12132600
Chicago/Turabian StyleNishad, Kaushal, Marcus Stein, Florian Ries, Viatcheslav Bykov, Ulrich Maas, Olaf Deutschmann, Johannes Janicka, and Amsini Sadiki. 2019. "Thermal Decomposition of a Single AdBlue® Droplet Including Wall–Film Formation in Turbulent Cross-Flow in an SCR System" Energies 12, no. 13: 2600. https://doi.org/10.3390/en12132600
APA StyleNishad, K., Stein, M., Ries, F., Bykov, V., Maas, U., Deutschmann, O., Janicka, J., & Sadiki, A. (2019). Thermal Decomposition of a Single AdBlue® Droplet Including Wall–Film Formation in Turbulent Cross-Flow in an SCR System. Energies, 12(13), 2600. https://doi.org/10.3390/en12132600