Design of Diamond Power Devices: Application to Schottky Barrier Diodes
Abstract
:1. Introduction
2. Brief Review of Diamond Diodes
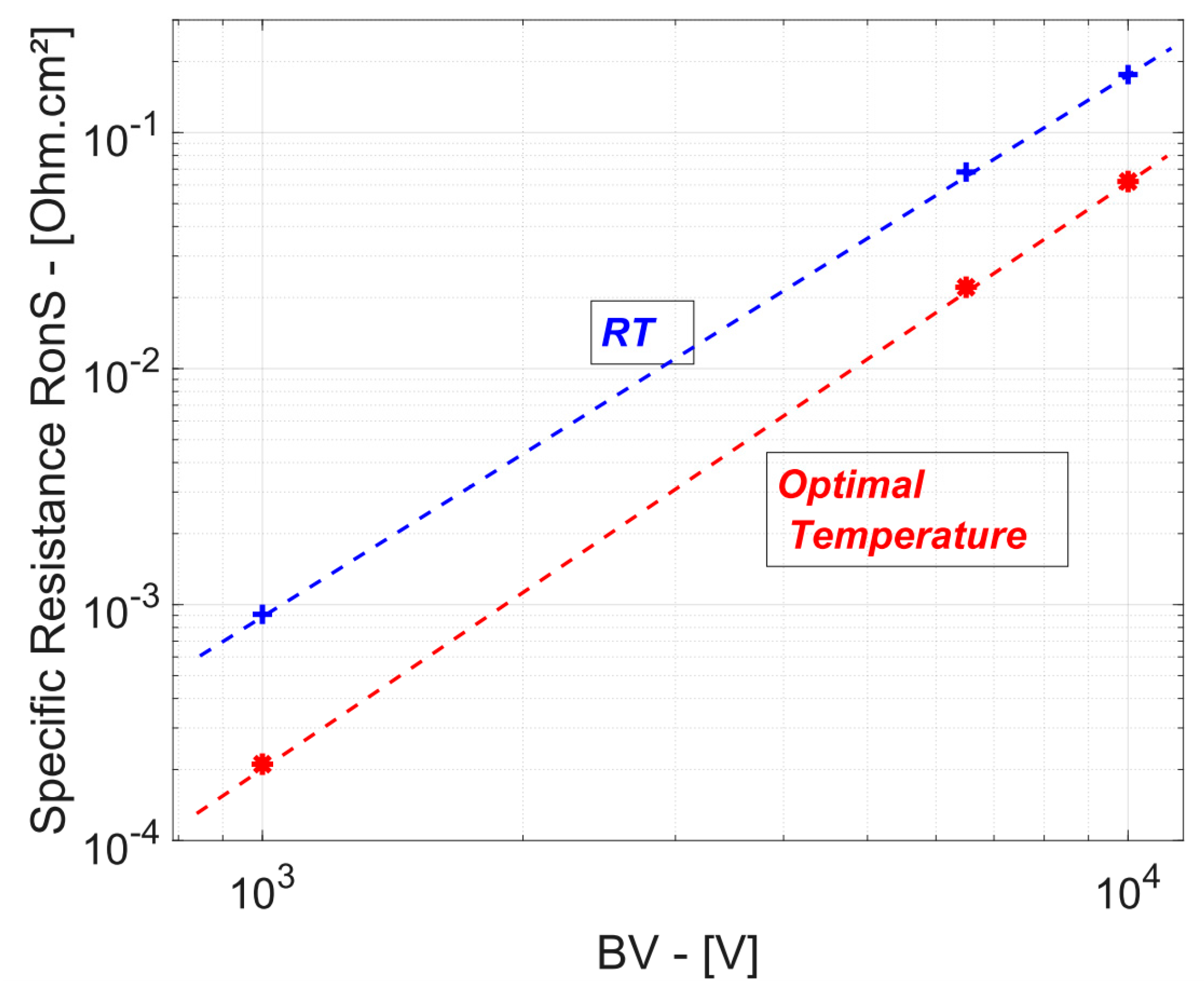
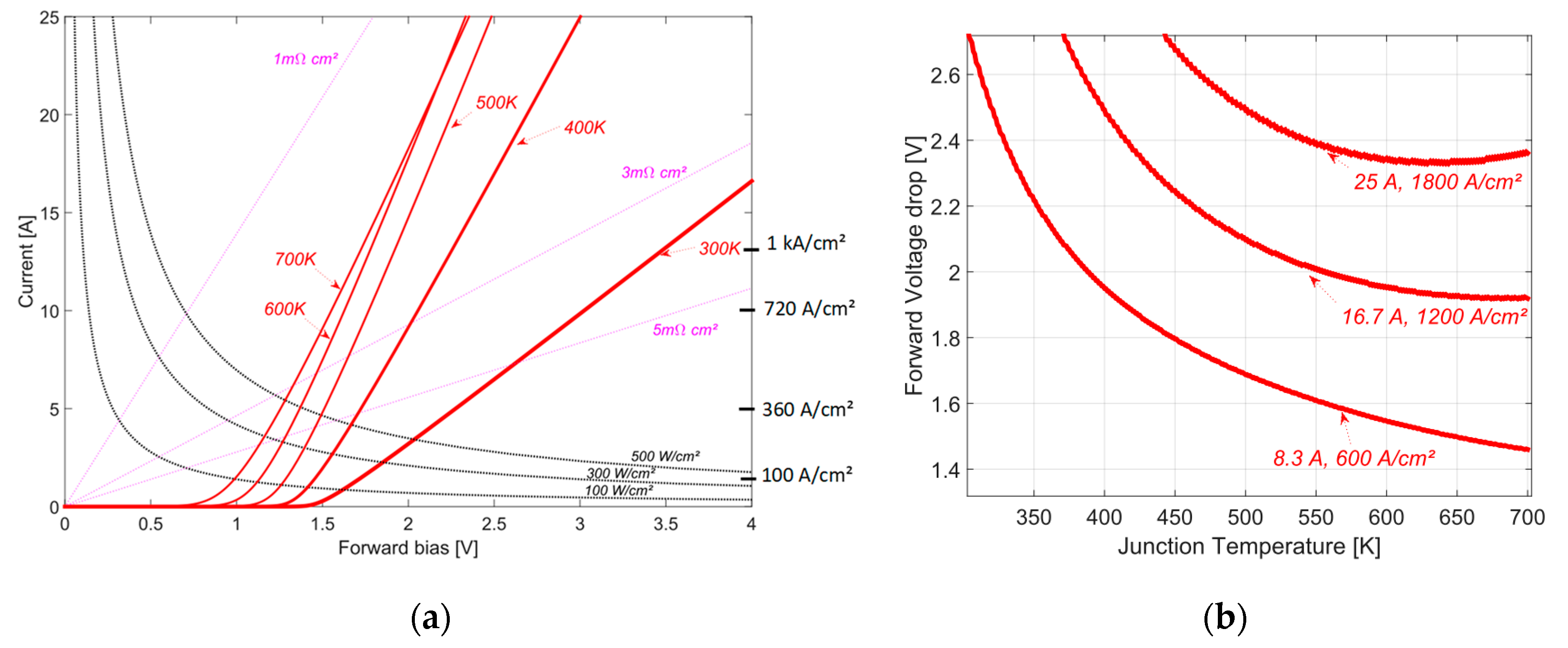
3. ON-State Versus OFF-State Trade-Off
4. Design and Optimization of OFF-State
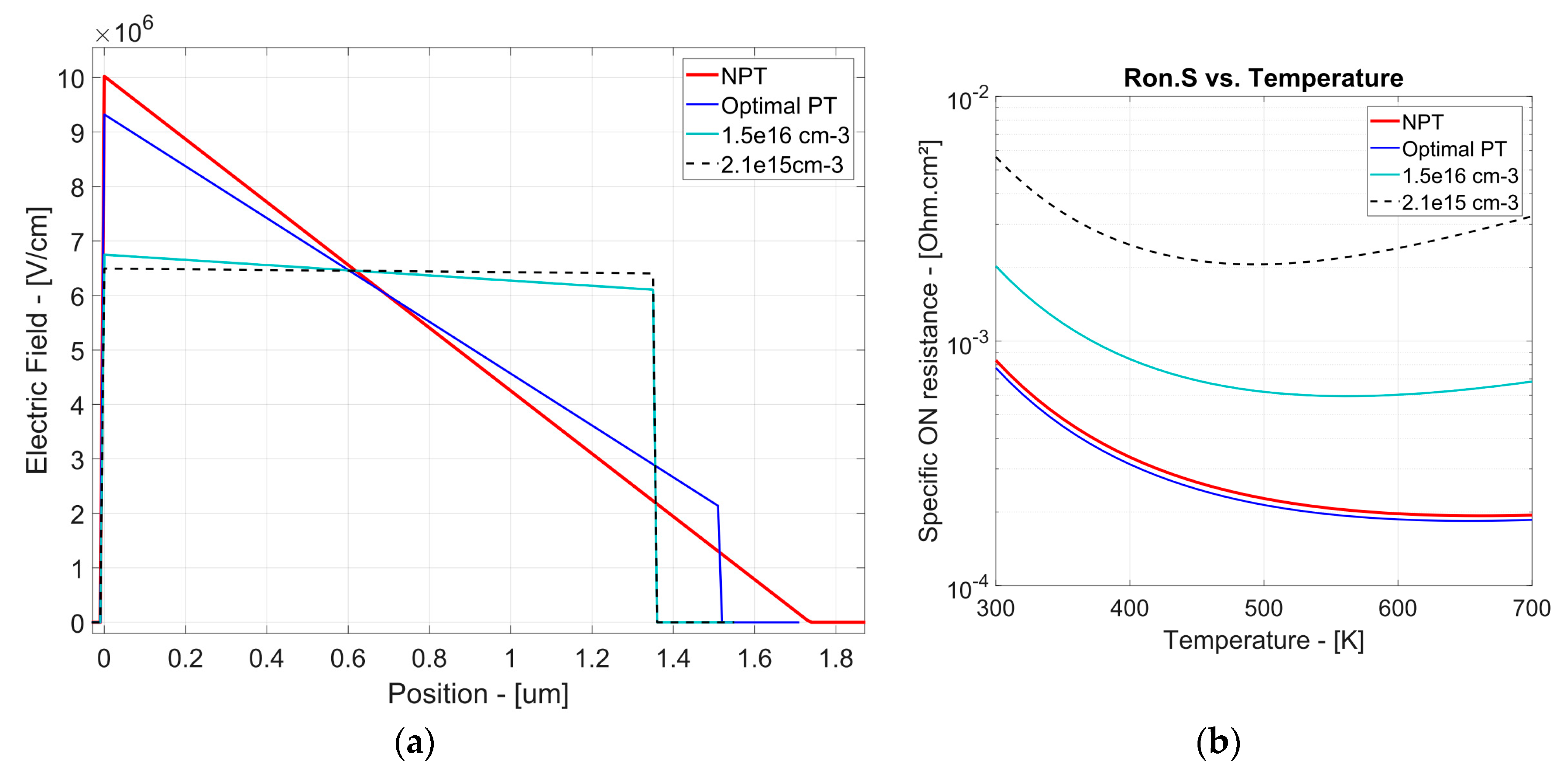
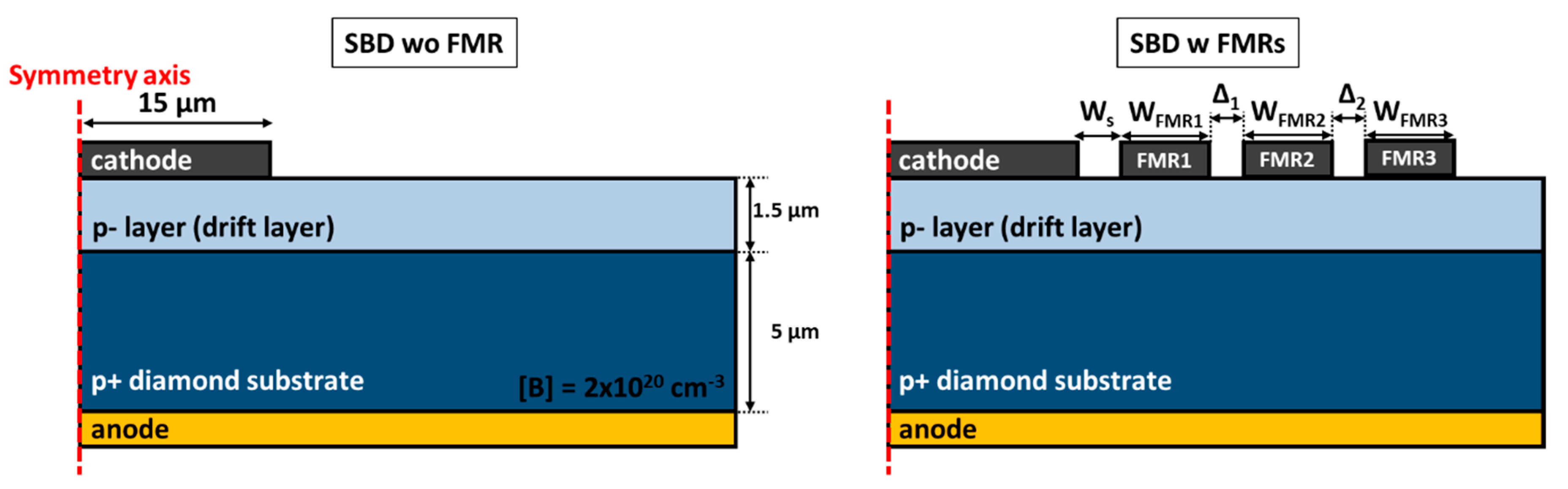
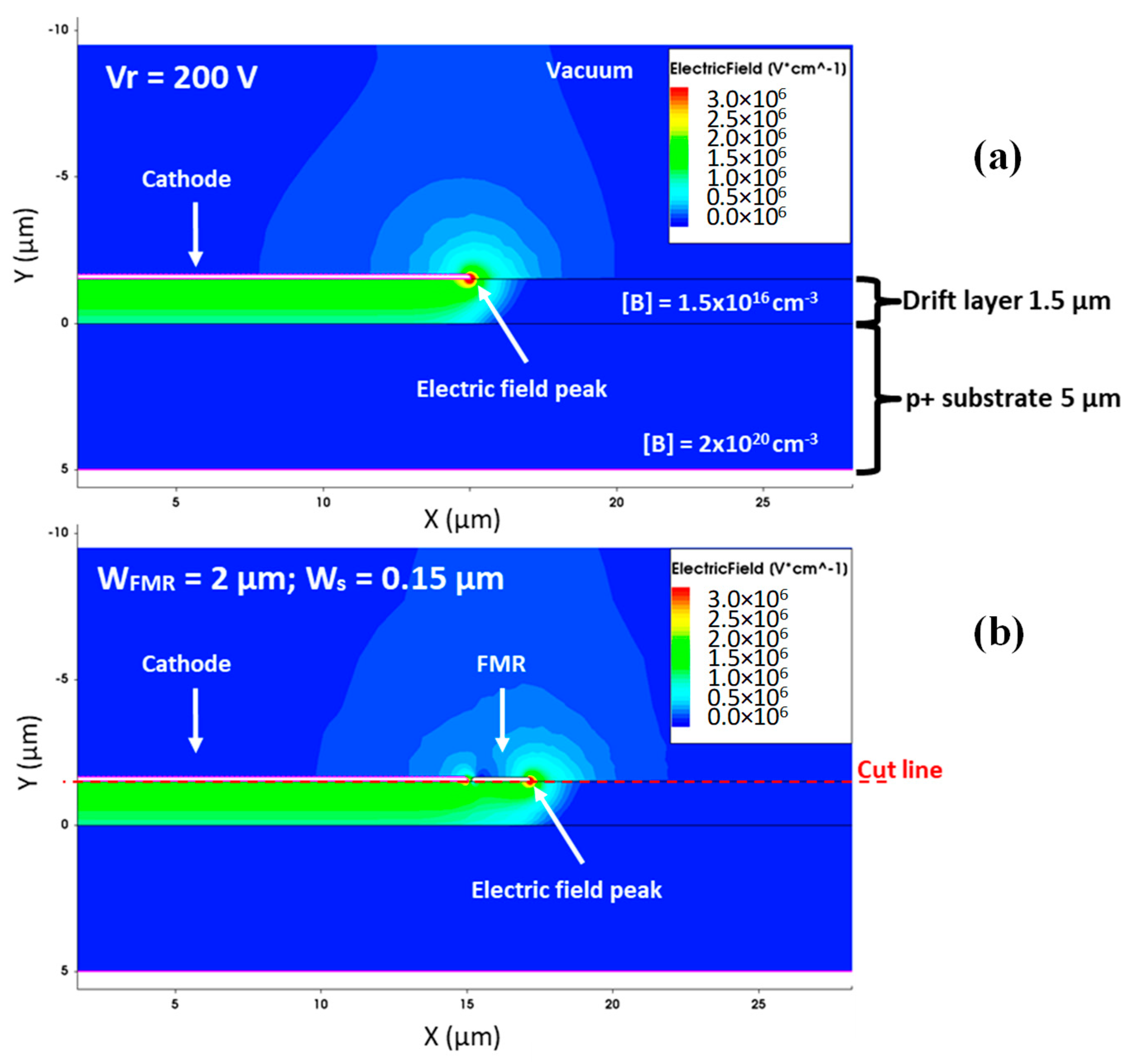
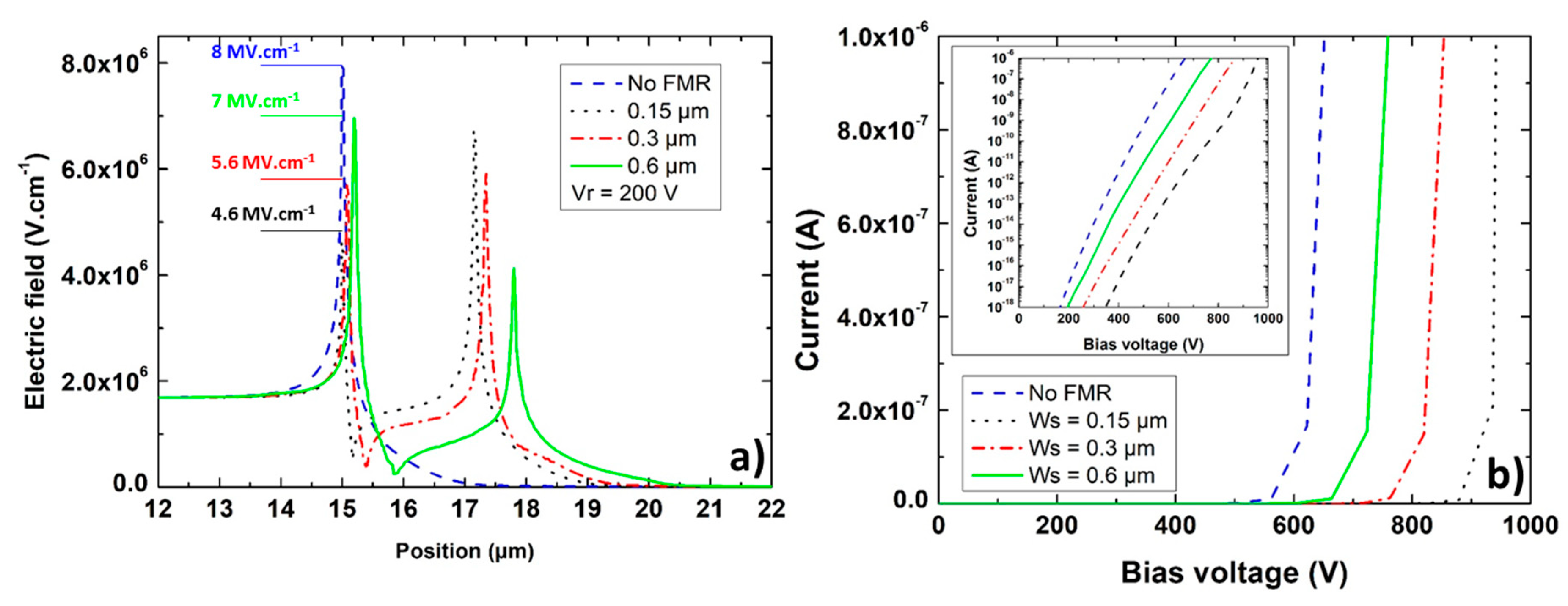
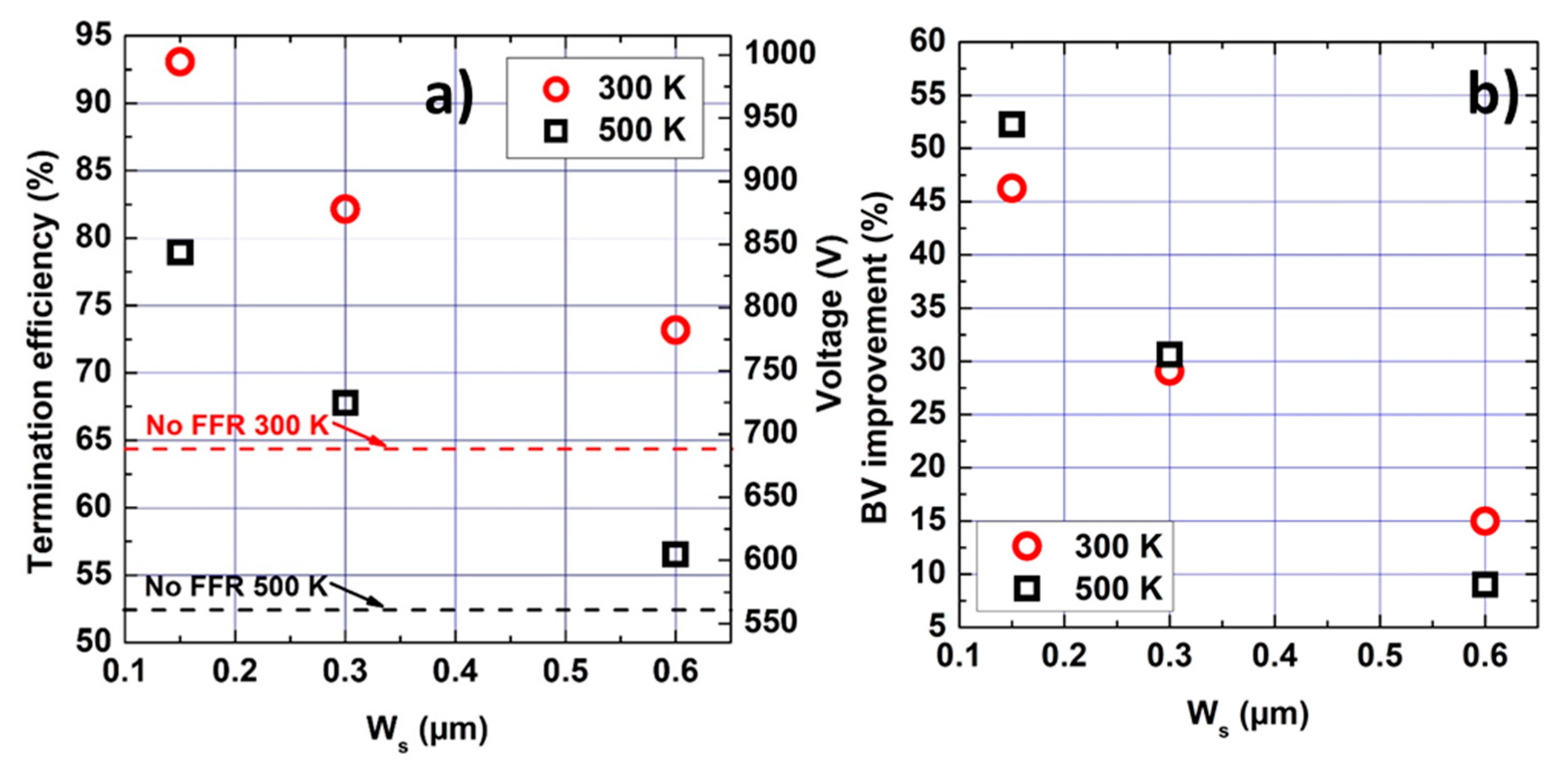
4.1. TCAD Simulations of OFF-State Diamond Diodes with FMR as Edge Termination
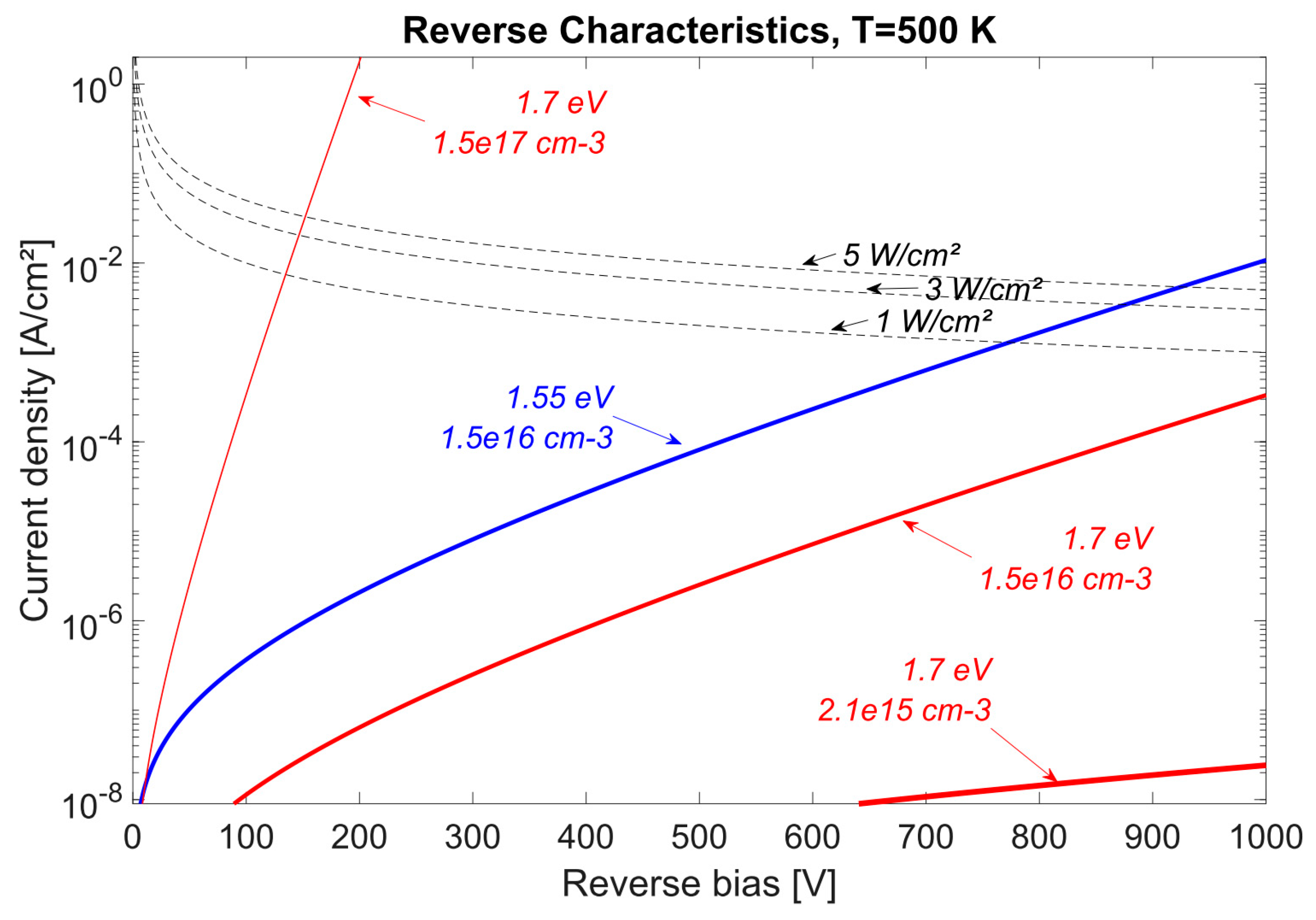
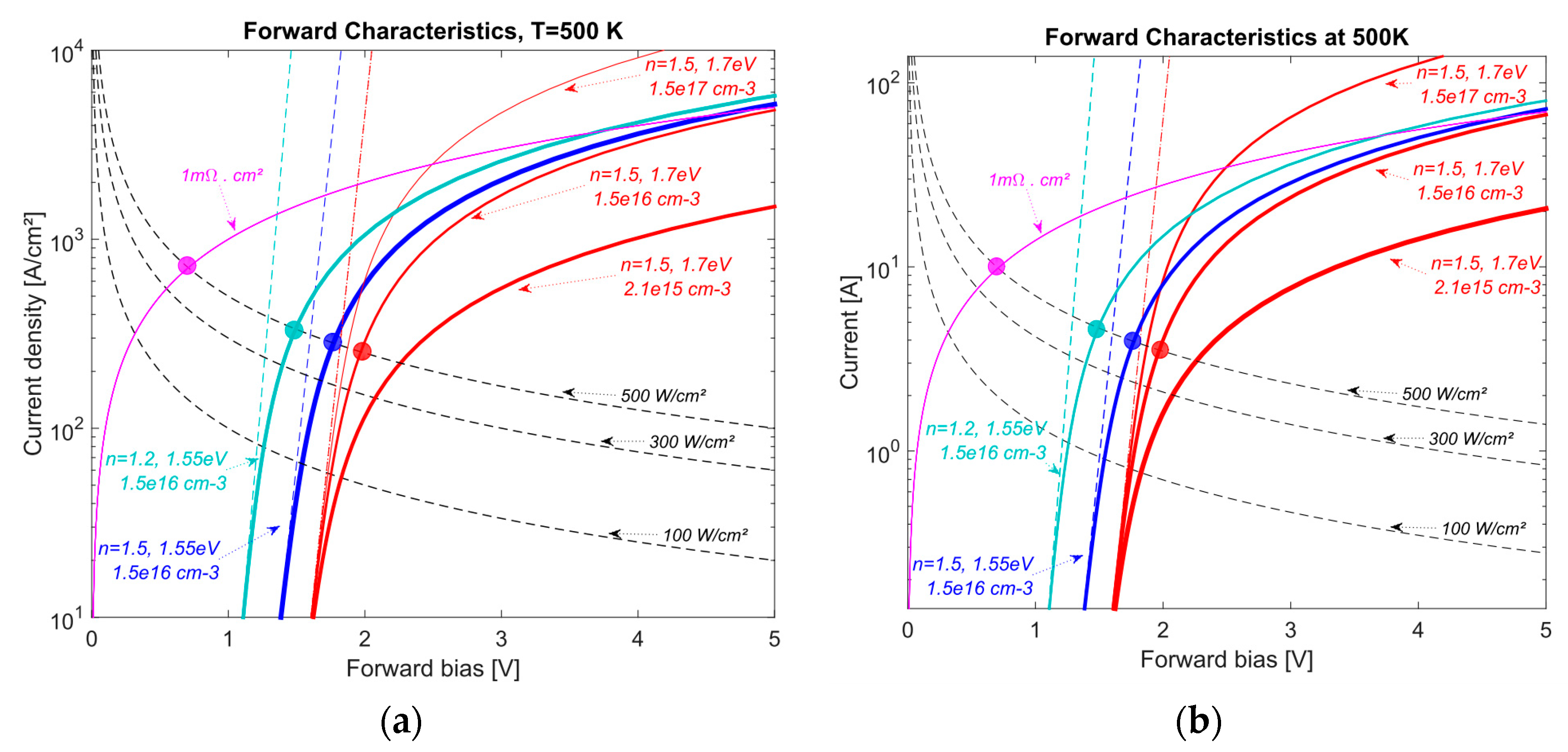
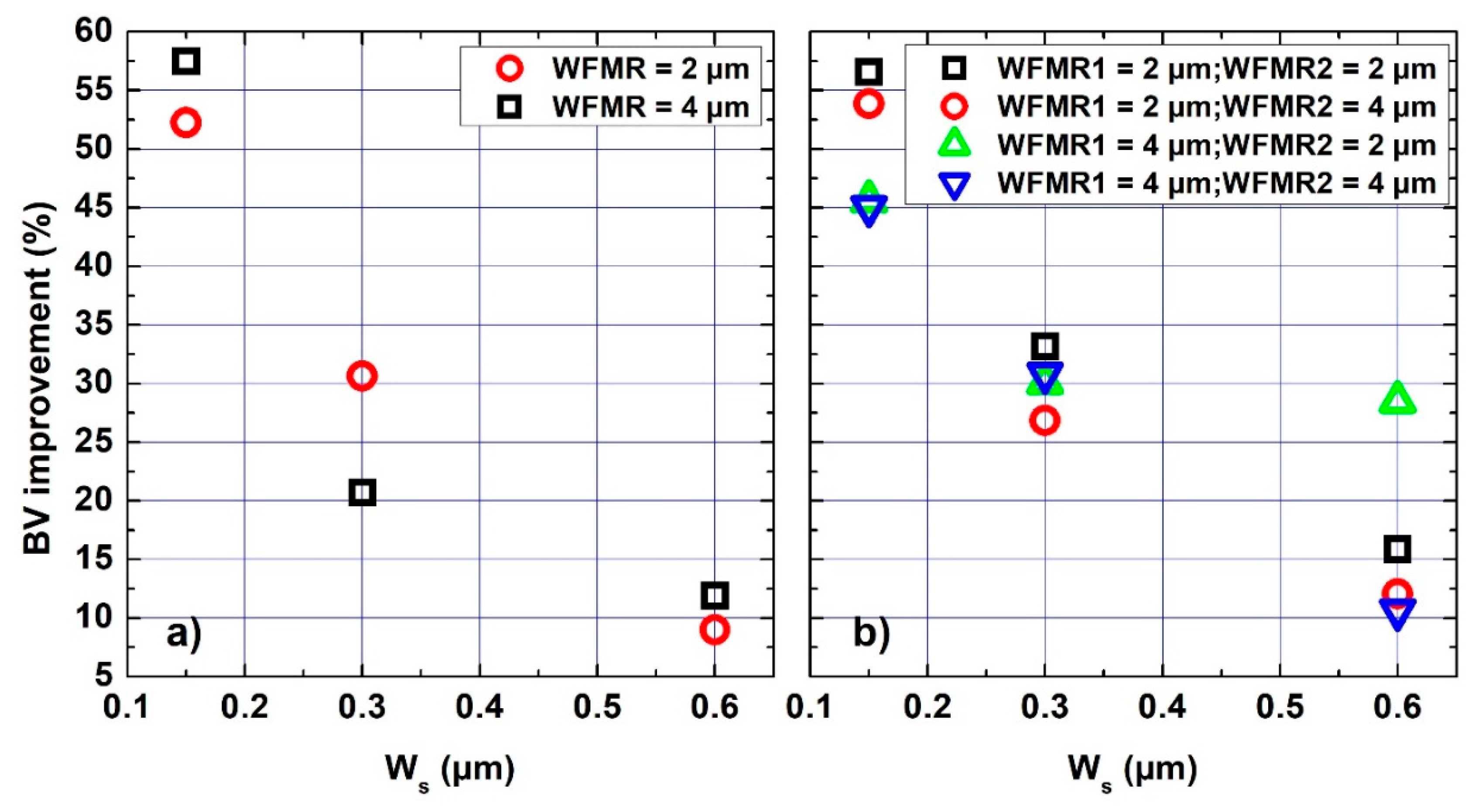
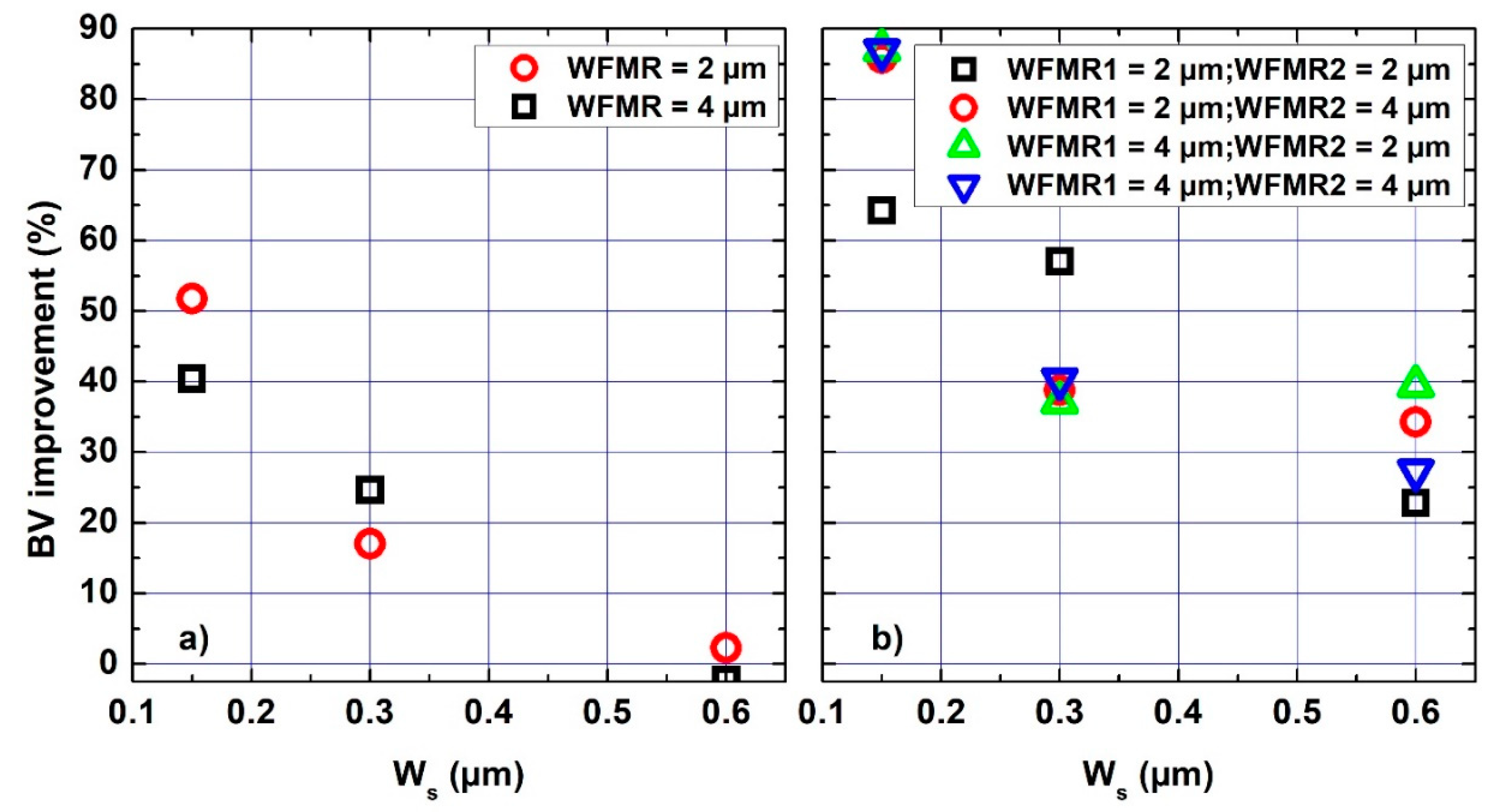
4.2. Design for 1kV Breakdown Voltage
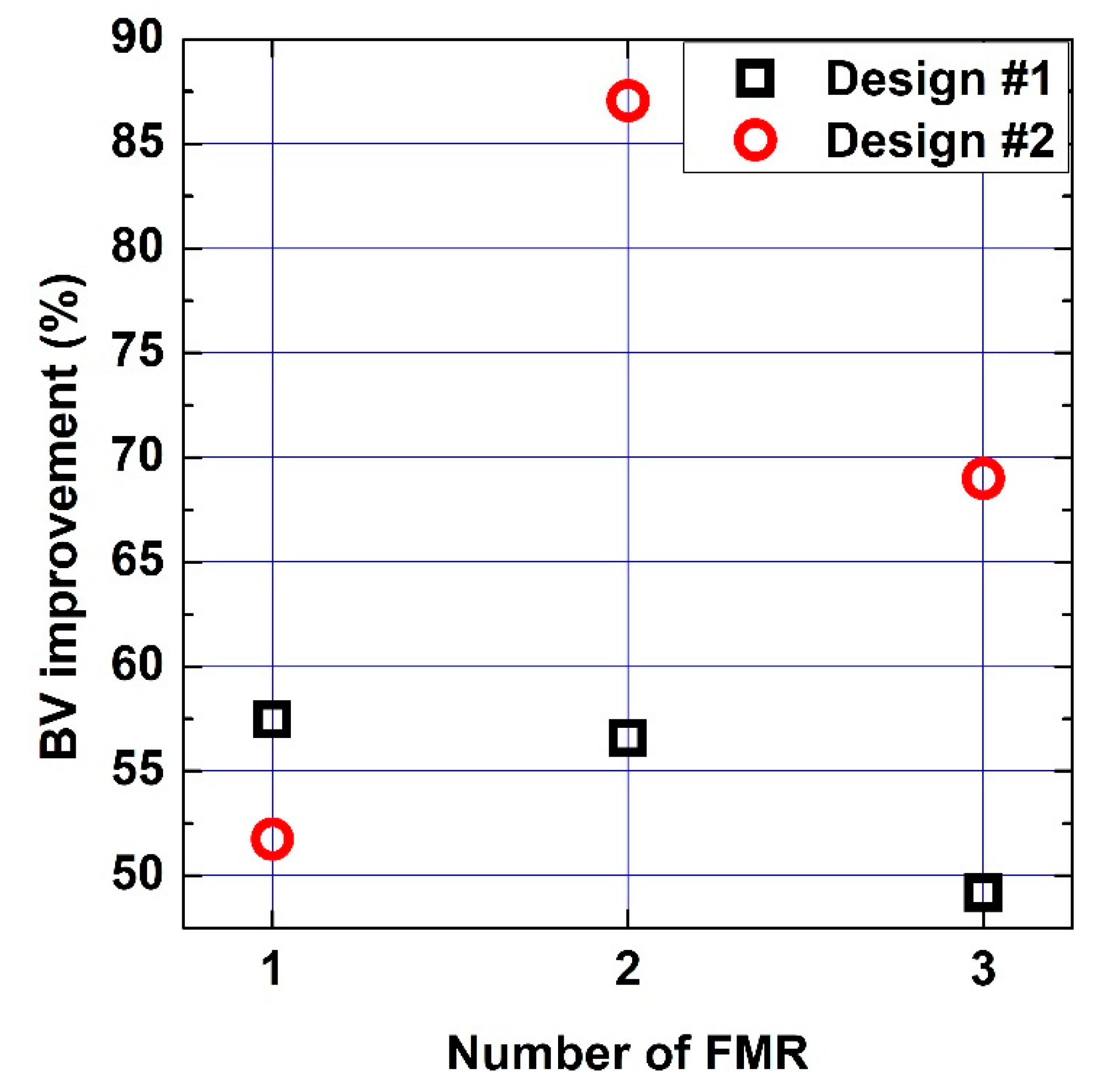
4.3. Influence of the Ring Number on the BV
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geis, M.W.; Gregory, J.A.; Pate, B.B. Capacitance-voltage measurements on metal-SiO2-diamond structures fabricated with (100)- and (111)-oriented substrates. IEEE Trans. Electron Devices 1991, 38, 619–626. [Google Scholar] [CrossRef]
- Shiomi, H.; Nakahata, H.; Imai, T.; Nishibayashi, Y.; Fujimori, N. Electrical Characteristics of Metal Contacts to Boron-Doped Diamond Epitaxial Film. Jpn. J. Appl. Phys. 1989, 28, 758. [Google Scholar] [CrossRef]
- Gildenblat, G.S.; Grot, S.A.; Wronski, C.R.; Badzian, A.R.; Badzian, T.; Messier, R. Electrical characteristics of Schottky diodes fabricated using plasma assisted chemical vapor deposited diamond films. Appl. Phys. Lett. 1988, 53, 586–588. [Google Scholar] [CrossRef]
- Volpe, P.N.; Muret, P.; Pernot, J.; Omnès, F.; Teraji, T.; Koide, Y.; Jomard, F.; Planson, D.; Brosselard, P.; Dheilly, N.; et al. Extreme dielectric strength in boron doped homoepitaxial diamond. Appl. Phys. Lett. 2010, 97, 223501. [Google Scholar] [CrossRef] [Green Version]
- Traoré, A.; Muret, P.; Fiori, A.; Eon, D.; Gheeraert, E.; Pernot, J. Zr/oxidized diamond interface for high power Schottky diodes. Appl. Phys. Lett. 2014, 104, 052105. [Google Scholar] [CrossRef]
- Makino, T.; Tanimoto, S.; Hayashi, Y.; Kato, H.; Tokuda, N.; Ogura, M.; Takeuchi, D.; Oyama, K.; Ohashi, H.; Okushi, H.; et al. Diamond Schottky-pn diode with high forward current density and fast switching operation. Appl. Phys. Lett. 2009, 94, 262101. [Google Scholar] [CrossRef]
- Traore, A.; Nakajima, A.; Makino, T.; Kuwabara, D.; Kato, H.; Ogura, M.; Takeuchi, D.; Yamazaki, S. Dynamic properties of diamond high voltage p–i–n diodes. Jpn. J. Appl. Phys. 2017, 56, 04CR14. [Google Scholar] [CrossRef]
- Umezawa, H.; Shikata, S.; Funaki, T. Diamond Schottky barrier diode for high-temperature, high-power, and fast switching applications. Jpn. J. Appl. Phys. 2014, 53, 05FP06. [Google Scholar] [CrossRef]
- Bormashov, V.S.; Terentiev, S.A.; Buga, S.G.; Tarelkin, S.A.; Volkov, A.P.; Teteruk, D.V.; Kornilov, N.V.; Kuznetsov, M.S.; Blank, V.D. Thin large area vertical Schottky barrier diamond diodes with low on-resistance made by ion-beam assisted lift-off technique. Diam. Relat. Mater. 2017, 75, 78–84. [Google Scholar] [CrossRef]
- Umezawa, H.; Nagase, M.; Kato, Y.; Shikata, S. High temperature application of diamond power device. Diam. Relat. Mater. 2012, 24, 201–205. [Google Scholar] [CrossRef]
- Makino, T.; Kato, H.; Tokuda, N.; Ogura, M.; Takeuchi, D.; Oyama, K.; Tanimoto, S.; Okushi, H.; Yamasaki, S. Diamond Schottky-pn diode without trade-off relationship between on-resistance and blocking voltage. Phys. Status Solidi A 2010, 207, 2105–2109. [Google Scholar] [CrossRef]
- Suzuki, M.; Sakai, T.; Makino, T.; Kato, H.; Takeuchi, D.; Ogura, M.; Okushi, H.; Yamasaki, S. Electrical characterization of diamond PiN diodes for high voltage applications. Phys. Status Solidi A 2013, 210, 2035–2039. [Google Scholar] [CrossRef]
- Blank, V.D.; Bormashov, V.S.; Tarelkin, S.A.; Buga, S.G.; Kuznetsov, M.S.; Teteruk, D.V.; Kornilov, N.V.; Terentiev, S.A.; Volkov, A.P. Power high-voltage and fast response Schottky barrier diamond diodes. Diam. Relat. Mater. 2015, 57 (Suppl. C), 32–36. [Google Scholar] [CrossRef]
- Kumaresan, R.; Umezawa, H.; Tatsumi, N.; Ikeda, K.; Shikata, S. Device processing, fabrication and analysis of diamond pseudo-vertical Schottky barrier diodes with low leak current and high blocking voltage. Diam. Relat. Mater. 2009, 18, 299–302. [Google Scholar] [CrossRef]
- Oyama, K.; Ri, S.G.; Kato, H.; Ogura, M.; Makino, T.; Takeuchi, D.; Tokuda, N.; Okushi, H.; Yamasaki, S. High performance of diamond p+-i-n+ junction diode fabricated using heavily doped p+ and n+ layers. Appl. Phys. Lett. 2009, 94, 152109. [Google Scholar] [CrossRef]
- Perez, G.; Lefranc, P.; Jeannin, P.; Eon, D.; Rouger, N. Parallel and interleaved structures for diamond Schottky diodes. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar]
- Perez, G.; Chicot, G.; Avenas, Y.; Lefranc, P.; Jeannin, P.O.; Eon, D.; Rouger, N. Integrated temperature sensor with diamond Schottky diodes using a thermosensitive parameter. Diam. Relat. Mater. 2017, 78, 83–87. [Google Scholar] [CrossRef]
- Matsumoto, T.; Mukose, T.; Makino, T.; Takeuchi, D.; Yamasaki, S.; Inokuma, T.; Tokuda, N. Diamond Schottky-pn diode using lightly nitrogen-doped layer. Diam. Relat. Mater. 2017, 75, 152–154. [Google Scholar] [CrossRef]
- Makino, T.; Kato, H.; Takeuchi, D.; Ogura, M.; Okushi, H.; Yamasaki, S. Device Design of Diamond Schottky-pn Diode for Low-Loss Power Electronics. Jpn. J. Appl. Phys. 2012, 51, 090116. [Google Scholar] [CrossRef]
- Dutta, M.; Koeck, F.A.M.; Li, W.; Nemanich, R.J.; Chowdhury, S. High Voltage Diodes in Diamond Using (100)- and (111)- Substrates. IEEE Electron Device Lett. 2017, 38, 600–603. [Google Scholar] [CrossRef]
- Chicot, G.; Eon, D.; Rouger, N. Optimal drift region for diamond power devices. Diam. Relat. Mater. 2016, 69, 68–73. [Google Scholar] [CrossRef]
- Baliga, B.J. Fundamentals of Power Semiconductor Devices; Springer: New York, NY, USA, 2008. [Google Scholar]
- Hiraiwa, A.; Kawarada, H. Figure of merit of diamond power devices based on accurately estimated impact ionization processes. J. Appl. Phys. 2013, 114, 034506. [Google Scholar]
- Volpe, P.-N.; Pernot, J.; Muret, P.; Omnès, F. High hole mobility in boron doped diamond for power device applications. Appl. Phys. Lett. 2009, 94, 092102. [Google Scholar] [CrossRef]
- Maréchal, A.; Rouger, N.; Crebier, J.C.; Pernot, J.; Koizumi, S.; Teraji, T.; Gheeraert, E. Model implementation towards the prediction of J(V) characteristics in diamond bipolar device simulations. Diam. Relat. Mater. 2014, 43 (Suppl. C), 34–42. [Google Scholar] [CrossRef]
- Traoré, A.; Koizumi, S.; Pernot, J. Effect of n- and p-type doping concentrations and compensation on the electrical properties of semiconducting diamond. Phys. Status Solidi A 2016, 213, 2036–2043. [Google Scholar] [CrossRef]
- Pernot, J.; Volpe, P.N.; Omnès, F.; Muret, P.; Mortet, V.; Haenen, K.; Teraji, T. Hall hole mobility in boron-doped homoepitaxial diamond. Phys. Rev. B 2010, 81, 205203. [Google Scholar] [CrossRef]
- Koizumi, S.; Umezawa, H.; Pernot, J.; Suzuki, M. 3- Fundamental material’s nature of diamond. In Power Electronics Device Applications of Diamond Semiconductors; Woodhead Publishing: Sawston, UK, 2018; pp. 191–217. [Google Scholar]
- Koizumi, S.; Umezawa, H.; Pernot, J.; Suzuki, M. (Eds.) 5-Device formation and the characterizations. In Power Electronics Device Applications of Diamond Semiconductors; Woodhead Publishing: Sawston, UK, 2018; pp. 295–382. [Google Scholar]
- Umezawa, H.; Saito, T.; Tokuda, N.; Ogura, M.; Ri, S.G.; Yoshikawa, H.; Shikata, S.I. Leakage current analysis of diamond Schottky barrier diode. Appl. Phys. Lett. 2007, 90, 073506. [Google Scholar] [CrossRef] [Green Version]
- Traoré, A. High Power Diamond Schottky Diode. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2015. [Google Scholar]
- Driche, K.; Rugen, S.; Kaminski, N.; Umezawa, H.; Okumura, H.; Gheeraert, E. Electric field distribution using floating metal guard rings edge-termination for Schottky diodes. Diam. Relat. Mater. 2018, 82, 160–164. [Google Scholar] [CrossRef]
- CPW4-1200-S010B 1200V Z-Rec Schottky Diode|Wolfspeed [En ligne]. Available online: https://www.wolfspeed.com/cpw4-1200-s010b (accessed on 18 April 2019).
- Umezawa, H.; Kato, Y.; Shikata, S. 1 Ω On-Resistance Diamond Vertical-Schottky Barrier Diode Operated at 250 °C. Appl. Phys. Express 2013, 6, 011302. [Google Scholar] [CrossRef]
- Landstrass, M.I.; Plano, M.A.; Moreno, M.A.; McWilliams, S.; Pan, L.S.; Kania, D.R.; Han, S. Device properties of homoepitaxially grown diamond. Diam. Relat. Mater. 1993, 2, 1033–1037. [Google Scholar] [CrossRef]
- Koizumi, S.; Umezawa, H.; Pernot, J.; Suzuki, M. (Eds.) 2-Doping and semiconductor characterizations. In Power Electronics Device Applications of Diamond Semiconductors; Woodhead Publishing: Sawston, UK, 2018; pp. 99–189. [Google Scholar]
- Ikeda, K.; Umezawa, H.; Shikata, S. Edge termination techniques for p-type diamond Schottky barrier diodes. Diam. Relat. Mater. 2008, 17, 809–812. [Google Scholar] [CrossRef]
- Nawawi, A.; Tseng, K.J.; Amaratunga, G.A.J.; Umezawa, H.; Shikata, S. Design and optimization of planar mesa termination for diamond Schottky barrier diodes. Diam. Relat. Mater. 2013, 36, 51–57. [Google Scholar]
- Brezeanu, M.; Butler, T.; Rupesinghe, N.L.; Amaratunga GA, J.; Rashid, S.J.; Udrea, F.; Avram, M.; Brezeanu, G. Ramp oxide termination structure using high-k dielectrics for high voltage diamond Schottky diodes. Diam. Relat. Mater. 2007, 16, 1020–1024. [Google Scholar] [CrossRef]
- Brezeanu, M.; Avram, M.; Rashid, S.J.; Amaratunga GA, J.; Butler, T.; Rupesinghe, N.L. Termination Structures for Diamond Schottky Barrier Diodes. In Proceedings of the 2006 IEEE International Symposium on Power Semiconductor Devices and IC’s, Naples, Italy, 4–8 June 2006; pp. 1–4. [Google Scholar]
- Gupta, S.K.; Pradhan, N.; Shekhar, C.; Akhtar, J. Design, Fabrication, and Characterization of Ni/4H-SiC (0001) Schottky Diodes Array Equipped with Field Plate and Floating Guard Ring Edge Termination Structures. IEEE Trans. Semicond. Manuf. 2012, 25, 664–672. [Google Scholar] [CrossRef]
- Chang, S.-C.; Wang, S.-J.; Uang, K.-M.; Liou, B.-W. Design and fabrication of high breakdown voltage 4H-SiC Schottky barrier diodes with floating metal ring edge terminations. Solid-State Electron. 2005, 49, 437–444. [Google Scholar] [CrossRef]
- Lee, S.C.; Ha, M.W.; Her, J.C.; Kim, S.S.; Lim, J.Y.; Seo, K.S.; Han, M.K. High breakdown voltage GaN Schottky barrier diode employing floating metal rings on AlGaN/GaN hetero-junction. In Proceedings of the ISPSD ’05, 17th International Symposium on Power Semiconductor Devices and ICs, Santa Barbara, CA, USA, 23–26 May 2005; pp. 247–250. [Google Scholar]
- Synopsys. SentaurusTM Device User Guide; Synopsys Inc.: Mountain View, CA, USA, 2015. [Google Scholar]
- Donato, N.; Antoniou, M.; Napoli, E.; Amaratunga, G.; Udrea, F. On the models used for TCAD simulations of Diamond Schottky Barrier Diodes. In Proceedings of the 2015 International Semiconductor Conference (CAS), Sinaia, Romania, 12–14 October 2015; pp. 223–226. [Google Scholar]
- Donato, N.; Pagnano, D.; Napoli, E.; Longobardi, G.; Udrea, F. Design of a normally-off diamond JFET for high power integrated applications. Diam. Relat. Mater. 2017, 78, 73–82. [Google Scholar] [CrossRef] [Green Version]
- Nawawi, A. Study of Single Crystal Diamond Schottky Barrier Diodes for Power Electronics Applications. Ph.D. Thesis, Nanyang Technological University, Singapore, 2014. [Google Scholar]
- Shirafuji, J.; Sugino, T. Electrical properties of diamond surfaces. Diam. Relat. Mater. 1996, 5, 706–713. [Google Scholar] [CrossRef]
- Rouger, N. Electric field distribution and voltage breakdown modeling for any PN junction. COMPEL 2015, 35, 137–156. [Google Scholar] [CrossRef]

| Device | Vertical SBD | Pseudo-Vertical SBD | Schottky pn Diode | PiN Diode |
|---|---|---|---|---|
| Conduction type | Unipolar | Unipolar | Unipolar | Bipolar |
| BV2/RonS (MW∙cm−2) | 25 [13] | 166.7 [5] | 30.25 [11] | 2.9 [12] |
| BV (V) | 1.8 kV [10] | 1.6 kV [14] | 55 V [11] | 920 V [12] |
| On state current density (A∙cm−2) | 3 kA∙cm−2 at V = 8 V [10] | 1 kA∙cm−2 at V = 6 V [5] | 60 kA∙cm−2 at V = 6 V [11] | 15 kA∙cm−2 at 35 V [15] |
| Switching speed | 1.5 V∙ns−1 at 20 A∙µs−1 [8] | 16 V∙ns−1 100 V and 200 mA [16] | Turn off speed ≈ 10 ns [6], lack of information | 6 V∙ns−1 at 4 A∙µs−1 [7] |
| 1 kV | 6.5 kV | 10 kV | |
|---|---|---|---|
| Drift region Boron doping | 1.8 × 1017 cm−3 | 5.5 × 1015 cm−3 | 2.7 × 1015 cm−3 |
| Drift region thickness in NPT condition | 1.75 µm | 27 µm | 48 µm |
| RonS at Room Temperature | 0.85 mΩ∙cm2 | 70 mΩ∙cm2 | 180 mΩ∙cm2 |
| “Optimal” Temperature minimizing RonS | 660 K | 540 K | 500 K |
| Design Drift #a | Design Drift #b | Design Drift #c | Design Drift #d | |
|---|---|---|---|---|
| 1 kV NPT | 1 kV Optimal PT | 1 kV lower doping | 1 kV lightly doped | |
| Drift region Boron doping | 1.8 × 1017 cm−3 | 1.5 × 1017 cm−3 | 1.5 × 1016 cm−3 | 2.1 × 1015 cm−3 |
| Drift region thickness in NPT condition | 1.75 µm | 1.51 µm | 1.35 µm | 1.35 µm |
| Peak electric Field | 10 MV/cm | 9.3 MV/cm | 6.75 MV/cm | 6.5 MV/cm |
| RonS at Room Temperature | 0.85 mΩ∙cm2 | 0.77 mΩ∙cm2 | 2 mΩ∙cm2 | 5.5 mΩ∙cm2 |
| RonS at optimal temperature | 0.195 mΩ∙cm2 | 0.183 mΩ∙cm2 | 0.6 mΩ∙cm2 | 2 mΩ∙cm2 |
| “Optimal” Temperature minimizing RonS | 660 K | 650 K | 560 K | 490 K |
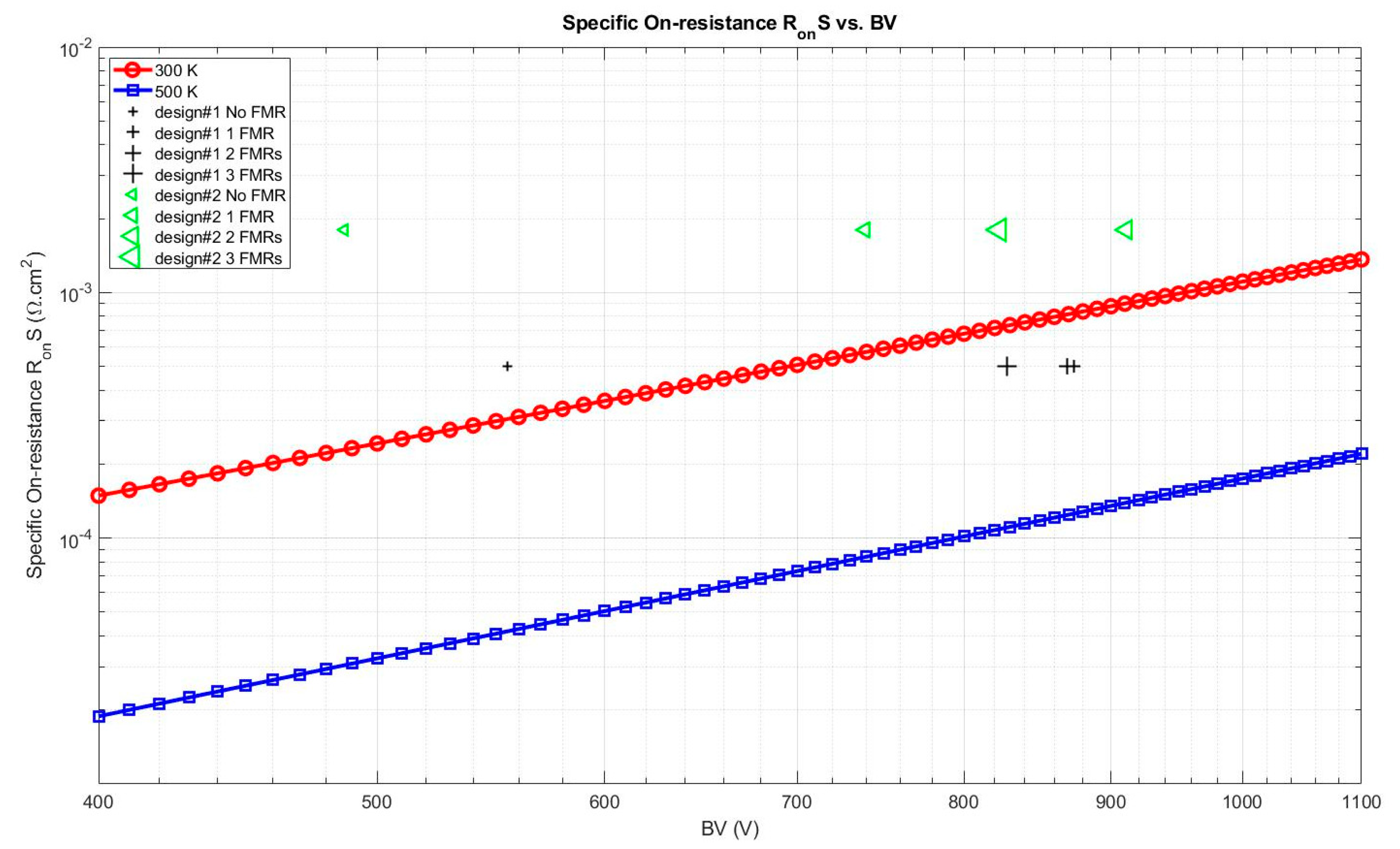
| 1 kV Design | #1 | #2 |
|---|---|---|
| Drift layer thickness (µm) | 1.5 | 1.5 |
| Doping (cm−3) | 1.5 × 1016 | 2.1 × 1015 |
| 1D BV (kV) | 1.07 | 1.07 |
| RonS300 K (mΩ∙cm2) | 2 | 6.3 |
| RonS500 K (mΩ∙cm2) | 0.5 | 1.8 |
| Design #1 | Design #2 | |||||
|---|---|---|---|---|---|---|
| Number of ring | 1 | 2 | 3 | 1 | 2 | 3 |
| BV improvement @ 500 K (%) | 57.4 | 56.6 | 49.2 | 51.7 | 87 | 69 |
| Optimized BV @ 500 K (V) | 874 | 869 | 828 | 739 | 911 | 823 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouger, N.; Maréchal, A. Design of Diamond Power Devices: Application to Schottky Barrier Diodes. Energies 2019, 12, 2387. https://doi.org/10.3390/en12122387
Rouger N, Maréchal A. Design of Diamond Power Devices: Application to Schottky Barrier Diodes. Energies. 2019; 12(12):2387. https://doi.org/10.3390/en12122387
Chicago/Turabian StyleRouger, Nicolas, and Aurélien Maréchal. 2019. "Design of Diamond Power Devices: Application to Schottky Barrier Diodes" Energies 12, no. 12: 2387. https://doi.org/10.3390/en12122387





