Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery
Abstract
1. Introduction
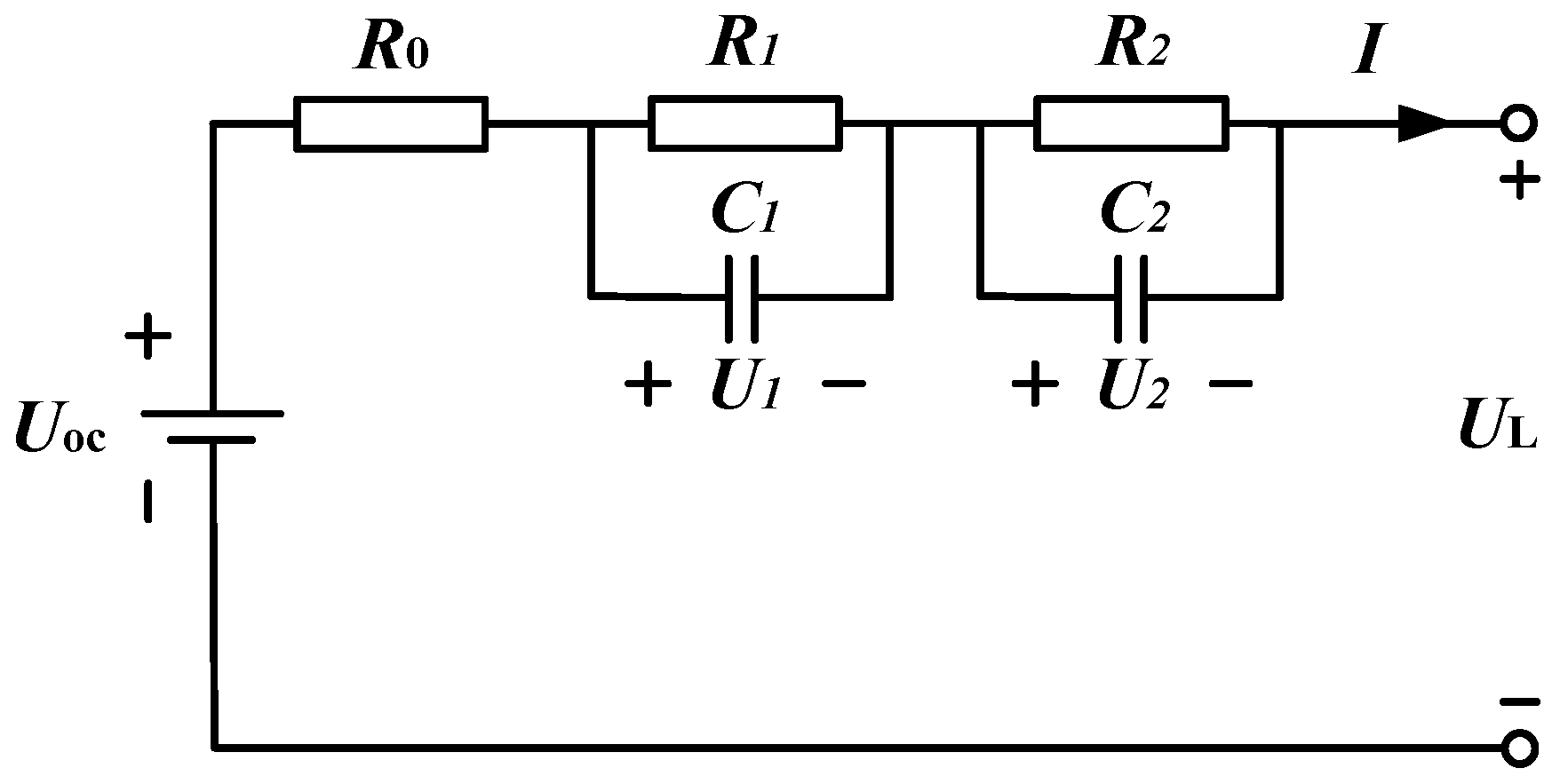
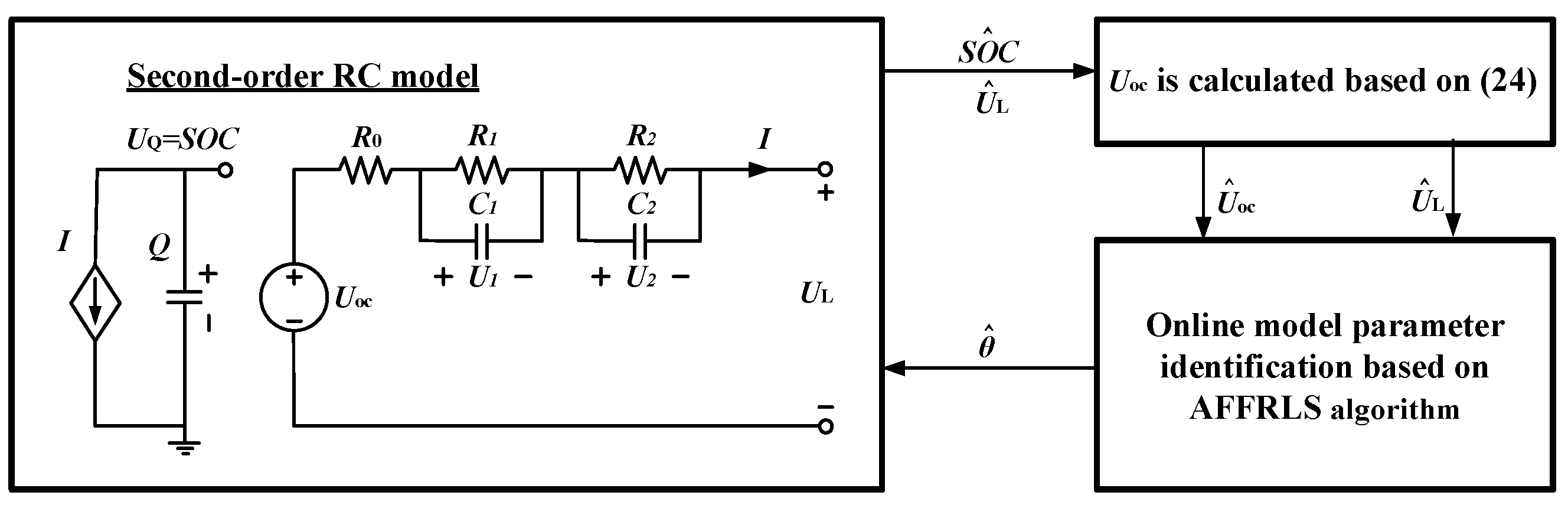
2. Lithium-Ion Battery Modeling
3. Online Parameter Identification Principle
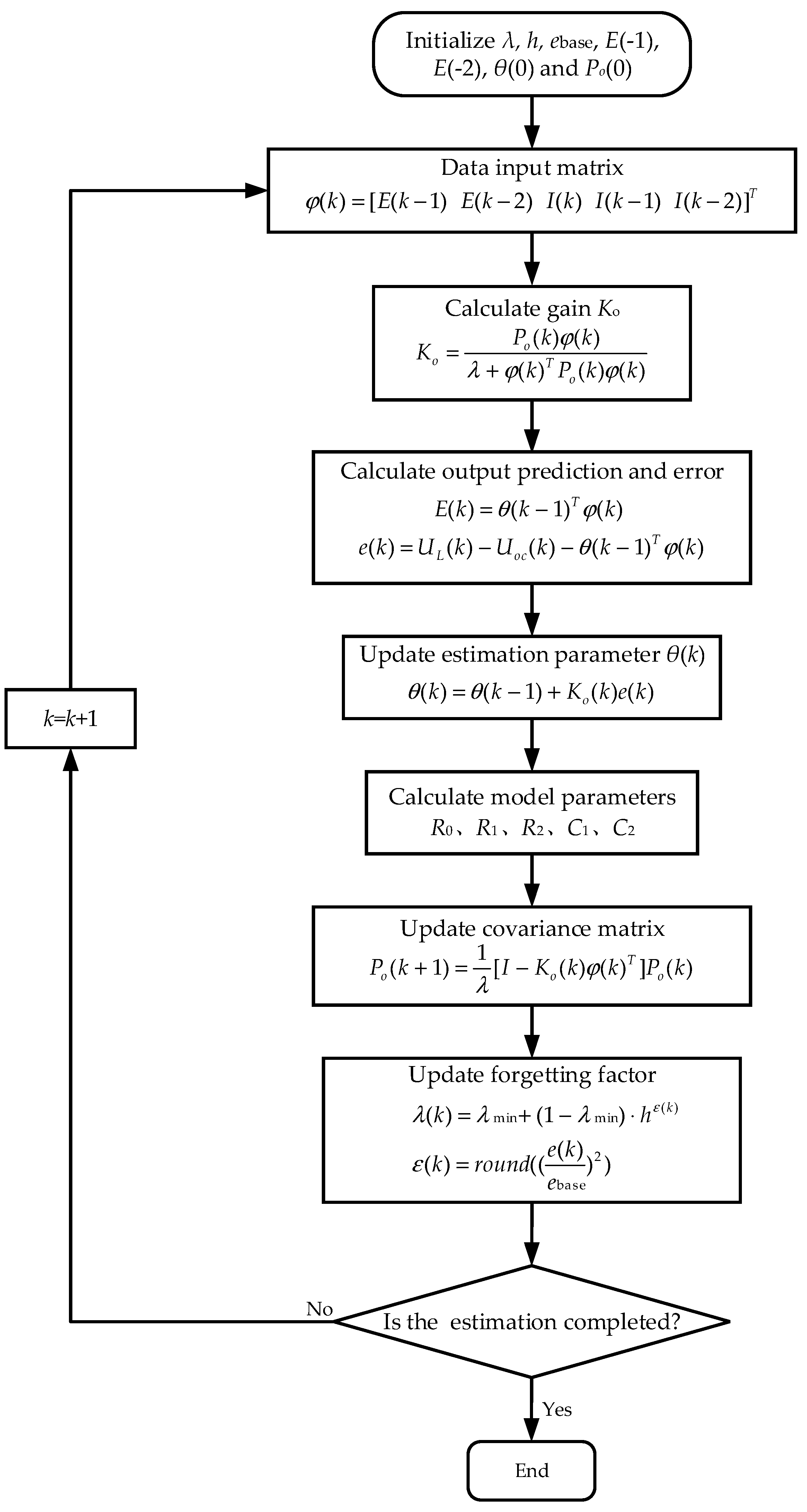
3.1. Forgetting Factor Recursive Least Square Method
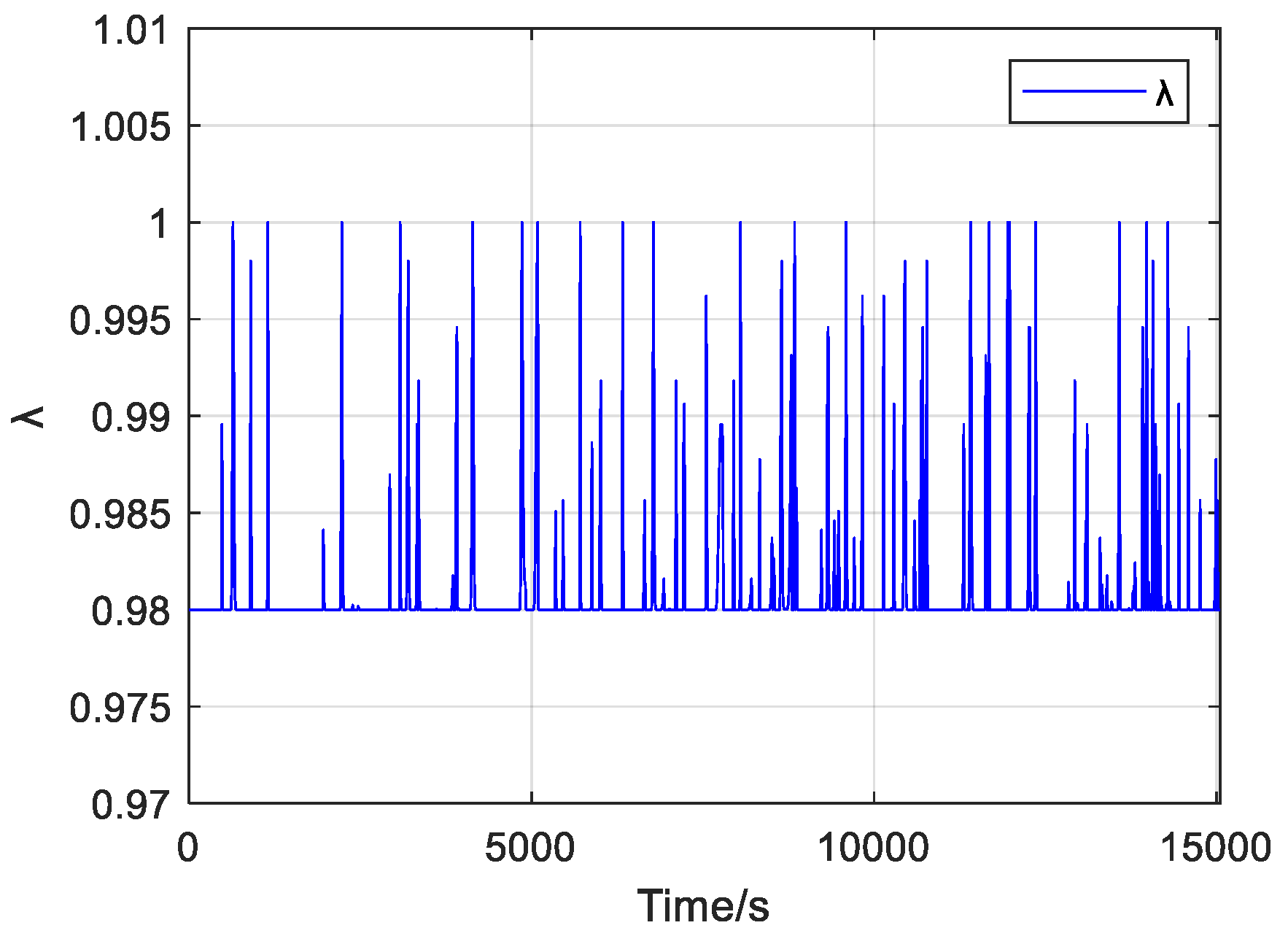
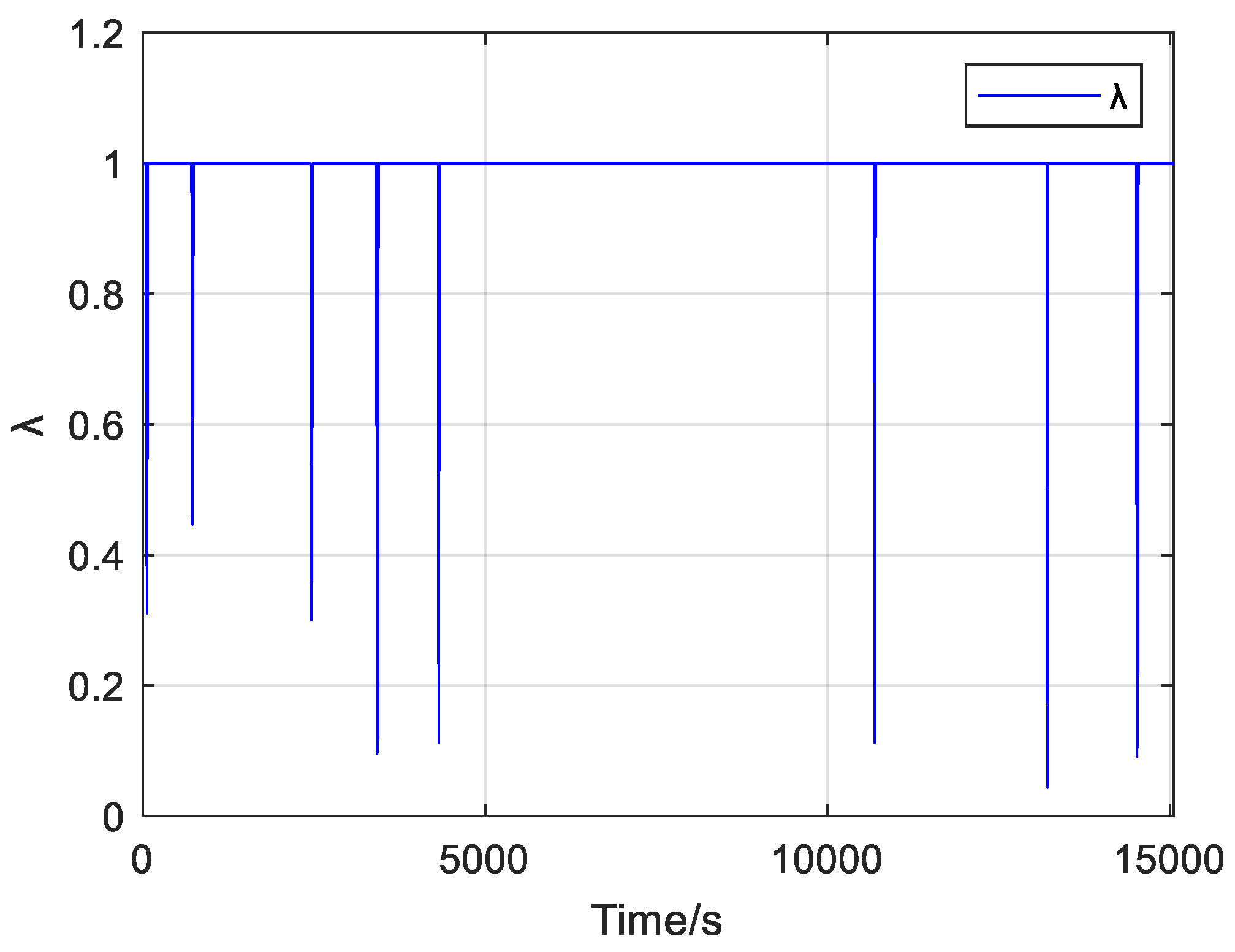
3.2. Adaptive Forgetting Factor Analysis
3.3. Implementation of Online Parameter Identification Algorithm Based on AFFRLS
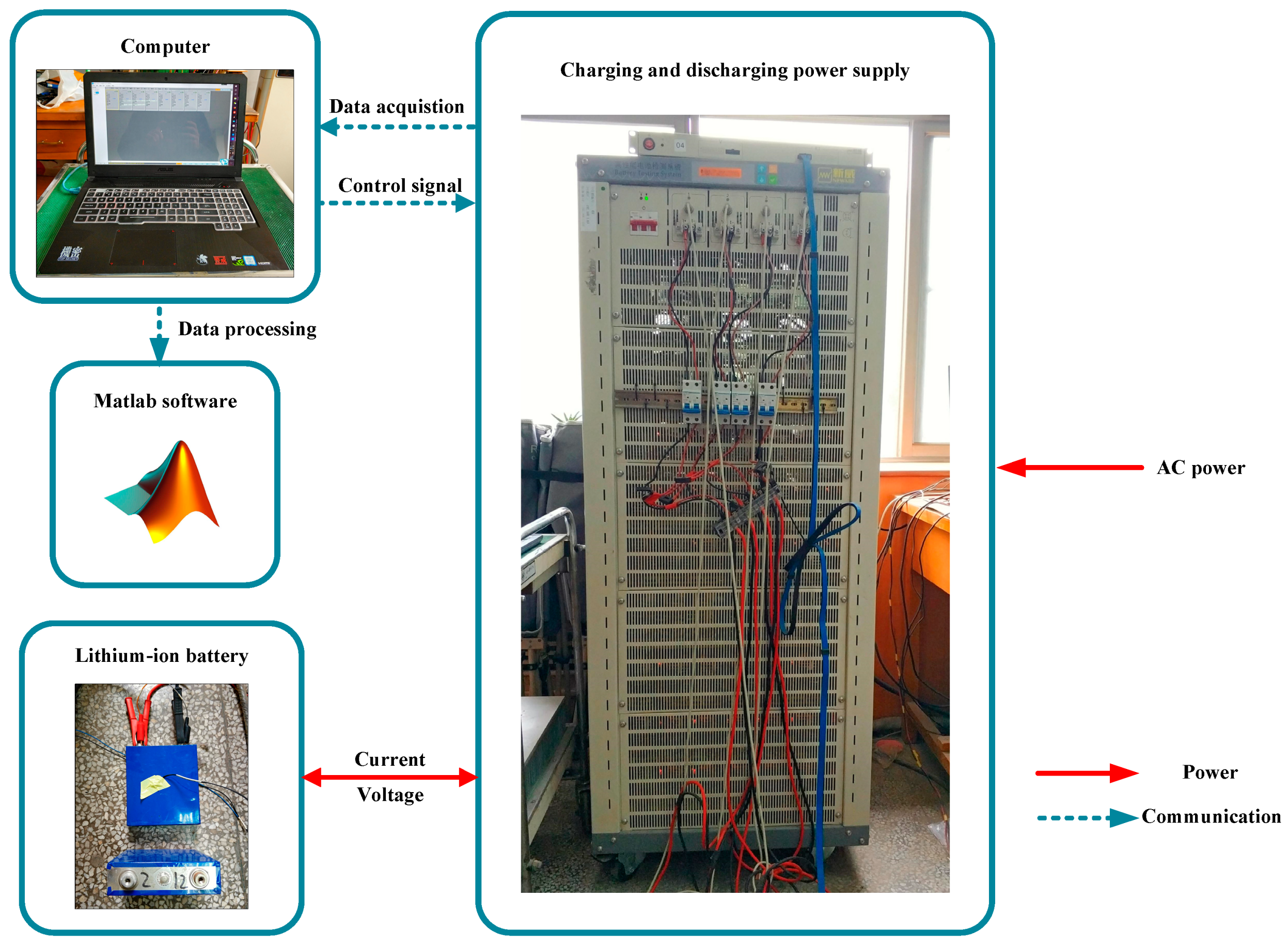
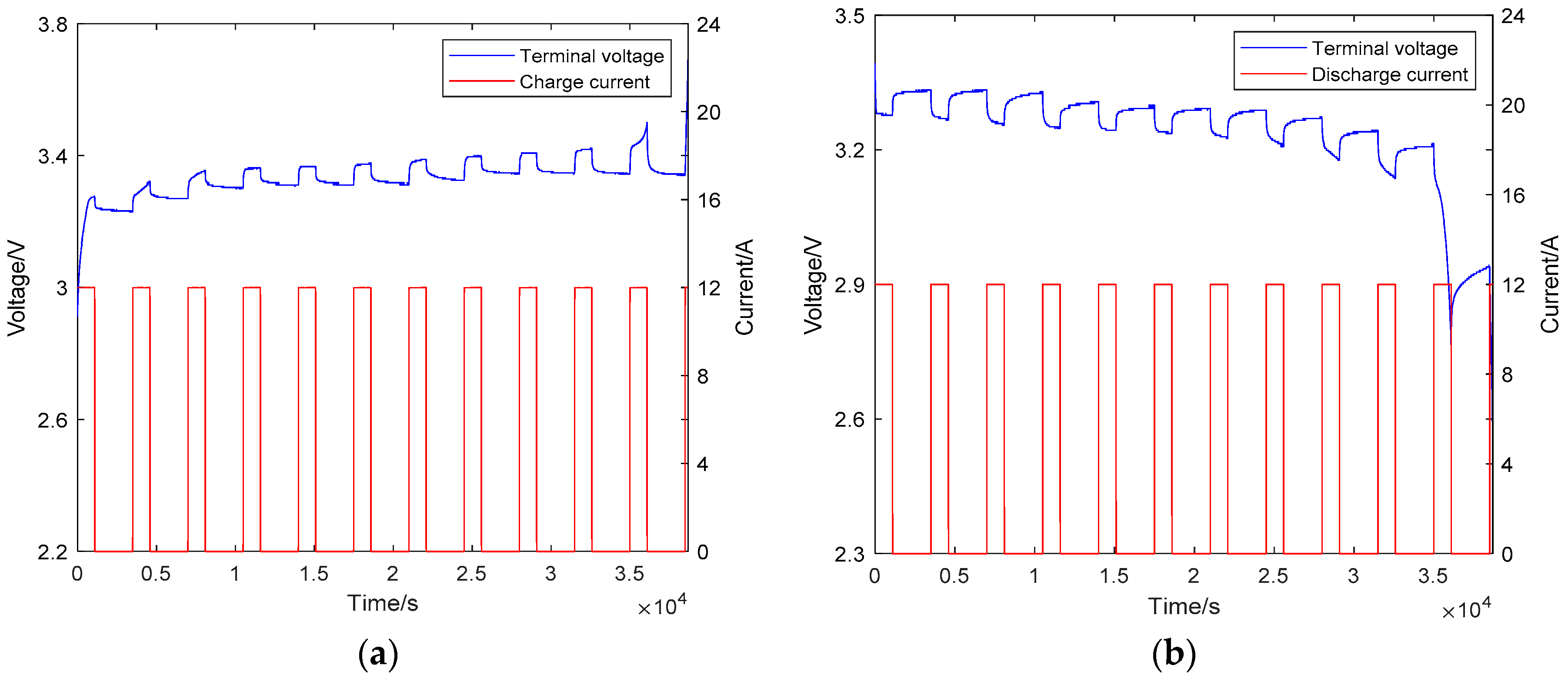
4. Experimental Verification and Analysis
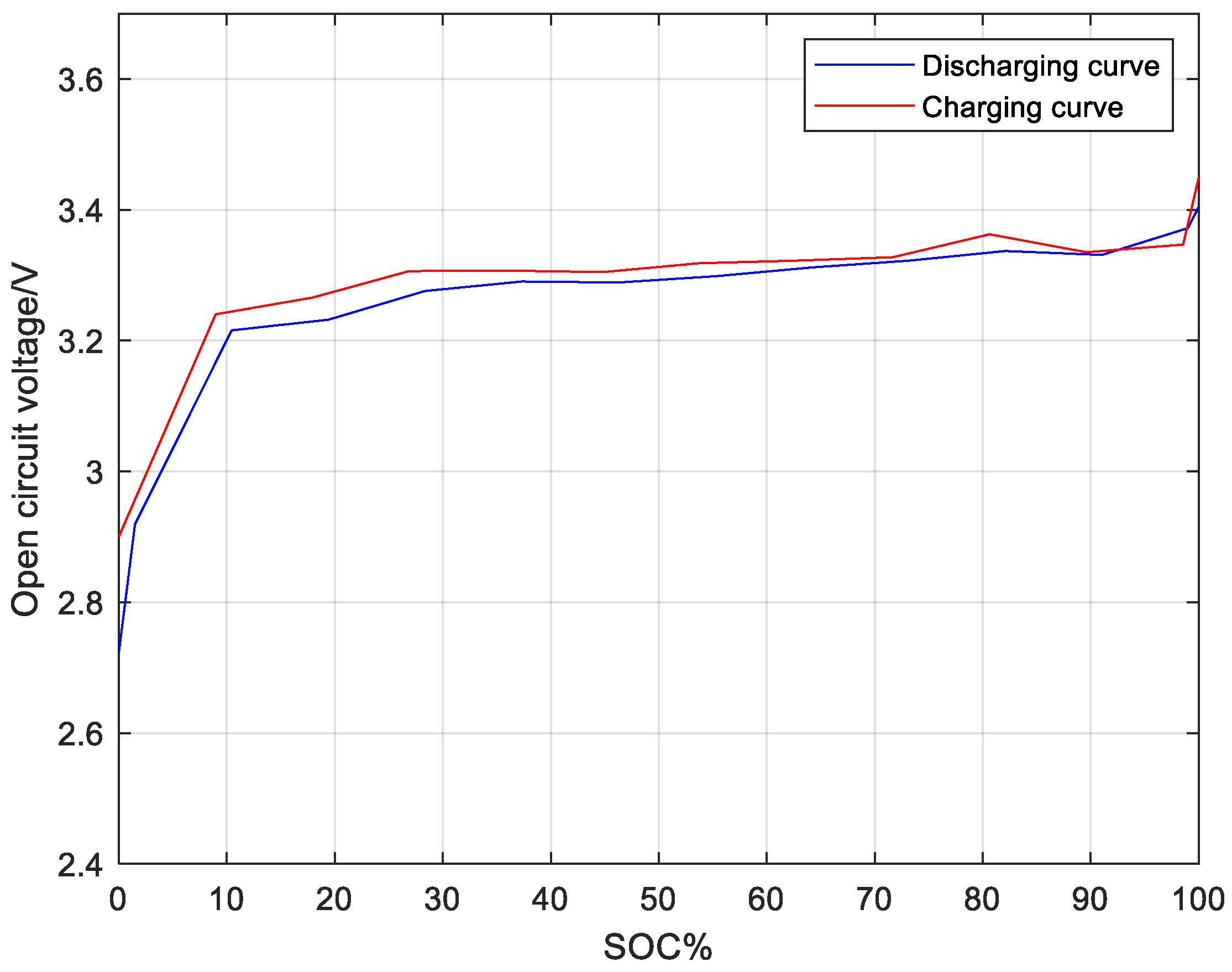
4.1. OCV-SOC Curve
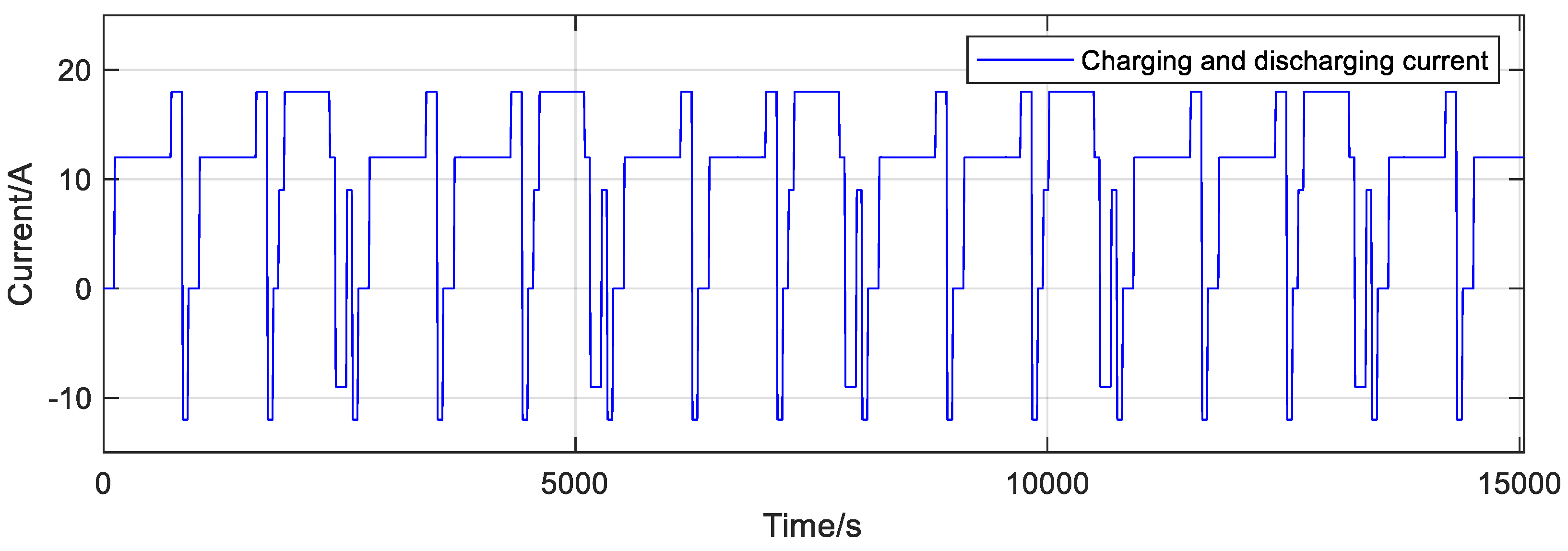
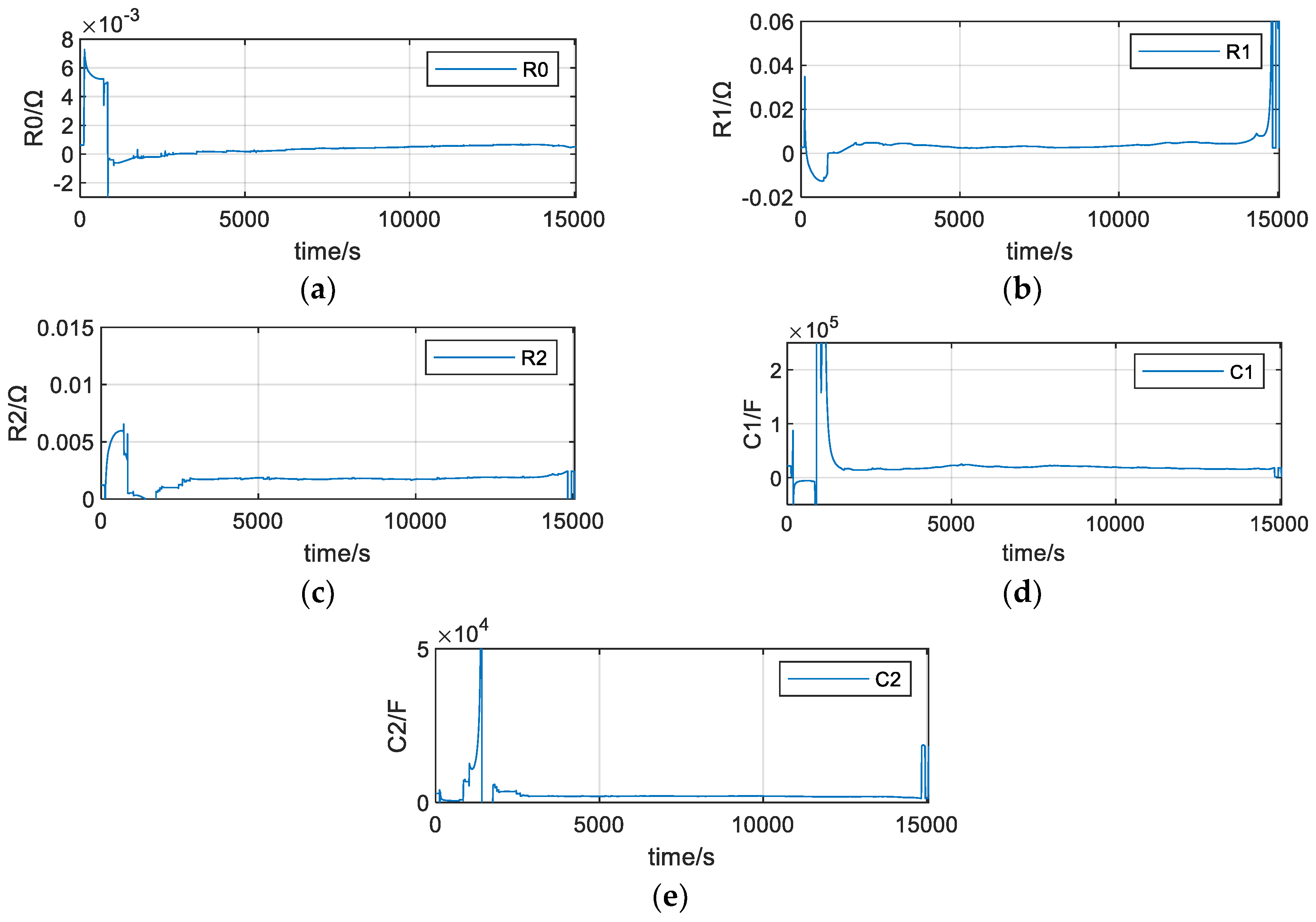
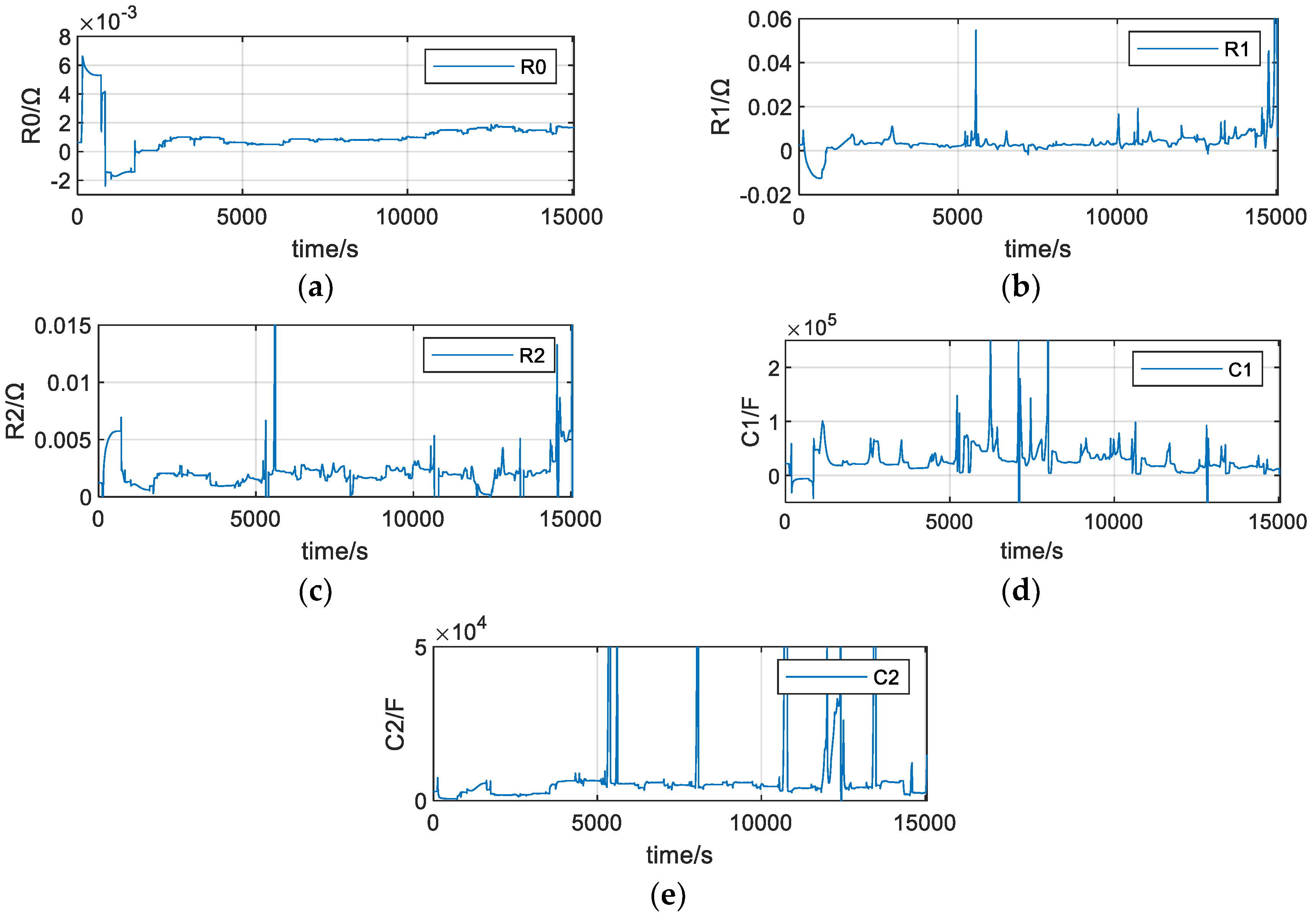
4.2. Online Parameter Identification of Lithium-Ion Battery Equivalent Model
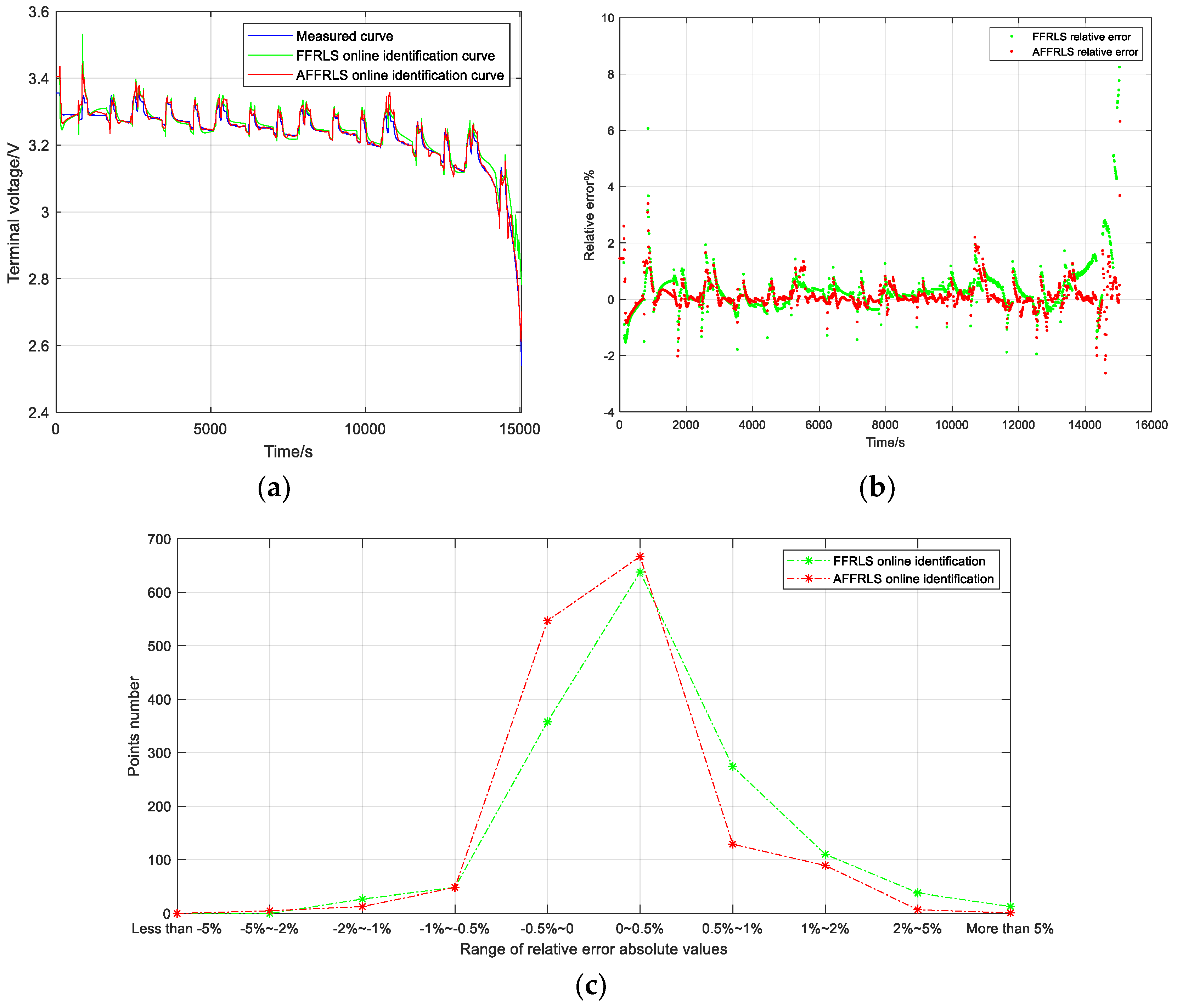
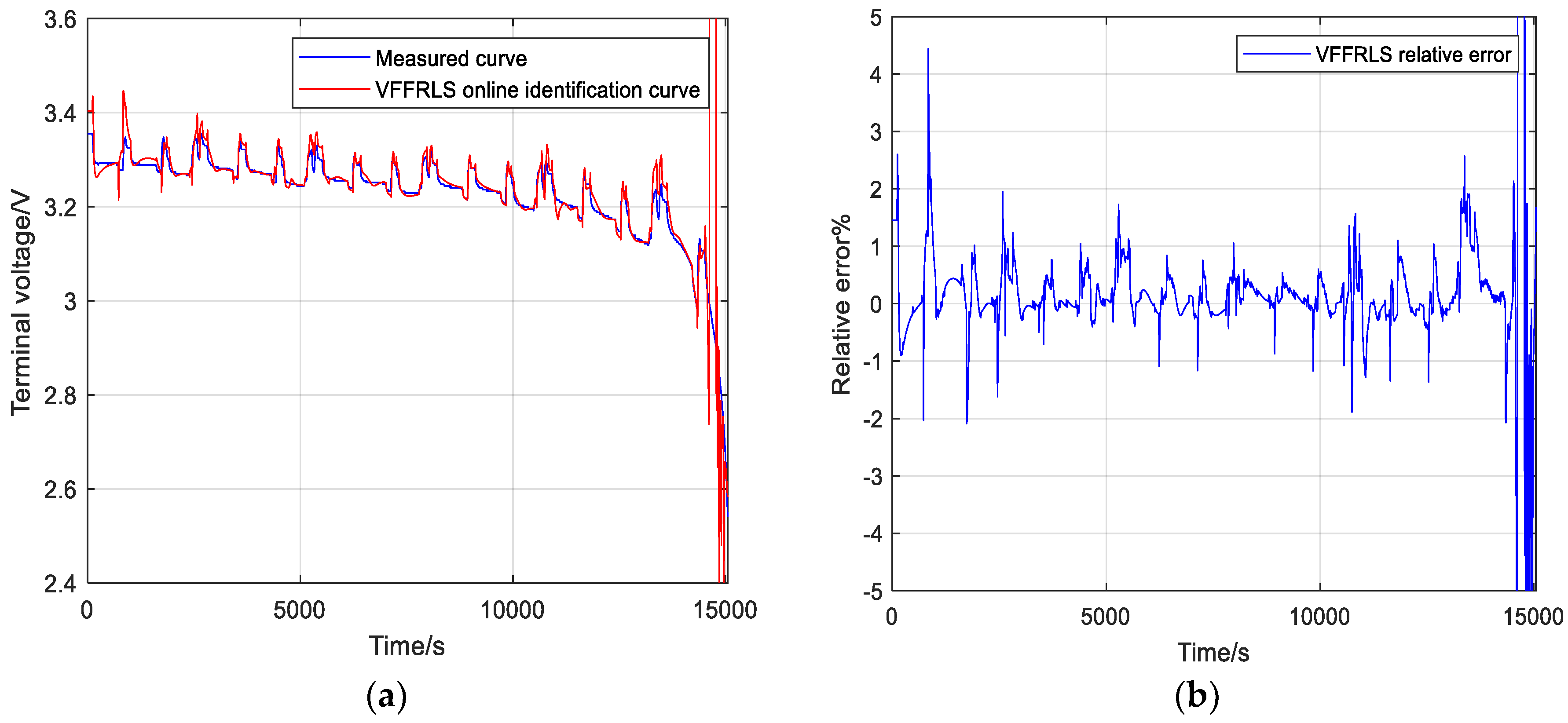
4.3. Comparative Analysis of the Prediction Effect of the Lithium-Ion Battery Terminal Voltage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hannan, M.A.; Hoque, M.M.; Hussain, A.; Yusof, Y.; Ker, P.J. State-of-the-art and energy management system of lithium-ion batteries in electric vehicle applications: Issues and recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Xu, J.; Mi, C.C.; Cao, B.; Deng, J.; Chen, Z.; Li, S. The state of charge estimation of lithium-ion batteries based on a proportional-integral observer. IEEE Trans. Veh. Technol. 2014, 63, 1614–1621. [Google Scholar]
- Paschero, M.; Storti, G.L.; Rizzi, A.; Mascioli, F.M.F.; Rizzoni, G. A novel mechanical analogy based battery model for SoC estimation using a multi-cell EKF. IEEE Trans. Sustain. Energy 2016, 7, 1695–1702. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Cheng, X.; Lu, Z.Y.; Gu, D.J. SOC estimation of lithium-ion batteries with AEKF and wavelet transform matrix. IEEE Trans. Power Electron. 2017, 32, 7626–7634. [Google Scholar] [CrossRef]
- Hardik, K.; Jesse, T.; Taha, S.U. Comparison of lead-acid and lithium ion batteries for stationary storage in off-grid energy systems. In Proceedings of the 4th IET Clean Energy and Technology Conference (CEAT 2016), Kuala Lumpur, Malaysia, 14–15 November 2016; pp. 1–7. [Google Scholar]
- Daniel, R.; Alfredo, P.; Marco, R.; Michele, O. 12V battery modeling: Model development, simulation and validation. In Proceedings of the 2017 International Conference of Electrical and Electronic Technologies for Automotive, Torino, Italy, 15–16 June 2017; pp. 1–5. [Google Scholar]
- Yang, J.; Wei, X.; Dai, H.; Zhu, J.; Xu, X. Lithium-ion battery internal resistance model based on the porous electrode theory. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Liu, X.; Li, W.; Zhou, A. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Putra, W.S.; Dewangga, B.R.; Cahyadi, A.; Wahyunggoro, O. Current estimation using Thevenin battery model. In Proceedings of the Joint International Conference on Electric Vehicular Technology and Industrial, Mechanical, Electrical and Chemical Engineering (ICEVT & IMECE), Surakarta, Indonesia, 4–5 November 2015; pp. 5–9. [Google Scholar]
- Ceraolo, M. New dynamical models of lead-acid batteries. IEEE Trans. Power Syst. 2000, 15, 1184–1190. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J.X. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Chen, S.; Fu, Y.; Mi, C.C. State of charge estimation of lithium ion batteries in electric drive vehicles using extended Kalman filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Wang, X.Y.; Yuan, H.M. Estimation for SOC of Li-ion battery based on two-order RC temperature model. In Proceedings of the 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; pp. 2158–2297. [Google Scholar]
- Diniz, P.S.R. Fundamentals of adaptive filtering. Adaptive Filtering; Springer: Boston, MA, USA, 2013; pp. 13–78. [Google Scholar]
- Tian, Y.; Zeng, Z.; Tian, J.; Zhou, S.; Hu, C. Joint estimation of model parameters and SOC for lithium-ion batteries in wireless charging systems. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 263–267. [Google Scholar]
- Albu, F. Improved variable forgetting factor recursive least square algorithm. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV), Guangzhou, China, 5–7 December 2012; pp. 1789–1793. [Google Scholar]
- Leung, S.H.; So, C.F. Gradient-based variable forgetting factor RLS algorithm in time-varying environments. IEEE Trans. Signal Process. 2005, 53, 3141–3150. [Google Scholar] [CrossRef]
- Chan, S.C.; Chu, Y.J. A new state-regularized QRRLS algorithm with a variable forgetting factor. IEEE Trans. Cir. Syst. II Express Briefs 2012, 59, 183–187. [Google Scholar] [CrossRef]
- Chen, Q.; Gu, Y.; Ding, F. Data filtering based recursive least squares estimation algorithm for a class of Wiener nonlinear systems. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 1848–1852. [Google Scholar]
- Chen, X.P.; Shen, W.X.; Dai, M.X.; Cao, Z.W.; Jin, J.; Ajay, K. Robust adaptive sliding-mode observer using RBF neural network for lithium-ion battery state of charge estimation in electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1936–1947. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Rated capacity (Ah) | 36 |
| Nominal voltage (V) | 3.2 |
| Standard charging/discharging current (A) | 12 |
| Charging cut-off voltage (V) | 3.7 |
| Discharging cut-off voltage (V) | 2.5 |
| Maximum continuous discharging current (A) | 108 |
| Item | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intermittent constant current charging experiments with 0.33 C standard current | |||||||||||||
| SOC/% | 0 | 8.96 | 17.92 | 26.88 | 35.84 | 44.80 | 53.76 | 62.72 | 71.68 | 80.64 | 89.60 | 98.56 | 100 |
| OCV/V | 2.902 | 3.233 | 3.270 | 3.304 | 3.311 | 3.311 | 3.311 | 3.326 | 3.344 | 3.348 | 3.344 | 3.341 | 3.615 |
| Intermittent constant current discharging experiments with 0.33 C standard current | |||||||||||||
| SOC/% | 0 | 1.49 | 10.45 | 19.40 | 28.36 | 37.31 | 46.27 | 55.22 | 64.18 | 73.13 | 82.09 | 91.04 | 100 |
| OCV/V | 2.683 | 2.939 | 3.214 | 3.244 | 3.270 | 3.289 | 3.292 | 3.300 | 3.307 | 3.330 | 3.333 | 3.333 | 3.393 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies 2019, 12, 2242. https://doi.org/10.3390/en12122242
Sun X, Ji J, Ren B, Xie C, Yan D. Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies. 2019; 12(12):2242. https://doi.org/10.3390/en12122242
Chicago/Turabian StyleSun, Xiangdong, Jingrun Ji, Biying Ren, Chenxue Xie, and Dan Yan. 2019. "Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery" Energies 12, no. 12: 2242. https://doi.org/10.3390/en12122242
APA StyleSun, X., Ji, J., Ren, B., Xie, C., & Yan, D. (2019). Adaptive Forgetting Factor Recursive Least Square Algorithm for Online Identification of Equivalent Circuit Model Parameters of a Lithium-Ion Battery. Energies, 12(12), 2242. https://doi.org/10.3390/en12122242





