Figure 1.
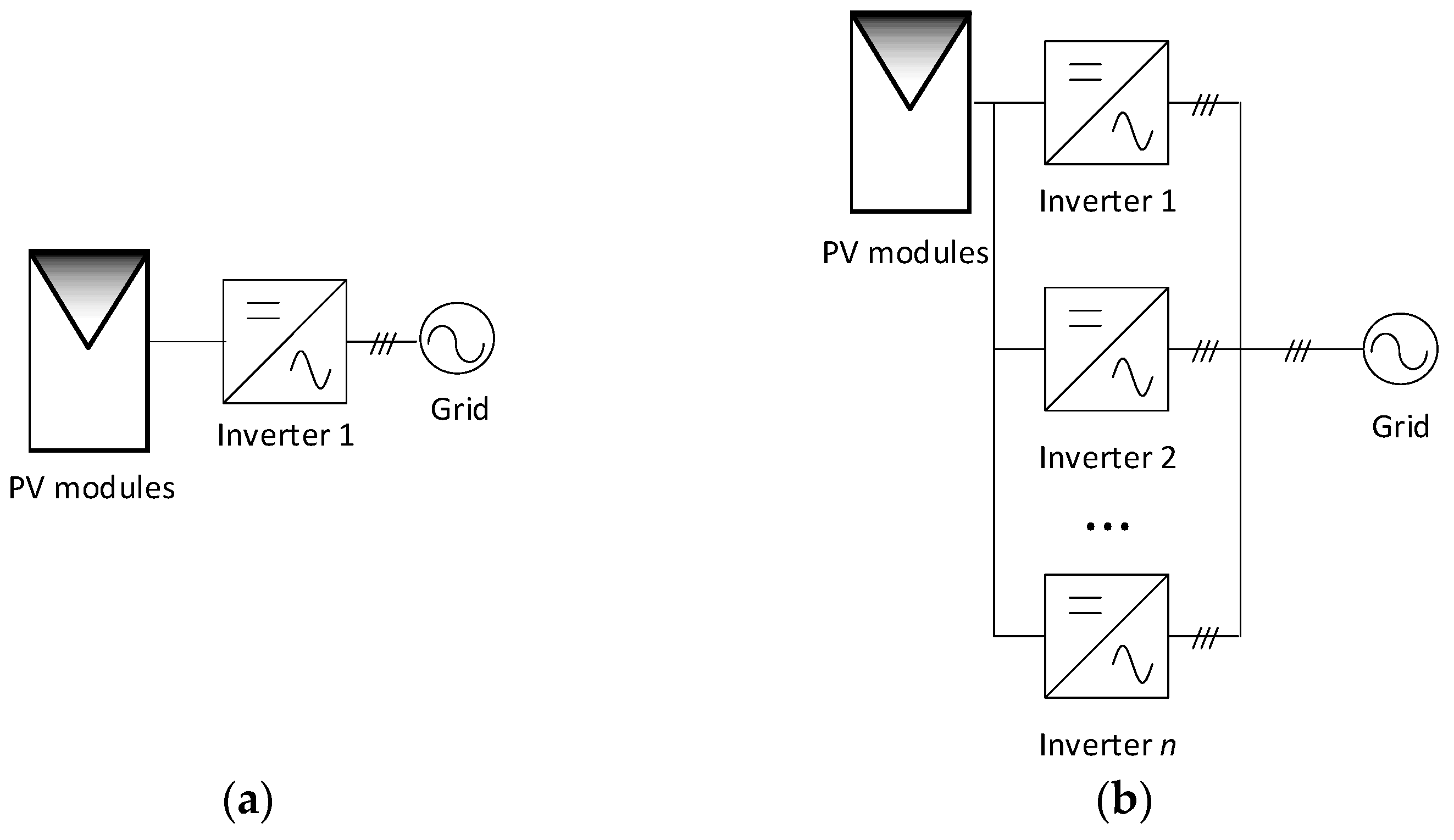
Topologies of high power central inverters. (a) Centralized inverter composed by a single power stage; (b) centralized inverter composed by n parallel modules.
Figure 1.
Topologies of high power central inverters. (a) Centralized inverter composed by a single power stage; (b) centralized inverter composed by n parallel modules.
Figure 2.
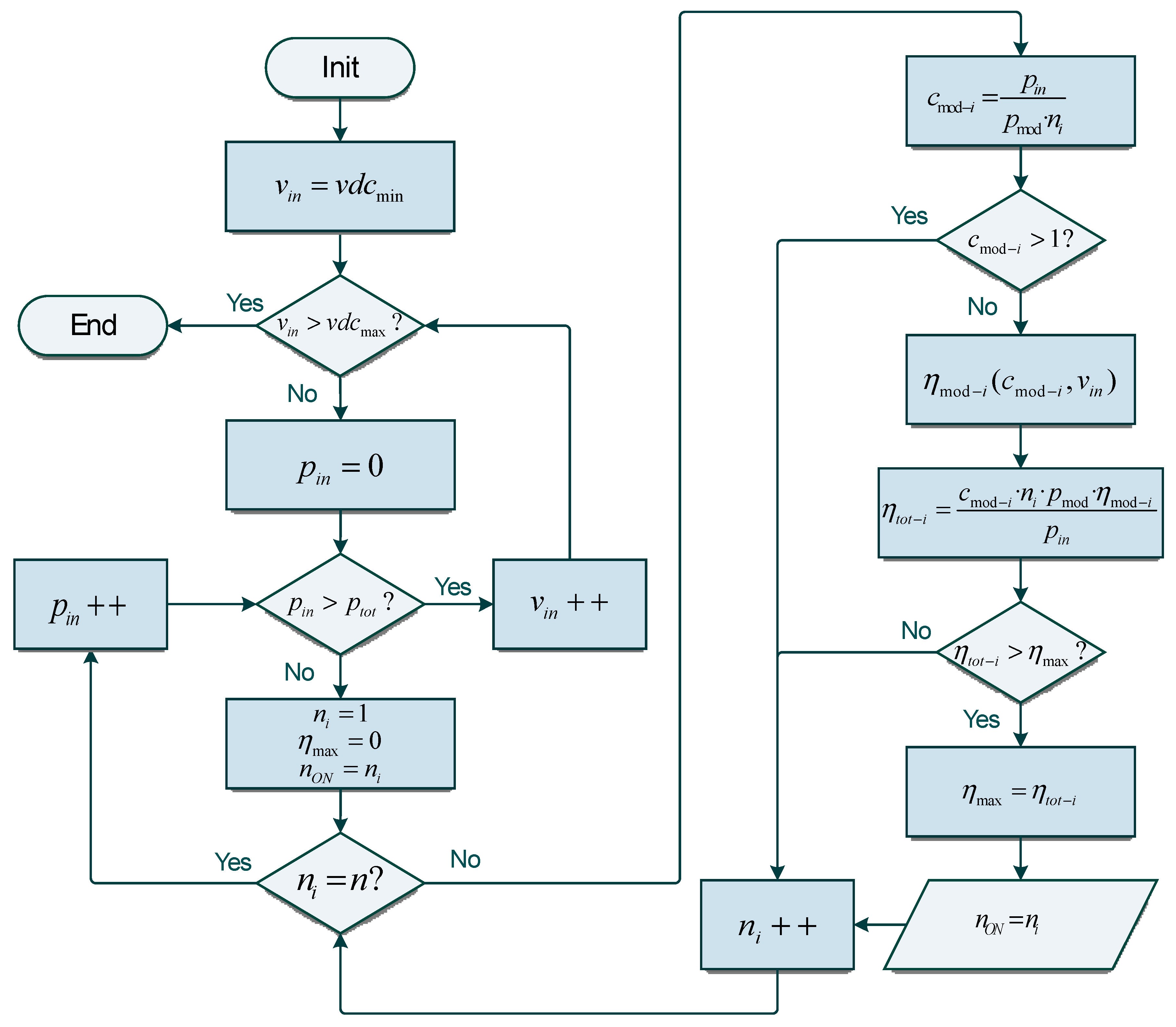
Efficiency-oriented algorithm.
Figure 2.
Efficiency-oriented algorithm.
Figure 3.
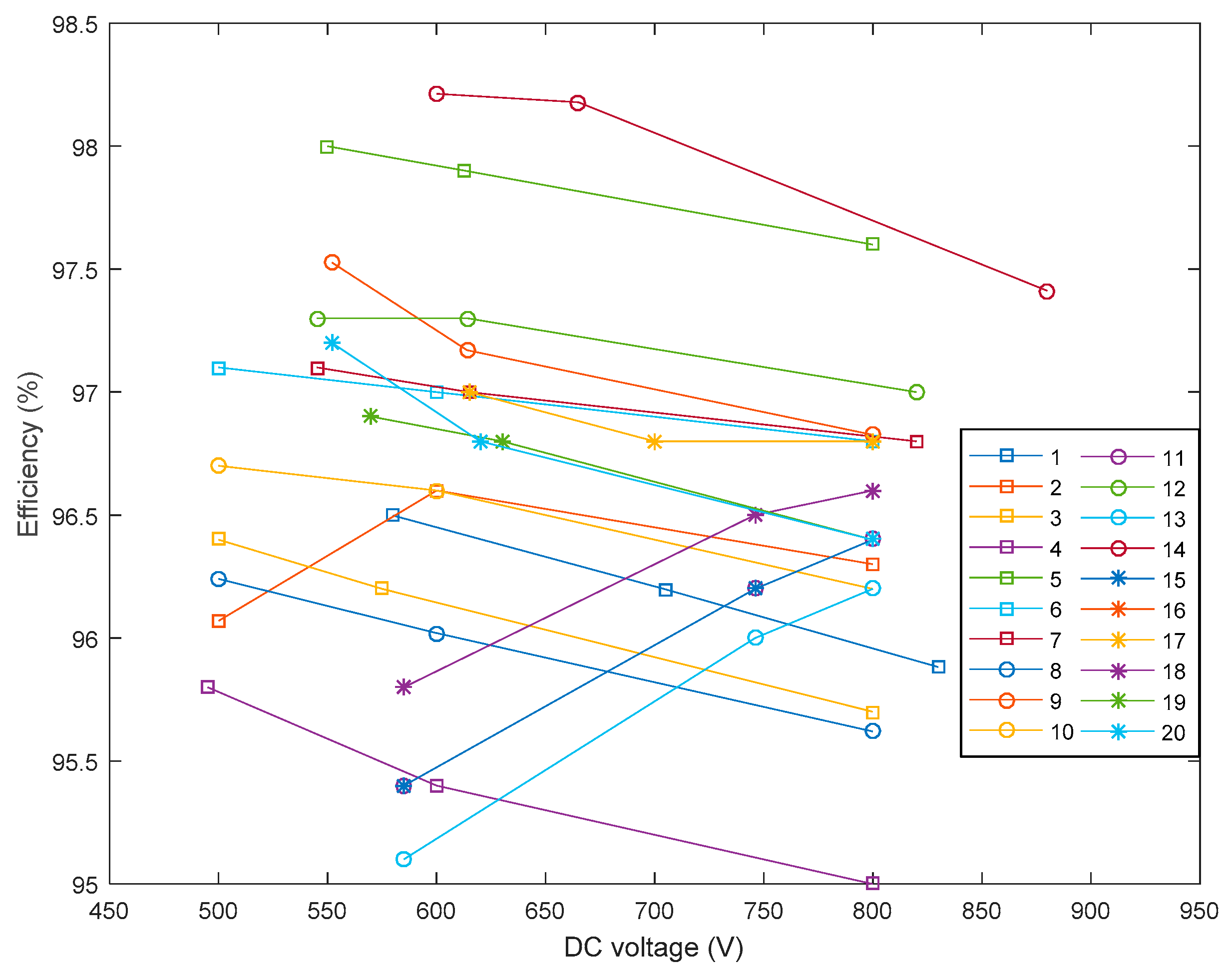
Relationship between the input voltage and the efficiency of the inverters extracted from the CEC Grid Support Inverters List.
Figure 3.
Relationship between the input voltage and the efficiency of the inverters extracted from the CEC Grid Support Inverters List.
Figure 4.
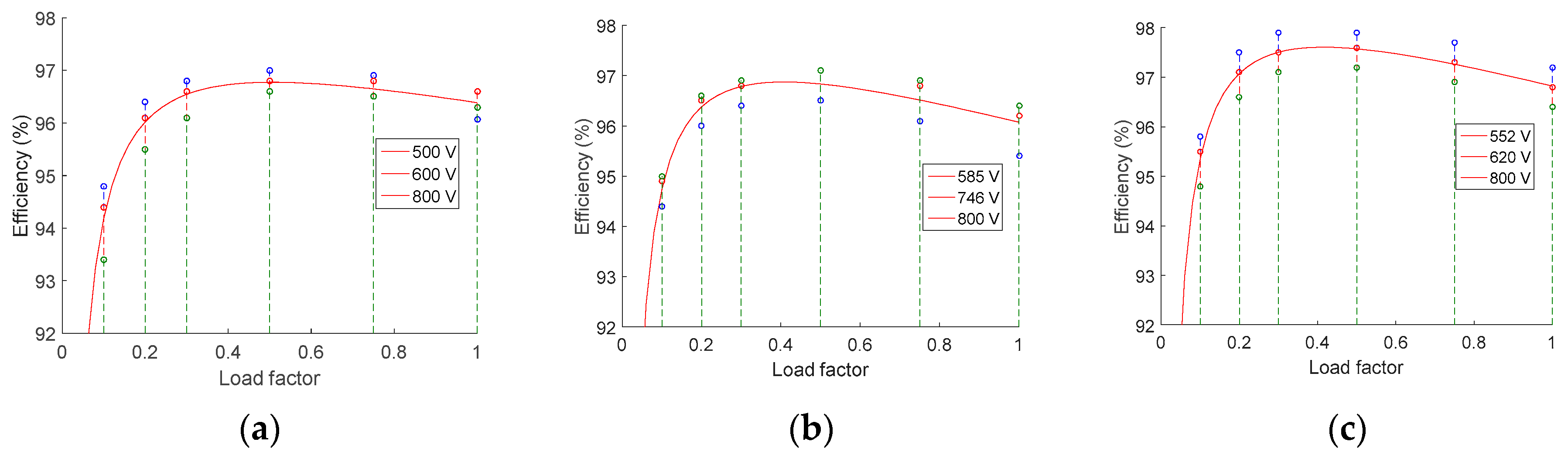
Efficiency curves calculated by means of the Jantsch model. (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US (c) Power Electronics FS0900CU.
Figure 4.
Efficiency curves calculated by means of the Jantsch model. (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US (c) Power Electronics FS0900CU.
Figure 5.
Efficiency curves calculated by means of the Dupont model. (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US. (c) Power Electronics FS0900CU.
Figure 5.
Efficiency curves calculated by means of the Dupont model. (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US. (c) Power Electronics FS0900CU.
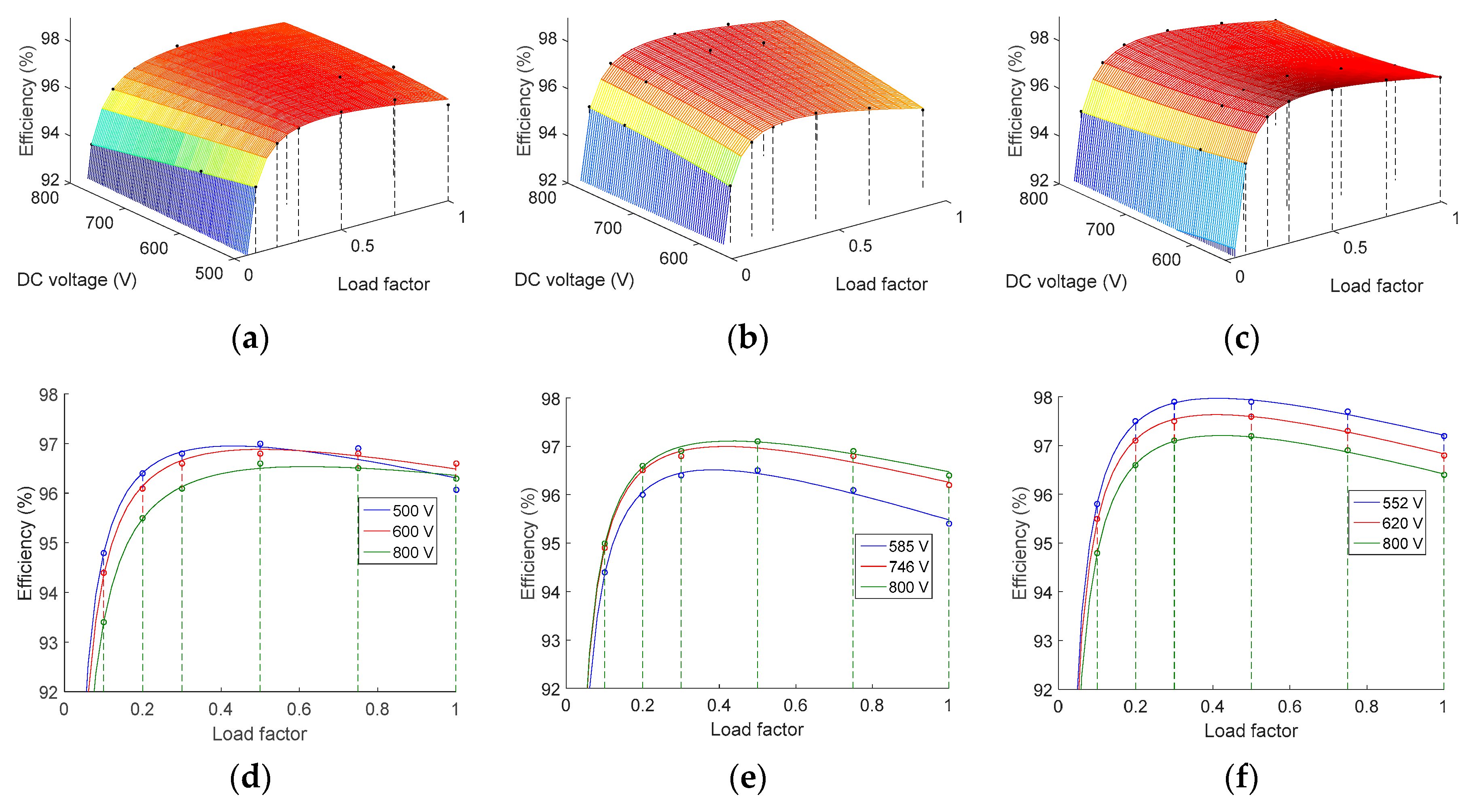
Figure 6.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Rampinelli model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 6.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Rampinelli model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
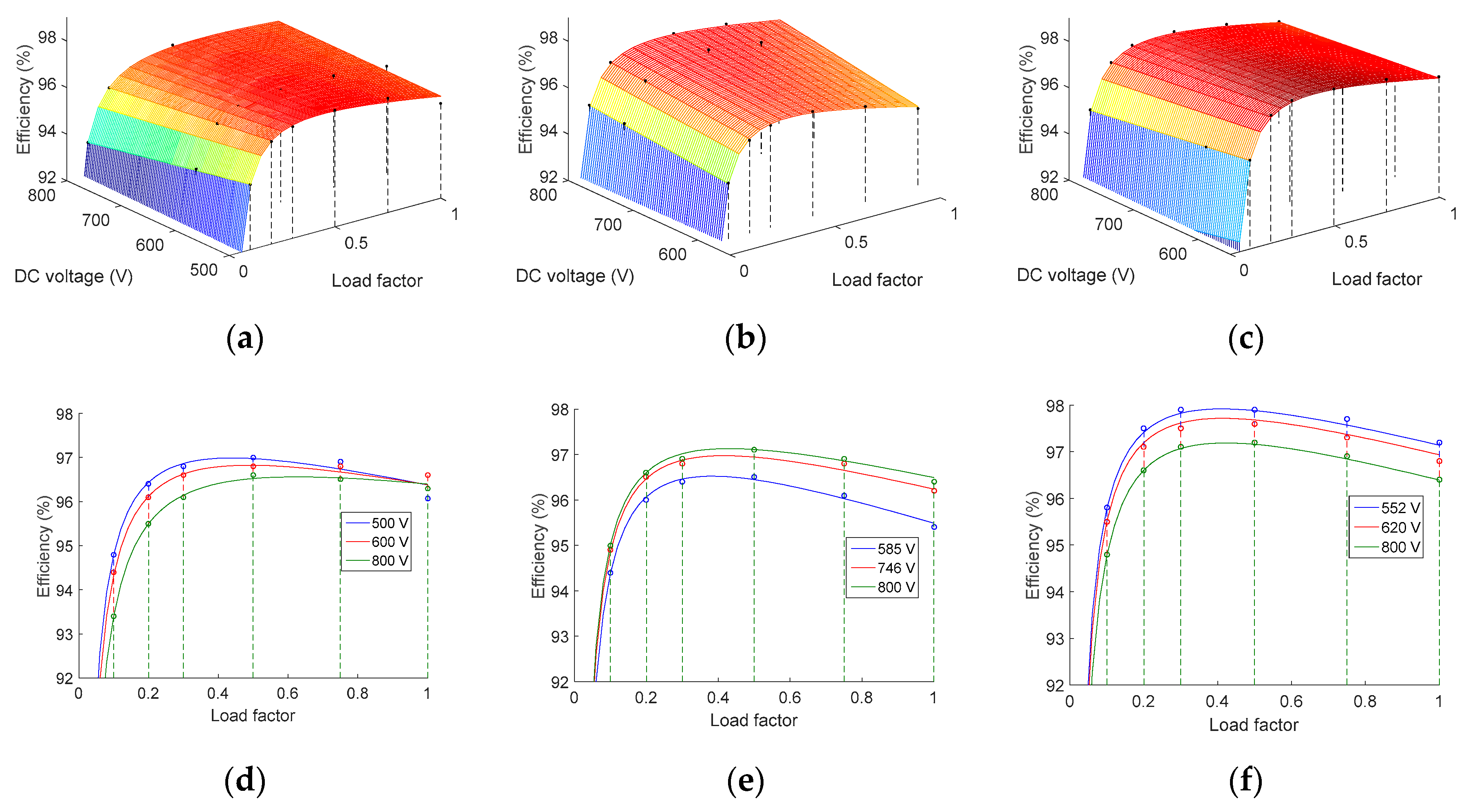
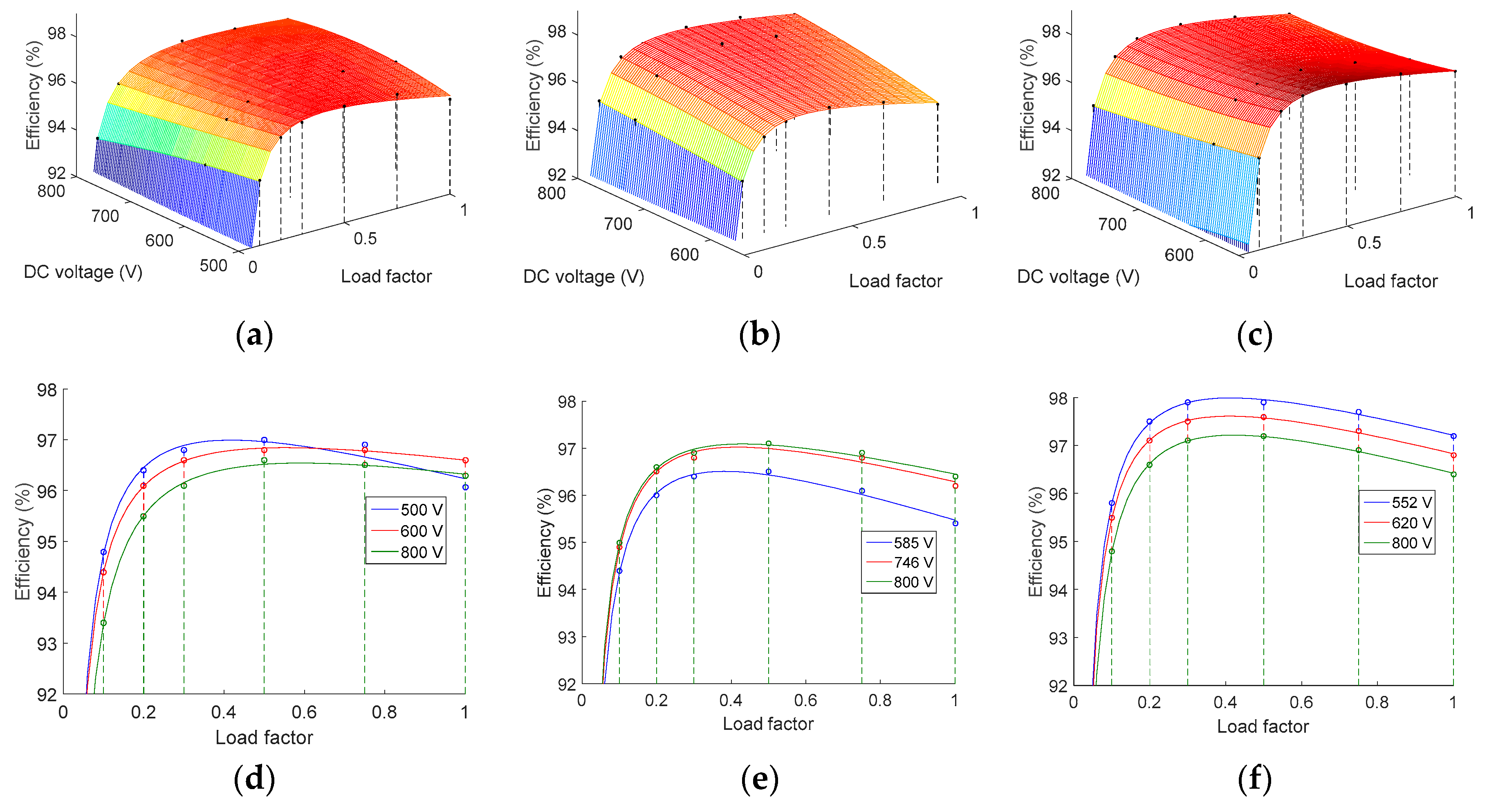
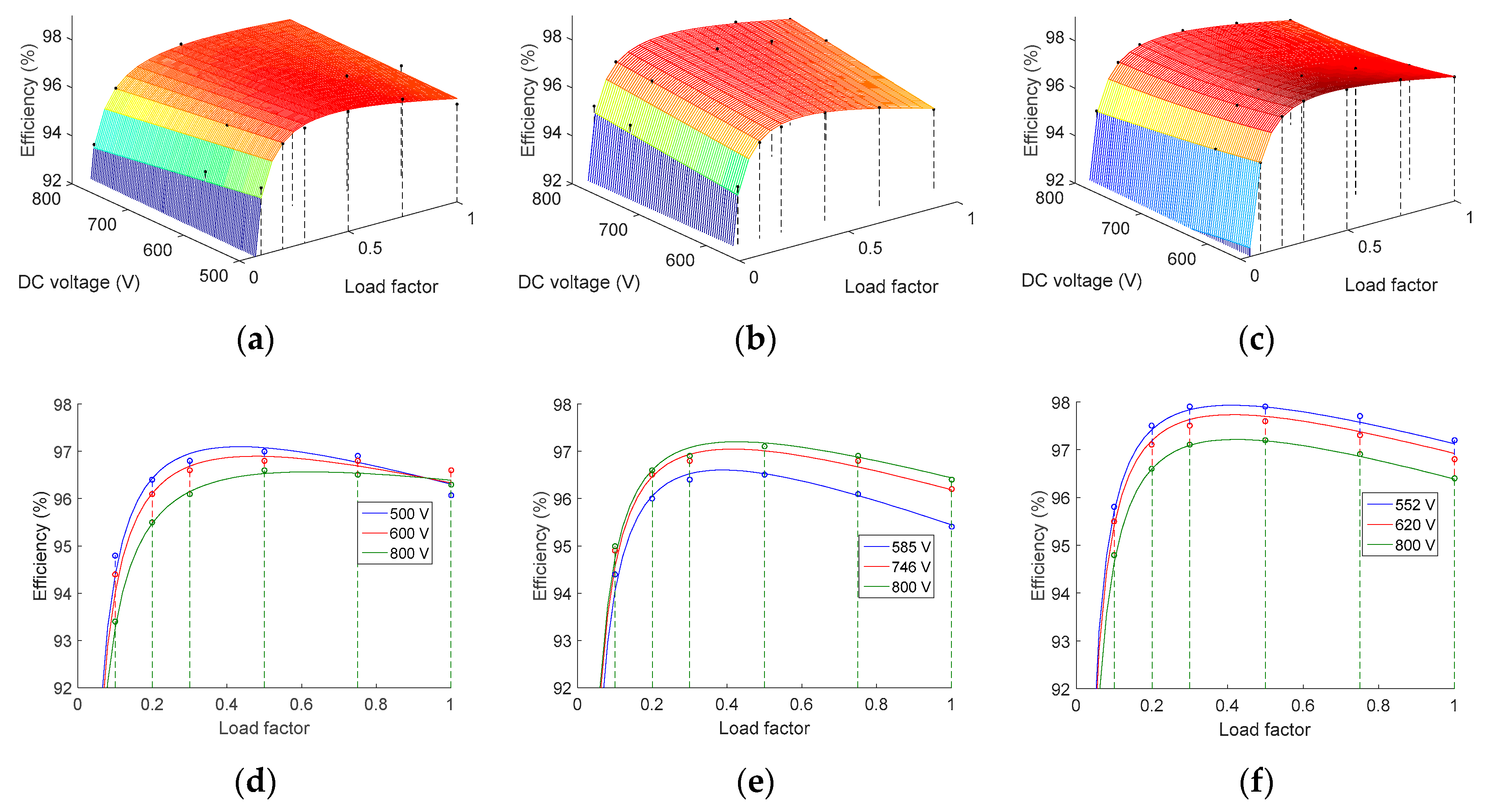
Figure 7.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Rampinelli nonlinear model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 7.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Rampinelli nonlinear model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 8.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Sandia model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 8.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Sandia model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 9.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Driesse model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
Figure 9.
Efficiency surfaces and detail of curves for three values of the DC voltage calculated by means of the Driesse model. (a,d) Perfect Galaxy International Ltd. EQX0250UV480TN. (b,e) Power-One ULTRA-750-TL-OUTD-4-US. (c,f) Power Electronics FS0900CU.
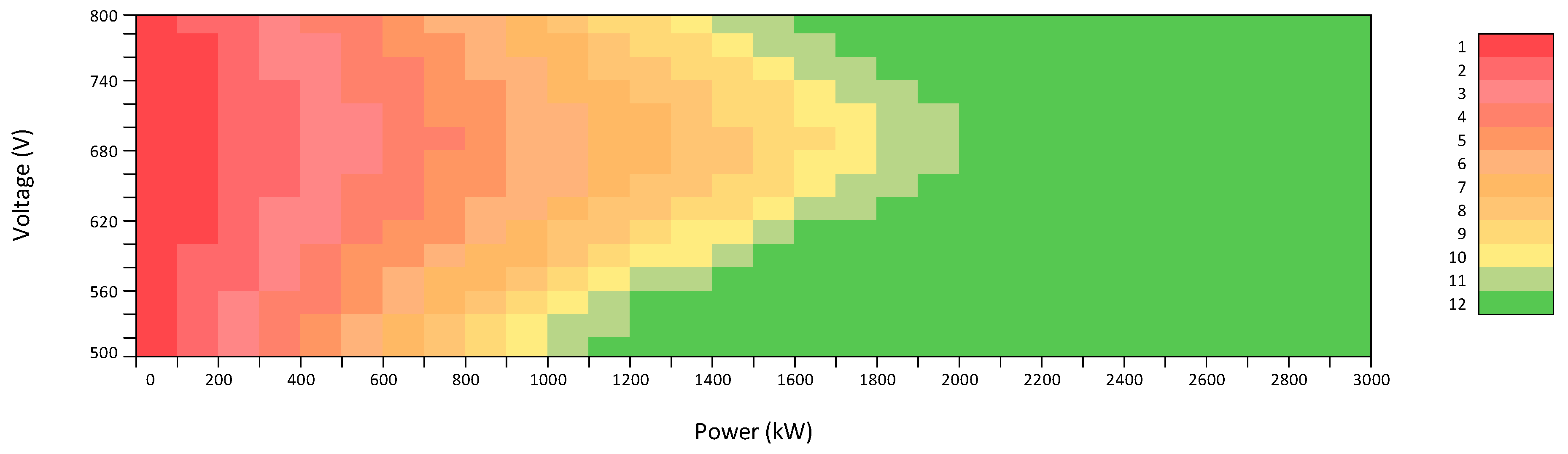
Figure 10.
Number of inverters in operation depending on the power generation and the maximum power point tracking (MPPT) voltage.
Figure 10.
Number of inverters in operation depending on the power generation and the maximum power point tracking (MPPT) voltage.
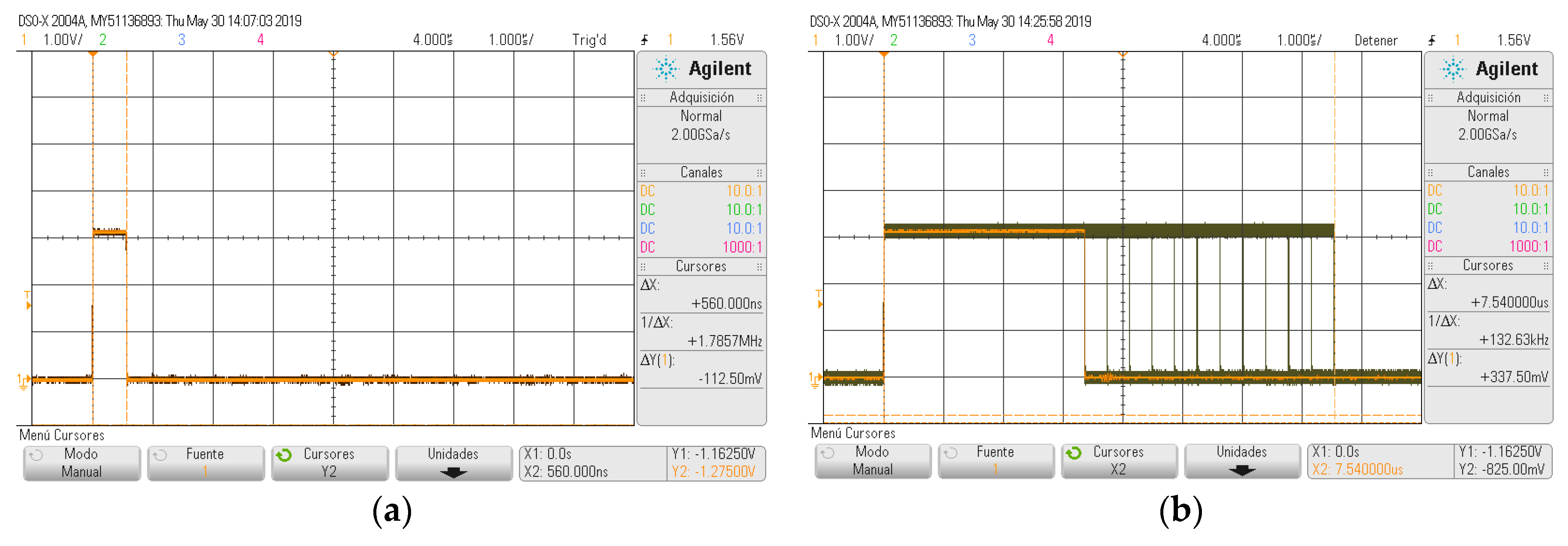
Figure 11.
Execution time of the algorithm (a) lookup table implementation. (b) equations implemented and solved in real time.
Figure 11.
Execution time of the algorithm (a) lookup table implementation. (b) equations implemented and solved in real time.
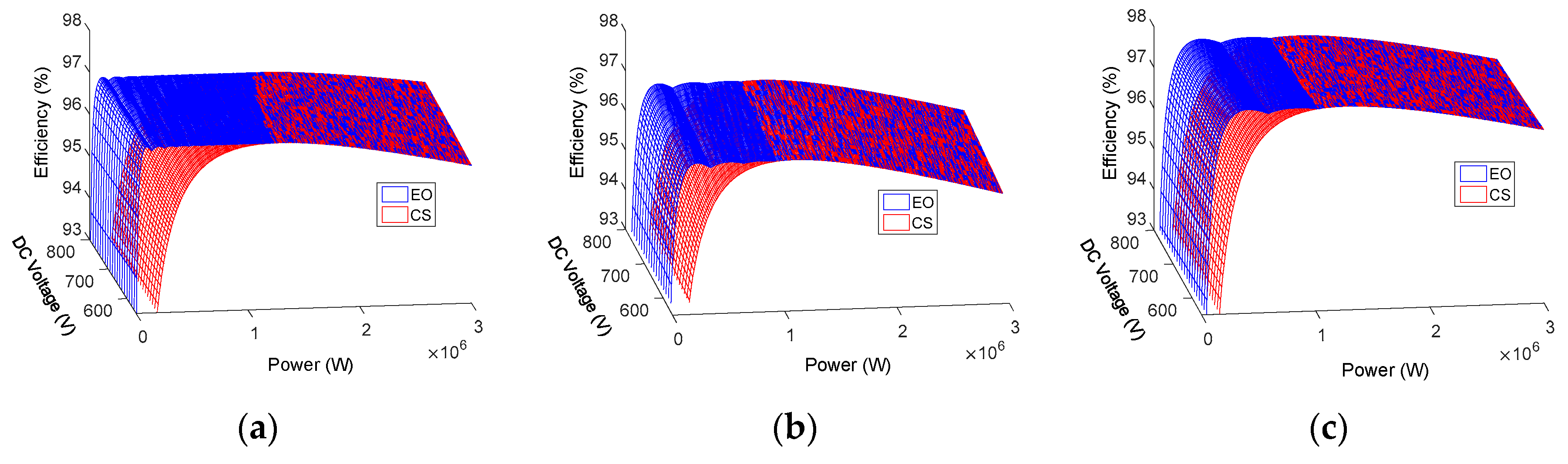
Figure 12.
Efficiency surfaces with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US. (c) Power Electronics FS0900CU.
Figure 12.
Efficiency surfaces with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Perfect Galaxy International Ltd. EQX0250UV480TN. (b) Power-One ULTRA-750-TL-OUTD-4-US. (c) Power Electronics FS0900CU.
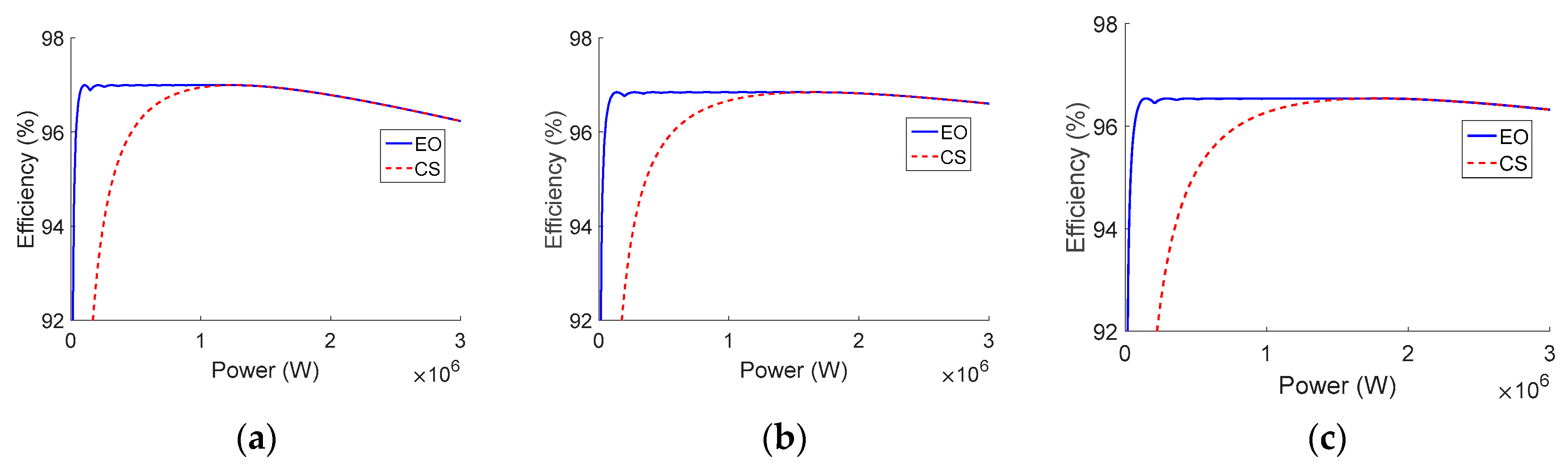
Figure 13.
Efficiency of Perfect Galaxy International Ltd. EQX0250UV480TN with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 500 V. (b) 600 V. (c) 800 V.
Figure 13.
Efficiency of Perfect Galaxy International Ltd. EQX0250UV480TN with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 500 V. (b) 600 V. (c) 800 V.
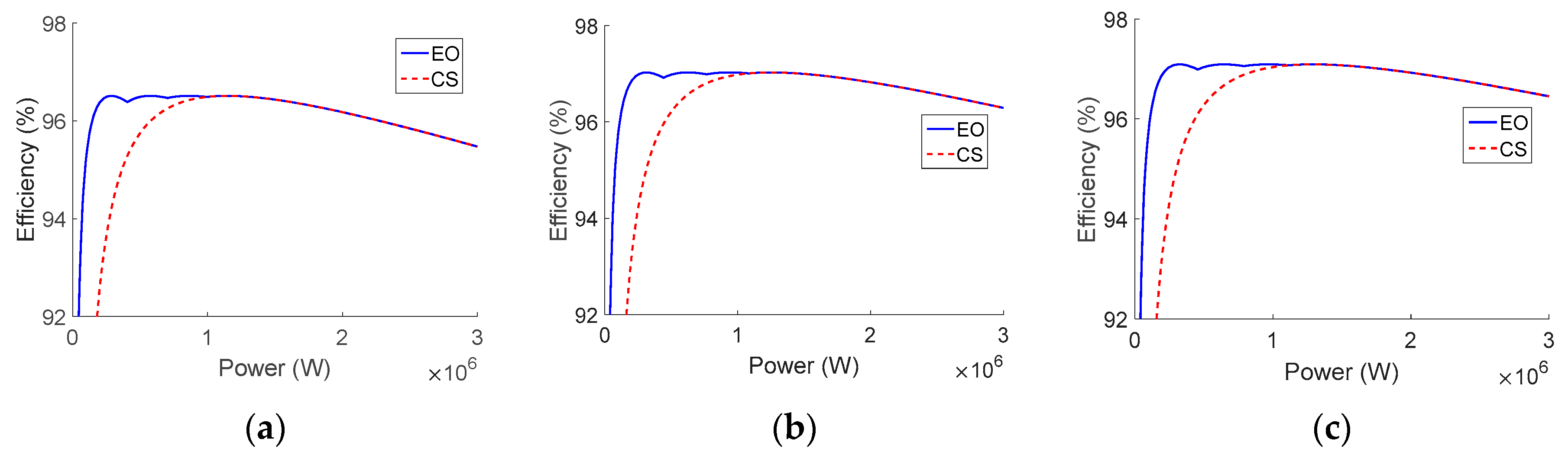
Figure 14.
Efficiency of Power-One ULTRA-750-TL-OUTD-4-US with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 585 V. (b) 746 V. (c) 800 V.
Figure 14.
Efficiency of Power-One ULTRA-750-TL-OUTD-4-US with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 585 V. (b) 746 V. (c) 800 V.
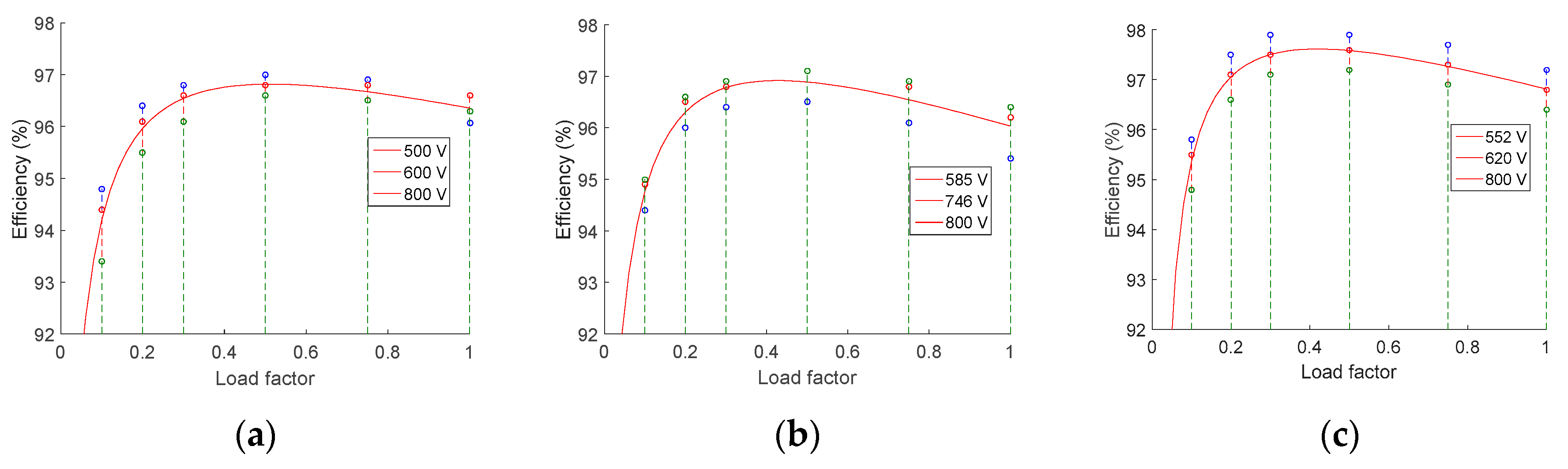
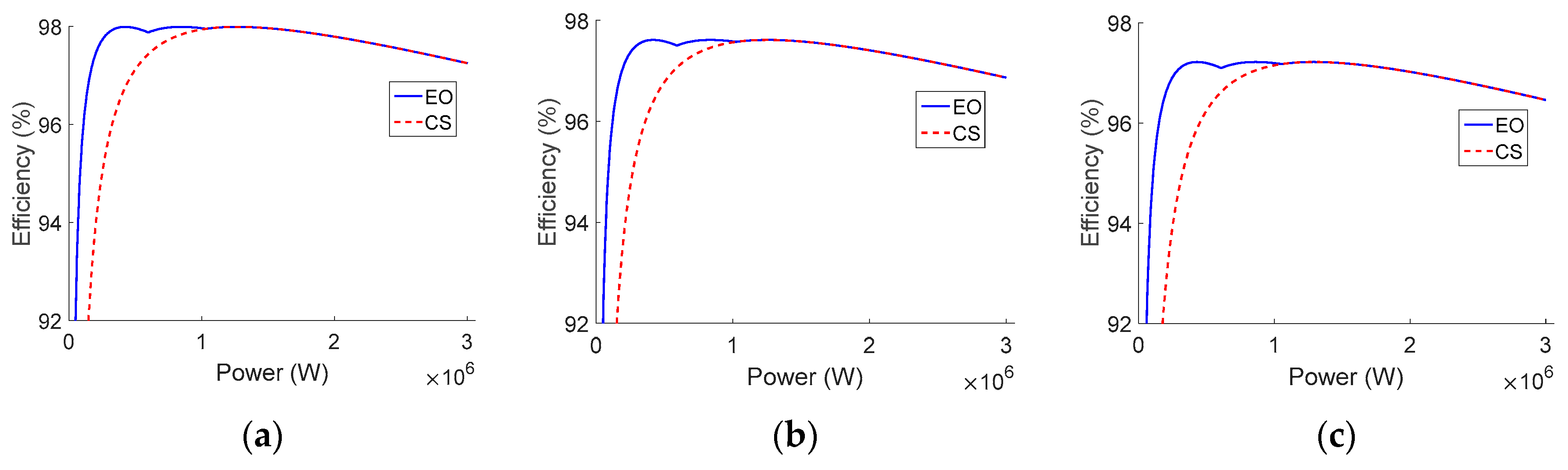
Figure 15.
Efficiency of Power Electronics FS0900CU with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 552 V. (b) 620 V. (c) 800 V.
Figure 15.
Efficiency of Power Electronics FS0900CU with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) 552 V. (b) 620 V. (c) 800 V.
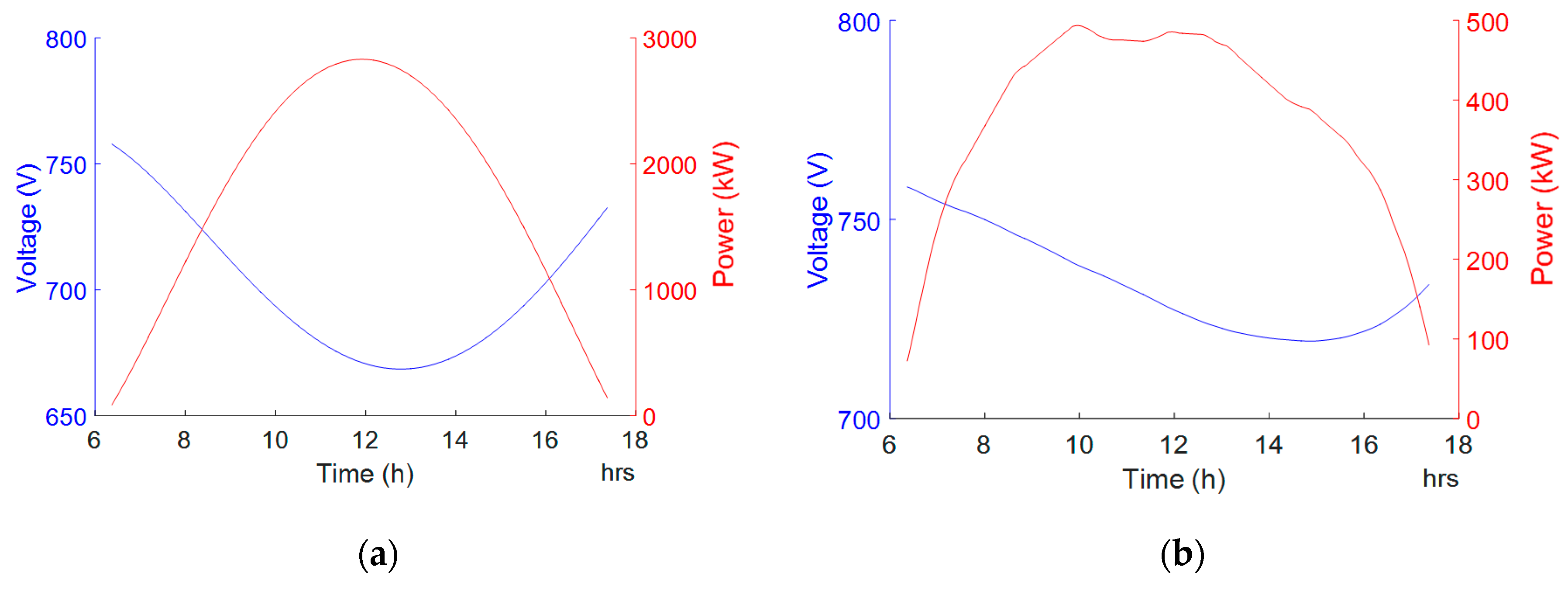
Figure 16.
Daily power generation and MPPT voltage curves. (a) Sunny day. (b) Cloudy day.
Figure 16.
Daily power generation and MPPT voltage curves. (a) Sunny day. (b) Cloudy day.
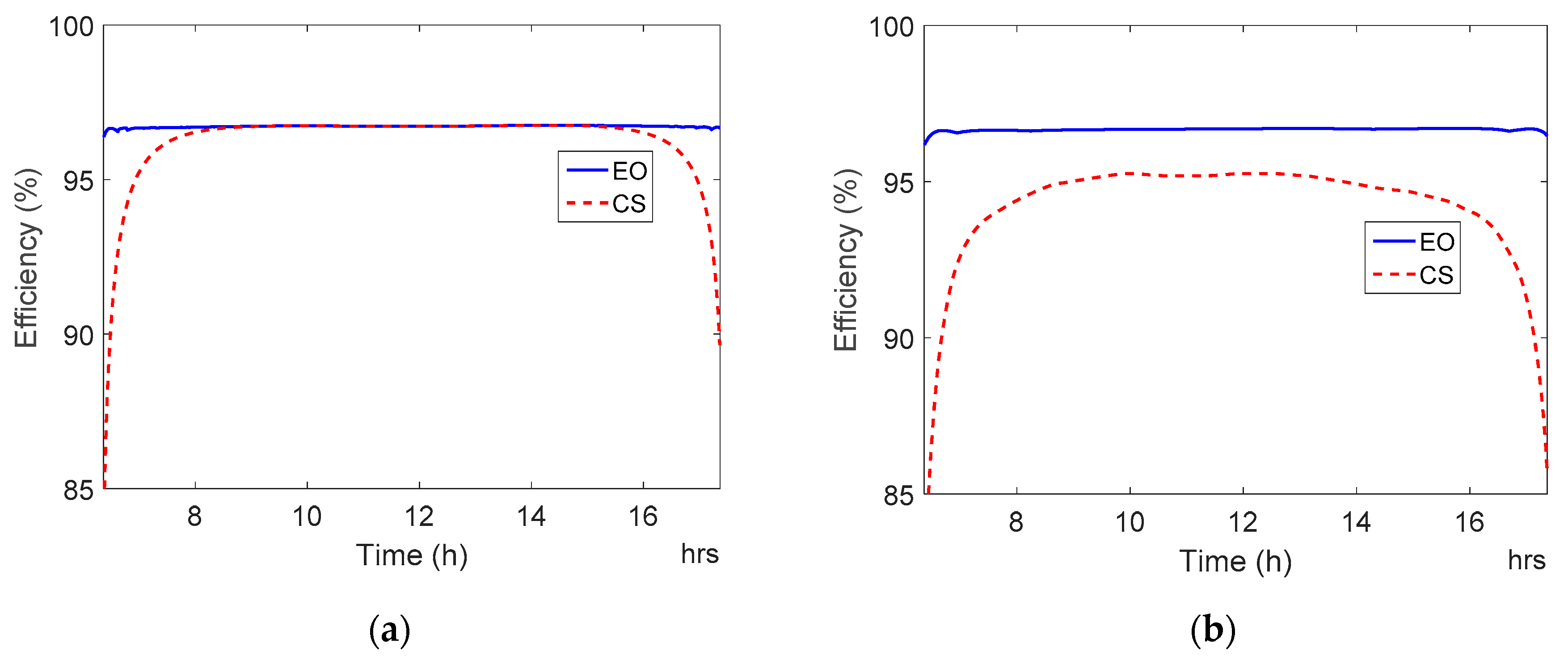
Figure 17.
Daily efficiency curves of Perfect Galaxy International Ltd. EQX0250UV480TN with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
Figure 17.
Daily efficiency curves of Perfect Galaxy International Ltd. EQX0250UV480TN with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
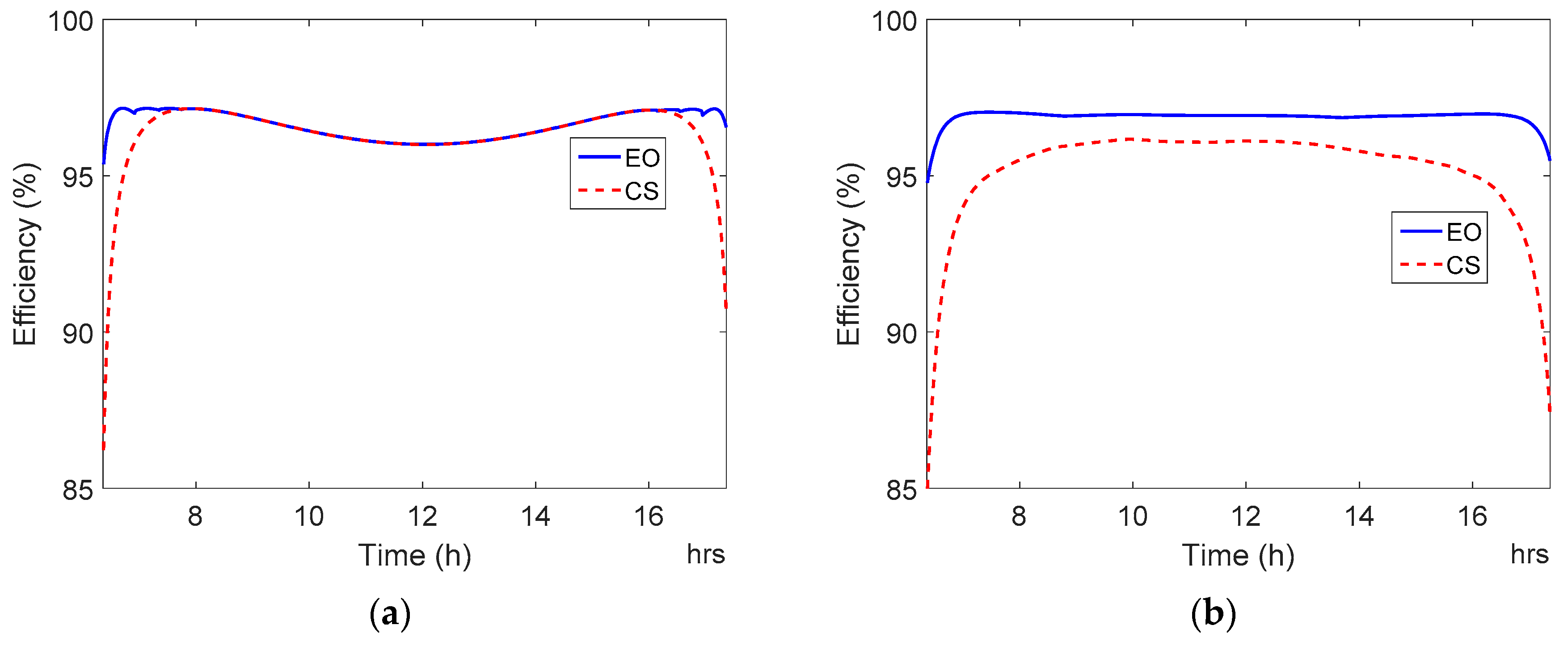
Figure 18.
Daily efficiency curves of Power-One ULTRA-750-TL-OUTD-4-US with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
Figure 18.
Daily efficiency curves of Power-One ULTRA-750-TL-OUTD-4-US with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
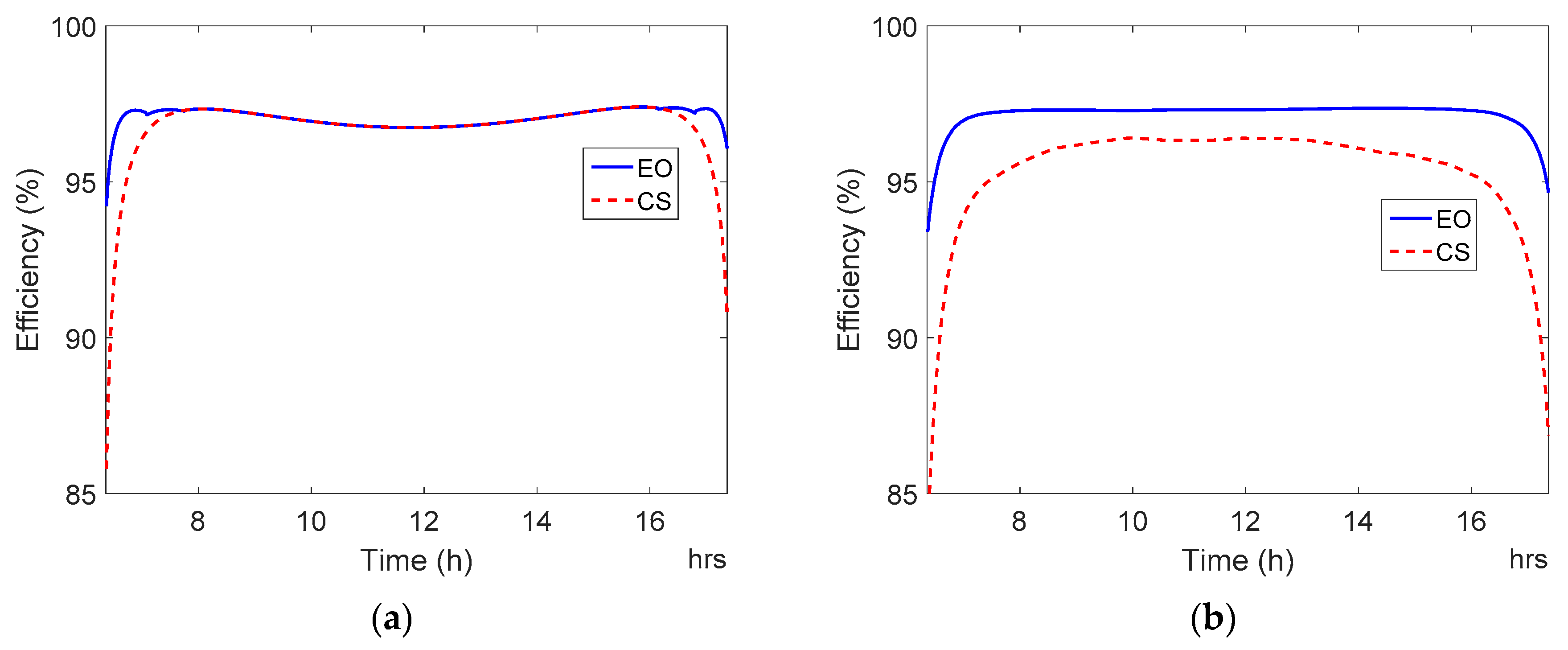
Figure 19.
Daily efficiency curves of Power Electronics FS0900CU with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
Figure 19.
Daily efficiency curves of Power Electronics FS0900CU with average current-sharing control method (CS) and efficiency-oriented method (EO). (a) Sunny day. (b) Cloudy day.
Table 1.
List of inverters under study (Source: CEC (California Energy Commission) Grid Support Inverters List).
Table 1.
List of inverters under study (Source: CEC (California Energy Commission) Grid Support Inverters List).
| Number of Inverter | Inverter | Company | Nominal Power |
|---|
| 1 | MPS-250HV | Dynapower | 250 kW |
| 2 | EQX0250UV480TN | Perfect Galaxy International Ltd. | 250 kW |
| 3 | FS0501CU | Power Electronics | 500 kW |
| 4 | IF500TL-UL OUTDOOR | Jema Energy | 500 kW |
| 5 | XP500U-TL | KACO new energy | 500 kW |
| 6 | EQMX0500UV320XP | Perfect Galaxy International Ltd. | 500 kW |
| 7 | SGI 500XTM | Yaskawa Solectria Solar | 500 kW |
| 8 | PV-625-XRLS-VV-STG | Perfect Galaxy International Ltd. | 625 kW |
| 9 | Conext Core XC680-NA | Schneider Electric | 680 kW |
| 10 | EQX0750UV320XP | Perfect Galaxy International Ltd. | 750 kW |
| 11 | ULTRA-750-TL-OUTD-4-US | Power-One | 750 kW |
| 12 | SC750CP-US | SMA America | 770 kW |
| 13 | ULTRA-750-TL-OUTD-1-US | ABB | 780 kW |
| 14 | HS-P1000GLO-U | Hyosung Heavy Industries | 1 MW |
| 15 | ULTRA-1100-TL-OUTD-2-US | ABB | 1 MW |
| 16 | ULTRA-1100-TL-OUTD-4-US | ABB | 1 MW |
| 17 | EQX1000UV400XP | Perfect Galaxy International Ltd. | 1 MW |
| 18 | ULTRA-1100-TL-OUTD-4-US | Power-One | 1 MW |
| 19 | SG1000MX | Sungrow Power Supply | 1 MW |
| 20 | FS0900CU | Power Electronics | 1 MW |
Table 2.
Perfect Galaxy International Ltd. EQX0250UV480TN efficiency data.
Table 2.
Perfect Galaxy International Ltd. EQX0250UV480TN efficiency data.
| vin | 10% | 20% | 30% | 50% | 75% | 100% |
|---|
| 500 V | 94.8% | 96.4% | 96.8% | 97% | 96.9% | 96.07% |
| 600 V | 94.4% | 96.1% | 96.6% | 96.8% | 96.8% | 96.6% |
| 800 V | 93.4% | 95.5% | 96.1% | 96.6% | 96.5% | 96.3% |
Table 3.
Power-One ULTRA-750-TL-OUTD-4-US efficiency data.
Table 3.
Power-One ULTRA-750-TL-OUTD-4-US efficiency data.
| vin | 10% | 20% | 30% | 50% | 75% | 100% |
|---|
| 585 V | 94.4% | 96% | 96.4% | 96.5% | 96.1% | 95.4% |
| 746 V | 94.9% | 96.5% | 96.8% | 97.1% | 96.8% | 96.2% |
| 800 V | 95% | 96.6% | 96.9% | 97.1% | 96.9% | 96.4% |
Table 4.
Power Electronics FS0900CU efficiency data.
Table 4.
Power Electronics FS0900CU efficiency data.
| vin | 10% | 20% | 30% | 50% | 75% | 100% |
|---|
| 552 V | 95.8% | 97.5% | 97.9% | 97.9% | 97.7% | 97.2% |
| 620 V | 95.5% | 97.1% | 97.5% | 97.6% | 97.3% | 96.8% |
| 800 V | 94.8% | 96.6% | 97.1% | 97.2% | 96.9% | 96.4% |
Table 5.
Jantsch coefficients.
Table 5.
Jantsch coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| k0 | 0.0044 | 0.0041 | 0.0042 |
| k1 | 0.016 | 0.0123 | 0.0044 |
| k2 | 0.0171 | 0.02245 | 0.0243 |
Table 6.
Dupont coefficients.
Table 6.
Dupont coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| α0 | 1.2204 | 1.2469 | 0.2538 |
| α1 | 46.9698 | 33.3255 | 39.5753 |
| β0 | 1.5224 | 1.4687 | 0.4354 |
| β1 | 47.4906 | 33.5318 | 39.704 |
Table 7.
Rampinelli coefficients.
Table 7.
Rampinelli coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| k0′ | k0,0 | 0.0024 | 0.0055 | 0.0028 |
| k0,1 | 3.2176 × 10−6 | −1.9691 × 10−6 | 2.1341 × 10−6 |
| k1′ | k1,0 | 0.0013 | 0.0189 | −0.0105 |
| k1,1 | 2.3093 × 10−5 | −9.3061 × 10−6 | 2.2688 × 10−5 |
| k2′ | k2,0 | 0.0342 | 0.0526 | 0.0195 |
| k2,1 | −2.6958 × 10−5 | −3.9468 × 10−5 | 7.3485 × 10−6 |
Table 8.
Rampinelli nonlinear model coefficients.
Table 8.
Rampinelli nonlinear model coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| k0″ | k0,0 | 0.013 | 0.002 | 0.0099 |
| k0,1 | −3.0294 × 10−5 | 8.2289 × 10−6 | −1.9309 × 10−5 |
| k0,2 | 2.5508 × 10−8 | −7.4294 × 10−9 | 1.5703 × 10−8 |
| k1″ | k1,0 | −0.0961 | 0.0764 | −0.0982 |
| k1,1 | 3.3111 × 10−4 | −1.8013 × 10−4 | 2.8608 × 10−4 |
| k1,2 | −2.3442 × 10−7 | 1.2444 × 10−7 | −1.9289 × 10−7 |
| k2″ | k2,0 | 0.1967 | −0.0461 | −0.0343 |
| k2,1 | −5.4074 × 10−4 | −3.9468 × 10−5 | −3.7155 × 10−5 |
| k2,2 | 3.9098 × 10−7 | −1.4074 × 10−8 | 3.259 × 10−8 |
Table 9.
Sandia coefficients.
Table 9.
Sandia coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| pac_o | 250,000 | 750,000 | 1.02 × 106 |
| vdc_o | 600 | 746 | 620 |
| pdc_o | 259,520 | 779,730 | 1.0524 × 106 |
| pso | 1216.1 | 3395.1 | 4260.9 |
| co | −7.8878 × 10−8 | −3.2207 × 10−8 | −2.2411 × 10−8 |
| c1 | −2.9565 × 10−6 | −4.9517 × 10−5 | 3.1507 × 10−5 |
| c2 | 1.1491 × 10−4 | −4.858 × 10−4 | 5.7319 × 10−4 |
| c3 | −0.002 | −0.0014 | 2.9497 × 10−4 |
Table 10.
Driesse coefficients.
Table 10.
Driesse coefficients.
| Coefficient | Perfect Galaxy International Ltd. EQX0250UV480TN | Power-One ULTRA-750-TL-OUTD-4-US | Power Electronics FS0900CU |
|---|
| b0 | b0,0 | −0.302 | 2.96 | 0.0755 |
| b0,1 | 2.4712 × 10−6 | 4.465 × 10−6 | 2.2934 × 10−6 |
| b0,2 | −0.3054 | 2.9634 | 0.073 |
| b1 | b1,0 | 3.9675 | 7.7702 | −22.9922 |
| b1,1 | 3.283 × 10−5 | 7.5838 × 10−6 | −2.8361 × 10−5 |
| b1,2 | 3.9788 | 7.7744 | −23.0511 |
| b2 | b2,0 | 17.3126 | 4.4107 | −15.3265 |
| b2,1 | 1.5323 × 10−5 | −2.9989 × 10−5 | −2.6754 × 10−5 |
| b2,2 | 17.3335 | 4.3712 | −15.3923 |
Table 11.
Number of modules to achieve 3 MW with the inverters under study.
Table 11.
Number of modules to achieve 3 MW with the inverters under study.
| Inverter | Company | Nominal Power | Number of Modules |
|---|
| EQX0250UV480TN | Perfect Galaxy International Ltd. | 250 kW | 12 |
| ULTRA-750-TL-OUTD-4-US | Power-One | 750 kW | 4 |
| FS0900CU | Power Electronics | 1 MW | 3 |
Table 12.
Execution time and memory resources.
Table 12.
Execution time and memory resources.
| Implementation | Data Memory | Program Memory | Execution Time |
|---|
| Option #1 | 1800 bytes | 47 words | 540 ns |
| Option #2 | - | 37 words | 3.5–7.4 µs |