Volumetric Measurements of Methane-Coal Adsorption and Desorption Isotherms—Effects of Equations of State and Implication for Initial Gas Reserves
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
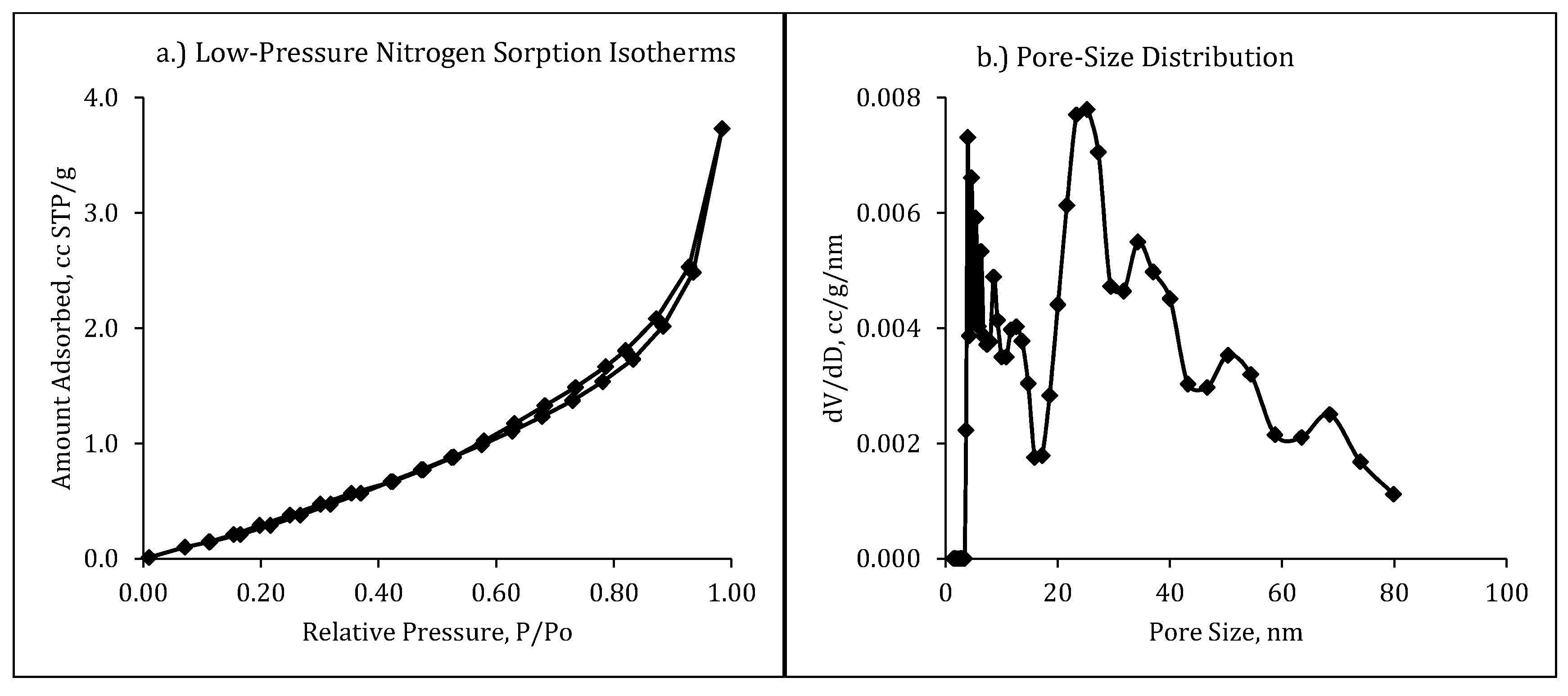
2.2. Sample Characterization Using Low-Pressure Nitrogen Adsorption
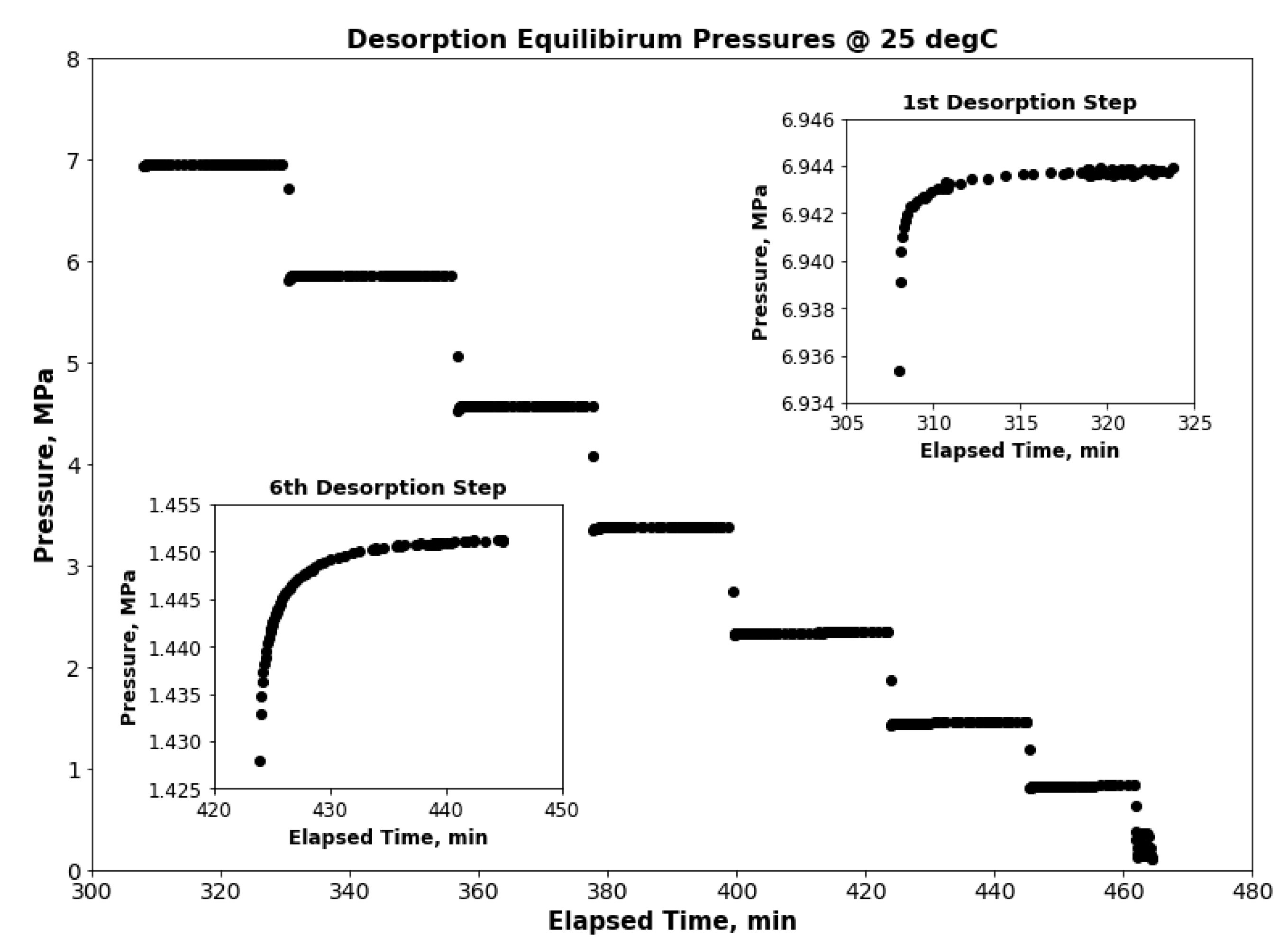
2.3. Measurement of Methane Sorption Isotherms
- (1)
- Negligible (or Zero) Hysteresis in which the isotherms overlay even though
- (2)
- Positive Hysteresis in which and as such, desorption isotherm lies above the adsorption curve
- (3)
- Negative Hysteresis in which and as such, desorption isotherm lies below the adsorption curve
2.4. Theory
2.4.1. Isotherm Modeling
2.4.2. Gas in-Place Calculation
- Case 1:
- Gas FVF equals the value calculated for each EOS.
- Case 2:
- Gas FVF equals constant for all EOS. The constant value was set as the value obtained for the reference EOS.
3. Results and Discussion
3.1. Low-Pressure Nitrogen Sorption Isotherms and Pore-Size Distribution
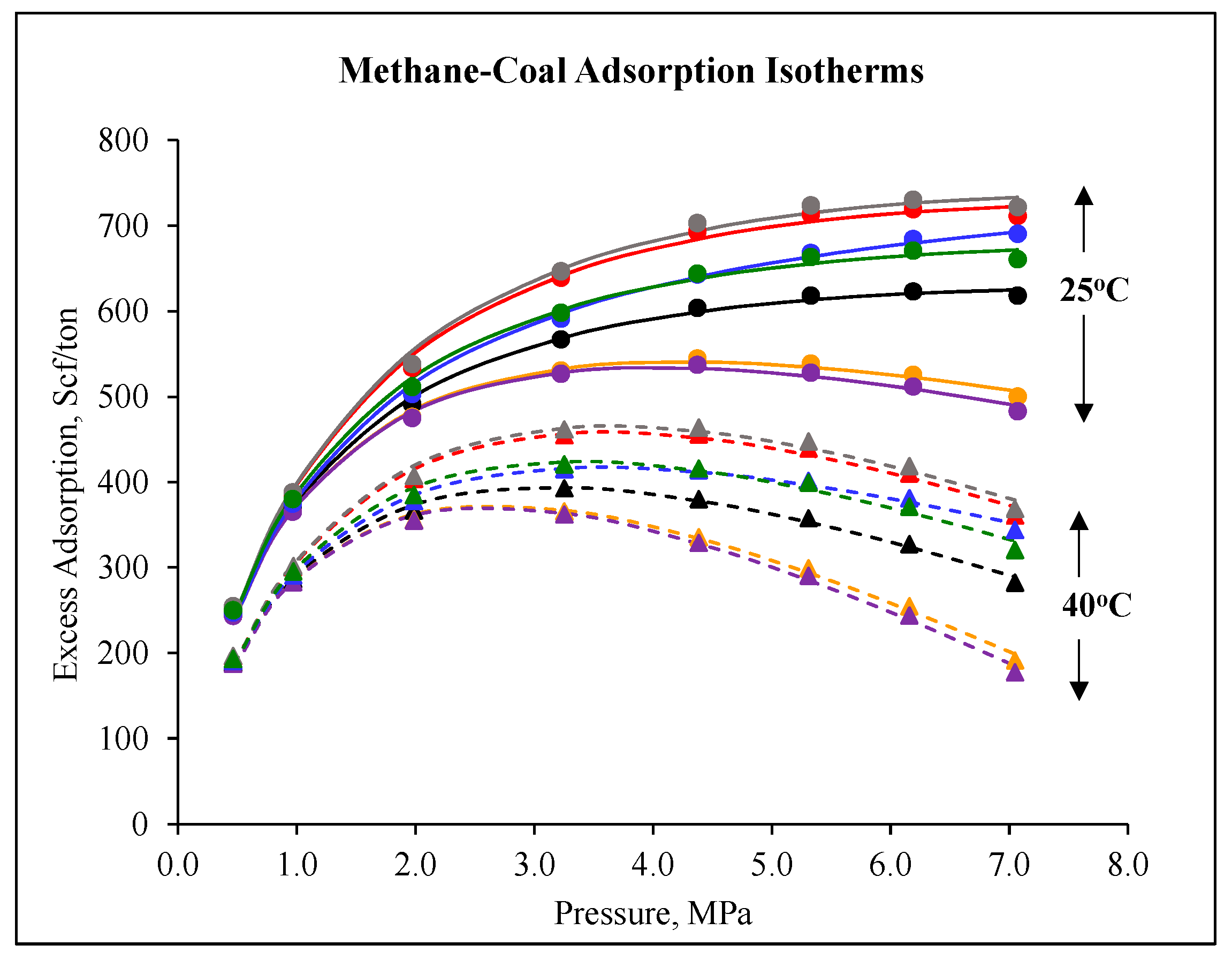
3.2. Methane-Coal Adsorption Isotherms
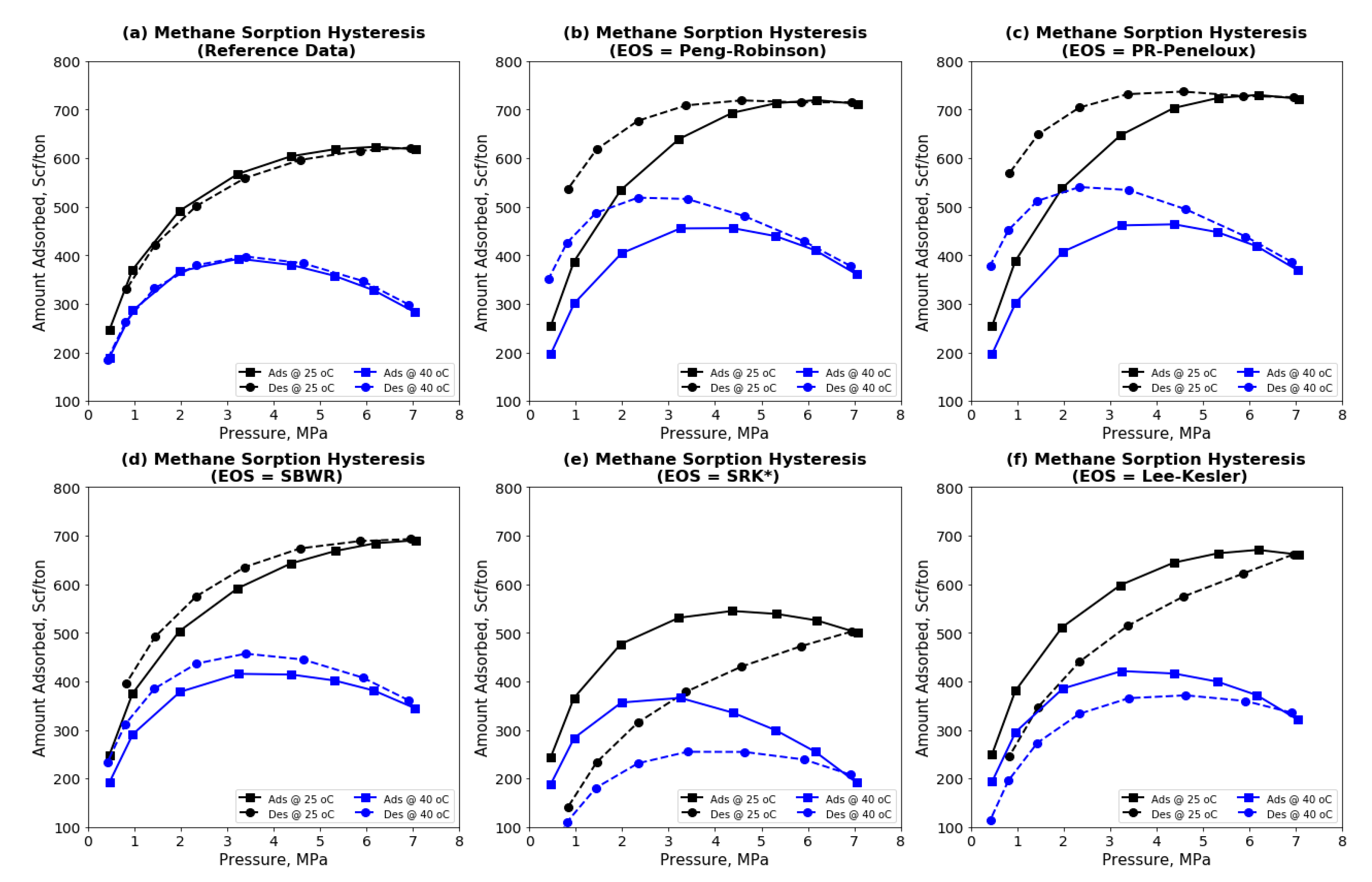
3.3. Methane-Coal Desorption Isotherms & Sorption Hysteresis
3.4. Langmuir Parameters
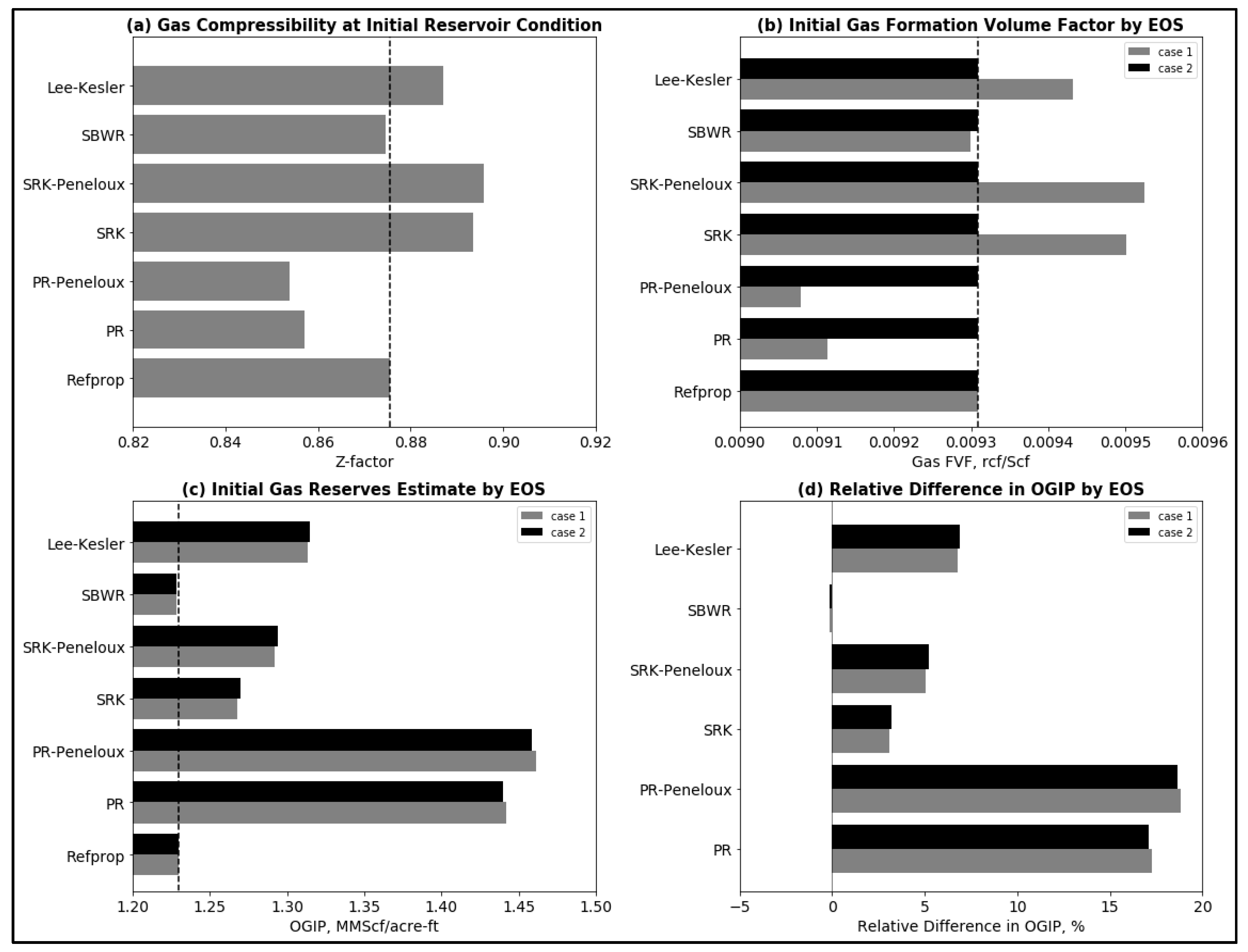
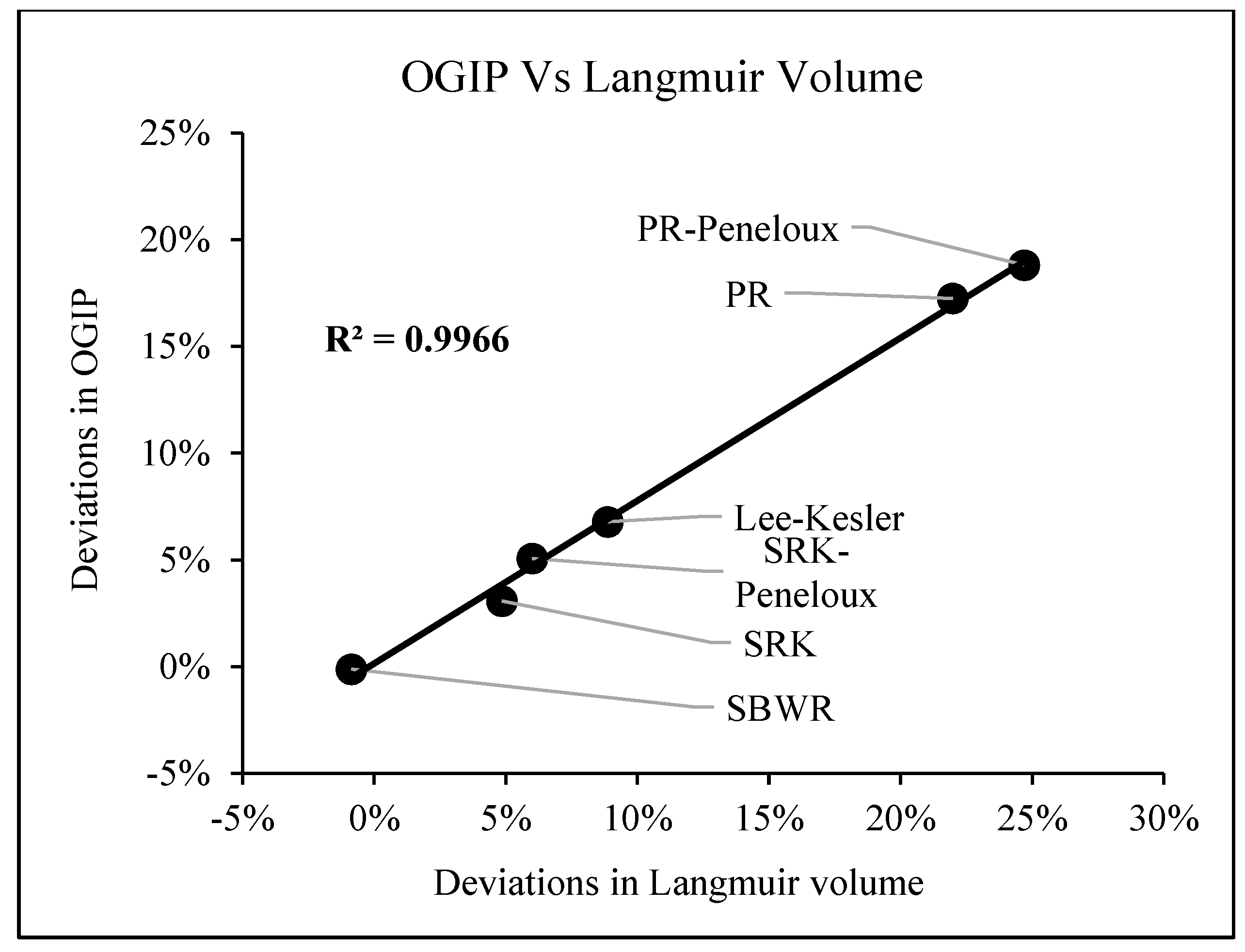
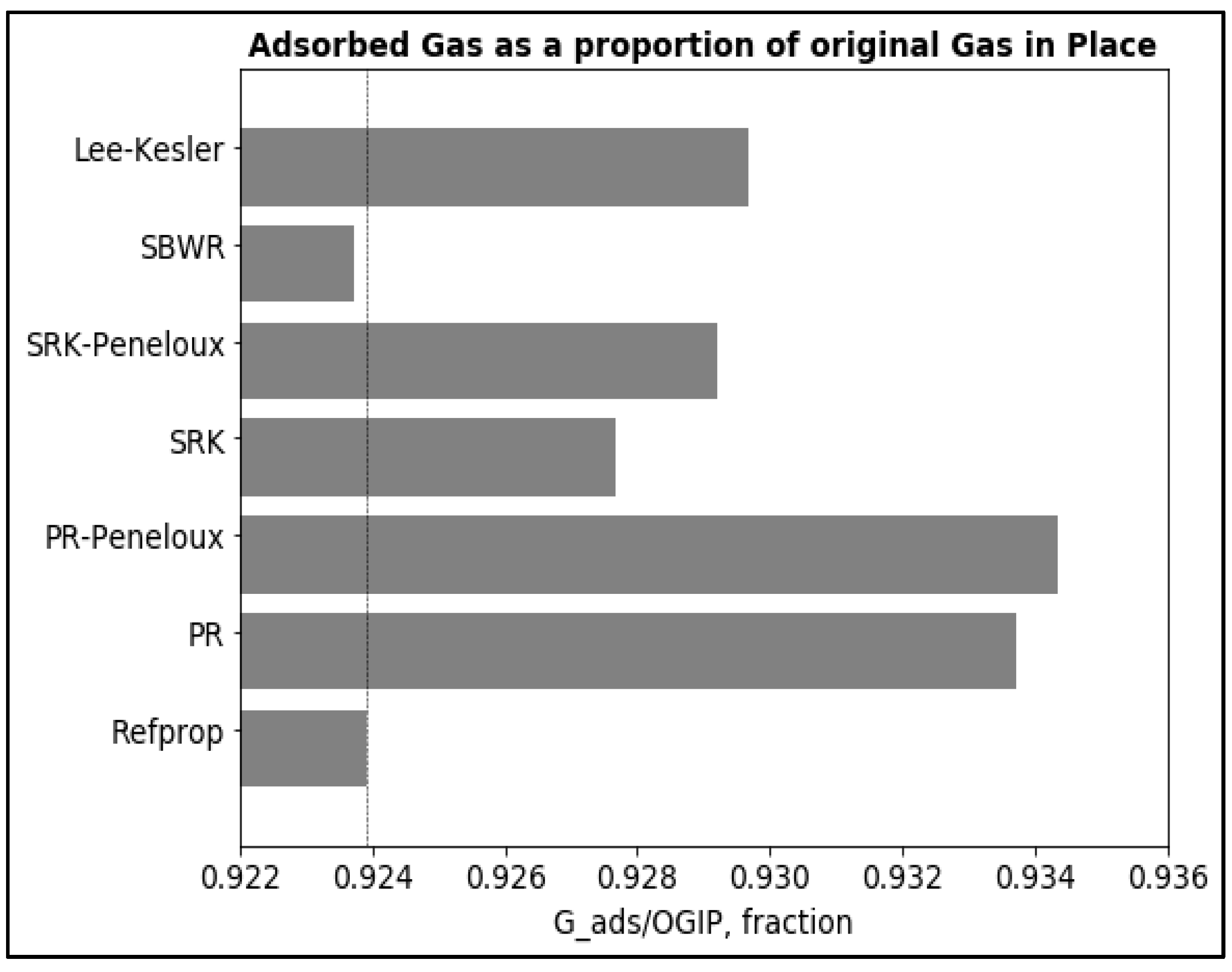
3.5. Original Gas in-Place
4. Conclusions
- (1)
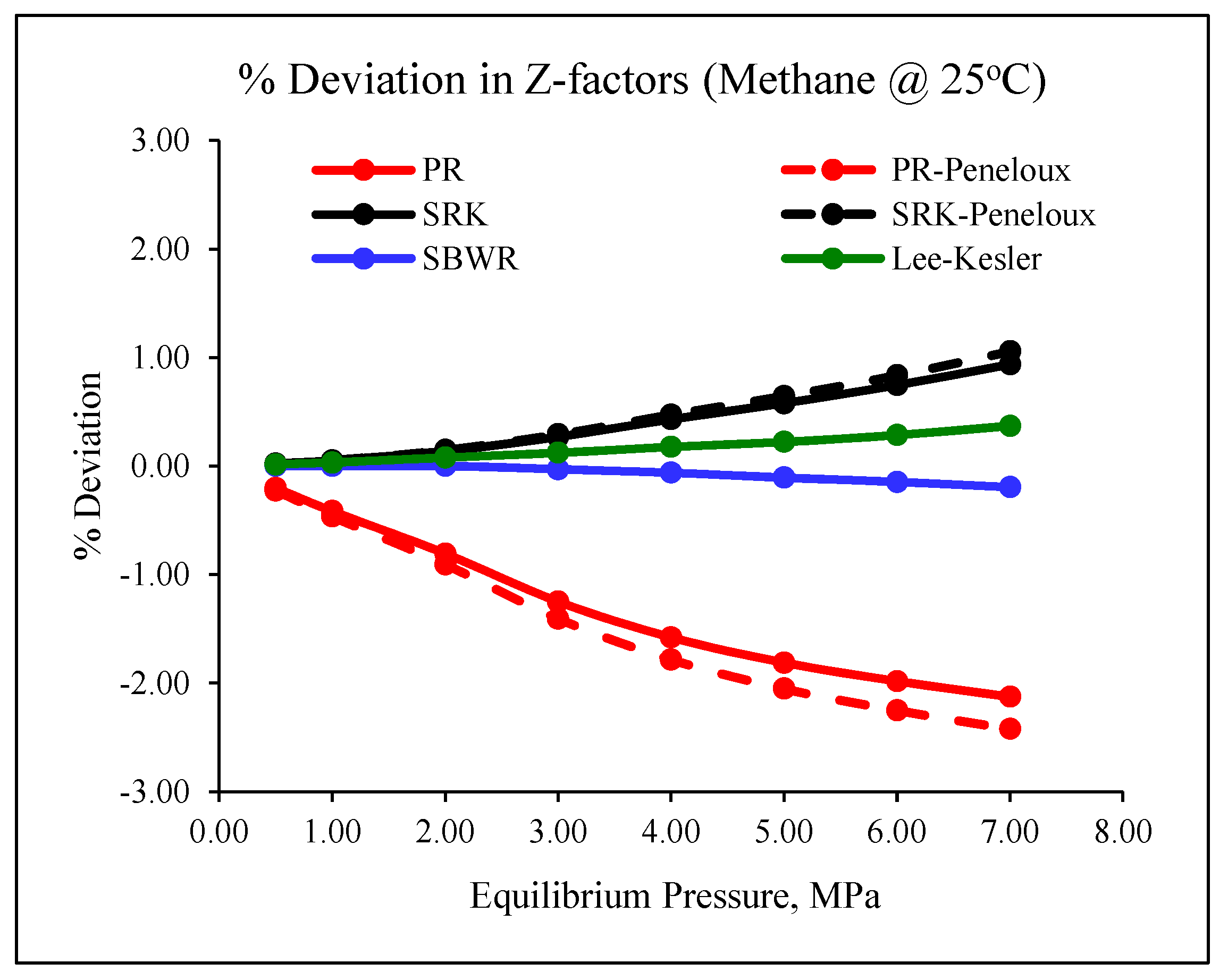
- Gas compressibility factors have significant effects on high-pressure adsorption and desorption isotherms of methane on coal.
- (2)
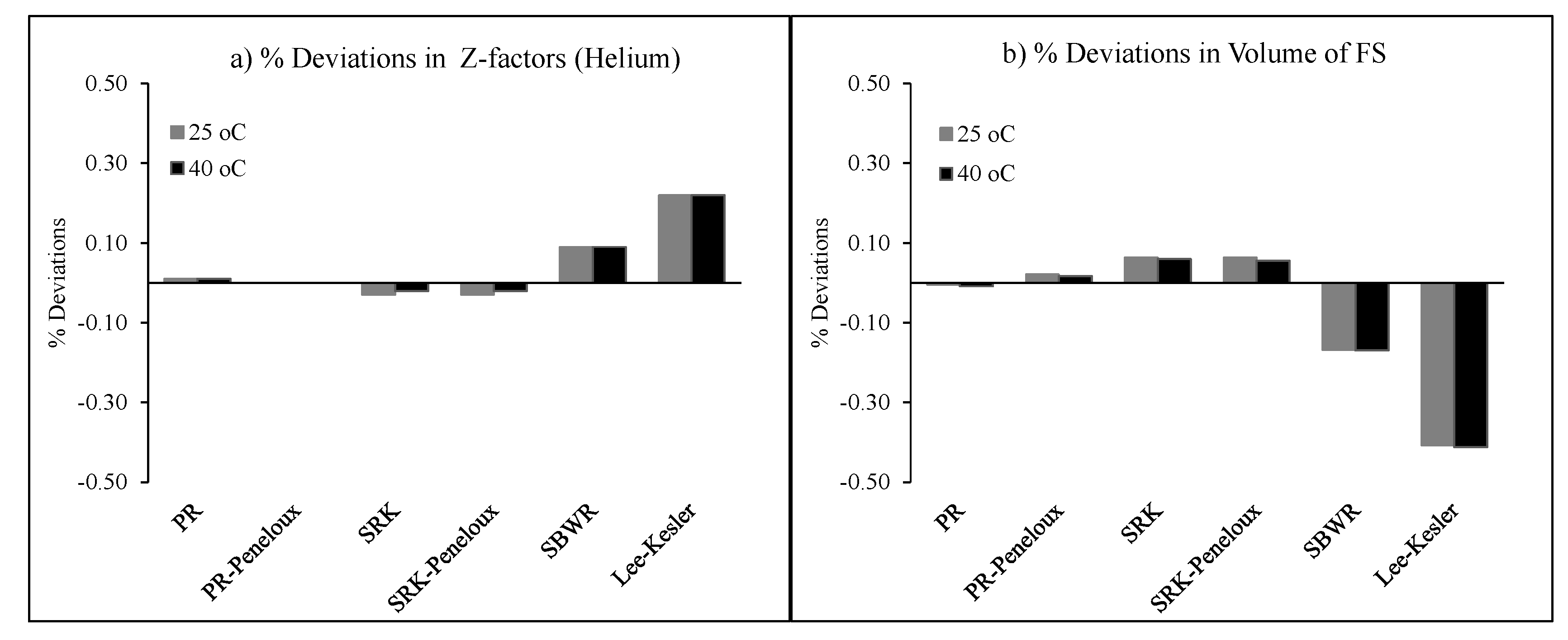
- Langmuir parameters also varied significantly with the choice of EOS with the SBWR-EOS having the closest values of Langmuir volumes and pressures to NIST-refprop at both test temperatures.
- (3)
- For each EOS, Langmuir volume and adsorbed phase density are lower at 40 °C than the corresponding values at 25 °C because of the negative effect of temperature on adsorption.
- (4)
- High-pressure methane-coal adsorption-desorption hysteresis is not a unique phenomenon; its existence, degree and type depend on the applied EOS.
- (5)
- For both test temperatures, negligible hysteresis was observed for the reference EOS while a relationship was observed between the deviations of methane Z-factor for each EOS (relative to Setzmann and Wagner’s) and the type of sorption hysteresis observed. Negatively deviating EOSs produced positive sorption hysteresis while positively deviating ones gave negative sorption hysteresis for the same dataset.
- (6)
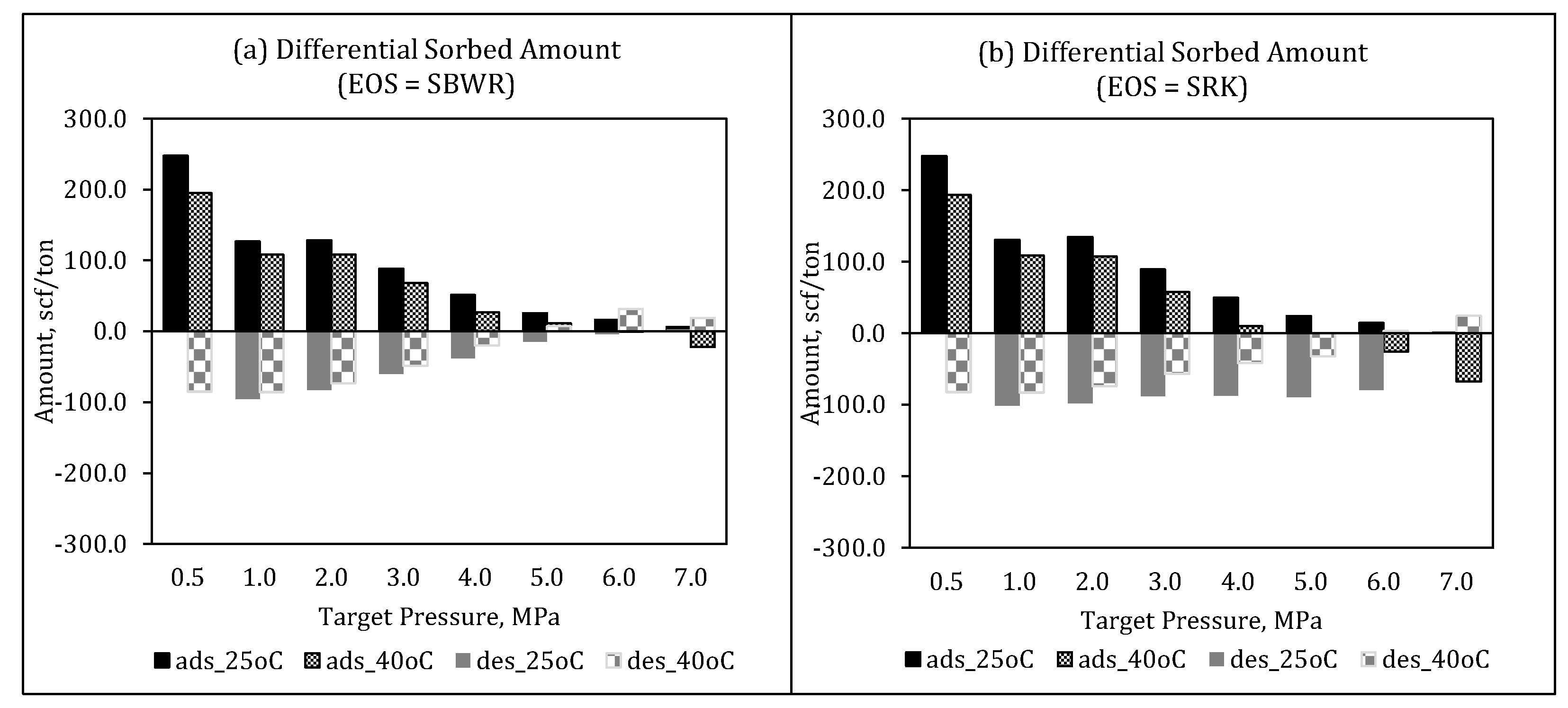
- Calculated OGIP is predominantly in adsorbed phase and as such, varies with Langmuir volume.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rachmat, S.; Pramana, A.A.; Febriana, L. Indonesia’s Unconventional Resources, Modified Resource Triangle, and a Typical Example of Stimulation of Coalbed Methane Reservoir. Mod. Appl. Sci. 2012, 6, 99–111. [Google Scholar] [CrossRef][Green Version]
- Seidle, J. Sorption of Gas on Coals. In Fundamentals of Coalbed Methane Reservoir Engineering; PennWell: Tulsa, OK, USA, 2011; pp. 125–153. [Google Scholar]
- Penuela, G.; Ordonez, A.; Bejarano, A. A Generalized Material Balance Equation for Coal Seam Gas Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 27–30 September 1998. [Google Scholar]
- King, G.R. Material-Balance Techniques for Coal-Seam and Devonian Shale Gas Reservoirs With Limited Water Influx. SPE Reserv. Eng. 1993, 8, 67–72. [Google Scholar] [CrossRef]
- Bell, G.J.; Rakop, K.C. Hysteresis of Methane/Coal Sorption Isotherms. In Proceedings of the 61st SPE-ATCE, New Orleans, LA, USA, 5–8 October 1986. [Google Scholar]
- Keller, J.U.; Staudt, R. Gas Adsorption Equilibria: Experimental Methods and Adsorptive Isotherms; Springer: Berlin, Germany, 2005. [Google Scholar]
- Gasparik, M.; Rexer, T.F.T.; Aplin, A.C.; Billemont, P.; Weireld, G.D.; Gensterblum, Y.; Henry, M.; Krooss, B.M.; Liu, S.; Ma, X.; et al. First international inter-laboratory comparison of high-pressure CH4, CO2 and C2H6 sorption isotherms on carbonaceous shales. Int. J. Coal Geol. 2014, 132, 131–146. [Google Scholar] [CrossRef]
- Goodman, A.L.; Busch, A.; Duffy, G.J.; Fitzgerald, J.E.; Gasem, K.A.M.; Gensterblum, Y.; Krooss, B.M.; Levy, J.; Ozdemir, E.; Pan, Z.; et al. An Inter-laboratory Comparison of CO2 Isotherms Measured on Argonne Premium Coal Samples. Energy Fuels 2004, 18, 1175–1182. [Google Scholar] [CrossRef]
- Lutynski, M.A.; Battistutta, E.; Bruining, H.; Wolf, K.H.A. Discrepancies inthe assessment of CO2 storage capacity and methane recovery from coal with selected equation of states Part I. Experimental isotherm calculation. Physicochem. Probl. Miner. Process. 2011, 47, 159–168. [Google Scholar]
- Ekundayo, J.; Rezaee, R. Effect of Equation of States on High Pressure Volumetric Measurements of Methane-Coal Sorption Isotherms—Part 1: Volumes of Free Space and Methane Adsorption Isotherms. Energy Fuels 2019, 33, 1029–1036. [Google Scholar] [CrossRef]
- Al-Fatlawi, O.; Hossain, M.M.; Osborne, J. Determination of best possible correlation for gas compressibility factor to accurately predict the initial gas reserves ingas-hydrocarbon reservoirs. Int. J. Hydrogen Energy 2017, 42, 25492–25508. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Z.; Ripepi, N.; Kang, B.; Yue, G. Adsorption Affinity of Different Types of Coal: Mean Isosteric Heat of Adsorption. Energy Fuels 2015, 29, 3609–3615. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, W.; Liu, S.; Liu, Y.; Yang, M.; Zhao, J.; Song, Y. Pure methane, carbon dioxide, and nitrogen adsorption on anthracite from China over a wide range of pressures and temperatures: Experiments and modeling. RSC Adv. 2015, 5, 52612–52623. [Google Scholar] [CrossRef]
- Yang, F.; Hu, B.; Xu, S.; Meng, Q.; Krooss, B.M. Thermodynamic Characteristic of Methane Sorption on Shales from Oil, Gas, and Condensate Windows. Energy Fuels 2018, 32, 10443–10456. [Google Scholar] [CrossRef]
- Ozdemir, E. Dynamic nature of supercritical CO2 adsorption on coals. Adsorption 2017, 23, 25–36. [Google Scholar] [CrossRef]
- Dutta, P.; Bhowmik, S.; Das, S. Methane and carbon dioxide sorption on a set of coals from India. Int. J. Coal Geol. 2011, 85, 289–299. [Google Scholar] [CrossRef]
- Battistutta, E.; van Hemert, P.; Lutynski, M.; Bruining, H.; Wolf, K.H. Swelling and sorption experiments on methane, nitrogen and carbon dioxide on dry Selar Cornish coal. Int. J. Coal Geol. 2010, 84, 39–48. [Google Scholar] [CrossRef]
- Busch, A.; Gensterblum, Y.; Krooss, B.M. Methane and CO2 sorption and desorption measurements on dry Argonne premium coals: Pure components and mixtures. Int. J. Coal Geol. 2003, 55, 205–224. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Yang, W.; Chu, W. Coalbed methane adsorption and desorption characteristics related to coal particle size. Chin. Phys. B 2016, 25, 068102. [Google Scholar] [CrossRef]
- Zhang, L.; Aziz, N.; Ren, T.; Nemcik, J.; Tu, S. Influence of coal particle size on coal adsorption and desorption characteristics. Arch. Min. Sci. 2014, 59, 807–820. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, S. Experimental and theoretical characterization of methane and CO2 sorption hysteresis in coals based on Langmiur desorption. Int. J. Coal Geol. 2016, 171, 49–60. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Lu, Y.; Choi, S.K.; Liu, X. Sorption Hysteresis Characterization of CH4 and CO2 on Anthracite, Bituminous Coal, and Lignite at Low Pressure. J. Energy Resour. Technol. 2017, 140, 012203. [Google Scholar] [CrossRef]
- Weishauptová, Z.; Přibyl, O.; Sýkorová, I.; Machovič, V. Effect of bituminous coal properties on carbon dioxide and methane high pressure sorption. Fuel 2015, 139, 115–124. [Google Scholar] [CrossRef]
- Jessen, K.; Tang, G.Q.; Kovscek, A.R. Laboratory and Simulation Investigation of Enhanced Coalbed Methane Recovery by Gas Injection. Transp. Porous Media 2008, 73, 141–159. [Google Scholar] [CrossRef]
- Kim, H.J.; Shi, Y.; He, J.; Lee, H.H.; Lee, C.H. Adsorption characteristics of CO2 and CH4 on dry and wet coal from subcritical to supercritical conditions. Chem. Eng. J. 2011, 171, 45–53. [Google Scholar] [CrossRef]
- He, J.; Shi, Y.; Ahn, S.; Kang, J.W.; Lee, C.H. Adsorption and Desorption of CO2 on Korean Coal under Subcritical to Supercritical Conditions. J. Phys. Chem. B 2010, 114, 4854–4861. [Google Scholar] [CrossRef]
- Rodrigues, C.F.A.; da Silva, J.M.M.; Dinis, M.A.P.; de Sousa, M.J.L. Effect of gas compressibility factor estimation in coal sorption isotherms accuracy. Int. J. Oil Gas Coal Technol. 2018, 19, 230–247. [Google Scholar] [CrossRef]
- Wang, K.; Wang, G.; Ren, T.; Cheng, Y. Methane and CO2 sorption hysteresis on coal: A critical review. Int. J. Coal Geol. 2014, 132, 60–80. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Zou, J.; Rezaee, R. Effect of particle size on high-pressure methane adsorption of coal. Pet. Res. 2016, 1, 53–58. [Google Scholar] [CrossRef]
- Zou, J.; Rezaee, R.; Liu, K. Effect of Temperature on Methane Adsorption in Shale Gas Reservoirs. Energy Fuels 2017, 31, 12081–12092. [Google Scholar] [CrossRef]
- Gasparik, M.; Ghanizadeh, A.; Bertier, P.; Gensterblum, Y.; Bouw, S.; Krooss, B.M. High-Pressure Methane Sorption Isotherms of Black Shales from the Netherlands. Energy Fuels 2012, 26, 4995–5004. [Google Scholar] [CrossRef]
- Seidle, J. Gas and Water Mass Balances in Coals. In Fundamentals of Coalbed Methane Reservoir Engineering; PennWell: Tulsa, OK, USA, 2011; pp. 217–246. [Google Scholar]
- Thommes, M.; Kanero, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Jun-yi, L.; Zheng-song, Q.; Wei-an, H.; Yang, L.; Ding-ding, S. Nano-pore structure characterization of shales using gas adsorption and mercury intrusion techniques. J. Chem. Pharm. Res. 2014, 6, 850–857. [Google Scholar]
- McCarty, R.D.; Arp, V.D. New wide range equation of state for helium. Adv. Cryog. Eng. 1990, 35, 1465–1475. [Google Scholar]
- Rouquerol, J.; Rouquerol, F.; Llewellyn, P.; Denoyel, R. Surface excess amounts in high-pressure gas adsorption: Issues and benefits. Colloids Surf. A Physicochem. Eng. Asp. 2016, 496, 3–12. [Google Scholar] [CrossRef]
- Do, D.D.; Do, H.D. Appropriate volumes for adsorption isotherm studies: The absolute void volume, accessible pore volume and enclosing particle volume. J. Colloid Interface Sci. 2007, 316, 317–330. [Google Scholar] [CrossRef]
- Harpalani, S.; Prusty, B.K.; Dutta, P. Methane/CO2 Sorption Modeling for Coalbed Methane Production and CO2 Sequestration. Energy Fuels 2006, 20, 1591–1599. [Google Scholar] [CrossRef]
| Components | Composition (%) |
|---|---|
| A. Petrographic Analysis | |
| Vitrinite | 75.0 |
| Fusinite | 3.3 |
| Semi-fusinite | 13.0 |
| Macrinite | 0.3 |
| Inertodetrinite | 4.0 |
| Mineral matter | 4.5 |
| Mean maximum reflectance | 1.43 |
| B. Proximate Analysis | |
| Ash content | 9.6 |
| Moisture content | 1.2 |
| Volatile matter | 21.2 |
| Fixed carbon | 68.0 |
| Parameters | |
|---|---|
| Reservoir Temperature, °C | 40 |
| Initial Res. Pressure, MPa | 10.34 |
| Rock density, g/cc | 1.34 * |
| Initial porosity, fraction | 0.1 * |
| Initial water saturation, fraction | 0.8 * |
| EOS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Temp. | Parameters | Refprop | PR | PR-Pen. | SRK | SRK-Pen. | SBWR | Lee-Kesler |
| 25 °C | VL, Scf/ton | 772.9 | 943.3 | 964.6 | 806.6 | 815 | 800 | 836.8 |
| PL, MPa | 1.02 | 1.34 | 1.38 | 1.08 | 1.1 | 1.09 | 1.13 | |
| ρads, Kg/m3 | 689.9 | 590.9 | 578.8 | 183.8 | 165.4 | 1.30E+09 | 742.9 | |
| R2 | 0.9985 | 0.9969 | 0.9966 | 0.9978 | 0.9977 | 0.9983 | 0.9973 | |
| 40 °C | VL, Scf/ton | 705.8 | 860.9 | 880.1 | 740 | 748.2 | 699.7 | 768.4 |
| PL, MPa | 1.26 | 1.63 | 1.68 | 1.34 | 1.35 | 1.23 | 1.39 | |
| ρads, Kg/m3 | 92.1 | 103.7 | 104.6 | 69.4 | 66.9 | 116.6 | 98.2 | |
| R2 | 0.9953 | 0.9918 | 0.9915 | 0.9946 | 0.9947 | 0.9957 | 0.9911 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ekundayo, J.M.; Rezaee, R. Volumetric Measurements of Methane-Coal Adsorption and Desorption Isotherms—Effects of Equations of State and Implication for Initial Gas Reserves. Energies 2019, 12, 2022. https://doi.org/10.3390/en12102022
Ekundayo JM, Rezaee R. Volumetric Measurements of Methane-Coal Adsorption and Desorption Isotherms—Effects of Equations of State and Implication for Initial Gas Reserves. Energies. 2019; 12(10):2022. https://doi.org/10.3390/en12102022
Chicago/Turabian StyleEkundayo, Jamiu M., and Reza Rezaee. 2019. "Volumetric Measurements of Methane-Coal Adsorption and Desorption Isotherms—Effects of Equations of State and Implication for Initial Gas Reserves" Energies 12, no. 10: 2022. https://doi.org/10.3390/en12102022
APA StyleEkundayo, J. M., & Rezaee, R. (2019). Volumetric Measurements of Methane-Coal Adsorption and Desorption Isotherms—Effects of Equations of State and Implication for Initial Gas Reserves. Energies, 12(10), 2022. https://doi.org/10.3390/en12102022






