Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems
Abstract
:1. Introduction
- (1)
- We propose harmonic objective effectively: optimization tools can focus on power loss reduction since IHD and THD can satisfy required limits.
- (2)
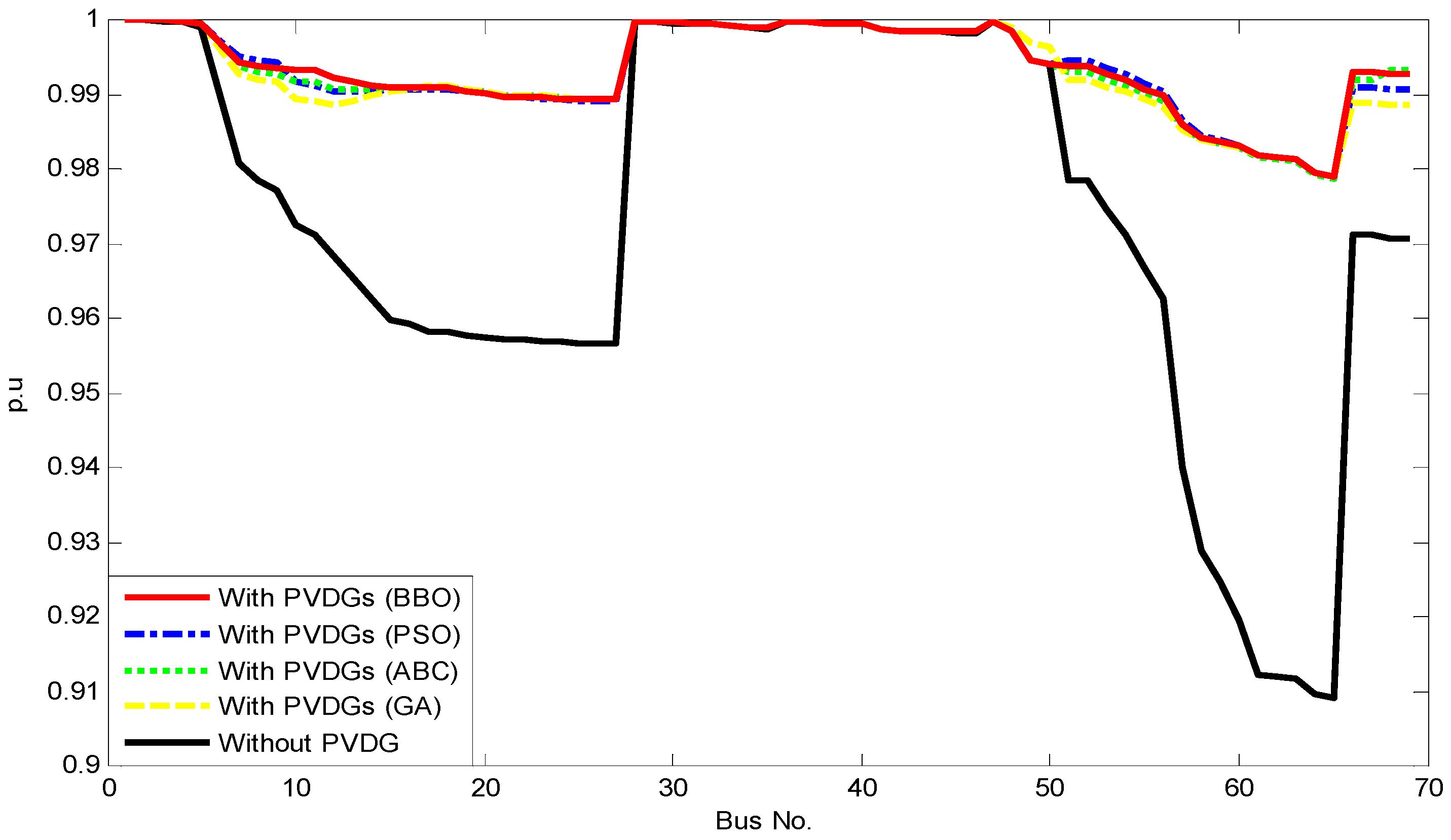
- We demonstrate the high performance of installing PVDG units in distribution power network: power loss can be reduced optimally while IHD, THD and voltage profile are improved significantly.
- (3)
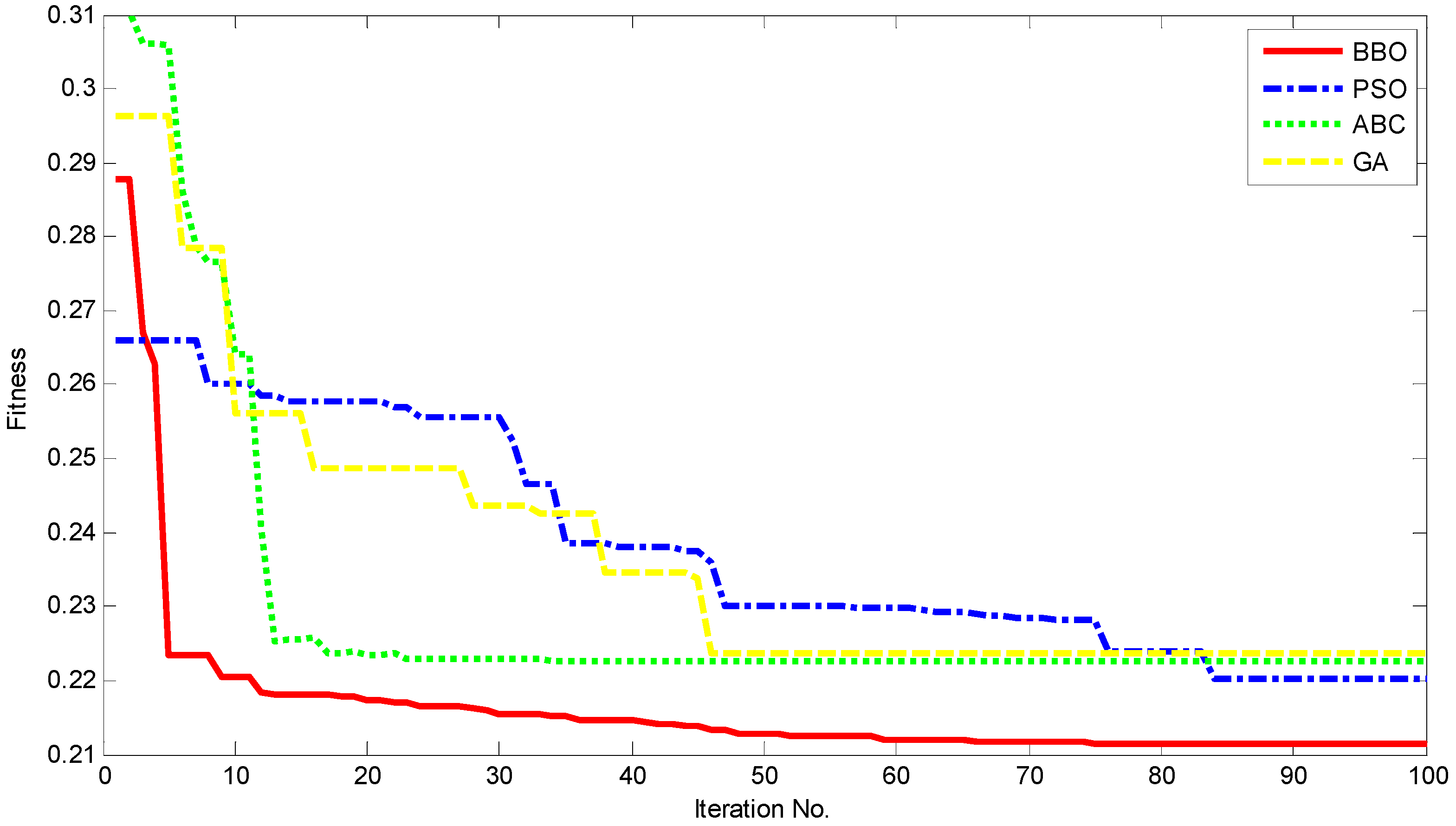
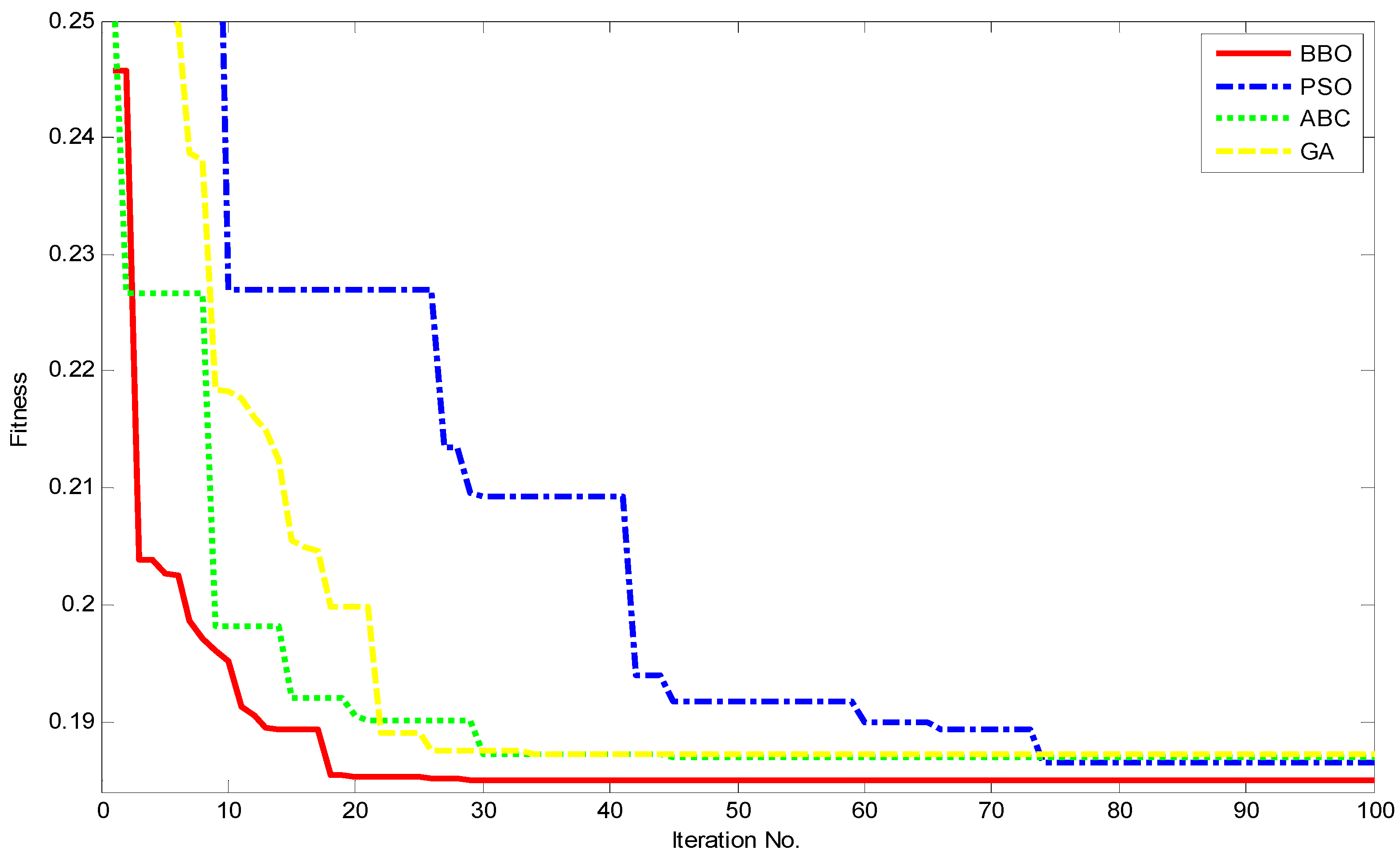
- We test the effectiveness level of four applied methods: BBO is the best one in finding the best location and the most appropriate capacity of PVDG units. All results from the distribution power network such as power loss, IHD, THD, voltage profile and together with the total capacity of al all PVDG units obtained by BBO are more effectively than other methods. In addition, BBO is also superior to other ones in terms of faster solution search.
2. Problem Formulation
2.1. Objective Function
2.1.1. Total Active Power Loss
2.1.2. Harmonic Distortion
2.2. Constraints
2.2.1. The power Balance Constraints
2.2.2. The Voltage Limits
2.2.3. Total Voltage Harmonic Distortion & Individual Voltage Harmonic Distortion Limits
2.2.4. The PVDG Units’ Capacity Limits
3. Biogeography-Based Optimization Algorithm (BBO)
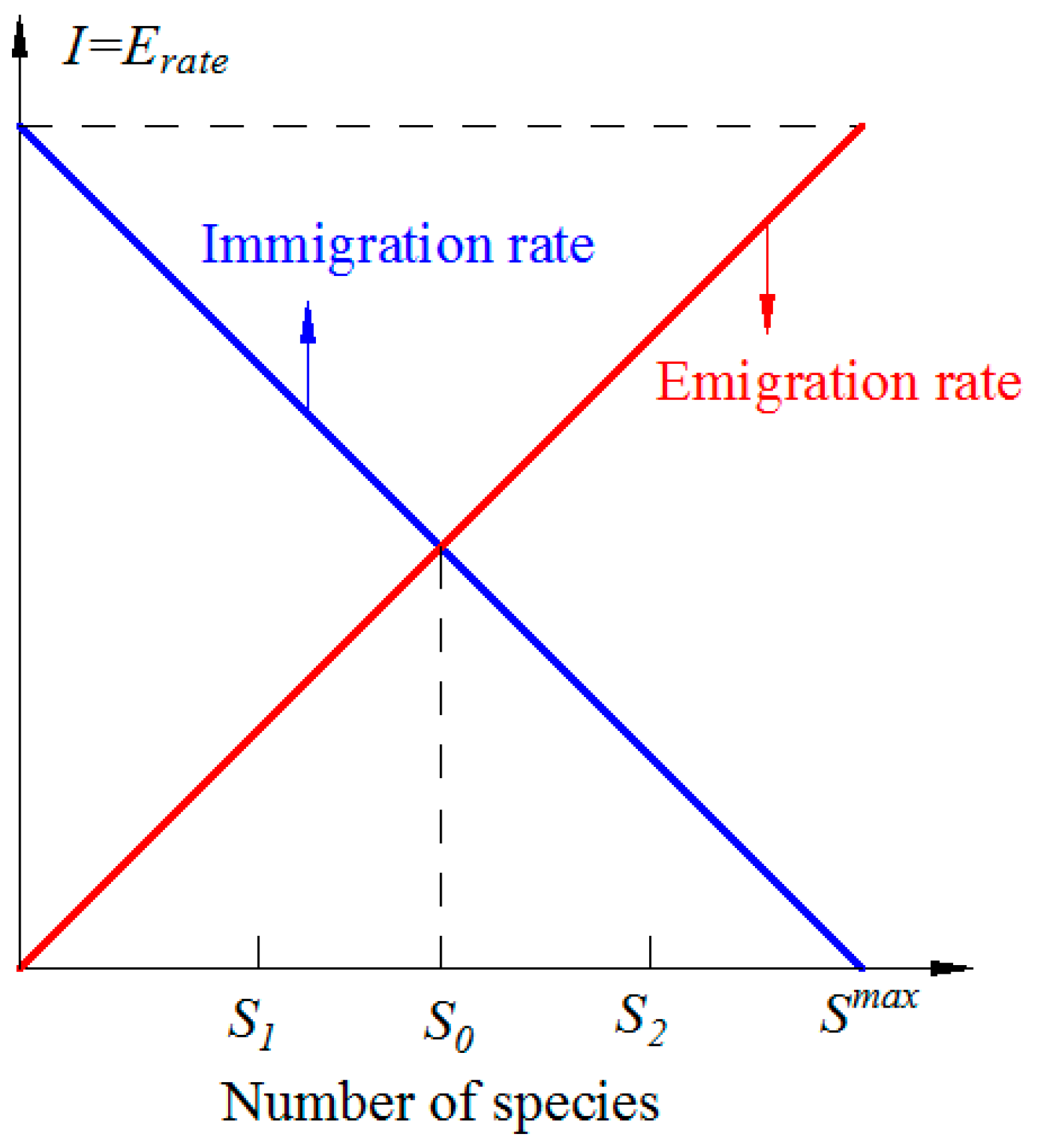
3.1. Basic Description of BBO
3.2. Migration Operation
3.3. Mutation Operation
3.4. Procedures for Implementing BBO Algorithm
- Step 1:
- Initialize BBO parameters that are necessary for the algorithm. These parameters include population size (the number of habitats), maximum immigration rate, emigration rate, mutation coefficient, the elite keeping rate, the habitat modification probability, number of control variables.
- Step 2:
- Randomly generate population in the acceptable limits. Each member in the population contains the value of all the variations and every variation in the population indicates SIVs for that member.
- Step 3:
- Calculate and collect the value of objective function for all population members. This value indicates the HSI for that Habitat. In this case, if the problem is a constrained optimization problem, then a specific approach such as penalty is used for converting the constrained optimization problem into the unconstrained optimization problem.
- Step 4:
- Map the HSI value to obtain the species count. Here, the species count with high value is allotted to the population member having high HSI for maximization optimization problem.
- Step 5:
- Calculate immigration rate and emigration rate for Hm. Calculate λm and μm by using Equations (19) and (20), respectively.
- Step 6:
- Migration operation [29]. Migration operation is applied for modifying habitats, which are selected probabilistically (roulette wheel method can be used for selection). In this step, the selected habitat Hm,d will be replaced by another habitat Hj,d. While, the probability of election of Hm is proportional to immigration rate (λm) and the probability of election of Hj is proportional to emigration rate (μm).After applying migration operation, HSI must be calculated.
- Step 7:
- Mutation operator [29]. Mutation operation is applied for each selected habitat. Select Hm,d according to mutation rate of Equation (21). The quantity of HSI for selected mutation habitat must be calculated again:
- Step 8:
- Best obtained solution is saved using elitism. Select population for next generation.
- Step 9:
- Repeat from step 3 until the specified number of generations or termination criterion is reached.
4. Biogeography-Based Optimization Algorithm for PVDG Units
4.1. Producting Initial Solutions
4.2. Produce New Solutions and Fix Violated Variables
4.3. Calculate of Fitness Function Value
4.4. Termination of Iterative Algorithm
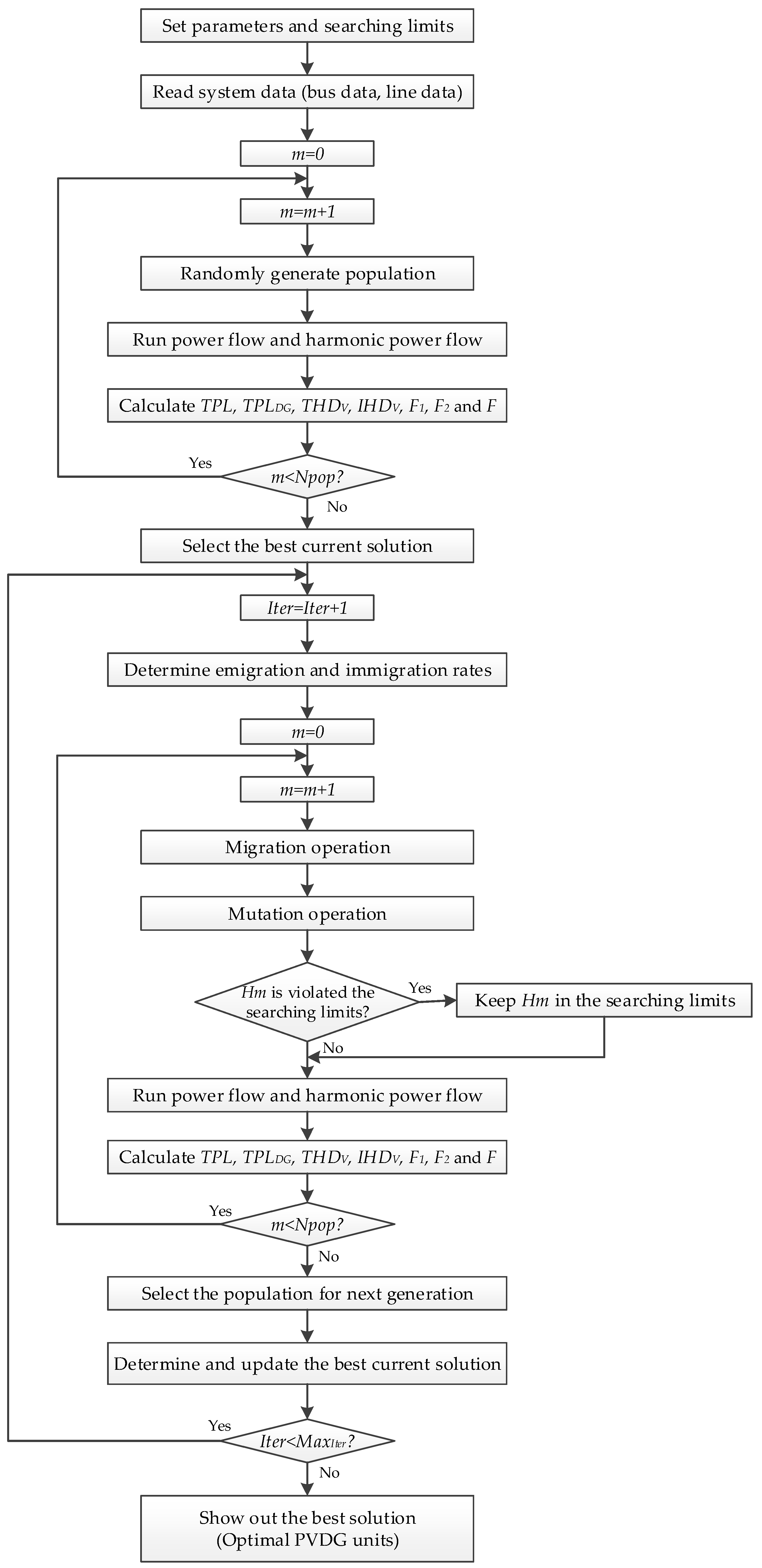
4.5. The Whole Search Procedure of BBO for Considered Problem
- Step 1:
- Assign values to main parameters of BBO such as maximum immigration rate, emigration rate, mutation coefficient, kept population rate in percent, maximum number of iterations, population size, the number of installed PVDG units and rated power of each PVDG unit.
- Step 2:
- Read system data, which includes line data and bus data of the radial distributed system.
- Step 3:
- Generate population by using Equation (25).
- Step 4:
- Run power flow and harmonic power flow based on FW/BWTS to obtain all remaining variables In,m and Vi,m for the mth solution.
- Step 5:
- Calculate total power loss and F1 by using Equations (1) and (2)Calculate THD and IHD by employing Equations (4) and (5)Calculate F2_THD and F2_IHD by using Equations (6) and (7)Determine F2 by using Equation (10)Calculate multi-objective function F by using Equation (11)Evaluate quality of the solution m by calculating Equation (29).
- Step 6: Select the best current solution based on the fitness values.
- Step 7:
- Set the computation to the first iteration (Iter = 1).
- Step 8:
- Determine the emigration rate and immigration rate for Hm by using Equations (19) and (20), respectively.
- Step 9:
- Migration operation: Follow the step 6 at procedures for implementing BBO algorithm.
- Step 10:
- Mutation operation: Follow the step 7 at procedures for implementing BBO algorithm.
- Step 11:
- Check limit violation for all new solutions and correct them by using Equation (28)
- Step 12:
- Run power flow and harmonic power flow based on FW/BWTS to obtain all remaining variables In,m and Vi,m for the mth solution.
- Step 13:
- Calculate total power loss and F1 by using Equations (1) and (2)Calculate THD and IHD by employing Equations (4) and (5)Calculate F2_THD and F2_IHD by using Equations (6) and (7)Determine F2 by using Equation (10)Calculate multi objective function F by using Equation (11)Evaluate quality of the mth solution by calculating Equation (29).
- Step 14:
- Select the population for next generation by combining the top solution at previous generation with the top solution at current generation.
- Step 15:
- Determine and update the best current solution.
- Step 16:
- If Iter < MaxIter, back to step 8. Otherwise, stop searching new solutions and report the best optimal solution.
5. Simulation Results
5.1. Case 1: IEEE 33-Bus Distribution Network
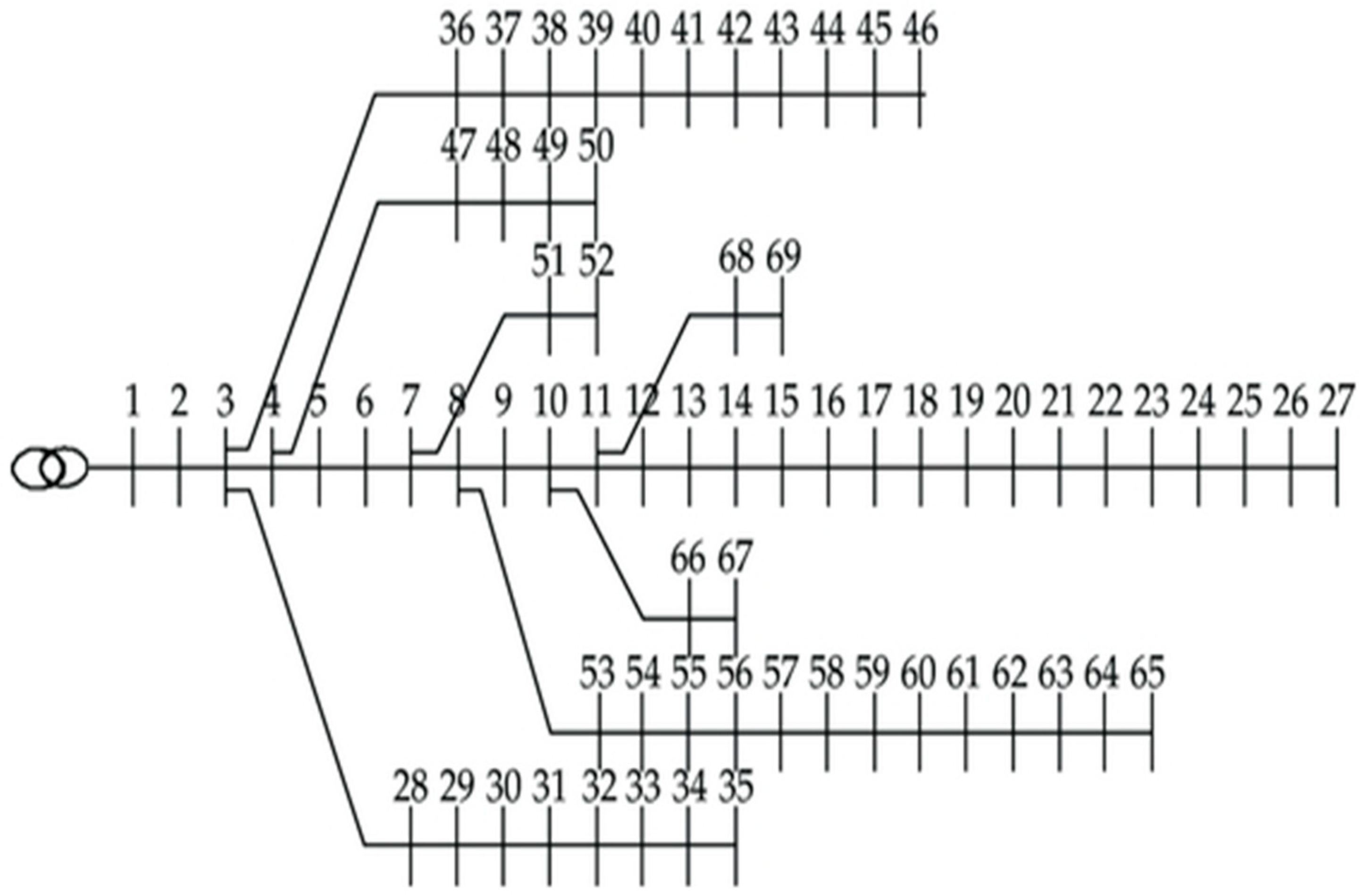
5.2. Case 2: IEEE 69-Bus Distribution Network
- (1)
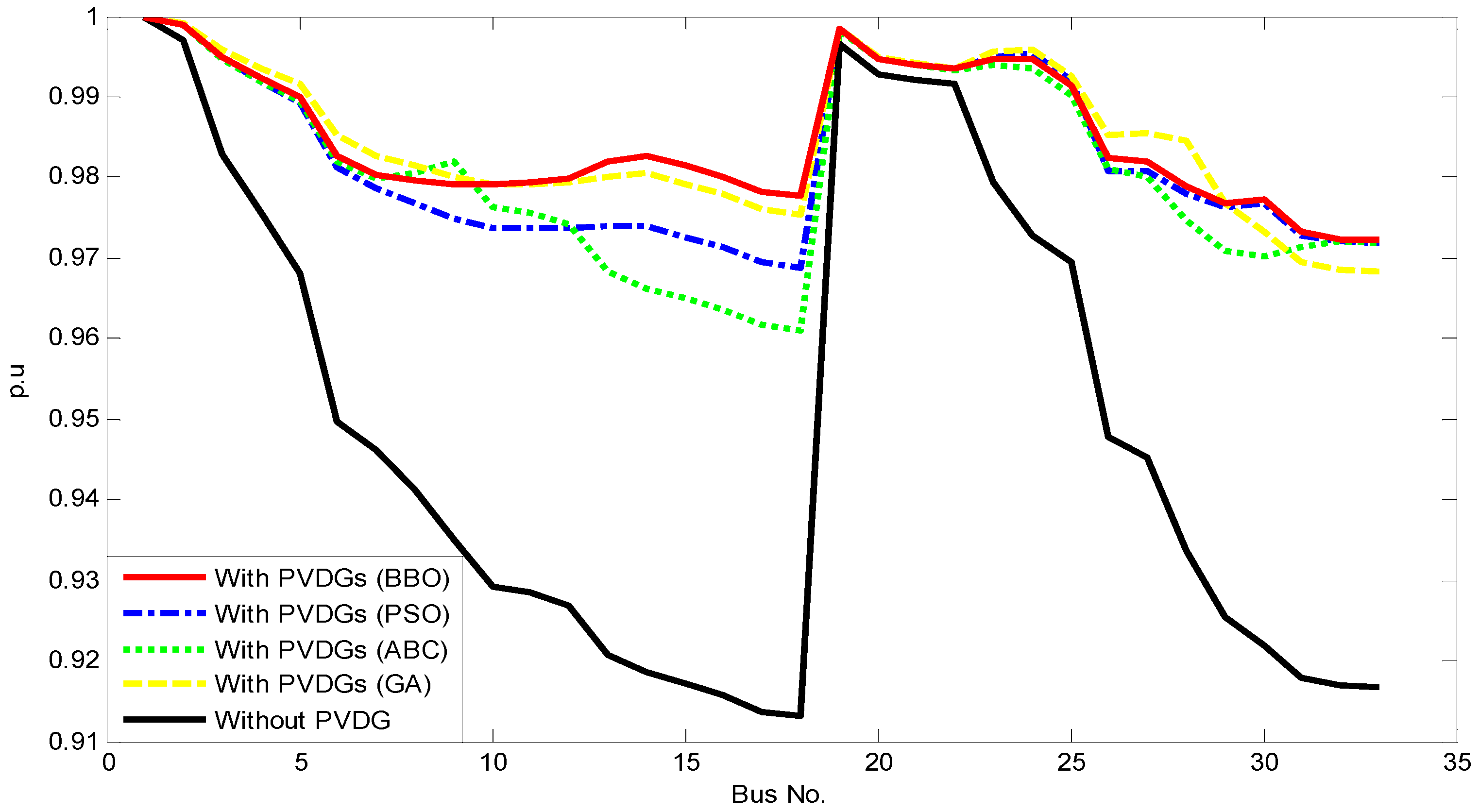
- Installing PVDG units in a distribution power network can bring benefits such as destroying harmonic flows acceptably, improving voltage profiles, and reducing total power losses;
- (2)
- Among the four implemented methods, including GA, ABC, PSO and BBO, the most effective method for determining location and size of PVDG units in distribution power network is BBO. BBO can reduce harmonic magnitude harmfully influencing loads, improve voltage profile, reduce total power loss and minimize capacity of PVDG units.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| μI | The current penalty factor |
| μV | The volt penalty factor |
| α2 | The component in the F2_IHD |
| α1 | The component in the F2_THD |
| μm | Emigration rate |
| λm | Immigration rate |
| ΔIn,m | The current difference at the nth branch of the mth solution |
| γ | The maximum allowable limit of the individual harmonic distortion |
| δ | The maximum allowable limit of the total harmonic distortion |
| ΔVn,m | The voltage difference at the ith bus of the mth solution |
| ω1 | The weight factor of F1 |
| ω2 | The weight factor of F2 |
| E and I | Maximum possible emigration rate and immigration rate, respectively |
| F1 | The objective function of the total power loss |
| F2 | The objective function of the harmonic distortion |
| F2_IHD | The component in the objective function of the individual harmonic distortion |
| F2_THD | The component in the objective function of the total harmonic distortion |
| FFm | The fitness function of the mth solution |
| Fm | The objective function of the mth solution |
| Hj | The jth habitat |
| Hm | The mth habitat |
| H | The number of order harmonic under consideration |
| Hj,d | The jth emigrating habitat with dth control variable |
| Hmin | The lower bound in the searching space |
| Hm,d | The mth immigrating habitat with the dth control variable |
| Hmax | The upper bound in the searching space |
| HSI | The habitat suitable index |
| In | The current magnitude of the nth branch before installing PVDG units |
| InDG | The current magnitude of the nth branch after installing PVDG units |
| The voltage individual harmonic distortion of the hth order harmonic at the ith bus | |
| The maximum voltage individual harmonic distortion at the system | |
| In,m | The current of the mth solution at the nth branch |
| The maximum current at the nth branch | |
| Iter | Current iteration number |
| Lj,m | The location of the jth PVDG unit at the mth solution |
| The lower bound in the location of the jth PVDG unit | |
| The upper bound in the location of the jth PVDG unit | |
| m(s) | The mutation rate of an individual solution |
| MaxIter | Maximum iteration number |
| mmax | The maximum mutation rate |
| Nbr | The number of branches in the system |
| Nbus | The number of buses in the system |
| NDG | The total number of PVDG units |
| Nload | The number of loads in the system |
| Npop | Population size |
| Pmod | The habitat modification probability |
| The maximum value of the PVDG sizing | |
| The minimum value of the PVDG sizing | |
| PDG,i | Active power of the ith PVDG unit |
| Pgrid | Total active power of grid |
| Pj,m | The capacity of the jth PVDG unit at the mth solution |
| The lower bound in the capacity of the jth PVDG unit | |
| The upper bound in the capacity of the jth PVDG unit | |
| Pload,i | Total active power of the ith load |
| Ploss,n | Total active power loss of the nth branch |
| Pmax | The maximum probability of species count |
| Ps | The probability of the habitat |
| Rn | The resistance of the nth branch in the distribution system |
| SIV | The suitability index variable |
| Sm | The mth species count |
| Smax | The maximum of the species number in the habitat |
| THDv,i | The voltage harmonic distortion at the ith bus |
| The maximum voltage harmonic distortion at the system | |
| TPL | The total power loss of all branches before installing PVDG units |
| TPLDG | The total power loss of all branches after installing PVDG units |
| Vh | The hth order harmonic voltage of the ith bus |
| The fundamental voltage at the ith bus | |
| The maximum voltage at the ith bus | |
| The minimum voltage at the ith bus | |
| Vi | The voltage at the ith bus |
| Vi,m | The voltage at the ith bus of the mth solution |
| Vmax | The maximum voltage |
| Vmin | The minimum voltage |
Appendix A
| From | To | R (Ohms) | X (Ohms) | P (kW) | Q (kVAR) | Imax (A) |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.0922 | 0.0470 | 100 | 60 | 400 |
| 2 | 3 | 0.4930 | 0.2511 | 90 | 40 | 400 |
| 3 | 4 | 0.3660 | 0.1864 | 120 | 80 | 400 |
| 4 | 5 | 0.3811 | 0.1941 | 60 | 30 | 400 |
| 5 | 6 | 0.8190 | 0.7070 | 60 | 20 | 400 |
| 6 | 7 | 0.1872 | 0.6188 | 200 | 100 | 300 |
| 7 | 8 | 0.7114 | 0.2351 | 200 | 100 | 300 |
| 8 | 9 | 1.0300 | 0.7400 | 60 | 20 | 200 |
| 9 | 10 | 1.0440 | 0.7400 | 60 | 20 | 200 |
| 10 | 11 | 0.1966 | 0.0650 | 45 | 30 | 200 |
| 11 | 12 | 0.3744 | 0.1238 | 60 | 35 | 200 |
| 12 | 13 | 1.4680 | 1.1550 | 60 | 35 | 200 |
| 13 | 14 | 0.5416 | 0.7129 | 120 | 80 | 200 |
| 14 | 15 | 0.5910 | 0.5260 | 60 | 10 | 200 |
| 15 | 16 | 0.7463 | 0.5450 | 60 | 20 | 200 |
| 16 | 17 | 1.2890 | 1.7210 | 60 | 20 | 200 |
| 17 | 18 | 0.7320 | 0.5740 | 90 | 40 | 200 |
| 2 | 19 | 0.1640 | 0.1565 | 90 | 40 | 200 |
| 19 | 20 | 1.5042 | 1.3554 | 90 | 40 | 200 |
| 20 | 21 | 0.4095 | 0.4784 | 90 | 40 | 200 |
| 21 | 22 | 0.7089 | 0.9373 | 90 | 40 | 200 |
| 3 | 23 | 0.4512 | 0.3083 | 90 | 50 | 200 |
| 23 | 24 | 0.8980 | 0.7091 | 420 | 200 | 200 |
| 24 | 25 | 0.8960 | 0.7011 | 420 | 200 | 200 |
| 6 | 26 | 0.2030 | 0.1034 | 60 | 25 | 300 |
| 26 | 27 | 0.2842 | 0.1447 | 60 | 25 | 300 |
| 27 | 28 | 1.0590 | 0.9337 | 60 | 20 | 300 |
| 28 | 29 | 0.8042 | 0.7006 | 120 | 70 | 200 |
| 29 | 30 | 0.5075 | 0.2585 | 200 | 600 | 200 |
| 30 | 31 | 0.9744 | 0.9630 | 150 | 70 | 200 |
| 31 | 32 | 0.3105 | 0.3619 | 210 | 100 | 200 |
| 32 | 33 | 0.3410 | 0.5302 | 60 | 40 | 200 |
| From | To | R (Ohms) | X (Ohms) | P (kW) | Q (kVAR) | Imax (A) |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.0005 | 0.0012 | 0 | 0 | 400 |
| 2 | 3 | 0.0005 | 0.0012 | 0 | 0 | 400 |
| 3 | 4 | 0.0015 | 0.0036 | 0 | 0 | 400 |
| 4 | 5 | 0.0251 | 0.0294 | 0 | 0 | 400 |
| 5 | 6 | 0.3660 | 0.1864 | 2.6 | 2.2 | 400 |
| 6 | 7 | 0.3811 | 0.1941 | 40.4 | 30 | 400 |
| 7 | 8 | 0.0922 | 0.0470 | 75 | 54 | 400 |
| 8 | 9 | 0.0493 | 0.0251 | 30 | 22 | 400 |
| 9 | 10 | 0.8190 | 0.2707 | 28 | 19 | 400 |
| 10 | 11 | 0.1872 | 0.0619 | 145 | 104 | 200 |
| 11 | 12 | 0.7114 | 0.2351 | 145 | 104 | 200 |
| 12 | 13 | 1.0300 | 0.3400 | 8 | 5 | 200 |
| 13 | 14 | 1.0440 | 0.3450 | 8 | 5.5 | 200 |
| 14 | 15 | 1.0580 | 0.3496 | 0 | 0 | 200 |
| 15 | 16 | 0.1966 | 0.0650 | 45.5 | 30 | 200 |
| 16 | 17 | 0.3744 | 0.1238 | 60 | 35 | 200 |
| 17 | 18 | 0.0047 | 0.0016 | 60 | 35 | 200 |
| 18 | 19 | 0.3276 | 0.1083 | 0 | 0 | 200 |
| 19 | 20 | 0.2106 | 0.0690 | 1 | 0.6 | 200 |
| 20 | 21 | 0.3416 | 0.1129 | 114 | 81 | 200 |
| 21 | 22 | 0.0140 | 0.0046 | 5 | 3.5 | 200 |
| 22 | 23 | 0.1591 | 0.0526 | 0 | 0 | 200 |
| 23 | 24 | 0.3463 | 0.1145 | 28 | 20 | 200 |
| 24 | 25 | 0.7488 | 0.2475 | 0 | 0 | 200 |
| 25 | 26 | 0.3089 | 0.1021 | 14 | 10 | 200 |
| 26 | 27 | 0.1732 | 0.0572 | 14 | 10 | 200 |
| 3 | 28 | 0.0044 | 0.0108 | 26 | 18.6 | 200 |
| 28 | 29 | 0.0640 | 0.1565 | 26 | 18.6 | 200 |
| 29 | 20 | 0.3978 | 0.1315 | 0 | 0 | 200 |
| 30 | 31 | 0.0702 | 0.0232 | 0 | 0 | 200 |
| 31 | 32 | 0.3510 | 0.1160 | 0 | 0 | 200 |
| 32 | 33 | 0.8390 | 0.2816 | 14 | 10 | 200 |
| 33 | 34 | 1.7080 | 0.5646 | 19.5 | 14 | 200 |
| 34 | 35 | 1.4740 | 0.4873 | 6 | 4 | 200 |
| 3 | 36 | 0.0044 | 0.0108 | 26 | 18.55 | 200 |
| 36 | 37 | 0.0640 | 0.11565 | 26 | 18.55 | 200 |
| 37 | 38 | 0.1053 | 0.1230 | 0 | 0 | 200 |
| 38 | 39 | 0.0304 | 0.0355 | 24 | 17 | 200 |
| 39 | 40 | 0.0018 | 0.0021 | 24 | 17 | 200 |
| 40 | 41 | 0.7283 | 0.8509 | 1.2 | 1 | 200 |
| 41 | 42 | 0.3100 | 0.3623 | 0 | 0 | 200 |
| 42 | 43 | 0.0410 | 0.0478 | 6 | 4.3 | 200 |
| 43 | 44 | 0.0092 | 0.0116 | 0 | 0 | 200 |
| 44 | 45 | 0.1089 | 0.1373 | 39.22 | 26.3 | 200 |
| 45 | 46 | 0.0009 | 0.0012 | 39.22 | 26.3 | 200 |
| 4 | 47 | 0.0034 | 0.0084 | 0 | 0 | 300 |
| 47 | 48 | 0.0851 | 0.2083 | 79 | 56.4 | 300 |
| 48 | 49 | 0.2898 | 0.7091 | 384.7 | 274.5 | 300 |
| 49 | 50 | 0.0822 | 0.2011 | 384.7 | 274.5 | 300 |
| 8 | 51 | 0.0928 | 0.0473 | 40.5 | 28.3 | 200 |
| 51 | 52 | 0.3319 | 0.1114 | 3.6 | 2.7 | 200 |
| 9 | 53 | 0.1740 | 0.0886 | 4.35 | 3.5 | 300 |
| 53 | 54 | 0.2030 | 0.1034 | 26.4 | 19 | 300 |
| 54 | 55 | 0.2842 | 0.1447 | 24 | 17.2 | 300 |
| 55 | 56 | 0.2813 | 0.1433 | 0 | 0 | 300 |
| 56 | 57 | 1.5900 | 0.5337 | 0 | 0 | 300 |
| 57 | 58 | 0.7837 | 0.2630 | 0 | 0 | 300 |
| 58 | 59 | 0.3042 | 0.1006 | 100 | 72 | 300 |
| 59 | 60 | 0.3861 | 0.1172 | 0 | 0 | 300 |
| 60 | 61 | 0.5075 | 0.2585 | 1244 | 888 | 300 |
| 61 | 62 | 0.0974 | 0.0496 | 32 | 23 | 300 |
| 62 | 63 | 0.1450 | 0.0738 | 0 | 0 | 300 |
| 63 | 64 | 0.7105 | 0.3619 | 227 | 162 | 300 |
| 64 | 65 | 1.0410 | 0.5302 | 59 | 42 | 300 |
| 11 | 66 | 0.2012 | 0.0611 | 18 | 13 | 200 |
| 66 | 67 | 0.0047 | 0.0014 | 18 | 13 | 200 |
| 12 | 68 | 0.7394 | 0.2444 | 28 | 20 | 200 |
| 68 | 69 | 0.0047 | 0.0016 | 28 | 20 | 200 |
References
- Pandey, R.R.; Arora, S. Distributed generation system: A review and its impact on India. Int. Res. J. Eng. Technol. (IRJET) 2016, 3, 758–765. [Google Scholar]
- Kamaruzzaman, A.Z.; Mohamed, A.; Shareef, H. Effect of grid-connected photovoltaic systems on static anddynamic voltage stability with analysis techniques—A review. Universiti Kebangsaan Malays. 2015, 134–138. [Google Scholar] [CrossRef]
- Sahib, J.T.; Ghani, A.R.M.; Jano, Z.; Mohamed, H.I. Optimum allocation of distributed generation using PSO: IEEE test case studies evaluation. Int. J. Appl. Eng. Res. 2017, 12, 2900–2906. [Google Scholar]
- Saad, M.N.; Sujod, Z.M.; Ming, H.L.; Abas, F.M.; Jadin, M.S.; Ishak, R.M.; Abdullah, H.R.N. Impacts of photovoltaic distributed generation location and size on distribution power system network. Int. J. Power Electron. Drive Syst. (IJPEDS). 2018, 9, 905–913. [Google Scholar]
- Sadeghian, H.; Athari, H.M.; Wang, Z. Optimized solar photovoltaic generation in a real local distribution network. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; pp. 2472–8152. [Google Scholar]
- Khorasany, M.; Aalami, H. Determination of the optimal location and sizing of DGs in radial distribution network using modified PSO and ABC algorithms. Int. J. Mod. Trends Eng. Res. 2016, 3, 429–436. [Google Scholar]
- Kumawat, A.; Singh, P. Optimal placement of capacitor and DG for minimization of power loss using genetic algorithm and artificial bee colony algorithm. Int. Res. J. Eng. Technol. (IRJET) 2016, 3, 2482–2488. [Google Scholar]
- Phuangpornpitak, W.; Bhumkittipich, K. Optimal placement and sizing of distributed generation for power loss reduction using particle swarm optimization. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 1211–1216. [Google Scholar] [CrossRef]
- Sedighizadeh, M.; Rezazadeh, A. Using genetic algorithm for distributed generation allocation to reduce losses and improve voltage profile. Int. Sch. Sci. Res. Innov. 2008, 2, 50–55. [Google Scholar]
- Sulistyowati, R.; Rianwan, C.D.; Ashari, M. PV farm placement and sizing using GA for area development plan of distribution network. In Proceedings of the 2016 International Seminar on Intelligent Technology and Its Application, Lombok, Indonesia, 28–30 July 2016. [Google Scholar] [CrossRef]
- Othman, M.M.; El-Khattam, W.; Hegazy, G.Y.; Abdelaziz, Y.A. Optimal placement and sizing of distributed generators in unbalanced distribution systems using supervised big bang-big crunch method. IEEE Trans. Power Syst. 2014, 30, 911–919. [Google Scholar] [CrossRef]
- Ameli, A.; Bahrami, S.; Khazaeli, F.; Haghifam, M. A multiobjective particle swarm optimization for sizing and placement of DGs from DG owner’s and distribution company’s viewpoints. IEEE Trans. Power Deliv. 2014, 29, 1831–1840. [Google Scholar] [CrossRef]
- Umar; Firdaus; Ashari, M.; Penangsang, O. Optimal location, size and type of DGs to reduce power loss and voltage deviation considering THD in radial unbalanced distribution systems. In Proceedings of the 2016 International Seminar on Intelligent Technology and Its Application (ISITIA), Lombok, Indonesia, 28–30 July 2016; Volume 29, pp. 1831–1840. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evolut. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Kadir, A.F.A.; Mohamed, A.; Shareef, H.; Wanik, C.Z.M.; Ibrahim, A.A. Optimal sizing and placement of distributed generation in distribution system considering losses and THDv using gravitational search algorithm. Przegląd Elektrotechniczny 2013, 89, 132–136. [Google Scholar]
- Teng, H.J.; Chang, Y.C. Backward/Forward sweep-based harmonic analysis method for distribution system. IEEE Trans. Power Deliv. 2007, 22, 1665–1672. [Google Scholar] [CrossRef]
- Beránek, V.; Olšan, T.; Libra, M.; Poulek, V.; Sedláček, J.; Dang, M.-Q.; Tyukhov, I.I. New Monitoring System for Photovoltaic Power Plants’ Management. Energies 2018, 11, 2495. [Google Scholar] [CrossRef]
- Allah, A.B.; Djamel, L. Control of power and voltage of solar grid connected. Int. J. Electr. Comput. Eng. (IJECE) 2016, 6, 26–33. [Google Scholar] [CrossRef]
- Hu, H.; Shi, Q.; He, Z.; He, J.; Gao, S. Potential harmonic resonance impact of PV inverter filters on distribution systems. IEEE Trans. Sustain. Energy 2015, 6, 151–161. [Google Scholar] [CrossRef]
- Sariraja, R.M.; Muthulakshmi, K.; Kumar, S.V.; Abinaya, T. PSO based optimal distributed generation placement and capacity by considering harmonic limits. Tech. Gaz. 2017, 24, 391–398. [Google Scholar]
- Prakash, P.; Khatod, K.D. Optimal sizing and siting techniques for distributed generation in distribution system: A review. Renew. Sustain. Energy Rev. 2016, 111–130. [Google Scholar] [CrossRef]
- Wazir, A.; Arbab, N. Analysis and optimization of IEEE 33 bus radial distributed system using optimization algorithm. J. Eng. Trends Appl. Eng. 2016, 1, 17–21. [Google Scholar]
- Rao, R.V.V.P.; Raju, S.S. Voltage regulator placement in radial distribution system using plant growth simulation algorithm. Int. J. Eng. Sci. Technol. 2010, 2, 207–217. [Google Scholar] [CrossRef]
- Lim, L.W.; Wibowo, A.; Desa, I.M.; Haron, H. A Biogeography-based optimization algorithm hybridized with tabu search for the quadratic assignment problem. Comput. Intell. Neurosci. 2016. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, H.; Ghaffarzadeh, N. A simultaneous biogeography based optimal location of DG units and capacitor bank in distribution systems with nonlinear loads. J. Electr. Eng. 2016, 67, 351–357. [Google Scholar] [CrossRef]
- Kumar, R.A.; Premalatha, L. Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization. Electr. Power Energy Syst. 2015, 73, 393–399. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, P.; Ren, M.; Yang, Y.; Tian, X. Improved biogeography-based optimization based on affinity propagation. Int. J. Geo-Inf. 2016, 5, 129. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J. Chapter 2: Advanced optimization techniques. Mech. Des. Opt. Using Adv. Opt. Tech. 2012, 7, 11–14. [Google Scholar]
- Wang, C.Z.; Wu, B.X. Hybrid biogeography-based optimization for integer programming. Sci. World J. 2014, 2014, 672983. [Google Scholar] [CrossRef]
- Palomino, G.G.; Barragán, A.A.L.; Trujillo, R.E. Locating distributed generation units radial systems. Contemp. Eng. Sci. 2017, 10, 1035–1046. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, B.G.; Bakar, A.H.A.; Mokhlis, H. A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system load ability using HPSO (hybrid particle swarm optimization) algorithm. Energy 2014, 66, 202–215. [Google Scholar] [CrossRef]
- Sajeevan, S.; Padmavathy, N. Optimal allocation and sizing of distributed generation using artificial bee colony algorithm. Int. Res. J. Eng. Technol. (IRJET) 2016, 3, 1244–1252. [Google Scholar]
- Pandey, D.; Bhadoriya, S.J. Optimal placement & sizing of distributed generation (DG) to minimize active power loss using particle swarm optimization (PSO). Int. J. Sci. Technol. Res. 2014, 3, 246–254. [Google Scholar]
- Vita, V. Development of a decision-making algorithm for the optimum size and placement of distributed generation units in distribution networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Harmonic Spectrum. Available online: https://github.com/tshort/OpenDSS/blob/master/Test/indmachtest/Spectrum.DSS (accessed on 7 January 2014).
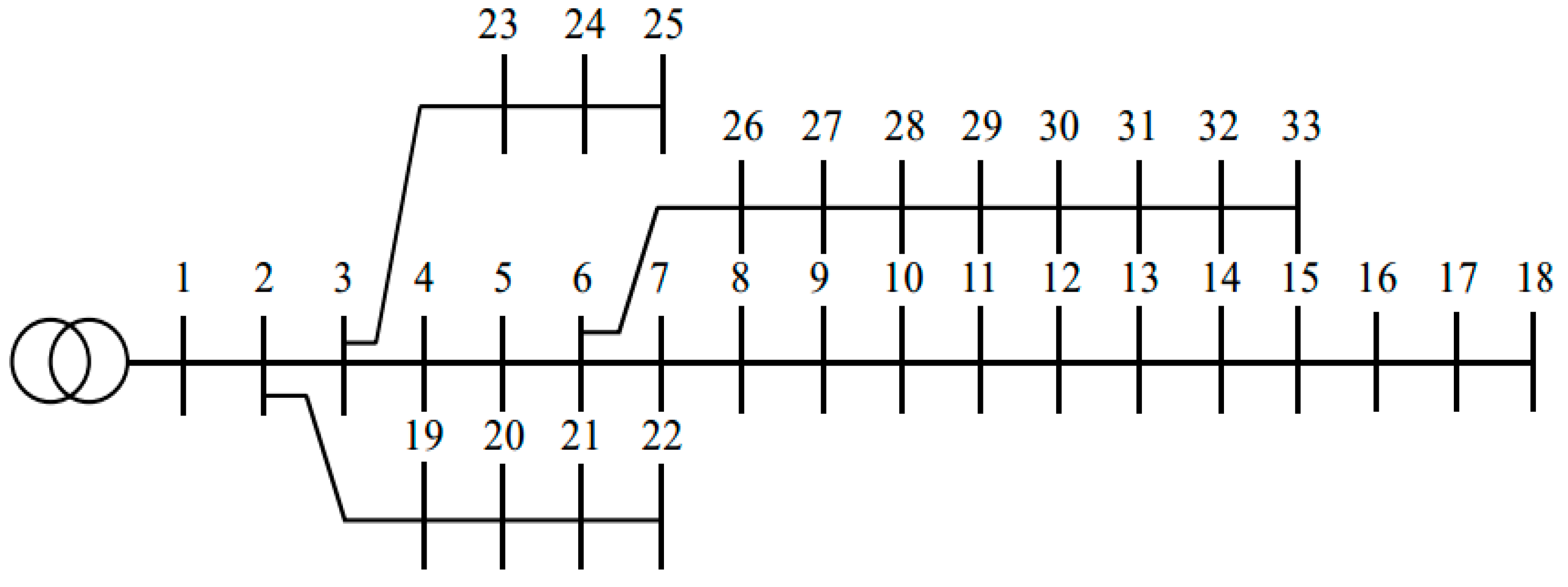
| Harmonic Order | Magnitude (%) | Angle (°) |
|---|---|---|
| 5; 7; 11; 13; 17 | 0.765; 0.627; 0.248; 0.127; 0.071 | 28; −180; −59; 79; −253 |
| Method | GA | ABC | PSO | BBO |
|---|---|---|---|---|
| The worst F | 0.2570 | 0.2401 | 0.2523 | 0.2219 |
| Average F | 0.2375 | 0.2313 | 0.2291 | 0.2152 |
| The best F | 0.2238 | 0.2227 | 0.2203 | 0.2115 |
| The best F1 | 0.3730 | 0.3712 | 0.3672 | 0.3525 |
| The best F2 | 0 | 0 | 0 | 0 |
| Case | Without PVDG | With PVDGs and GA | With PVDGs and ABC | With PVDGs and PSO | With PVDGs and BBO |
|---|---|---|---|---|---|
| (%) | 6.0331 | 4.1902 | 4.1627 | 4.2749 | 3.9355 |
| (%) | 3.9133 | 2.7187 | 2.7009 | 2.7736 | 2.5535 |
| Total active power loss (MW) | 0.2027 | 0.0756 | 0.0752 | 0.0744 | 0.0715 |
| Method | The Best Solution | Total Capacity of PVDG Units |
|---|---|---|
| GA | Bus: 14–Size: 0.6947 MW | 3.3419 MW |
| Bus: 24–Size: 1.1844 MW | ||
| Bus: 28–Size: 1.4628 MW | ||
| ABC | Bus: 09–Size: 1.1372 MW | 3.0077 MW |
| Bus: 24–Size: 1.0674 MW | ||
| Bus: 32–Size: 0.8031 MW | ||
| PSO | Bus: 09–Size: 1.0625 MW | 3.0590 MW |
| Bus: 24–Size: 1.0447 MW | ||
| Bus: 30–Size: 0.9518 MW | ||
| BBO | Bus: 14–Size: 0.7539 MW | 2.9247 MW |
| Bus: 24–Size: 1.0994 MW | ||
| Bus: 30–Size: 1.0714 MW |
| Method | GA | ABC | PSO | BBO |
|---|---|---|---|---|
| The worst F | 0.2499 | 0.1931 | 0.1955 | 0.1871 |
| Average F | 0.1902 | 0.1892 | 0.1881 | 0.1859 |
| The best F | 0.1873 | 0.1870 | 0.1864 | 0.1850 |
| The best F1 | 0.3122 | 0.3117 | 0.3107 | 0.3083 |
| The best F2 | 0 | 0 | 0 | 0 |
| Case | Without PVDG | With PVDGs and GA | With PVDGs and ABC | With PVDGs and PSO | With PVDGs and BBO |
|---|---|---|---|---|---|
| (%) | 5.3964 | 3.7720 | 3.9330 | 3.3511 | 3.3037 |
| (%) | 3.4878 | 2.4372 | 2.5414 | 2.1619 | 2.1305 |
| Total active power loss (MW) | 0.2245 | 0.0701 | 0.0700 | 0.0698 | 0.0692 |
| Method | The Best Solution | Total Capacity of PVDG Units |
|---|---|---|
| GA | Bus: 18–Size: 0.5239 MW | 3.2451 MW |
| Bus: 49–Size: 0.9356 MW | ||
| Bus: 61–Size: 1.7856 MW | ||
| ABC | Bus: 18–Size: 0.4290 MW | 2.5015 MW |
| Bus: 61–Size: 1.7405 MW | ||
| Bus: 69–Size: 0.3320 MW | ||
| PSO | Bus: 09–Size: 0.6385 MW | 2.7678 MW |
| Bus: 17–Size: 0.4390 MW | ||
| Bus: 61–Size: 1.6903 MW | ||
| BBO | Bus: 11–Size: 0.5388 MW | 2.6241 MW |
| Bus: 18–Size: 0.3669 MW | ||
| Bus: 61–Size: 1.7184 MW |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Tran, H.V. Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies 2019, 12, 174. https://doi.org/10.3390/en12010174
Duong MQ, Pham TD, Nguyen TT, Doan AT, Tran HV. Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies. 2019; 12(1):174. https://doi.org/10.3390/en12010174
Chicago/Turabian StyleDuong, Minh Quan, Thai Dinh Pham, Thang Trung Nguyen, Anh Tuan Doan, and Hai Van Tran. 2019. "Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems" Energies 12, no. 1: 174. https://doi.org/10.3390/en12010174
APA StyleDuong, M. Q., Pham, T. D., Nguyen, T. T., Doan, A. T., & Tran, H. V. (2019). Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies, 12(1), 174. https://doi.org/10.3390/en12010174






