In Operando Neutron Radiography Analysis of a High-Temperature Polymer Electrolyte Fuel Cell Based on a Phosphoric Acid-Doped Polybenzimidazole Membrane Using the Hydrogen-Deuterium Contrast Method
Abstract
1. Introduction
2. Experimental
2.1. Cell Design and MEA Preparation
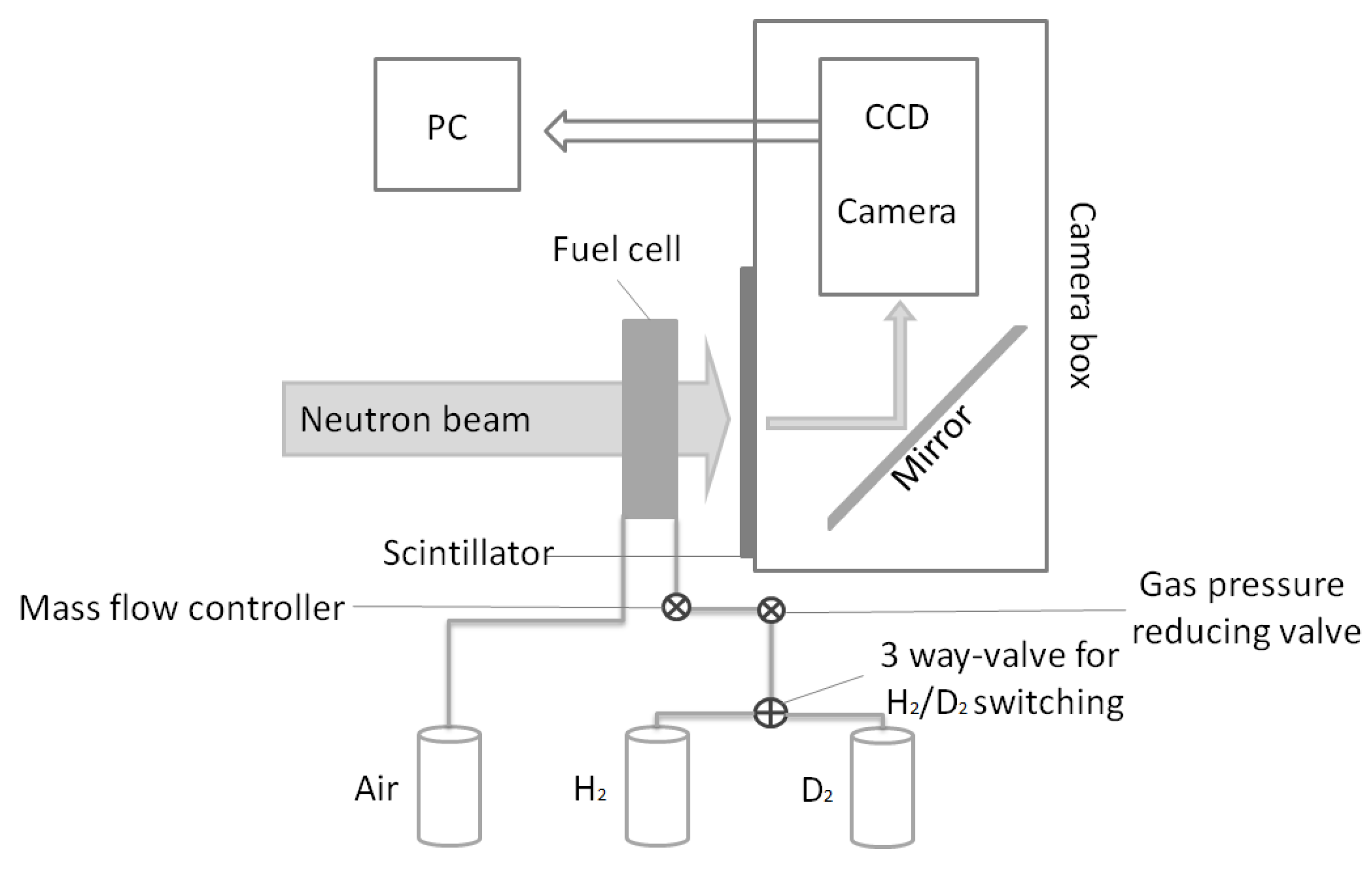
2.2. Neutron Radiography Setup
2.3. Mobile Single Cell Test Station
2.4. Electrochemical Impedance Spectroscopy (EIS)
3. Results and Discussion
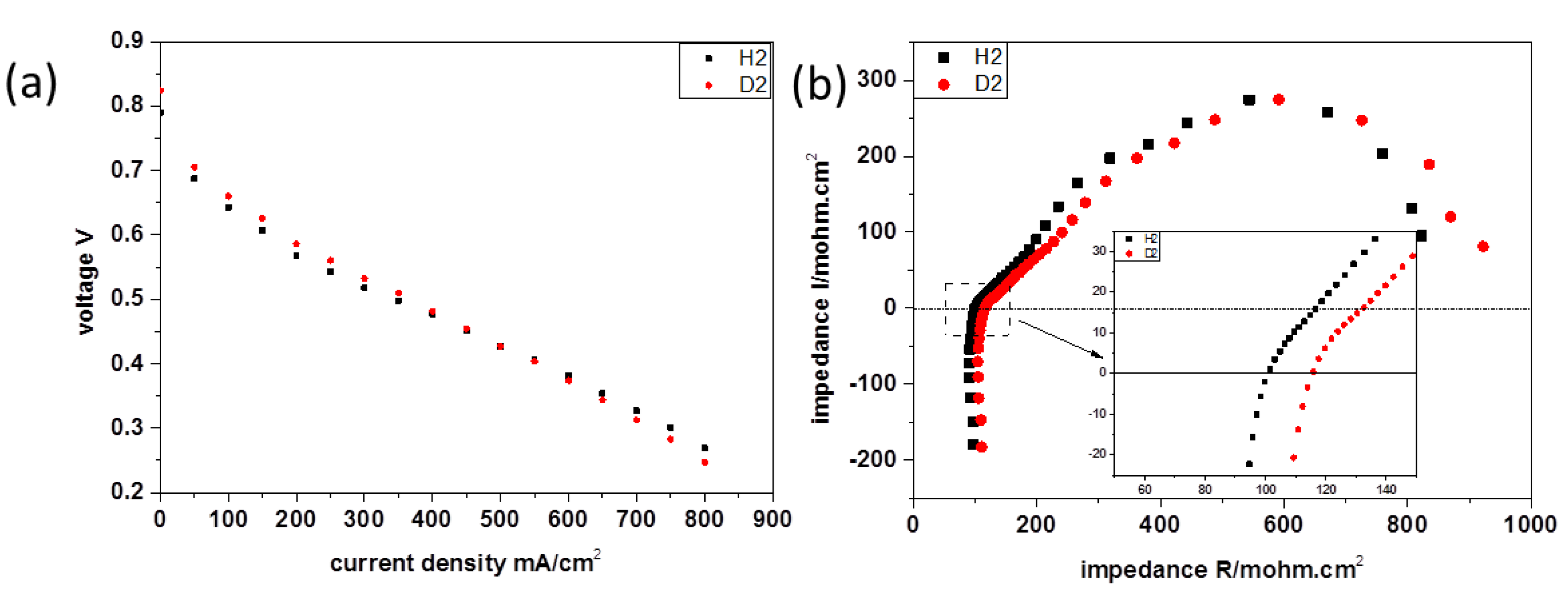
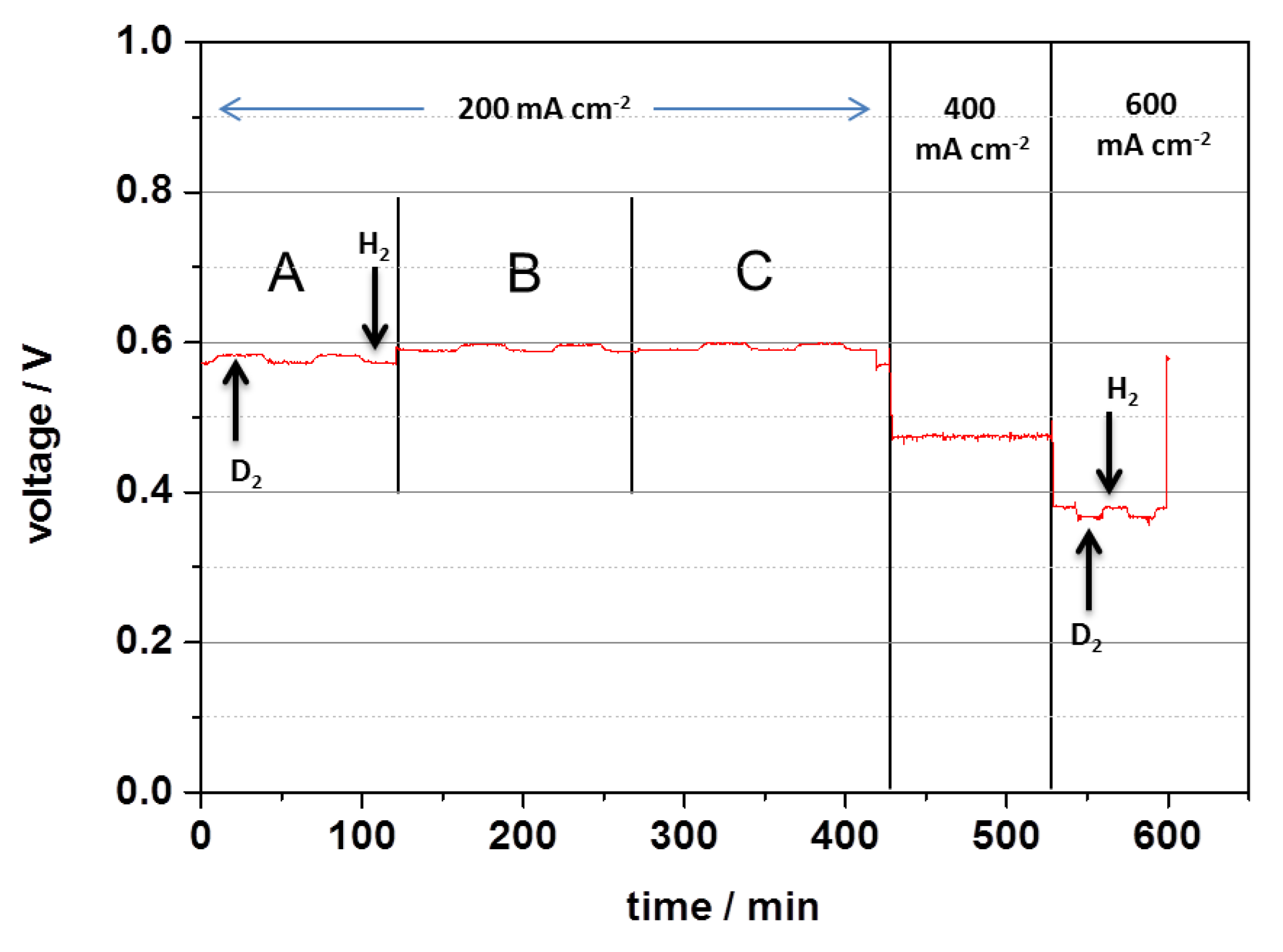
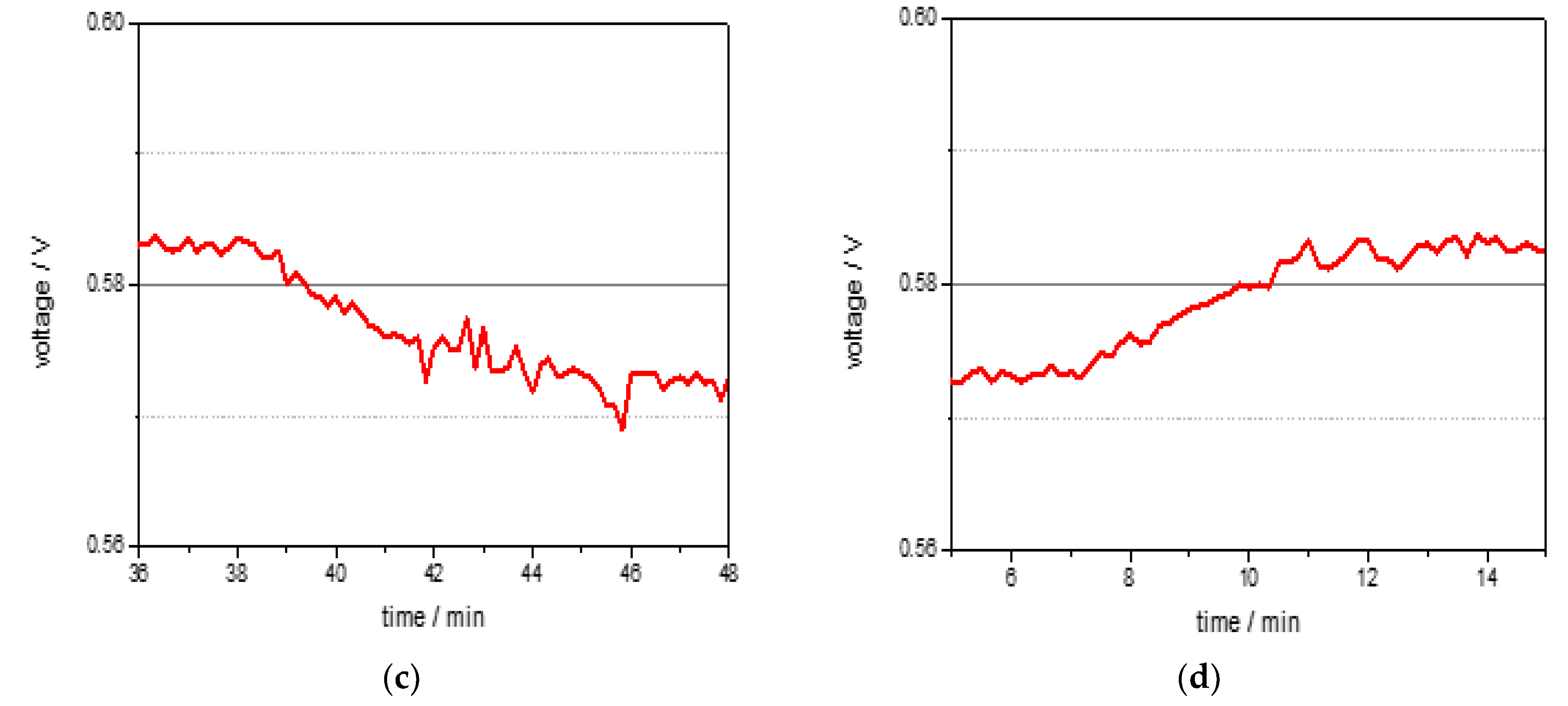
3.1. Cell Performance and Electrochemical Impedance Spectroscopy
3.1.1. Basic Electrochemical Theory
3.1.2. Results and Discussion
3.2. Image Results and Discussion
3.2.1. Overall H/D Exchange Process in the MEA
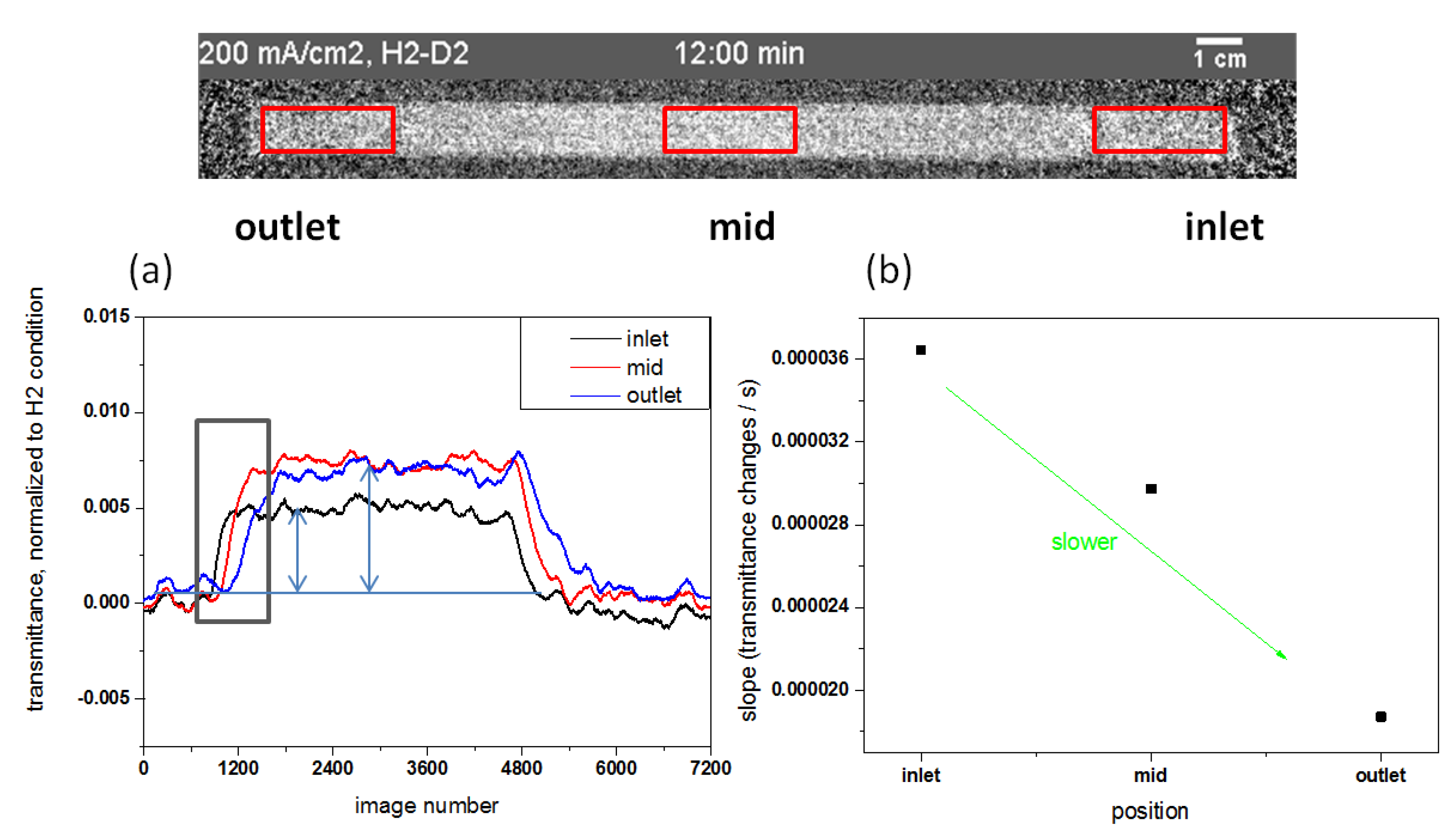
3.2.2. Local H/D Exchange Process of MEA
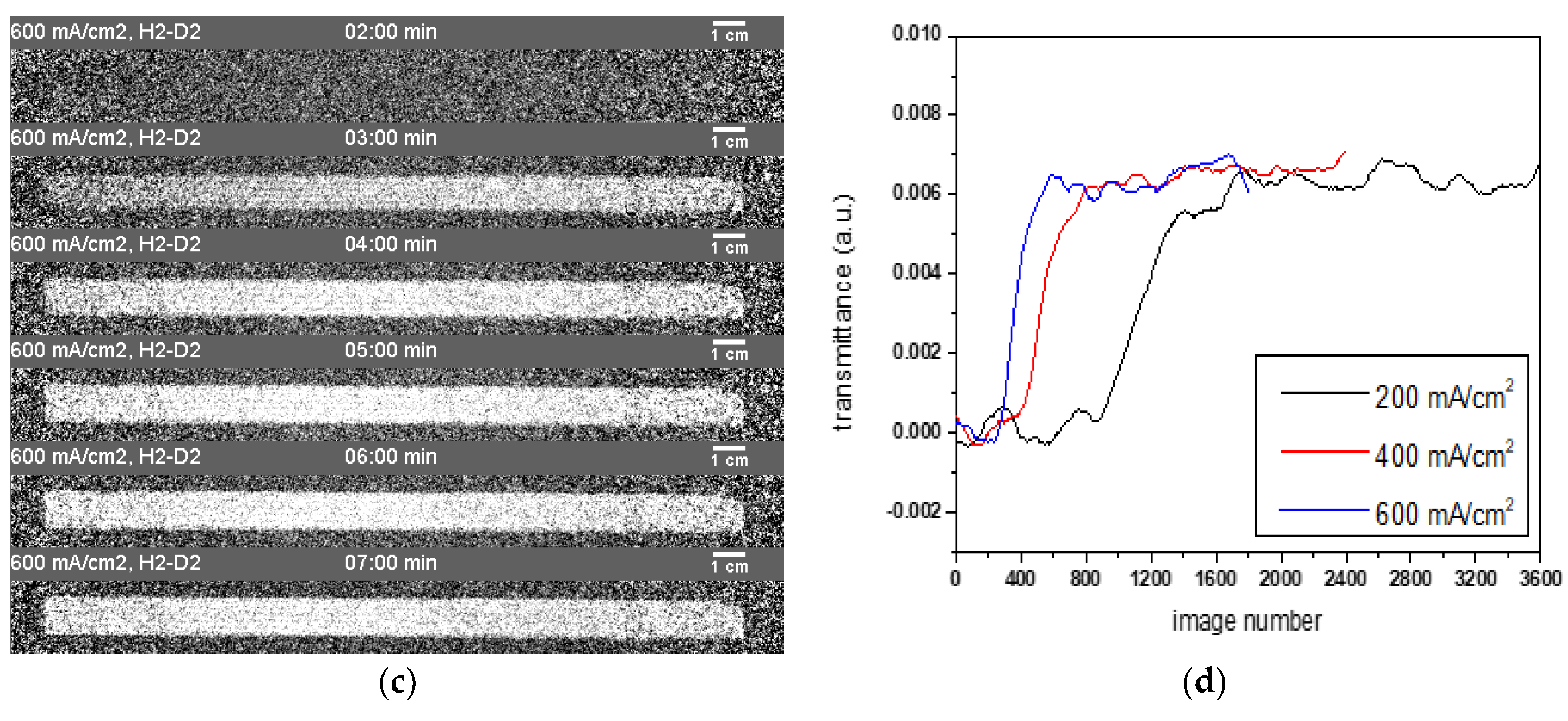
3.2.3. Impact of Different Current Densities on the H/D Exchange Process in the MEA
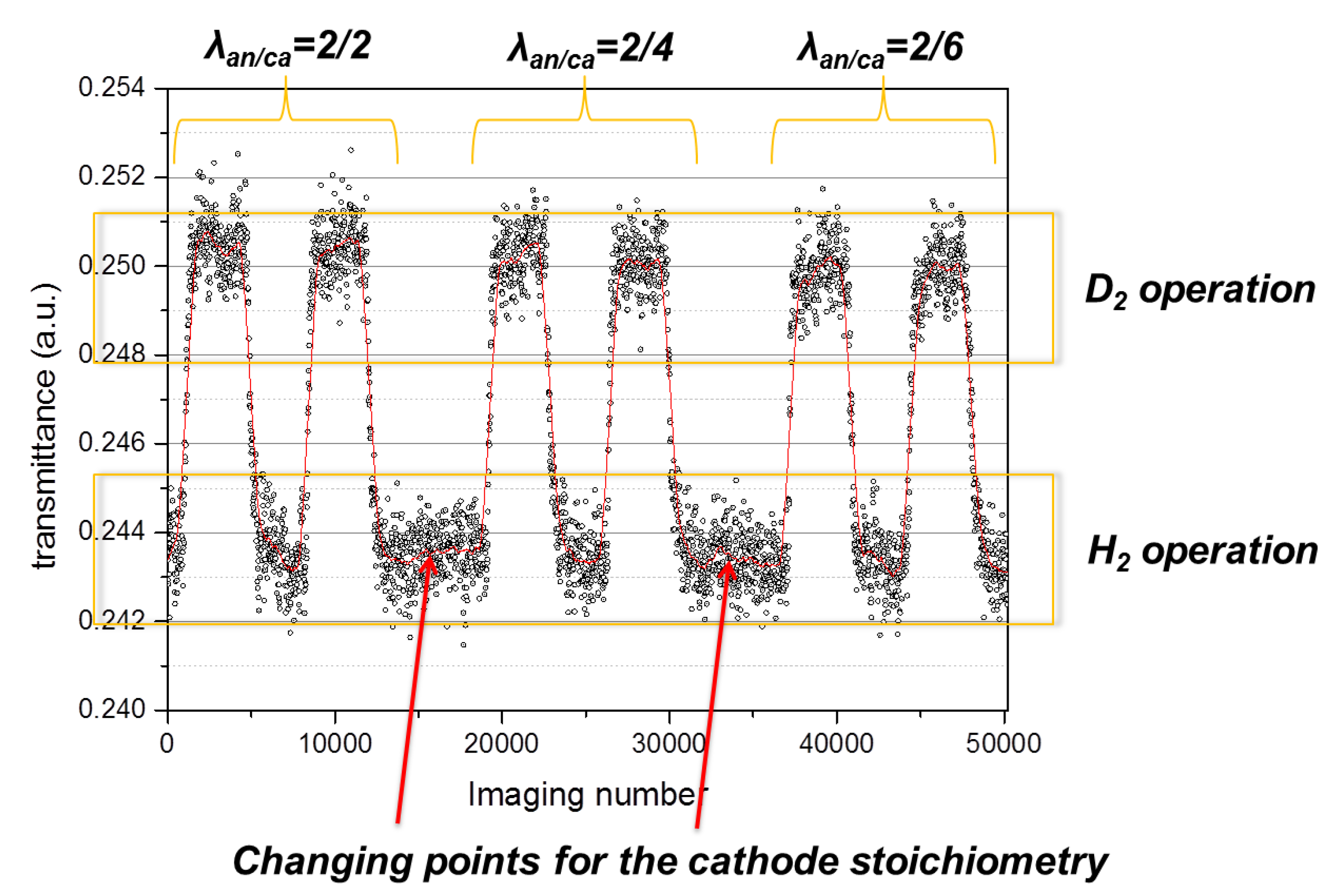
3.2.4. Transmittance Changes Independent of Different Gas Flow Rates at the Cathode
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zaidi, S.J.; Rauf, M.A. Fuel Cell Fundamentals; Springer: New York, NY, USA, 2009; pp. 1–5. [Google Scholar]
- Wannek, C.; Konradi, I.; Mergel, J.; Lehnert, W. Redistribution of phosphoric acid in membrane electrode assemblies for high-temperature polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2009, 34, 9479–9485. [Google Scholar] [CrossRef]
- Li, Q.; Jensen, J.O.; Savinell, R.F.; Bjerrum, N.J. High temperature proton exchange membranes based on polybenzimidazoles for fuel cells. Prog. Polym. Sci. 2009, 34, 449–477. [Google Scholar] [CrossRef]
- Wainright, J.S.; Wang, J.T.; Weng, D.; Savinell, R.F.; Litt, M. Acid-doped polybenzimidazoles: A new polymer electrolyte. J. Electrochem. Soc. 1995, 142, 121–123. [Google Scholar] [CrossRef]
- Maier, W.; Arlt, T.; Wannek, C.; Manke, I.; Riesemeier, H.; Krüger, P.; Scholta, J.; Lehnert, W.; Banhart, J.; Stolten, D. In-situ synchrotron X-ray radiography on high temperature polymer electrolyte fuel cells. Electrochem. Commun. 2010, 12, 1436–1438. [Google Scholar] [CrossRef]
- Maier, W.; Arlt, T.; Wippermann, K.; Wannek, C.; Manke, I.; Lehnert, W.; Stolten, D. Correlation of synchrotron X-ray radiography and electrochemical impedance spectroscopy for the investigation of ht-pefcs. J. Electrochem. Soc. 2012, 159, F398–F404. [Google Scholar] [CrossRef]
- Majerus, A.; Labus, M.; Korte, C.; Bettermann, H.; Lehnert, W. In situ Raman spectroscopy on HT-PEM fuel cell. In Proceedings of the 4th European PEFC & H2 Forum, The European Fuel Cell Forum, Lucerne, Switzerland, 2–5 July 2013. [Google Scholar]
- Eberhardt, S.H.; Büchi, F.N.; Schmidt, T.J. Localization of Phosphoric Acid in HT-PEFCs by X-ray Tomographic Microscopy. In Proceedings of the 4th European PEFC & H2 Forum, The European Fuel Cell Forum, Lucerne, Switzerland, 2–5 July 2013. [Google Scholar]
- Niemöller, A.; Jakes, P.; Kayser, S.; Lin, Y.; Lehnert, W.; Granwehr, J. 3d printed sample holder for in-operando epr spectroscopy on high temperature polymer electrolyte fuel cells. J. Magn. Reson. 2016, 269, 157–161. [Google Scholar] [CrossRef] [PubMed]
- Boillat, P.; Scherer, G.G.; Wokaun, A.; Frei, G.; Lehmann, E.H. Transient observation of 2h labeled species in an operating pefc using neutron radiography. Electrochem. Commun. 2008, 10, 1311–1314. [Google Scholar] [CrossRef]
- Hartnig, C.; Manke, I.; Kardjilov, N.; Hilger, A.; Grünerbel, M.; Kaczerowski, J.; Banhart, J.; Lehnert, W. Combined neutron radiography and locally resolved current density measurements of operating pem fuel cells. J. Power Sources 2008, 176, 452–459. [Google Scholar] [CrossRef]
- Cho, K.T.; Mench, M.M. Investigation of the role of the micro-porous layer in polymer electrolyte fuel cells with hydrogen deuterium contrast neutron radiography. Phys. Chem. Chem. Phys. 2012, 14, 4296. [Google Scholar] [CrossRef] [PubMed]
- Putra, A.; Iwase, H.; Yamaguchi, D.; Koizumi, S.; Maekawa, Y.; Matsubayashi, M.; Hashimoto, T. In-situ observation of dynamic water behavior in polymer electrolyte fuel cell by combined method of small-angle neutron scattering and neutron radiography. J. Phys. Conf. Ser. 2010, 247, 012044. [Google Scholar] [CrossRef]
- Manke, I.; Hartnig, C.; Kardjilov, N.; Messerschmidt, M.; Hilger, A.; Strobl, M.; Lehnert, W.; Banhart, J. Characterization of water exchange and two-phase flow in porous gas diffusion materials by hydrogen-deuterium contrast neutron radiography. Appl. Phys. Lett. 2008, 92, 244101. [Google Scholar] [CrossRef]
- Schröder, A.; Wippermann, K.; Lehnert, W.; Stolten, D.; Sanders, T.; Baumhöfer, T.; Kardjilov, N.; Hilger, A.; Banhart, J.; Manke, I. The influence of gas diffusion layer wettability on direct methanol fuel cell performance: a combined local current distribution and high resolution neutron radiography study. J. Power Sources 2010, 195, 4765–4771. [Google Scholar] [CrossRef]
- Boillat, P.; Biesdorf, J.; Oberholzer, P.; Kaestner, A.; Schmidt, T.J. Evaluation of Neutron Imaging for Measuring Phosphoric Acid Distribution in High Temperature PEFCs. J. Electrochem. Soc. 2014, 161, F192–F198. [Google Scholar] [CrossRef]
- Arlt, T.; Lüke, W.; Kardjilov, N.; Banhart, J.; Lehnert, W.; Manke, I. Monitoring the hydrogen distribution in poly(2,5-benzimidazole)-based (ABPBI) membranes in operating high-temperature polymer electrolyte fuel cells by using H-D contrast neutron imaging. J. Power Sources 2015, 299, 125–129. [Google Scholar] [CrossRef]
- Lüke, L. Analyse des Betriebsverhaltens von Hochtemperature-Polymerelektrolyt-Brennstoffzellen. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2013. [Google Scholar]
- Kardjilov, N.; Hilger, A.; Manke, I.; Banhart, J. Conrad-2: the neutron imaging instrument at hzb. Neutron News 2014, 25, 23–26. [Google Scholar] [CrossRef]
- Josic, L.; Lehmann, E.H.; Mannes, D.; Kardjilov, N.; Hilger, A. Investigation of phase transfer properties of light and heavy water by means of energy selective neutron imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 670, 68–72. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Wippermann, K.; Wannek, C.; Oetjen, H.-F.; Mergel, J.; Lehnert, W. Cell resistances of poly(2,5-benzimidazole)-based high temperature polymer membrane fuel cell membrane electrode assemblies: time dependence and influence of operating parameters. J. Power Sources 2010, 195, 2806–2809. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells; Springer: London, UK, 2006; pp. 27–49. [Google Scholar]
- Chaplin, M. Water Structure and Science. Available online: http://www1.lsbu.ac.uk/water/water_properties.html#tcoef (accessed on 9 January 2017).
- Standard Reference Database of National Institute of Standards and Technology. Available online: http://cccbdb.nist.gov/hf0k.asp (accessed on 9 January 2017).
- Aylward, G.H.; Findlay, T.J. Datensammlung Chemie in SI-Einheiten; VCH: Weinheim, Germany, 1986. [Google Scholar]
- NIST Center for Neutron Research. Available online: https://www.ncnr.nist.gov/instruments/bt1/neutron.html (accessed on 10 March 2017).
- Zeis, R. Materials and characterization techniques for high-temperature polymer electrolyte membrane fuel cells. Beilstein J. Nanotechnol. 2015, 6, 68–83. [Google Scholar] [CrossRef] [PubMed]
- Vilciauskas, L.; Tuckerman, M.E.; Bester, G.; Paddison, S.J.; Kreuer, K.D. The mechanism of proton conduction in phosphoric acid. Nat. Chem. 2012, 4, 461–466. [Google Scholar] [CrossRef] [PubMed]
- Aihara, Y.; Sonai, A.; Hattori, M.; Hayamizu, K. Ion conduction mechanisms and thermal properties of hydrated and anhydrous phosphoric acids studied with 1 h, 2 h, and 31 p nmr. J. Phys. Chem. B 2006, 110, 24999–25006. [Google Scholar] [CrossRef] [PubMed]
- Korte, C. Phosphoric acid, an electrolyte for fuel cells-Temperature and composition dependence of vapor pressure and proton conductivity. Fuel Cell Sci. Eng. 2012, 335–359. [Google Scholar] [CrossRef]
- Kreuer, K.D. Proton Conductivity: Materials and Applications. Chem. Mater. 1996, 8, 610–641. [Google Scholar] [CrossRef]
- Vuilleumier, R.; Borgis, D. Proton conduction: Hopping along hydrogen bonds. Nat. Chem. 2012, 4, 432–433. [Google Scholar]
- Mesmer, R.E.; Herting, D.L. Thermodynamics of Ionization of D2O and D2PO4−. J. Solut. Chem. 1978, 7, 901–912. [Google Scholar] [CrossRef]
- Nowick, A.; Vaysleyb, A. Isotope effect and proton hopping in high-temperature protonic conductors. Solid State Ion. 1997, 97, 17–26. [Google Scholar] [CrossRef]
- Sluyters, J.H.; Sluyters-Rehbach, M. The mechanism of the hydrogen ion conduction in liquid light and heavy water derived from the temperature dependence of their limiting conductivities. J. Phys. Chem. B 2010, 114, 15582–15589. [Google Scholar] [CrossRef] [PubMed]
- Layfield, J.P.; Hammes-schiffer, S. Hydrogen tunneling in enzymes and biomimetic models. Chem. Rev. 2014, 114, 3466–3494. [Google Scholar] [CrossRef] [PubMed]
- Heres, M.; Wang, Y.; Griffin, P.J.; Gainaru, C.; Sokolov, A.P. Proton conductivity in phosphoric acid: The role of quantum effects. Phys. Rev. Lett. 2016, 117, 156001. [Google Scholar] [CrossRef]
- Reimer, U.; Ehlert, J.; Lehnert, W. Water distribution in high temperature polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2016, 41, 1837–1845. [Google Scholar] [CrossRef]
- Pinar, F.J.; Cañizares, P.; Rodrigo, M.A.; Úbeda, D.; Lobato, J. Long-term testing of a high-temperature proton exchange membrane fuel cell short stack operated with improved polybenzimidazole-based composite membranes. J. Power Sources 2015, 274, 177–185. [Google Scholar] [CrossRef]



| Reaction | ||
|---|---|---|
| H2 + 0.5 O2 → H2O (liq.) | −237.18 | 1.229 |
| D2 + 0.5 O2 → D2O (liq.) | −243.44 | 1.262 |
| D2 + 0.5 O2 → D2O (gas) | −234.54 | 1.215 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Arlt, T.; Kardjilov, N.; Manke, I.; Lehnert, W. In Operando Neutron Radiography Analysis of a High-Temperature Polymer Electrolyte Fuel Cell Based on a Phosphoric Acid-Doped Polybenzimidazole Membrane Using the Hydrogen-Deuterium Contrast Method. Energies 2018, 11, 2214. https://doi.org/10.3390/en11092214
Lin Y, Arlt T, Kardjilov N, Manke I, Lehnert W. In Operando Neutron Radiography Analysis of a High-Temperature Polymer Electrolyte Fuel Cell Based on a Phosphoric Acid-Doped Polybenzimidazole Membrane Using the Hydrogen-Deuterium Contrast Method. Energies. 2018; 11(9):2214. https://doi.org/10.3390/en11092214
Chicago/Turabian StyleLin, Yu, Tobias Arlt, Nikolay Kardjilov, Ingo Manke, and Werner Lehnert. 2018. "In Operando Neutron Radiography Analysis of a High-Temperature Polymer Electrolyte Fuel Cell Based on a Phosphoric Acid-Doped Polybenzimidazole Membrane Using the Hydrogen-Deuterium Contrast Method" Energies 11, no. 9: 2214. https://doi.org/10.3390/en11092214
APA StyleLin, Y., Arlt, T., Kardjilov, N., Manke, I., & Lehnert, W. (2018). In Operando Neutron Radiography Analysis of a High-Temperature Polymer Electrolyte Fuel Cell Based on a Phosphoric Acid-Doped Polybenzimidazole Membrane Using the Hydrogen-Deuterium Contrast Method. Energies, 11(9), 2214. https://doi.org/10.3390/en11092214





