The Impact of Pulse Charging Parameters on the Life Cycle of Lithium-Ion Polymer Batteries
Abstract
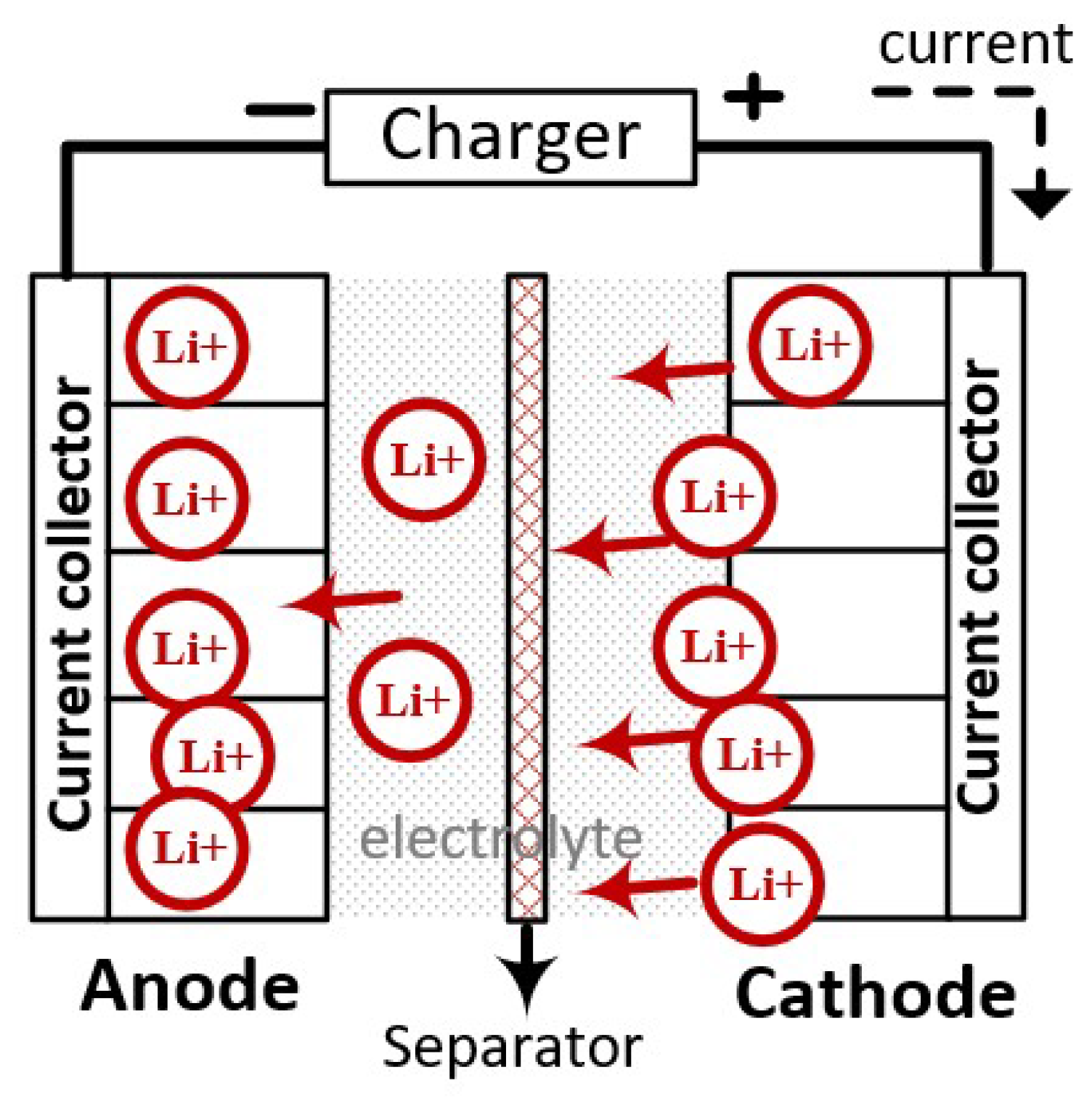
1. Introduction
2. Background on Pulse Charging and Taguchi Orthogonal Array (OA)
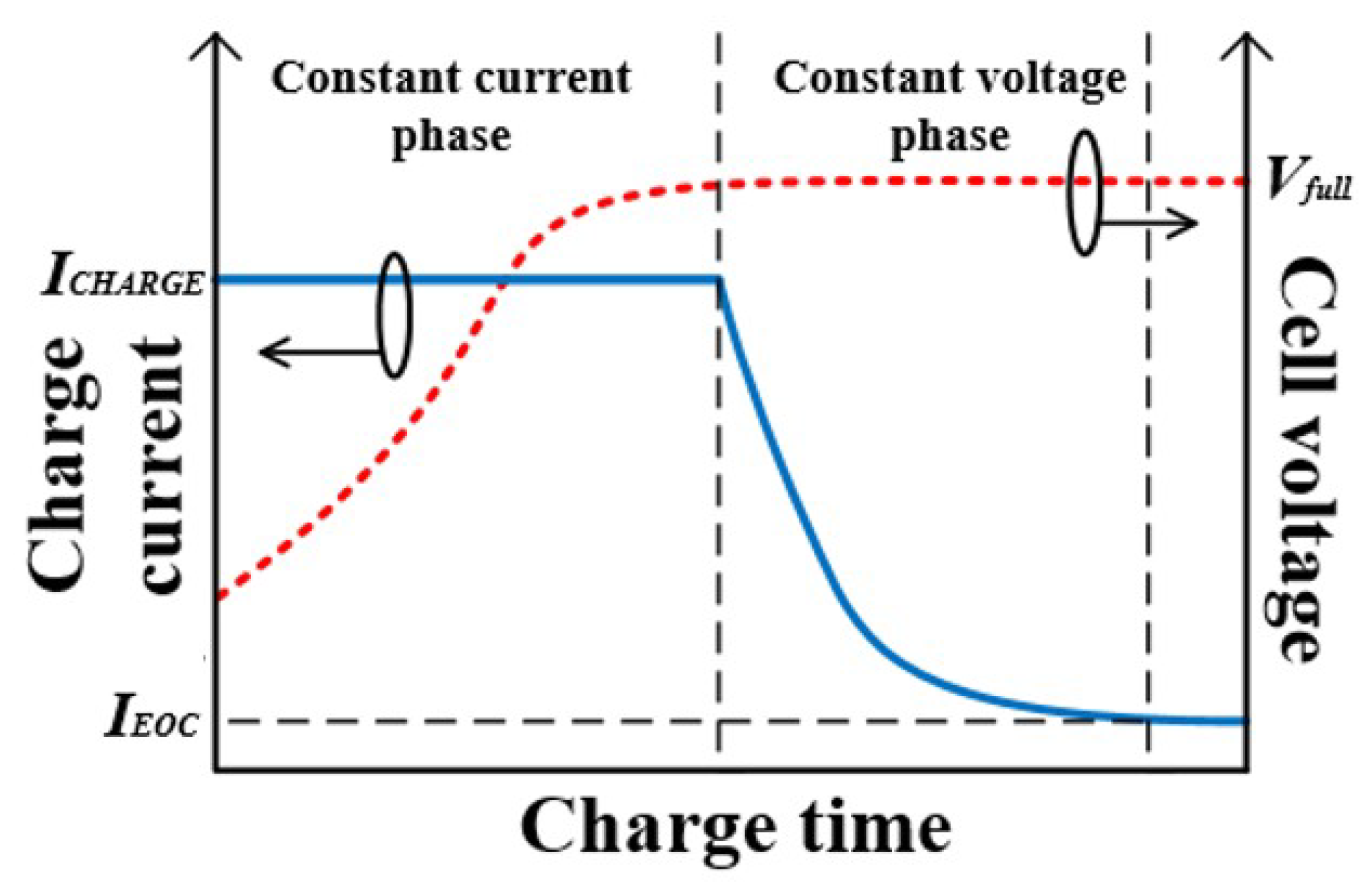
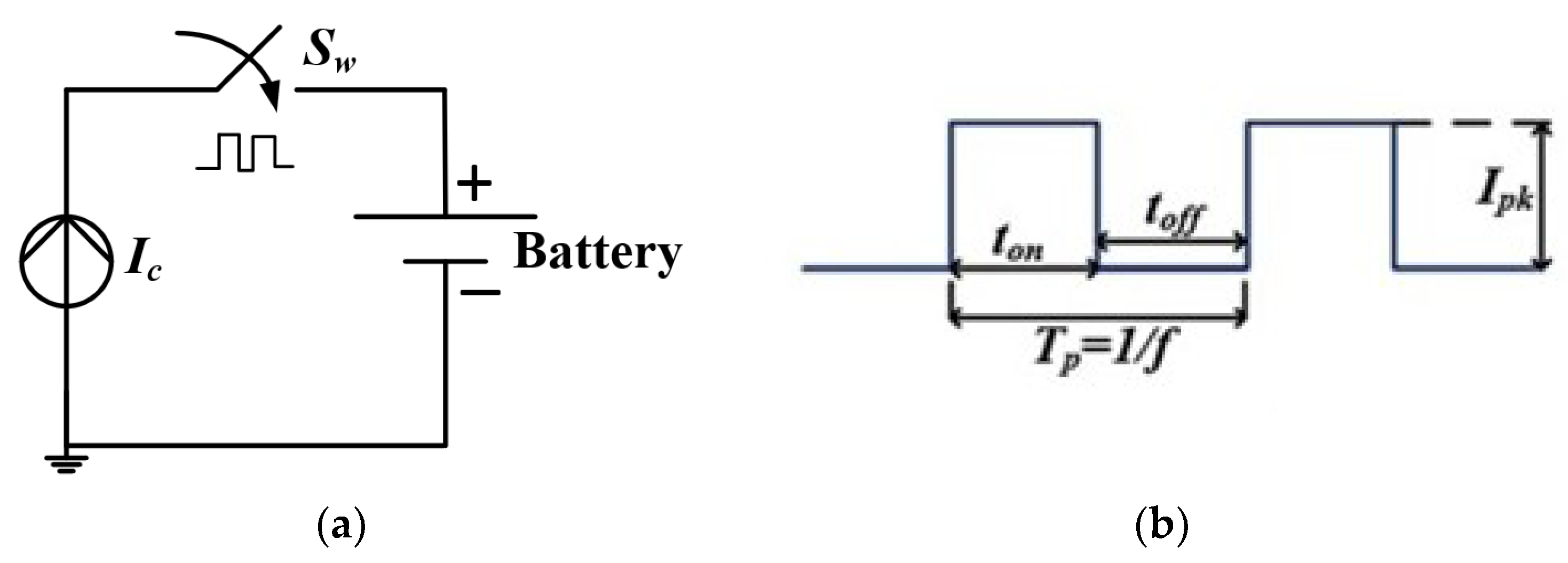
2.1. Pulse Charging
2.2. Taguchi Orthogonal Arrays
3. Techniques for Evaluation of Impact of Charging Parameters on Battery Characteristics
3.1. Destructive Techniques
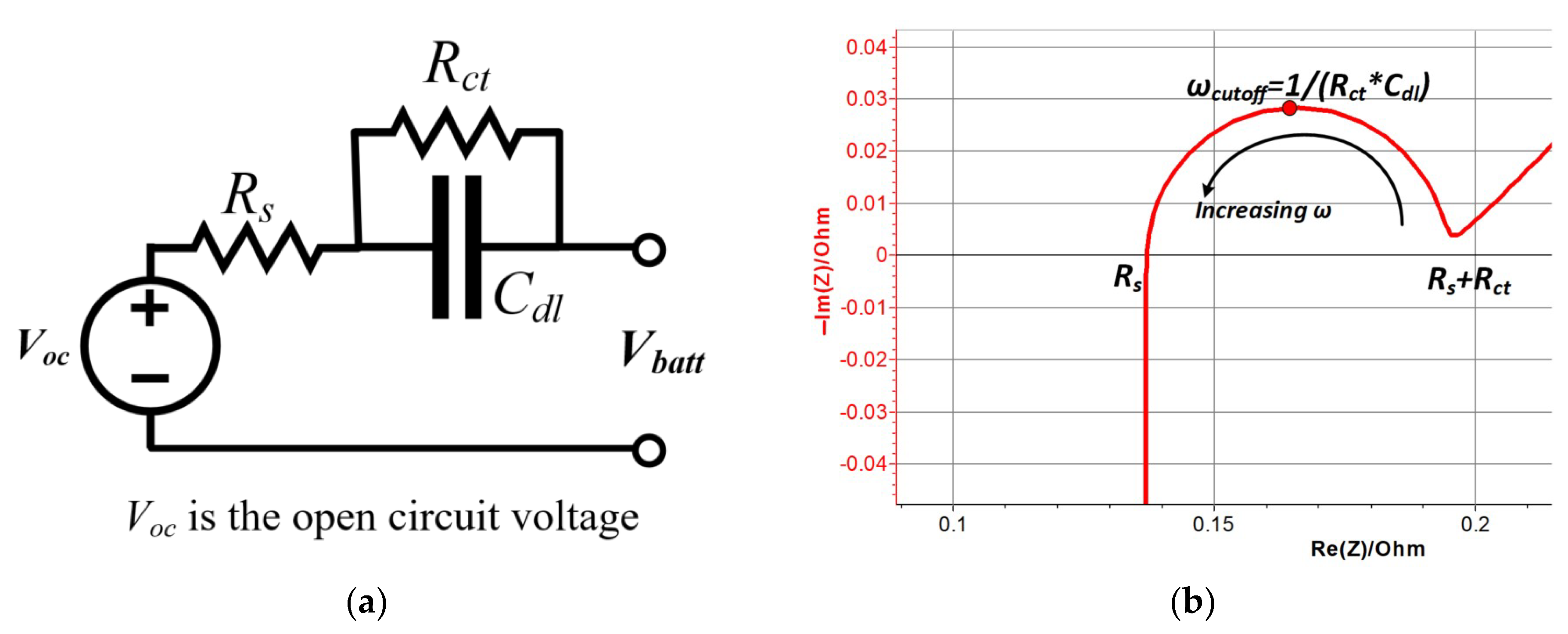
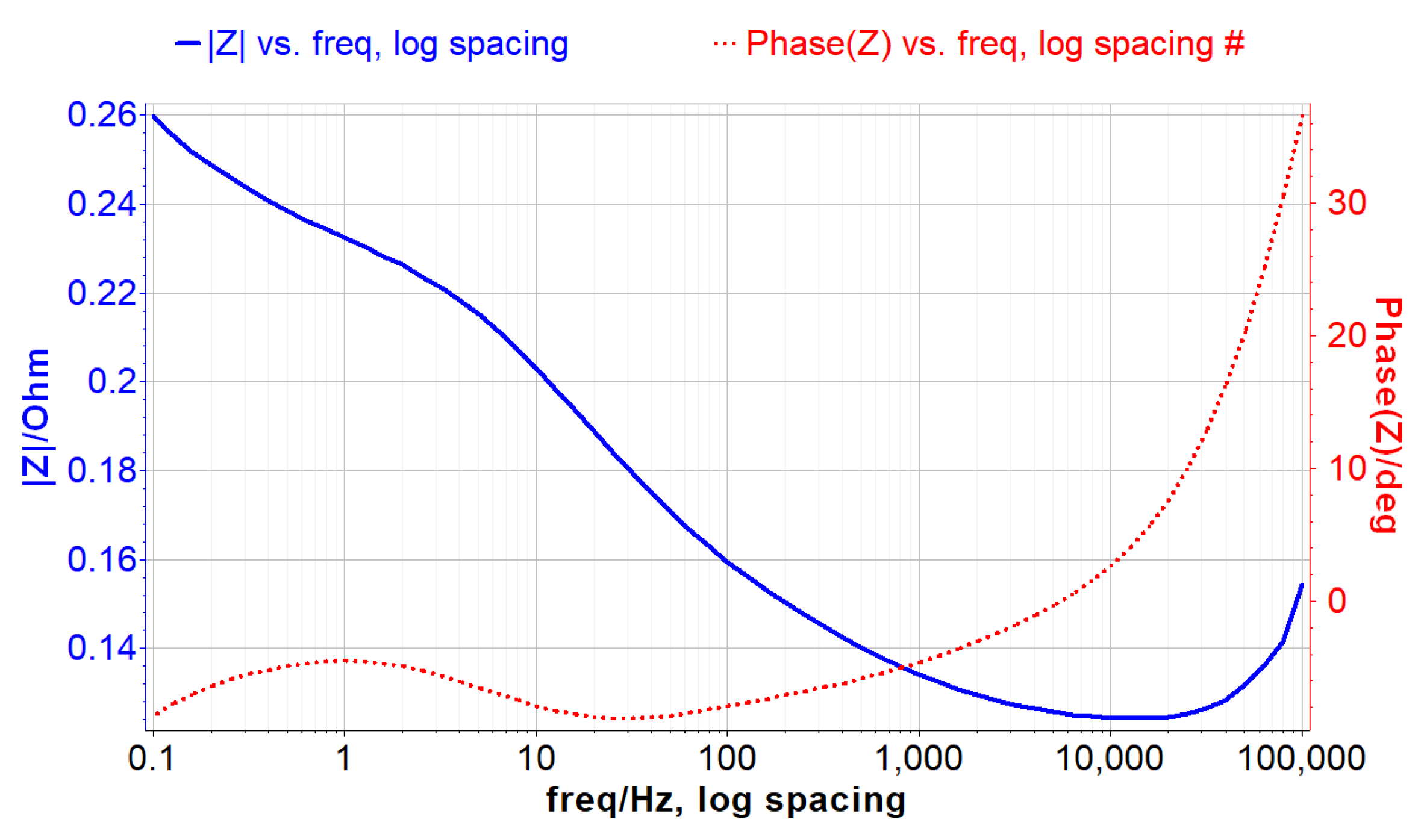
3.2. Non-Destructive Techniques
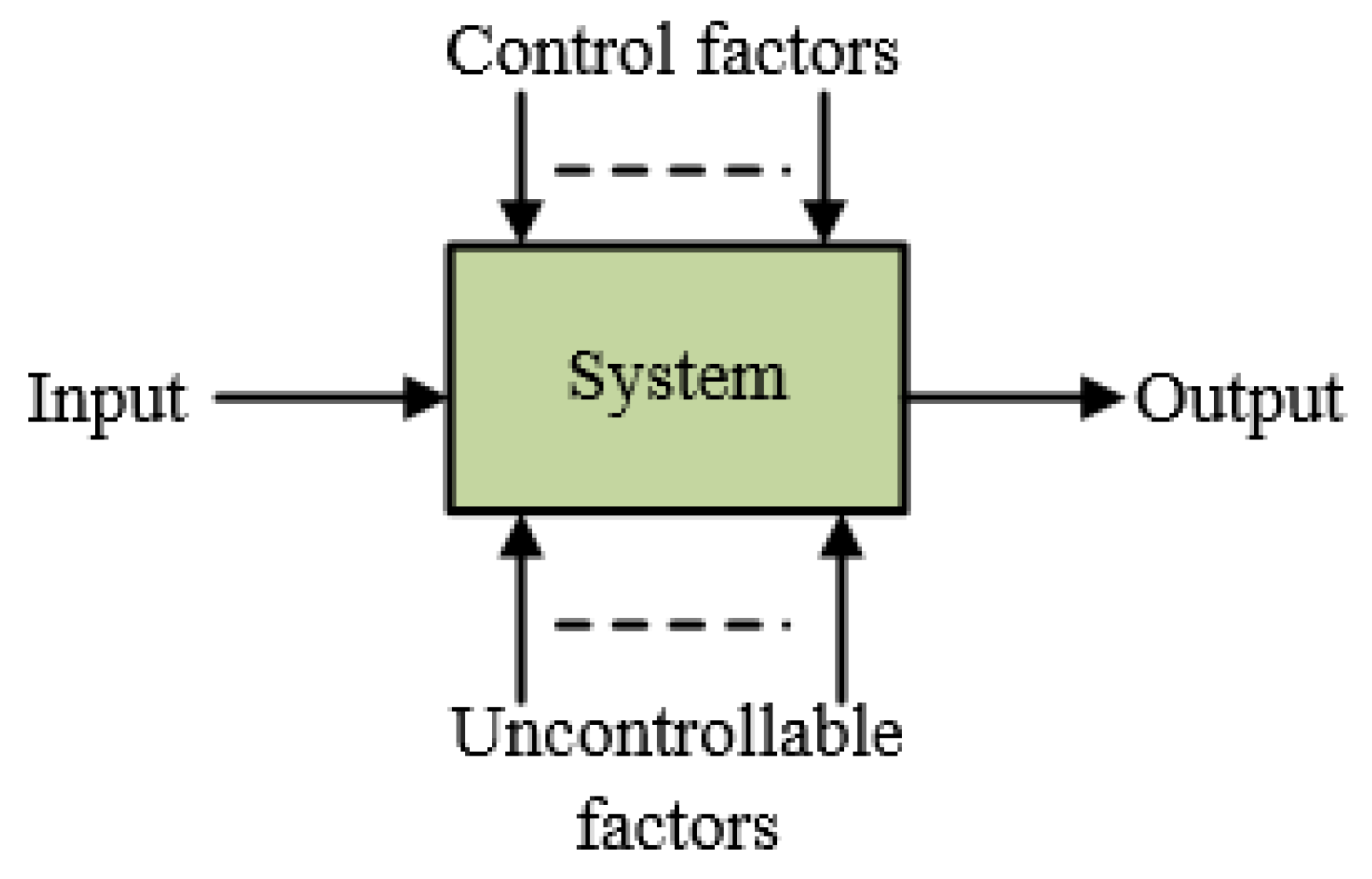
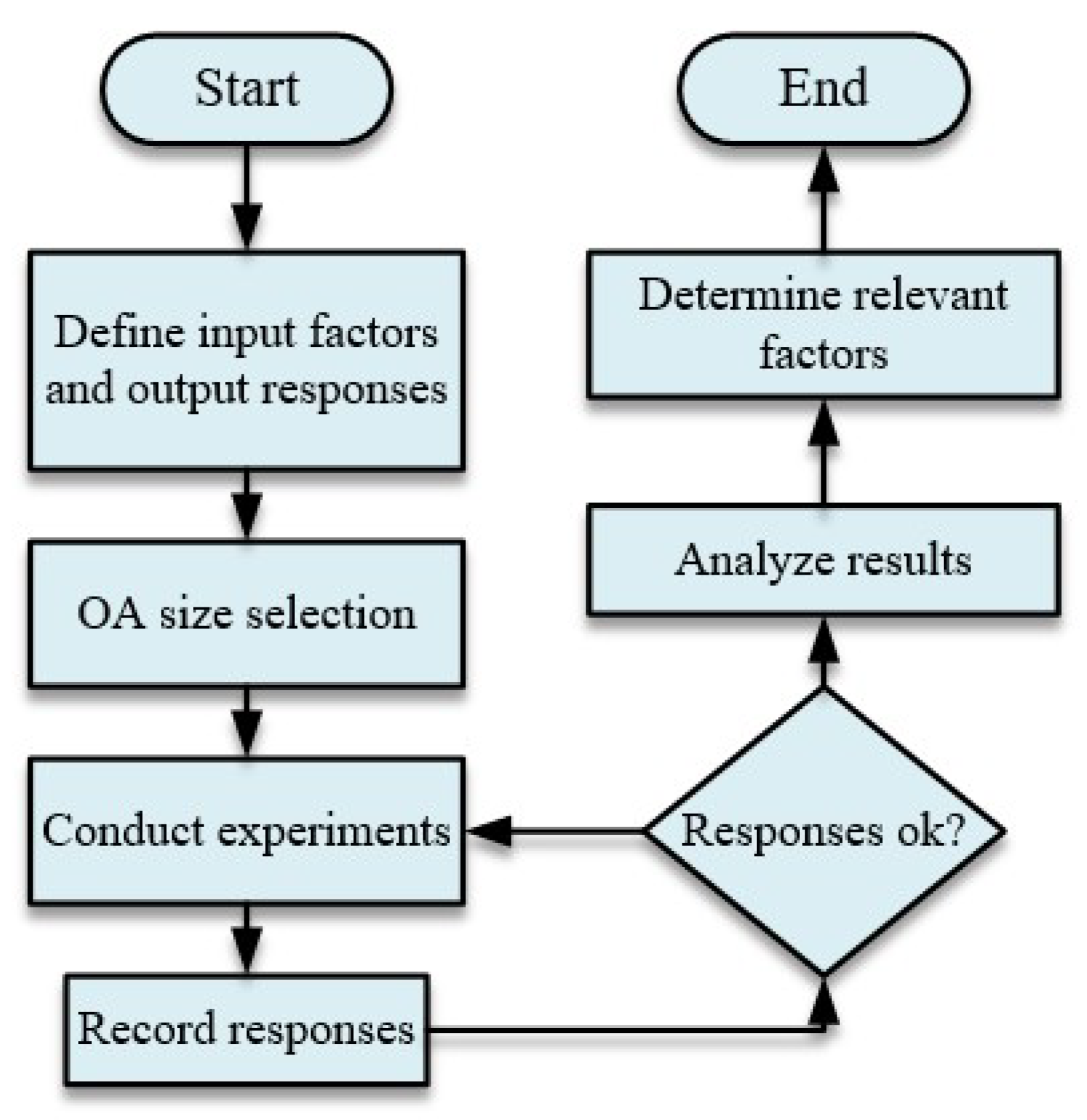
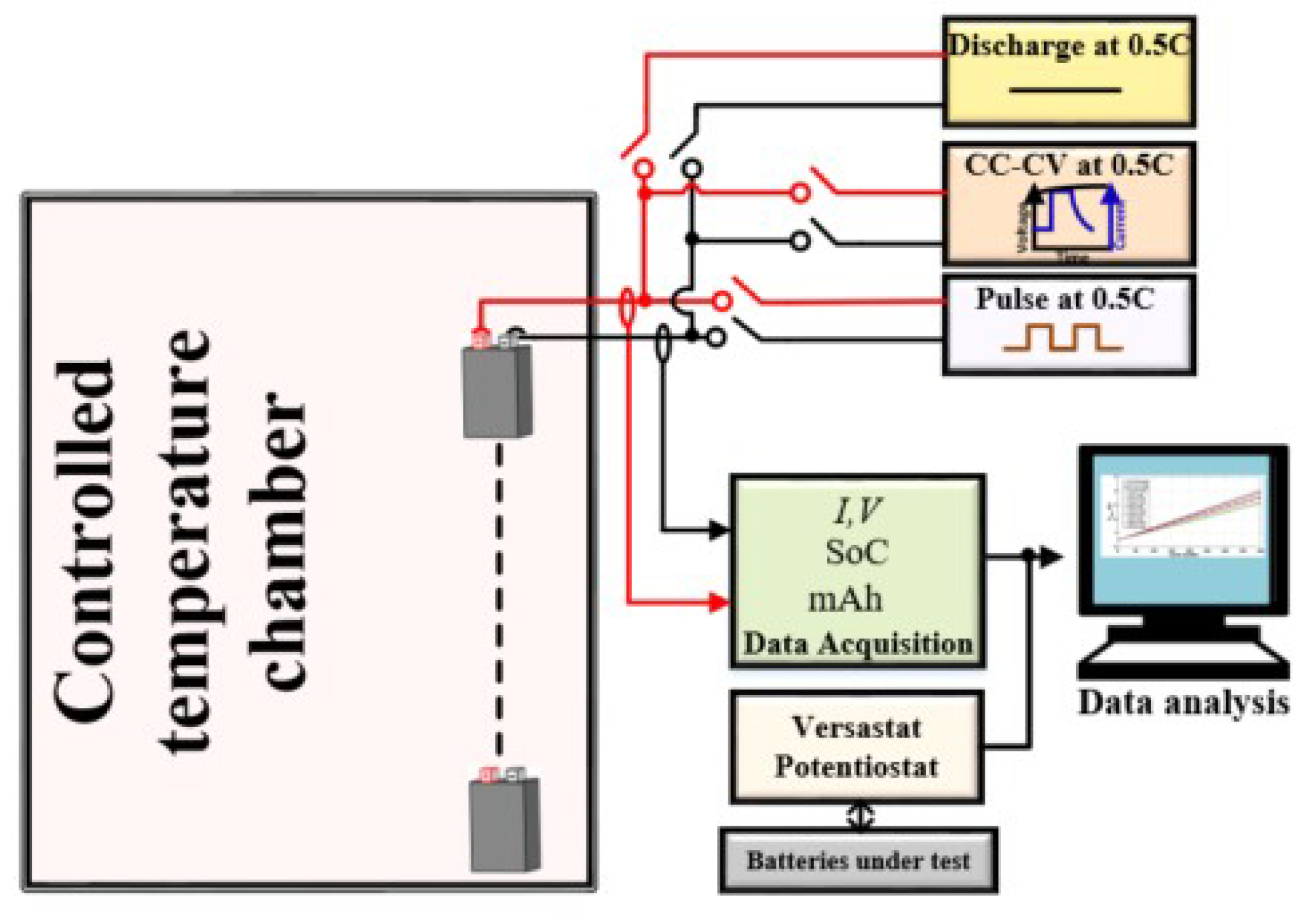
4. Design Procedure
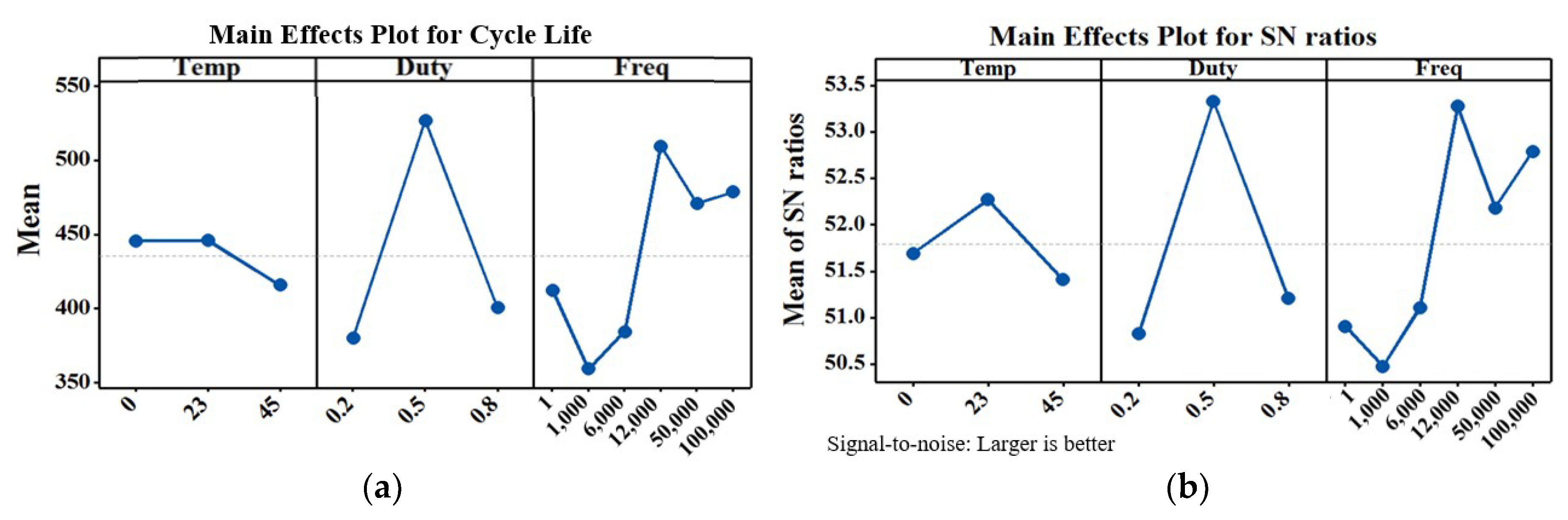
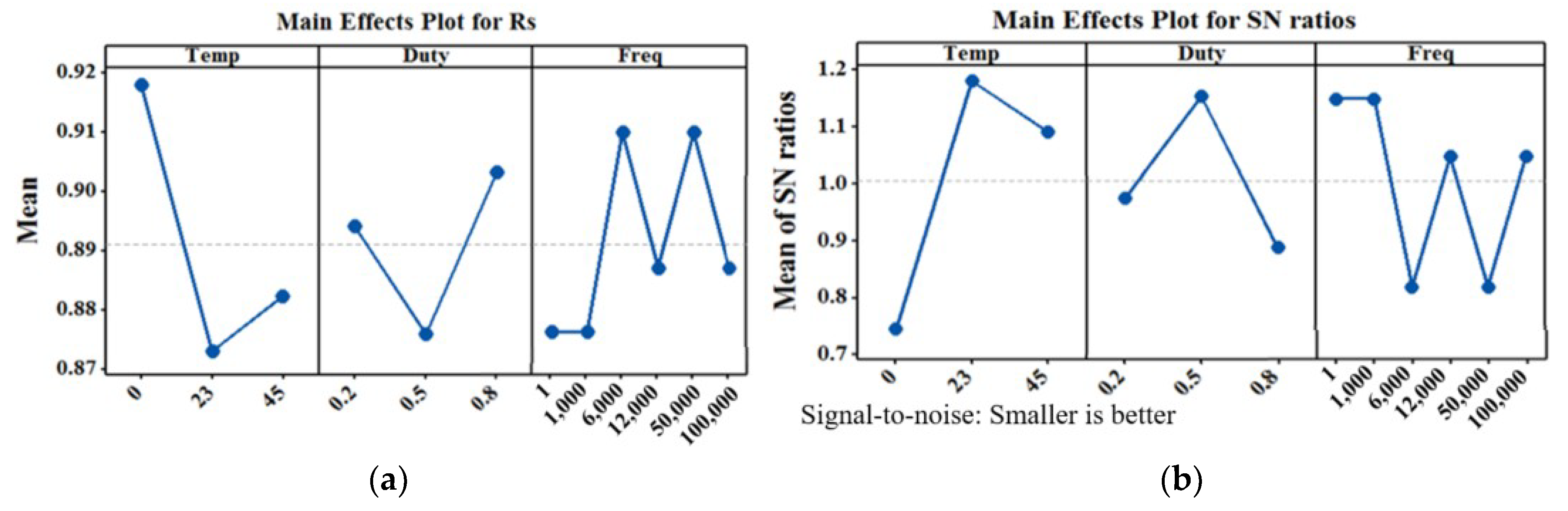
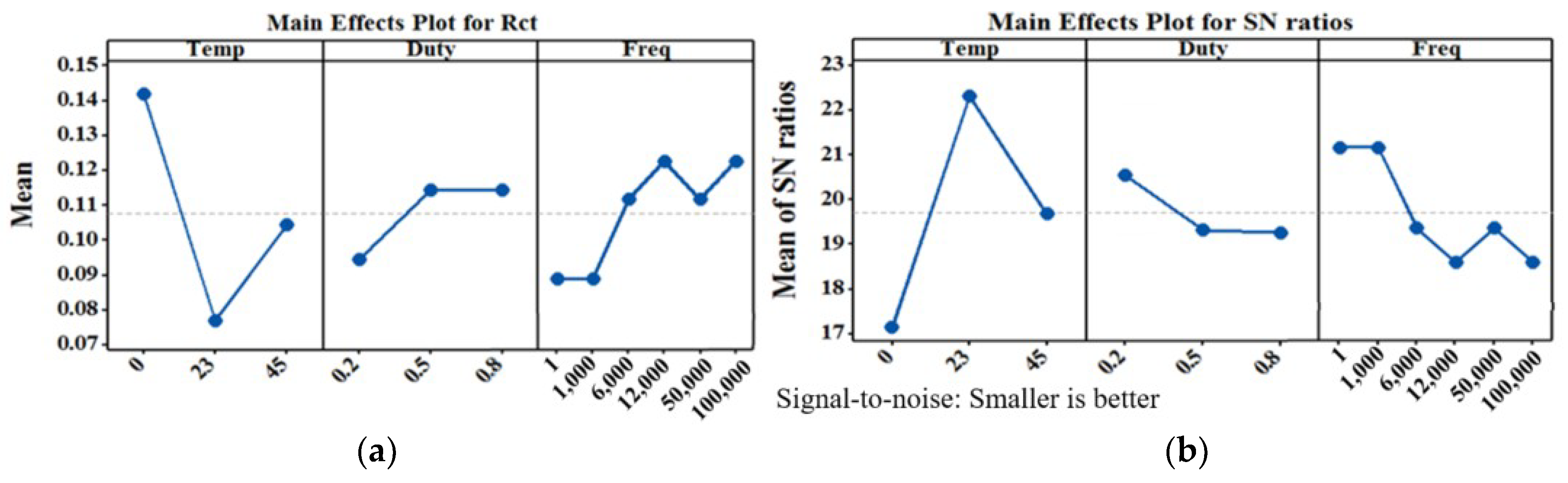
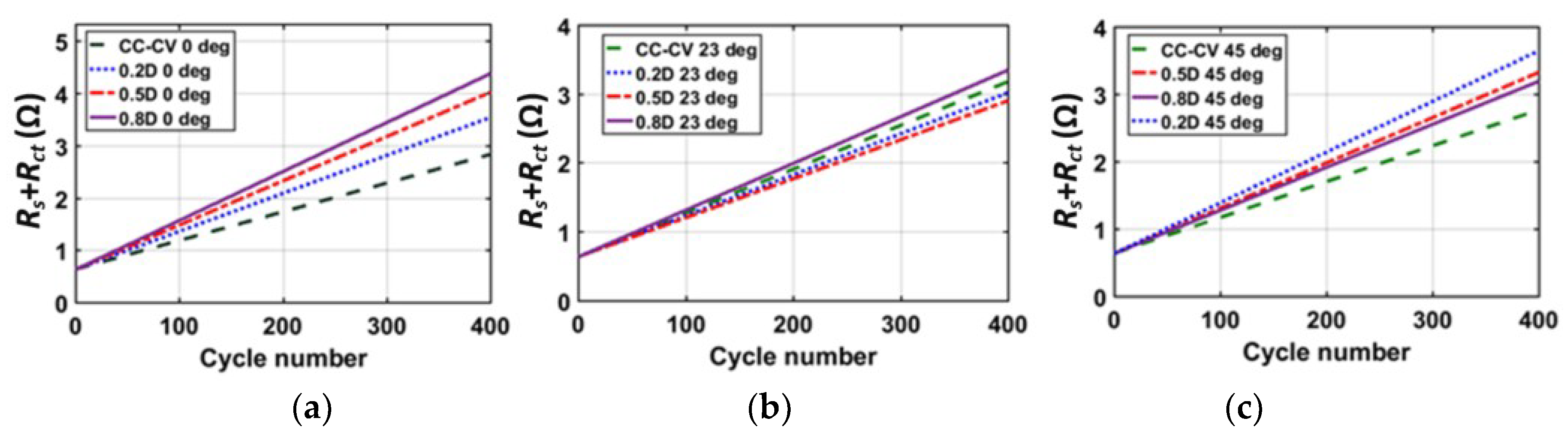
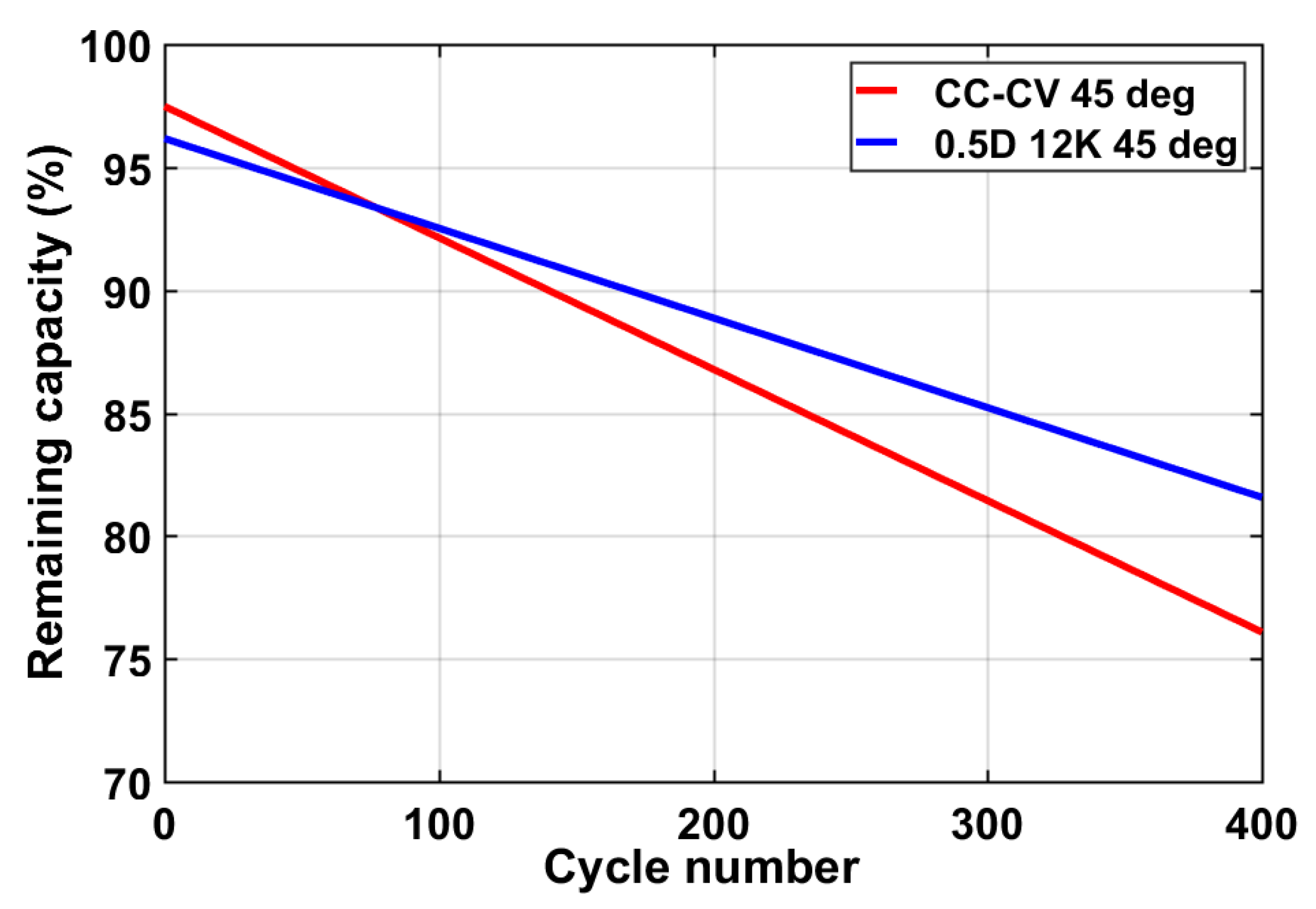
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- PR Newswire Association LLC, Lithium-Ion Battery Market is Expected to Reach $46.21 Billion, Worldwide, by 2022. Available online: https://www.prnewswire.com/news-releases/lithium-ion-battery-market-is-expected-to-reach-4621-billion-worldwide-by-2022-575386231.html (accessed on 12 March 2018).
- Global Market for Lithium-Ion Batteries—Forecast, Trends & Opportunities 2014–2020. Available online: https://www.researchandmarkets.com/reports/2904215/global-market-for-lithium-ion-batteries (accessed on 12 March 2018).
- Grand View Research, Battery Market Size, Share | Industry Research Report, 2024. Available online: https://www.grandviewresearch.com/industry-analysis/battery-marketvol (accessed on 23 March 2018).
- Reddy, T.B. Linden’s Handbook of Batteries, 4th ed.; McGraw Hill Professional: New York, NY, USA, 2010. [Google Scholar]
- Meyer, W.H. Polymer electrolytes for lithium-ion batteries. Adv. Mater. (Deerfield Beach, Fla.) 1998, 10, 439–448. [Google Scholar] [CrossRef]
- Piqué, G.V.; Bergveld, H.J. State-of-the-Art of Integrated Switching Power Converters. In Analog Circuit Design: Low Voltage Low Power; Short Range Wireless Front-Ends; Power Management and DC-DC; Steyaert, M., Roermund, A.v., Baschirotto, A., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2012; pp. 259–281. [Google Scholar]
- Iyenggar, A.; Tripathi, A.; Basarur, A.; Roy, I. Unified Power Management Framework for Portable Media Devices. In Proceedings of the IEEE International Conference on Portable Information Devices, Orlando, FL, USA, 25–29 May 2007; pp. 1–5. [Google Scholar]
- Lu, Y.H.; Simunic, T.; Micheli, G.d. Software controlled power management. Available online: http://seelab.ucsd.edu/papers/ylu_codes99.pdf (accessed on 1 April 2018).
- Yin, M.D.; Cho, J.; Park, D. Pulse-Based Fast Battery IoT Charger Using Dynamic Frequency and Duty Control Techniques Based on Multi-Sensing of Polarization Curve. J. Energies 2016, 9, 209. [Google Scholar] [CrossRef]
- Chen, L.-R. A Design of an Optimal Battery Pulse Charge System by Frequency-Varied Technique. IEEE TiE 2007, 54, 398–405. [Google Scholar] [CrossRef]
- Purushothaman, B.K.; Landau, U. Rapid Charging of Lithium-Ion Batteries Using Pulsed Currents. JES 2006, 153, A533. [Google Scholar] [CrossRef]
- Popov, B.N.; Haran, B.S.; Durairajan, A.; White, R.; Podrazhansky, Y.; Cope, R.C. Studies on capacity fade of Li-ion cells cycled using pulse and DC charging protocols. In Proceedings of the Name of the 197th Electrochemical Society meeting, Toronto, ON, Canada, 14–18 May 2000. [Google Scholar]
- Li, J.; Murphy, E.; Winnick, J.; Kohl, P.A. The effects of pulse charging on cycling characteristics of commercial lithium-ion batteries. J. Power Sources 2001, 102, 302–309. [Google Scholar] [CrossRef]
- Ely, D.R.; García, R.E. Heterogeneous Nucleation and Growth of Lithium Electrodeposits on Negative Electrodes. JES 2013, 160, A668. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Shen, W.; Vo, T.T.; Kapoor, A. Charging algorithms of lithium-ion batteries: An overview. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, Singapore, 18–20 July 2012; pp. 1567–1572. [Google Scholar]
- Boadu, J.M.A.; Abouzied, M.; Sanchez-Sinencio, E. An Efficient and Fast Li-ion Battery Charging System Using Energy Harvesting or Conventional Sources. IEEE TIE 2018, 65, 7383–7394. [Google Scholar]
- Boadu, J.M.A.; Guiseppi-Elie, A.; Sanchez-Sinencio, E. Search for Optimal Pulse Charging Parameters for Li-ion Polymer Batteries Using Taguchi Orthogonal Arrays. IEEE TIE 2018, 65, 8982–8992. [Google Scholar]
- Randles, J.E.B. Kinetics of rapid electrode reactions. Discuss. Faraday Soc. 1947, 1, 11–19. [Google Scholar] [CrossRef]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of Periodic Current Pulses on Li-Ion Battery Performance. IEEE TIE 2012, 59, 348–3488. [Google Scholar] [CrossRef]
- Chen, L.-R. Design of Duty-Varied Voltage Pulse Charger for Improving Li-Ion Battery-Charging Response. IEEE TIE 2009, 56, 480–487. [Google Scholar]
- Pundir, R.; Chary, G.H.V.C.; Dastidar, M.G. Application of Taguchi method for optimizing the process parameters for the removal of copper and nickel by growing Aspergillus sp. Water Resour. Ind. 2016. [Google Scholar] [CrossRef]
- Shahbazian, A.; Davood, A.; Dabirsiaghi, A. Application of Taguchi Method to Investigate the Effects of Process Factors on the Production of Industrial Piroxicam Polymorphs and Optimization of Dissolution Rate of Powder. Iran. J. Pharm. Res. IJPR 2016, 15, 395. [Google Scholar] [PubMed]
- Pang, J.S.; Ansari, M.N.M.; Zaroog, O.S.; Ali, M.H.; Sapuan, S.M. Taguchi design optimization of machining parameters on the CNC end milling process of halloysite nanotube with aluminium reinforced epoxy matrix (HNT/Al/Ep) hybrid composite. HBRC J. 2014, 10, 138–144. [Google Scholar] [CrossRef]
- Hsu, C.C.; Chien, C.S.; Wei, T.Y.; Li, Y.T.; Li, H.F. Taguchi DoE for ceramic substrate SMT defects improvement. In Proceedings of the 2016 11th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 26–28 October 2016; pp. 381–384. [Google Scholar]
- Dudhe, R.; Ayyalusamy, S.; Desai, T. Optimization of BAW Resonator for Wireless Applications using Taguchi’s Orthogonal Array Method. Available online: https://www.researchgate.net/profile/Ravishankar_Dudhe2/publication/303719442_Optimization_of_BAW_Resonator_for_Wireless_Applications_using_Taguchi’s_Orthogonal_Array_Method/links/574f1e0b08ae1880a820f7f4.pdf (accessed on 23 January 2018).
- Deo, R.; Likhite, A.A.; Zanwar, D.R.; Majumdar, G. Design of experiments by Taguchi method in agricultural research. J. Soils Crop. 2007, 17, 320–325. [Google Scholar]
- Wang, S.C.; Chen, Y.L.; Liu, Y.H.; Huang, Y.S. A fast-charging pattern search for li-ion batteries with fuzzy-logic-based Taguchi method. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 855–859. [Google Scholar]
- Liu, Y.H.; Luo, Y.F. Search for an Optimal Rapid-Charging Pattern for Li-Ion Batteries Using the Taguchi Approach. IEEE TIE 2010, 57, 3963–3971. [Google Scholar] [CrossRef]
- Wang, S.C.; Huang, J.W.; Liu, Y.H.; Hsieh, C.H. The implementation of consecutive orthogonal array method on searching optimal five step charging pattern for Lithium-ion batteries. In Proceedings of the 2011 9th World Congress on Intelligent Control and Automation, Taipei, Taiwan, 21–25 June 2011; pp. 358–363. [Google Scholar]
- Phadke, M.S. Quality Engineering Using Robust Design, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Taguchi, G. Experimental Designs; Maruzen Publishing Company: Tokyo, Japan, 1976. [Google Scholar]
- Williard, N.; Sood, B.; Osterman, M.; Pecht, M. Disassembly methodology for conducting failure analysis on lithium–ion batteries. J. Mater. Sci. Mater. Electron. 2011, 22, 1616. [Google Scholar] [CrossRef]
- Scipioni, R.; Jørgensen, P.S.; Ngo, D.; Simonsen, S.B.; Liu, Z.; Yakal-Kremski, K.J.; Wang, H.; Hjelm, J.; Norby, P.; Barnett, S.A.; Jensen, S.H. Electron microscopy investigations of changes in morphology and conductivity of LiFePO4/C electrodes. J. Power Sources 2016, 307, 259–269. [Google Scholar] [CrossRef]
- Freitag, S.; Berger, C.; Gelb, J.; Weisenberger, T.B.C. Li-Ion Battery Components—Cathode, Anode, Binder, Separator—Imaged at Low Accelerating Voltages with ZEISS FE-SEMs, Zeiss White Paper, Carl Zeiss Microscopy GmbH. Available online: https://p.widencdn.net/nih1gr/EN_wp_Battery_Low_Accelerating_Voltages_ZEISS-FE_SEMs (accessed on 23 March 2018).
- Kong, L.; Xing, Y.; Pecht, M.G. In-Situ Observations of Lithium Dendrite Growth. IEEE Access 2018, 6, 8387–8393. [Google Scholar] [CrossRef]
- Orsini, F.; Pasquier, A.D.; Beaudoin, B.; Tarascon, J.M.; Trentin, M.; Langenhuizen, N.; de Beer, E.; Notten, P. In situ Scanning Electron Microscopy (SEM) observation of interfaces within plastic lithium batteries. J. Power Sources 1998, 76, 19–29. [Google Scholar] [CrossRef]
- Chan, J.Y.; Kim, J.H.; Seunghoon, N.; Park, C.R.; Yang, S.J. Rational Design of Nanostructured Functional Interlayer/Separator for Advanced Li–S Batteries. Adv. Funct. Mater. 2018, 1707411. [Google Scholar] [CrossRef]
- Jeong, S.; Inaba, M.; Iriyama, Y.; Abe, T.; Ogumi, Z. Surface film formation on a graphite negative electrode in lithium-ion batteries: AFM study on the effects of co-solvents in ethylene carbonate-based solutions. Electrochimica Acta 2002, 47, 1975–1982. [Google Scholar] [CrossRef]
- Waag, W.; Käbitz, S.; Sauer, D.U. Experimental investigation of the lithium-ion battery impedance characteristic at various conditions and aging states and its influence on the application. Appl. Energy 2013, 102, 885–897. [Google Scholar] [CrossRef]
- Aurbach, D.; Zinigrad, E.; Cohen, Y.; Teller, H. A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions. Solid State Ion. 2002, 148, 405–416. [Google Scholar] [CrossRef]
- Jeong, S.; Inaba, M.; Mogi, R.; Iriyama, Y.; Abe, T.; Ogumi, Z. Surface Film Formation on a Graphite Negative Electrode in Lithium-Ion Batteries: Atomic Force Microscopy Study on the Effects of Film-Forming Additives in Propylene Carbonate Solutions. Langmuir 2001, 17, 8281–8286. [Google Scholar] [CrossRef]
- Shim, J.; Kostecki, R.; Richardson, T.; Song, X.; Striebel, K.A. Electrochemical analysis for cycle performance and capacity fading of a lithium-ion battery cycled at elevated temperature. J. Power Sources 2002, 112, 222–230. [Google Scholar] [CrossRef]
- Ramadass, P.; Durairajan, A.; Haran, B.S.; White, R.E.; Popov, B.N. Capacity fade studies on spinel based Li-ion cells. In Proceedings of the Seventeenth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 18 January 2002; pp. 25–30. [Google Scholar]
- Itou, Y.; Ukyo, Y. Performance of LiNiCoO2 materials for advanced lithium-ion batteries. J. Power Sources 2005, 146, 39–44. [Google Scholar] [CrossRef]
- Zhang, D.; Haran, B.S.; Durairajan, A.; White, R.E.; Podrazhansky, Y.; Popov, B.N. Studies on capacity fade of lithium-ion batteries. J. Power Sources 2000, 91, 122–129. [Google Scholar] [CrossRef]
- Lundgren, C.A.; Xu, K.; Jow, T.R.; Allen, J.; Zhang, S.S. Springer Handbook of Electrochemical Energy; Springer: Berlin Heidelberg, 2017; pp. 449–494. Available online: https://www.springer.com/us/book/9783662466568 (accessed on 20 March 2018).
- UTröltzsch; Kanoun, O.; Tränkler, H. Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochimica Acta 2006, 51, 1664–1672. [Google Scholar]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Ametek Scientific Instruments, VersaSTAT 4|Potentiostat Galvanostat|Princeton Applied Research. Available online: https://www.ameteksi.com/products/potentiostats/single-channel/versastat-series/versastat-4 (accessed on 20 April 2018).
- Dincer, I. Comprehensive Energy Systems. Elsevier, Posted February 21, 2018. Available online: https://www.sciencedirect.com/referencework/9780128149256/comprehensive-energy-systems (accessed on 2 March 2018).
- TestEquity, TestEquity 107 Benchtop Temperature Chamber (Environmental Chamber). Available online: https://www.testequity.com/products/1592/ (accessed on 20 April 2018).
- Leng, F.; Tan, C.M.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [PubMed]
- Ning, G.; Haran, B.; Popov, B.N. Capacity fade study of lithium-ion batteries cycled at high discharge rates. J. Power Sources 2003, 117, 160–169. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
| Factors | |||||||
|---|---|---|---|---|---|---|---|
| ⋯⋯ | ⋯⋯ | ||||||
| ⋯⋯ | |||||||
| ⋮ ⋮ | ⋮ ⋮ | ⋮ ⋮ | |||||
| Control factors | Factor levels | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| D | 0.2 | 0.5 | 0.8 | - | - | - |
| T (°C) | 0 | 23 | 45 | - | - | - |
| f (kHz) | 0.1 | 1 | 6 | 50 | 100 | |
| Factors | Factors | ||||||
|---|---|---|---|---|---|---|---|
| No. | No. | ||||||
| 1 | 23 | 0.2 | 12k | 19 | 0 | 0.8 | 12k |
| 2 | 45 | 0.8 | 100 | 20 | 0 | 0.5 | 6k |
| 3 | 45 | 0.2 | 50k | 21 | 0 | 0.2 | 1k |
| 4 | 45 | 0.2 | 6k | 22 | 0 | 0.2 | 100 |
| 5 | 45 | 0.5 | 100k | 23 | 23 | 0.2 | 100k |
| 6 | 0 | 0.8 | 12k | 24 | 0 | 0.5 | 6k |
| 7 | 0 | 0.2 | 100 | 25 | 45 | 0.5 | 100k |
| 8 | 45 | 0.8 | 1k | 26 | 23 | 0.2 | 100k |
| 9 | 23 | 0.5 | 1k | 27 | 23 | 0.8 | 50k |
| 10 | 0 | 0.2 | 1k | 28 | 45 | 0.2 | 50k |
| 11 | 0 | 0.5 | 50k | 29 | 23 | 0.8 | 6k |
| 12 | 45 | 0.5 | 12k | 30 | 23 | 0.5 | 100 |
| 13 | 23 | 0.8 | 50k | 31 | 0 | 0.5 | 50k |
| 14 | 45 | 0.5 | 12k | 32 | 0 | 0.8 | 100k |
| 15 | 45 | 0.8 | 1k | 33 | 45 | 0.2 | 6k |
| 16 | 45 | 0.8 | 100 | 34 | 23 | 0.5 | 1k |
| 17 | 23 | 0.5 | 100 | 35 | 23 | 0.8 | 6k |
| 18 | 23 | 0.2 | 12k | 36 | 0 | 0.8 | 100k |
| Factors | Factors | ||||||
|---|---|---|---|---|---|---|---|
| No. | Cycle Life | No. | Cycle Life | ||||
| 1 | 583 | 0.8604 | 0.08091 | 19 | 873 | 0.9420 | 0.16680 |
| 2 | 370 | 0.8680 | 0.09468 | 20 | 308 | 0.9100 | 0.15500 |
| 3 | 239 | 0.9200 | 0.09845 | 21 | 438 | 0.9020 | 0.10390 |
| 4 | 421 | 0.9200 | 0.09845 | 22 | 360 | 0.9020 | 0.10390 |
| 5 | 763 | 0.8590 | 0.12000 | 23 | 295 | 0.8604 | 0.08091 |
| 6 | 446 | 0.9420 | 0.16680 | 24 | 214 | 0.9100 | 0.15500 |
| 7 | 213 | 0.9020 | 0.10390 | 25 | 755 | 0.8590 | 0.12000 |
| 8 | 258 | 0.8680 | 0.09468 | 26 | 250 | 0.8604 | 0.08091 |
| 9 | 545 | 0.8589 | 0.06816 | 27 | 486 | 0.9000 | 0.08174 |
| 10 | 303 | 0.9020 | 0.10390 | 28 | 408 | 0.9200 | 0.09845 |
| 11 | 512 | 0.9100 | 0.15500 | 29 | 377 | 0.9000 | 0.08174 |
| 12 | 388 | 0.8590 | 0.12000 | 30 | 828 | 0.8589 | 0.06816 |
| 13 | 309 | 0.9000 | 0.08174 | 31 | 871 | 0.9100 | 0.15500 |
| 14 | 311 | 0.8590 | 0.12000 | 32 | 401 | 0.9420 | 0.16680 |
| 15 | 215 | 0.8680 | 0.09468 | 33 | 593 | 0.9200 | 0.09845 |
| 16 | 268 | 0.8680 | 0.09468 | 34 | 396 | 0.8589 | 0.06816 |
| 17 | 434 | 0.8589 | 0.06816 | 35 | 393 | 0.9000 | 0.08174 |
| 18 | 456 | 0.8604 | 0.08091 | 36 | 408 | 0.9420 | 0.16680 |
| Cycle Life | ||||
| Factor | Degrees of Freedom | Sum of Squares | Mean Square | F |
| Duty Cycle | 2 | 152,562 | 76,281 | 2.41 |
| Frequency | 5 | 105,460 | 21,092 | 0.58 |
| Temperature | 2 | 7221 | 3611 | 0.1 |
| Total | 265,243 | |||
| RS | ||||
| Factor | Degrees of Freedom | Sum of Squares | Mean Square | F |
| Duty Cycle | 2 | 0.004654 | 0.002327 | 3.02 |
| Frequency | 5 | 0.007104 | 0.001421 | 1.85 |
| Temperature | 2 | 0.013494 | 0.006747 | 13.41 |
| Total | 0.025252 | |||
| Rct | ||||
| Factor | Degrees of Freedom | Sum of Squares | Mean Square | F |
| Duty Cycle | 2 | 0.003193 | 0.001596 | 1.59 |
| Frequency | 5 | 0.007084 | 0.001417 | 1.45 |
| Temperature | 2 | 0.025525 | 0.012762 | 38.84 |
| Total | 0.035802 | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amanor-Boadu, J.M.; Guiseppi-Elie, A.; Sánchez-Sinencio, E. The Impact of Pulse Charging Parameters on the Life Cycle of Lithium-Ion Polymer Batteries. Energies 2018, 11, 2162. https://doi.org/10.3390/en11082162
Amanor-Boadu JM, Guiseppi-Elie A, Sánchez-Sinencio E. The Impact of Pulse Charging Parameters on the Life Cycle of Lithium-Ion Polymer Batteries. Energies. 2018; 11(8):2162. https://doi.org/10.3390/en11082162
Chicago/Turabian StyleAmanor-Boadu, J. M., A. Guiseppi-Elie, and E. Sánchez-Sinencio. 2018. "The Impact of Pulse Charging Parameters on the Life Cycle of Lithium-Ion Polymer Batteries" Energies 11, no. 8: 2162. https://doi.org/10.3390/en11082162
APA StyleAmanor-Boadu, J. M., Guiseppi-Elie, A., & Sánchez-Sinencio, E. (2018). The Impact of Pulse Charging Parameters on the Life Cycle of Lithium-Ion Polymer Batteries. Energies, 11(8), 2162. https://doi.org/10.3390/en11082162






