Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting
Abstract
1. Introduction
- (1)
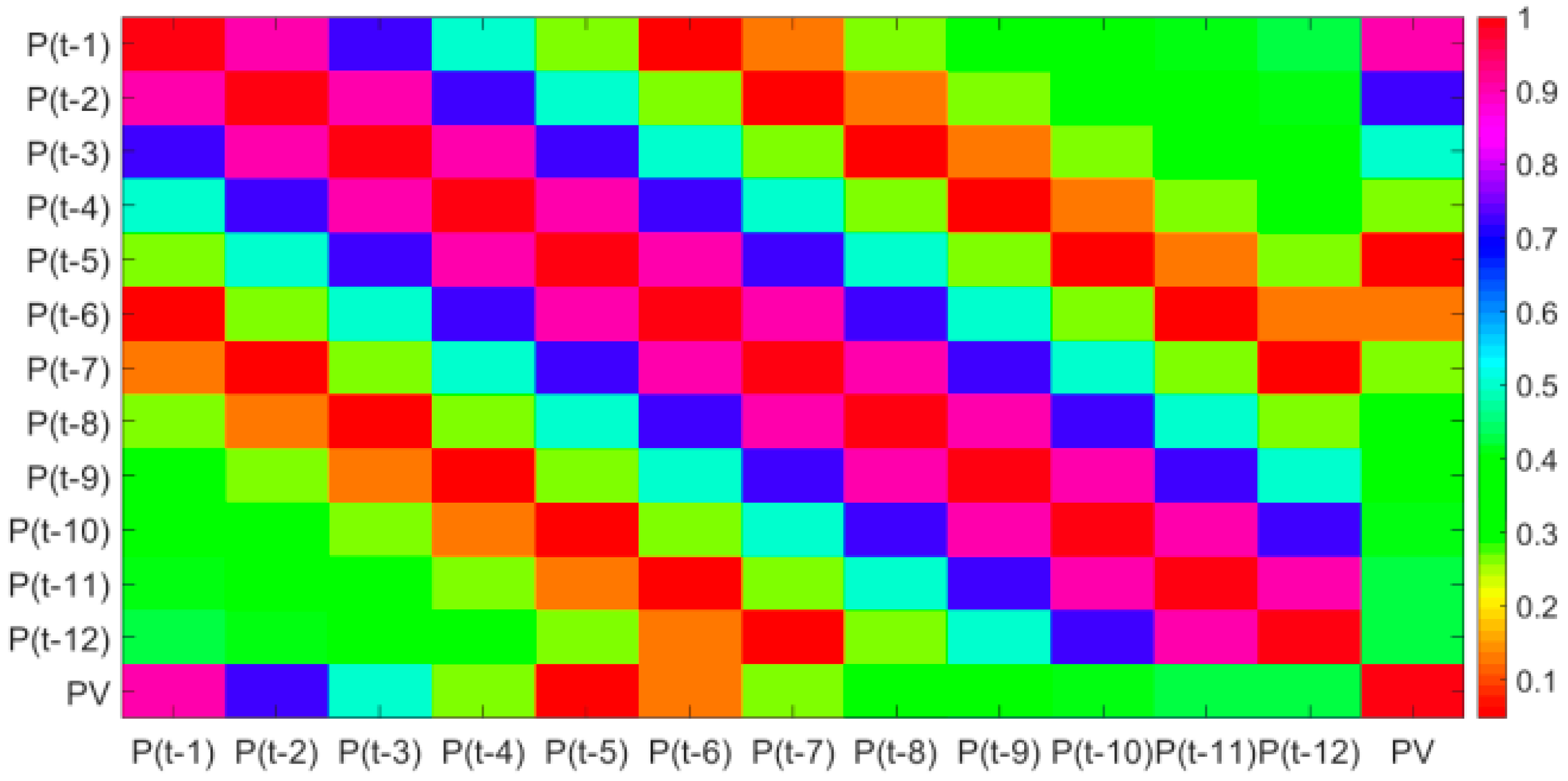
- The Pearson coefficient method is used to extract the main features that affect the photovoltaic power and analyze the relationship between historical photovoltaic power and the future photovoltaic power output.
- (2)
- The K-means method is utilized to divide the data into several groups based on the similarity of the features, so as to improve the accuracy of prediction.
- (3)
- The GRU network that can simultaneously consider the influence of features and historical photovoltaic power output trend on the future photovoltaic power output is designed for forecasting short-term photovoltaic power. It not only inherits the advantages of LSTM network, but also shortens training time.
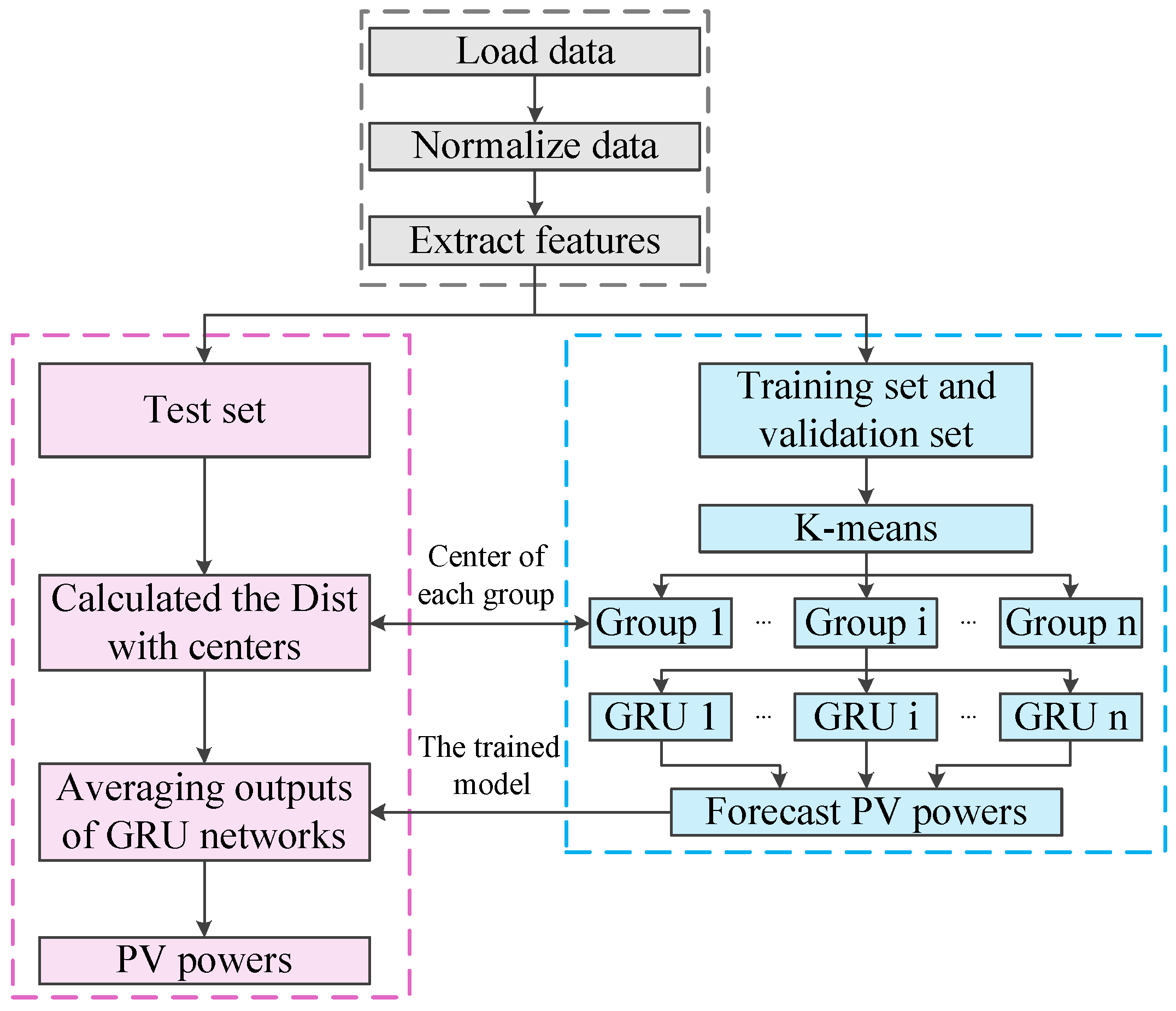
2. The Forecasting Framework of Proposed Approaches
3. Feature Extraction and Cluster Analysis
3.1. Introduction of the Dataset
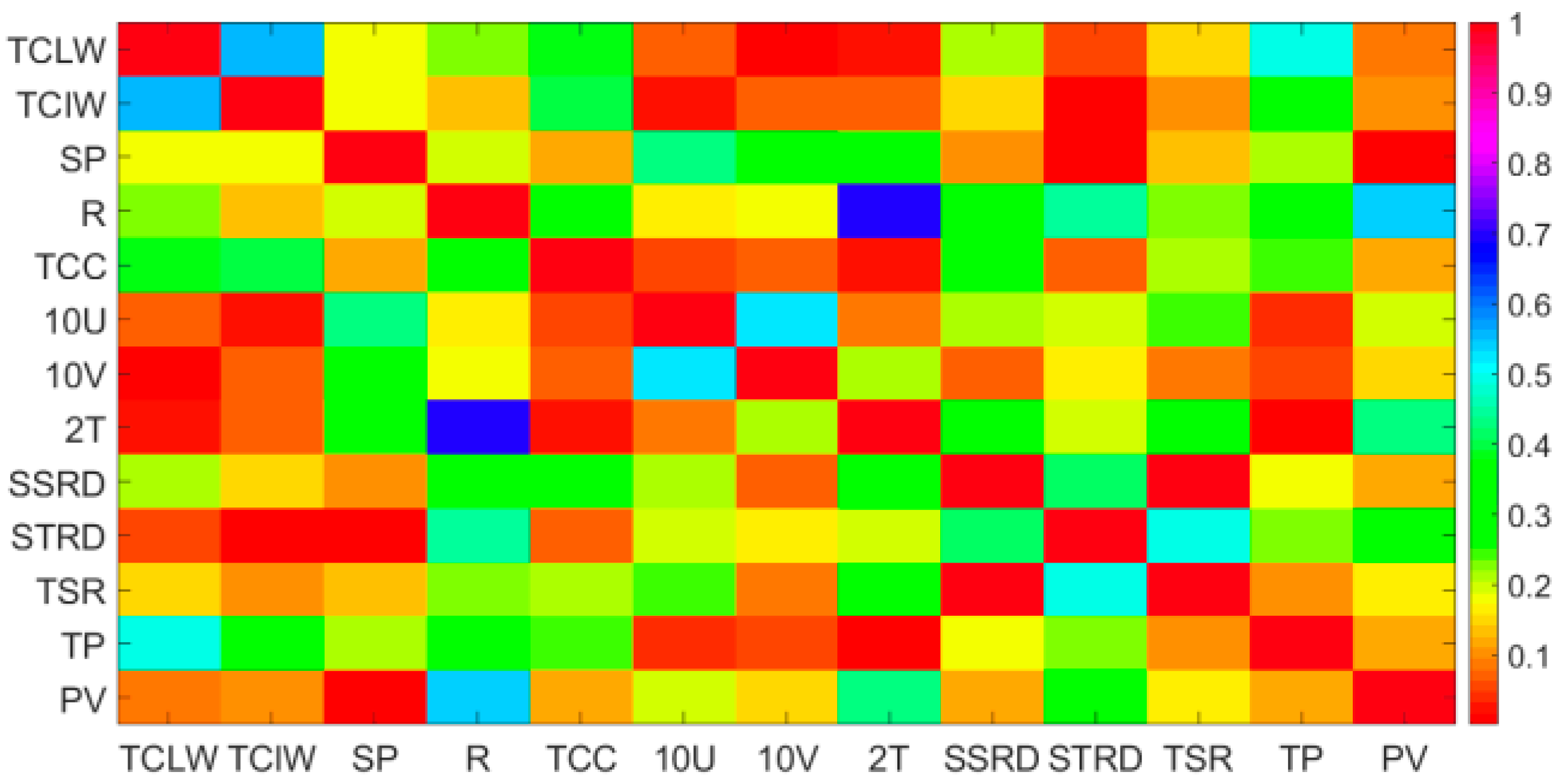
3.2. Feature Extraction
3.3. Cluster Analysis
- (1)
- Initializing the K centers of K groups: To eliminate the influence of dimension, the min-max normalization is used to standardize each feature. K samples are randomly selected as the initial centers of each group.
- (2)
- Assigning each sample to each group: The Euclidean distance between each sample and the center of each group is calculated, and each sample is allocated to the nearest group.
- (3)
- Recalculating the center of each group: The center of each group is recalculated based on the sample data of each group, and the results will be output if all the centers are not changed. Otherwise, return to step (2).
4. The Forecasting Framework Based on GRU Network
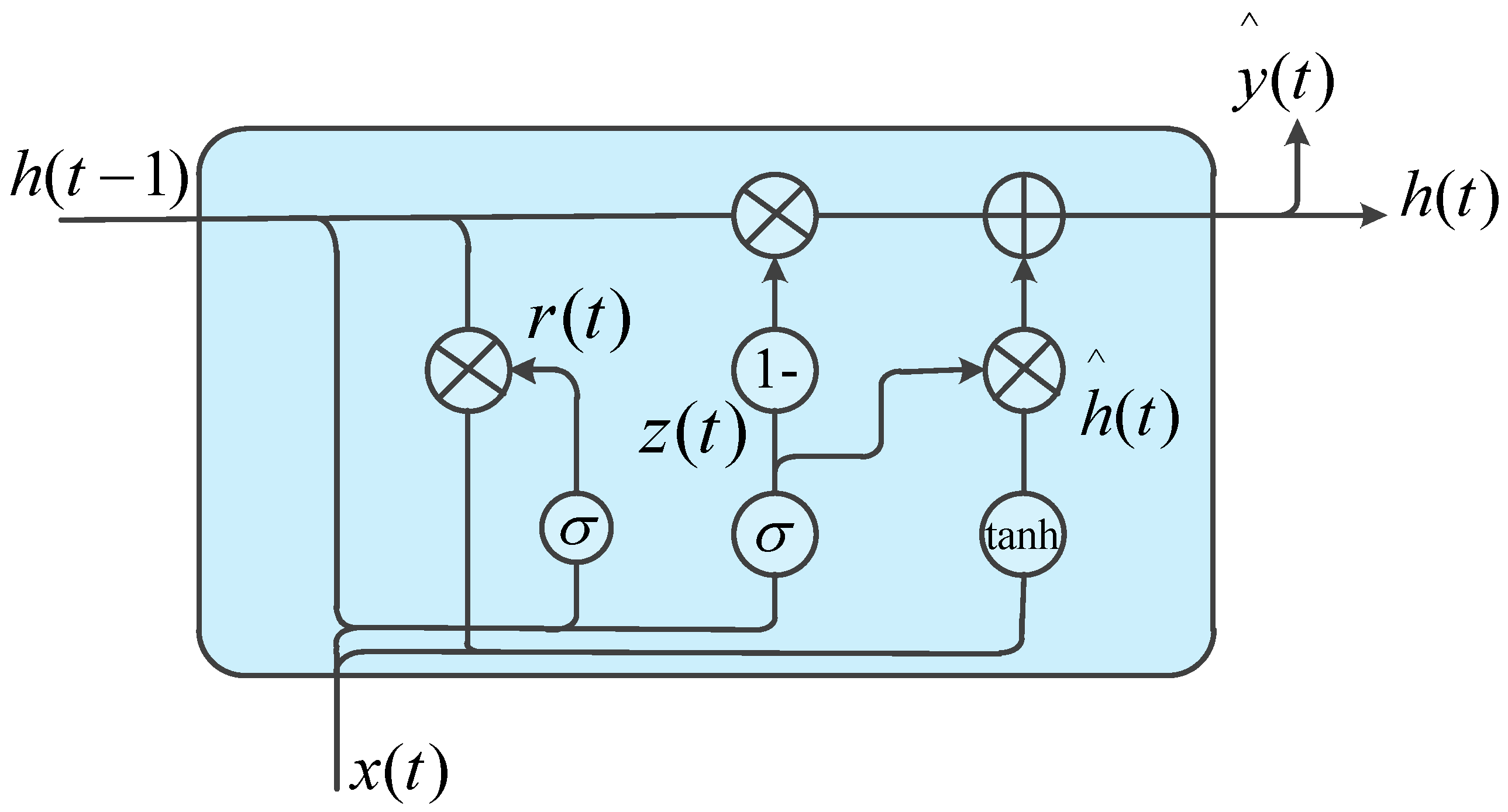
4.1. The GRU Network
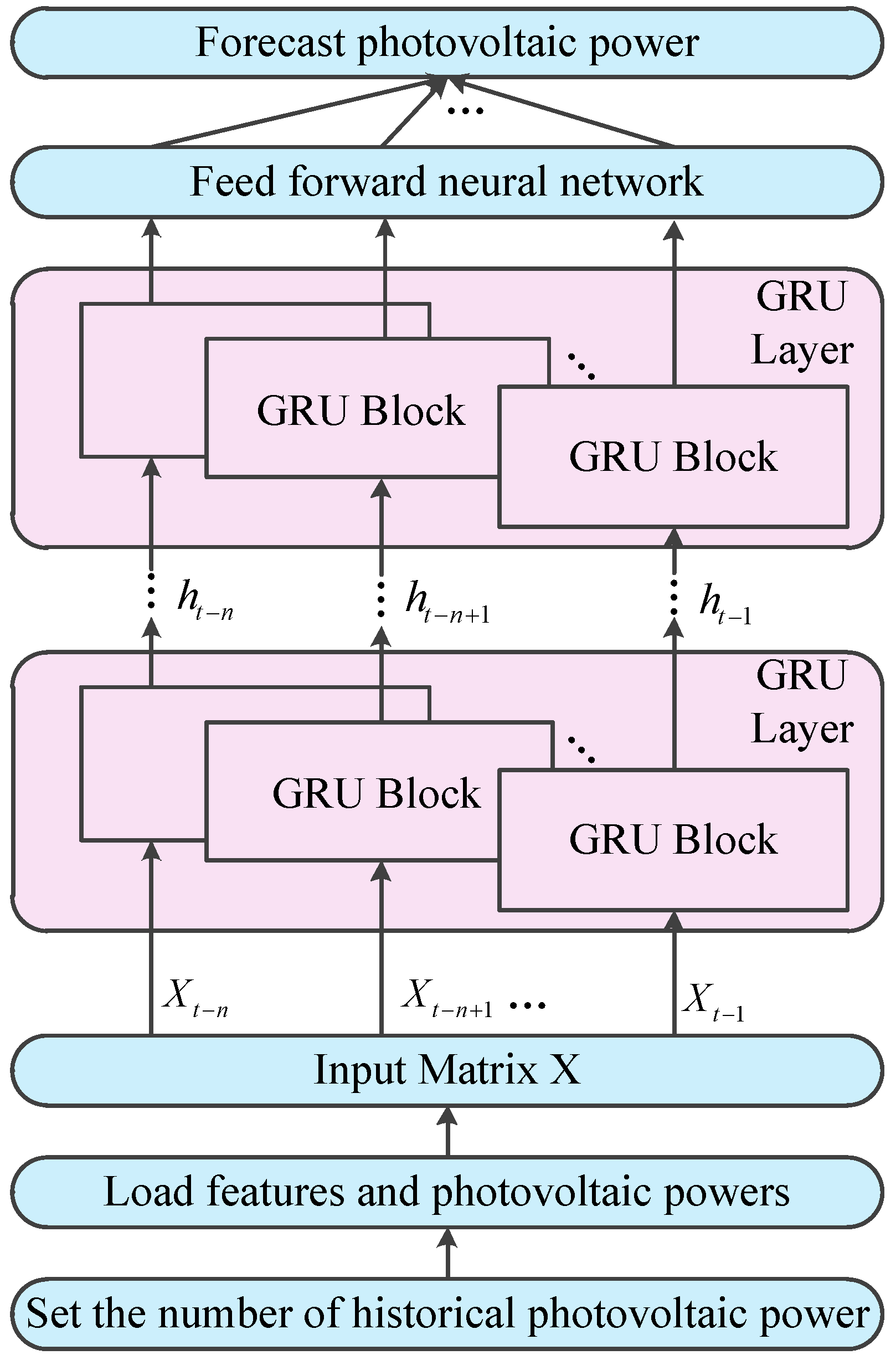
4.2. The Process for Forecasting Photovoltaic Power Based on GRU Network
- (1)
- Set a historical photovoltaic power series that will be used to predict the next photovoltaic power. The matrix X consists of historical photovoltaic power and 9 features that include R,TCC,10U,10V,2T,SSRD,STRD,TSR and TP.
- (2)
- Every row of the matrix X is the scaled features and the time step is fed to corresponding GRU block in the GRU layer. Since the sequential nature of the output of a GRU layer, the number of GRU layers that are stacked to form a recurrent neural network can be arbitrary.
- (3)
- The output of the top GRU layer are fed to a feed forward neural network that maps the output of GRU layer to photovoltaic power.
4.3. Program Implementation
4.4. Indicators for Evaluating the Results
5. Case Study
- (1)
- The number of neurons in the input layer of the GRU is equal to the sum of the number of features plus the number of historical photovoltaic power. The output layer with sigmoid activation function has one neuron. After several experiments, the best choice is to use one GRU layer, and the number of neurons is 15. The epochs are set to 100. In addition, LSTM uses the same parameters as GRU.
- (2)
- After several experiments, the best choice of BP network is to use two hidden layers, and the number of neurons in each layer is 15 and 5 respectively. The epochs are set to 100.
- (3)
- The radial basis function (RBF) is used as a kernel function for SVM. (4) After several experiments, the best parameters of ARIMA are set as follows: The number of autoregressive terms (p) is equal to 4. The degree of differencing (d) is equal to 2. The number of lagged forecast errors in the prediction equation (q) is set to 4.
5.1. The Optimal Number of Groups
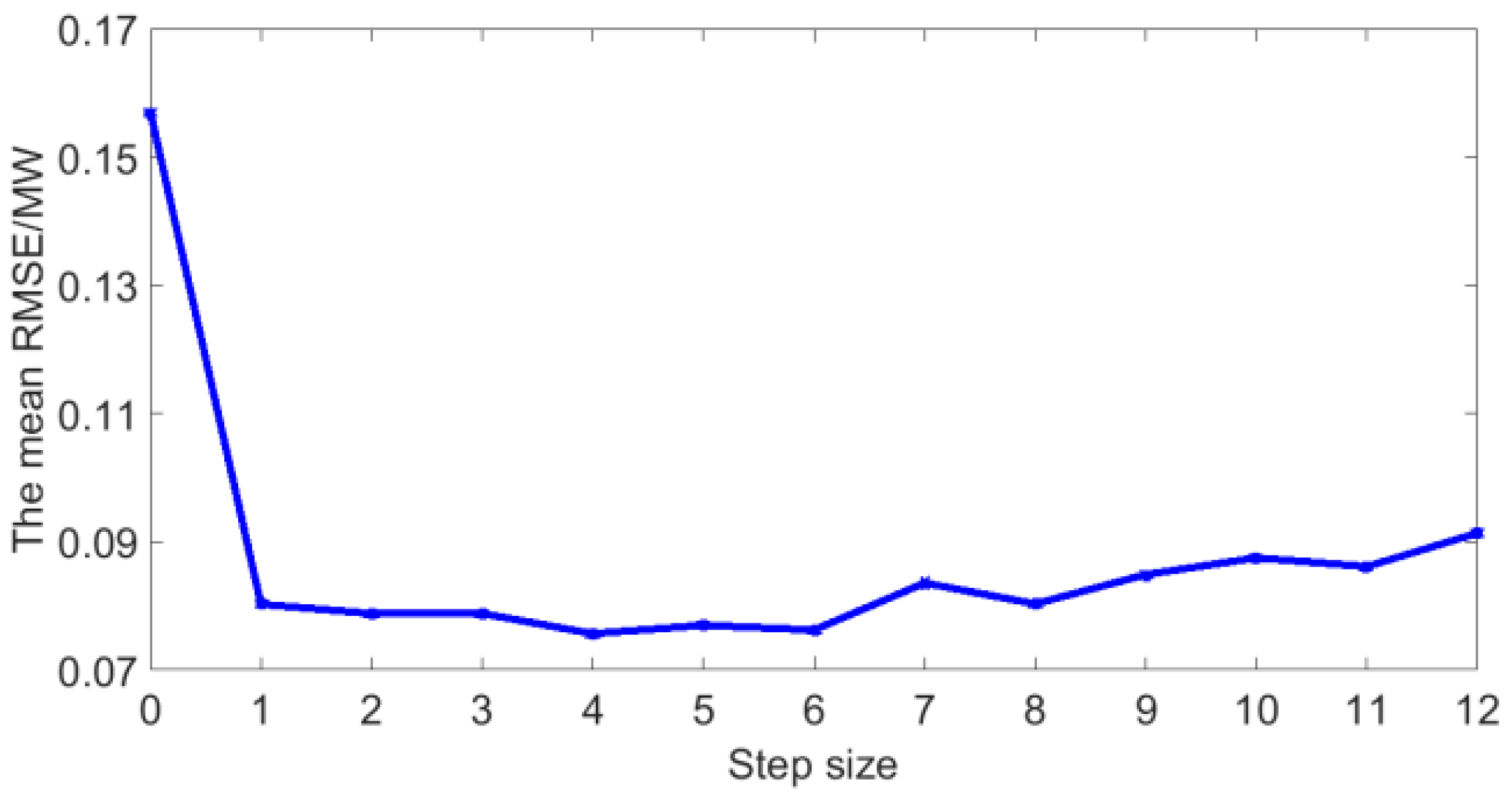
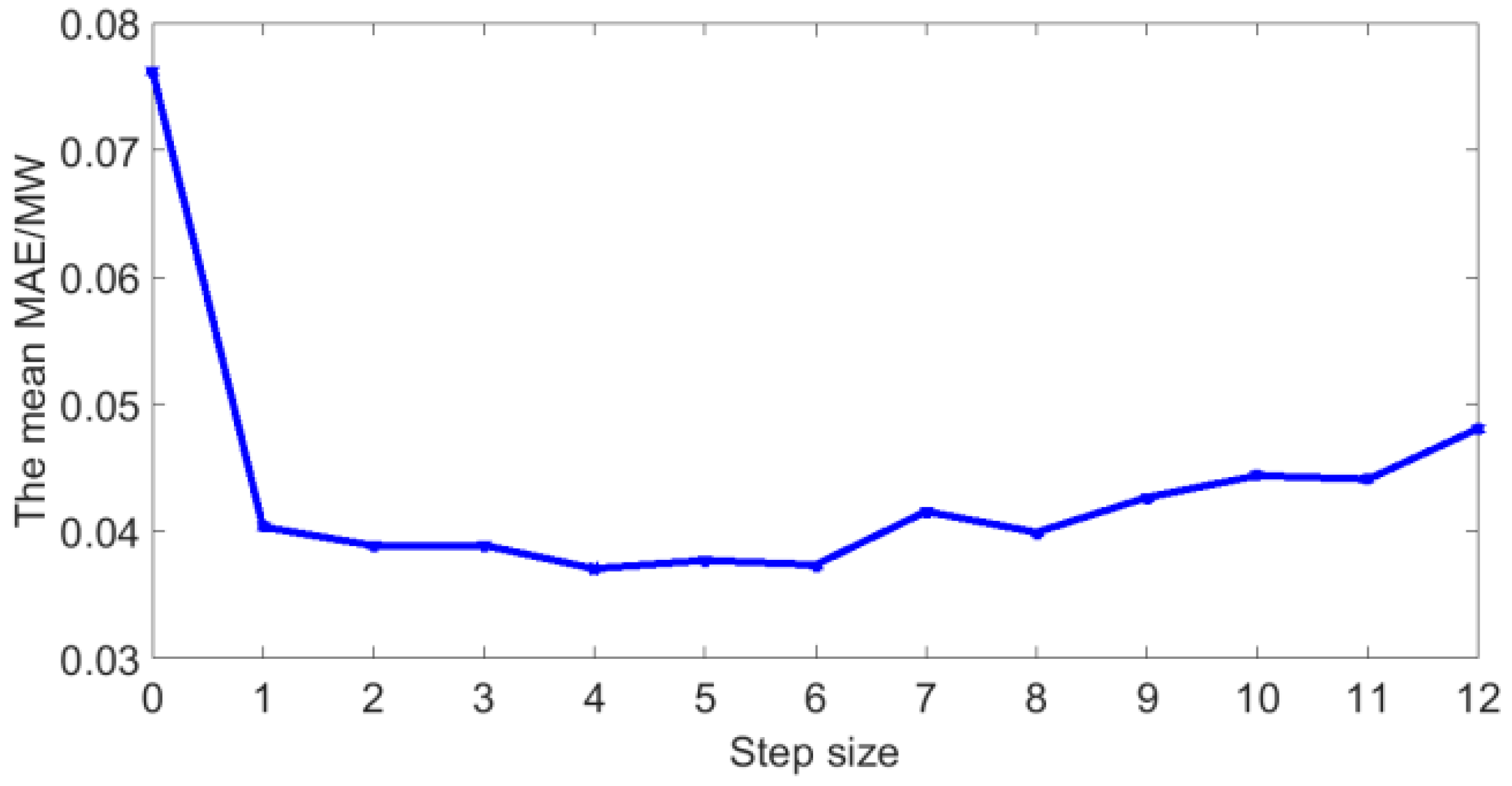
5.2. The Optimal Step Size
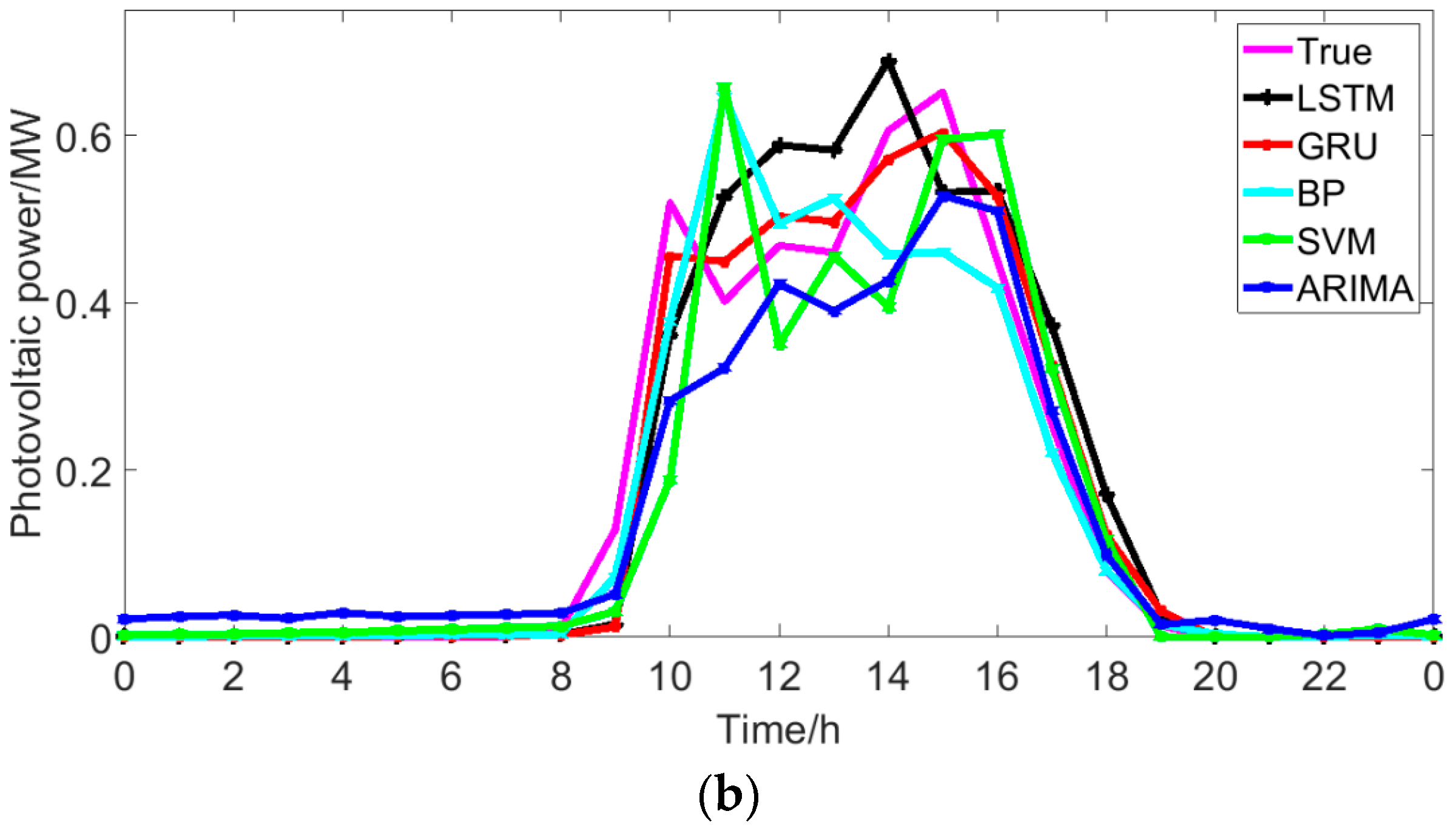
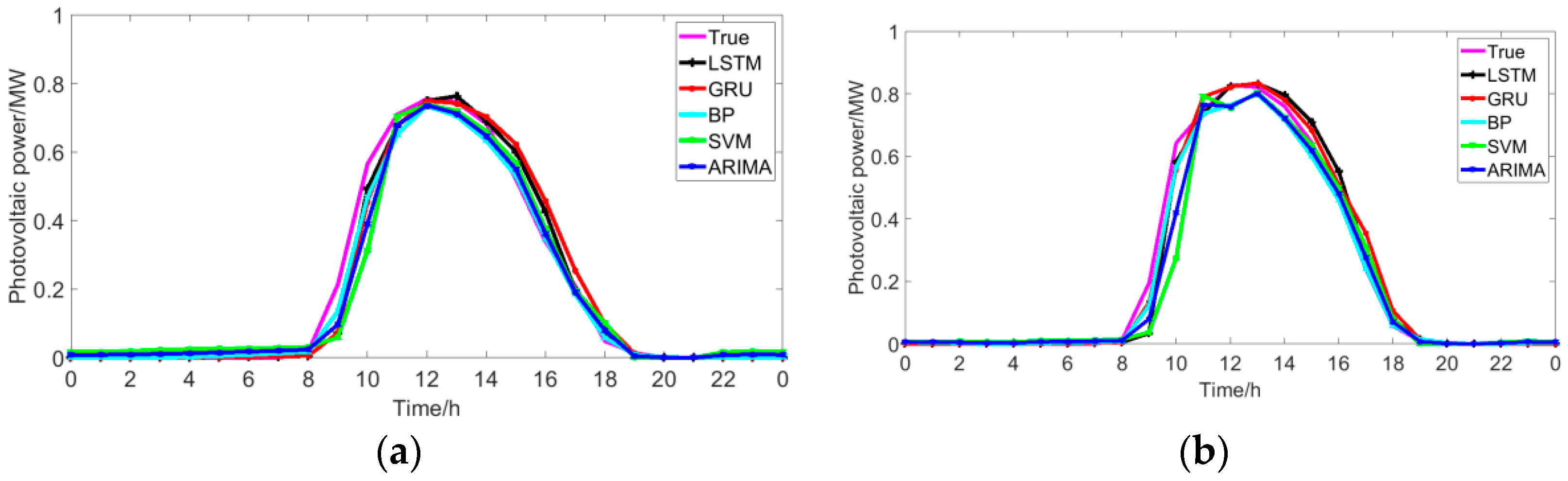
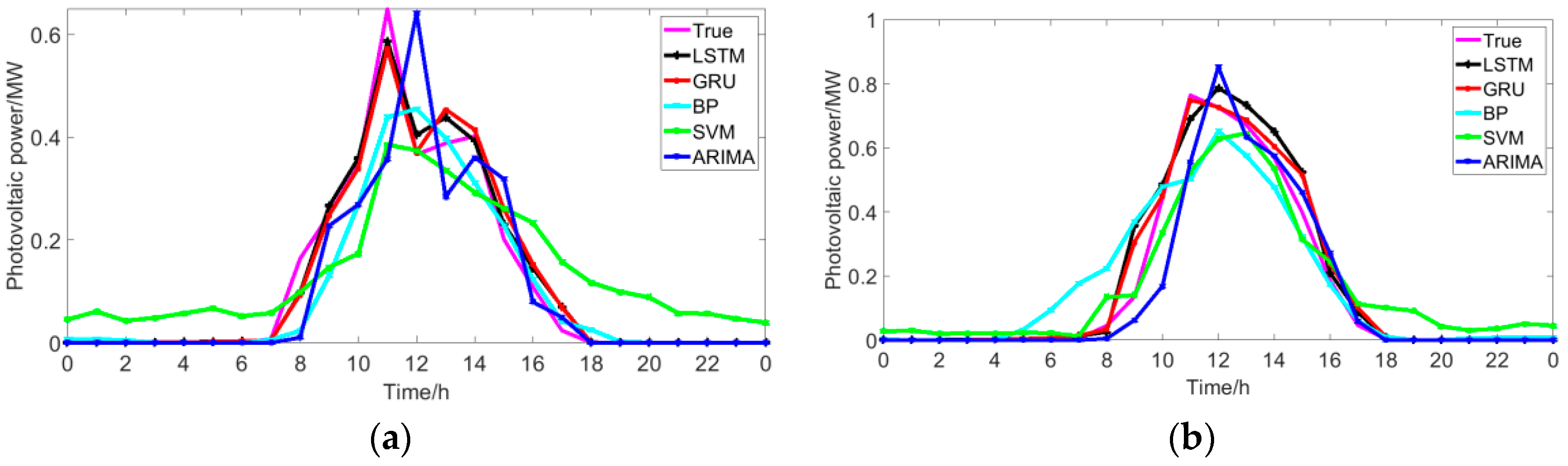
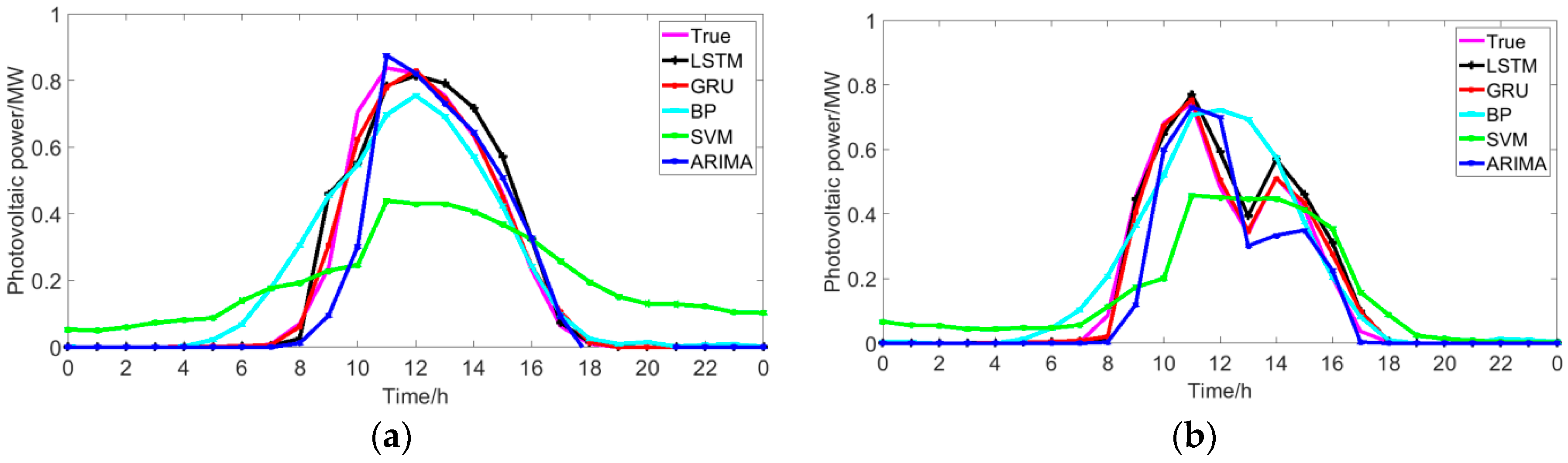
5.3. Comparison with Traditional Methods
6. Conclusions
- (1)
- Grouping training sets based on the similarity of input features and using the GRU network of the group to which the current object belongs can improve the accuracy of the prediction. The error decreases as the number of groups increases.
- (2)
- The Pearson coefficient can not only extract the main features that affect the photovoltaic power, but also qualitatively analyze the relationship between historical photovoltaic power and next moment’s power. Through qualitative analysis and quantitative analysis, it is found that a suitable number of historical time series of photovoltaic power can improve the forecasting accuracy. In this dataset, the optimal number of historical time series is 4.
- (3)
- As for the forecasting accuracy, the GRU network can simultaneously consider the influence of features and historical photovoltaic power output on the next moment’s photovoltaic power, which leads to a higher accuracy of the GRU than that of BP, SVM, ARIMA, and LSTM. In addition, compared with LSTM, GRU has fewer parameters and shorter training time. Compared to LSTM, the advantage of GRU is even more obvious when the data set is particularly large.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fonseca, A.G.; Tortelli, O.L.; Lourenço, E.M. A reconfiguration analysis tool for distribution networks using fast decoupled power flow. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015; pp. 182–187. [Google Scholar]
- Hu, Y.; Lian, W.; Han, Y.; Dai, S.; Zhu, H. A seasonal model using optimized multi-layer neural networks to forecast power output of pv plants. Energies 2018, 11, 326. [Google Scholar] [CrossRef]
- Liu, W.; Liu, C.; Lin, Y.; Ma, L.; Xiong, F.; Li, J. Ultra-short-term forecast of photovoltaic output power under fog and haze weather. Energies 2018, 11, 528. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J.; Cheng, Y.; Ni, Q.; Wang, S. Short-term solar power forecasting based on weighted gaussian process regression. IEEE Trans. Ind. Electr. 2018, 65, 300–308. [Google Scholar] [CrossRef]
- Huang, C.Y.; Tzeng, W.C.; Liu, Y.W.; Wang, P.Y. Forecasting the global photovoltaic market by using the gm(1,1) grey forecasting method. In Proceedings of the 2011 IEEE Green Technologies Conference (IEEE-Green), Baton Rouge, LA, USA, 14–15 April 2011; pp. 1–5. [Google Scholar]
- Qijun, S.; Fen, L.; Jialin, Q.; Jinbin, Z.; Zhenghong, C. Photovoltaic power prediction based on principal component analysis and support vector machine. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016; pp. 815–820. [Google Scholar]
- Jang, H.S.; Bae, K.Y.; Park, H.S.; Sung, D.K. Solar power prediction based on satellite images and support vector machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Bai, K.; Zhang, Z.; Lu, X.; Zhang, X. Short-term power-forecasting method of distributed pv power system for consideration of its effects on load forecasting. J. Eng. 2017, 2017, 865–869. [Google Scholar] [CrossRef]
- Ojha, U.; Adhikari, U.; Singh, D.K. Image annotation using deep learning: A review. In Proceedings of the 2017 International Conference on Intelligent Computing and Control (I2C2), Coimbatore, India, 23–24 June 2017; pp. 1–5. [Google Scholar]
- Neo, Y.Q.; Teo, T.T.; Woo, W.L.; Logenthiran, T.; Sharma, A. Forecasting of photovoltaic power using deep belief network. In Proceedings of the TENCON 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017; pp. 1189–1194. [Google Scholar]
- Yacef, R.; Benghanem, M.; Mellit, A. Prediction of daily global solar irradiation data using bayesian neural network: A comparative study. Renew. Energy 2012, 48, 146–154. [Google Scholar] [CrossRef]
- Cao, J.C.; Cao, S.H. Study of forecasting solar irradiance using neural networks with preprocessing sample data by wavelet analysis. Energy 2006, 31, 3435–3445. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by lstm. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Ferdowsi, M.; Dagli, C. Solar irradiance forecasting using deep recurrent neural networks. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 988–994. [Google Scholar]
- Liu, B.; Fu, C.; Bielefield, A.; Liu, Q.Y. Forecasting of chinese primary energy consumption in 2021 with gru artificial neural network. Energies 2017, 10, 1453. [Google Scholar] [CrossRef]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity price forecasting using recurrent neural networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global energy forecasting competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Wang, X.; Lee, W.J.; Huang, H.; Szabados, R.L.; Wang, D.Y.; Olinda, P.V. Factors that impact the accuracy of clustering-based load forecasting. IEEE Trans. Ind. Appl. 2016, 52, 3625–3630. [Google Scholar] [CrossRef]
- Wu, W.; Peng, M. A Data Mining Approach Combining K-Means Clustering With Bagging Neural Network for Short-Term Wind Power Forecasting. IEEE Internet Things J. 2017, 4, 979–986. [Google Scholar] [CrossRef]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A short-term wind power forecasting approach with adjustment of numerical weather prediction input by data mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Agrawal, R.K.; Muchahary, F.; Tripathi, M.M. Long term load forecasting with hourly predictions based on long-short-term-memory networks. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using rnn encoder-decoder for statistical machine translation. arXiv, 2014; arXiv:1406.1078. [Google Scholar]
- Jesus, O.D.; Hagan, M.T. Backpropagation algorithms for a broad class of dynamic networks. IEEE Trans. Neural Netw. 2007, 18, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Yazan, E.; Talu, M.F. Comparison of the stochastic gradient descent based optimization techniques. In Proceedings of the 2017 International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 16–17 September 2017; pp. 1–5. [Google Scholar]

| Variable Name | Unit |
|---|---|
| Total column liquid water (TCLW) | |
| Total column ice water (TCIW) | |
| Surface pressure (SP) | |
| Relative humidity at 1000 mbar (R) | % |
| Total cloud cover (TCC) | 0–1 |
| 10-m U wind component (10 U) | |
| 10-m V wind component (10 V) | |
| 2-m temperature (2 T) | K |
| Surface solar rad down (SSRD) | |
| Surface thermal rad down (STRD) | |
| Top net solar rad (TSR) | |
| Total precipitation (TP) | m |
| Program: Codes for Building the GRU Network |
|---|
| #1. Define Network from keras.models import Sequential from keras.layers import Dense from keras.layers.recurrent import GRU model = Sequential() model.add(GRU(units=10,input_shape=(trainX.shape [1], trainX.shape[2]),return_sequences=True)) model.add(GRU(units=10,return_sequences=True)) model.add(GRU(units=10)) model.add(Dense(units=1, kernel_initializer=‘normal’,activation=‘sigmoid’)) #2. compile the network model.compile(loss=‘mae’, optimizer=‘adam’) #3. fit the network history=model.fit(trainX,trainY,epochs=100,batch_size=10,validation_data=(validX,validY),verbose=2,shuffle=False) #4. forecasting photovoltaic power PV = model.predict(testX) |
| Group No. | MAE/MW | RMSE/MW | Group No. | MAE/MW | RMSE/MW |
|---|---|---|---|---|---|
| 1 | 0.0409 | 0.0725 | 6 | 0.0396 | 0.0701 |
| 2 | 0.0407 | 0.0717 | 7 | 0.0395 | 0.0701 |
| 3 | 0.0404 | 0.0725 | 8 | 0.0395 | 0.0698 |
| 4 | 0.0409 | 0.0718 | 9 | 0.0379 | 0.0683 |
| Method | The Best Case/s | The Worst Case/s | The Average Case/s | Standard Deviation/s |
|---|---|---|---|---|
| LSTM | 393.01 | 400.57 | 396.27 | 1.80 |
| GRU | 354.92 | 379.57 | 365.40 | 7.25 |
| BP | 7.87 | 14.55 | 10.62 | 1.58 |
| SVM | 30.03 | 32.05 | 30.65 | 0.35 |
| ARIMA | 2.64 | 5.99 | 3.66 | 0.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liao, W.; Chang, Y. Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies 2018, 11, 2163. https://doi.org/10.3390/en11082163
Wang Y, Liao W, Chang Y. Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies. 2018; 11(8):2163. https://doi.org/10.3390/en11082163
Chicago/Turabian StyleWang, Yusen, Wenlong Liao, and Yuqing Chang. 2018. "Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting" Energies 11, no. 8: 2163. https://doi.org/10.3390/en11082163
APA StyleWang, Y., Liao, W., & Chang, Y. (2018). Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies, 11(8), 2163. https://doi.org/10.3390/en11082163




