Impact of Demand-Side Management on the Reliability of Generation Systems
Abstract
:1. Introduction
- The CLS program is modelled for the first time to simulate the dynamic load shifting strategy during the inadequacy of power supply. The superiority of the CLS program is highlighted by comparing its performance with the well-known PLS program.
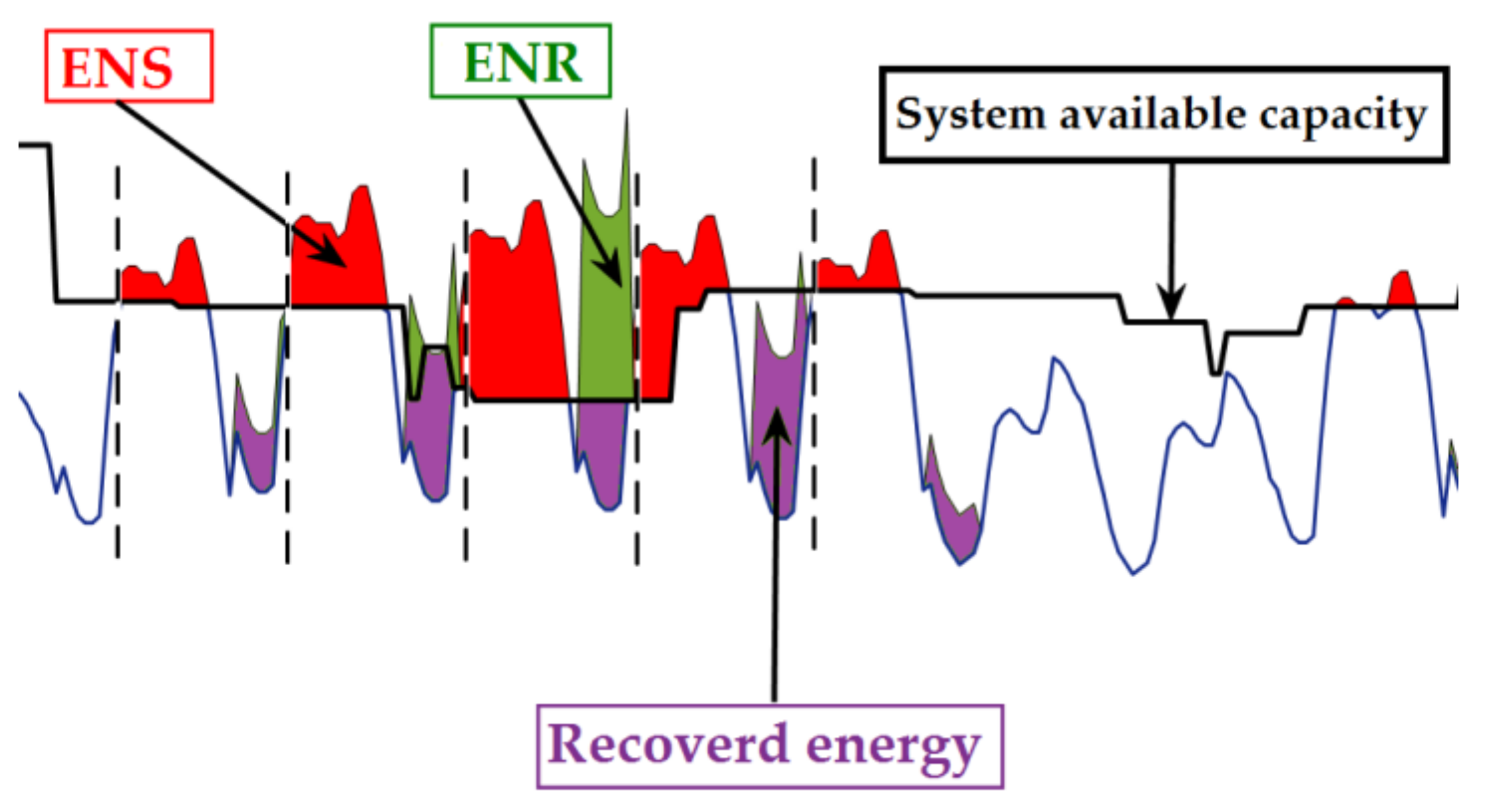
- A new index known as the expected-energy-not-recovered (EENR) is proposed to measure the inability of both the PLS and CLS in recovering the curtailed load.
- The modelling of the generation system in this study considers the two-state, four-state, and planned maintenance models. Load forecast uncertainty (LFU) is considered for the load model. The reliability impacts of these models are considered in PLS and CLS programs and their reliability performances are compared.
2. Methodology
2.1. Generation System Model
2.1.1. Two-State Model
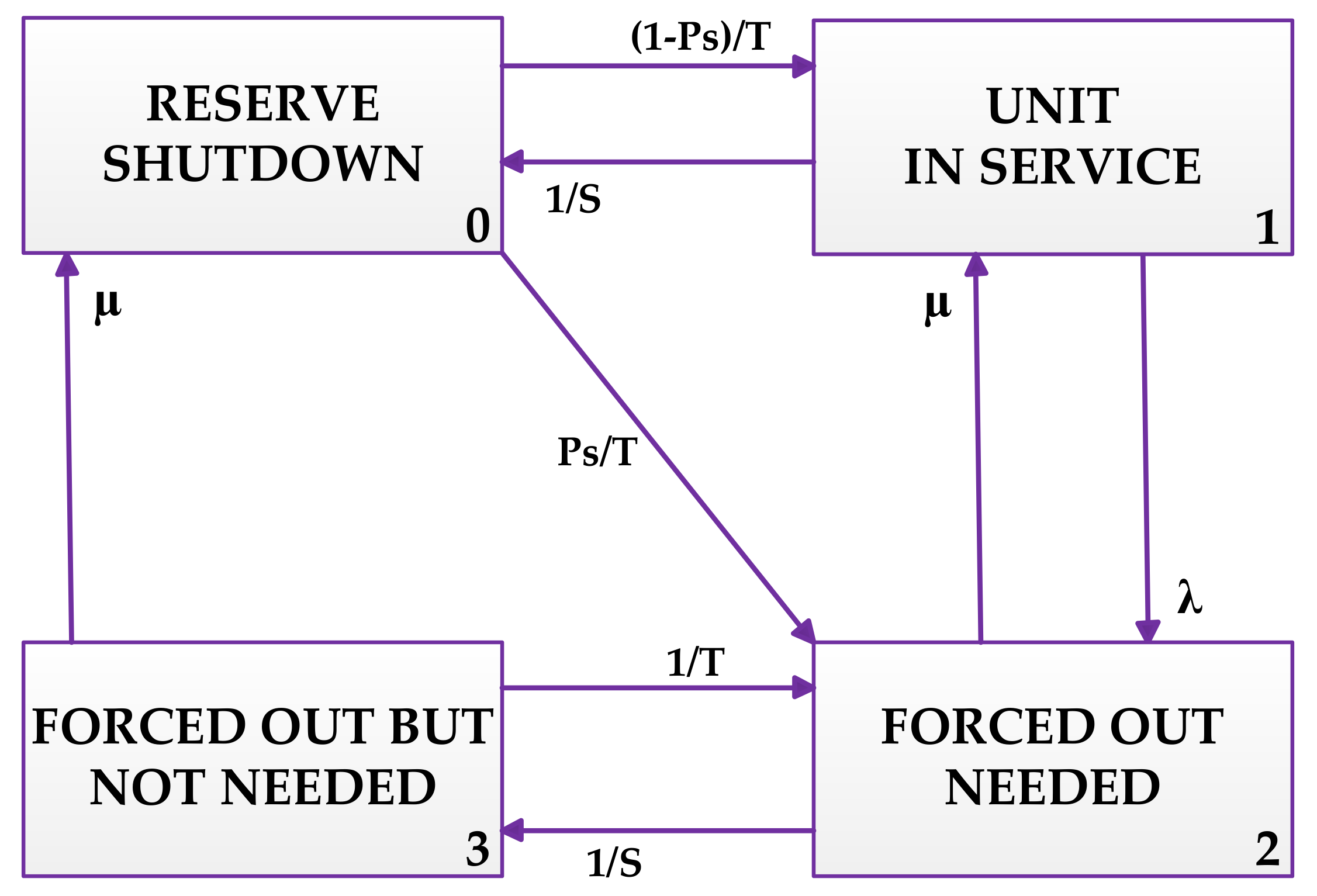
2.1.2. Four-State Model
- Reserve shutdown state: The generation unit is shutdown but ready for loading.
- Service state: The generation unit is in operating condition.
- Forced out needed: The generation unit is in down state and in need.
- Forced out not needed: The generation unit is in down state and not needed.
- The total available capacity of base units is calculated after accumulating the and of all base units according to Equations (4) and (5).
- Chronological load is intersected with base units of available capacity to determine the needs (corresponding to ) for peaking and cycling units.
- Available capacity of each peaking and cycling unit is calculated using the two-state model initially, then modified using the following:where is the unit available capacity of the peaking and cycling unit and is the corresponding unit capacity. From Equation (6), if the random number is greater or equal to , the unit is considered start-up, otherwise it fails. Generators in the period of reserve shutdown (corresponding to ) are in the up state.
- Corresponding units of available capacity is accumulated and added to the base units of available capacity to form total system available capacity.
- Chronological load is subtracted from total system available capacity to determine the amount of curtailed energy and duration of loss of the load.
2.1.3. Scheduled Maintenance
2.2. Demand-Side Management
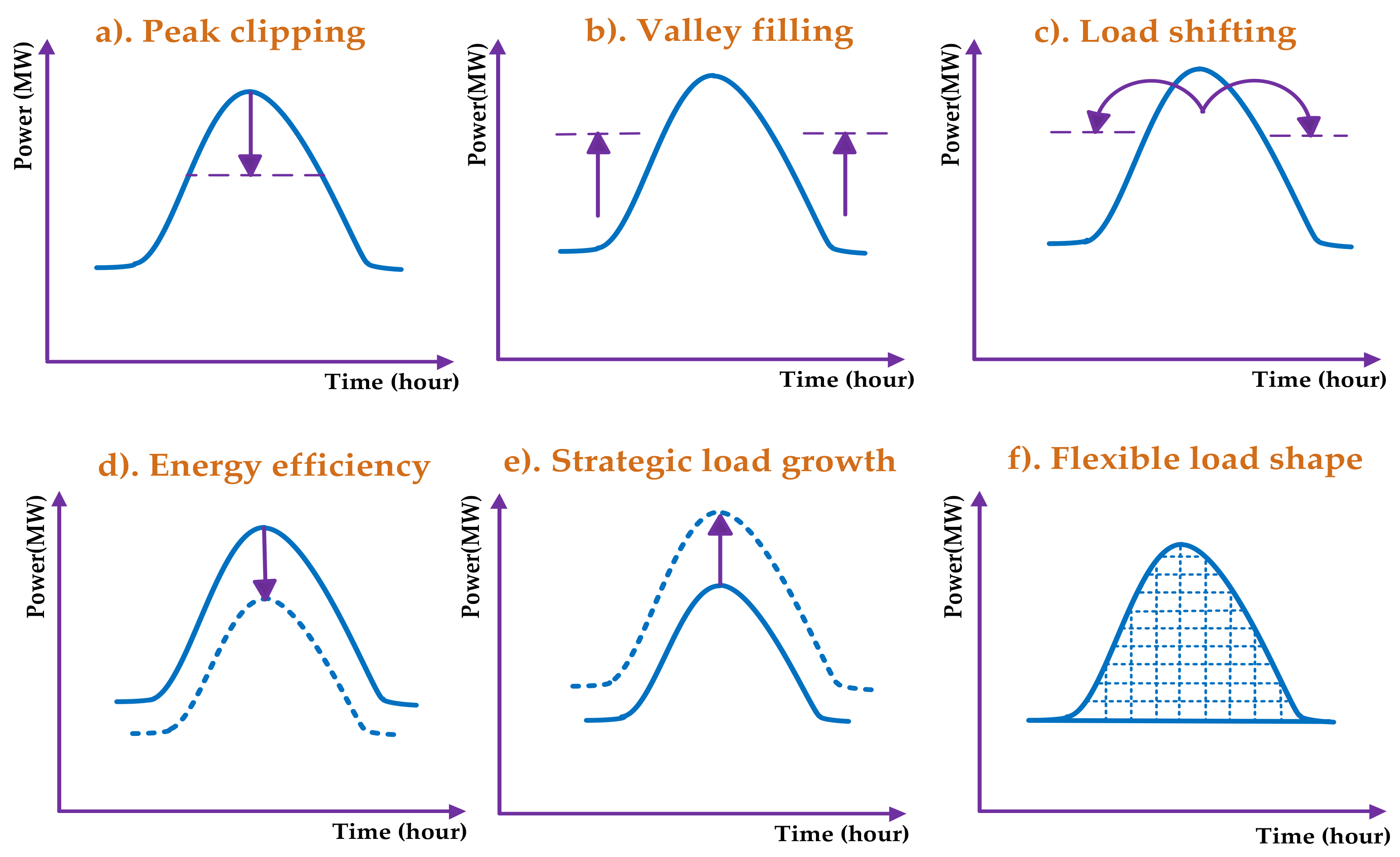
2.2.1. Load-Shifting Model
2.2.2. Load Forecast Uncertainty
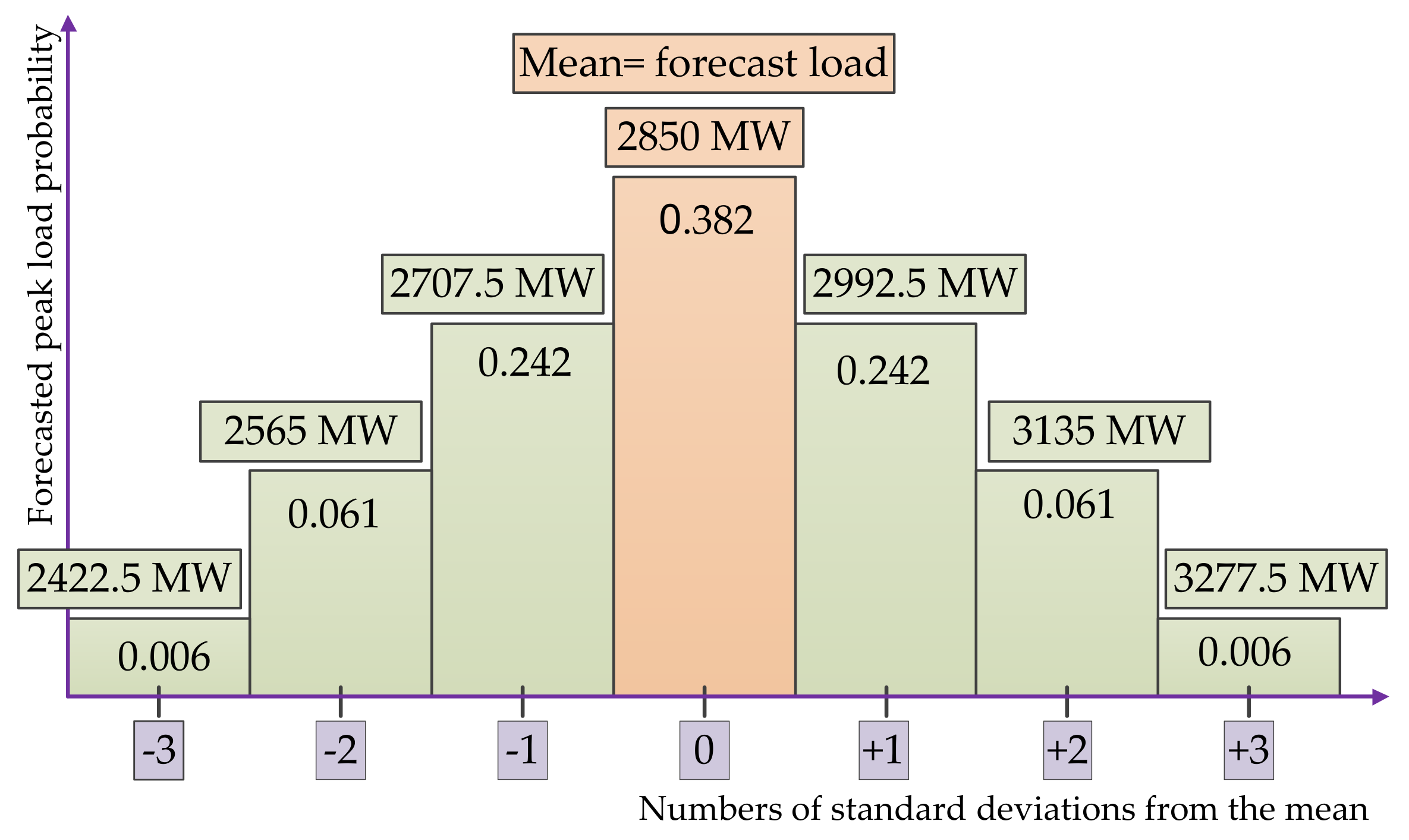
- Load level is selected based on the standard deviation from mean (peak level). Each load level is obtained by multiplying the peak value by the percentage of uncertainty. This value is added to the peak value to represent the increase in peak uncertainty or subtracted from peak to represent the decrease in peak uncertainty.
- The load level is multiplied by the probability that the load level occurs to obtain the weighted values for each level.
- The sum of all weighted load is the corresponding reliability index for the forecast load.
2.3. Overview of Methodology
- Step 1:
- Specify the chronological hourly load curve.
- Step 2:
- Model the load as one of the following cases:
- Case 1:
- Original load, without any consideration.
- Case 2:
- Preventive load-shifting scenarios (peak clipping is 15% of peak load, and energy recovery range from 90% to 100% of clipped load).
- Case 3:
- Load with forecast uncertainty (LFU is 1% to 15% of the peak value).
- Step 3:
- Calculate ENR for PLS which represents the total summation of the corresponding .
- Step 4:
- Model the generation system with one of the following cases:
- Case 1:
- Two-state model: all generation units are modelled as base load units.
- Case 2:
- Four-state model: peaking and cycling generation units are modelled using four state model. As the four-state model is irrelevant to base load units, they are modelled using the two-state model.
- Case 3:
- Considering planned maintenance: Planned maintenance for each generation unit is considered once every year. In the event of planned maintenance and failure of a certain generation unit, the available capacity of the corresponding unit is zero.
- Step 5:
- Generate the random statuses of each generator and obtain the total system available capacity by summing the generation capacity of each generator.
- Step 6:
- Compare the generation capacity margin with the system demand. If the margin is greater, then Step 7 is executed; otherwise, go to Step 6.
- Step 7:
- Acquire .
- Step 8:
- Divide by the number of off-peak hours.
- Step 9:
- Calculate for CLS.
- Step 10:
- Check the number of simulations that have been performed. If the maximum number of simulations is not yet met, go to Step 2, otherwise proceed to Step 11.
- Step 11:
- Calculate EENR for CLS.
- Step 12:
- The total EENS for PLS is the ENR added to all the expected unserved load due to the inadequacy of generation capacity, while the total EENS for CLS is equal to EENR.
3. Result and Discussions
3.1. Comparisons of PLS and CLS
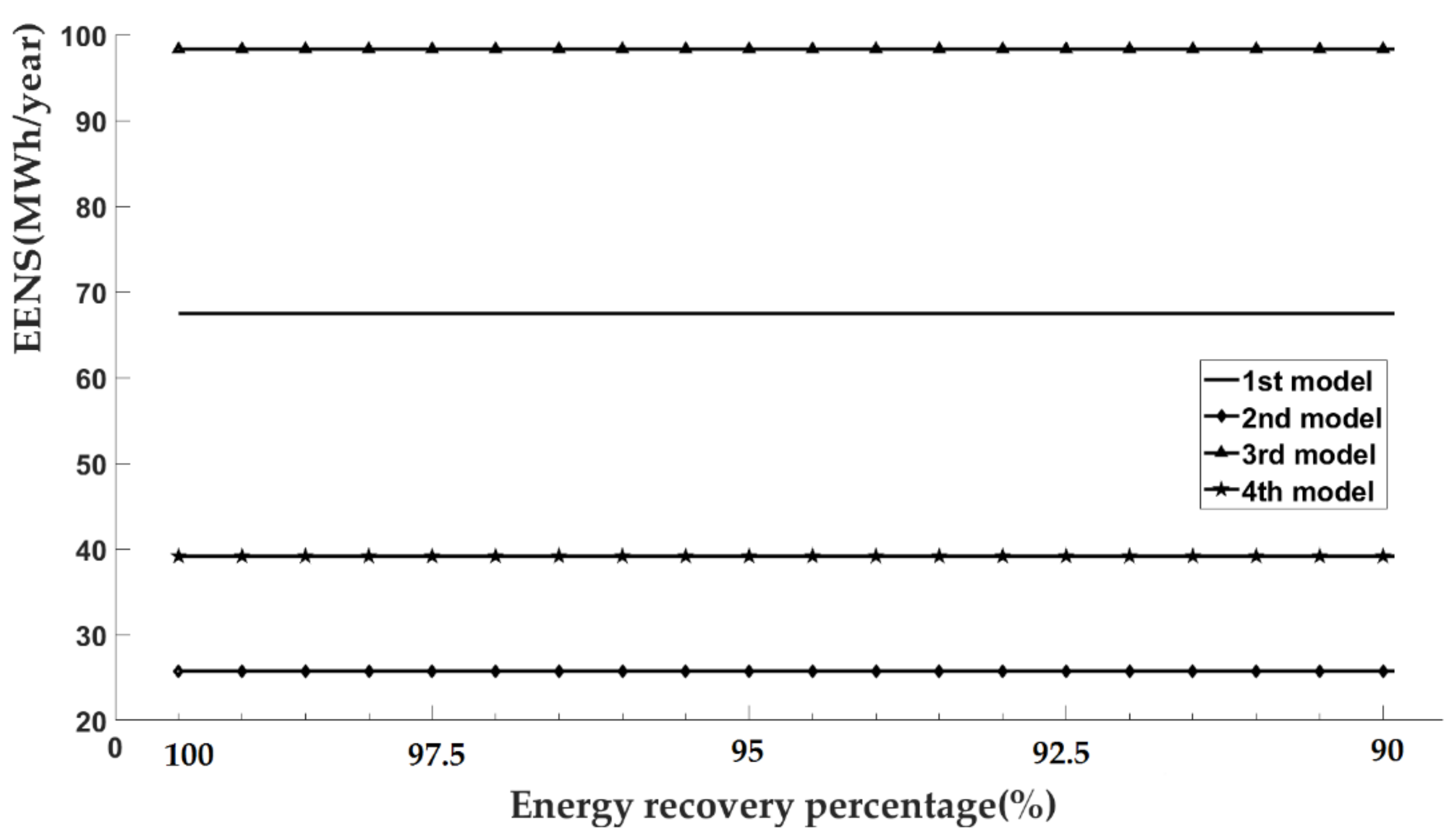
- The results in each case vary depending on the employed model:
- Case 1:
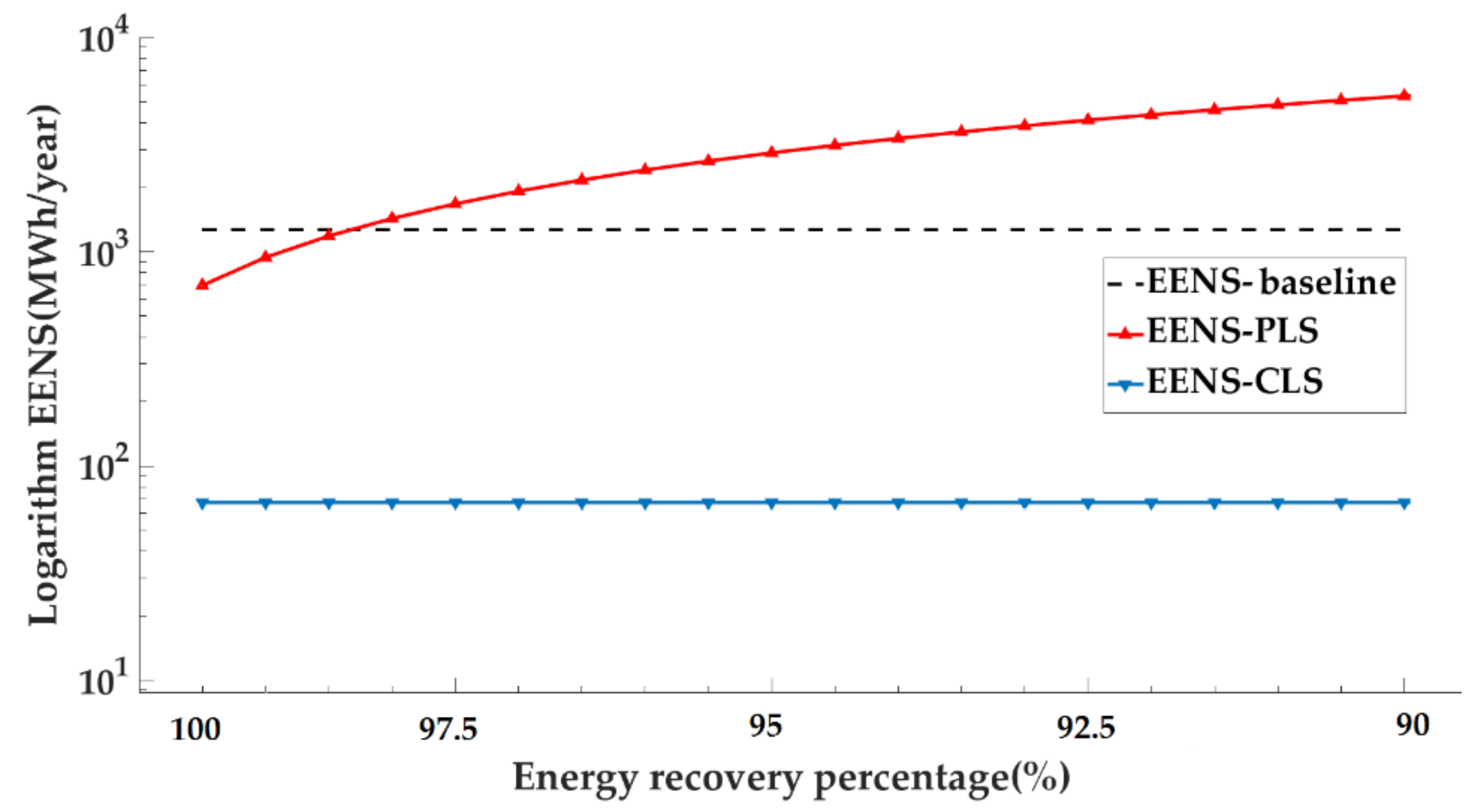
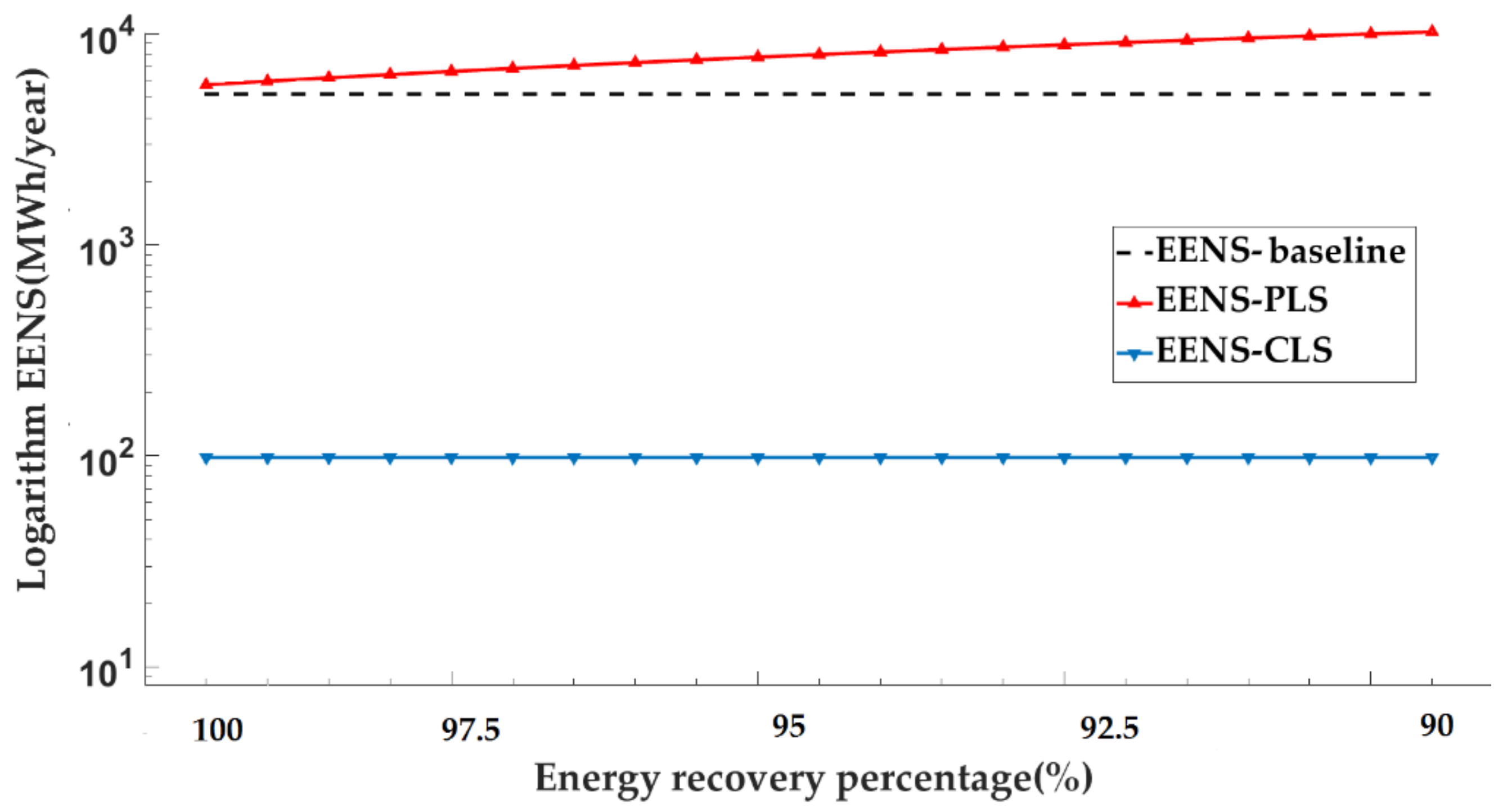
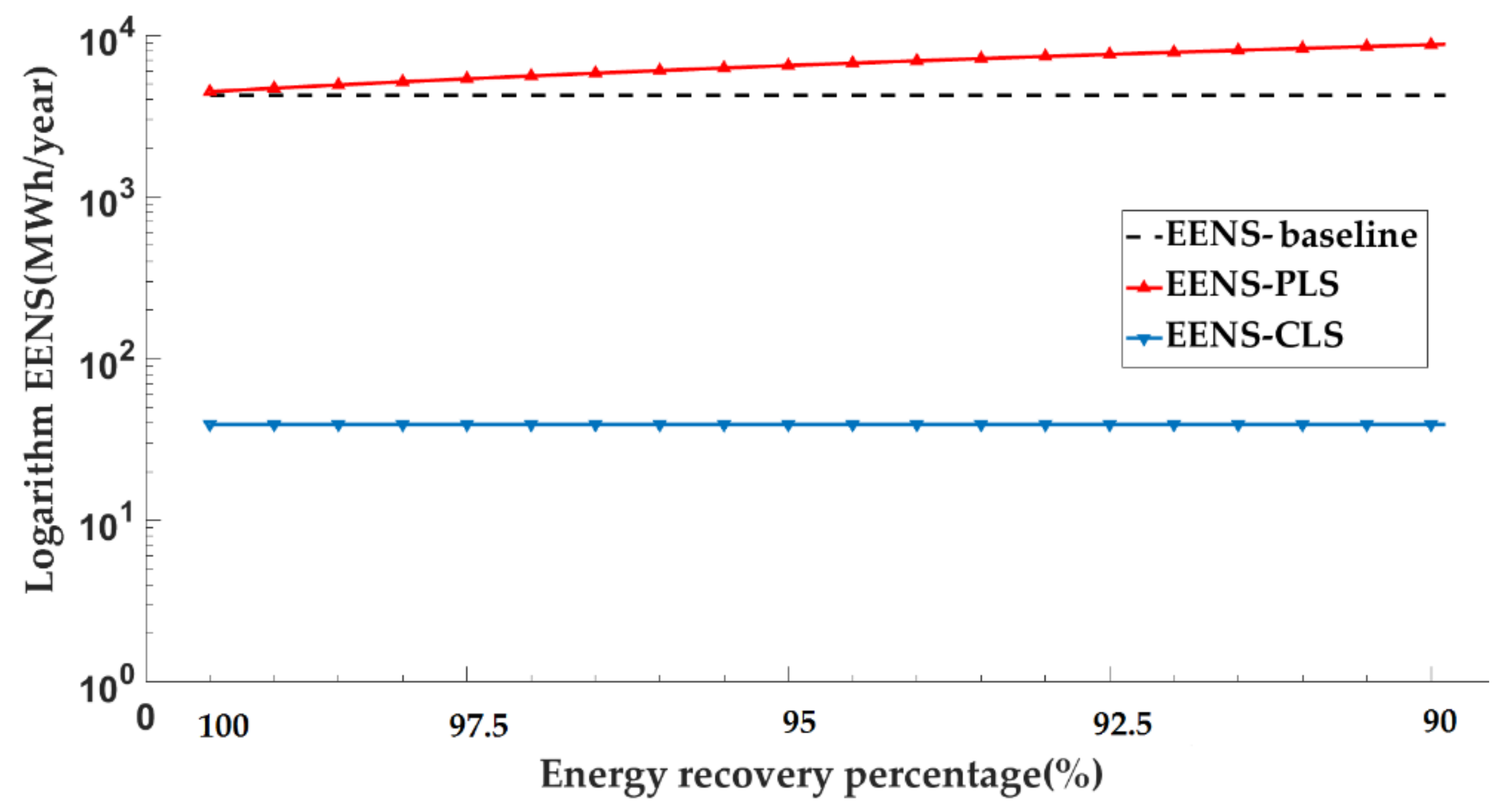
- When no load shifting is considered, the EENS of Model 4 2 is 24% lower than Model 1, and the EENS of Model 4 is 16% lower than Model 3.
- Case 2:
- When PLS is considered, the EENS of Model 2 is 14% lower than Model 1, and the EENS of Model 4 is 28% lower than Model 3.
- Case 3:
- When CLS is considered, the EENS of Model 2 is 62% lower than Model 1, and the EENS of Model 4 is 60% lower than Model 3.
The two-state model does not consider the duty cycle of peaking load units. The reduction in EENS in the three cases above represents the error in the EENS evaluation of the two-state model. Therefore, the four-state model is more accurate and realistic in assessing the EENS of the generating system than the two-state model. - When planned maintenance and LFU are used in Models 3 and 4, the EENS value increases significantly as compared to Models 1 and 2 for all cases. The reason for this is planned maintenance of the generators tends to reduce the overall available generation capacity, while, at the same time, there is the possibility that the fixed load level may increase under LFU consideration.
- The effect of PLS and CLS on EENS is discussed as follows:
- Case 1:
- When load shifting is not used, the EENS value is always higher than other cases. This highlights the reliability benefits of the load-shifting measures.
- Case 2:
- When PLS is implemented, the EENS improves in the first and Model 2s by 21% and 0.05%, respectively. In Model 4, the EENS is decreased by 11.5% only. This shows that PLS has lesser impact on EENS when planned maintenance and LFU are considered.
- Case 3:
- When CLS is considered, EENS values reduce significantly, improving the index values of the first case by 93%, 97%, 98% and 99% in Models 1–4, respectively. This proves that CLS has a significant impact on the reliability of generation systems. The reason for this significant improvement is that the CLS program is used when the power supply is unable to meet the load demand, providing a more specific treatment to the manipulation of the load curve.
3.2. Discussion
- The results show that the EENS of PLS and CLS differs. The dynamic considerations of available system capacity and load in CLS have significant impacts towards the generation system adequacy and thus must be accurately modelled.
- The benefit of Load shifting depends on the ability of the system operator to recover clipped or curtailed load, which is affected by mismatch between the generation and load levels, the percentage limits of energy to be recovered, the willingness of consumers to participate in the load rescheduling program and the availability of the ancillary services that connect system operator with demand-side.
- During the inadequacy of power supply, most of the energy curtailed can be recovered in the same day. The unrecovered energy is due to the insufficient capacity of the off-peak period and this excess amount of energy is classified as the EENR in this paper.
- Power systems usually have reserve capacity margin to account for load uncertainty and generator outages as well as planned maintenance. The CLS program proposed in this paper is shown to be able to improve the adequacy of power supply without introducing additional power generating facility, presenting a viable alternative that is much cheaper and faster to be implemented.
- The above results show that CLS is clearly more effective than PLS in terms of improving the reliability of power supply. In CLS, optimal regulatory incentives can be determined by considering only the EENR instead of the entire clipped energy as in PLS. However, its benefit can only be realised if electricity suppliers are allowed to curtail and cycle load.
- The complexity of power systems couple with continuous load growth require applicable LFU and planned maintenance models to estimate future energy demands. Although this increases the EENS value, it provides a more realistic assessment. The results have shown that the application of the CLS program can overcome the unwanted reduction of the generation system. Thus, CLS is suitable in such considerations to mitigate the EENS deterioration. Moreover, the CLS program is also a more economic option as the system operators are able to add new generation facilities only after the load shifting program is unable to achieve the desired reliability level.
- In the four-state model, the duty cycle of peaking and cycling generation units are considered. These type of generation units, when compared to the based load unit, undergo more frequent start-up and shutdown but with lesser operating hours because they are only needed during peak periods, or when there is inadequate power supply. However, the frequently ramping generators burn more fuel and, therefore, incur more cost than if the generators are operating continuously. For this reason, peaking and cycling units are expensive to operate and should be minimised. The load shifting programs can help to achieve this by reducing the peak load levels, leading to the lesser needs of peaking and cycling units.
- As a whole, the load shifting programs investigated in this paper fit into the wider agenda of DSM. DSM programmes have received considerable attention in recent years due to their significant impacts on reliability. DSM programmes are expected to be implemented substantially in the next few decades to satisfy the requirements of new challenges, such as the intermittent nature of renewable energies, global environmental concerns and economic constraints. These programmes are significant, should be considered in the planning and operation phases of electrical power systems and must be integrated with generation-side management to maintain the reliability and increase the efficiency of power systems. The adequacy planning of generation systems has changed recently due to new trends and technologies, i.e., smart grids, advanced communication systems and the digital revolution. Power system planners currently have to consider various resources to satisfy the residential and industrial demand growth.
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Pi | The probability of system state |
| Ci | The loss of load for system state |
| The number of simulation year | |
| The mean time to failure | |
| The mean time to repair | |
| The time to failure | |
| The time to repair | |
| Uniformly distributed random number between [0, 1] | |
| The failure rate | |
| The repair rate | |
| The average reserve shutdown time amongst periods of need, excluding scheduled outage | |
| The average in-need time per occasion of demand | |
| The starting failure probability of a generator | |
| The unit available capacity of the peaking and cycling generation unit | |
| The corresponding unit capacity | |
| A uniformly distributed random number between [0, 1] | |
| The original demand of the system | |
| , | The modified system load curves which result from implementing a load-shifting activity |
| The pre-specified peak demand | |
| The percentage of energy recovered amount, its range is | |
| The first time of the day when the original load is greater than the pre-specified peak (, | |
| The last time of the day when the original load is greater than the pre-specified peak | |
| , | The starting and ending times for the off-peak recovery of energy. |
| The duration of energy recovery, calculated as the difference between and | |
| The first modified load curve after subtracting from the original load | |
| The energy that must be shed during the period of adequacy deficiency. | |
| The second modified load curve after recovering energy to the first modified load curve | |
| The amount of added energy to each hour of recovery period | |
| The energy not recovered for each hour of energy recovery period | |
| The range of recovered energy, | |
| The first time during the day when the original load exceeds the system available capacity | |
| The last time during the day when the original load becomes equal or less than system capacity | |
| , | The starting and ending times for the off-peak recovery of energy |
| The instantaneous system available capacity | |
| Expected energy not supplied |
References
- Dehnavi, E.; Abdi, H. Determining optimal buses for implementing demand response as an effective congestion management method. IEEE Trans. Power Syst. 2017, 32, 1537–1544. [Google Scholar] [CrossRef]
- Allan, R. Reliability Evaluation of Power Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Li, W. Reliability Assessment of Electric Power Systems Using Monte Carlo Methods; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Gellings, C.W. Evolving practice of demand-side management. J. Mod. Power Syst. Clean Energy 2017, 5, 1–9. [Google Scholar] [CrossRef]
- Gellings, C.W. The concept of demand-side management for electric utilities. Proc. IEEE 1985, 73, 1468–1470. [Google Scholar] [CrossRef]
- Gellings, C.W.; Chamberlin, J.H. Demand-Side Management: Concepts and Methods; The Fairmont Press Inc.: Lilburn, GA, USA, 1987. [Google Scholar]
- Gellings, C.W. Standars Corner IEEE PES Demand-Side Management Subcommittee. IEEE Power Eng. Rev. 1986, PER-6, 9–12. [Google Scholar]
- De Almeida, A.; Rosenfeld, A.H. Demand-Side Management and Electricity End-Use Efficiency 149; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Teh, J.; Ooi, C.A.; Cheng, Y.-H.; Zainuri, M.A.A.M.; Lai, C.-M. Composite Reliability Evaluation of Load Demand Side Management and Dynamic Thermal Rating Systems. Energies 2018, 11, 466. [Google Scholar] [CrossRef]
- Patton, A.; Singh, C. Evaluation of load management effects using the OPCON generation reliability model. IEEE Trans. Power App. Syst. 1984, 11, 3229–3238. [Google Scholar] [CrossRef]
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impacts of Demand-Side Management on Electrical Power Systems: A Review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef]
- Huang, D.; Billinton, R. Effects of Load Sector Demand Side Management Applications in Generating Capacity Adequacy Assessment. IEEE Trans. Power Syst. 2012, 27, 335–343. [Google Scholar] [CrossRef]
- Sinsukprasert, P. Effects of Demand Side Management on Power System Reliability: A Case Study of Thailand, 1998. Available online: https://repository.upenn.edu/dissertations/AAI9829992 (accessed on 6 July 2018).
- Malik, A.S. Simulation of DSM resources as generating units in probabilistic production costing framework. IEEE Trans. Power Syst. 1998, 13, 1528–1533. [Google Scholar] [CrossRef]
- Malik, A. Modelling and economic analysis of DSM programs in generation planning. Int. J. Electr. Power Energy Syst. 2001, 23, 413–419. [Google Scholar] [CrossRef]
- Narimani, M.R.; Nauert, P.J.; Joo, J.Y.; Crow, M.L. Reliability assesment of power system at the presence of demand side management. In Proceedings of the IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 19–20 February 2016; pp. 1–5. [Google Scholar]
- Malik, A.S. Dynamic generating costs in DSM planning. Energy 1999, 24, 1–8. [Google Scholar] [CrossRef]
- Tanrioven, M.; Alam, M. Impact of load management on reliability assessment of grid independent PEM fuel cell power plants. J. Power Sources 2006, 157, 401–410. [Google Scholar] [CrossRef]
- Karunanithi, K.; Saravanan, S.; Prabakar, B.; Kannan, S.; Thangaraj, C. Integration of Demand and Supply Side Management strategies in Generation Expansion Planning. Renew. Sustain. Energy Rev. 2017, 73, 966–982. [Google Scholar] [CrossRef]
- Diewvilai, R.; Nidhiritdhikrai, R.; Eua-arporn, B. Demand side management worth evaluation under generation system planning framework. In Proceedings of the 2012 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phetchaburi, Thailand, 16–18 May 2012; pp. 1–4. [Google Scholar]
- Salehfar, H.; Patton, A. Modeling and evaluation of the system reliability effects of direct load control. IEEE Trans. Power Syst. 1989, 4, 1024–1030. [Google Scholar] [CrossRef]
- Ahsan, Q. Load management: Impacts on the reliability and production costs of interconnected systems. Int. J. Electr. Power Energy Syst. 1990, 12, 257–262. [Google Scholar] [CrossRef]
- Billinton, R.; Lakhanpal, D. Impacts of demand-side management on reliability cost/reliability worth analysis. IEE Proc. Gener. Transm. Distrib. 1996, 143, 225–231. [Google Scholar] [CrossRef]
- Calsetta, A.; Albrecht, P.; Cook, V.; Ringlee, R.; Whooley, J. A four-state model for estimate of outage risk for units in peaking service. IEEE Trans. Power App. Syst. 1972, 618–627. [Google Scholar] [CrossRef]
- Allan, R.N.; Billinton, R.; Abdel-Gawad, N. The IEEE reliability test system-extensions to and evaluation of the generating system. IEEE Trans. Power Syst. 1986, 1, 1–7. [Google Scholar] [CrossRef]
- Billinton, R.; El-Sheikhi, F.A. Preventive maintenance scheduling in power generation systems using a quantitative risk criterion. Can. Electr. Eng. J. 1983, 8, 28–39. [Google Scholar] [CrossRef]
- Limaye, D. Implementation of demand-side management programs. Proc. IEEE 1985, 73, 1503–1512. [Google Scholar] [CrossRef]
- Abaravicius, J. Demand Side Activities for Electric Load Reduction. Ph.D. Thesis, Lund University, Lund, Sweden, 2007. [Google Scholar]
- Billinton, R.; Huang, D. Effects of load forecast uncertainty on bulk electric system reliability evaluation. IEEE Trans. Power Syst. 2008, 23, 418–425. [Google Scholar] [CrossRef]
- El-Sheikhi, F.A.; Billinton, R. Load forecast uncertainty consideration in generating unit preventive maintenance scheduling for single systems. In Proceedings of the Third International Conference on Probabilistic Methods Applied to Electric Power Systems, London, UK, 3–5 July 1991; pp. 241–245. [Google Scholar]
- Zhai, D.; Breipohl, A.; Lee, F.; Adapa, R. The effect of load uncertainty on unit commitment risk. IEEE Trans. Power Syst. 1994, 9, 510–517. [Google Scholar] [CrossRef]
- Subcommittee, P.M. IEEE Reliability Test System. IEEE Trans. Power App. Syst. 1979, 98, 2047–2054. [Google Scholar] [CrossRef]






| Capacity (MW) | Scheduled Maintenance (Weeks/Year) | Outage Schedule (Number in Bracket Is Week) |
|---|---|---|
| 2 × 400 | 6 | (10–15) and (35–40) |
| 1 × 350 | 5 | (31–35) |
| 3 × 197 | 4 | (8–11), (15–18) and (40–43) |
| 4 × 155 | 4 | (6–9), (12–15), (26–29) and (36–39) |
| 3 × 100 | 3 | (20–22), (27–29) and (41–43) |
| 4 × 76 | 3 | (3–5), (15–17), (30–32) and (34–36) |
| 6 × 50 | 2 | (16–17), (21–22), (27–28), (31–32), (38–39) and (41–42) |
| 4 × 20 | 2 | (9–10), (12–13), (12,13) and (33–34) |
| 5 × 12 | 2 | (9–10), (26–27), (33–34), (38–39) and (41–42) |
| Std. Deviations from Mean | Load Level (MW) | Reliability Index | Probability | Weighted |
|---|---|---|---|---|
| −3 | 2850 − (15% × 2850) = 2422.5 | a | 0.006 | a × 0.06 |
| −2 | 2850 − (10% × 2850) = 2565.0 | b | 0.061 | b × 0.61 |
| −1 | 2850 − (5% × 2850) = 2707.5 | c | 0.242 | c × 0.242 |
| 0 | 2850 − (0% × 2850) = 2850.0 | d | 0.382 | d × 0.382 |
| +1 | 2850 + (5% × 2850) = 2992.5 | e | 0.242 | e × 0.242 |
| +2 | 2850 + (10% × 2850) = 3135.0 | f | 0.061 | f × 0.061 |
| +3 | 2850 + (15% × 2850) = 3277.5 | g | 0.006 | g × 0.006 |
| Reliability index = Σ weighted of reliability index = a × 0.06 + b × 0.61 + c × 0.242 + d × 0.382 + e × 0.242 + f × 0.061 + g × 0.006 | ||||
| Priority Order | Capacity (MW) | Unit Type | Expected Energy Production (GWh) | Load Supplied |
|---|---|---|---|---|
| 1–6 | 50 × 6 | Hydro | 2594.592 | Base |
| 7–8 | 400 × 2 | Nuclear | 6142.754 | |
| 9 | 350 × 1 | Coal | 2521.737 | |
| 10–12 | 197 × 3 | Oil | 3002.401 | |
| 13–16 | 155 × 4 | Coal | 680.454 | |
| 17–19 | 100 × 3 | Oil | 333.287 | Cycling |
| 20–23 | 76 × 4 | Coal | 18.638 | |
| 24–28 | 12 × 5 | Oil | 1.149 | Peaking |
| 29–32 | 20 × 5 | Oil | 0.885 |
| Model No. | EENS MW h/year | ||
|---|---|---|---|
| 1st Case: No Load Shifting | 2nd Case: PLS | 3rd Case: CLS | |
| Model 1: 2-state for all units | 1144.6422 | 898.9592 | 68.9158 |
| Model 2: 4-state for peaking and cycling units | 869.7892 | 822.5749 | 25.7486 |
| Model 3: Model 1 + LFU & maintenance | 6235.3378 | 6258.9655 | 98.3171 |
| Model 4: Model 2 + LFU & maintenance | 5208.4484 | 4607.0723 | 39.1608 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impact of Demand-Side Management on the Reliability of Generation Systems. Energies 2018, 11, 2155. https://doi.org/10.3390/en11082155
Jabir HJ, Teh J, Ishak D, Abunima H. Impact of Demand-Side Management on the Reliability of Generation Systems. Energies. 2018; 11(8):2155. https://doi.org/10.3390/en11082155
Chicago/Turabian StyleJabir, Hussein Jumma, Jiashen Teh, Dahaman Ishak, and Hamza Abunima. 2018. "Impact of Demand-Side Management on the Reliability of Generation Systems" Energies 11, no. 8: 2155. https://doi.org/10.3390/en11082155
APA StyleJabir, H. J., Teh, J., Ishak, D., & Abunima, H. (2018). Impact of Demand-Side Management on the Reliability of Generation Systems. Energies, 11(8), 2155. https://doi.org/10.3390/en11082155






