Efficient and Privacy-Preserving Data Aggregation and Dynamic Billing in Smart Grid Metering Networks

Abstract

The smart grid enables convenient data collection between smart meters and operation centers via data concentrators. However, it presents security and privacy issues for the customer. For instance, a malicious data concentrator cannot only use consumption data for malicious purposes but also can reveal life patterns of the customers. Recently, several methods in different groups (e.g., secure data aggregation, etc.) have been proposed to collect the consumption usage in a privacy-preserving manner. Nevertheless, most of the schemes either introduce computational complexities in data aggregation or fail to support privacy-preserving billing against the internal adversaries (e.g., malicious data concentrators). In this paper, we propose an efficient and privacy-preserving data aggregation scheme that supports dynamic billing and provides security against internal adversaries in the smart grid. The proposed scheme actively includes the customer in the registration process, leading to end-to-end secure data aggregation, together with accurate and dynamic billing offering privacy protection. Compared with the related work, the scheme provides a balanced trade-off between security and efficacy (i.e., low communication and computation overhead while providing robust security).

1. Introduction

Smart grid (SG) has been envisioned as offering a great potential to remould the traditional power distribution network by integrating several desirable features, e.g., flexibility, reliability, and efficiency for the next-generation power plants in the foreseeable future [1]. Moreover, the integration of new renewable energy resources (solar, wind, etc.) will make the energy grid more sustainable and environmentally friendly. In SG, advanced metering infrastructure (AMI) is a major application domain that integrates the energy companies and end-consumers to take part in the utility management. An AMI typically consists of many entities, e.g., smart meter (SM), data concentrator gateway (CG), database, trusted authority, and others. A SM mainly measures the consumption data within the home and sends it periodically to the CG utilizing two-way communication technologies. Finally, the consumption data arrives at the supplier’s main servers via the CG. The data can be used for the real-time energy management systems. For instance, consumption usage data is being utilized for the dynamic pricing and billing, and for energy feedback purposes. Moreover, based on the billing, the utility suppliers are now able to balance and manage bulk generation and consumption by looking at how much energy is being consumed by the consumers at different times of the day/week or what kind of tariff plan is used by a customer [2].

The SM sends consumption data periodically using a two-way communication technology to the CG and then to the utility company; however, the two-way communication raises many potential security and privacy threats. For instance, as consumption data is utilized for energy feedback together with dynamic pricing and billing purposes, the opportunity to inject false data (in transit and/or from data origin) would allow an attacker to unbalance the load management and the dynamic pricing systems. More precisely, in a power grid, an attacker can send the manipulated meters’ readings by installing several fake SMs (or other false data injection techniques [3]) and these false readings can unbalance the load management (e.g., demand response) program. Such unbalancing may disrupt the smooth functionality of a power grid, cause higher energy generation cost, and sometimes even energy blackout in a local region. Form a billing perspective, a customer with ill intent may send an incorrect report (or zero uses report) of his/her energy consumptions from the home area network to the utility company. The rate of incorrect reports does not seem very large, though the cumulative effect on utilities is significant. Moreover, such incorrect reports may create revenue collection issues and/or a perturbation of energy price control in the energy market due to the incorrect reports. Thus, security of a smart meter’s data (i.e., consumption report) is paramount in the SG. From the perspective of customers’ privacy, the consumption data may disclose the smallest routine of daily activities of individuals (such as, sleeping patterns, office time, and other activities) [4,5]. Moreover, a lower/zero power consumption on a normal day may point to the property being unoccupied. Therefore, the SM data (i.e., consumption usages) that is utilized for the pricing and billing, and energy feedback purposes, must be transmitted and recorded in a secure and privacy-preserving manner in the SG.

1.1. Contribution

In this paper, we propose an efficient and privacy-preserving data aggregation and billing scheme that thwarts security and privacy attacks, considering both outsider and insider attackers in smart grid metering networks. Specifically, the main contributions of this paper can be summarized as follows.

• First, we propose a new and efficient data generation and aggregation scheme to preserve the security and privacy of consumption usage data between the smart meter and data concentrator. The CGs are not able to derive the aggregated sum of the consumption data, but can only check the validity of the received reports. Moreover, to attain the efficiency at resource-constrained SM, we employed the elliptic curve cryptography, symmetric encryption, and one-way hashing operations.
• Second, we propose a price determining and dynamic billing mechanism that derives the dynamic price for different time-slots and computes the accurate bills for the customers. In addition, a customer can verify whether the energy bill received is accurate.
• Third, we successfully evaluate the security strength of the proposed scheme under the indistinguishability against adaptive chosen ciphertext attacks (IND-CGCCA) and unforgeability (also called existential forgeability against adaptive chosen message attacks—EUFCMA). Thus, the proposed scheme is also provably secure.
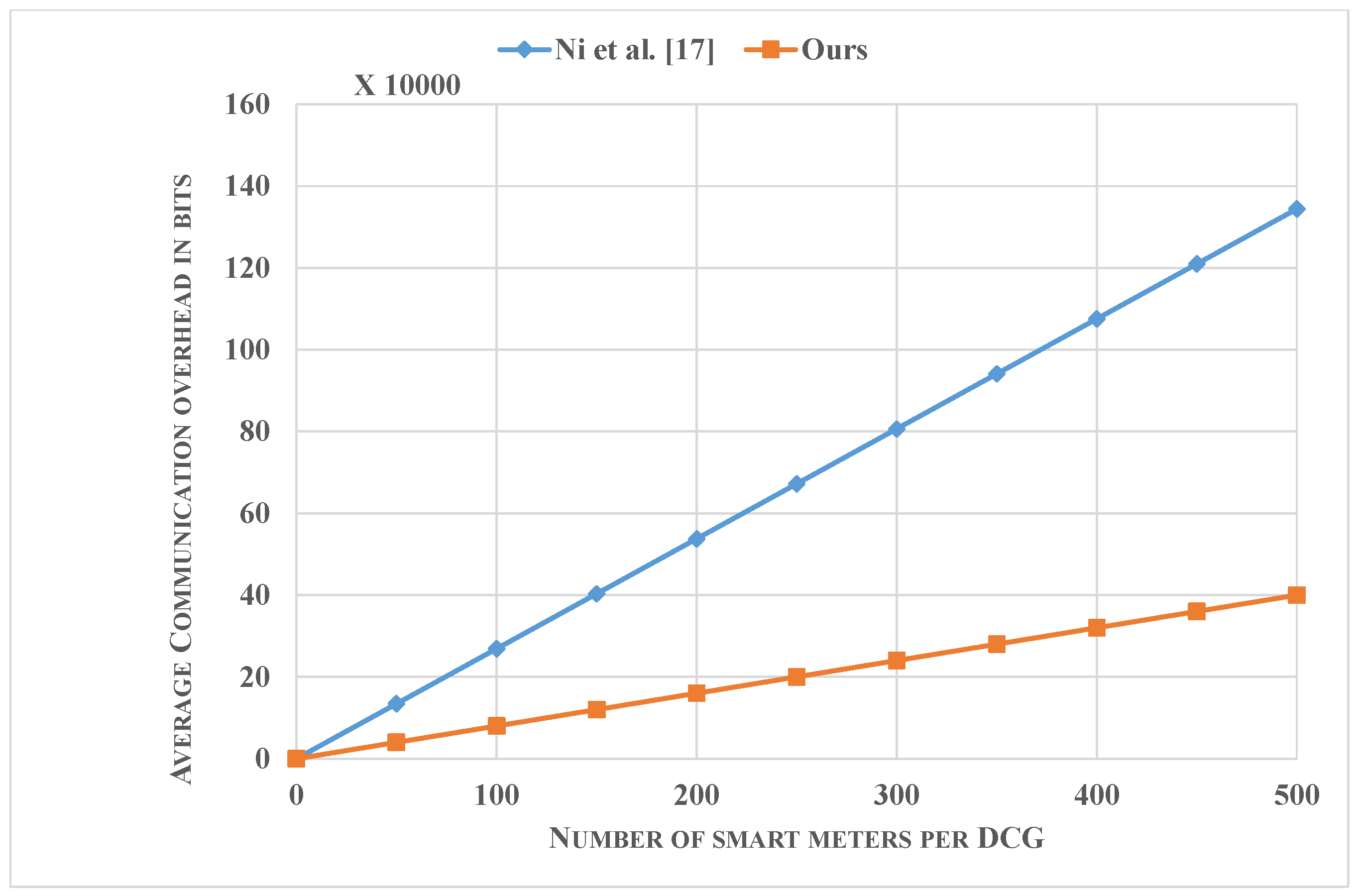
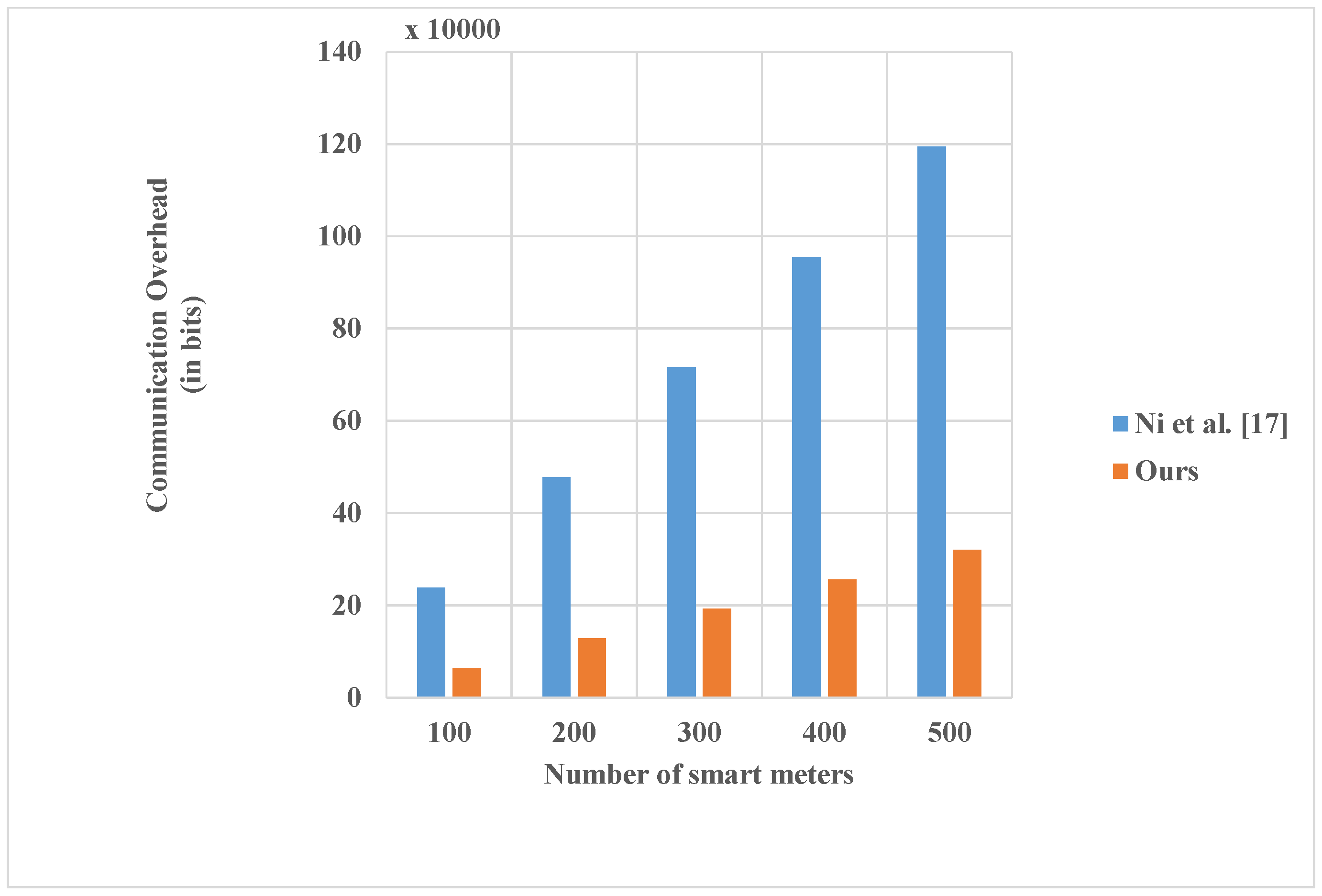
• Finally, we present performance comparisons of the proposed scheme, showing that our scheme requires lower computation and communication costs than the existing schemes. To be more specific, the total computational time for the report generation for until the computation of the bill by the customer would require 632 µs. With respect to communication costs, the security related information requires a payload of 1920 bits. We also show the scalability of our scheme regarding communication overhead from SM to CG and CG to OC for a varying number of SMs.

1.2. Outline of the Paper

The rest of this paper is organized as follows. Section 2 describes related work on privacy preserving data aggregation schemes with and without billing functionalities. In Section 3, the system, adversary models and design goals are explained. Section 4 deals with some preliminaries. In Section 5 the proposed scheme is elaborated. The security and performance analysis are provided in Section 6 and Section 7 respectively. Finally, we end with conclusions in Section 8.

2. Related Work

To address security and privacy threats in smart grids, recently a significant number of secure and privacy-preserving schemes have been proposed. These schemes present different types and/or levels of security protections at different costs in the energy distribution networks. We have divided them into two categories.

2.1. Privacy-Preserving Data Aggregation

Chen et al. proposed a fault tolerant privacy-preserving data aggregation scheme in [6]. In this scheme, a smart meter sends measurement data encrypted by the Paillier encryption scheme to the CG. After aggregating encrypted data by the CG, the info is sent to the control center, which consists of several working servers. Each server can decrypt aggregated data using the Paillier decryption algorithm. The authors claimed that their proposed scheme can protect the privacy of customers against the malicious CG and the control center.

An efficient identity-based data aggregation protocol is proposed by Zhiwei Wang [7]. To aggregate consumption usage report, the main idea of the scheme is to employ an identity-based encryption scheme along with the signature. To execute the scheme, a SM computes the ciphertext on the metering data and computes a signature on the consumption data. Finally, it sends the report to the aggregator unit (AU). Upon collecting data from SMs, the AU performs batch verification to verify all the signatures, which are received from the SMs. At the end, it computes its own signature and sends the signature and ciphertext to the energy service provider (ESP). The authors claimed that their scheme is secure against man-in-the-middle, replay, and internal and external attacks (i.e., AU and ESP). However, the computation cost of batch processing is significantly high at the AU (e.g., a batch of 80 SMs takes more than 3 s). The scheme, therefore may not be efficient, if a batch consists of many hundreds of smart meters.

Badra-Zeadally [8] proposed an efficient, lightweight privacy-preserving data aggregation approach that makes use of symmetric homomorphic encryption and Elliptic Curve Diffie Hellman (ECDH) key exchange methods to aggregate the SM data in a privacy-preserving manner. However, the scheme cannot defend against the internal adversary. In the similar vein, Abdallah-Shen proposed a lightweight security and privacy-protection scheme for customer-side network [9]. The scheme utilized the concept of lattice-based cryptography, which is based on finding short almost-orthogonalized vectors, e.g., shortest vector problem (SVP). However, the SVP-based algorithm required high time complexities [10]. In [11], the authors proposed a lightweight data aggregation against internal adversary. The scheme utilized the elliptic curve cryptography, and achieved efficiency. However, it does not support the billing.

Vahedi et al. discussed a ECC-based data aggregation scheme that provides privacy to the consumption usage data [12]. In the scheme, a SM measures energy consumption usage data within the home and encrypts them. It then signs ciphertext (i.e., energy consumption data) and transmits it to the AU. Upon receiving the message, the AU checks integrity of the messages and collects them. The AU then signs the aggregated messages and forwards them to the main operation center (OC) in a secure manner. Finally, consumption usage data is obtained and verified by the OC. To achieve security and privacy, the authors utilized elliptic curve-based ElGamal encryption scheme and homomorphic mapping including a blinding factor that can provide security against internal/external attackers.

Please note that most of the current state of the art schemes indeed provide security and privacy protections in data aggregation but do not solve the privacy issues in the billing system as the CGs are able to derive the aggregated consumption data. As the billing system together with the feedback system being utilized to balance the bulk generation and consumption, this results that the above mentioned schemes cannot be directly implemented for both data aggregation and billing systems in smart grid metering networks.

2.2. Privacy-Preserving Data Aggregation and Billing

To address privacy-preserving billing including secure data aggregation, a handful schemes have been proposed, recently.

In [13], Li et al. proposed a privacy-preserving multi-subset data aggregation (PPMA) scheme in the SG network. In PPMA, SMs are divided into a multi-subset according to their electricity consumptions for each period in a residential area. The control center (CC) can obtain the sum of electricity usage data for each subset in a secure and privacy-preserving manner via the AU. The authors utilized a homomorphic cryptosystem to aggregate electricity consumption data in a privacy-preserving way. The scheme proposed in [13] is computationally expensive for a resource-constrained smart meter. As concerns the proposed PPMA supported the dynamic billing system, however, the authors recognized themselves that PPMA cannot be effective if a SM is compromised.

Borges et al. [14] proposed a privacy-enhancing scheme to aggregate the metering data in-network. The authors utilized homomorphic commitment with a homomorphic encryption scheme in order to aggregate smart meter data. However, the main drawback of this scheme is that the authors have neither provided proof-of-concepts nor simulation results, therefore it is not easy to discuss its feasibility and security.

In [15], the authors investigated two billing protocols (simple protocol, and third-party protocol) for the SG networks. The both proposed protocols mainly focus on the privacy-preserving billing but do not focus on the data aggregation. Moreover, as specified by the authors, more research work would be needed to find a better substitute of Pedersen Commitments in the three-party protocol to achieve the efficiency on the microcontrollers.

Ni et al. [16] proposed a secure data aggregation and billing scheme (also called P2SM) against the misbehaving data collector. The authors built a new attack model (i.e., semi-honest attacker and malicious attacker). The scheme in this paper can determine the misbehavior of a data collector. To achieve security against a malicious data collector, the authors utilized a proxy re-encryption scheme and homomorphic authentication. However, these mechanisms make use of compute intensive bilinear pairing operations, leading to high communication and computation costs. Moreover, the scheme may vulnerable to impersonation attack at data collector level. In [17], Ohara et al. proposed a privacy-preserving billing and energy management scheme in SG networks. The authors utilized different and computationally expensive mechanisms, e.g., homomorphic commitment and encryption, and standard digital signature, to achieve their security and privacy goals. Moreover, in [17] there is no protection against malicious CGs.

In [18], Gope-Sikdar proposed an efficient data aggregation scheme for privacy-friendly dynamic pricing-based billing and demand response management in SG. The authors utilized the symmetric key cryptography and hashing operations, and achieved low-computation cost at resource-constrained smart meter. In the scheme, the anonymity of a smart meter is attained by issuing several temporary identities to the smart meter. However, the scheme may have practical issues. For instance, upon finishing the temporary identities, reissuing temporary identities are not trivial, and that may require the user involvement. Moreover, the scheme may not work under the malicious aggregator.

Please note that it can be noticed from aforementioned schemes, most of the schemes are either computationally expensive for the resource-constrained smart meter or may vulnerable against malicious CG or other attacks (e.g., impersonation attack). In addition, the schemes proposed in [13,14,15,16,17] mainly focuses on the static billing with standard tariff plans. Whereas in several countries, for example the United Kingdom, Norway, the Netherlands, Finland, and so on, the utility companies have been proposed to implement “dynamic-price based billing systems” [18]. Consequently, this allows us to rethink to design and analyze a privacy-preserving scheme that not only aggregates data in a secure and efficient manner but also protects privacy of dynamic billing in AMI.

3. System and Adversary Models, and Design Goals

3.1. System Model

A high-level network model of our scheme is depicted in Figure 1. Eight different phases can be distinguished in the scheme. In the system initialization phase (1), the system parameters are fixed by the OC and also the CGs receive the required key material. In the smart meter deployment phase (2), the smart meter receives the key material. In the customer registration phase (3), the customer gets linked to the SM by installing its own secret key. The transmission of the encrypted smart meter measurements is done in the report generation (4). Based on the report generations over different time periods, the CG is able to make an aggregated report, which is done in the report generation phase (5). After receiving the aggregated reports from the CG, the OC first needs to decrypt the reports in order to derive the aggregated consumption data for each SM. This phase is called the price determination phase (6), as this info is used by the OC to determine the fluctuant prices for different time periods. After sending the fluctuant prices to the CG, the CG derives a new aggregated report, which is used by the OC to derive the resulting price. These activities are executed in the dynamic billing phase (7). Finally, upon receiving the prices from the CG (i.e., for the different time periods), the customer is also able to verify the resulting price of the OC in the customer verification phase (8). In the scheme, six different entities are involved. A detailed description and role of each entity is given, as follows.

• Operation Center (OC): In general, this entity is responsible for the realtime maintenance, the analysis of the power quality, and the determination of dynamic prices for the electricity consumption in a certain region at different time slots per day. Please note that this paper will mainly concentrate further on the last aspect and show how the OC is able to compute the final price to be paid by each individual customer based on these variable prices. In our system model, the OC is considered to be a trusted entity, which generates and publishes the system parameters in the scheme. It also registers all entities participating. Although it is able to derive the final price to be paid by the customer, the OC should not have the possibility to derive the individual user consumption at each moment of the day. Instead, the OC must check the integrity of the received aggregated consumption data and be ensured that the dynamic prices are applied in a correct way.
• Data Collector Gateway (CG): This entity is responsible for the collection and aggregation of the information sent by the SMs in a certain region. Please note that from the information sent by the SMs, the CG is not able to derive the real user consumption usage data for a specific time period or even aggregated period. The CG can verify the integrity of the transmitted messages of the SMs. Later, based on the received dynamic prices, the CG can make computations on the encrypted data such that only the OC and customer are able to derive the real price. The CG is assumed to perform all the required actions. The CG is also considered to be a resource rich device and that to possess sufficient tamper proof storage for storing the secret shared keys with the SMs.
• Smart meter (SM): In a home area network even a building area network, the SM sends every fixed period (encrypted) information related to the realtime measured electricity consumption to the CG [19]. The SM is assumed to be a resource constrained device. The communication between the SM and CG can be established with the low power and/or long range technology, such as LoRa or by means of Power Line Communication (PLC) as studied in [20,21,22,23].
• Utility company: The utility company generates the customer’s bill based on the data received by the OC.
• Customer: The customer integrates own security material onto the SM via, e.g., USB. Moreover, based on the published dynamic prices of the OC and the data stored at the CG, the customer can check the validity of own bill that is generated by the Utility.
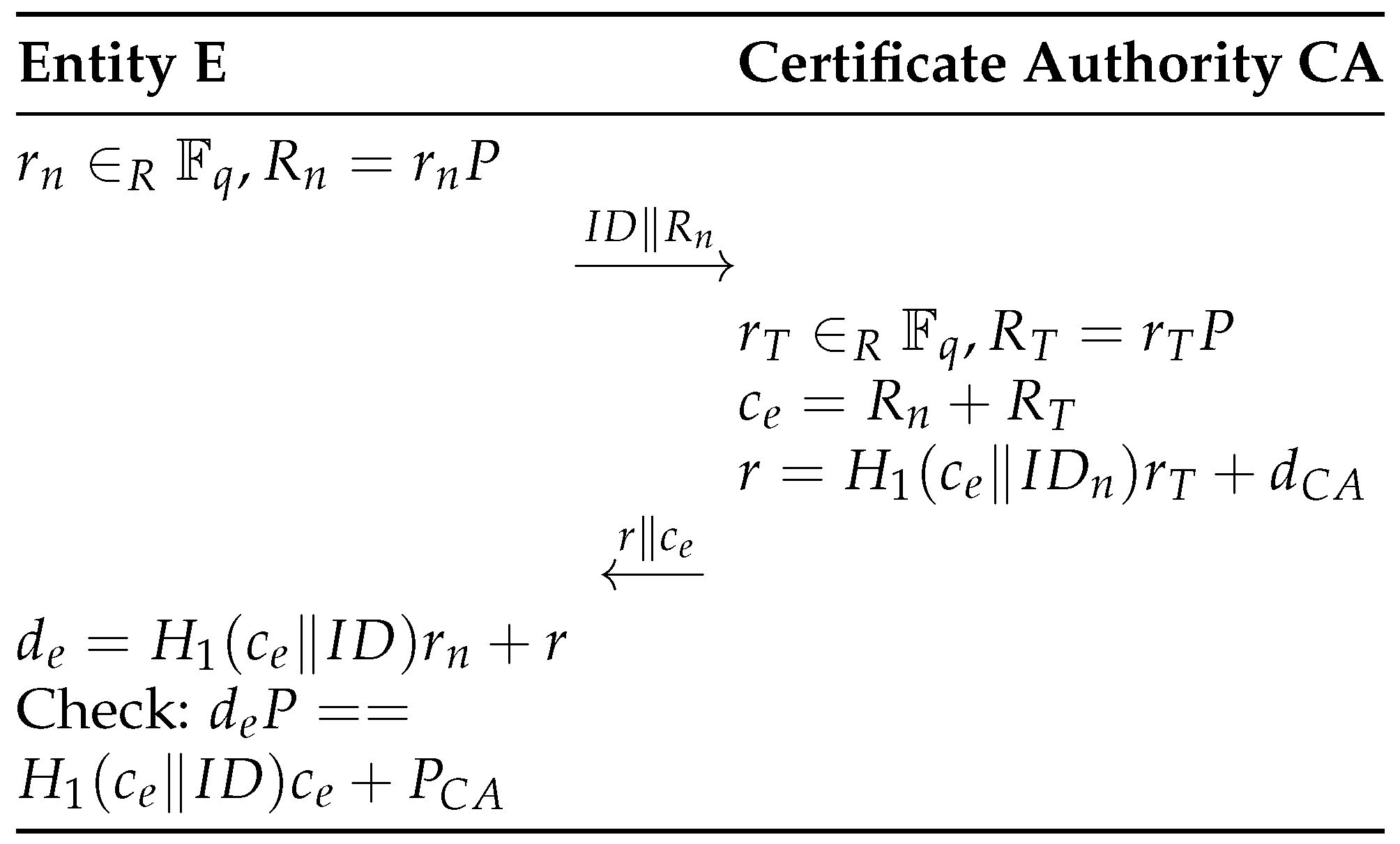
• Central Authority (CA): This trusted third party consists of two divisions. One division manages the distribution of the legitimate SMs. Each SM is installed with two pre-stored keys, one shared with the CG and another with the OC. The other division is responsible for the generation of a certificate for each legitimate entity (i.e., CG, OC and the customer related to a particular SM). This certificate allows to compute the corresponding public key.

3.2. Adversary Model

In the smart metering networks, a data concentrator gateway (i.e., CG) is deployed to collect consumption usage data via the SM from the home area network. The CG is not only responsible to send the consumption reports to the utility but it is also responsible to generate the billing reports for the utility company and customers. However, the CG is typically installed at a public place which is vulnerable to be attacked/hacked by the adversaries (e.g., external and insider) [16]. Therefore, we consider the following attacks:

• The adversaries can eavesdrop on the communication messages sent between SM-to-CG, CG-to-OC, inject new messages, or replay and change messages following the Yao-Dolev security model [24]. This involves the real man-in-the-middle and replay attacks.
• For the sake of reality, consider an (insider) adversary, he/she can attack the CG’s database (e.g., aggregation reports, billings, feedback, etc.). The adversary can retrieve the information stored in the non tamper resistant part of the memory. These information may include encrypted consumption data and/or corresponding auxiliary data of the different SMs over the different periods of time. More precisely, the insider may aim the following attacks. First, an internal attacker, can inject the false data that provides wrong energy feedback to unbalance load management in a power grid. Second, the insider attacker (e.g., CG) might be interested to derive the individual consumption data in order to sell this information to other parties, e.g., social media, etc. Third, the CG might also be trying to deceive the OC by including other fake consumption data. Fourth, the CG might be trying to attack a particular SM in order to increase its electricity bill or contribute with a malicious SM to decrease the bill.
• An adversary may perform an impersonation attack on one or a group of SMs to send fake data on behalf of non-compromised SMs to the CG. Moreover, an attacker can also be a malicious customer, being aware of the private key of the SM, that tries to modify the real consumption data.

Finally, we do not consider the possibility where the CG and the OC collaborate to derive the measurement data (e.g., in the report generation phase) and the possibility that secret information stored in the tamper resistant part of the memory (SM, CG or OC) can be retrieved.

3.3. Design Goals

Following the literature [16,18,25], a secure scheme should satisfy the following design goals.

• Confidentiality: The individual user consumption for each specific fine grained period should not be leaked to any entity, including the CG and the OC, at any circumstance. This information is very sensitive as it could be used to derive user’s behaviour. In addition, no information on the aggregated consumption at SM or regional level should be leaked to both the CG and any other outsider. Finally, the total price to be paid, should only be derivable by the OC and the customer.
• Integrity: The integrity of the messages should be checked at several places into the scheme in order to be sure that the correct electricity bills are derived. First, the CG should check that the consumption reports sent by the SMs at the different periods are unaltered by outsiders, and hence coming from legitimate registered SMs. Second, the OC should be ensured that the derived aggregated consumption data is based on the received consumption data of legitimate SMs and thus, does not include data coming from outsiders or a corrupted CG. Finally, the OC should also be able to verify that the derived final price for a certain SM is based on the sum of correct combinations between the received consumption data of that particular SM and the defined price in that region for each period.
• Authentication: This feature ensures that the transmitted data is coming from a registered SM and legitimate CG. Correct establishment of the authenticity feature avoids impersonation and man-in-the-middle attacks.
• Efficiency: Typically the SM is a resource constrained device, therefore, a security scheme should take communication and computation efficiency into consideration.

4. Preliminaries

4.1. Brief Background of Elliptic Curve Cryptography

The proposed scheme relies on Elliptic Curve Cryptography (ECC) [26], which is based on the algebraic structure of elliptic curves (ECs) over finite fields.

We denote the curve in the finite field $F_p$ by $E_{p(a,b)}$, defined by the equation $y^2=x^3+ax+b$ with a and b two constants in $F_p$ and $\Delta =4a^3+27b^2\ne 0$. We denote by P the base point generator of $E_{p(a,b)}$ of prime order q. All points on $E_{p(a,b)}$, together with the infinite point form an additive group G. In [27] standardised curve parameters are described.

The product $R=rP=(R_x,R_y)=P+\cdots +P$ (r times) with $r\in F_q$ and $R_x,R_y\in F_p$ results in a point of the EC and represents an EC multiplication. When we send an EC point, it is sufficient to send its x coordinate. The scheme relies on the two computational hard problems.

• The Elliptic Curve Discrete Logarithm Problem (ECDLP): This problem states that given two EC points R and Q of $E_{p(a,b)}$, it is computationally hard for any polynomial-time bounded algorithm to determine a parameter $x\in F_q^{\ast }$, such that $Q=xR$.
• The Elliptic Curve Diffie Hellman Problem (ECDHP): Given two EC points $R=xP,Q=yP$ with two unknown parameters $x,y\in F_q^{\ast }$, it is computationally hard for any polynomial-time bounded algorithm to determine the EC point $xyP$.

Furthermore, we denote the operation $H_i$ with $i=\{1,\dots ,7\}$ as the one-way cryptographic hash function (e.g., Secure Hash Algorithms SHA2 or SHA3) that results in several $F_p$. The concatenation of two messages $M_1$ and $M_2$ is denoted by $M_1\parallel M_2$. We assume that these functions and the EC parameters, together with the EC operations, are implemented in each entity participating the scheme.

4.2. Private-Public Key Generation

To guarantee the link between the identity and the public key of the entity, we make use of the implicit Qu Vanstone implicit certificates [28]. The advantage of this mechanism is that it is able to offer certificates in a very efficient way, with the assumption of the existence of a honest but curious certificate authority (CA). The final private key can only be computed by the entity E requesting a certificate $c_e$. The secret key pair of the CA is denoted by $(d_{CA},P_{CA})$. Figure 2 shows the different steps in the derivation of the private-public key pair $(d_e,P_e)$ of an entity E with identity $ID$. Consequently, the public key $P_e$ can be obtained by the publicly available information $ID,c_e$ of the node and the public key $P_{CA}$ of the CA as $P_e=H_1(c_e\parallel ID)c_e+P_{CA}=d_{e}P$.

5. Proposed Scheme

The scheme consists of eight different phases: (1) system initialization; (2) smart meter deployment; (3) customer registration; (4) report generation; (5) report aggregation; (6) price determination; (7) dynamic billing; and (8) customer verification, as follows.

• System initialization: The OC fixes the cryptographic mechanisms to be used (EC, generator P, Hash function H), retrieves a certificate $c_o$ with the CA, generates its corresponding private $d_o$ and public key $P_o$ and publishes $(P_o,c_o)$. Also the CGs retrieve a certificate $c_c$ with the CA, generate their corresponding private $d_c$ and public $P_c$ key and publish $(P_c,c_c)$.
• Smart meter deployment: In this phase, the CA installs two secret keys, $k_c$ and $k_o$, in the tamper resistant module (e.g., low cost TPM [29]) of the SM. The group key $k_c$ is shared with the CG to which the SM will report, and $k_o$ is shared with the OC. Please note that these keys can be renewed by the CG and OC respectively through dedicated unicast communications to all active registered SMs. In addition, the public key of the CA, $P_{CA}$, together with the EC parameters and required security functions are also installed on the device.
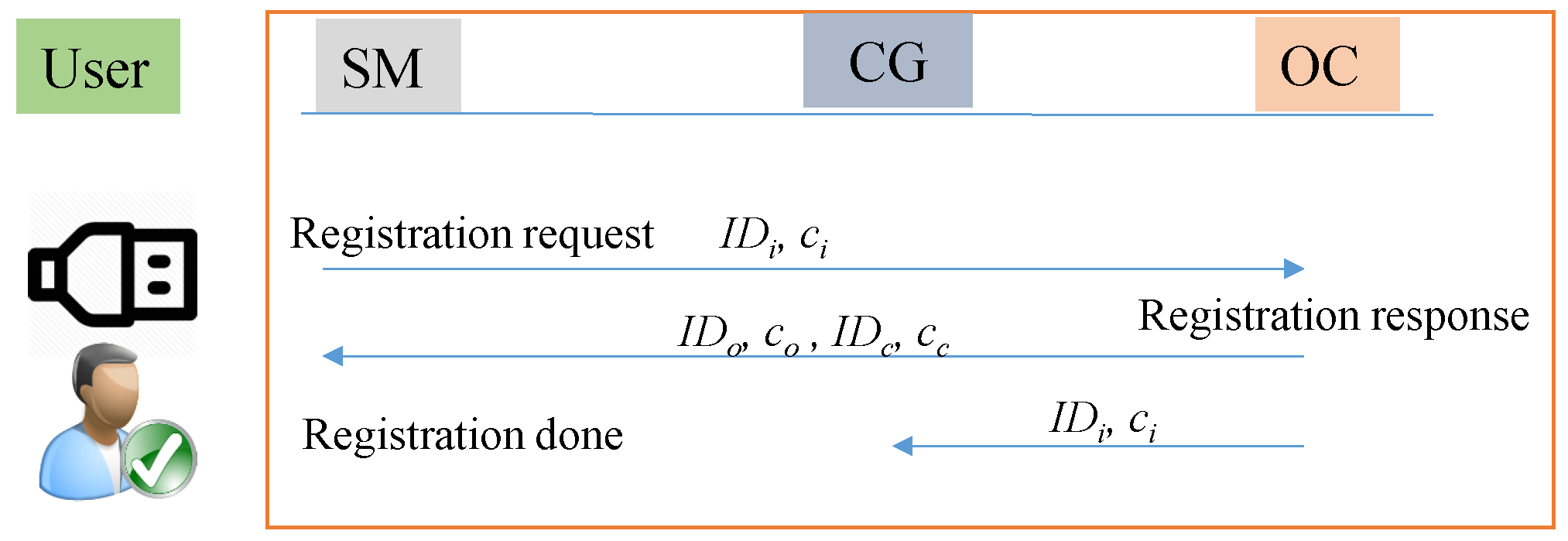
• Customer registration phase: In this phase, the customer belonging to region R receives a SM with pre-stored keys $k_c$ and $k_o$. Please note that the device possesses a USB connection, which is used by the customer to install its own secret keys. To activate the device $S{M}_i$ installed in its house, the customer $C_i$ needs to undergo three processes. Therefore, the OC provides as a service to the customer a secure web portal for the communication with the CA and with itself. Moreover, a secure offline program is also provided, which needs to be downloaded by the customer and will prepare the required script, used to install the secret keys into the SM. As a first step, the customer contacts the CA and receives a certificate $c_i$, which is bounded to its identity $I{D}_i$, consisting of its personal identity and the serial number of the SM. Second, the customer registers with the OC by sending the message containing the parameters $I{D}_i,c_i$. Following the ECQV scheme, the OC is able to compute the public key $P_i$ of the $S{M}_i$ using $I{D}_i,c_i$. The OC responds with sending the certificates and identities $c_o,I{D}_o$ and $c_c,I{D}_c$ of itself and the CG to which it should communicate. The customer now enters $c_i,c_o,I{D}_o,c_c,I{D}_c,I{D}_i$ and the secret random value $r_i$ used to initiate the certificate process of $c_i$ into the offline program. Based on this input, the program is able to derive the private and public key pair $(d_i,P_i)$ and the public keys $P_o$ and $P_c$ of the OC and CG respectively. Also the secret shared keys $d_i{P}_o$ and $d_i{P}_c$ with the OC and CG respectively are computed. Through the USB connection, the customer is now able to install $d_i,d_i{P}_o,d_i{P}_c$ in the tamper resistant part of the hardware of the $S{M}_i$.
  The OC also sends to the CG the identity $I{D}_i$ and certificate $c_i$ of the $S{M}_i$, joining its region. The CG computes the corresponding public key of the $S{M}_i$ and securely stores $(I{D}_i,P_i,d_c{P}_i)$ in its memory. The flow of customer registration phase is summarised in Figure 3.
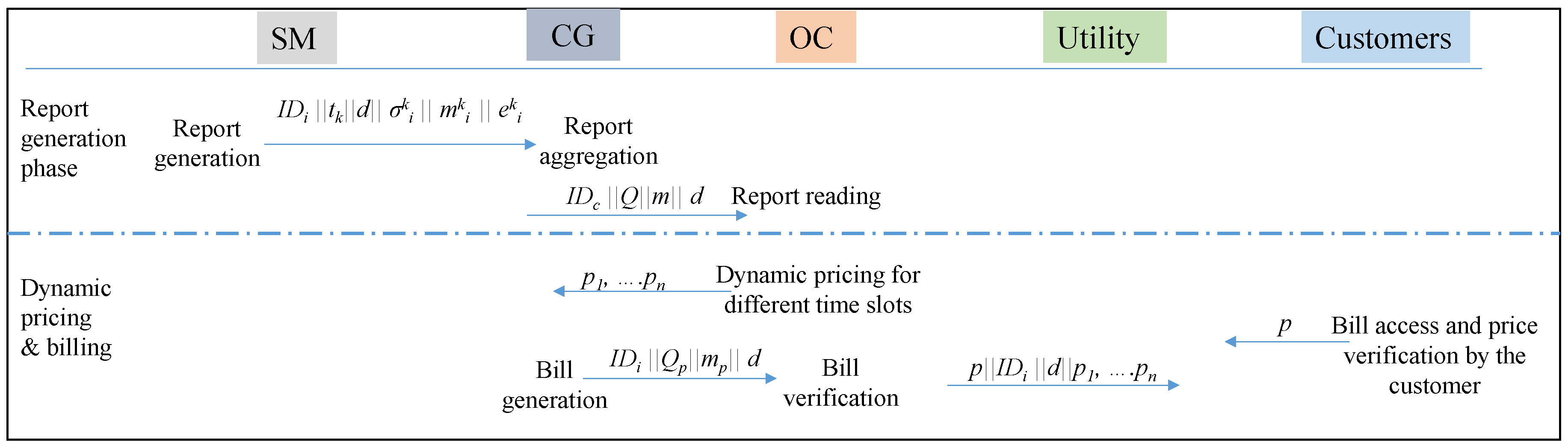
• Report generation: At the beginning of the day d, the $S{M}_i$ generates $H_5(k_o\parallel d)$. Please note that this value is similar for all legitimate and registered SMs.
  After a fixed period T, at timestamp $t_k=kT$, with $1\le k\le n$, the $S{M}_i$ reads the consumption measurement $m_i^k$ and computes the following operations:

  $$\begin{array}{ccc}\hfill {\beta }_i^k& =& H_2(d_i{P}_c\parallel t_k\parallel d)\hfill \\ \hfill {\gamma }_i^k& =& H_2(d_i{P}_o\parallel t_k\parallel d)\hfill \\ \hfill {\sigma }_i^k& =& H_3({\beta }_i^k\parallel I{D}_i\parallel t_k\parallel d)+H_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d)+m_i^k\hfill \\ \hfill m_i^{k^{\prime }}& =& H_4(k_c\parallel t_k\parallel d)H_5(k_o\parallel d){\beta }_i^k{m}_i^k\hfill \\ \hfill e_i^k& =& H_6(I{D}_i\parallel t_k\parallel d\parallel {\sigma }_i^k\parallel m_i^{k^{\prime }}\parallel {\beta }_i^k)\hfill \end{array}$$
  Next, the message $I{D}_i\parallel t_k\parallel d\parallel {\sigma }_i^k\parallel m_i^{k^{\prime }}\parallel e_i^k$ is sent to CG.
• Report aggregation: For each received message, the CG first checks the integrity and authenticity of the message by verifying the correctness of $e_i^k$ using ${\beta }_i^k=H_2(d_c{P}_i\parallel t_k\parallel d)$. If negative, a correction message is requested. If the SM fails to send a correct message, it will be excluded and reported to the OC. If positive, the CG stores all the received messages $I{D}_i\parallel t_k\parallel d\parallel {\sigma }_i^k\parallel m_i^{k^{\prime }}\parallel e_i^k$ with $1\le k\le n$ during day d by the N different $S{M}_i$ with $1\le i\le N$ and identity $I{D}_i$ from its region. Please note that the customer has access to the database where this information is stored.
  There are in general 6 (each 4 h) or 24 (each hour) periods per day in which the data is aggregated. At the end of a particular period $\rho$, for instance a period consisting of s different time slots (e.g., $1\le k\le s$), the following operations to aggregate the different consumption messages of all $S{M}_i$ with $1\le i\le N$ in its region are made.

  $$\begin{array}{ccc}& & choosez{\in }_R{F}_p,Z=zP\hfill \\ \hfill Q& =& \left(\sum _{i=1}^N\sum _{k=1}^s(({\sigma }_i^k-H_3({\beta }_i^k\parallel I{D}_i\parallel t_k\parallel d))\right)P\hfill \\ & & +H_2(z{P}_0\parallel \rho \parallel d)d_c{P}_o\hfill \\ \hfill m& =& H_2(z{P}_o\parallel \rho \parallel d)\sum _{i=1}^N\sum _{k=1}^s({\beta }_i^k{H}_4(k_c\parallel t_k{\parallel d))}^{-1}{m}_i^{k^{\prime }}\hfill \\ & =& H_2(z{P}_o\parallel \rho \parallel d)H_5(k_o\parallel d)\sum _{i=1}^N\sum _{k=1}^s{m}_i^k\hfill \end{array}$$
  The message $I{D}_c\parallel Q\parallel m\parallel \rho \parallel d$ is sent to the OC.
• Price determination: In this phase, the received report first needs to be read by the OC. Upon arrival of the message $I{D}_c\parallel Q\parallel m\parallel \rho \parallel d$, the OC first computes for all N SMs at the time period with $1\le k\le s$ in its region

  $$\begin{array}{ccc}\hfill {\gamma }_i^k& =& H_2(d_o{P}_i\parallel t_k\parallel d),1\le k\le s,1\le i\le N\hfill \end{array}$$
  Then, the OC checks the following equality:

  $$\begin{array}{cc}& Q-\left(\sum _{i=1}^N\sum _{k=1}^s{H}_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d)\right)P\hfill \\ & -H_2(d_{o}Z\parallel \rho \parallel d)d_o{P}_c\hfill \\ ==& (H_5(k_o\parallel d)H_2(d_o{Z\parallel \rho \parallel d))}^{-1}mP\hfill \end{array}$$

  (1)
  If the equality is correct, then the actual consumption data M for that period of the N SMs in its region equals to

  $$\begin{array}{c}\hfill M=\sum _{i=1}^N\sum _{k=1}^s{m}_i^k=(H_5(k_o\parallel d)H_2(d_o{Z\parallel \rho \parallel d))}^{-1}m\end{array}$$
  Based on these aggregated consumption data in a specific region, the OC defines the fluctuant electricity prices $(p_1,\dots ,p_n)$ for that region, corresponding to the different time slots $t_k$ with $1\le k\le n$. These prices are sent to the CG and officially published.
• Dynamic billing: Based on the received prices, the CG now performs the following operations for computing the bill of the $S{M}_i$:

  $$\begin{array}{ccc}& & choosey{\in }_R{F}_p,Y=yP\hfill \\ \hfill m_p& =& H_7(y{P}_o\parallel d)\sum _{k=1}^n({\beta }_i^k{H}_4(k_c\parallel t_k{\parallel d))}^{-1}{m}_i^{k^{\prime }}{p}_k\hfill \\ & =& H_7(y{P}_o\parallel d)H_5(k_o\parallel d)\sum _{k=1}^n{m}_i^k{p}_k\hfill \\ \hfill Q_p& =& \sum _{k=1}^n({\sigma }_i^k-H_3({\beta }_i^k\parallel I{D}_i\parallel t_k\parallel d)p_{k}P\hfill \\ & & +H_7(y{P}_o\parallel d)d_c{P}_o\hfill \end{array}$$
  The message $I{D}_i\parallel Q_p\parallel m_p\parallel d$ is sent to the OC. The OC can then verify the computation of the CG, and after a positive validation compute the effective price. Thus, in order to verify the operation of the CG, the following equality should hold:

  $$\begin{array}{cc}& Q_p-\sum _{k=1}^n{H}_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d)p_{k}P\hfill \\ & -H_7(d_{o}Y\parallel d)d_o{P}_c\hfill \\ ==& {(H_5(k_o\parallel d)H_7(d_{o}Y\parallel d))}^{-1}{m}_{p}P\hfill \end{array}$$

  (2)
  If so, the effective price p equals to

  $$\begin{array}{c}\hfill p={(H_5(k_o\parallel d)H_7(d_{o}Y\parallel d))}^{-1}{m}_p.\end{array}$$
  The message $p\parallel I{D}_i\parallel d\parallel (p_1,\dots ,p_n)$ is securely sent to the utility company.
• Customer verification: The customer can now verify the computed price p, by consulting both the stored values $({\sigma }_i^1,\dots ,{\sigma }_i^n)$ with the CG and the published prices $(p_1,\dots ,p_n)$ for that particular day d, using its private key $d_i$. This key allows reconstruction of ${\beta }_i^k$ and ${\gamma }_i^k$ for all $1\le k\le n$, and thus the determination of the equation:

  $$\begin{array}{ccc}\hfill p& =& \sum _{k=1}^n(({\sigma }_i^k-H_3({\beta }_i^k\parallel I{D}_i\parallel t_k\parallel d)\hfill \\ & & -H_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d))p_k\hfill \end{array}$$

The flow of the proposed scheme (i.e., report generation and aggregation, and dynamic pricing and billing) is shown in Figure 4.

6. Security Analysis

6.1. Formal Proof

First of all, for the report generation of the SMs, authentication and integrity is obtained thanks to the hardness of the ECDLP. This follows from the fact that only the CG is able to compute $d_i{P}_c=d_c{P}_i$ and thus ${\beta }_i^k$, to perform the integrity check by verifying the received value $e_i^k$ with the result of $H_6$.

We will now formally prove that the report aggregation phase and dynamic billing phase between the CG-to-OC communication satisfy both confidentiality (also called indistinguishability against adaptive chosen ciphertext attacks—IND-CGCCA) and unforgeability (also called existential forgeability against adaptive chosen message attacks—EUFCMA). Due to the similarity between both phases, it suffices to give the proof for the report aggregation phase. The proof is based on the security model proposed in [11], which is using mechanisms defined for signcryption schemes [30].

In the security model, two games are defined to be executed by a Challenger, denoted by $\mathcal{C}$, and an Attacker, denoted by $\mathcal{A}$. Five queries of $\mathcal{A}$ to $\mathcal{C}$ are allowed.

• $H_i(m)$: In this query, $\mathcal{C}$ randomly selects a value $r\in F_q^{\ast }$, sends r as response to $\mathcal{C}$ and stores in table $L_{H_i}$ the tuple $(m,r)$ with $i=1,\dots ,7$.
• CreateSM($I{D}_i$): In this query, $\mathcal{C}$ generates a private key and certificate for the SM, and stores it in the table $L_{SM}$.
• CreateReportSM($I{D}_i,d,t_k$): First, $\mathcal{C}$ checks if $I{D}_i$ exists in $L_{SM}$. If not, $\mathcal{C}$ does a CreateSM($I{D}_i$) query. Else, for a given $t_k,d$, it generates a tuple $(I{D}_i\parallel t_k\parallel d\parallel {\sigma }_i^k\parallel m_i^{k^{\prime }}\parallel e_i^k)$ and stores it in the table $L_{RSM}$.
• CreateAggregatedReport($I{D}_c,I{D}_1,\dots ,I{D}_n,\rho ,d$): In this query, $\mathcal{C}$ first checks if the reports of the SMs are available. If not, CreateReportSM queries are executed. Else, a random value z and private key $d_c$ for the CG are chosen and used to compute the aggregated report $I{D}_c,Q,m,d$. This value is stored in the table $L_{ASM}$.
• Retrieve($I{D}_c,Q,m$): Here, $\mathcal{C}$ checks the validity of the report and decrypts it to get the aggregated consumption data m.

We now distinguish two games and their corresponding definitions related to security.

6.1.1. Game 1

In this game, $\mathcal{C}$ first produces the system parameters and sends them to $\mathcal{A}$. Next, $\mathcal{A}$ selects a set of challenging identities $\{I{D}_1^{\ast },\dots ,I{D}_n^{\ast }\}$, chooses two sets of messages $\{m_1^0,\dots ,m_n^0\}$ and $\{m_1^1,\dots ,m_n^n\}$ and sends them to $\mathcal{C}$. Then, $\mathcal{C}$ picks a random value $b\in \{0,1\}$ to select one of the two sets of messages for which an aggregated data report $(I{D}_c,Q,m)$ is generated and sent to $\mathcal{A}$. Finally, using the five queries (except the Retrieve query) defined above, $\mathcal{A}$ guesses the value of b in order to distinguish which set of messages has been used in the aggregated report.

Definition 1.

The scheme provides confidentiality (also called indistinguishability against adaptive chosen ciphertext attacks—IND-CCA) if an attacker is not able to win Game 1 with a non-negligible advantage, i.e., to guess $b^{\prime }$ as the correct value of b. The advantage of $\mathcal{A}$ is defined by

$$\begin{array}{c}\hfill Ad{v}_{\mathcal{A}}^{IND-CCA}=2\parallel Pr(b=b^{\prime })-1\parallel \end{array}$$

6.1.2. Game 2

In this game, $\mathcal{C}$ first produces the system parameters and sends them to $\mathcal{A}$. Next, $\mathcal{A}$ selects a challenging CG $I{D}_c^{\ast }$ and outputs the aggregated report $(I{D}_c^{\ast },m,Q)$ corresponding with the challenging identity $I{D}_c^{\ast }$, by using the five queries defined above (except the CreateAggregatedReport with identity $I{D}_c^{\ast }$).

Definition 2.

The scheme provides unforgeability (also called existential forgeability against adaptive chosen message attacks—EUFCMA) if no attacker is able to win Game 2 with a non-negligible advantage, i.e. if $\mathcal{A}$ is not able to make a valid data aggregated report without the usage of the CreateAggregatedReport query.

Theorem 1.

The scheme is able to provide confidentiality if the ECDHP is hard.

Proof. 

We will prove that if $\mathcal{A}$ succeeds to win the game with non-negligible advantage $ϵ$, then also $\mathcal{C}$ will be able to solve the ECDHP with non-negligible advantage, which is a contradiction against the hardness of the problem. ☐

Consequently, we consider an instance of the ECDHP, being $R=sP,Q=yP$. First, $\mathcal{C}$ sets $P_o=R$ and publishes it together with the system parameters $E_{p(a,b)},P,H_1(.),\dots ,H_7(.),$$T,n,s,P_{CA},P_c$.

Then, $\mathcal{A}$ randomly selects a set of challenging identities $\{I{D}_1^{\ast },\dots ,I{D}_n^{\ast }\}$, chooses two sets of messages $\{m_1^0,\dots ,m_n^0\}$ and $\{m_1^1,\dots ,m_n^n\}$ and sends them to $\mathcal{C}$. Then, $\mathcal{C}$ picks a random value $b\in \{0,1\}$ to select one of the two sets of messages. Then, $\mathcal{C}$ extracts the identity related information with $I{D}_I$ of the table $L_{SM}$ and also creates their report. The variable Z used in the derivation of the aggregated report is set to Q by $\mathcal{C}$. Then, $\mathcal{C}$ also computes the aggregated report. All computed values are put in the tables $L_{H_i}$. Finally, the aggregated data report $(I{D}_c,Q,m)$ is sent to $\mathcal{A}$.

Now, using the five queries (except the Retrieve query) defined above, $\mathcal{A}$ guesses the value of b in order to distinguish which set of messages has been used in the aggregated report. If $\mathcal{A}$ is able to win the game with non-negligible advantage, then $\mathcal{C}$ can also solve the ECDLP. To do that, $\mathcal{C}$ computes $m{({\sum }_{i=1}^n{m}_i)}^{-1}{H}_5{(k_0\parallel d)}^{-1}$, which equals to $H_2(z{P}_o\parallel \rho \parallel d)$. After consulting $L_{H_2}$, $\mathcal{C}$ is able to reveal $z{P}_o$, corresponding with R as the solution of the considered problem.

If $q_{H_2}$ corresponds with the number of $H_2$ queries, the probability that $\mathcal{C}$ can solve the ECDHP equals to $\frac{ϵ}{q_{H_2}}$. Consequently, this leads to a contradiction and we can conclude that the scheme provides confidentiality.

Theorem 2.

The scheme is able to provide unforgeability if the ECDLP is hard.

Proof. 

We proof with contradiction that if $\mathcal{A}$ is able to win the game, then $\mathcal{C}$ is able to solve the ECDLP. Let $Q=xP$ and the derivation of x be the instance of the ECDLP that we will consider. ☐

First, $\mathcal{C}$ randomly selects $P_o$ and sets $P_o=Q$. Next, it determines the system parameters $E_{p(a,b)},P,H_1(.),\dots ,H_7(.),T$$n,s,P_{CA}$. Then, $\mathcal{A}$ selects a challenging CG $I{D}_c^{\ast }$ and outputs the aggregated report $(I{D}_c^{\ast },m,Q)$ corresponding with the challenging identity $I{D}_c^{\ast }$, by using the five queries defined above (except the CreateAggregatedReport with identity $I{D}_i^{\ast }$). If $\mathcal{A}$ is able to generate a valid ciphertext, then we show that $\mathcal{C}$ will be able to solve the ECDLP.

Using the forking lemma of [31], $\mathcal{C}$ is able to construct another valid ciphertext $(I{D}_c^{\ast },m^{\ast },Q^{\ast })$ by choosing a different Hash function $H_2$. This leads to the following two equations:

$$\begin{array}{c}\hfill Q-\left(\sum _{i=1}^N\sum _{k=1}^s{H}_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d)\right)P-\\ \hfill H_2(d_{o}Z\parallel \rho \parallel d)d_o{P}_c==(H_5(k_o\parallel d)H_2(d_o{Z\parallel \rho \parallel d))}^{-1}mP\\ \hfill Q-\left(\sum _{i=1}^N\sum _{k=1}^s{H}_3({\gamma }_i^k\parallel I{D}_i\parallel t_k\parallel d)\right)P-\\ \hfill H_2^{\ast }(d_{o}Z\parallel \rho \parallel d)d_o{P}_c==(H_5(k_o\parallel d)H_2^{\ast }(d_o{Z\parallel \rho \parallel d))}^{-1}{m}^{\ast }P\end{array}$$

Subtracting both equations, leads to the following equality

$$\begin{array}{c}\hfill (-H_2(z{P}_o\parallel \rho \parallel d)+H_2^{\ast }(z{P}_o\parallel \rho \parallel d))d_c{d}_{o}P==\\ \hfill (H_5(k_o\parallel d)(H_2(z{P}_o{\parallel \rho \parallel d)}^{-1}m-H_2^{\ast }(z{P}_o{\parallel \rho \parallel d)}^{-1}{m}^{\ast })P\end{array}$$

and thus the solution of the ECDLP challenge equals to

$$\begin{array}{c}\hfill ((-H_2(z{P}_o\parallel \rho \parallel d)+H_2^{\ast }(z{P}_o\parallel \rho \parallel d))d_c{)}^{-1}\\ \hfill (H_5(k_o\parallel d)(H_2(z{P}_o{\parallel \rho \parallel d)}^{-1}m-H_2^{\ast }(z{P}_o{\parallel \rho \parallel d)}^{-1}{m}^{\ast })\end{array}$$

Denote the size of $L_{H_2}$ by $q_{h_2}$. To compute the hardness of this challenge, the probability is equal to the probability that a different hash value can be chosen $1/q_{h_2}$ times the probability $ϵ$ that $\mathcal{A}$ is able to win the game, resulting in $\frac{ϵ}{q_{h_2}}$. Consequently if $ϵ$ is non-negligible, this ECDLP challenge too, which is a contradiction.

6.2. Informal Proof

• Confidentiality: The individual user consumption $m_i^k$ of a SM with identity $I{D}_i$ for each time slot $t_k$ cannot be retrieved by an outsider, other SM, CG or OC. This follows from the fact that the only two parameters containing this information, ${\sigma }_i^k,m_i^{k^{\prime }}$, include knowledge which is either uniquely known by the CG or the OC, taking into account the hardness of the ECDHP. The aggregated consumption data of the SMs can also not be leaked to an outsider or another SM, as the parameter m containing information on the aggregated sum depends either on knowledge uniquely known by the OC or by the CG. Similar reasoning holds for the price to be payed.
• Integrity: The integrity is checked at three places. First, the CG checks that the reports sent by the SMs are unaltered and are coming from legitimate registered SMs. This follows from the fact that ${\beta }_i^k$ is included in the hash value to be checked by the CG. This parameter ${\beta }_i^k$ can only be computed by registered SMs, which is verified through the usage of its public key that is stored in the CG’s database.
  In the second place, the OC checks that the aggregated consumption data does not include data coming from outsiders, a corrupted CG, or a corrupted SM. To validate this fact, Equation (1) plays a major role. If a SM is sending corrupt info on the consumption data, then two different values of $m_i^k$ are included during the computation of the variables ${\sigma }_i^k,m_i^{k^{\prime }}$. Also if the CG has the intention to corrupt the sum of aggregated data, it would change the value ${\sigma }_i^k$ by simply adding or subtracting a certain amount. However, this operation will always be noticed by the OC, as in that case Equation (1) will not be satisfied.
  Similarly, the OC can also verify that the derived final price for a certain SM is based on the sum of correct combinations between the received consumption data of that particular SM and the defined price in that region for each period, thanks to verification of Equation (2). This follows from the fact that in the calculation of $H_3$, the parameters $t_k,I{D}_i$ and ${\gamma }_i^k$ are involved.
• Authentication: Identities and certificates are shared among the legitimate entities during initialization and registration, such that the corresponding public key can be unambiguously derived of it thanks to the ECQV mechanism. Authentication of the sender and receiver is obtained as the transmitted messages heavily rely on the usage of the private key of the sender and public key of the receiver. As a consequence, the message is only meaningful for the receiver and sender with the corresponding private and public key respectively.

7. Performance Analysis

This section compares computation and communication costs of the proposed scheme with the most relevant and recent protocol in [11,16,17]. Let $sm$—the time for executing scalar multiplication, $pa$—the time for executing point addition, $pm$—the time for executing point multiplication, $bp$—the time for executing bilinear pairing, h—the time for executing hash-operation. The comparisons on total computing cost among [11,16,17] and the proposed scheme are given in

Table 1. Performance comparison among [11,16,17], and Proposed scheme.

	Registration Phase (SM)	Report Generation (SM)	Report Aggregation (CG)	Report Reading Phase (OC)	Billing phase
					OC	CG	Customer
[16]	$3sm+h+2pa$	$4sm+h+2pa+4pm$	$(2Ns-2)pa+(Ns)bp$	$(2Ns+1)pa+(Ns+4)sm$ $+(Ns)h+pm+bp$	$(72s)sm+(24s-3)pa$	$Nsm+(2N-1)pm+sm+bp$	$(24)2sm+2pa+(24)h+bp$
[17]	–	$2c+2sm+sig+comm$	–	$2cN+2smN+Nsig+Ncommt$	$2c+2sm+sig+commt$	–	$2c+2sm+sig$
[11]	–	$2pm+2h$	$3N+(2N)pa+(3N)h$	–	–	–	–
Ours	$4pm+pa$	$7h$	$(Ns+3)pm+4(Ns+2)h$	$3pm+pa+(Ns+3)h$	$3pm+(2n+2)h$	$3pm+pa+(n+3)h$	$(2n+1)h$

$sm$—the time for executing scalar multiplication; $pa$—the time for executing point addition; $pm$—the time for executing point multiplication; N—the number of smart meter; s—the number of individual reports (of smart meter) received in a period s; $bp$—the time for executing bilinear pairing; h—the time for executing hash-operation; $sig$—the time for generating/verifying signature; $commt$—the time for executing commitment/decommitment; c—the time for performing public key cryptosystem (i.e., encryption and decryption).

.

As shown in Table 1, the proposed scheme requires $4pm+1pa$ during registration, which is one time cost. In the report generation phase, the SM needs to compute $7h$. The report aggregation phase requires $(Ns+3)pm+4(Ns+2)h$ of the CG. In the report reading, the OC needs to compute $3pm+pa+(Ns+3)h$. Finally for the dynamic billing, the CG performs $3pm+pa+(n+3)h$ operations, the OC computes $3pm+(2n+2)h$ operations and the customer performs $(2n+1)h$ operations. We can discover from Table 1 that our scheme outperforms in report generation phase as it requires only seven hash operations whereas the schemes proposed in [16,17] require high computation costs (i.e., $4sm+h+2pa+4pm$, $2c+2sm+sig+comm$, respectively) at the SM. Likewise, the proposed scheme outperforms in other phases too, e.g., report aggregation phase, report reading phase, and billing phase as compared to Ni et al. [16] and Ohara et al. [17] schemes. The biggest drawback of Ohara et al. scheme is that it cannot provide security against the malicious CG. Whereas Ni et al. scheme can provide security against the malicious CG but incurred high computational costs. We also compare the proposed scheme with a recently proposed data aggregation scheme, which is based on ECC operations [11]. Here we only obtain performance results for the report generation phase, as we can see from Table 1, computation overhead of our scheme is lower than the [11] scheme. Moreover, there is no billing mechanism considered in [11] scheme.

Moreover, in order to estimate the execution times for various phases, we use the same computation costs as obtained in [11] using an Intel I5-3210M 2.5 GHz CPU with 8GB RAM and Windows 7 as OS. Likewise [16], we consider a smart metering network that consists of N number of computational-constrained smart meter, sending 1 measurement during 24 different periods of the day, i.e. $N=100$, $s=1$, $n=24$ to the CG. Here, s is the number of individual reports (of SM) received in a period s. The comparisons on execution time (in µs) of among [11,16,17], and the proposed scheme are given in

Table 2. Computation costs of our scheme in the different phases (µs).

Phase	[16]	[17]	[11]	Our
Report generation (SM)	24.7	96.2	1.97	0.7
Report aggregation (CG)	2355.4	1657.23	-	565.06
Report reading (OC)	328.1	174.3	Null	16.56
Dynamic billing (CG)	2254.7	Null	Null	16.51
Dynamic billing (OC)	3564.1	26.5	Null	16.48
Dynamic billing (Customer)	54.9	183.4	Null	0.05

. It can be seen from Table 2 that the computation timing values in [16] are not efficient because the authors used expensive Weil pairing as bilinear pairing operations. Ohara et al.’s scheme [17] is much more efficient than Ni et al.’s scheme [16] but it cannot provide privacy-protection against the malicious CG. Similarly, the scheme proposed in [11] is efficient at the report generation as compared to [16,17] but it does not consider the billing scenario. On the contrary, the proposed protocol achieves high efficiency because we do not utilise additional EC operations, besides the existing stored values in the report generation of the SM. It is just at the point of the CG that EC operations are included. Here, we used the associative property of the EC addition, to limit the number of EC multiplications. Consequently, we can conclude that the scheme proposed in this paper is more efficient both in data aggregation and dynamic billing, compared to [11,16,17].

To estimate the required communication bits in proposed scheme, we have adopted and compared the bit lengths of various parameters from [16], since it has similar architecture and also offers the same features of dynamic pricing and resistance against pollution attacks of malicious CG, as the proposed scheme. We assume that the length of the identity and timestamp equals to 160 bits. Taking into account the size of a 160 bit EC, as discussed before,

Table 3. Comparison of the communication costs (expressed in bits).

Message	SM Report	Aggregated Report	Bill
[16]	2688	2388	2880
Proposed scheme	800	640	480

describes the number of bits to be transmitted in different phases (e.g., SM-to-CG communication and CG-to-OC communication) in [16] and the proposed scheme. It can be seen from Table 3, in the proposed scheme, a SM needs to send 800 bits in the SM-to-CG communication whereas the Ni et al’s scheme requires 2688 bits to send to the CG. Likewise, the CG requires to send 640 bits to the OC (i.e., CG-to-OC communication) in the proposed scheme, on the other hand, Ni et al’s scheme needs to send 2388 bits to the OC. The number of bits in billing phase will always be constant in the proposed scheme and [16], as 480, and 2880, receptively, as shown in Table 3.

In the SG, as the SM reports consumption usage data to the CG, the efficiency of a security model also depends on the total traffic volume gain (i.e., overhead) at the aggregator. For the sake of example purposes, consider a virtual smart village, where each CG serves N number of consumers (i.e., SM). Let each SM generates a message (i.e., power consumption report) periodically (every 15/30 min) and sends the report to the CG. The total volume of messages that require to be verified periodically by the CG will be significantly high. If the average packet size is p then the communication overhead at the CG is $N\times p$.

Figure 5 depicts the communication overhead comparisons at the CG between the Ni et al.’s scheme and the proposed scheme. In this experiment, we vary the number of smart meters from 50 to 500 smart meters per CG and investigate the overhead impacts at the CG. It can be observed from Figure 5, the communication overhead is significantly reduced in the proposed scheme as compared to [16], at the CG. This is due to the shorter ciphertext of the proposed scheme. Likewise, Figure 6 shows the communication overhead comparisons in CG-to-OC communication between the Ni et al.’s scheme and the proposed scheme. No matter how the number of households varies, the total traffic volume between CG-to-OC communication will be drastically lower in the proposed scheme than the Ni et al.’s scheme. In summary, this shows that the proposed scheme is much more efficient than the scheme proposed in [16].

8. Conclusions

In this paper, we propose an efficient and secure solution for smart grids to be used for the collection of data of the customer’s smart meter. Also the billing functionality, where different prices for different time periods are considered, has been included in the scheme. Based on aggregated data coming from different time periods, the individual customer’s bill taking into account different time prices for each period, can still be derived by the OC and checked afterwards by the customer. Special attention in the scheme has been given to the privacy of the customer as no other entity is able to derive the individual user consumption for a specific time period. Also the integrity is guaranteed at each possible step in the scheme and mutual identity based authentication is obtained thanks to the usage of ECQV certificates. In particular, the security features of confidentiality and unforgeability are proven in the random oracle model. Another important feature of our scheme is that the customer is actively involved into the activation of the SM by including its security material, leading to an increased trust of the customer into the SG. Moreover, compared with the existing schemes in literature, our scheme has significantly reduced computation and communication costs as the required operations are limited to elliptic curve operations (multiplications and additions) and hashes. The total computational time for the report generation until the computation of the bill by the customer would need approximately 632 µs and the security related information to be transmitted requires 1920 bits.

With the new EU General Data Privacy Regulation (GDPR), user privacy has become a major concern for each company collecting user’s data. Therefore, it is of utmost importance to immediately use the correct and efficient cryptographic mechanisms to derive as little as possible user information by at little as possible different entities. Moreover, also in the GDPR users need to explicitly approve that data will be collected of them. Because of these aspects, we believe that the proposed scheme in this paper offers the best possible solution. On the one hand, the user needs to explicitly include own security material into the SM, which is a guarantee that no other entity (including the CA, OC, company supplying SMs, etc.) is able to derive fine grained user consumption data. Thanks to the cryptographic mechanisms, only the OC and not the CGs as proposed in many schemes in literature, are able to derive the aggregated consumption data. Consequently, as we have shown that the overhead of including these additional cryptographic operations is reasonable, there are no privacy or technical obstacles anymore that can prohibit the mass scale distribution of SG.