Exploiting Artificial Neural Networks for the Prediction of Ancillary Energy Market Prices
Abstract
1. Introduction
- identify what sources of data are relevant and openly available for the predictions of the FCR-N ancillary service market.
- identify and present a methodology that can be utilized for the prediction of ancillary market prices and the key design decisions to be made, highlighting the differences between ancillary market (such as FCR-N) and spot market prices’ prediction, as well as employing the Artificial Neural Network (ANN) model in which numerous hyper-parameters are to be tuned for the ANN, with no prior work existing for ancillary service price prediction with ANN.
- evaluate the prediction performance of the FCR-N price. The experimental results show that the proposed ANN model was capable of adapting to the fast-changing price patterns of the FCR-N market. Moreover, the ANN outperforms the two state of the art models, Support Vector Regression (SVR) and the ARIMA model, in the prediction of the FCR-N prices.
2. Related Work
3. Problem Analysis
3.1. Data Collection
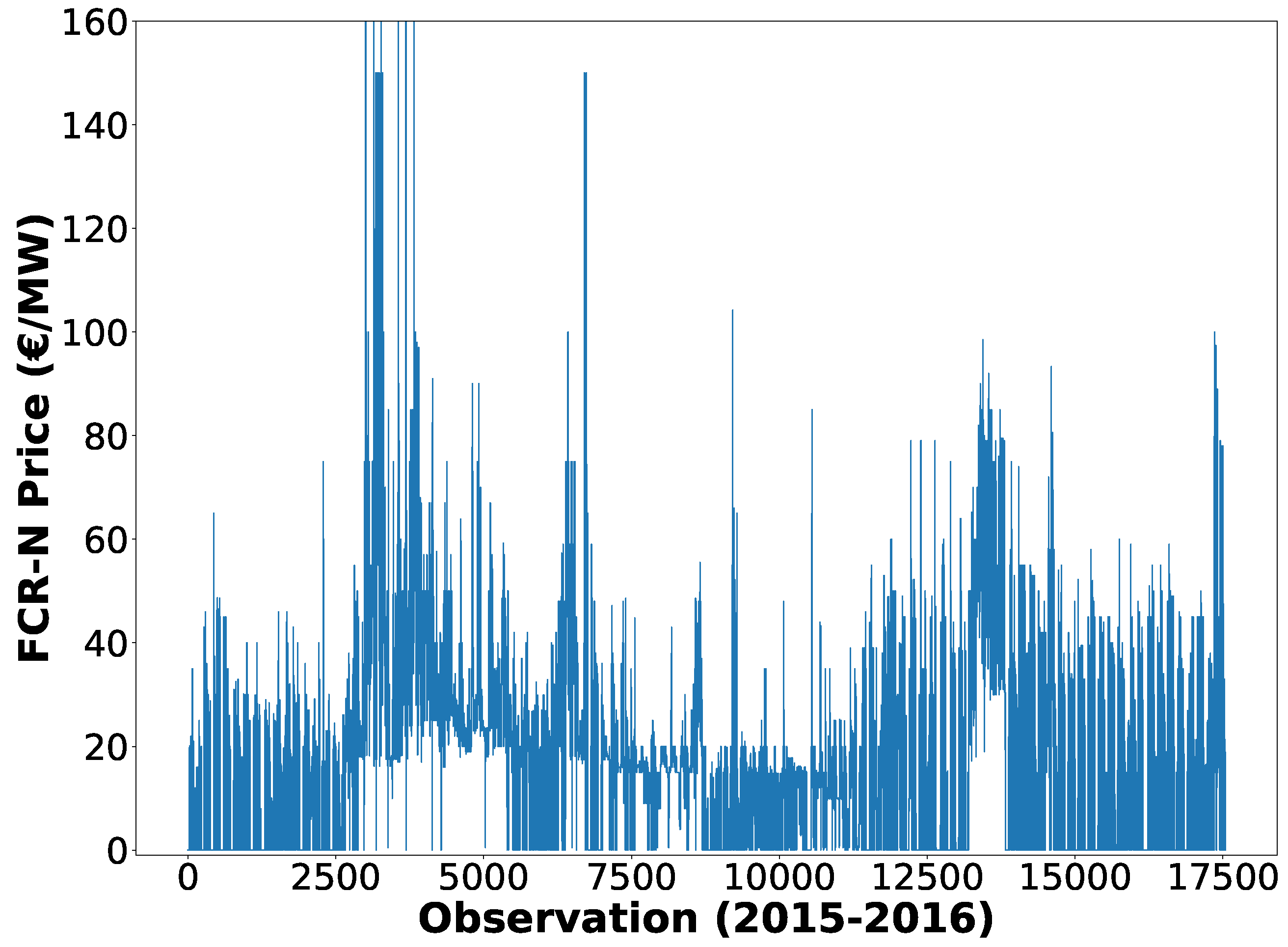
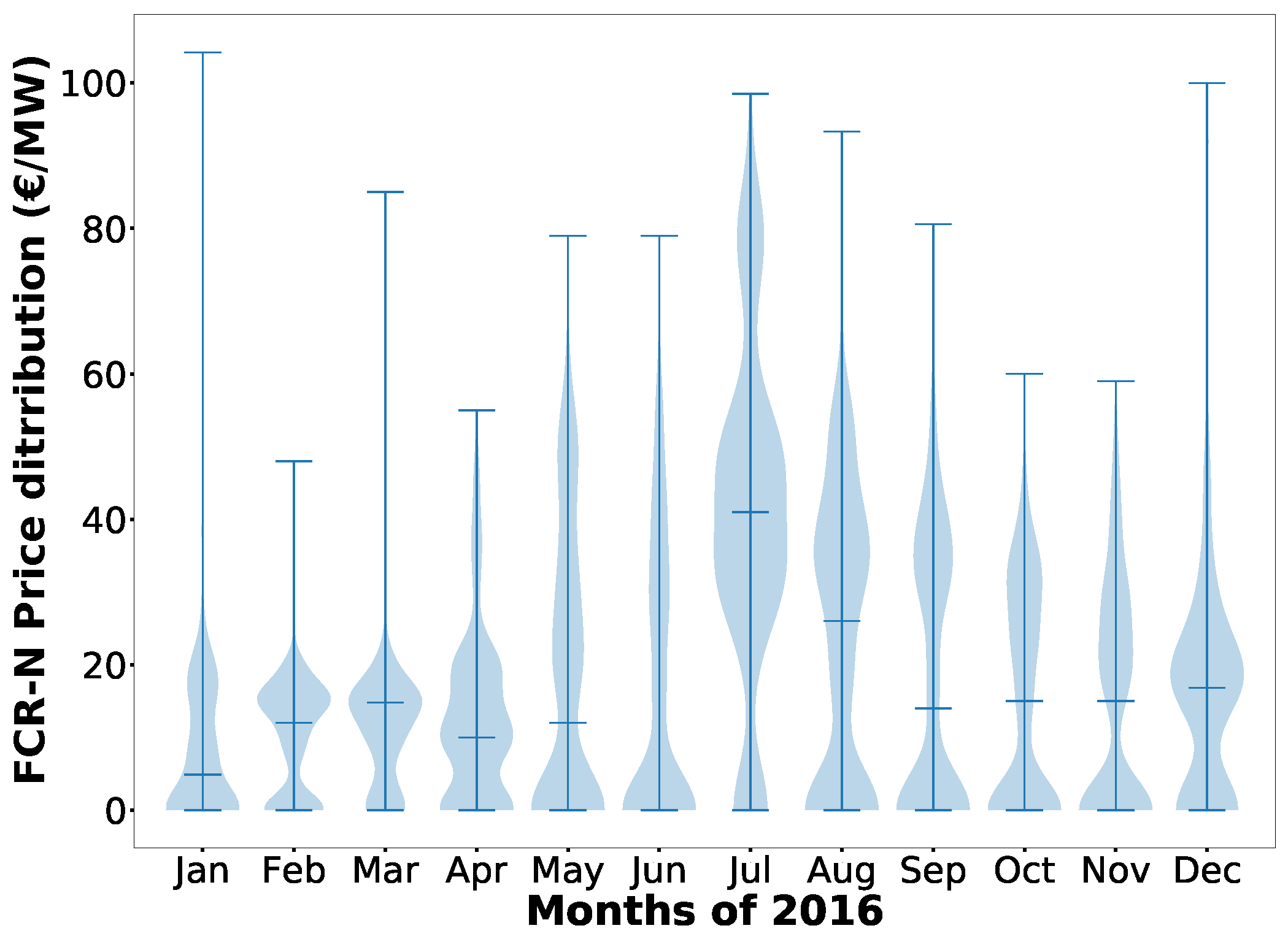
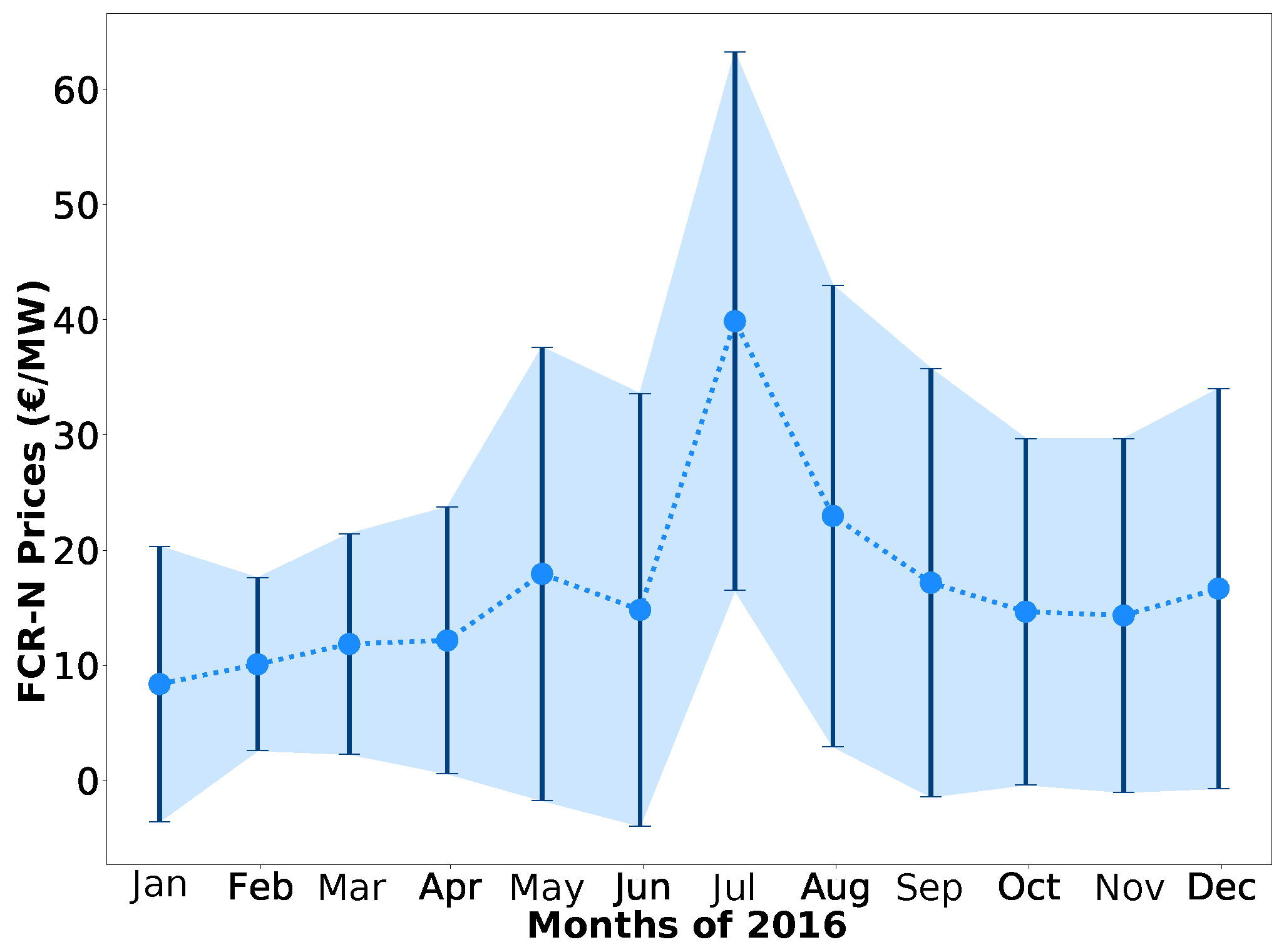
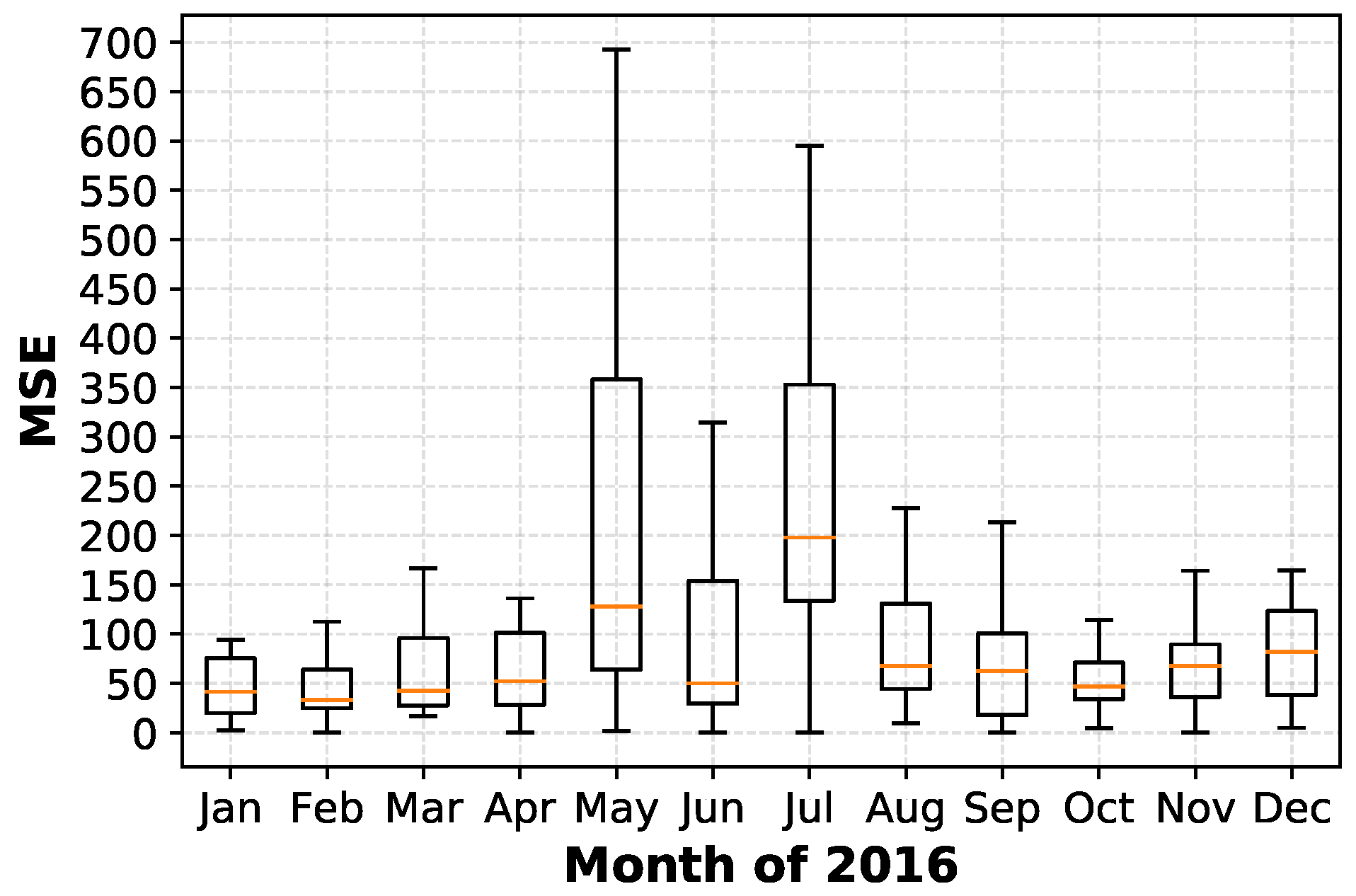
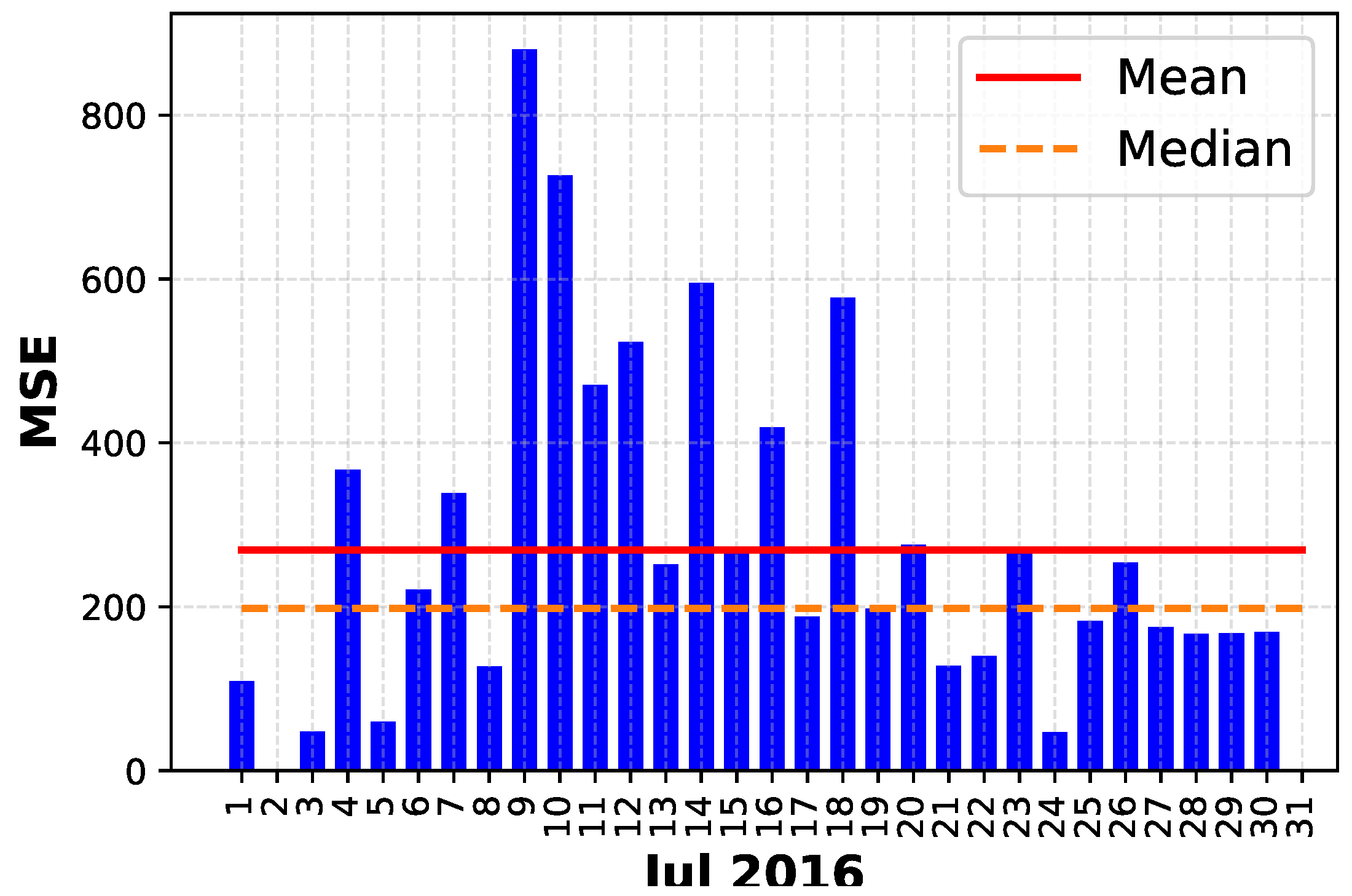
3.2. FCR-N Price Analysis
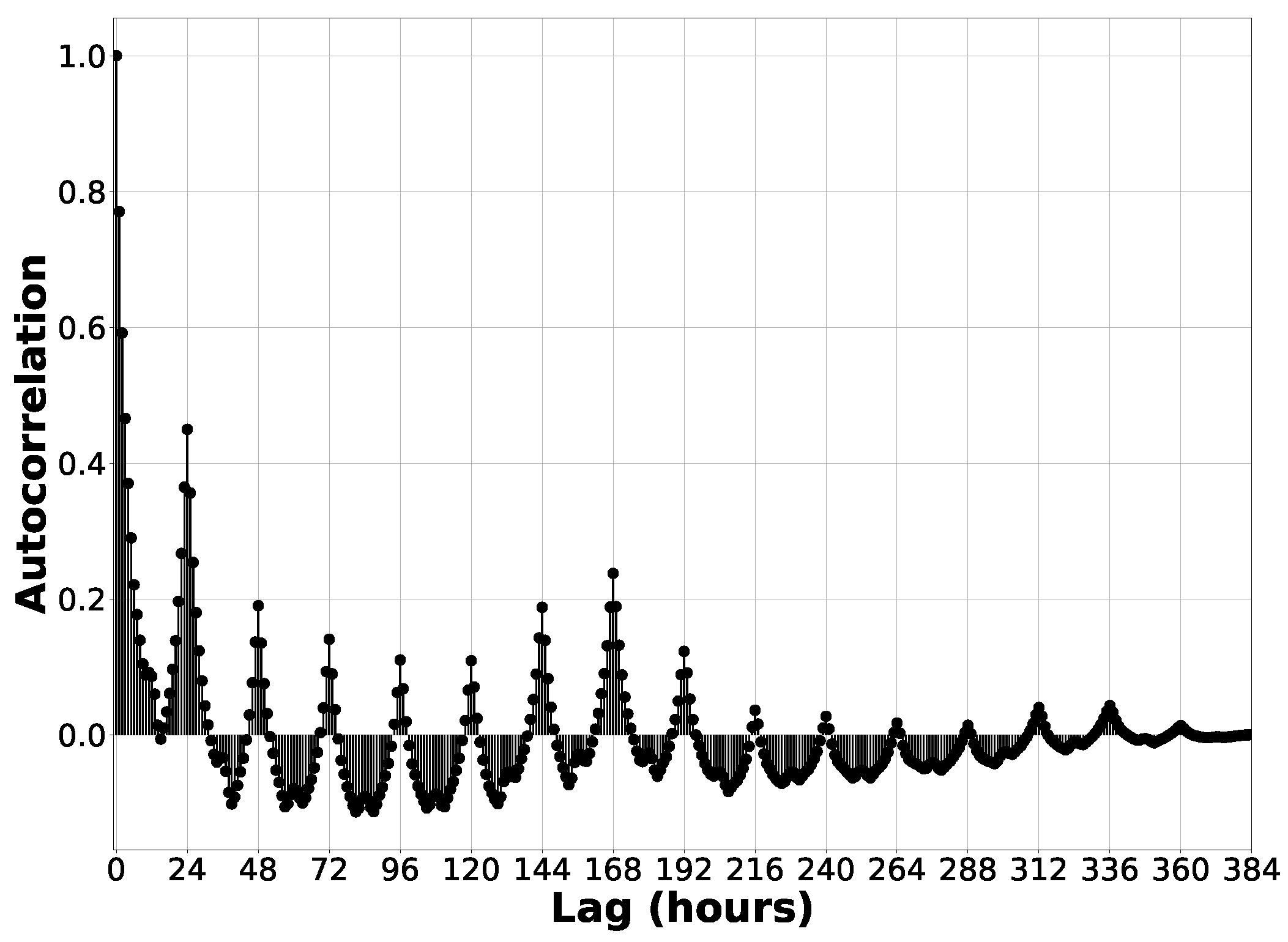
3.3. Autocorrelation and Variable Lag
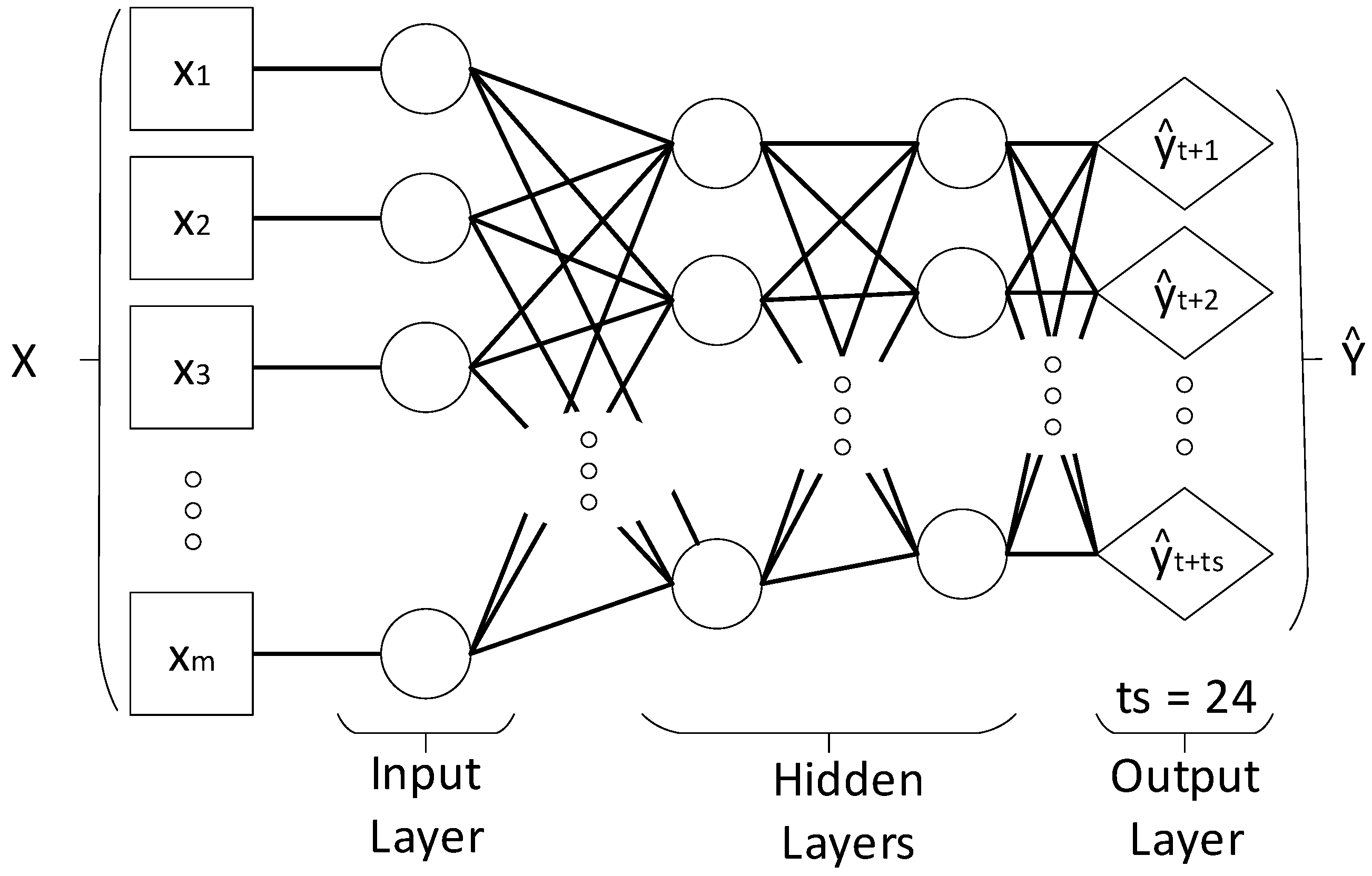
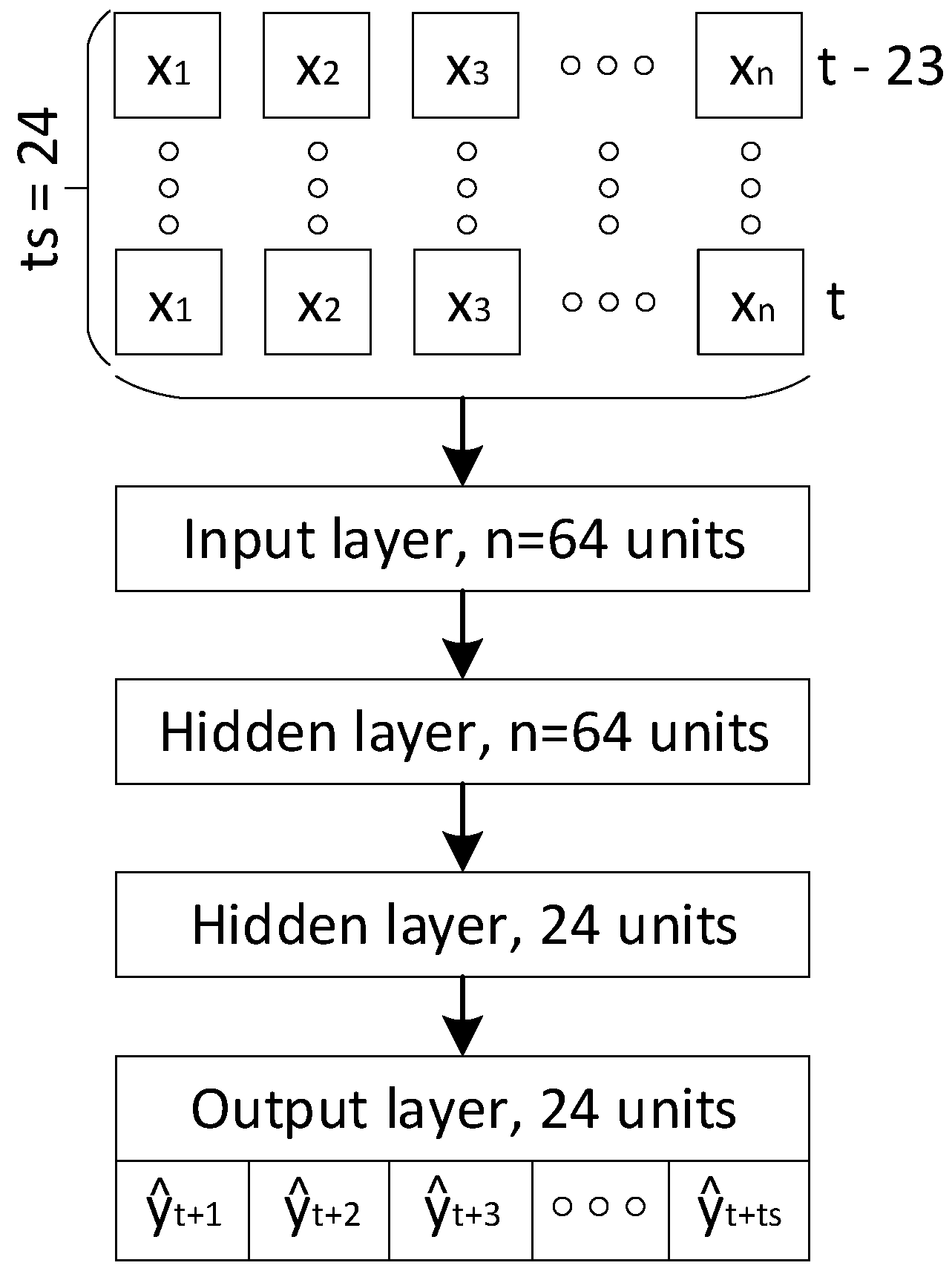
4. Methodology
4.1. Prediction Model Formulation
4.2. Data Preprocessing
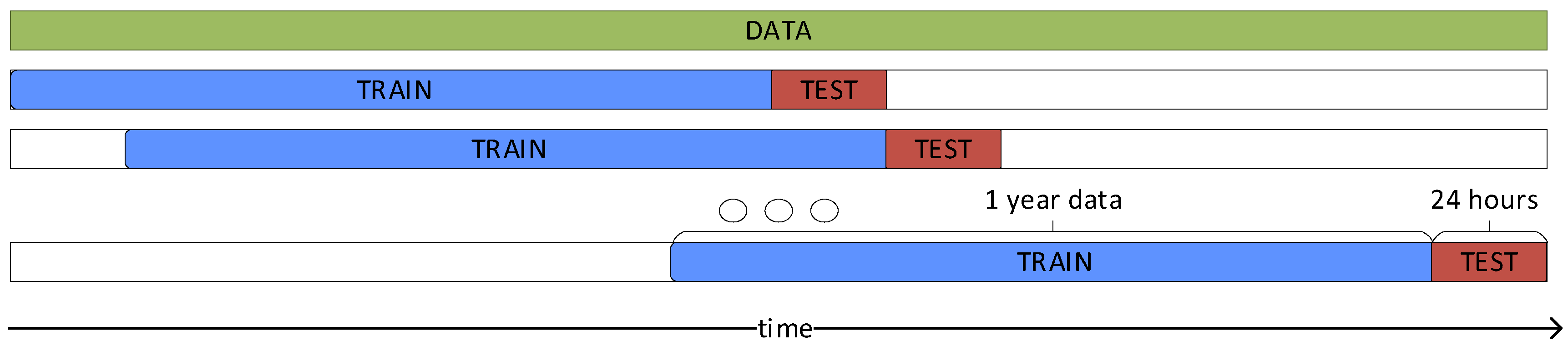
4.3. Model Validation
4.4. Prediction Performance Evaluation
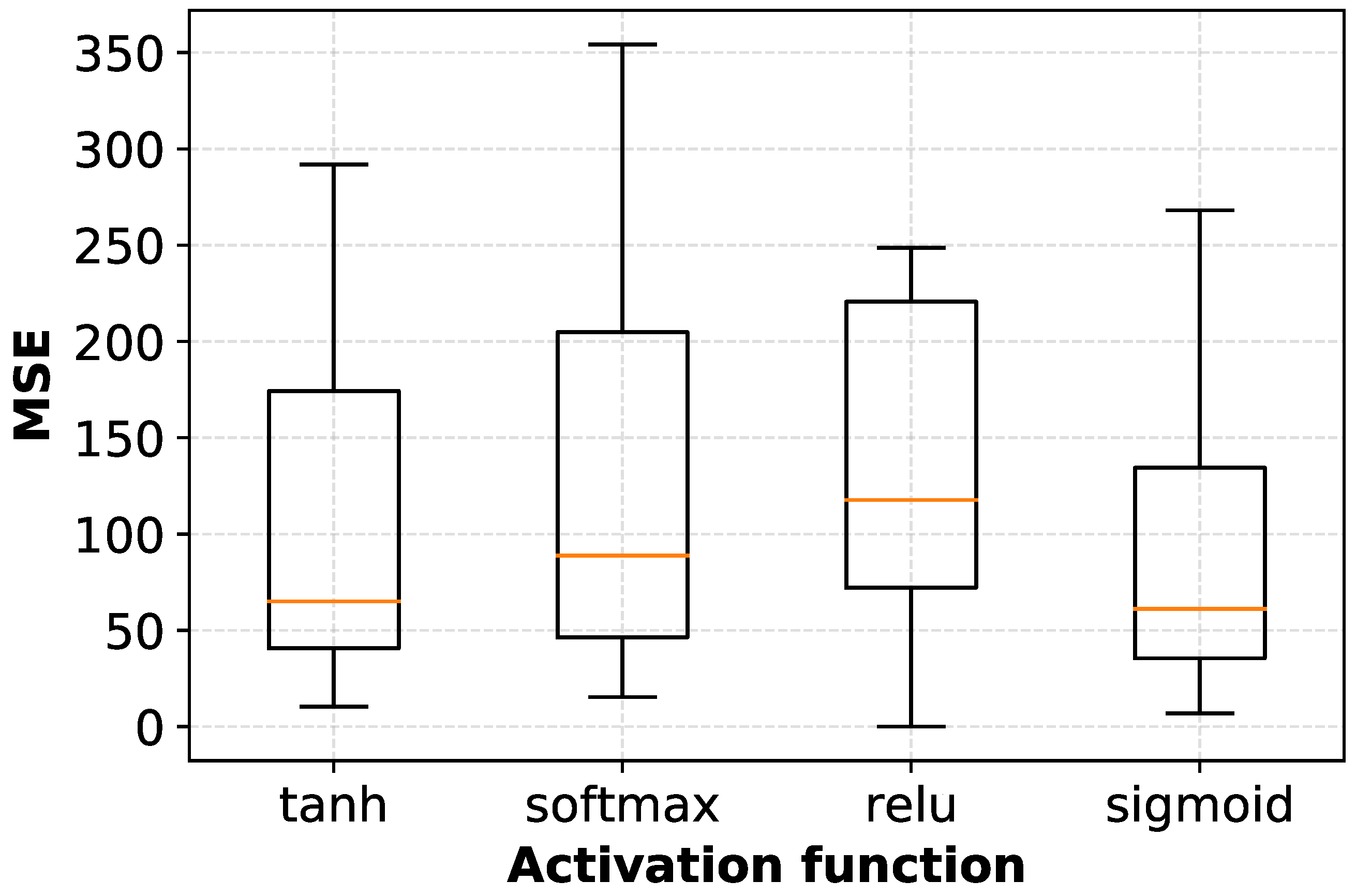
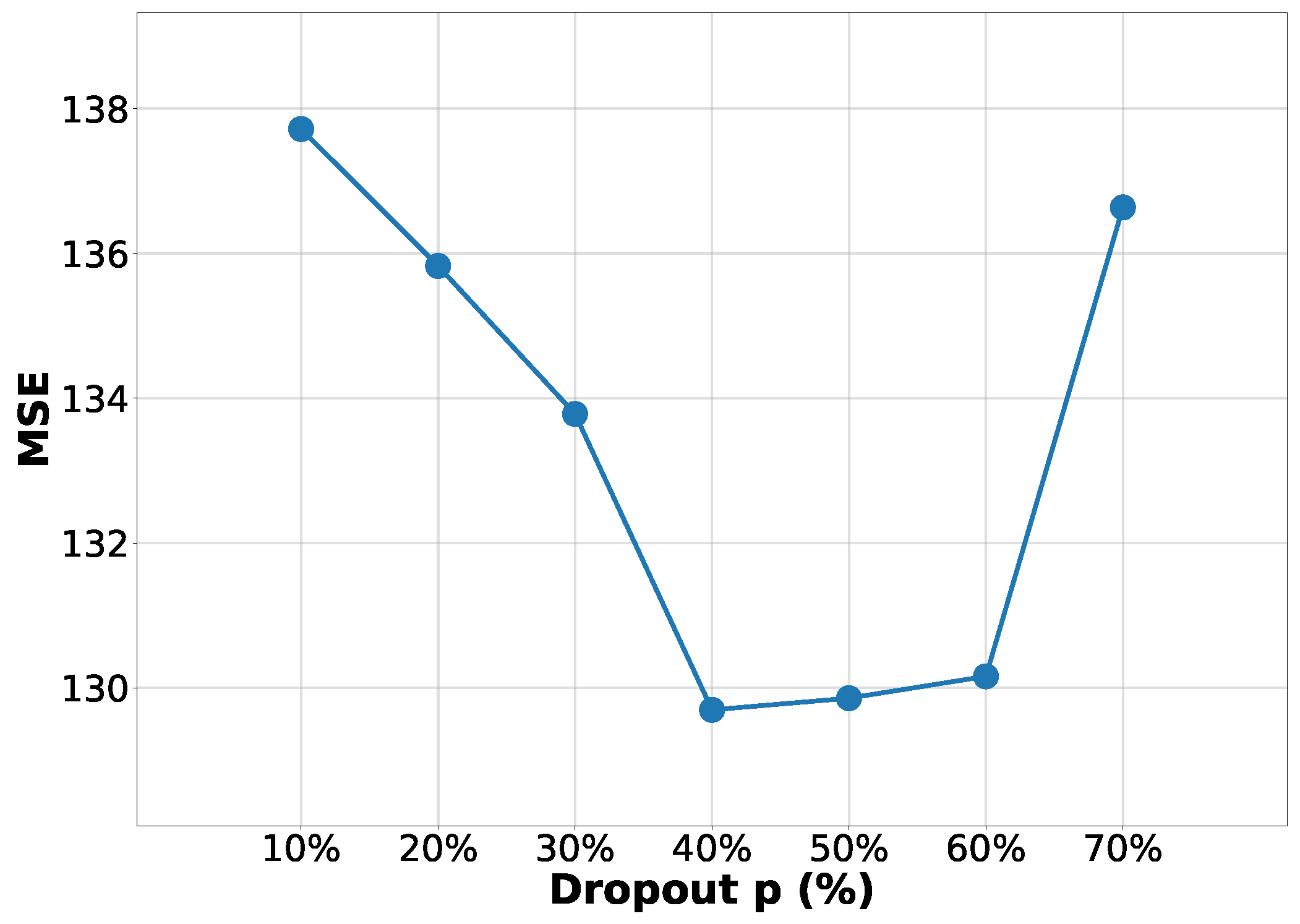
4.5. Empirical Configuration of an Artificial Neural Network
5. Empirical Results and Discussion
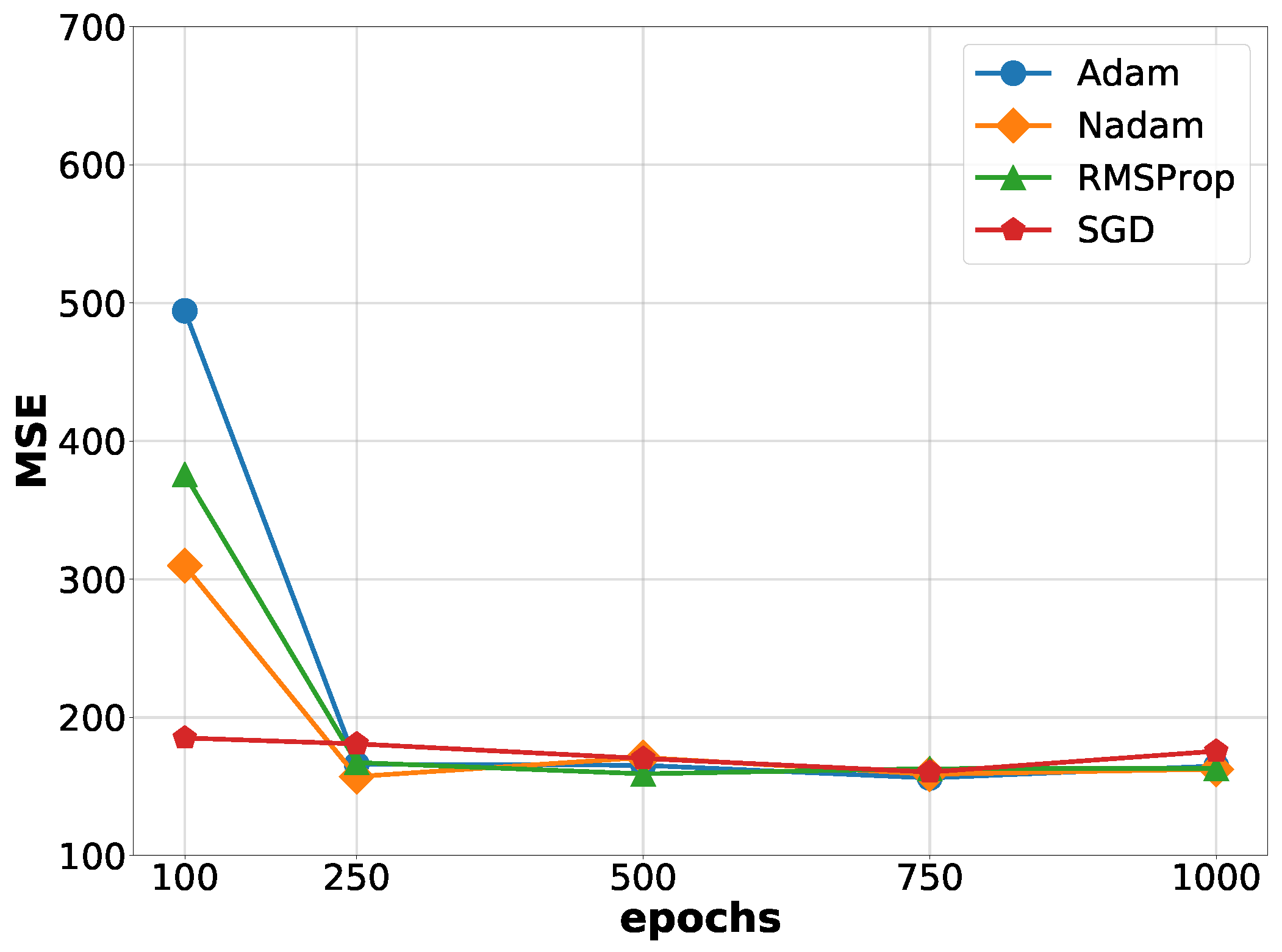
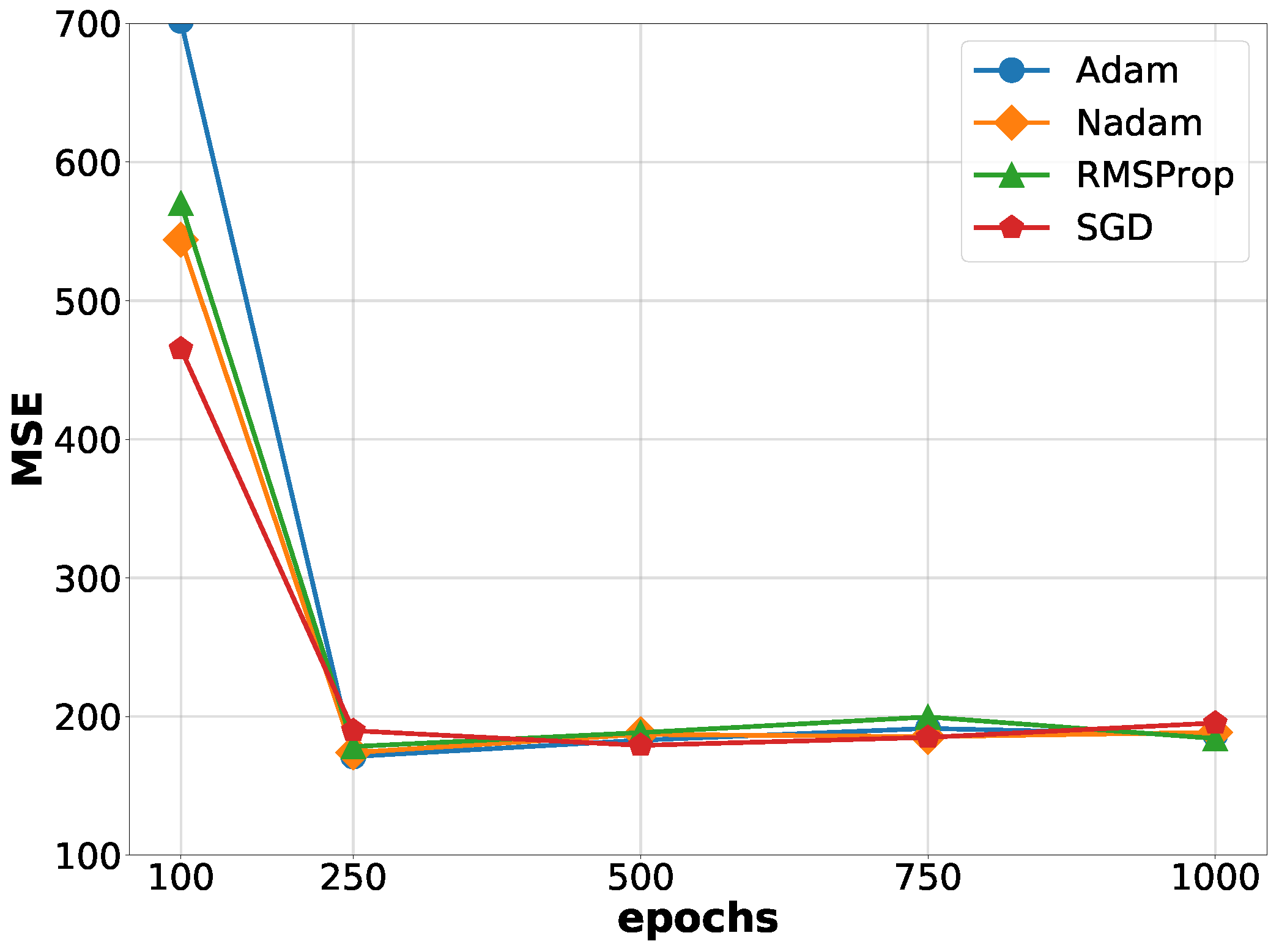
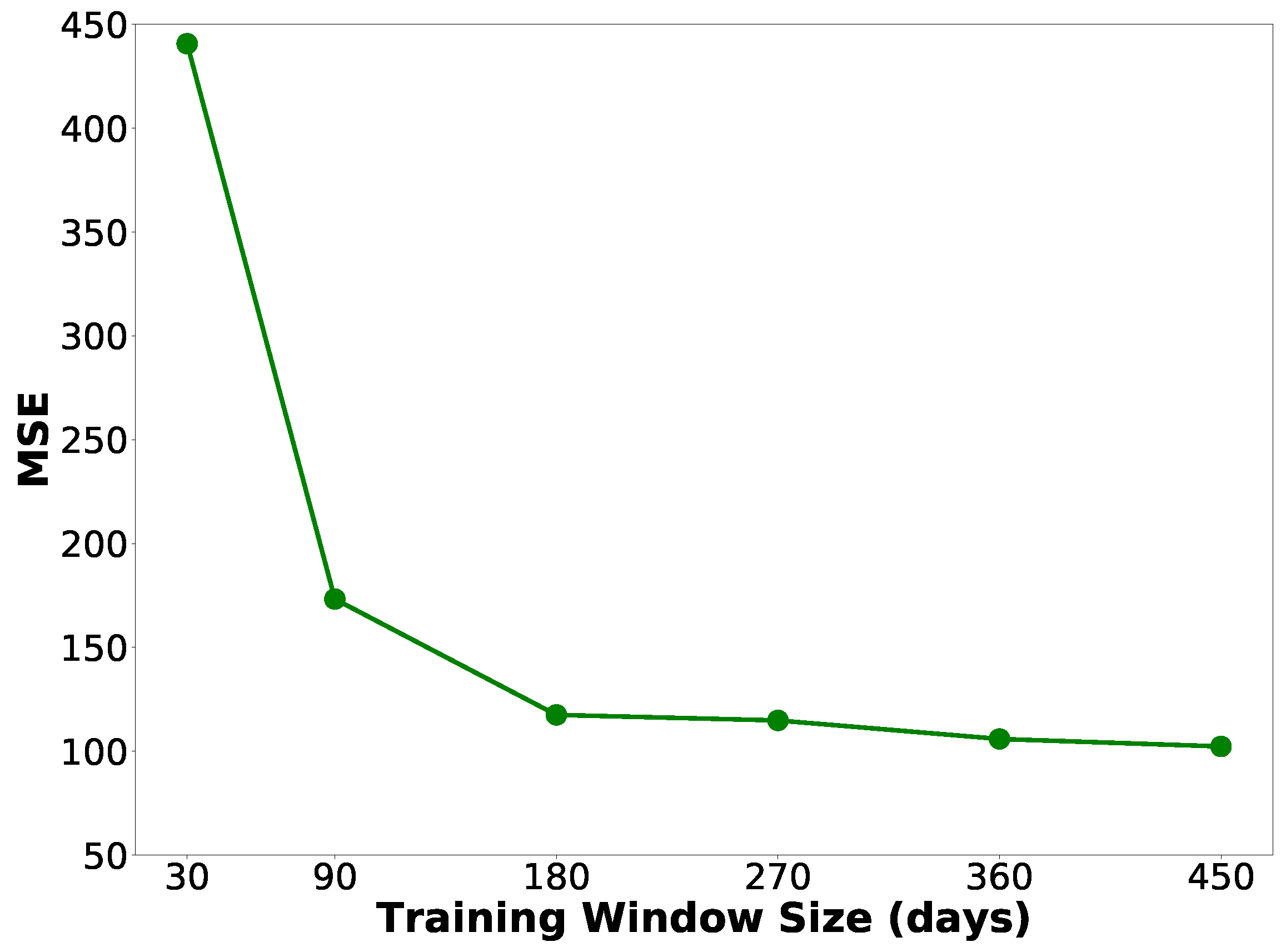
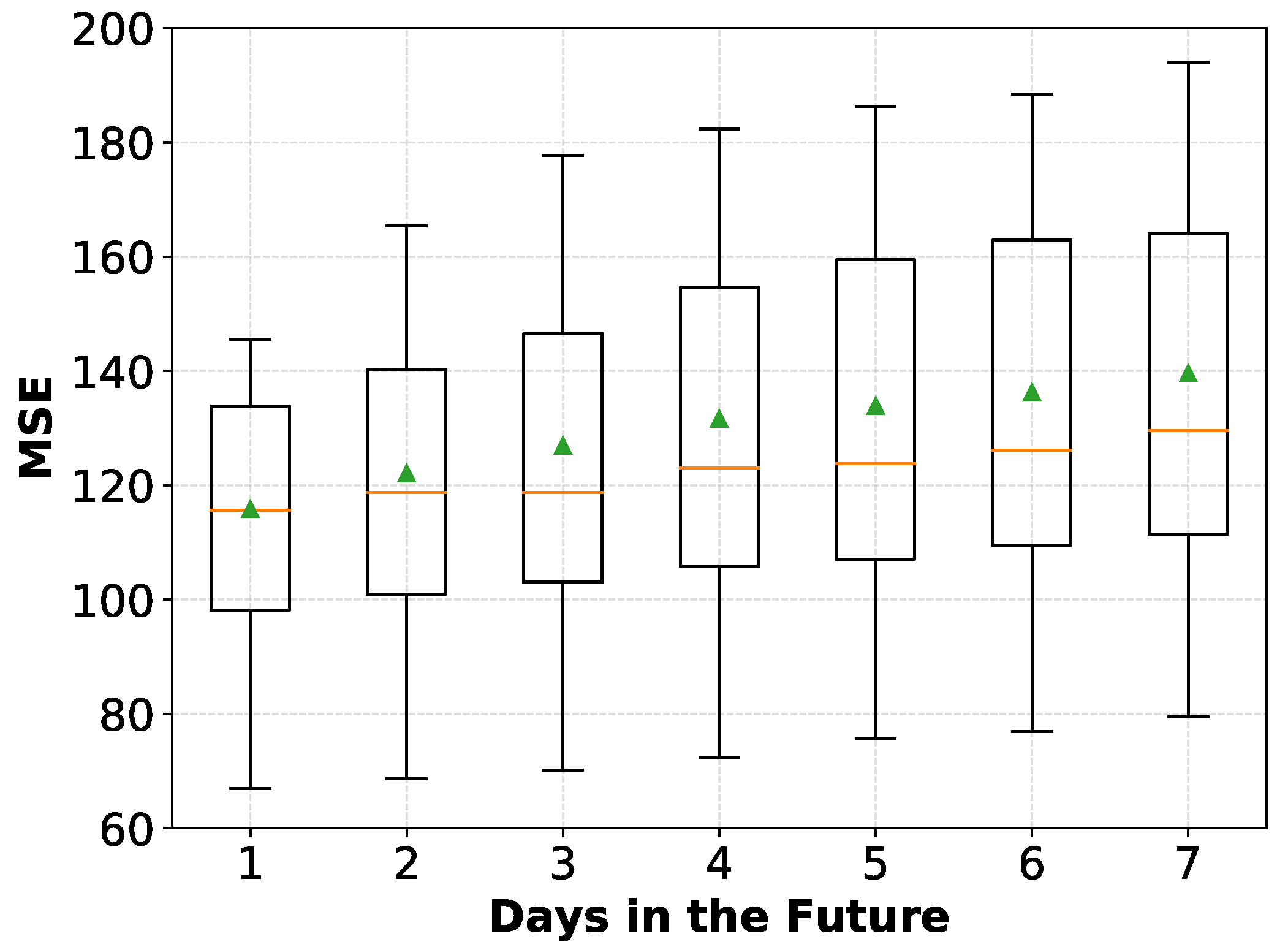
5.1. Determining the Training Window Size
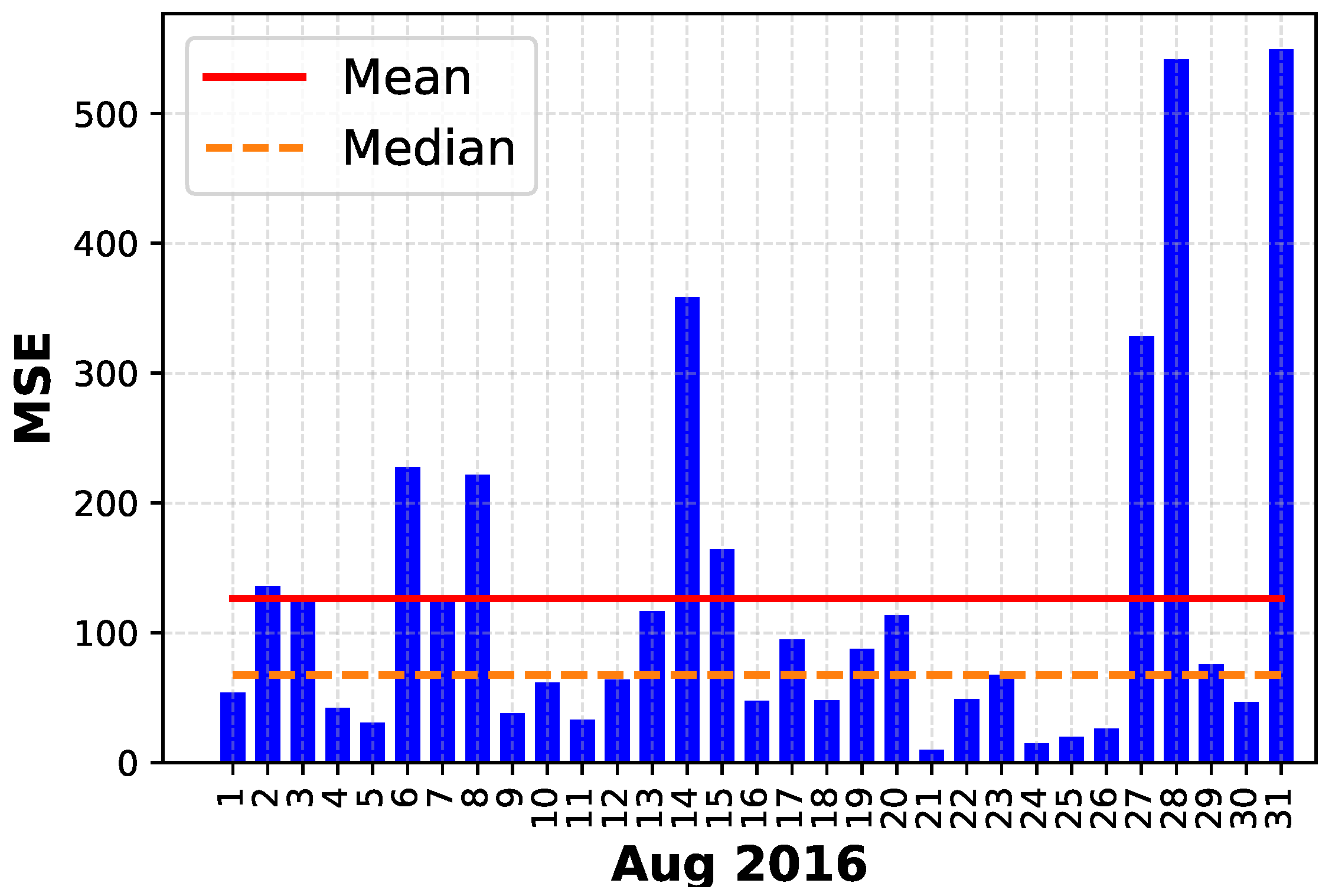
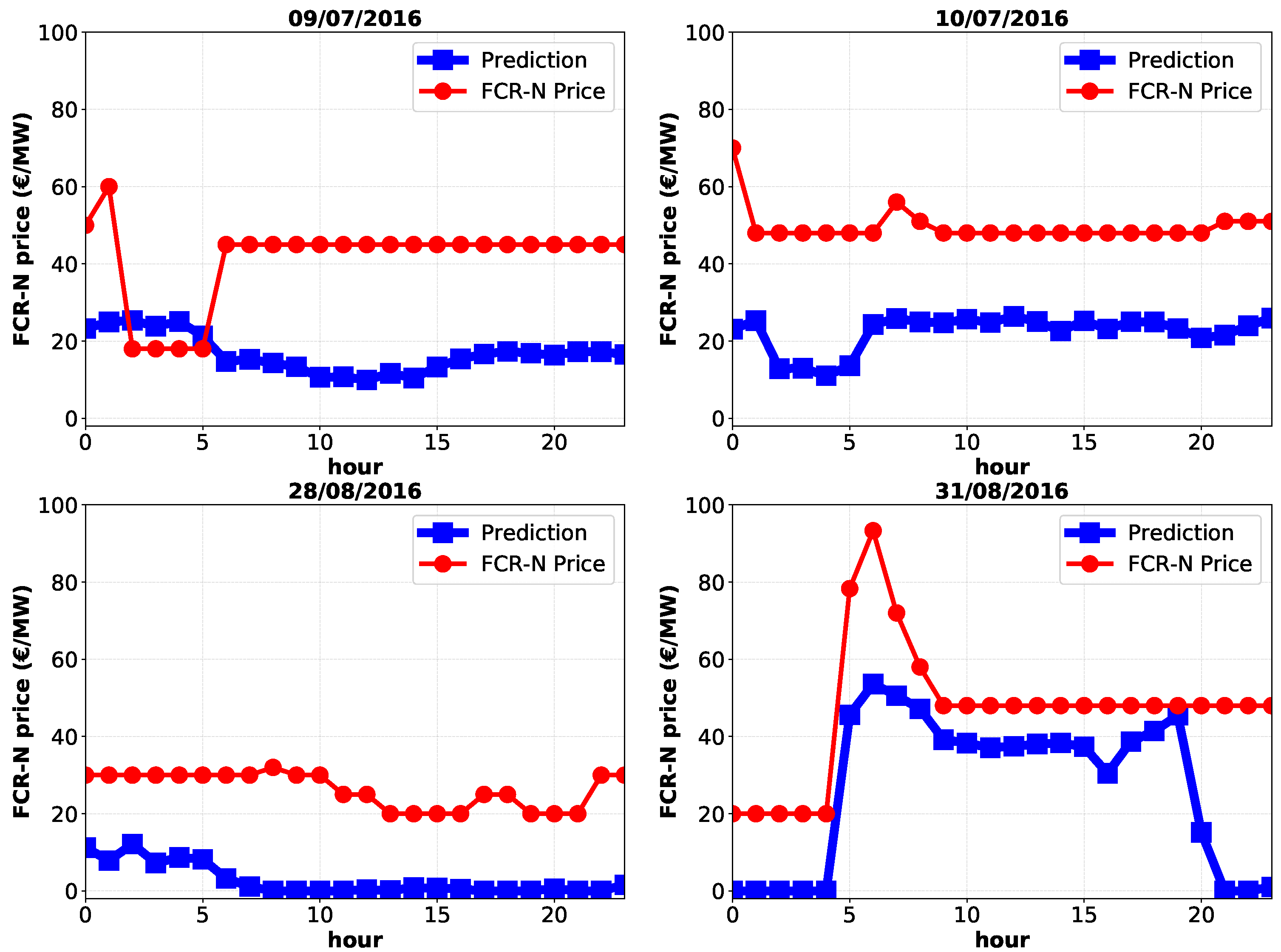
5.2. Prediction Performance Analysis
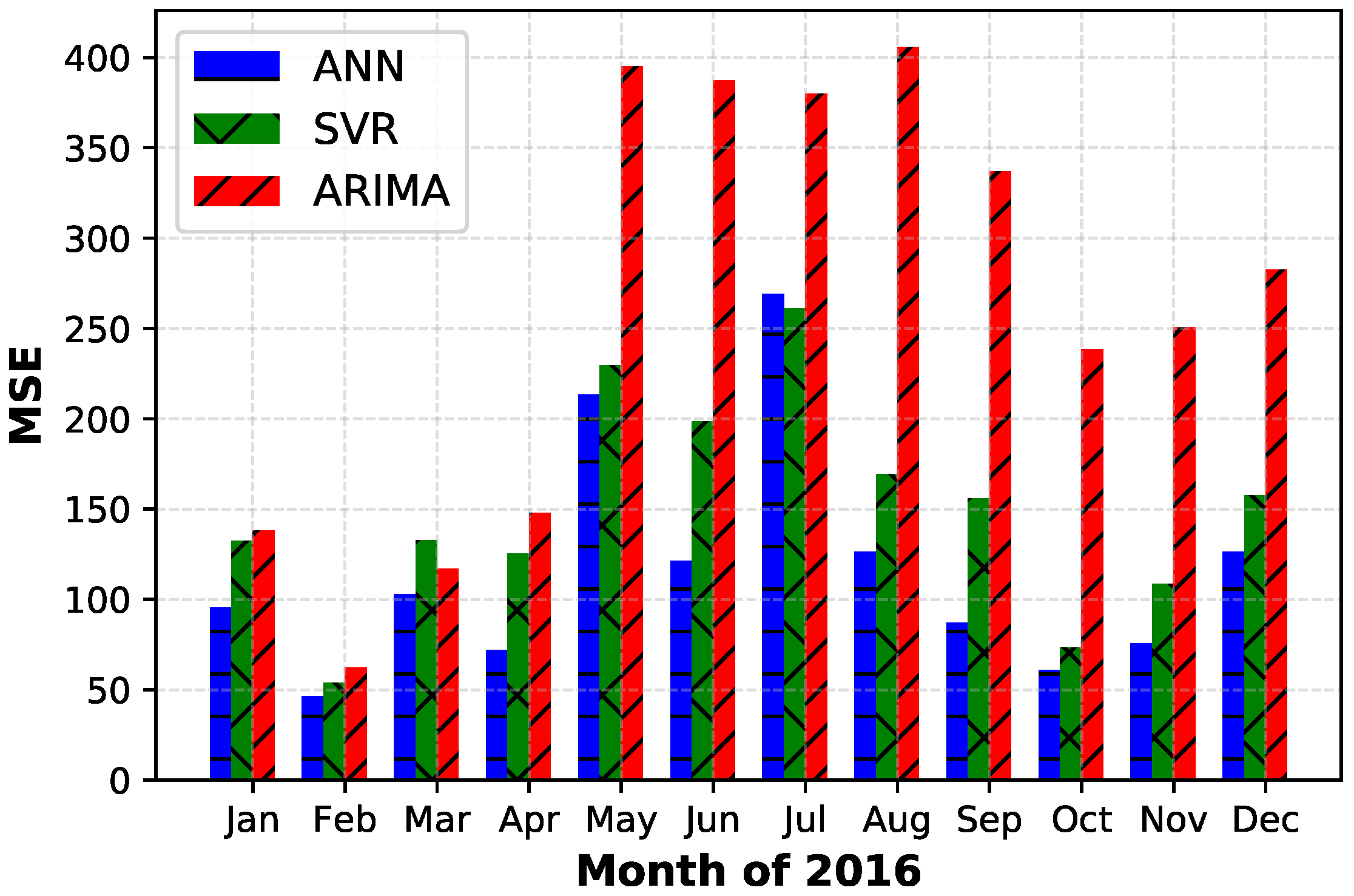
5.3. Comparison with the State of the Art
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| aFRR | Automatic Frequency Restoration Reserve |
| ANN | Artificial Neural Network |
| ARIMA | AutoRegressive Integrated Moving Average |
| DER | Distributed Energy Resources |
| DR | Demand Response |
| EV | Electric Vehicle |
| FCR | Frequency Containment Reserve |
| FCR-D | Frequency Containment Reserve for Disturbance |
| FCR-N | Frequency Containment Reserve for Normal operation |
| MIMO | Multi-Input Multi-Output |
| MSE | Mean Squared Error |
| RNN | Recurrent Neural Network |
| SGD | Stochastic Gradient Descent |
| SVR | Support Vector Regression |
| V2B | Vehicle-to-Building |
| V2H | Vehicle-to-Home |
References
- Gkatzikis, L.; Koutsopoulos, I.; Salonidis, T. The role of aggregators in smart grid demand response markets. IEEE J. Sel. Areas Commun. 2013, 31, 1247–1257. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L. Adaptive negotiation agent for facilitating bi-directional energy trading between smart building and utility grid. IEEE Trans. Smart Grid 2013, 4, 702–710. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Xie, D.; Chu, H.; Gu, C.; Li, F.; Zhang, Y. A novel dispatching control strategy for EVs intelligent integrated stations. IEEE Trans. Smart Grid 2017, 8, 802–811. [Google Scholar] [CrossRef]
- Berthold, F.; Ravey, A.; Blunier, B.; Bouquain, D.; Williamson, S.; Miraoui, A. Design and development of a smart control strategy for plug-in hybrid vehicles including vehicle-to-home functionality. IEEE Trans. Trans. Electrif. 2015, 1, 168–177. [Google Scholar] [CrossRef]
- Pang, C.; Dutta, P.; Kezunovic, M. BEVs/PHEVs as dispersed energy storage for V2B uses in the smart grid. IEEE Trans. Smart Grid 2012, 3, 473–482. [Google Scholar] [CrossRef]
- Jia, Q.S.; Shen, J.X.; Xu, Z.B.; Guan, X.H. Simulation-based policy improvement for energy management in commercial office buildings. IEEE Trans. Smart Grid 2012, 3, 2211–2223. [Google Scholar] [CrossRef]
- Venayagamoorthy, G.K.; Sharma, R.K.; Gautam, P.K.; Ahmadi, A. Dynamic energy management system for a smart microgrid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1643–1656. [Google Scholar] [CrossRef] [PubMed]
- De Angelis, F.; Boaro, M.; Fuselli, D.; Squartini, S.; Piazza, F.; Wei, Q. Optimal home energy management under dynamic electrical and thermal constraints. IEEE Trans. Ind. Inform. 2013, 9, 1518–1527. [Google Scholar] [CrossRef]
- Wu, D.; Aliprantis, D.C.; Ying, L. Load scheduling and dispatch for aggregators of plug-in electric vehicles. IEEE Trans. Smart Grid 2012, 3, 368–376. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, W.; Han, Z.; Cao, Z. Charging scheduling of electric vehicles with local renewable energy under uncertain electric vehicle arrival and grid power price. IEEE Trans. Veh. Technol. 2014, 63, 2600–2612. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalao, J.P. A decentralized electricity market scheme enabling demand response deployment. IEEE Trans. Power Syst. 2018, 33, 4218–4227. [Google Scholar] [CrossRef]
- Callaway, D.S.; Hiskens, I.A. Achieving controllability of electric loads. Proc. IEEE 2011, 99, 184–199. [Google Scholar] [CrossRef]
- Zhang, X.; Hug, G.; Kolter, J.Z.; Harjunkoski, I. Demand response of ancillary service from industrial loads coordinated with energy storage. IEEE Trans. Power Syst. 2018, 33, 951–961. [Google Scholar] [CrossRef]
- Wandhare, R.G.; Agarwal, V. Novel stability enhancing control strategy for centralized PV-grid systems for smart grid applications. IEEE Trans. Smart Grid 2014, 5, 1389–1396. [Google Scholar] [CrossRef]
- Liu, M.; Shi, Y.; Liu, X. Distributed MPC of aggregated heterogeneous thermostatically controlled loads in smart grid. IEEE Trans. Ind. Electron. 2016, 63, 1120–1129. [Google Scholar] [CrossRef]
- Jin, C.; Lu, N.; Lu, S.; Makarov, Y.V.; Dougal, R.A. A coordinating algorithm for dispatching regulation services between slow and fast power regulating resources. IEEE Trans. Smart Grid 2014, 5, 1043–1050. [Google Scholar] [CrossRef]
- Lu, N.; Zhang, Y. Design considerations of a centralized load controller using thermostatically controlled appliances for continuous regulation reserves. IEEE Trans. Smart Grid 2013, 4, 914–921. [Google Scholar] [CrossRef]
- Galus, M.D.; Koch, S.; Andersson, G. Provision of load frequency control by PHEVs, controllable loads, and a cogeneration unit. IEEE Trans. Ind. Electron. 2011, 58, 4568–4582. [Google Scholar] [CrossRef]
- Ota, Y.; Taniguchi, H.; Nakajima, T.; Liyanage, K.M.; Baba, J.; Yokoyama, A. Autonomous distributed V2G (vehicle-to-grid) satisfying scheduled charging. IEEE Trans. Smart Grid 2012, 3, 559–564. [Google Scholar] [CrossRef]
- Gu, Y.; Bakke, J.; Zhou, Z.; Osborn, D.; Guo, T.; Bo, R. A novel market simulation methodology on hydro storage. IEEE Trans. Smart Grid 2014, 5, 1119–1128. [Google Scholar] [CrossRef]
- Ilić, M.D.; Popli, N.; Joo, J.Y.; Hou, Y. A possible engineering and economic framework for implementing demand side participation in frequency regulation at value. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Fingrid. Rules and Fees for the Hourly Market of Frequency Controlled Reserves. 2018. Available online: https://goo.gl/Lx62YR (accessed on 21 July 2018).
- Wu, D.; Zeng, H.; Lu, C.; Boulet, B. Two-stage energy management for office buildings with workplace EV charging and renewable energy. IEEE Trans. Transp. Electrif. 2017, 3, 225–237. [Google Scholar] [CrossRef]
- Wang, P.; Zareipour, H.; Rosehart, W.D. Descriptive models for reserve and regulation prices in competitive electricity markets. IEEE Trans. Smart Grid 2014, 5, 471–479. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Kyriazidis, D.K.; Bakirtzis, A.G. Real-time charging management framework for electric vehicle aggregators in a market environment. IEEE Trans. Smart Grid 2016, 7, 948–957. [Google Scholar] [CrossRef]
- Shafie-khah, M.; Catalão, J.P. A stochastic multi-layer agent-based model to study electricity market participants behavior. IEEE Trans. Power Syst. 2015, 30, 867–881. [Google Scholar] [CrossRef]
- Sánchez-Martín, P.; Lumbreras, S.; Alberdi-Alén, A. Stochastic programming applied to EV charging points for energy and reserve service markets. IEEE Trans. Power Syst. 2016, 31, 198–205. [Google Scholar] [CrossRef]
- Jin, C.; Tang, J.; Ghosh, P. Optimizing electric vehicle charging with energy storage in the electricity market. IEEE Trans. Smart Grid 2013, 4, 311–320. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an optimal vehicle-to-grid aggregator for frequency regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Melo, D.R.; Trippe, A.; Gooi, H.B.; Massier, T. Robust electric vehicle aggregation for ancillary service provision considering battery aging. IEEE Trans. Smart Grid 2016, 9. [Google Scholar] [CrossRef]
- Ela, E.; Gevorgian, V.; Tuohy, A.; Kirby, B.; Milligan, M.; O’Malley, M. Market designs for the primary frequency response ancillary service—Part I: Motivation and design. IEEE Trans. Power Syst. 2014, 29, 421–431. [Google Scholar] [CrossRef]
- Ela, E.; Gevorgian, V.; Tuohy, A.; Kirby, B.; Milligan, M.; O’Malley, M. Market designs for the primary frequency response ancillary service—Part II: Case studies. IEEE Trans. Power Syst. 2014, 29, 432–440. [Google Scholar] [CrossRef]
- González, P.; Villar, J.; Díaz, C.A.; Campos, F.A. Joint energy and reserve markets: Current implementations and modeling trends. Electr. Power Syst. Res. 2014, 109, 101–111. [Google Scholar] [CrossRef]
- Raineri, R.; Rios, S.; Schiele, D. Technical and economic aspects of ancillary services markets in the electric power industry: An international comparison. Energy Policy 2006, 34, 1540–1555. [Google Scholar] [CrossRef]
- Fingrid. Frequency Containment Reserves. 2018. Available online: https://goo.gl/aY2PSE (accessed on 21 July 2018).
- ENTSO-E. Nordic Balancing Philosophy. 2016. Available online: https://goo.gl/Hn6o3D (accessed on 21 July 2018).
- Yang, J.; Zhao, J.; Luo, F.; Wen, F.; Dong, Z.Y. Decision-making for electricity retailers: A brief survey. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Croonenbroeck, C.; Hüttel, S. Quantifying the economic efficiency impact of inaccurate renewable energy price forecasts. Energy 2017, 134, 767–774. [Google Scholar] [CrossRef]
- Wang, P.; Zareipour, H.; Rosehart, W.D. Characteristics of the prices of operating reserves and regulation services in competitive electricity markets. Energy Policy 2011, 39, 3210–3221. [Google Scholar] [CrossRef]
- Fingrid. Market Places. 2017. Available online: https://goo.gl/QfddQ1 (accessed on 21 July 2018).
- Karthikeyan, S.P.; Raglend, I.J.; Kothari, D.P. A review on market power in deregulated electricity market. Int. J. Electr. Power Energy Syst. 2013, 48, 139–147. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Domanski, P.D.; Gintrowski, M. Alternative approaches to the prediction of electricity prices. Int. J. Energy Sect. Manag. 2017, 11, 3–27. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A.J. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Keles, D.; Scelle, J.; Paraschiv, F.; Fichtner, W. Extended forecast methods for day-ahead electricity spot prices applying artificial neural networks. Appl. Energy 2016, 162, 218–230. [Google Scholar] [CrossRef]
- Gao, G.; Lo, K.; Fan, F. Comparison of ARIMA and ANN models used in electricity price forecasting for power market. Energy Power Eng. 2017, 9, 120–126. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; Mit Press: Cambridge, MA, USA, 1997; pp. 155–161. [Google Scholar]
- Zhao, J.H.; Dong, Z.Y.; Xu, Z.; Wong, K.P. A statistical approach for interval forecasting of the electricity price. IEEE Trans. Power Syst. 2008, 23, 267–276. [Google Scholar] [CrossRef]
- Shayeghi, H.; Ghasemi, A.; Moradzadeh, M.; Nooshyar, M. Simultaneous day-ahead forecasting of electricity price and load in smart grids. Energy Convers. Manag. 2015, 95, 371–384. [Google Scholar] [CrossRef]
- Shiri, A.; Afshar, M.; Rahimi-Kian, A.; Maham, B. Electricity price forecasting using Support Vector Machines by considering oil and natural gas price impacts. In Proceedings of the 2015 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–5. [Google Scholar]
- Giovanelli, C.; Liu, X.; Sierla, S.; Vyatkin, V.; Ichise, R. Towards an aggregator that exploits big data to bid on frequency containment reserve market. In Proceedings of the IECON 2017 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7514–7519. [Google Scholar]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead electricity price forecasting via the application of artificial neural network based models. Appl. Energy 2016, 172, 132–151. [Google Scholar] [CrossRef]
- Saâdaoui, F. A seasonal feedforward neural network to forecast electricity prices. Neural Comput. Appl. 2017, 28, 835–847. [Google Scholar] [CrossRef]
- Sharma, V.; Srinivasan, D. A hybrid intelligent model based on recurrent neural networks and excitable dynamics for price prediction in deregulated electricity market. Eng. Appl. Artif. Intell. 2013, 26, 1562–1574. [Google Scholar] [CrossRef]
- Kaastra, I.; Boyd, M. Designing a neural network for forecasting financial and economic time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Ahlstrom, M.; Ela, E.; Riesz, J.; O’Sullivan, J.; Hobbs, B.F.; O’Malley, M.; Milligan, M.; Sotkiewicz, P.; Caldwell, J. The Evolution of the Market: Designing a Market for High Levels of Variable Generation. IEEE Power Energy Mag. 2015, 13, 60–66. [Google Scholar] [CrossRef]
- Fingrid. Fingrid Open Data Service. 2017. Available online: https://data.fingrid.fi (accessed on 21 July 2018).
- Energia.fi. Finnish Electricity Consumption. 2017. Available online: https://energia.fi/EN (accessed on 21 July 2018).
- NordPool. Day-ahead Elspot prices. 2017. Available online: http://www.nordpoolspot.com/historical-market-data/ (accessed on 21 July 2018).
- Finnish Meteorological Institute. Finnish Meteorological Institute’s Open Data. Available online: https://en.ilmatieteenlaitos.fi/open-data (accessed on 21 July 2018).
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar]
- Marcjasz, G.; Uniejewski, B.; Weron, R. On the importance of the long-term seasonal component in day-ahead electricity price forecasting with NARX neural networks. Int. J. Forecast. 2018. [Google Scholar] [CrossRef]
- Zhou, Z.; Chan, W.K.V. Reducing electricity price forecasting error using seasonality and higher order crossing information. IEEE Trans. Power Syst. 2009, 24, 1126–1135. [Google Scholar] [CrossRef]
- Bontempi, G.; Ben Taieb, S.; Le Borgne, Y.A. Machine Learning Strategies for Time Series Forecasting; Springer: Berlin/Heidelberg, Germany, 2013; pp. 62–77. [Google Scholar]
- An, N.H.; Anh, D.T. Comparison of Strategies for Multi-step-Ahead Prediction of Time Series Using Neural Network. In Proceedings of the 2015 International Conference on Advanced Computing and Applications (ACOMP), Ho Chi Minh City, Vietnam, 23–25 November 2015; pp. 142–149. [Google Scholar]
- Aksoy, S.; Haralick, R.M. Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 2001, 22, 563–582. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing neural network architectures using reinforcement learning. arXiv, 2016; arXiv:1611.02167. [Google Scholar]
- Heaton, J. Introduction to Neural Networks with Java; Heaton Research, Inc.: St. Louis, MO, USA, 2008. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv, 2016; arXiv:1609.04747. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-RMSProp: Divide the gradient by a running average of its recent magnitude. Coursera Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Dozat, T. Incorporating Nesterov momentum into Adam. In Proceedings of the ICLR 2016 Workshop Track International Conference on Learning Representations, San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Karlik, B.; Olgac, A.V. Performance analysis of various activation functions in generalized MLP architectures of neural networks. Int. J. Artif. Intell. Expert Syst. 2011, 1, 111–122. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]

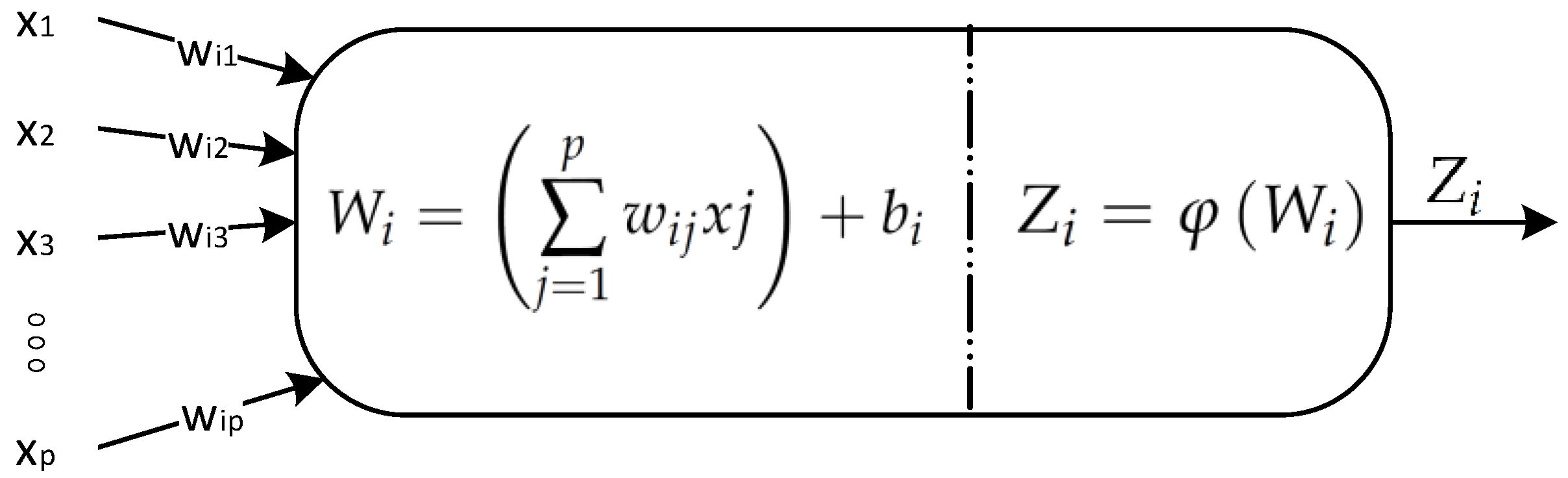
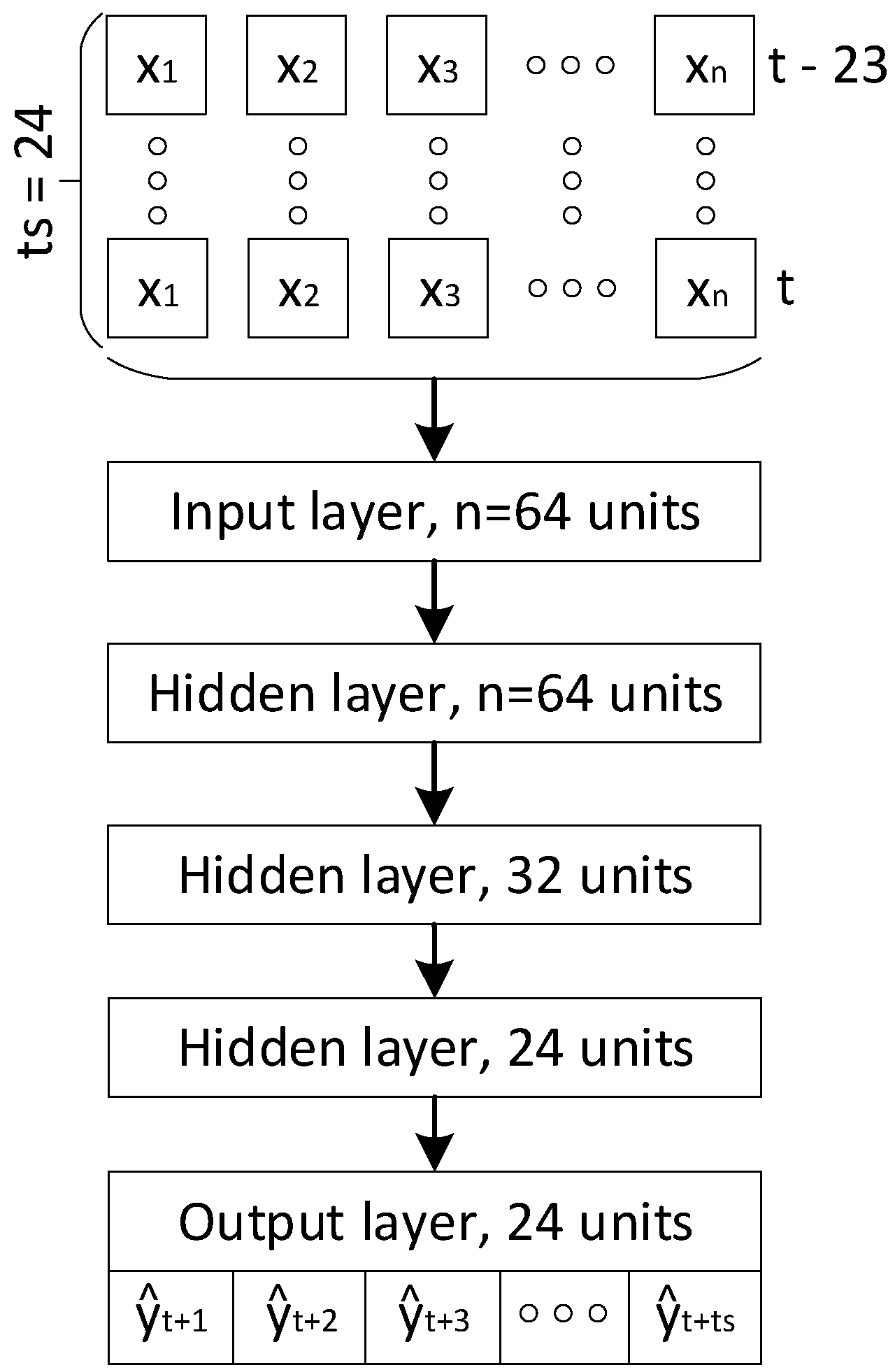

| Market | Minimum Bid | Activation Time | Activation Frequency | How Often It Is Activated |
|---|---|---|---|---|
| FCR-N | 0.1 MW | 3 min | Fully after a frequency step change of ± 0.1 Hz, max deadband ±0.05 Hz | Several times a day |
| Category Name | # | Data Source |
|---|---|---|
| FCR market data | 5 | Fingrid [58] |
| Electricity Import/Export | 12 | Fingrid [58] |
| Electricity Load | 2 | Fingrid [58] |
| Electricity Generation | 12 | Fingrid [58] and Energia.fi [59] |
| Day-ahead Elspot Prices | 1 | Nord Pool [60] |
| Oil Prices | 1 | |
| Weather | 26 | Finnish Meteorological Institute [61] |
| Calendar | 5 | |
| Total | 64 |
| Mean | 19.560 | Skewness | 89.335 |
| Median | 17.725 | Kurtosis | 37.686 |
| Min | 0.0 | Jarque–Bera | 1,065,031.561 |
| Max | 500.0 | % 0-value | 29.10% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giovanelli, C.; Sierla, S.; Ichise, R.; Vyatkin, V. Exploiting Artificial Neural Networks for the Prediction of Ancillary Energy Market Prices. Energies 2018, 11, 1906. https://doi.org/10.3390/en11071906
Giovanelli C, Sierla S, Ichise R, Vyatkin V. Exploiting Artificial Neural Networks for the Prediction of Ancillary Energy Market Prices. Energies. 2018; 11(7):1906. https://doi.org/10.3390/en11071906
Chicago/Turabian StyleGiovanelli, Christian, Seppo Sierla, Ryutaro Ichise, and Valeriy Vyatkin. 2018. "Exploiting Artificial Neural Networks for the Prediction of Ancillary Energy Market Prices" Energies 11, no. 7: 1906. https://doi.org/10.3390/en11071906
APA StyleGiovanelli, C., Sierla, S., Ichise, R., & Vyatkin, V. (2018). Exploiting Artificial Neural Networks for the Prediction of Ancillary Energy Market Prices. Energies, 11(7), 1906. https://doi.org/10.3390/en11071906







