The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments
Abstract
1. Introduction
- A crucial factor in the accuracy of performance measurements arises from the control strategy imposed on the tidal turbine. The capability of the control system to keep the rotor operating near its optimum Tip Speed Ratio (TSR), when driven by an unsteady and non-uniform inflow velocity, and avoiding ‘stall’, is a key element in a successful commercial turbine. Similarly, the control strategy adopted during an experiment can increase the error bounds in derived performance indicators, such as CP. Control strategies used in previous tidal turbine performance testing vary. For devices at low Technology Readiness Level (TRL) scales [16], such as those used in laboratory scale experiments, an open-loop control may suffice [9]. However, more commonly, a closed-loop, proportional–integral–derivative (PID) feedback control strategy is found [17,18] in higher TRL devices.It is recognised that in order to develop the industry, advanced control strategies require development and testing in highly parameterised conditions. Efforts are being made in this field in both research and industry. The use of overspeed, pitch or stall control strategies with peak power tracking, or surface mapping algorithms for condition monitoring purposes are under development [19,20]. Furthermore, future options may include the possibility of feed-forward algorithms such as those being trialled in the wind sector [21].
- The second source of increased uncertainty comes from the increased variability of the inflow velocity. This is of particularly significance since the power density scales with the cube of the inflow velocity. Furthermore, both genuine variability and sampling errors are compounded in real velocimetry data. Separating and quantifying their effects requires care in calibration of instruments and data analysis. In order to promote consistent best practice in the power performance testing of Tidal Energy Converters (TECs), Johnstone et al. published best practices for the wave and tidal sector [22] which specifies the requirements for clear uncertainty analysis. Further to this the IEC (Geneva, Switzerland) published a Technical Specification IEC/TS 62600-200 [23]. The specification provides the methodology for determining an average value for velocity at a site, enabling the time average performance of a turbine to be captured and reported to a common standard. The IEC specification has been used in other research projects and across the industry [10,13,24] and will be used to guide the data analysis in this paper.
2. Experimental Setup
2.1. Flow Instrumentation
2.2. Flow Instrumentation Validation
2.3. Control Strategy
3. Non-Dimensional Performance Characteristics
4. Results
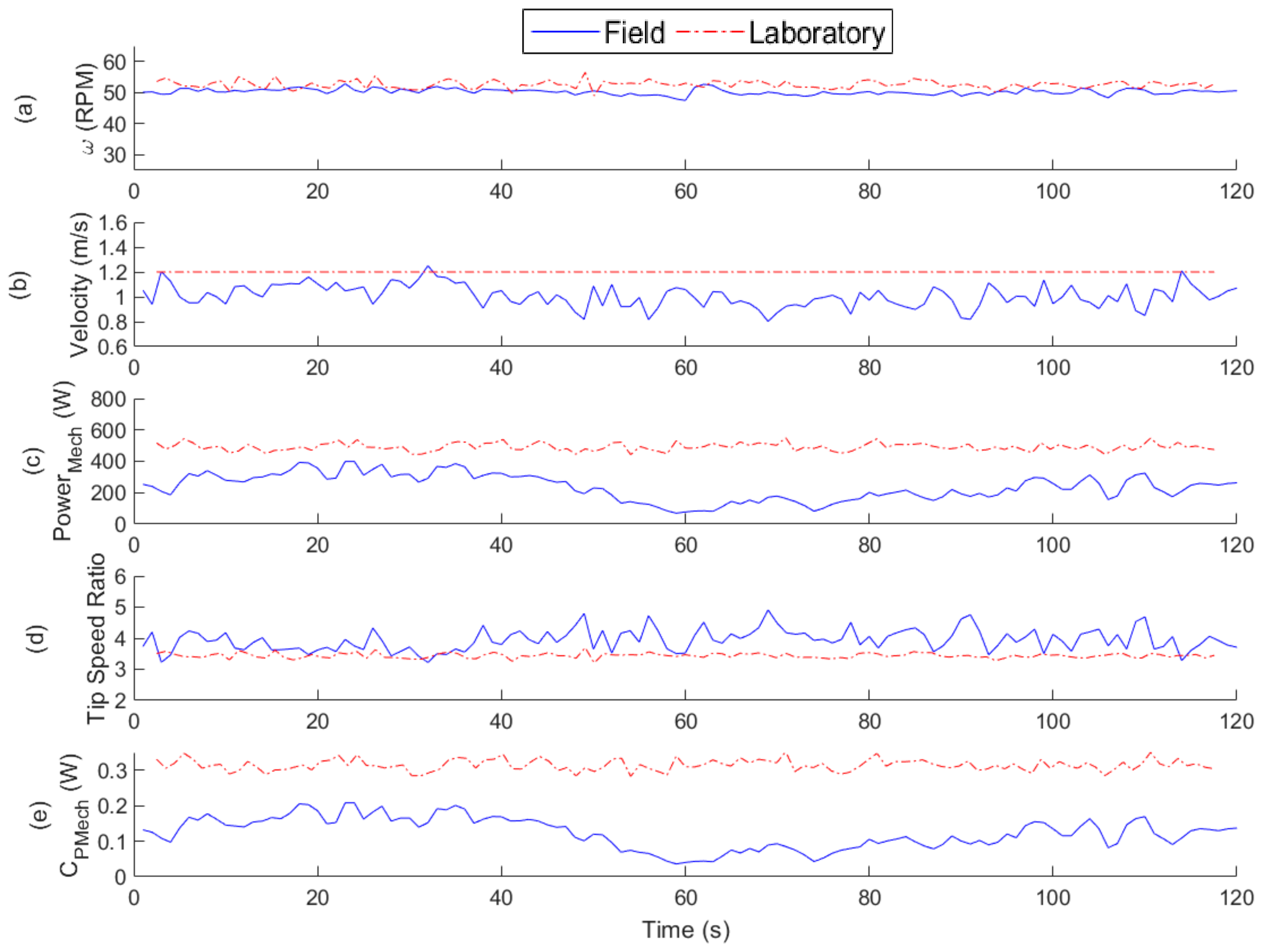
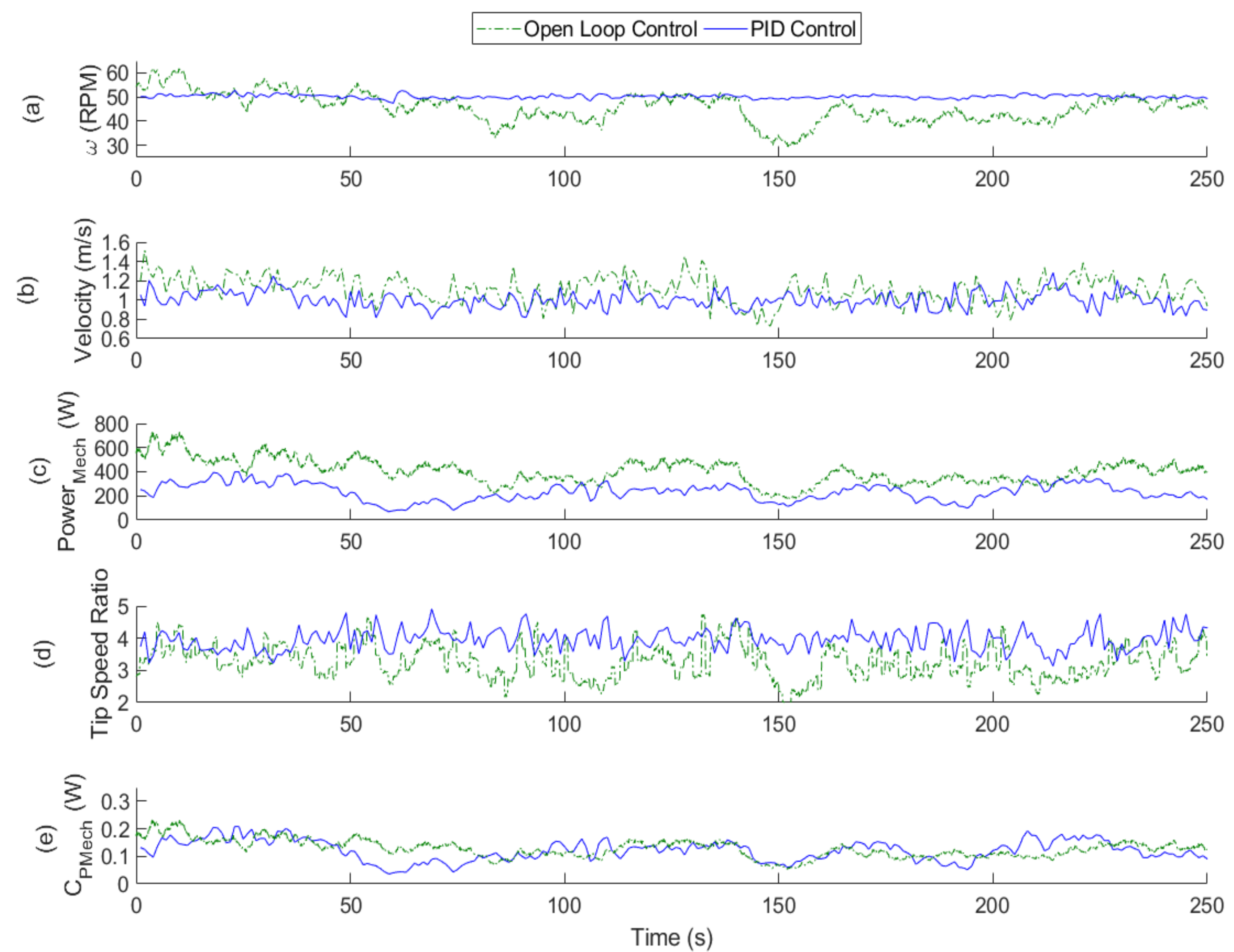
4.1. Time Series Results
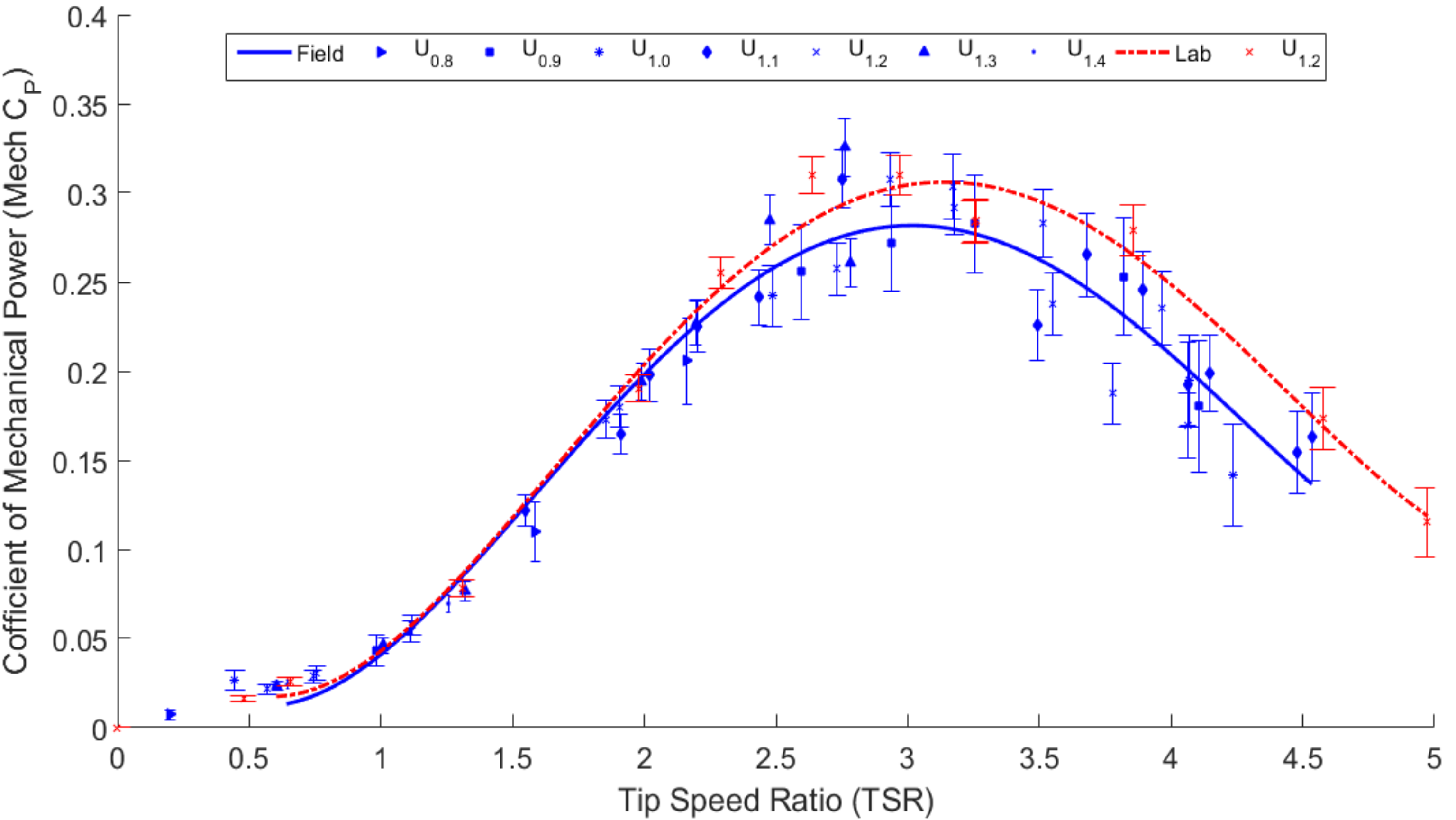
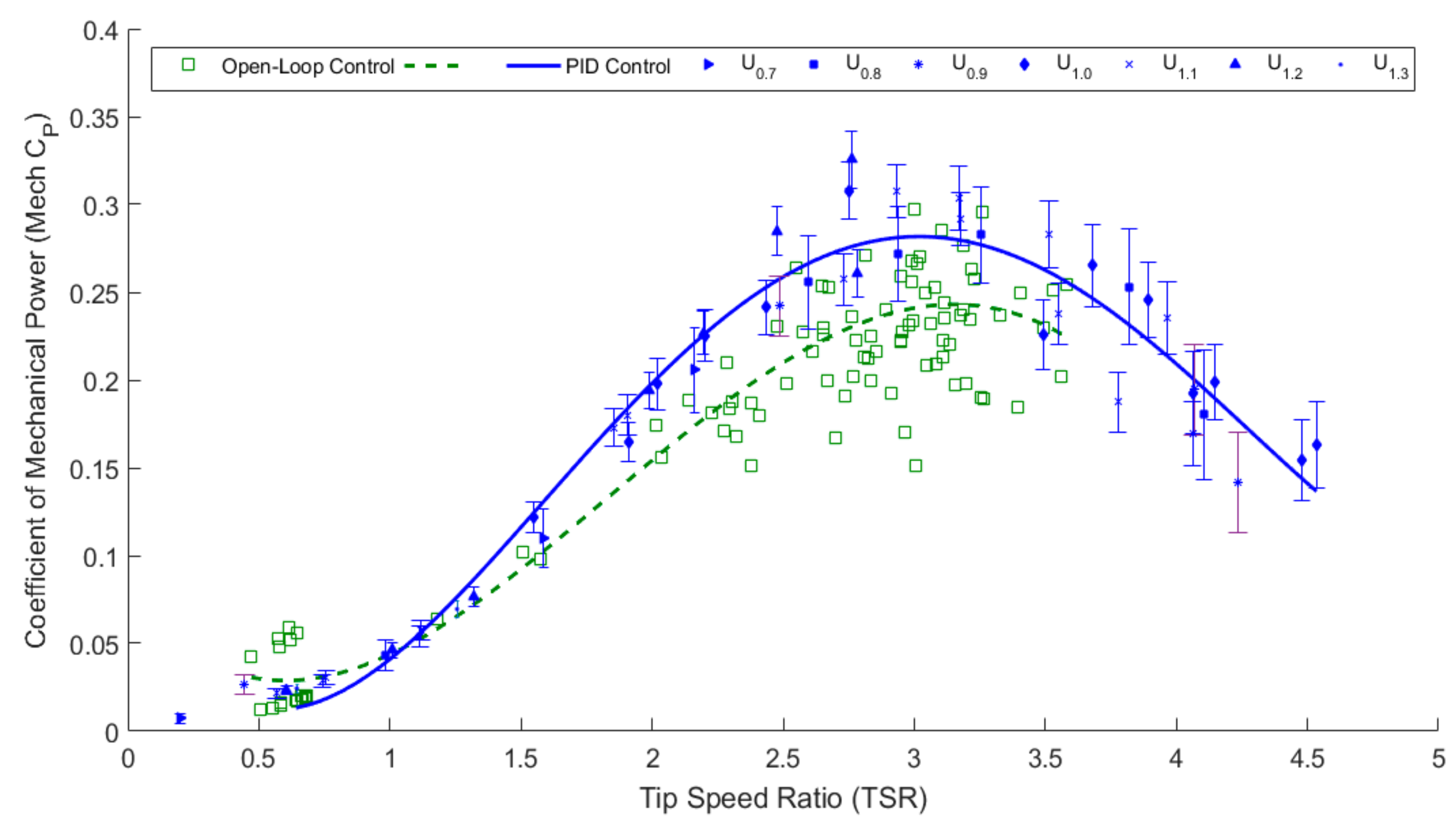
4.2. Derived Performance Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter | Symbol |
| Area of turbine (m2) | A |
| Velocity Bin Identifier | i |
| Time Instant Identifier | j |
| Depth Profile Bin Identifier | k |
| Number of samples | n |
| Density (kg/m3) | |
| Extracted Power | |
| Extracted Torque | Q |
| Turbine Radius (m) | |
| Sample Identifier | s |
| Extracted Thrust | |
| Mean Velocity (m/s) | |
| Rotational Speed (rad/s) | |
| Standard Deviation | σ |
| Two Standard Deviation (95% confidence interval) | 2σ |
Appendix A
ADP Towing Tank Calibration Results
| Variable S (Percentage Disagreement between Vector and Aquadopp) | Prediction from Calibration | Whole Validation Dataset | Validation for Yaw within ±15 Degrees |
|---|---|---|---|
| Bias = Mean(S) | −0.08% | +1.03% | +0.27% |
| Precision = Standard Deviation(S) | ±1.1% | ±2.53% | ±2.02% |
Appendix B
B.1. Deriving Single Measurement for Inflow Velocity
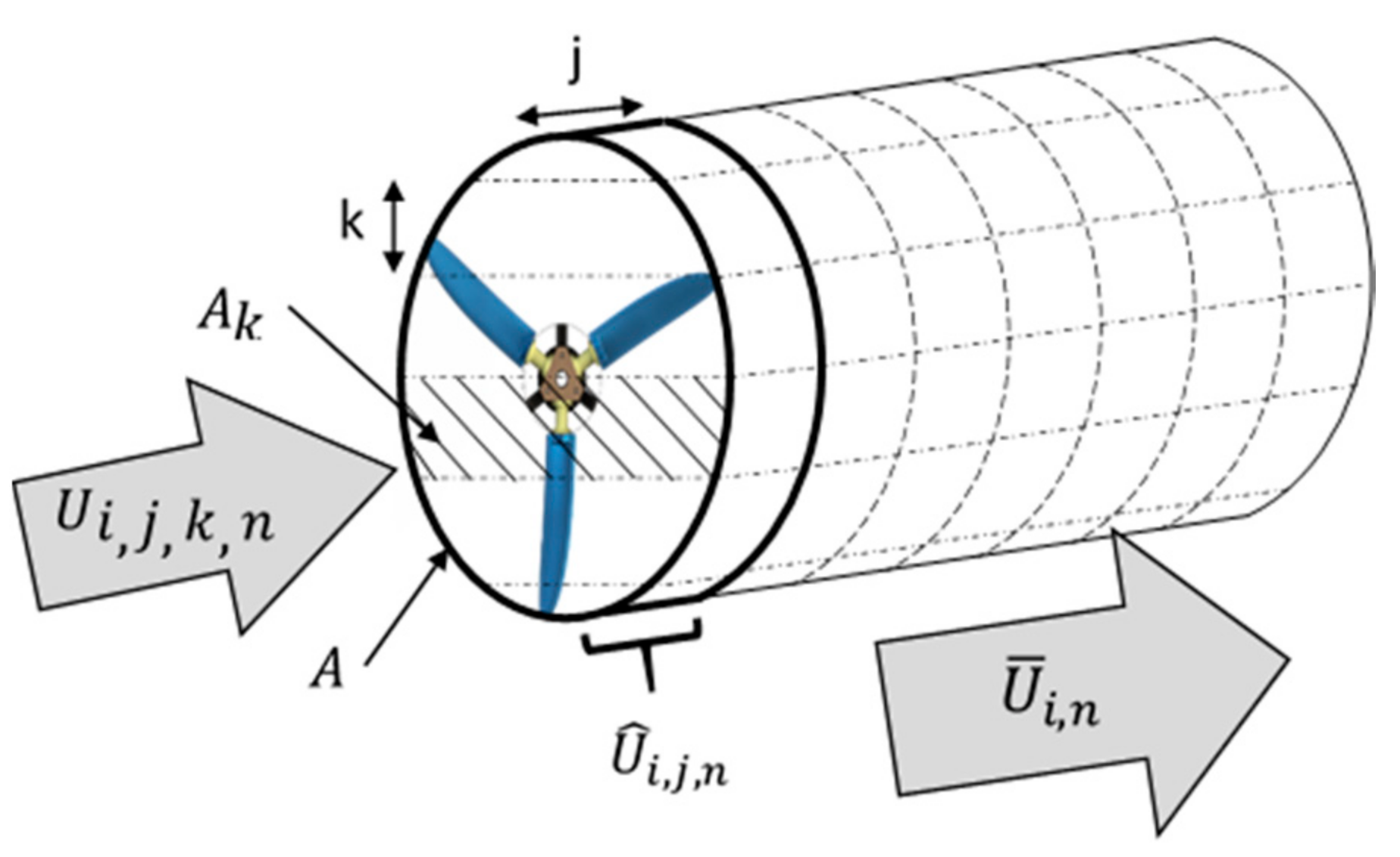
B.2. Propagation of Uncertainty
References
- Department for Buisness, Energy & Industrial Stragety. Contracts for Difference Second Allocation Round Results. 2017. Available online: https://www.gov.uk/government/publications/contracts-for-difference-cfd-second-allocation-round-results (accessed on 20 January 2018).
- Mason-Jones, A.; O’Doherty, D.M.; Morris, C.E.; O’Doherty, T.; Byrne, C.B.; Prickett, P.W.; Grosvenor, R.I.; Owen, I.; Tedds, S.; Poole, R.J. Non-dimensional scaling of tidal stream turbines. Energy 2012, 44, 820–829. [Google Scholar] [CrossRef]
- Clarke, J.A.; Connor, G.; Grant, A.D.; Johnstone, C.M. Design and testing of a contra-rotating tidal current turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 171–179. [Google Scholar] [CrossRef]
- Gaurier, B.; Germain, G.; Facq, J.V.; Johnstone, C.M.; Grant, A.D.; Day, A.H.; Nixon, E.; Di Felice, F.; Costanzo, M. Tidal energy “Round Robin” tests comparisons between towing tank and circulating tank results. Int. J. Mar. Energy 2015, 12, 87–109. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Whittaker, T.; Boake, C.; Elsaesser, B. Field tests of multiple 1/10 scale tidal turbines in steady flows. Renew. Energy 2016, 87, 240–252. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Elsaesser, B.; Whittaker, T.; Boake, C. Testing Tidal Turbines—Part 1: Steady Towing Tests vs. Tidal Mooring Tests. In Proceedings of the ASRANet International Conference on Offshore Renewable Energy, Glasgow, UK, September 2014; Volume 68, pp. 55–87. Available online: https://pure.qub.ac.uk/portal/files/11366206/ASRANet_2014_PJeffcoate.pdf (accessed on 20 January 2018).
- Atcheson, M.; MacKinnon, P.; Elsaesser, B. A large scale model experimental study of a tidal turbine in uniform steady flow. Ocean Eng. 2015, 110, 51–61. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Salvatore, F.; Boake, C.; Elsaesser, B.; Vallerano, V. Effect of Submergence on Tidal Turbine Performance. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 3–9. [Google Scholar]
- Jeffcoate, P.; Starzmann, R.; Elsaesser, B.; Scholl, S.; Bischoff, S. Field measurements of a full scale tidal turbine. Int. J. Mar. Energy 2015, 12, 3–20. [Google Scholar] [CrossRef]
- Starzmann, R.; Jeffcoate, P.; Scholl, S.; Bischof, S.; Elsaesser, B. Field testing a full-scale tidal turbine Part 1: Power Performance Assessment. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–7. [Google Scholar]
- Schmitt, P.; Elsaesser, B.; Bischof, S.; Starzmann, R. Field testing a full-scale tidal turbine Part 2: In-line Wake Effects. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015; pp. 1–7. [Google Scholar]
- Frost, C.; Benson, I.; Elsäßer, B.; Starzmann, R.; Whittaker, T. Mitigating Uncertainty in Tidal Turbine Performance Characteristics from Experimental Testing. In Proceedings of the European Wave & Tidal Energy Conference, Cork, Ireland, 27 August 2017. [Google Scholar]
- Forbush, D.; Polagye, B.; Thomson, J.; Kilcher, L.; Donegan, J.; McEntee, J. Performance characterization of a cross-flow hydrokinetic turbine in sheared inflow. Int. J. Mar. Energy 2016, 16, 150–161. [Google Scholar] [CrossRef]
- Blackmore, T.; Myers, L.E.; Bahaj, A.S. Effects of turbulence on tidal turbines: Implications to performance, blade loads, and condition monitoring. Int. J. Mar. Energy 2016, 14, 1–26. [Google Scholar] [CrossRef]
- European Commission Technology readiness levels (TRL). Horizon 2020 General Annexes; European Commission: Brussels, Belgium, 2015; p. 4995. [Google Scholar]
- Mason-Jones, A.; O’Doherty, D.M.; Morris, C.E.; O’Doherty, T. Influence of a velocity profile & support structure on tidal stream turbine performance. Renew. Energy 2013, 52, 23–30. [Google Scholar] [CrossRef]
- Payne, G.S.; Stallard, T.; Martinez, R. Design and manufacture of a bed supported tidal turbine model for blade and shaft load measurement in turbulent flow and waves. Renew. Energy 2017, 107, 312–326. [Google Scholar] [CrossRef]
- Harrold, M.J. Experimental and Numerical Assessment of a Tidal Turbine Control Strategy, University of Strathclyde, 2016. Available online: http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.723008 (accessed on 20 January 2018).
- Allmark, M.; Grosvenor, R.; Prickett, P. An approach to the characterisation of the performance of a tidal stream turbine. Renew. Energy 2017, 111, 849–860. [Google Scholar] [CrossRef]
- Schlipf, D.; Pao, L.Y.; Cheng, P.W. Comparison of Feedforward and Model Predictive Control of Wind Turbines Using LIDAR. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3050–3055. [Google Scholar]
- Johnstone, C.M.; McCombes, T.; Bahaj, A.S.; Myers, L.E.; Holmes, B.; Koefoed, J.P.; Bittencourt, C. EquiMar: Development of Best Practices for the Engineering Performance Appraisal of Wwave and Tidal Energy Converters. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011. [Google Scholar]
- IEC/TS 62600-200 Power Performance Assessment of Electricity Producing Tidal Energy Converters Commissioned by: IEC. 2011. Available online: https://webstore.iec.ch/publication/7242 (accessed on 20 January 2018).
- Clark, T.; Black, K.; Ibrahim, J.; Minns, N.; Fisher, S.; Roc, T.; Hernon, J.; White, R. MRCF-TiME-KS9b Turbulence: Best Practices for Data Processing, Classification and Characterisation of Turbulent Flows. Ocean Array Systems: Edinburgh, UK. 2015. Available online: http://www.oceanarraysystems.com/publications (accessed on 20 January 2018).
- Shih, H.H.; Payton, C.; Sprenke, J.; Mero, T. Towing Basin Speed Calibration of Acoustic Doppler Current Profiling Instruments. In Joint Conference on Water Resource Engineering and Water Resources Planning and Management 2000; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 1–10. [Google Scholar]
- Oberg, K.; Mueller, D.S. Validation of Streamflow Measurements Made with Acoustic Doppler Current Profilers. J. Hydraul. Eng. 2007, 133, 1421–1432. [Google Scholar] [CrossRef]
- Elsaesser, B.; Torrens-Spence, H.; Schmitt, P.; Kregting, L. Comparison of Four Acoustic Doppler Current Profilers in a High Flow Tidal Environment—Queen’s University Belfast Research Portal—Research Directory & Institutional Repository for QUB. In Proceedings of the 3rd Asian Wave and Tidal Energy Conference, Singapore, 24–28 October 2016. [Google Scholar]
- Pao, L.Y.; Johnson, K.E. Control of Wind Turbines. IEEE Control Syst. 2011, 31, 44–62. [Google Scholar] [CrossRef]
- Bennett, S. The past of pid controllers. Annu. Rev. Control 2001, 25, 43–53. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. J. Dyn. Syst. Meas. Control 1993, 115, 220. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Moments of the distributions of power and products of normal variates. Biometrika 1942, 32, 226–242. [Google Scholar] [CrossRef]
- Doman, D.A.; Murray, R.E.; Pegg, M.J.; Gracie, K.; Johnstone, C.M.; Nevalainen, T. Tow-tank testing of a 1/20th scale horizontal axis tidal turbine with uncertainty analysis. Int. J. Mar. Energy 2015, 11, 105–119. [Google Scholar] [CrossRef]

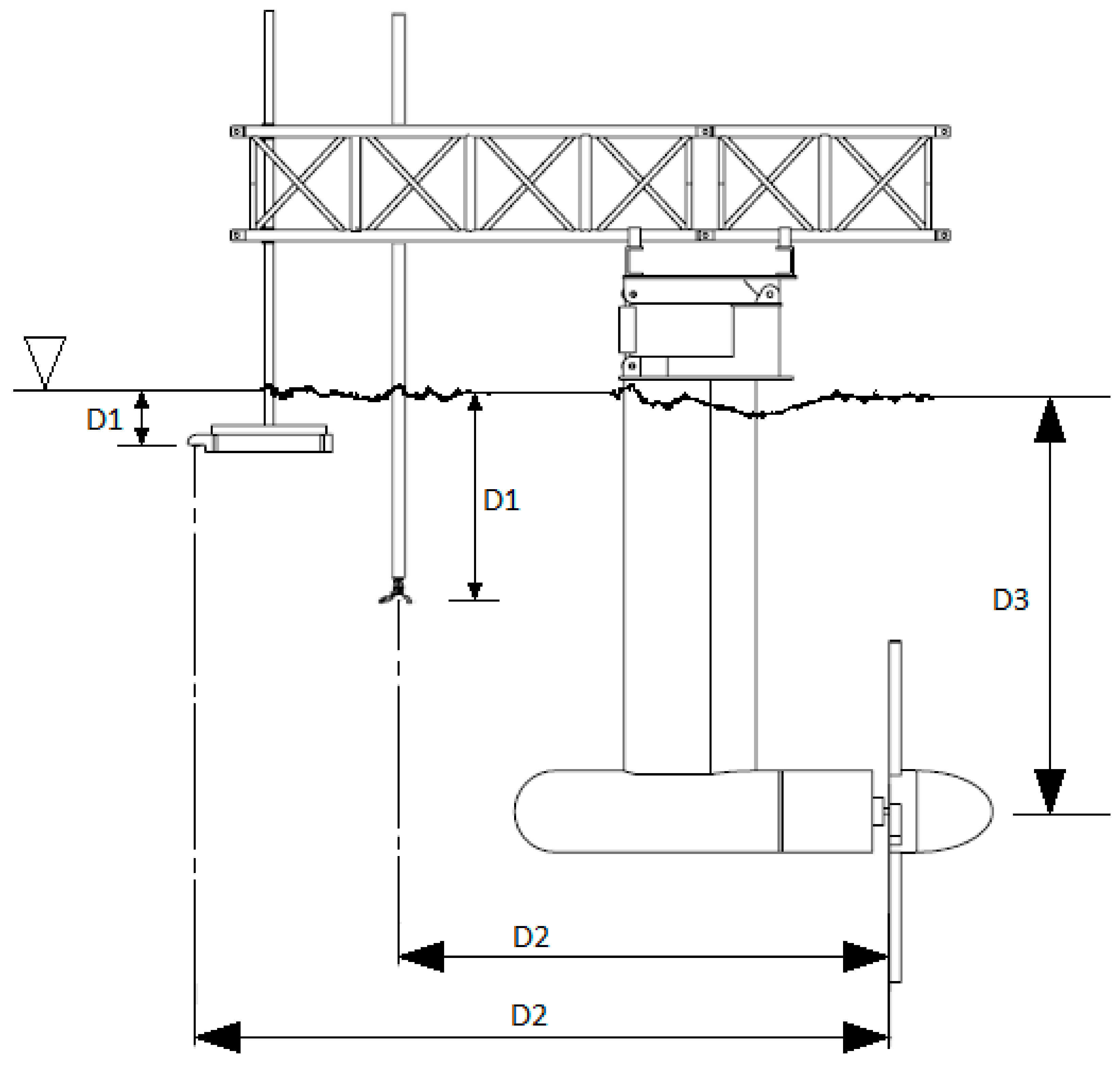
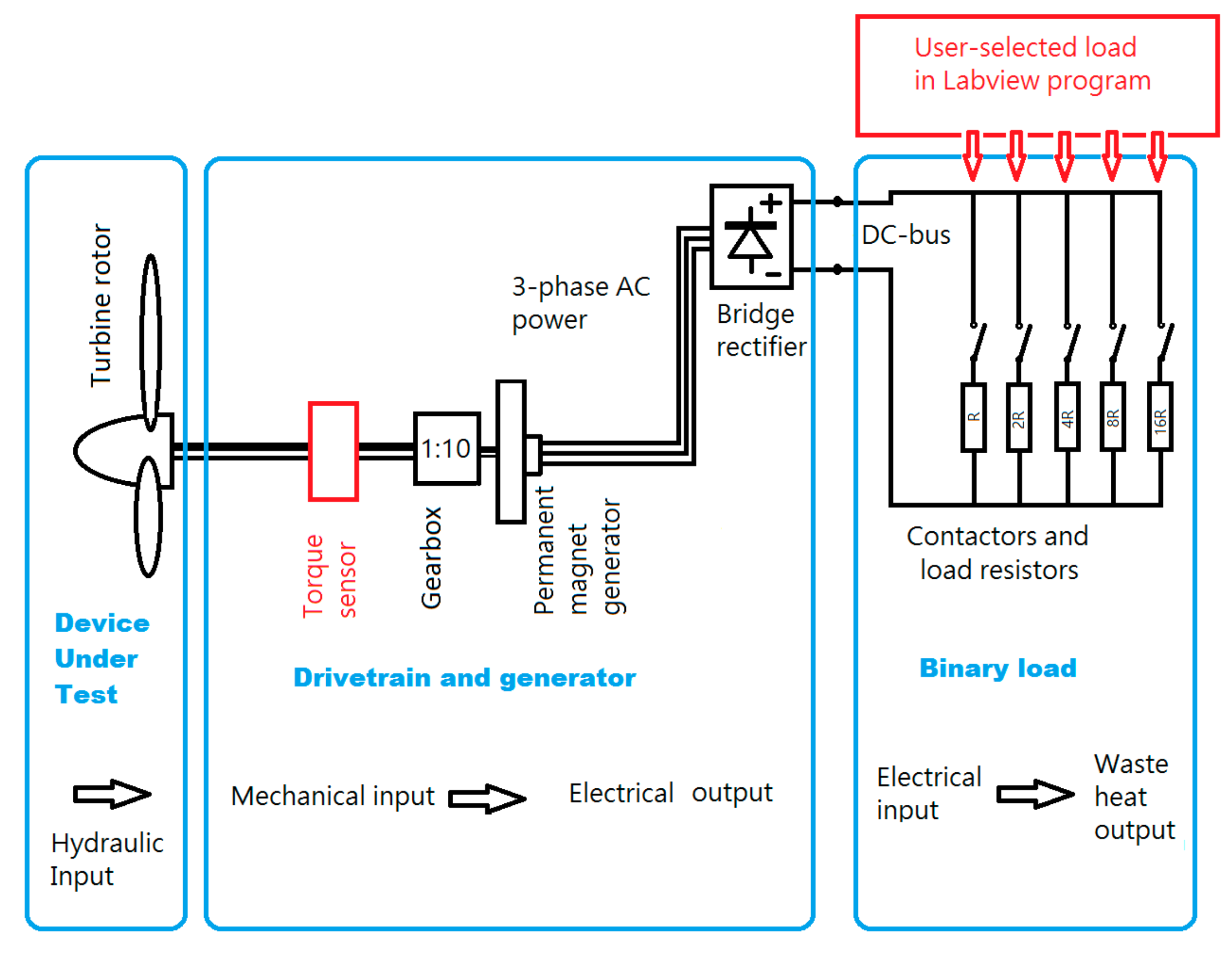
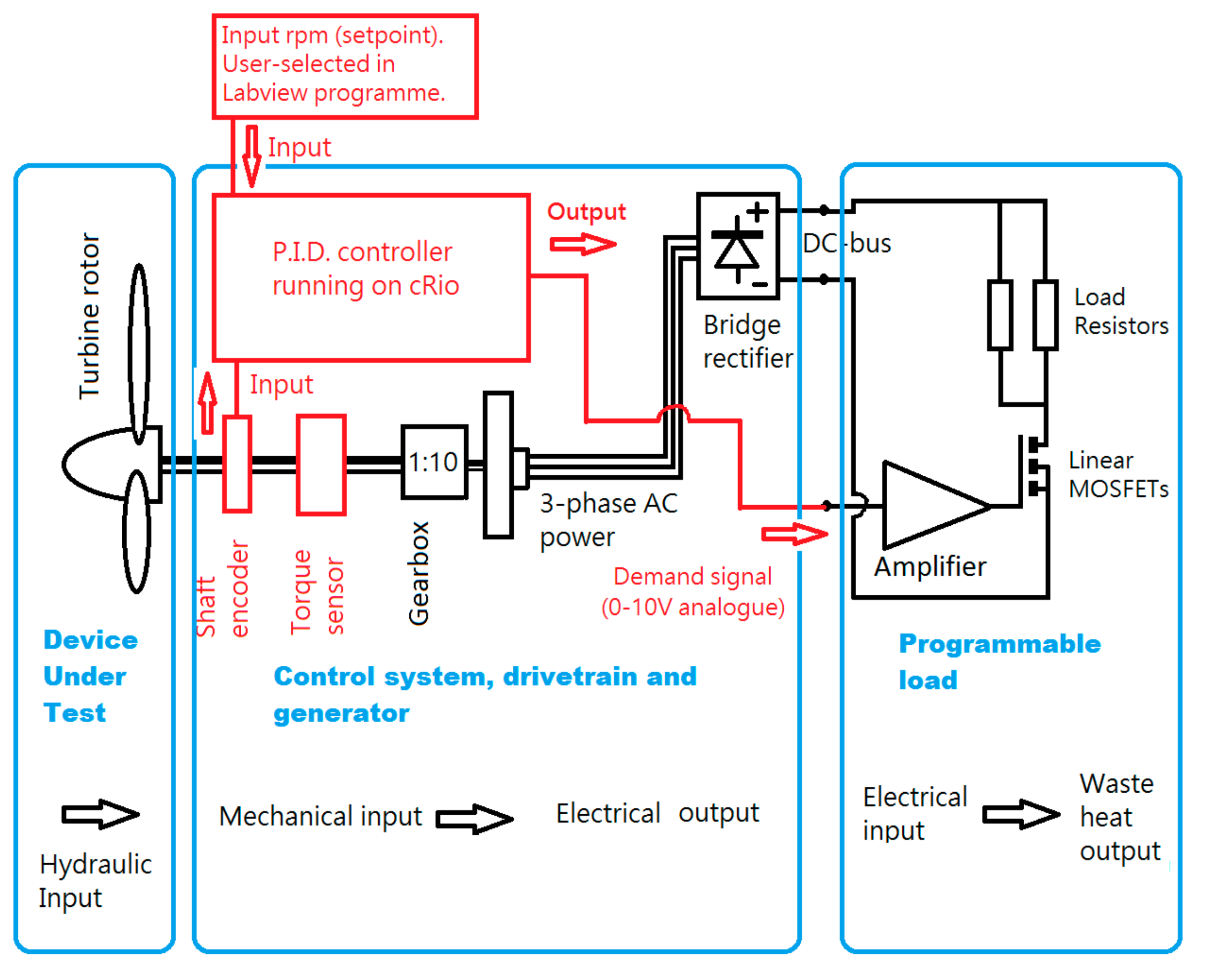
| Project | Date | Experiment Description | Publications |
|---|---|---|---|
| TTT | 2013–2014 |
| [6,7,8] |
| TTT 2 | 2014–2015 |
| [9,10,11,12] |
| TTT 3 | 2015–2017 |
| [13] |
| Parameter | ADP | ADV | ||
|---|---|---|---|---|
| Strangford | CNR-INSEAN | Strangford | CNR-INSEAN | |
| Distance D1 (m) | 0.30 m | 0.30 m | 0.86 m | 0.86 m |
| Distance D2 (m) | 2.99 m | 3.80 m | 3.10 m | 3.7 m |
| Distance D3 (m) | 1.75 m | 1.75 m | 1.75 m | 1.75 m |
| Power | high | high | high | high |
| Transmit length | N/A | N/A | 8 mm | 8 mm |
| Number of cells | 20 | 20 | N/A | N/A |
| Cell Size (m) | 0.25 m | 0.25 m | N/A | N/A |
| Blanking Distance (m) | 0.25 m | 0.25 m | N/A | N/A |
| Co-ordinate System | Beam | Beam | Beam | Beam |
| Sample Frequency (Hz) | 1 Hz | 1 Hz | 16 Hz | 16 Hz |
| Sample Period (s) | 120–600 s | 90–140 s | 120–600 s | 90–140 s |
| Nortek Transform Matrix Output | ADP—Aquadopp | ADV—Vector |
|---|---|---|
| x | U = −1.0124x + 4.97 | U = −1.0042x + 6.4 |
| y | V = −1.0124y + 0 | V = +1.0042y + 0 |
| z | W = −1.0124z + 0 | W = −1.0042z + 0 |
| Bias in U (1 σ) | −0.03% | +0.05% |
| Precision in U (1 σ) | ±0.6% | ±0.9% |
| Symbol | Description | Value |
|---|---|---|
| Kc | Proportional constant | 2.2 (no dimensions) |
| Ti | Integration time constant | 0.003 (min) |
| Td | Differential time constant | 0.001 (min) |
| Velocity Bin (ms−1) | Mean Current Velocity, () | Mean Power Output, () | Mean SD of Power Output, () | Number of Data Sets, n |
|---|---|---|---|---|
| 0.65–0.75 | 0.720 | 37.972 | 7.088 | 3 |
| 0.75–0.85 | 0.802 | 100.929 | 45.999 | 6 |
| 0.85–0.95 | 0.922 | 113.202 | 59.554 | 4 |
| 0.95–1.05 | 1.012 | 193.498 | 94.951 | 13 |
| 1.05–1.15 | 1.100 | 215.158 | 91.195 | 16 |
| 1.15–1.25 | 1.183 | 264.867 | 78.834 | 8 |
| 1.25–1.35 | 1.254 | 83.518 | 15.557 | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frost, C.; Benson, I.; Jeffcoate, P.; Elsäßer, B.; Whittaker, T. The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments. Energies 2018, 11, 1533. https://doi.org/10.3390/en11061533
Frost C, Benson I, Jeffcoate P, Elsäßer B, Whittaker T. The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments. Energies. 2018; 11(6):1533. https://doi.org/10.3390/en11061533
Chicago/Turabian StyleFrost, Carwyn, Ian Benson, Penny Jeffcoate, Björn Elsäßer, and Trevor Whittaker. 2018. "The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments" Energies 11, no. 6: 1533. https://doi.org/10.3390/en11061533
APA StyleFrost, C., Benson, I., Jeffcoate, P., Elsäßer, B., & Whittaker, T. (2018). The Effect of Control Strategy on Tidal Stream Turbine Performance in Laboratory and Field Experiments. Energies, 11(6), 1533. https://doi.org/10.3390/en11061533






