Boundary Conditions Accuracy Effect on the Numerical Simulations of the Thermal Performance of Building Elements
Abstract
1. Introduction
2. Theoretical Background
2.1. Boundary Conditions in Standardized Methods
2.2. Boundary Condition Common Practices in the Literature
3. Methodology
3.1. Numerical Simulation
- a solar exposed vertical building element in sunny spring conditions (ESS);
- a solar non-exposed vertical building element in sunny spring conditions (NESS); and
- a solar exposed vertical building element in sunny winter conditions (ESW).
3.2. Temperature Reconstruction Algorithm Using Elementary Signals
- A set of elementary signals were discretized using the sampling period of the measurement vector P and defined similarly to Equation (5) as:where and .Moreover , , and , are discrete sets from which the parameter values were selected.
- The residue measurement vector was set to be the original measurement vector as for . The best matching elementary signal in Equation (6) for was determined by identifying the maximum inner product between each elementary signal and the measured data points, where the inner product was given by:and the best set of parameters was selected using Equation (7) as:with amplitude scaling:for .
- The selected discretized elementary signal was constructed as in Equation (6):
- The residue was calculated as:and the discretised function that models the data was constructed using Equations (7) and (8) as:
- The root mean squared error (RMSE) was calculated as:
- Index j was increased by 1 and the process continued until the maximum number of iterations Jmax was reached or when the RMSE representing the data dropped below a threshold defined by .
- When the process was completed then as in Equations (4) and (5) were set.
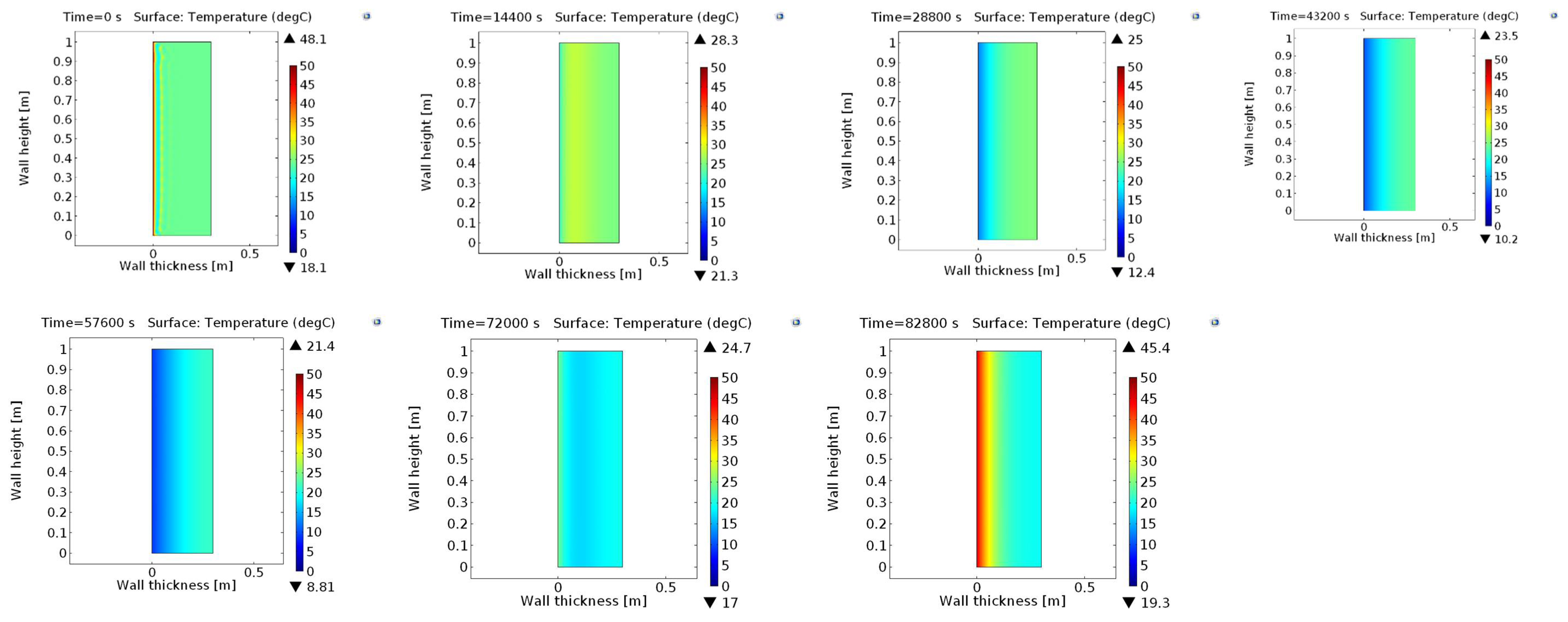
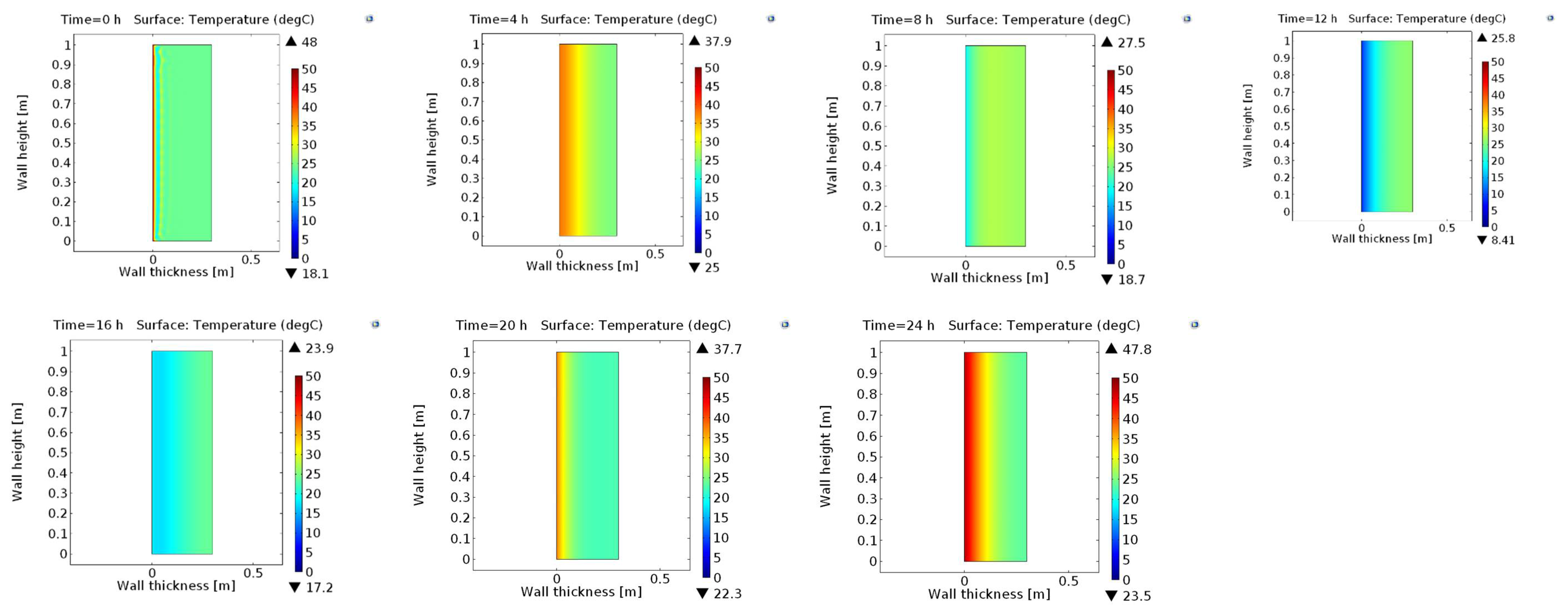
4. Numerical Simulation Results and Discussion
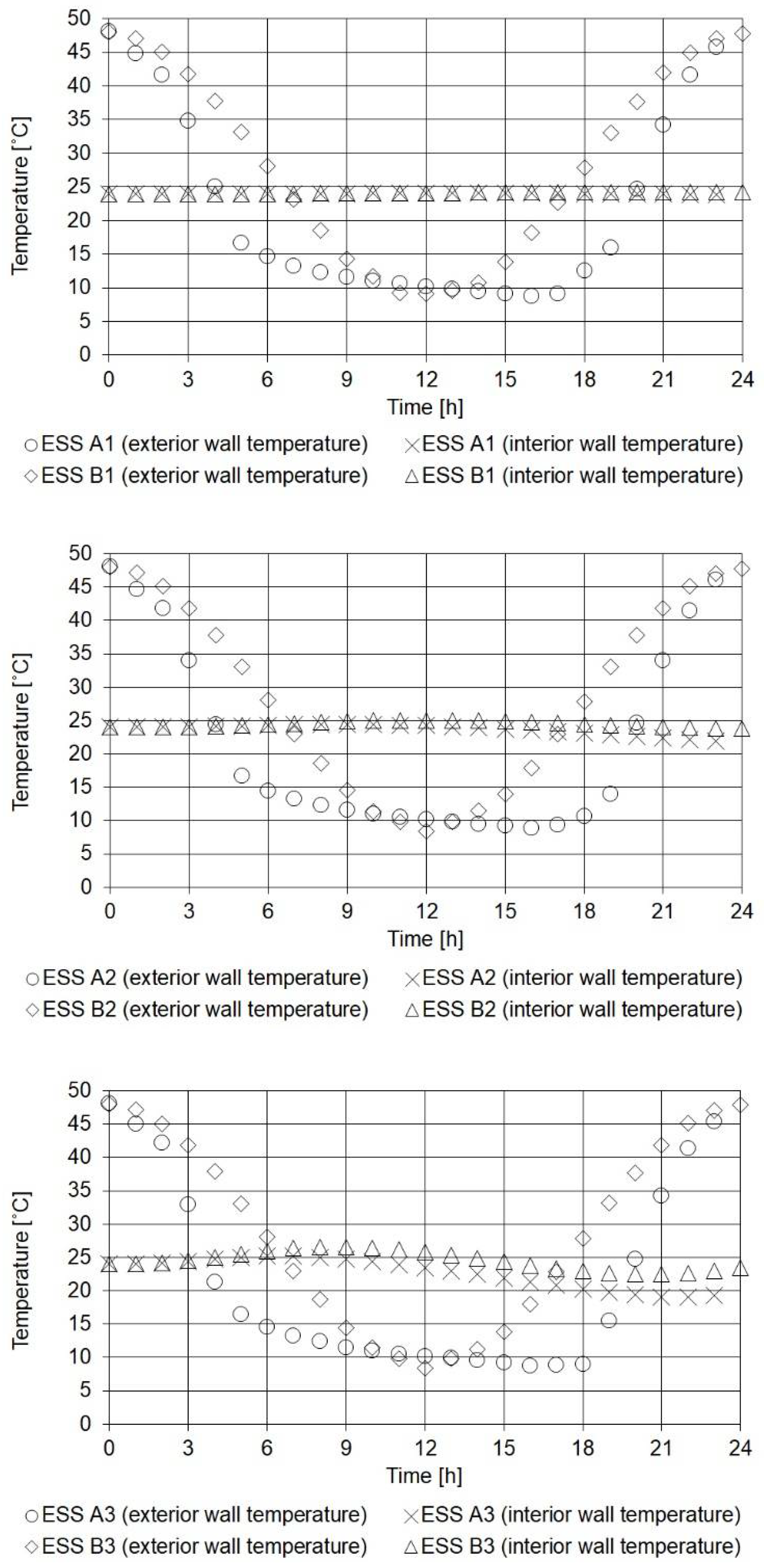
4.1. Exposed Wall in Sunny Spring Conditions (ESS)
4.2. Exposed Wall in Sunny Spring Conditions (ESS)
4.3. Non-Exposed Wall in Sunny Spring Conditions (NESS)
4.4. Exposed Wall in Sunny Winter Conditions (ESW)
4.5. Heat Flux of Building Walls Under Investigation
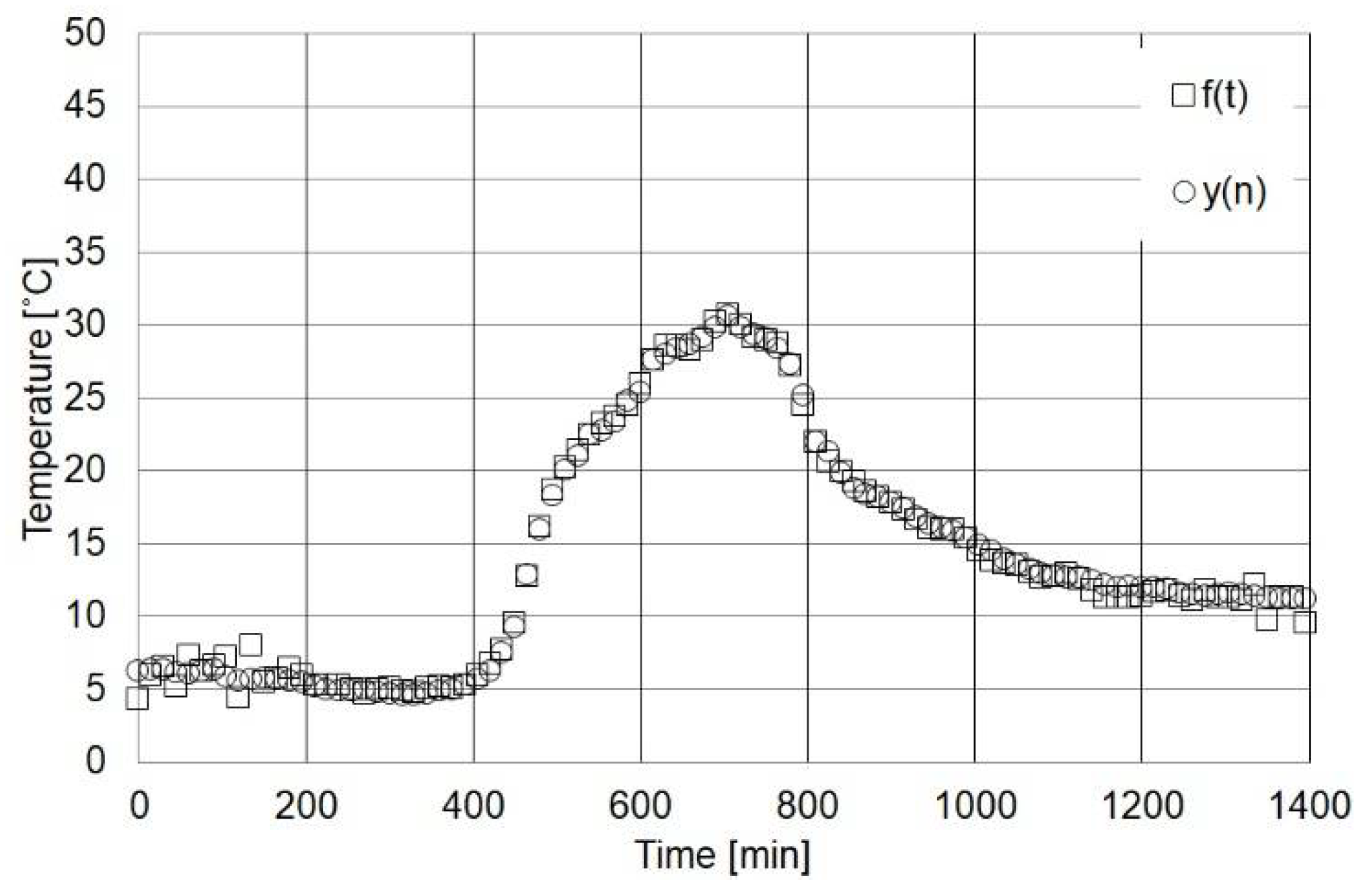
5. Function Modeling from Measured Data
- an exposed wall in sunny spring conditions (ESS);
- a non-exposed wall in sunny spring conditions (NESS); and
- an exposed wall in sunny winter conditions (ESW)
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| ESS | Exposed wall in Sunny Spring conditions |
| ESW | Exposed wall in Sunny Winter conditions |
| HVAC | Heating Ventilating and Air-Conditioning |
| NESS | Non-Exposed wall in Sunny Spring conditions |
| Symbols | |
| Heat Capacity at constant pressure (J/kg K) | |
| E | Root Mean Squared Error (°C) |
| f | Function |
| j | Unit on the imaginary axis for a complex number; |
| Thermal Conductivity (W/m K) | |
| N | Number of data (–) |
| Q | Heat flux (W) |
| r | Residue vector (°C) |
| P | Sampling period (s) |
| P’ | Duration of elementary signal (s) |
| s | Elementary signal |
| T | Temperature (°C) |
| t | Time (s) |
| Velocity (m/s) | |
| y | Temperature data vector (°C) |
| Greek Letter | |
| α | Time scale (1/s2) |
| e | Element |
| μ | Amplitude scale (unitless) |
| v | Frequency shift (Hz) |
| ξ | Signal |
| Density (kg/m3) | |
| τ | Time shift (s) |
| ψ | Phase difference (rad) |
| ω | Angular frequency (rad/s) |
| Other Symbols | |
 | Mean value |
 | Complex amplitude |
| arg | Argument of a complex number |
| max | Maximum value |
| Subscript | |
| n | For the thermal zone |
Appendix A
| Time (s) | Recorded Temperature on Building’s Exterior Wall Surface (°C) | ||
|---|---|---|---|
| Solar Exposed Wall in Sunny Spring Conditions (ESS) | Solar Non-Exposed Wall in Sunny Spring Conditions (NESS) | Solar Exposed in Sunny Winter Conditions (ESW) | |
| 0 | 8.35 | 13.98 | 6.29 |
| 60 | 10.37 | 12.77 | 6.10 |
| 120 | 20.17 | 12.37 | 5.62 |
| 180 | 29.51 | 12.42 | 5.58 |
| 240 | 39.52 | 11.47 | 4.86 |
| 300 | 44.38 | 11.21 | 4.72 |
| 360 | 47.35 | 12.11 | 4.86 |
| 420 | 46.60 | 16.51 | 6.29 |
| 480 | 44.53 | 18.90 | 15.92 |
| 540 | 39.72 | 21.73 | 22.44 |
| 600 | 28.21 | 27.51 | 25.38 |
| 660 | 17.92 | 32.01 | 28.68 |
| 720 | 15.20 | 34.13 | 29.84 |
| 780 | 14.09 | 36.06 | 27.28 |
| 840 | 12.70 | 34.12 | 19.80 |
| 900 | 11.59 | 28.88 | 17.80 |
| 960 | 11.22 | 25.97 | 16.03 |
| 1020 | 10.86 | 22.88 | 14.52 |
| 1080 | 10.39 | 19.99 | 12.98 |
| 1140 | 9.94 | 18.10 | 12.45 |
| 1200 | 9.80 | 17.02 | 11.98 |
| 1260 | 9.24 | 16.23 | 11.50 |
| 1320 | 8.99 | 15.73 | 11.54 |
| 1380 | 8.72 | 15.35 | 11.25 |
| 1440 | 8.52 | 15.02 | 11.19 |
References
- 13790:2008. Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling; ISO: Geneva, Switzerland, 2008.
- Fokaides, P.A.; Maxoulis, C.N.; Panayiotou, G.P.; Neophytou, M.K.A.; Kalogirou, S.A. Comparison between measured and calculated energy performance for dwellings in a summer dominant environment. Energy Build. 2011, 43, 3099–3105. [Google Scholar] [CrossRef]
- Kylili, A.; Fokaides, P.A. Numerical simulation of phase change materials for building applications: A review. Adv. Build. Energy Res. 2015, 11, 1–25. [Google Scholar] [CrossRef]
- 13786:2007. Thermal Performance of Building Components—Dynamic Thermal Characteristics—Calculation Methods; ISO: Geneva, Switzerland, 2007.
- Kontoleon, K.J.; Eumorfopoulou, E.A. The influence of wall orientation and exterior surface solar absorptivity on time lag and decrement factor in the Greek region. Renew. Energy 2008, 33, 1652–1664. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Wachenfeldt, B.J. Numerical study on the heat storing capacity of concrete walls with air cavities. Energy Build. 2009, 41, 769–773. [Google Scholar] [CrossRef]
- Viot, H.; Sempey, A.; Pauly, M.; Mora, L. Comparison of different methods for calculating thermal bridges: Application to wood-frame buildings. Build. Environ. 2015, 93, 339–348. [Google Scholar] [CrossRef]
- Yang, J.; Yu, J.; Xiong, C. Heat Transfer Analysis of Hollow Block Ventilated Wall Based on CFD Modeling. Procedia Eng. 2015, 121, 1312–1317. [Google Scholar] [CrossRef]
- Tariku, F.; Kumaran, K.; Fazio, P. Integrated analysis of whole building heat, air and moisture transfer. Int. J. Heat Mass Transf. 2010, 53, 3111–3120. [Google Scholar] [CrossRef]
- Abahri, K.; Belarbi, R.; Trabelsi, A. Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials. Build. Environ. 2011, 46, 1354–1360. [Google Scholar] [CrossRef]
- Kontoleon, K.J. Dynamic thermal circuit modelling with distribution of internal solar radiation on varying façade orientations. Energy Build. 2012, 47, 139–150. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Ge, H.; Fazio, P.; Chen, G.; Guo, X. Determination of optimum insulation thickness for building walls with moisture transfer in hot summer and cold winter zone of China. Energy Build. 2015, 109, 361–368. [Google Scholar] [CrossRef]
- Mazzeo, D.; Oliveti, G.; Arcuri, N. Multiple Bi-phase Interfaces in a PCM Layer Subject to Periodic Boundary Conditions Characteristic of Building External Walls. Energy Procedia 2015, 82, 472–479. [Google Scholar] [CrossRef]
- Fokaides, P.A.; Christoforou, E.A.; Kalogirou, S.A. Legislation driven scenarios based on recent construction advancements towards the achievement of nearly zero energy dwellings in the southern European country of Cyprus. Energy 2014, 66, 588–597. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Kylili, A.; Fokaides, P.A. European smart cities: The role of zero energy buildings. Sustain. Cities Soc. 2015, 15, 86–95. [Google Scholar] [CrossRef]
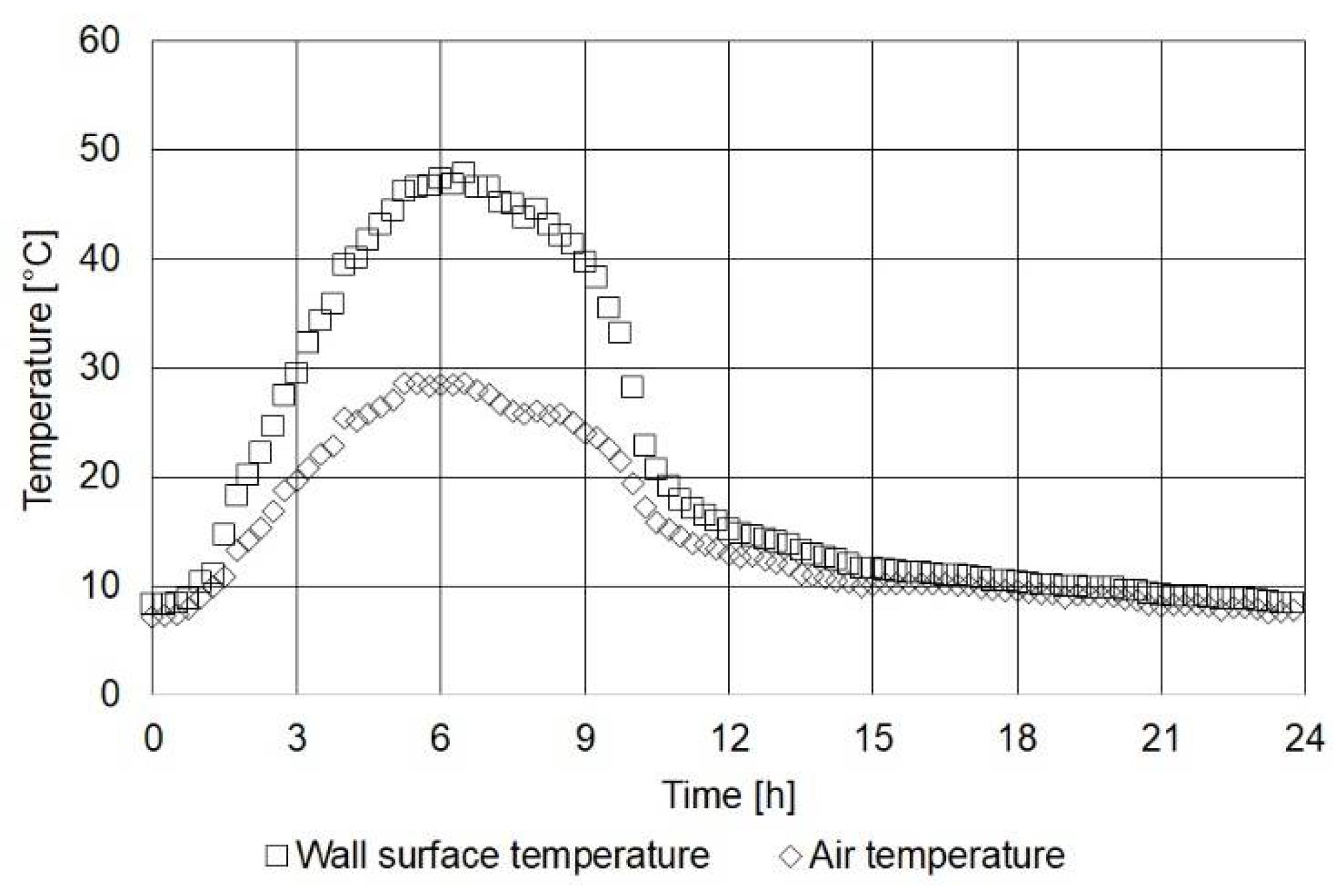
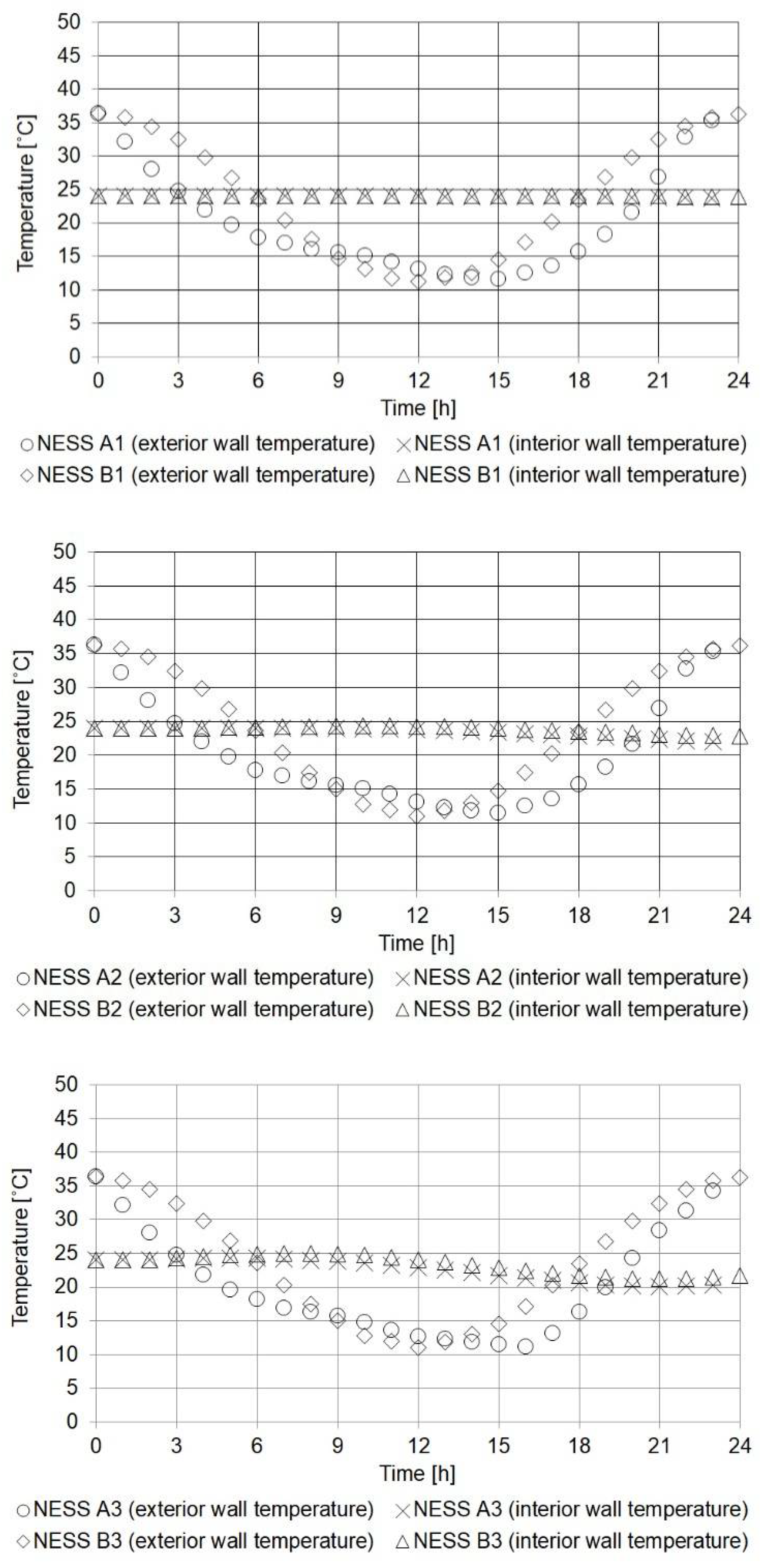
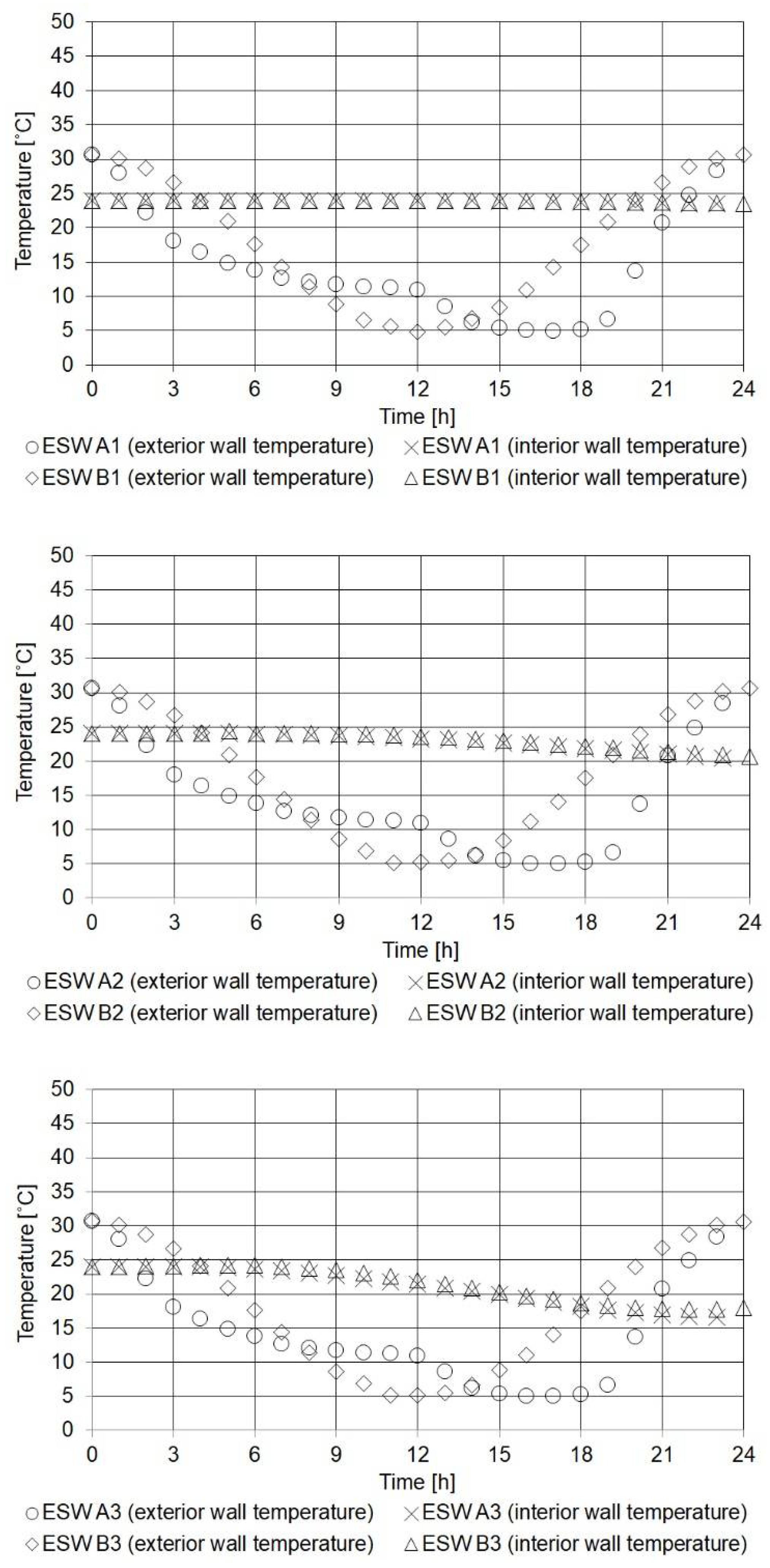
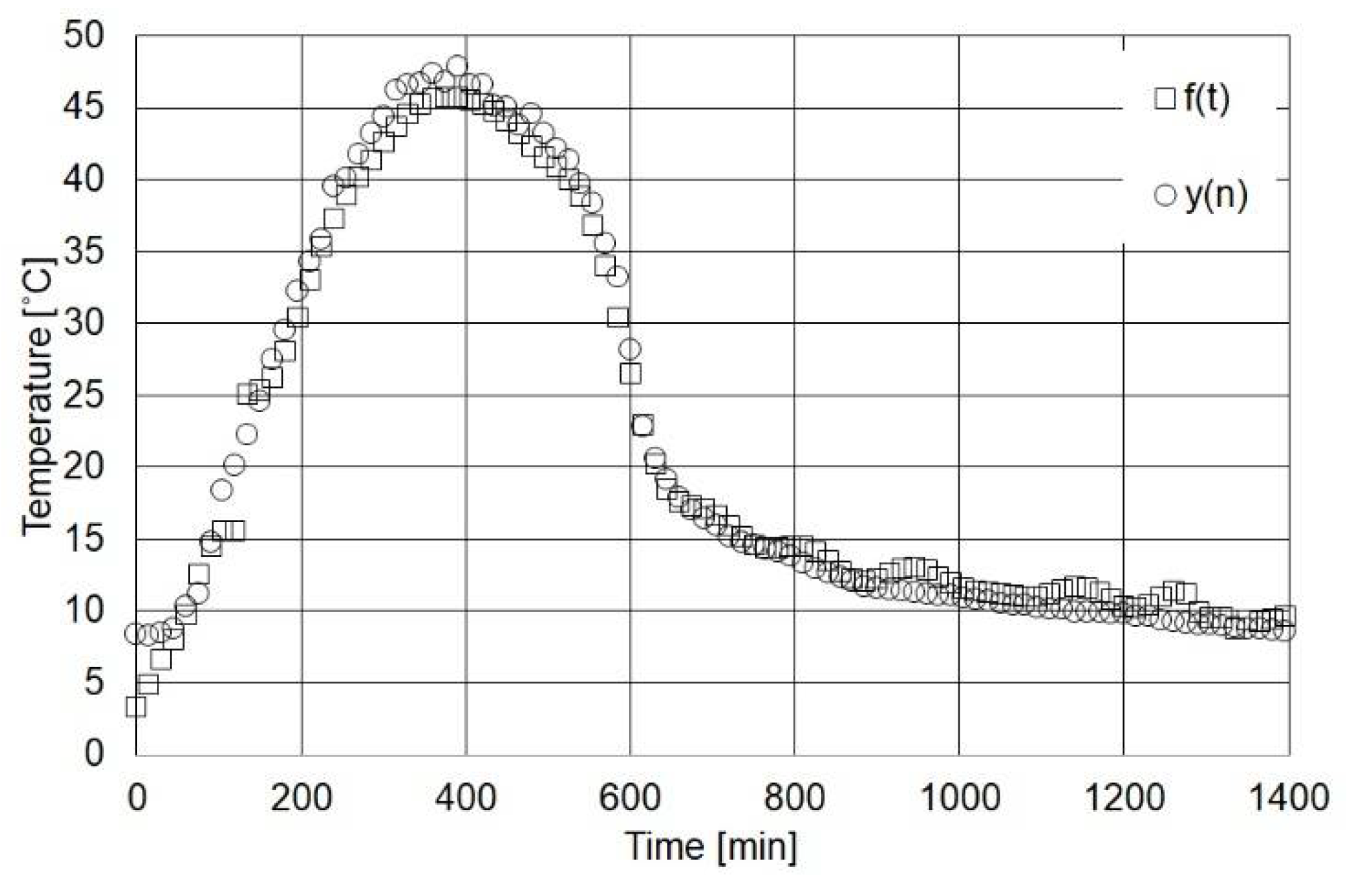
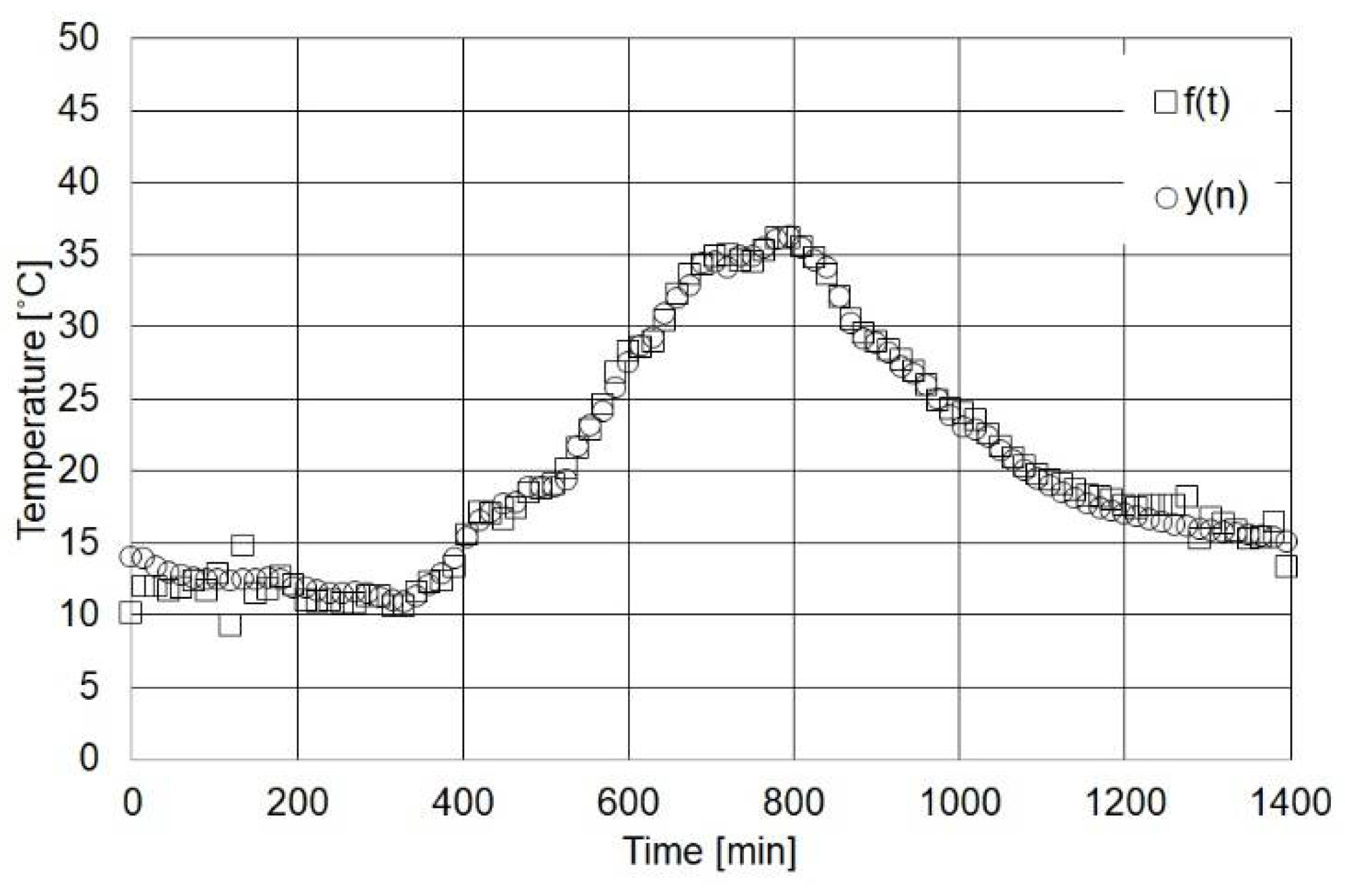
| Work | Title | Tin (°C) | Tint (°C) | Text (°C) | hint (W/m2 K) | hext (W/m2 K) | α | ε |
|---|---|---|---|---|---|---|---|---|
| Kontoleon and Eumorfopoulou (2008) [5] | The influence of wall orientation and exterior surface solar absorptivity on time lag and decrement factor in the Greek region | - | 24 | 22–30 sinusoidal | - | - | - | - |
| Zhang and Wachenfeldt (2009) [6] | Numerical study on the heat storing capacity of concrete walls with air cavities | 20 | - | 20–30 sinusoidal | 8 | - | - | - |
| Tariku et al. (2010) [9] | Integrated analysis of whole building heat, air and moisture transfer | - | 20–27 | real weather conditions | 8.3 | 29.3 | 0.6 | 0.9 |
| Abahri et al. (2011) [10] | Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials | 10 | 25 | meteorological data for one year period | - | - | - | - |
| Kontoleon (2012) [11] | Dynamic thermal circuit modelling with distribution of internal solar radiation on varying façade orientations | - | - | daily temperature variation using real data | 8.33 | 16.67 | - | - |
| Liu et al. (2015) [12] | Determination of optimum insulation thickness for building walls with moisture transfer in hot summer and cold winter zone of China | - | 26 (summer); 18 (winter) | typical meteorological year data | 8.72 | 23.26 | - | - |
| Mazzeo et al. (2015) [13] | Multiple bi-phase interfaces in a PCM layer subject to periodic boundary conditions characteristic of building external walls | - | 26 (summer); 20 (winter); 23 (spring) | meteorological data based on average monthly days | 7.7 | 20 | 0.6 | - |
| Viot et al. (2015) [6] | Comparison of different methods for calculating thermal bridges: Application to wood-frame buildings | - | 20 | 10–30 sinusoidal | - | - | - | - |
| Yang et al. (2015) [8] | Heat transfer analysis of hollow block ventilated wall based on CFD modeling | - | 26 | 28–46 sinusoidal | 8.6 | 18.3 | - | - |
| ● For j = 1,…,Jmax |
| –With , , |
| –Let {} = |
| –Let = |
| –Calculate residue as |
| –Let reconstructed function as |
| –Calculate RMSE as |
| –If < Eth then let J = j , break loop |
| ● Let reconstructed signal |
| ● Let final RMSE error E = |
| Simulation Building Wall Model | Total Heat Flux, Q (W/m2) | Deviation of Model B from Model A (%) |
|---|---|---|
| ESS A1 | 206.91 | - |
| ESS A2 | 529.34 | |
| ESS A3 | 1066.58 | |
| ESS B1 | 202.80 | 1.99 |
| ESS B2 | 519.84 | 1.79 |
| ESS B3 | 1074.97 | 0.79 |
| NESS A1 | 125.53 | - |
| NESS A2 | 310.50 | |
| NESS A3 | 603.57 | |
| NESS B1 | 127.68 | 1.71 |
| NESS B2 | 325.84 | 4.94 |
| NESS B3 | 675.68 | 11.95 |
| ESW A1 | 175.17 | - |
| ESW A2 | 418.36 | |
| ESW A3 | 766.07 | |
| ESW B1 | 146.70 | 16.25 |
| ESW B2 | 368.77 | 11.86 |
| ESW B3 | 716.78 | 6.43 |
| Simulation Building Wall Model | Material Properties | Boundary Conditions | |
|---|---|---|---|
| Thermal Conductivity, k (W/m K) | Weather Conditions | Exterior Boundary Conditions, Text (°C) | |
| ESS A1 | 0.2 | ESS | 24-h actual surface temperature data (see Appendix A) |
| ESS A2 | 0.5 | ||
| ESS A3 | 1.0 | ||
| ESS B1 | 0.2 | ESS | 28.05 + 19.75 sin [2π (t/24)] |
| ESS B2 | 0.5 | ||
| ESS B3 | 1.0 | ||
| NESS A1 | 0.2 | NESS | 24-h actual surface temperature data (see Appendix A) |
| NESS A2 | 0.5 | ||
| NESS A3 | 1.0 | ||
| NESS B1 | 0.2 | NESS | 23.58 + 12.67 sin [2π (t/24)] |
| NESS B2 | 0.5 | ||
| NESS B3 | 1.0 | ||
| ESW A1 | 0.2 | ESW | 24-h actual surface temperature data (see Appendix A) |
| ESW A2 | 0.5 | ||
| ESW A3 | 1.0 | ||
| ESW B1 | 0.2 | ESW | 17.62 + 12.98 sin [2π (t/24)] |
| ESW B2 | 0.5 | ||
| ESW B3 | 1.0 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fokaides, P.A.; Kylili, A.; Kyriakides, I. Boundary Conditions Accuracy Effect on the Numerical Simulations of the Thermal Performance of Building Elements. Energies 2018, 11, 1520. https://doi.org/10.3390/en11061520
Fokaides PA, Kylili A, Kyriakides I. Boundary Conditions Accuracy Effect on the Numerical Simulations of the Thermal Performance of Building Elements. Energies. 2018; 11(6):1520. https://doi.org/10.3390/en11061520
Chicago/Turabian StyleFokaides, Paris A., Angeliki Kylili, and Ioannis Kyriakides. 2018. "Boundary Conditions Accuracy Effect on the Numerical Simulations of the Thermal Performance of Building Elements" Energies 11, no. 6: 1520. https://doi.org/10.3390/en11061520
APA StyleFokaides, P. A., Kylili, A., & Kyriakides, I. (2018). Boundary Conditions Accuracy Effect on the Numerical Simulations of the Thermal Performance of Building Elements. Energies, 11(6), 1520. https://doi.org/10.3390/en11061520






