Interaction of Wind Turbine Wakes under Various Atmospheric Conditions
Abstract
1. Introduction
2. Methodology
2.1. LES Framework
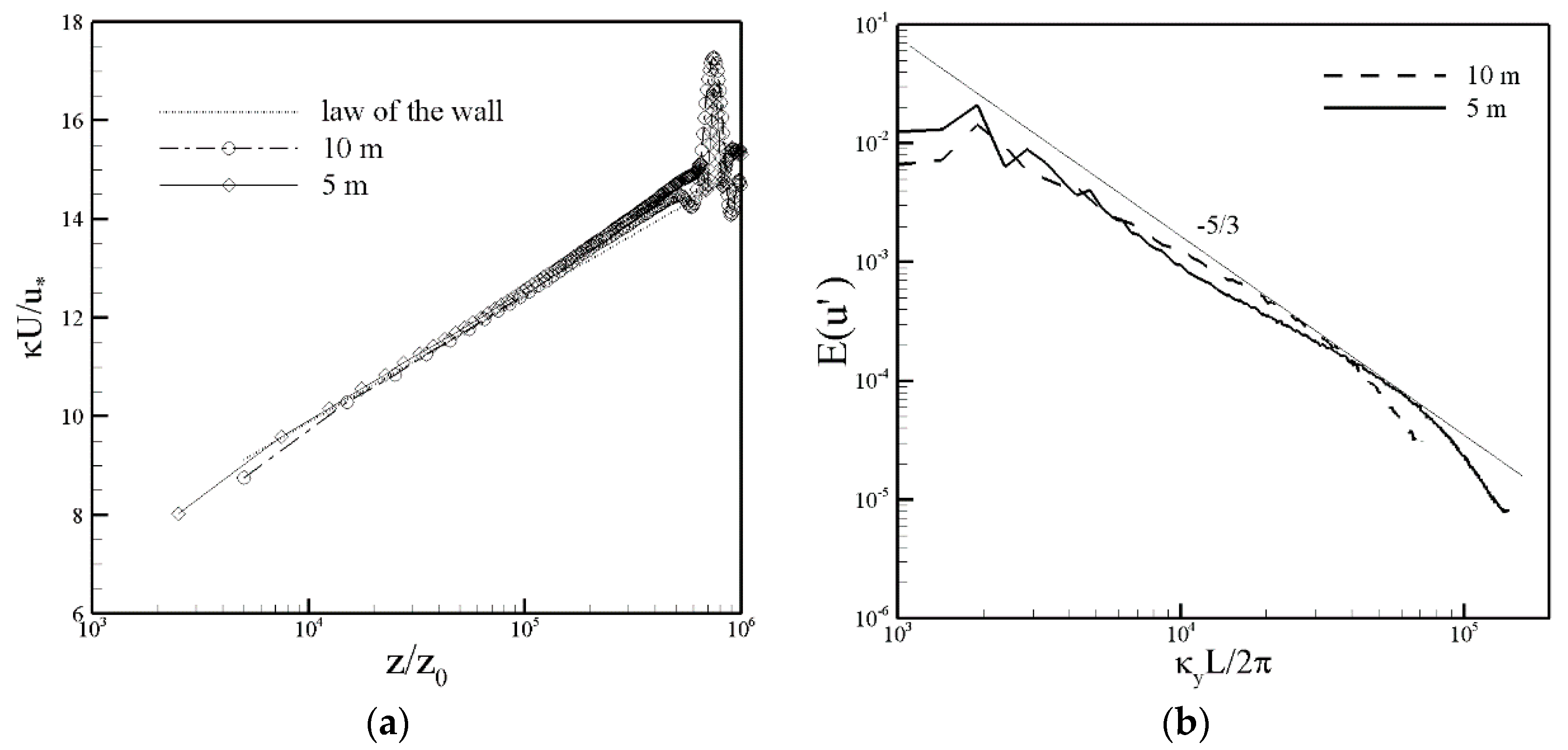
2.2. Atmospheric Boundary Layer
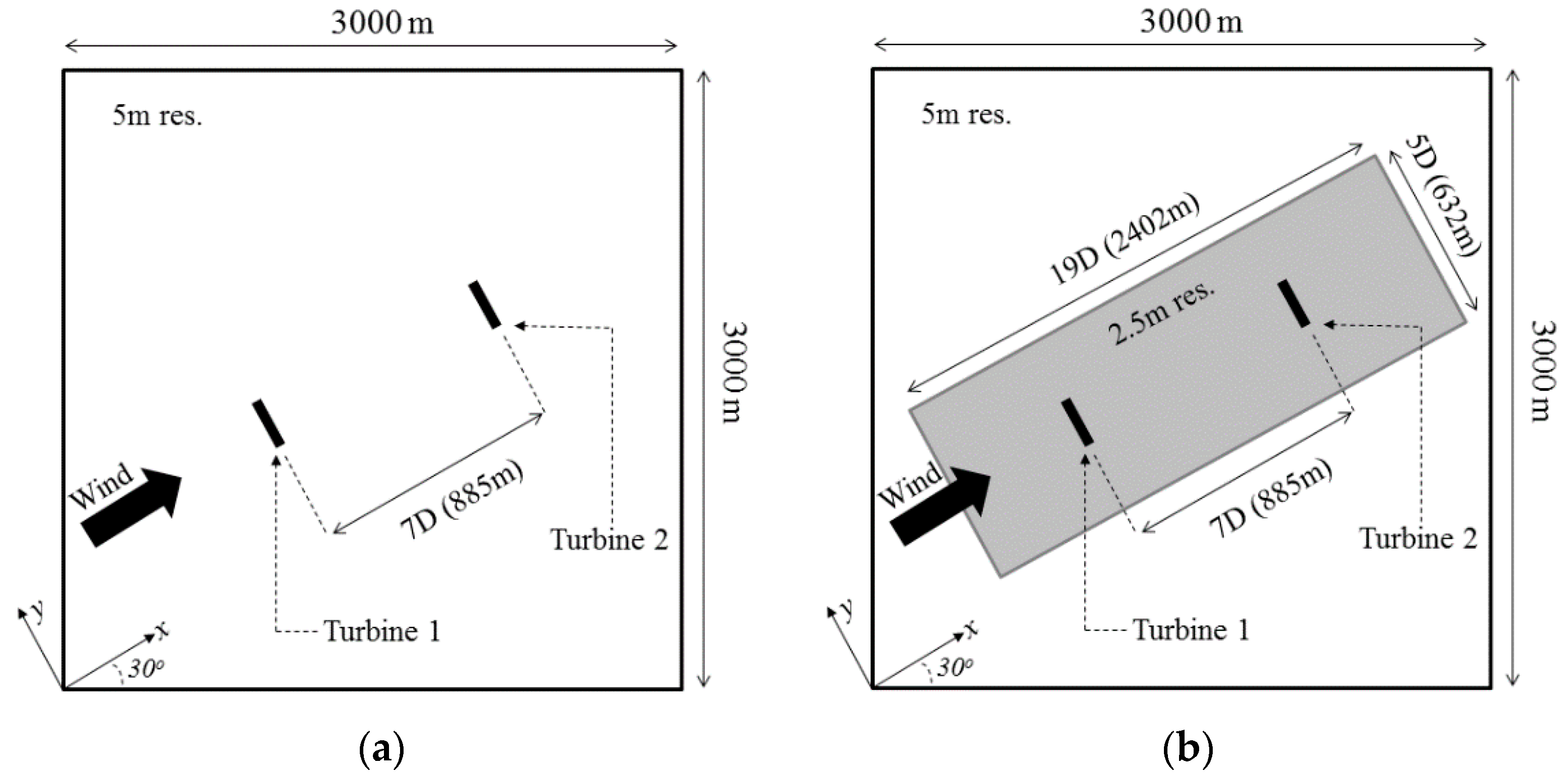
2.3. Computational Domain
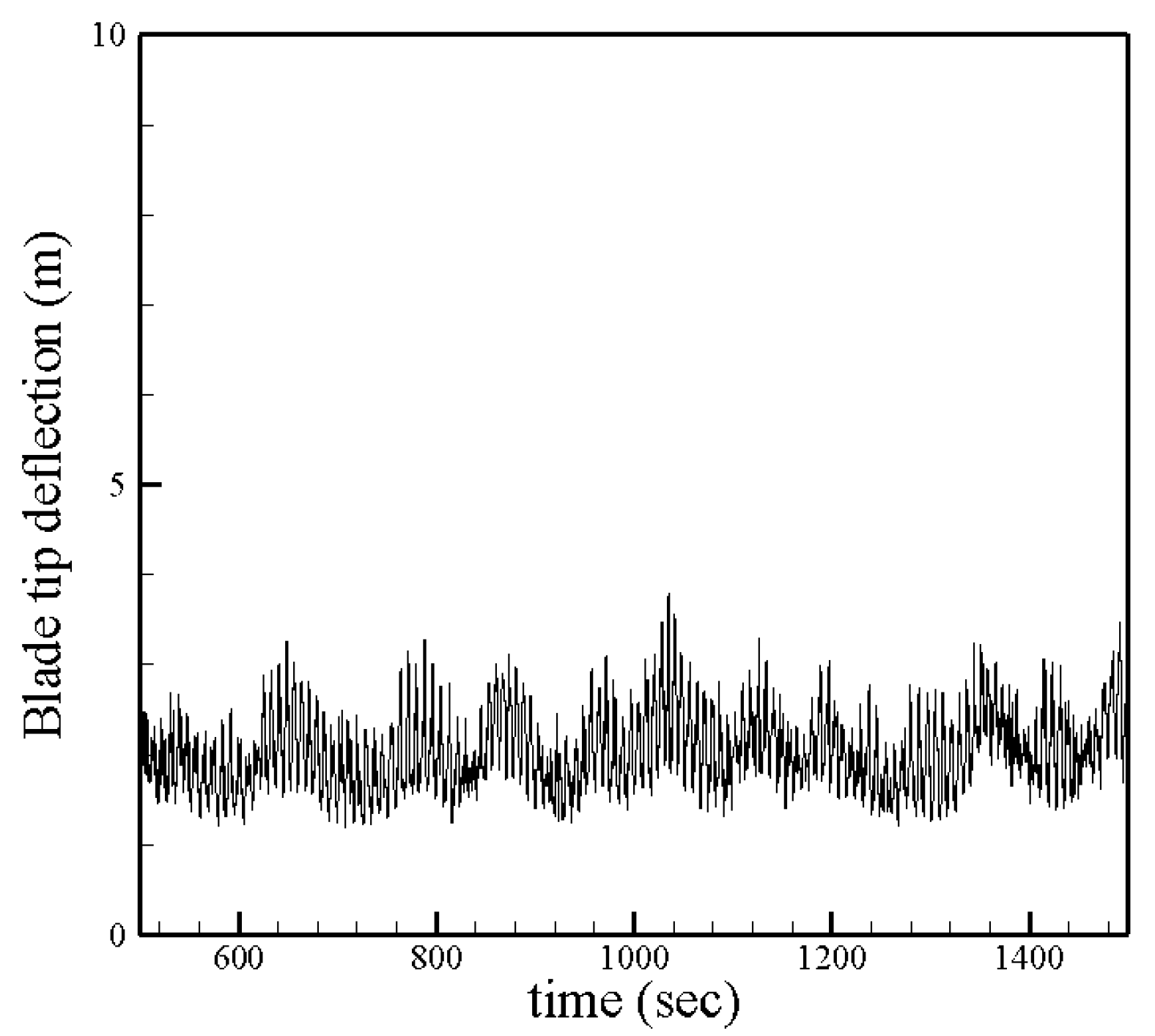
2.4. Wind Turbine Model
3. Results
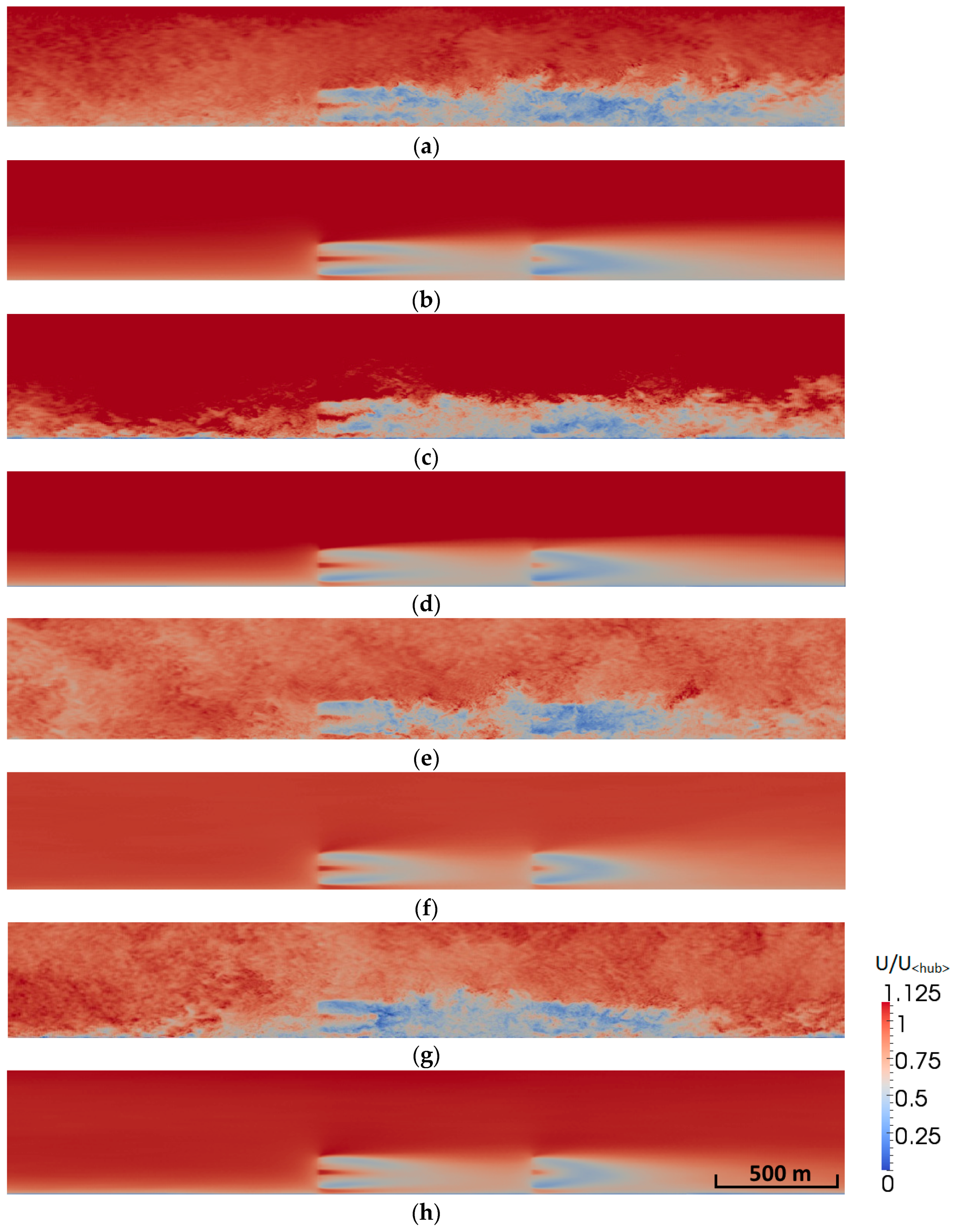
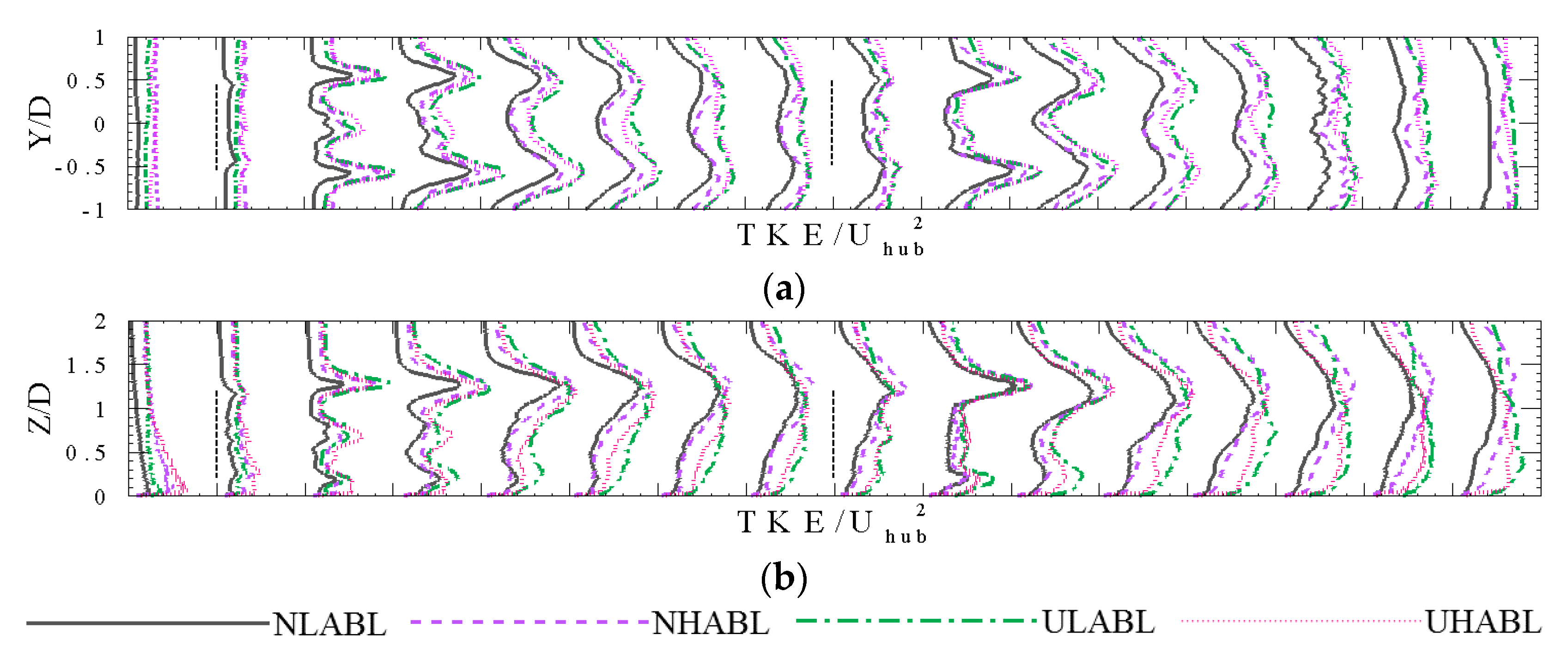
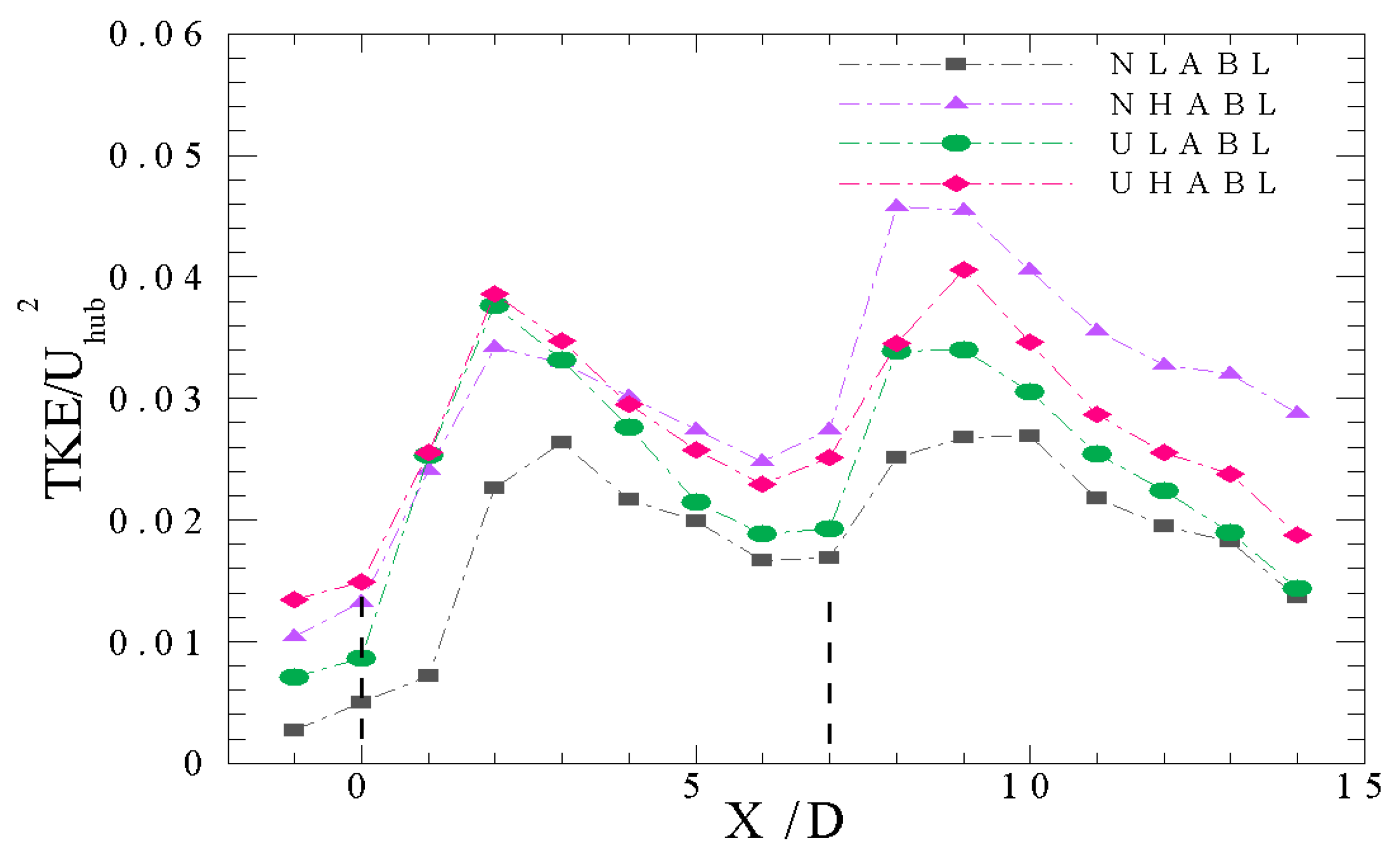
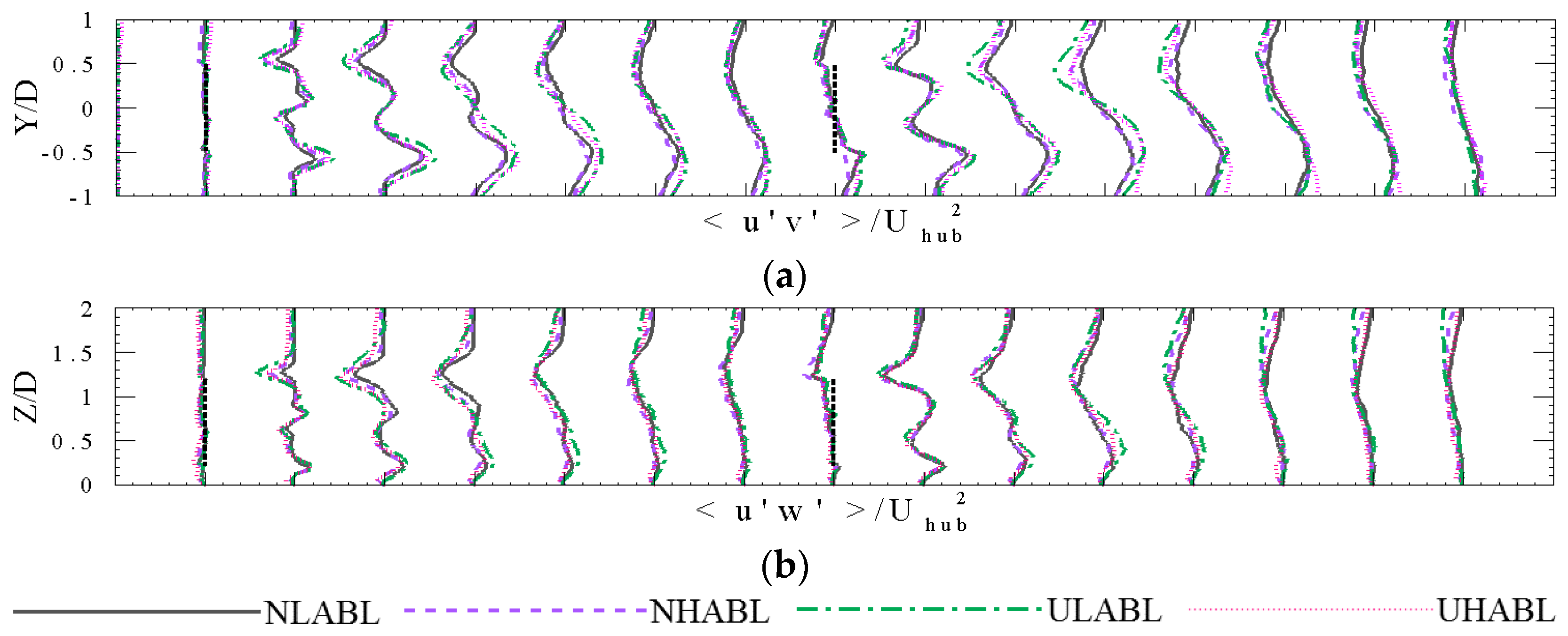
3.1. Velocity and Turbulent Kinetic Energy
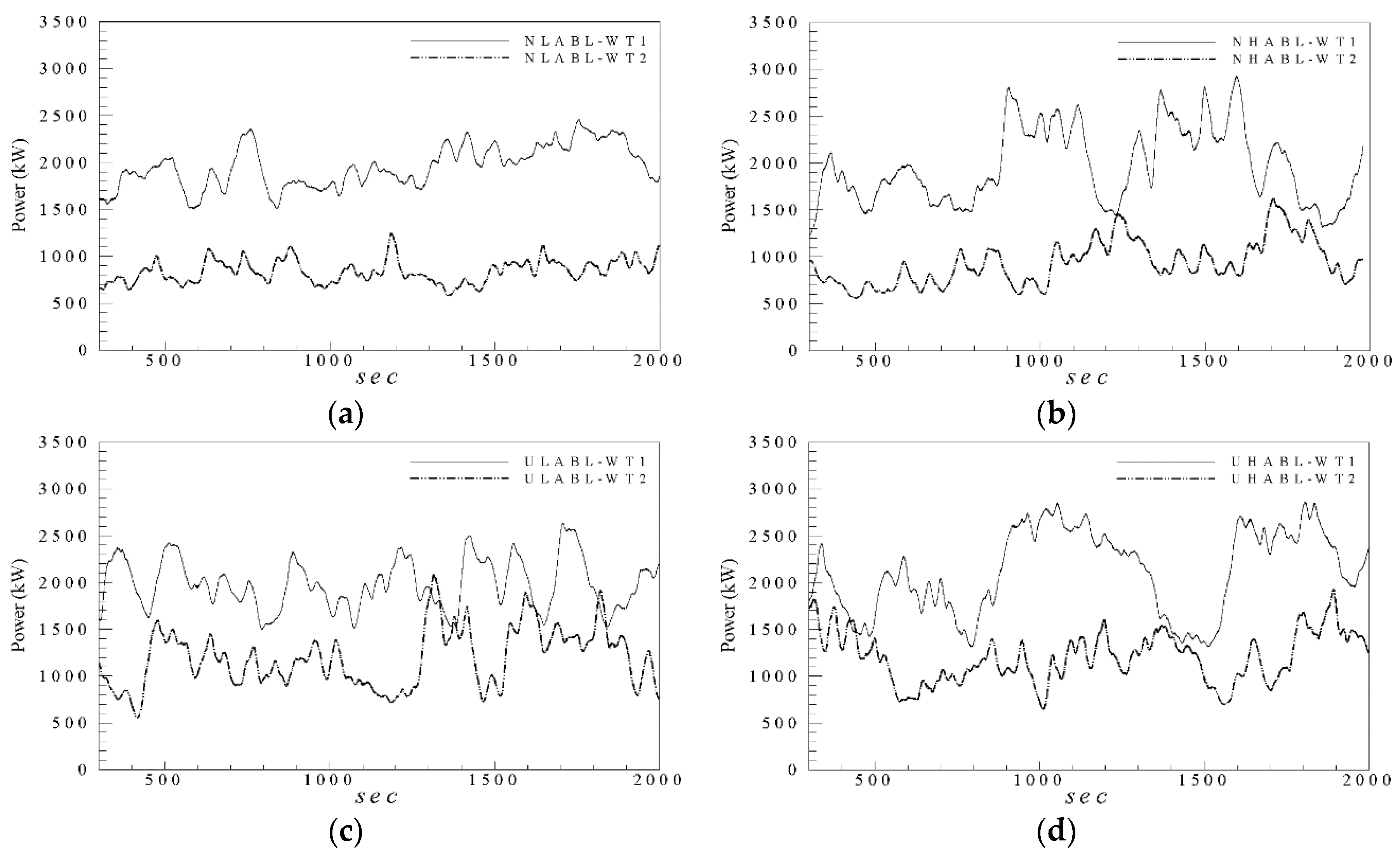
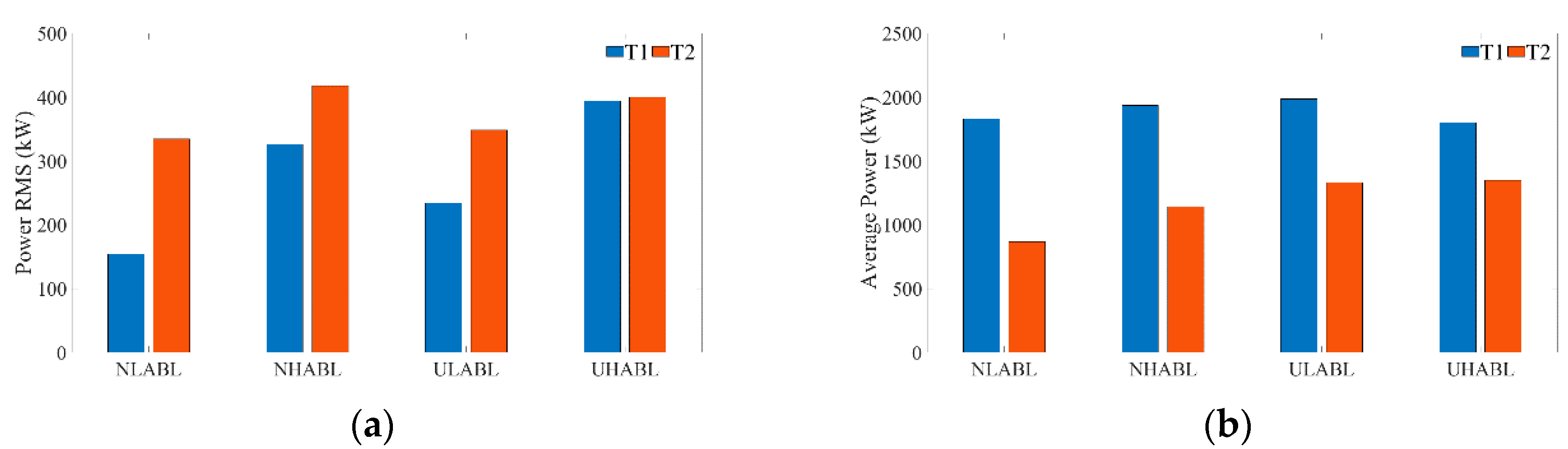
3.2. Power Generation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- US Energy Information Administration. Electric Power Monthly with Data for January 2018. Available online: https://www.eia.gov/electricity/monthly/epm_table_grapher.php?t=epmt_es1a (accessed on 22 May 2018).
- Kumar, Y.; Ringenberg, J.; Depuru, S.S.; Devabhaktuni, V.K.; Lee, J.W.; Nikolaidis, E.; Andersen, B.; Afjeh, A. Wind energy: Trends and enabling technologies. Renew. Sustain. Energ. Rev. 2016, 53, 209–224. [Google Scholar] [CrossRef]
- Sarlak, H.; Meneveau, C.; Sørensen, J.N. Role of Subgrid-scale Modeling in Large Eddy Simulation of Wind Turbine Wake Interactions. Renew. Energy 2015, 77, 386–399. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Navarro, J.; Palomares, A.M.; Dudhia, J. Mesoscale Modeling of Offshore Wind Turbine Wakes at the Wind Farm Resolving Scale: A Composite-based Analysis with the Weather Research and Forecasting model over Horns Rev. Wind Energy 2015, 18, 559–566. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling Turbine Wakes and Power Losses Within a Wind Farm Using LES: An Application to the Horns Rev Offshore Wind Farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Whale, J.; Anderson, C.G.; Bareiss, R.; Wagner, S. An Experimental and Numerical Study of the Vortex Structure in the Wake of a Wind Turbine. J. Wind Eng. Ind. Aerodyn. 2000, 84, 1–21. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sorensen, J.N.; Crespo, A. Wind Turbine Wake Aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Medici, D.; Alfredsson, P.H. Measurement on a Wind Turbine Wake: 3D Effects and Bluff Body Vortex Shedding. Wind Energy 2006, 9, 219–236. [Google Scholar] [CrossRef]
- Sorensen, J.N.; Myken, A. Unsteady Actuator Disc Model for Horizontal Axis Wind Turbines. J. Wind Eng. Ind. Aerodyn. 1992, 39, 139–149. [Google Scholar] [CrossRef]
- Jimenez, A.; Crespo, A.; Migoya, E.; Garcia, J. Advances in Large-eddy Simulation of a Wind Turbine Wake. J. Phys. Conf. Ser. 2007, 75, 012041. [Google Scholar] [CrossRef]
- Cleijne, J.W. Results of Sexbierum Wind Farm Report; TNO: The Hague, The Netherlands, 1993. [Google Scholar]
- Sorensen, J.N.; Shen, W.Z. Numerical modeling of Wind Turbine Wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2008. [Google Scholar]
- Chamorro, L.P.; Porte-Agel, F. A Wind-Tunnel Investigation of Wind Turbine Wakes: Boundary Layer Turbulence Effects. Bound.-Layer Meteorol. 2009, 132, 129–149. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porte-Agel, F. Large-eddy Simulation of Wind-turbine Wakes: Evaluation of Turbine Parametrizations. Bound.-Layer Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porte-Agel, F. Simulations of Turbulent Flow inside and above Wind Farms: Model Validation and Layout Effects. Bound.-Layer Meteorol. 2013, 146, 181–205. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Terzi, L. A Study of Wind Turbine Wakes in Complex Terrain through RANS Simulations and SCADA. J. Sol. Energy Eng. 2018, 140, 031001. [Google Scholar] [CrossRef]
- Subramanian, B.; Chokani, N.; Abhari, R.S. Aerodynamics of Wind Turbine Wakes in Flat and Complex Terrains. Renew. Energy 2016, 85, 454–463. [Google Scholar] [CrossRef]
- Hansen, K.S.; Larsen, G.C.; Menke, R.; Vasiljevic, N.; Angelou, N.; Feng, J.; Zhu, W.J.; Vignaroli, A.; Liu, W.; Xu, C.; et al. Wind Turbine Wake Measurement in Complex Terrain. J. Phys. Conf. Ser. 2016, 753, 032013. [Google Scholar] [CrossRef]
- Berg, J.; Troldborg, N.; Sorensen, N.N.; Patton, E.G.; Sullivan, P.P. Large-eddy Simulation of Turbine Wake in Complex Terrain. J. Phys. Conf. Ser. 2017, 854, 012003. [Google Scholar] [CrossRef]
- Castellani, F.; Astolfi, D.; Terzi, L.; Hansen, K.S.; Rodrigo, J.S. Analyzing Wind Farm Efficiency on Complex Terrains. J. Phys. Conf. Ser. 2014, 524, 012142. [Google Scholar] [CrossRef]
- Hansen, K.S.; Barthelmie, R.J.; Jensen, L.E.; Sommer, A. The Impact of Turbulence Intensity and Atmospheric Stability on Power Deficits Due to Wind Turbine Wakes at Horns Rev wind farm. Wind Energy 2012, 15, 183–196. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L. FAST User’s Guide; NREL/EL-500-38230; NTRS: Chicago, IL, USA, 2005.
- Stull, R.B. Meteorology for Scientists and Engineers, 2nd ed.; Brooks Cole: Belmont, CA, USA, 1999. [Google Scholar]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Moeng, C.H. A large eddy Simulation Model for the Study of Planetary Boundary Layer Turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Simulator for Off/Onshore Wind Farm Applications. Available online: http://wind.nrel.gov/designcodes/simulators/sowfa/ (accessed on 18 May 2018).
- Rhie, C.M.; Chow, W.L. Numerical Study of the Turbulent Flow Past an Airfoil with Trailing Edge Separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Issa, R. Solution of the Implicitly Discretized Fluid Flow Equations by Operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Monin, A.S.; Ohukhov, A.M. Basic Laws of Turbulent Mixing in the Surface Layer of the Atmosphere. Tr. Akad. Nauk SSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Lab.: Golden, CO, USA, 2009.
- Churchfield, M.J.; Lee, S.; Moriarty, P.; Martinez, L.; Leonardi, S.; Vijayakumar, G.; Brasseur, J. A Large-Eddy Simulation of Wind-plant Aerodynamics. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012. [Google Scholar]
- Barthelmie, R.J.; Jensen, L.E. Evaluation of Wind Farm Efficiency and Wind Turbine Wakes at the Nysted Offshore Wind Farm. Wind Energy 2010, 13, 573–586. [Google Scholar] [CrossRef]
- Jensen, L.E. Analysis of Array Efficiency at Horns Rev and the Effect of Atmospheric Stability. In Proceedings of the 2007 EWEC Conference, Milan, Italy, 7–10 May 2007. [Google Scholar]



| Atmospheric Stability | Surface Roughness | |
|---|---|---|
| Low | High | |
| Neutral | NLABL | NHABL |
| Unstable | ULABL | UHABL |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Vorobieff, P.; Poroseva, S. Interaction of Wind Turbine Wakes under Various Atmospheric Conditions. Energies 2018, 11, 1442. https://doi.org/10.3390/en11061442
Lee S, Vorobieff P, Poroseva S. Interaction of Wind Turbine Wakes under Various Atmospheric Conditions. Energies. 2018; 11(6):1442. https://doi.org/10.3390/en11061442
Chicago/Turabian StyleLee, Sang, Peter Vorobieff, and Svetlana Poroseva. 2018. "Interaction of Wind Turbine Wakes under Various Atmospheric Conditions" Energies 11, no. 6: 1442. https://doi.org/10.3390/en11061442
APA StyleLee, S., Vorobieff, P., & Poroseva, S. (2018). Interaction of Wind Turbine Wakes under Various Atmospheric Conditions. Energies, 11(6), 1442. https://doi.org/10.3390/en11061442






