Single-Ended Protection Scheme for VSC-Based DC Microgrid Lines

Abstract

With the promotion of distributed energy and direct current (DC) loads, the DC microgrid is able to provide a higher power quality and improve the grid efficiency. Various technical issues in DC microgrids are still to be addressed, particularly a proper protection scheme for fault detection and isolation in DC microgrids utilizing voltage source converters (VSCs). In this paper, the pole-to-pole DC fault transient behavior of the VSC-based microgrids is firstly analyzed with four successive stages, and then the exact requirements for protections are presented. Furthermore, a novel single-ended protection scheme based on local transient signals is proposed, which needs no data transmission or synchronization between two ends, ensuring the speed. A four-terminal DC microgrid model was built in PSCAD/EMTDC. Numerous simulations have demonstrated the validity of the proposed scheme.

1. Introduction

DC microgrids provide a highly efficient pattern to combine conventional alternative current (AC) utility powers, distributed energy generators, electronic DC appliances, and energy storage. Compared with AC microgrid systems, the voltage source converter (VSC)-based DC microgrids show many advantages, including a high power-converting efficiency, greater power capacity, better power quality, and thus a lower discarding rate of distributed energies [1,2]. The converters in a microgrid allow the power flow to be bidirectional, catering for the flexible locations of loads and renewable energy. In recent years, plenty of strategies have been proposed for the electronic device design, control module, and optimal operation of DC microgrids [3,4,5,6].

However, various technical challenges still need to be overcome to realize the safe and reliable operation of DC microgrids on a large scale. One of these issues is addressed in the study on the protection principle under DC fault conditions, particularly for the networks with VSCs [7,8]. Conventional converters with thyristors do not experience a high level of overcurrent during DC fault scenarios, whereas in VSCs, insulated-gate bipolar transistors (IGBTs) in converters are blocked as a result of instant self-protection. In this case, the anti-parallel freewheeling diodes together act as an uncontrolled rectifier, allowing the feeding of AC fault current and the discharging of capacitors. These transient stages generate a very large overcurrent, reaching more than 8–10-fold that rated in the worst cases. This overcurrent would flow quickly to all other connected lines if there were no instant protections, posing a great threat to the whole system [9].

In existing AC microgrids, current protection schemes involve the isolation of faulted lines via AC circuit breakers [6,7]. However, these protections are not totally applicable to DC microgrids because of the low impedance of DC lines, as well as the non-existence of zero crossings in DC current signals. Therefore, it is necessary to investigate a novel protection scheme aimed at DC microgrids, to detect and isolate only the faulted segments, thus protecting large numbers of power electronic devices in converters, and meanwhile maintaining the power supply security in healthy areas [10,11]. In recent years, DC circuit breakers have been utilized in low-voltage DC microgrids, and double-ended DC line protections are gradually being put forward [12,13,14]. Usually, methods using double-ended signals and data processing in the frequency domain are more accurate [15,16]. However, single-ended schemes are advantageous in the accessing of local measurements, no need for synchronization, and lower industrial cost. Voltage and current signals are preferred in protection designs for microgrids, as these data are originally restored in the line terminals. The authors in [17] propose a new single-ended differential protection using data measured from distributed optical sensors along the transmission line. A novel single-ended protection principle based on time-domain transient electrical signals is proposed in [18], where the DC line current change and voltage change rate are used as criterions.

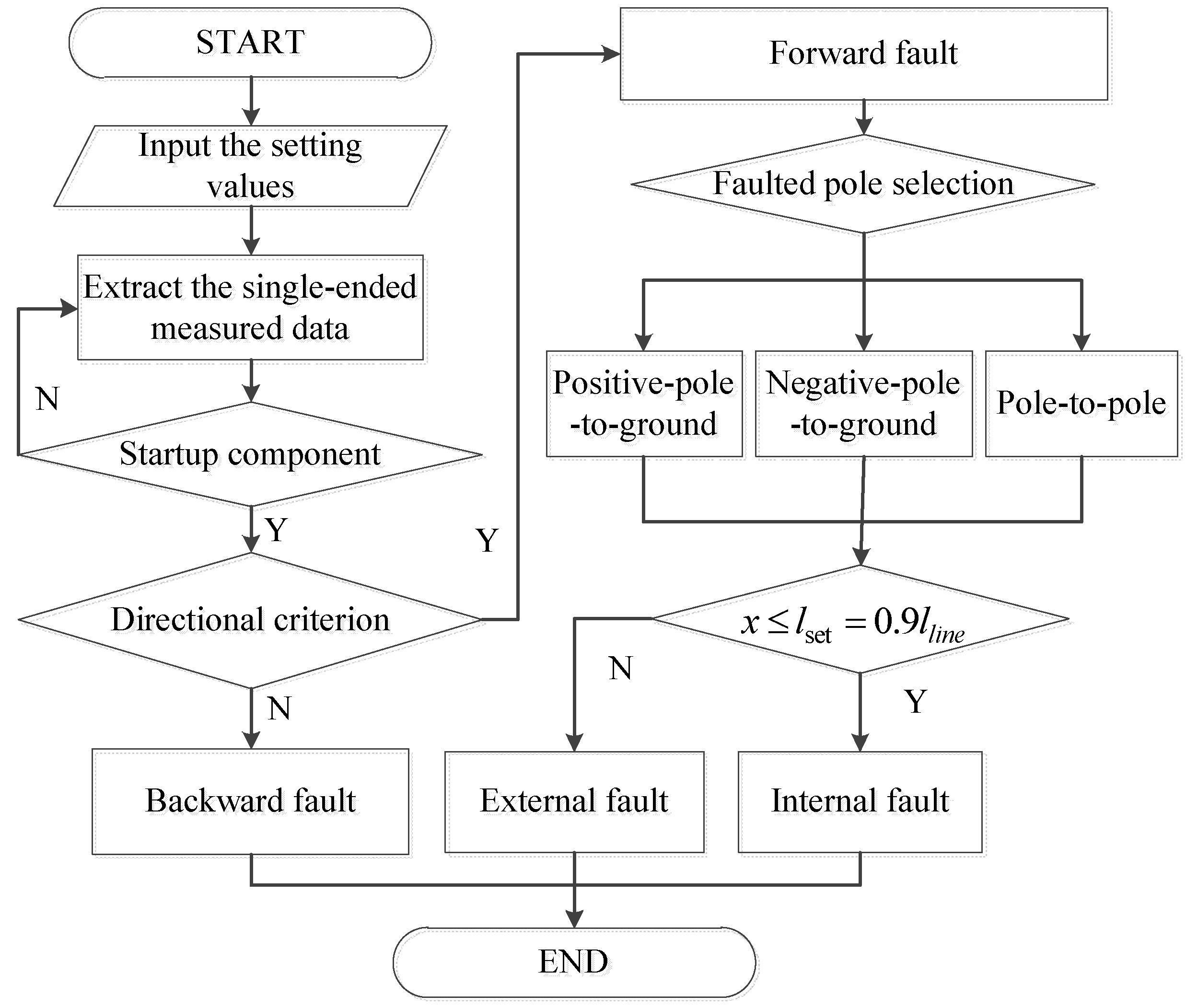
In this paper, the basic structures of DC microgrids are firstly introduced. The pole-to-pole fault transient characteristics of VSC-based DC microgrids are then analyzed in four stages. A novel protection scheme is proposed using the single-ended transient signals. In the proposed scheme, the voltage criterion of DC inductance is employed as a directional element, which can identify forward faults of the protected line. Features of the pole voltage change criterion are used as the pole selection element, through which the faulted pole can be distinguished. This method needs no communication between the two ends, ensuring the speed and reliability. Finally, various simulation results demonstrated the validity of the proposed protection in PSCAD/EMTDC.

2. Pole-to-Pole Fault Characteristics of DC Microgrids

2.1. Structures of DC Microgrids

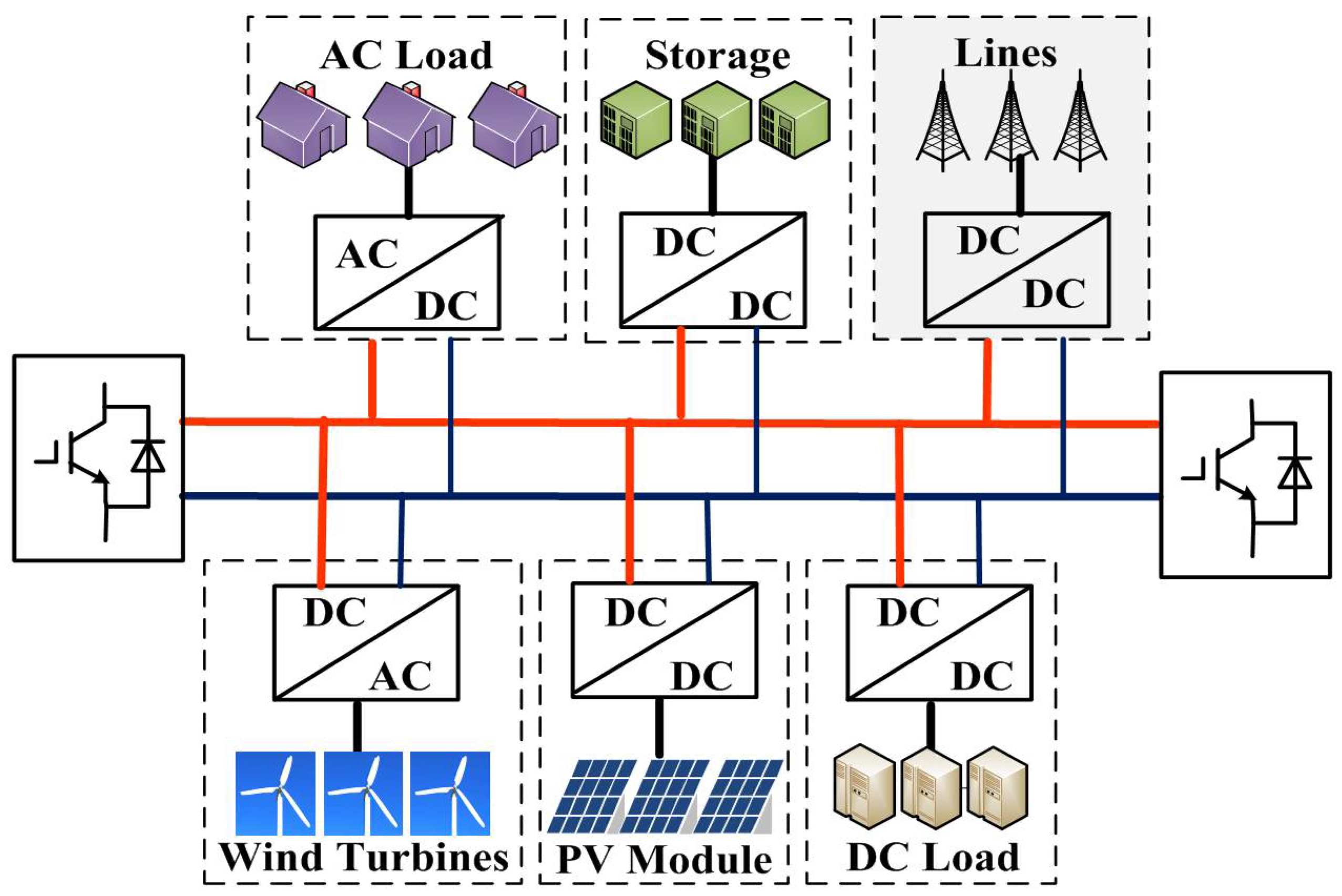
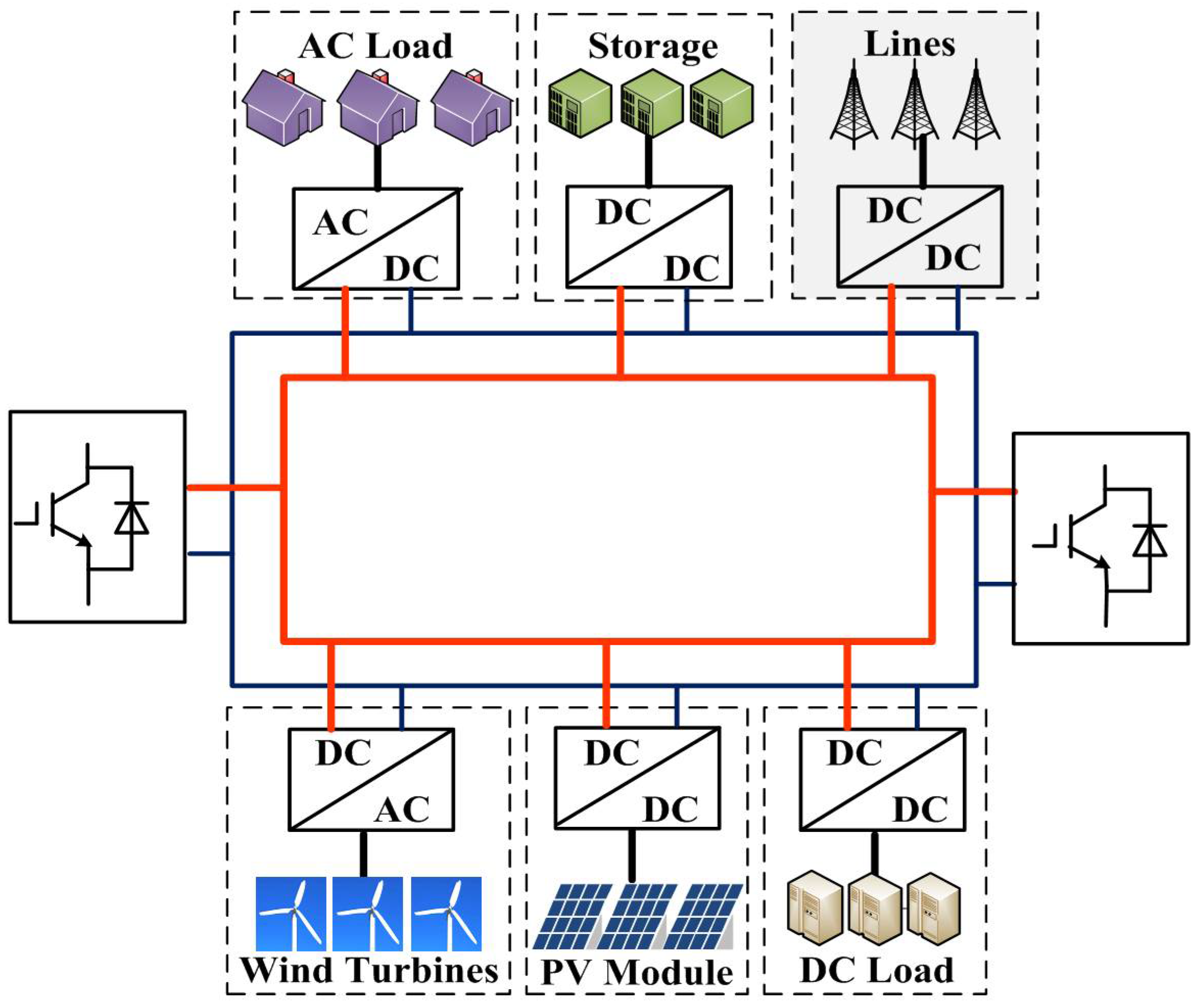
The scale of a DC microgrid has a strong relationship with its location, construction purpose, and the number of connected distributed generations. In general, DC microgrid networking is very flexible with regard to its plan, design, control, and operation. Figure 1 shows the radial structure of a multi-terminal DC microgrid, and Figure 2 shows the ring structure, the grey zone indicating adjacent lines. As a result of its reliable and flexible operation, the ring structure is more commonly used in multi-terminal systems [15,16]. Sources in a DC microgrid could be of various types. Photovoltaic modules and fuel cells provide DC voltage, which makes these sources suitable to be connected via a DC/DC converter. Microturbines featuring high-frequency voltage depend on conversions to join in the DC grid. AC/DC converters are also needed when connecting wind turbines to DC buses. Besides sources, some energy storage devices such as batteries and supercapacitors are crucial to microgrids for their functions of power-quality improvement, load leveling, and an emergency power supply [19]. Additionally, DC microgrids are also able to supply AC or DC loads in need of high reliability, for example, monitoring systems, safety systems, and equipment for ventilation or heat [20].

It is illustrated that both AC/DC and DC/DC converters are used in the system to interconnect the different modules to the DC bus. These AC/DC converters are required to generate a sinusoidal voltage and current wave, to transmit the power flow bidirectionally. The converters should be galvanic isolated and able to deal with imbalance or voltage dips. In this case, the VSC is a preferable alternative to improve the efficiency of conversion.

2.2. Fault Transient Stages

The extensive usage of VSCs brings about the issue of fault analysis and the protection principle, a vital part of microgrid systems [21]. Faults on the DC side consist mainly of pole-to-pole faults, pole-to-ground faults, and break faults, which should be detected as quickly as possible. Pole-to-pole faults raise the most concern among these types, as severe transient characteristics may lead to destructive consequences, on both the DC and AC sides. For this reason, the proposed protection scheme is based on detailed insight into DC faults, which is discussed in this section.

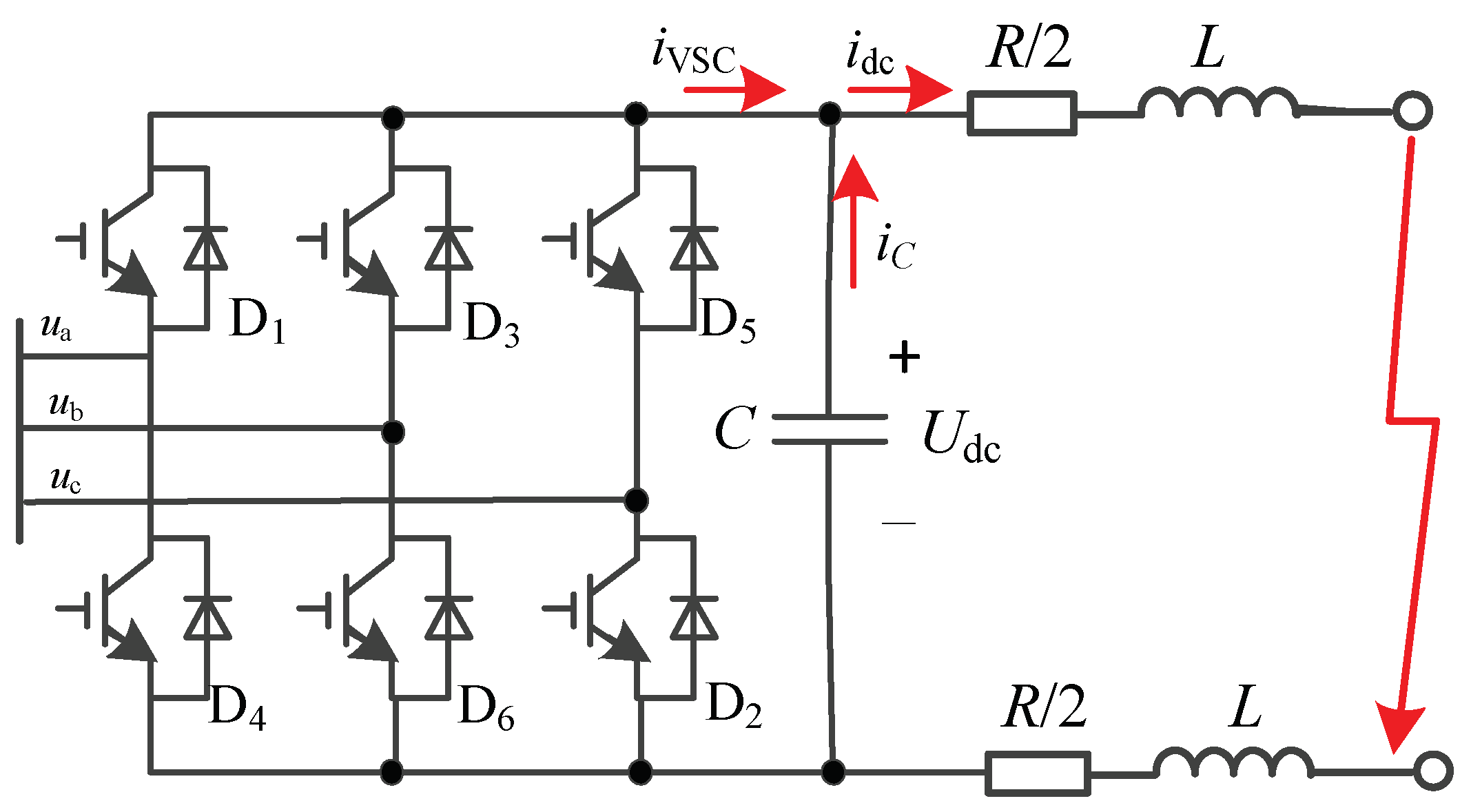
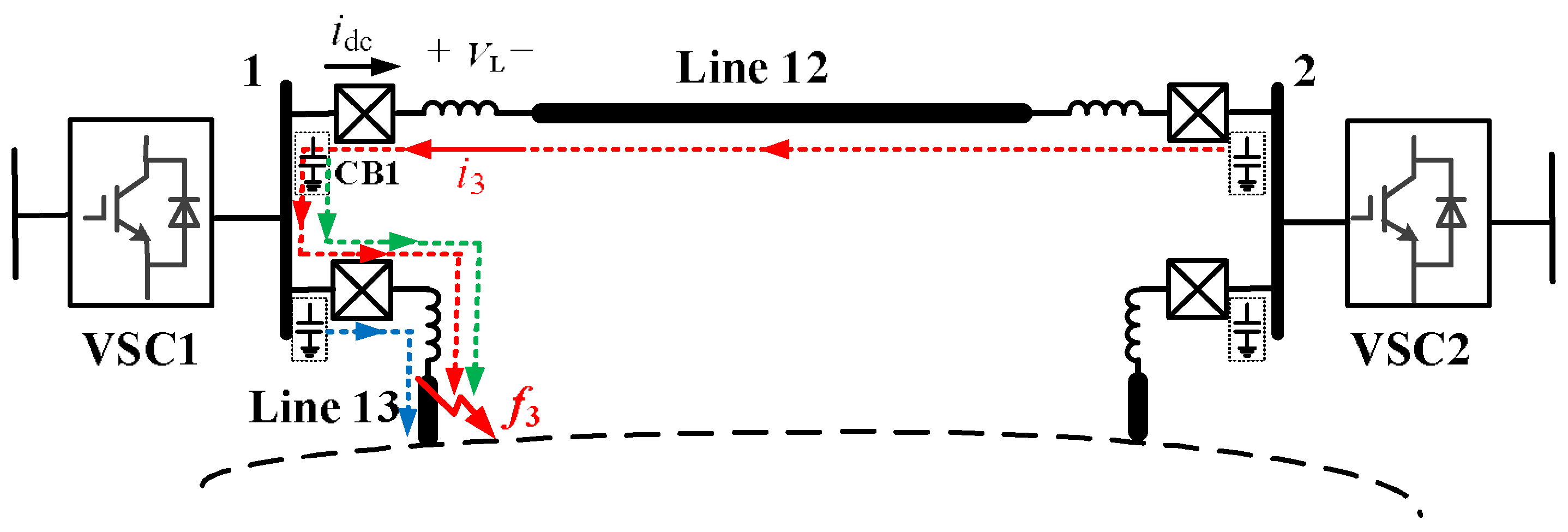
Figure 3 shows the equivalent circuit of a pole-to-pole short-circuit fault in a DC microgrid, where R and L represent the equivalent resistance and inductance of the DC line, respectively; C represents the paralleled DC capacitor; and u_a, u_b, u_c represent the AC voltage connected point. Under this fault condition, the capacitor discharges through the fault point (i_C). As for the AC system, it is collapsed to a three-phase short-circuit because of the low impedance of DC lines. The converter is then blocked by its overcurrent protection. 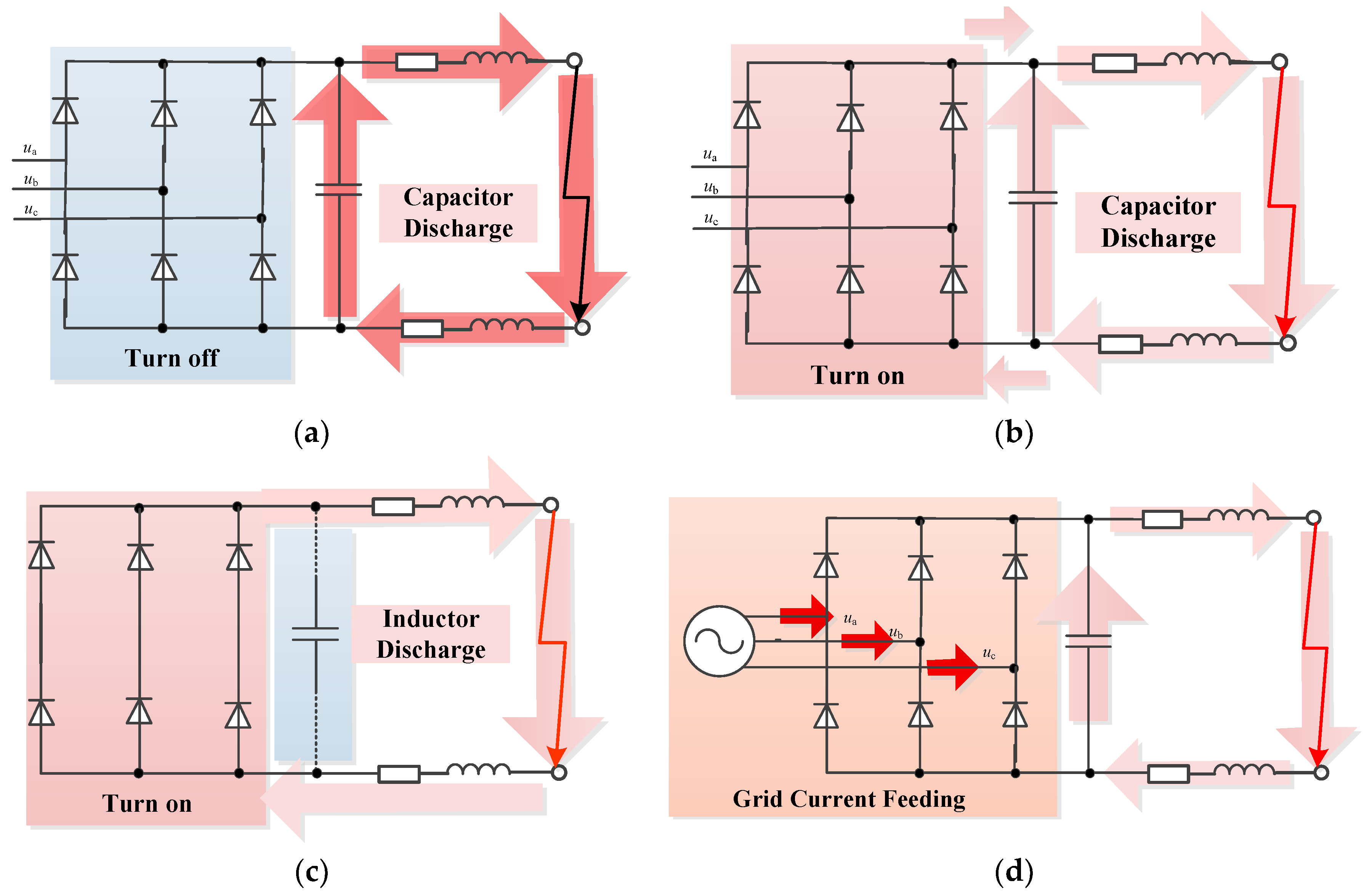Therefore, the AC power would feed in the fault point through the parallel diodes in the VSC (i_VSC) [18,19]. Because the equivalent circuit is nonlinear, it can be divided into four stages in detail for the mathematical analysis, as shown in Figure 4.

As shown in Figure 4, the DC fault current has two energy sources in principle: the connecting AC grids, which contribute to a steady-state fault current through the VSC, and the DC capacitor, which contributes largely to a transient current. The DC capacitor discharges rapidly during the bipolar fault when the IGBTs are blocked, contributing to a large DC current. The AC voltage is normally smaller than the DC voltage, which leaves the diodes turned off at the very beginning.

2.3. DC Fault Analysis of VSC

As shown in Figure 4, stage 1 has an overcurrent through the DC lines without the joining of the AC system. The discharging circuit in Figure 4a can be described as a second-order transient equation of the DC voltage:

$$LC\frac{{\mathrm{d}}^2{u}_{\mathrm{dc}}}{\mathrm{d}{t}^2}+RC\frac{\mathrm{d}{u}_{\mathrm{dc}}}{\mathrm{d}t}+u_{\mathrm{dc}}=0$$

(1)

To solve this equation, the parameters R, L, and C play a part in the expression. For a DC microgrid system, the resistance of DC lines is relatively small enough to fulfill the underdamping condition $R<2\sqrt{L/C}$. In this case, the eigenvalues of the nonlinear Equation (1) are a pair of conjugate complex numbers in Equation (2). Supposing the pole-to-pole fault happens at t = 0 with the initial conditions U₀ and I₀, the fault voltage and current can be solved as follows:

$${\lambda }_{1,2}=-\frac{R}{2L}\pm \sqrt{{\left(\frac{R}{2L}\right)}^2-\frac{1}{LC}}=-\alpha \pm \mathrm{j}\omega ,$$

(2)

$$u_{\mathrm{dc}}=\frac{U_0{\omega }_0}{\omega }{e}^{-\alpha t}\sin \left(\omega t+\theta \right)-\frac{I_0}{\omega C}{e}^{-\alpha t}\sin \omega t,$$

(3)

$$i_{\mathrm{dc}}=-\frac{I_0{\omega }_0}{\omega }{e}^{-\alpha t}\sin \left(\omega t-\theta \right)+\frac{U_0}{\omega L}{e}^{-\alpha t}\sin \omega t,$$

(4)

where $\alpha =\frac{R}{2L}$, $\omega =\sqrt{\frac{1}{LC}-{\left(\frac{R}{2L}\right)}^2}$, ${\omega }_0= \sqrt{{\alpha }^2+{\omega }^2}=1/\sqrt{LC}$, and $\theta = \arctan \left(\omega /\alpha \right)$.

For DC microgrids, particularly when additional DC inductances are installed at the terminals, line parameters satisfy the condition (R/2L)² < 1/LC in Equation (4) if a metallic fault occurs, indicating $\omega = {\omega }_0$. The DC fault current of Equation (4) can therefore be rewritten simply as follows:

$$i_{\mathrm{dc}}=e^{-\alpha t}\left(U_0\sqrt{\frac{C}{L}}\sin \omega t+I_0\cos \omega t\right).$$

(5)

Assuming $\delta =\arctan \left(\frac{I_0}{U_0}\sqrt{\frac{L}{C}}\right)$, the DC current can be clearly seen as a function of initial states and line parameters L and C in Equation (6):

$$i_{\mathrm{dc}}=e^{-\alpha t}\left(\sqrt{\frac{C}{L}{U}_0^2 + I_0^2}\sin \left(\omega t+\delta \right)\right).$$

(6)

When the voltage of the capacitor drops to the same level as the AC link, it reaches stage 2, at which point the diodes turn on because of the forward voltage. Meanwhile the capacitor continues to discharge. The time at which the voltage of the capacitor discharges to zero can be obtained as follows:

$$t_1=t_0+\left(\pi -\phi \right)/\omega ,$$

(7)

where $\phi = \arctan \left(U_0{\omega }_{0}C\sin \theta /\left(U_0{\omega }_{0}C\cos \theta -I_0\right)\right)$.

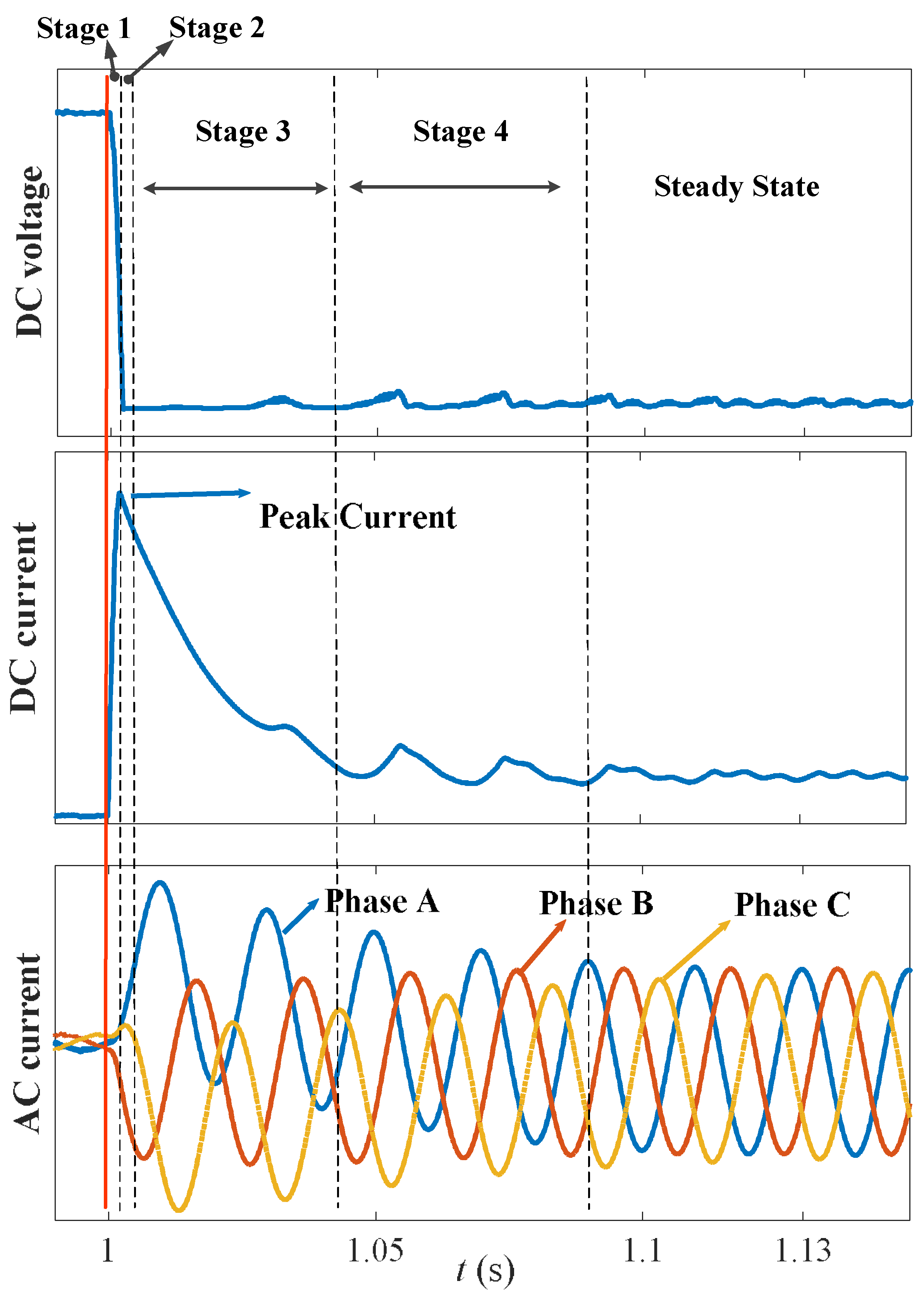
Figure 5 illustrates the transient waveforms responding to a pole-to-pole fault at t₀ = 1 s, with the four stages each labeled.

Stages 1 and 2 last several milliseconds, and during these stages the transient features are used to compose protection schemes. Some interesting features in stages 3 and 4 may be noticed. As the DC voltage becomes less than zero because of the damping, the inductor discharges through diodes and resistance, again charging the capacitor in stage 3. With the increase in the capacitor voltage, the DC voltage between the two poles slightly rises from zero. At this time, the AC grid performs as a three-phase fault with current increasing sharply. In stage 4, the AC grid current feeds in the DC link through paralleled diodes, posing a great threat to electronic devices. In general, DC faults should be cleared in 3–5 ms to avoid the collapse of the system and thus the restart of the VSC (charging, synchronization, etc.), which may otherwise take a long time in the order of seconds.

3. Single-Ended Protection Scheme

3.1. Requirements for Protection

The DC microgrid is featured with low inertia and is connected with many distributed energies and AC/DC loads. Figure 5 shows that the DC voltage drops dramatically in 2 ms during the fault, which demands a fast protection to be detected. Therefore, the DC protection should utilize the transient characteristics to distinguish the faults as quickly as possible, which means the action by the protection should be between stages 1 and 2 when the capacitor discharges.

A multi-terminal VSC-based microgrid DC system is shown in Figure 6, for which wind turbines and a DC load are connected to the DC buses. The paralleled DC capacitors are used to stabilize the DC voltage. The supplemental inductors are installed at each end of DC lines, which could reduce the peak value and rising rate of the fault current to a lower level. These supplemental inductors naturally act as the boundary of DC lines, blocking the high-frequency components of current. Meanwhile, these boundary cells could be used to extract information to reliably distinguish between the internal faults and external faults.

Considering the protection at CB1 in Figure 6, for example, the fault locations are illustrated: f₁ suggests an internal fault, f₄ and f₅ suggest external forward faults, and f₂ and f₃ suggest backward DC faults. The role of protection at CB1 is to ensure the power transfer security and stability of the system under DC fault conditions. This is achieved by isolating the faulty segments in such way that the remaining healthy part operates normally. The characteristics of the terminal fault f₁ on line 12 are very similar to those of the terminal fault f₅ on line 24. In this aspect, the protection should be selective enough, sufficiently fast, reliable, and robust. In general, the transient characteristics of DC capacitors and inductors are important for designing a single-ended protection scheme. The scheme should satisfy the selectivity, speed, sensitivity, and reliability simultaneously. The action of protections should be made in 2 ms at stages 1 and 2.

3.2. Startup Component

In a DC microgrid, it is desirable to use only local signals to detect faults because of the sharp increase in fault DC current during the first two stages when the DC capacitor discharges. If the local controller can distinguish this feature accurately, the startup signal could be transmitted to the local DC breaker without data communications between the two ends, which is very advantageous in terms of saving time, contributing to the fast detection of faults. Hence the absolute-value integration method is adopted as the startup component, as formulated in Equation (8):

$$\frac{1}{N}{\displaystyle \sum _{k=1}^N\left|I_k\right|}>I_{op\_set},$$

(8)

where I_k indicates the measured current, and k = 1, 2, …, N. N is the total number of sampling points in the time window. I_{op_set} indicates the setting value, where normally I_{op_set} = K_rel I_rate K_rel, the reliability coefficient, is equal to 1.3–1.5, and I_rate is the DC current rating.

3.3. Directional Criterion

A proper directional criterion is important for the protection scheme for multiterminal systems. Figure 7 shows forward pole-to-pole faults at two locations for CB1. The current through the inductor flows from the bus to the line, which is the same direction as for the reference current i_dc. For the backward fault in Figure 8, however, the inductor current flows in the other direction. This paper proposes a practical directional criterion utilizing the voltage over the supplemental inductor to distinguish the forward faults from the backward faults, formulated as follows:

$$V_L=L\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t},$$

(9)

where V_L is the voltage of inductance L, and i_dc is the reference current through the inductor as labeled in Figure 7 and Figure 8.

To further investigate the voltage in Equation (9), the DC current in Equation (6) can be used to achieve the derivative of the DC current at the fault time t = 0 as follows:

$${\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}|}_{t=0}=-\sqrt{C^2{U}_0^2+LC{I}_0^2}\sin \left(\delta -\theta \right).$$

(10)

The sign of Equation (10) depends on the sign of $\delta -\theta$ as follows:

$$\delta -\theta =\arctan \left(\frac{I_0}{U_0}\sqrt{\frac{L}{C}}\right)-\arctan \left(\omega /\alpha \right).$$

(11)

If faults happen with an initial current I₀ of less than zero, that is, $-\frac{\pi }{2}<\delta <0$, then $-\pi <\delta -\theta <0$ can hence be derived, which means the changing rate (Equation (10)) is greater than zero.

On the other hand, if faults happen with an initial current I₀ of greater than 0, the relationship between these two angles in Equation (11) should be further determined. Here some simulations using parameters from the projects were investigated, as shown in Figure 9. A typical group of parameters from a DC microgrid were chosen: U₀ = 1000 V, L₀ = 0.56 mH/km, R₀ = 0.078 Ohm/km, L_r = 1 mH, and C = 2 mF. The fault distance varied from 0 to 30 km, and the initial current varied from 50 to 500 A. The mathematical analysis results show that the angle was always around −69° to −70°.

Because the angle in Equation (11) is less than zero regardless of the initial current and fault distance, the changing rate of the DC current in Equation (10) is always greater than zero, making the DC voltage of the inductor also greater than zero. For backward faults, however, the current reverses the direction and similarly increases, with the inductor voltage being less than zero. Thus, the direction criterion of the proposed protection scheme is that composed in Equation (12):

$$\{\begin{array}{c}\begin{array}{cc}{V}_L=L\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}>0,& \mathrm{forward} \mathrm{fault};\end{array}\\ \begin{array}{cc}{V}_L=L\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}<0,& \mathrm{backward}\end{array} \mathrm{fault}.\end{array}$$

(12)

3.4. Faulted Pole Selection

Faulted pole selection is an essential step in protection schemes that allows the power transfer security among healthy segments. In this paper, the transient characteristics of pole DC voltage are used to identify faulted poles.

As presented in Section 3, when a pole-to-pole fault occurs, the voltages of both poles decline at the same rate, in principle, whereas when a pole-to-ground fault happens, a faulted pole experiences a higher changing rate. During a positive-pole-to-ground fault, the positive-pole voltage drops to zero at a rate faster than that of the negative-pole voltage. Similarly, the negative-pole voltage rises to zero at a rate faster than that of the positive voltage during a negative-pole-to-ground fault, as illustrated in Figure 10, where the dashed lines are voltage rating ±500 V and zero reference.

The coefficient of the changing rate of pole voltage (CRU) is introduced to quantify the changing characteristics of the transient pole voltage waveform.

$$K_{\mathrm{U}}=\frac{CR{U}^{+}}{CR{U}^{-}}=\frac{\sqrt{\frac{1}{N-1}{\displaystyle \sum _{k=1}^N{\left[u^{+}(k)-u_0^{+}\right]}^2}}}{\sqrt{\frac{1}{N-1}{\displaystyle \sum _{k=1}^N{\left[u^{-}(k)-u_0^{-}\right]}^2}}},$$

(13)

where CRU⁺ and CRU⁻ represent the change rate coefficients of positive and negative pole voltages, respectively; K_U is the ratio of CRU⁺ to CRU⁻; u⁺(k) and u⁻(k) represent the kth samples of positive and negative pole voltages, respectively; u₀⁺ and u₀⁻ represent the initial voltages; N represents the number of samples in the time window of 2 ms; and the corresponding N is equal to 100 for the sampling frequency of 50 kHz.

The CRU⁺ coefficient is much greater than CRU⁻ for a positive-pole-to-ground fault, $K_{\mathrm{U}}\gg 1$; on the other hand, CRU⁺ is much smaller than CRU⁻ for a negative-pole-to-ground fault, $0<K_{\mathrm{U}}<1$. When a pole-to-pole fault happens, $K_{\mathrm{U}}= 1$ can be concluded theoretically. The ratio K_U, therefore, can be taken as a faulted pole selection criterion in Equation (14). This criterion was generally useful in the various simulations, as an adequate margin was considered. To guarantee its reliability in industrial project usage, a further field test with project parameters is recommended.

$$\{\begin{array}{l}{K}_{\mathrm{U}}\ge 1.3,\\ K_{\mathrm{U}}<0.7,\\ 0.7<K_{\mathrm{U}}<1.3,\end{array}\begin{array}{c}{\mathrm{positive}\text{-}\mathrm{pole}}_{}{\mathrm{grounded}}_{}\mathrm{fault};\\ {\mathrm{negative}\text{-}\mathrm{pole}}_{}{\mathrm{grounded}}_{}\mathrm{fault};\\ {{}_{}}_{}{{}_{}}_{}{}_{}{\mathrm{pole}\text{-}\mathrm{to}\text{-}\mathrm{pole}}_{}\mathrm{fault}.\end{array}$$

(14)

3.5. Identification of Fault Areas

The forward faults f₂ and f₅ have similar features, as explained above. This section proposes a criterion to identify an internal fault on the basis of the idea of distance protection. For a pole-to-pole fault, at a distance x from CB1 on line 12, the time-domain equation containing the distance is Equation (15):

$$u_t=2\left(L_{0}x+L_r\right)\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}+2R_{0}x{i}_{\mathrm{dc}},$$

(15)

where L₀ and R₀ are the inductance and resistance per kilometer of lines, respectively; L_r is the supplemental inductance; and u_t is the local measured voltage. The shunt capacitor of the line has been omitted for its limited contribution. The fault distance can then be solved for as follows:

$$x=\frac{u_t-2L_r\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}}{2L_0\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}+2R_0{i}_{\mathrm{dc}}}.$$

(16)

For positive-pole or negative-pole-to-ground faults, the distance can also be similarly written as follows:

$$x=\frac{u_t-L_r\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}}{L_0\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}+R_0{i}_{\mathrm{dc}}}.$$

(17)

Here, the time window is 2 ms and the sampling frequency is 50 kHz, ensuring a sufficient number of data samples to obtain the fault distance. The line protection zone is generally set to be 90% of the whole line, and thus the internal fault criterion in this paper is set as

$$x\le l_{set}=0.9l_{line}.$$

(18)

To conclude, the flowchart of the proposed single-ended DC fault protection scheme is illustrated in Figure 11.

4. Verification

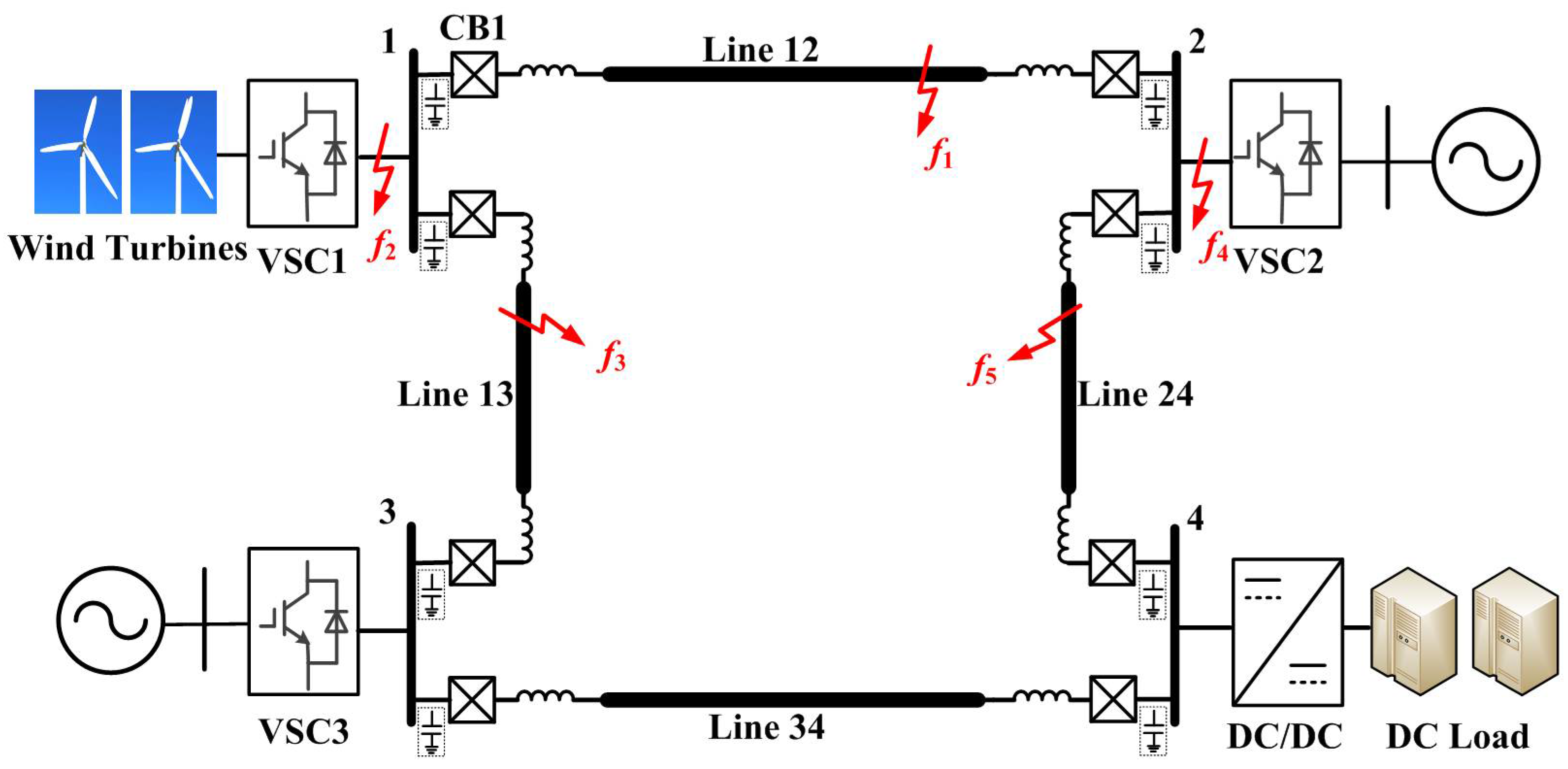
The four-terminal DC microgrid of Figure 8 was established in PSCAD/EMTDC to test the proposed single-ended protection scheme. The system parameters were the same as those stated in Section 3.3: the nominal voltage was ±500 V, and four 1 km lines were used with the π-model.

4.1. Simulation of Directional Criterion

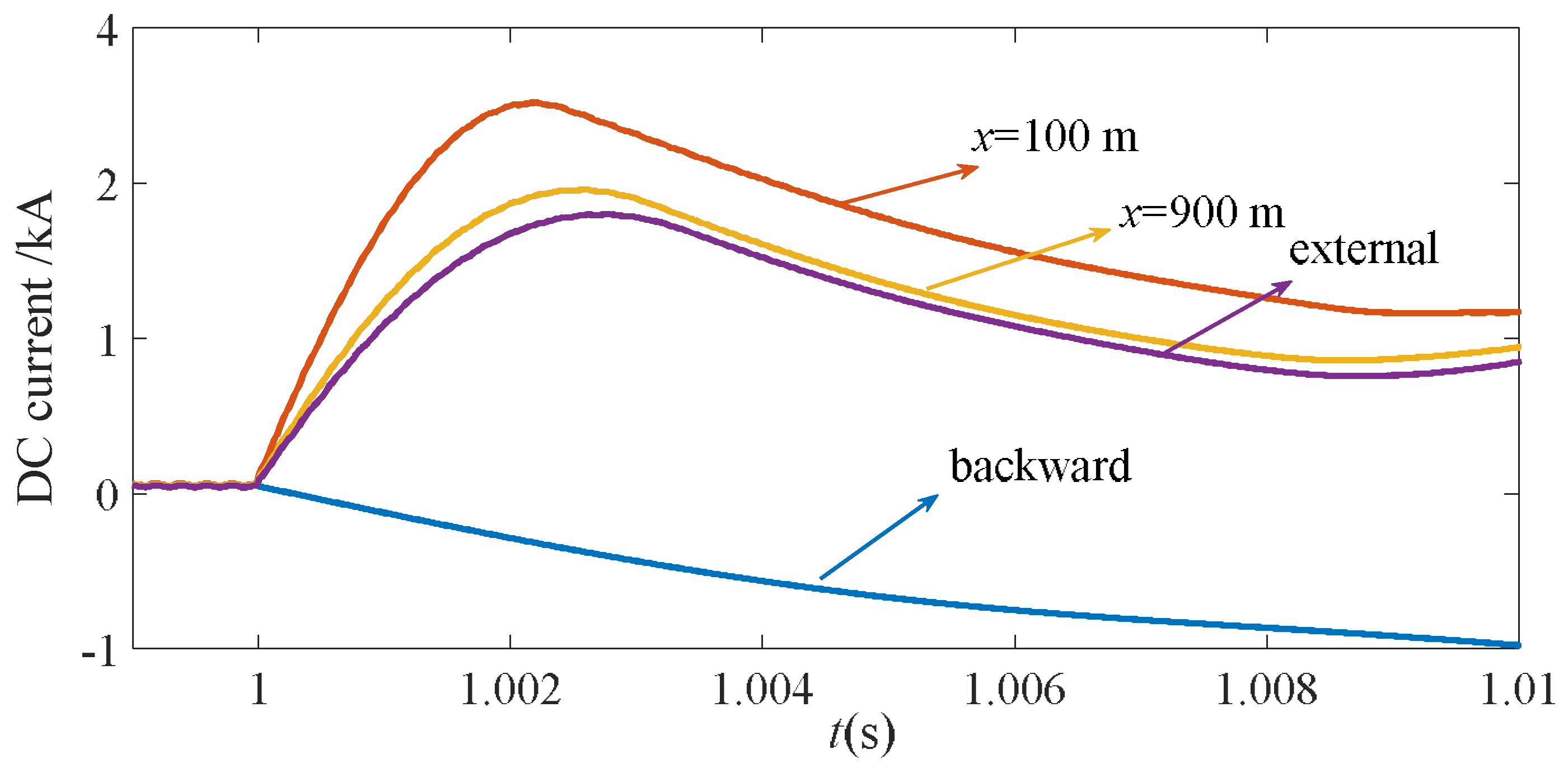
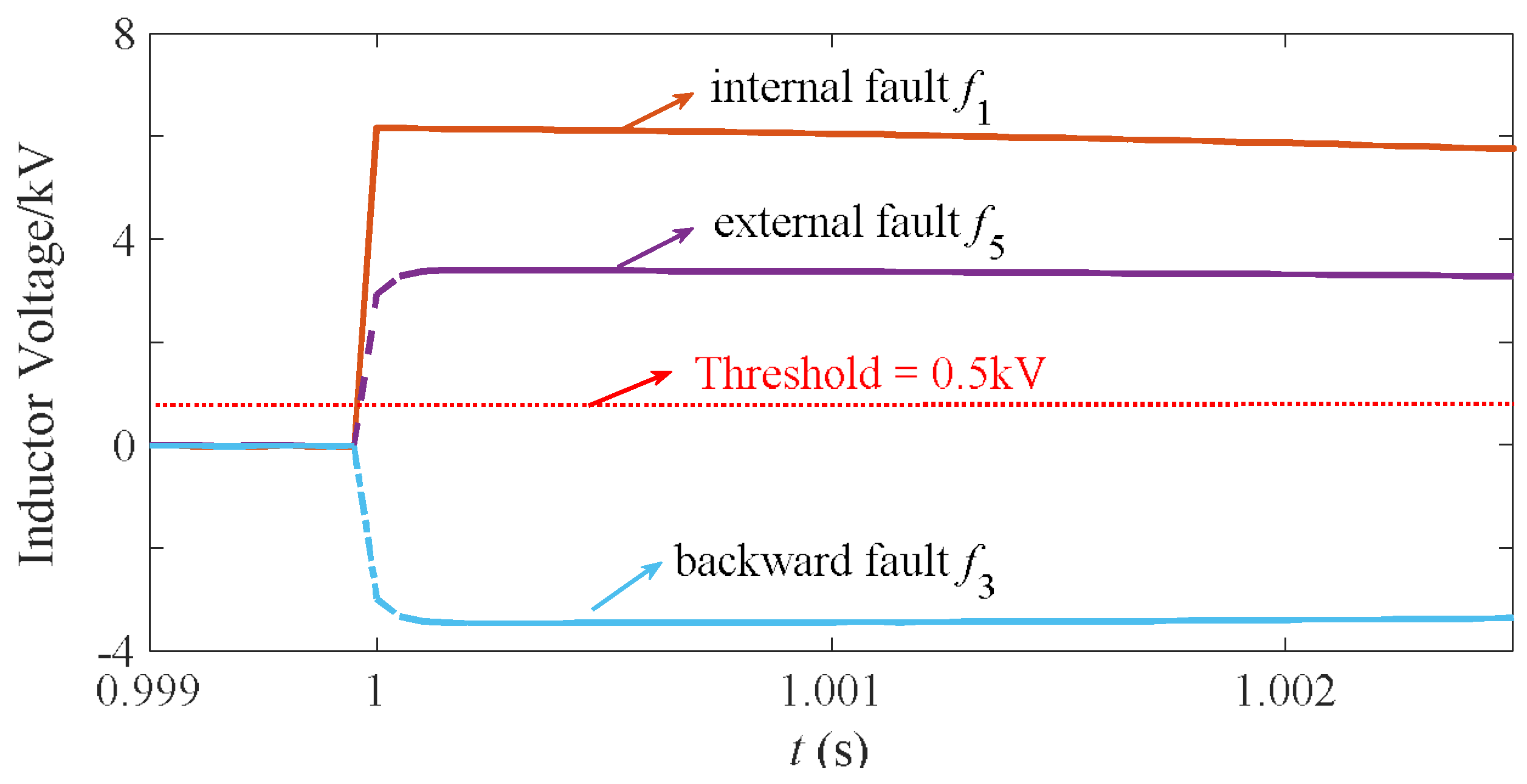
Figure 12 illustrates the simulation results for the DC current of pole-to-pole faults at different locations. The reference forward direction of CB1 was set from the bus to the line. From the picture, it is seen that the rising rate of the fault current was reduced, because of the placement of supplemental inductors at both ends of the lines.

The simulation results for the three fault types in Figure 8 and Figure 9 are shown in Figure 13. The forward faults were the following: the internal fault f₁ at the terminal end (fault distance x = 900 m) of line 12, and the external fault f₅ at line 24 close to VSC2. The backward fault f₃ was located at line 13, which was near VSC1. As is seen from the results, the directional criterion could selectively distinguish the forward faults and backward faults by the threshold of 0.5 kV, the dashed line in Figure 13.

4.2. Simulation of Faulted Pole Selection

The results of the faulted pole selection for CB1 are displayed in

Table 1. Simulation results of faulted pole selection for forward faults.

Fault Type	x/m	Rfault/Ω	KU	Fault Type	x/m	Rfault/Ω	KU
Internal PG fault 1	100	0.1	29.8425	Internal PP fault 1	100	0.1	1.0492
		1	18.6964			1	1.0772
	500	0.1	17.9425		500	0.1	1.0375
		1	12.1508			1	1.0575
	900	0.1	13.6224		900	0.1	1.0541
		1	10.0290			1	1.0887
Internal NG fault 1	100	0.1	0.0177	External PP fault	100	0.1	1.0832
		1	0.0434			1	1.1373
	500	0.1	0.0131		500	0.1	1.0816
		1	0.0421			1	1.1258
	900	0.1	0.0220		900	0.1	1.1132
		1	0.0608			1	1.1763

¹ PG (NG) fault: positive (negative)-pole-to-ground fault; PP fault: pole-to-pole fault.

. Here, the internal faults were located on line 12 and the external faults were set on line 24. The fault distances were 100, 500, and 900 m, respectively. The fault resistances were 0.1 and 1 Ω, respectively, as the line was 1 km in length and the DC voltage was rated at 1000 V.

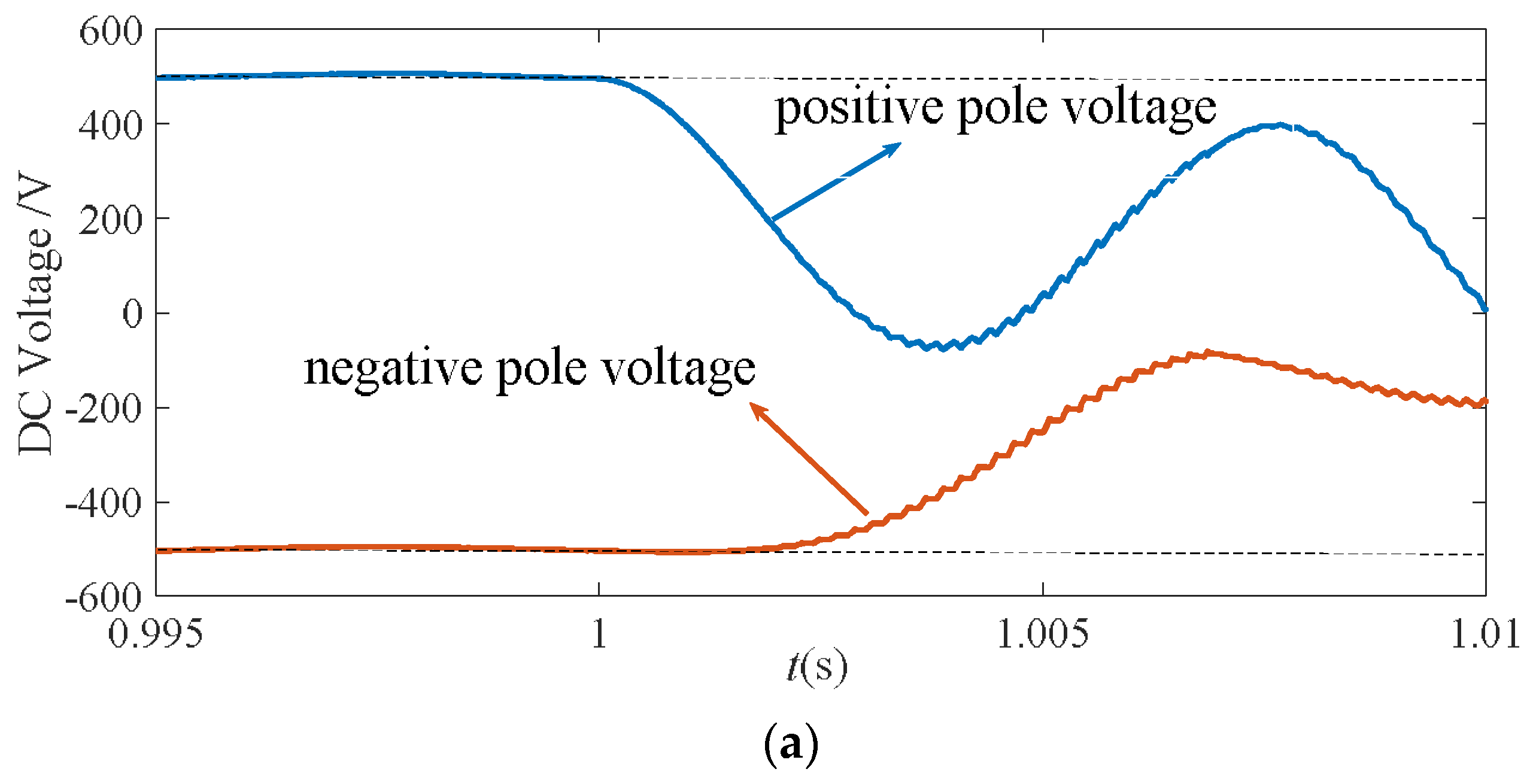
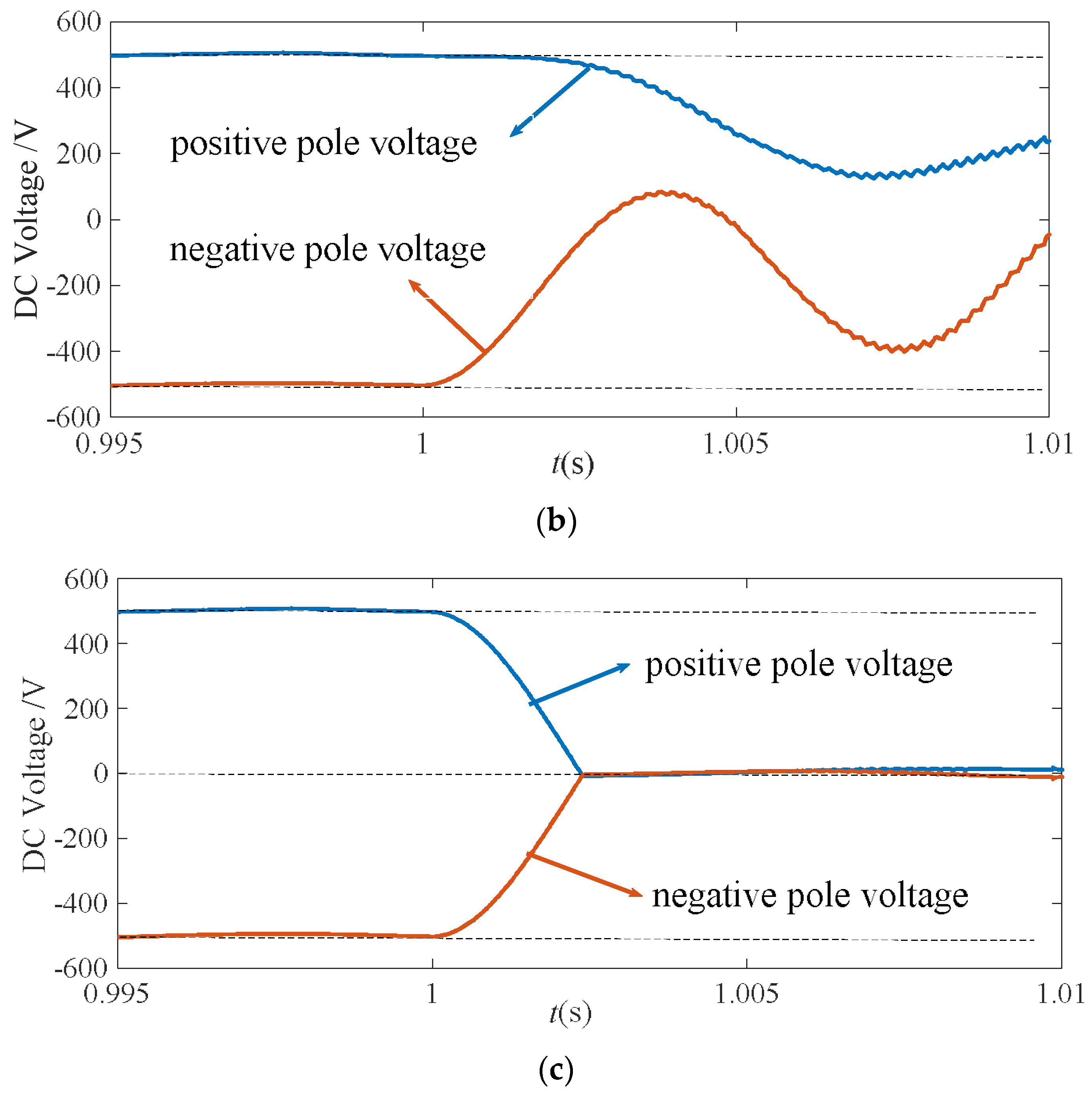
The calculated K_U values were all greater than 1.3 for positive-pole faults-smaller than the setting value of 0.7 and around 1.0 for pole-to-pole faults, which is demonstrated by Equation (14). The proposed faulted pole selection criterion works properly, regardless of the fault resistance and fault distance.

4.3. Simulation of Fault Area Identification

The distance criterion was used to primarily identify the internal faults and forward external faults following the faulted pole selection. Similarly, various distances and fault resistances were considered for PG faults, NG faults, and PP faults. The results are shown in

Table 2. Simulation results of internal fault identification.

Fault Type	x/m	Rfault/Ω	Results
Internal PG, NG, and PP faults	100	0.1	Internal
		1	Internal
	500	0.1	Internal
		1	Internal
	900	0.1	Internal
		1	Internal
External PG, NG, and PP faults	100	0.1	External
		1	External
	500	0.1	External
		1	External
	900	0.1	External
		1	External

¹ PG (NG) fault: positive (negative)-pole-to-ground fault; PP fault: pole-to-pole fault.

, where the internal and external faults are identified correctly.

In this section, the protection zone of the proposed scheme was set as 90% of the length of the whole line. Hence the remaining part should be covered by the backup protection, which was added with a time delay.

4.4. Sensitivity Analysis

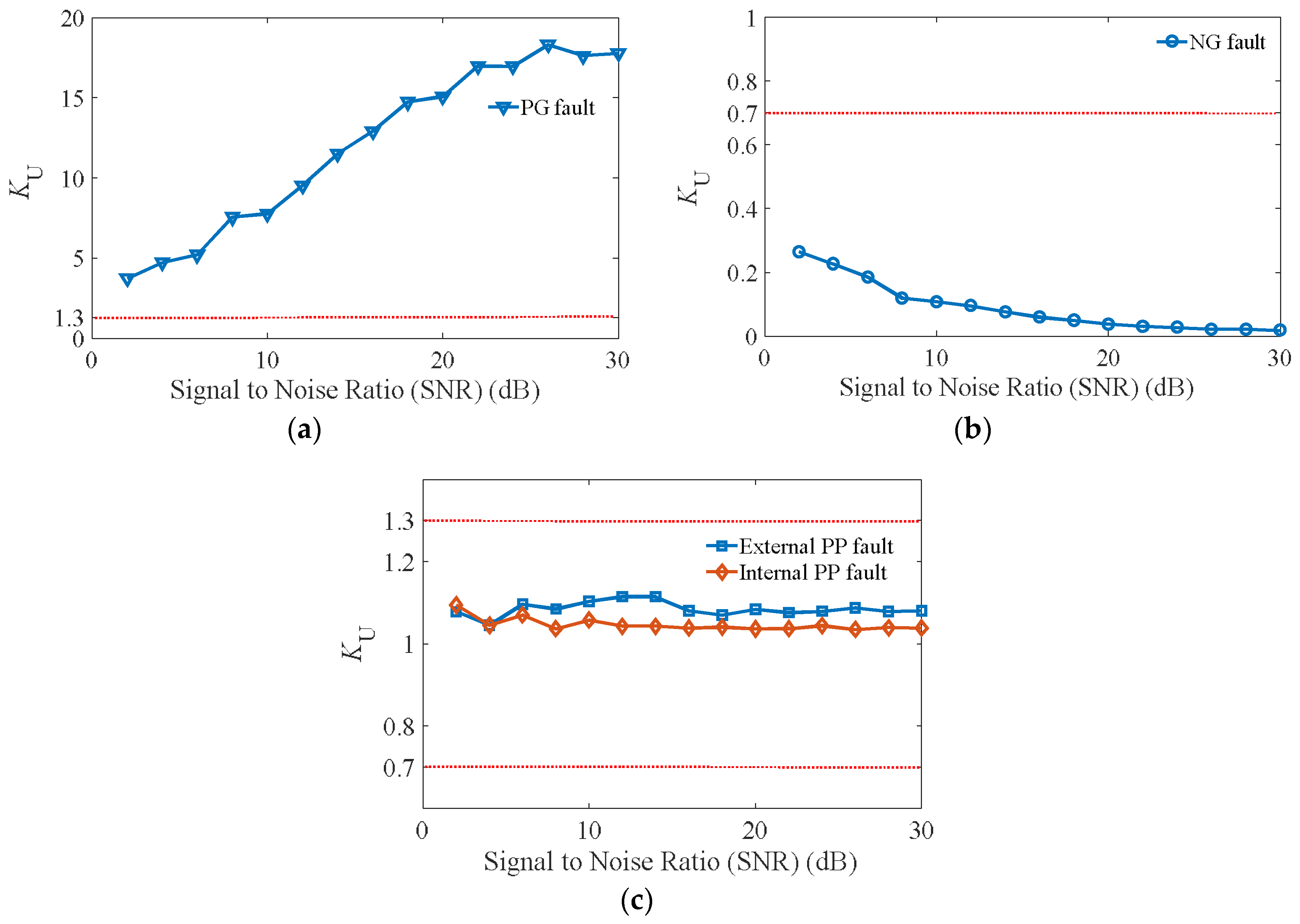
4.4.1. Influence of Signal Noise

This section investigates the impact of signal noise on the proposed protection. The three types of internal faults at the middle of line 12 and the external PP fault on line 24 were simulated. White Gaussian noise was added to the sampling voltage in various levels, with a maximum of 30 dB. Then, the protection scheme was employed. The simulation results for the protections on line 12 with different signal-to-noise ratios (SNRs) are presented in Figure 14. As shown in Figure 14, the ratio K_U was still greater than 1.3 for PG faults and smaller than 0.7 for NG faults even with the high level of additive noise. Meanwhile, the ratio for PP faults did not exceed either of the two thresholds. The results demonstrate that the proposed protection scheme has a high robustness to additive noise.

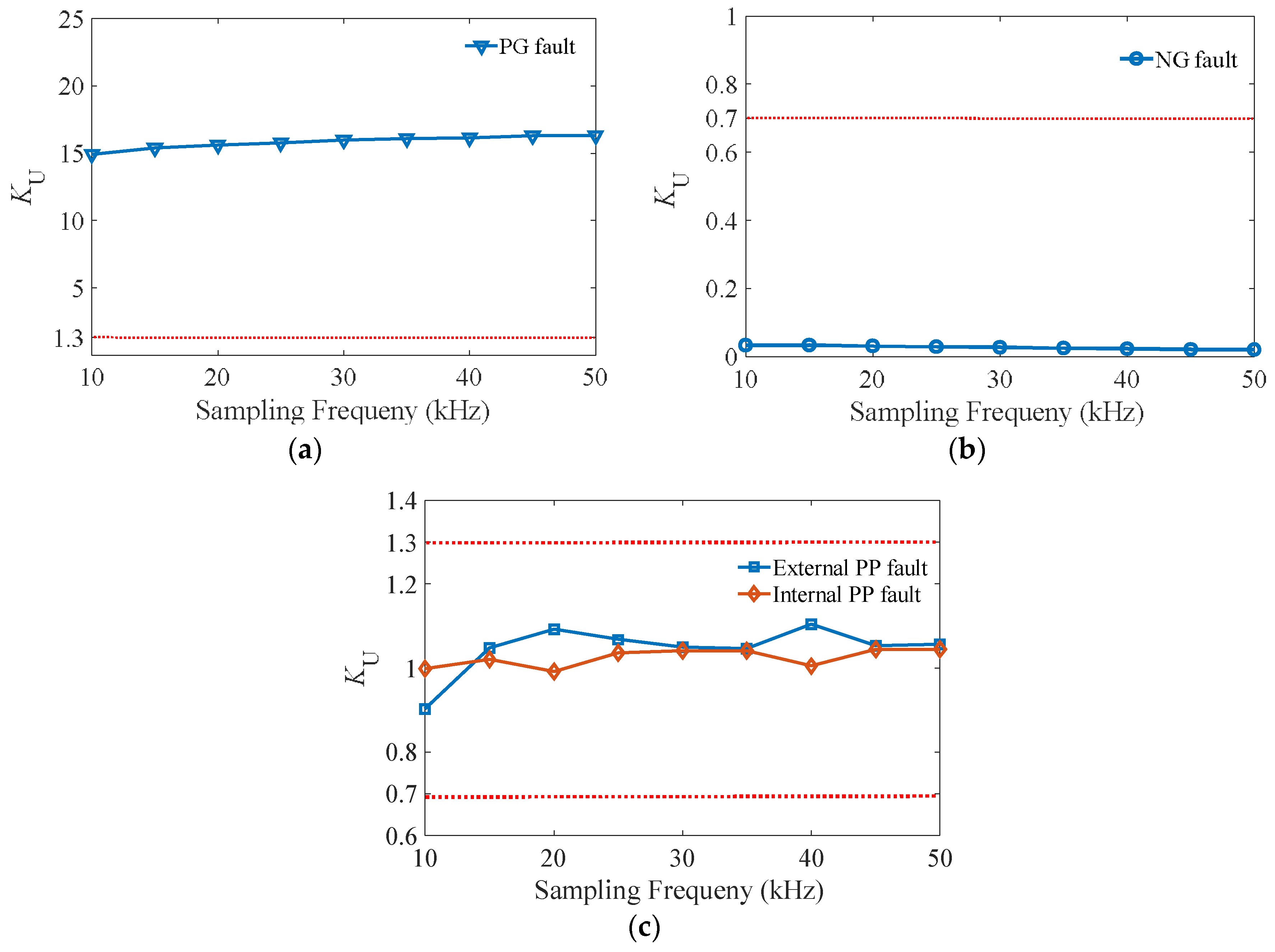
4.4.2. Influence of Sampling Frequency

The impact of the sampling frequency on the proposed scheme could be analyzed by down-sampling the DC voltage signals. The frequency band in this section was from 50 to 10 kHz. The internal faults were simulated at the middle of line 12, while the external fault happened on line 24, with a fault resistance of 0.1 Ω. The K_U value calculated by the pole voltages at CB1 are presented in Figure 15. It is seen that K_U was greater than 1.3 for PG faults and less than 0.7 for NG faults, even with a low level of sampling frequency. Meanwhile, the ratio for PP faults did not exceed either of the two thresholds. Therefore, the proposed protection scheme performs well, undisturbed by the sampling frequency.

5. Conclusions

In this paper, pole-to-pole fault characteristics for VSC-based DC microgrids are investigated, and four transient stages are quantitatively analyzed. On the basis of single-ended transient signals, a protection scheme for DC lines in microgrids is proposed to act as the main protection, which consists of three main steps: a directional criterion, faulted pole selection, and fault area identification. The performance of the proposed protection scheme was tested in a four-terminal system under various conditions in PSCAD/EMTDC. The results demonstrated that the scheme can effectively detect and isolate the forward internal faults only by local information, without data transmission or synchronization. The proposed scheme is robust to the fault distance, resistances, sampling frequency, and signal noise and can satisfy the protection requirements of speed and selectivity.