3D Numerical Study of Multiphase Counter-Current Flow within a Packed Bed for Post Combustion Carbon Dioxide Capture
Abstract
:1. Introduction
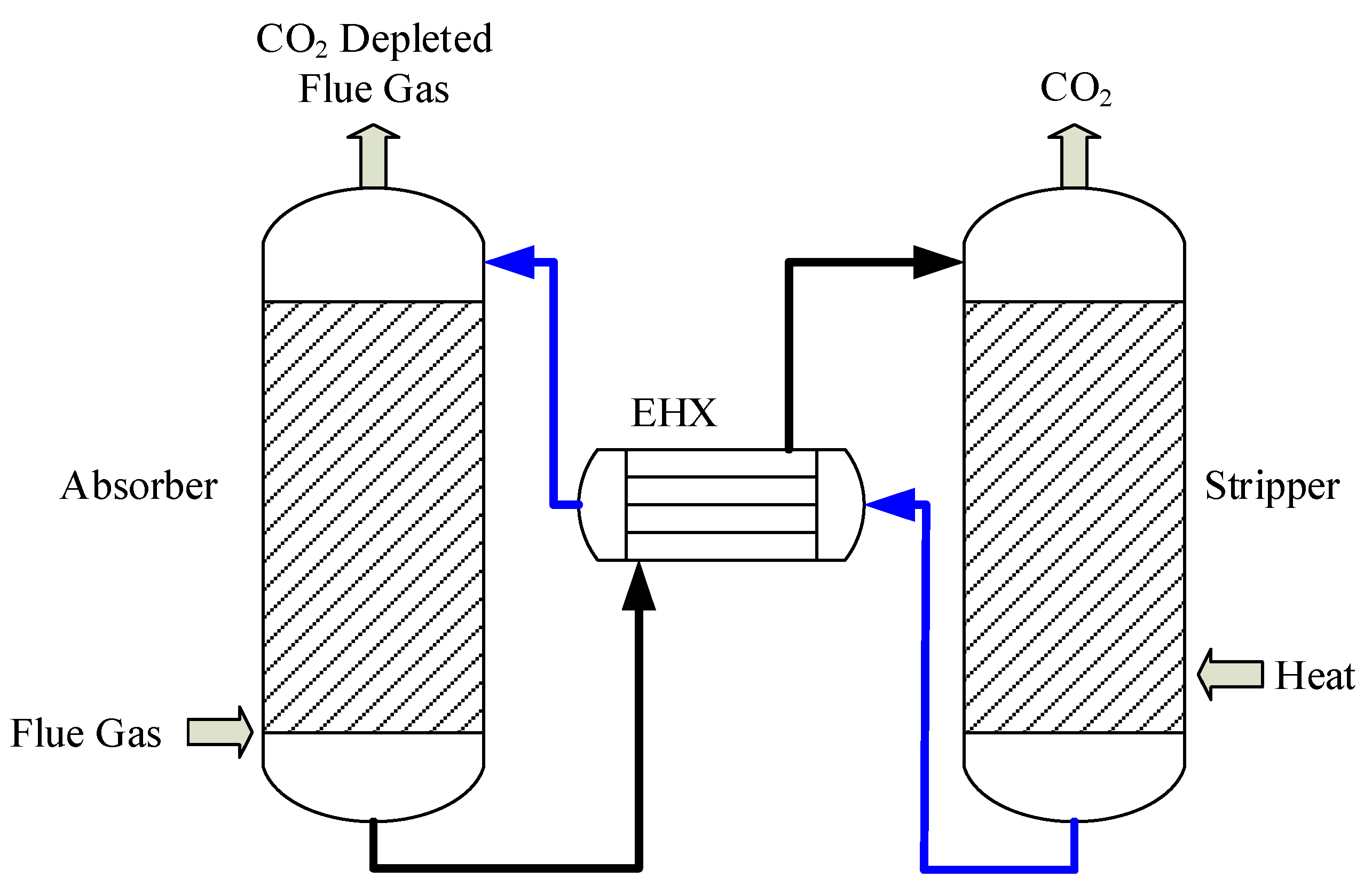
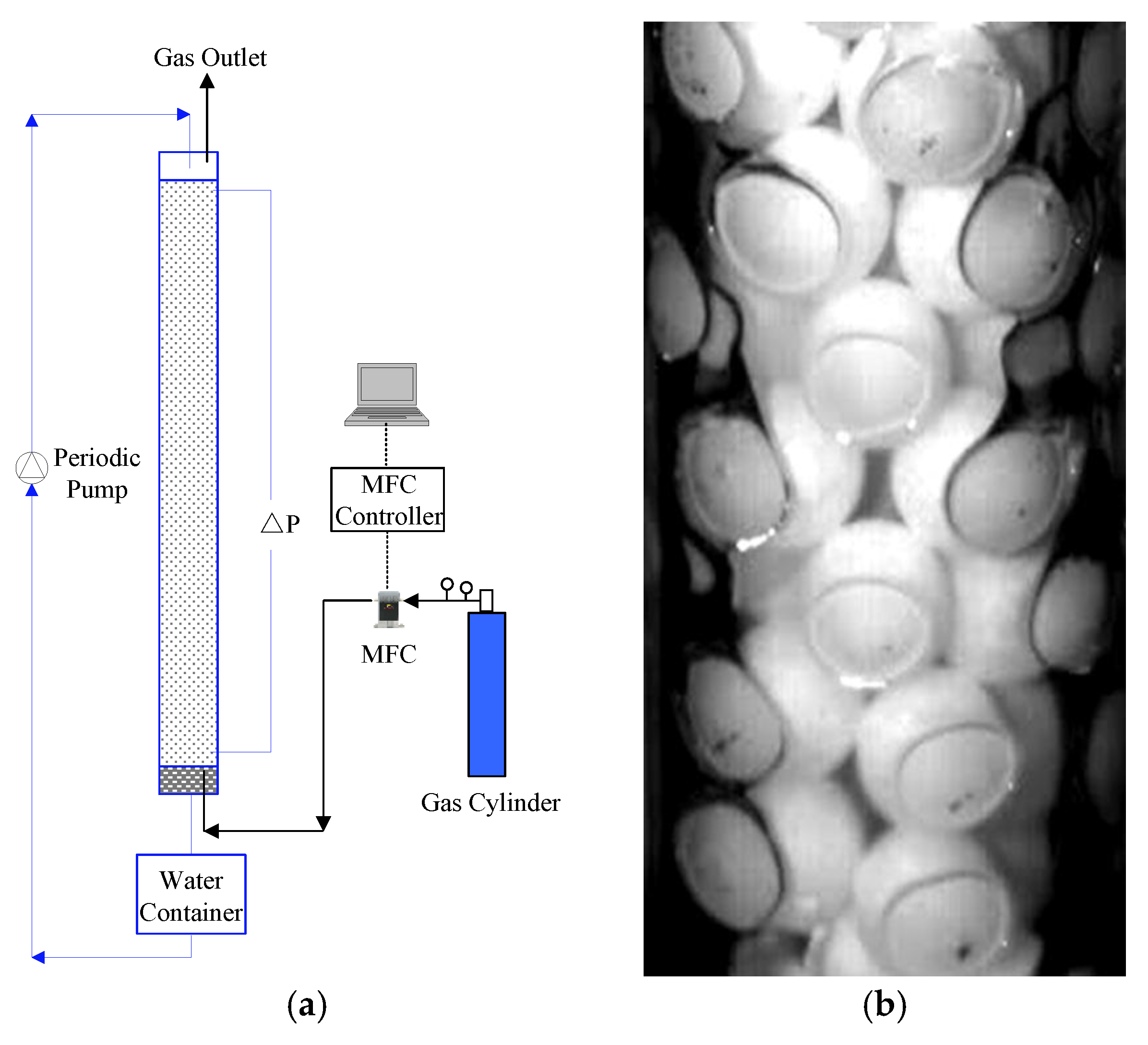
2. Experimental Methods
3. Development of the Numerical Model
3.1. Mesh Generation
3.2. Governing Equation in the VOF Model
3.3. Turbulence Model
3.4. Model Parameters and Boundary Conditions
4. Results and Discussions
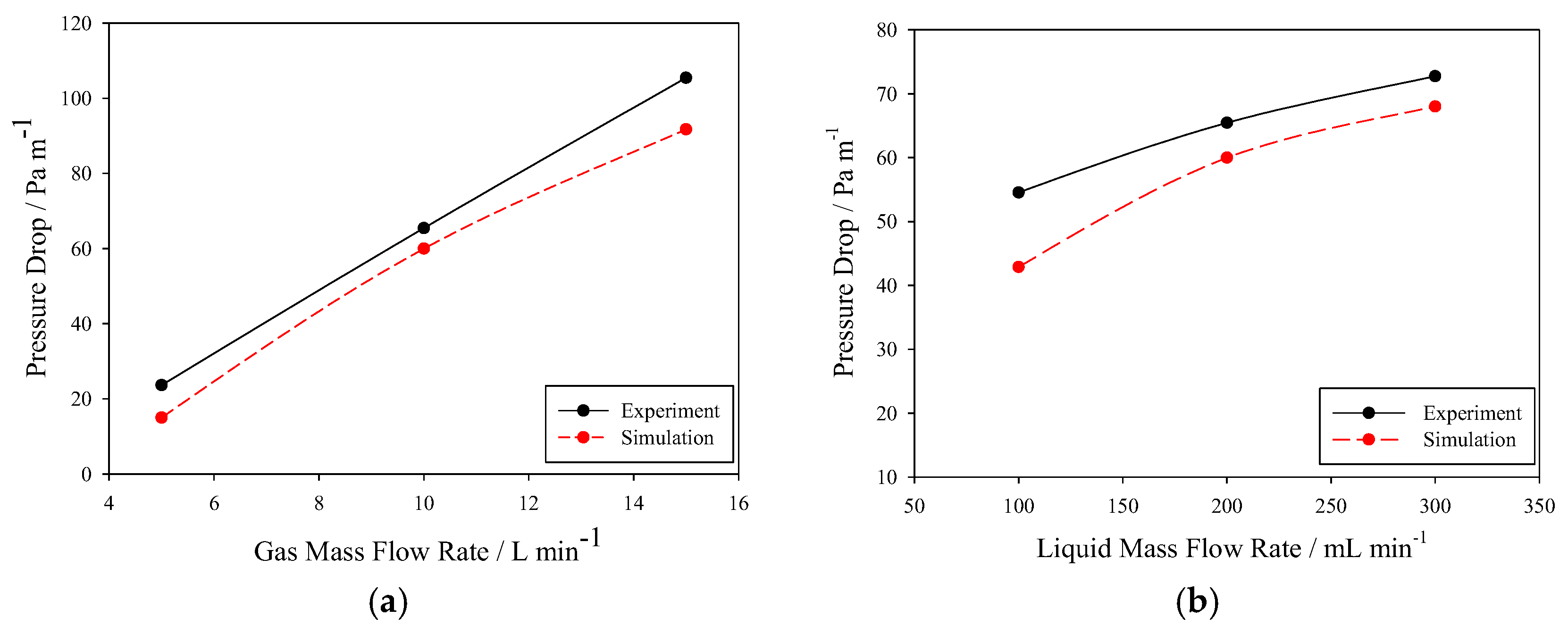
4.1. Model Validation
4.2. Liquid Distribution Characterization
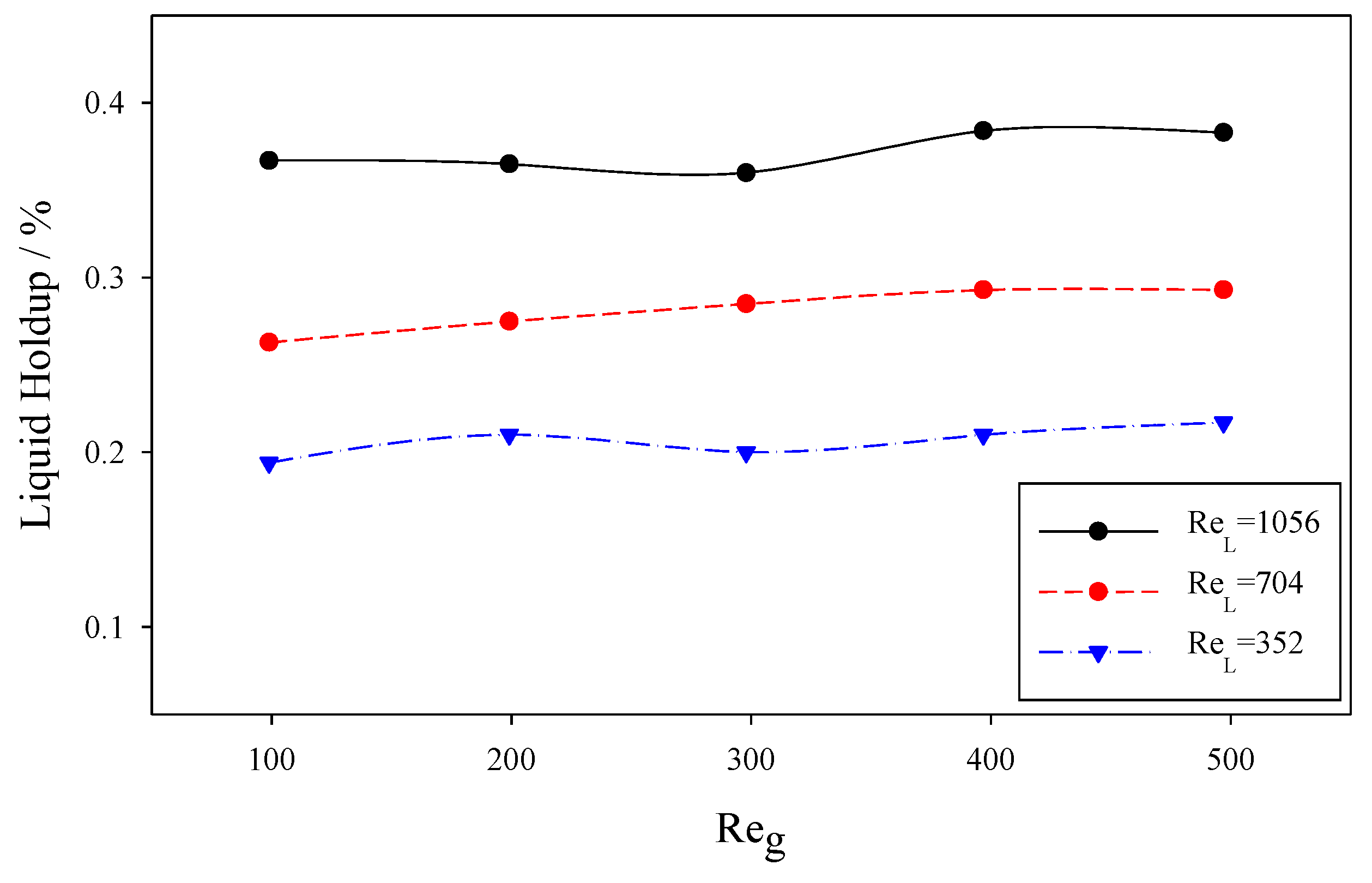
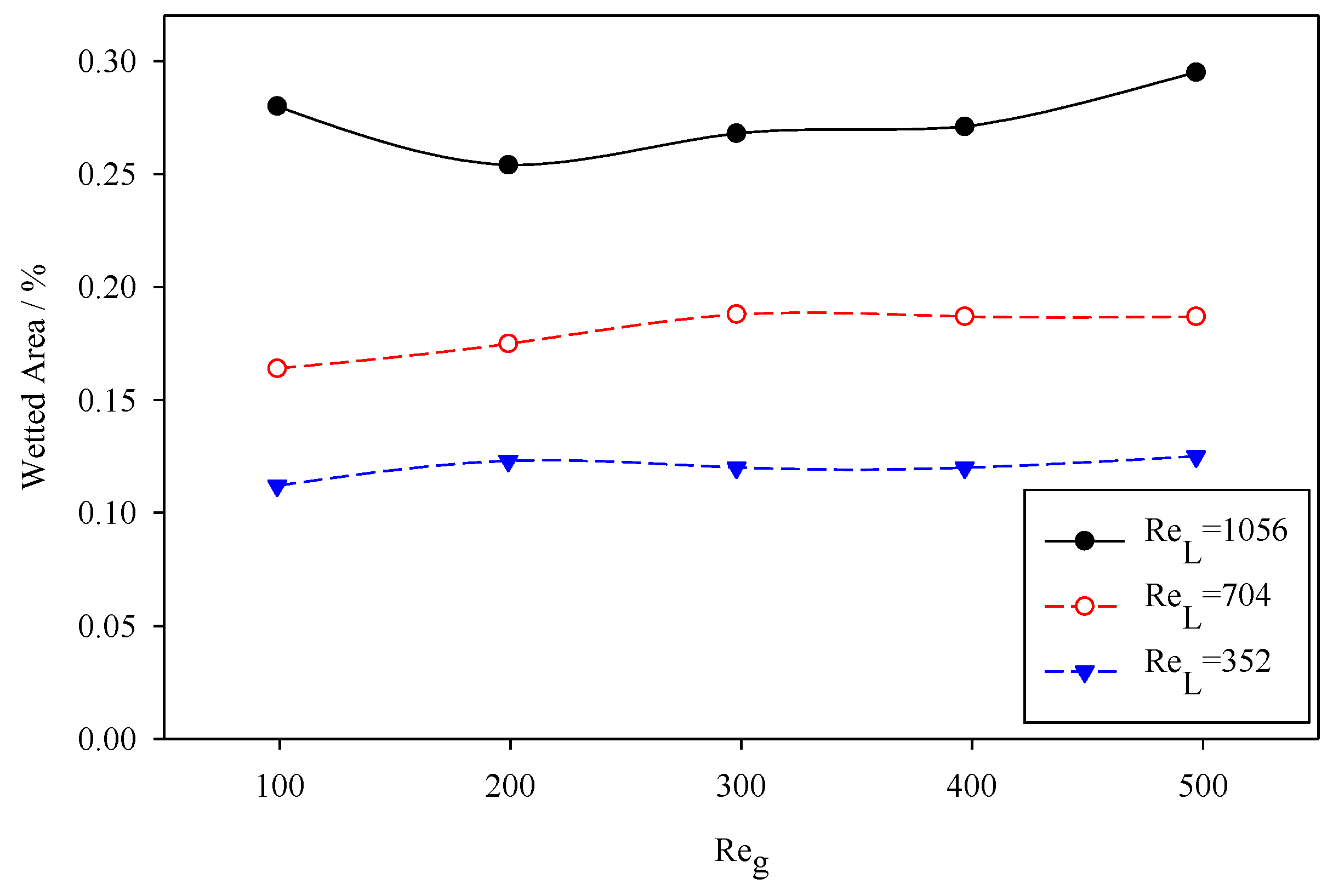
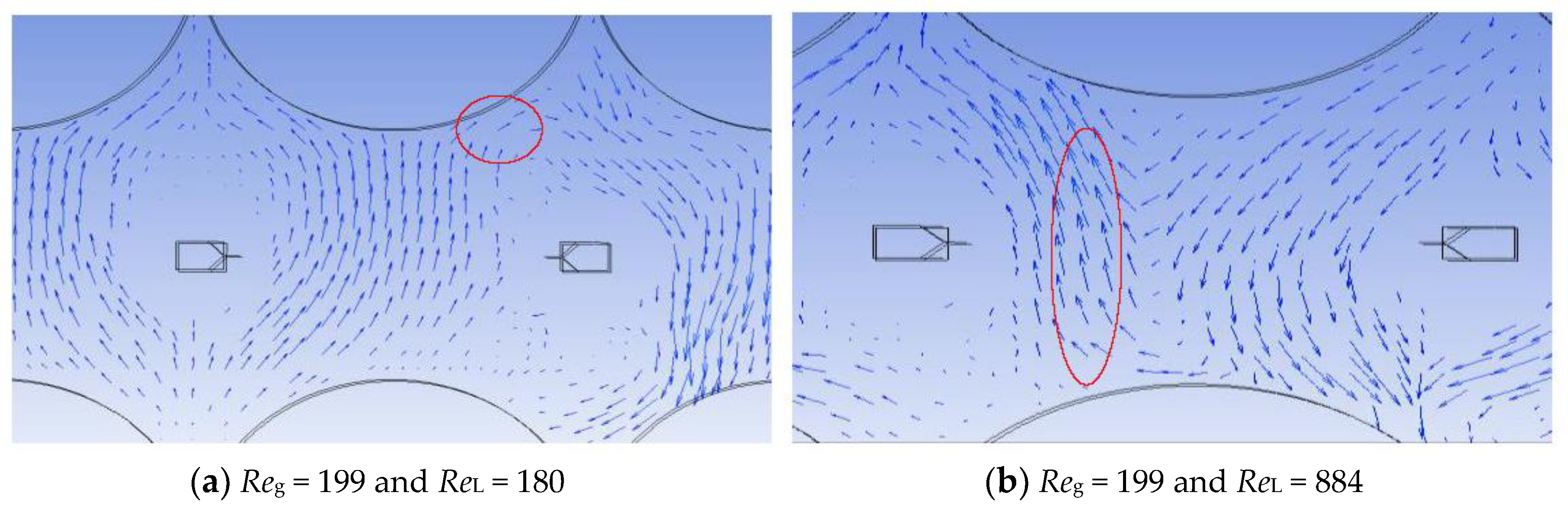
4.3. Gas–Liquid Interactions
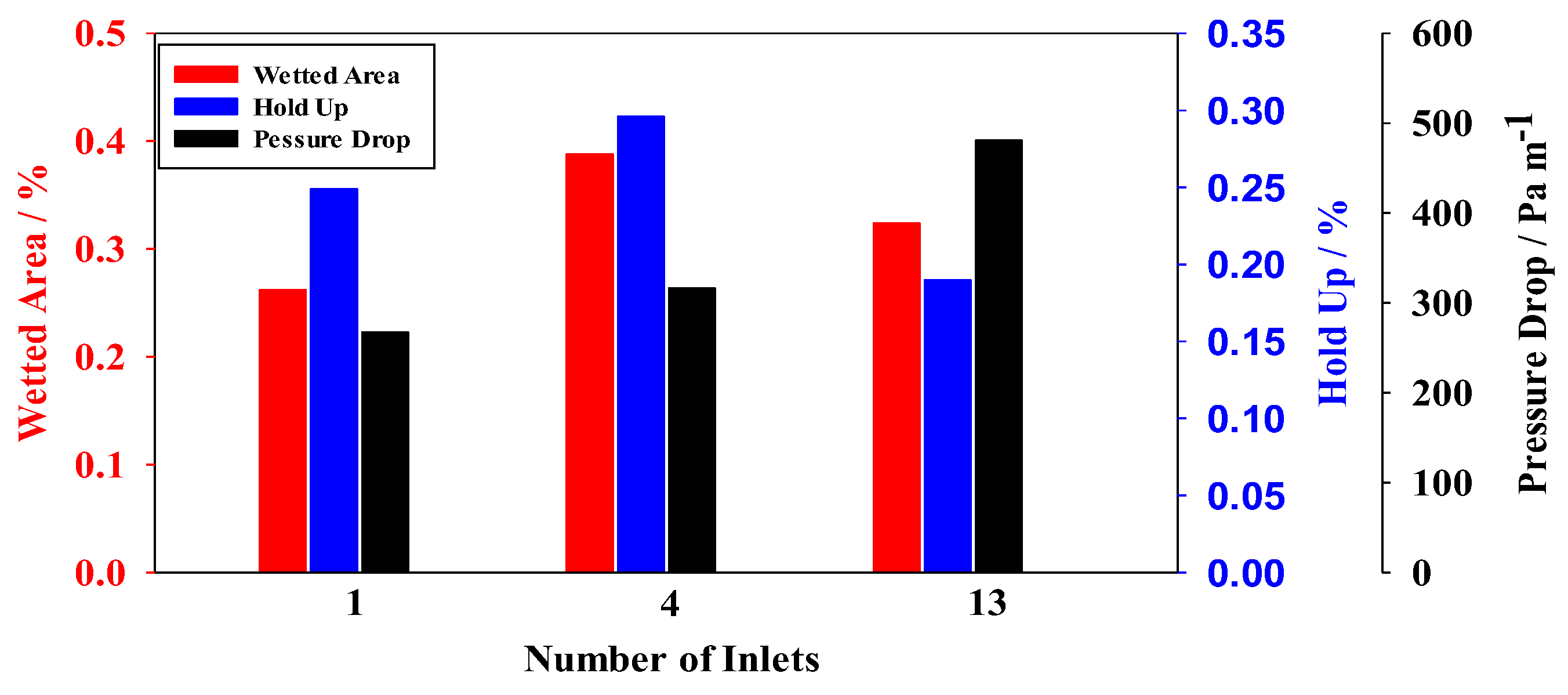
4.4. Effect of the Number of Liquid Inlets
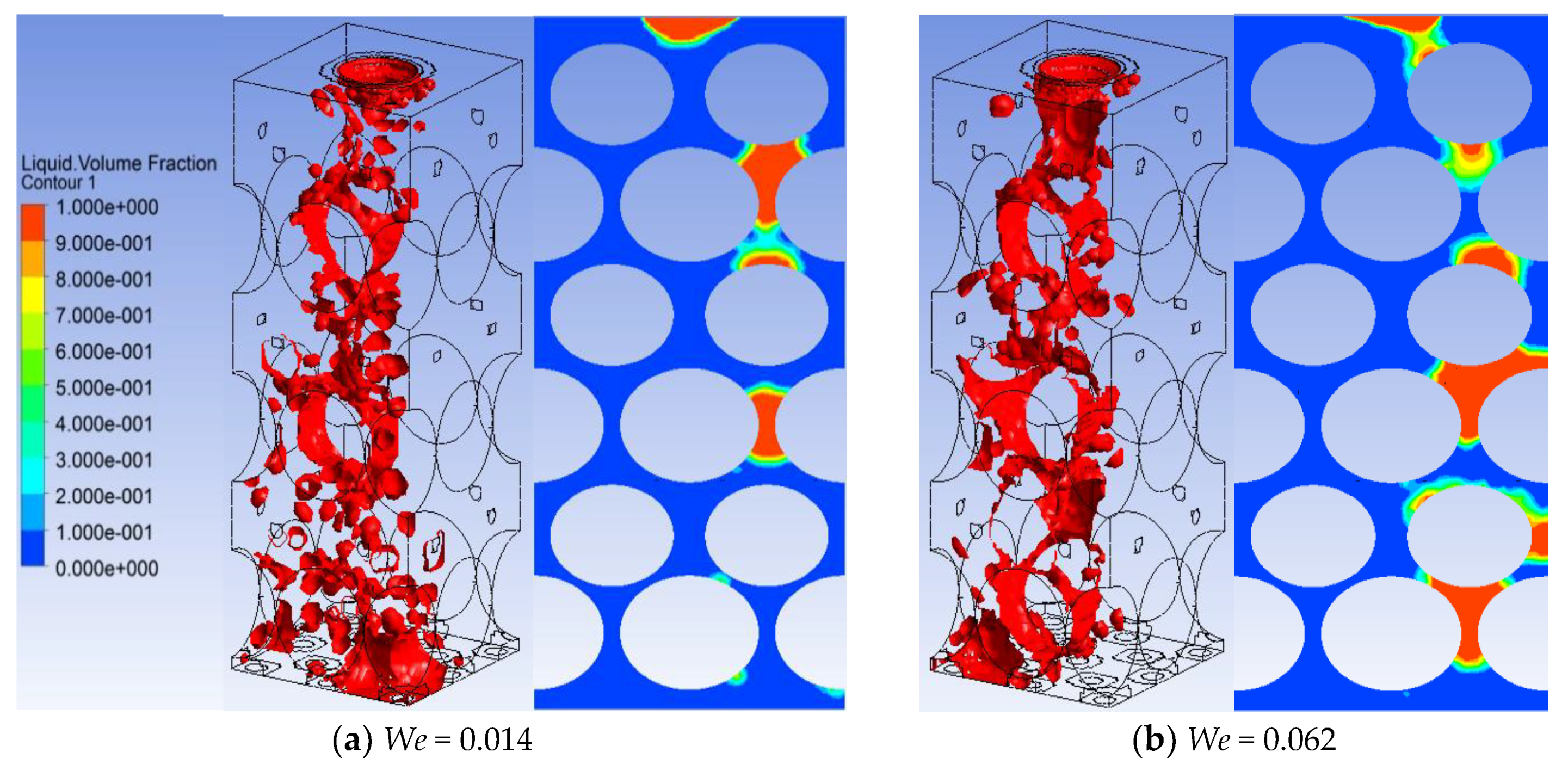
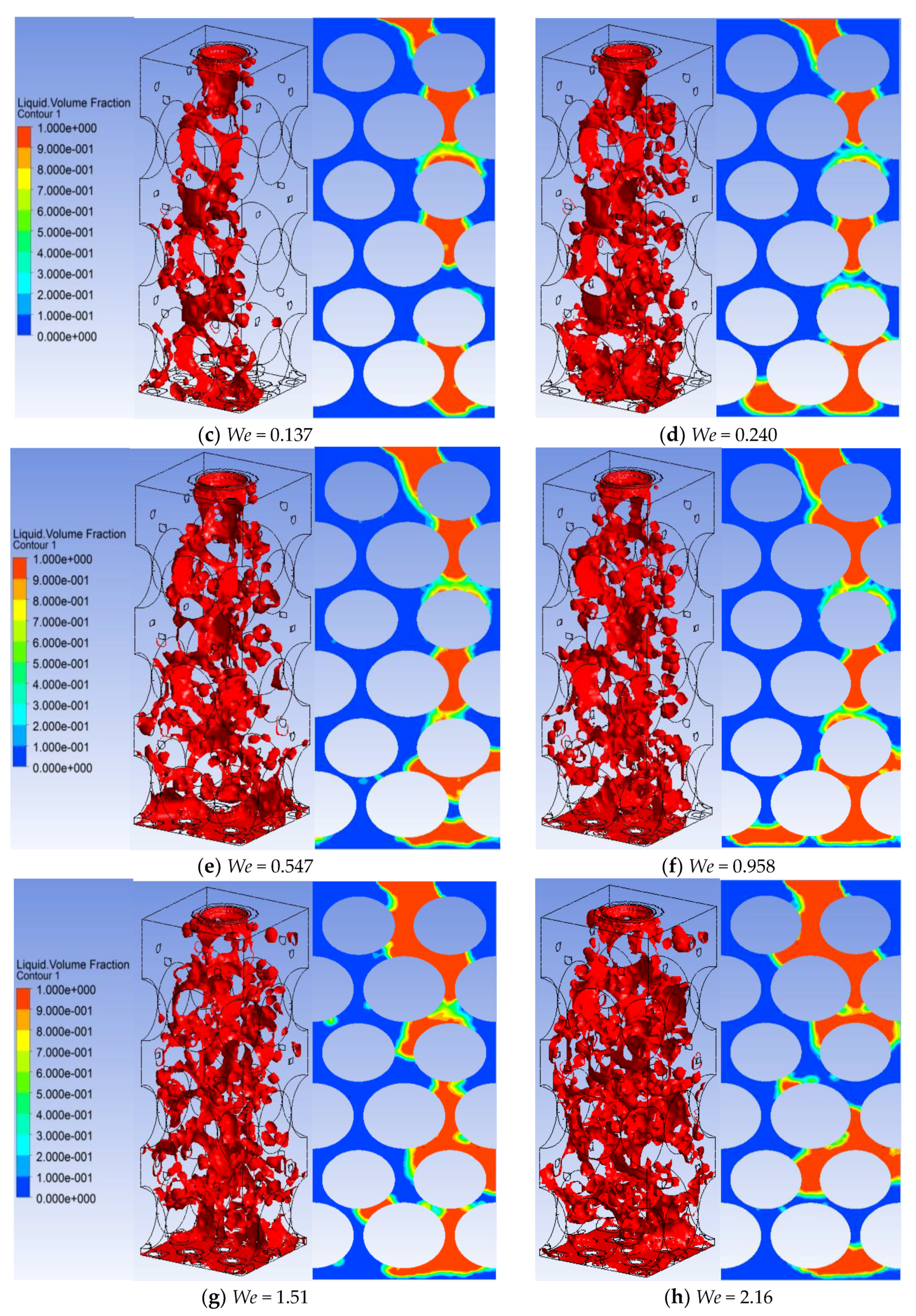
4.5. Effect of Liquid Surface Tension
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muradova, N.Z.; Veziroğlub, T.N. Green path from fossil-based to hydrogen economy: An overview of carbon-neutral technologies. Int. J. Hydrog. Energy 2008, 33, 6804–6839. [Google Scholar] [CrossRef]
- Climate Change 2007: Synthesis Report. Available online: http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_synthesis_report.htm (accessed on 3 June 2018).
- Liu, F.; Chen, L.; Neathery, J.K.; Saito, K.; Liu, K. Cerium oxide promoted iron-based oxygen carrier for chemical looping combustion. Ind. Eng. Chem. Res. 2014, 53, 16341–16348. [Google Scholar] [CrossRef]
- Feron, P.H. Exploring the potential for improvement of the energy performance of coal fired power plants with post-combustion capture of carbon dioxide. Int. J. Greenh. Gas Control 2010, 4, 152–160. [Google Scholar] [CrossRef]
- Mahr, B.; Mewes, D. CFD modelling and calculation of dynamic two-phase flow in columns equipped with structured packing. Chem. Eng. Res. Des. 2007, 85, 1112–1122. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Kashid, M.N.; Ranade, V.V.; Chaudhari, R.V. Hydrodynamics of trickle bed reactors: Experiments and CFD modeling. Ind. Eng. Chem. Res. 2005, 44, 6278–6294. [Google Scholar] [CrossRef]
- Ismail, I.; Gamio, J.C.; Bukhari, S.F.A.; Yang, W.Q. Tomography for multi-phase flow measurement in the oil industry. Flow Meas. Instrum. 2005, 16, 145–155. [Google Scholar] [CrossRef]
- Stapf, S.; Han, S.-I. NMR Imaging in Chemical Engineering; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2006. [Google Scholar]
- Elkins, C.J.; Alley, M.T. Magnetic resonance velocimetry: Applications of magnetic resonance imaging in the measurement of fluid motion. Exp. Fluids 2007, 43, 823–858. [Google Scholar] [CrossRef]
- Llamas, J.-D.; Pérat, C.; Lesage, F.; Weber, M.; D’Ortona, U.; Wild, G. Wire mesh tomography applied to trickle beds: A new way to study liquid maldistribution. Chem. Eng. Process. 2008, 47, 1765–1770. [Google Scholar] [CrossRef]
- Li, L.; Zou, X.; Wang, H.; Zhang, S.; Wang, K. Investigations on two-phase flow resistances and its model modifications in a packed bed. Int. J. Multiphase Flow 2018, 101, 24–34. [Google Scholar] [CrossRef]
- Toukan, A.; Alexander, V.; AlBazzaz, H.; Al-Dahhan, M.H. Identification of flow regime in a cocurrent gas-liquid upflow moving packed bed reactor using gamma ray densitometry. Chem. Eng. Sci. 2017, 168, 380–390. [Google Scholar] [CrossRef]
- Kuzeljevic, Z. Hydrodynamics of Trickle Bed Reactors: Measurements and Modeling. Ph.D. Thesis, Washington University, Saint Louis, MO, USA, 2010. [Google Scholar]
- Attou, A.; Ferschneider, G. Two-fluid model for flow regime transition in gas-liquid trickle-bed reactors. Chem. Eng. Sci. 1999, 54, 5031. [Google Scholar] [CrossRef]
- Propp, R.M.; Colella, P.; Crutchfield, W.Y.; Day, M.S. A numerical model for trickle bed reactors. J. Comput. Phys. 2000, 165, 311–333. [Google Scholar] [CrossRef]
- Souadnia, A.; Latifi, M.A. Analysis of two-phase flow distribution in trickle-bed reactors. Chem. Eng. Sci. 2001, 56, 5977–5985. [Google Scholar] [CrossRef]
- Jiang, Y. Flow Distribution and Its Impact on Performance of Packed-Bed Reactors. Ph.D. Thesis, Washington University, St. Louis, MO, USA, 2000. [Google Scholar]
- Gunjal, P.R.; Ranade, V.V.; Chaudhari, R.V. Liquid phase residence time distribution in trickle bed reactors: Experiments and CFD simulations. Can. J. Chem. Eng. 2003, 81, 821. [Google Scholar] [CrossRef]
- Bednarz, A.; Weber, B.; Jupke, A. Development of a CFD model for the simulation of a novel multiphase counter-current loop reactor. Chem. Eng. Sci. 2017, 161, 350–359. [Google Scholar] [CrossRef]
- Zhao, B. Post-combustion CO2 capture with ammonia by vortex fow-based multistage spraying. Energy 2016, 102, 106–117. [Google Scholar] [CrossRef]
- Tong, Z.; Marek, A.; Hong, W. Experimental and numerical investigation on gravity-driven film flow over triangular corrugations. Ind. Eng. Chem. Res. 2013, 52, 15946–15958. [Google Scholar] [CrossRef]
- Saito, K.; Williams, F.A. Scale modeling in the age of high speed computation. In Progress in Scale Modeling; Springer: Cham, Switzerland, 2014; Volume II, pp. 1–16. ISBN 978-3-319-10308-2. [Google Scholar]
- Liu, F.; Saito, K.; Liu, K. Scale-up of chemical looping combustion. In Progress in Scale Modeling; Springer: Cham, Switzerland, 2014; Volume II, pp. 239–248. ISBN 978-3-319-10308-2. [Google Scholar]
- Lopes, R.J.; Quinta-Ferreira, R.M. Quinta-Ferreira: CFD modelling of multiphase flow distribution in trickle beds. Chem. Eng. J. 2009, 147, 342–355. [Google Scholar] [CrossRef]
- Dybbs, A.; Edwards, R.V. A New Look at Porous Media Fluid Mechanics—Darcy to Turbulent. In Fundamentals of Transport Phenomena in Porous Media; Bear, J., Corapcioglu, M.Y., Eds.; NATO ASI Series (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1984; Volume 82. [Google Scholar]
- Labourasse, E.; Lacanette, D.; Toutant, A.; Lubin, P.; Vincent, S.; Lebaigue, O.; Caltagirone, J.-P.; Sagaut, P. Towards Large Eddy Simulation of isothermal two-phase flows: Governing equations and a priori tests. Int. J. Multiphase Flow 2007, 33, 1–39. [Google Scholar] [CrossRef]
- Vincent, S.; Larocque, J.; Lacanette, D.; Toutant, A.; Lubin, P.; Sagaut, P. Numerical simulation of phase separation and a priori two-phase LES filtering. Comput. Fluids 2008, 37, 898–906. [Google Scholar] [CrossRef]
- Christensen, D.E.; Deigaard, R. Large eddy simulation of breaking waves. Coast. Eng. 2001, 42, 53–86. [Google Scholar] [CrossRef]
- Sebastia-Saez, D.; Gu, S.; Ranganathan, P.; Papadikis, K. 3D modeling of hydrodynamics and physical mass transfer characteristics of liquid film flows in structured packing elements. Int. J. Greenh. Gas Control 2013, 19, 492–502. [Google Scholar] [CrossRef]
- Fu, D.; Wei, L.; Liu, S. Experiment and model for the surface tension of carbonated MEA–MDEA aqueous solutions. Fluid Phase Equilib. 2013, 337, 83–88. [Google Scholar] [CrossRef]
- Johnston, P.M.; Zhu, J.-X.; Lasa, H.I.; Zhang, H. Effect of distributor designs on the flow development in downer reactor. AIChE J. 1999, 45, 1587–1592. [Google Scholar] [CrossRef]



| Boundary | Materials | Type | Value | Velocity (m/s) | Reynolds Number | We Number |
|---|---|---|---|---|---|---|
| Liquid inlet | Water | Mass flow rate | 100–1200 mL/min | 0.012–0.147 | 180–1100 | 0.014–2.2 |
| Gas inlet | Air | Mass flow rate | 5–25 L/min | 0.076–0.382 | 99–500 | |
| Liquid outlet | Pressure-outlet | 0 Pa | ||||
| Gas outlet | Pressure-outlet | 0 Pa |
| Cases | Gas Phase Mass Flow Rate (L/min) | Liquid Phase Mass Flow Rate (mL/min) | Gas Side Pressure Drop (Pa/m) |
|---|---|---|---|
| 1 | 5 | 200 | 23.64 |
| 1 | 10 | 200 | 65.45 |
| 1 | 15 | 200 | 105.45 |
| 2 | 10 | 100 | 54.55 |
| 2 | 10 | 200 | 65.45 |
| 2 | 10 | 300 | 72.73 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Liu, F.; Song, Z.; Liu, K.; Saito, K. 3D Numerical Study of Multiphase Counter-Current Flow within a Packed Bed for Post Combustion Carbon Dioxide Capture. Energies 2018, 11, 1441. https://doi.org/10.3390/en11061441
Yang L, Liu F, Song Z, Liu K, Saito K. 3D Numerical Study of Multiphase Counter-Current Flow within a Packed Bed for Post Combustion Carbon Dioxide Capture. Energies. 2018; 11(6):1441. https://doi.org/10.3390/en11061441
Chicago/Turabian StyleYang, Li, Fang Liu, Zhengchang Song, Kunlei Liu, and Kozo Saito. 2018. "3D Numerical Study of Multiphase Counter-Current Flow within a Packed Bed for Post Combustion Carbon Dioxide Capture" Energies 11, no. 6: 1441. https://doi.org/10.3390/en11061441
APA StyleYang, L., Liu, F., Song, Z., Liu, K., & Saito, K. (2018). 3D Numerical Study of Multiphase Counter-Current Flow within a Packed Bed for Post Combustion Carbon Dioxide Capture. Energies, 11(6), 1441. https://doi.org/10.3390/en11061441





