1. Introduction
The super capacitor energy storage system (SCESS) with the advantages of a high-power density, long life, and widely operating temperature, is widely used in industrial applications. The super capacitors (SCs) are low voltage devices, the rated voltage of which with organic electrolytes is <3.0 V per cell, whereas with aqueous electrolytes, it is <1.23 V per cell [
1]. However, the SCESS is often used with a high voltage, such as the SCESS used in the metro regenerative braking energy absorption system [
2] and wind farms or photovoltaic plants [
3]. The high voltage SCESS is composed of a large number of SCs connected in series. Because of the limitation of the manufacturing process and inconsistent parameters attenuation during use, the parameters such as capacitance, internal resistance, and leakage are inconsistent, which will cause voltage inconsistency, and the overvoltage phenomena of SCs even appear, which will reduce the life of SCs [
4,
5]. A fast voltage equalizer is needed for high voltage SCESS to avoid the SCs’ overvoltage phenomena and ensure the security of the SCESS.
During use, the voltage of SC is usually from 0.5 times U
N to U
N (the rated voltage). A voltage lower than 0.5U
N but higher than zero will be harmless to SC, which is different from batteries, because a low voltage can damage the batteries. Once the voltage is higher than U
N, it will cause irreversible damage to SCs and results in life reduction [
5]. The focus of the equalizer for SCESS should be discharging the higher voltage SCs with high speed. The SCESS usually works with instantaneous high-power, while the balancing current of the equalizer is relatively small, so the effects of the equalizer can be ignored during the working of SCESS. In most high-power applications, the SCESS works with a high current for a short time and is then left to stand for a time
ts to prepare next power rush [
6]. When the SCESS is charged from 0.5U
N to U
N, the SC with the minimum capacitance
Cmin will have the highest voltage
VSCmax. The equalizer should discharge the highest voltage SC and make the voltage drop to the average voltage
VSCav within the time
ts. Then, the desired balancing speed for SCESS can be described as (1), where
idis is the value of discharging current which represents the desired balancing speed and ∆
Q is the charge to be discharged. Different applications have different standing times
ts, so the desired balancing speed will also be different; in any case, the faster the better.
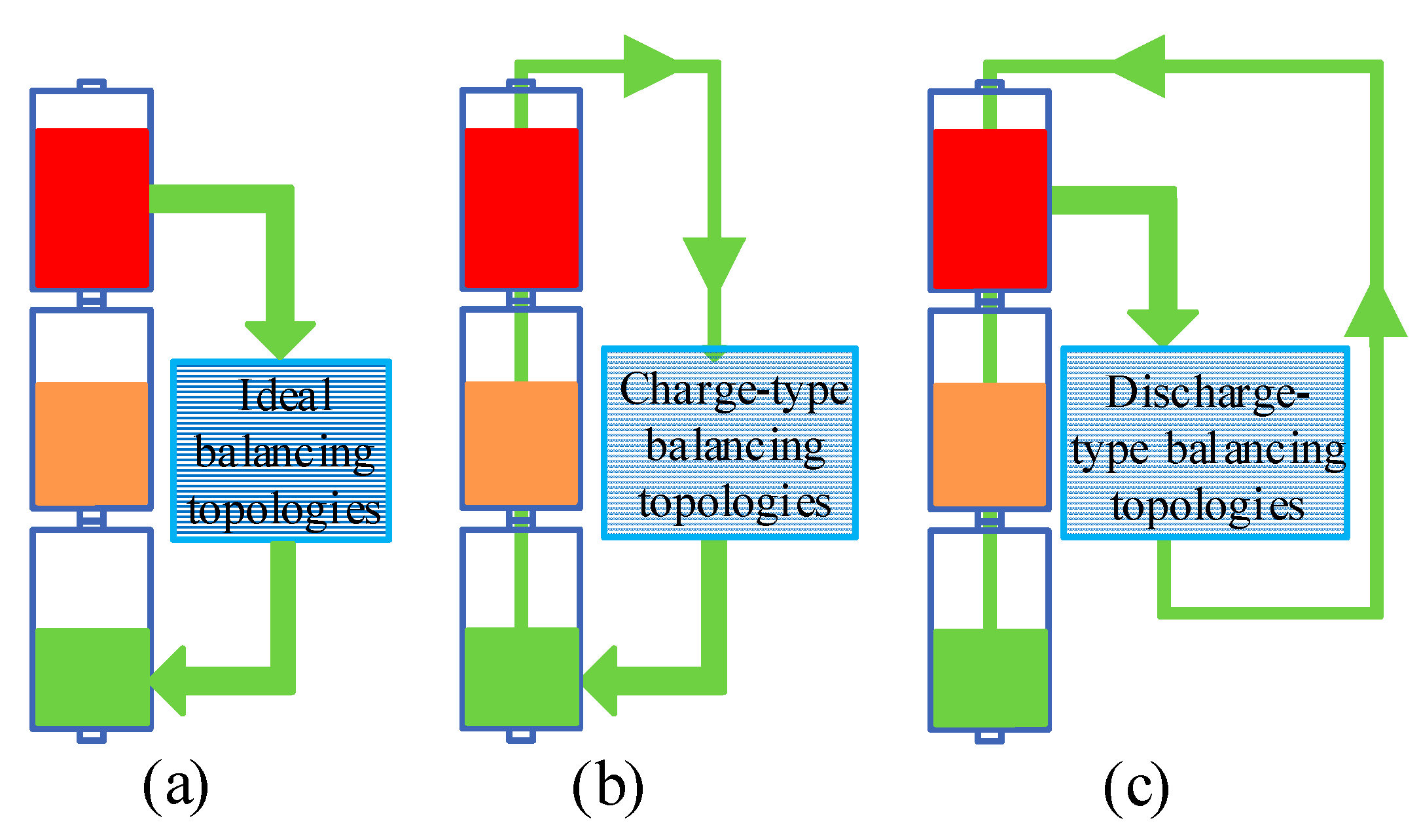
Numerous balancing topologies have been developed by scholars and engineers. According to the ways in which energy can be transferred, the voltage balancing system can be divided into ideal balancing topologies, charge-type balancing topologies, and discharge-type balancing topologies, which are shown in
Figure 1.
As shown in
Figure 1a, the technical characteristics of ideal balancing topology are: the energy from the higher voltage SCs is transferred to the lower voltage SCs directly and simultaneously. In the literature [
7,
8], the ideal balancing topology is realized by using switches connecting each SC to the transformer windings. These windings with the same turn ratio share the same transformer core. When the switches are turned on simultaneously, the energy from the higher voltage SCs is transferred to the lower voltage SCs directly by the transformer core. However, with these balancing topologies, the turn ratio of windings should be strictly consistent. Furthermore, it is difficult to use in the high voltage SCESS, because the number of windings which share the same core are limited. The modularization technique can be used to make the multi-winding transformer balancing topology suitable for the high voltage energy storage system (ESS) [
7,
9,
10]. These voltage equalizers with a high efficiency and small balancing current between modules are very suitable for the battery energy storage system (BESS). However, they are not suitable for SCESS, which needs a faster balancing speed. Because the SCESS will be repeatedly charged and discharged with an instantaneous high current and the terminal voltage will be changed frequently, the fast voltage equalizers are needed to avoid the SCs’ overvoltage phenomena.
The isolation bi-directional DC/DC converters with the properties of being easily cascaded and low-cost are one of the perfect candidates for the realization of an ideal balancing topology. In [
11], the bidirectional DC/DC converter balancing topologies are used to realize the ideal balancing topology; however, the cost of the bidirectional DC/DC converters is high. Quasi ideal balancing topologies are easier to implement, including the buck/boost converter balancing topologies [
12,
13], the switched capacitor balancing topologies [
14,
15], and so on. These balancing topologies can discharge the higher voltage SCs and charge the lower voltage SCs, but not directly and simultaneously, so the balancing speed is slower than the ideal balancing topology. Beside the ideal balancing topologies, the charge-type topologies and discharge-type topologies are widely researched and used.
As shown in
Figure 1b, the technical characteristics of the charge-type balancing topologies are: the lower voltage SCs are charged with the energy from the SCESS directly. The higher voltage SCs are discharged indirectly with a small current. Many charge-type balancing topologies are researched, such as the topology based on the voltage multiplier [
16,
17], based on the fly-back circuit [
18,
19], based on the forward circuit [
20,
21], and so on. These topologies are not aimed at the discharging of the higher voltage SCs, but the charging of the lower voltage SCs and the discharging speed of the higher voltage SCs is slow. Once the voltage of an SC is much higher than the average voltage, it will take a long time to discharge it, so the overvoltage phenomena may then occur. So, the charging-type topologies can do little to protect the overvoltage SCs, which are not the absolute security topologies.
The discharge-type balancing topologies are security topologies, shown in
Figure 1c, and the technical characteristics are: the higher voltage SCs are discharged directly, and the extra energy from the higher voltage SCs is fed back to the SCESS. The discharge-type topologies discharge the higher voltage SCs directly and the overvoltage phenomena of SCs will not occur. The passive balancing topologies belong to discharge-type topologies, but with zero efficiency [
22]. This is because the extra energy of the higher voltage SCs is dissipated in the form of heat by resistance, Zener diodes, and so on. In the literature [
23], the higher voltage SCs are discharged by the fly-back converters and the extra energy is fed back to the SCESS by making the output voltage of the fly-back converters higher than the voltage of SCESS, the high step-up ratio fly-back converters are needed, which are difficult to implement in a small size, and high voltage stress of switches will cause a power loss increase. Furthermore, if the output current passes through lots of diodes then the efficiency is reduced.
In some applications, the ESS can work without the additional equalizer and voltage balancing is achieved by the control of a cascaded multilevel converter (CMC) or modular multilevel converter (MMC). The cells or cell units are connected in series by means of a half-bridge or full-bridge multilevel converter to form MMC or CMC, and the voltage balancing is realized by the control of MMC or CMC [
24,
25,
26,
27,
28]. It is easy to achieve voltage balancing of SCESS with MMC or CMC and each cell can be removed from the current path without interrupting the operation of the system. However, there are some drawbacks that limit the wide use of MMC or CMC. First, the control strategy of MMC or CMC is usually complex. Furthermore, the MMC or CMC is high-cost and has a poor efficiency with high current applications. Because the high load current passes through each half-bridge or full-bridge converter, the high-current level switches are costly and the high current will cause high on-resistance of switches, which can reduce the efficiency of the system. Besides, large numbers of switches working with a high current will give rise to hidden faults, which will reduce the reliability of the system.
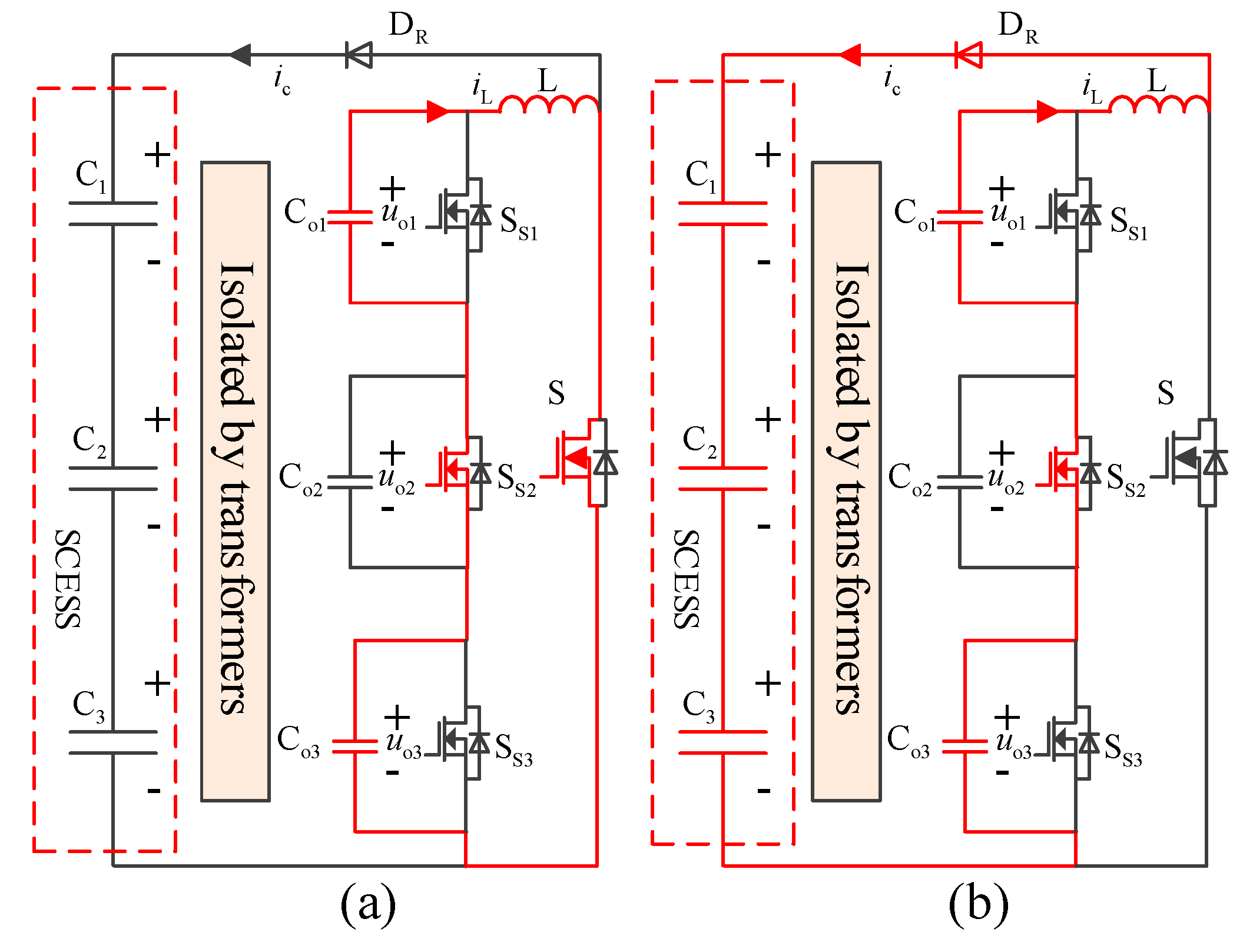
To achieve a fast and security balancing topology for series-connected super capacitor string, a novel modularized discharge-type equalizer for a series-connected SC string is proposed in this paper. With the proposed topology, the higher voltage SCs are discharged by the cascaded converter modules with a big current, so the overvoltage phenomena of the SCs can be avoided. The energy from the higher voltage SCs is transferred to the cascaded converter modules and will be fed back to the SCESS by a boost converter. The critical characteristics of the proposed balancing topology are: (a) Modularized converter makes the balancing system suitable for different voltage levels SCESS; (b) it belongs to discharge-type balancing topology and has an excellent discharge performance which can avoid the over voltage phenomenon of SCs and increase the security of the system; (c) it is suitable for series-connected SC string due to the excellent isolation performance; (d) the voltage stress of the switches inside the cascaded converter modules is low, which is different from the existing modularized discharge-type balancing topology [
23]; and (e) the control of the cascaded converter modules and boost converter can be implemented by analog devices which will simplify the control of the system. The next part of this paper is organized as follows: In the second section, the working principle of the proposed balancing topology is discussed. In the third section, the control strategy of the proposed topology is discussed and an in-depth comparative analysis with the charge-type balancing topology is made from the perspectives of balancing speed and round-trip energy efficiency. In the fourth section, the experiment is implemented to verify the proposed topology. Following this, a conclusion to this paper is presented.
2. Working Principle of the Propose Balancing Topology
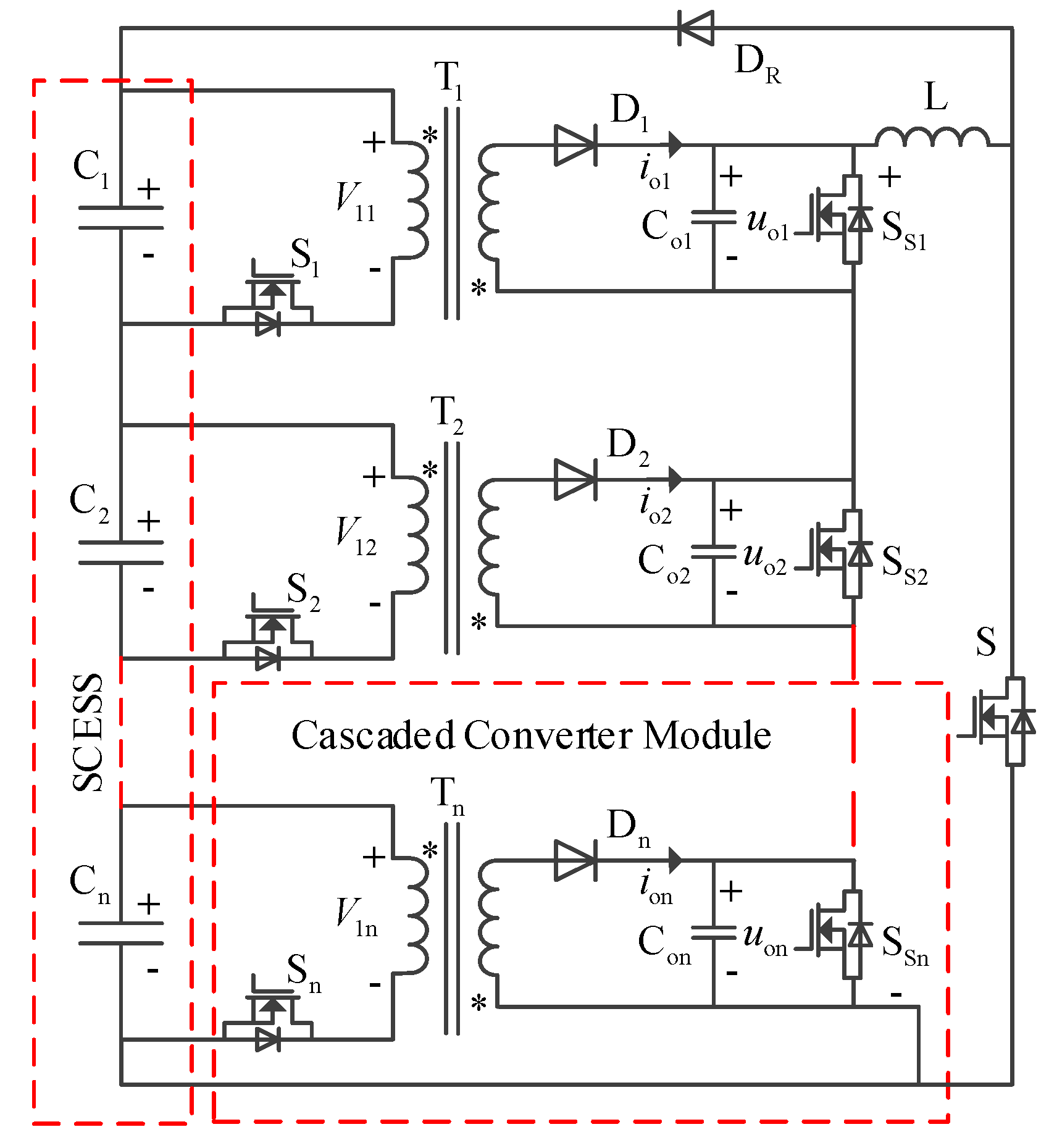
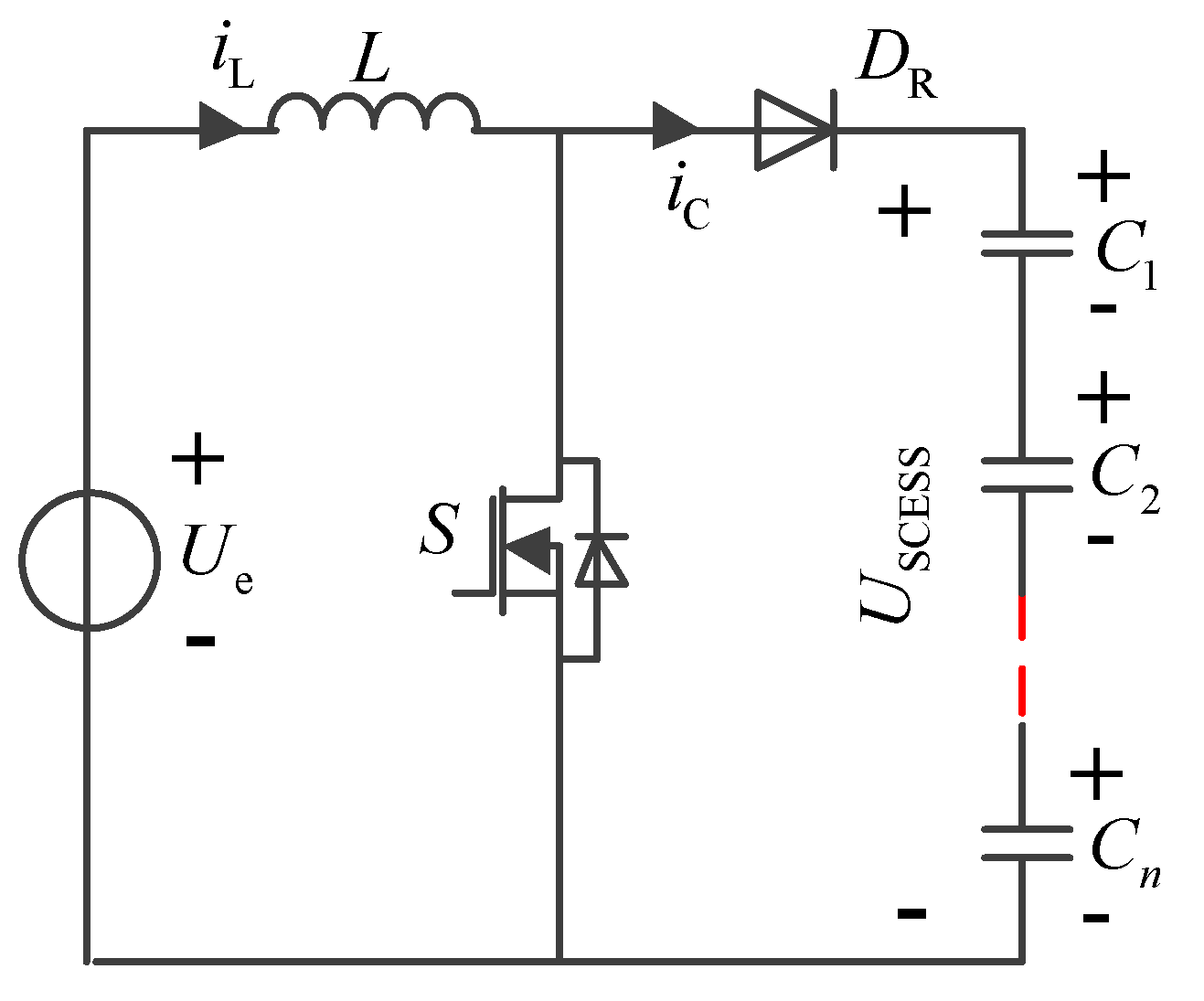
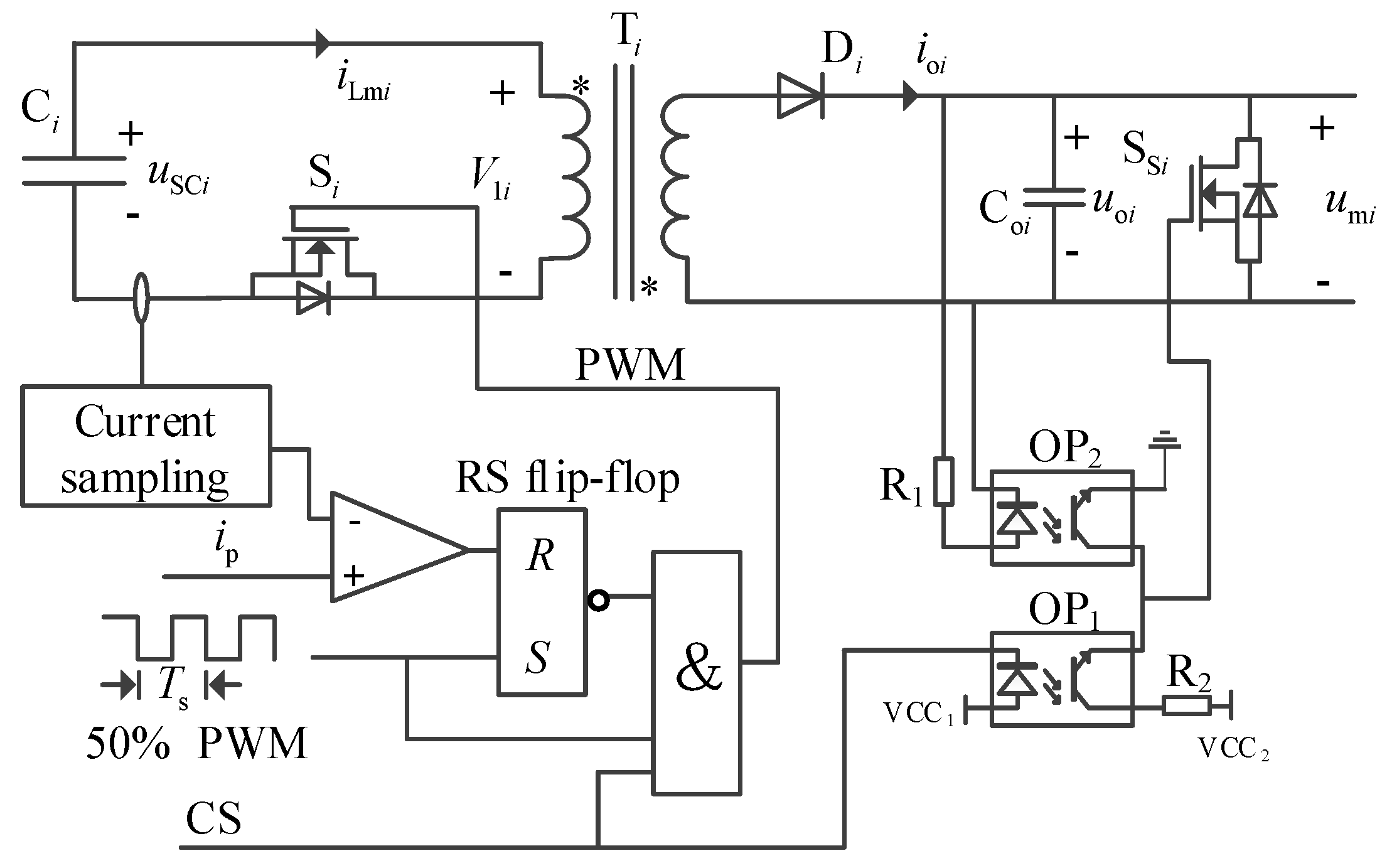
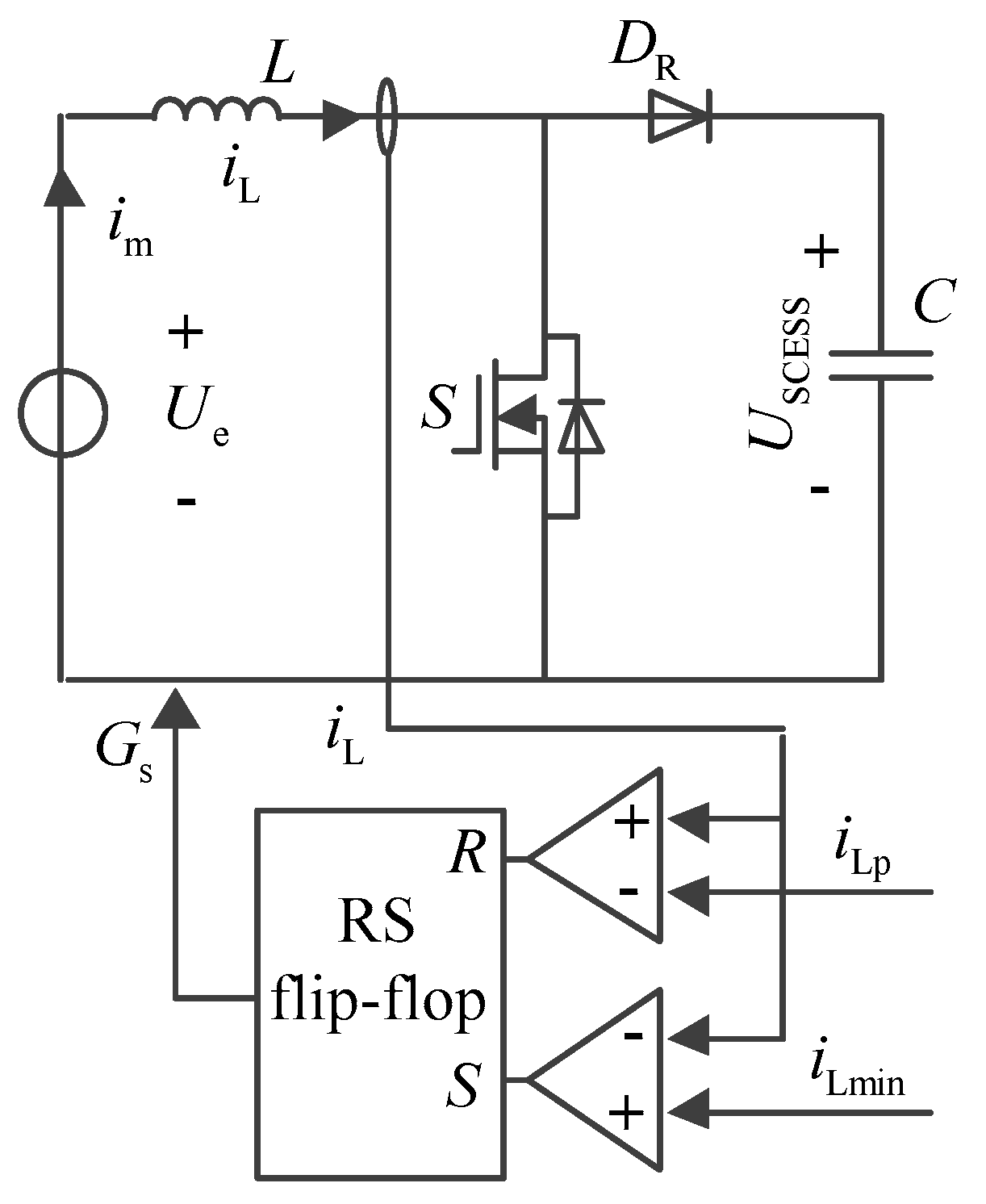
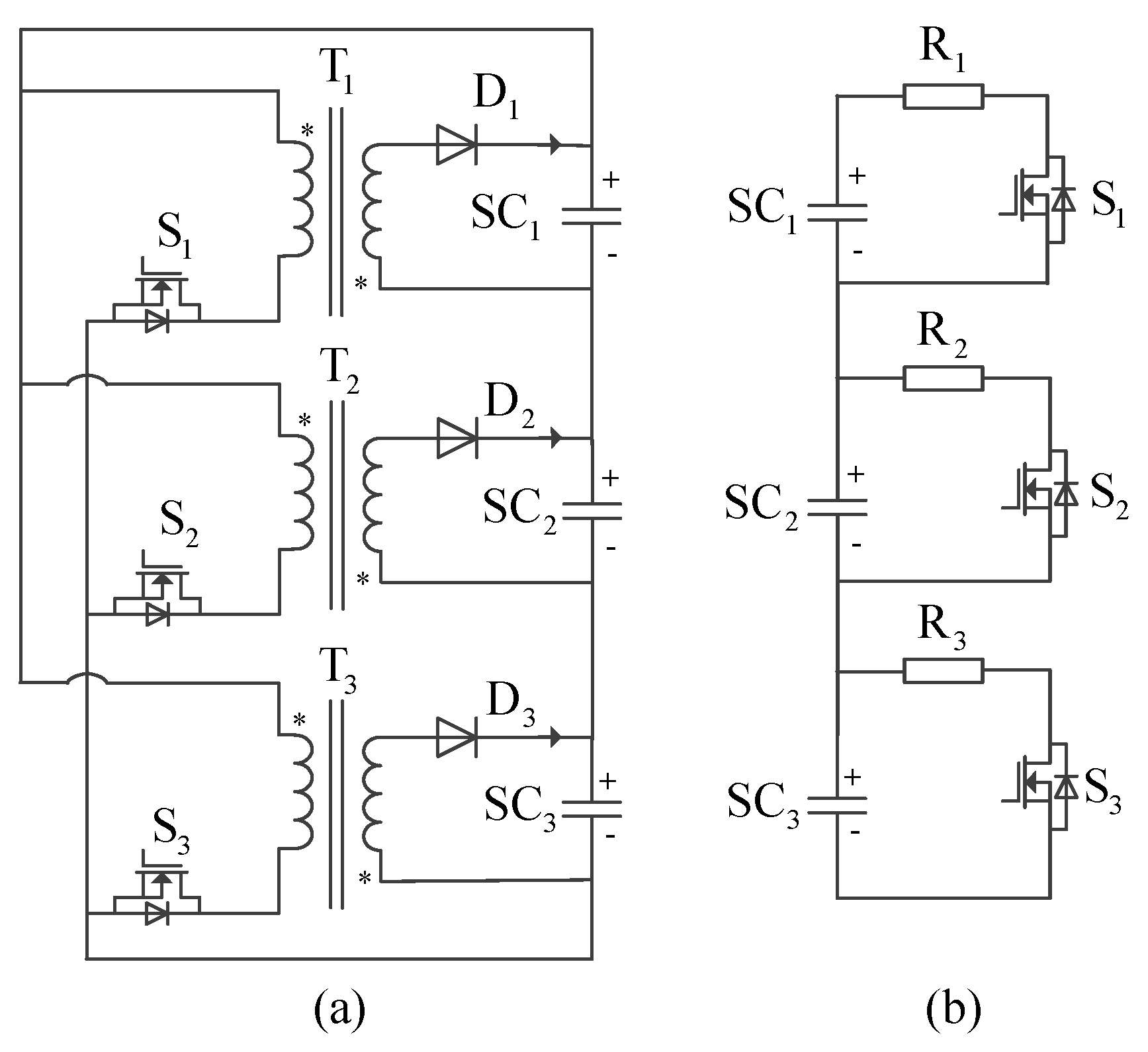
The proposed discharge-type modularized equalizer is shown in
Figure 2, which is composed of
n (the number of series-connected SCs) cascaded converter modules, a boost converter. The boost converter consists of a filter inductor
L, a diode
DR, and a switch
S. Each SC corresponds to a cascaded converter module, and the outputs of the cascaded converter modules are connected in series to form a cascaded converter. The cascaded converter module consists of a fly-back converter and a switch S
Si paralleled with the output capacitor C
oi.
In order to better illustrate the working principles of the proposed balancing topology, an SCESS that consists of three SCs is analyzed in detail. Assume that the SCs named C
1, C
2, C
3 and the voltage satisfy
uSC1 >
uSC3 >
uaverage >
uSC2. The higher voltage SCs C
1 and C
3 should be discharged and the extra energy is transferred to the filter capacitors C
o1 and C
o3, while the lower voltage SC C
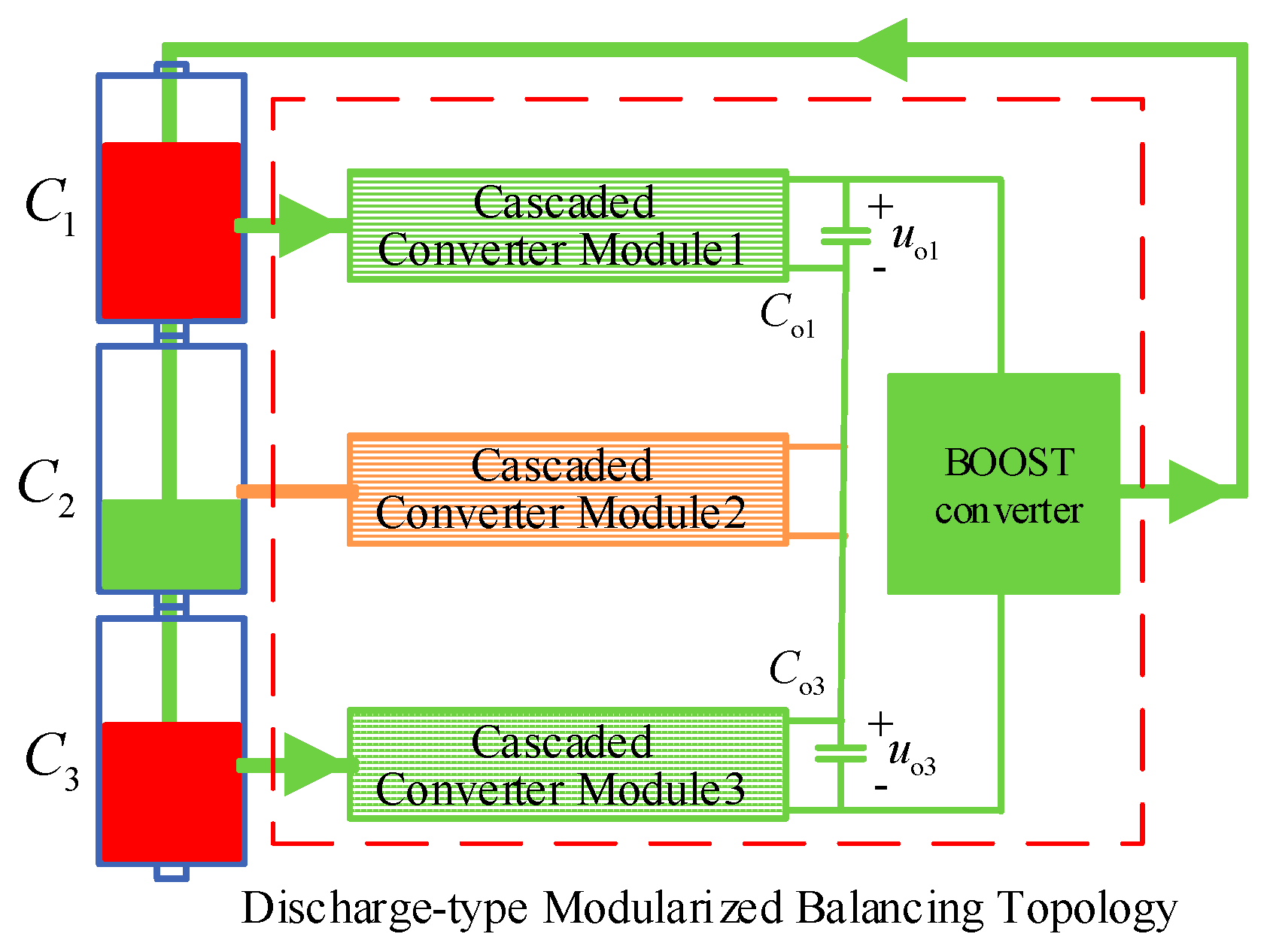
2 should not be discharged, and the corresponding cascaded converter module acts as wires. The block diagram of the balancing principle is shown in
Figure 3. The outputs of the cascaded converter modules are connected in series to form a cascaded converter and the cascaded output voltage is
uo1 +
uo3. The boost converter feedbacks the energy stored in the filter capacitors C
o1 and C
o3 to the SCESS.
The cascaded converter modules are controlled by the control signal CS
i, which is generated by the balancing controller. For the higher voltage SCs, the control signal is CS
i = 1, while for the lower voltage SCs, it is CS
i = 0. When CS
i = 1, the fly-back converter of the
ith cascaded converter module starts working to discharge the higher voltage SC and transfer the excess energy to the filter capacitor
Coi. When CS
i = 0, the fly-back converter does not work, and the switch S
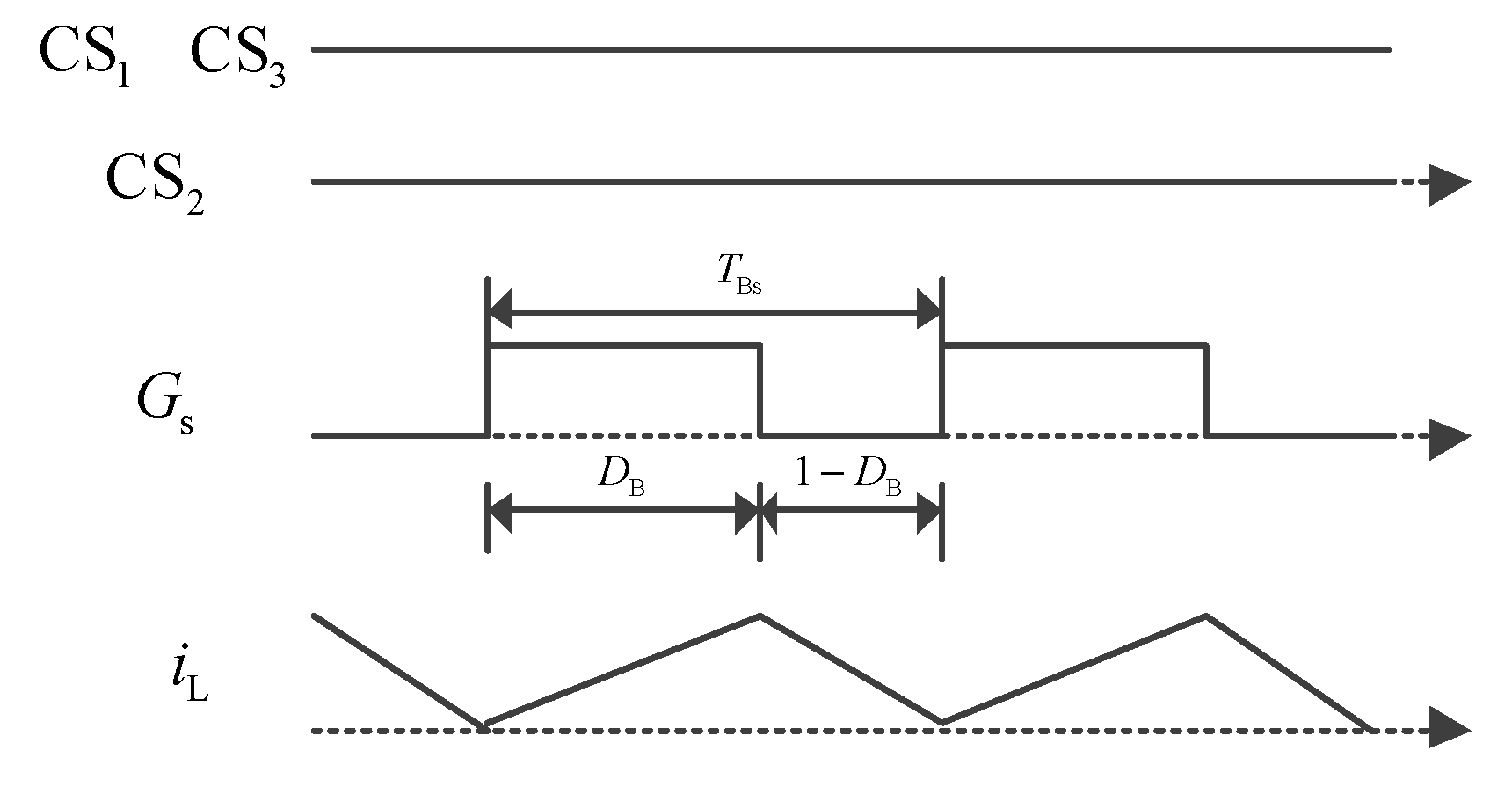
si is turned on, so that the output of the cascaded converter module acts as wires. The drives of the cascaded converter modules and the main waveforms of the boost converter are shown in
Figure 4, and the currents of the boost converter are shown in
Figure 5.
As shown in
Figure 4, the control signals CS
1 = 1 and CS
3 = 1, while CS
2 = 0. The output of the cascaded converter is equal to
uo1 +
uo3. The boost converter is driven by the PWM signal
Gs, and the current is shown in
Figure 5. As shown in
Figure 5a, when the PWM is high, the inductor current
iL increases. As shown in
Figure 5b, when the PWM is low, the inductor current decreases and the energy is fed back to the SCESS.
The energy transferred process of the proposed balancing topology is divided into two parts: one is the cascaded converter modules, which discharge the higher voltage SCs and transfer the extra energy to the filter capacitors; and the other is the boost converter, which transfers the energy stored in the filter capacitors to the SCESS. The energy transferred process works simultaneously with an independent control sequence. Next, the working principle of the cascaded converter module is discussed in detail.
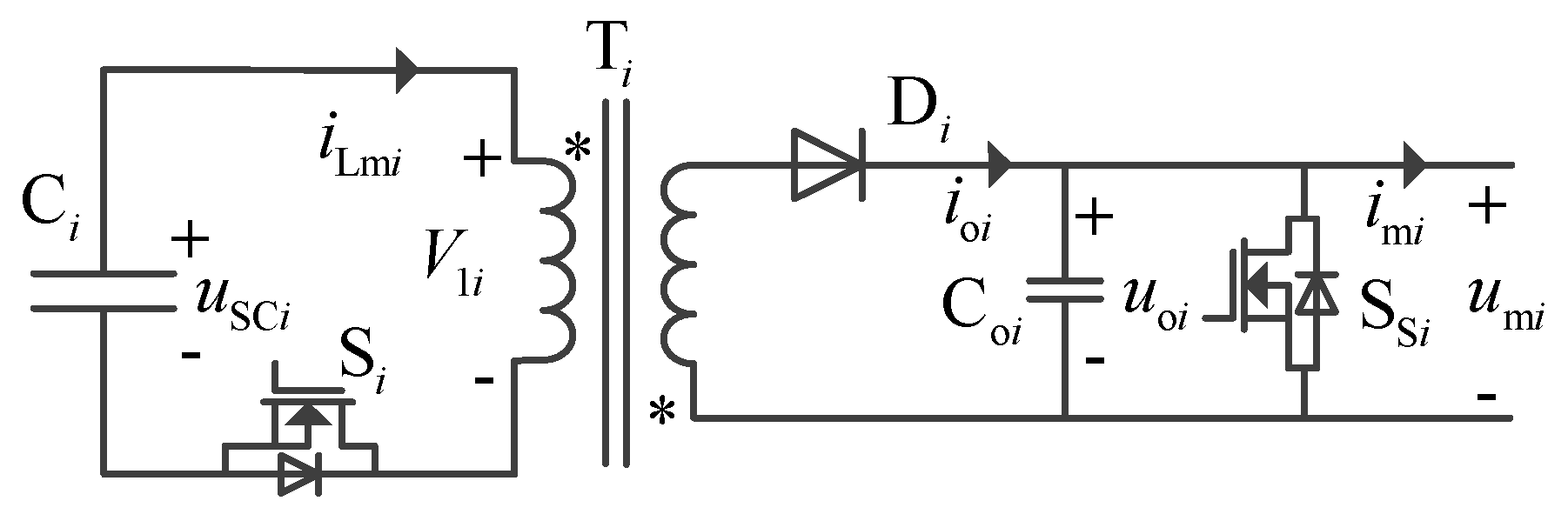
The topology of the cascaded converter module is shown in
Figure 6, which consists of a fly-back converter and a switch S
Si paralleled with the output capacitor C
oi. The fly-back converter has the function of isolation and discharge. Compared to the forward converter, the fly-back converter has the advantages of avoiding the use of output filter inductance, a freewheeling diode, and a specialized transformer reset circuit, which will make the converter small in size. The switch S
Si is used to make a short circuit of the output capacitor C
oi to make the cascaded converter module act as wires.
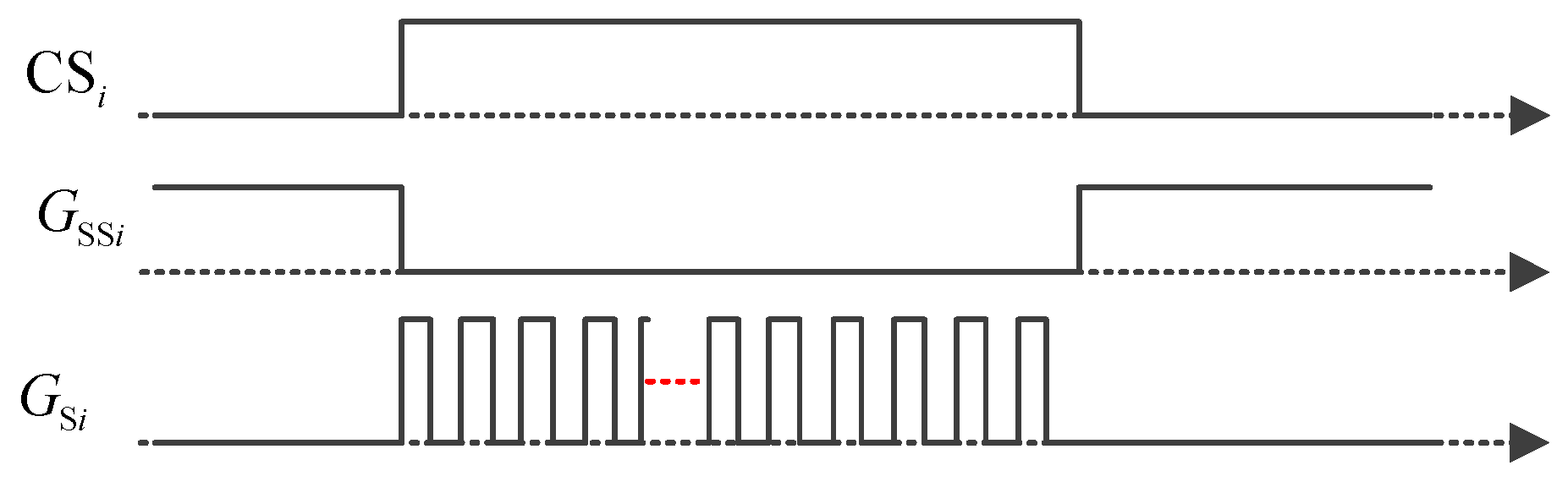
The drive of the cascaded converter module is shown as
Figure 7, where the control signal CS
i is used to control the working of the fly-back converter. The switch S
Si is driven by the complementary signals of CS
i. If the voltage of
ith SC is higher than the average voltage, CS
i = 1, the corresponding cascaded converter module starts discharging the SC. If the voltage of
ith SC is lower than the average voltage, the CS
i is low, the fly-back converter does not work and the short circuit switch S
Si is on, and the cascaded converter module acts as wires.
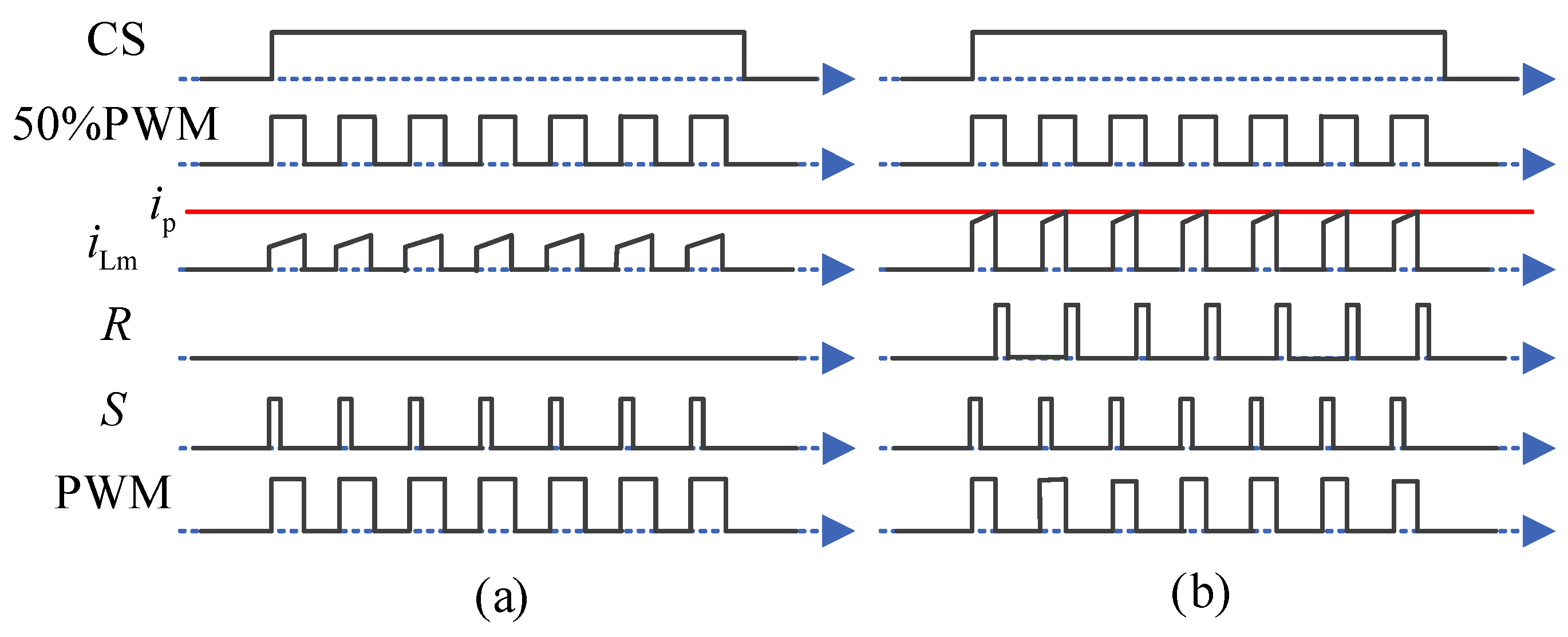
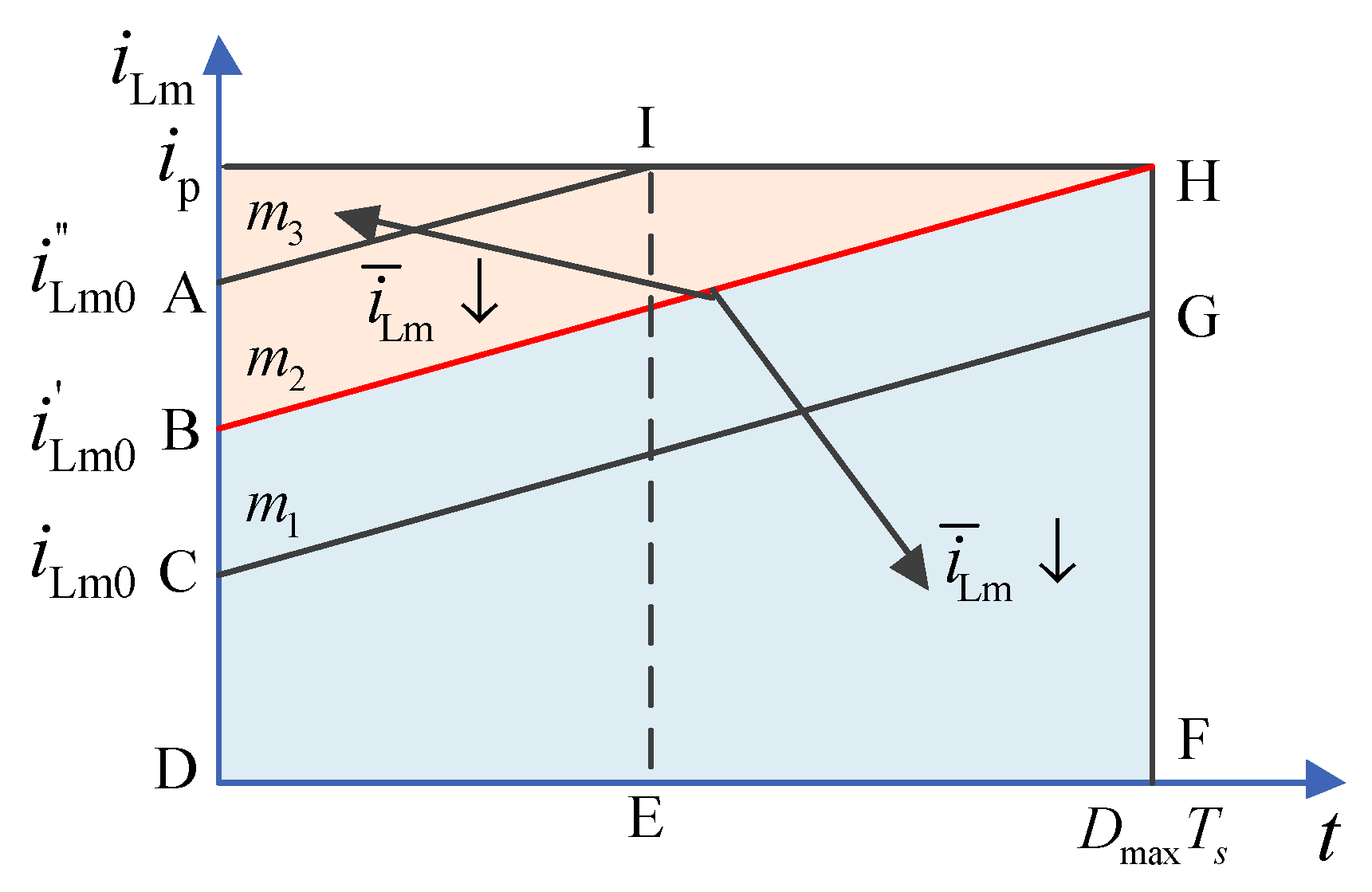
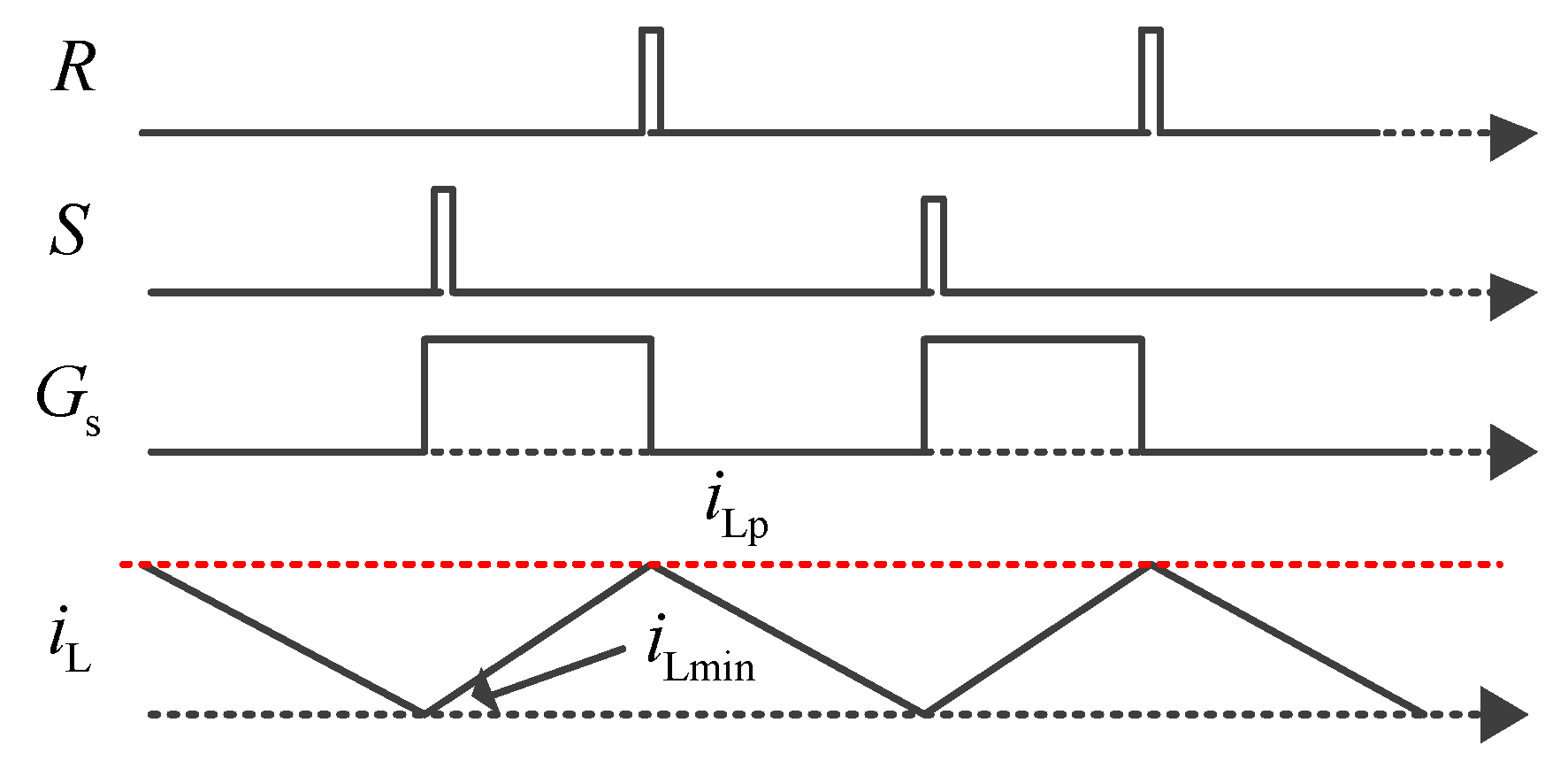
To improve the discharging power of the modularized converter module, the fly-back converters are operated in continuous current mode (CCM) [
29]. The switch S
i is driven by high frequency PWM
Gsi. In the time interval 0~
DTs, the switch
Si is on, and the current
iLmi increases linearly, which can be expressed as (2). In the time interval
DTs~
Ts, the switch
Si is off, and the energy stored in the magnetizing inductance is transferred to the filter capacitor. The peak current control strategy with the peak current
ip is used to control the fly-back converter. The discharging power of the fly-back converter can be expressed as (3).
where
iLm0 is affected by the load current;
Lm is the magnetizing inductance; △
i is the increment of current
iLm during the time interval 0~
DTs;
D is the duty cycle of the PWM and
Ts is the period; and
usci is the voltage of
ith SC.
The output voltage of the cascaded converter module is controlled by the control signal CS
i. When CS
i = 1,
GSSi = 0, the output of the cascaded converter module is
uoi. When CS
i = 0,
GSSi = 1, the output of the cascaded converter module is zero. Thus, the output voltage of the cascaded converter module
umi can be expressed as (4). The outputs of the cascaded converter modules are connected in series to form a cascaded converter, thus, the cascaded output voltage
Ue can be expressed as (5).
where
n is the number of series-connected SCs; CS
i is the control signal of
ith SC; and
uoi is the voltage of
ith filter capacitor
Coi, which will be calculated in the next part.
The boost converter can be simplified as shown in
Figure 8, where the input voltage of the boost converter is
Ue and the output voltage is the voltage of SCESS
USCESS. The working principle of the boost converter is very classic and familiar, and control of the boost converter will be discussed in the next part.
Through the above analysis, the voltage stress of switches can be ascertained. The voltage of SC is usc, and the turn ratio of transformer is n. Then, the voltage stress of switch Si is (usc + uoi/n), and the voltage stress of switch Ssi is uoi. Because the values of usc and uoi are small, the voltage stress of switches inside the cascaded converter modules is low. The voltage stress of switch S in the boost converter is USCESS, which is high. However, only one switch S is used in one balancing system and the current stress of switch S is low, so the price of switch S is acceptable.
4. Experiment and Results
The 7500 F, 2.7 V organic electrolyte carbon electrode SCs manufactured by china railway rolling stock corporation are used in this experiment and the SCESS consists of three SCs. The input of the cascaded converter module can be selected as 1.5–3 V. The peak current of the fly-back converter is
ip = 20 A and the frequency is
fs = 50 KHz. The UC3844 ICs are used to control the fly-back converters which have the cycle-by-cycle peak current limit function with a 50% maximum duty cycle. The comparator LM319 and the flip-flop HEF4027B (NXP Semiconductors, Washington, WA, USA) are used to achieve hysteresis current control of the boost converter. An STM32F407 control board (ST Microelectronics, Geneva, Switzerland) is used to control the whole system, including the voltage sampling, generating the control signal CS. Other experiment conditions are summarized in
Table 1 and the photograph of the experiment platform is shown in
Figure 19.
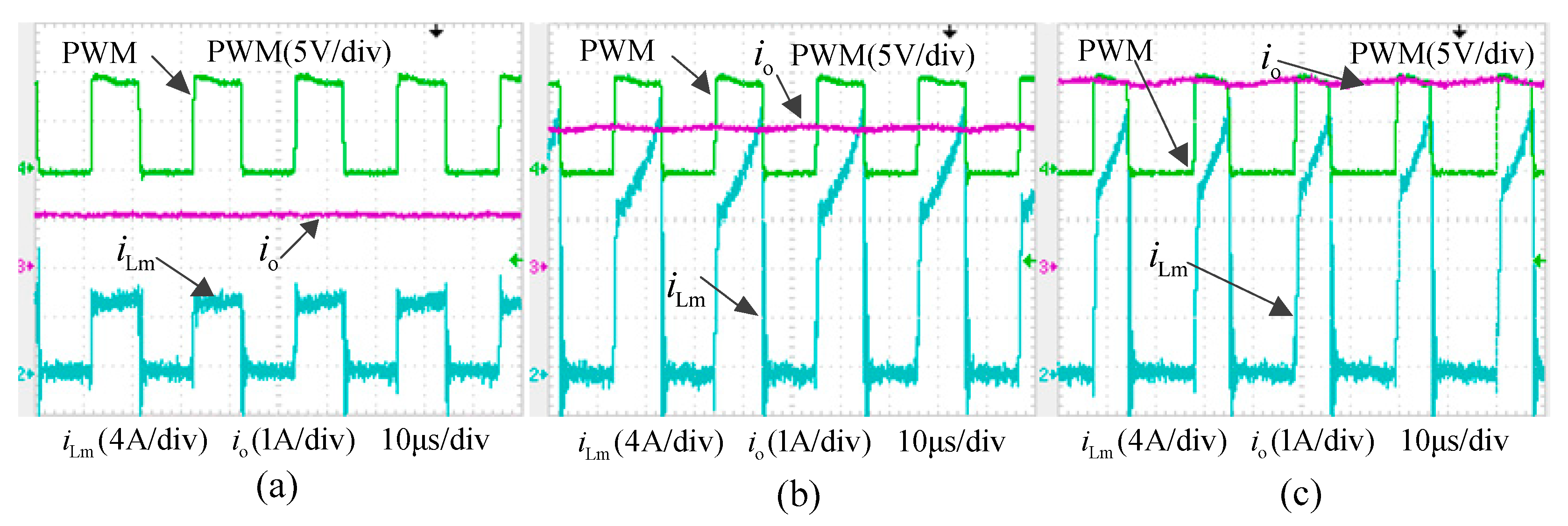
The waveforms of the output current
io, current
iLm, and PWM of the cascaded converter module are shown as
Figure 20. As shown in
Figure 20a, the output current
io = 1 A, the PWM duty cycle is 50%, and the peak current of
iLm is 6 A which does not reach the designed 20 A peak current. As shown in
Figure 20b, the output current
io = 3.1 A, the PWM duty cycle is 50%, and the peak current of
iLm is 20 A. As shown in
Figure 20c, the output current
io = 4 A, the PWM duty cycle is 35%, and the peak current of
iLm is 20 A. The ideal output current
is 3.2 A, which is calculated as (11). When
, the discharge current
iLm increases with the increase of output current
io, while
iLm decreases with the increase of
io when
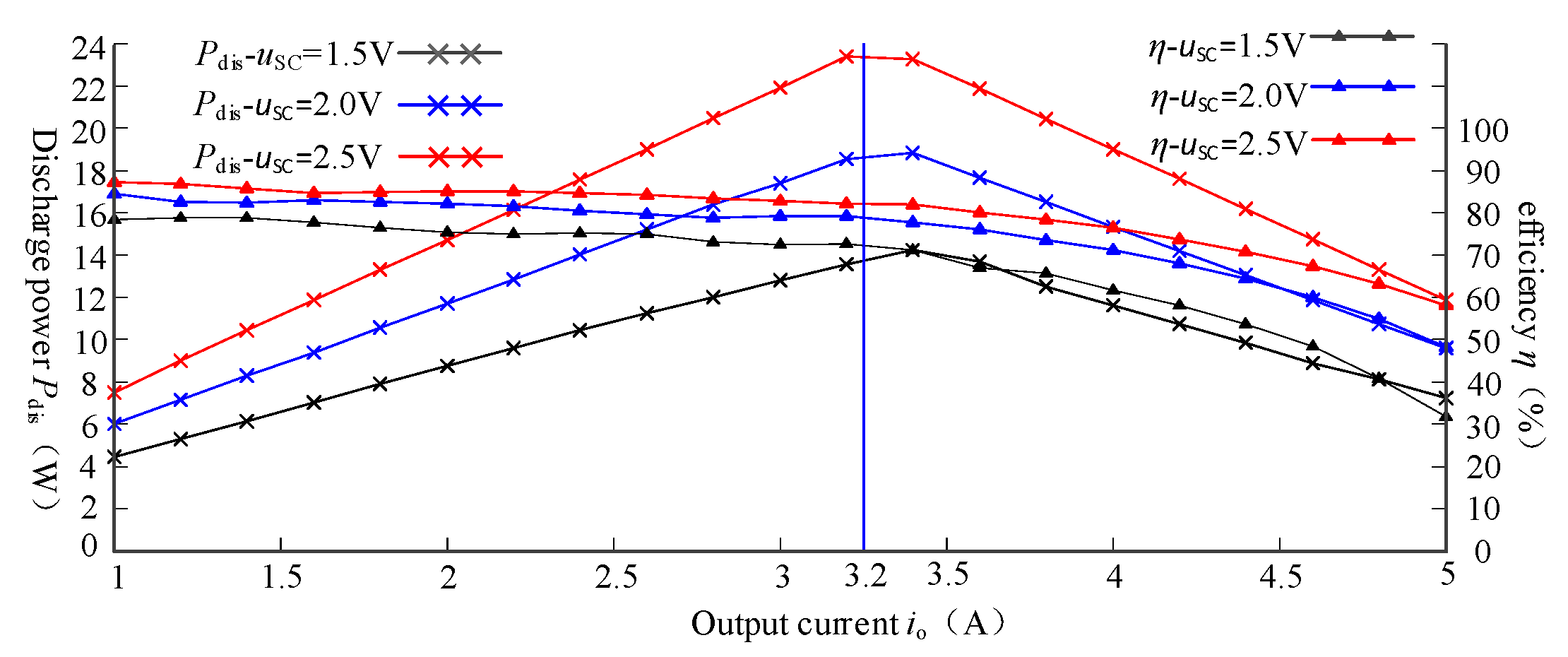
. The discharging power and efficiency change with output current
io are shown as
Figure 21. The discharging power first increases and then decreases with the increase of output current
io. When
io = 3.2 A, the discharging power reaches the maximum, which is consistent with the calculated ideal output current. The ideal output current hardly changes with the changing of
uSC and the discharging power increases with the increase of u
SC. The efficiency of the cascaded converter module decreases with the increase of the output current and the efficiency is 80% at the ideal output current. The drive of short circuit switch S
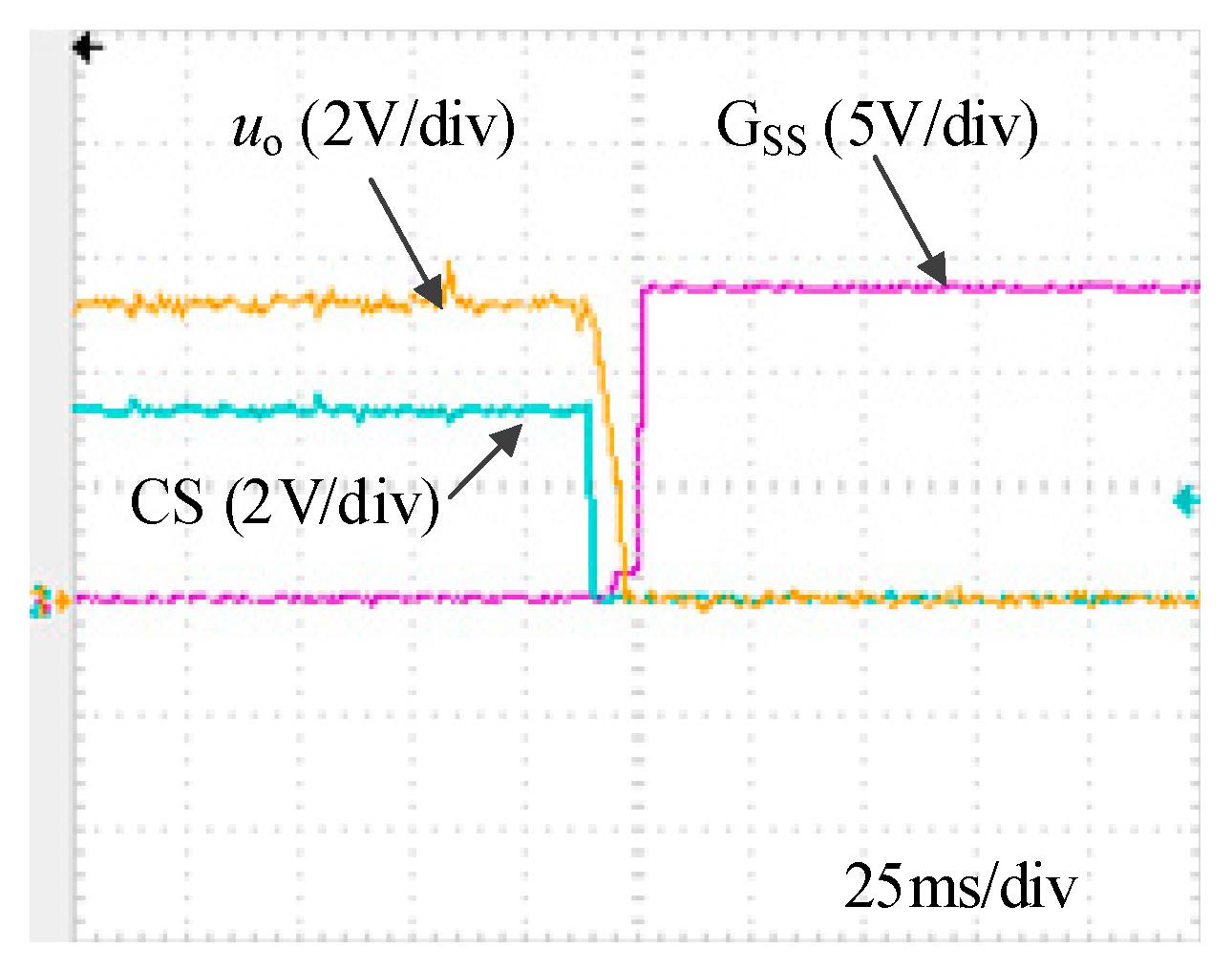
S is decided by the control signal CS and the voltage of the output capacitor
uoi. As shown in
Figure 22, CS is the control signal,
uo is the voltage of the output capacitor, and G
SS is the drive of the short circuit switch S
S. The short circuit switch S
S will not turn on until CS = 0 and the voltage
uo reaches an acceptable low value.
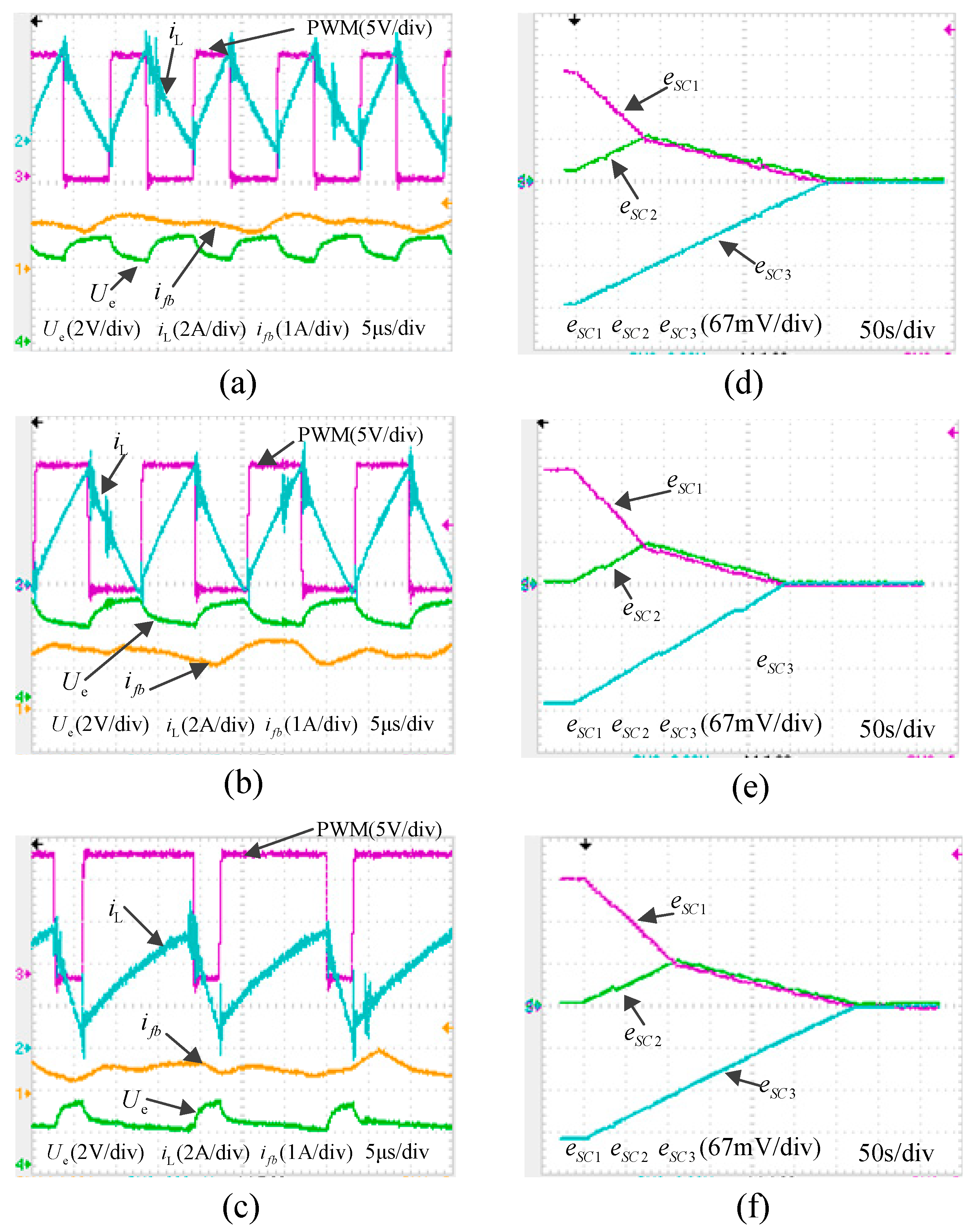
The voltages of the SCs are
uSC1 = 2.6 V,
uSC2 = 2.4 V, and
uSC3 = 2.2 V. The main waveforms of the boost converter and balancing time are shown as
Figure 23. As shown in
Figure 23,
iL is the inductor current of the boost converter which is controlled with the hysteresis current control strategy, and the average value can be calculated as Equation (12).
Ue is the input voltage of the boost converter, and is also the output voltage of the cascaded converter. The periodic fluctuation of
Ue is caused by the periodic variation of
iL, and the average value of
Ue remains unchanged at a certain
iL value.
ifb is the output current of the boost converter which feeds back the extra energy to the SCESS, and
ifb increases with the increasing of the discharging power of the cascaded converter. The PWM waveform is the drive of the boost converter and the duty cycle of the PWM increases with the increase of
iL, while the frequency decreases with the increase of
iL. The initial voltages of the SCs are
uSC1 = 2.6 V,
uSC2 = 2.4 V, and
uSC3 = 2.2 V, and
Esci (
i = 1,2,3) represents the errors between the voltages of SCs and the average voltage. When the SCESS reaches the balanced state,
Esci =0 (
i = 1,2,3). As shown in
Figure 23d, the balancing time is 300 s with the average inductor current
. As shown in
Figure 23e, the balancing time is 220 s with the average inductor current
. As shown in
Figure 23f, the balancing time is 320 s with the average inductor current
. The maximum balancing speed is reached near the ideal output current of the cascaded converter; if the output current is too large or too small, it will reduce the balancing speed. So, the control strategy based on the maximum discharging power of the boost converter will achieve the maximum balancing speed of the proposed topology.
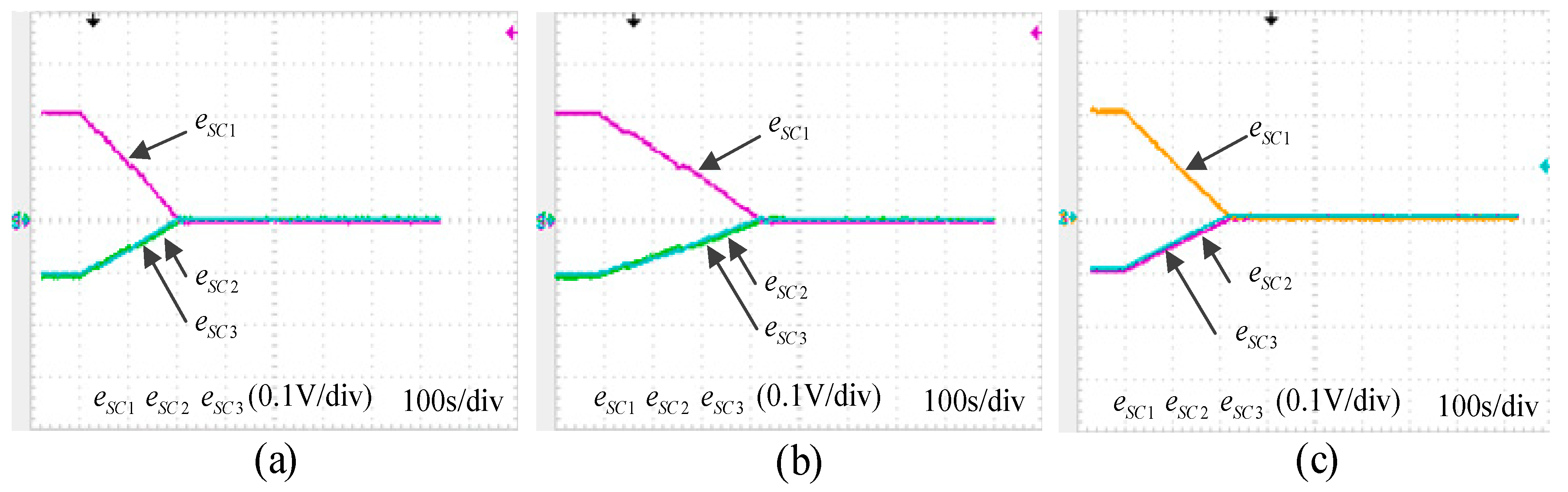
A comparative experiment is conducted to compare the balancing speed and round-trip energy efficiency. As shown in
Figure 24a [
18], the fly-back converters which are powered by the SCESS with 10 A output current to charge the lower voltage SCs are used as the charge-type balancing topology. As shown in
Figure 24b [
22], the 0.25 Ω 50 W resistor is used to discharge the higher voltage SC in the switched resistance balancing topology. The SCESS consists of three SCs with the voltages
uSC1 = 2.6 V,
uSC2 = 2.3 V, and
uSC3 = 2.3 V. The balancing time is shown in
Figure 25 and the experimental results are shown in
Table 2.
The experiment results are shown in
Table 2. The balancing time of charge-type topology is 340 s, while the balancing time is 200 s of the proposed topology and 220 s of the switched resistor method. The proposed modularized discharge-type topology has the fastest balancing speed and the balancing speed of the switched resistor method is close to the proposed topology. However, the 0.25 Ω 50 W resistor has a big size and the round-trip energy efficiency is zero because the extra energy is dissipated in the form of heat. The round-trip energy efficiency of the charge-type method is higher than the switched resistor method but lower than the proposed topology. This experiment proved that the proposed modularized discharge-type topology has an excellent discharging performance. The balancing speed is faster and the round-trip energy efficiency is higher than the charge-type balancing topology and the switched resistor method when the voltage of an SC is much higher than the average voltage.
There are many other excellent balancing topologies; however, most of them are designed for the BESS with a small balancing current. Few papers discussed the round-trip energy efficiency of the equalizer for BESS, because the round-trip energy efficiency for BESS is difficult to calculate or measure. Fortunately, the efficiency of many topologies is given. It will be interesting to compare the proposed balancing topology with the conventional ones and the comparison results are summed as
Table 3. In
Table 3, five index parameters are employed to evaluate the balancing performances, which are the discharging current (P
1), average efficiency of converter (P
2), voltage stress (P
3), number of circuit components (P
4), and control degree of freedom (P
5). The discharging current (P
1) refers to the balancing speed and the desired balancing speed of SCESS is described in (1). The average efficiency of the converter (P
2) reflects the round-trip energy efficiency; generally, high efficiency of a converter will result in a high round-trip energy efficiency. The voltage stress (P
3) refers to the voltage stress of the switches or diodes which have the largest number in the balancing system. The number of circuit components (P
4) represents the hardware cost. The control degree of freedom (P
5) refers to the control ability of SC’s voltage or state of charge (SOC), which is evaluated by “high (refer to each SC’s voltage can be controlled)” and “low (refer to the voltages of SCs are automatic balanced which can’t be controlled)”.
In
Table 3, some discharging currents are represented by inequality <
ipeak A, which means that the discharging current is a triangular current with a peak value
ipeak and the average current changing with duty cycle
D. The voltage stress of diodes in [
16] is
VB/2 (
VB is the voltage of battery or battery module). However, the charging current flows through two diodes and the voltage drop of diodes is big. The voltage
VB should be much larger than the voltage drop, otherwise the efficiency will be low. Thus, in the experiment in [
16],
VB = 16.4 V, and the voltage stress is 8.2 V in
Table 3. In [
20], the voltage stress is not mentioned; however, it can be calculated from the experimental data. In [
23], the voltage stress is 3.4N − 0.7 = 2.7 N + 0.7(N − 1), where 0.7 is the diode forward voltage.
As shown in
Table 3, each conventional balancing topology has its own advantages. For example, the topology in [
11] has a high control degree of freedom, has a high converter efficiency in [
9], has a small number of circuit components in [
20], and has a low voltage stress in [
22]. However, most of them are designed for BESS, not for SCESS, which needs a large discharge current. Although the topology in [
23] has a large discharge current, the voltage stress is high and the efficiency is low. The proposed balancing topology has a large discharge current which can avoid the SCs’ overvoltage phenomena and ensure the security of the SCESS. The efficiency is acceptable at a large discharge current. If the voltage stress is lower than 10 V, then the 20 V voltage level MOSFET can be used as switches. The drawback of the proposed balancing topology is the number of circuit components, which is slightly large. However, this will result in a high control degree of freedom. Thus, each SC’s voltage can be controlled and an advanced voltage balancing strategy can be used to enhance the lifetime of energy storage systems [
22].