Microgrids Real-Time Pricing Based on Clustering Techniques
Abstract
:1. Introduction
1.1. Background, Motivations and Aims
1.2. Literature Review and Contributions
- This paper proposes a clustering-based pricing scheme for microgrids through which a microgrid operator can assign proper price tariffs on its consumers based on the load curves clustered in distinctive classes.
- As for clustering techniques, this paper applies an improved weighted fuzzy average k-means to overcome the drawbacks of the traditional k-means techniques.
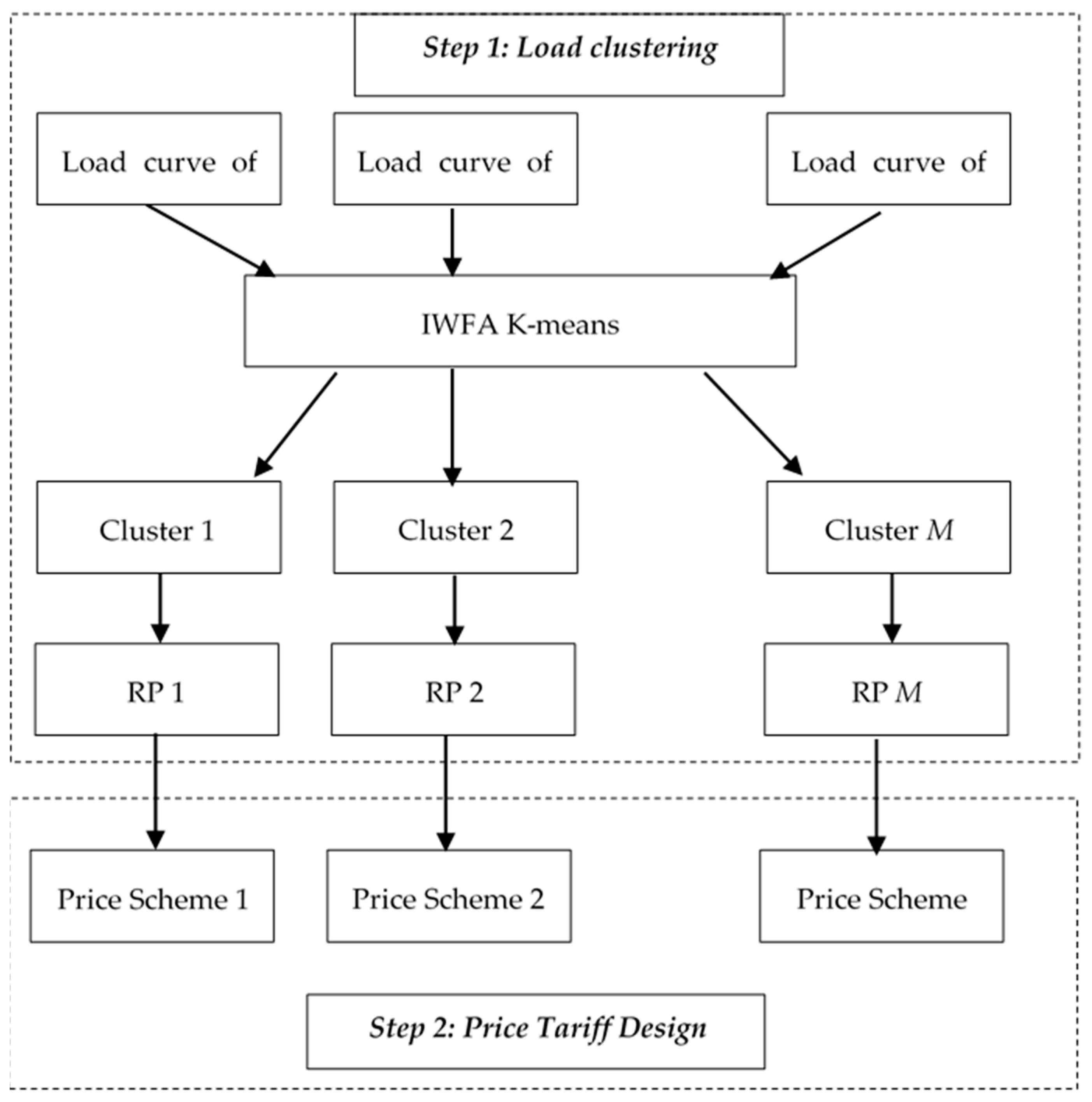
2. Methodology Framework
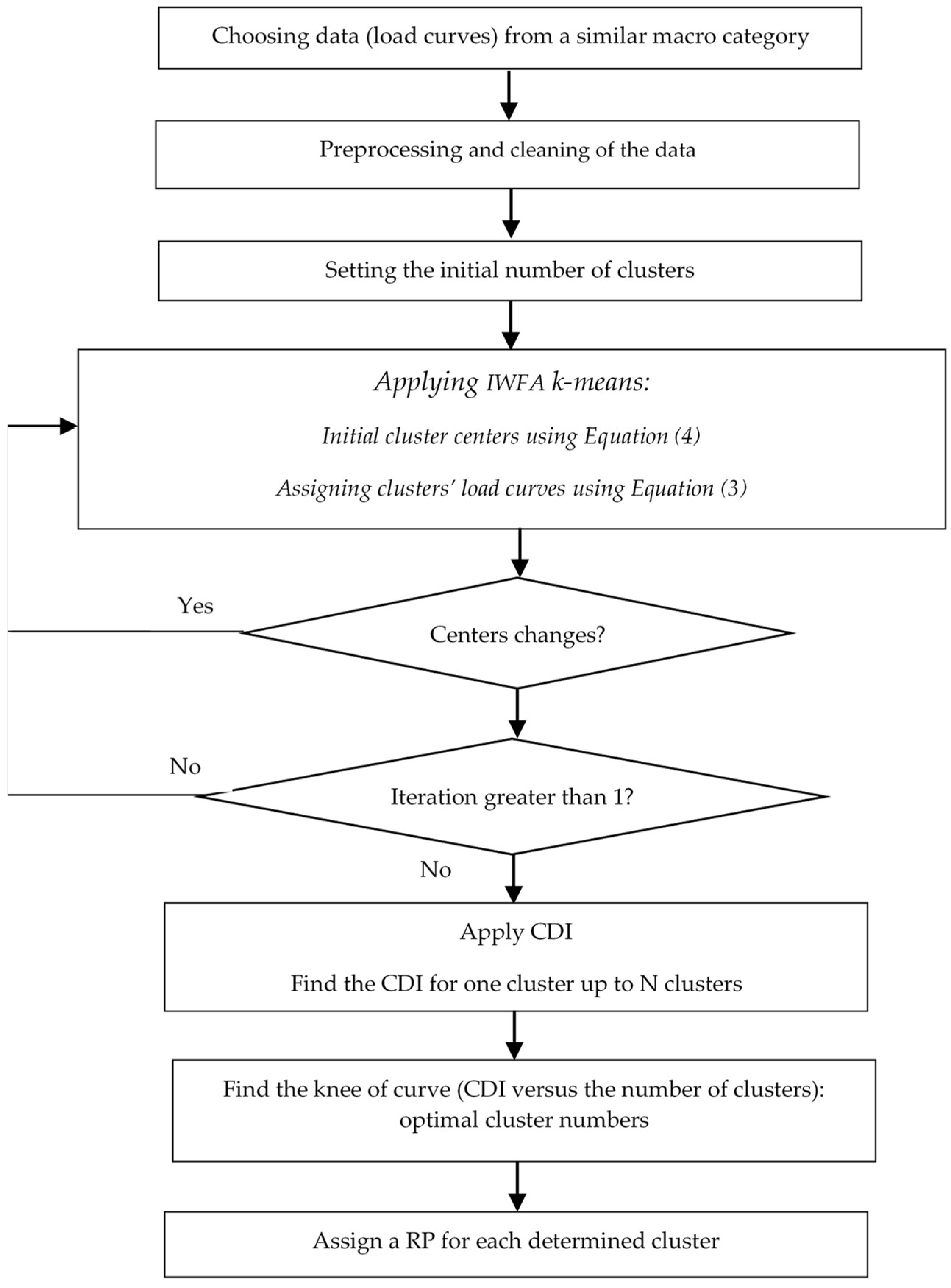
2.1. Clustering Process
- The distance between two load curves (e.g., between two hours l(i) and l(j), of the set L(k)) is defined as:where H is the number of intervals of each load curve.
- The distance between a cluster center r(k) and the subset L(k) is:where n(k) is the number of load curves in k-th cluster.
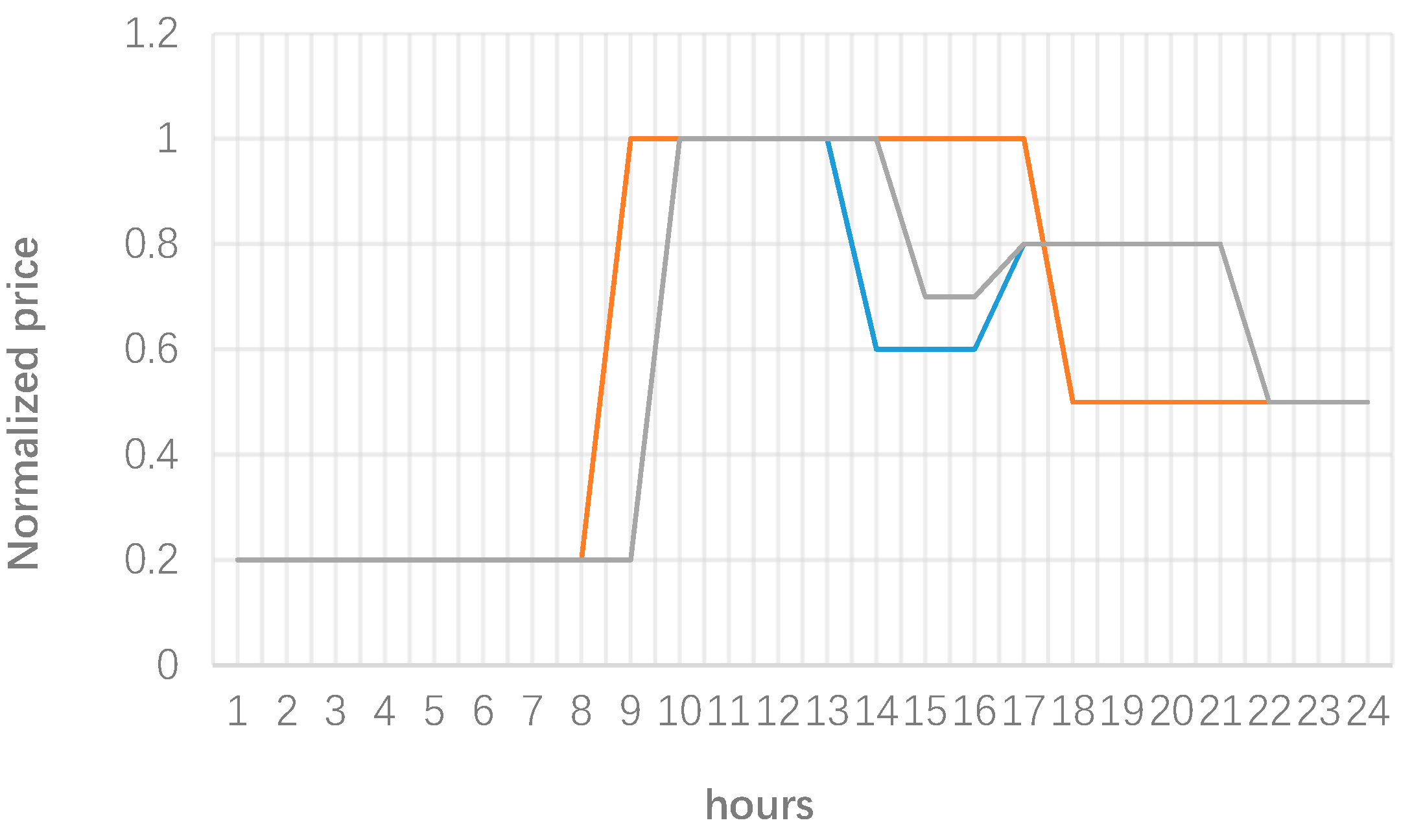
2.2. Microgrid Pricing Scheme
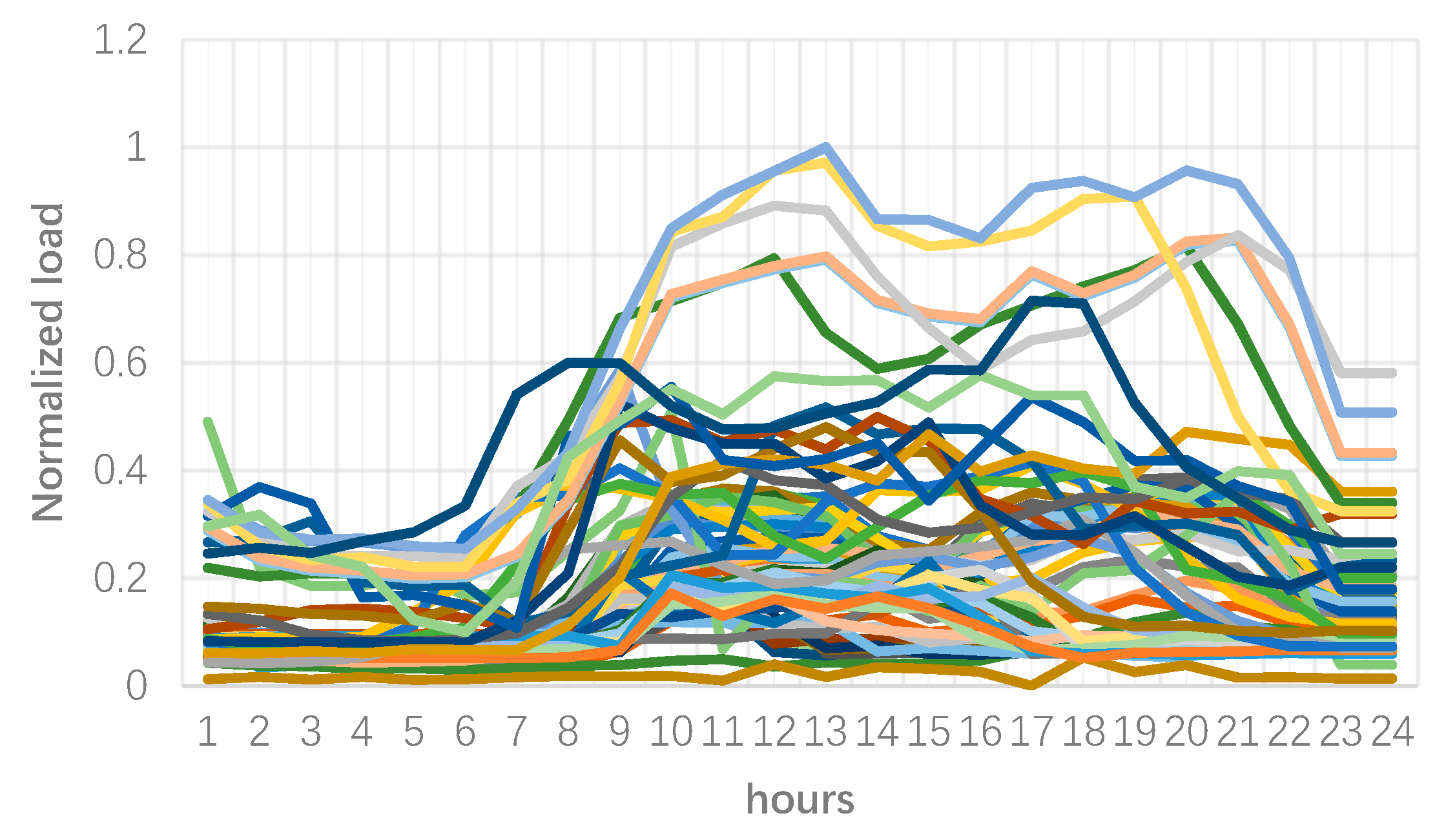
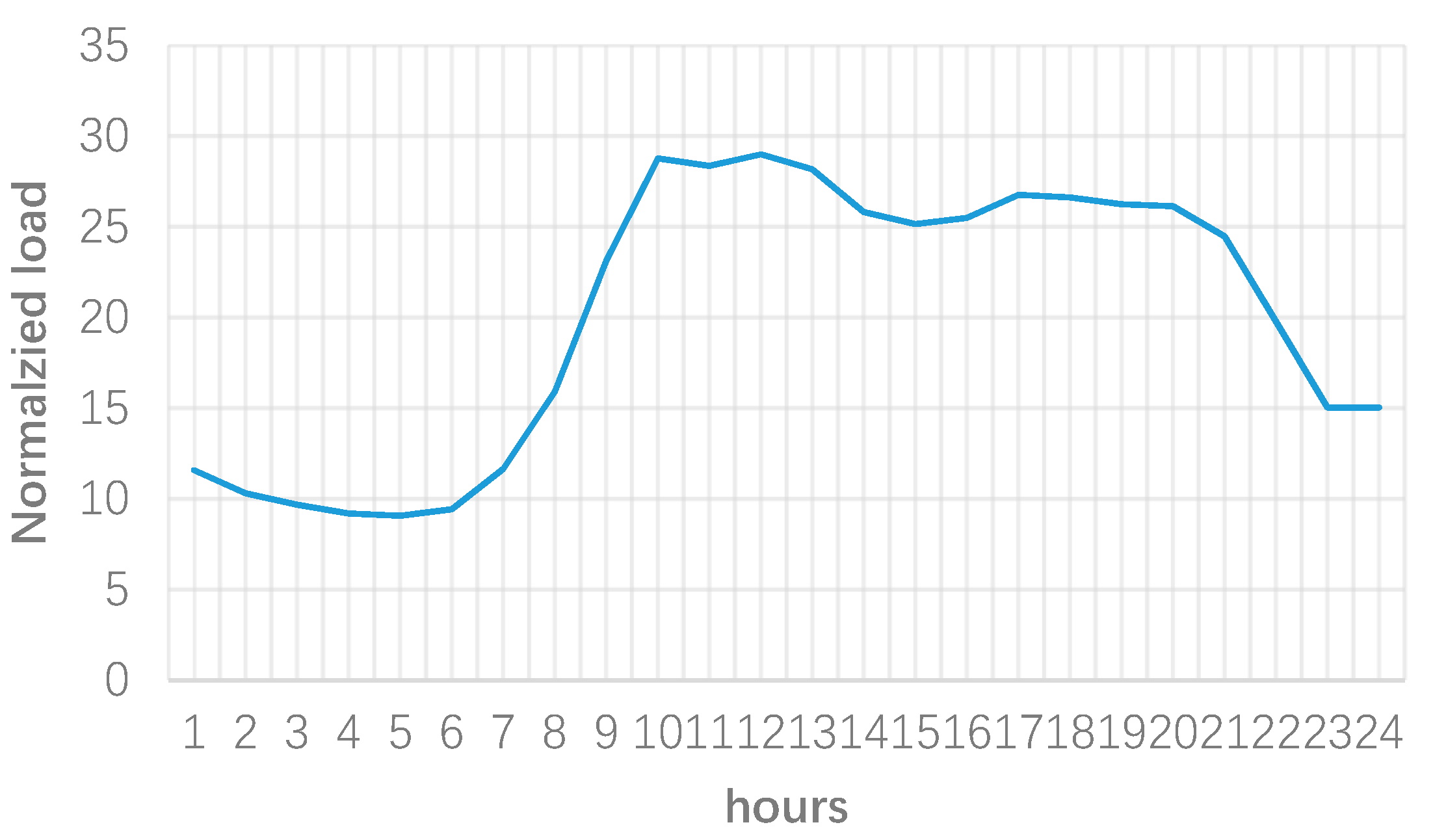
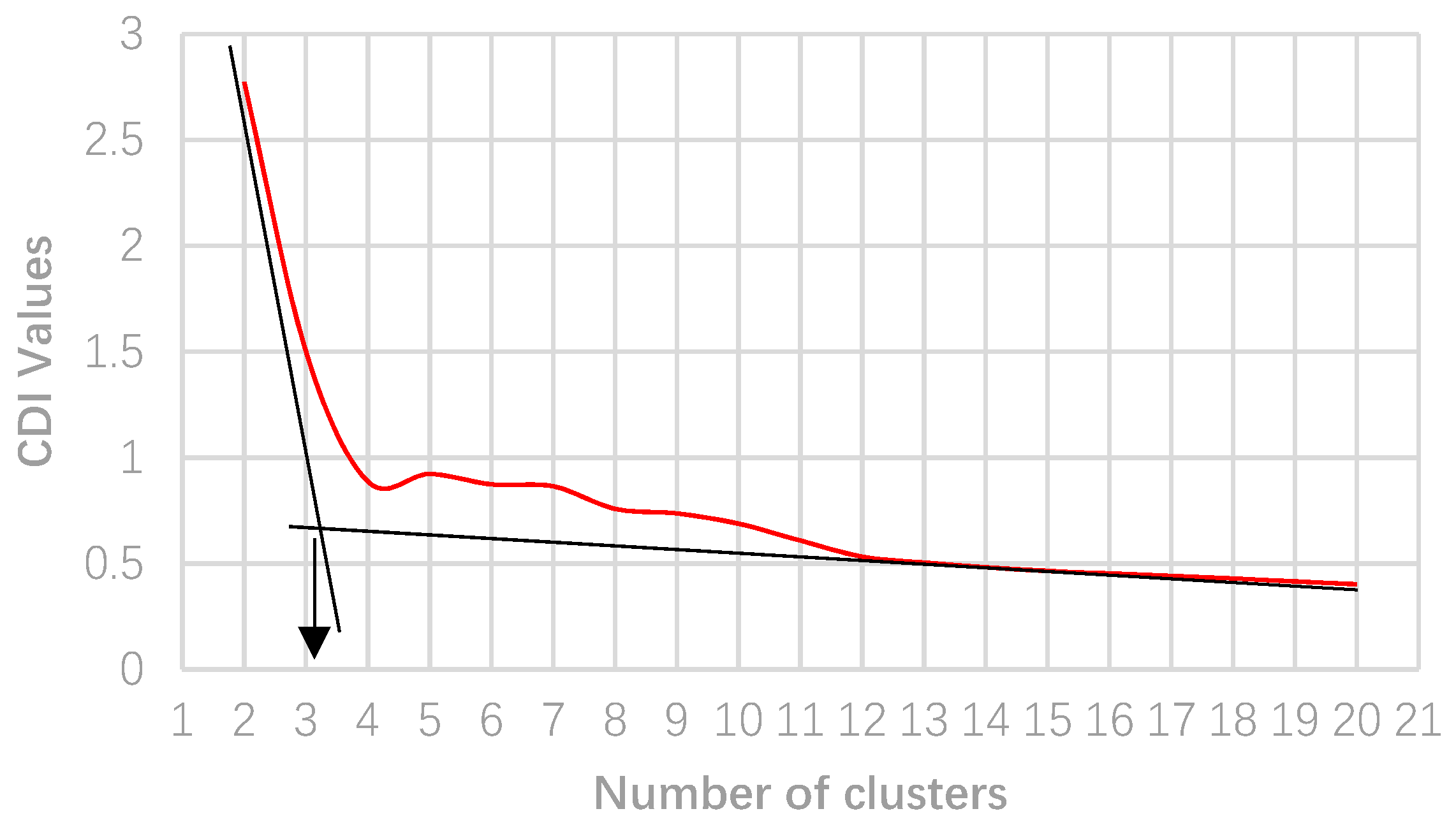
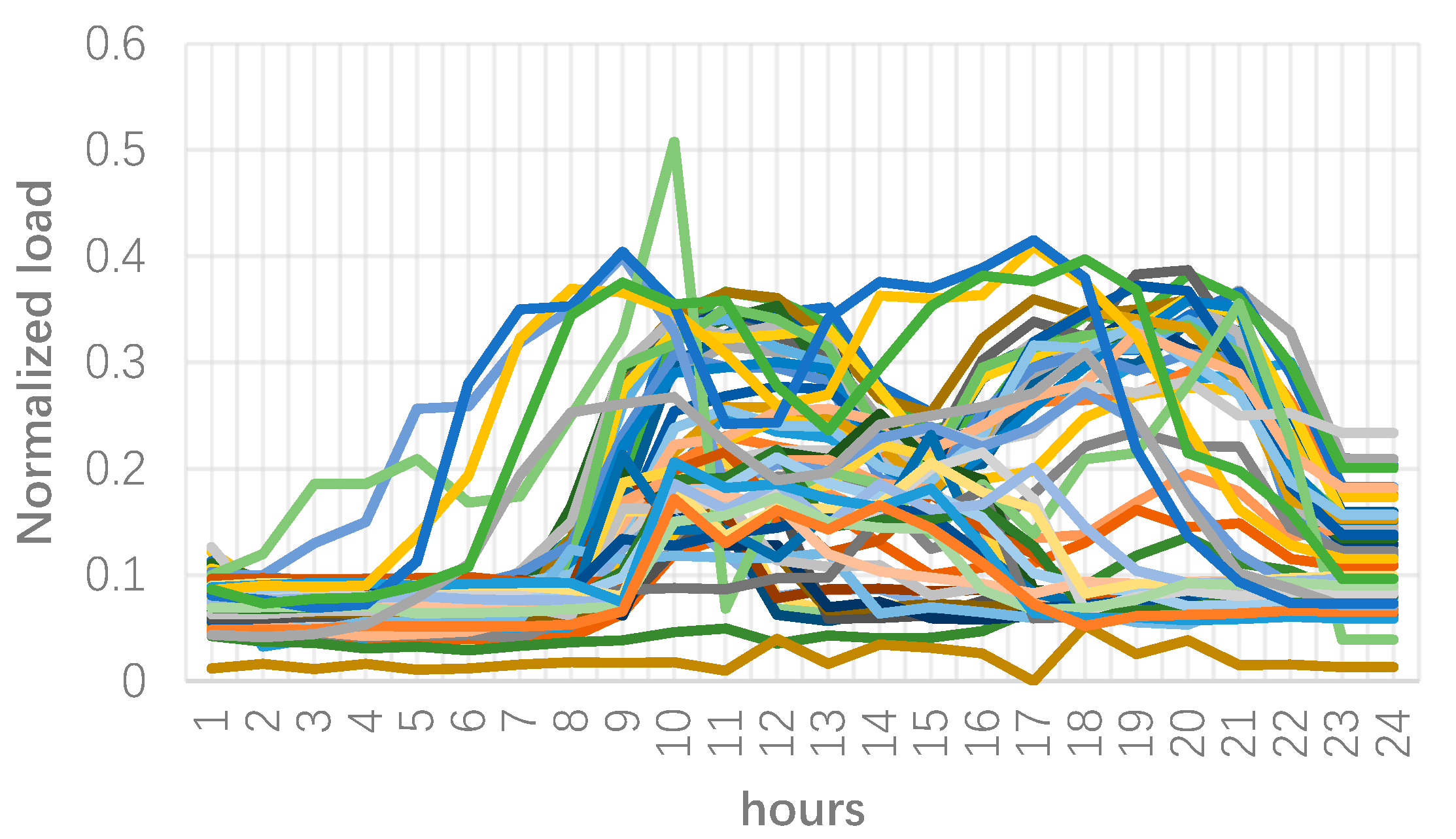
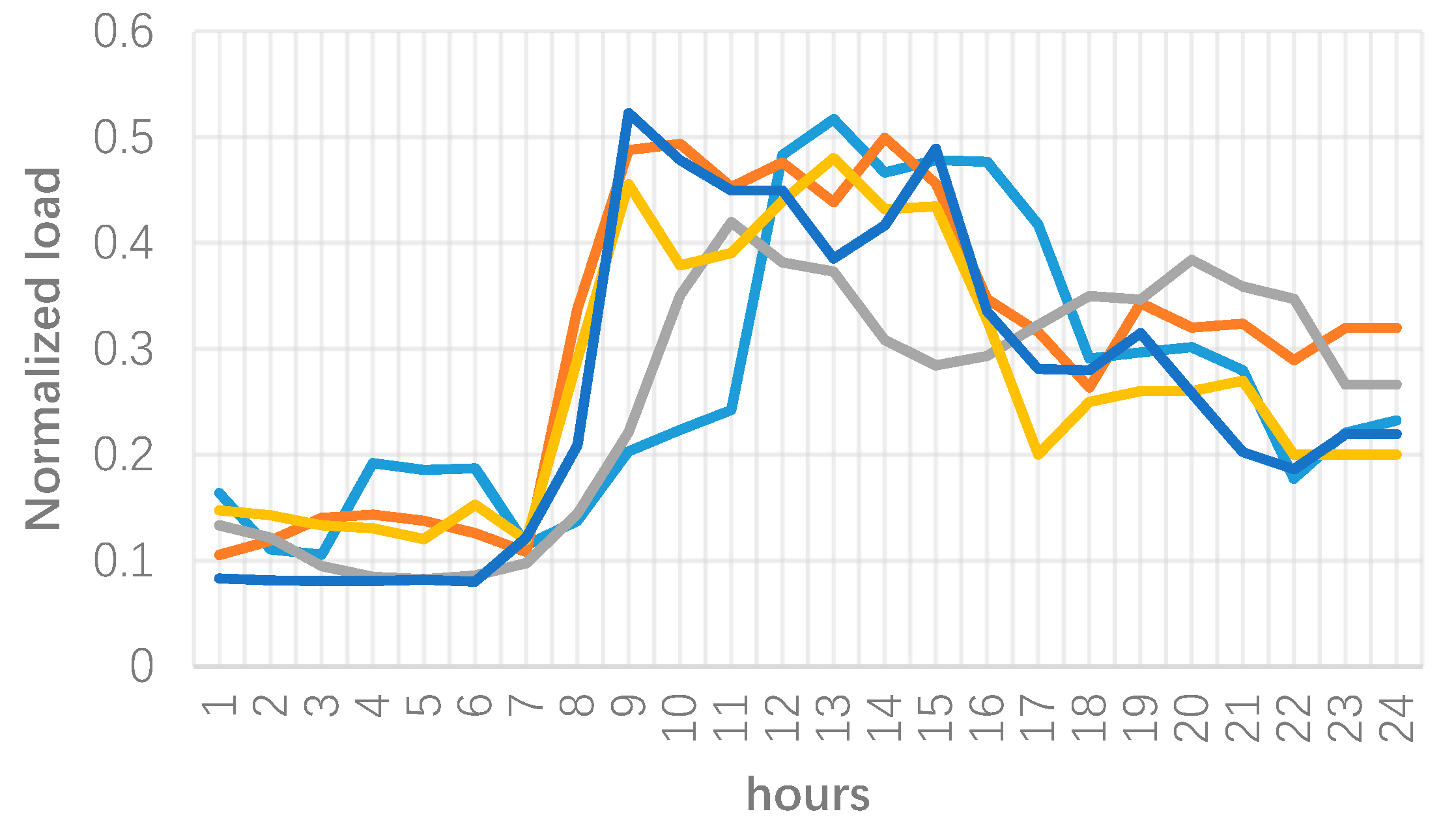
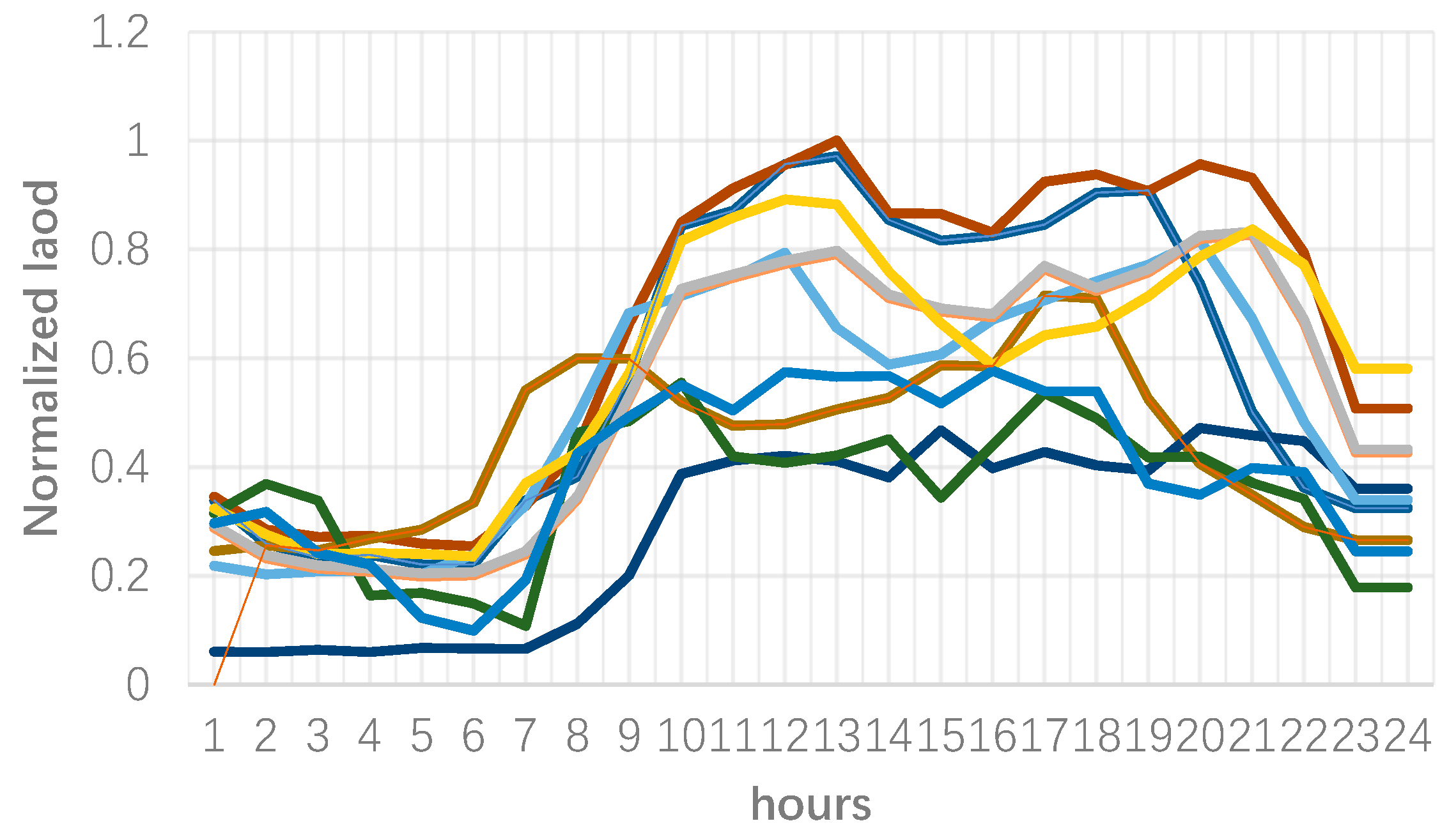
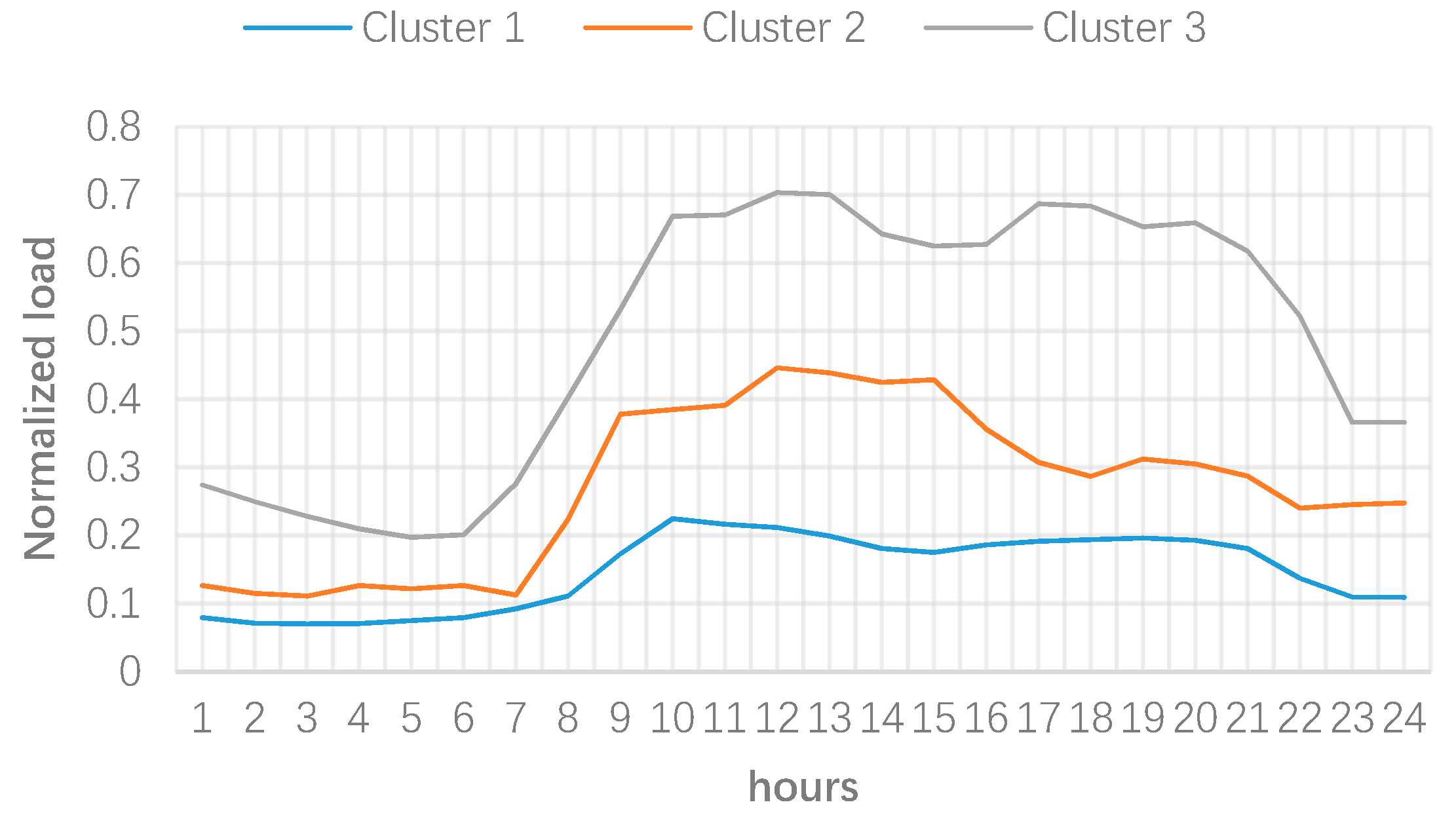
3. Numerical Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclatures
| The hth component of weighted fuzzy average in the rth iteration | |
| Variance of WFA k-means | |
| Variance of the hth component of load profiles | |
| Average variance | |
| Adjusting parameter | |
| Adjusting parameter | |
| The pth input curve | |
| The hth component of pth input curve | |
| Centeriod of the kth cluster | |
| The hth component of centeriod of the kth cluster | |
| The hth component of initial centeriod of the kth cluster | |
| The hth component of computed weight of the pth curve in the rth iteration |
References
- Yu, J.; Ni, M.; Jiao, Y.; Wang, X. Plug-in and plug-out dispatch optimization in microgrid clusters based on flexible communication. J. Mod. Power Syst. Clean Energy 2016, 5, 663–670. [Google Scholar] [CrossRef]
- Lo Prete, C.; Hobbs, B.F.; Norman, C.S.; Cano-Andrade, S.; Fuentes, A.; von Spakovsky, M.R.; Mili, L. Sustainability and reliability assessment of microgrids in a regional electricity market. Energy 2012, 41, 192–202. [Google Scholar] [CrossRef]
- Satapathy, P.; Dhar, S.; Dash, P.K. Stability improvement of PV-BESS diesel generator-based microgrid with a new modified harmony search-based hybrid firefly algorithm. IET Renew. Power Gener. 2017, 11, 566–577. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Z.; Lingyu, R.; Orekan, T. A Geršgorin theory for robust microgrid stability analysis. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Xu, X.; Wang, T.; Mu, L.; Mitra, J. Predictive Analysis of Microgrid Reliability Using a Probabilistic Model of Protection System Operation. IEEE Trans. Power Syst. 2017, 32, 3176–3184. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Ge, L.; Wu, L. 2-D Wind Speed Statistical Model for Reliability Assessment of Microgrid. IEEE Trans. Sustain. Energy 2016, 7, 1159–1169. [Google Scholar] [CrossRef]
- Guo, Y.; Xiong, J.; Xu, S.; Su, W. Two-Stage Economic Operation of Microgrid-Like Electric Vehicle Parking Deck. IEEE Trans. Smart Grid 2016, 7, 1703–1712. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Risk-Constrained Profit Maximization for Microgrid Aggregators with Demand Response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Honarmand, M.; Zakariazadeh, A.; Jadid, S. Integrated scheduling of renewable generation and electric vehicles parking lot in a smart microgrid. Energy Convers. Manag. 2014, 86, 745–755. [Google Scholar] [CrossRef]
- Wu, T.; Yang, Q.; Bao, Z.; Yan, W. Coordinated Energy Dispatching in Microgrid with Wind Power Generation and Plug-in Electric Vehicles. IEEE Trans. Smart Grid 2013, 4, 1453–1463. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Chang, W.-C.; Chang, Y.-R.; Lee, Y.-D.; Ouyang, D.-C. Optimal sizing of renewable energy generations in a community microgrid using Markov model. Energy 2017, 135, 68–74. [Google Scholar] [CrossRef]
- Jin, M.; Feng, W.; Marnay, C.; Spanos, C. Microgrid to enable optimal distributed energy retail and end-user demand response. Appl. Energy 2017, 210, 1321–1335. [Google Scholar] [CrossRef]
- Liu, G.; Starke, M.; Xiao, B.; Zhang, X.; Tomsovic, K. Microgrid optimal scheduling with chance-constrained islanding capability. Electr. Power Syst. Res. 2017, 145, 197–206. [Google Scholar] [CrossRef]
- Colley, D.; Mahmoudi, N.; Eghbal, D.; Saha, T.K. Queensland load profiling by using clustering techniques. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014; pp. 1–6. [Google Scholar]
- Tiefeng, Z.; Guangquan, Z.; Jie, L.; Xiaopu, F.; Wanchun, Y. A New Index and Classification Approach for Load Pattern Analysis of Large Electricity Customers. IEEE Trans. Power Syst. 2012, 27, 153–160. [Google Scholar]
- Tsekouras, G.J.; Kotoulas, P.B.; Tsirekis, C.D.; Dialynas, E.N.; Hatziargyriou, N.D. A pattern recognition methodology for evaluation of load profiles and typical days of large electricity customers. Electr. Power Syst. Res. 2008, 78, 1494–1510. [Google Scholar] [CrossRef]
- Kohan, N.M.; Moghaddam, M.; Bidaki, S.; Yousefi, G. Comparison of modified k-means and hierarchical algorithms in customers load curves clustering for designing suitable tariffs in electricity market. In Proceedings of the 43rd International Universities Power Engineering Conference, Padova, Italy, 1–4 September 2008; pp. 1–5. [Google Scholar]
- Wenyuan, L.; Jiaqi, Z.; Xiaofu, X.; Jiping, L. A Statistic-Fuzzy Technique for Clustering Load Curves. IEEE Trans. Power Syst. 2007, 22, 890–891. [Google Scholar]
- Mahmoudi-Kohan, N.; Eghbal, M.; Moghaddam, M. Customer recognition-based demand response implementation by an electricity retailer. In Proceedings of the 2011 21st Australasian Universities Power Engineering Conference (AUPEC), Brisbane, Australia, 25–28 September 2011; pp. 1–6. [Google Scholar]
- Chicco, G.; Napoli, R.; Piglione, F. Comparisons among clustering techniques for electricity customer classification. IEEE Trans. Power Syst. 2006, 21, 933–940. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Saha, T.K.; Eghbal, M. Wind offering strategy in the Australian National Electricity Market: A two-step plan considering demand response. Electr. Power Syst. Res. 2015, 119, 187–198. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Saha, T.K.; Eghbal, M. A new demand response scheme for electricity retailers. Electr. Power Syst. Res. 2014, 108, 144–152. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Eghbal, M.; Saha, T.K. Employing demand response in energy procurement plans of electricity retailers. Int. J. Electr. Power Energy Syst. 2014, 63, 455–460. [Google Scholar] [CrossRef]
- Eghbal, M.; Saha, T.K.; Mahmoudi-Kohan, N. Utilizing demand response programs in day ahead generation scheduling for micro-grids with renewable sources. In Proceedings of the Innovative Smart Grid Technologies Asia (ISGT), Perth, Australia, 13–16 November 2011; pp. 1–6. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Mahmoudi, N.; Chen, K. Microgrids Real-Time Pricing Based on Clustering Techniques. Energies 2018, 11, 1388. https://doi.org/10.3390/en11061388
Liu H, Mahmoudi N, Chen K. Microgrids Real-Time Pricing Based on Clustering Techniques. Energies. 2018; 11(6):1388. https://doi.org/10.3390/en11061388
Chicago/Turabian StyleLiu, Hao, Nadali Mahmoudi, and Kui Chen. 2018. "Microgrids Real-Time Pricing Based on Clustering Techniques" Energies 11, no. 6: 1388. https://doi.org/10.3390/en11061388
APA StyleLiu, H., Mahmoudi, N., & Chen, K. (2018). Microgrids Real-Time Pricing Based on Clustering Techniques. Energies, 11(6), 1388. https://doi.org/10.3390/en11061388




