Wire Mesh Dampers for Semi-Floating Ring Bearings in Automotive Turbochargers: Measurements of Structural Stiffness and Damping Parameters
Abstract
1. Introduction
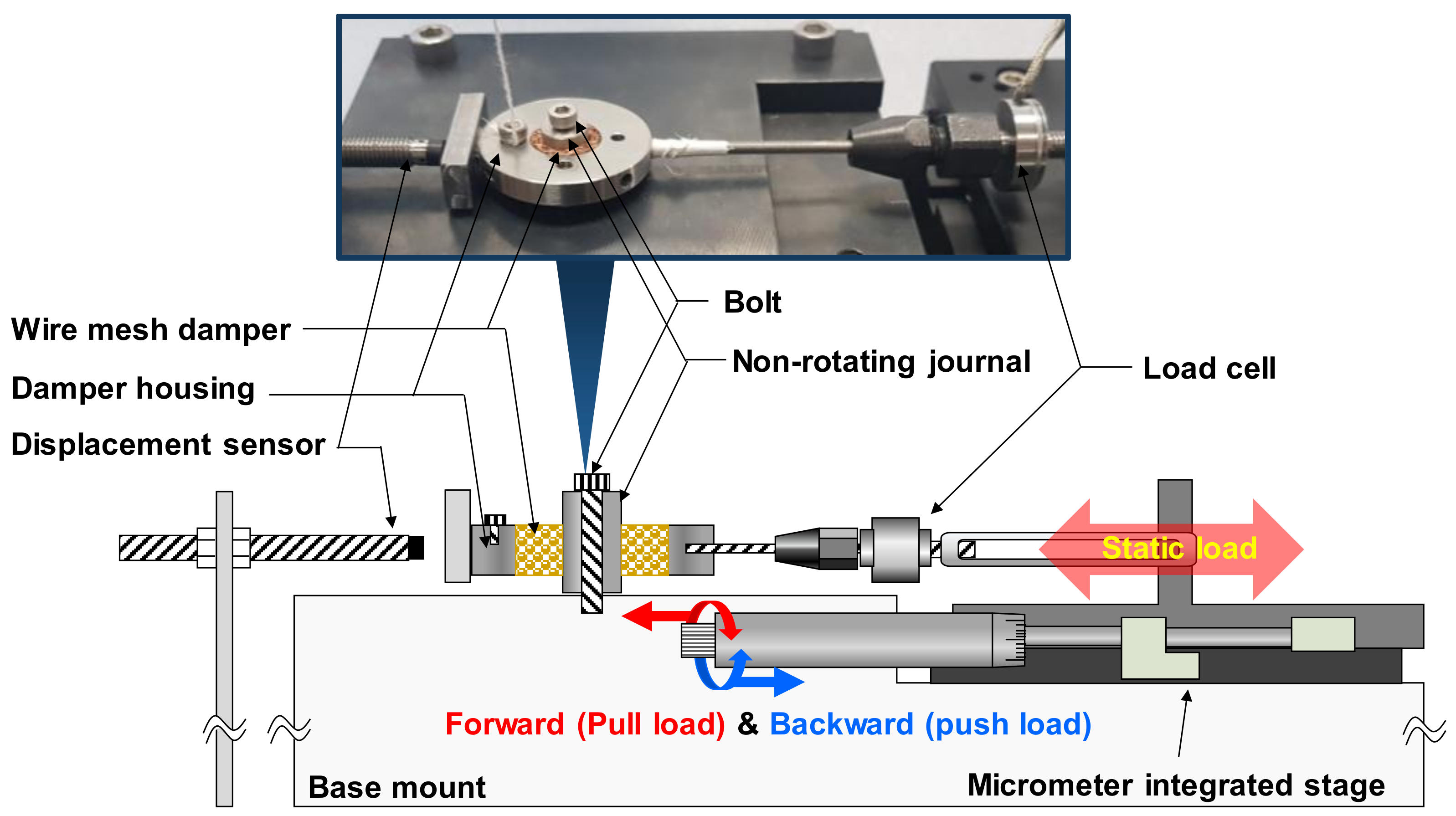
2. Experimental Facility and Procedure
3. Identification Procedure of WMD Structural Stiffness and Damping Parameters
3.1. Structural Stiffness
3.2. Damping Parameters
4. Experimental Results and Discussion
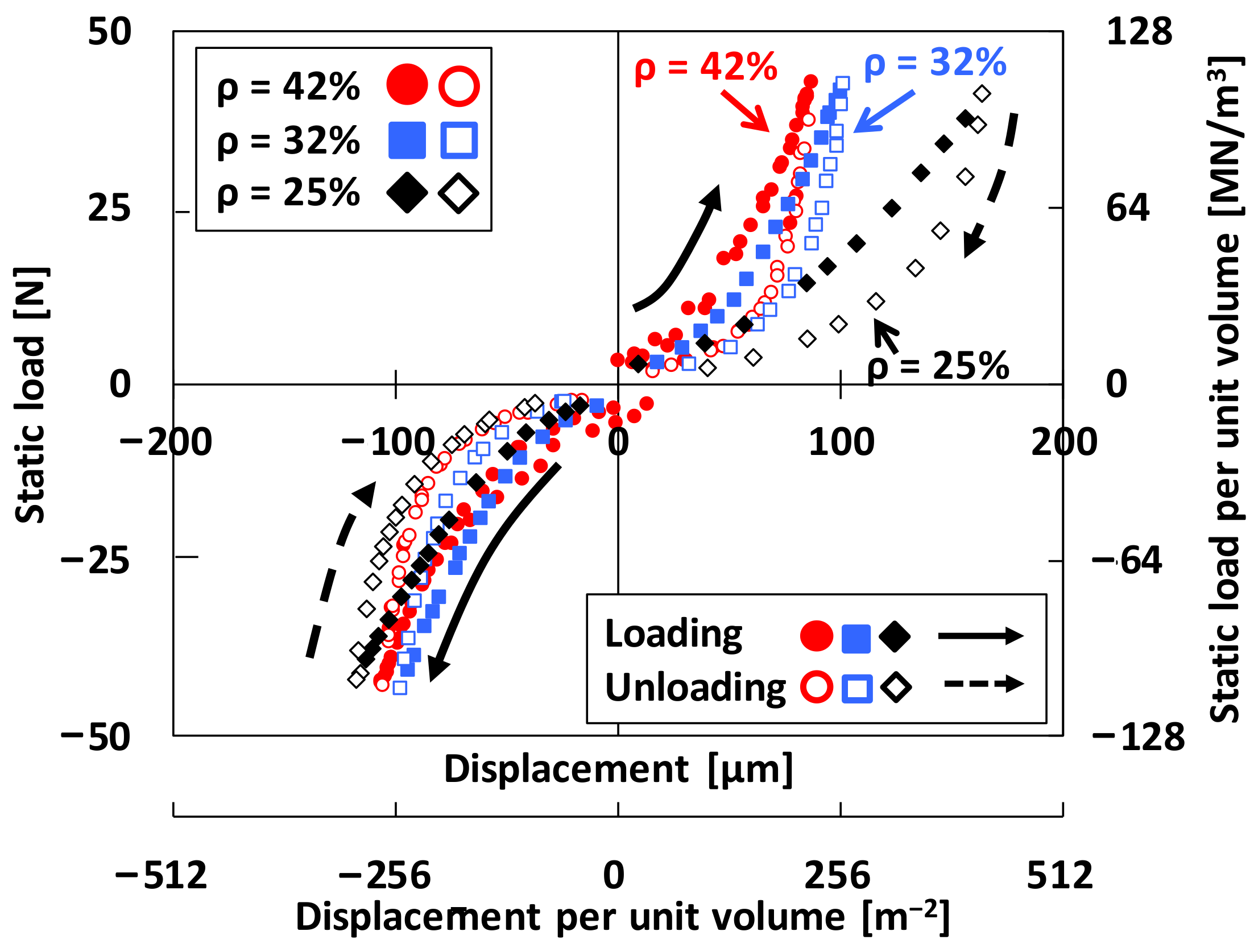
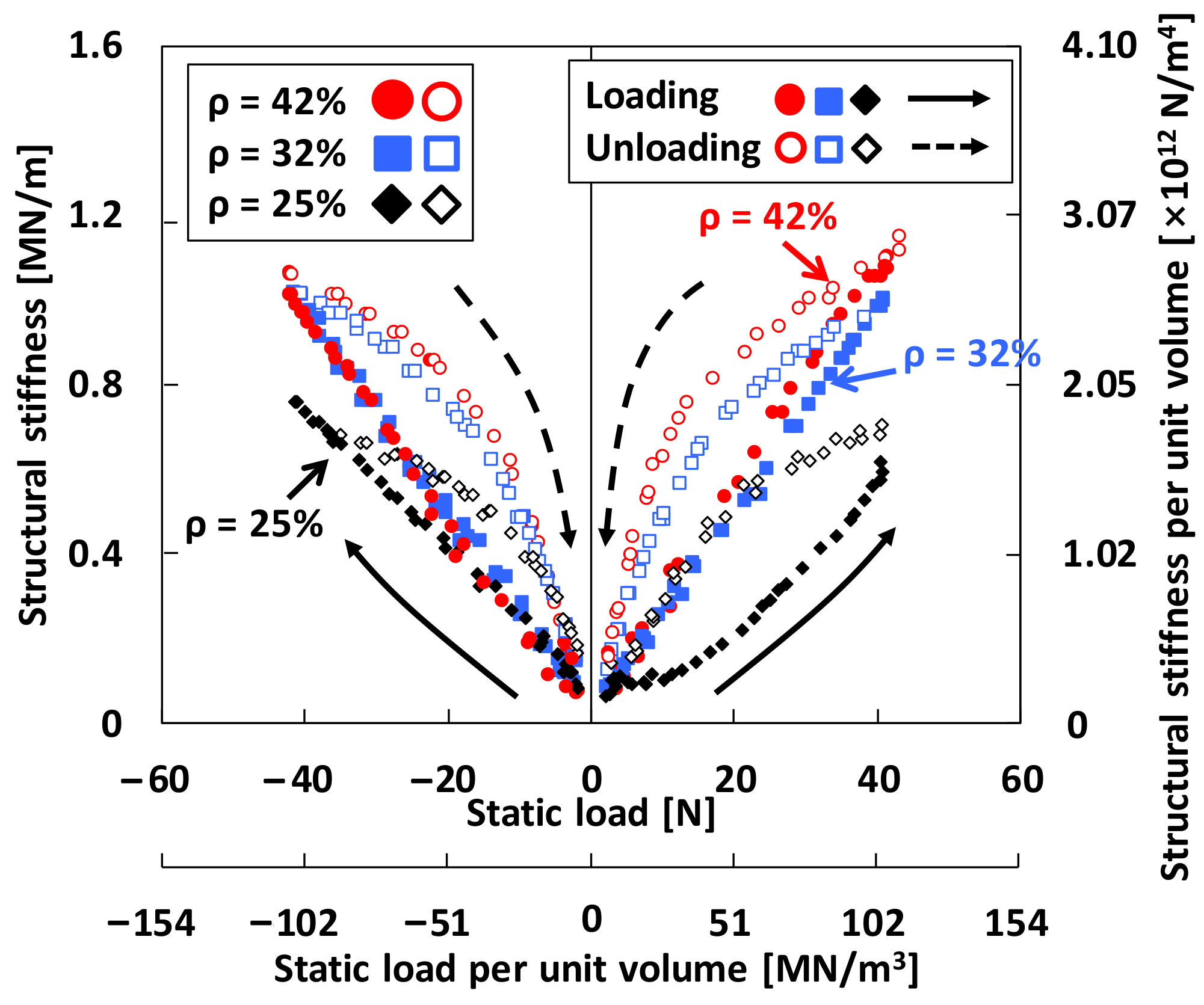
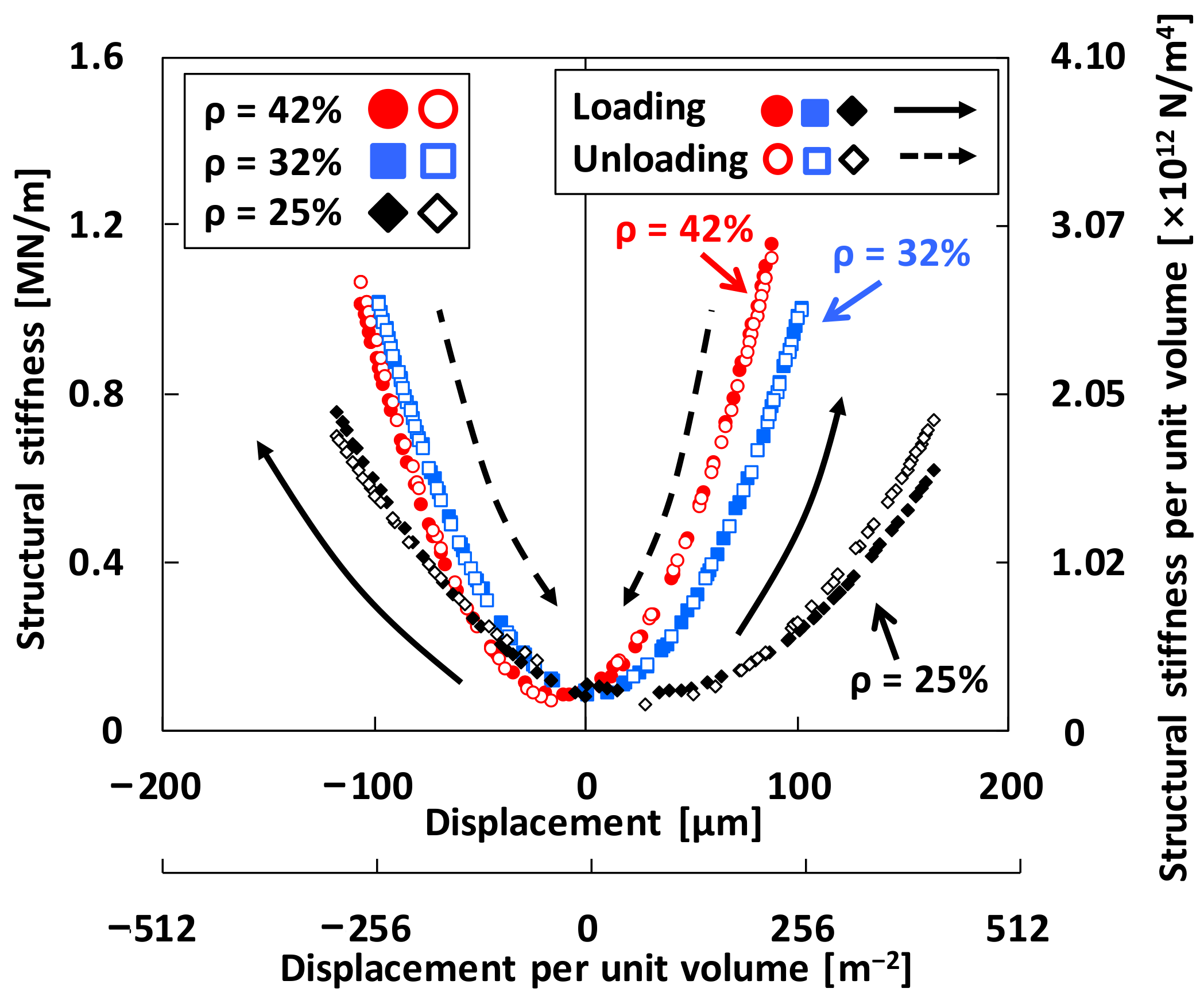
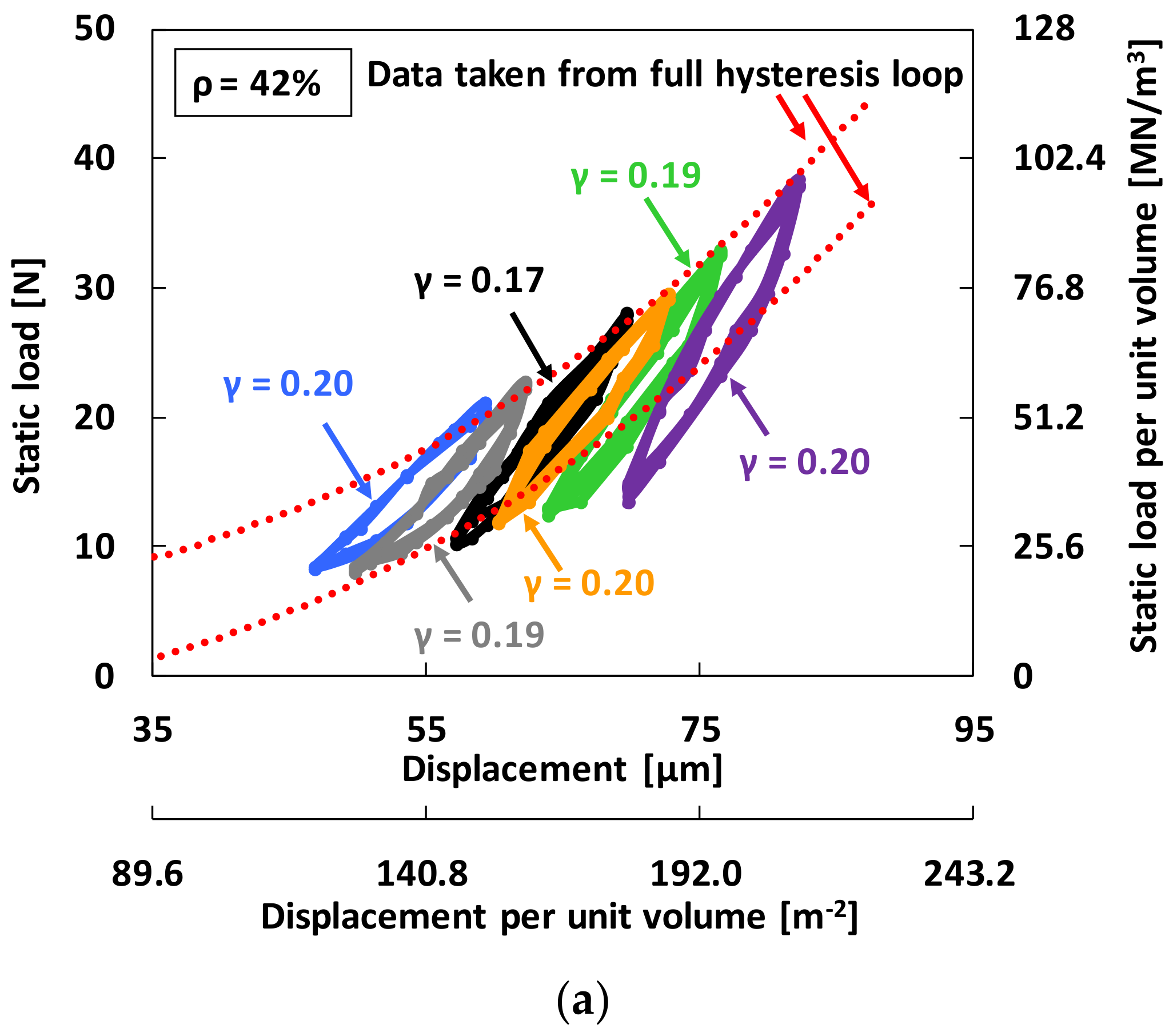
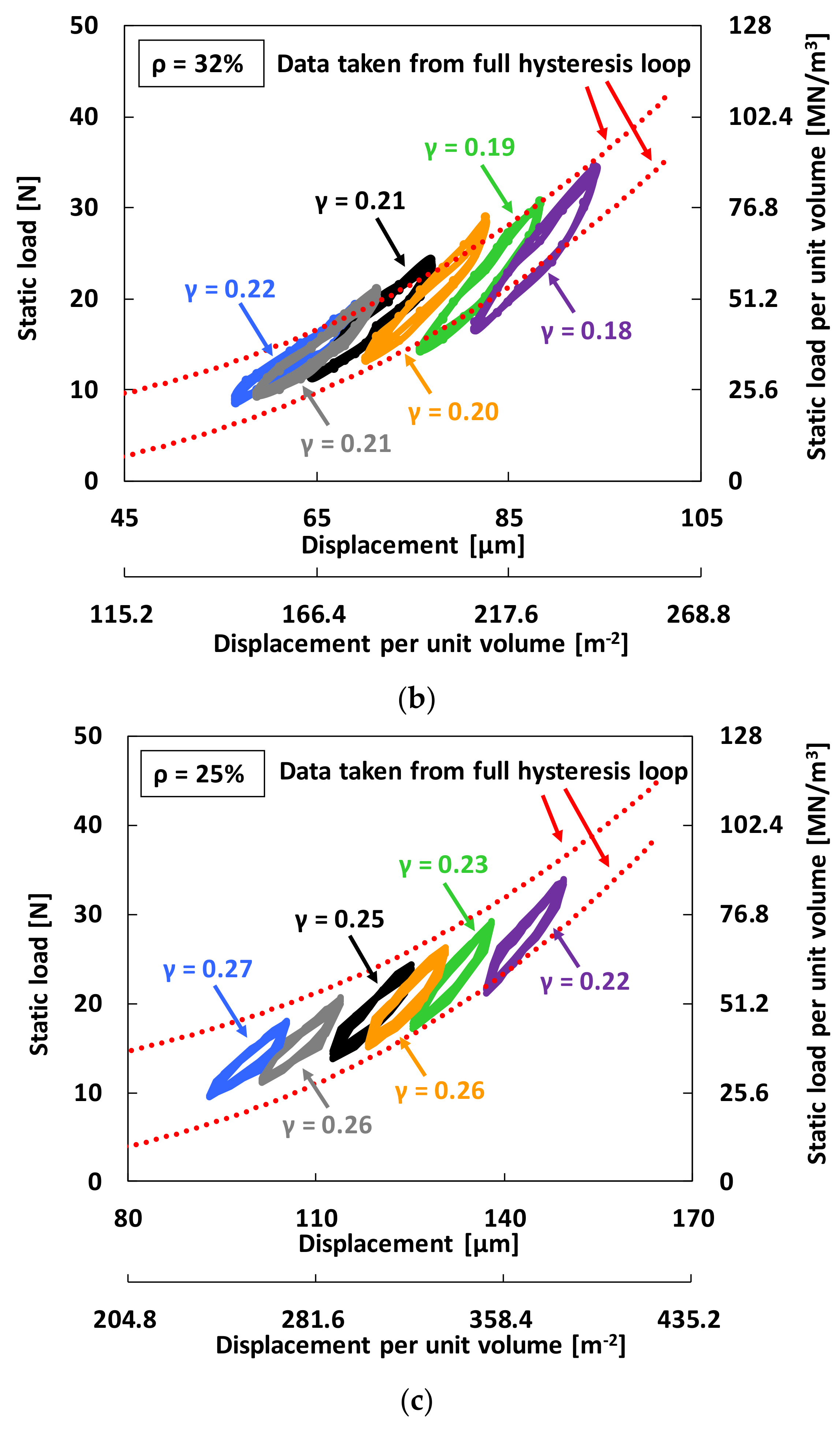
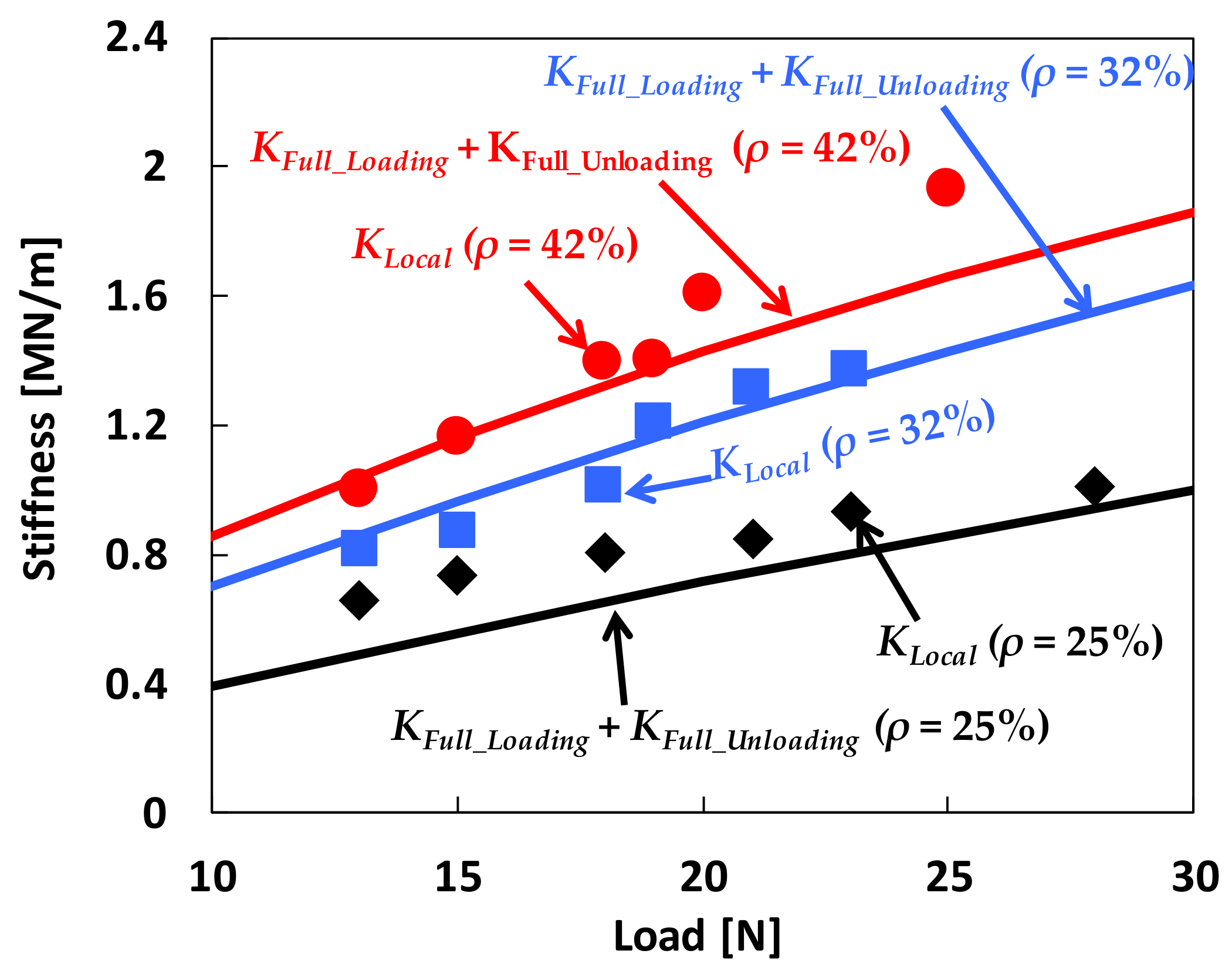
4.1. Structural Stiffness from Full Hysteresis Loop Measurements
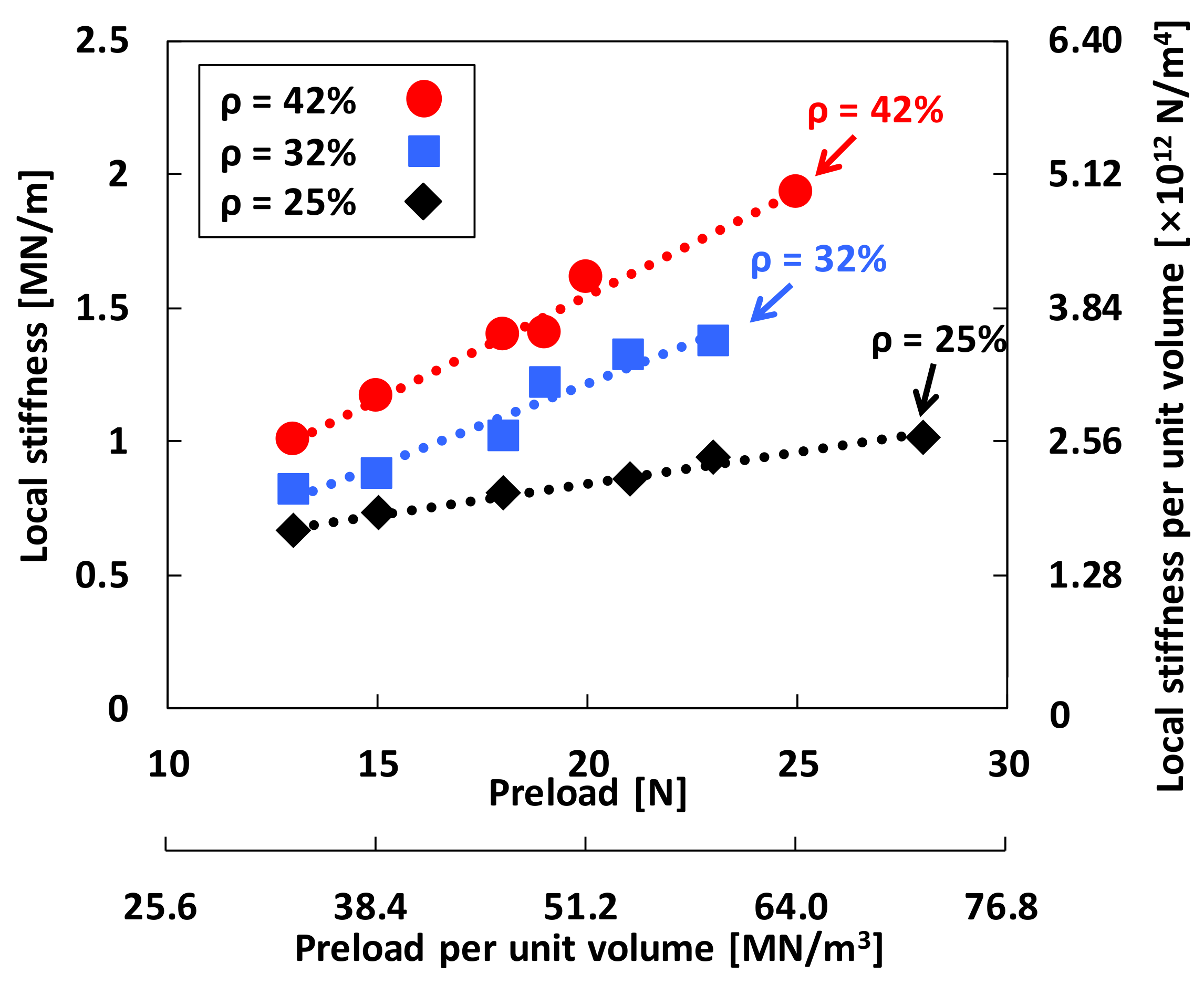
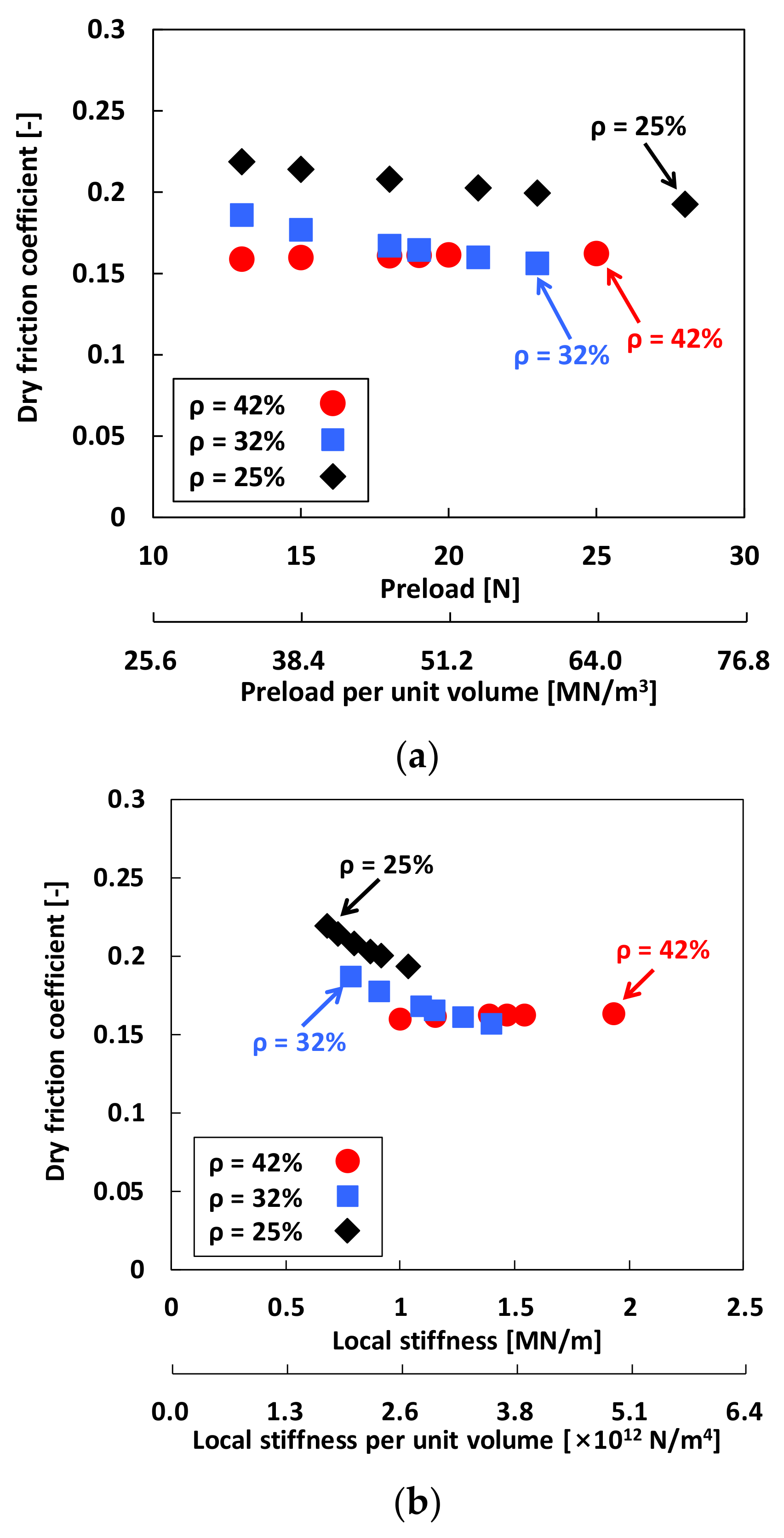
4.2. Structural Stiffness and Damping Parameters from Local Hysteresis Loop Measurements
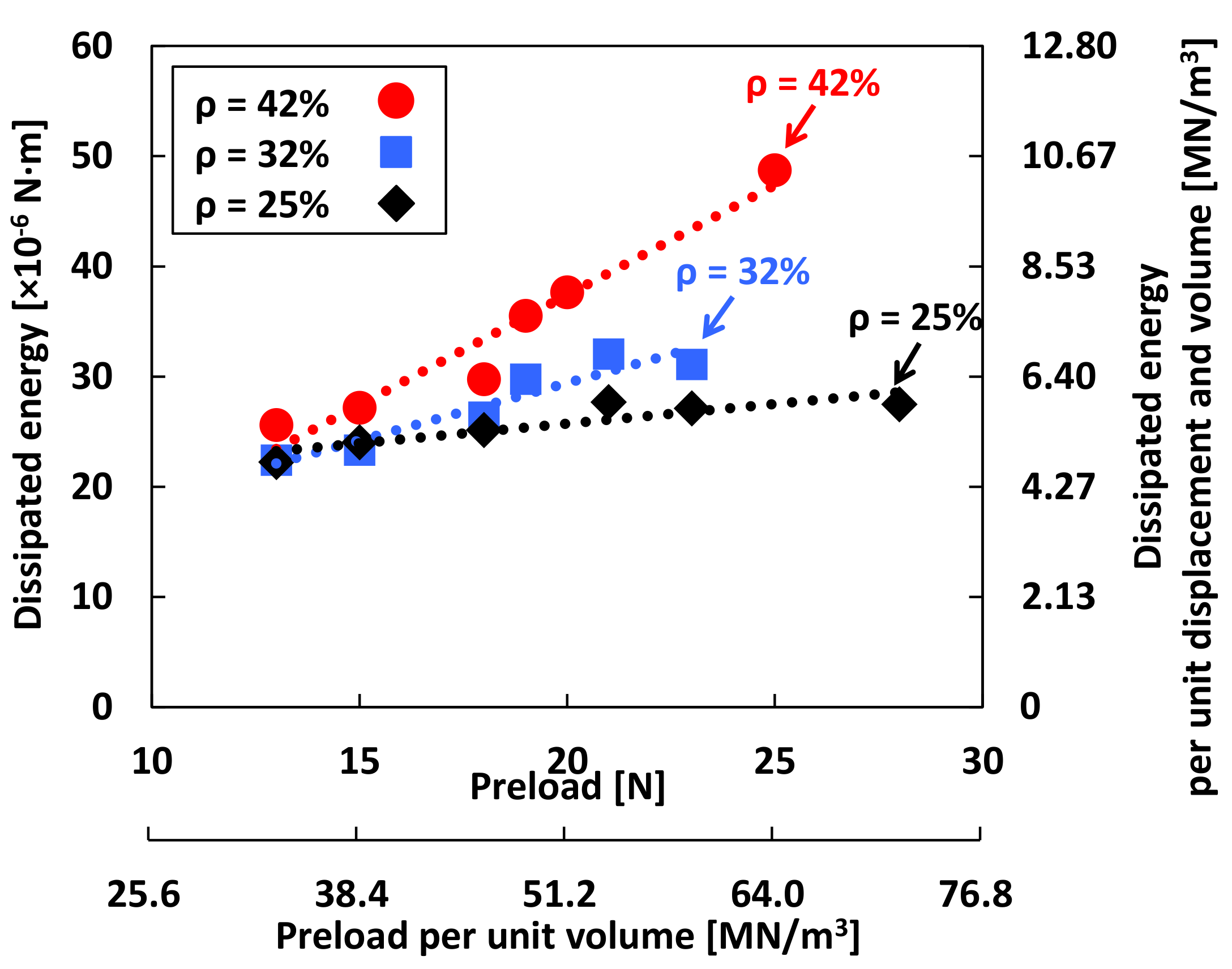
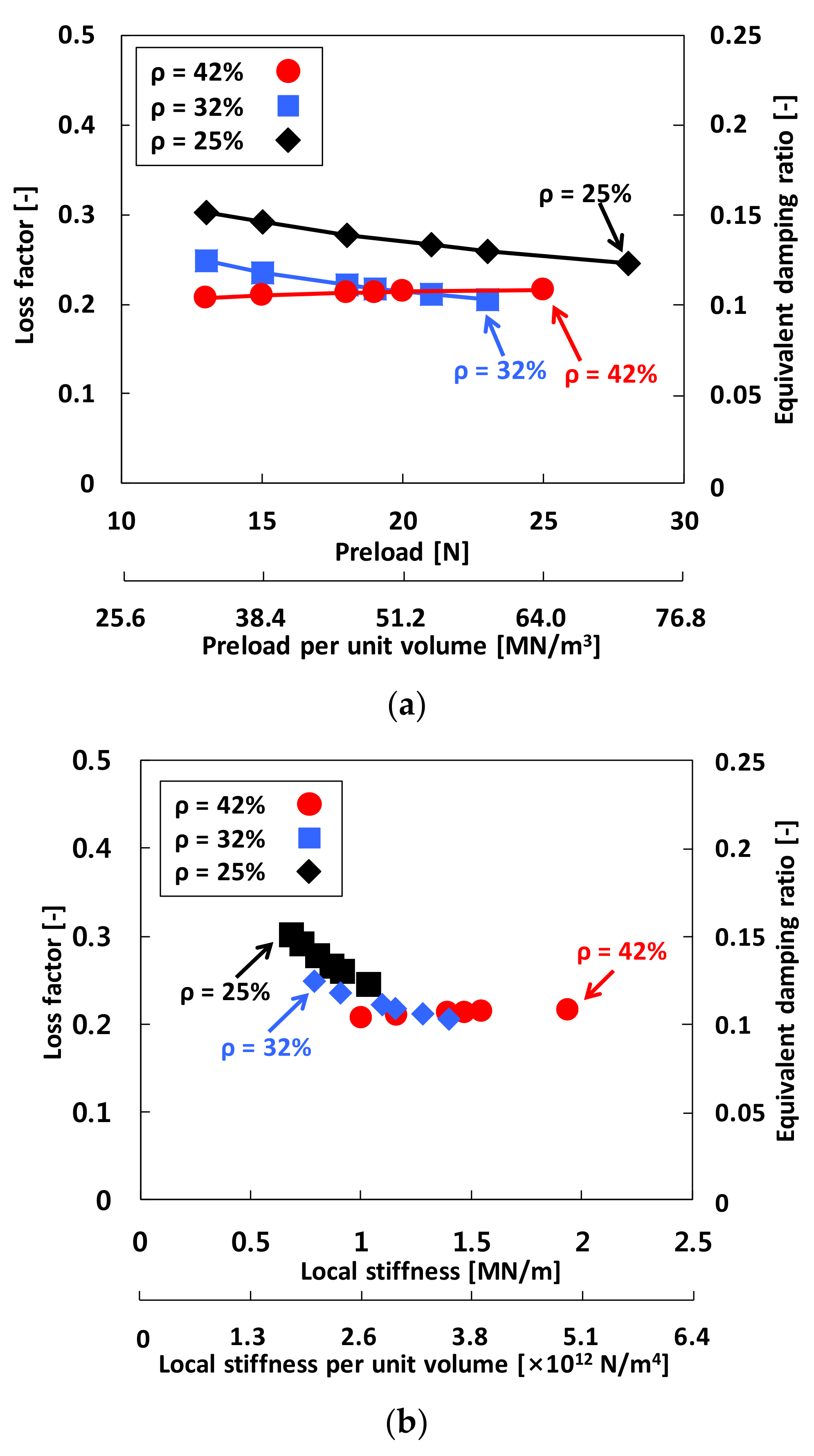
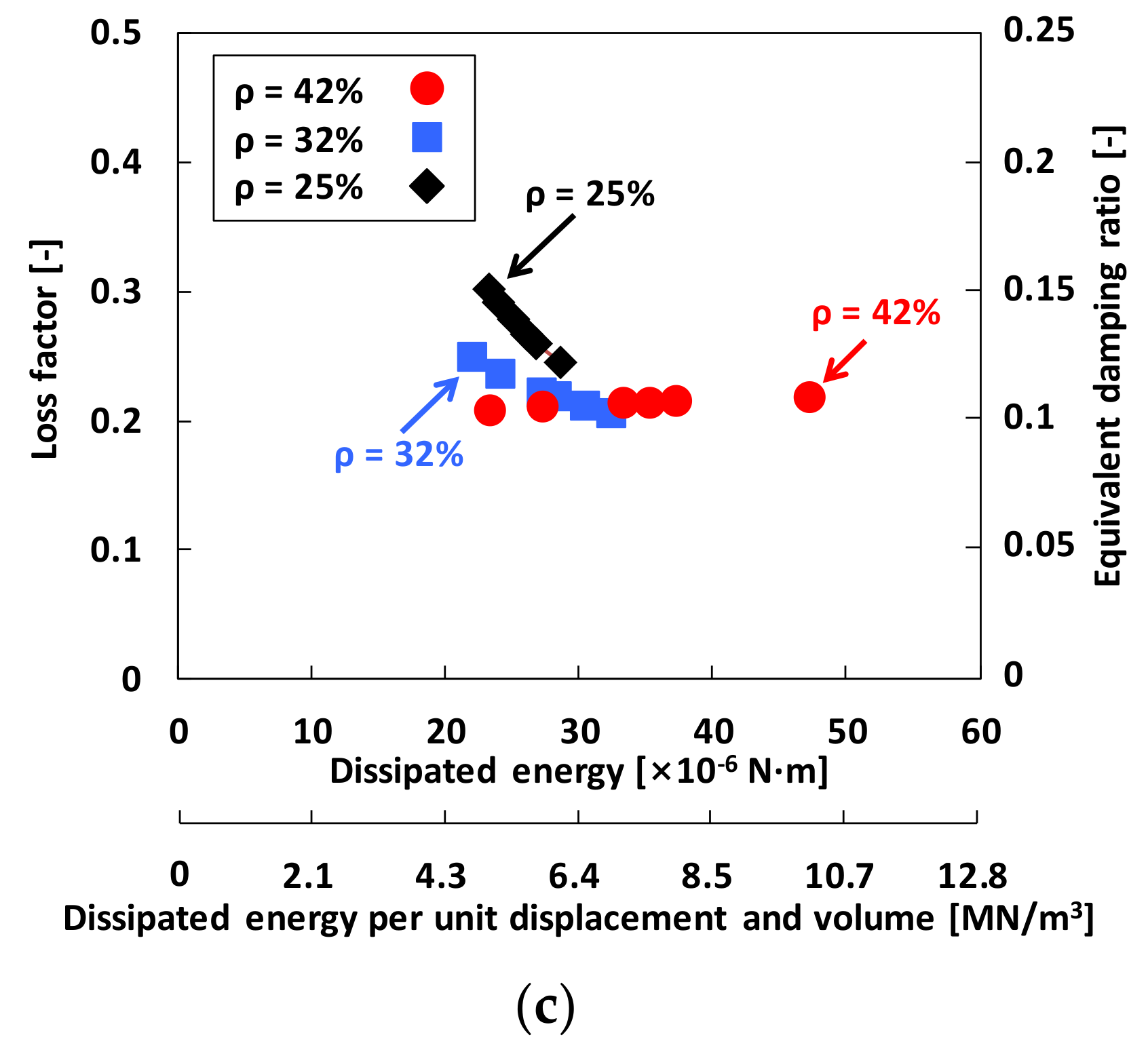
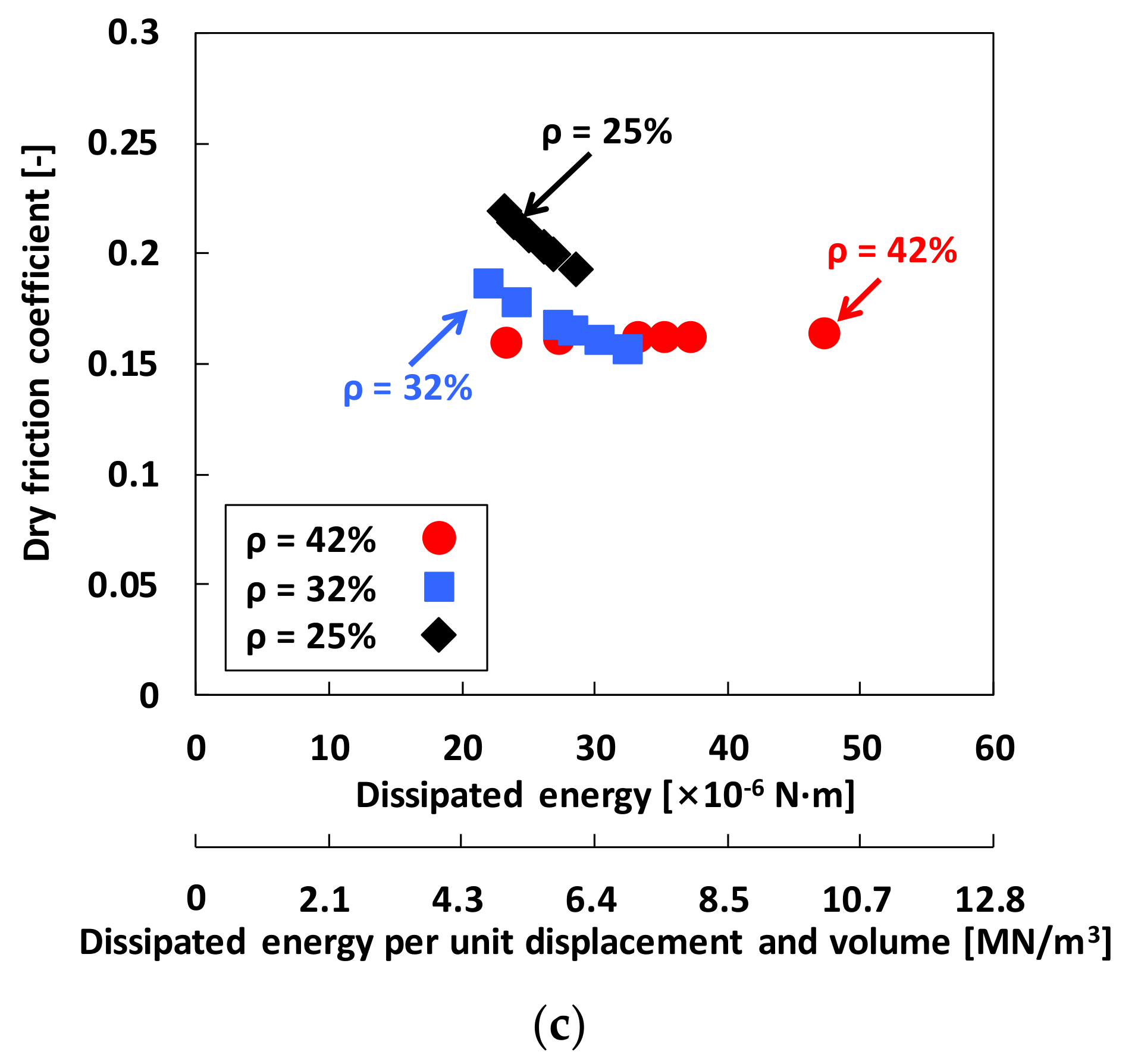
4.3. Damping Parameters from Local Hysteresis Loop Measurements
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
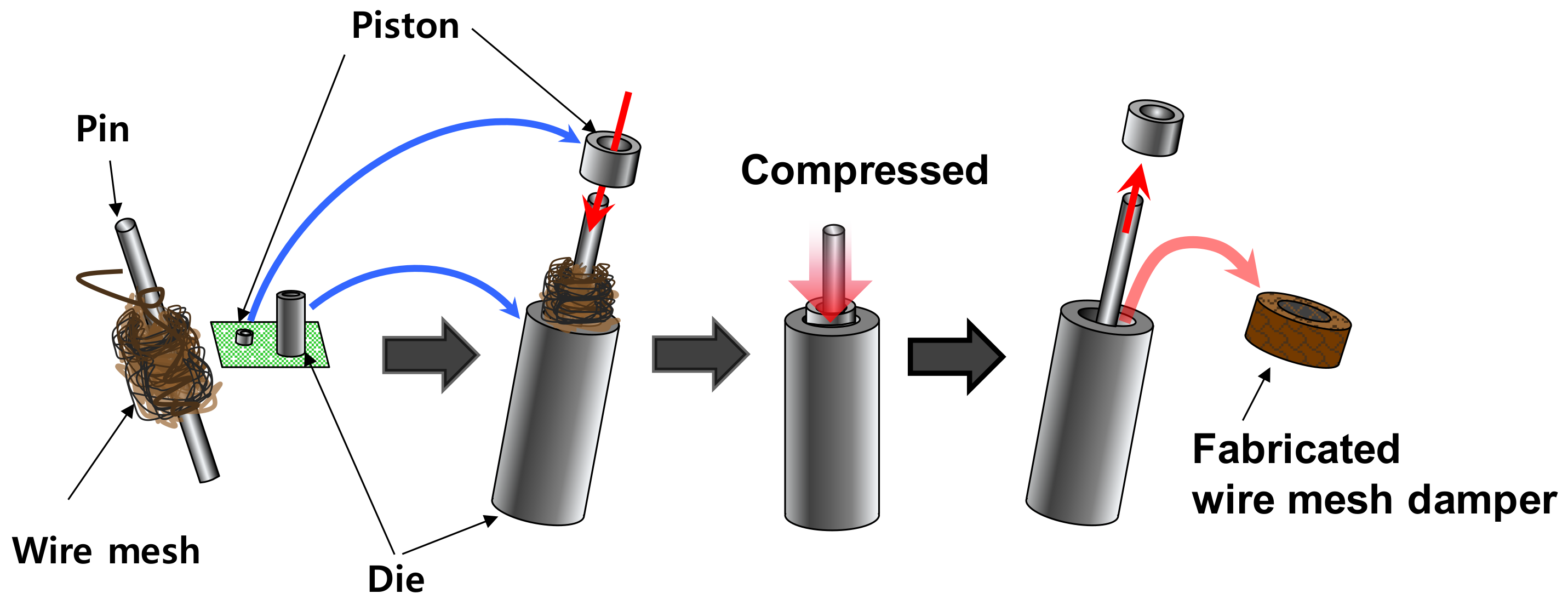
Appendix B
| WMD Density | Preload | Identified Value | Uncertainty (Uc) | % Uncertainty |
|---|---|---|---|---|
| ρ = 42% | 13 N | 1.001 MN/m | 0.103 MN/m | 10% |
| 15 N | 1.161 MN/m | 0.137 MN/m | 12% | |
| 18 N | 1.397 MN/m | 0.046 MN/m | 3% | |
| 19 N | 1.402 MN/m | 0.053 MN/m | 4% | |
| 20 N | 1.608 MN/m | 0.092 MN/m | 6% | |
| 25 N | 1.931 MN/m | 0.121 MN/m | 6% | |
| ρ = 32% | 13 N | 0.820 MN/m | 0.083 MN/m | 10% |
| 15 N | 0.873 MN/m | 0.087 MN/m | 10% | |
| 18 N | 1.015 MN/m | 0.080 MN/m | 8% | |
| 19 N | 1.215 MN/m | 0.064 MN/m | 5% | |
| 21 N | 1.319 MN/m | 0.080 MN/m | 6% | |
| 23 N | 1.373 MN/m | 0.135 MN/m | 10% | |
| ρ = 25% | 13 N | 0.662 MN/m | 0.030 MN/m | 5% |
| 15 N | 0.734 MN/m | 0.011 MN/m | 2% | |
| 18 N | 0.807 MN/m | 0.030 MN/m | 4% | |
| 21 N | 0.854 MN/m | 0.063 MN/m | 7% | |
| 23 N | 0.937 MN/m | 0.058 MN/m | 6% | |
| 28 N | 1.015 MN/m | 0.135 MN/m | 13% |
| WMD Density | Preload | Identified Value | Uncertainty (Uc) | % Uncertainty |
|---|---|---|---|---|
| ρ = 42% | 13 N | 25.602 μN·m | 5.450 μN·m | 21% |
| 15 N | 27.173 μN·m | 4.340 μN·m | 16% | |
| 18 N | 29.752 μN·m | 10.707 μN·m | 36% | |
| 19 N | 35.525 μN·m | 10.734 μN·m | 30% | |
| 20 N | 37.664 μN·m | 1.656 μN·m | 4% | |
| 25 N | 48.721 μN·m | 15.307 μN·m | 31% | |
| ρ = 32% | 13 N | 22.425 μN·m | 4.908 μN·m | 22% |
| 15 N | 23.332 μN·m | 2.325 μN·m | 10% | |
| 18 N | 26.323 μN·m | 1.453 μN·m | 5% | |
| 19 N | 29.765 μN·m | 11.512 μN·m | 39% | |
| 21 N | 32.040 μN·m | 4.614 μN·m | 14% | |
| 23 N | 31.102 μN·m | 11.903 μN·m | 38% | |
| ρ = 25% | 13 N | 22.252 μN·m | 1.345 μN·m | 6% |
| 15 N | 24.149 μN·m | 4.701 μN·m | 20% | |
| 18 N | 25.149 μN·m | 6.272 μN·m | 25% | |
| 21 N | 27.691 μN·m | 1.744 μN·m | 6% | |
| 23 N | 27.109 μN·m | 6.594 μN·m | 24% | |
| 28 N | 27.493 μN·m | 4.216 μN·m | 15% |
| WMD Density | Preload | Identified Value | Uncertainty (Uc) | % Uncertainty |
|---|---|---|---|---|
| ρ = 42% | 13 N | 0.207 | 0.021 | 10% |
| 15 N | 0.210 | 0.025 | 12% | |
| 18 N | 0.212 | 0.008 | 3% | |
| 19 N | 0.213 | 0.008 | 4% | |
| 20 N | 0.214 | 0.013 | 6% | |
| 25 N | 0.216 | 0.014 | 6% | |
| ρ = 32% | 13 N | 0.249 | 0.026 | 11% |
| 15 N | 0.236 | 0.023 | 10% | |
| 18 N | 0.221 | 0.016 | 7% | |
| 19 N | 0.218 | 0.013 | 6% | |
| 21 N | 0.211 | 0.013 | 6% | |
| 23 N | 0.206 | 0.020 | 10% | |
| ρ = 25% | 13 N | 0.302 | 0.014 | 4% |
| 15 N | 0.292 | 0.005 | 2% | |
| 18 N | 0.278 | 0.011 | 4% | |
| 21 N | 0.266 | 0.019 | 7% | |
| 23 N | 0.259 | 0.017 | 6% | |
| 28 N | 0.245 | 0.032 | 13% |
| WMD Density | Preload | Identified Value | Uncertainty (Uc) | % Uncertainty |
|---|---|---|---|---|
| ρ = 42% | 13 N | 0.159 | 0.009 | 6% |
| 15 N | 0.160 | 0.006 | 4% | |
| 18 N | 0.161 | 0.013 | 8% | |
| 19 N | 0.161 | 0.012 | 8% | |
| 20 N | 0.161 | 0.002 | 1% | |
| 25 N | 0.162 | 0.013 | 8% | |
| ρ = 32% | 13 N | 0.186 | 0.010 | 6% |
| 15 N | 0.177 | 0.004 | 2% | |
| 18 N | 0.167 | 0.002 | 1% | |
| 19 N | 0.164 | 0.017 | 10% | |
| 21 N | 0.160 | 0.006 | 4% | |
| 23 N | 0.156 | 0.014 | 9% | |
| ρ = 25% | 13 N | 0.219 | 0.003 | 1% |
| 15 N | 0.214 | 0.011 | 5% | |
| 18 N | 0.208 | 0.013 | 6% | |
| 21 N | 0.203 | 0.003 | 2% | |
| 23 N | 0.200 | 0.012 | 6% | |
| 28 N | 0.193 | 0.007 | 4% |
References
- Ryu, K.; Ashton, Z. Bump-Type Foil Bearings and Flexure Pivot Tilting Pad Bearings for Automotive Oil-Free Turbochargers: Highlights in Rotordynamic Performance. ASME J. Eng. Gas Turbines Power 2016, 138, 042501. [Google Scholar] [CrossRef]
- San Andrés, L.; Vistamehr, A. Nonlinear Rotordynamics of Vehicle Turbochargers: Parameters Affecting Sub Harmonic Whirl Frequencies and Their Jump. In Proceedings of the 8th IFToMM International Conference on Rotordynamics, Seoul, Korea, 12–15 September 2010. [Google Scholar]
- Ehrich, F.; Childs, D. Self-Excited Vibration in High-Performance Turbomachinery. Mech. Eng. 1984, 106, 66–79. [Google Scholar]
- San Andrés, L.; Rivadeneira, J.; Chinta, M.; Gjika, K.; LaRue, G. Nonlinear Rotordynamics of Automotive Turbochargers: Predictions and Comparisons to Test Data. ASME J. Eng. Gas Turbines Power 2007, 129, 488–493. [Google Scholar] [CrossRef]
- San Andrés, L.; Rivadeneira, J.C.; Gjika, K.; Groves, C.; LaRue, G. A Virtual Tool for Prediction of Turbocharger Nonlinear Dynamic Response: Validation against Test Data. ASME J. Eng. Gas Turbines Power 2007, 129, 1035–1046. [Google Scholar] [CrossRef]
- San Andrés, L.; Barbarie, V.; Bhattacharya, A.; Gjika, K. On the Effect of Thermal Energy Transport to the Performance of (Semi) Floating Ring Bearing Systems for Automotive Turbochargers. ASME J. Eng. Gas Turbines Power 2012, 134, 102507. [Google Scholar] [CrossRef]
- Kim, K.; Ryu, K. Rotordynamic Analysis of Automotive Turbochargers Supported on Ball Bearings and Squeeze Film Dampers in Series: Effect of Squeeze Film Damper Design Parameters and Rotor Imbalances. Tribol. Lubr. 2018, 34, 8–15. [Google Scholar] [CrossRef]
- Zeidan, F.; San Andrés, L.; Vance, J. Design and Application of Squeeze Film Dampers in Rotating Machinery. In Proceedings of the 25th Turbomachinery Symposium, College Station, TX, USA, 17–19 September 1996; pp. 169–188. [Google Scholar]
- San Andrés, L.; Jeung, S.-H.; Den, S.; Savela, G. Squeeze Film Damper: An Experimental Appraisal of Their Dynamic Performance. In Proceedings of the 2016 Asia Turbomachinery & Pump Symposium, Marina Bay Sands, Singapore, 22–25 February 2016; pp. 1–23. [Google Scholar]
- Childs, D.W. Turbomachinery Rotordynamics with Case Studies; Minter Spring Publishing: Wellborn, TX, USA, 2013; pp. 281–317. ISBN 978-0-615-85272-0. [Google Scholar]
- Delgado, A.; San Andrés, L. A Model for Improved Prediction of Force Coefficients in Grooved Squeeze Film Dampers and Grooved Oil Seal Rings. ASME J. Tribol. 2010, 132, 032202. [Google Scholar] [CrossRef]
- San Andrés, L. Squeeze Film Damper: Operation, Models and Technical Issues, Modern Lubrication Theory, Notes 13, Texas A&M University, 2012. Available online: http://hdl.handle.net/1969.1/93253 (accessed on 27 February 2018).
- San Andrés, L. Force Coefficients for a Large Clearance Open Ends Squeeze Film Damper with a Central Groove: Experiments and Predictions. Tribol. Int. 2014, 71, 17–25. [Google Scholar] [CrossRef]
- Jeung, S.-H.; San Andrés, L.; Bradley, G. Forced Coefficients for a Short Length, Open-Ends Squeeze Film Damper with End Grooves: Experiments and Predictions. ASME J. Gas Turbines Power 2016, 138, 022501. [Google Scholar] [CrossRef]
- Vance, J.; Zeidan, F.; Murphy, B. Machinery Vibration and Rotordynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 214–216. ISBN 978-0-471-46213-2. [Google Scholar]
- Chirathadam, T.A. Measurements of Drag Torque and Lift off Speed and Identification of Stiffness and Damping in A Metal Mesh Foil Bearing. Master’s Thesis, Texas A&M University, College Station, TX, USA, December 2009. [Google Scholar]
- Childs, D.W. The Space Shuttle Main Engine High-Pressure Fuel Turbopump Rotordynamic Instability Problem. AMSE J. Eng. Power 1978, 100, 48–57. [Google Scholar] [CrossRef]
- Okayasu, A.; Ohta, T.; Azuma, T.; Fujita, T.; Aoki, H. Vibration Problem in the LE-7 LH2 Turbopump. In Proceedings of the 26th Joint Propulsion Conference, Orlando, FL, USA, 16–18 July 1990. [Google Scholar]
- Zarzour, M.; Vance, J. Experimental Evaluation of a Metal Mesh Bearing Damper. ASME J. Eng. Gas Turbines Power 2000, 122, 1–4. [Google Scholar] [CrossRef]
- Ertas, B.H.; Al-Khateeb, E.M.; Vance, J.M. Rotordynamic Bearing Dampers for Cryogenic Rocket Engine Turbopumps. AIAA J. Propul. Power 2003, 119, 674–682. [Google Scholar] [CrossRef]
- Ertas, B.; Luo, H.; Hallman, D. Dynamic Characteristics of Shape Memory Alloy Metal Mesh Dampers. In Proceedings of the 50th AIAA Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
- San Andrés, L.; Chirathadam, T.A. A Metal Mesh Foil Bearing and a Bump-Type Foil Bearing: Comparison of Performance for Two Similar Size Gas Bearings. ASME J. Eng. Gas Turbines Power 2012, 134, 102501. [Google Scholar] [CrossRef]
- Feng, K.; Zhao, X.; Zhang, Z.; Zhang, T. Numerical and Compact Model of Metal Mesh Foil Bearings. STLE Trib. Trans. 2016, 59, 480–490. [Google Scholar] [CrossRef]
- Ertas, B. Compliant Hybrid Journal Bearings Using Integral Wire Mesh Dampers. ASME J. Eng. Gas Turbines Power 2009, 131, 1–11. [Google Scholar] [CrossRef]
- Feng, K.; Liu, W.; Zhang, Z.; Zhang, T. Theoretical Model of a Flexure Pivot Tilting Pad Gas Bearings with Metal Mesh Dampers in Parallel. Tribol. Int. 2016, 94, 26–38. [Google Scholar] [CrossRef]
- Ryu, K. Fluid Film Hydrodynamic Flexure Pivot Tilting Pad Semi-Floating Ring Journal Bearing with Compliant Dampers. U.S. Patent 9,599,149 B2, 21 March 2017. [Google Scholar]
- Juvinall, R.C.; Marshek, K.M. Machine Component Design, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; p. 817. ISBN 978-1-118-09226-2. [Google Scholar]
- San Andrés, L.; Ryu, K.; Kim, T.H. Identification of Structural Stiffness and Energy Dissipation Parameters in a Second Generation Foil Bearing—Effect of Shaft Temperature. ASME J. Eng. Gas Turbines Power 2011, 133, 032501. [Google Scholar] [CrossRef]
- Larsen, J.S.; Varela, A.C.; Santos, I.F. Numerical and Experimental Investigation of Bump Foil Mechanical Behavior. Tribol. Int. 2014, 74, 46–56. [Google Scholar] [CrossRef]
- Ginsberg, J.H. Mechanical and Structural Vibrations: Theory and Application, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 130–139. ISBN 0-471-12808-2. [Google Scholar]
- Rao, S.S. Mechanical Vibration, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011; pp. 192–198. ISBN 978-0-13-212819-3. [Google Scholar]
- De Silva, C.W. Vibration: Fundamentals and Practice, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007; pp. 385–427. ISBN 0-8493-1987-0. [Google Scholar]
- San Andrés, L.; Ryu, K. On the Nonlinear Dynamics of Rotor-Foil Bearing Systems: Effects of Shaft Acceleration, Mass Imbalance and Bearing Mechanical Energy Dissipation. In Proceedings of the ASME 2011 Turbo Expo, Vancouver, British Columbia, Canada, 6–10 June 2011. [Google Scholar]
- Park, E.Q. Effect of Bearing Design Parameters on Rotordynamic Stability and Shaft Motion Amplitudes for Automotive Turbocharges Supported on Fully Floating Ring Bearings. Master’s Thesis, Hanyang University, Seoul, Korea, February 2018. [Google Scholar]
- Bang, J. Experimental Identification of Structural Stiffness and Damping Coefficients in Bump-type Foil Bearings. Master’s Thesis, Hanyang University, Seoul, Korea, February 2017. [Google Scholar]
- Hoffmann, R.; Liebich, R. Characterization and Calculation of Nonlinear Vibrations in Gas Foil Bearing Systems—An Experimental and Numerical investigation. J. Sound Vib. 2018, 412, 389–409. [Google Scholar] [CrossRef]


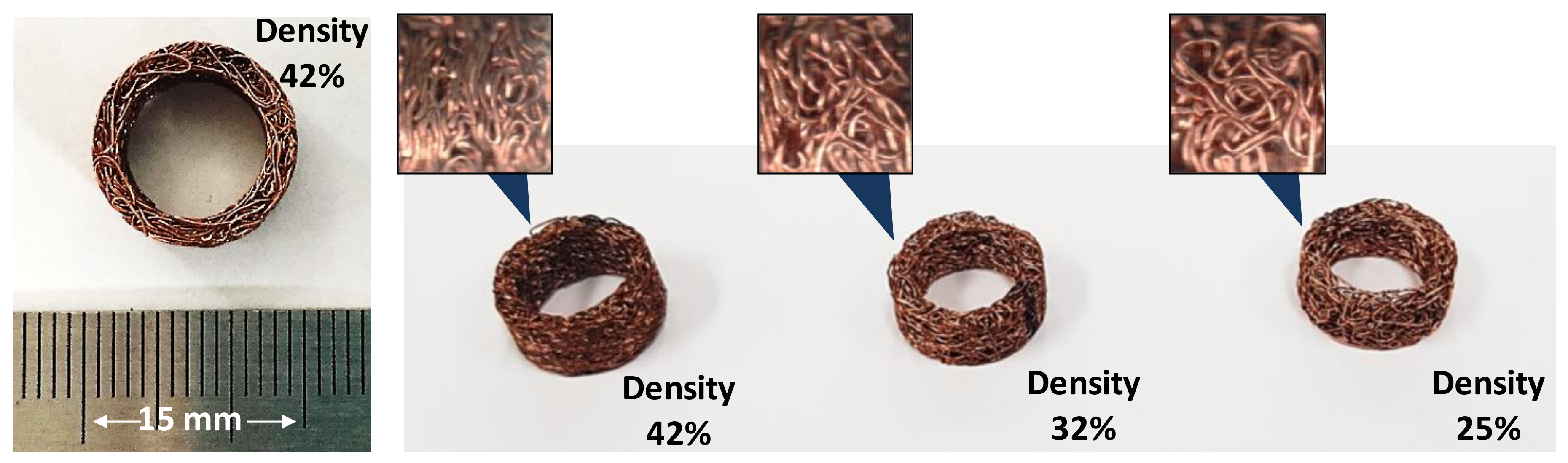
| Parameters | WMDρ=42% | WMDρ=32% | WMDρ=25% |
|---|---|---|---|
| Mass | 1.453 g | 1.062 g | 0.854 g |
| Outer diameter | 13.430 mm | 13.284 mm | 13.352 mm |
| Inner diameter | 9.713 mm | 9.206 mm | 9.320 mm |
| Width | 5.782 mm | 5.127 mm | 5.322 mm |
| Volume | 3.906 × 10−7 m3 | 3.693 × 10−7 m3 | 3.820 × 10−7 m3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryu, K.; Yi, H. Wire Mesh Dampers for Semi-Floating Ring Bearings in Automotive Turbochargers: Measurements of Structural Stiffness and Damping Parameters. Energies 2018, 11, 812. https://doi.org/10.3390/en11040812
Ryu K, Yi H. Wire Mesh Dampers for Semi-Floating Ring Bearings in Automotive Turbochargers: Measurements of Structural Stiffness and Damping Parameters. Energies. 2018; 11(4):812. https://doi.org/10.3390/en11040812
Chicago/Turabian StyleRyu, Keun, and Howon Yi. 2018. "Wire Mesh Dampers for Semi-Floating Ring Bearings in Automotive Turbochargers: Measurements of Structural Stiffness and Damping Parameters" Energies 11, no. 4: 812. https://doi.org/10.3390/en11040812
APA StyleRyu, K., & Yi, H. (2018). Wire Mesh Dampers for Semi-Floating Ring Bearings in Automotive Turbochargers: Measurements of Structural Stiffness and Damping Parameters. Energies, 11(4), 812. https://doi.org/10.3390/en11040812






