A Novel Direct Torque Control Method Based on Asymmetric Boundary Layer Sliding Mode Control for PMSM
Abstract
:1. Introduction
2. Review of Classical DTC for PMSM
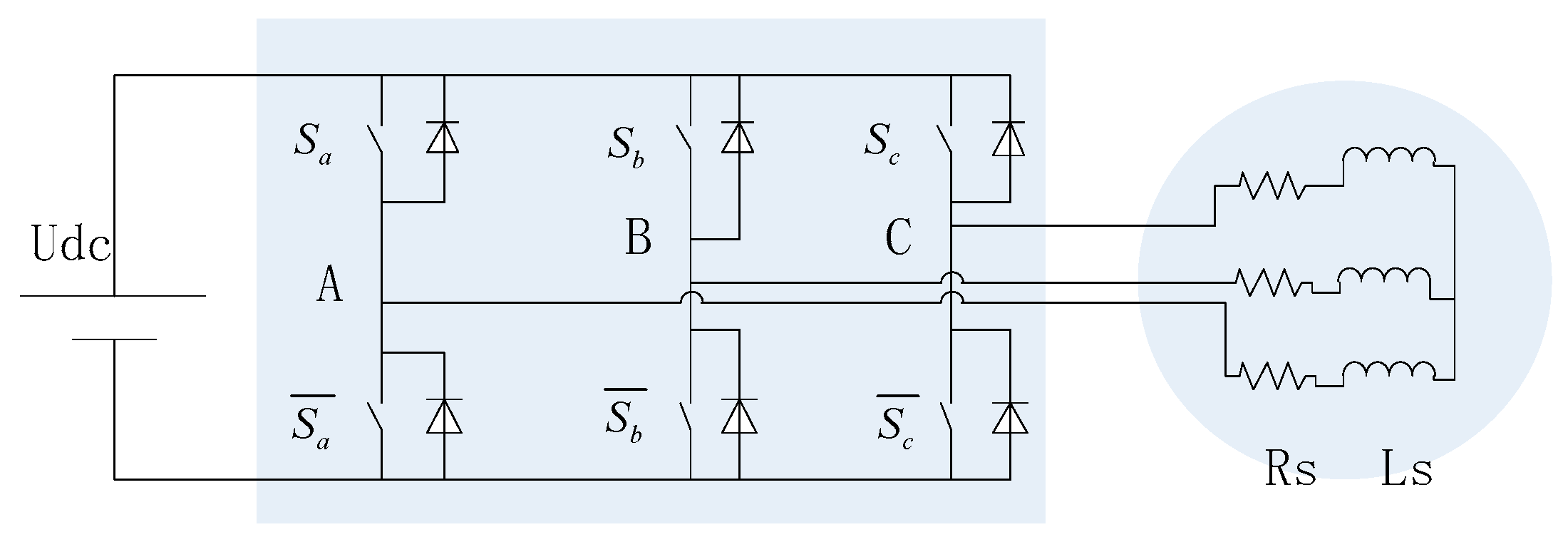
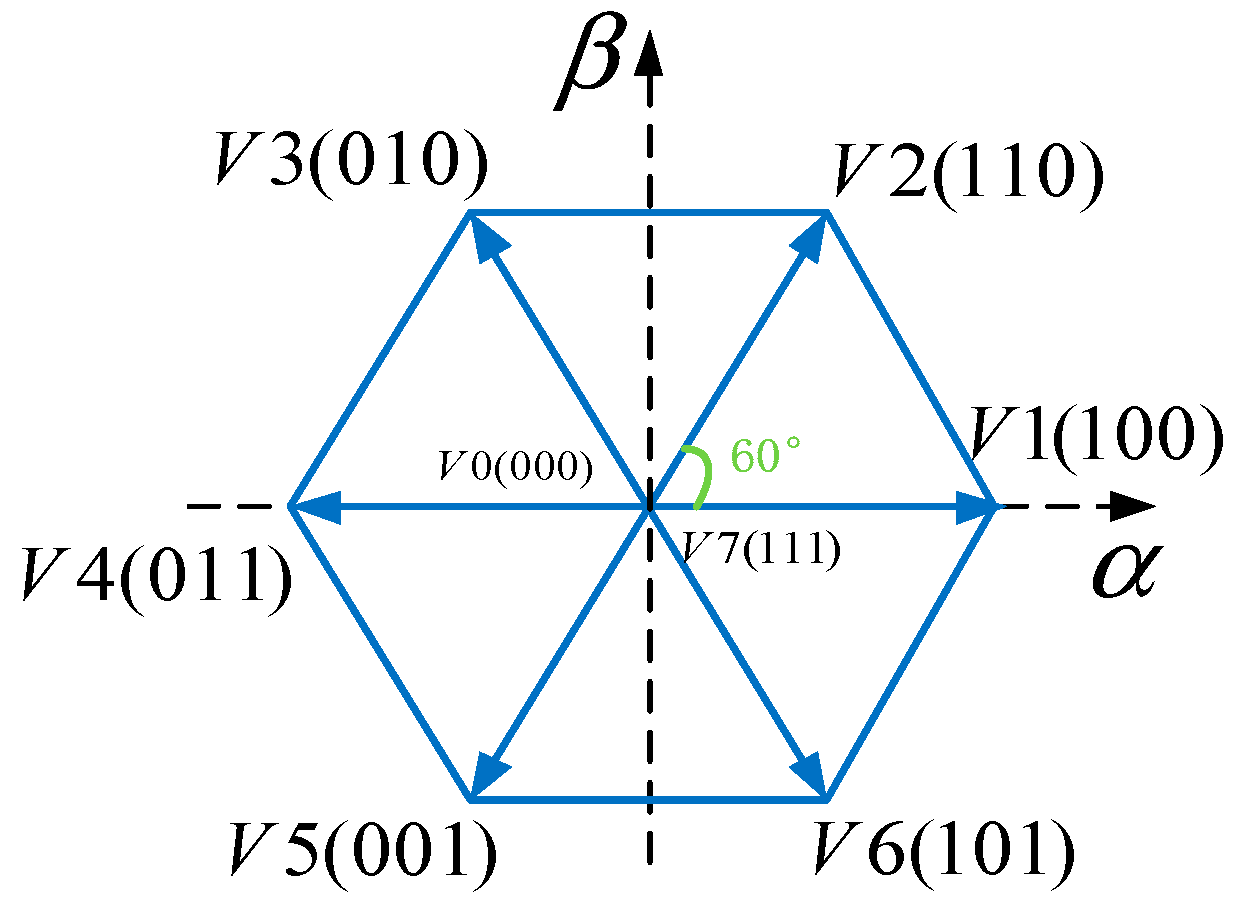
2.1. The Definition of Primary Voltage Vectors
2.2. Model of PMSM
- , —stator voltage of d and q-axis,
- , —stator current of d and q axis,
- , —stator flux linkage of d and q-axis,
- , —inductances of d and q-axis,
- —stator resistance,
- —permanent magnet flux, and
- —rotor mechanical speed.
2.3. The Control of the Amplitude of Stator Flux Linkage
2.4. Implementation of DTC for PMSM
3. Proposed DTC Method
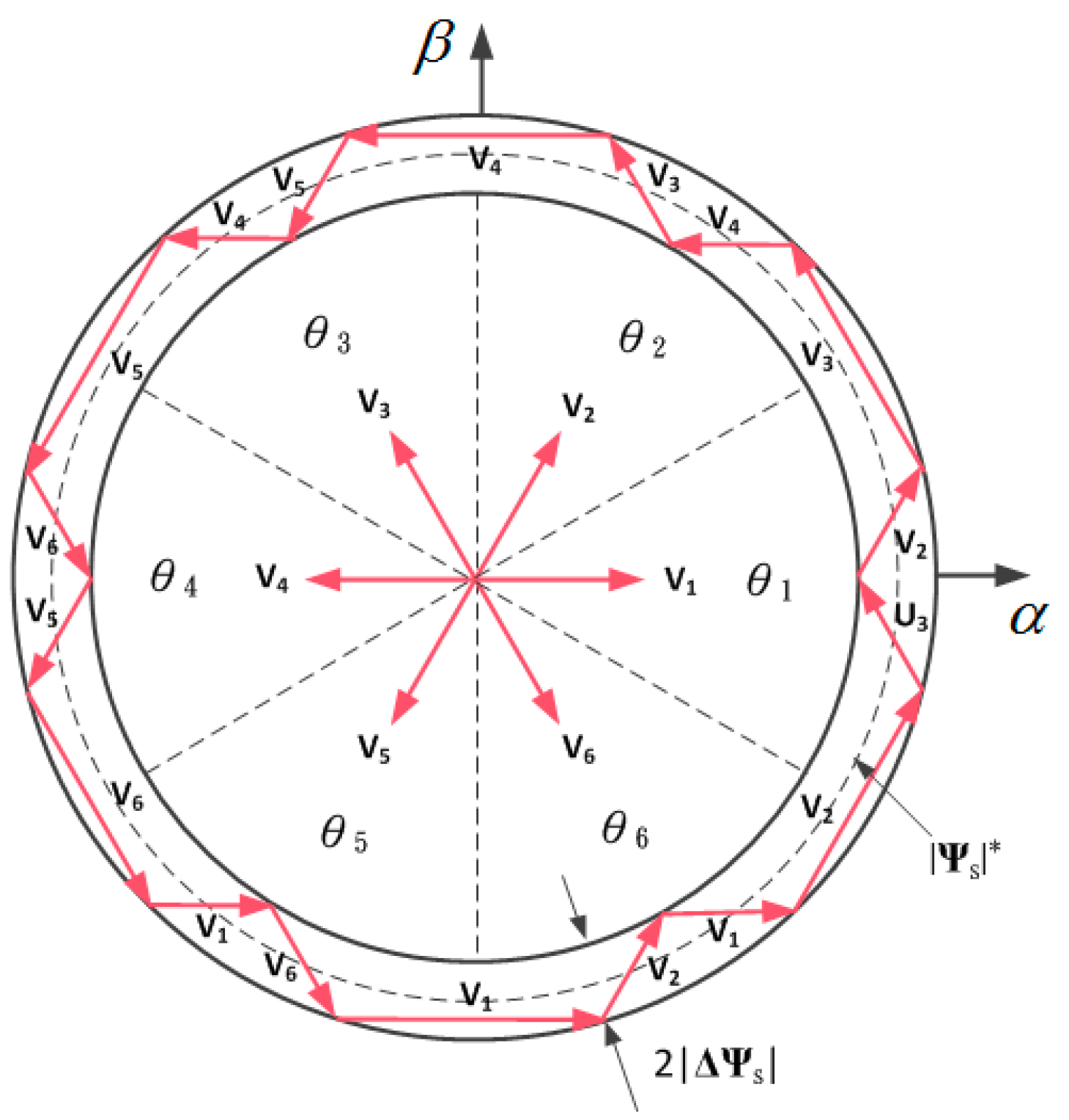
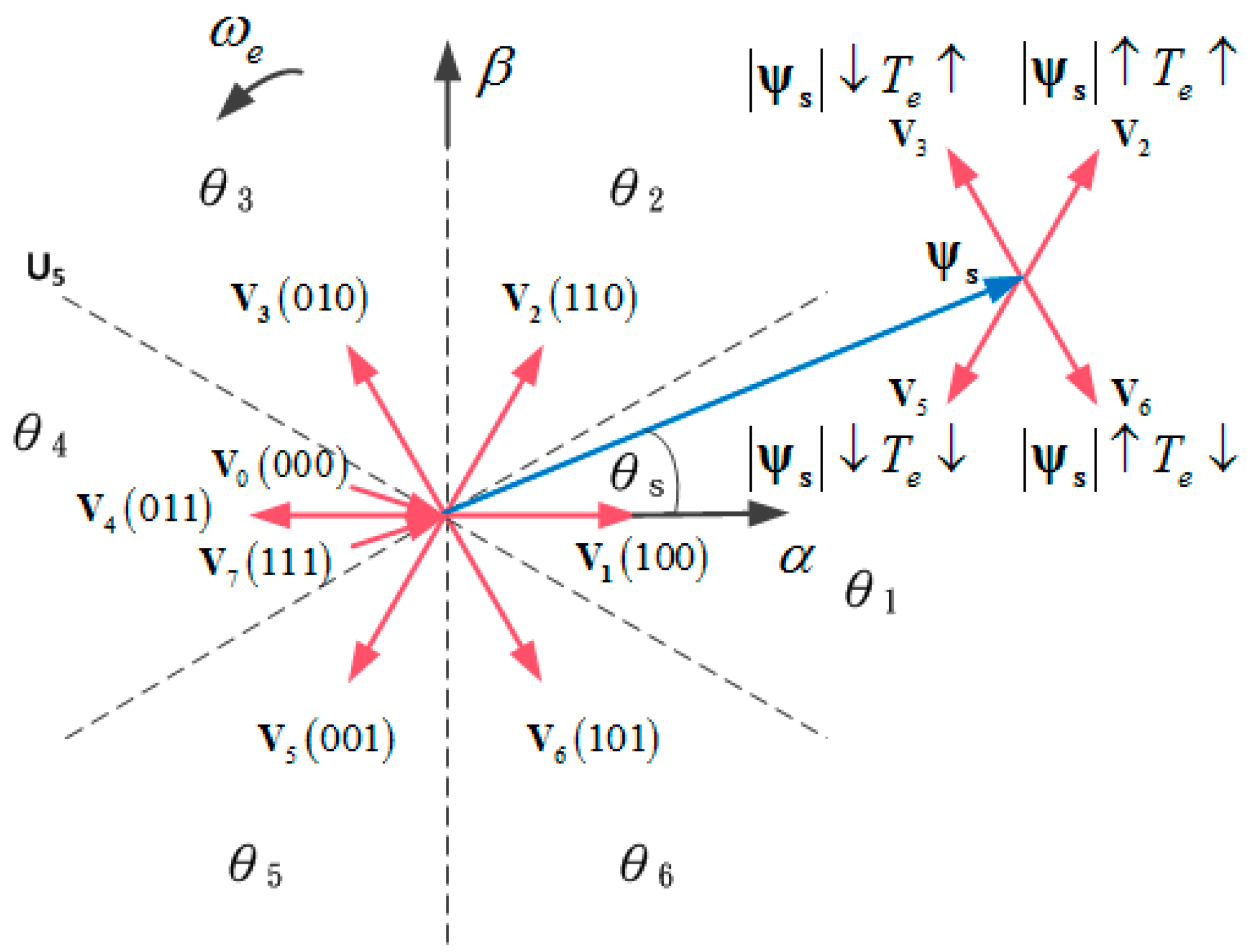
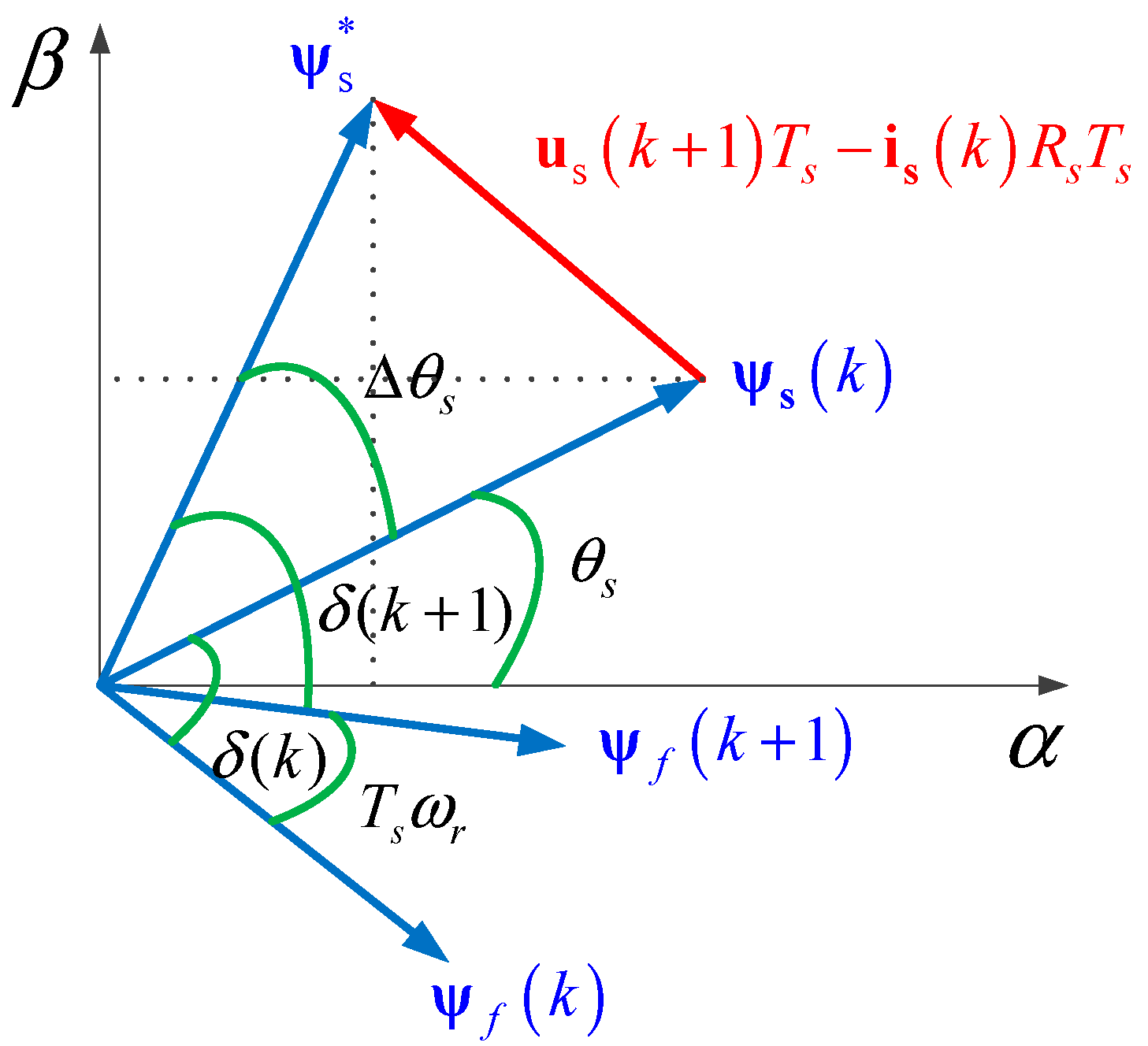
3.1. Generation of Reference Voltage Vector
3.2. Design of SMC-Based Torque Controller
3.3. Design of SMC-Based Speed Controller
4. Simulation Results and Comparison
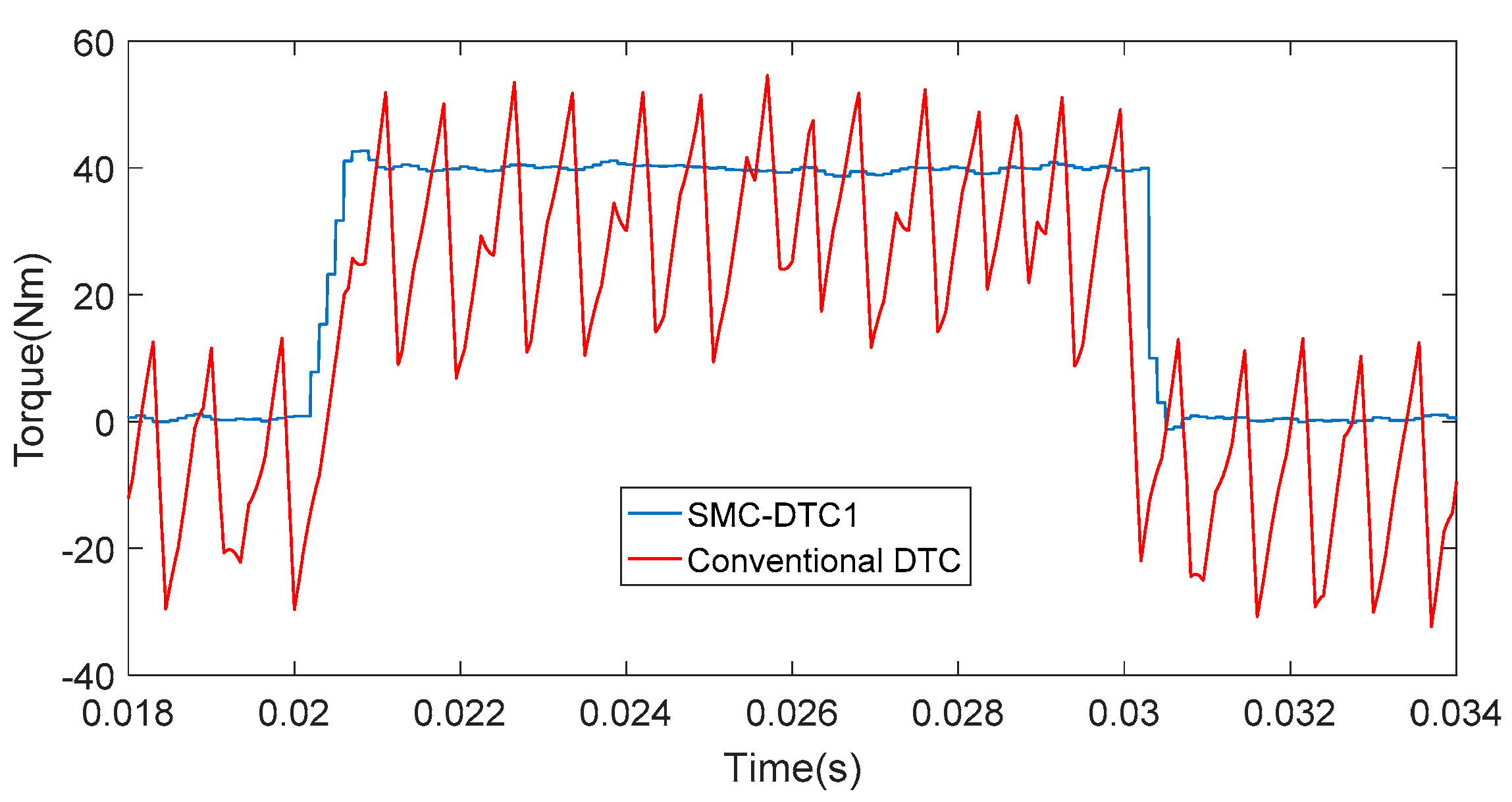
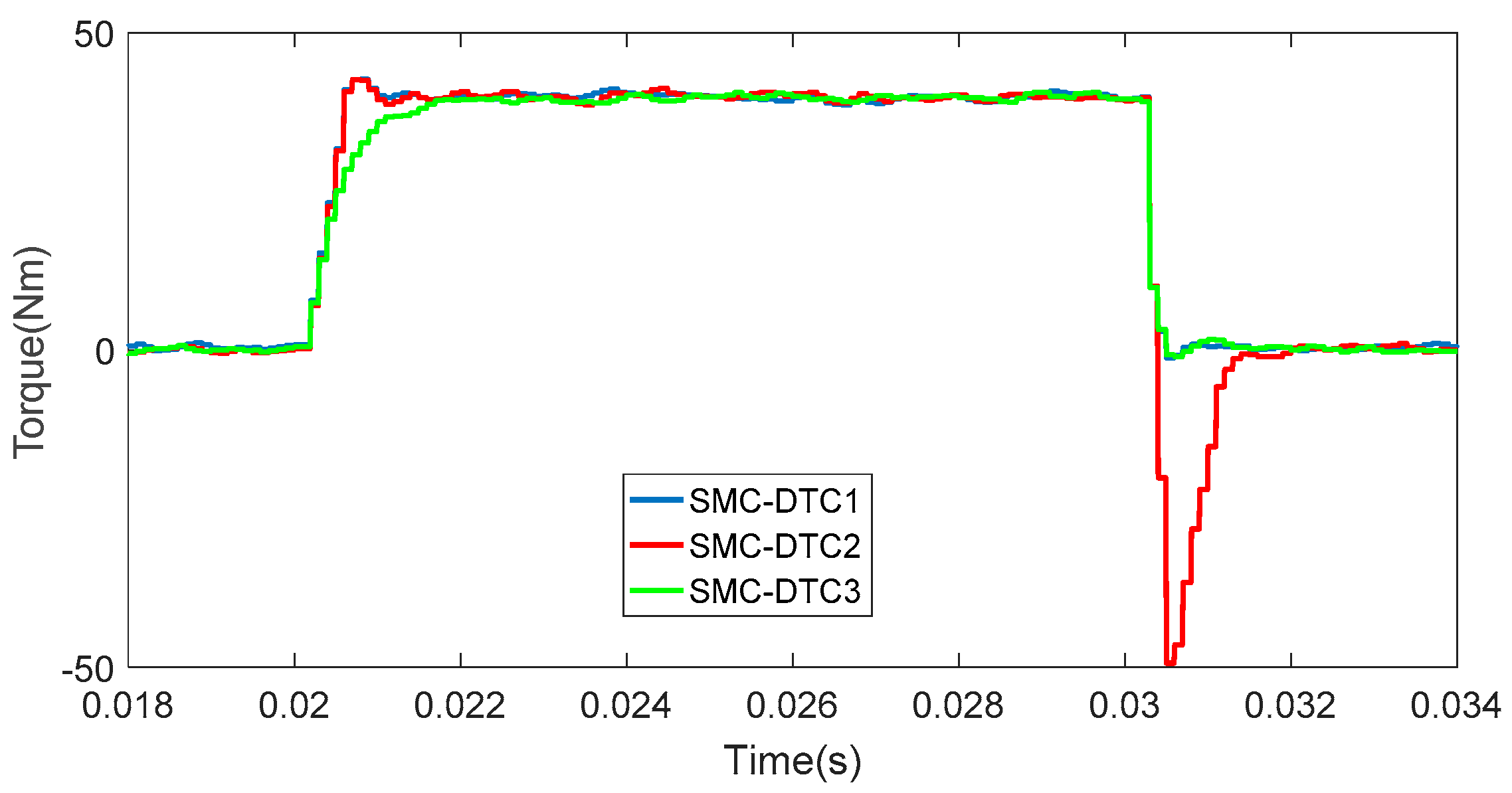
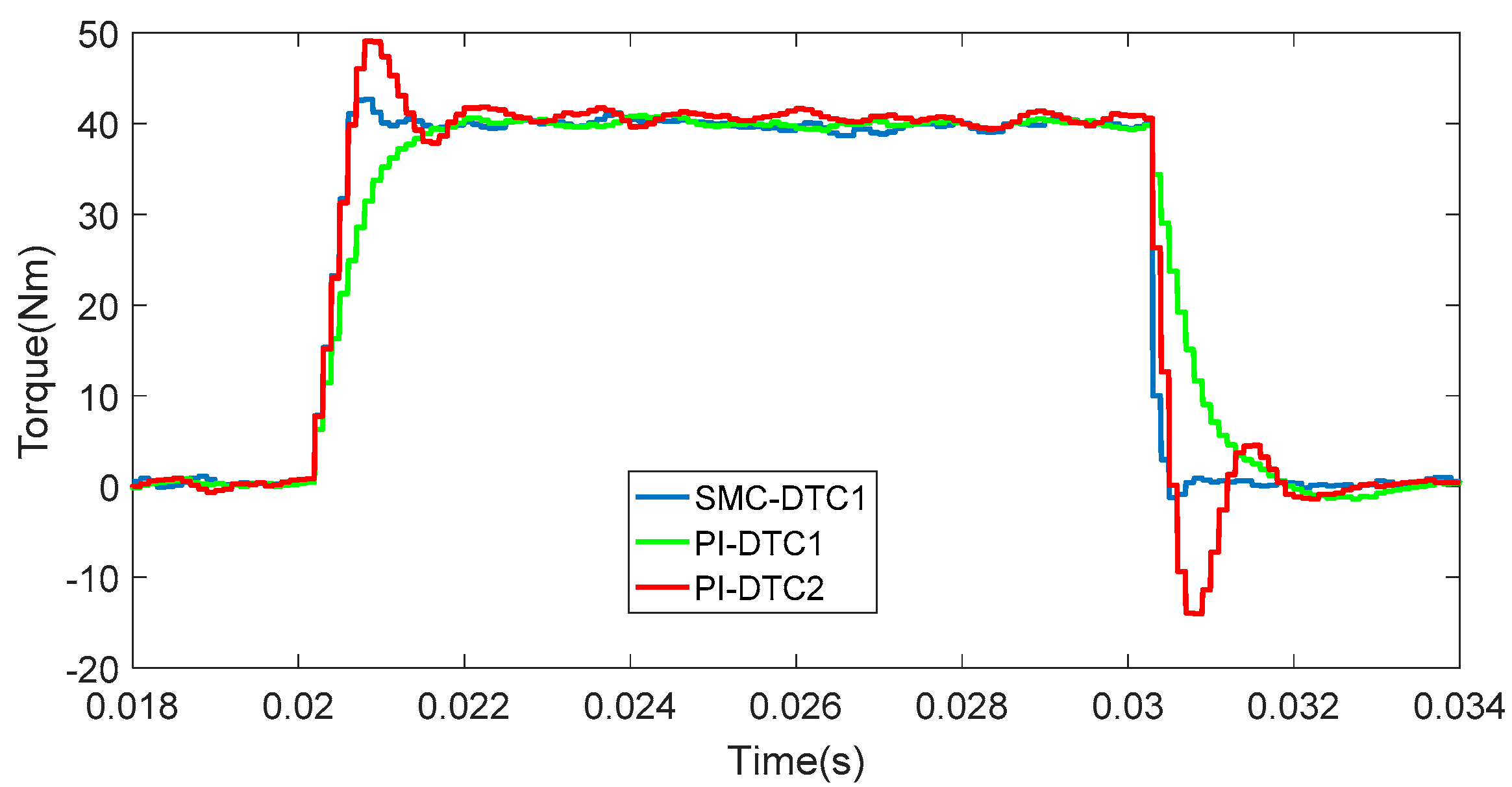
4.1. Torque Response in Transient-State Operation
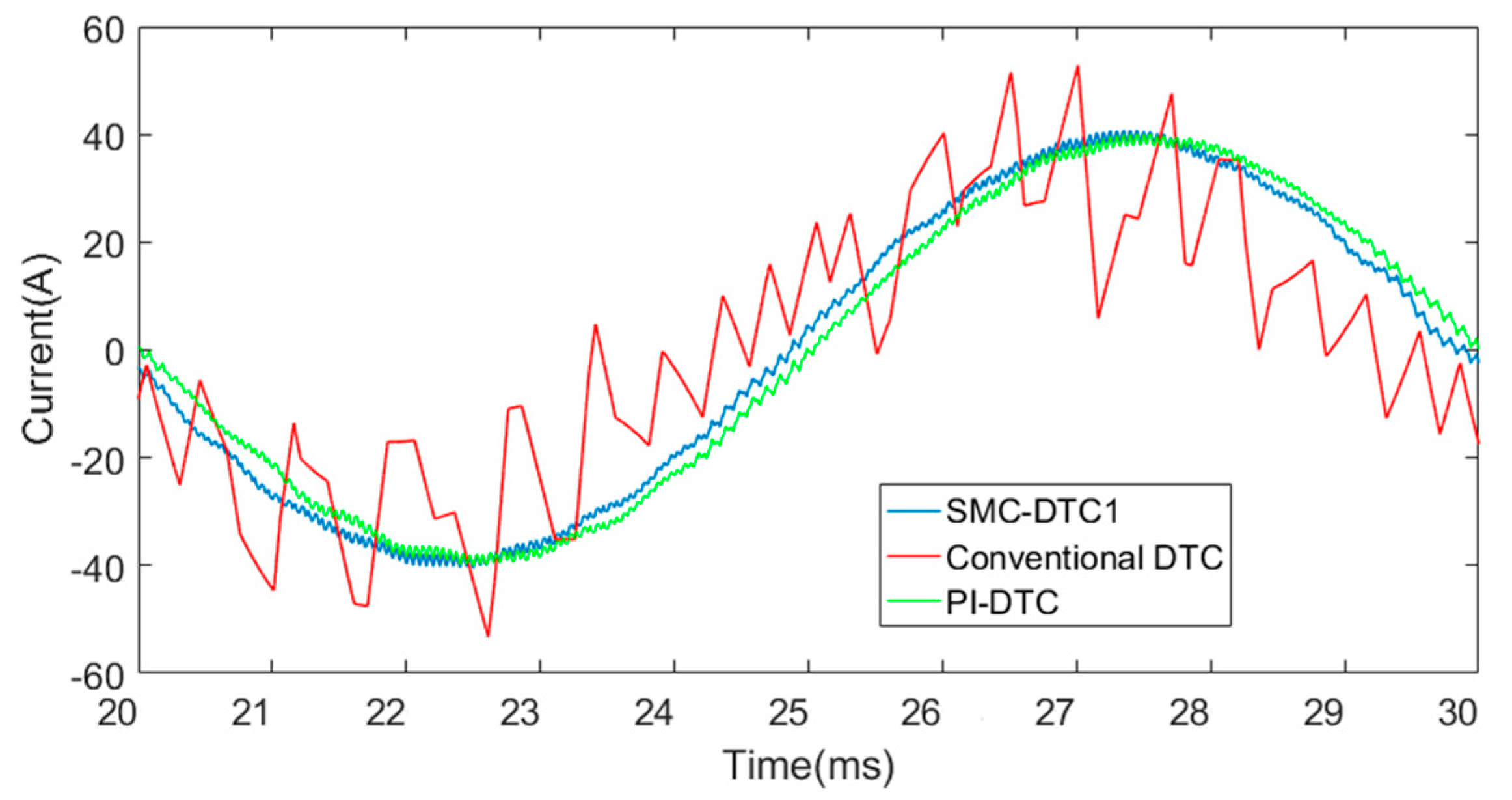
4.2. Stator Phase Current in Steady-State Operation
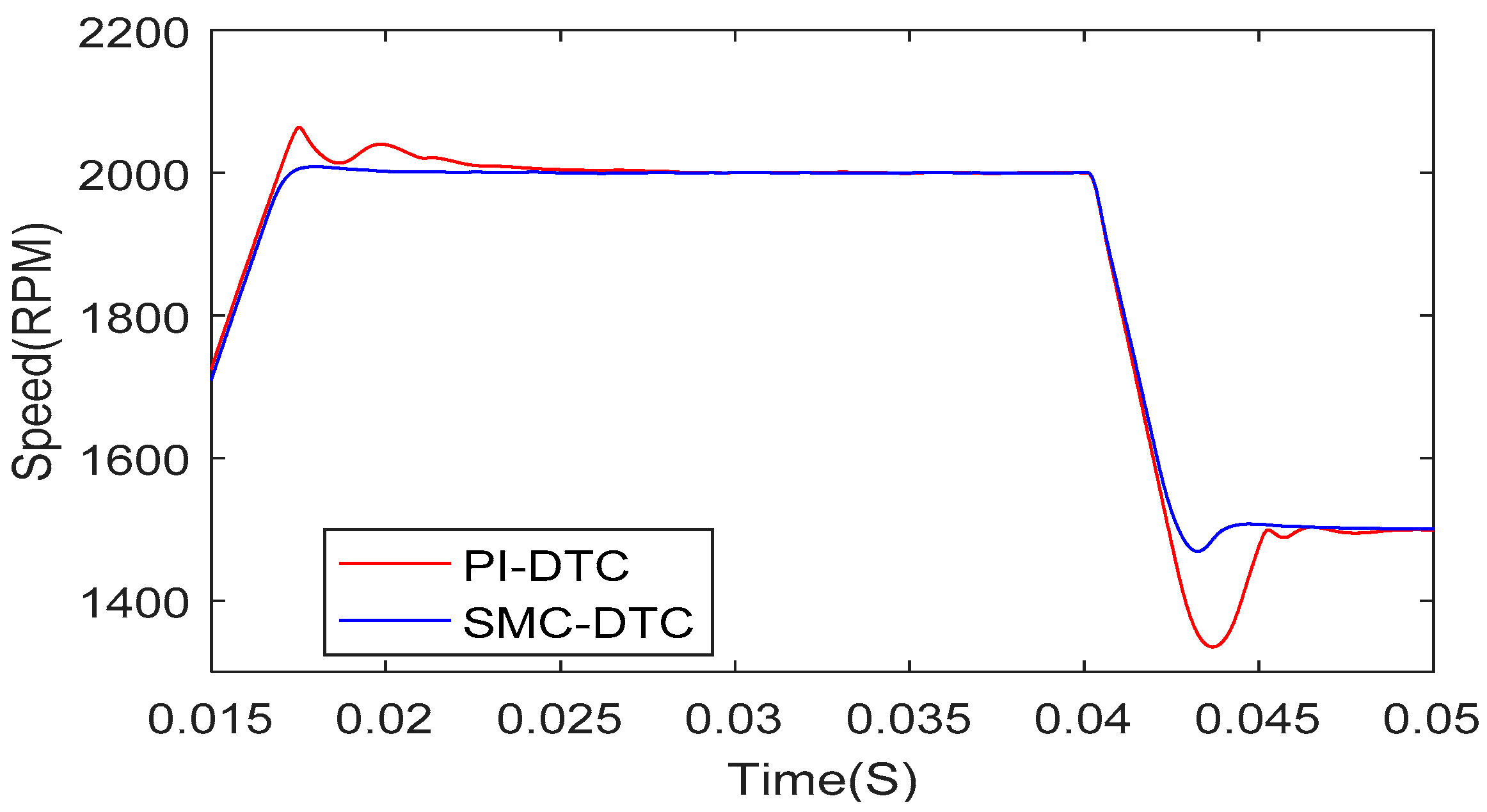
4.3. Speed Response
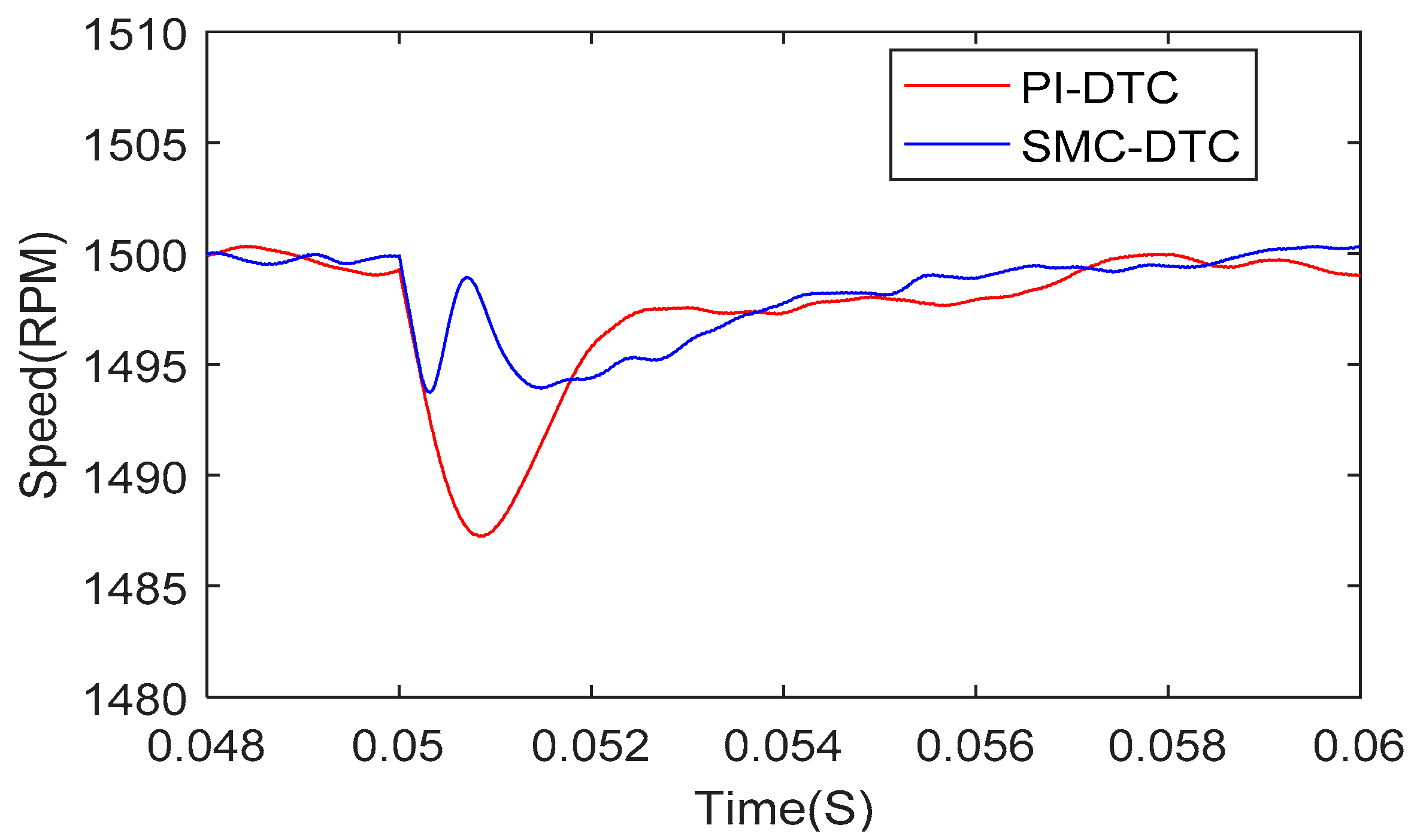
4.4. Robustness against the Load Disturbances
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chan, C.C. The state of the art of electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Do, T.D.; Choi, H.H.; Jung, J.W. θ-D approximation technique for nonlinear optimal speed control design of surface-mounted PMSM drives. IEEE/ASME Trans. Mechatron. 2015, 20, 1822–1831. [Google Scholar] [CrossRef]
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power electronics and motor drives in electric, hybrid electric, and plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Qiao, W.; Qu, L. A discrete-time direct torque control for direct-drive PMSG-based wind energy conversion systems. IEEE Trans. Ind. Appl. 2015, 51, 3504–3514. [Google Scholar] [CrossRef]
- Martins, C.A.; Roboam, X.; Meynard, T.A.; Carvalho, A.S. Switching frequency imposition and ripple reduction in DTC drives by using a multilevel converter. IEEE Trans. Power Electron. 2002, 17, 286–297. [Google Scholar] [CrossRef]
- Xia, C.; Zhao, J.; Yan, Y.; Shi, T. A novel direct torque control of matrix converter-fed PMSM using duty cycle control for torque ripple reduction. IEEE Trans. Ind. Electron. 2014, 61, 2700–2713. [Google Scholar] [CrossRef]
- Kang, J.K.; Sul, S.K. New direct torque control of induction motor for minimum torque ripple and constant switching frequency. IEEE Trans. Ind. Appl. 1999, 35, 1076–1082. [Google Scholar]
- Pacas, M.; Weber, J. Predictive direct torque control for the PM synchronous machine. IEEE Trans. Ind. Electron. 2005, 52, 1350–1356. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J. A novel duty cycle control strategy to reduce both torque and stator flux ripples for DTC of permanent-magnet synchronous motor drives with switching frequency reduction. IEEE Trans. Power Electron. 2011, 26, 3055–3067. [Google Scholar] [CrossRef]
- Kenney, B.; Lorenz, R. Stator- and rotor-flux-based deadbeat direct torque control of induction machine. IEEE Trans. Ind. Appl. 2003, 39, 1093–1101. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, X.; Li, Y. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2012, 59, 871–877. [Google Scholar] [CrossRef]
- Lai, Y.S.; Chen, J.H. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar]
- Yu, C.H.; Tseng, C.Y. Research on gear-change control technology for the clutchless automatic-manual transmission of an electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1446–1458. [Google Scholar] [CrossRef]
- Ren, Y.; Zhu, Z.Q.; Liu, J. Direct torque control of permanent-magnet synchronous machine drives with a simple duty ratio regulator. IEEE Trans. Ind. Electron. 2014, 61, 5249–5258. [Google Scholar] [CrossRef]
- Tang, L.; Zhong, L.; Rahman, M.F.; Hu, Y. A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency. IEEE Trans. Power Electron. 2004, 19, 346–354. [Google Scholar] [CrossRef]
- Swierczynski, D.; kazmierkowski, M. Direct torque control of permanent magnet synchronous motor (PMSM) using space vector modulation (DTC-SVM)—Simulation and experimental results. In Proceedings of the 28th Annual Conference of the IEEE Industrial Electronics Society, Sevilla, Spain, 5–8 November 2002; Volume 1, pp. 751–755. [Google Scholar]


| Parameter | Value | Unit |
|---|---|---|
| Voltage supply | 300 | V |
| Rated speed | 2000 | rpm |
| Rated torque | 40 | N·m |
| Rated current (RMS) | 28 | A |
| Flux linkage | 0.1821 | Wb |
| Number of pole pairs | 4 | - |
| Stator resistance | 0.129 | Ω |
| q-axis inductance | 0.00153 | H |
| d-axis inductance | 0.00153 | H |
| Inertia moment | 0.001 | kg·m2 |
| Viscous friction coefficient | 0.0019 | N·m·s/rad |
| Result- | Conventional DTC | SMC-DTC1 | SMC-DTC2 | SMC-DTC3 | PI-DTC1 | PI-DTC2 | Unit |
|---|---|---|---|---|---|---|---|
| Rising time | 0.95 | 0.58 | 0.6 | 1.7 | 1.7 | 0.6 | ms |
| Falling time | 0.13 | 0.46 | 0.4 | 0.5 | 1.9 | 0.5 | ms |
| 31.9 | 39.9 | 39.9 | 3.98 | 40 | 40 | N·m | |
| 11.55 | 0.58 | 0.5 | 0.46 | 0.39 | 0.38 | N·m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Li, Y.; Jia, C. A Novel Direct Torque Control Method Based on Asymmetric Boundary Layer Sliding Mode Control for PMSM. Energies 2018, 11, 657. https://doi.org/10.3390/en11030657
Song Q, Li Y, Jia C. A Novel Direct Torque Control Method Based on Asymmetric Boundary Layer Sliding Mode Control for PMSM. Energies. 2018; 11(3):657. https://doi.org/10.3390/en11030657
Chicago/Turabian StyleSong, Qiang, Yiting Li, and Chao Jia. 2018. "A Novel Direct Torque Control Method Based on Asymmetric Boundary Layer Sliding Mode Control for PMSM" Energies 11, no. 3: 657. https://doi.org/10.3390/en11030657
APA StyleSong, Q., Li, Y., & Jia, C. (2018). A Novel Direct Torque Control Method Based on Asymmetric Boundary Layer Sliding Mode Control for PMSM. Energies, 11(3), 657. https://doi.org/10.3390/en11030657





