High-Efficiency Isolated Photovoltaic Microinverter Using Wide-Band Gap Switches for Standalone and Grid-Tied Applications
Abstract
:1. Introduction
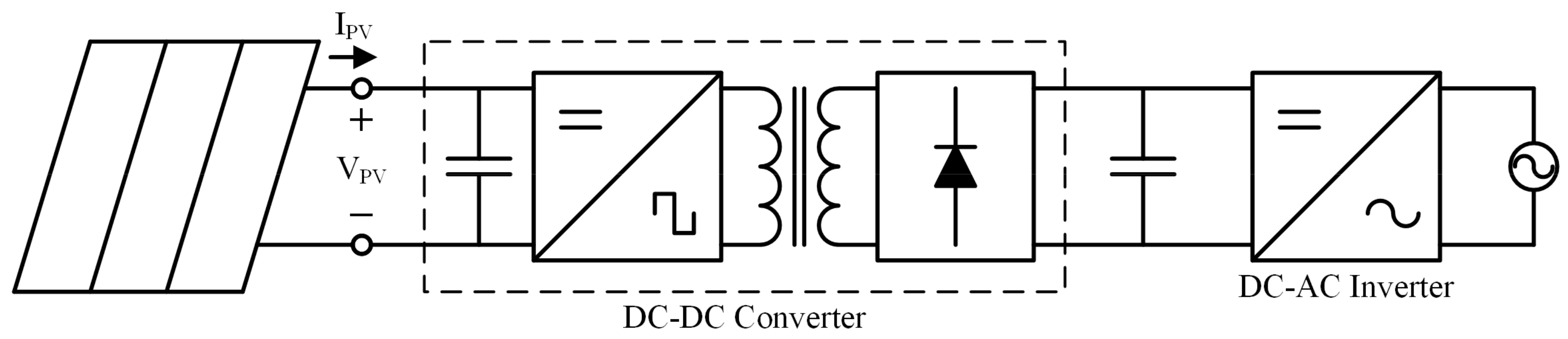
2. System Design and Considerations
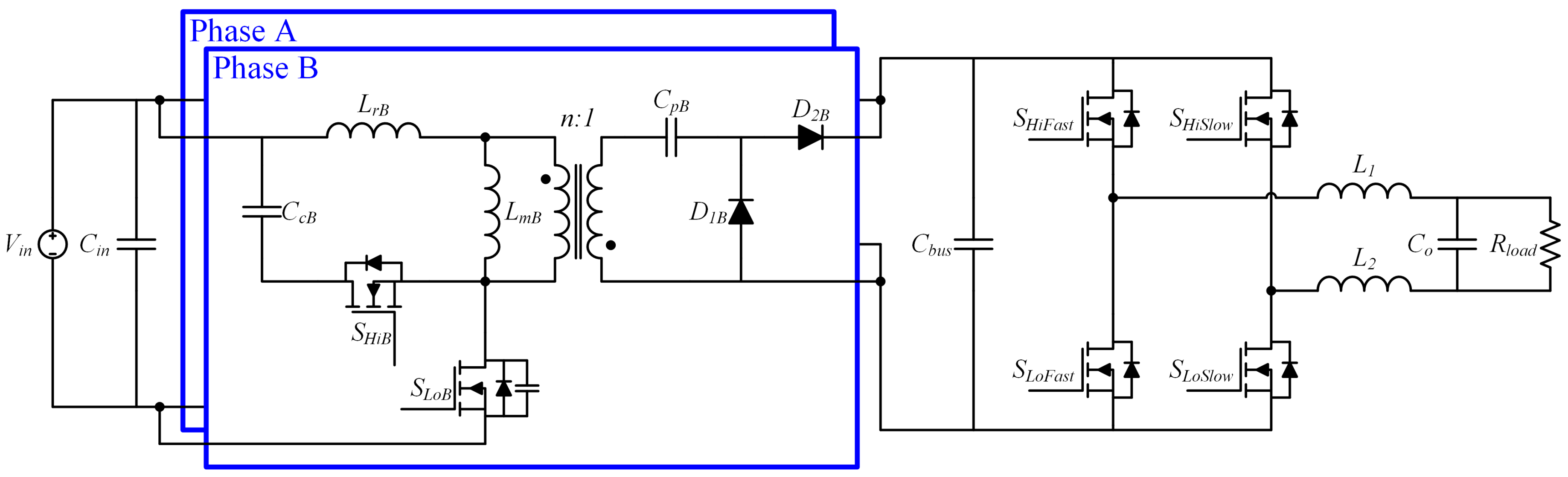
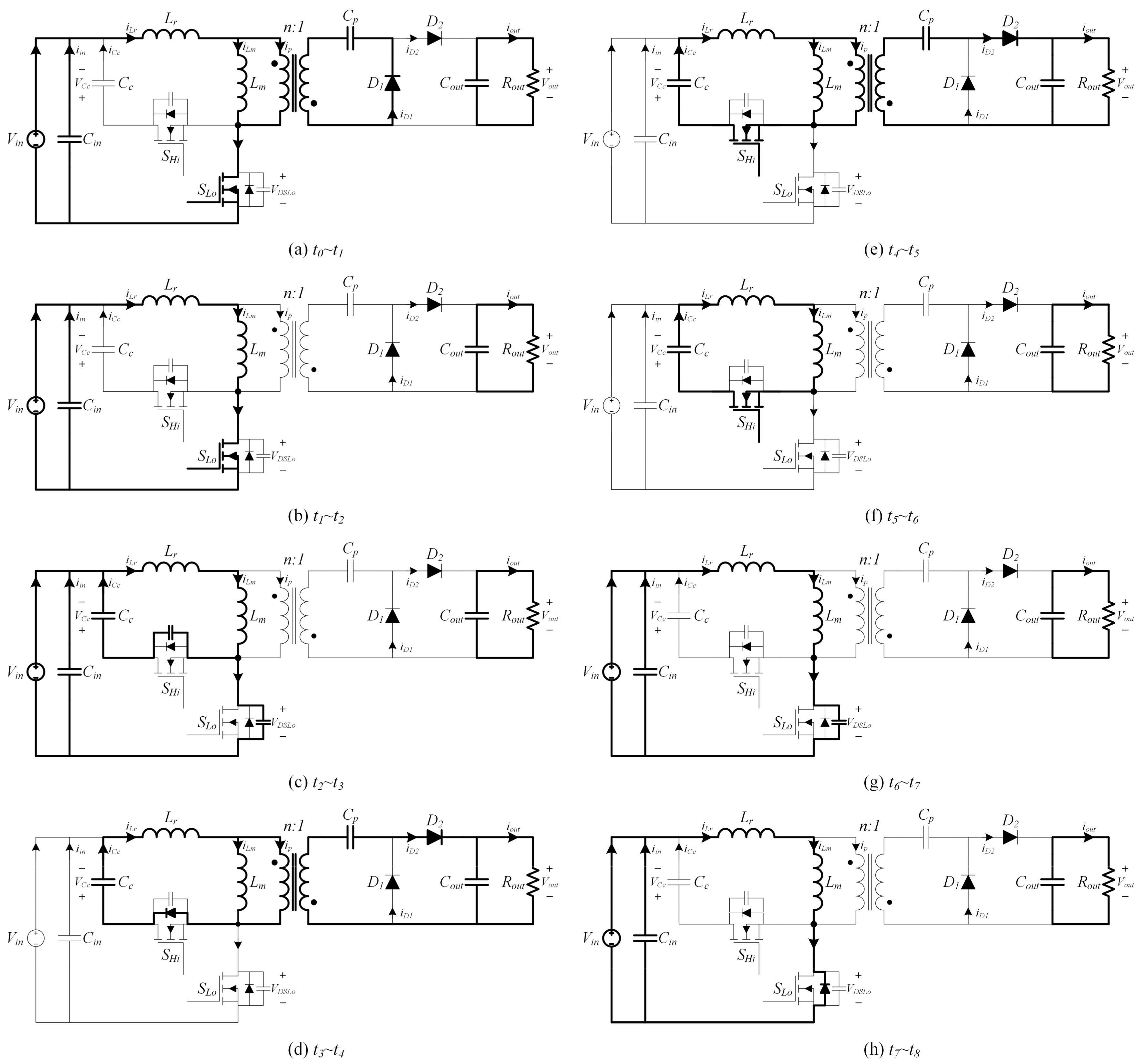
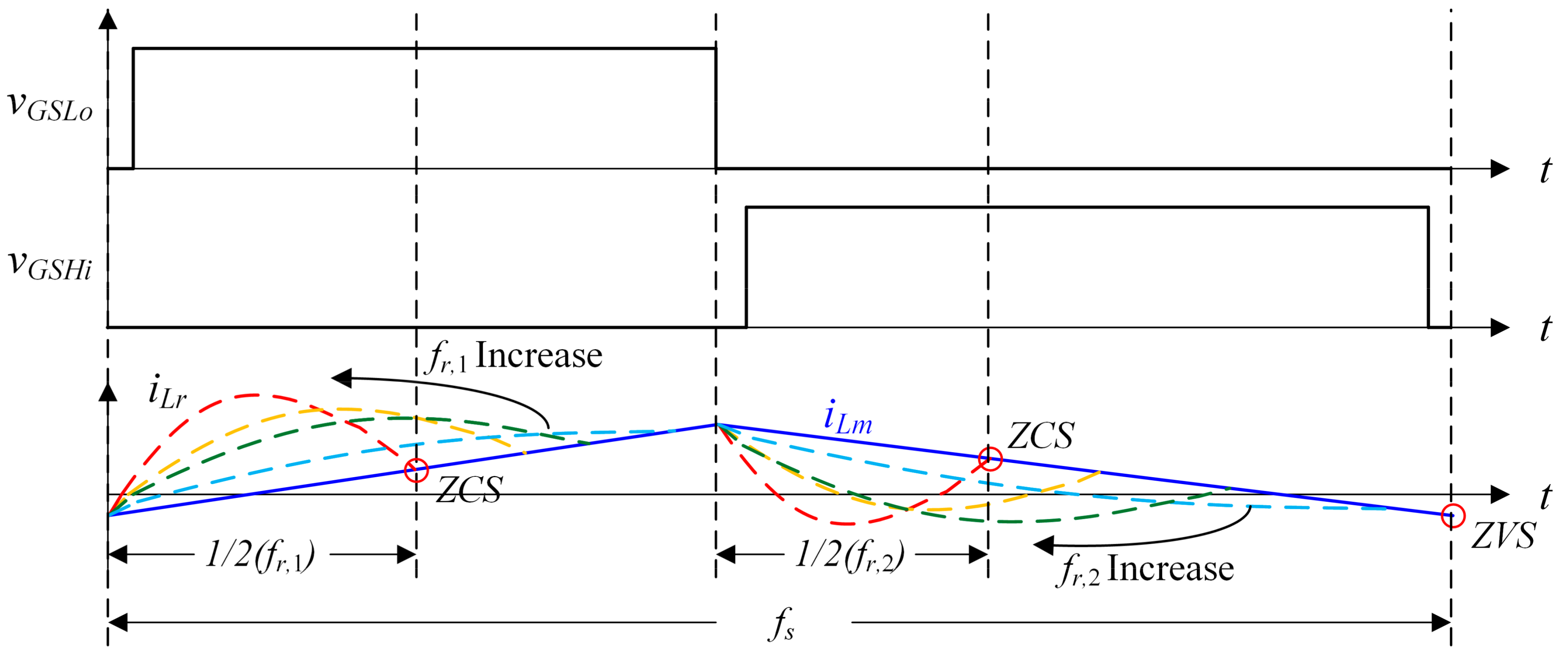
2.1. Active-Clamp Forward-Flyback Resonant Converter
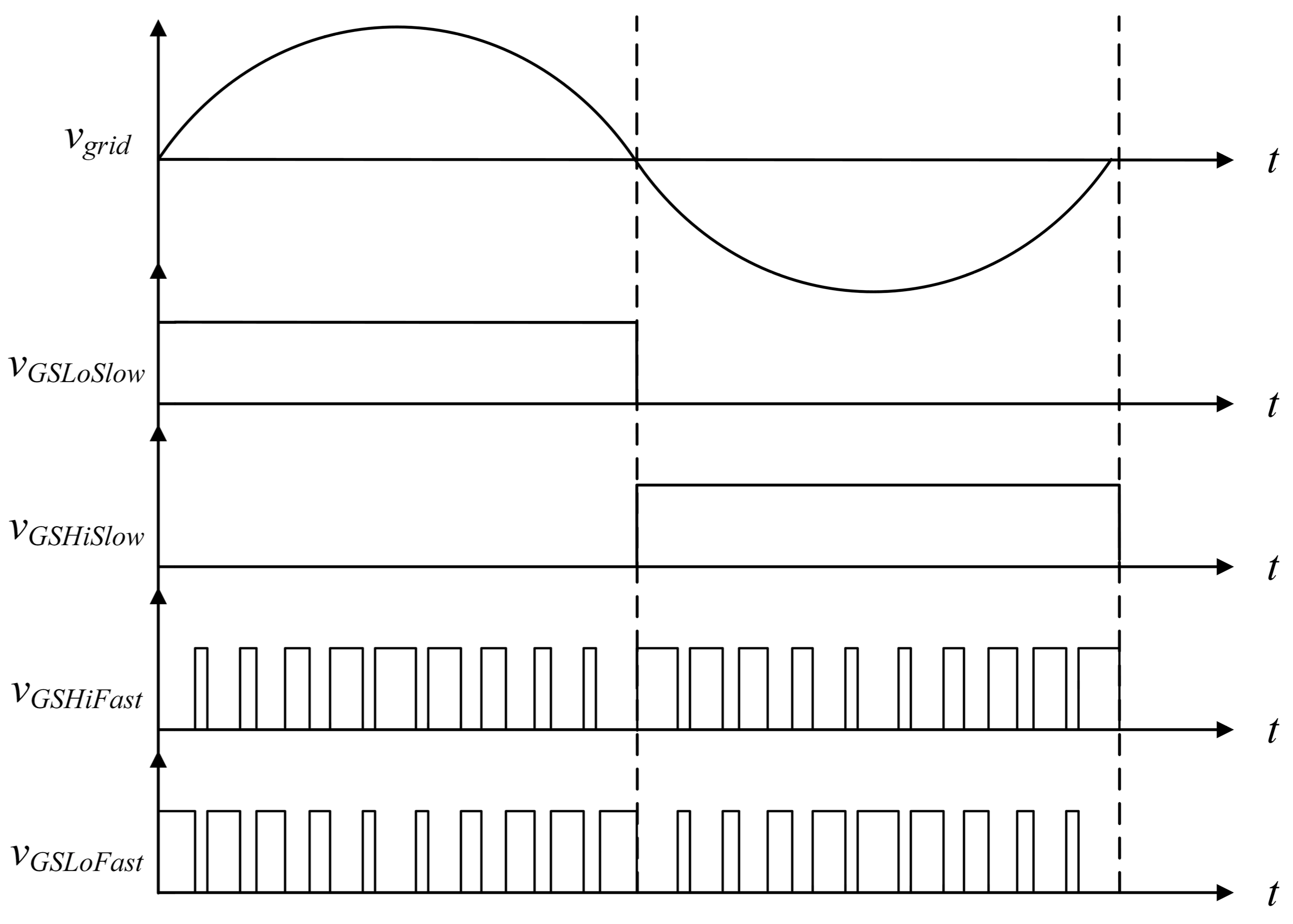
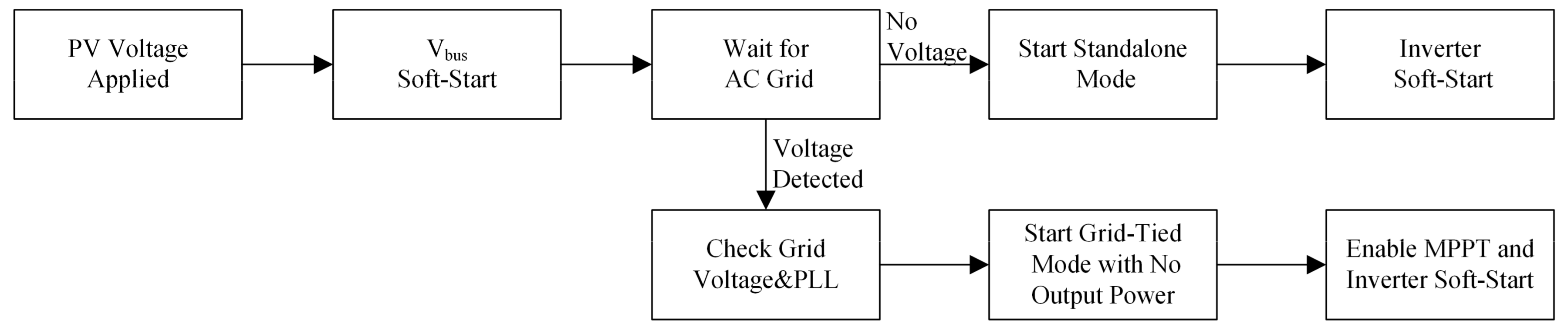
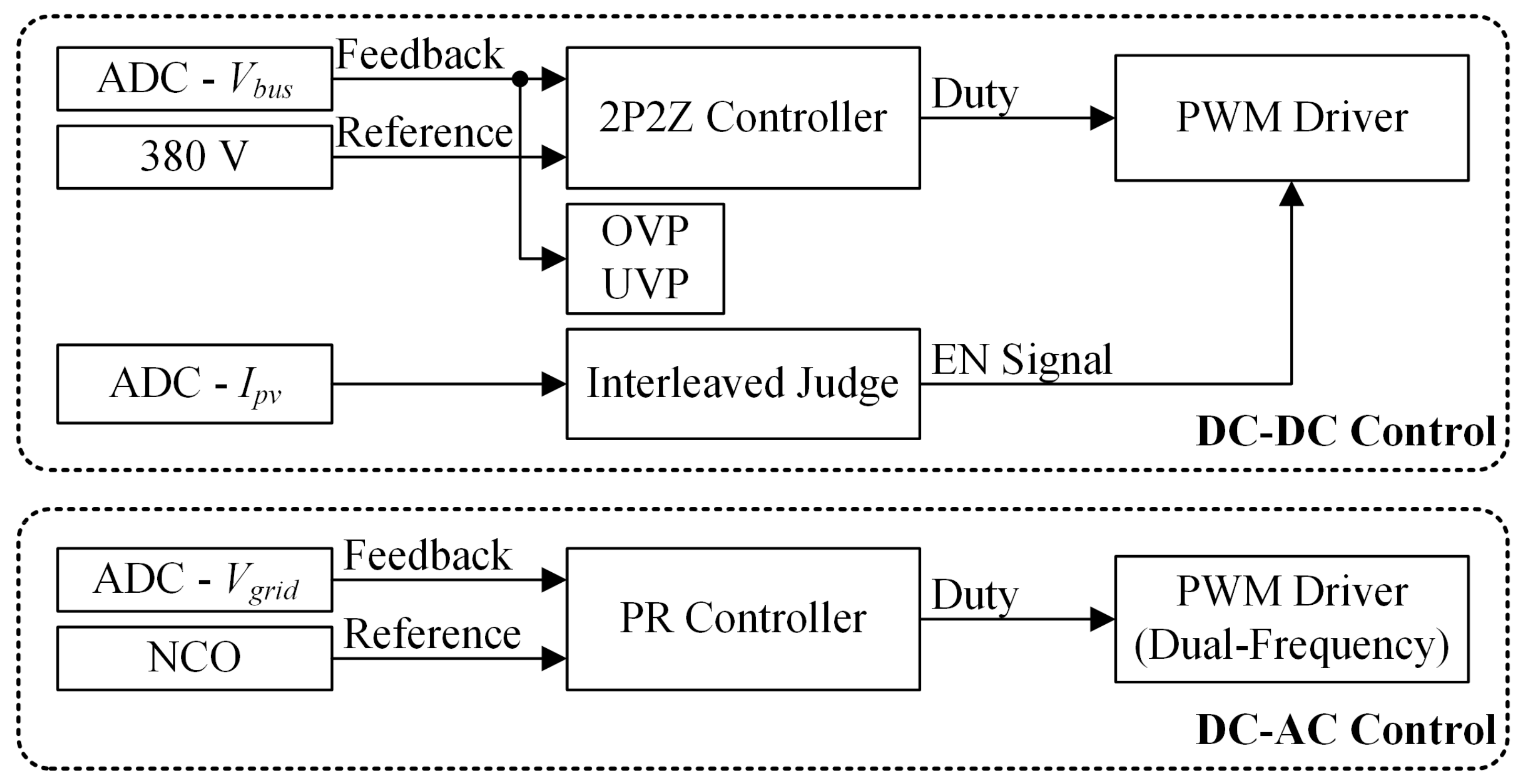
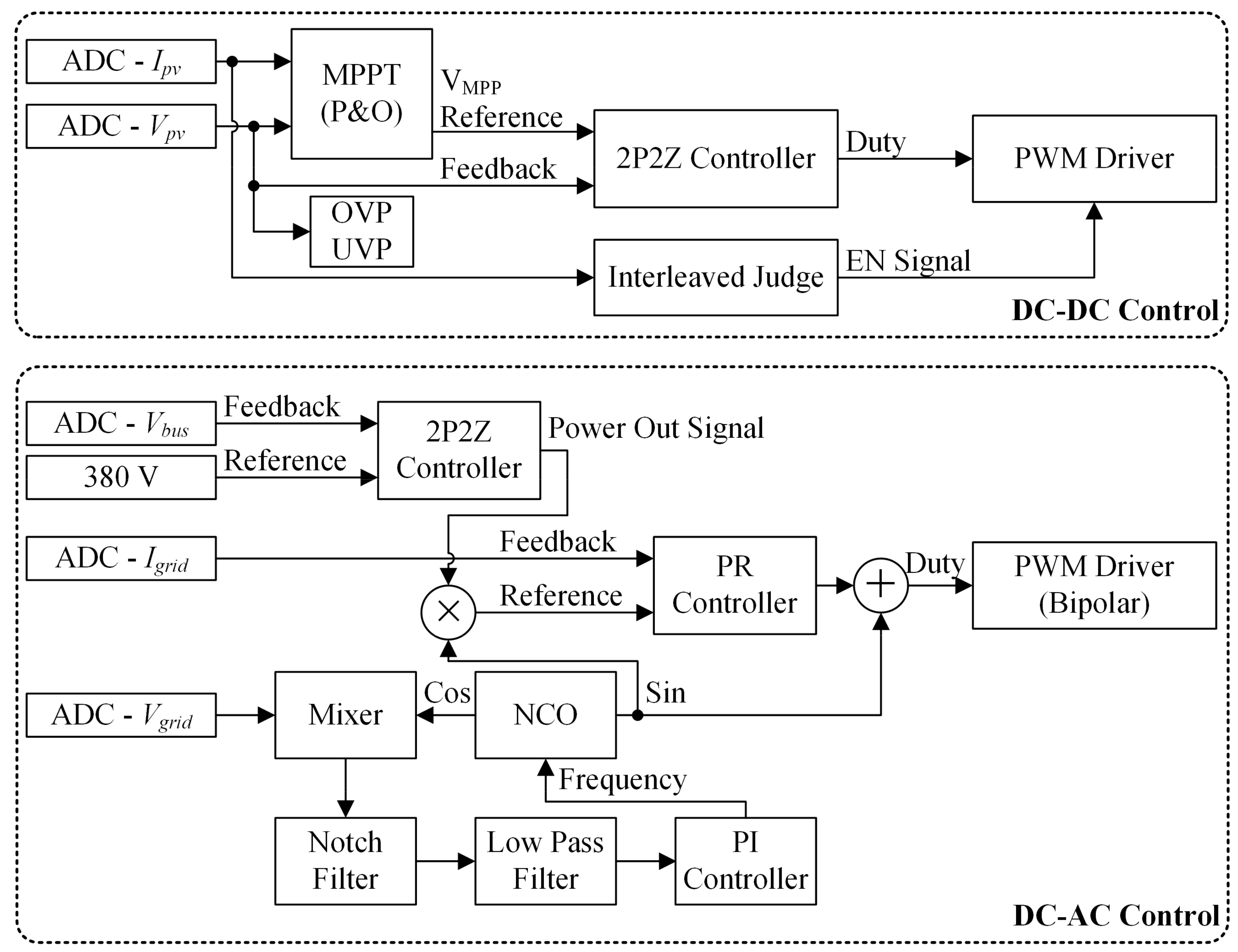
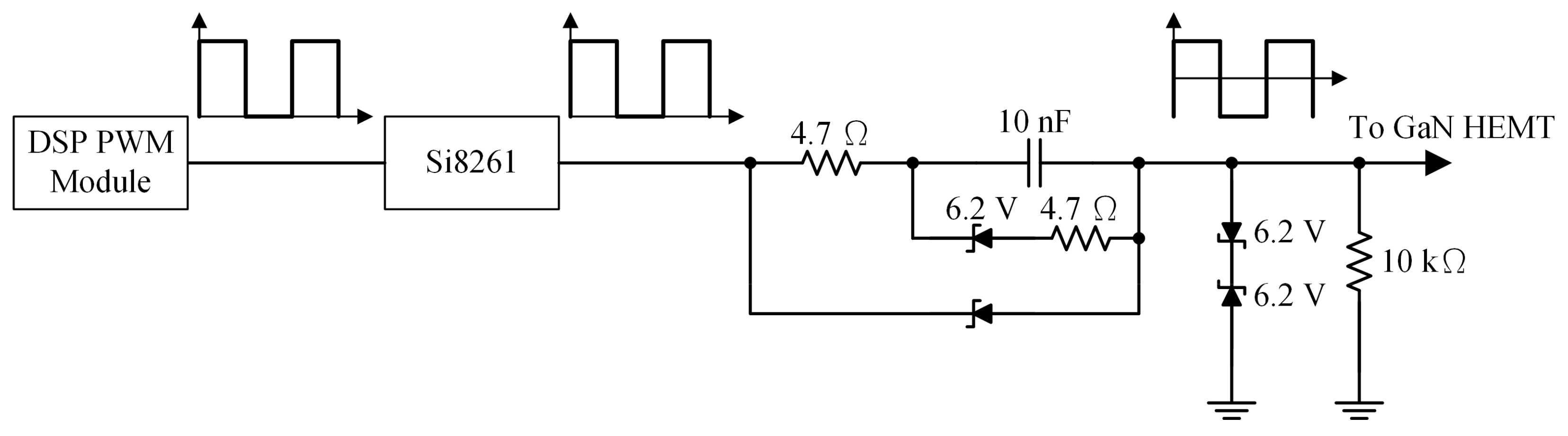
2.2. System Control
3. Results
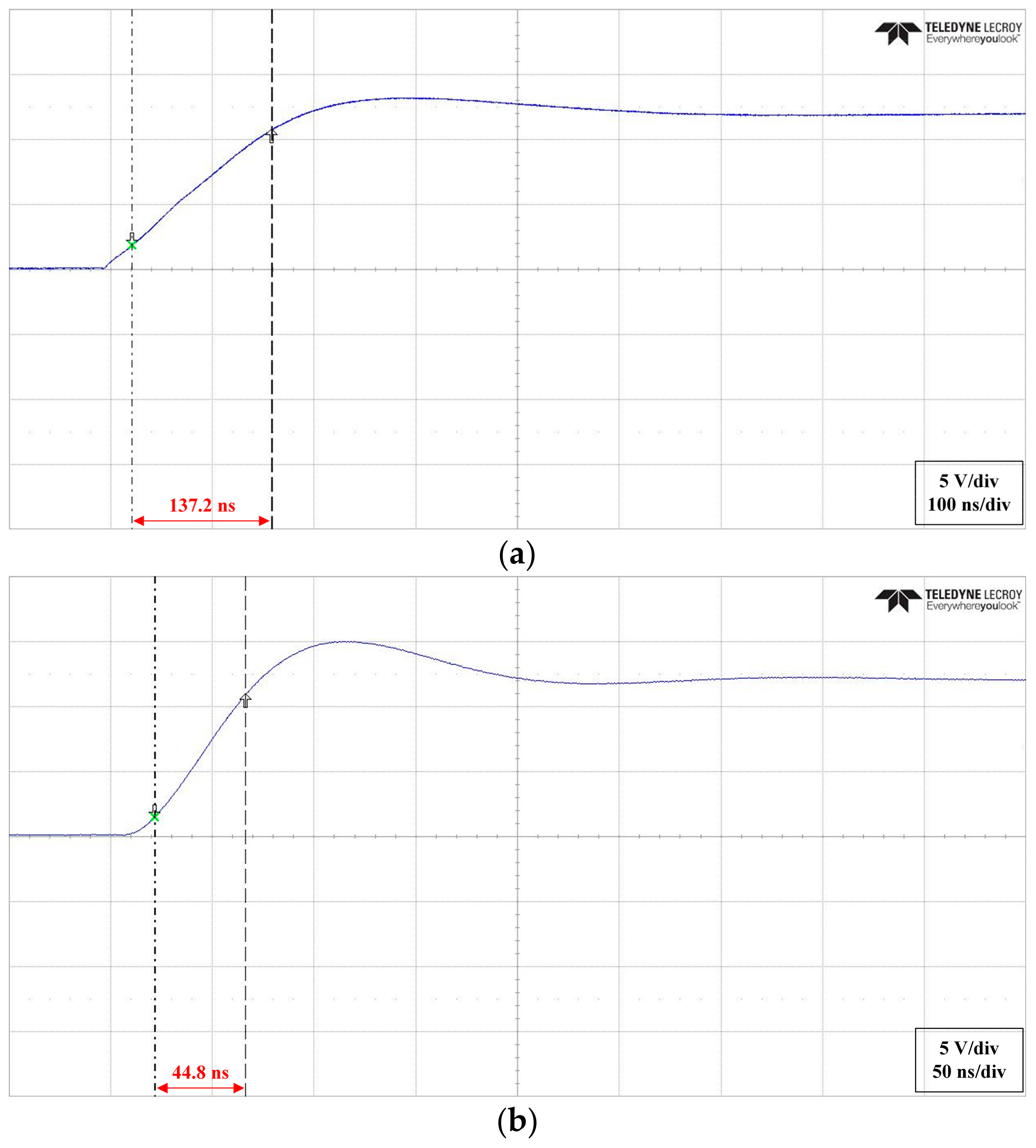
3.1. Power Switch Comparison
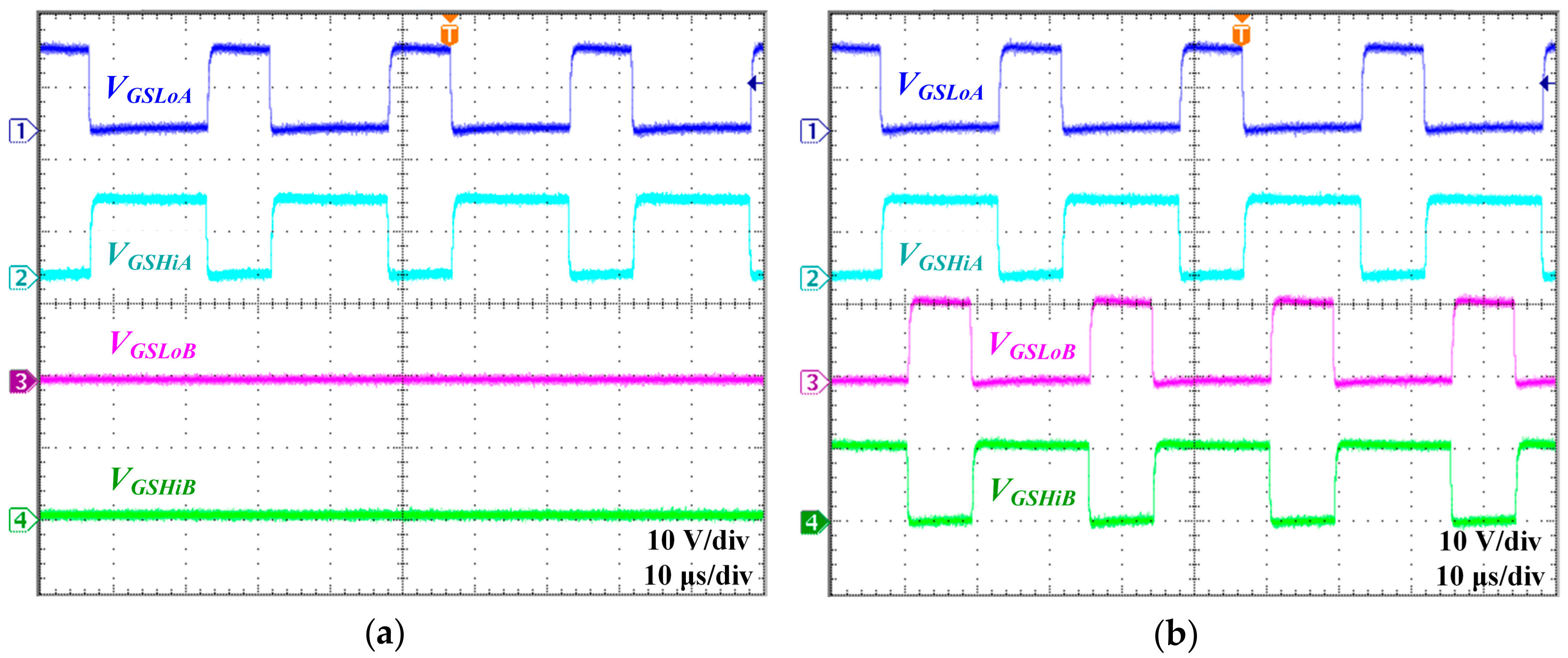
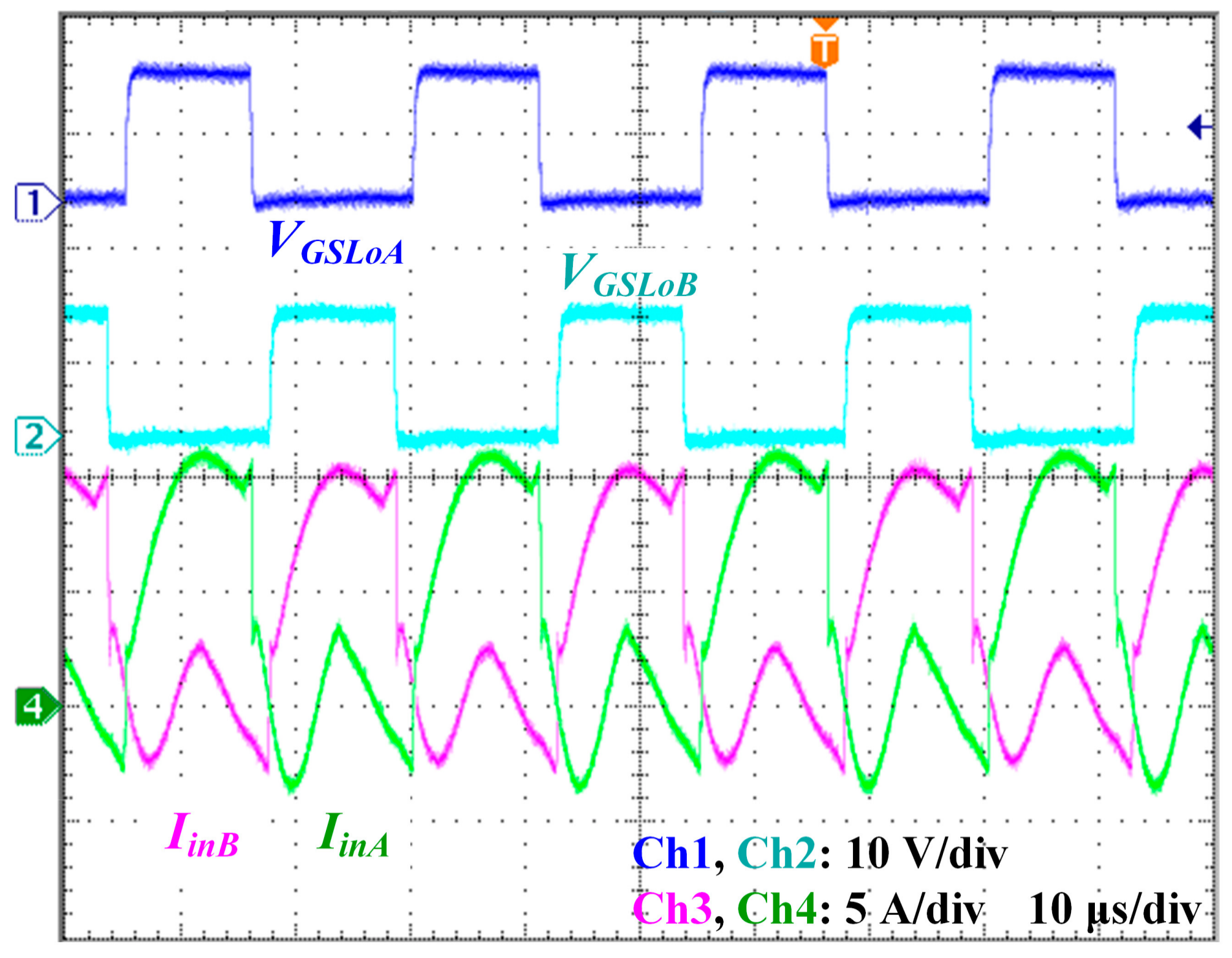
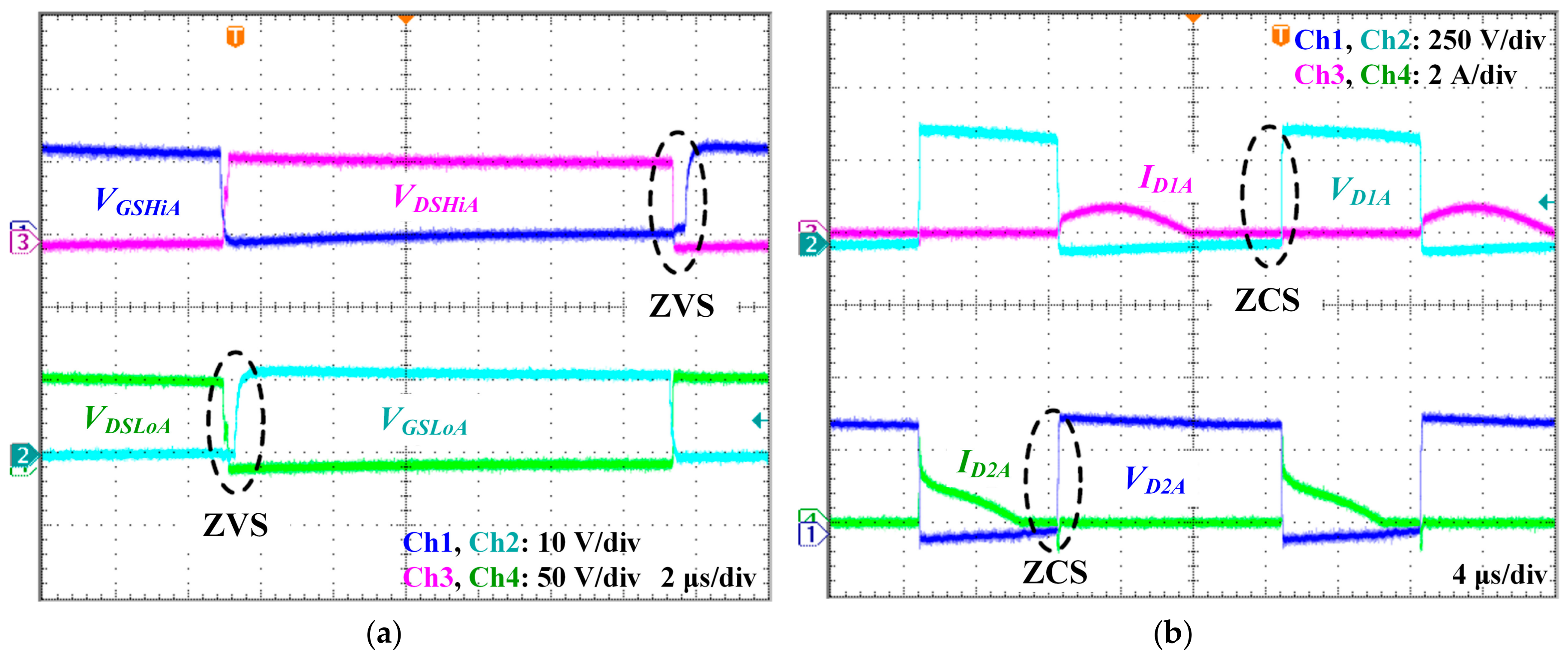
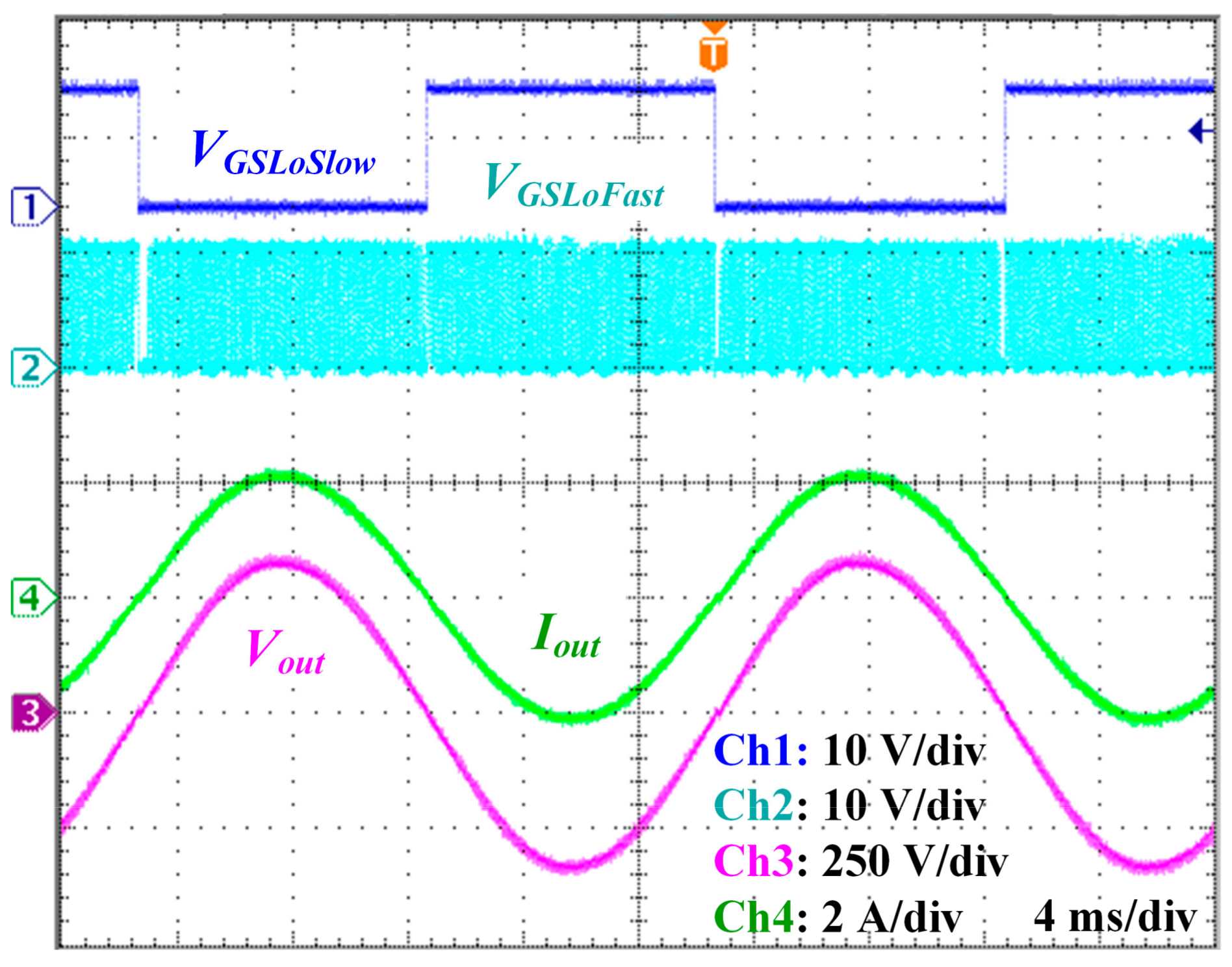
3.2. Experimental Verification
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paz, F.; Ordonez, M. High-performance solar MPPT using switching ripple identification based on a lock-in amplifier. IEEE Trans. Ind. Electron. 2016, 63, 3595–3604. [Google Scholar] [CrossRef]
- Debnath, D.; Chatterjee, K. Two-stage solar photovoltaic-based stand-alone scheme having battery as energy storage element for rural deployment. IEEE Trans. Ind. Electron. 2015, 62, 4148–4157. [Google Scholar] [CrossRef]
- Sahan, B.; Vergara, A.N.; Henze, N.; Engler, A.; Zacharias, P. A single-stage PV module integrated converter based on a low-power current-source inverter. IEEE Trans. Ind. Electron. 2008, 55, 2602–2609. [Google Scholar] [CrossRef]
- Suntio, T.; Leppaaho, J.; Huusari, J.; Nousiainen, L. Issues on Solar-Generator Interfacing With Current-Fed MPP-Tracking Converters. IEEE Trans. Power Electron. 2010, 25, 2409–2419. [Google Scholar] [CrossRef]
- Huusari, J.; Suntio, T. Dynamic Properties of Current-Fed Quadratic Full-Bridge Buck Converter for Distributed Photovoltaic MPP-Tracking Systems. IEEE Trans. Power Electron. 2012, 27, 4681–4689. [Google Scholar] [CrossRef]
- Femia, N.; Lisi, G.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Distributed maximum power point tracking of photovoltaic arrays: Novel approach and system analysis. IEEE Trans. Ind. Electron. 2008, 55, 2610–2621. [Google Scholar] [CrossRef]
- Khan, O.; Xiao, W.; Zeineldin, H.H. Gallium-nitride-based submodule integrated converters for high-efficiency distributed maximum power point tracking PV applications. IEEE Trans. Ind. Electron. 2016, 63, 966–975. [Google Scholar] [CrossRef]
- Vázquez, M.J.V.; Márquez, J.M.A.; Manzano, F.S. A methodology for optimizing stand-alone PV-system size using parallel-connected DC/DC converters. IEEE Trans. Ind. Electron. 2008, 55, 2664–2673. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. An adaptive voltage-sensor-based MPPT for photovoltaic systems with SEPIC converter including steady-state and drift analysis. IEEE Trans. Ind. Electron. 2015, 62, 7609–7619. [Google Scholar] [CrossRef]
- Xiao, W.; Ozog, N.; Dunford, W.G. Topology study of photovoltaic interface for maximum power point tracking. IEEE Trans. Ind. Electron. 2007, 54, 1696–1704. [Google Scholar] [CrossRef]
- Lin, F.J.; Chiang, H.C.; Chang, J.K. Modeling and Controller Design of PV Micro Inverter without Using Electrolytic Capacitors and Input Current Sensors. Energies 2016, 9, 993. [Google Scholar] [CrossRef]
- Nousiainen, L.; Puukko, J.; Mäki, A.; Messo, T.; Huusari, J.; Jokipii, J.; Viinamäki, J.; Lobera, D.T.; Valkealahti, S.; Suntio, T. Photovoltaic Generator as an Input Source for Power Electronic Converters. IEEE Trans. Power Electron. 2013, 28, 3028–3038. [Google Scholar] [CrossRef]
- Suntio, T.; Messo, T.; Aapro, A.; Kivimäki, J.; Kuperman, A. Review of PV Generator as an Input Source for Power Electronic Converters. Energies 2017, 10, 1076. [Google Scholar] [CrossRef]
- Zapata, J.W.; Kouro, S.; Carrasco, G.; Renaudineau, H. Step-Up Partial Power DC-DC Converters for Two-Stage PV Systems with Interleaved Current Performance. Energies 2018, 11, 357. [Google Scholar] [CrossRef]
- Suntio, T.; Messo, T.; Puukko, J. Power Electronic Converters: Dynamics and Control in Conventional and Renewable Energy Applications; Wiley: Weinheim, Germany, 2017; ISBN 978-3-527-34022-4. [Google Scholar]
- Park, J.H.; Ahn, J.Y.; Cho, B.H.; Yu, G.J. Dual-module-based maximum power point tracking control of photovoltaic systems. IEEE Trans. Power Electron. 2006, 53, 1036–1047. [Google Scholar] [CrossRef]
- Sree, K.R.; Rathore, A.K. Hybrid modulated extended secondary universal current-fed ZVS converter for wide voltage range: Analysis, design, and experimental results. IEEE Trans. Power Electron. 2015, 62, 4471–4480. [Google Scholar] [CrossRef]
- Mutoh, N.; Inoue, T. A control method to charge series-connected ultraelectric double-layer capacitors suitable for photovoltaic generation systems combining MPPT control method. IEEE Trans. Power Electron. 2007, 54, 374–383. [Google Scholar] [CrossRef]
- Chakraborty, C.; Iu, H.H.C.; Lu, D.D.C. Power converters, control, and energy management for distributed generation. IEEE Trans. Power Electron. 2015, 62, 4466–4470. [Google Scholar] [CrossRef]
- Huang, Z.; Recht, F.; Wu, Y. PCB Layout and Probing for GaN Power Switches; Application Note AN-0003, Rev. 2; Transphorm Inc.: Goleta, CA, USA, 2015. [Google Scholar]
- Kolar, J.; Krismer, F.; Lobsiger, Y.; Muhlethaler, J.; Nussbaumer, T.; Minibock, J. Extreme efficiency power electronics. In Proceedings of the International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012; pp. 1–22. [Google Scholar]
- Viinamäki, J.; Kuperman, A.; Suntio, T. Grid-Forming-Mode Operation of Boost-Power-Stage Converter in PV-Generator-Interfacing Applications. Energies 2017, 10, 1033. [Google Scholar] [CrossRef]



| Device | On-Resistance (Ω) | Gate-Charge (nC) | FOM |
|---|---|---|---|
| GaN HEMT TPH3006PS | 0.15 | 6.2 | 0.93 |
| CoolMOS 20N60CFD | 0.19 | 95 | 18.05 |
| Parameter | Symbol | Specification |
|---|---|---|
| Input voltage | Vin | 18–40 V |
| Output voltage | Vo | 240 Vrms |
| Output current | Io | 2.1 Arms (rated) |
| Efficiency | ŋ | ≥0.95 (at 375 W) |
| Voltage THD | THDv | ≤5% (at nominal output) |
| Mode | Po (W) | Efficiency (%) |
|---|---|---|
| single | 100 | 97.10 |
| interleaved | 250 | 97.25 |
| interleaved | 375 | 97.10 |
| interleaved | 500 | 96.50 |
| Vbus (V) | Vo (Vrms) | Po (W) | Efficiency (%) |
|---|---|---|---|
| 380 | 240 | 100 | 96.65 |
| 380 | 240 | 250 | 97.80 |
| 380 | 240 | 375 | 98.00 |
| 380 | 240 | 500 | 98.15 |
| Vpv (V) | Vo (Vrms) | Po (W) | Efficiency (%) |
|---|---|---|---|
| 34 | 240 | 100 | 94.15 |
| 34 | 240 | 250 | 95.25 |
| 34 | 240 | 375 | 95.17 |
| 34 | 240 | 500 | 94.70 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C.; Chen, M.-C.; Yang, C.-Y.; Kim, K.A.; Chiu, H.-J. High-Efficiency Isolated Photovoltaic Microinverter Using Wide-Band Gap Switches for Standalone and Grid-Tied Applications. Energies 2018, 11, 569. https://doi.org/10.3390/en11030569
Liu Y-C, Chen M-C, Yang C-Y, Kim KA, Chiu H-J. High-Efficiency Isolated Photovoltaic Microinverter Using Wide-Band Gap Switches for Standalone and Grid-Tied Applications. Energies. 2018; 11(3):569. https://doi.org/10.3390/en11030569
Chicago/Turabian StyleLiu, Yu-Chen, Ming-Cheng Chen, Chun-Yu Yang, Katherine A. Kim, and Huang-Jen Chiu. 2018. "High-Efficiency Isolated Photovoltaic Microinverter Using Wide-Band Gap Switches for Standalone and Grid-Tied Applications" Energies 11, no. 3: 569. https://doi.org/10.3390/en11030569
APA StyleLiu, Y.-C., Chen, M.-C., Yang, C.-Y., Kim, K. A., & Chiu, H.-J. (2018). High-Efficiency Isolated Photovoltaic Microinverter Using Wide-Band Gap Switches for Standalone and Grid-Tied Applications. Energies, 11(3), 569. https://doi.org/10.3390/en11030569






