Towards Optimal Power Management of Hybrid Electric Vehicles in Real-Time: A Review on Methods, Challenges, and State-Of-The-Art Solutions
Abstract
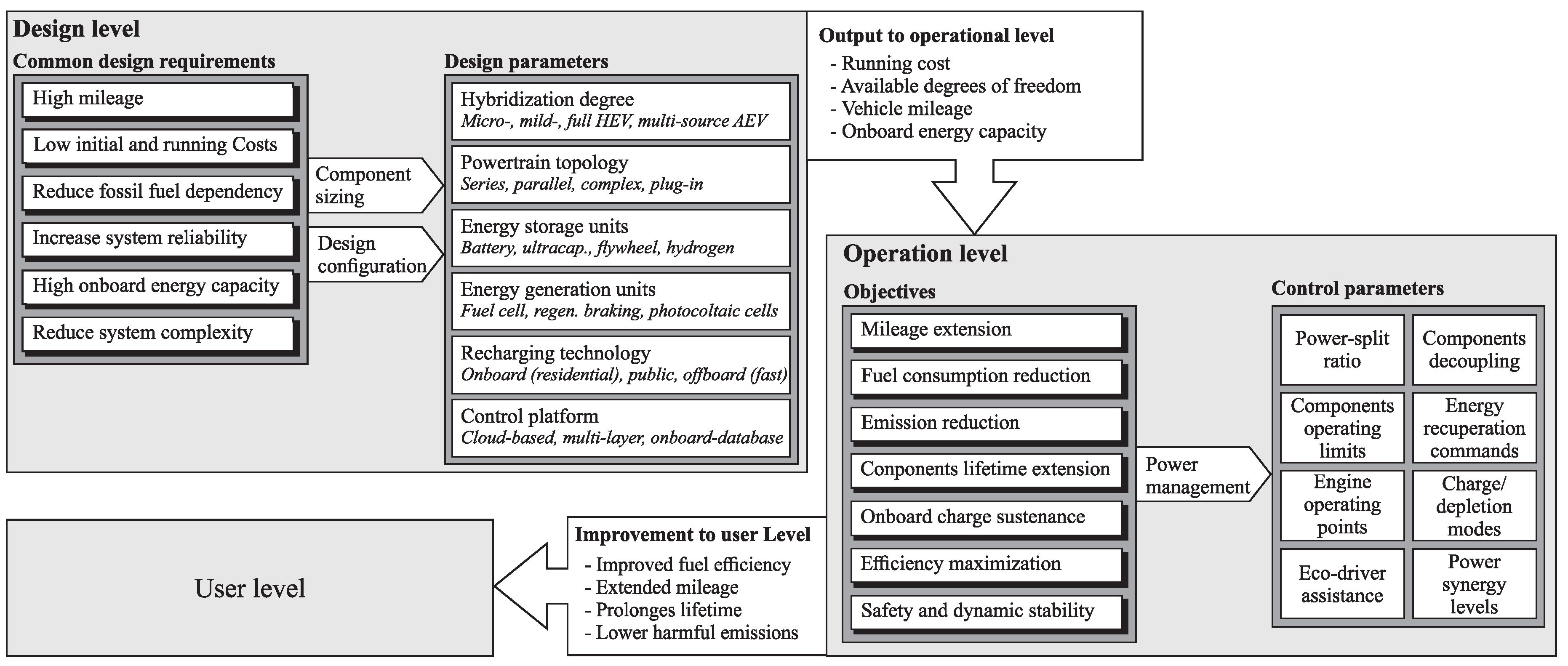
:1. Introduction
1.1. Problem Statement
1.2. Contribution and Novelty
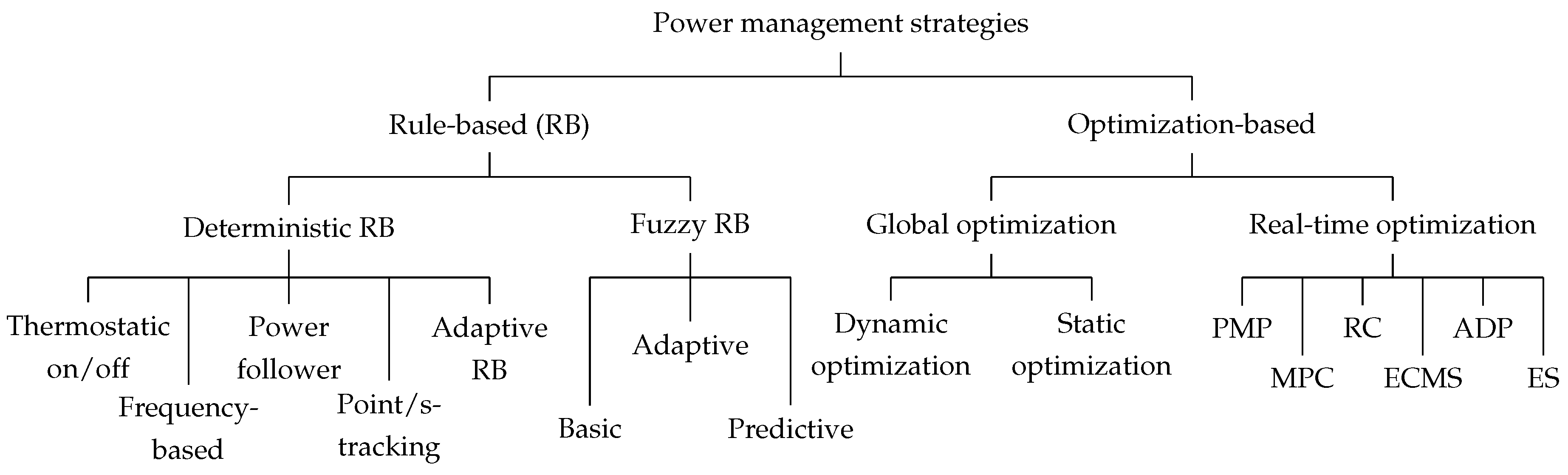
2. Rule-Based Methods
2.1. Deterministic Rule-Based Methods
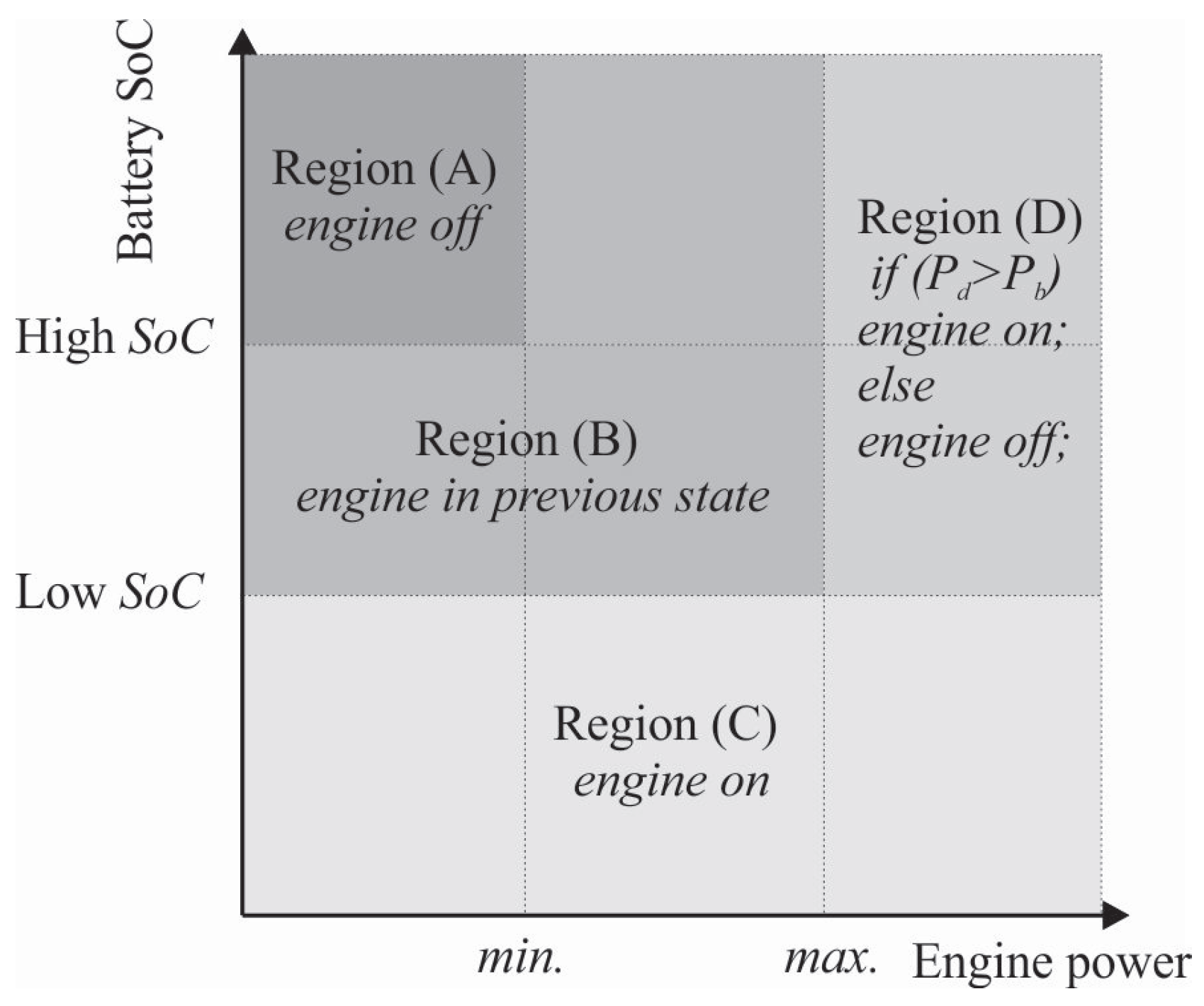
2.1.1. Thermostat (on/off) Control Strategy
2.1.2. Power Follower (Baseline) Control Strategy
2.1.3. Modified Power Follower—Adaptive RB (ARB)
2.1.4. Frequency-Based Approach
2.1.5. Optimal Points Tracking
2.2. Fuzzy Rule-Based Methods
2.2.1. Basic Fuzzy
2.2.2. Adaptive Fuzzy
2.2.3. Predictive Fuzzy
3. Optimization-Based Methods
3.1. Global Optimization
3.1.1. Linear Programming
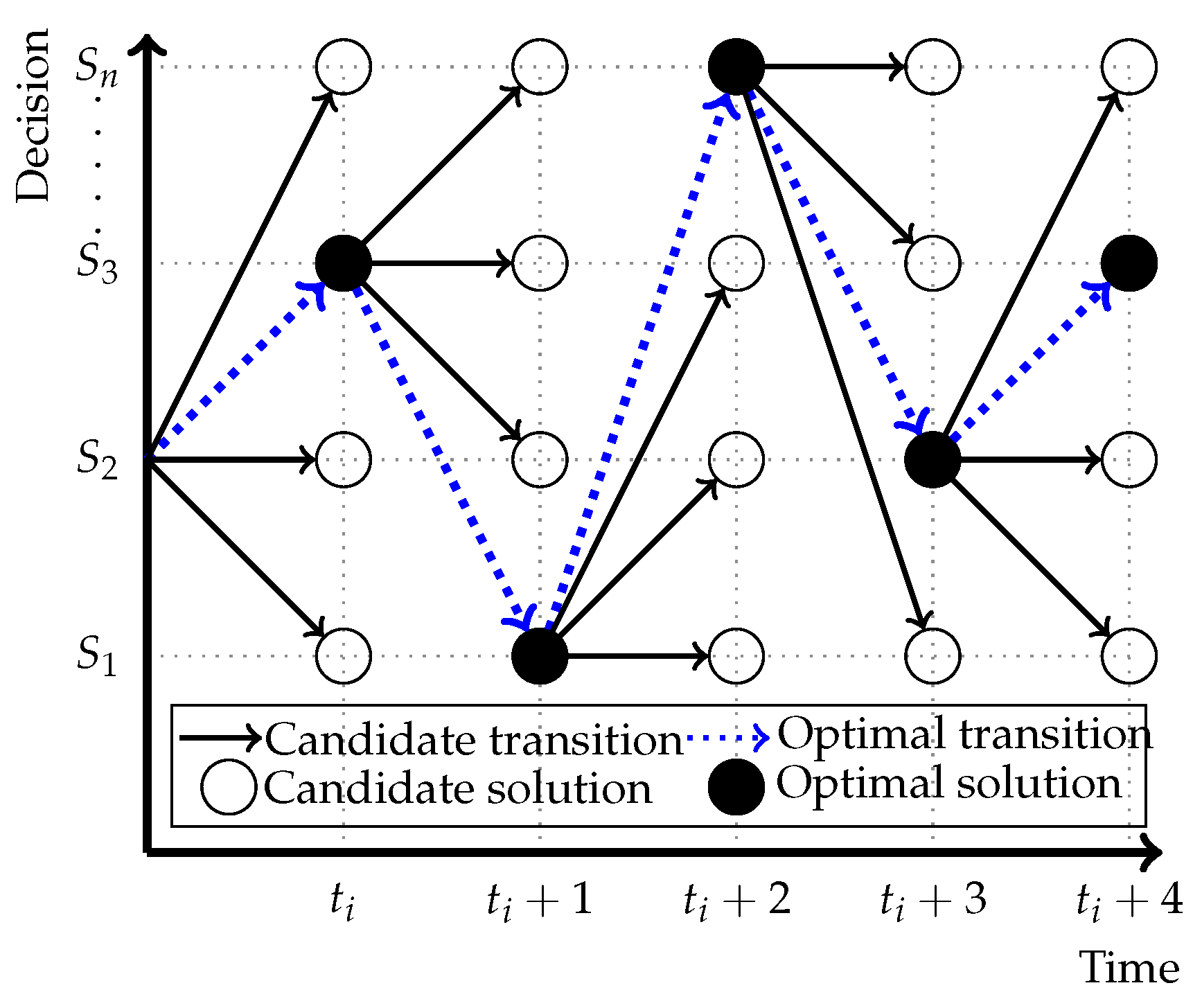
3.1.2. Dynamic Programming (DP)
3.1.3. Genetic Algorithm (GA)
3.1.4. Optimal Control Theory
3.1.5. Particle Swarm Optimization (PSO)
3.1.6. Further Methods
3.2. Real-time Optimization
3.2.1. ECMS
3.2.2. Pontryagin’s Minimum Principle (PMP)
3.2.3. Model Predictive Control (MPC)
3.2.4. Adaptive Dynamic Programming (ADP)
3.2.5. Extremum Seeking (ES)
3.2.6. Robust Control (RC)
4. Towards Optimality in Real-time
4.1. Subsidiary Adaptation Tools
4.2. Integration to Power Management Methods
4.3. Insight Into Optimal Real-Time Methods
4.4. Evaluation and Discussion
5. Summary and Conclusions
Author Contributions
Conflicts of Interest
References
- Onori, S.; Serrao, L.; Rizzoni, G. Hybrid Electric Vehicles; Springer: London, UK, 2016. [Google Scholar]
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, L.F.P.; Steinbuch, M. Review of Optimization Strategies for System-Level Design in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef]
- Amjad, S.; Neelakrishnan, S.; Rudramoorthy, R. Review of design considerations and technological challenges for successful development and deployment of plug-in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2010, 14, 1104–1110. [Google Scholar] [CrossRef]
- Emadi, A.; Rajashekara, K.; Williamson, S.S.; Lukic, S.M. Topological overview of hybrid electric and fuel cell vehicular power system architectures and configurations. IEEE Trans. Veh. Technol. 2005, 54, 763–770. [Google Scholar] [CrossRef]
- Malikopoulos, A.A. Impact of Component Sizing in Plug-In Hybrid Electric Vehicles for Energy Resource and Greenhouse Emissions Reduction. J. Energy Resour. Technol. 2013, 135, 041201. [Google Scholar] [CrossRef]
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- Salmasi, F.R. Control Strategies for Hybrid Electric Vehicles: Evolution, Classification, Comparison, and Future Trends. IEEE Trans. Veh. Technol. 2007, 56, 2393–2404. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and Review of Control Strategies for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 111–122. [Google Scholar] [CrossRef]
- Sabri, M.; Danapalasingam, K.; Rahmat, M. A review on hybrid electric vehicles architecture and energy management strategies. Renew. Sustain. Energy Rev. 2016, 53, 1433–1442. [Google Scholar] [CrossRef]
- Hofman, T.; Steinbuch, M.; Druten, R.V.; Serrarens, A. Rule-based energy management strategies for hybrid vehicles. Int. J. Electr. Hybrid Veh. 2007, 1, 71. [Google Scholar] [CrossRef]
- Zhang, P.; Yan, F.; Du, C. A comprehensive analysis of energy management strategies for hybrid electric vehicles based on bibliometrics. Renew. Sustain. Energy Rev. 2015, 48, 88–104. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ali, A.; Sharaf, A.; Kamel, H.; Hegazy, S. A Theo-Practical Methodology for Series Hybrid Vehicles Evaluation and Development; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Cheng, Y.; Chen, K.; Chan, C.; Bouscayrol, A.; Cui, S. Global modeling and control strategy simulation for a hybrid electric vehicle using electrical variable transmission. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008. [Google Scholar]
- Johnson, V.H.; Wipke, K.B.; Rausen, D.J. HEV Control Strategy for Real-Time Optimization of Fuel Economy and Emissions; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A user-friendly advanced powertrain simulation using a combined backward/forward approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B. Energy Management Based on Frequency Approach for Hybrid Electric Vehicle Applications: Fuel-Cell/Lithium-Battery and Ultracapacitors. IEEE Trans. Veh. Technol. 2012, 61, 3375–3386. [Google Scholar] [CrossRef]
- Kim, Y.; Salvi, A.; Siegel, J.B.; Filipi, Z.S.; Stefanopoulou, A.G.; Ersal, T. Hardware-in-the-loop validation of a power management strategy for hybrid powertrains. Control Eng. Pract. 2014, 29, 277–286. [Google Scholar] [CrossRef]
- Park, J.; Park, Y.; Park, J. Optimal power distribution strategy for series—Parallel hybrid electric vehicles. Proc. Inst. Mech. Eng. D 2008, 222, 989–1000. [Google Scholar] [CrossRef]
- Ahn, K.; Papalambros, P.Y. Engine optimal operation lines for power-split hybrid electric vehicles. Proc. Inst. Mech. Eng. D 2009, 223, 1149–1162. [Google Scholar] [CrossRef]
- Lee, H.D.; Sul, S.K. Fuzzy-logic-based torque control strategy for parallel-type hybrid electric vehicle. IEEE Trans. Ind. Electron. 1998, 45, 625–632. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Mahmoodi-k, M. Development a new power management strategy for power split hybrid electric vehicles. Transp. Res. D Transp. Environ. 2015, 37, 79–96. [Google Scholar] [CrossRef]
- Langari, R.; Won, J.S. Intelligent Energy Management Agent for a Parallel Hybrid Vehicle—Part I: System Architecture and Design of the Driving Situation Identification Process. IEEE Trans. Veh. Technol. 2005, 54, 925–934. [Google Scholar] [CrossRef]
- Won, J.S.; Langari, R. Intelligent Energy Management Agent for a Parallel Hybrid Vehicle—Part II: Torque Distribution, Charge Sustenance Strategies, and Performance Results. IEEE Trans. Veh. Technol. 2005, 54, 935–953. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive energy management of a plug-in hybrid electric vehicle based on driving pattern recognition and dynamic programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Hajimiri, M.H.; Salmasi, F.R. A Fuzzy Energy Management Strategy for Series Hybrid Electric Vehicle with Predictive Control and Durability Extension of the Battery. In Proceedings of the 2006 IEEE Conference on Electric and Hybrid Vehicles, Pune, India, 18–20 December 2006; pp. 1–5. [Google Scholar]
- Montazeri-Gh, M.; Mahmoodi-K, M. Optimized predictive energy management of plug-in hybrid electric vehicle based on traffic condition. J. Clean. Prod. 2016, 139, 935–948. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, Y.; Tian, G.; Wu, H.; Chen, Q. A four-step method to design an energy management strategy for hybrid vehicles. In Proceedings of the 2004 IEEE American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 1, pp. 156–161. [Google Scholar]
- Oh, K.; Min, J.; Choi, D.; Kim, H. Optimization of control strategy for a single-shaft parallel hybrid electric vehicle. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2007, 221, 555–565. [Google Scholar] [CrossRef]
- Tate, E.D.; Boyd, S.P. Finding Ultimate Limits of Performance for Hybrid Electric Vehicles; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2000. [Google Scholar]
- Wu, G.; Boriboonsomsin, K.; Barth, M.J. Development and Evaluation of an Intelligent Energy-Management Strategy for Plug-in Hybrid Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2014, 15, 1091–1100. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Wegmann, R.; Döge, V.; Becker, J.; Sauer, D.U. Optimized operation of hybrid battery systems for electric vehicles using deterministic and stochastic dynamic programming. J. Energy Storage 2017, 14, 22–38. [Google Scholar] [CrossRef]
- Romaus, C.; Gathmann, K.; Bocker, J. Optimal energy management for a hybrid energy storage system for electric vehicles based on Stochastic Dynamic Programming. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Madanipour, V.; Montazeri-Gh, M.; Mahmoodi-k, M. Optimization of the component sizing for a plug-in hybrid electric vehicle using a genetic algorithm. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2015, 230, 692–708. [Google Scholar] [CrossRef]
- Bertram, C.; Buecherl, D.; Thanheiser, A.; Herzog, H.G. Multi-objective optimization of a parallel hybrid electric drive train. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–5. [Google Scholar]
- Jozefowiez, N.; Semet, F.; Talbi, E.G. Enhancements of NSGA II and Its Application to the Vehicle Routing Problem with Route Balancing. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 131–142. [Google Scholar]
- Li, Y.; Lu, X.; Kar, N.C. Rule-Based Control Strategy With Novel Parameters Optimization Using NSGA-II for Power-Split PHEV Operation Cost Minimization. IEEE Trans. Veh. Technol. 2014, 63, 3051–3061. [Google Scholar] [CrossRef]
- Serrao, L.; Sciarretta, A.; Grondin, O.; Chasse, A.; Creff, Y.; Domenico, D.D.; Pognant-Gros, P.; Querel, C.; Thibault, L. Open Issues in Supervisory Control of Hybrid Electric Vehicles: A Unified Approach Using Optimal Control Methods. Oil Gas Sci. Technol. 2013, 68, 23–33. [Google Scholar] [CrossRef]
- Paganelli, G.; Guerra, T.; Delprat, S.; Guezennec, Y.; Rizzoni, G. Optimal control theory applied to hybrid fuel cell powered vehicle. IFAC Proc. Vol. 2002, 35, 253–258. [Google Scholar] [CrossRef]
- Delprat, S.; Hofman, T. Hybrid vehicle optimal control: Linear interpolation and singular control. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Lei, Z.; Cheng, D.; Liu, Y.; Qin, D.; Zhang, Y.; Xie, Q. A Dynamic Control Strategy for Hybrid Electric Vehicles Based on Parameter Optimization for Multiple Driving Cycles and Driving Pattern Recognition. Energies 2017, 10, 54. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Shen, P.; Zhao, Z.; Zhan, X.; Li, J. Particle swarm optimization of driving torque demand decision based on fuel economy for plug-in hybrid electric vehicle. Energy 2017, 123, 89–107. [Google Scholar] [CrossRef]
- Dosthosseini, R.; Kouzani, A.; Sheikholeslam, F. Direct method for optimal power management in hybrid electric vehicles. Int. J. Automot. Technol. 2011, 12, 943–950. [Google Scholar] [CrossRef]
- Pérez, L.; García, G. State constrained optimal control applied to supervisory control in HEVs. Oil Gas Sci. Technol. 2010, 65, 191–201. [Google Scholar] [CrossRef]
- Dextreit, C.; Kolmanovsky, I.V. Game theory controller for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2014, 22, 652–663. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, C.; Li, M.; Ma, C.; Chow, M.Y. A Game Theory Approach to Energy Management of An Engine–Generator/Battery/Ultracapacitor Hybrid Energy System. IEEE Trans. Ind. Electron. 2016, 63, 4266–4277. [Google Scholar] [CrossRef]
- Younis, A.; Zhou, L.; Dong, Z. Application of the new SEUMRE global optimisation tool in high efficiency EV/PHEV/EREV electric mode operations. Int. J. Electr. Hybrid Veh. 2011, 3, 176–190. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.; Rimaux, J.; Santin, J. Equivalent consumption minimization strategy for parallel hybrid powertrains. In Proceedings of the VTC Spring: 2002 IEEE 55th Vehicular Technology Vehicular Technology Conference, Birmingham, Alabama, 6–9 May 2002. [Google Scholar]
- Pisu, P.; Rizzoni, G. A Comparative Study of Supervisory Control Strategies for Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2007, 15, 506–518. [Google Scholar] [CrossRef]
- Park, J.; Park, J.H. Development of equivalent fuel consumption minimization strategy for hybrid electric vehicles. Int. J. Automot. Technol. 2012, 13, 835–843. [Google Scholar] [CrossRef]
- Pei, D.; Leamy, M.J. Dynamic programming-informed equivalent cost minimization control strategies for hybrid-electric vehicles. J. Dyn. Syst. Meas. Control 2013, 135, 051013. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Zhang, C.; Vahid, A. Real-time optimal control of plug-in hybrid vehicles with trip preview. In Proceedings of the IEEE American Control Conference (ACC), Baltimore, MD, USA, 30 June–2 July 2010; pp. 6917–6922. [Google Scholar]
- Sun, C.; Sun, F.; He, H. Investigating adaptive-ECMS with velocity forecast ability for hybrid electric vehicles. Appl. Energy 2017, 185, 1644–1653. [Google Scholar] [CrossRef]
- Zhang, C.; Vahidi, A. Route preview in energy management of plug-in hybrid vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 546–553. [Google Scholar] [CrossRef]
- Optimal Control with Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2007.
- Rousseau, G.; Sinoquet, D.; Rouchon, P. Constrained Optimization of Energy Management for a Mild-Hybrid Vehicle. Oil Gas Sci. Technol. 2007, 62, 623–634. [Google Scholar] [CrossRef]
- Kessels, J.; Koot, M.; van den Bosch, P.; Kok, D. Online Energy Management for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2008, 57, 3428–3440. [Google Scholar] [CrossRef]
- Juanjuan, S.; Xinhao, Y.; Ze, L.; Fudong, W. Smooth control for hybrid electric vehicle based on the Pontryagin’s Minimum Principle and the observer. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 741–744. [Google Scholar]
- Hou, C.; Ouyang, M.; Xu, L.; Wang, H. Approximate Pontryagin’s minimum principle applied to the energy management of plug-in hybrid electric vehicles. Appl. Energy 2014, 115, 174–189. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Allgöwer, F.; Zheng, A. (Eds.) Nonlinear Model Predictive Control; Birkhäuser: Basel, Switzerland, 2000. [Google Scholar]
- Murphey, Y.L.; Park, J.; Chen, Z.; Kuang, M.L.; Masrur, M.A.; Phillips, A.M. Intelligent hybrid vehicle power control—Part I: Machine learning of optimal vehicle power. IEEE Trans. Veh. Technol. 2012, 61, 3519–3530. [Google Scholar] [CrossRef]
- Huang, Y.; Khajepour, A.; Wang, H. A predictive power management controller for service vehicle anti-idling systems without a priori information. Appl. Energy 2016, 182, 548–557. [Google Scholar] [CrossRef]
- Li, L.; You, S.; Yang, C.; Yan, B.; Song, J.; Chen, Z. Driving-behavior-aware stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2016, 162, 868–879. [Google Scholar] [CrossRef]
- Trovao, J.P.; Dubois, M.R.; Gomozov, O.; Kestelyn, X.; Bouscayrol, A. A Model Predictive Control with Non-Uniform Sampling Times for a Hybrid Energy Storage System in Electric Vehicle Application. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Gomozov, O.; Trovao, J.P.F.; Kestelyn, X.; Dubois, M.R. Adaptive Energy Management System Based on a Real-Time Model Predictive Control With Nonuniform Sampling Time for Multiple Energy Storage Electric Vehicle. IEEE Trans. Veh. Technol. 2017, 66, 5520–5530. [Google Scholar] [CrossRef]
- Ali, A.M.; Söffker, D. Realtime Application of Progressive Optimal Search and Adaptive Dynamic Programming in Multi-Source HEVs. In Proceedings of the ASME DSCC 2017—Dynamic Systems and Control Conference, Tysons, Virginia, 11–13 October 2017; Volume 2. [Google Scholar]
- LUUS, R. Optimal control by dynamic programming using systematic reduction in grid size. Int. J. Control 1990, 51, 995–1013. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Yin, C.; Zhang, H.; Wang, C. Hardware-in-the-loop simulation for the design and verification of the control system of a series–parallel hybrid electric city-bus. Simul. Model. Pract. Theory 2012, 25, 148–162. [Google Scholar] [CrossRef]
- Johri, R.; Liang, W.; McGee, R. Hybrid electric vehicle energy management with battery thermal considerations using multi-rate dynamic programming. In Proceedings of the ASME 2013 Dynamic Systems and Control Conference, American Society of Mechanical Engineers, Palo Alto, CA, USA, 21–23 October 2013; p. V001T05A003. [Google Scholar]
- Gong, Q.; Li, Y.; Peng, Z.R. Trip Based Optimal Power Management of Plug-in Hybrid Electric Vehicle with Advanced Traffic Modeling. SAE Int. J. Engines 2008, 1, 861–872. [Google Scholar] [CrossRef]
- Boyali, A.; Güvenç, L. Real-time controller design for a parallel hybrid electric vehicle using neuro-dynamic programming method. In Proceedings of the 2010 IEEE International Conference on Systems Man and Cybernetics (SMC), Istanbul, Turkey, 10–13 October 2010; pp. 4318–4324. [Google Scholar]
- Ali, A.M.; Söffker, D. Realtime Power Management of a Multi-Source HEV Using Adaptive Dynamic Programing and Probabilistic Drive State Model. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE 2017), Cleveland, OH, USA, 6–9 August 2017; Volume 3. [Google Scholar]
- Krstić, M.; Wang, H.H. Stability of extremum seeking feedback for general nonlinear dynamic systems. Automatica 2000, 36, 595–601. [Google Scholar] [CrossRef]
- Liu, S.J.; Krstic, M. Stochastic Averaging and Stochastic Extremum Seeking; Springer: London, UK, 2012. [Google Scholar]
- Zhou, D.; Ravey, A.; Al-Durra, A.; Gao, F. A comparative study of extremum seeking methods applied to online energy management strategy of fuel cell hybrid electric vehicles. Energy Convers. Manag. 2017, 151, 778–790. [Google Scholar] [CrossRef]
- Bizon, N. Energy optimization of fuel cell system by using global extremum seeking algorithm. Appl. Energy 2017, 206, 458–474. [Google Scholar] [CrossRef]
- Pisu, P.; Silani, E.; Rizzoni, G.; Savaresi, S. A LMI-based supervisory robust control for hybrid vehicles. In Proceedings of the 2003 IEEE American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Delprat, S.; Guerra, T.M.; Paganelli, G.; Lauber, J.; Delhom, M. Control strategy optimization for an hybrid parallel powertrain. In Proceedings of the IEEE American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 2, pp. 1315–1320. [Google Scholar]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, J.; Halim, D. HEV Energy Management Fuzzy Logic Control Based on Dynamic Programming. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–5. [Google Scholar]
- Lin, C.C.; Peng, H.; Jeon, S.; Lee, J.M. Control of a hybrid electric truck based on driving pattern recognition. In Proceedings of the 2002 Advanced Vehicle Control Conference, Hiroshima, Japan, 9–13 September 2002. [Google Scholar]
- Rezaei, A.; Burl, J.B.; Zhou, B. Estimation of the ECMS Equivalent Factor Bounds for Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2017, PP, 1–8. [Google Scholar] [CrossRef]
- Ericsson, E. Independent driving pattern factors and their influence on fuel-use and exhaust emission factors. Transp. Res. D Transp. Environ. 2001, 6, 325–345. [Google Scholar] [CrossRef]
- Venditti, M. Analysis of the Performance of Different Machine Learning Techniques for the Definition of Rule-based Control Strategies in a Parallel HEV. Energy Procedia 2016, 101, 685–692. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Y.; Bogdan, P.; Chang, N.; Pedram, M. Optimizing fuel economy of hybrid electric vehicles using a Markov decision process model. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 718–723. [Google Scholar]
- Payri, F.; Guardiola, C.; Pla, B.; Blanco-Rodriguez, D. On a stochastic approach of the ecms method for energy management in hybrid electric vehicles. IFAC Proc. Vol. 2012, 45, 341–348. [Google Scholar] [CrossRef]
- Bhangu, B.S.; Bentley, P.; Stone, D.A.; Bingham, C.M. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Marano, V.; Rizzoni, G.; Tulpule, P.; Gong, Q.; Khayyam, H. Intelligent Energy Management for Plug-in Hybrid Electric Vehicles: The Role of ITS Infrastructure in Vehicle Electrification. Oil Gas Sci. Technol. 2012, 67, 575–587. [Google Scholar] [CrossRef]
- Ravey, A.; Blunier, B.; Miraoui, A. Control Strategies for Fuel-Cell-Based Hybrid Electric Vehicles: from Offline to Online and Experimental Results. IEEE Trans. Veh. Technol. 2012, 61, 2452–2457. [Google Scholar] [CrossRef]
- Shen, D.; Lu, L.; Müller, S. Utilization of predictive information to optimize driving and powertrain control of series hybrid vehicles. Automot. Engine Technol. 2017. [Google Scholar] [CrossRef]
- Rajagopalan, A.; Washington, G. Intelligent Control of Hybrid Electric Vehicles Using GPS Information; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2002. [Google Scholar]
- Montazeri-Gh, M.; Ahmadi, A.; Asadi, M. Driving condition recognition for genetic-fuzzy HEV Control. In Proceedings of the 2008 3rd International Workshop on Genetic and Evolving Systems, Witten-Bommerholz, Germany, 4–7 March 2008; pp. 65–70. [Google Scholar]
- Yi, T.; Xin, Z.; Liang, Z.; Xinn, Z. Intelligent Energy Management Based on Driving Cycle Identification Using Fuzzy Neural Network. In Proceedings of the 2009 Second International Symposium on Computational Intelligence and Design, Changsha, China, 12–14 December 2009; Volume 2, pp. 501–504. [Google Scholar]
- Rajagopalan, A.; Washington, G.; Rizzoni, G.; Guezennec, Y. Development of Fuzzy Logic and Neural Network Control and Advanced Emissions Modeling for Parallel Hybrid Vehicles; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 2003.
- Onori, S.; Serrao, L. On Adaptive-ECMS strategies for hybrid electric vehicles. In Proceedings of the International Scientific Conference on Hybrid and Electric Vehicles, Rueil-Malmaison, France, 6–7 December 2011; pp. 6–7. [Google Scholar]
- Sun, C.; He, H.; Sun, F. The Role of Velocity Forecasting in Adaptive-ECMS for Hybrid Electric Vehicles. Energy Procedia 2015, 75, 1907–1912. [Google Scholar] [CrossRef]
- Jeong, J.; Lee, D.; Kim, N.; Park, Y.i.; Cha, S.W. Fuel economy analysis of a parallel hybrid bus using the optimal control theory. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 6–9 September 2011; pp. 1–5. [Google Scholar]
- Karbowski, D.; Kim, N.; Rousseau, A. Route-Based Online Energy Management of a PHEV and Sensitivity to Trip Prediction. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Onori, S.; Tribioli, L. Adaptive Pontryagin’s Minimum Principle supervisory controller design for the plug-in hybrid GM Chevrolet Volt. Appl. Energy 2015, 147, 224–234. [Google Scholar] [CrossRef]
- Johannesson, L.; Asbogard, M.; Egardt, B. Assessing the Potential of Predictive Control for Hybrid Vehicle Powertrains Using Stochastic Dynamic Programming. IEEE Trans. Intell. Transp. Syst. 2007, 8, 71–83. [Google Scholar] [CrossRef]
- Cairano, S.D.; Bernardini, D.; Bemporad, A.; Kolmanovsky, I.V. Stochastic MPC With Learning for Driver-Predictive Vehicle Control and its Application to HEV Energy Management. IEEE Trans. Control Syst. Technol. 2014, 22, 1018–1031. [Google Scholar] [CrossRef]
- Johannesson, L.; Pettersson, S.; Egardt, B. Predictive energy management of a 4QT series-parallel hybrid electric bus. Control Eng. Pract. 2009, 17, 1440–1453. [Google Scholar] [CrossRef]
- Chen, Z.; Masrur, M.A.; Murphey, Y.L. Intelligent vehicle power management using machine learning and fuzzy logic. In Proceedings of the 2008 IEEE International Conference on Fuzzy Systems (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 2351–2358. [Google Scholar]
- Lv, Y.M.; Yuan, H.W.; Liu, Y.Y.; Wang, Q.S. Fuzzy Logic Based Energy Management Strategy of Battery-Ultracapacitor Composite Power Supply for HEV. In Proceedings of the 2010 First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 17–19 September 2010; pp. 1209–1214. [Google Scholar]
- Xu, L.; Wang, J.; Chen, Q. Kalman filtering state of charge estimation for battery management system based on a stochastic fuzzy neural network battery model. Energy Convers. Manag. 2012, 53, 33–39. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, L.; Yan, B.; Yan, T.; Ma, P. An Online Rolling Optimal Control Strategy for Commuter Hybrid Electric Vehicles Based on Driving Condition Learning and Prediction. IEEE Trans. Veh. Technol. 2016, 65, 4312–4327. [Google Scholar] [CrossRef]
- Li, W.; Xu, G.; Wang, Z.; Xu, Y. Dynamic energy management for hybrid electric vehicle based on approximate dynamic programming. In Proceedings of the 2008 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 7864–7869. [Google Scholar]
- Chen, Z.; Mi, C.C.; Xu, J.; Gong, X.; You, C. Energy Management for a Power-Split Plug-in Hybrid Electric Vehicle Based on Dynamic Programming and Neural Networks. IEEE Trans. Veh. Technol. 2014, 63, 1567–1580. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, J. A Parallel Hybrid Electric Vehicle Energy Management Strategy Using Stochastic Model Predictive Control With Road Grade Preview. IEEE Trans. Control Syst. Technol. 2015, 23, 2416–2423. [Google Scholar] [CrossRef]
- Hu, X.; Sun, F.; Zou, Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies 2010, 3, 1586–1603. [Google Scholar] [CrossRef]
- Li, S.; Bao, K.; Fu, X.; Zheng, H. Energy Management and Control of Electric Vehicle Charging Stations. Electr. Power Compon. Syst. 2014, 42, 339–347. [Google Scholar] [CrossRef]
- Mohamed, A.; Salehi, V.; Ma, T.; Mohammed, O. Real-Time Energy Management Algorithm for Plug-In Hybrid Electric Vehicle Charging Parks Involving Sustainable Energy. IEEE Trans. Sustain. Energy 2014, 5, 577–586. [Google Scholar] [CrossRef]
- HomChaudhuri, B.; Lin, R.; Pisu, P. Hierarchical control strategies for energy management of connected hybrid electric vehicles in urban roads. Transp. Res. C Emerg. Technol. 2016, 62, 70–86. [Google Scholar] [CrossRef]
- Zhang, F.; Xi, J.; Langari, R. Real-Time Energy Management Strategy Based on Velocity Forecasts Using V2V and V2I Communications. IEEE Trans. Intell. Transp. Syst. 2017, 18, 416–430. [Google Scholar] [CrossRef]
- Du, Z.; Qiu, L.; Pisu, P. Hierarchical Energy Management Control of Connected Hybrid Electric Vehicles on Urban Roads with Efficiencies Feedback. In Proceedings of the ASME 2016 Dynamic Systems and Control Conference Minneapolis, Minneapolis, MN, USA, 12–14 October 2016; p. V001T16A002. [Google Scholar]
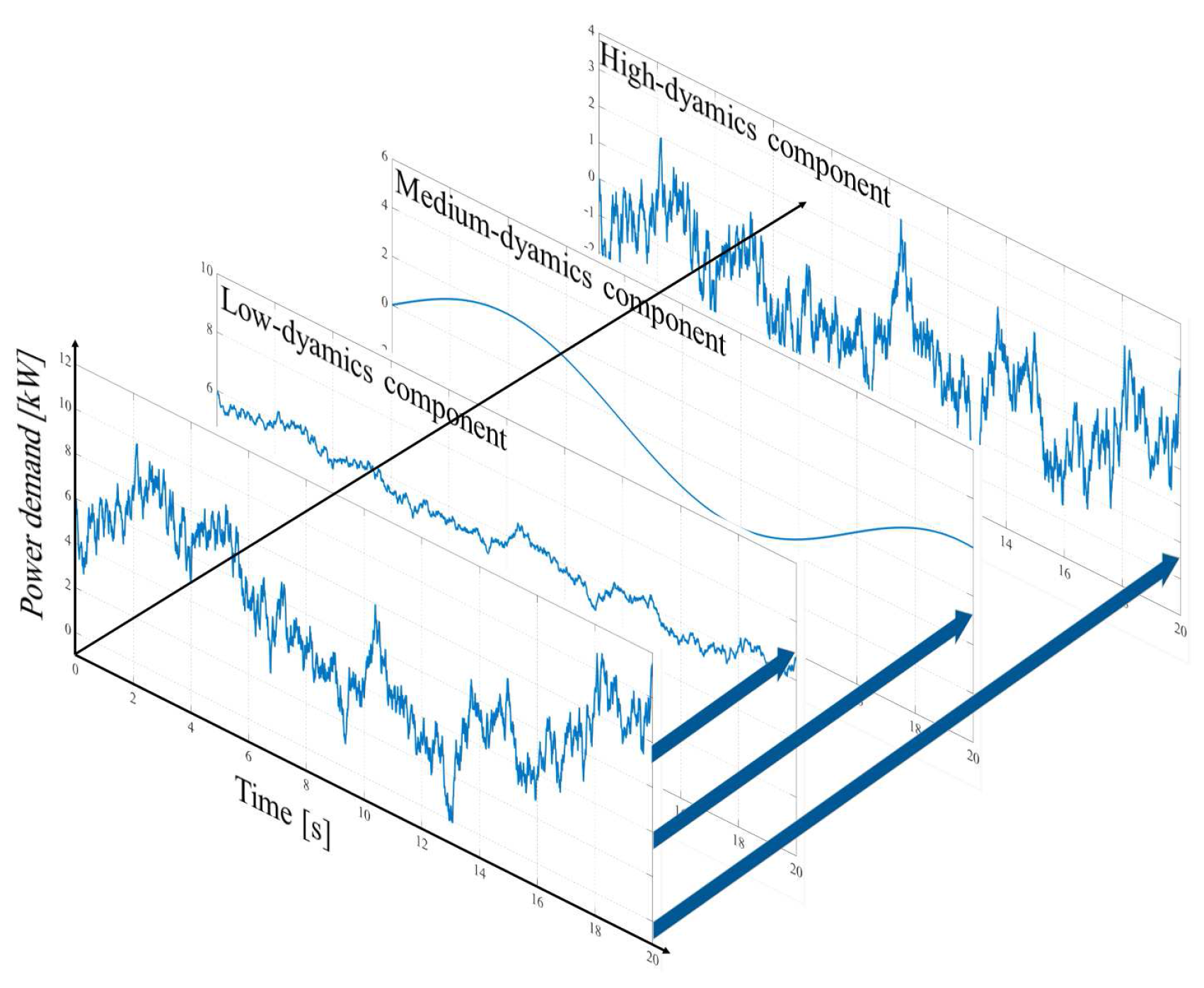
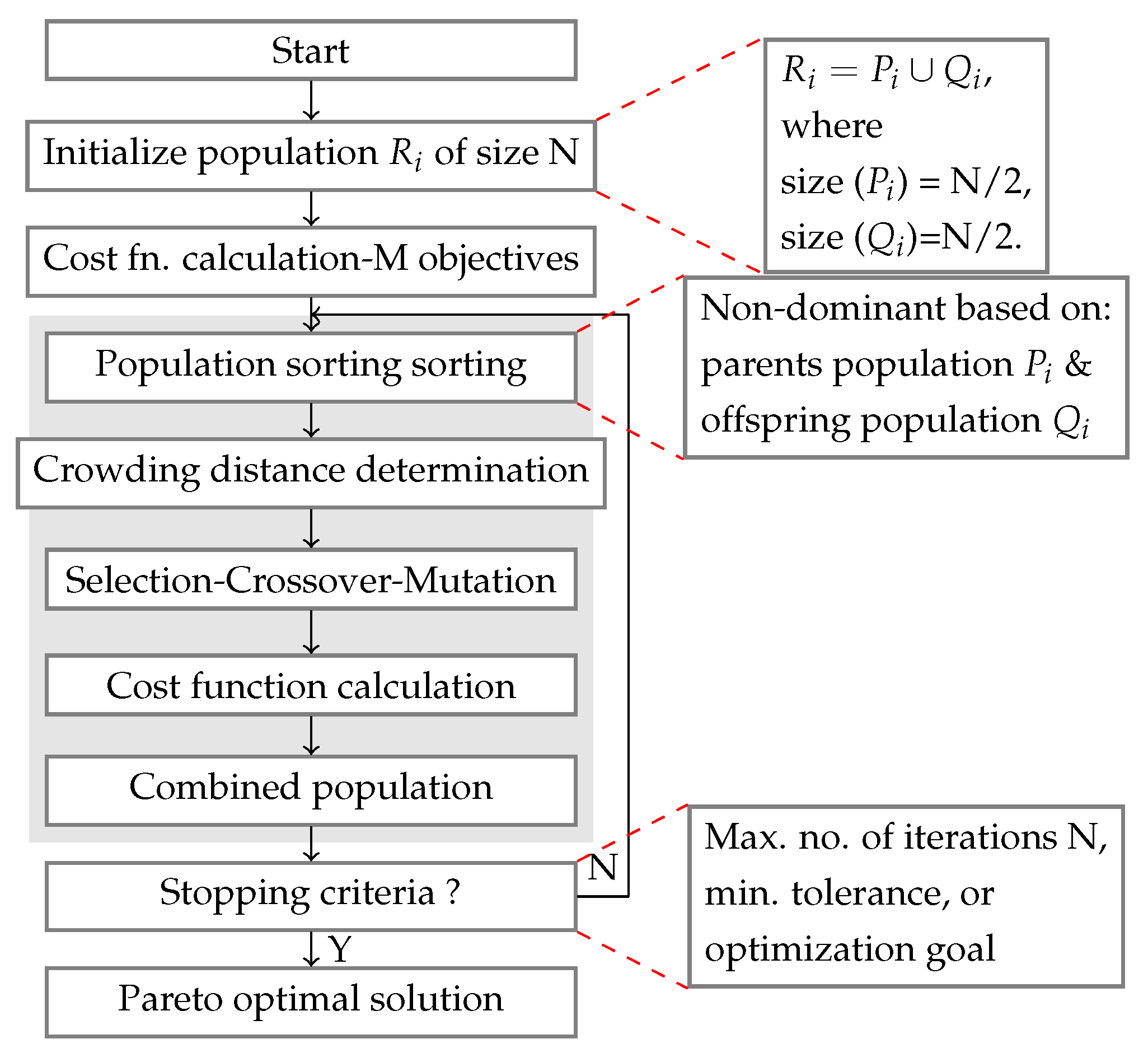

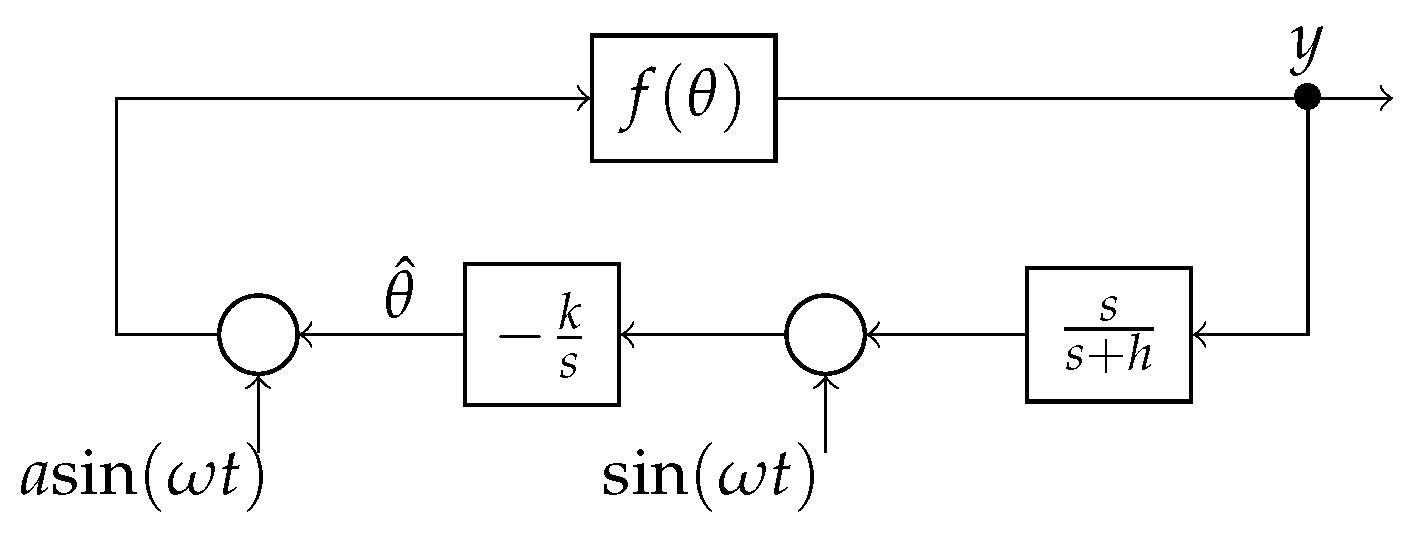

| Auxiliary Tools | Types | Conducted by | Integrated to | Achievement/Output |
|---|---|---|---|---|
| Rules optimization | - qualitative - quantitative | Static optimization | Rule-based | Robustnes of RB methods |
| Multi-rate computing | - fixed rate - adaptive rate | - case-based - parallel computing | Opt-based | Computational time reduction |
| Pattern recognition | - driving patterns - route/road type | - machine learning - fuzzy logic/NN | Rule-based & opt-based | Case-based optimized solutions |
| Prediction/estimation | - driving conditions - estimation | - statistics/HMM - observers/filter | Opt-based | Priori knowledge of future drive conditions |
| Intelligent traffic systems (ITS) | - V2V - V2I | Communication technologies | Rule-based & opt-based | - current traffic conditions - next refuelling options |
| * | DRB | FRB | ECMS | PMP | DP | MPC |
|---|---|---|---|---|---|---|
| 1 | [44,86] | [87,96] | [89] | [54] | – | – |
| 2 | – | – | – | – | [76,77] | [71,97] |
| 3 | [44,88] [77,98] | [25,99,100] [101] | [57,102] [103] | [104] [105,106] | [25] [77,107] | [108] [109] |
| 4 | [92] [91] | [99] [110] [111] [112] | [93] | [113] [106] [64] | [114] [115] | [116] [94] [117] |
| 5 | [118] | [119] | [120,121] | – | – | [122] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.M.; Söffker, D. Towards Optimal Power Management of Hybrid Electric Vehicles in Real-Time: A Review on Methods, Challenges, and State-Of-The-Art Solutions. Energies 2018, 11, 476. https://doi.org/10.3390/en11030476
Ali AM, Söffker D. Towards Optimal Power Management of Hybrid Electric Vehicles in Real-Time: A Review on Methods, Challenges, and State-Of-The-Art Solutions. Energies. 2018; 11(3):476. https://doi.org/10.3390/en11030476
Chicago/Turabian StyleAli, Ahmed M., and Dirk Söffker. 2018. "Towards Optimal Power Management of Hybrid Electric Vehicles in Real-Time: A Review on Methods, Challenges, and State-Of-The-Art Solutions" Energies 11, no. 3: 476. https://doi.org/10.3390/en11030476
APA StyleAli, A. M., & Söffker, D. (2018). Towards Optimal Power Management of Hybrid Electric Vehicles in Real-Time: A Review on Methods, Challenges, and State-Of-The-Art Solutions. Energies, 11(3), 476. https://doi.org/10.3390/en11030476






