Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil
Abstract
:1. Introduction
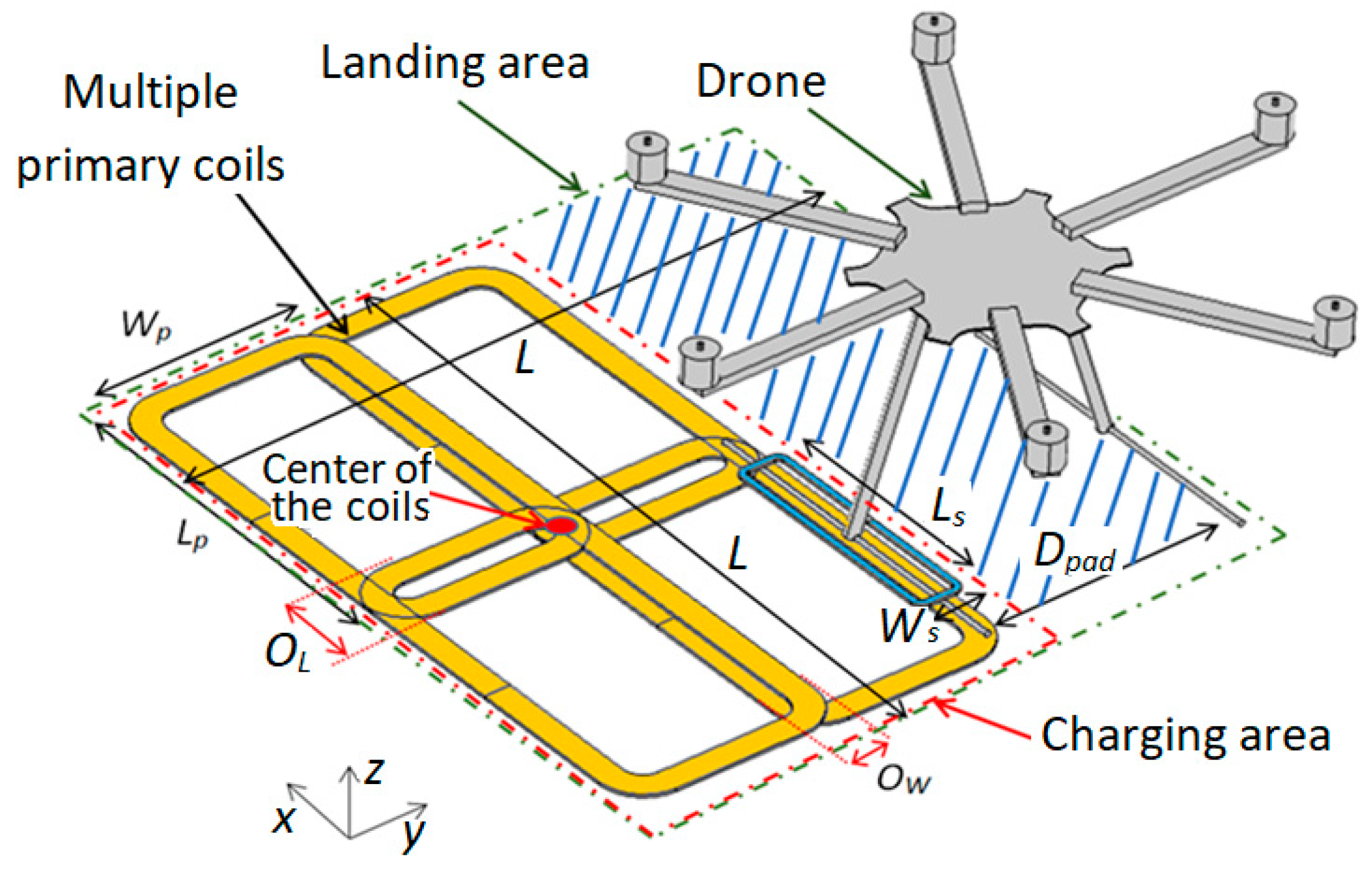
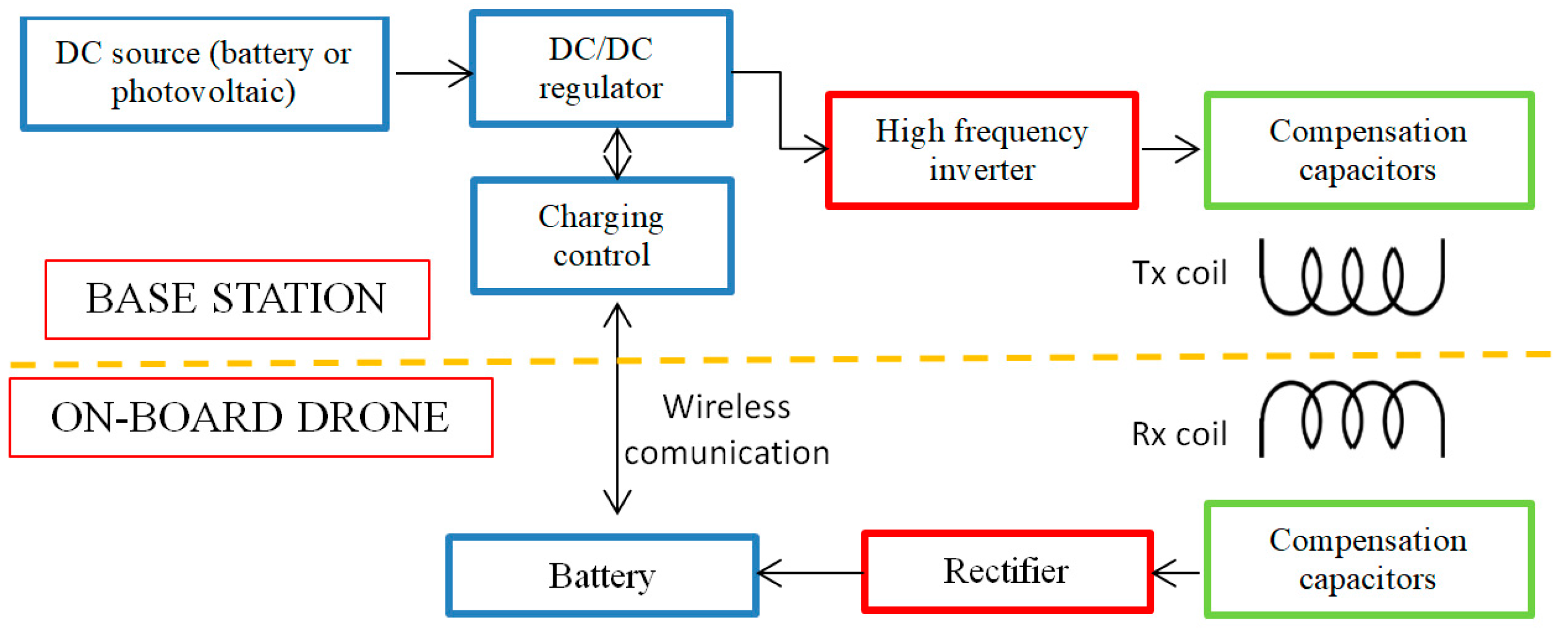
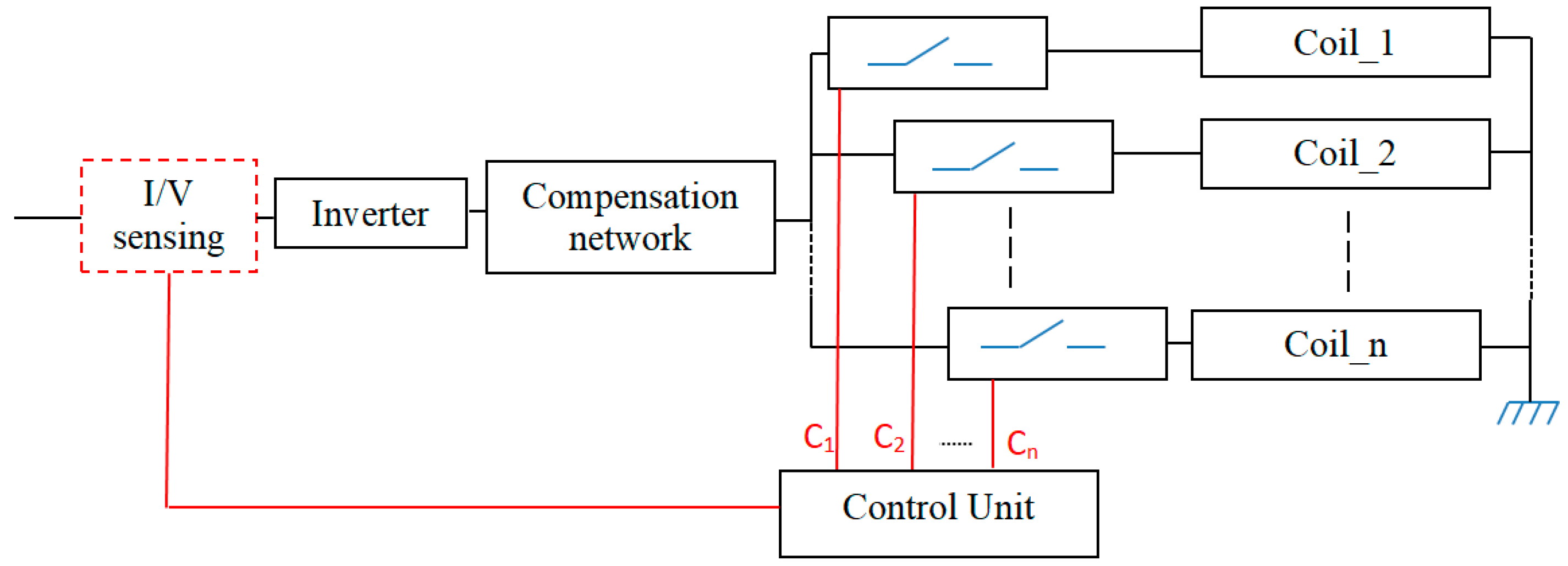
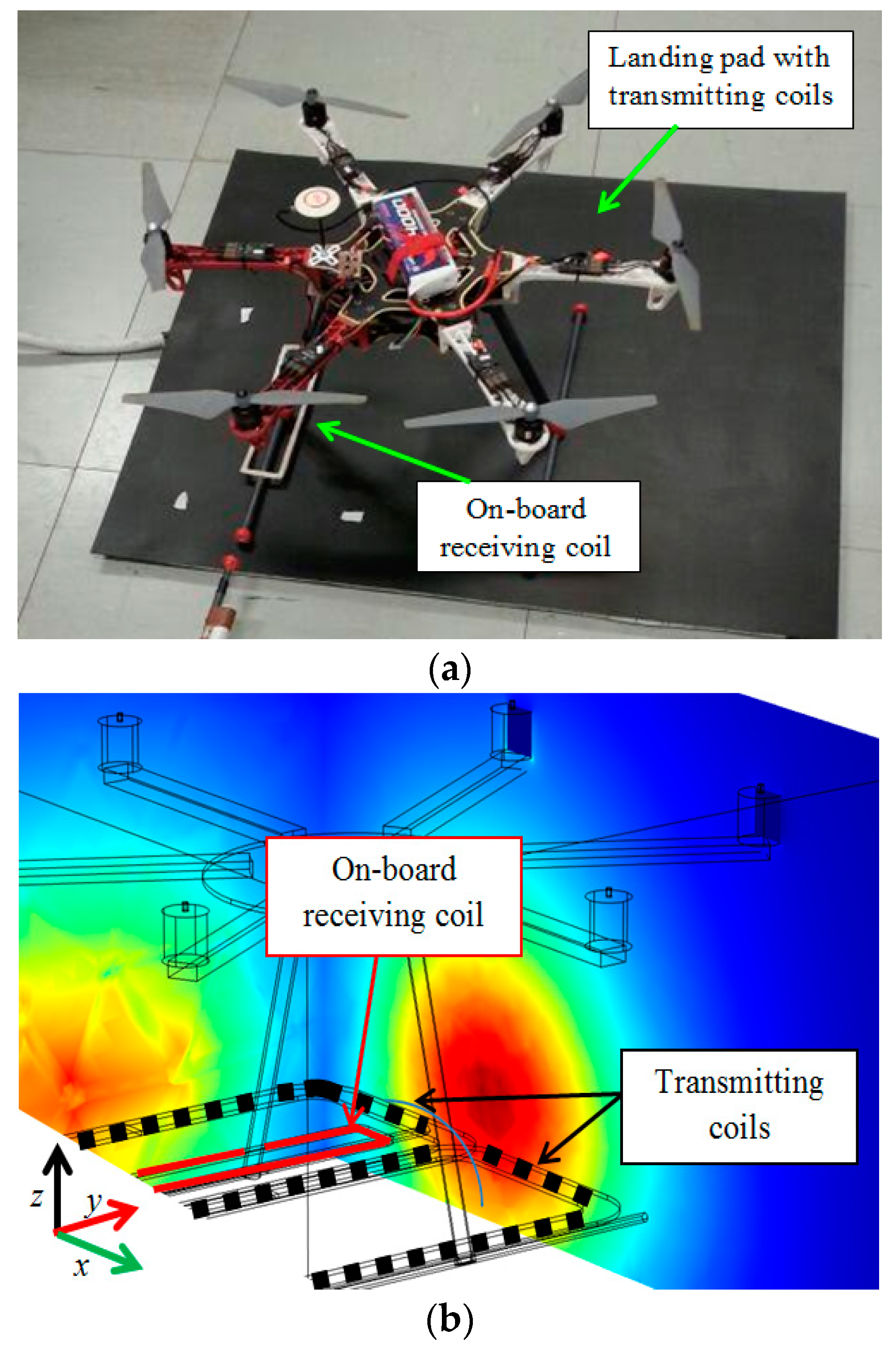
2. System Configuration
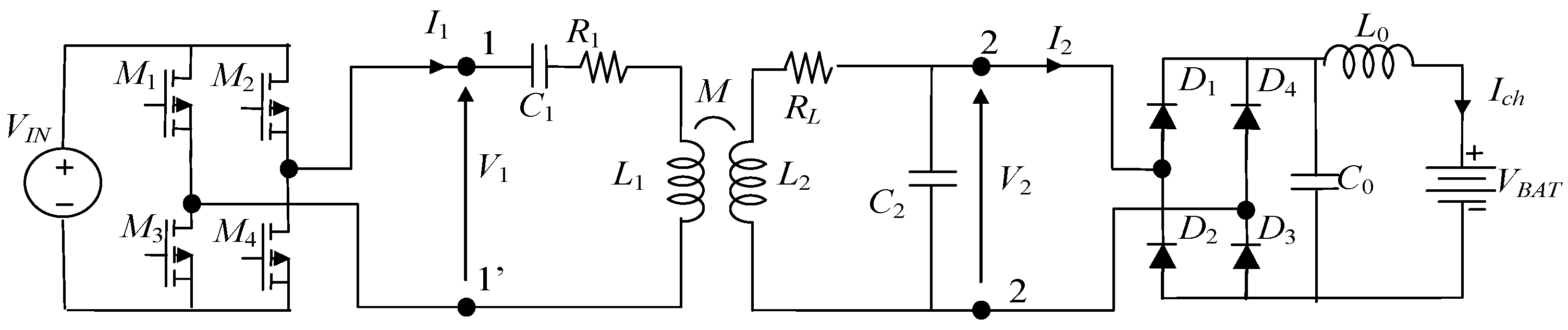
3. WPT Design
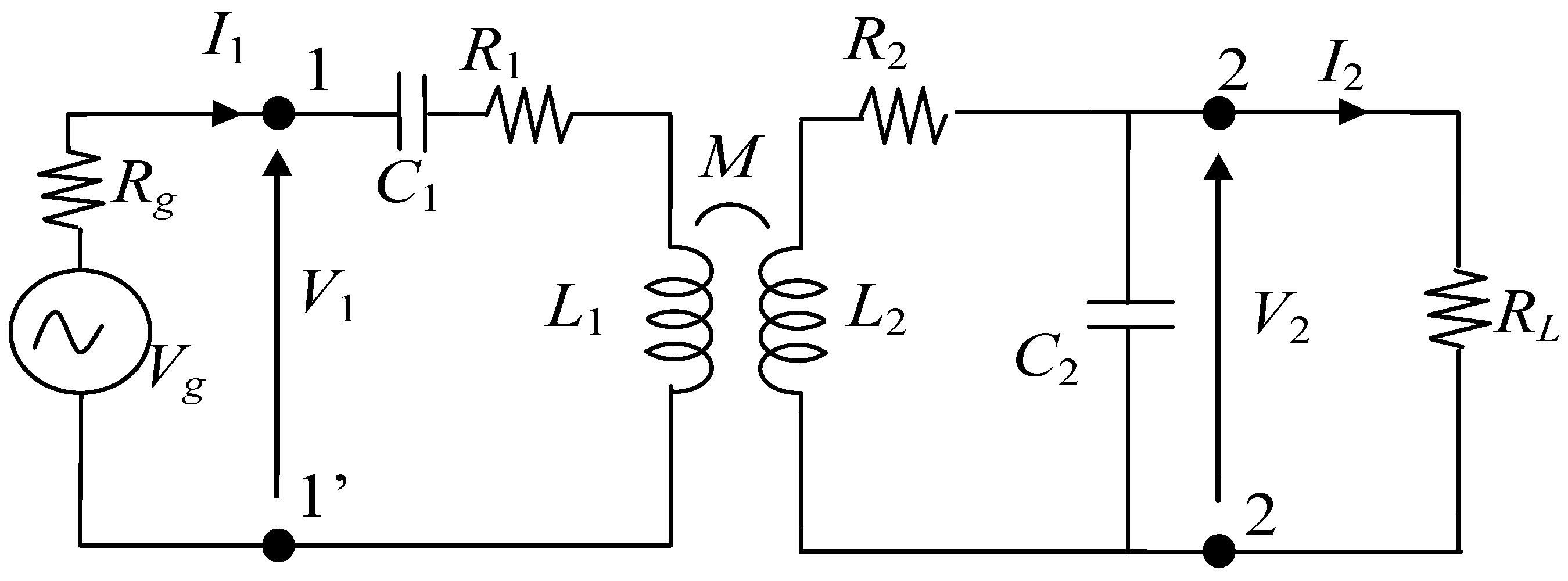
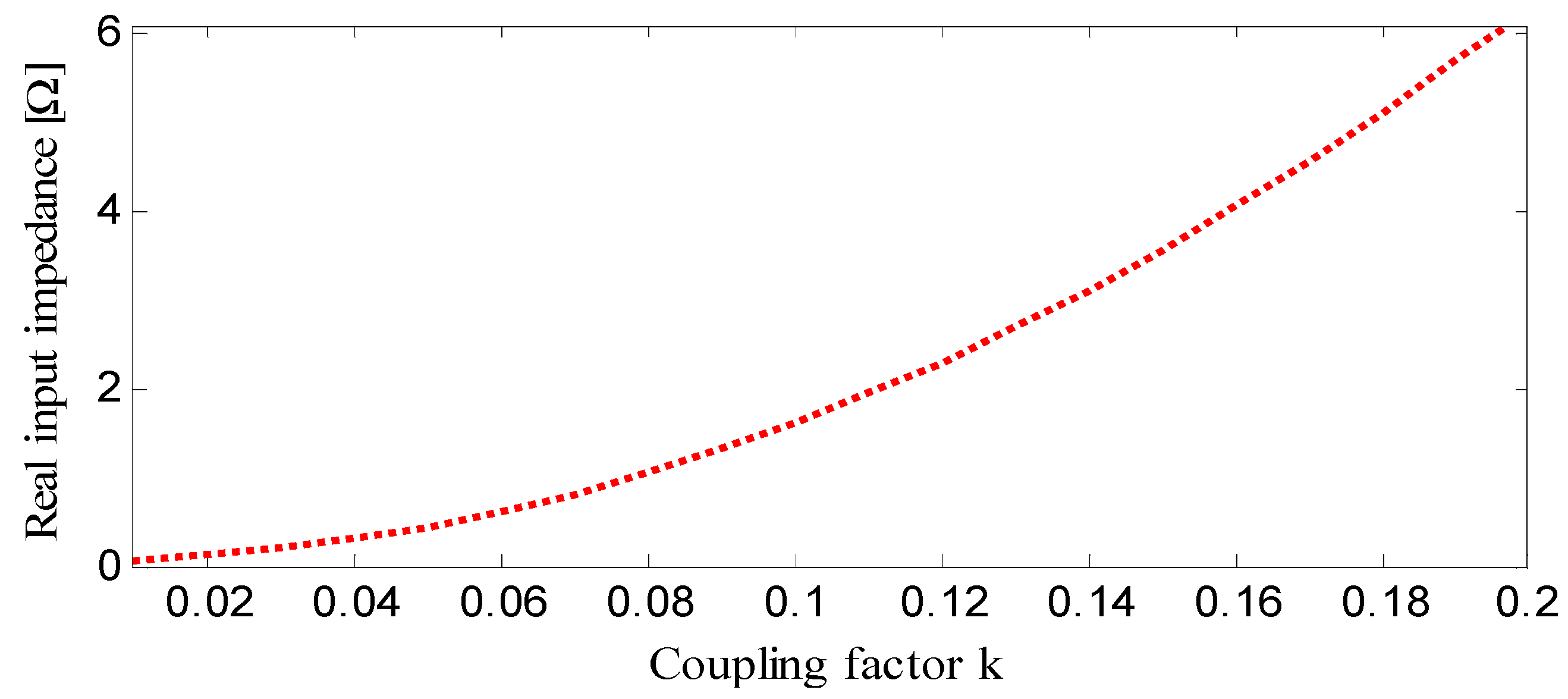
3.1. WPT Equivalent Circuit
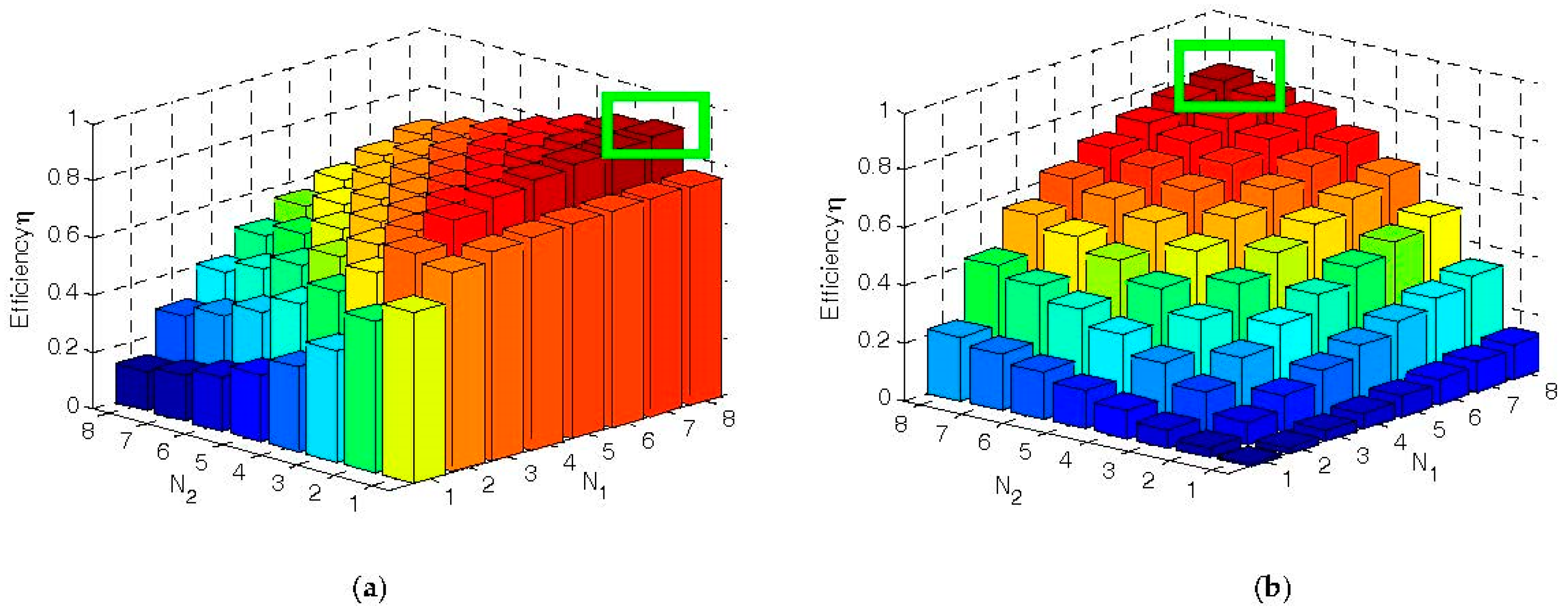
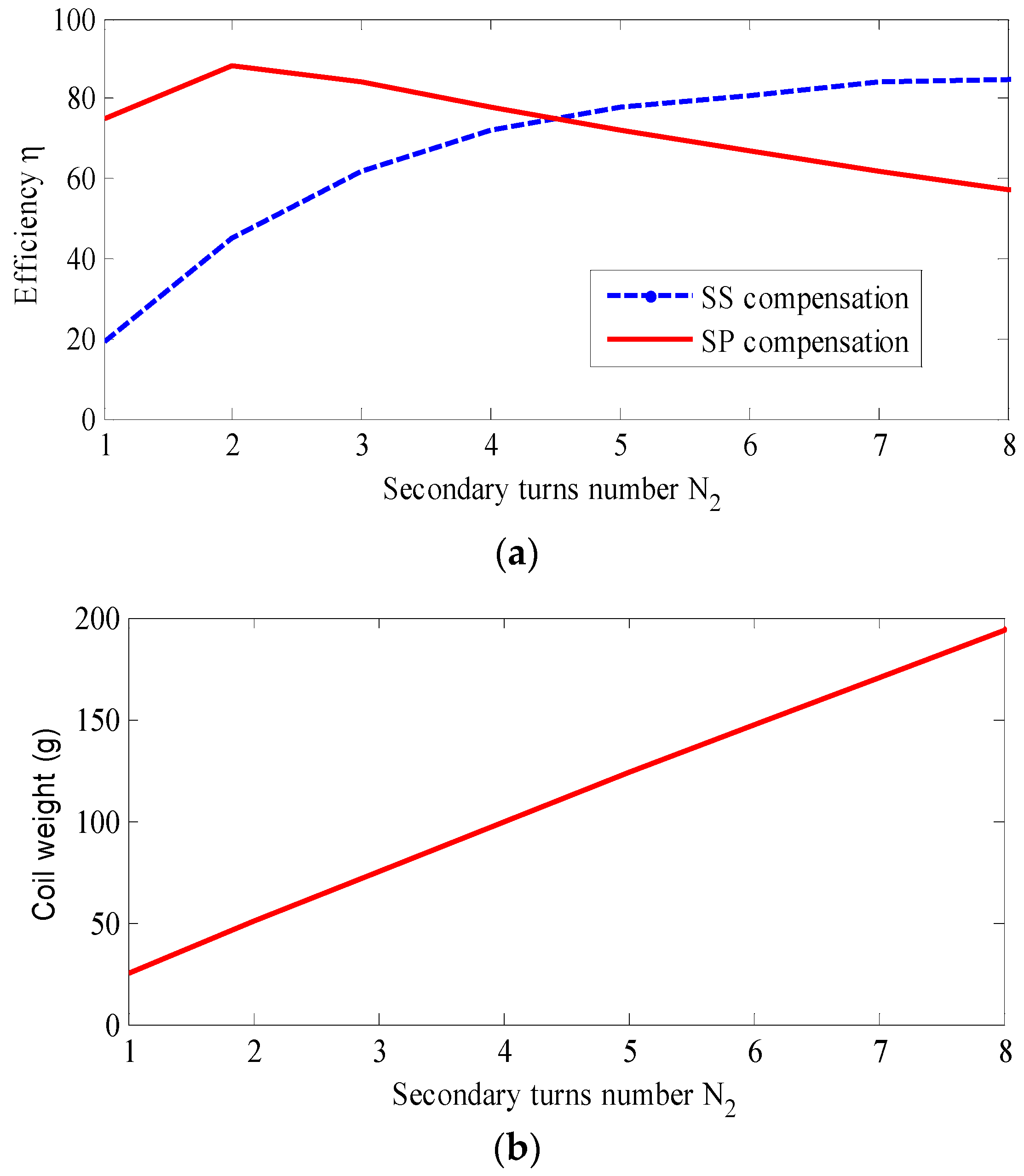
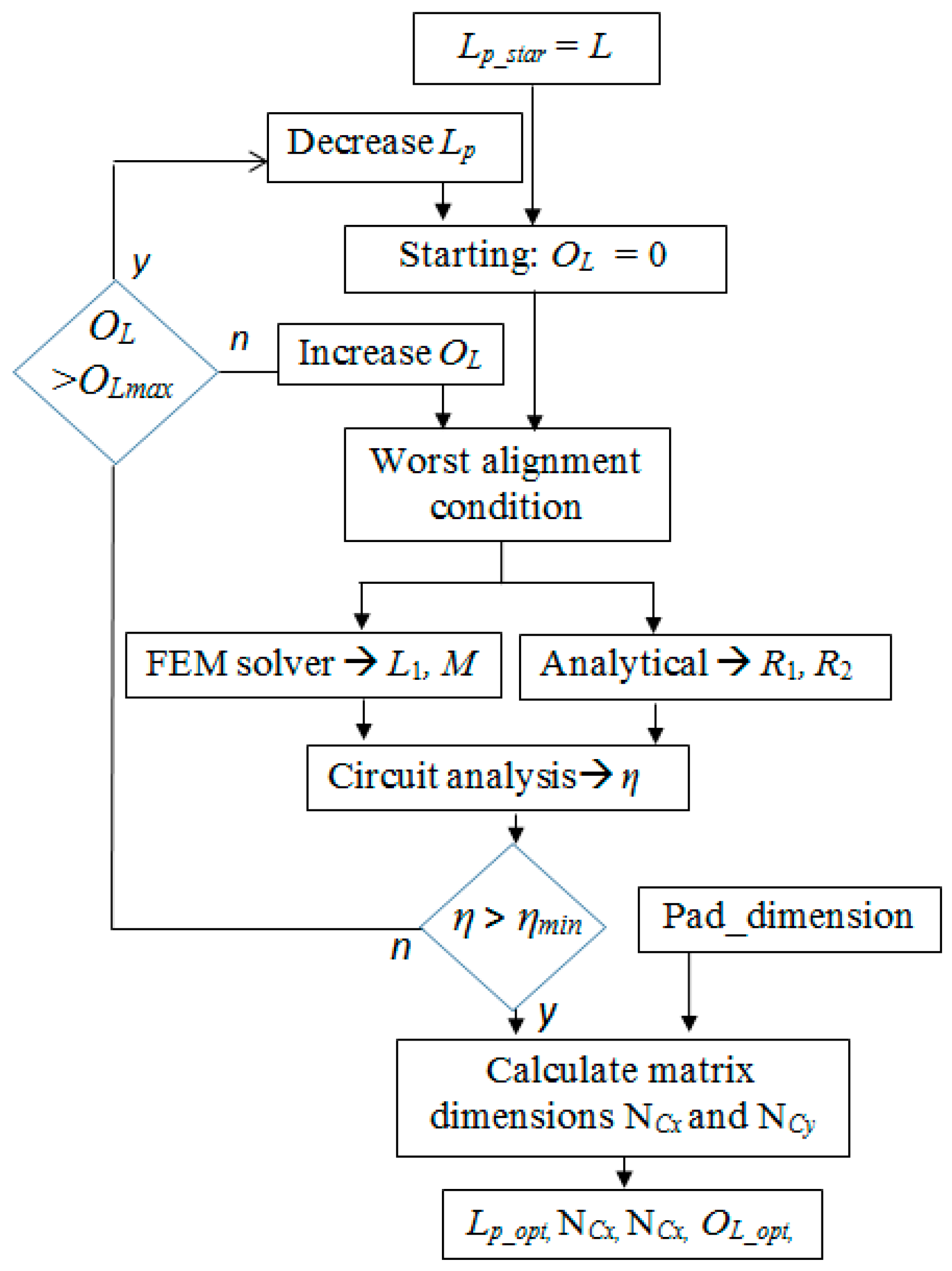
3.2. Coil Design
- Resonance frequency f.
- Coil side Lp equal to the side L of the landing area.
- Overlapping OL = 0.
4. Applications
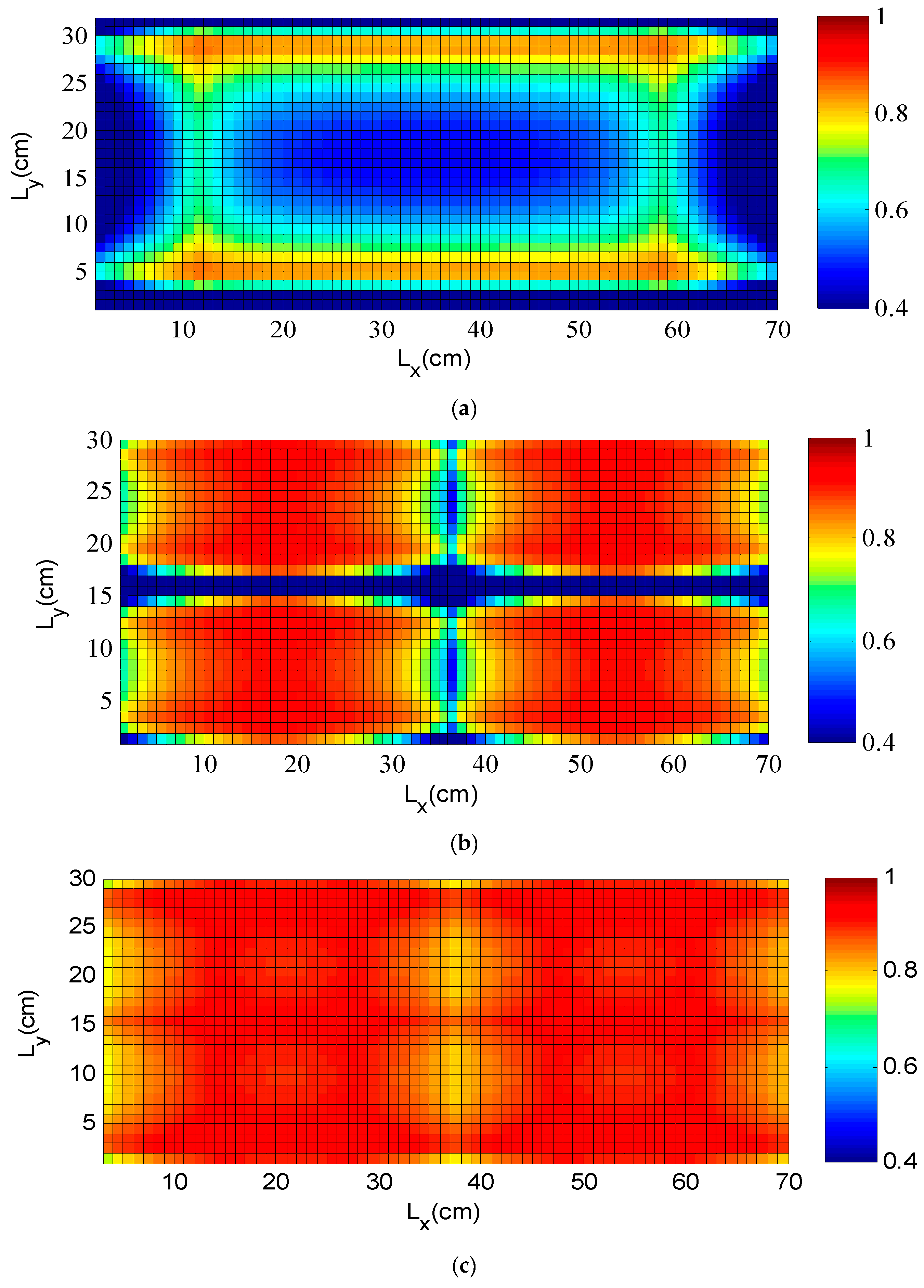
4.1. Coil Design
- Primary coil dimension Lp_opt = 375 mm.
- Array size NCx × NCy with NCx = 2 and NCy = 2.
- Overlapping distance OL_opt = 50 mm.
- Side of the square landing area L = 700 mm.
4.2. Numerical Results
- Output voltage Vbat = 16 V.
- Output current Ibat = 4 A.
- Output power PL = 64 W.
4.3. Electrical Performance
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Sujit, P.B.; Ghose, D. Search using multiple UAVs with flight time constraints. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 491–509. [Google Scholar] [CrossRef]
- Sarunic, P.; Evans, R. Hierarchical model predictive control of UAVs performing multitarget-multisensor tracking. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2253–2268. [Google Scholar] [CrossRef]
- Lee, B.; Kwon, S.; Park, P.; Kim, K. Active power management system for an unmanned aerial vehicle powered by solar cells, a fuel cell, and batteries. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2253–2268. [Google Scholar] [CrossRef]
- DIJ. Available online: https://www.dji.com/ (accessed on 14 September 2017).
- Lee, D.; Zhou, J.; Lin, W.T. Autonomous battery swapping system for quadcopter. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 118–124. [Google Scholar]
- Knorr, S.; Puiatti, L.; Dallachiesa, M.; Puiatti, A. Charging Apparatus and Method for Electrically Charging Energy Storage Devices. Patent WO2015107199 A1, 23 July 2015. [Google Scholar]
- Covic, G.A.; Boys, J.T. Inductive power transfer. Proc. IEEE 2013, 101, 1276–1289. [Google Scholar] [CrossRef]
- Shinohara, N. Power without wires. IEEE Microw. Mag. 2011, 11, 64–73. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Maradei, F.; Feliziani, M. Near Field reduction in a Wireless Power Transfer System using LCC compensation. IEEE Trans. Electromagn. Compat. 2017, 59, 686–694. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; De Santis, V.; Feliziani, M. EMF safety and thermal aspects in a pacemaker equipped with a wireless power transfer system working at low frequency. IEEE Trans. Microw. Theory Tech. 2016, 64, 375–382. [Google Scholar] [CrossRef]
- Jawad, A.M.; Nordin, R.; Gharghan, S.K.; Jawad, H.M.; Ismail, M. Opportunities and Challenges for Near-Field Wireless Power Transfer: A Review. Energies 2017, 10, 1022. [Google Scholar] [CrossRef]
- Vijayakumaran Nair, V.; Choi, J.R. An Efficiency Enhancement Technique for a Wireless Power Transmission System Based on a Multiple Coil Switching Technique. Energies 2016, 9, 156. [Google Scholar] [CrossRef]
- Feliziani, M.; Campi, T.; Cruciani, S.; Maradei, F.; Grasselli, U.; Macellari, M.; Schirone, L. Robust LCC compensation in wireless power transfer with variable coupling factor due to coil misalignment. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015. [Google Scholar]
- Campi, T.; Dionisi, F.; Cruciani, S.; De Santis, V.; Feliziani, M.; Maradei, F. Magnetic field levels in drones equipped with wireless power transfer technology. In Proceedings of the 2016 Asia-Pacific International Symposium on Electromagnetic Compatibility (APEMC), Shenzhen, China, 17–21 May 2016; pp. 544–547. [Google Scholar]
- Junaid, A.B.; Konoiko, A.; Zweiri, Y.; Sahinkaya, M.N.; Seneviratne, L. Autonomous Wireless Self-Charging for Multi-Rotor Unmanned Aerial Vehicles. Energies 2017, 10, 803. [Google Scholar] [CrossRef]
- Choi, C.H.; Jang, H.J.; Lim, S.G.; Lim, H.C.; Cho, S.H.; Gaponov, I. Automatic wireless drone charging station creating essential environment for continuous drone operation. In Proceedings of the 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, Korea, 26–29 October 2016; pp. 132–136. [Google Scholar]
- He, X.; Bito, J.; Tentzeris, M.M. A drone-based wireless power transfer and communications platform. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; pp. 1–4. [Google Scholar]
- Mostafa, T.M.; Muharam, A.; Hattori, R. Wireless battery charging system for drones via capacitive power transfer. In Proceedings of the 2017 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Chongqing, China, 20–22 May 2017; pp. 1–6. [Google Scholar]
- Simic, M.; Bil, M.; Vojisavljevic, V. Investigation in Wireless Power Transmission for UAV Charging. Proc. Comput. Sci. 2015, 40, 1846–1855. [Google Scholar] [CrossRef]
- Cruciani, S.; Campi, T.; Feliziani, M.; Maradei, F. Optimum coil configuration of wireless power transfer system in presence of shields. In Proceedings of the 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 16–22 August 2015; pp. 720–725. [Google Scholar]
- Campi, T.; Cruciani, S.; Feliziani, M. Magnetic shielding of Wireless Power Transfer systems. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, (EMC’14/Tokyo), Tokyo, Japan, 12–16 May 2014. [Google Scholar]
- COMSOL Multiphysics Software. Available online: http://www.comsol.com (accessed on October 2017).
- Round Litz Datasheet. Available online: http://litzwire.com/nepdfs/Round_Litz_Catalog.pdf (accessed on 14 September 2017).
- D’Amore, M.; De Santis, V.; Feliziani, M. Equivalent circuit modeling of frequency-selective surfaces based on nanostructured transparent thin films. IEEE Trans. Magn. 2012, 48, 703–706. [Google Scholar] [CrossRef]
- Buccella, C.; Feliziani, M. A hybrid model to compute the effects of a direct lightning stroke on three-dimensional structures. IEEE Trans. Magn. 2003, 39, 1586–1589. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Palandrani, F.; De Santis, V.; Hirata, A.; Feliziani, M. Wireless Power Transfer charging system for AIMDs and pacemakers. IEEE Trans. Microw. Theory Tech. 2016, 64, 633–642. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M. Autonomous Landing of a Quadrotor on a Moving Platform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1504–1519. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Maradei, F.; Feliziani, M. High efficiency and lightweight wireless charging system for drone batteries. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Cagliari, Italy, 20–22 September 2017; pp. 1–5. [Google Scholar]
- Zhang, W.; Mi, C.C. Compensation topologies of high-power Wireless Power Transfer systems. IEEE Trans. Veh. Technol. 2016, 65, 4768–4778. [Google Scholar] [CrossRef]
- Liu, X.; Wang, T.; Yang, X.; Jin, N.; Tang, H. Analysis and Design of a Wireless Power Transfer System with Dual Active Bridges. Energies 2017, 10, 1588. [Google Scholar] [CrossRef]
- Aldhaher, S.; Kkelis, D.; Yates, D.C.; Mitcheson, P.D. Class EF2 inverters for wireless power transfer applications. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–4. [Google Scholar]


| Method | R1 (mΩ) | R2 (mΩ) | L1 (μH) | L2 (μH) | M (μH) |
|---|---|---|---|---|---|
| Numerical | - | - | 44.1 | 1.23 | 0.91 |
| Measured | 180 | 20 | 46.2 | 1.33 | 1.05 |
| Misalignment | Type | V1 (V) | I1 (A) | η (%) | P1 (W) | |
|---|---|---|---|---|---|---|
| Tx (mm) | Ty (mm) | |||||
| 0 | 0 | Calculated | 11.7 | 6.2 | 88 | 72.5 |
| Measured | 12.5 | 6 | 85 | 75 | ||
| 100 | 0 | Calculated | 10.2 | 7.6 | 83 | 77.5 |
| Measured | 10.8 | 7.3 | 81 | 78.8 | ||
| 200 | 0 | Calculated | 8.5 | 9.6 | 78 | 81.6 |
| Measured | 9.9 | 8.5 | 76 | 84.1 | ||
| 0 | 35 | Calculated | 12.0 | 6 | 89 | 71.9 |
| Measured | 12.6 | 5.9 | 87 | 73.5 | ||
| 0 | 70 | Calculated | 12.3 | 5.8 | 90 | 71.1 |
| Measured | 12.8 | 5.6 | 89 | 71.2 | ||
| Battery Status (%) | Vbat (V) | Ich (A) | Pbat (W) | Pdc (W) | ηtot (%) |
|---|---|---|---|---|---|
| 10 | 12.8 | 4.1 | 52.4 | 64.7 | 79 |
| 50 | 14.4 | 4.0 | 57.6 | 72.9 | 78 |
| 100 | 16.4 | 4.0 | 65.5 | 85.2 | 76 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campi, T.; Cruciani, S.; Feliziani, M. Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil. Energies 2018, 11, 352. https://doi.org/10.3390/en11020352
Campi T, Cruciani S, Feliziani M. Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil. Energies. 2018; 11(2):352. https://doi.org/10.3390/en11020352
Chicago/Turabian StyleCampi, Tommaso, Silvano Cruciani, and Mauro Feliziani. 2018. "Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil" Energies 11, no. 2: 352. https://doi.org/10.3390/en11020352
APA StyleCampi, T., Cruciani, S., & Feliziani, M. (2018). Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil. Energies, 11(2), 352. https://doi.org/10.3390/en11020352





