The PurdueTracer: An Energy-Efficient Human-Powered Hydraulic Bicycle with Flexible Operation and Software Aids
Abstract
:1. Introduction
- The safety risk to the rider in the form of entangling clothing in the chain and the sprocket due to the fact that the chain drive is typically exposed;
- The undesirable occurrence in variable-speed bicycles of shifting to the wrong gear and positioning the chain in an intermediate position between sprockets, which leads to surprising and dangerous slipping of the chain and the consequent unbalancing of the cyclist;
- The lubrication requirement of the chain, which attracts dust and dirt, causing aging and decay of the efficiency of the system and unpleasant effects due to possible contact with clothing.
- (1)
- Maximizes velocity while pedaling;
- (2)
- Minimizes overall weight;
- (3)
- Recovers energy while braking;
- (4)
- Allows for a power boost (use of energy from the accumulator);
- (5)
- Maximizes human comfort and implements all necessary safety features.
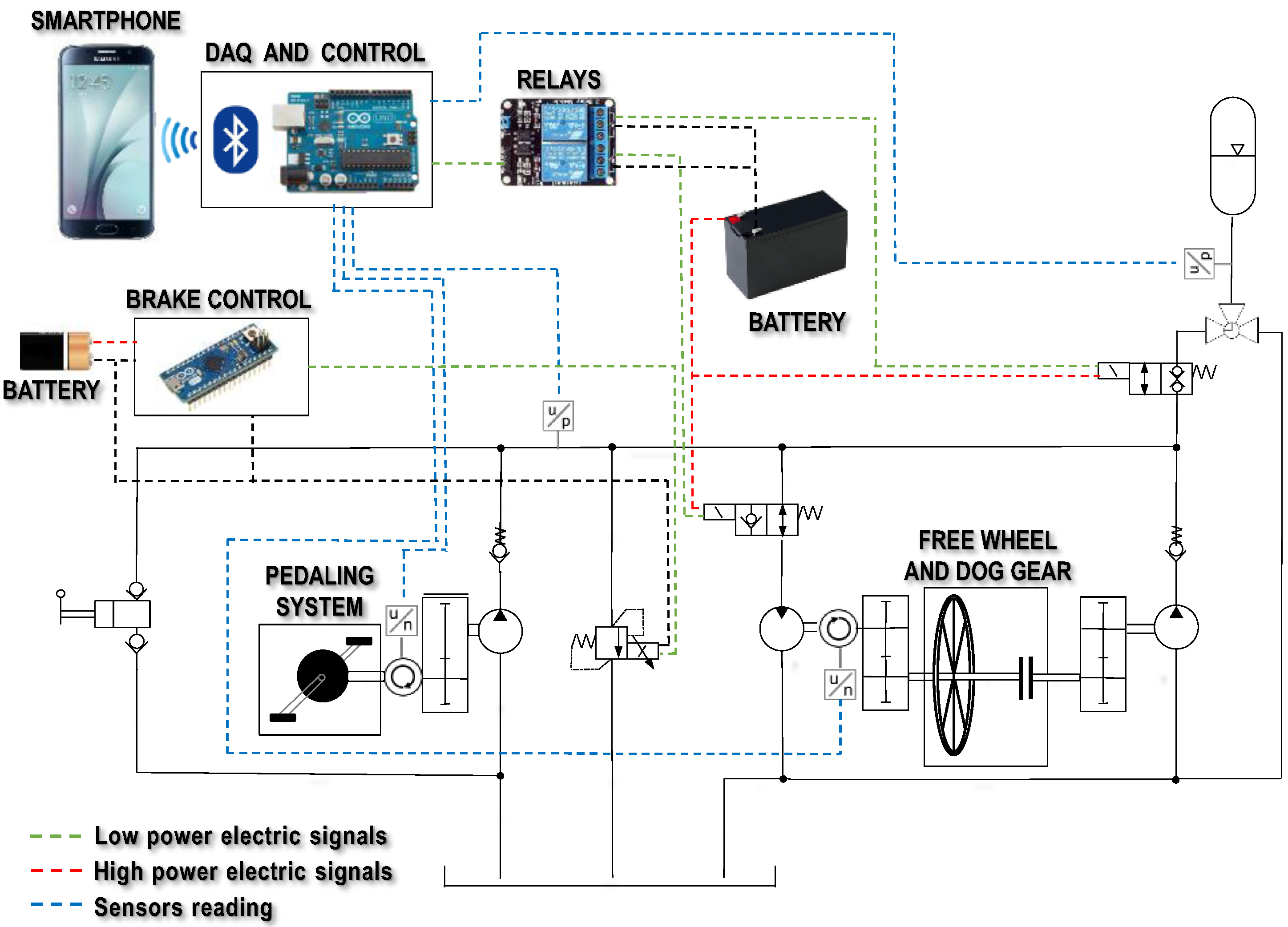
2. System Overview
3. Hydraulic System Design
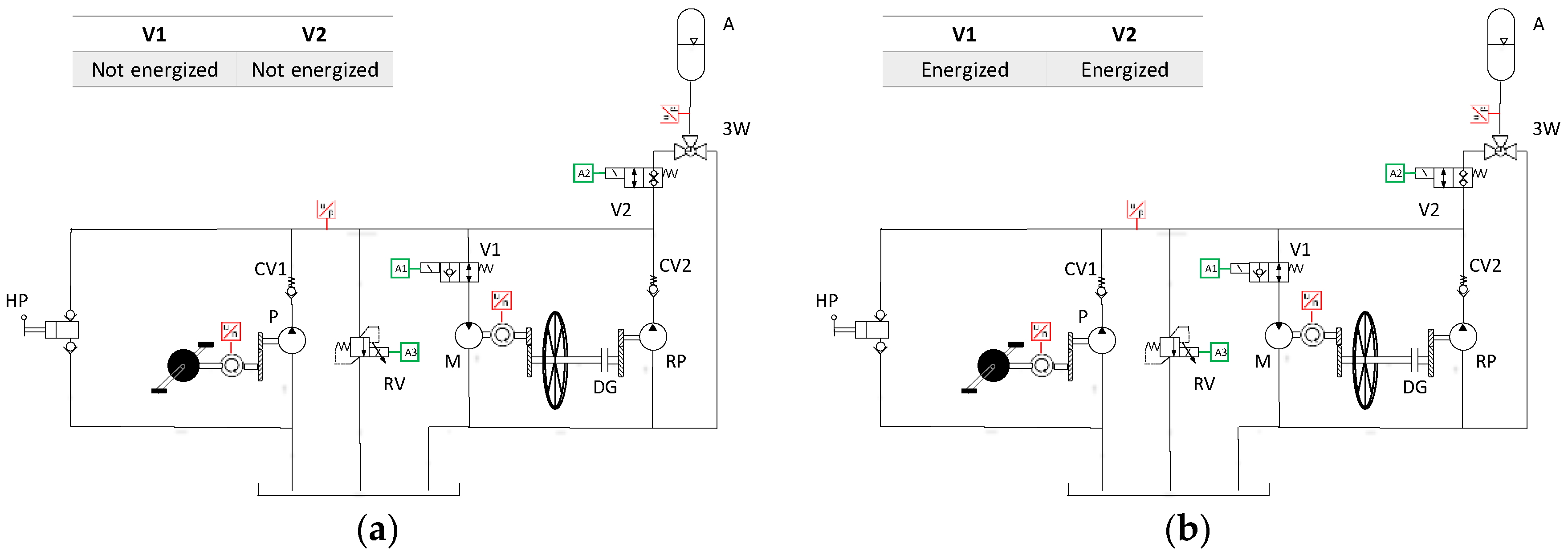
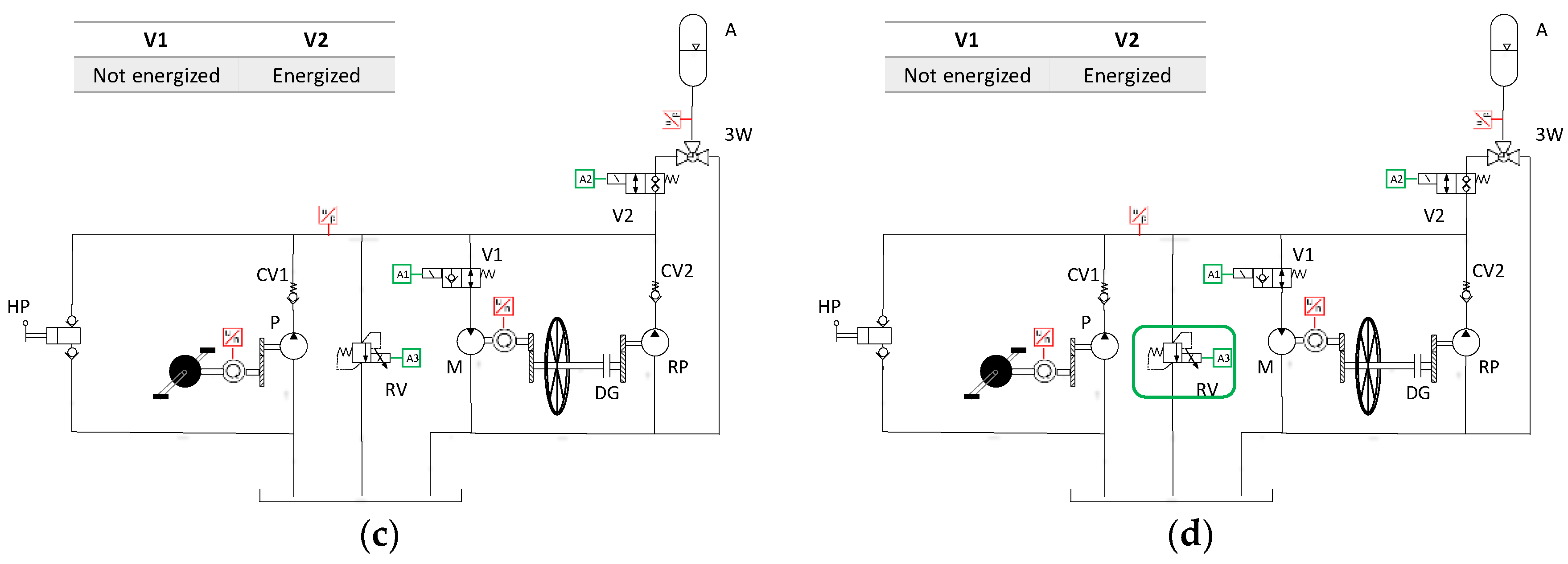
3.1. Hydraulic Hybrid Circuits
- It reduces the number of components (i.e., charge pump circuit). Closed-circuit HTs generally reduce the size of the reservoir. However, for this application, the reservoir size requirement given by the accumulator charge and discharge processes turned out to be more stringent than that related to the flow of the small pump used in the circuit.
- It allows easy implementation of different modes of operation through switching valves, without significant layout complications.
- Limited availability of lightweight material (i.e., aluminum) pumps and motors in the displacement range of interest for this application (<10 cm3/rev, as will be detailed in the Section 3.2).
- The use of an electrically controlled multiple-speed gear hub connected to the rear wheel can permit regulation similar to a secondary controlled HT, but avoids the use of a variable unit at partial displacement, where the energy efficiency can be low.
- An electro-hydraulic system for adjusting the instantaneous displacement of the units would add increased weight and complexity to the system.
- It permitted calculating the motor size independently from the needs of the regeneration circuit. In fact, the size of the hydraulic motor was determined based on the requirements of the Pedaling and Boost modes. A less advantageous size would have resulted if the needs of the Regeneration mode’s function were also considered.
- It permitted us to use a “free wheel” gear hub, like in a traditional bike. A free wheel hub allows for unidirectional transmission of the torque transmitted to the wheels, and allows for vehicle coasting (wheel spinning without involving angular velocity at the gear hub). A single pump/motor solution would have required a bidirectional hub, with the undesired consequence of eliminating the coasting function. In other words, the cyclist would feel the parasitic loss of the hydraulic motor while coasting.
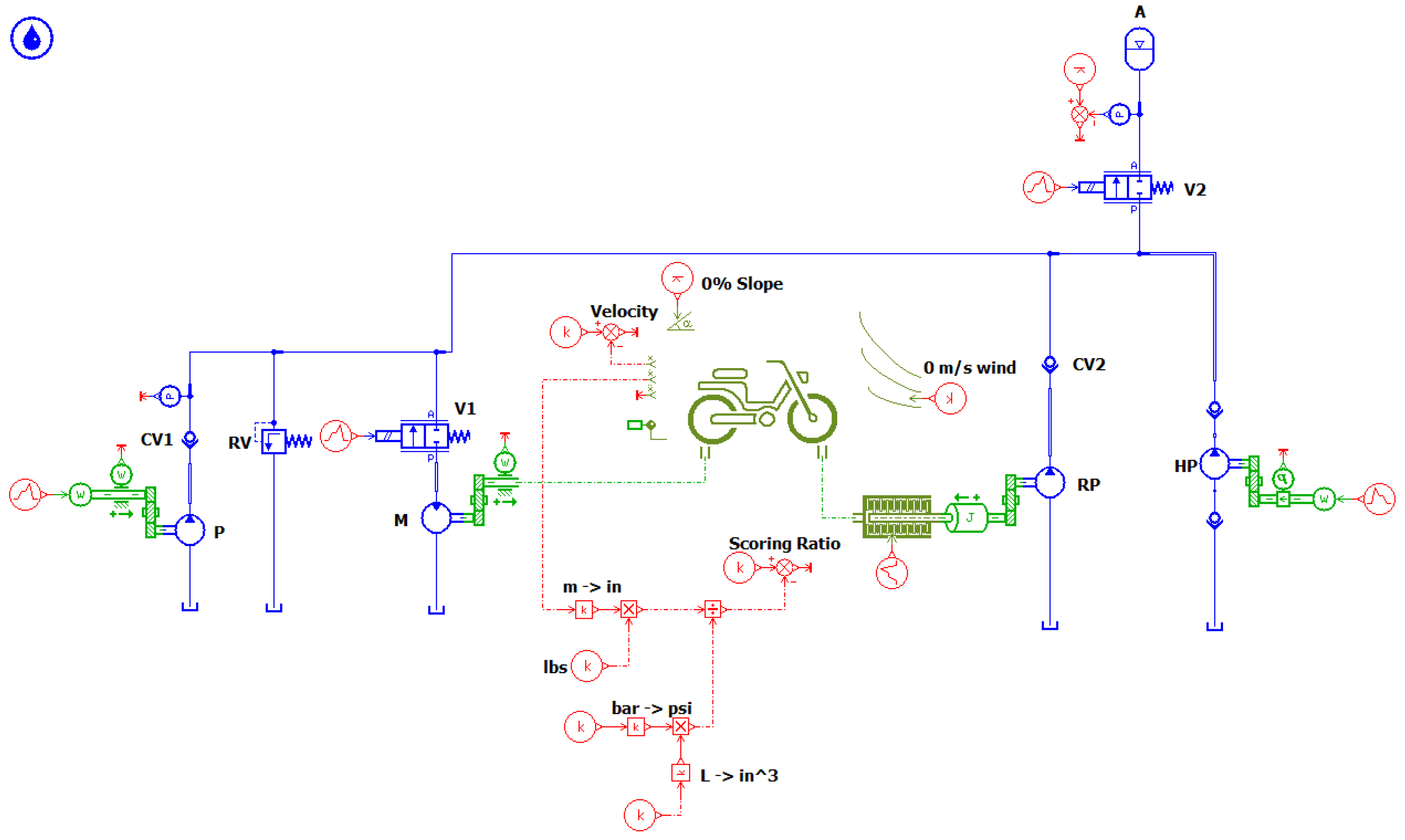
3.2. Simulation and Sizing of the System
3.2.1. Numerical Model of the PurdueTracer
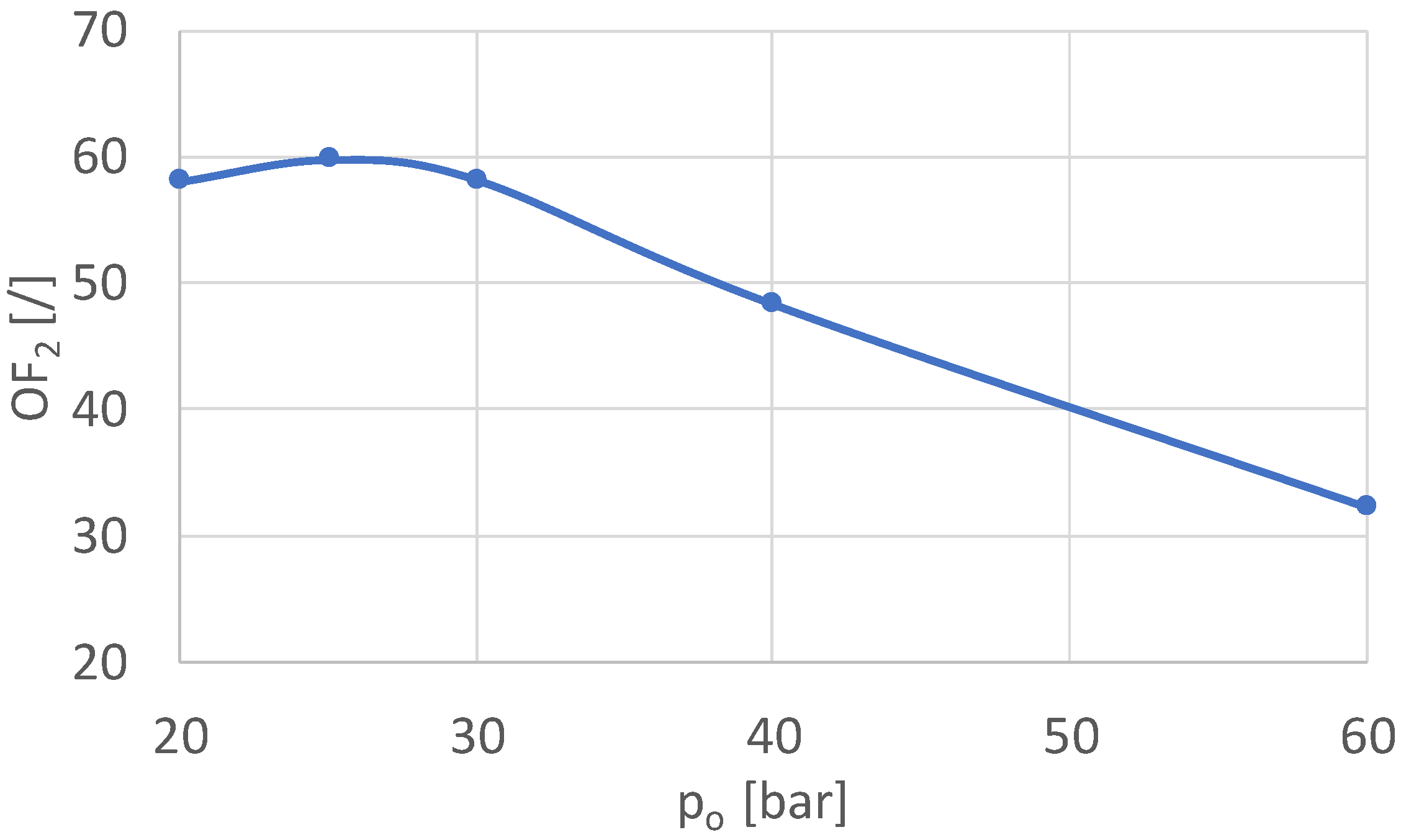
3.2.2. Numerical Optimization
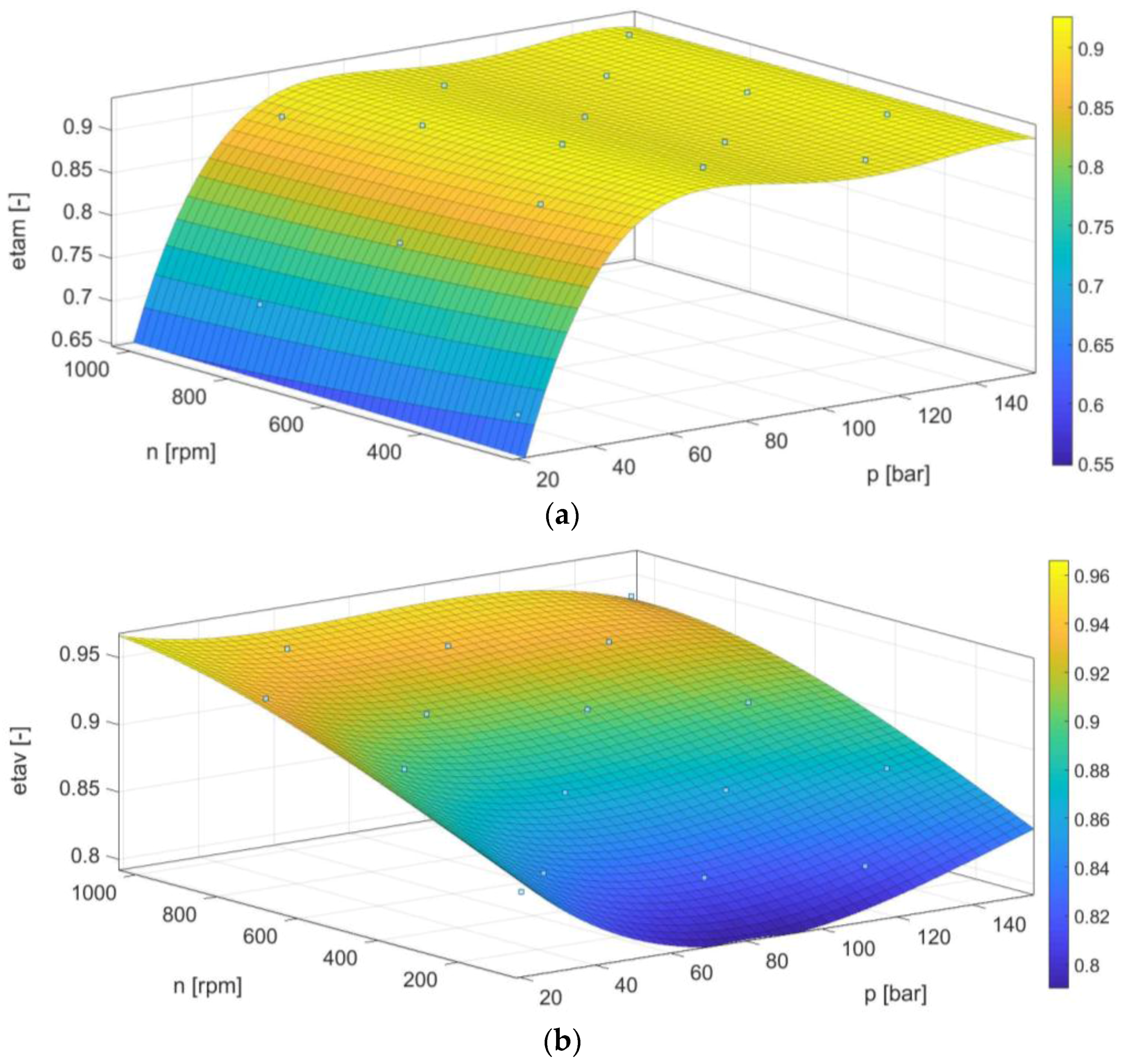
3.2.3. Optimization Results and Predicted Performance
4. Mechanical System Design
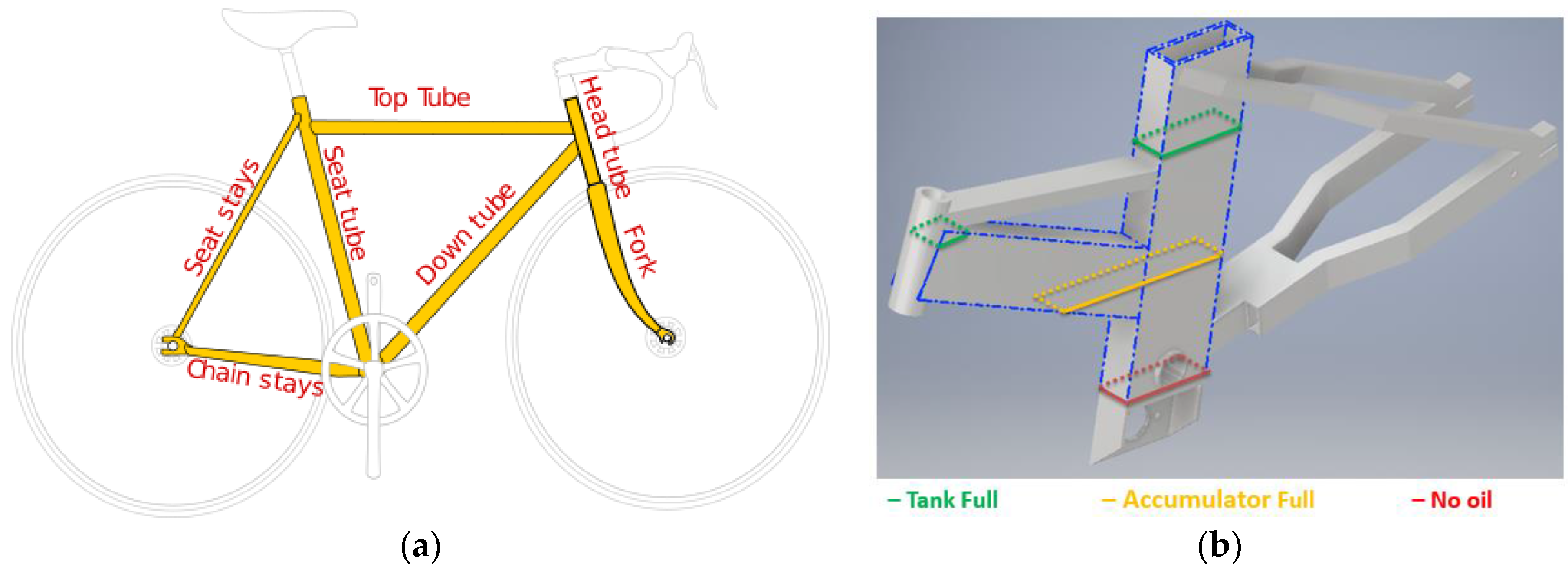
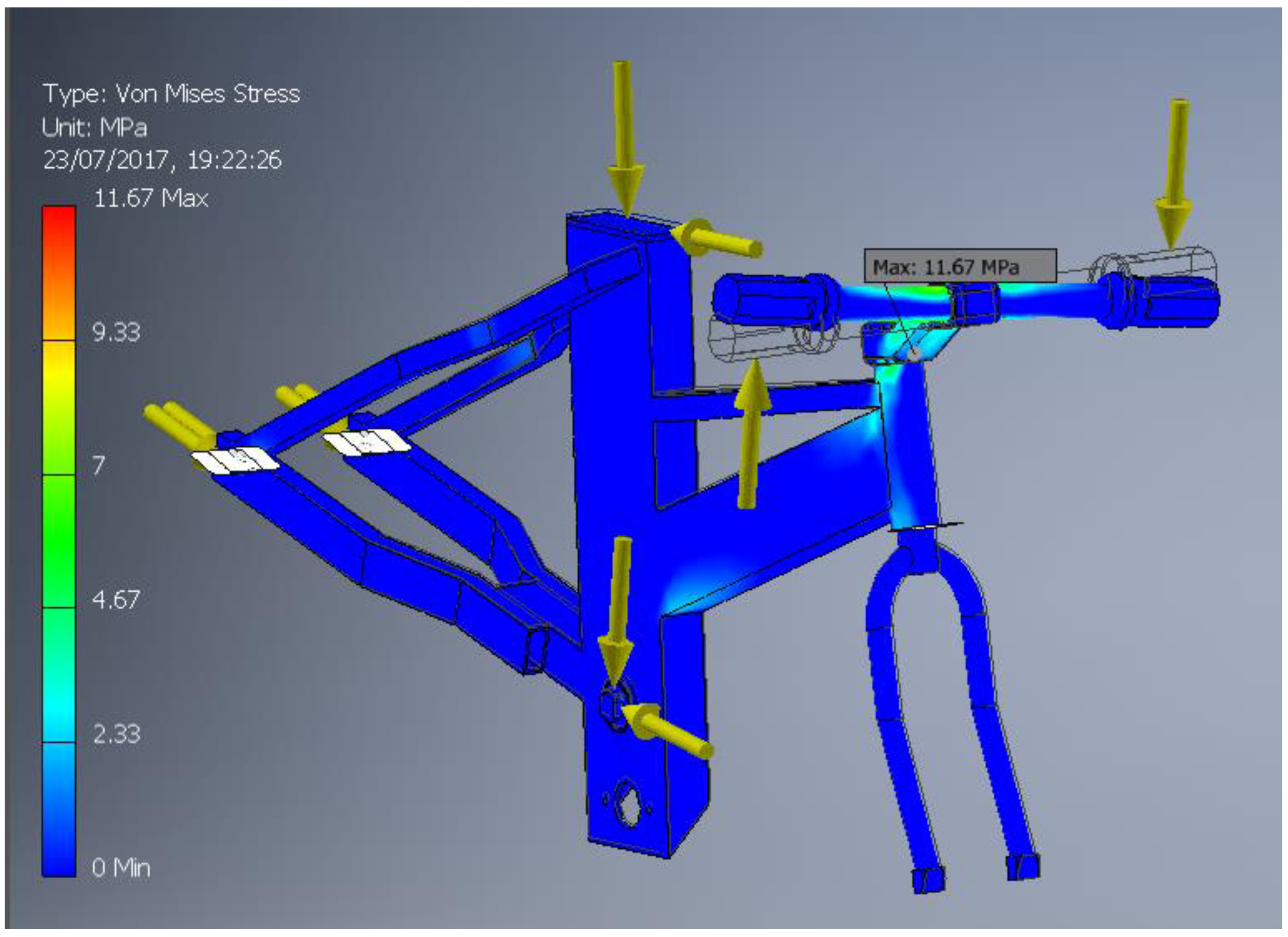
4.1. Frame
- Sitting pedaling, pushing on the right/left pedal: in which the rider is sitting on the saddle and pushing on the right/left pedal in an analysis (depending on the case analyzed);
- Braking: in which the rider is braking with both brakes;
- Road irregularity: in which the loads simulate the road deformity.
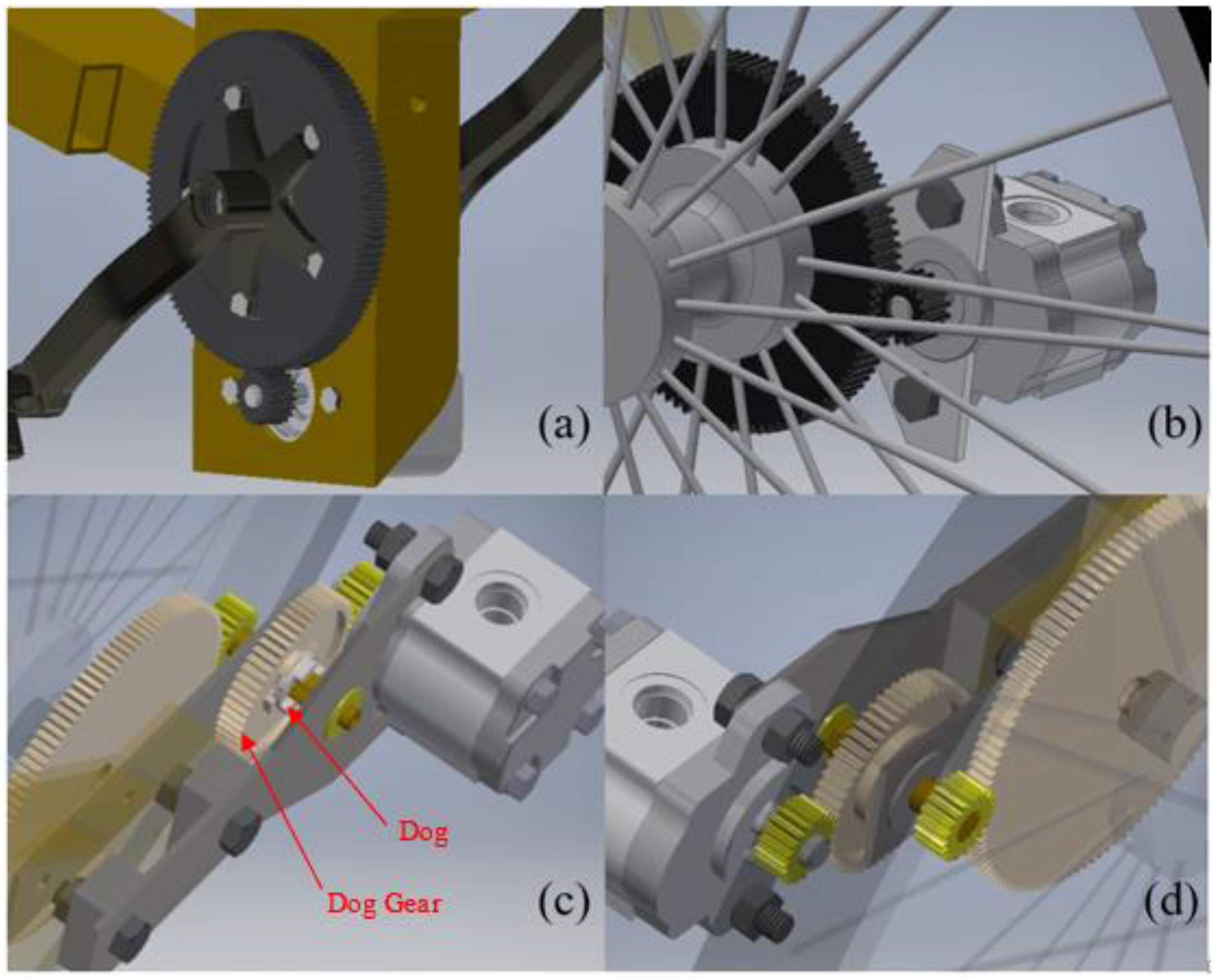
4.2. Gearboxes
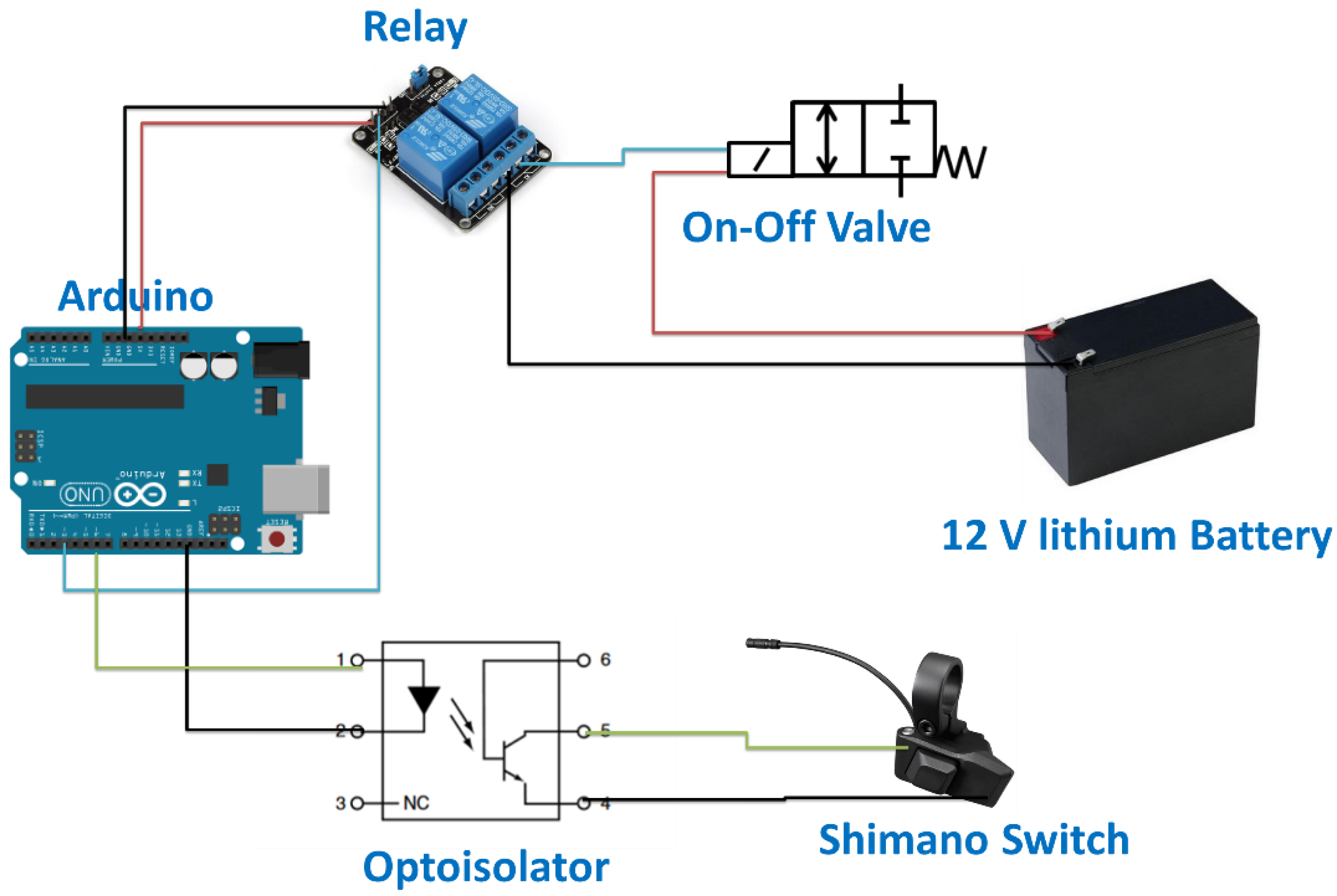
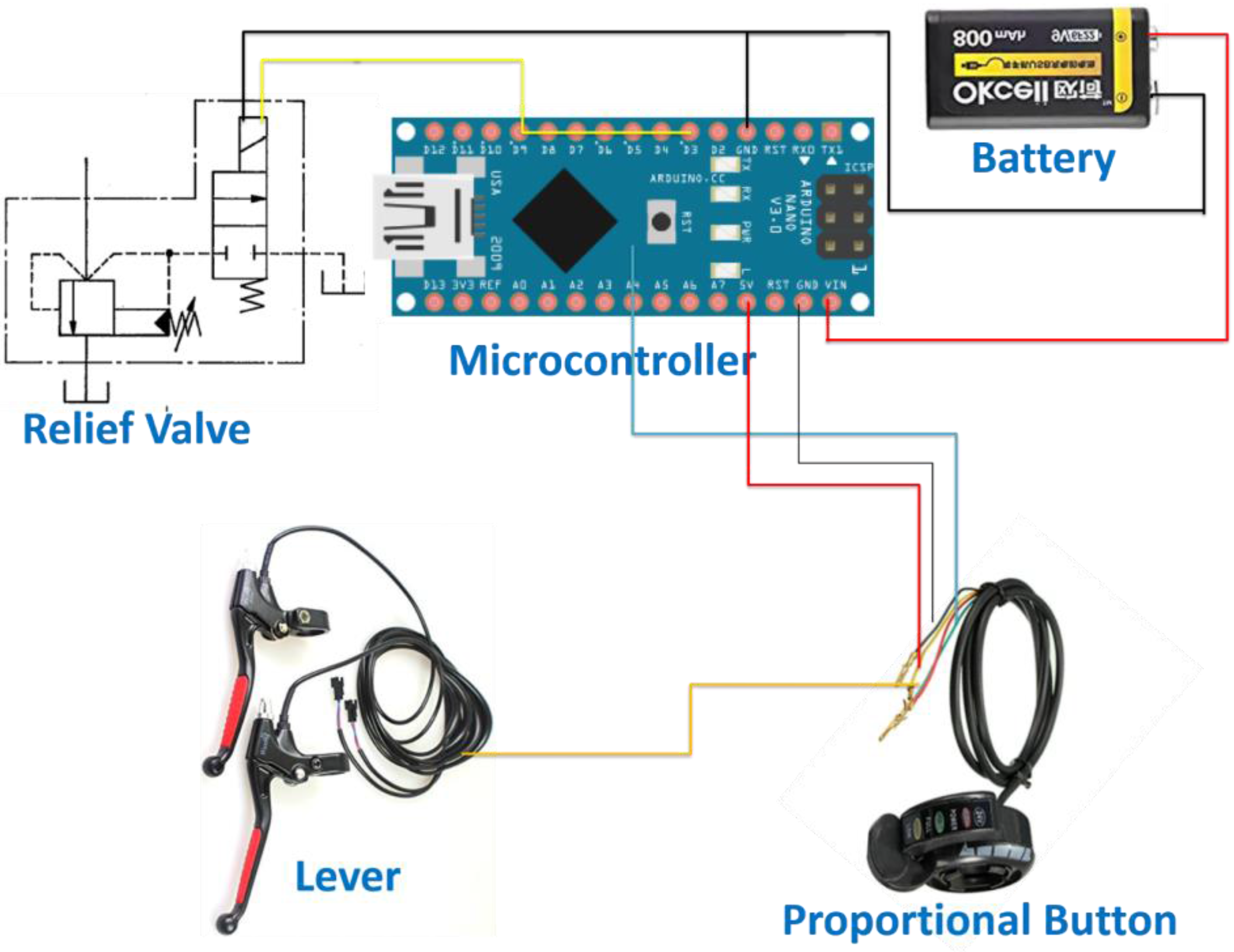
5. Electronic System Design
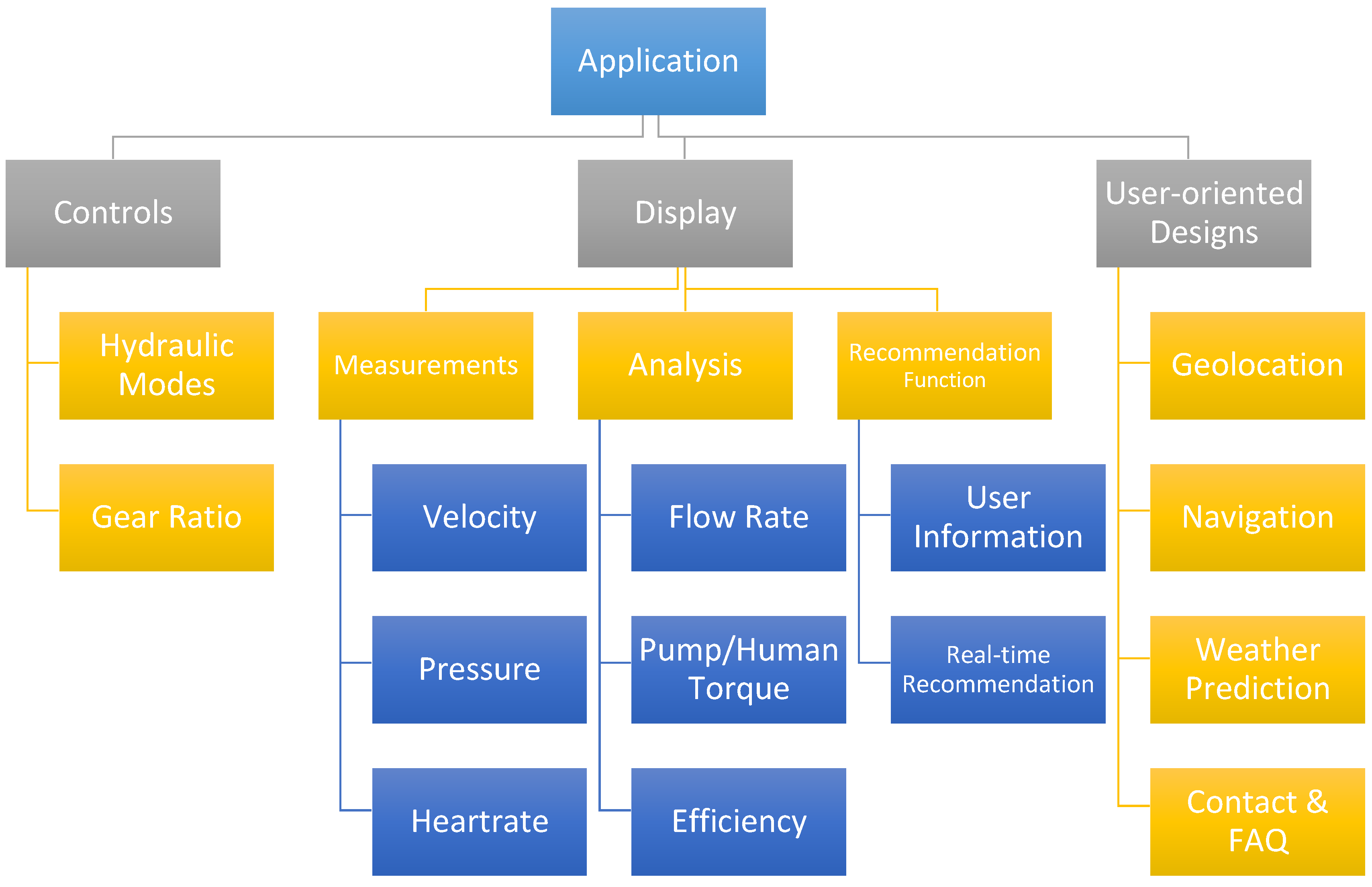
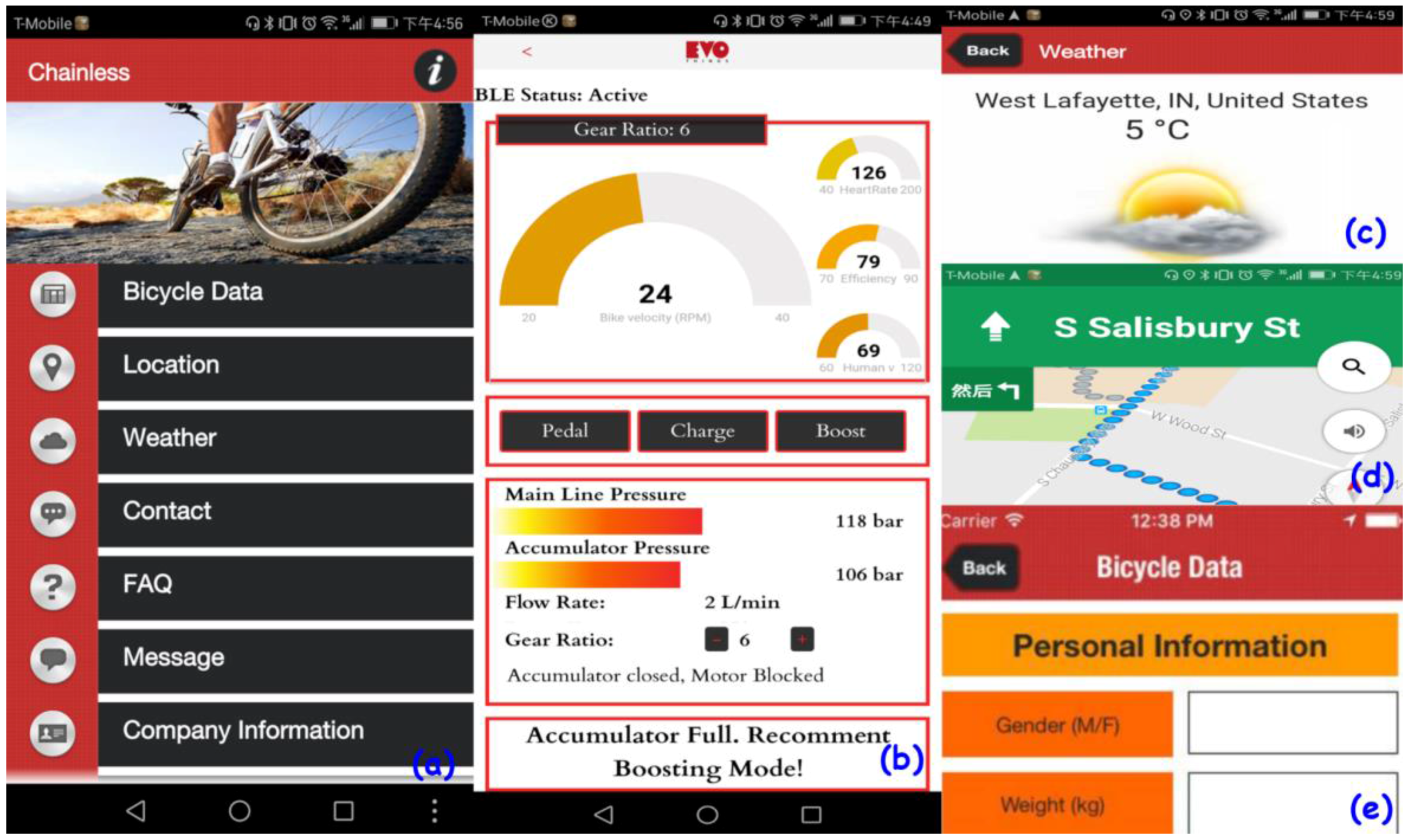
5.1. Software
- The control subsystem for gear and mode change;
- The display subsystem to show directed measured data from sensors, the analysis of bicycle and human performance, and recommendations for healthy riding;
- The user-oriented design to enable comprehensive guidance.
5.2. Data Measurement
5.3. Regeneration Mode Implementation
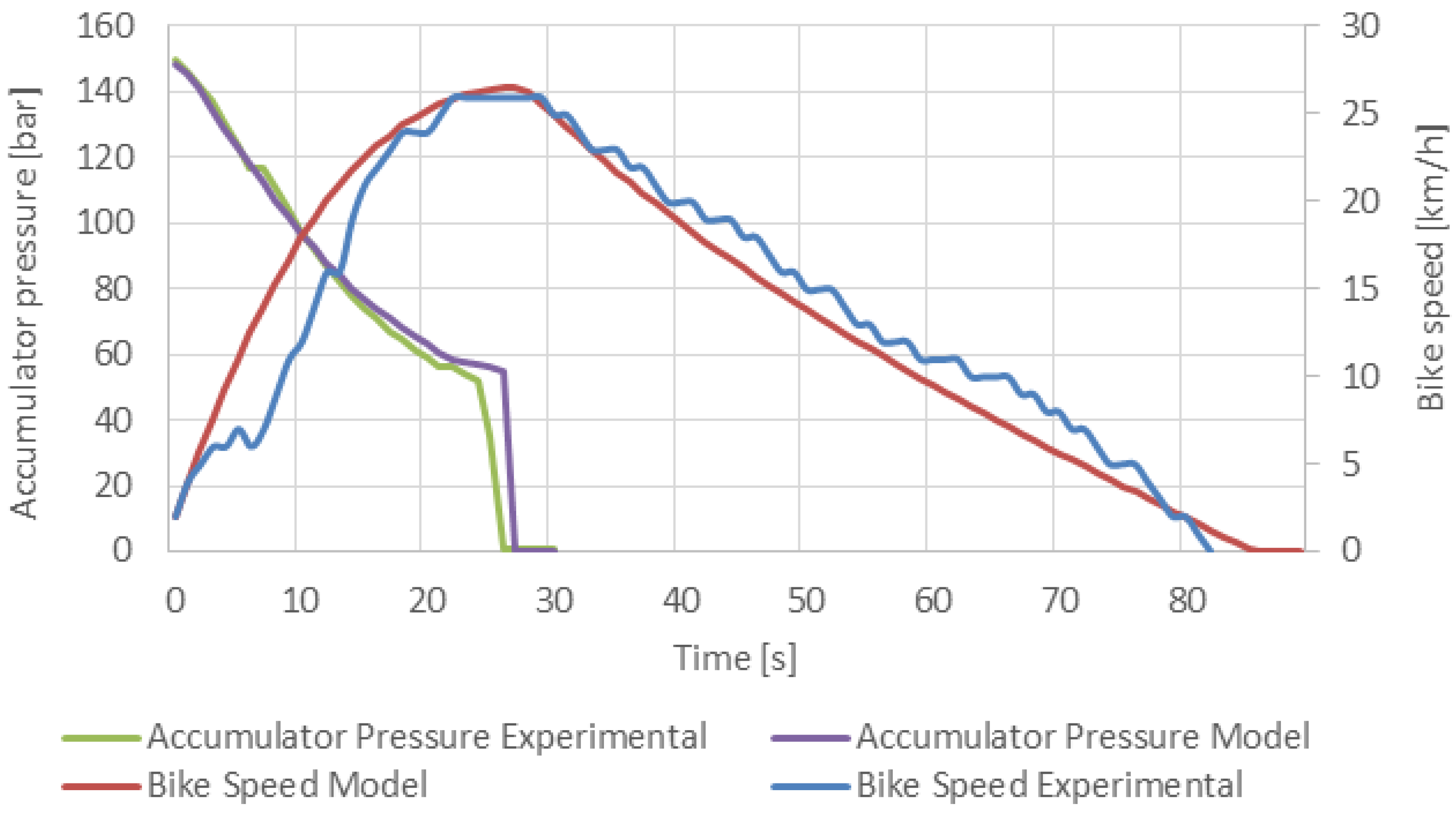
6. Results and Model Validation
6.1. Performance Experiment
6.2. Competition Performance
- Sprint race: demonstrated the ability of the vehicle to move a short distance (about 200 m) quickly.
- Efficiency challenge: demonstrated the ability of the vehicle to effectively store energy and efficiently use the stored energy to propel the unassisted vehicle.
- Endurance challenge: demonstrated the reliability, safety, replicability, and durability of the fluid power system design and assembly.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | user age, year |
| acceleration of the vehicle, | |
| drag coefficient in longitudinal direction | |
| coefficient of viscous friction, N/(m/s) | |
| aerodynamic force, N | |
| friction force, N | |
| slop force, N | |
| propelling force, N | |
| maximal user heart rate, bpm | |
| wheels inertia, kg·m2 | |
| distance traveled by the vehicle, inch | |
| cyclist and vehicle mass, lbs | |
| cyclist mass, kg | |
| vehicle mass, kg | |
| polytrophic exponent (ideal gas) | |
| motor shaft rotational speed, rpm | |
| pump shaft rotational speed, rpm | |
| objective function of the optimization problem | |
| wheel circumference, m | |
| accumulator pre-charge pressure, bar | |
| accumulator pre-charge pressure during the competition, psi | |
| initial accumulator pressure in regeneration mode, bar | |
| nitrogen gas pressure in the accumulator, bar | |
| accumulator max working pressure, bar | |
| measured pressure, bar | |
| accumulator min working pressure, bar | |
| flow needed for fluid motor speed, L/min | |
| pump flow, L/min | |
| gearbox ratio of the motor | |
| gearbox ratio of the motor | |
| wheel radius, m | |
| vehicle active area for air resistance, m2 | |
| torque on the rear wheel, N·m | |
| effective torque on the motor shaft, N·m | |
| effective torque on the pump shaft, N·m | |
| starting velocity in regeneration mode, m/s | |
| accumulator volume, in3 | |
| motor volumetric displacement, cm3/rev | |
| pump volumetric displacement, cm3/rev | |
| nitrogen gas volume in the accumulator, m3 | |
| vehicle velocity measured by electronic system, m/s | |
| voltage signal output of pressure sensors, V | |
| vehicle velocity in pedaling mode, m/s | |
| vehicle velocity, m/s | |
| wind velocity, m/s | |
| pressure difference between motor inlet and outlet, bar | |
| pressure difference between pump inlet and outlet, bar | |
| time interval for velocity measurement, s | |
| road slope, ° | |
| motor hydro-mechanic efficiency | |
| pump hydro-mechanic efficiency | |
| motor volumetric efficiency | |
| pump volumetric efficiency | |
| rolling friction coefficients, | |
| air density, kg/m3 | |
| air density, kg/m3 |
References
- Chen, J.S. Energy efficiency comparison between hydraulic hybrid and hybrid electric vehicles. Energies 2015, 8, 4697–4723. [Google Scholar] [CrossRef]
- Midgley, W.J.; Cebon, D. Comparison of regenerative braking technologies for heavy goods vehicles in urban environments. Proc. Inst. Mech. Eng. Part D J. Autom. Eng. 2012, 226, 957–970. [Google Scholar] [CrossRef]
- Harriger, G.A. Hydraulic Drive System for Bicycles and the Like. U.S. Patent 4,546,990, 15 October 1985. [Google Scholar]
- Schmidt, T.; Wilson, D.G. Human Power: Technical Journal of the IHPVA; IHPVA: San Luis Obispo, CA, USA, 2004; Volume 10, ISSN 0898-6908. [Google Scholar]
- Neptune, R.R.; Kautz, S.A.; Hull, M.L. The effect of pedaling rate on coordination in cycling. J. Biomech. 1997, 30, 1051–1058. [Google Scholar] [CrossRef]
- Chattin, J. Hydraulic Transmission for Bicycles. U.S. Patent 6,032,968, 7 March 2000. [Google Scholar]
- Davey, J.A. Bicycles. U.S. Patent 4,290,621, 22 September 1981. [Google Scholar]
- Brackett, D.C. Hydraulic Bicycle with Conjugate Drive Motors and Variable Stroke Crankshaft. U.S. Patent 5,938,224, 17 August 1999. [Google Scholar]
- Chang, L.; Yao, J.F. The development of the electro-hydraulic driving bicycle. Appl. Mech. Mater. 2013, 373, 2132–2135. [Google Scholar] [CrossRef]
- Yang, Y.H.; Zhong, X.Q. Design of Hydraulic Transmission Bicycle based on Top-down Method. Adv. Mater. Res. 2012, 468, 867–870. [Google Scholar] [CrossRef]
- Amarantos, J.G. Hydraulic Powered Bicycle. U.S. Patent 4,087,105, 2 May 1978. [Google Scholar]
- Swain, D.M.; Moore, J.Z.; Maurer, F.C.; Shih, A. Hydraulic Regenerative Braking for a Vehicle. U.S. Patent 7,992,948, 2 May 1978. [Google Scholar]
- Lagwankar, K.D. Hydraulic regenerative system for bicycle. Int. J. Eng. Res. Appl. 2013, 3, 869–875. [Google Scholar]
- Truong, D.Q.; Ahn, K.K.; Khoa, L.D.; Thinh, D.H. Development of a Smart Bicycle Based on a Hydrostatic Automatic Transmission. J. Adv. Mech. Des. Syst. Manuf. 2012, 6, 236–251. [Google Scholar] [CrossRef]
- Wang, F.; Bissen, M.; Ward, W.; Stelson, K. Modeling and design of a hybrid bicycle with hydraulic transmission. Int. J. Fluid Power Syst. 2014, 8, 99–106. [Google Scholar] [CrossRef]
- Foa, M.; Vacca, A.; Senatore, A. HYDROKART: A Human Powered Vehicle a Trasmissione Idrostatica; Oleodinamica e Pneumatica: Milan, Italy, 2017; ISSN 2421-4388. (In Italian) [Google Scholar]
- National Fluid Power Association. Fluid Power Vehicle Challenge, Rules and Awards. Available online: http://nfpahub.com/fpc/vehicle-challenge/rules-and-awards-fpvc/ (accessed on 14 October 2017).
- Wilson, D.G.; Papadopoulos, J. Bicycling Science, 3rd ed.; MIT Press: Cambridge, MA, USA, 2004; ISBN 9780262232371. [Google Scholar]
- Navarro, K.F.; Gay, V.; Golliard, L.; Johnston, B.; Leijdekkers, P.; Vaughan, E.; Wang, X.; Williams, M.A. Social Cycle: What can a mobile app do to encourage cycling. In Proceedings of the 38th Annual IEEE Conference on Local Computer Networks—Workshops, Sydney, Australia, 21–24 October 2013; pp. 24–30. [Google Scholar]
- Burke, E.R. High-Tech Cycling, 2nd ed.; Human Kinetics: Champion, IL, USA, 2002; ISBN 0-7360-4507-4. [Google Scholar]
- Maestrelli, L.; Falsini, A. Bicycle optimization by means of an advanced gradient method algorithm. In Proceedings of the 2nd European HyperWorks Technology Conference, Strasbourg, France, 30 September–1 October 2008. [Google Scholar]
- Tanaka, H.; Monahan, K.D.; Seals, D.R. Age-predicted maxima heart rate revisited. J. Am. Coll. Cariol. 2001, 37, 153–156. [Google Scholar] [CrossRef]



| Best Design | Selected Components | ||
|---|---|---|---|
| Component | Size | Company | Size |
| Pump displacement | 4.52 cc/rev | CASAPPA | 4.27 cc/rev |
| Motor displacement | 2.13 cc/rev | CASAPPA | 2.13 cc/rev |
| Accumulator volume | 2.00 L | STEELHEAD COMPOSITES | 2.00 L |
| Front gear ratio | 1/5.68 | MISUMI | 1/6.32 |
| Rear gear ratio | 4.00 | MISUMI | 4.00 |
| Regeneration gear ratio | 17.82 | ANDYMARK | 16.80 |
| Regeneration pump displacement | 4.23 cc/rev | CASAPPA | 4.27 cc/rev |
| Accumulator pre-charge gas pressure | 25 bar | - | 25 bar |
| Performances Performances in Pedaling Mode | ||
| Best Design from Optimization | Selected Components | |
| Power | 183 W | 223 W |
| Torque IN (Human) | 25 N·m | 30 N·m |
| Pump shaft | 435 rpm | 442 rpm |
| Bike speed | 5.10 m/s | 5.87 m/s |
| Main line pressure | 45.93 bar | 64.59 bar |
| Mainline flow rate | 1.81 L/min | 1.64 L/min |
| Pump volumetric efficiency | 88.91% | 86.36% |
| Pump mechanical efficiency | 86.76% | 90.85% |
| Motor volumetric efficiency | 94.62% | 90.81% |
| Motor mechanical efficiency | 85.55% | 90.43% |
| Hydraulic transmission efficiency | 62.44% | 64.44% |
| Performances in Boost Mode | ||
| Best Design from Optimization | Selected Components | |
| Max speed | 5.21 m/s | 4.86 m/s |
| Efficiency function (OF2) | 51.1232 | 50.5471 |
| Distance covered | 221 m | 214 m |
| First Stage | Second Stage | Total Ratio |
|---|---|---|
| 6:1 (120/20) | 2.8:1 (56/20) | 16.8: 1 |
| Measured Performance in Pedaling Mode * | |
| Bike speed | 10.0 m/s |
| Main line pressure | 101 bar |
| Measured Performance in Boost Mode | |
| Max speed | 7.22 m/s |
| Efficiency function (OF2) | 59.74 |
| Distance covered | 240 m |
| Podium Placement | |
|---|---|
| Overall Champion | 1st Place |
| Efficiency Challenge | 1st Place |
| Best Design | 1st Place |
| Reliability and Safety | 1st Place |
| Best Paper/Presentation | 2nd Place |
| Reliability/Durability Challenge | 2nd Place |
| Sprint Race | 3rd Place |
| Workmanship | 3rd Place |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marinaro, G.; Xu, Z.; Chen, Z.; Li, C.; Mao, Y.; Vacca, A. The PurdueTracer: An Energy-Efficient Human-Powered Hydraulic Bicycle with Flexible Operation and Software Aids. Energies 2018, 11, 305. https://doi.org/10.3390/en11020305
Marinaro G, Xu Z, Chen Z, Li C, Mao Y, Vacca A. The PurdueTracer: An Energy-Efficient Human-Powered Hydraulic Bicycle with Flexible Operation and Software Aids. Energies. 2018; 11(2):305. https://doi.org/10.3390/en11020305
Chicago/Turabian StyleMarinaro, Gianluca, Zhuangying Xu, Zhengpu Chen, Chenxi Li, Yizhou Mao, and Andrea Vacca. 2018. "The PurdueTracer: An Energy-Efficient Human-Powered Hydraulic Bicycle with Flexible Operation and Software Aids" Energies 11, no. 2: 305. https://doi.org/10.3390/en11020305
APA StyleMarinaro, G., Xu, Z., Chen, Z., Li, C., Mao, Y., & Vacca, A. (2018). The PurdueTracer: An Energy-Efficient Human-Powered Hydraulic Bicycle with Flexible Operation and Software Aids. Energies, 11(2), 305. https://doi.org/10.3390/en11020305






