Design Considerations for Parallel Differential Power Processing Converters in a Photovoltaic-Powered Wearable Application
Abstract
:1. Introduction
2. Design and Methodology
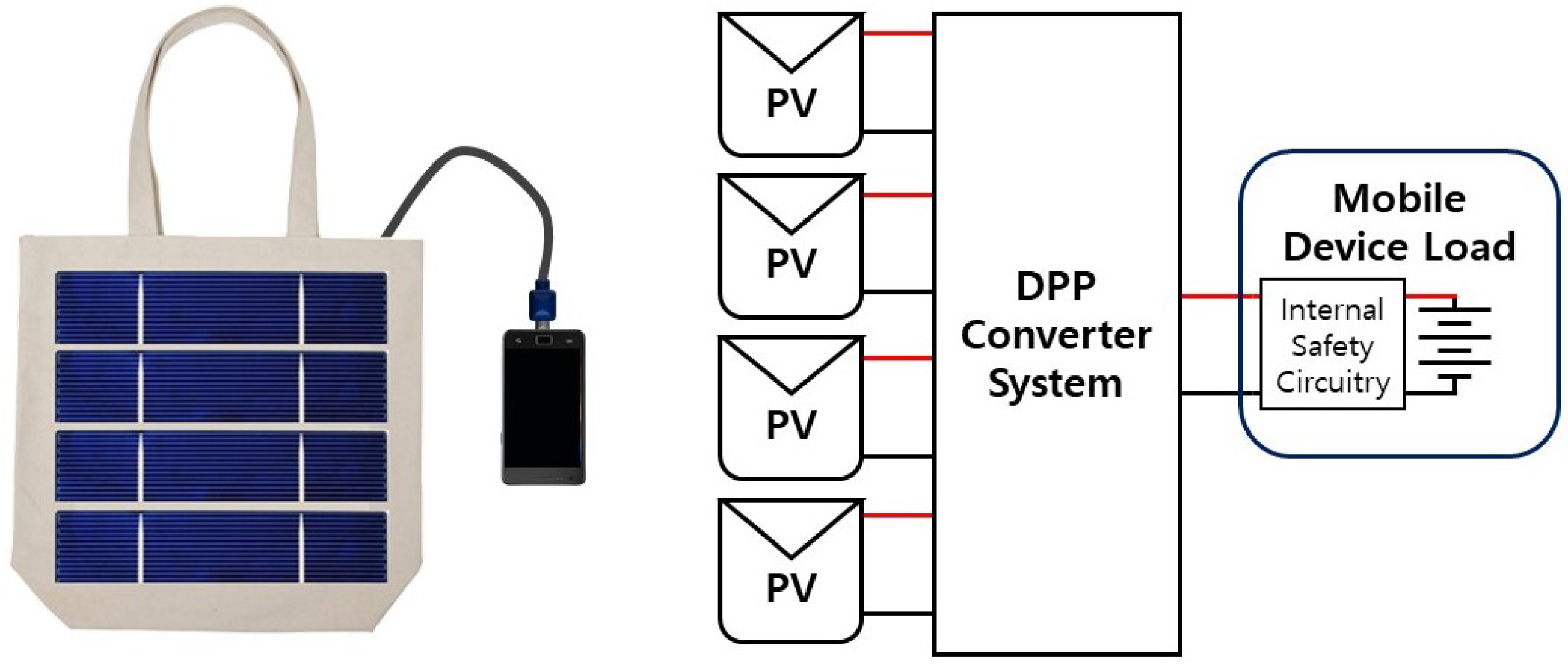
2.1. PV-Powered Bag Application
2.2. Parallel DPP System Analysis
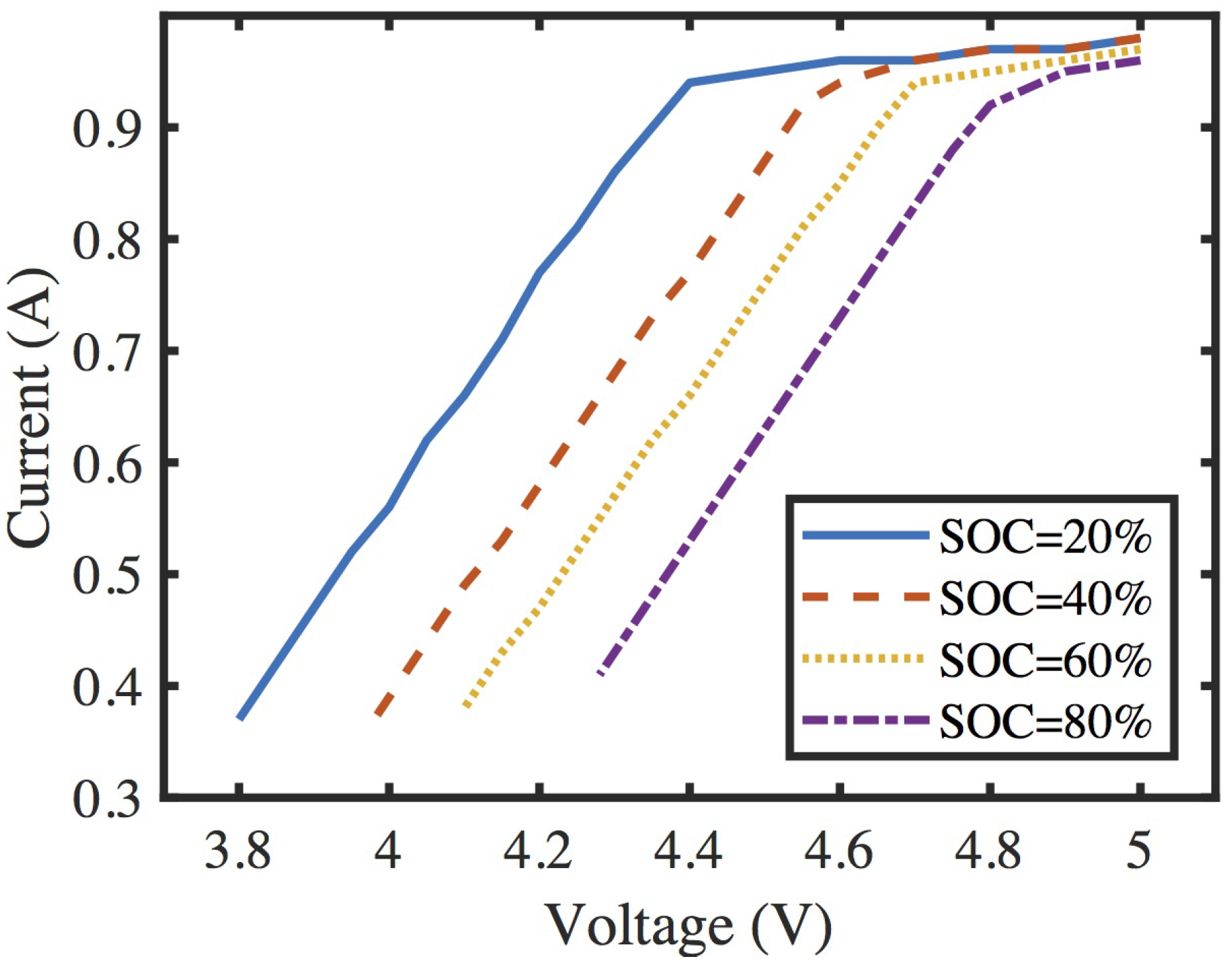
2.3. Battery Impedance
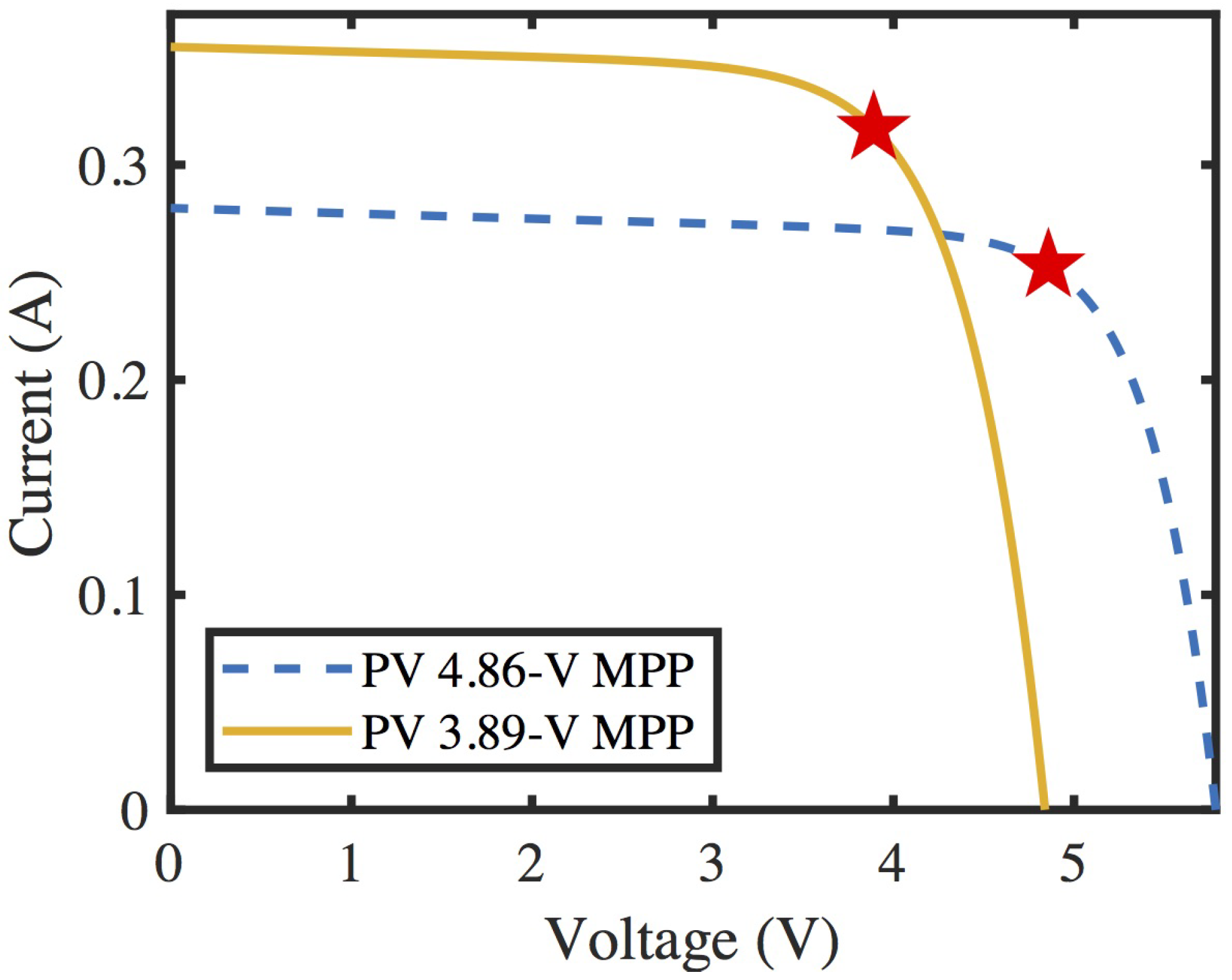
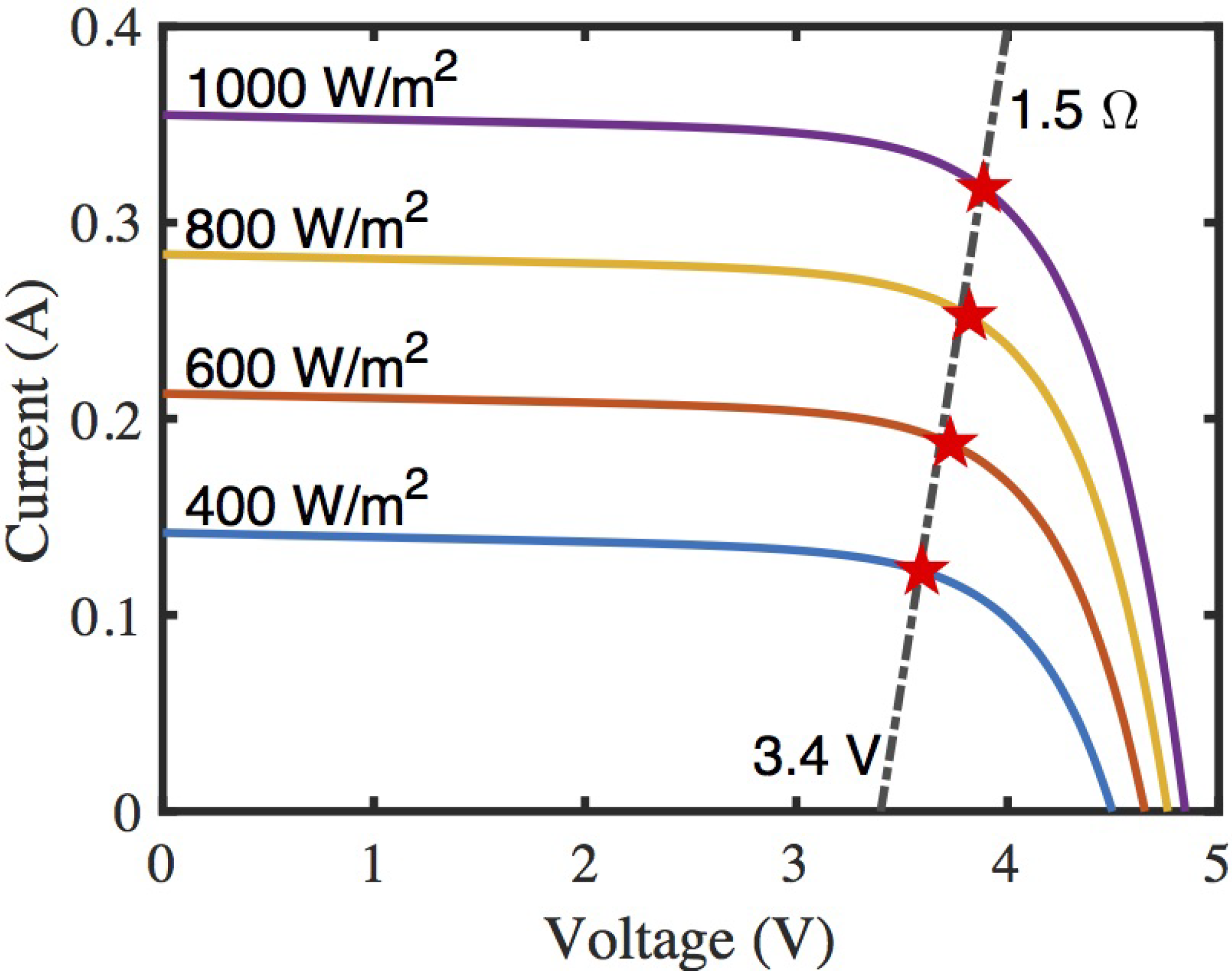
2.4. PV Module Selection
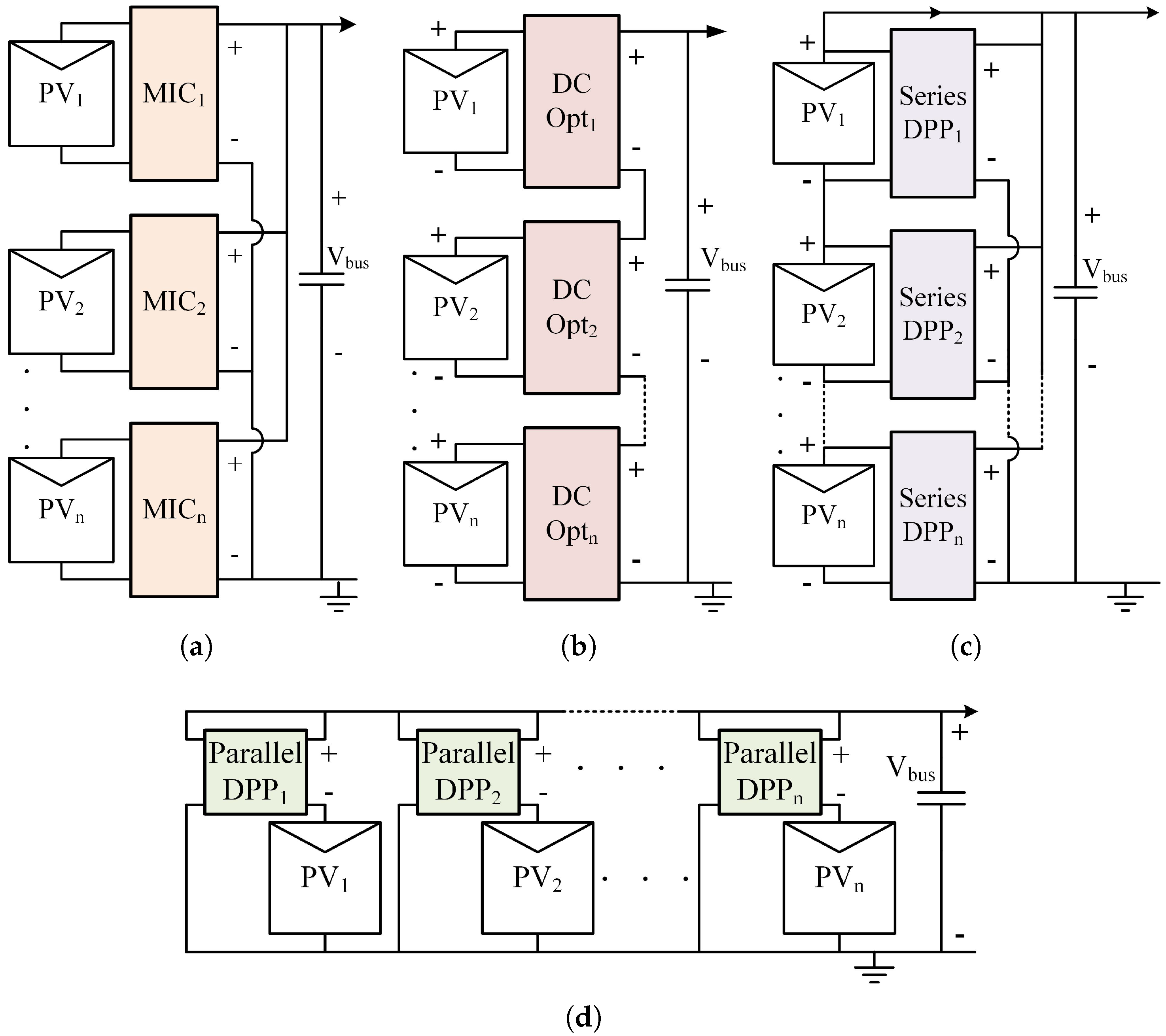
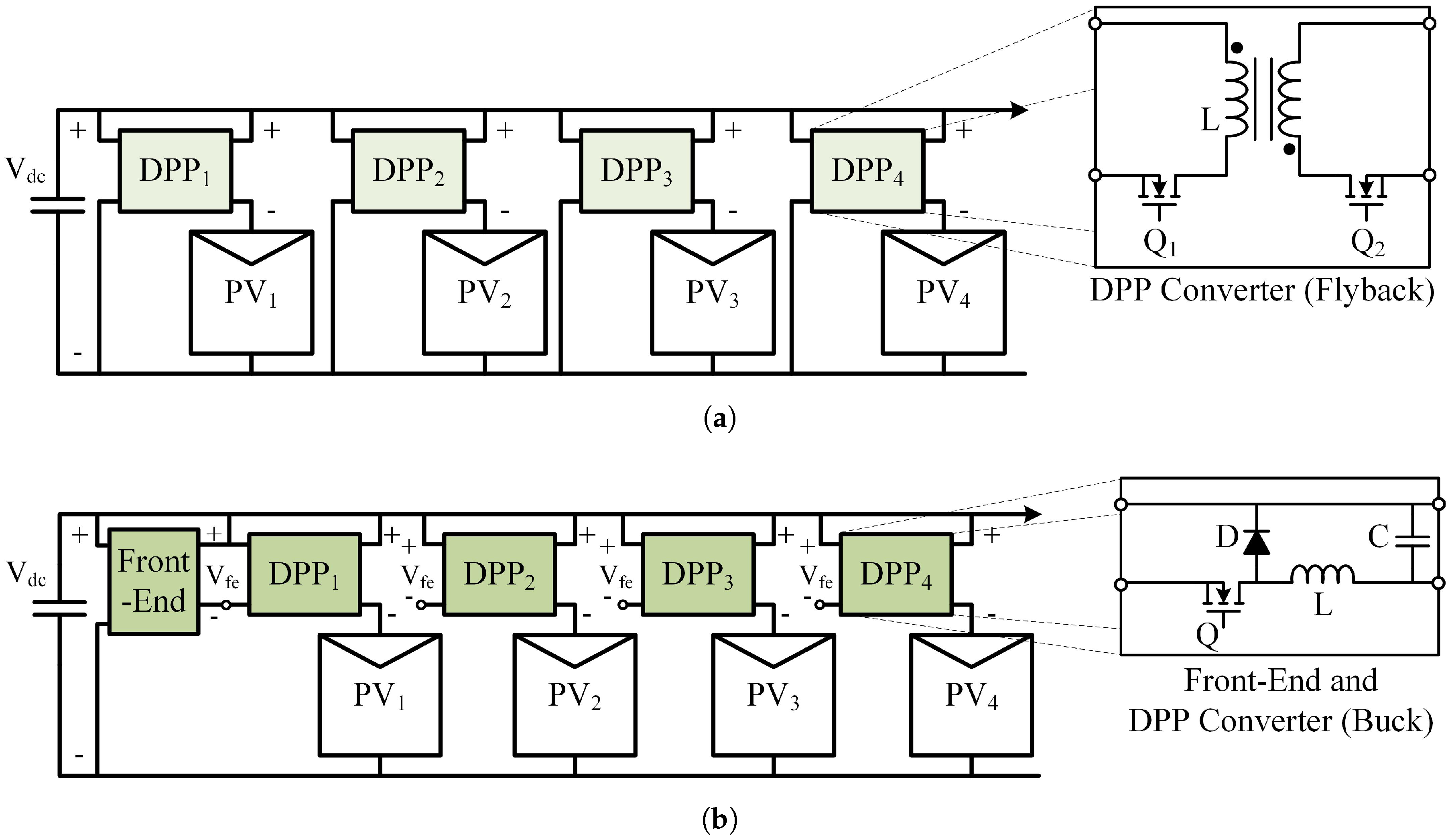
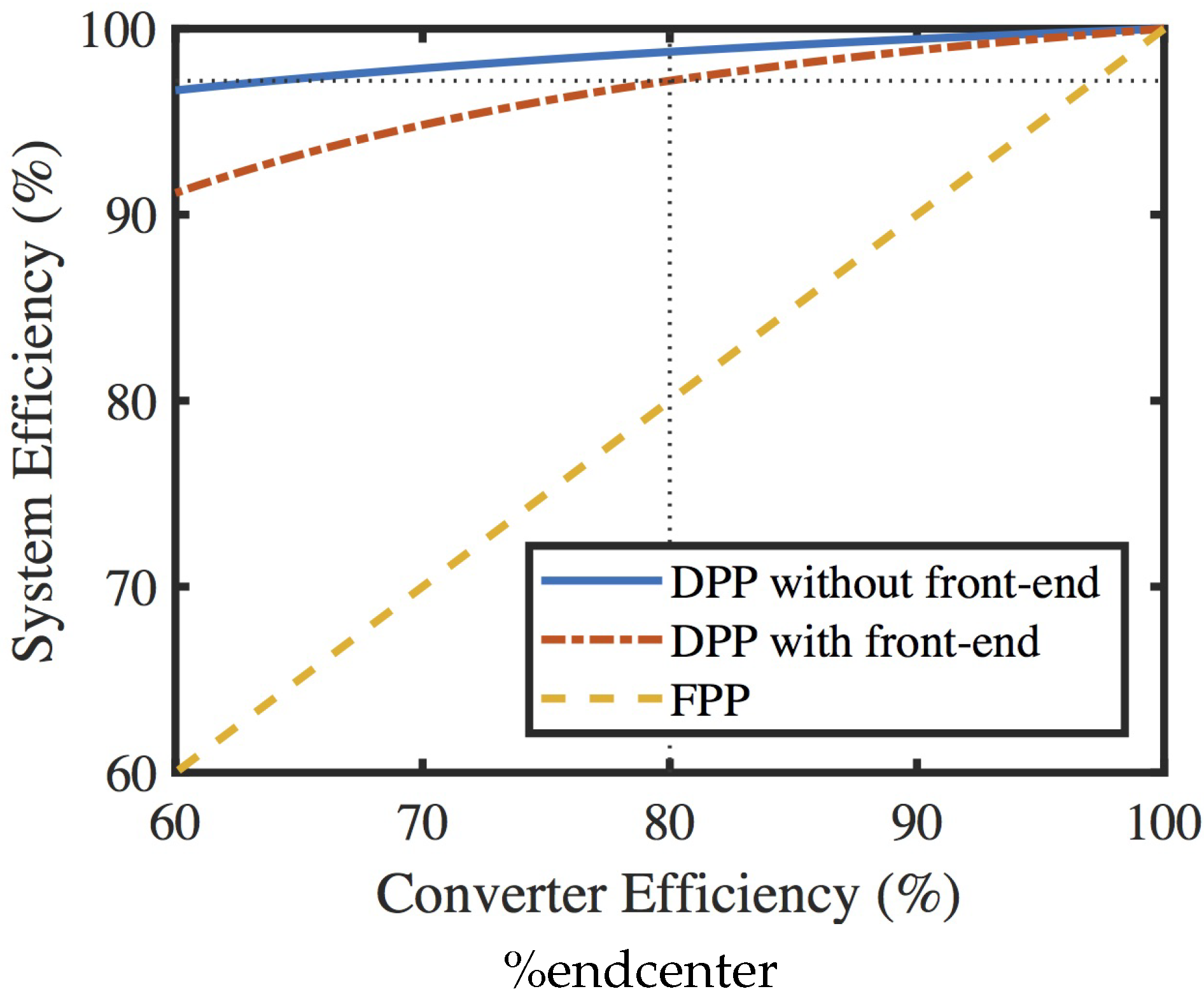
2.5. Parallel DPP Configuration Considerations
2.6. Maximum Power Point Tracking Control
3. Results and Discussion
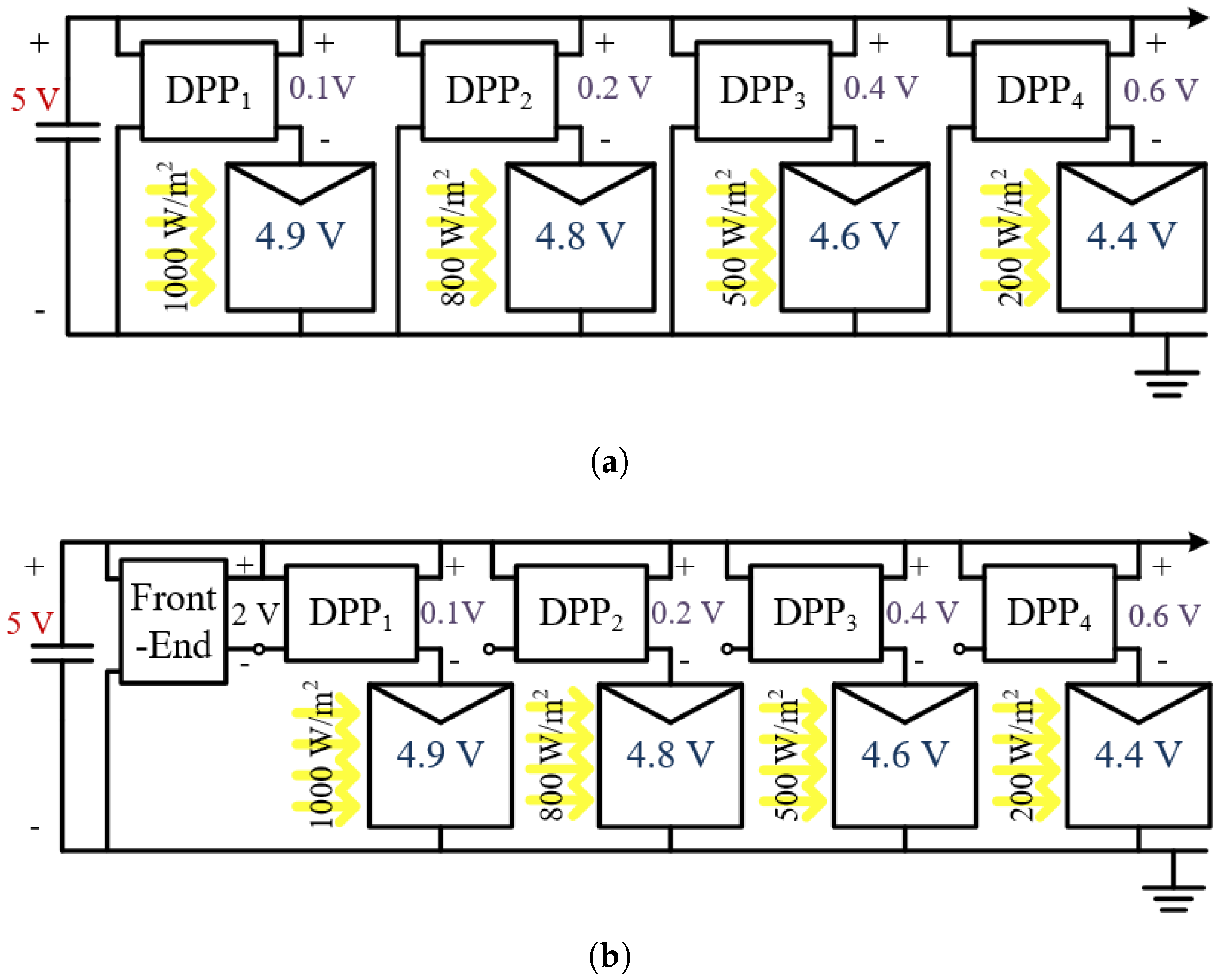
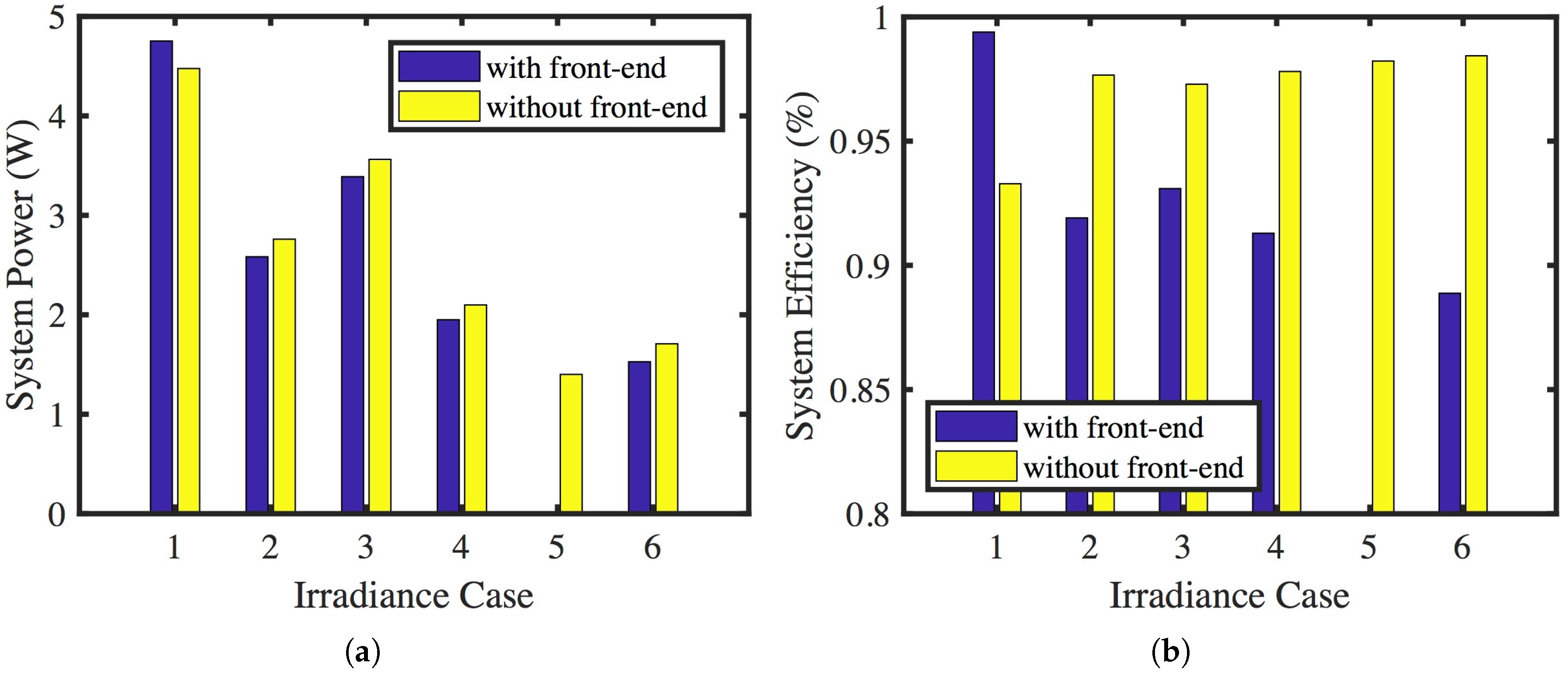
3.1. Parallel DPP Configuration Comparison
3.2. Simulation Setup
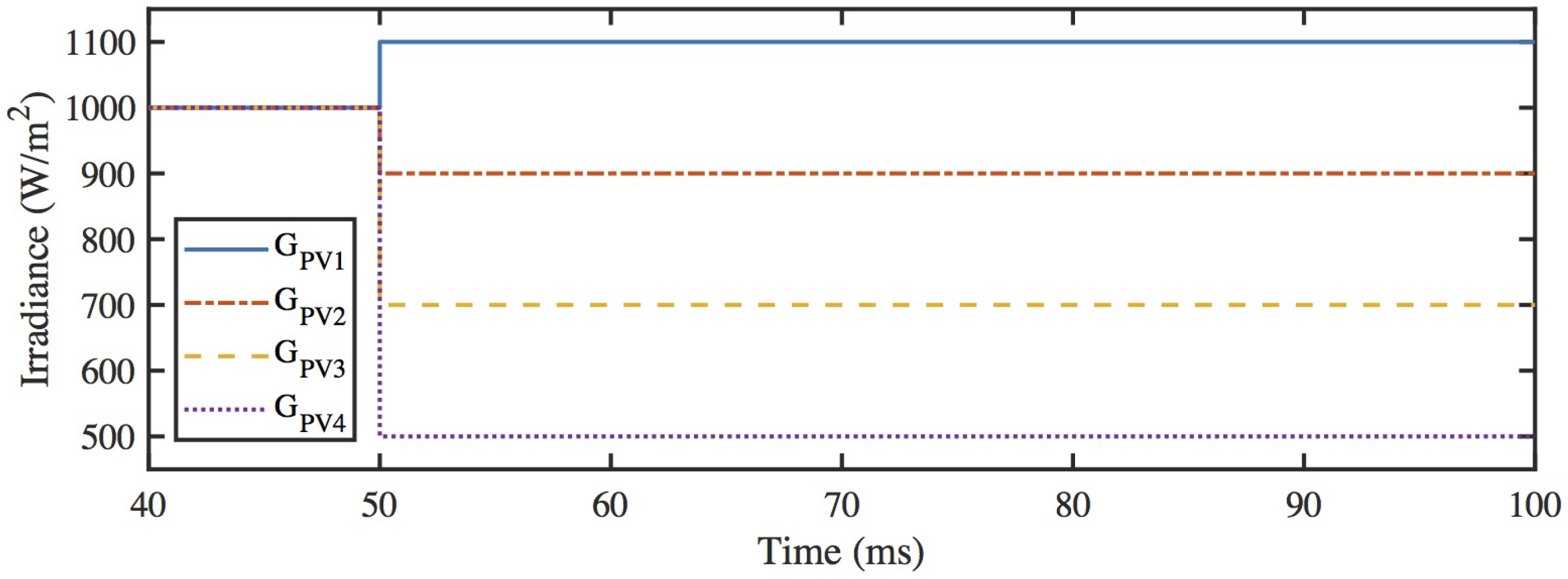
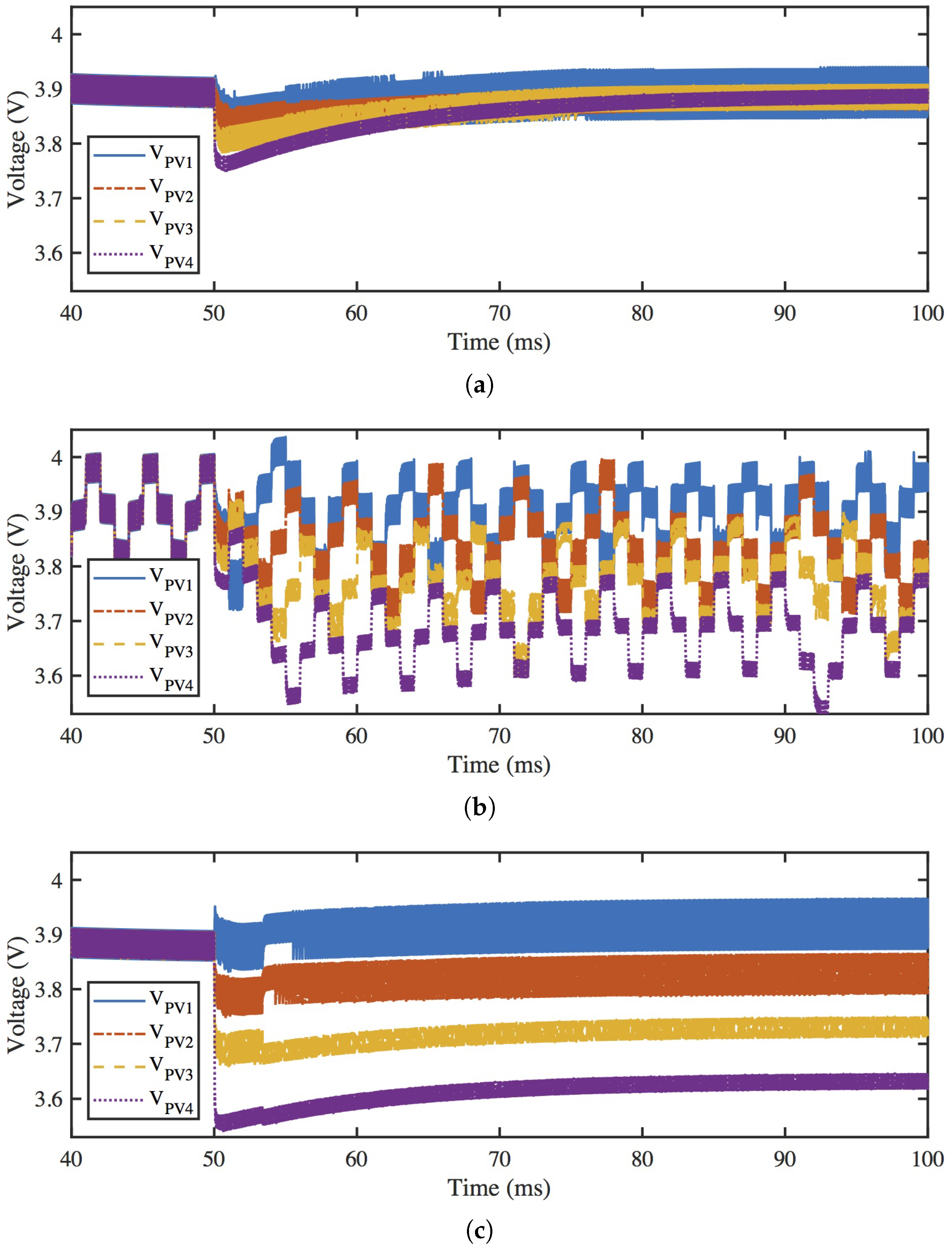
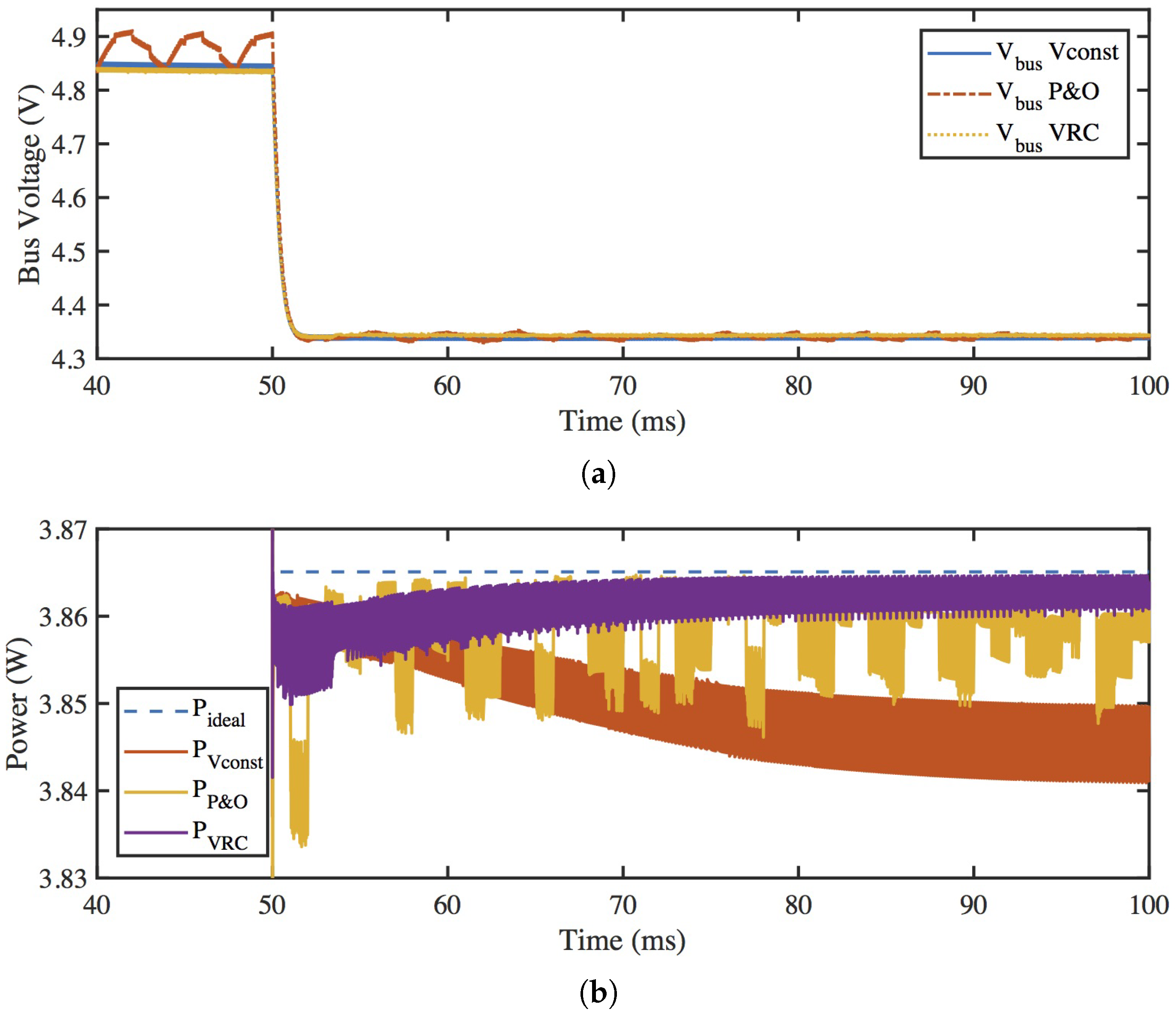
3.3. Simulation Results for MPPT Algorithm Comparison
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PV | photovoltaic |
| DPP | differential power processing |
| MPPT | maximum power point tracking |
| MPP | maximum power point |
| MIC | module-integrated converter |
| FPP | full power processing |
| P&O | perturb and observe |
| VRC | voltage-offset resistive control |
References
- Zsiborács, H.; Hegedűsné Baranyai, N.; Vincze, A.; Háber, I.; Pintér, G. Economic and Technical Aspects of Flexible Storage Photovoltaic Systems in Europe. Energies 2018, 11, 1445. [Google Scholar] [CrossRef]
- Pintér, G.; Baranyai, N.H.; Wiliams, A.; Zsiborács, H. Study of Photovoltaics and LED Energy Efficiency: Case Study in Hungary. Energies 2018, 11, 790. [Google Scholar] [CrossRef]
- Mardonova, M.; Choi, Y. Review of Wearable Device Technology and Its Applications to the Mining Industry. Energies 2018, 11, 547. [Google Scholar] [CrossRef]
- Gao, L.; Dougal, R.A.; Liu, S.; Iotova, A.P. Parallel-Connected Solar PV System to Address Partial and Rapidly Fluctuating Shadow Conditions. IEEE Trans. Ind. Electron. 2009, 56, 1548–1556. [Google Scholar] [Green Version]
- Olalla, C.; Deline, C.; Maksimovic, D. Performance of Mismatched PV Systems With Submodule Integrated Converters. IEEE J. Photovolt. 2014, 4, 396–404. [Google Scholar] [CrossRef]
- Kim, K.A.; Krein, P.T. Reexamination of Photovoltaic Hot Spotting to Show Inadequacy of the Bypass Diode. IEEE J. Photovolt. 2015, 5, 1435–1441. [Google Scholar] [CrossRef]
- Sahu, H.S.; Nayak, S.K.; Mishra, S. Maximizing the Power Generation of a Partially Shaded PV Array. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 626–637. [Google Scholar] [CrossRef]
- Manganiello, P.; Balato, M.; Vitelli, M. A Survey on Mismatching and Aging of PV Modules: The Closed Loop. IEEE Trans. Ind. Electron. 2015, 62, 7276–7286. [Google Scholar] [CrossRef]
- Olalla, C.; Hasan, M.N.; Deline, C.; Maksimovic, D. Mitigation of Hot-Spots in Photovoltaic Systems Using Distributed Power Electronics. Energies 2018, 11, 726. [Google Scholar] [CrossRef]
- Barth, C.; Pilawa-Podgurski, R.C.N. Dithering Digital Ripple Correlation Control for Photovoltaic Maximum Power Point Tracking. IEEE Trans. Power Electron. 2015, 30, 4548–4559. [Google Scholar] [CrossRef]
- Moon, S.; Yoon, S.G.; Park, J.H. A New Low-Cost Centralized MPPT Controller System for Multiply Distributed Photovoltaic Power Conditioning Modules. IEEE Trans. Smart Grid 2015, 6, 2649–2658. [Google Scholar] [CrossRef]
- Zsiborács, H.; Bai, A.; Popp, J.; Gabnai, Z.; Pályi, B.; Farkas, I.; Baranyai, N.H.; Veszelka, M.; Zentkó, L.; Pintér, G. Change of Real and Simulated Energy Production of Certain Photovoltaic Technologies in Relation to Orientation, Tilt Angle and Dual-Axis Sun-Tracking. A Case Study in Hungary. Sustainability 2018, 10, 1394. [Google Scholar] [CrossRef]
- Li, Q.; Wolfs, P. A Review of the Single Phase Photovoltaic Module Integrated Converter Topologies with Three Different DC Link Configurations. IEEE Trans. Power Electron. 2008, 23, 1320–1333. [Google Scholar]
- Maity, S.; Sahu, P.K. Modeling and Analysis of a Fast and Robust Module-Integrated Analog Photovoltaic MPP Tracker. IEEE Trans. Power Electron. 2016, 31, 280–291. [Google Scholar] [CrossRef]
- Walker, G.R.; Sernia, P.C. Cascaded dc-dc converter connection of photovoltaic modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
- Chen, S.M.; Liang, T.J.; Hu, K.R. Design, Analysis, and Implementation of Solar Power Optimizer for DC Distribution System. IEEE Trans. Power Electron. 2013, 28, 1764–1772. [Google Scholar] [CrossRef]
- Hanson, A.J.; Deline, C.A.; MacAlpine, S.M.; Stauth, J.T.; Sullivan, C.R. Partial-Shading Assessment of Photovoltaic Installations via Module-Level Monitoring. IEEE J. Photovolt. 2014, 4, 1618–1624. [Google Scholar] [CrossRef]
- Levron, Y.; Clement, D.; Choi, B.; Olalla, C.; Maksimovic, D. Control of Submodule Integrated Converters in the Isolated-Port Differential Power-Processing Photovoltaic Architecture. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 821–832. [Google Scholar] [CrossRef]
- Olalla, C.; Deline, C.; Clement, D.; Levron, Y.; Rodriguez, M.; Maksimovic, D. Performance of Power-Limited Differential Power Processing Architectures in Mismatched PV Systems. IEEE Trans. Power Electron. 2015, 30, 618–631. [Google Scholar] [CrossRef]
- Shimizu, T.; Hirakata, M.; Kamezawa, T.; Watanabe, H. Generation control circuit for photovoltaic modules. IEEE Trans. Power Electron. 2001, 16, 293–300. [Google Scholar] [CrossRef] [Green Version]
- Shenoy, P.S.; Kim, K.A.; Johnson, B.B.; Krein, P.T. Differential Power Processing for Increased Energy Production and Reliability of Photovoltaic Systems. IEEE Trans. Power Electron. 2013, 28, 2968–2979. [Google Scholar] [CrossRef]
- Olalla, C.; Clement, D.; Rodriguez, M.; Maksimovic, D. Architectures and Control of Submodule Integrated DC-DC Converters for Photovoltaic Applications. IEEE Trans. Power Electron. 2013, 28, 2980–2997. [Google Scholar] [CrossRef]
- Diab-Marzouk, A.; Trescases, O. SiC-Based Bidirectional Cuk Converter with Differential Power Processing and MPPT for a Solar Powered Aircraft. IEEE Trans. Transp. Electrification 2015, 1, 369–381. [Google Scholar] [CrossRef]
- Bell, R.; Pilawa-Podgurski, R.C.N. Decoupled and Distributed Maximum Power Point Tracking of Series-Connected Photovoltaic Submodules Using Differential Power Processing. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 881–891. [Google Scholar] [CrossRef]
- Qin, S.; Barth, C.B.; Pilawa-Podgurski, R.C.N. Enhancing Microinverter Energy Capture With Submodule Differential Power Processing. IEEE Trans. Power Electron. 2016, 31, 3575–3585. [Google Scholar] [CrossRef]
- Jeon, Y.T.; Lee, H.; Kim, K.A.; Park, J.H. Least Power Point Tracking Method for Photovoltaic Differential Power Processing Systems. IEEE Trans. Power Electron. 2017, 32, 1941–1951. [Google Scholar] [CrossRef]
- Kim, K.A.; Shenoy, P.S.; Krein, P.T. Converter Rating Analysis for Photovoltaic Differential Power Processing Systems. IEEE Trans. Power Electron. 2015, 30, 1987–1997. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Kim, K.A.; Xu, C.; Lei, J.; Krein, P.T. Dynamic photovoltaic model incorporating capacitive and reverse-bias characteristics. IEEE J. Photovolt. 2013, 3, 1334–1341. [Google Scholar] [CrossRef]
- Jena, D.; Ramana, V.V. Modeling of photovoltaic system for uniform and non-uniform irradiance: A critical review. Renew. Sustain. Energy Rev. 2015, 52, 400–417. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, J.; Han, Y. PV Balancers: Concept, Architectures, and Realization. IEEE Trans. Power Electron. 2015, 30, 3479–3487. [Google Scholar] [CrossRef]
- Lee, H.; Kim, K.A. Differential power processing converter design for photovoltaic wearable applications. In Proceedings of the International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 463–468. [Google Scholar]
- Lee, H.; Kim, K.A. Comparison of photovoltaic converter configurations for wearable applications. In Proceedings of the IEEE Workshop Control Modeling Power Electron, Vancouver, BC, Canada, 12–15 July 2015; pp. 1–6. [Google Scholar]
- Cobos, J.A.; Cristóbal, H.; Serrano, D.; Ramos, R.; Oliver, J.A.; Alou, P. Differential power as a metric to optimize power converters and architectures. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2168–2175. [Google Scholar]
- Esram, T.; Kimball, J.; Krein, P.; Chapman, P.; Midya, P. Dynamic Maximum Power Point Tracking of Photovoltaic Arrays Using Ripple Correlation Control. IEEE Trans. Power Electron. 2006, 21, 1282–1291. [Google Scholar] [CrossRef]
- Kim, K.A.; Li, R.M.; Krein, P.T. Voltage-offset resistive control for DC-DC converters in photovoltaic applications. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 2045–2052. [Google Scholar]
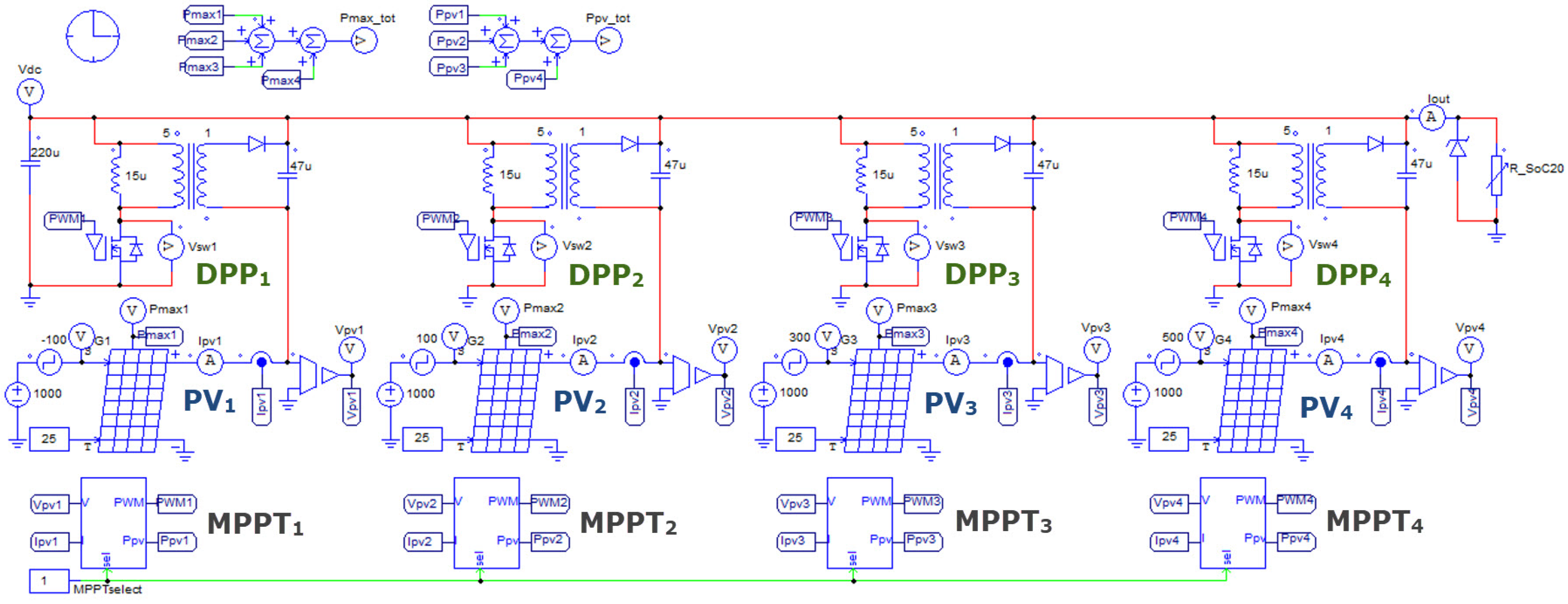
| Full Power Processing (FPP) Converters | |||
| PV No. | (W) | (W) | (W) |
| 1 | 1.23 | 0.25 | 0.59 |
| 2 | 0.96 | 0.19 | |
| 3 | 0.57 | 0.11 | |
| 4 | 0.19 | 0.04 | |
| Parallel DPP Converters | |||
| PV No. | (W) | (W) | (W) |
| 1 | 0.05 | 0.01 | 0.04 |
| 2 | 0.05 | 0.01 | |
| 3 | 0.05 | 0.01 | |
| 4 | 0.03 | 0.01 | |
| With Front-End Converter | |||
| Conv. | (W) | (W) | (W) |
| FE | 0.23 | 0.05 | 0.08 |
| Case | Irradiance (W/m) | |||
|---|---|---|---|---|
| PV 1 | PV 2 | PV 3 | PV 4 | |
| 1 | 1000 | 1050 | 900 | 950 |
| 2 | 1000 | 700 | 500 | 200 |
| 3 | 1000 | 1050 | 900 | 50 |
| 4 | 500 | 550 | 400 | 450 |
| 5 | 500 | 350 | 300 | 175 |
| 6 | 500 | 550 | 450 | 50 |
| Aspect | With Front-End | Without Front-End |
|---|---|---|
| MPPT with low DC bus | poor | good |
| Charging at low input power | fair | good |
| System power: nominal, uniform | excellent | good |
| System power: lower or nonuniform | poor | good |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, K.A. Design Considerations for Parallel Differential Power Processing Converters in a Photovoltaic-Powered Wearable Application. Energies 2018, 11, 3329. https://doi.org/10.3390/en11123329
Lee H, Kim KA. Design Considerations for Parallel Differential Power Processing Converters in a Photovoltaic-Powered Wearable Application. Energies. 2018; 11(12):3329. https://doi.org/10.3390/en11123329
Chicago/Turabian StyleLee, Hyunji, and Katherine A. Kim. 2018. "Design Considerations for Parallel Differential Power Processing Converters in a Photovoltaic-Powered Wearable Application" Energies 11, no. 12: 3329. https://doi.org/10.3390/en11123329
APA StyleLee, H., & Kim, K. A. (2018). Design Considerations for Parallel Differential Power Processing Converters in a Photovoltaic-Powered Wearable Application. Energies, 11(12), 3329. https://doi.org/10.3390/en11123329





