Control of a DC-DC Buck Converter through Contraction Techniques
Abstract
:1. Introduction
2. Mathematical Methods
2.1. Linear Transformations
2.2. Matrix Measure
2.3. Contraction Analysis for Filippov Systems
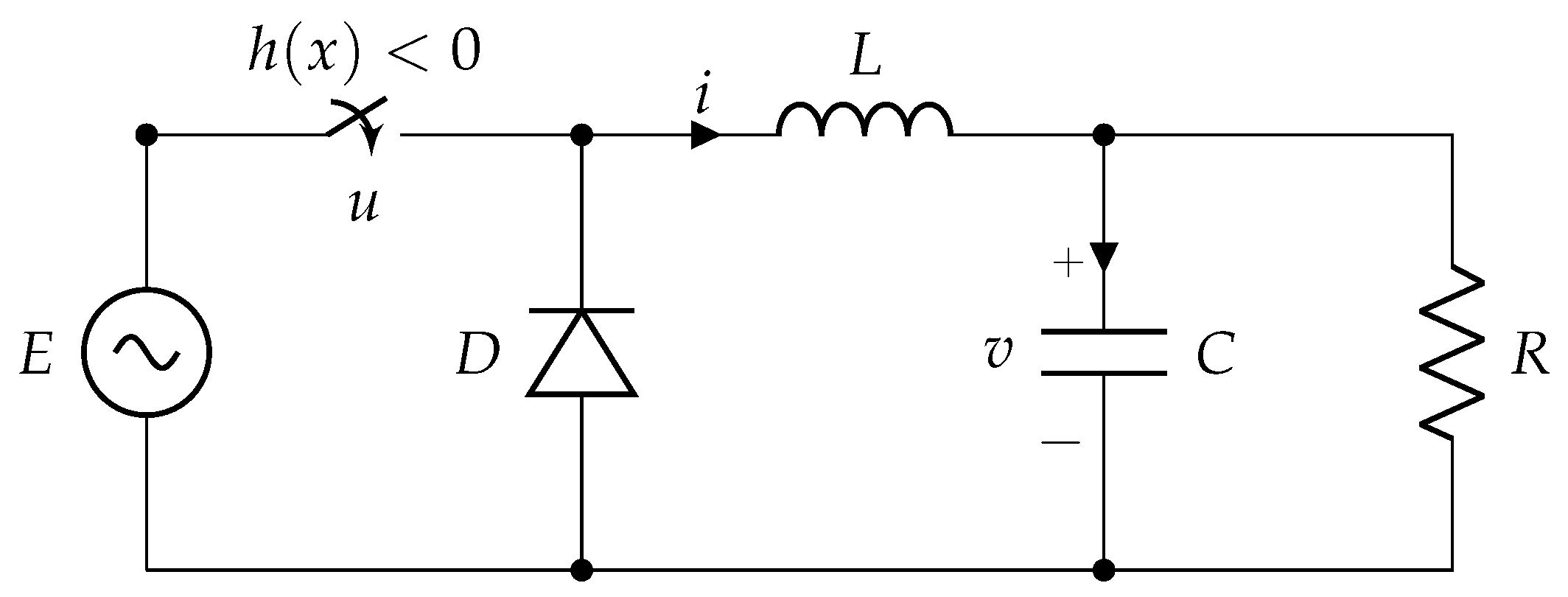
3. The Buck Power Converter
4. Application to 2D-Case
4.1. Controller Design
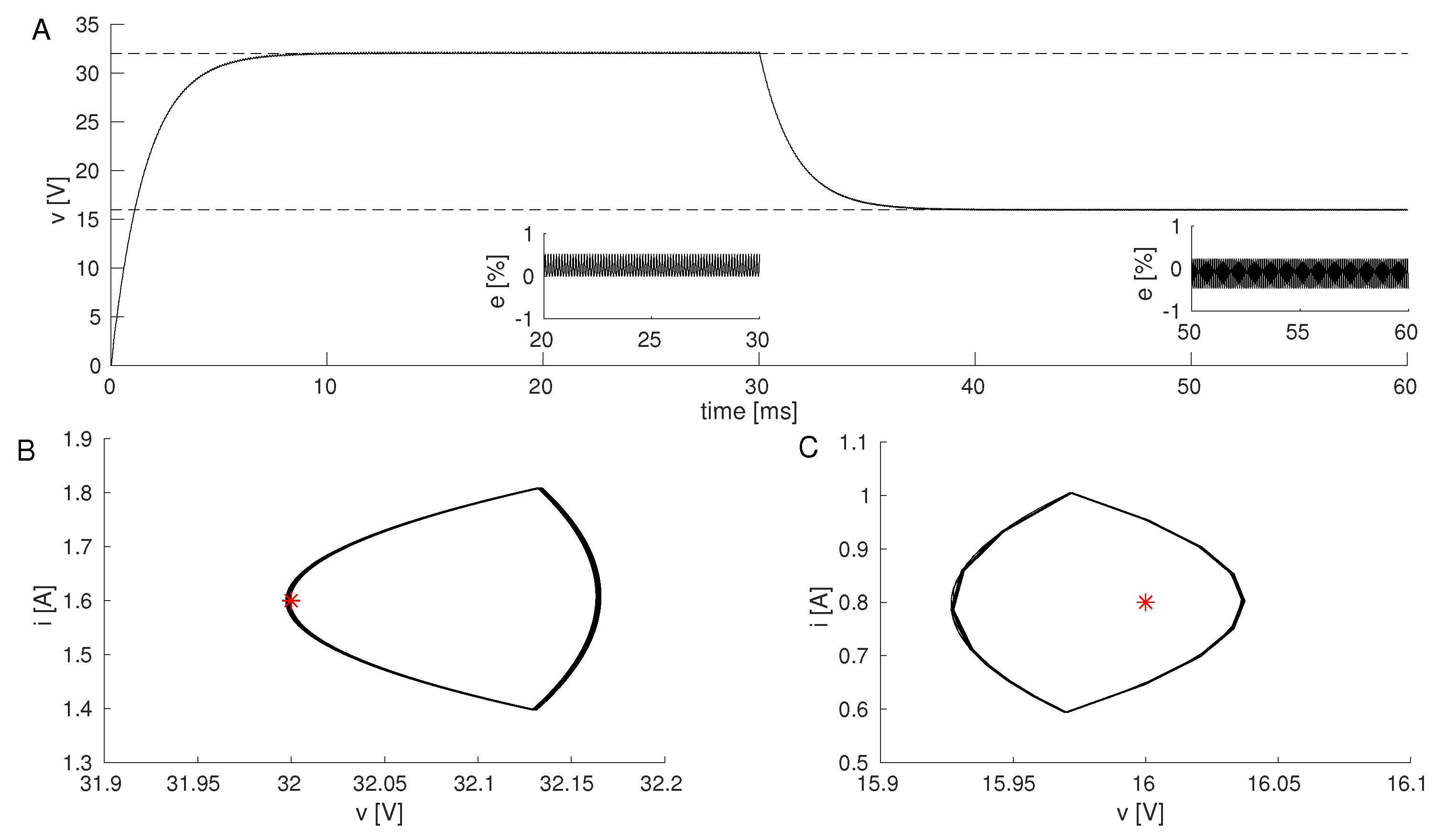
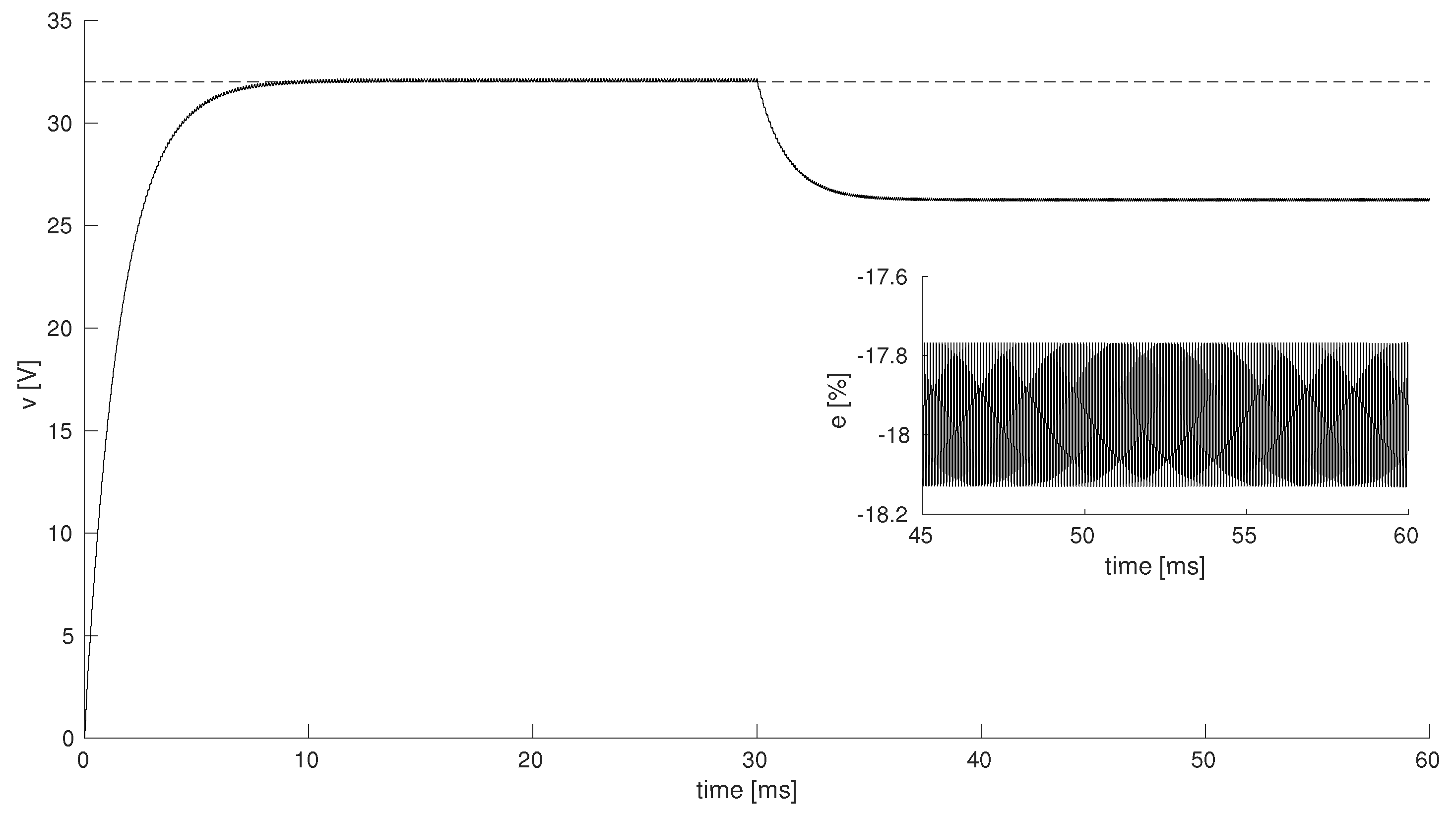
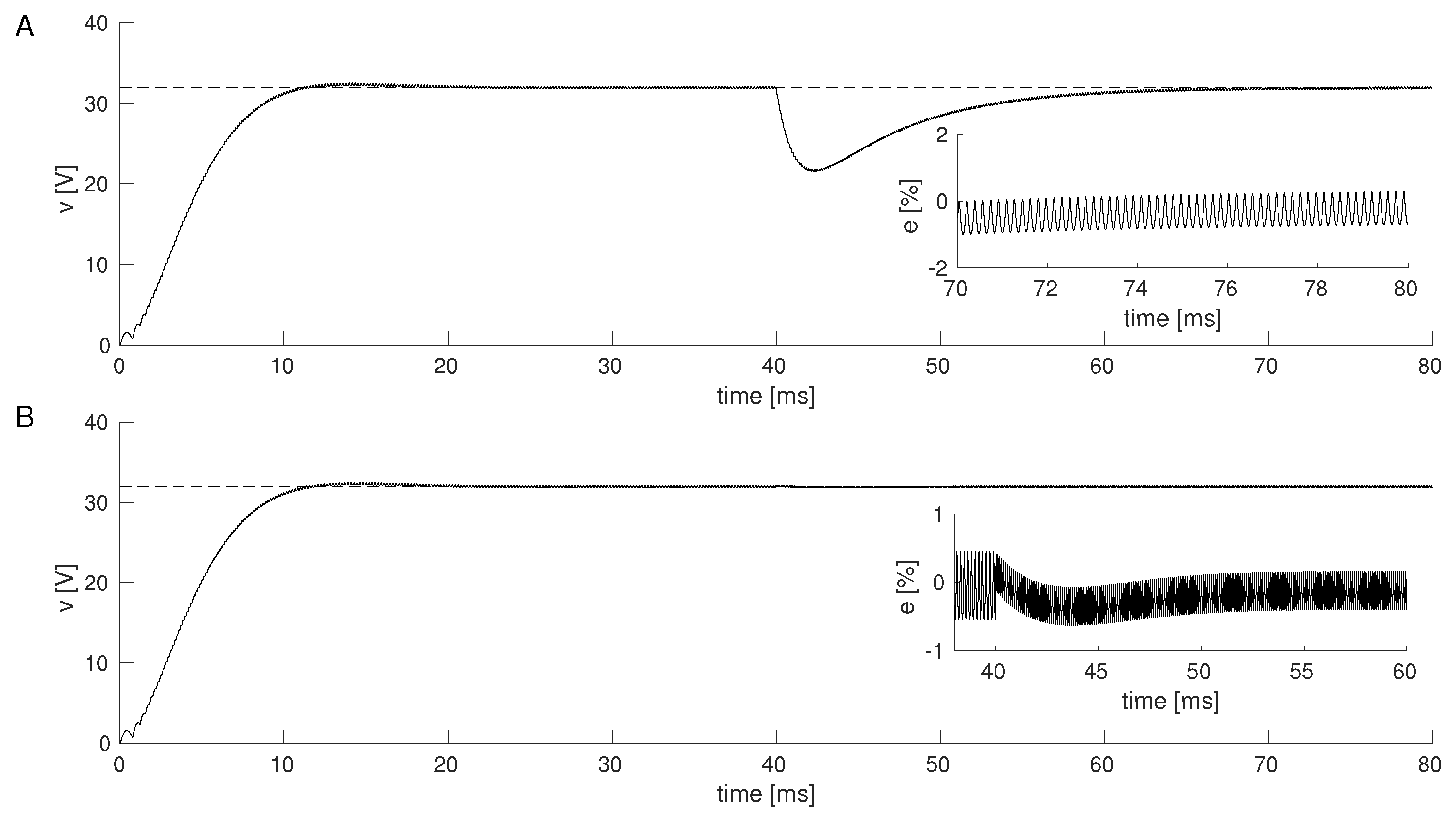
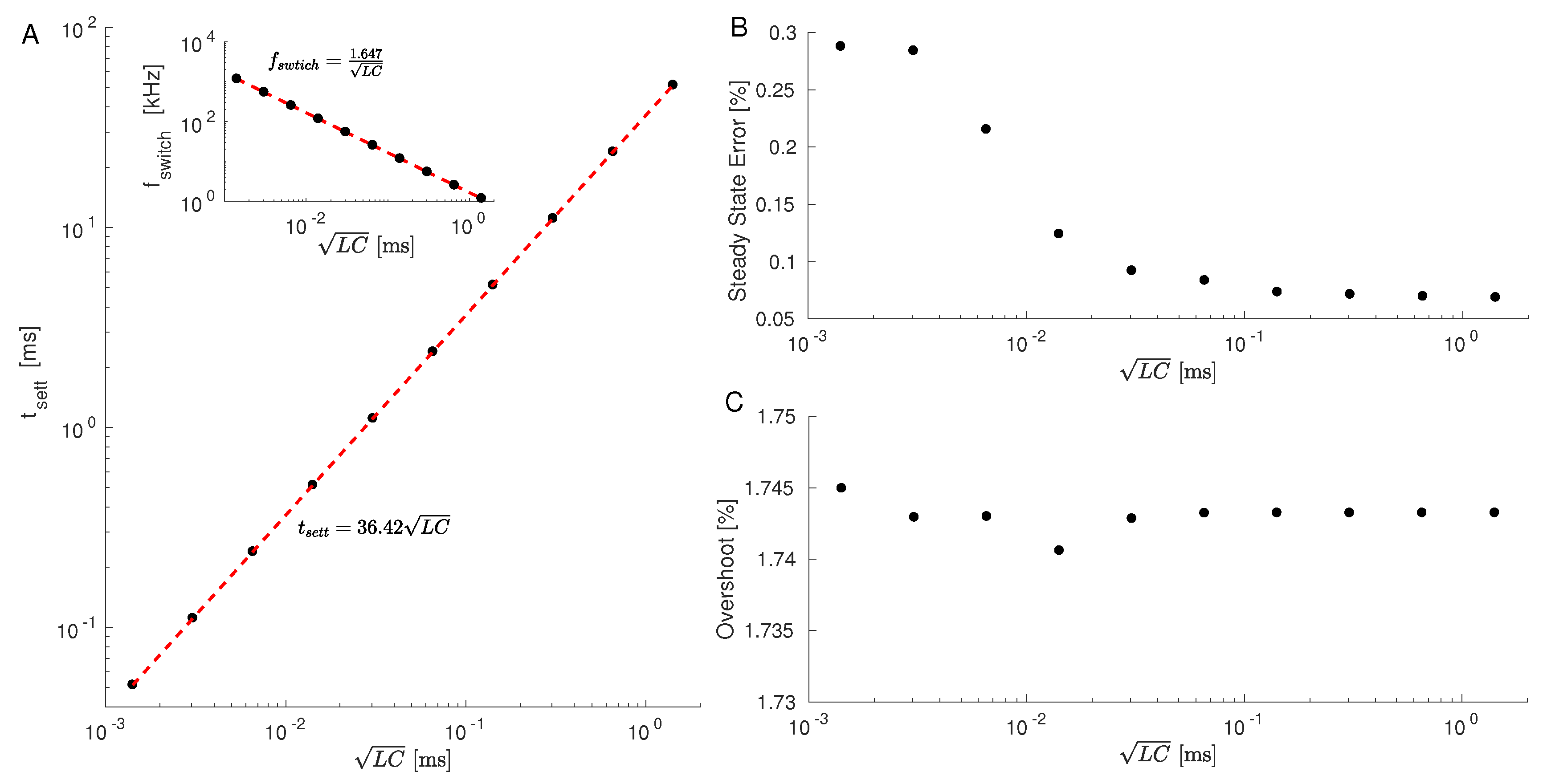
4.2. Simulation Results
5. Application to 3D-Case
5.1. Controller Design Based on a Modified Integral Control Action
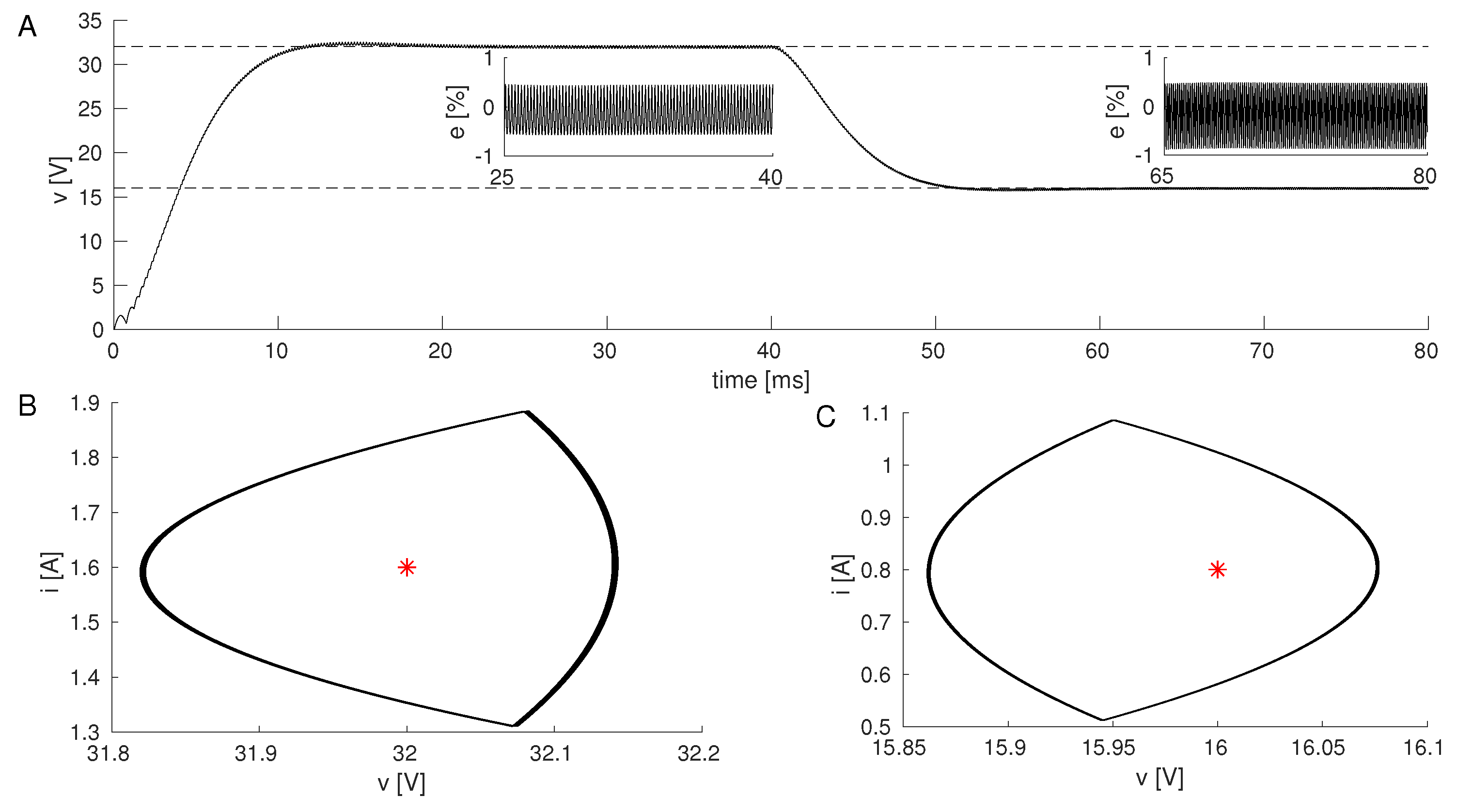
Simulation Results
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Matrix Measure for a 2D System
Appendix A.2. Matrix Measure for 3D System
References
- Chen, S.M.; Wang, C.Y.; Liang, T.J. A novel sinusoidal boost-flyback CCM/DCM DC-DC converter. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition–APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 3512–3516. [Google Scholar]
- Tseng, K.C.; Lin, J.T.; Cheng, C.A. An Integrated Derived Boost-Flyback Converter for fuel cell hybrid electric vehicles. In Proceedings of the 2013 1st International Future Energy Electronics Conference (IFEEC), Tainan, Taiwan, 3–6 November 2013; pp. 283–287. [Google Scholar]
- Siouane, S.; Jovanovic, S.; Poure, P. Service Continuity of PV Synchronous Buck/Buck-Boost Converter with Energy Storage. Energies 2018, 11, 1369. [Google Scholar] [CrossRef]
- Ortigoza, R.S.; Rodriguez, V.H.G.; Marquez, E.H.; Ponce, M.; Sanchez, J.R.G.; Juarez, J.N.A.; Ortigoza, G.S.; Perez, J.H. A Trajectory Tracking Control for a Boost Converter-Inverter-DC Motor Combination. IEEE Lat. Am. Trans. 2018, 16, 1008–1014. [Google Scholar] [CrossRef]
- Fernando, W.A.; Lu, D.D. Bi-directional converter for interfacing appliances with HFAC enabled power distribution systems in critical applications. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, S.; Singh, B.; Bhuvaneswari, G.; Bist, V. A Power Quality Improved Bridgeless Converter-Based Computer Power Supply. IEEE Trans. Ind. Appl. 2016, 52, 4385–4394. [Google Scholar] [CrossRef]
- Undeland, T.M.; Robbins, W.P.; Mohan, N. Power Electronics: Converters, Applications, and Design; John Wiley and Sons: New York, NY, USA, 2003. [Google Scholar]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Mueller, J.A.; Kimball, J. Modeling Dual Active Bridge Converters in DC Distribution Systems. IEEE Trans. Power Electron. 2018. [Google Scholar] [CrossRef]
- Banerjee, S.; Verghese, G.C. Nonlinear Phenomena in Power Electronics: Attractors, Bifurcations, Chaos, and Nonlinear Control; IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- Cheng, C.H.; Cheng, P.J.; Xie, M.J. Current sharing of paralleled DC–DC converters using GA-based PID controllers. Expert Syst. Appl. 2010, 37, 733–740. [Google Scholar] [CrossRef]
- Guo, L.; Hung, J.Y.; Nelms, R.M. Evaluation of DSP-Based PID and Fuzzy Controllers for DC-DC Converters. IEEE Trans. Ind. Electron. 2009, 56, 2237–2248. [Google Scholar]
- Rodríguez-Licea, M.A.; Pérez-Pinal, F.J.; Nuñez-Perez, J.C.; Herrera-Ramirez, C.A. Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads. Energies 2018, 11, 1130. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Quevedo, D.E. Predictive Control of Power Converters: Designs With Guaranteed Performance. IEEE Trans. Ind. Inf. 2015, 11, 53–63. [Google Scholar] [CrossRef]
- Alsmadi, Y.M.; Utkin, V.; Haj-ahmed, M.A.; Xu, L. Sliding mode control of power converters: DC/DC converters. Int. J. Control 2017. [Google Scholar] [CrossRef]
- Khaligh, A.; Rahimi, A.M.; Emadi, A. Modified Pulse-Adjustment Technique to Control DC/DC Converters Driving Variable Constant-Power Loads. IEEE Trans. Ind. Electron. 2008, 55, 1133–1146. [Google Scholar] [CrossRef]
- Gabian, G.; Gamble, J.; Blalock, B.; Costinett, D. Hybrid buck converter optimization and comparison for smart phone integrated battery chargers. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2148–2154. [Google Scholar]
- Lai, C.; Cheng, Y.; Hsieh, M.; Lin, Y. Development of a Bidirectional DC/DC Converter With Dual-Battery Energy Storage for Hybrid Electric Vehicle System. IEEE Trans. Veh. Technol. 2018, 67, 1036–1052. [Google Scholar] [CrossRef]
- Lukmana, M.A.; Nurhadi, H. Preliminary study on Unmanned Aerial Vehicle (UAV) Quadcopter using PID controller. In Proceedings of the 2015 International Conference on Advanced Mechatronics, Intelligent Manufacture, and Industrial Automation (ICAMIMIA), Surabaya, Indonesia, 15–17 October 2015; pp. 34–37. [Google Scholar] [CrossRef]
- Chiang, C.; Chen, C. Zero-Voltage-Switching Control for a PWM Buck Converter Under DCM/CCM Boundary. IEEE Trans. Power Electron. 2009, 24, 2120–2126. [Google Scholar] [CrossRef]
- Calderón, A.; Vinagre, B.; Feliu, V. Fractional order control strategies for power electronic buck converters. Signal Process. 2006, 86, 2803–2819. [Google Scholar] [CrossRef]
- Suh, J.; Seok, J.; Kong, B. A Fast Response PWM Buck Converter with Active Ramp Tracking Control in Load Transient period. IEEE Trans. Circuits Syst. II Express Briefs 2018. [Google Scholar] [CrossRef]
- Chang, C.; Yuan, Y.; Jiang, T.; Zhou, Z. Field programmable gate array implementation of a single-input fuzzy proportional-integral-derivative controller for DC-DC buck converters. IET Power Electron. 2016, 9, 1259–1266. [Google Scholar] [CrossRef]
- El Aroudi, A.; Giaouris, D.; Iu, H.H.C.; Hiskens, I.A. A review on stability analysis methods for switching mode power converters. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 302–315. [Google Scholar] [CrossRef]
- Fiore, D.; Hogan, S.J.; di Bernardo, M. Contraction analysis of switched systems via regularization. Automatica 2016, 73, 279–288. [Google Scholar] [CrossRef] [Green Version]
- di Bernardo, M.; Fiore, D. Switching control for incremental stabilization of nonlinear systems via contraction theory. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 2054–2059. [Google Scholar] [CrossRef]
- Lohmiller, W.; Slotine, J.J.E. On Contraction Analysis for Non-linear Systems. Automatica 1998, 34, 683–696. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.T. Linear Systems Theory and dEsign; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]
- Khalil, H.K. Nonlinear Control; Pearson: New York, NY, USA, 2015. [Google Scholar]
- Deane, J.H.; Hamill, D.C. Analysis, simulation and experimental study of chaos in the buck converter. In Proceedings of the PESC’90 Record 21st Annual IEEE Power Electronics Specialists Conference, San Antonio, TX, USA, 11–14 June 1990; pp. 491–498. [Google Scholar]
- Fossas, E.; Olivar, G. Study of chaos in the buck converter. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 13–25. [Google Scholar] [CrossRef] [Green Version]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angulo-Garcia, D.; Angulo, F.; Osorio, G.; Olivar, G. Control of a DC-DC Buck Converter through Contraction Techniques. Energies 2018, 11, 3086. https://doi.org/10.3390/en11113086
Angulo-Garcia D, Angulo F, Osorio G, Olivar G. Control of a DC-DC Buck Converter through Contraction Techniques. Energies. 2018; 11(11):3086. https://doi.org/10.3390/en11113086
Chicago/Turabian StyleAngulo-Garcia, David, Fabiola Angulo, Gustavo Osorio, and Gerard Olivar. 2018. "Control of a DC-DC Buck Converter through Contraction Techniques" Energies 11, no. 11: 3086. https://doi.org/10.3390/en11113086





