Thermo-Economic Analysis of a Bottoming Kalina Cycle for Internal Combustion Engine Exhaust Heat Recovery
Abstract
:1. Introduction
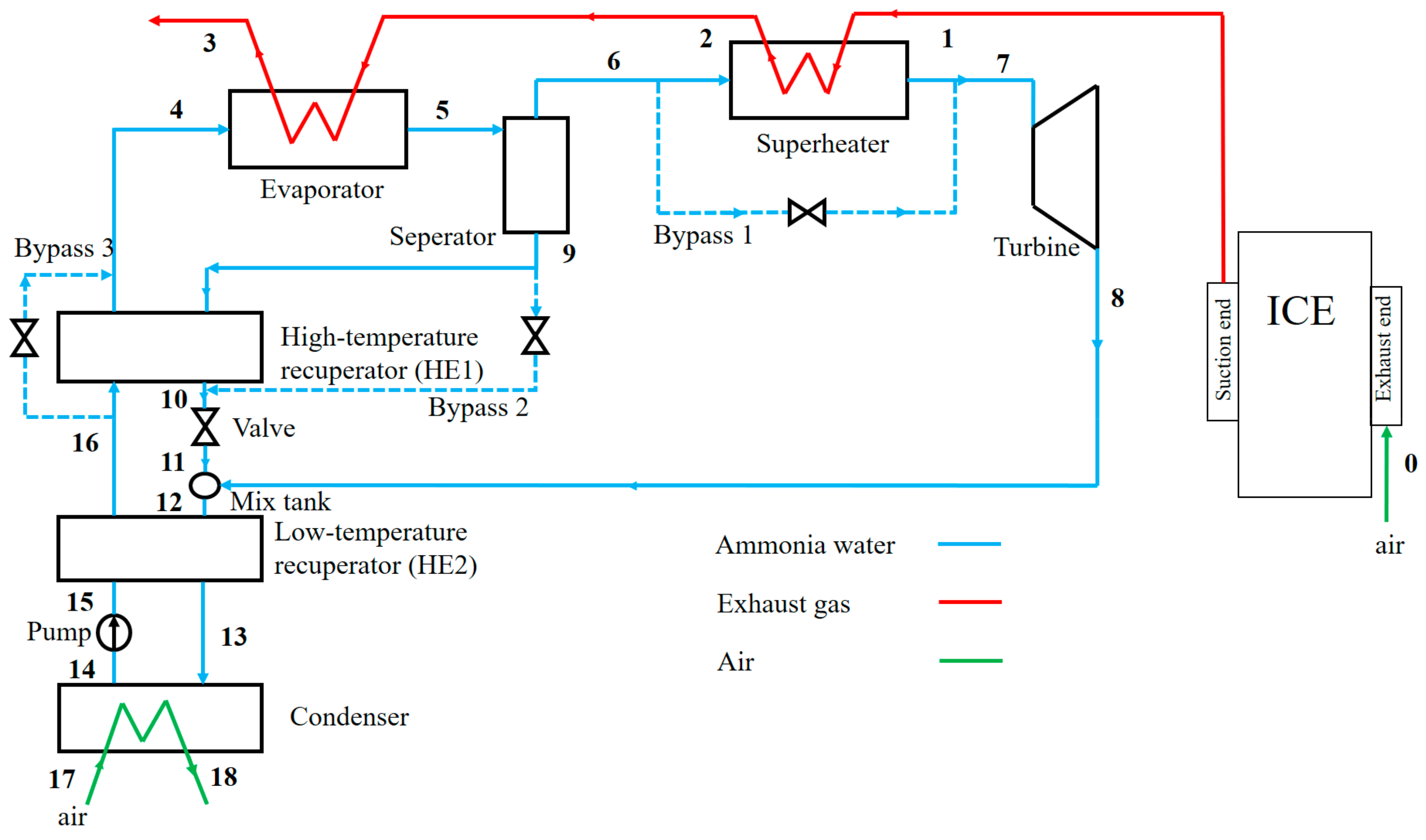
2. System Description and Assumptions
- The KC subsystem does not influence the operation condition of ICE.
- The KC system operates in a steady-state.
- Changes in kinetic and potential energies are negligible.
- The pressure loss due to frictional effects is negligible.
- The ammonia-water mixture leaving the condenser (state 14) is a saturated liquid.
- The minimum pinch-point temperature difference of all heat exchangers is 10K.
3. System Modeling
3.1. Thermodynamic Modeling
Verification of Ammonia-Water Thermodynamic Properties
3.2. Economic Modeling
4. Results and Discussion
4.1. Thermal Performance Analysis for KCs
4.2. Thermal Performance
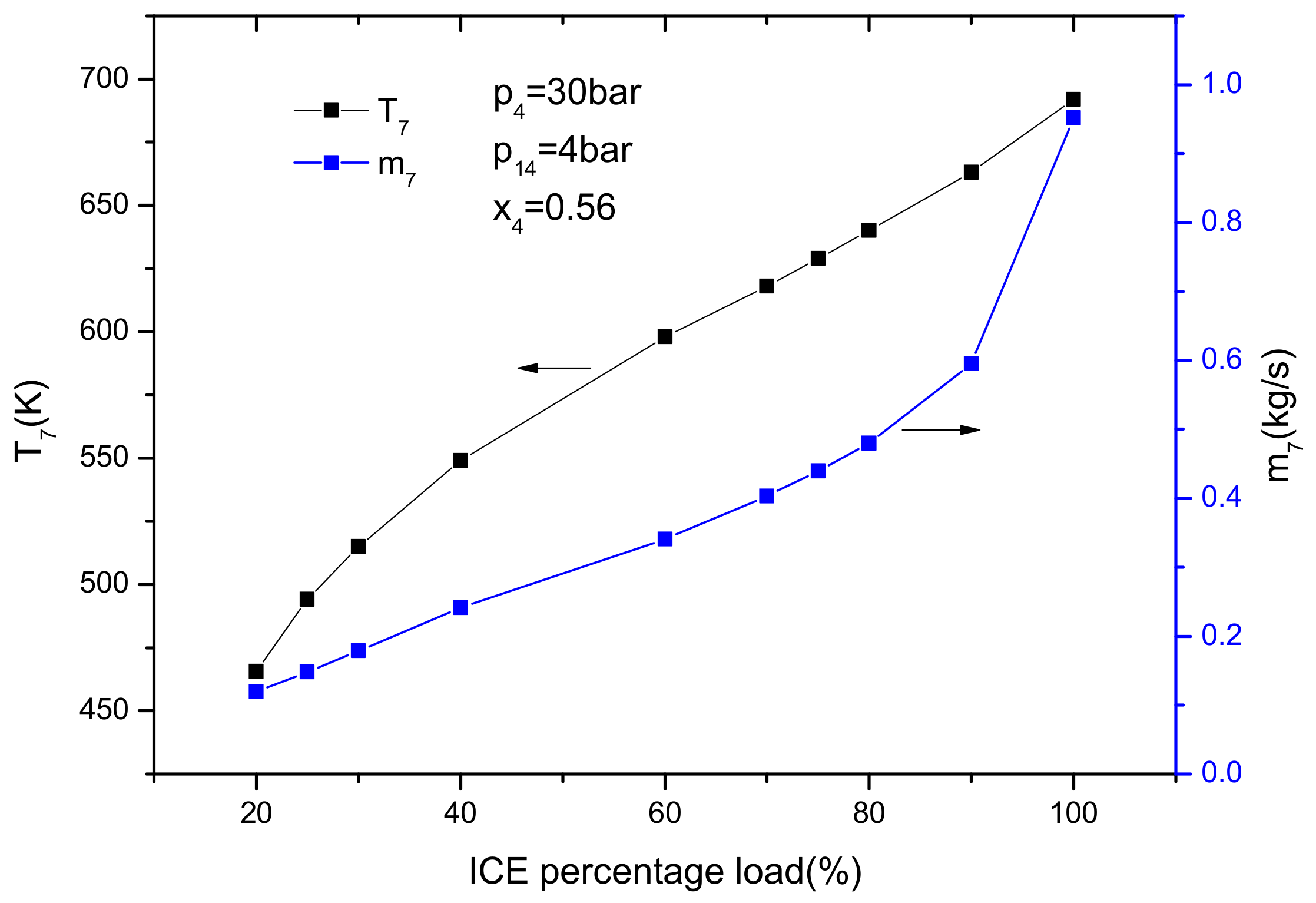
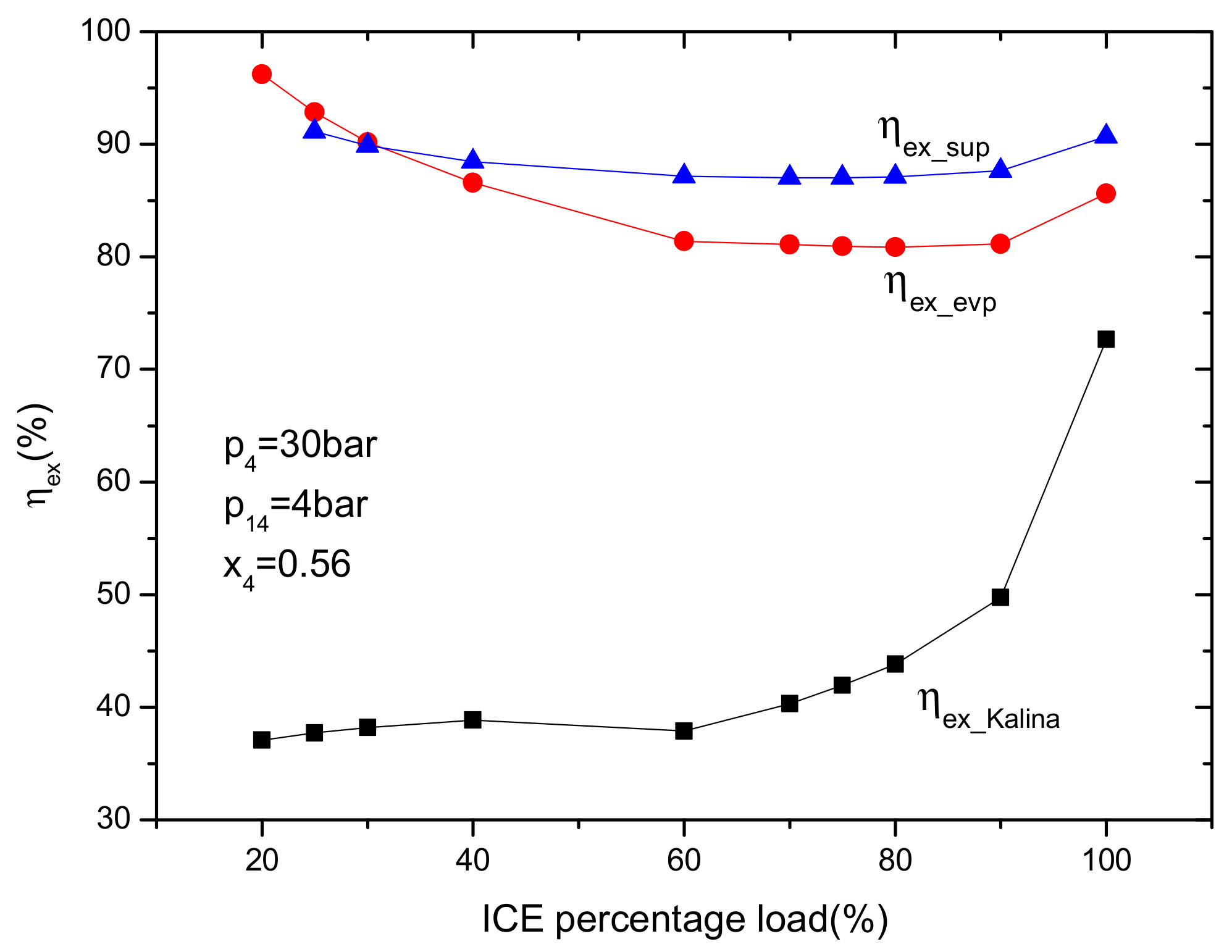
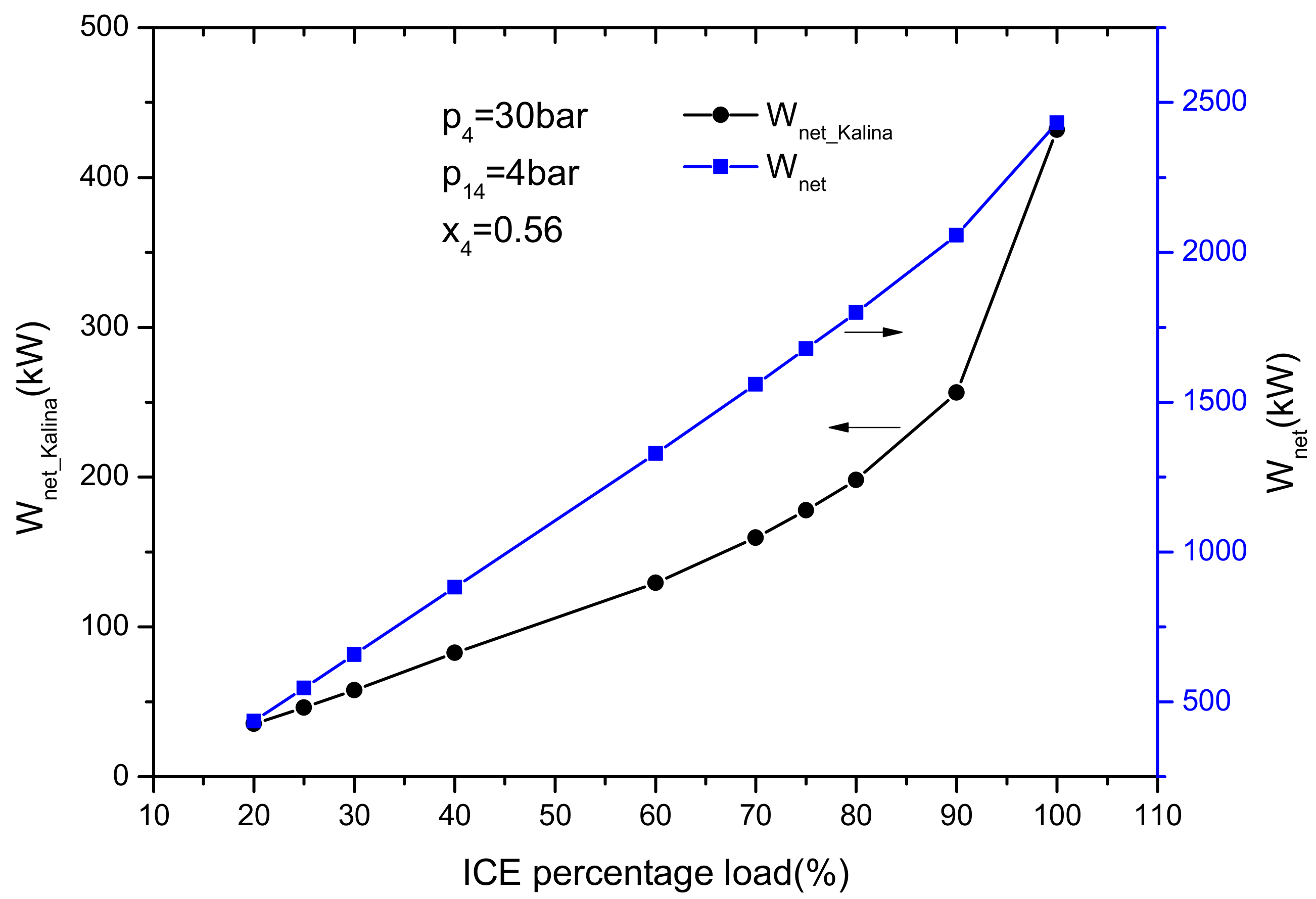
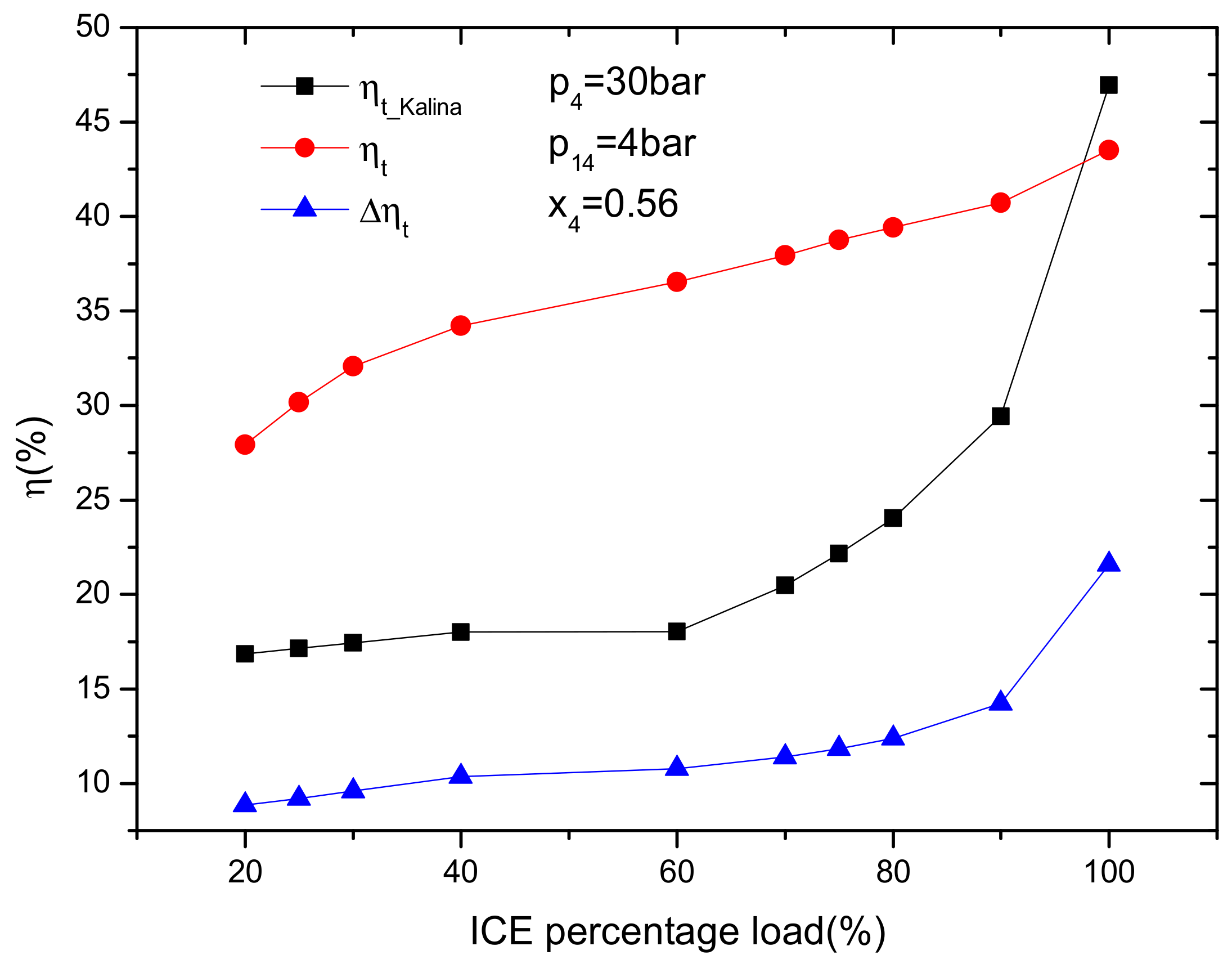
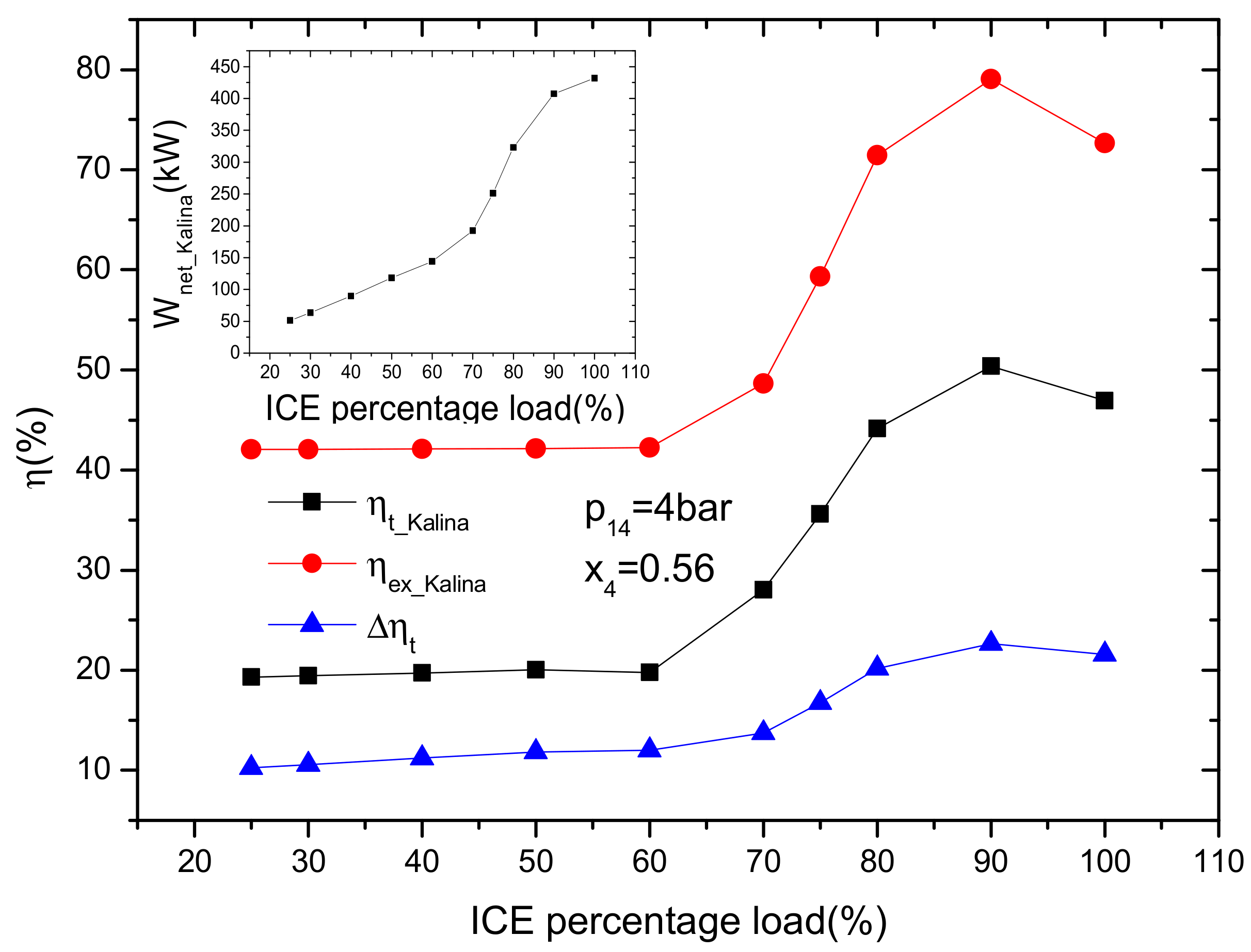
4.2.1. Effect of the ICE Load
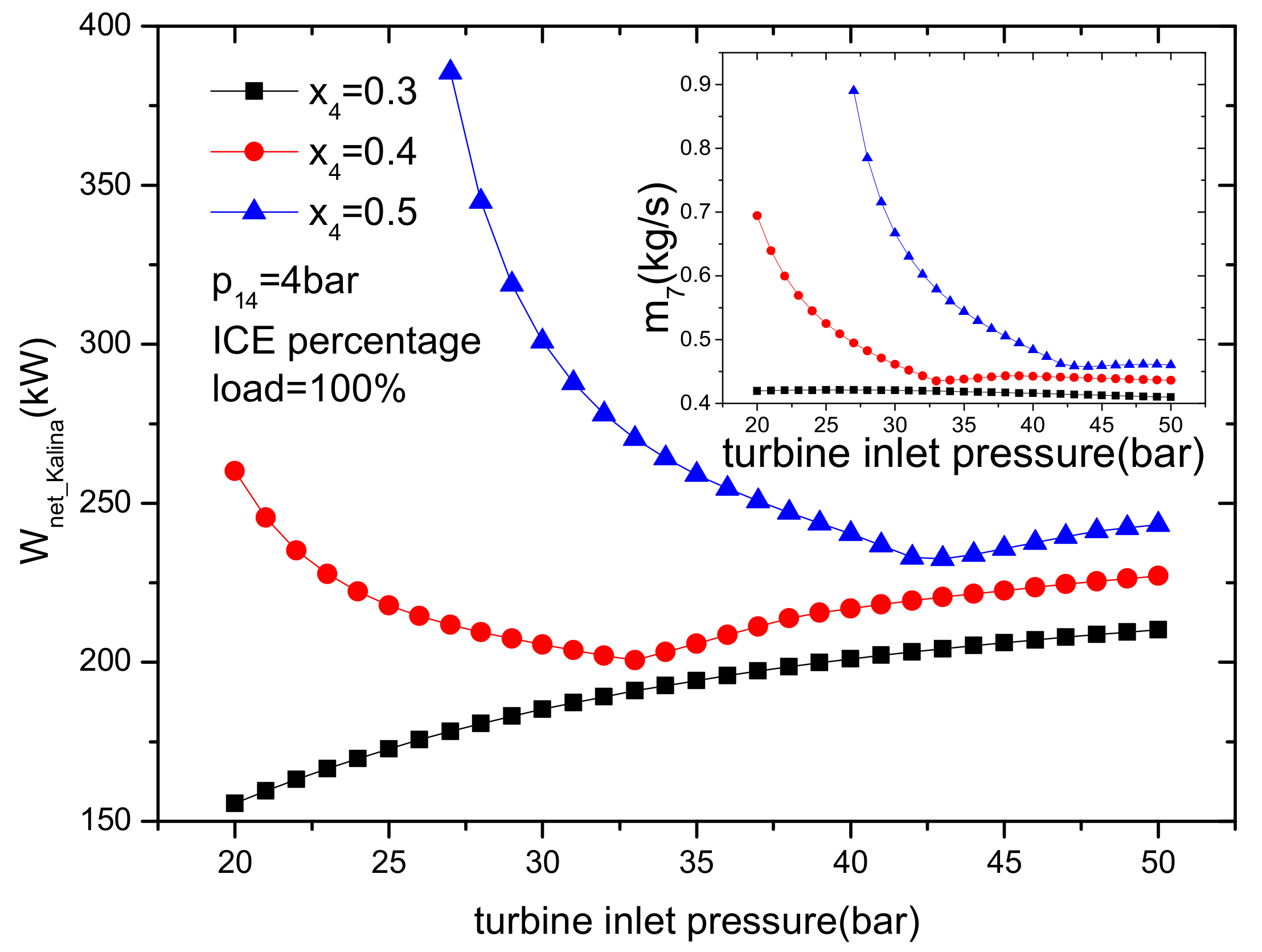
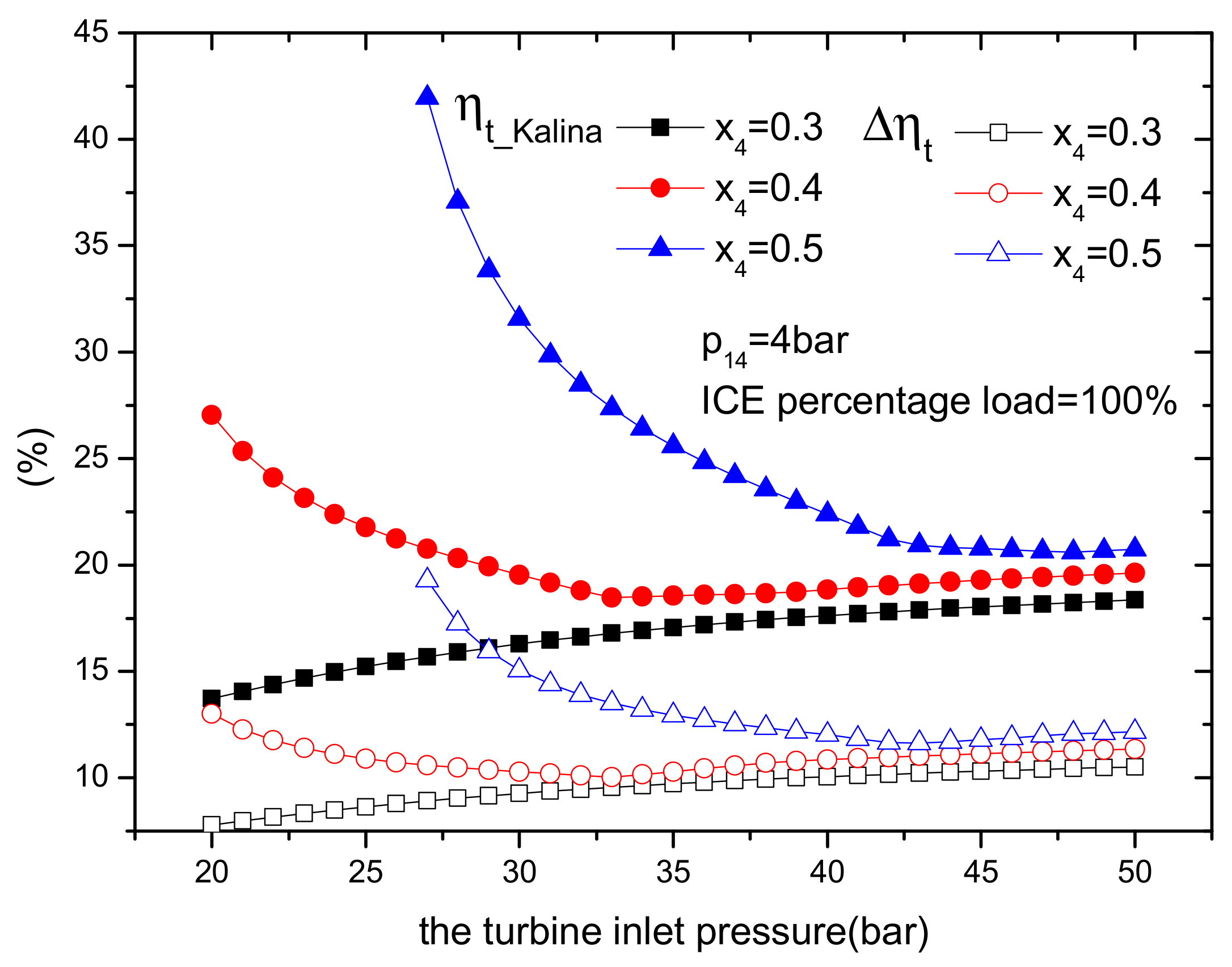
4.2.2. Effect of Turbine Inlet Pressure
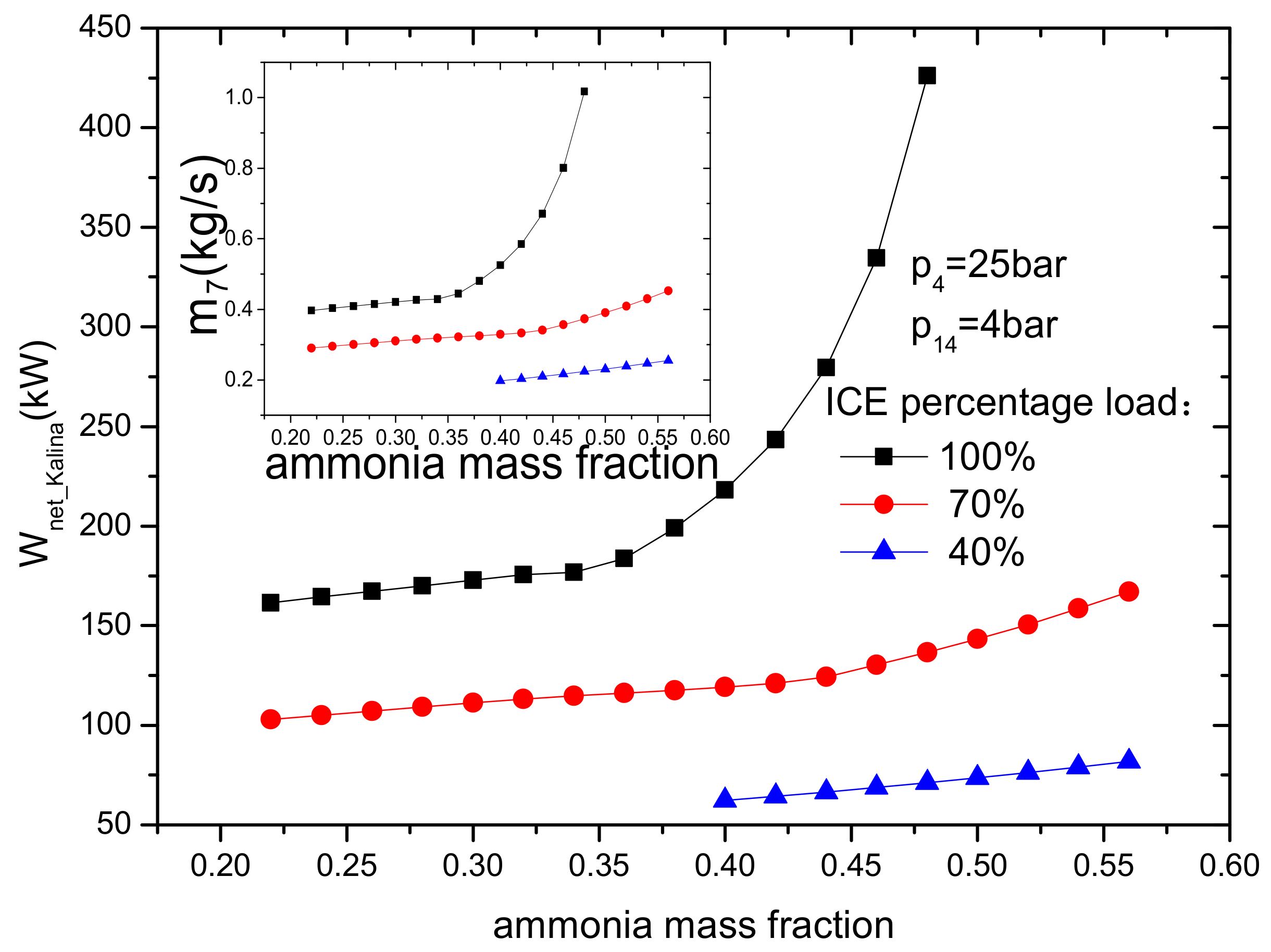
4.2.3. Effect of Ammonia Mass Fraction
4.3. Economic Performance
5. Conclusions
- (1)
- KC with a superheater is a promising cycle for waste heat recovery from ICE. The Kalina subsystem not only yields extra power output without extra petroleum consumption but also reduces the emissions of CO2. The maximum net power output and thermal efficiency of KC in this paper are greater than those in the published literature for all ICE loads, and the maximum exergy efficiency is greater than that in the published literature when the ICE load is greater than 40%.
- (2)
- The net power output, KC thermal efficiency and the improvement of the thermal efficiency of ICE increase with ICE percentage load and ammonia mass fraction. Compared with the single ICE, the increase of thermal efficiency is approximately 21.6% at 100% ICE percentage load. In addition, within the scope of this paper, if the ammonia mass fraction is below 0.34, a higher turbine inlet pressure is better for improving thermal performance. If the ammonia mass fraction is greater than 0.34, a lower turbine inlet pressure is better.
- (3)
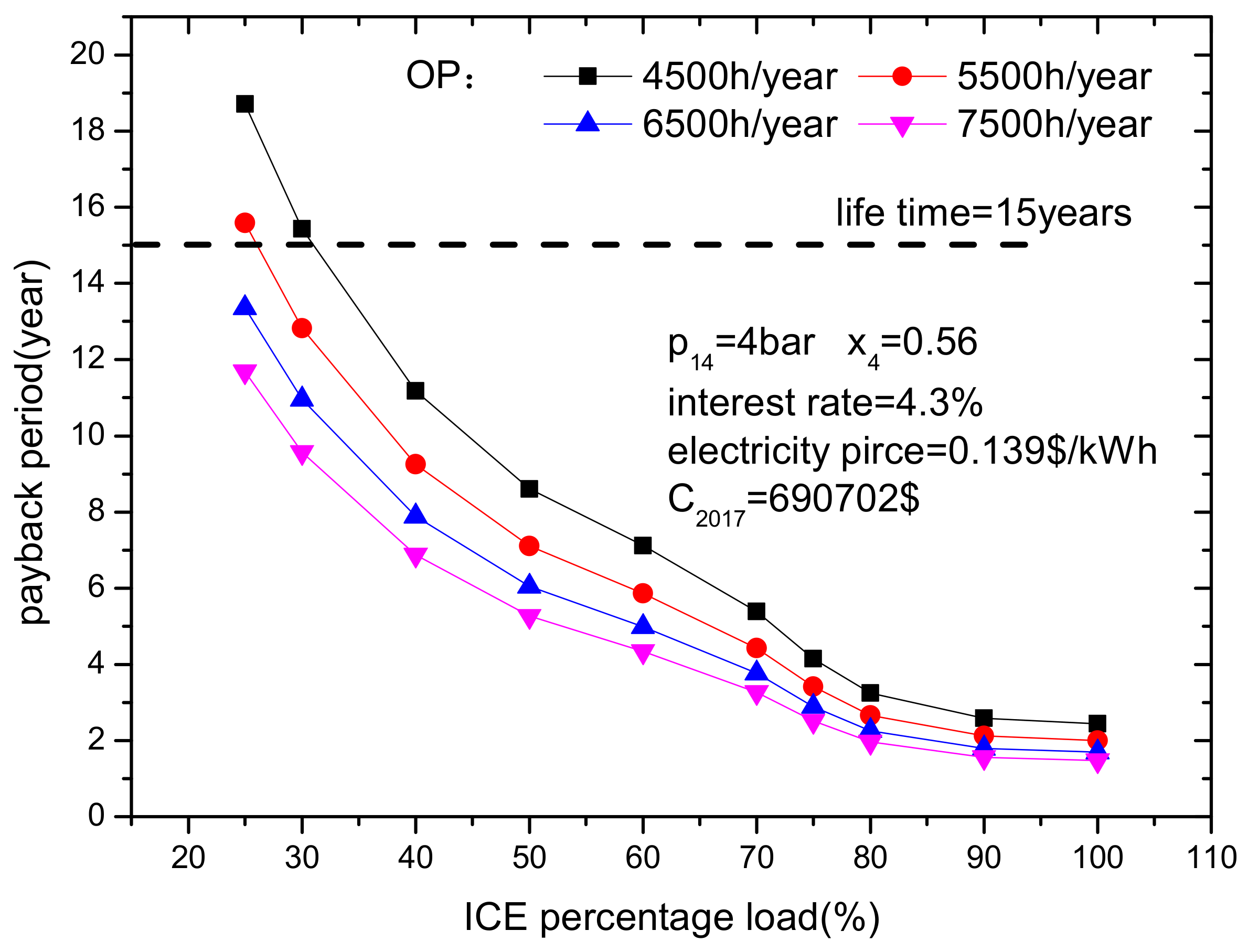
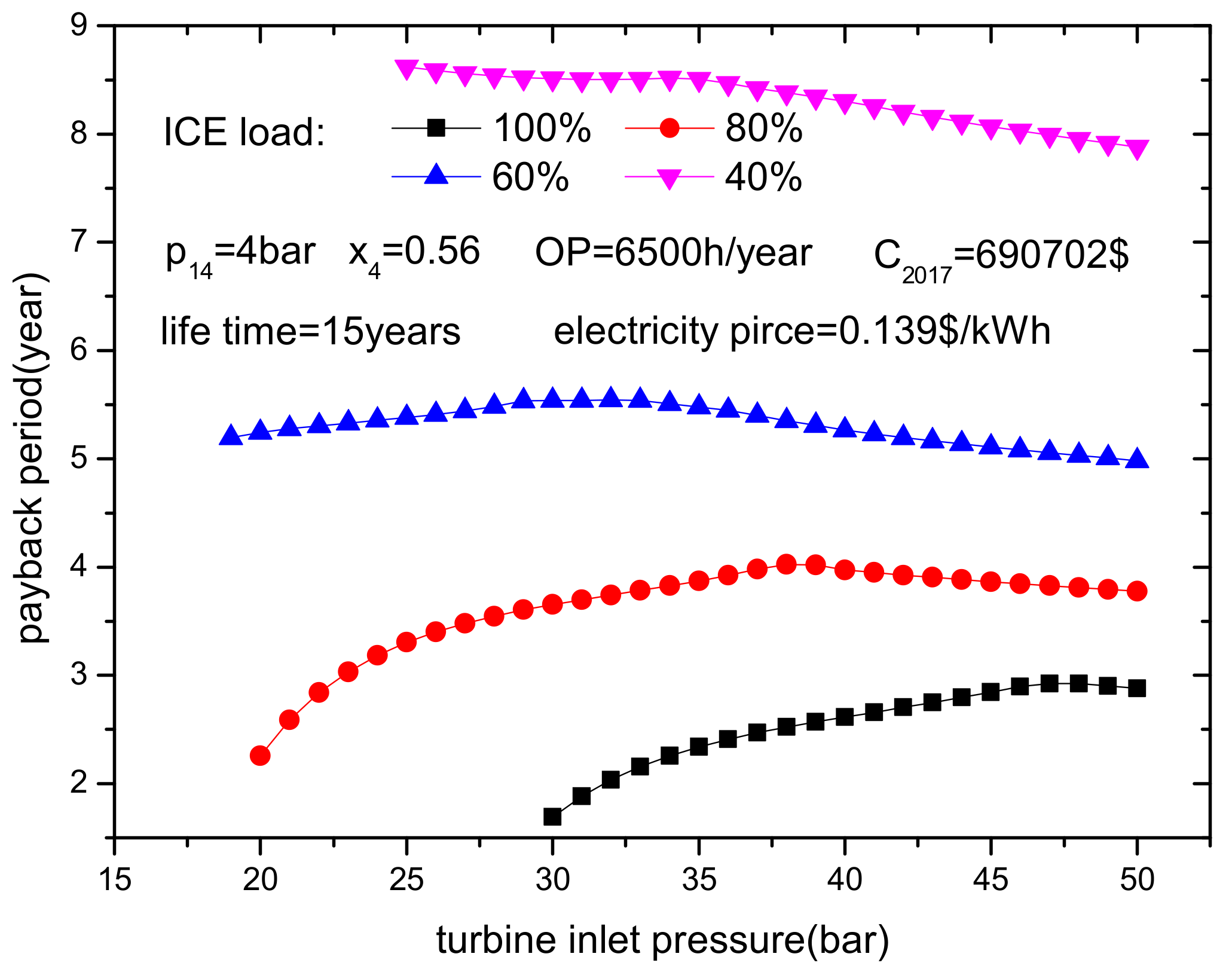
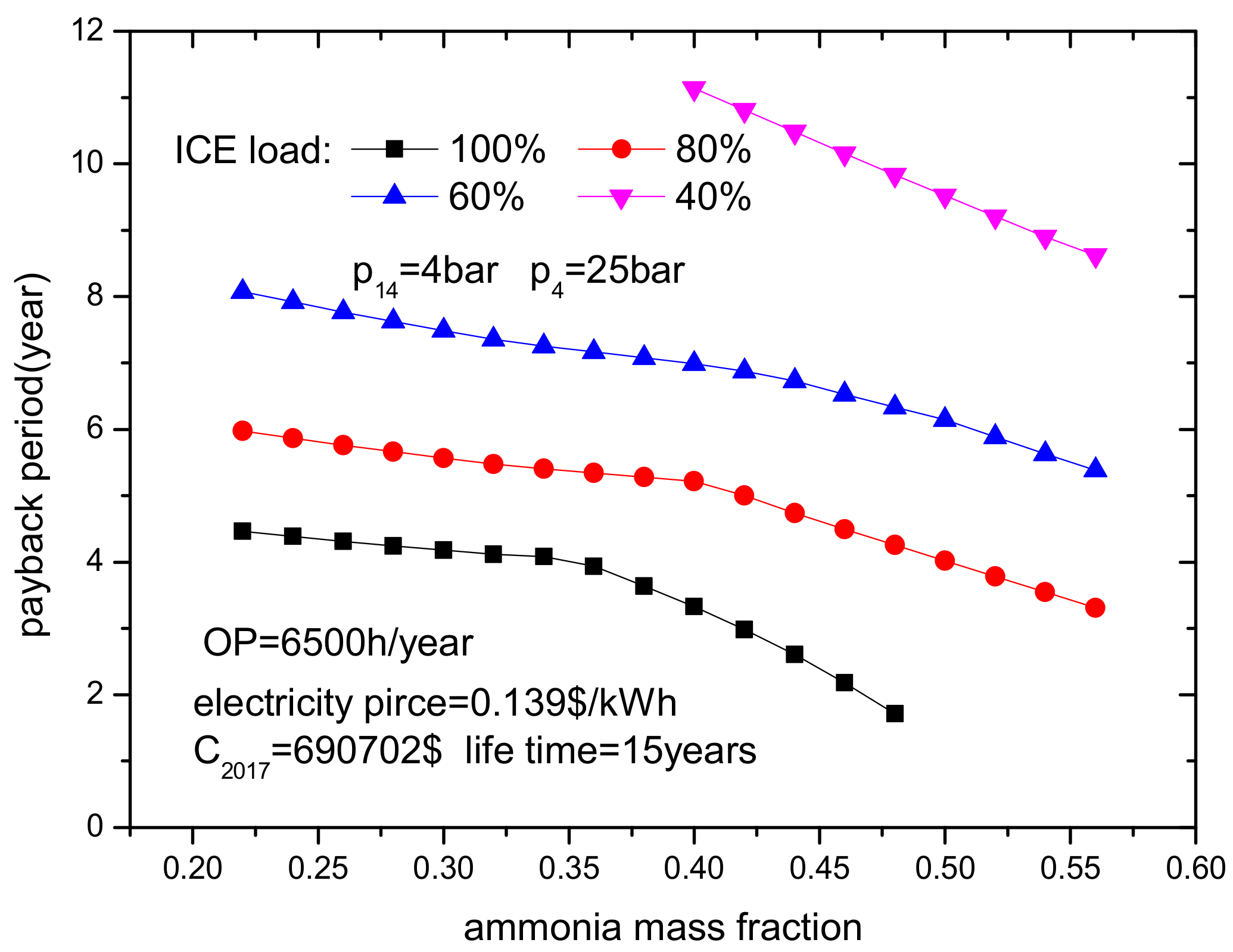
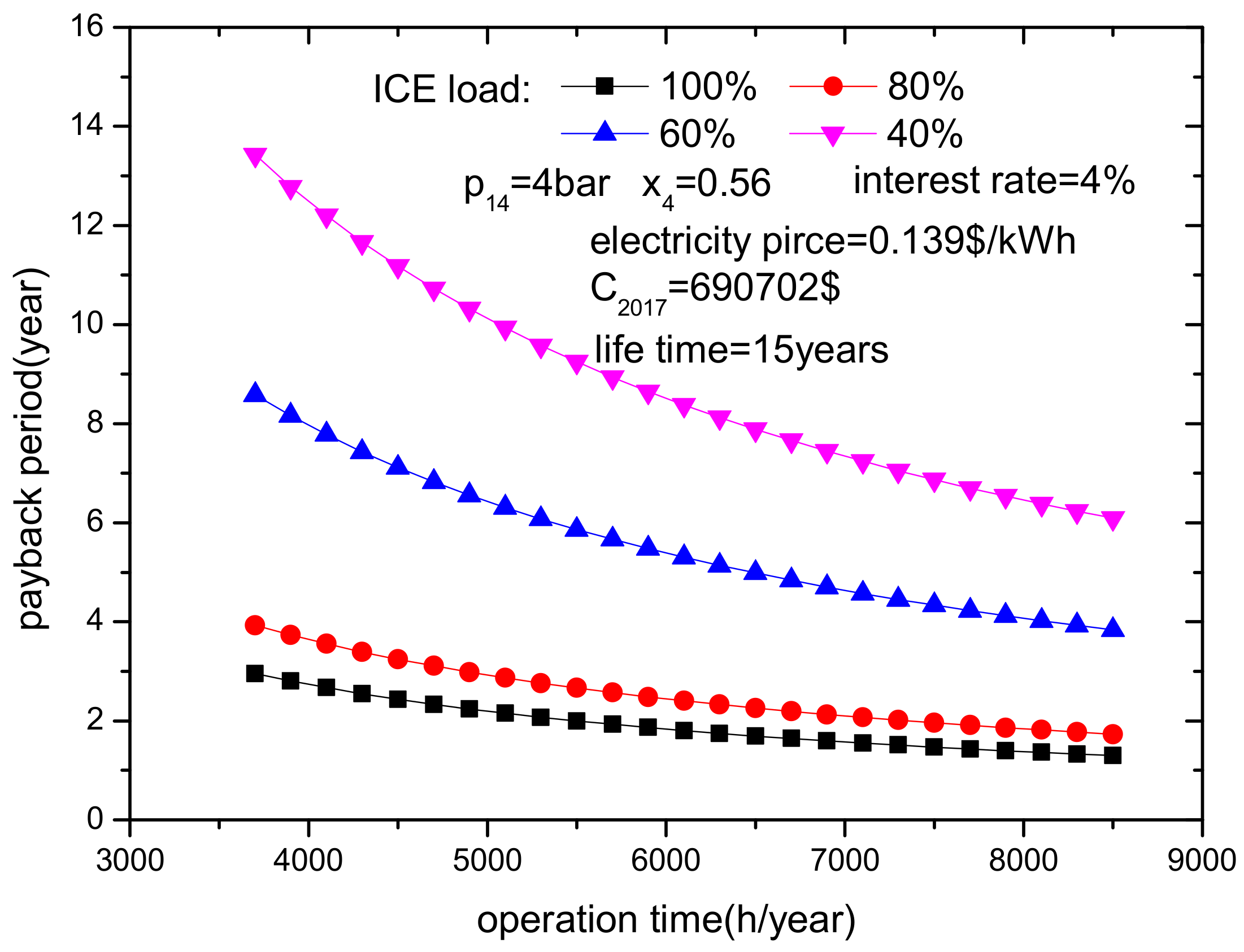
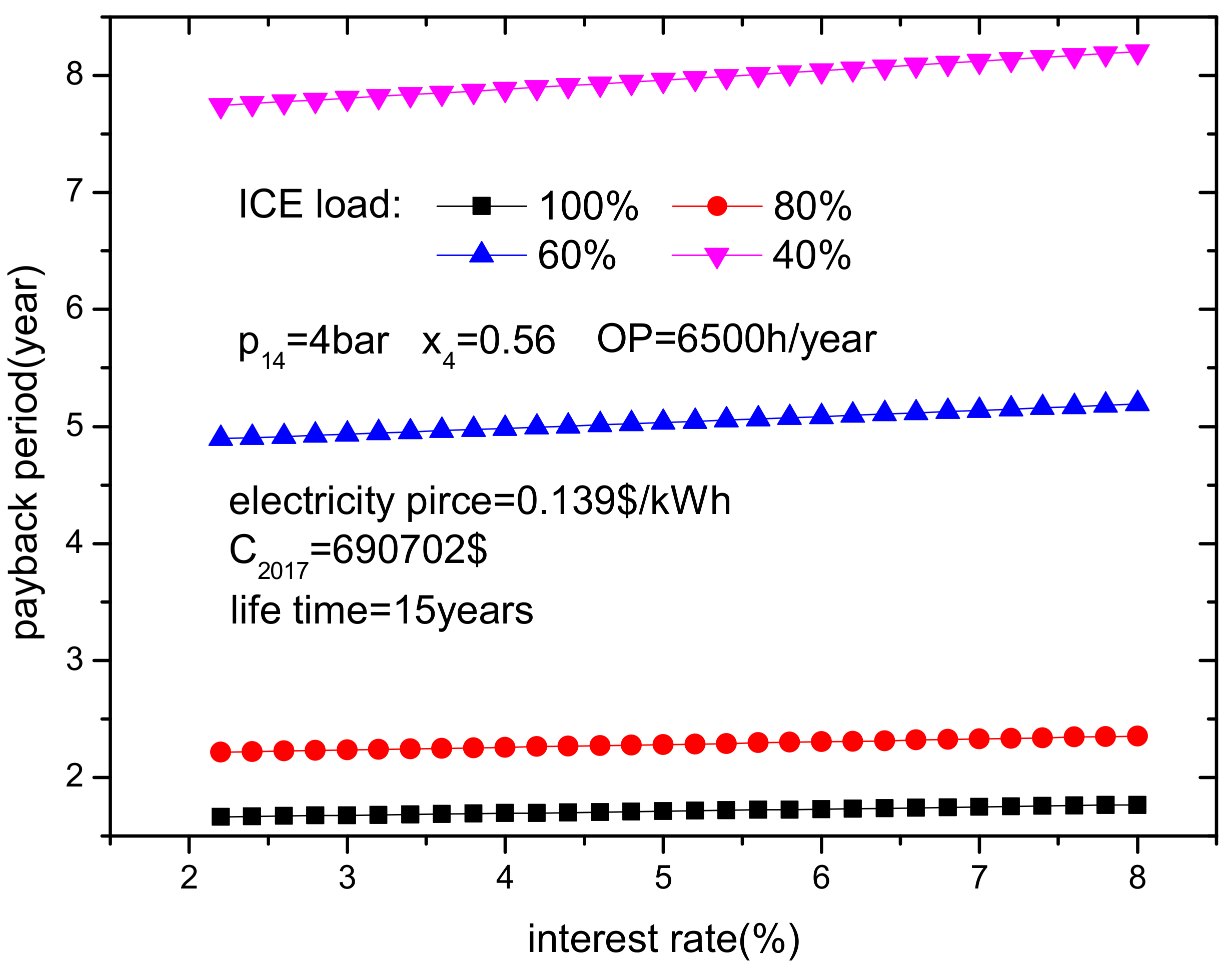
- The capital investment increases with ICE load because a high ICE load results in a high heat transfer area. It is assumed that the Kalina subsystem that requires the largest investment (C2017), is used at all ICE loads in the paper. Both higher ICE loads and higher ammonia mass fractions result in shorter payback periods. If ICE load is high, a lower turbine inlet pressure is better for reducing the payback period. In addition, both longer annual operation times and lower interest rates lead to shorter payback periods. However, it is worth noting that the payback period will be longer than the ICE lifetime if the ICE load is too low and the annual operation time is too short.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | heat exchanger area (m2) |
| C | cost rate ($) |
| COM | operating and maintenance cost |
| CRF | capital recovery factor |
| E | exergy (kJ/kg) |
| h | enthalpy (kJ/kg) |
| i | interest rate |
| m | mass flow rate (kg/s) |
| OP | operation hours |
| ORC | organic rankine cycle |
| p | pressure (bar) |
| P | net power output (W) |
| Q | heat transfer rate (W) |
| s | specific entropy (kJ/kg K) |
| T | temperature (K) |
| x | ammonia mass fraction |
| U | overall heat transfer coefficient |
| W | power output (W) |
| Subscripts abbreviations | |
| evp | evaporator |
| ex | exergy |
| net | net power output |
| ICE | international combustion engine |
| p | pump |
| s | isentropic |
| sup | superheater |
| t | thermal |
| T | turbine |
| Greek symbols | |
| η | Efficiency (%) |
| ΔT | temperature difference (K) |
References
- Wei, M.; Fang, J.; Ma, C.; Danish, S.N. Waste heat recovery from heavy-duty diesel engine exhaust gases by medium temperature orc system. Sci. China Technol. Sci. 2011, 54, 2746–2753. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, K.; Qu, S. Energy and exergy analyses of a bottoming Rankine cycle for engine exhaust heat recovery. Energy 2013, 58, 448–457. [Google Scholar] [CrossRef]
- Kostowski, W.J.; Usón, S. Comparative evaluation of a natural gas expansion plant integrated with an IC engine and an organic rankine cycle. Energy Convers. Manag. 2013, 75, 509–516. [Google Scholar] [CrossRef]
- Seyedkavoosi, S.; Javan, S.; Kota, K. Exergy-based optimization of an organic Rankine cycle (ORC) for waste heat recovery from an internal combustion engine (ICE). Appl. Therm. Eng. 2017, 126, 447–457. [Google Scholar] [CrossRef]
- Wang, X.; Shu, G.; Tian, H.; Liu, P.; Li, X.; Jing, D. Engine working condition effects on the dynamic response of organic Rankine cycle as exhaust waste heat recovery system. Appl. Therm. Eng. 2017, 123, 670–681. [Google Scholar] [CrossRef]
- Pili, R.; Pastrana, J.D.C.; Romagnoli, A.; Spliethoff, H.; Wieland, C. Working fluid selection and optimal power-to-weight ratio for orc in long-haul trucks. Energy Procedia 2017, 129, 754–761. [Google Scholar] [CrossRef]
- Wang, E.; Yu, Z.; Zhang, H.; Yang, F. A regenerative supercritical-subcritical dual-loop organic Rankine cycle system for energy recovery from the waste heat of internal combustion engines. Appl. Energy 2017, 190, 574–590. [Google Scholar] [CrossRef]
- Scaccabarozzi, R.; Tavano, M.; Invernizzi, C.M.; Martelli, E. Thermodynamic Optimization of heat recovery ORCs for heavy duty Internal Combustion Engine: Pure fluids vs. zeotropic mixtures. Energy Procedia 2017, 129, 168–175. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H.; Wang, X. Engine Load Effects on the Energy and Exergy Performance of a Medium Cycle/Organic Rankine Cycle for Exhaust Waste Heat Recovery. Entropy 2018, 20, 1–23. [Google Scholar]
- Wang, X.; Shu, G.; Tian, H.; Liu, P.; Jing, D.; Li, X. Dynamic analysis of the dual-loop Organic Rankine Cycle for waste heat recovery of a natural gas engine. Energy Convers. Manag. 2017, 148, 724–736. [Google Scholar] [CrossRef]
- Kalina, A.I. Combined-cycle system with novel bottoming cycle. J. Eng. Gas Turbines Power 1984, 106, 737–742. [Google Scholar] [CrossRef]
- Ibrahim, O.; Klein, S. Absorption power cycles. Energy 1996, 21, 21–27. [Google Scholar] [CrossRef]
- Fu, W.; Zhu, J.; Zhang, W.; Lu, Z. Performance evaluation of Kalina cycle subsystem on geothermal power generation in the oilfield. Appl. Therm. Eng. 2013, 54, 497–506. [Google Scholar] [CrossRef]
- Madhawa Hettiarachchi, H.D.; Golubovic, M.; Worek, W.M.; Ikegami, Y. The performance of the kalina cycle system 11(kcs-11) with low-temperature heat sources. J. Energy Resour. Technol. 2007, 129, 243–247. [Google Scholar] [CrossRef]
- Singh, O.K.; Kaushik, S.C. Energy and exergy analysis and optimization of Kalina cycle coupled with a coal fired steam power plant. Appl. Therm. Eng. 2013, 51, 787–800. [Google Scholar] [CrossRef]
- Li, S.; Dai, Y. Thermo-economic comparison of kalina and CO2 transcritical power cycle for low temperature geothermal sources in China. Appl. Therm. Eng. 2014, 70, 139–152. [Google Scholar] [CrossRef]
- Yari, M.; Mehr, A.S.; Zare, V.; Mahmoudi, S.M.S.; Rosen, M.A. Exergoeconomic comparison of TLC (trilateral rankine cycle), ORC (organic rankine cycle) and Kalina cycle using a low grade heat source. Energy 2015, 83, 712–722. [Google Scholar] [CrossRef]
- Wang, E.; Yu, Z. A numerical analysis of a composition-adjustable Kalina cycle power plant for power generation from low-temperature geothermal sources. Appl. Energy 2016, 180, 834–848. [Google Scholar] [CrossRef]
- Fallah, M.; Mahmoudi, S.M.S.; Yari, M.; Akbarpour Ghiasi, R. Advanced exergy analysis of the Kalina cycle applied for low temperature enhanced geothermal system. Energy Convers. Manag. 2016, 108, 190–201. [Google Scholar] [CrossRef]
- Nemati, A.; Nami, H.; Ranjbar, F.; Yari, M. A comparative thermodynamic analysis of ORC and Kalina cycles for waste heat recovery: A case study for CGAM cogeneration system. Case Stud. Therm. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Gharde, P.R.; Sali, N.V. Design of Kalina cycle for waste heat recovery from 1196 cc multi-cylinder petrol engine. Int. J. Adv. Res. Sci. Eng. 2015, 4, 75–84. [Google Scholar]
- Yue, C.; Han, D.; Pu, W.; He, W. Comparative analysis of a bottoming transcritical orc and a Kalina cycle for engine exhaust heat recovery. Energy Convers. Manag. 2015, 89, 764–774. [Google Scholar] [CrossRef]
- Xu, F.; Goswami, D.Y.; Bhagwat, S.S. A combined power/cooling cycle. Energy 2000, 25, 233–246. [Google Scholar] [CrossRef]
- Madhawa Hettiarachchi, H.D.; Golubovic, M.; Worek, W.M.; Ikegami, Y. Optimum design criteria for an organic Rankine cycle using low-temperature geothermal heat sources. Energy 2007, 32, 1698–1706. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Guo, T. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar] [CrossRef]
- Zhu, Y.; Qu, W.; Yu, P. Chemical Equipment Design Manual; Chemical Industry Press: Beijing, China, 2005. [Google Scholar]
- Qian, S. Heat Exchanger Design Handbook; Chemical Industry Press: Beijing, China, 2002. [Google Scholar]
- Rodríguez, C.E.C.; Palacio, J.C.E.; Venturini, O.J.; Lora, E.E.S.; Cobas, V.M.; dos Santos, D.M.; Dotto, F.R.L.; Gialluca, V. Exergetic and economic analysis of Kalina cycle for low temperature geothermal sources in Brazil. Appl. Therm. Eng. 2013, 52, 109–119. [Google Scholar] [CrossRef]
- Bahlouli, K.; Khoshbakhti Saray, R.; Sarabchi, N. Parametric investigation and thermo-economic multi-objective optimization of an ammonia–water power/cooling cycle coupled with an HCCI (homogeneous charge compression ignition) engine. Energy 2015, 86, 672–684. [Google Scholar] [CrossRef]
- Xia, J.; Wang, J.; Lou, J.; Zhao, P.; Dai, Y. Thermo-economic analysis and optimization of a combined cooling and power (CCP) system for engine waste heat recovery. Energy Convers. Manag. 2016, 128, 303–316. [Google Scholar] [CrossRef]
- Chemical Enineering. Available online: http://www.chemengonline.com/cepci-updates-january-2018-prelim-and-december-2017-final/ (accessed on 24 March 2018).
- Chen, Y.; Han, W.; Jin, H. Investigation of an ammonia-water combined power and cooling system driven by the jacket water and exhaust gas heat of an Internal combustion engine. Int. J. Refrig. 2017, 82, 174–188. [Google Scholar] [CrossRef]
- Wang, X.Q.; Li, X.P.; Li, Y.R.; Wu, C.M. Payback period estimation and parameter optimization of subcritical organic Rankine cycle system for waste heat recovery. Energy 2015, 88, 734–745. [Google Scholar] [CrossRef]
- State Grid. Available online: http://www.95598.cn/person/sas/es/expenses.jsp?partNo=PM06003001 (accessed on 30 August 2018).
- De Oliveira Neto, R.; Sotomonte, C.A.R.; Coronado, C.J.; Nascimento, M.A. Technical and economic analyses of waste heat energy recovery from internal combustion engines by the Organic Rankine Cycle. Energy Convers. Manag. 2016, 129, 168–179. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Zhang, X.R.; Fujima, K.; Enomoto, M.; Sawada, N. Solar energy powered Rankine cycle using supercritical CO2. Appl. Therm. Eng. 2006, 26, 2345–2354. [Google Scholar] [CrossRef]

| Subsystem | Equipment | Energy Equations |
|---|---|---|
| The topping ICE system | ||
| The bottoming Kalina cycle | Evaporator | |
| Superheater | ||
| Separator | ||
| HE1 | ||
| HE2 | ||
| Condenser | ||
| Turbine | ||
| Pump | ||
| Throttle valve | ||
| Mix tank |
| Parameter | Pressure/bar | Temperature/K | Mass Rate/m3/kg | Ammonia Mass Fraction | ||||
|---|---|---|---|---|---|---|---|---|
| No. | Simulation | Ref. [22] | Simulation | Ref. [22] | Simulation | Ref. [22] | Simulation | Ref. [22] |
| 4 | 53 | 53 | 437 | 433 | 2.07 | 2.06 | 0.37 | 0.37 |
| 5 | 53 | 53 | 494 | 494 | 2.07 | 2.06 | 0.37 | 0.37 |
| 6 | 53 | 53 | 494 | 494 | 0.71 | 0.668 | 0.584 | 0.616 |
| 8 | 3.97 | 3.97 | 382 | 381 | 0.71 | 0.668 | 0.584 | 0.616 |
| 9 | 53 | 53 | 494 | 494 | 1.36 | 1.39 | 0.247 | 0.252 |
| 10 | 53 | 53 | 388 | 380 | 1.36 | 1.39 | 0.247 | 0.252 |
| 11 | 3.97 | 3.97 | 352 | 345 | 1.36 | 1.39 | 0.247 | 0.252 |
| 13 | 3.97 | 3.97 | 337 | 334 | 2.07 | 2.06 | 0.37 | 0.37 |
| 14 | 3.97 | 3.97 | 301 | 301 | 2.07 | 2.06 | 0.37 | 0.37 |
| 15 | 53 | 53 | 302 | 302 | 2.07 | 2.06 | 0.37 | 0.37 |
| Component | Overall Heat Transfer Coefficient (W/m2K) |
|---|---|
| Evaporator | 1100 |
| Conderser | 500 |
| Superheater | 300 |
| Recuperator | 700 |
| Constant | Value | Constant | Value | Constant | Value |
|---|---|---|---|---|---|
| K1,he | 4.3247 | K2,pump | 0.0536 | C2,he | 0.11272 |
| K2,he | −0.303 | K3,pump | 0.1538 | C3,he | 0.08183 |
| K3,he | 0.1634 | B1,he | 1.63 | C1,pump | −0.3935 |
| K1,turb | 2.7051 | B2,he | 1.66 | C2,pump | 0.3957 |
| K2,turb | 1.4398 | B1,sup | 2.25 | C3,pump | −0.00226 |
| K1,sup | 3.4974 | B2,sup | 1.82 | FM,he | 1 |
| K2,sup | 0.4485 | B1,pump | 1.89 | FBM,turb | 3.5 |
| K3,sup | 3.4974 | B2,pump | 1.35 | FM,sep | 1 |
| K1,pump | 3.3892 | C1,he | 0.03881 | FM,pump | 2.2 |
| ICE Load Percentage | Fuel Total Heating Value Q0 (kW) | Power Output PICE (kW) | Thermal Efficiency of ICE ηt_ICE (%) | Exhaust Gases Temperature T1 (K) |
|---|---|---|---|---|
| 100 | 5590 | 2000 | 35.78 | 712 |
| 90 | 5050 | 1800 | 35.64 | 683 |
| 80 | 4560 | 1600 | 35.09 | 660 |
| 75 | 4330 | 1500 | 34.64 | 649 |
| 70 | 4110 | 1400 | 34.06 | 638 |
| 60 | 3640 | 1200 | 32.97 | 618 |
| 50 | 3120 | 1000 | 32.05 | 596 |
| 40 | 2580 | 800 | 31.01 | 569 |
| 30 | 2050 | 600 | 29.27 | 535 |
| 25 | 1810 | 500 | 27.62 | 514 |
| 20 | 1560 | 400 | 25.64 | 491 |
| 10 | 1060 | 200 | 18.87 | 419 |
| Items | Value | Value in Ref. [22] | Items | Value | Value in Ref. [22] |
|---|---|---|---|---|---|
| ICE load percentage (%) | 100% | 100% | Q3 (kW) | 920 | 1151 |
| fuel total heating value Q0 (kW) | 5590 | 5590 | Q4 (kW) | 448 | 935 |
| power output PICE (kW) | 2000 | 2000 | WT_Kalina (kW) | 436.6 | 217 |
| exhaust gases volume flow rate (m3/s) | 7.2 | 7.2 | Wnet_Kalina (kW) | 432 | |
| exhaust gases temperature T1 (K) | 712 | 712 | ηt_kalina (%) | 46.94 | 18.8 |
| turbine inlet temperature T7 (K) | 692 | 494 | ηt_ICE (%) | 35.78 | 35.78 |
| turbine inlet pressure p7 (bar) | 30 | 53 | Δηt (%) | 21.6 | 15.1 |
| ammonia mass fraction x4 | 0.56 | 0.37 | payback period (year) | 2.94 | |
| m4 (kg/s) | 0.985 | Mem (tons/year) | 1691 | ||
| m6 (kg/s) | 0.952 | Mpe (kL/year) | 503.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Chen, F. Thermo-Economic Analysis of a Bottoming Kalina Cycle for Internal Combustion Engine Exhaust Heat Recovery. Energies 2018, 11, 3044. https://doi.org/10.3390/en11113044
Gao H, Chen F. Thermo-Economic Analysis of a Bottoming Kalina Cycle for Internal Combustion Engine Exhaust Heat Recovery. Energies. 2018; 11(11):3044. https://doi.org/10.3390/en11113044
Chicago/Turabian StyleGao, Hong, and Fuxiang Chen. 2018. "Thermo-Economic Analysis of a Bottoming Kalina Cycle for Internal Combustion Engine Exhaust Heat Recovery" Energies 11, no. 11: 3044. https://doi.org/10.3390/en11113044
APA StyleGao, H., & Chen, F. (2018). Thermo-Economic Analysis of a Bottoming Kalina Cycle for Internal Combustion Engine Exhaust Heat Recovery. Energies, 11(11), 3044. https://doi.org/10.3390/en11113044




