A Numerical Study on the Diversion Mechanisms of Fracture Networks in Tight Reservoirs with Frictional Natural Fractures
Abstract
:1. Introduction
2. Problem Formulation
2.1. Governing Equations of Hydraulic Fracturing Problems
2.2. Crack Propagation Criterion
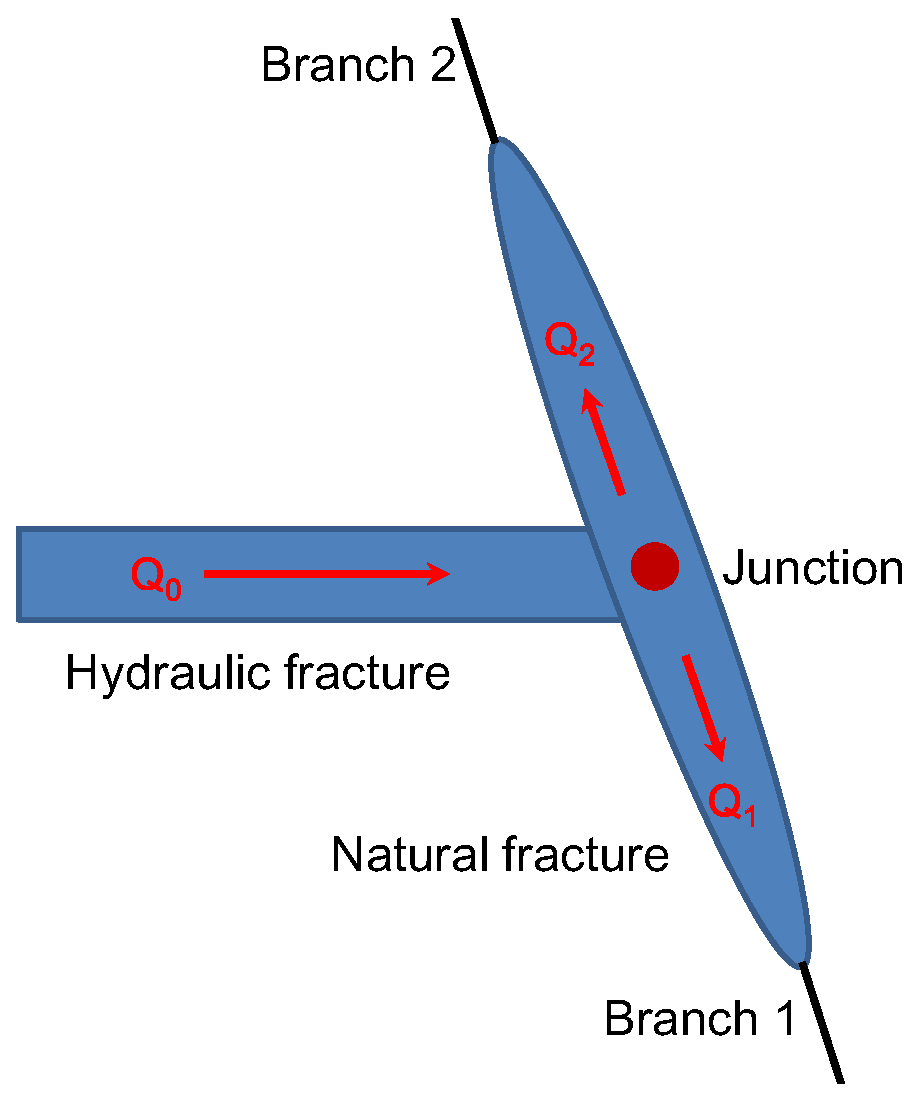
2.3. The Cross Criterion between HF and Frictional NF
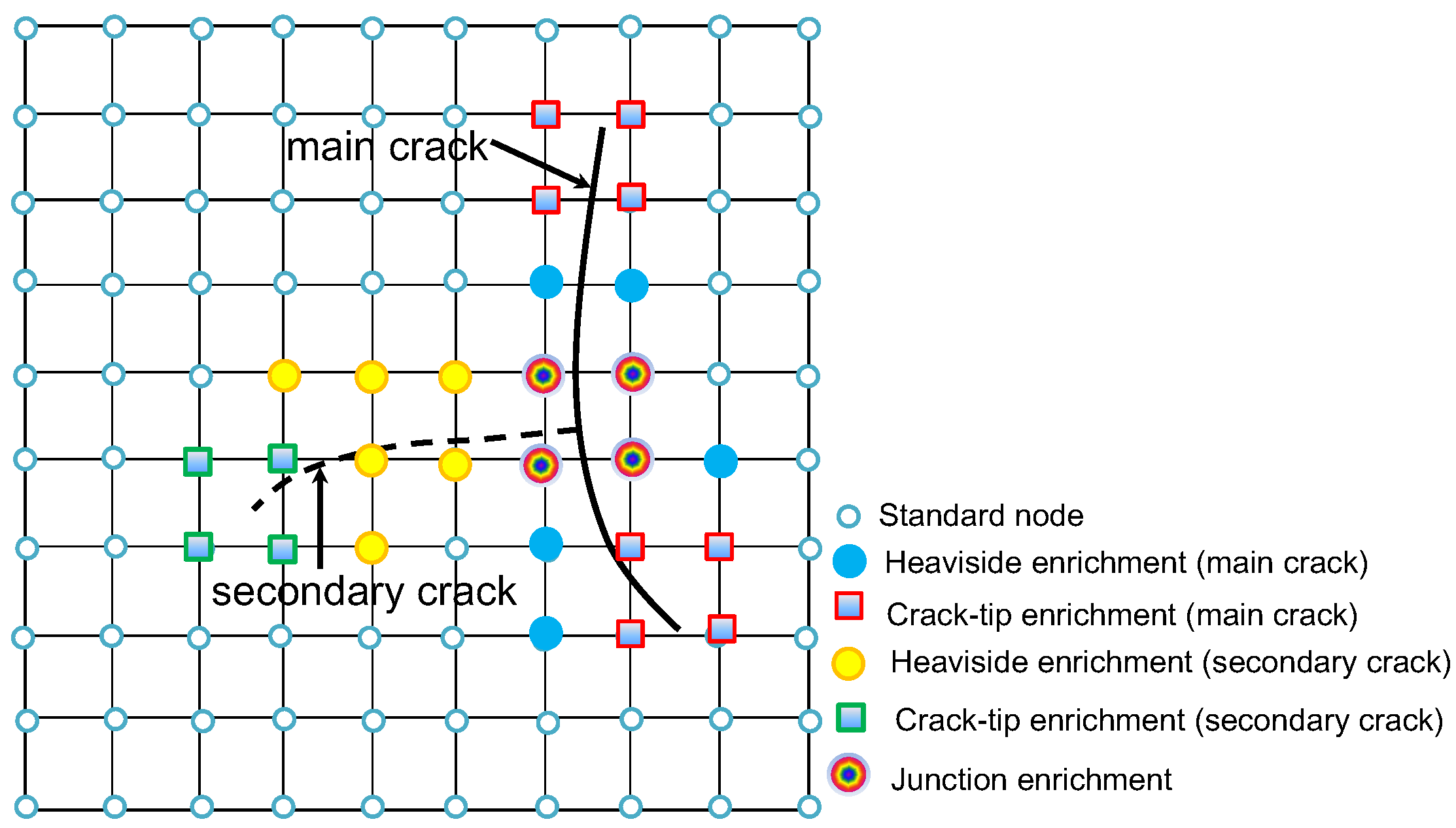
2.4. XFEM and Discretization of the Governing Equations of the Hydraulic Fracturing Problem
3. Results and Discussion
3.1. Verification of the XFEM Model
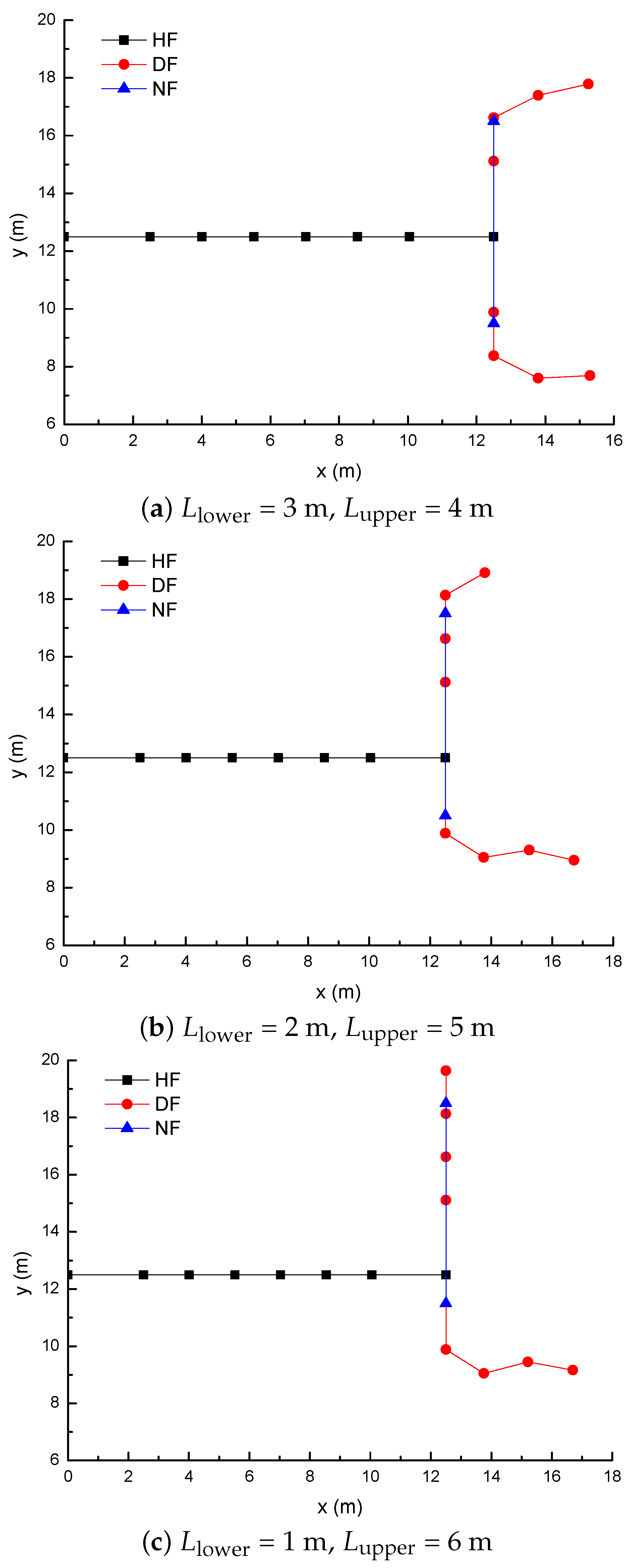
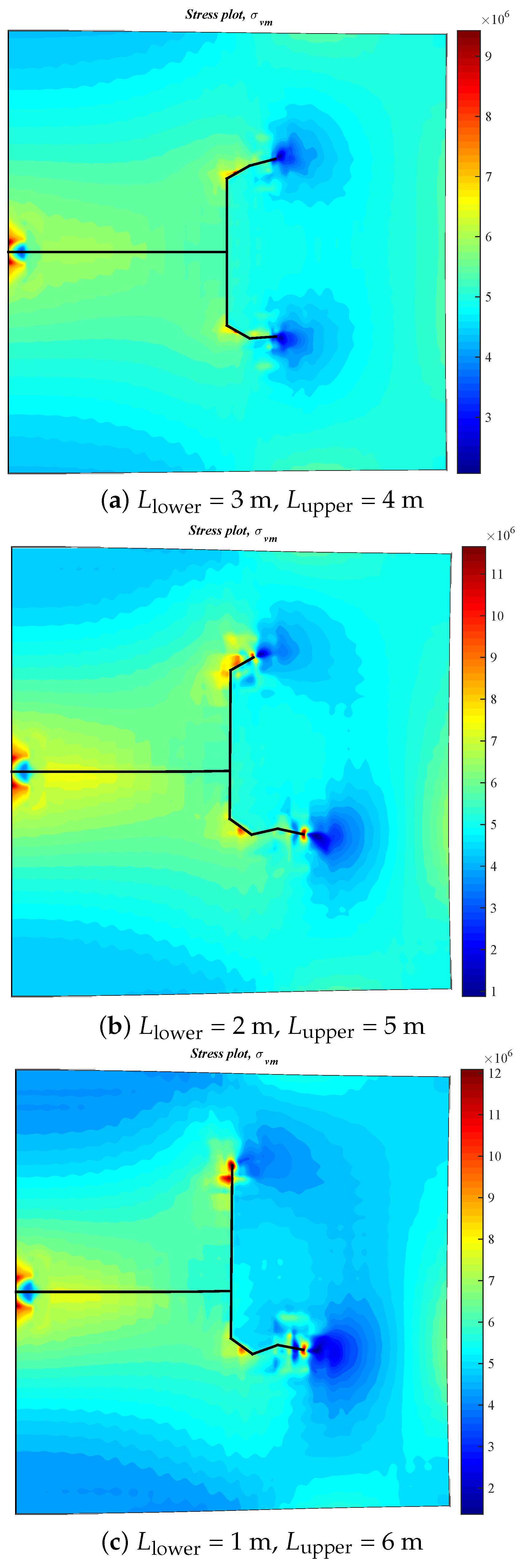
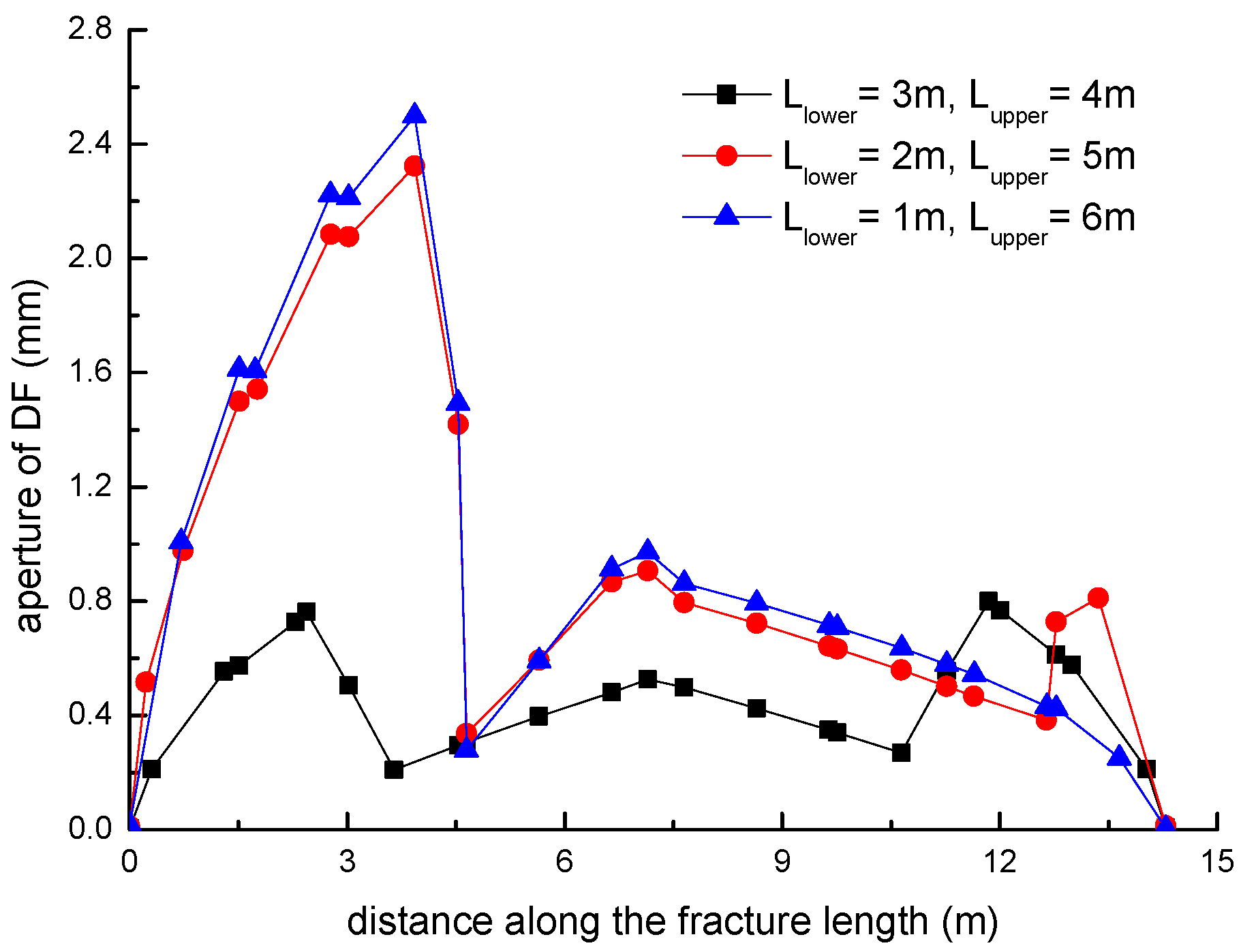
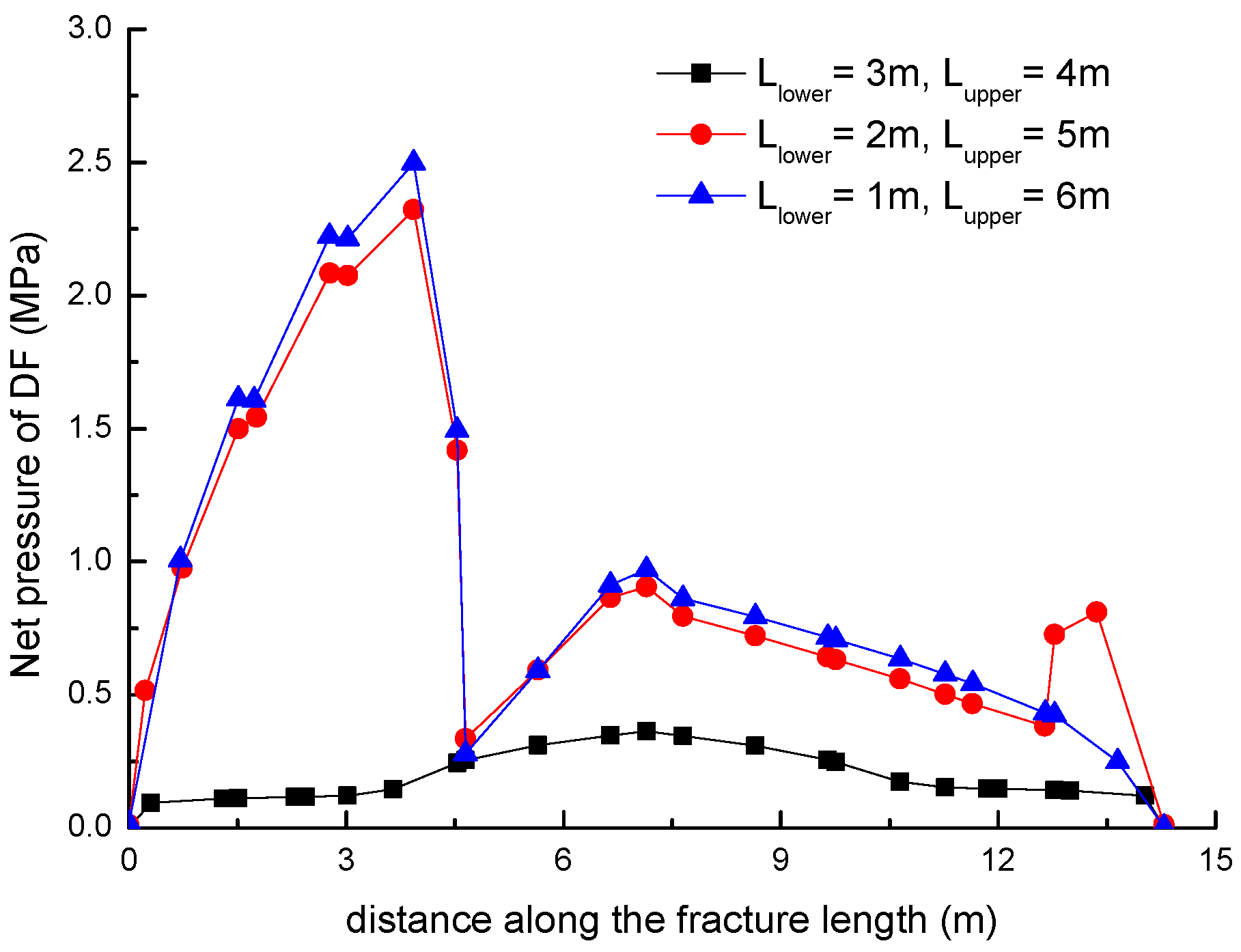
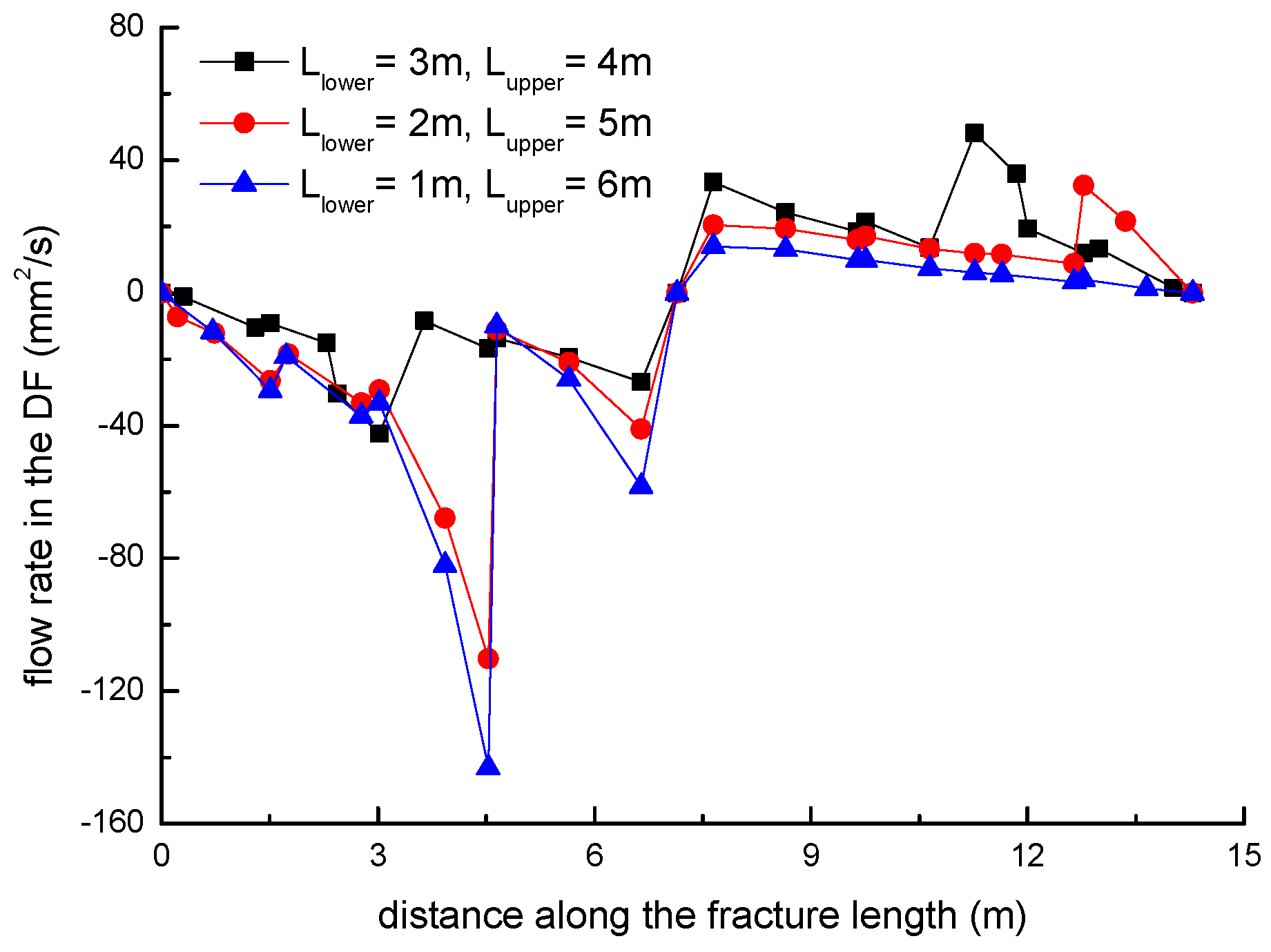
3.2. Effect of the Location of Natural Fractures on the Diversion of Fracture Network Propagation
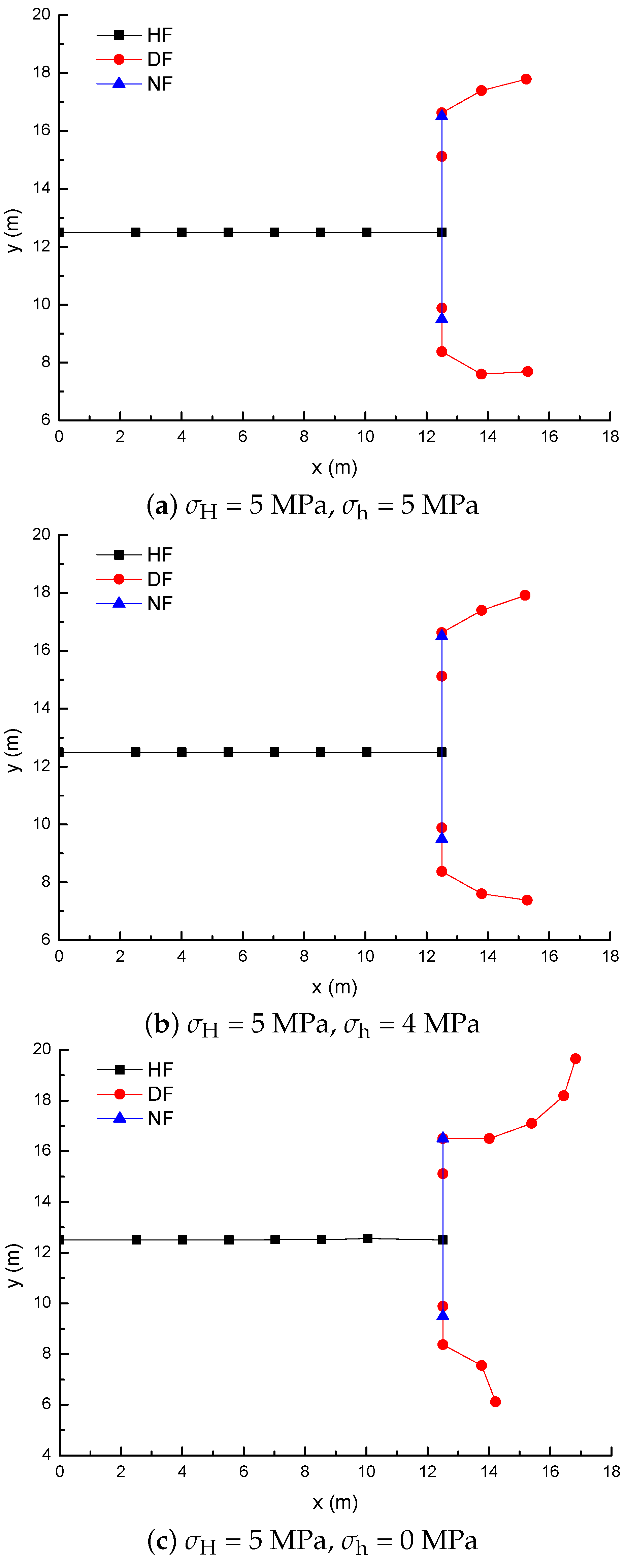
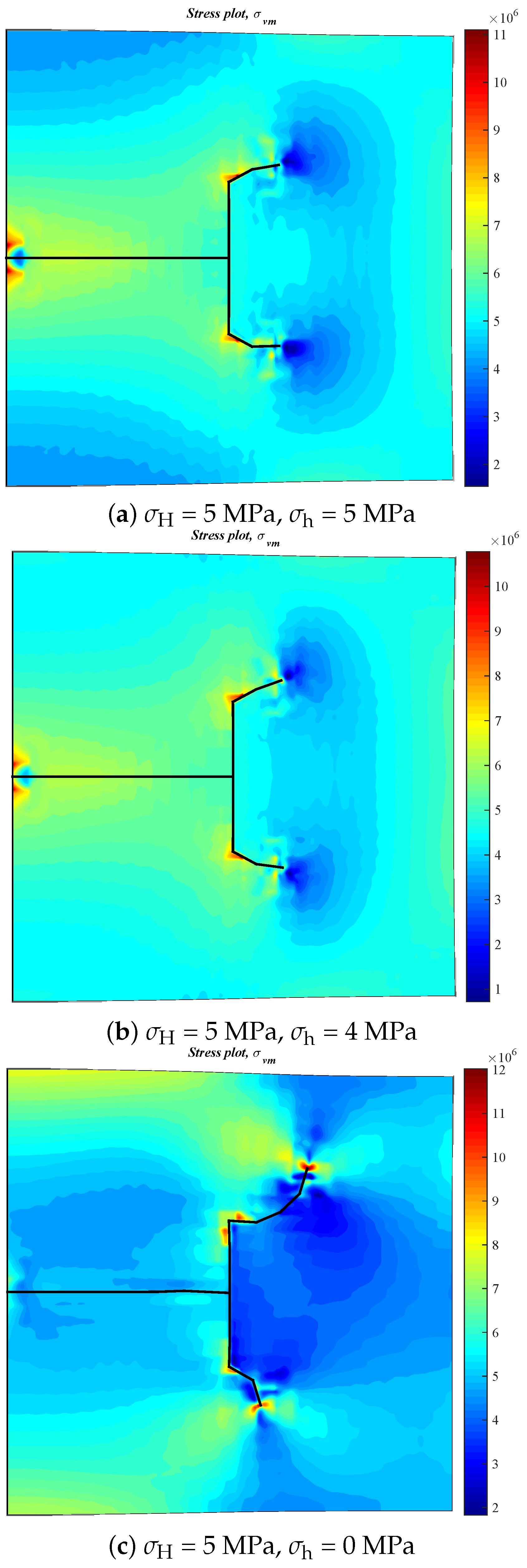
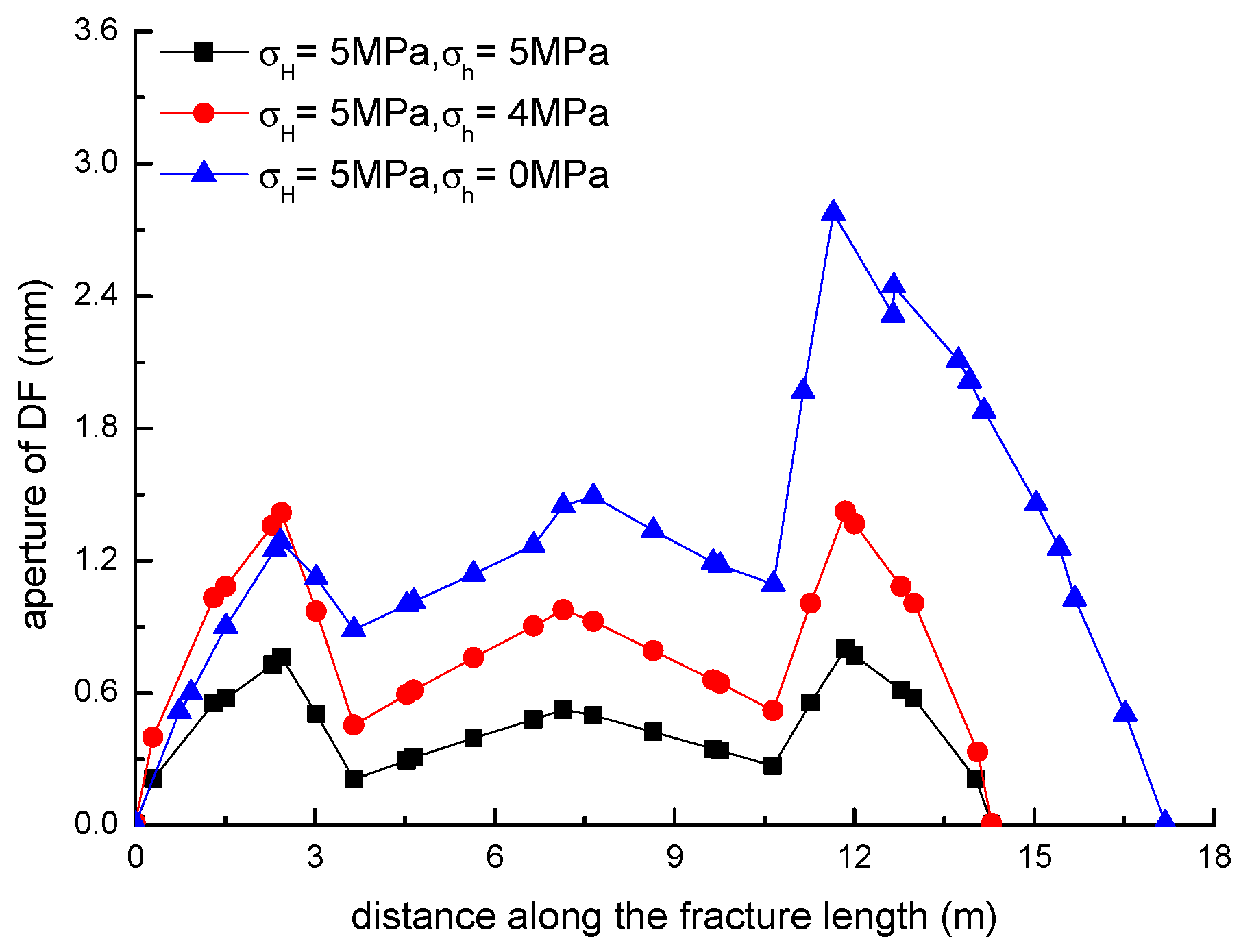
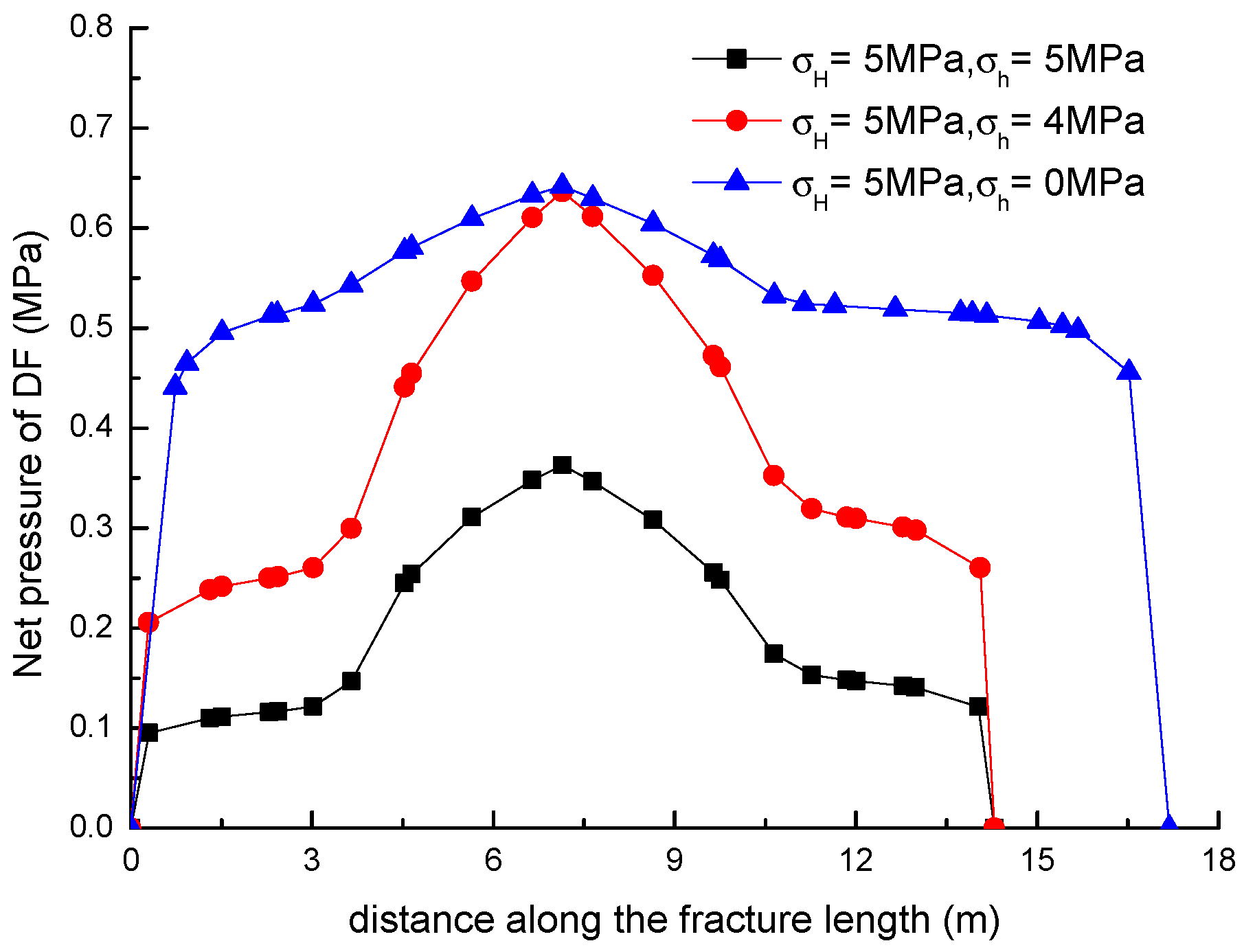
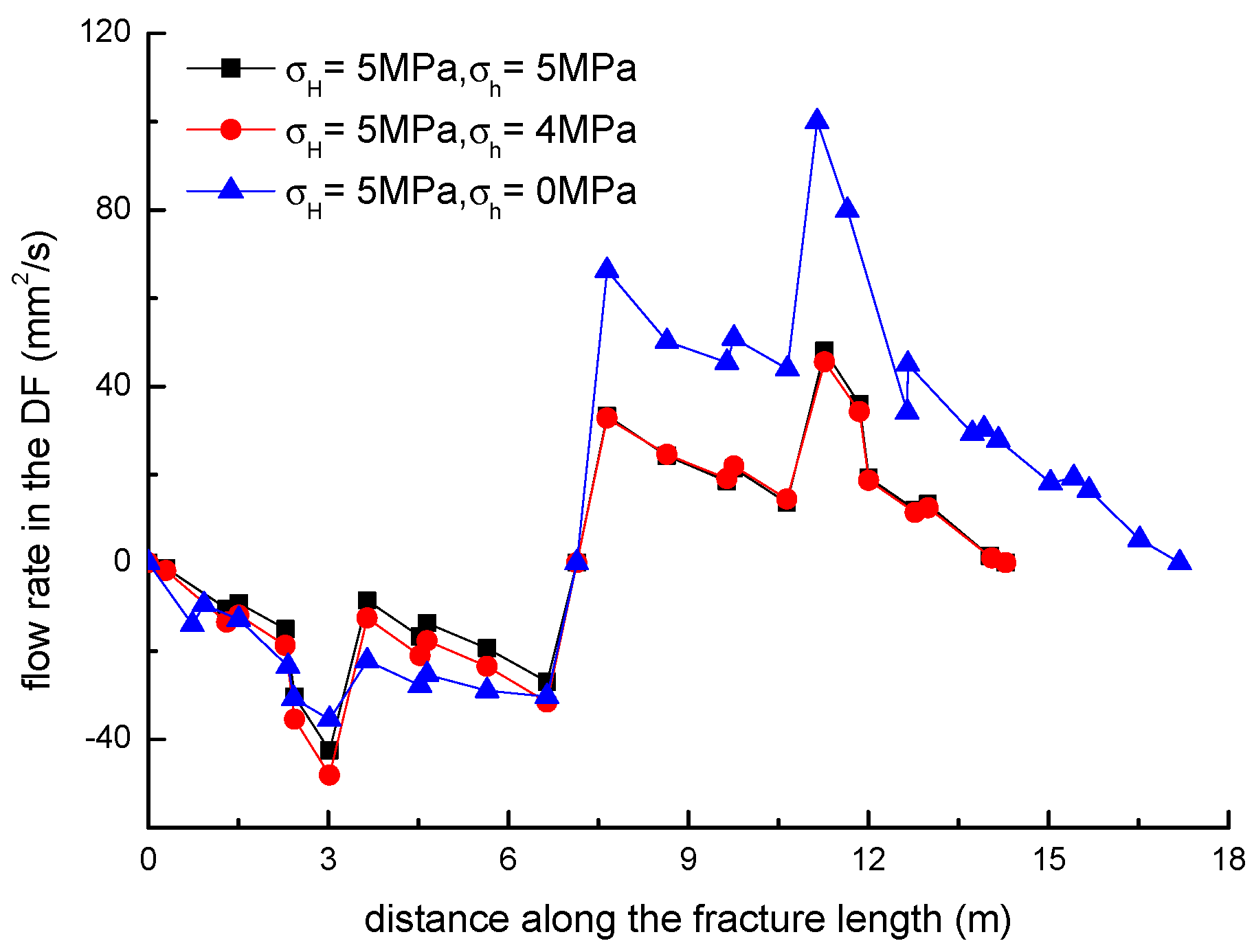
3.3. Effect of Horizontal Stress Differences on the Diversion of Fracture Network Propagation
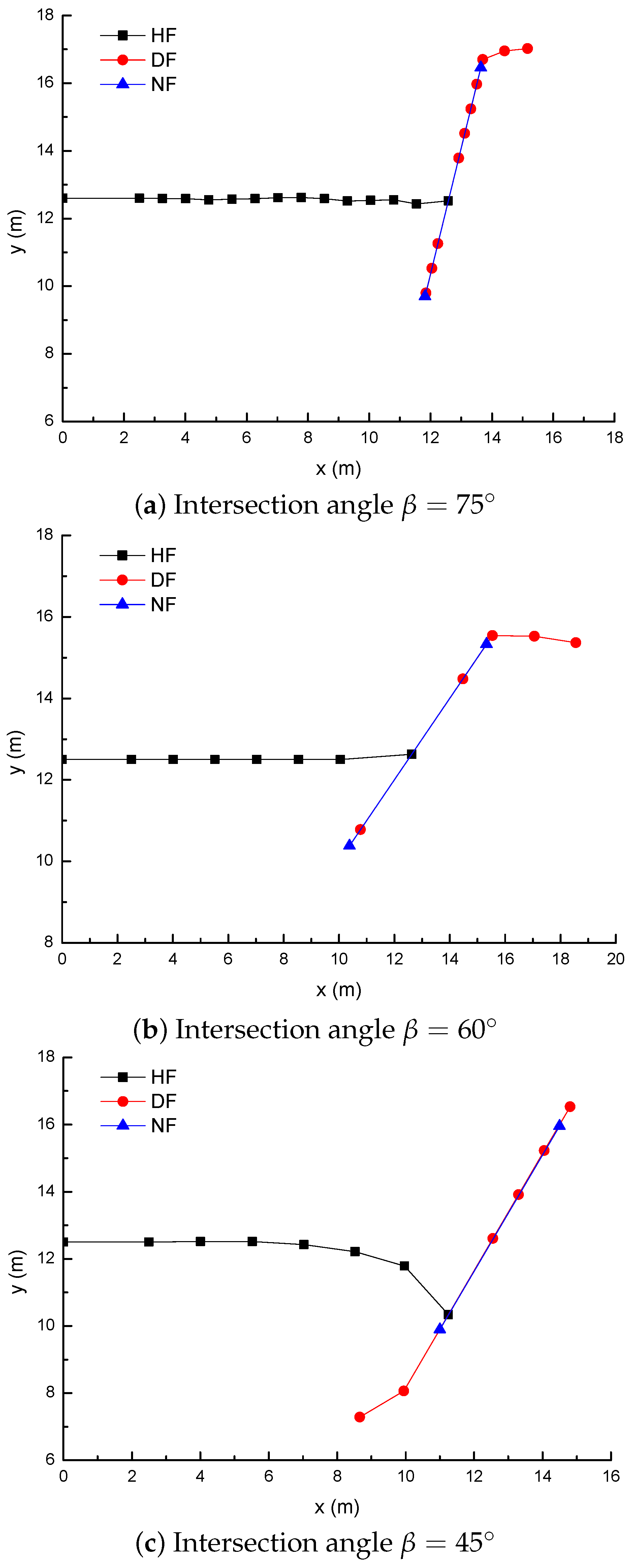
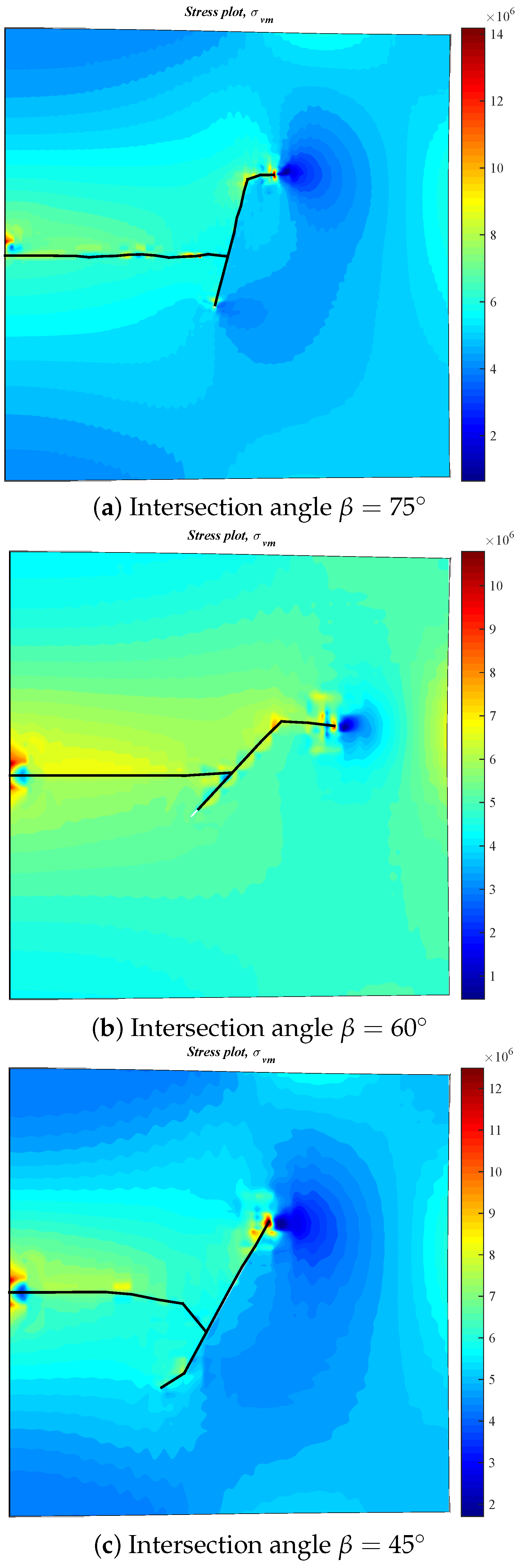
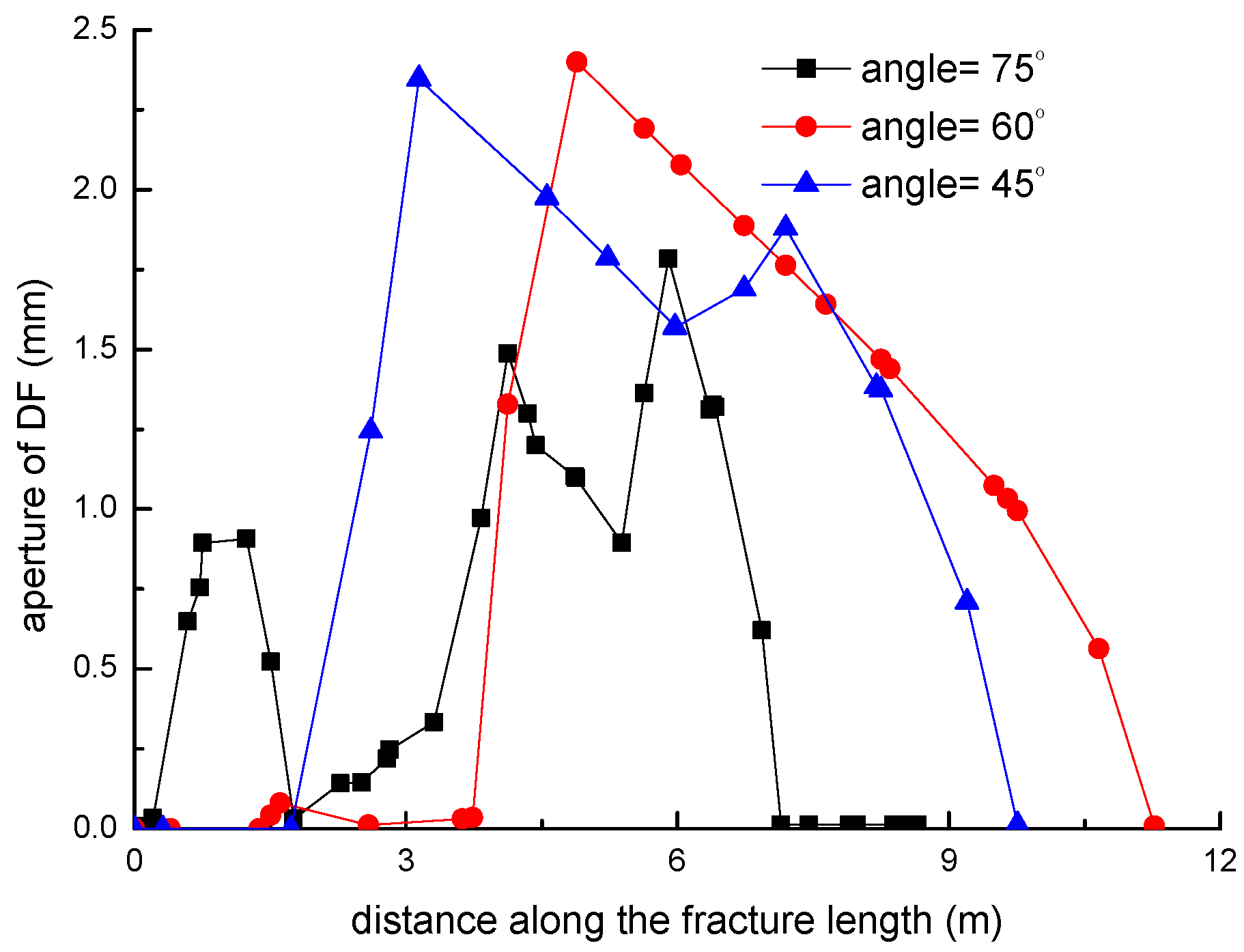
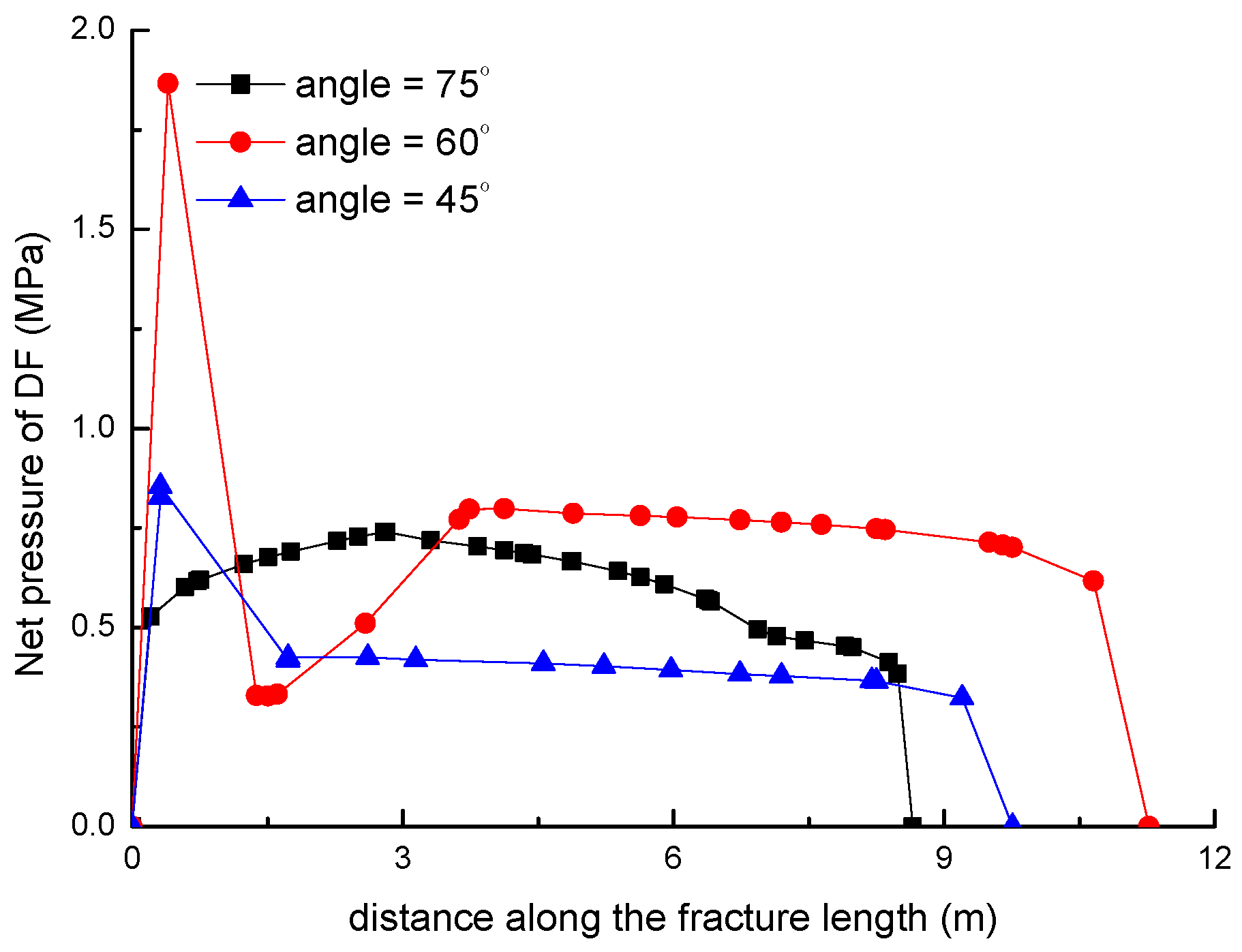
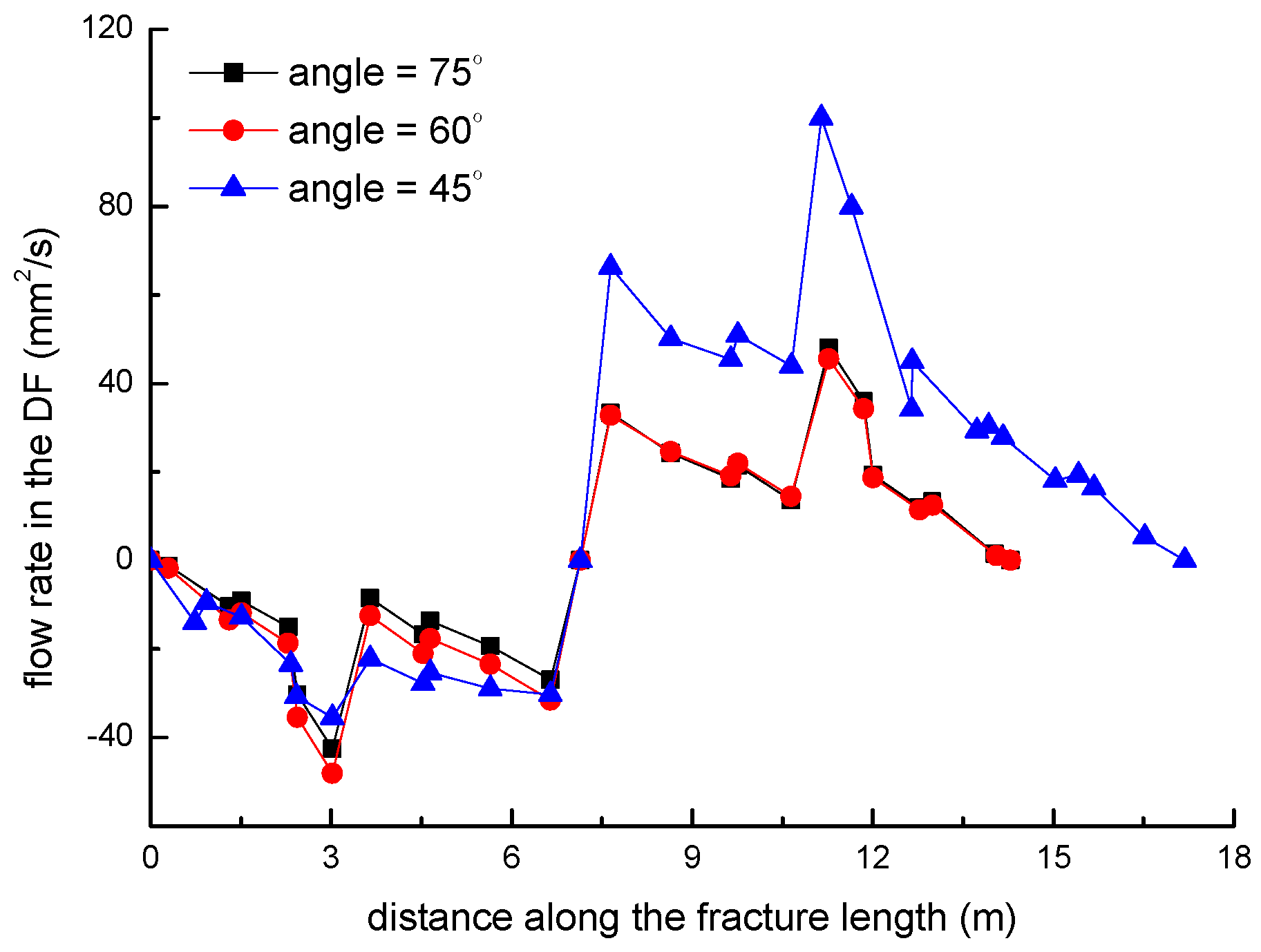
3.4. Effect of the NF–HF Intersection Angle on the Diversion of Fracture Network Propagation
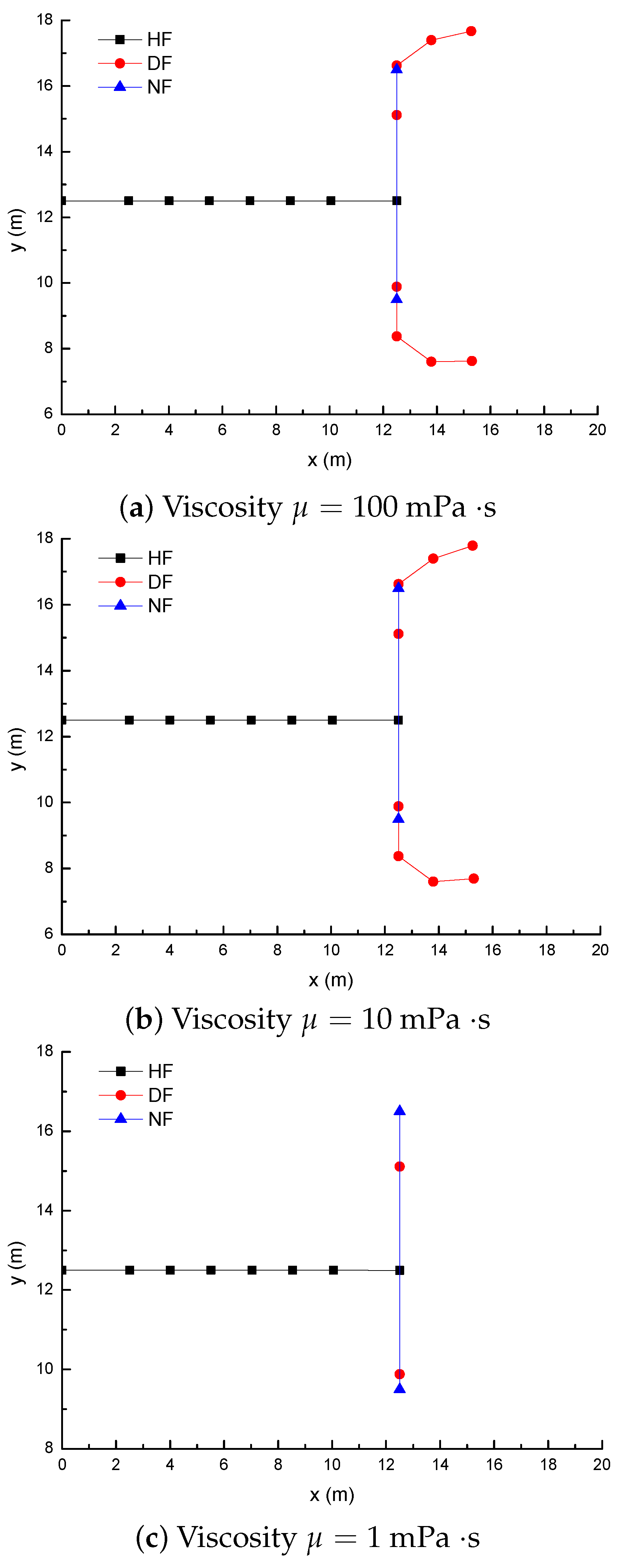
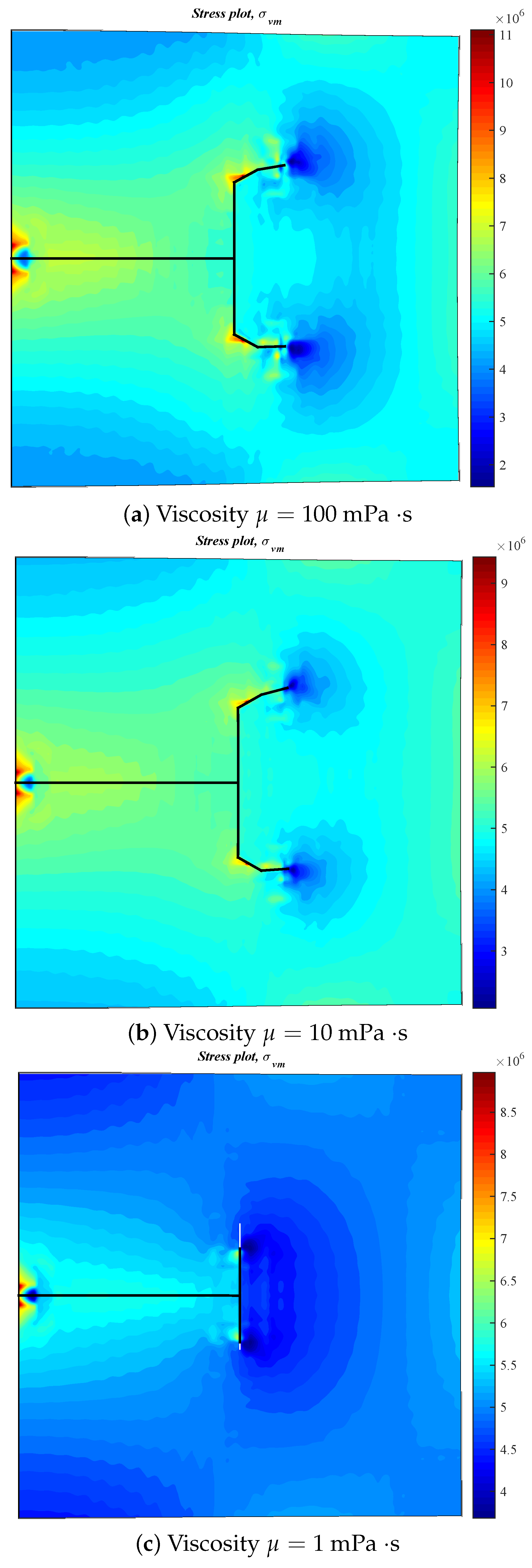
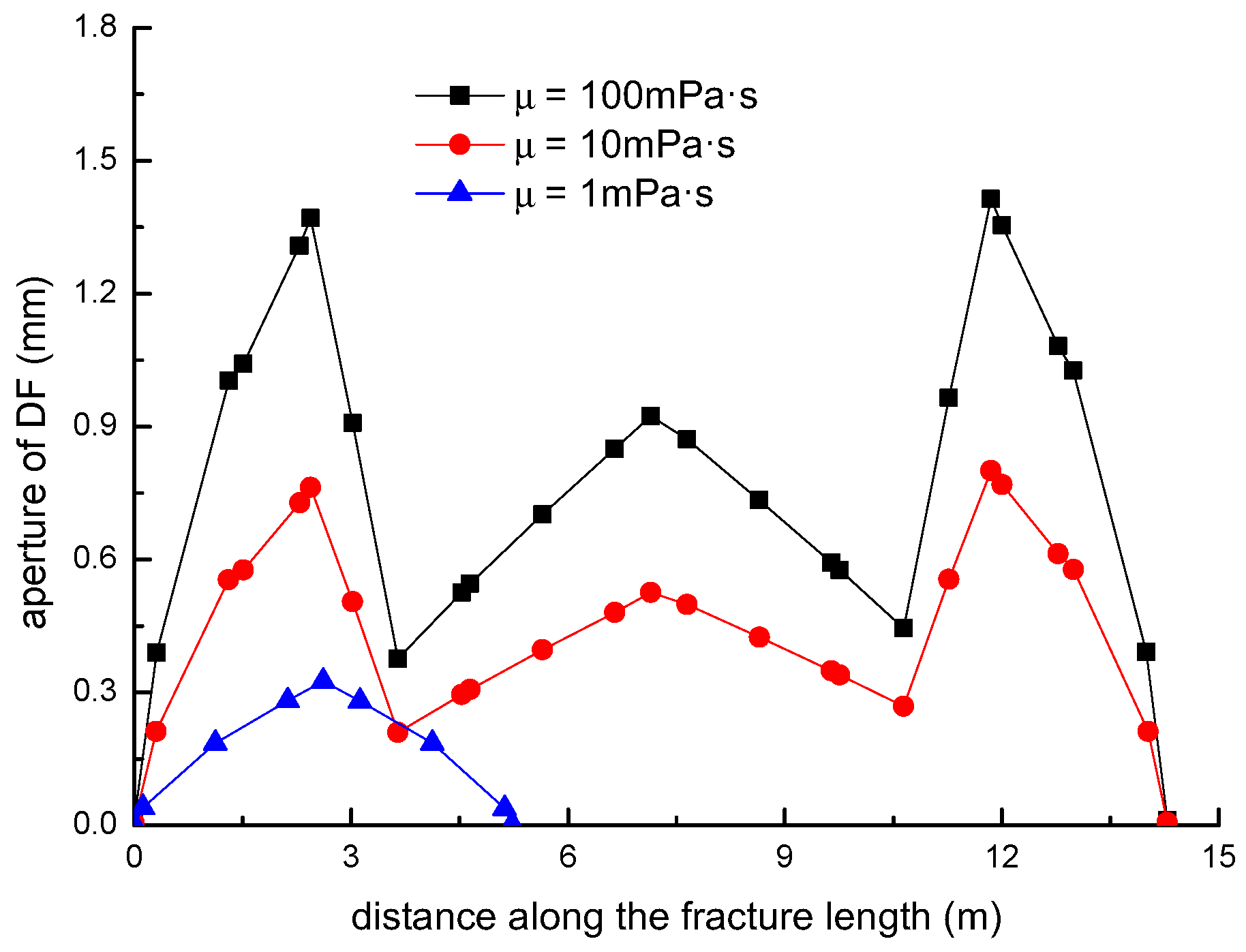
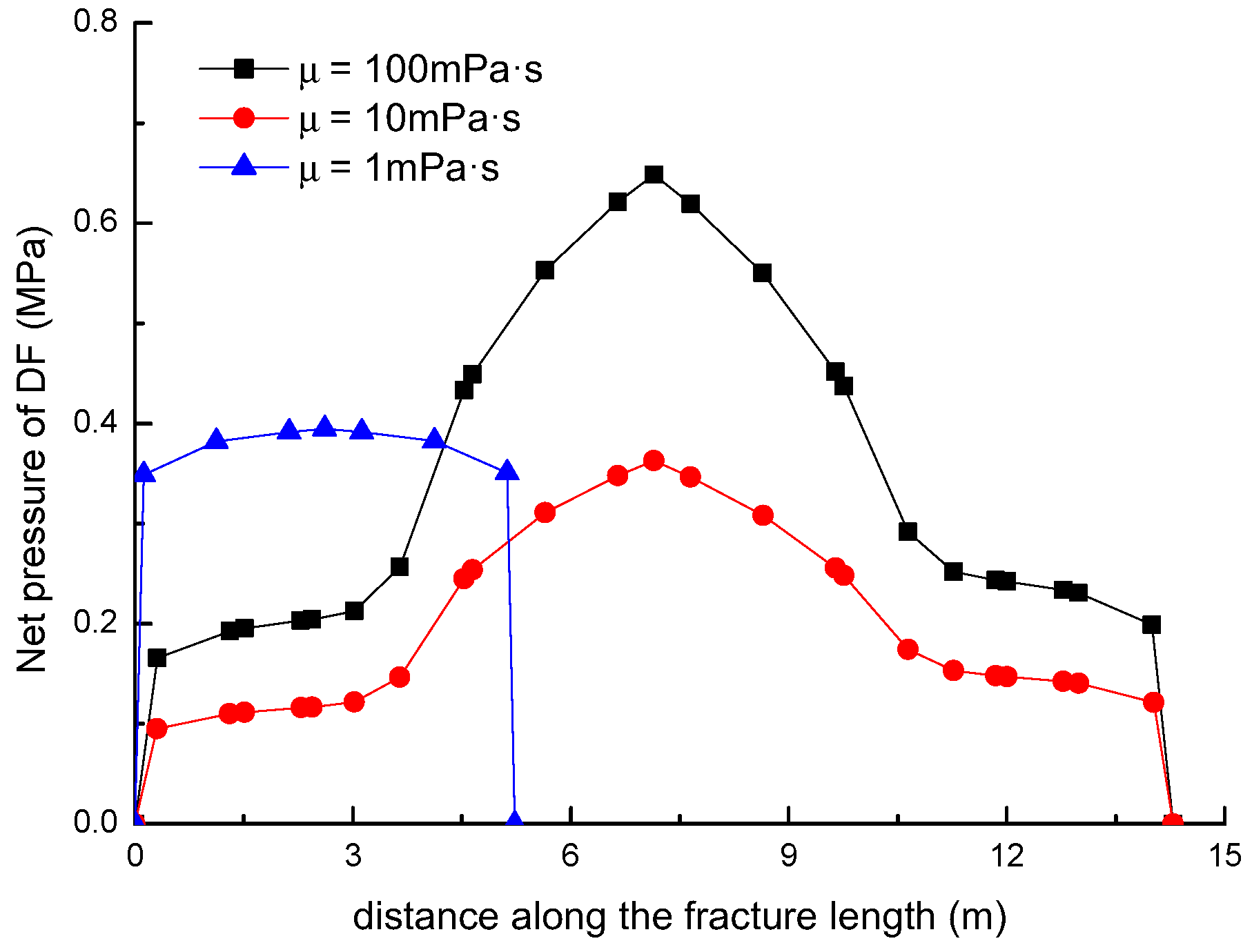
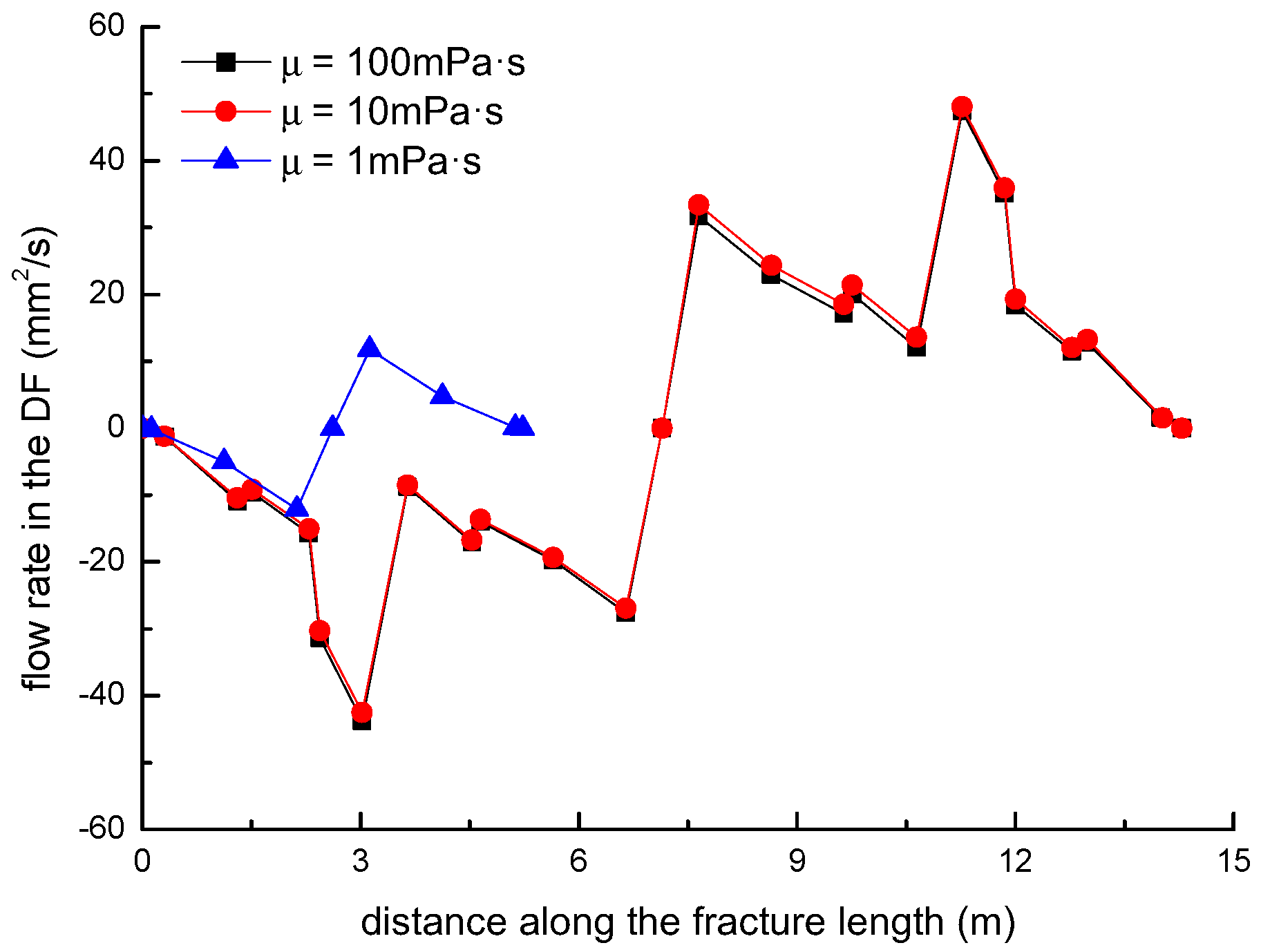
3.5. Effect of Fluid Viscosity on the Diversion of Fracture Network Propagation
4. Conclusions
- (1)
- Fracture diversion propagation will occur near the two tips of the opened NF after an HF is intersecting with an NF. The numerical results show that some key factors such as the NF position, the NF–HF intersection angle, the horizontal stress differences, and the fluid viscosity have a significant impact on the diversion propagation in the upper and lower parts of the opened NF.
- (2)
- For a constant length of NF (7 m), the upper length of the DF decreases by about 2 m with a 2 m increment of the upper length of the NF (), while the length of the DF increases 9.06 m, with the fluid viscosity increased from 1 to 100 mPa.s; (2) the deflection angle in the upper parts increases by 30.8° with the stress difference increased by 5 MPa, while the deflection angle increases by 61.2° with the intersection angle decreased from 75° to 45°.
- (3)
- The longer the upper parts of the original NF are, the more difficult it is for the opened NF to divert away from the upper tip of the NF under the conditions of an isotropic stress state, while the lower parts of the original NF is more easily diverted to the right-hand side than the upper parts of the original NF. The NF–HF intersection angle will have a significant impact on the diversion propagation of the primary HF and the secondary opened NFs.
- (4)
- In general, the distributions of fracture aperture, net pressure, and flow rate reveal asymmetrical characteristics for the secondary hydraulically driven fractures. For the distribution of Von-Mises stress, there is usually a concentrated stress zone area near the turning point of the secondary cracks, which corresponds to the inflection points on the curves of the fracture aperture and net pressure.
- (5)
- The diversion mechanisms of the fracture network are the results of the combined action of all factors. This will provide a new perspective on the mechanisms of fracture network generation. Future work should determine the primary and secondary relations of various factors by means of experiments and numerical calculation.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| XFEM | Extended Finite Element Method |
| DEM | Discrete Element Method |
| NMM | Numerical Manifold Method |
| SRV | Stimulated Reservoir Volume |
| HF | Hydraulic Fracture or Hydraulically Driven Fracture or Hydro-Fracture |
| NF | Natural Fracture |
| DF | Diverted Fracture |
| PFP | Preferred Fracture Plane |
| ELP | Enhanced Local Pressure |
Appendix A
| Input Parameter | Value |
|---|---|
| Young’s Modulus, E | 20 GPa |
| Poisson’s ratio, | 0.2 |
| Fracture toughness, | 0.1 |
| The consistency index of fracturing fluid, K | 0.84 |
| Injection rate, | 0.001 |
| Viscosity, | 0.1 |
| Dimensionless fracture toughness, | 0.313 |
| Injection time, t | 30 s |
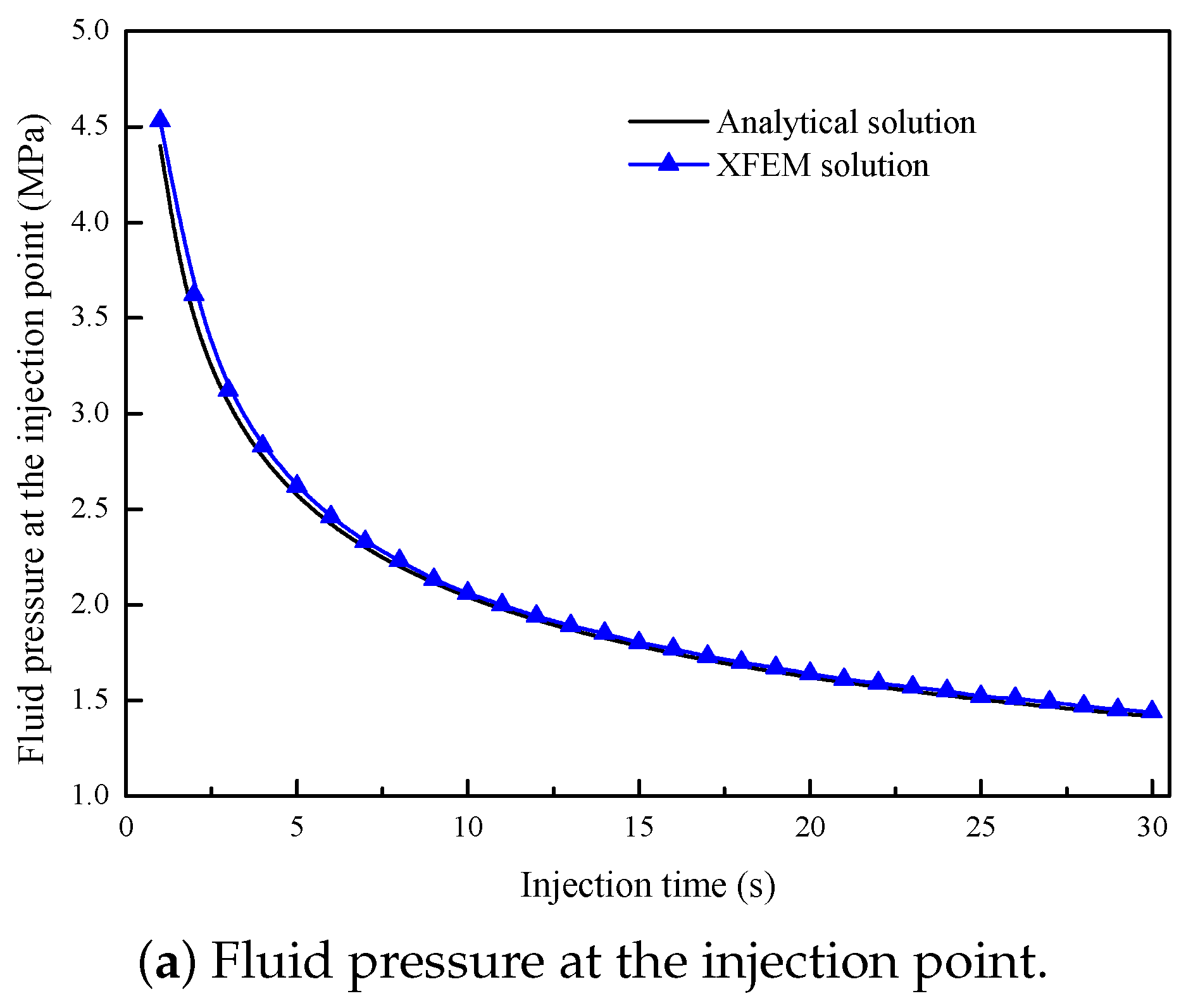
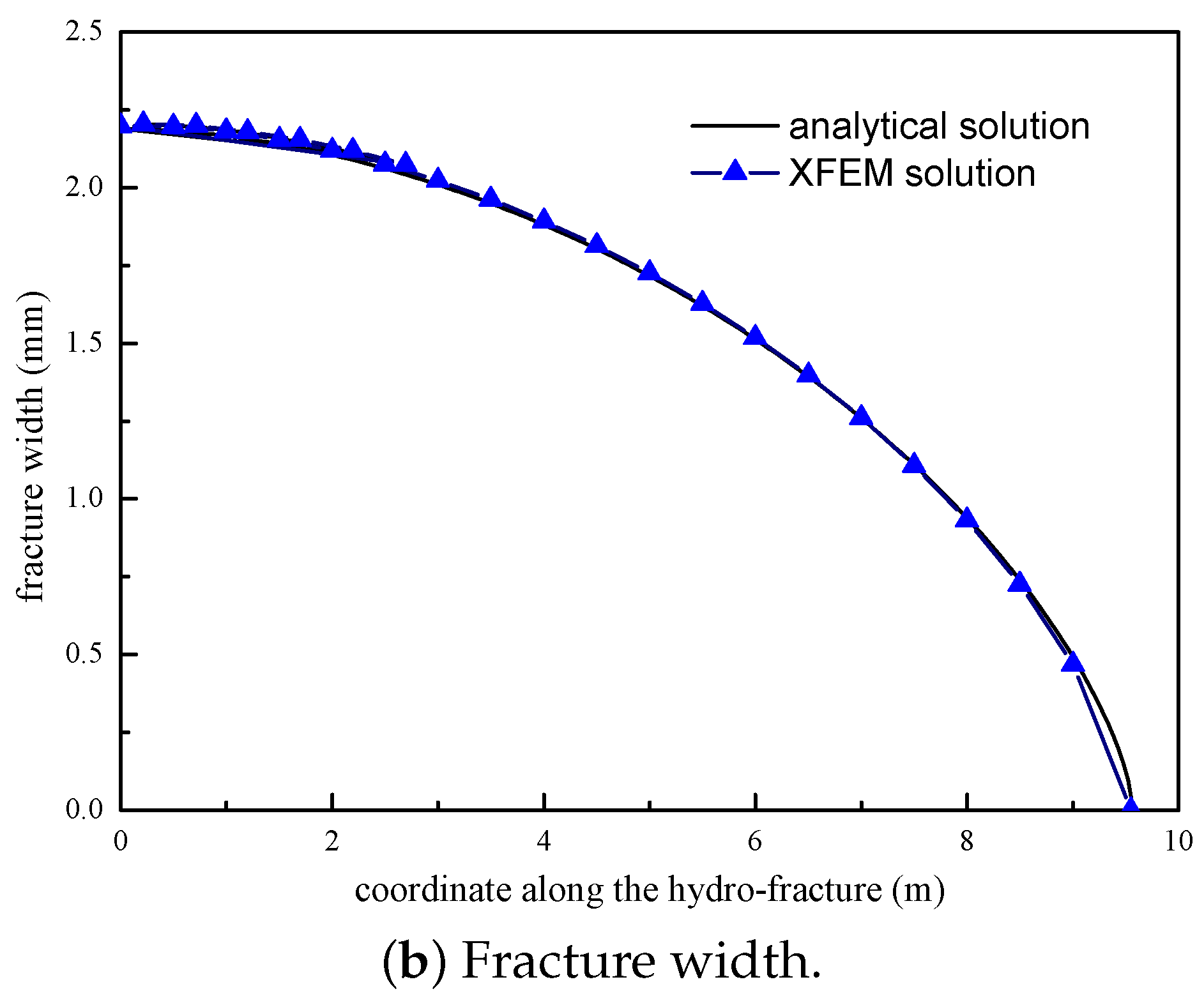
References
- Pang, Y.; Soliman, M.Y.; Deng, H.; Emadi, H. Analysis of effective porosity and effective permeability in shale-gas reservoirs with consideration of gas adsorption and stress effects. SPE J. 2017, 22, 1739–1759. [Google Scholar] [CrossRef]
- Shen, Y.; Ge, H.; Li, C.; Yang, X.; Ren, K.; Yang, Z.; Su, S. Water imbibition of shale and its potential influence on shale gas recovery—A comparative study of marine and continental shale formations. J. Nat. Gas Sci. Eng. 2016, 35, 1121–1128. [Google Scholar] [CrossRef]
- Pang, Y.; Soliman, M.; Deng, H.; Emadi, H. Effect of methane adsorption on stress-dependent porosity and permeability in shale gas reservoirs. In Proceedings of the SPE Low Perm Symposium, Denver, CO, USA, 5–6 May 2016. [Google Scholar]
- Matsunaga, I.; Kobayashi, H.; Sasaki, S.; Ishida, T. Studying hydraulic fracturing mechanism by laboratory experiments with acoustic emission monitoring. In Proceedings of the 34th U.S. Symposium on Rock Mechanics (USRMS), Madison, WI, USA, 28–30 June 1993. [Google Scholar]
- Wang, W.; Su, Y.; Sheng, G.; Cossio, M.; Shang, Y. A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional oil reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 139–147. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, L.; Zhu, D.; Hill, A. Experimental and numerical studies of reduced fracture conductivity due to proppant embedment in the shale reservoir. J. Pet. Sci. Eng. 2015, 130, 37–45. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Shahvali, M.; Su, Y. Analytical solutions for a quad-Linear flow model derived for multistage fractured horizontal wells in tight oil reservoirs. J. Energy Resour. Technol. 2017, 139, 012905. [Google Scholar] [CrossRef]
- Wang, W.; Shahvali, M.; Su, Y. A semi-analytical model for production from tight oil reservoirs with hydraulically fractured horizontal wells. Fuel 2015, 158, 612–618. [Google Scholar] [CrossRef]
- Cai, J.; Wei, W.; Liu, R.; Wang, J. Fractal characterization of dynamic fracture network extension in porous media. Fractals 2017, 25, 1750023. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Cai, J. Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Singh, H.; Cai, J. Screening improved recovery methods in tight-oil formations by injecting and producing through fractures. Int. J. Heat Mass Transf. 2018, 116, 977–993. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.D.; Roegiers, J.C.; McLennan, J. Poroelasticity considerations in In Situ stress determination by hydraulic fracturing. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 507–513. [Google Scholar] [CrossRef]
- Schmitt, D.; Zoback, M. Poroelastic effects in the determination of the maximum horizontal principal stress in hydraulic fracturing tests—A proposed breakdown equation employing a modified effective stress relation for tensile failure. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 499–506. [Google Scholar] [CrossRef]
- Mahrer, K.D. A review and perspective on far-field hydraulic fracture geometry studies. J. Pet. Sci. Eng. 1999, 24, 13–28. [Google Scholar] [CrossRef]
- Yew, C.H.; Weng, X. Mechanics of Hydraulic Fracturing, 2nd ed.; Gulf Professional Publishing: Houston, TX, USA, 2014. [Google Scholar]
- Hossain, M.M.; Rahman, M. Numerical simulation of complex fracture growth during tight reservoir stimulation by hydraulic fracturing. J. Pet. Sci. Eng. 2008, 60, 86–104. [Google Scholar] [CrossRef]
- Yuan, B.; Zheng, D.; Moghanloo, R.G.; Wang, K. A novel integrated workflow for evaluation, optimization, and production predication in shale plays. Int. J. Coal Geol. 2017, 180, 18–28. [Google Scholar] [CrossRef]
- Yuan, B.; Su, Y.; Moghanloo, R.G.; Rui, Z.; Wang, W.; Shang, Y. A new analytical multi-linear solution for gas flow toward fractured horizontal wells with different fracture intensity. J. Nat. Gas Sci. Eng. 2015, 23, 227–238. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, X.; Guo, C.; Wei, M. A model for multiple transport mechanisms through nanopores of shale gas reservoirs with real gas effect–adsorption-mechanic coupling. Int. J. Heat Mass Transf. 2016, 93, 408–426. [Google Scholar] [CrossRef]
- Wei, B.; Li, Q.; Jin, F.; Wang, C. The potential of a novel nanofluid in enhancing oil recovery. Energy Fuels 2016, 30, 2882–2891. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, Y.; Wang, W.; Lu, M.; Sheng, G. Gas transport behaviors in shale nanopores based on multiple mechanisms and macroscale modeling. Int. J. Heat Mass Transf. 2018, 125, 845–857. [Google Scholar] [CrossRef]
- Renshaw, C.; Pollard, D. An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 237–249. [Google Scholar] [CrossRef]
- Gu, H.; Weng, X. Criterion for fractures crossing frictional interfaces at non-orthogonal angles. In Proceedings of the 44th U.S. Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Chen, Z.; Jeffrey, R.G.; Zhang, X.; Kear, J. Finite-element simulation of a hydraulic fracture interacting with a natural fracture. SPE J. 2017, 22, 219–234. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, S.; Ma, X.; Zhou, T.; Zeng, B. Numerical investigation of hydraulic fracture network propagation in naturally fractured shale formations. J. Struct. Geol. 2016, 84, 1–13. [Google Scholar] [CrossRef]
- Wu, Z.; Wong, L.N.Y. Frictional crack initiation and propagation analysis using the numerical manifold method. Comput. Geotech. 2012, 39, 38–53. [Google Scholar] [CrossRef]
- Heider, Y.; Reiche, S.; Siebert, P.; Markert, B. Modeling of hydraulic fracturing using a porous-media phase-field approach with reference to experimental data. Eng. Fract. Mech. 2018, 202, 116–134. [Google Scholar] [CrossRef]
- Dahi-Taleghani, A.; Olson, J.E. Numerical modeling of multistranded-hydraulic-fracture propagation: Accounting for the interaction between induced and natural fractures. SPE J. 2011, 16, 575–581. [Google Scholar] [CrossRef]
- Gordeliy, E.; Peirce, A. Enrichment strategies and convergence properties of the XFEM for hydraulic fracture problems. Comput. Methods Appl. Mech. Eng. 2015, 283, 474–502. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Shah, S.; Lamb, A.R.; Bordas, S.P. Enriched finite elements for branching cracks in deformable porous media. Eng. Anal. Bound. Elem. 2015, 50, 435–446. [Google Scholar] [CrossRef] [Green Version]
- Klimenko, D.; Taleghani, A.D. A modified extended finite element method for fluid-driven fractures incorporating variable primary energy loss mechanisms. Int. J. Rock Mech. Min. Sci. 2018, 106, 329–341. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Sutula, D.; Tian, S.; Bordas, S.P. XFEM modeling of multistage hydraulic fracturing in anisotropic shale formations. J. Pet. Sci. Eng. 2018, 162, 801–812. [Google Scholar] [CrossRef]
- Shi, F.; Wang, X.; Liu, C.; Liu, H.; Wu, H. An XFEM-based method with reduction technique for modeling hydraulic fracture propagation in formations containing frictional natural fractures. Eng. Fract. Mech. 2017, 173, 64–90. [Google Scholar] [CrossRef]
- Wang, X.; Shi, F.; Liu, C.; Lu, D.; Liu, H.; Wu, H. Extended finite element simulation of fracture network propagation in formation containing frictional and cemented natural fractures. J. Nat. Gas Sci. Eng. 2018, 50, 309–324. [Google Scholar] [CrossRef]
- Ghaderi, A.; Taheri-Shakib, J.; Mohammad Nik, A.S. The distinct element method (DEM) and the extended finite element method (XFEM) application for analysis of interaction between hydraulic and natural fractures. J. Pet. Sci. Eng. 2018, 171, 422–430. [Google Scholar] [CrossRef]
- Paul, B.; Faivre, M.; Massin, P.; Giot, R.; Colombo, D.; Golfier, F.; Martin, A. 3D coupled HM–XFEM modeling with cohesive zone model and applications to non planar hydraulic fracture propagation and multiple hydraulic fractures interference. Comput. Methods Appl. Mech. Eng. 2018, 342, 321–353. [Google Scholar] [CrossRef]
- Remij, E.; Wand Remmers, J.J.C.; Huyghe, J.M.; Smeulders, D.M.J. On the numerical simulation of crack interaction in hydraulic fracturing. Comput. Geosci. 2018, 22, 423–437. [Google Scholar] [CrossRef]
- Vahab, M.; Khalili, N. X-FEM modeling of multizone hydraulic fracturing treatments within saturated porous media. Rock Mech. Rock Eng. 2018, 51, 3219–3239. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Ding, W.; Ge, H.; Jia, X.; Shi, Y.; Wang, X.; Yan, X. A numerical simulation study of fracture reorientation with a degradable fiber-diverting agent. J. Nat. Gas Sci. Eng. 2015, 25, 215–225. [Google Scholar] [CrossRef]
- Gravouil, A.; Moës, N.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets—Part II: Level set update. Int. J. Numer. Methods Eng. 2002, 53, 2569–2586. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez, M.; Shojaei, A. Overview of numerical models for interactions between hydraulic fractures and natural fractures: Challenges and limitations. Comput. Geotech. 2016, 71, 361–368. [Google Scholar] [CrossRef]
- Feng, Y.; Li, X.; Gray, K.E. Mudcake effects on wellbore stress and fracture initiation pressure and implications for wellbore strengthening. Pet. Sci. 2018, 15, 319–334. [Google Scholar] [CrossRef]
- Olson, J.E.; Bahorich, B.; Holder, J. Examining hydraulic fracture: Natural fracture interaction in hydrostone block experiments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Zhang, Q.; Su, Y.; Wang, W.; Lu, M.; Sheng, G. Apparent permeability for liquid transport in nanopores of shale reservoirs: Coupling flow enhancement and near wall flow. Int. J. Heat Mass Transf. 2017, 115, 224–234. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Ge, H.; Shi, Y.; Yi, X.; Xiong, C.; Liu, X.; Wu, Y.; Li, Y. An experimental study on the mechanism of degradable fiber-assisted diverting fracturing and its influencing factors. J. Nat. Gas Sci. Eng. 2015, 27, 260–273. [Google Scholar] [CrossRef]
- Cherny, S.; Lapin, V.; Esipov, D.; Kuranakov, D.; Avdyushenko, A.; Lyutov, A.; Karnakov, P. Simulating fully 3D non-planar evolution of hydraulic fractures. Int. J. Fract. 2016, 201, 181–211. [Google Scholar] [CrossRef]
- Gupta, P.; Duarte, C.A. Coupled hydromechanical-fracture simulations of nonplanar three-dimensional hydraulic fracture propagation. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 143–148. [Google Scholar] [CrossRef]
- Zlotnik, S.; Díez, P.; Fernández, M.; Vergés, J. Numerical modelling of tectonic plates subduction using X-FEM. Comput. Methods Appl. Mech. Eng. 2007, 196, 4283–4293. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Liu, Z.; Zeng, Q.; Gao, Y.; Zhuang, Z. XFEM modeling of hydraulic fracture in porous rocks with natural fractures. Sci. China-Phys. Mech. Astron. 2017, 60, 084612. [Google Scholar] [CrossRef]
- Haddad, M.; Sepehrnoori, K. XFEM-Based CZM for the simulation of 3D multiple-cluster hydraulic fracturing in quasi-brittle shale formations. Rock Mech. Rock Eng. 2016, 49, 4731–4748. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K. Modeling of curving hydraulic fracture propagation from a wellbore in a poroelastic medium. J. Nat. Gas Sci. Eng. 2018, 53, 83–93. [Google Scholar] [CrossRef]
- Chen, Z. A New Enriched Finite Element Method with Application to Static Fracture Problems with Internal Fluid Pressure. Int. J. Appl. Mech. 2015, 7, 1550037. [Google Scholar] [CrossRef]
- Meschke, G.; Leonhart, D. A Generalized Finite Element Method for hydro-mechanically coupled analysis of hydraulic fracturing problems using space-time variant enrichment functions. Comput. Methods Appl. Mech. Eng. 2015, 290, 438–465. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A.R. Hydro-mechanical modeling of cohesive crack propagation in multiphase porous media using the extended finite element method. Int. J. Numeri. Anal. Methods Geomech. 2013, 37, 1247–1279. [Google Scholar] [CrossRef]
- Taleghani, A.D.; Gonzalez-Chavez, M.; Yu, H.; Asala, H. Numerical simulation of hydraulic fracture propagation in naturally fractured formations using the cohesive zone model. J. Pet. Sci. Eng. 2018, 165, 42–57. [Google Scholar] [CrossRef]
- Kumar, D.; Ghassemi, A. Three-Dimensional Poroelastic Modeling of Multiple Hydraulic Fracture Propagation from Horizontal Wells. Int. J. Rock Mech. Min. Sci. 2018, 105, 192–209. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–151. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K.E. A fracture-mechanics-based model for wellbore strengthening applications. J. Nat. Gas Sci. Eng. 2016, 29, 392–400. [Google Scholar] [CrossRef]
- Khoei, A.R. Extended Finite Element Method: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Gu, H.; Weng, X.; Lund, J.B.; Mack, M.G.; Ganguly, U.; Suarez-Rivera, R. Hydraulic fracture crossing natural fracture at nonorthogonal angles: A criterion and its validation. SPE Prod. Oper. 2012, 27, 20–26. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.S.; Barati, R. A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoirs. Fuel 2019, 236, 404–427. [Google Scholar] [CrossRef]
- McGinley, M.J. The Effects of Fracture Orientation and Anisotropy on Hydraulic Fracture Conductivity in the Marcellus Shale. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2015. Available online: https://doi.org/http://hdl.handle.net/1969.1/155300 (accessed on 1 September 2018).
- Jia, B.; Tsau, J.S.; Barati, R. Experimental and numerical investigations of permeability in heterogeneous fractured tight porous media. J. Nat. Gas Sci. Eng. 2018, 58, 216–233. [Google Scholar] [CrossRef]
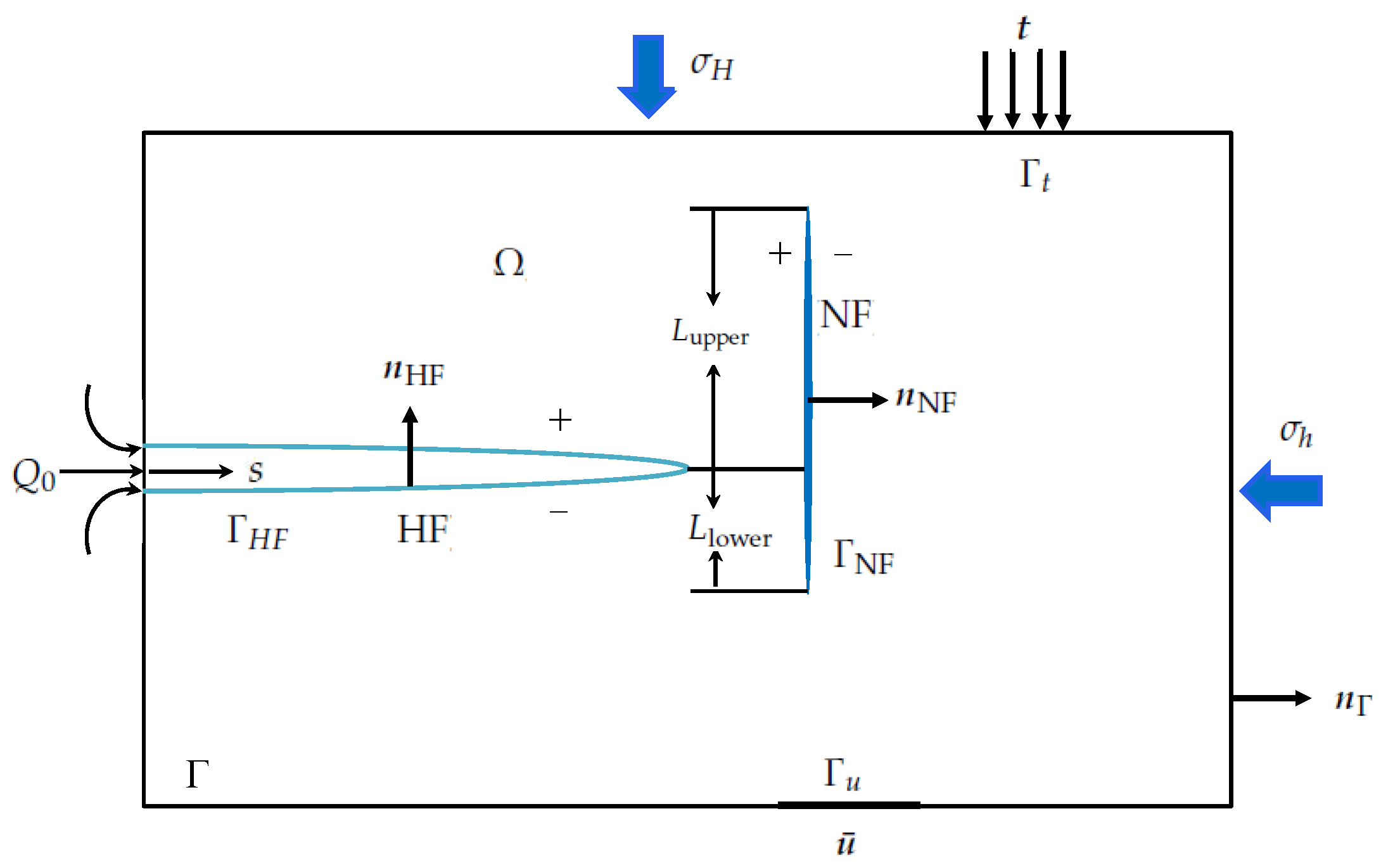
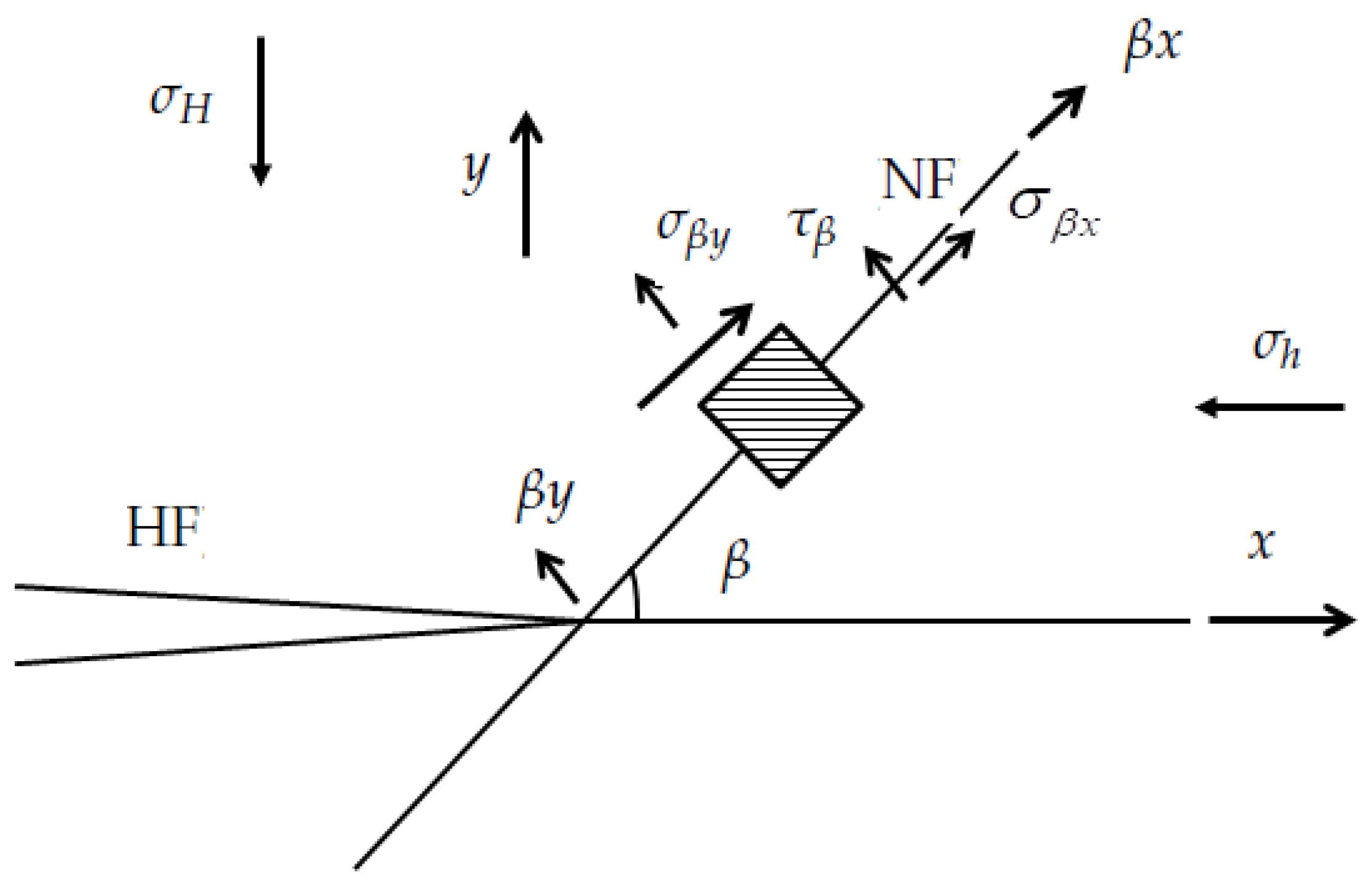
| Input Parameter | Value |
|---|---|
| Young’s Modulus, E | 20 GPa |
| Poisson’s ratio, | 0.2 |
| Rock density, | 2460 |
| Friction coefficient of NF, | 0.3 |
| Cohesion of the NF, | 0 MPa |
| Fracture toughness, | 1.0 |
| Tensile strength, | 1.5 MPa |
| Unconfined compression strength, | 100 MPa |
| Apparent viscosity of fracturing fluid, | 0.1 |
| The consistency index of fracturing fluid, K | 0.84 |
| The flow behavior index of fracturing fluid, n | 0.53 |
| Dynamic viscosity index, m | 2.0 |
| Fluid pump rate, | 0.001 |
| Pore pressure, | 5 MPa |
| Maximum horizontal stress, | 5 MPa |
| Minimum horizontal stress, | 5 MPa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Shi, F.; Yu, B.; Sun, D.; Li, X.; Han, D.; Tan, Y. A Numerical Study on the Diversion Mechanisms of Fracture Networks in Tight Reservoirs with Frictional Natural Fractures. Energies 2018, 11, 3035. https://doi.org/10.3390/en11113035
Wang D, Shi F, Yu B, Sun D, Li X, Han D, Tan Y. A Numerical Study on the Diversion Mechanisms of Fracture Networks in Tight Reservoirs with Frictional Natural Fractures. Energies. 2018; 11(11):3035. https://doi.org/10.3390/en11113035
Chicago/Turabian StyleWang, Daobing, Fang Shi, Bo Yu, Dongliang Sun, Xiuhui Li, Dongxu Han, and Yanxin Tan. 2018. "A Numerical Study on the Diversion Mechanisms of Fracture Networks in Tight Reservoirs with Frictional Natural Fractures" Energies 11, no. 11: 3035. https://doi.org/10.3390/en11113035
APA StyleWang, D., Shi, F., Yu, B., Sun, D., Li, X., Han, D., & Tan, Y. (2018). A Numerical Study on the Diversion Mechanisms of Fracture Networks in Tight Reservoirs with Frictional Natural Fractures. Energies, 11(11), 3035. https://doi.org/10.3390/en11113035






