Assessing the Factors Impacting on the Reliability of Wind Turbines via Survival Analysis—A Case Study
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Survival Analysis
3.1.1. Non-Parametric Survival Analyses: Kaplan–Meier and Nelson–Aalen Estimators
3.1.2. Log-Rank Test for the Significance of Survival
3.1.3. Semi-Parametric Survival Analysis: Cox Proportional Hazard Model
- Standard error (SE): the SE of the estimate shows the accuracy of the estimation for the observed value.
- Wald statistic: The Wald statistic is the ratio of the regression coefficient B to SE. It is used to evaluate the significance of the B coefficients of factors.
- Degrees of freedom: df represents the number of sub-factors that are compared against a factor. For example, design type has two sub-factors, direct and geared, thus the df is 2 − 1 = 1.
- Significance level (sig.): The probability of the coefficient occurring by chance for a specific factor.
- Exp (B): The hazard ratio from the Cox regression is given as Exp (B).
- Confidence intervals (CI) of 95%: 95% upper and lower levels of coefficients resulting from the regression.
4. Case Study Based on WMEP Data
4.1. Survival Analysis Factors
4.1.1. Koppen–Geiger Climatic Regions
- Cfa: Temperate—without dry season—hot summer
- Cfb: Temperate—without dry season—warm summer
- Dfb: Cold—without dry season—warm summer
- Dfc: Cold—without dry season—cold summer
4.1.2. Elevational Location
4.1.3. Distance to Coast
4.1.4. Mean Annual Wind Speed (MAWS)
4.1.5. Turbine Age
4.1.6. Turbine Type
4.1.7. Number of Previous Failures (NOPF)
4.1.8. Scheduled Maintenance History
4.2. Selected Turbine Aspects
5. Results
5.1. Wind Turbine System Approach
5.2. Survival Analysis of the Electrical Subsystem
5.3. Survival Analysis for Components of the Electrical Subsystems
5.3.1. Survival Analysis for Fuses
5.3.2. Survival Analysis for Switches
6. Conclusions
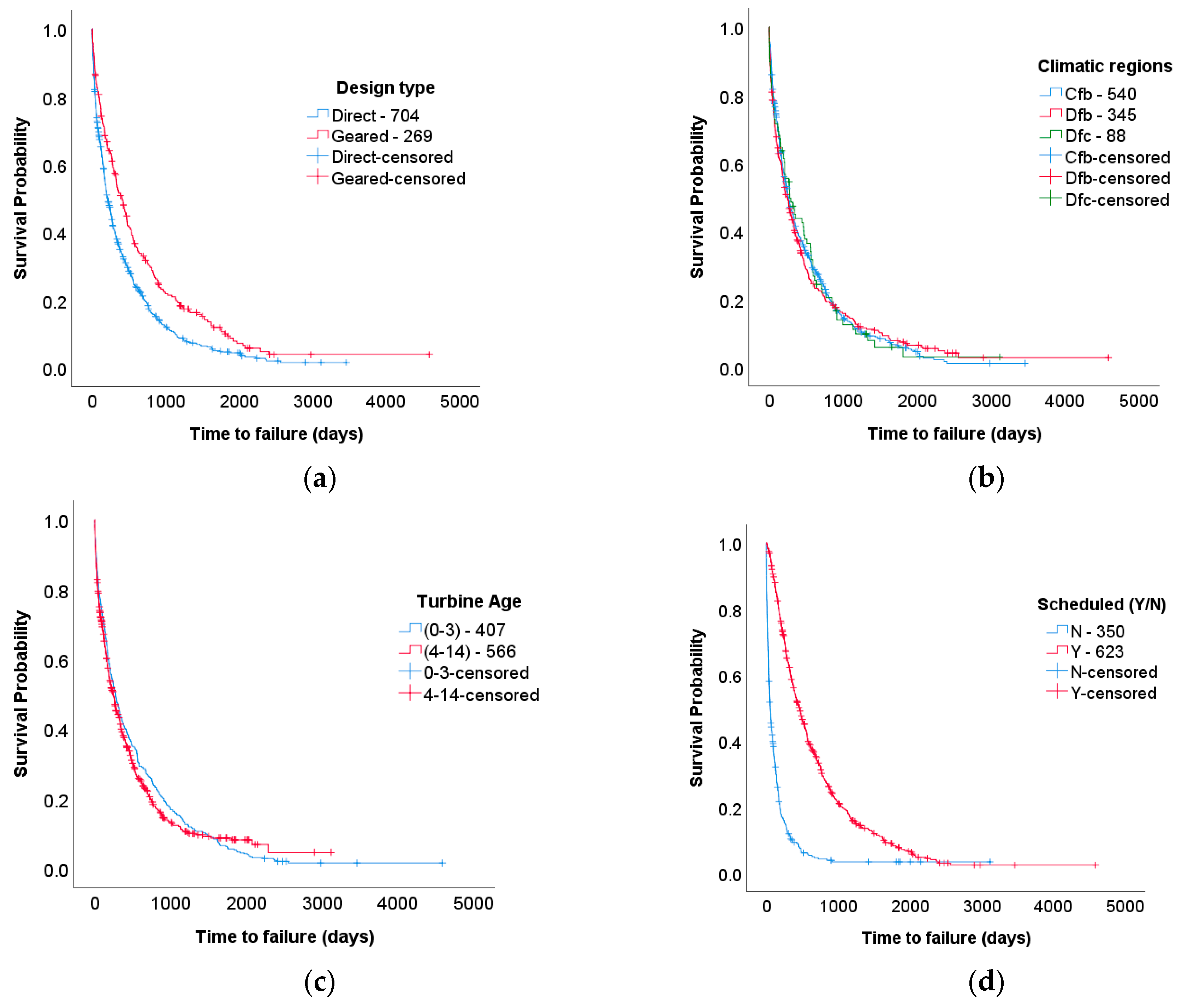
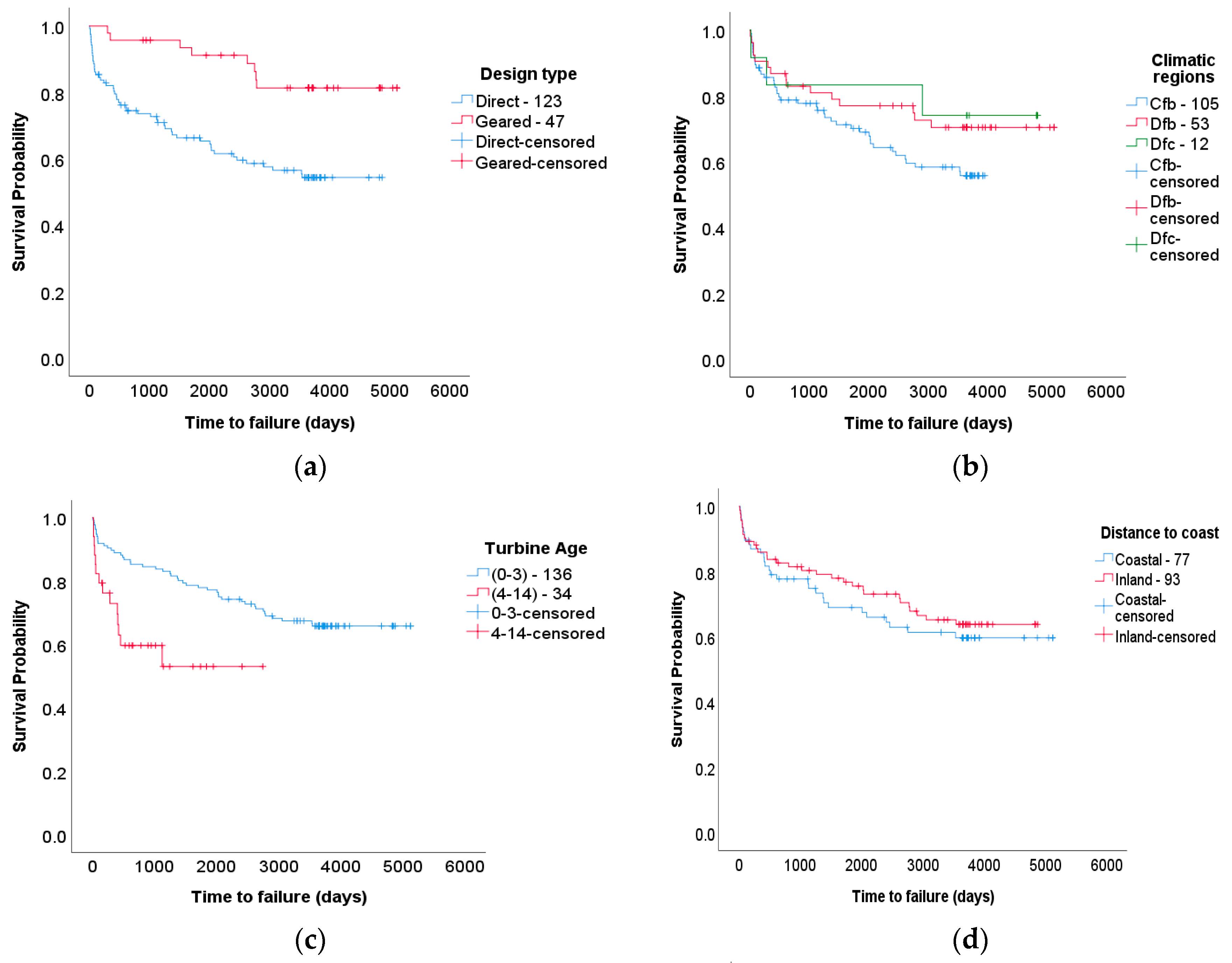
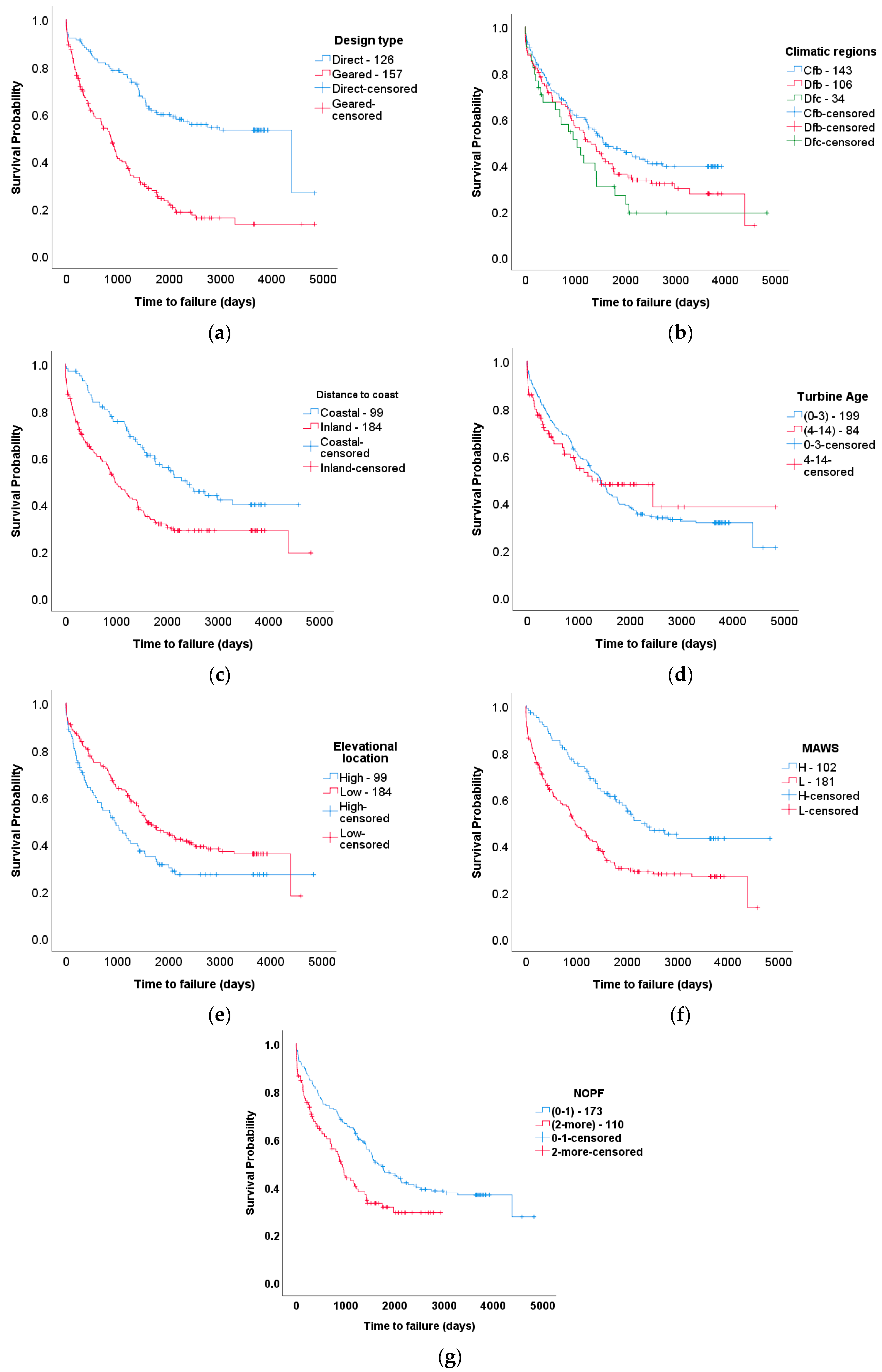
- Geared-drive wind turbines and their electrical systems were observed to have 1.3- and 1.4- times higher survival rates, respectively, compared to direct-drive wind turbines and their electrical systems. This distinction in survival was also true for fuses, while switches showed the exact opposite trend—switches in direct-drive turbines were less likely to fail compared to switches in geared-drive wind turbines. The geared-drive type of wind turbines might improve the survival of certain components while reducing the survival of other components. For example, the survival of fuses was two times higher in direct-drive turbines than in geared-drive turbines, whereas the survival of switches was reduced by 66%.
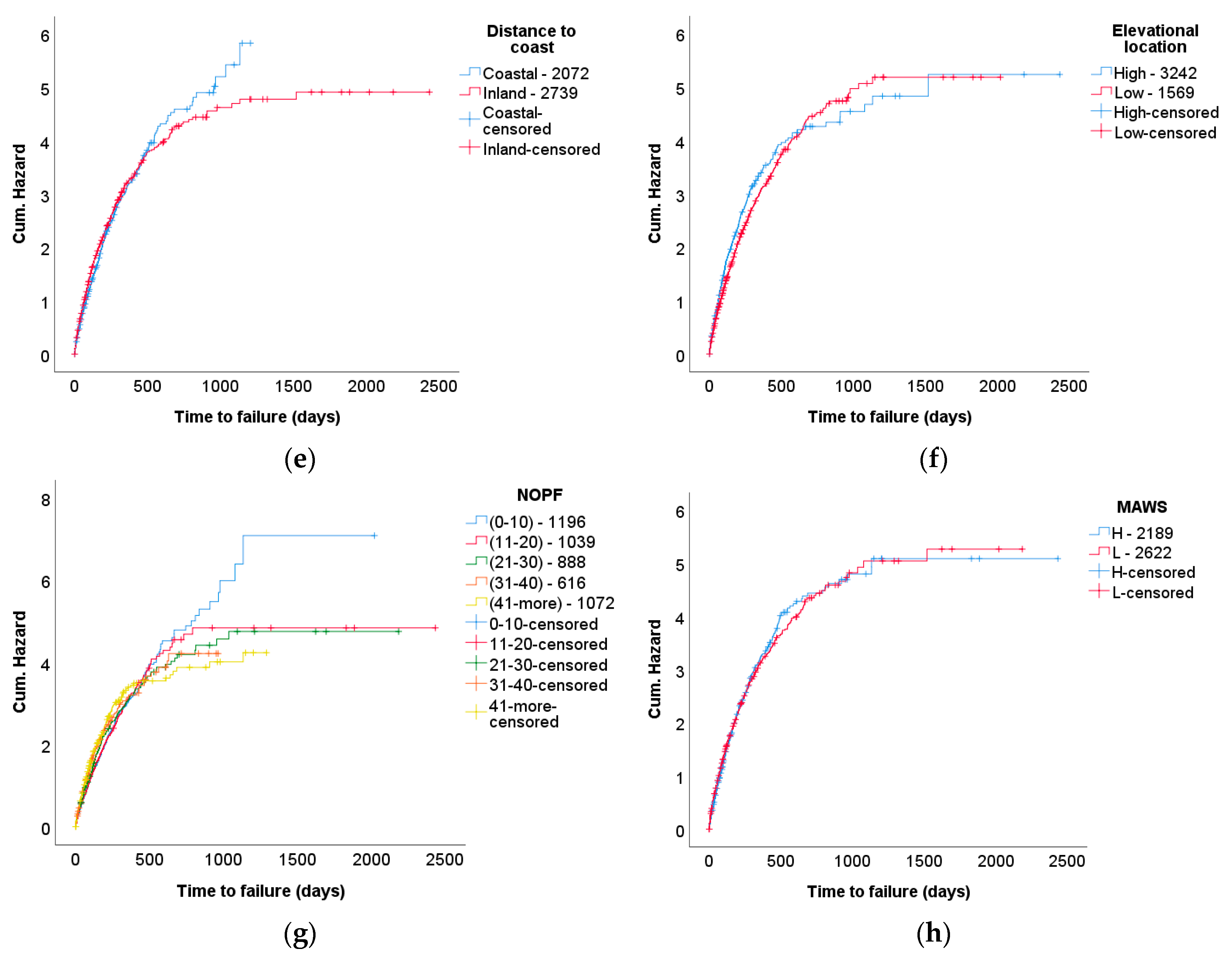
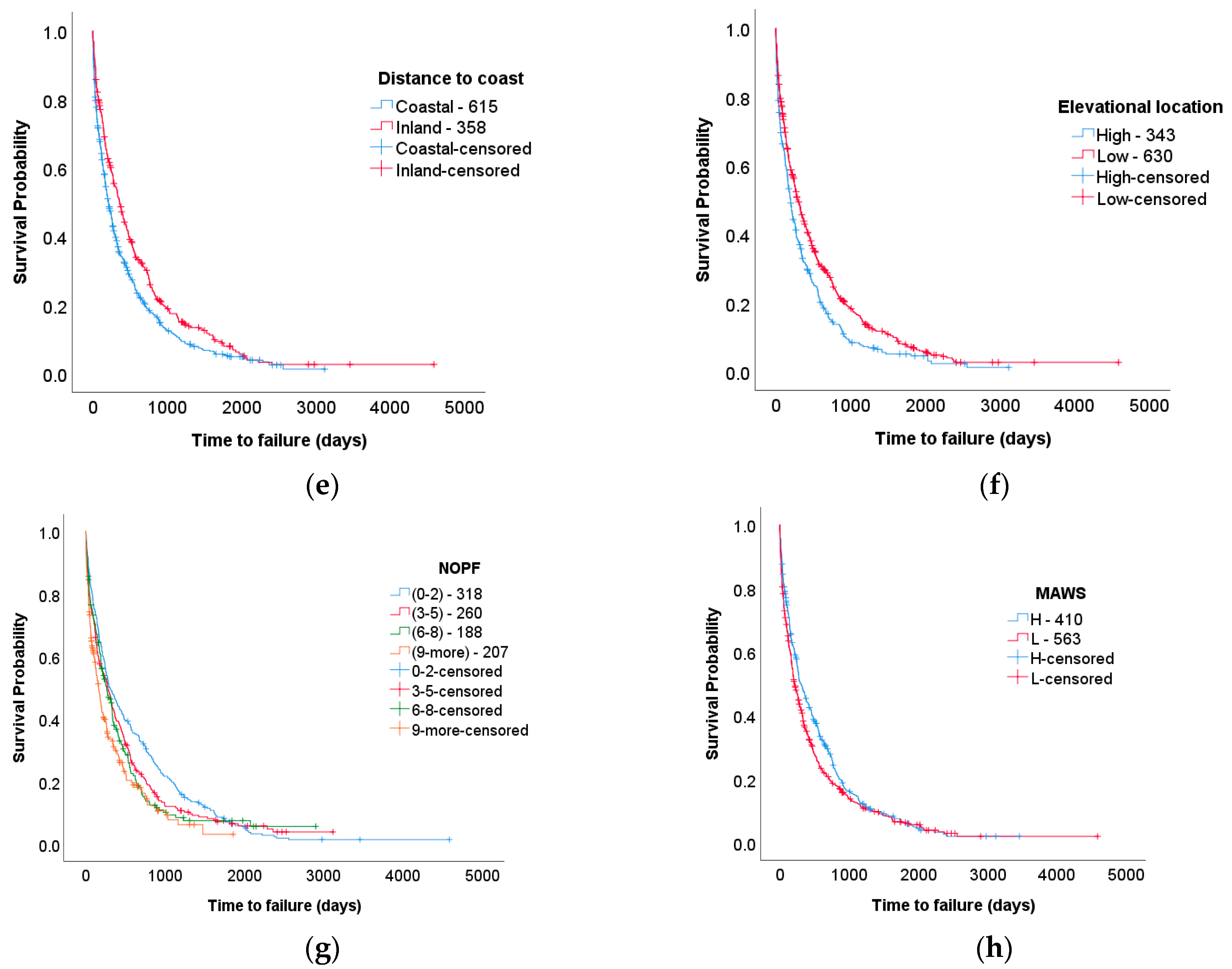
- Although the survival probability graphs show some differences between the climatic regions, these were not significant to the survival of wind turbines, the electrical subsystem and components of the electrical systems. However, this significance is related to the number of data points and the relative number of data points among the factors as well as the investigated subsystems and components. The lack of expected significance for the climatic regions in this study may be attributed to data scarcity, specifically for the Dfc region with a cold climate in the summer.
- The impact of turbine age on the survival of turbine systems and electrical subsystems varied with time. However, fuses had a 60% lower survival in the “mature” age group (4–14 years) than in their early years.
- Scheduled maintenance reporting significantly improved the survival of wind turbines; our data and analysis showed a 2.8- and 3.8-times improvement in survival for wind turbines as a system and for the electrical subsystems, respectively. In other words, at any time there was 2.8 times higher probability of survival for a wind turbine and a 3.8 times higher probability of survival for an electrical subsystem with a history of scheduled maintenance than one without such a history.
- Distance to the coast was not found to be a significant reliability factor for wind turbine systems and electrical subsystems. However, the shorter distance to the coast increased the survival of switches by 39%. A potential explanation for this is that wind patterns in coastal regions fluctuate less than ones on land.
- Elevational location was found not to be a significant factor for the survival of turbine systems, electrical subsystems and fuse and switch components. It must be noted that the maximum elevation of the considered turbines in this study was 800 m.
- Although the hazard rate cannot be quantified due to the violation of proportionality, it was found that a high number of previous failures (NOPF) reduced the survival of wind turbines as a system and of the electrical systems compared to low NOPF. It was also found that a high NOPF showed a lower survival rate for wind turbine components, however in order to determine the significance more data are required.
- MAWS was not shown to be a significantly reliable factor for wind turbine systems and electrical subsystems. However, higher MAWS increased the survival of switches by 35%, which can be attributed to more consistent wind patterns.
Author Contributions
Funding
Conflicts of Interest
References
- GWEC. Global Wind Report 2016—Annual Market Update. [online] Gwec.net. 2017. Available online: http://gwec.net/publications/global-wind-report-2/global-wind-report-2016/ (accessed on 3 March 2018).
- Faulstich, S.; Hahn, B.; Tavner, P.J. Wind Turbine Downtime and Its Importance for Offshore Deployment. Wind Energy 2011, 14, 327–337. [Google Scholar] [CrossRef]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind Turbine Condition Monitoring: State-of-the-Art Review, New Trends, and Future Challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef] [Green Version]
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A Brief Status on Condition Monitoring and Fault Diagnosis in Wind Energy Conversion Systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef] [Green Version]
- Sheng, S.; O’Connor, R. Chapter 15—Reliability of Wind Turbines. In Wind Energy Engineering; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Ghodrati, B.; Uday, K. Reliability and Operating Environment-based Spare Parts Estimation Approach: A Case Study in Kiruna Mine, Sweden. J. Qual. Maint. Eng. 2005, 11, 169–184. [Google Scholar] [CrossRef]
- Tavner, P.; Edwards, C.; Brinkman, A.; Spinato, F. Influence of Wind Speed on Wind Turbine Reliability. Wind Eng. 2006, 30, 55–72. [Google Scholar] [CrossRef]
- Leite, A.P.; Borges, C.L.T.; Falcao, D.M. Probabilistic Wind Farms Generation Model for Reliability Studies Applied to Brazilian Sites. IEEE Trans. Power Syst. 2006, 21, 1493–1501. [Google Scholar] [CrossRef]
- Hau, E. Wind Turbine Installation and Operation. Wind Turbines 2013, 719–787. [Google Scholar] [CrossRef]
- Faulstich, S.; Lyding, P.; Hahn, B. Component Reliability Ranking with Respect to WT Concept and External Environmental Conditions. Available online: https://scholar.google.com.tw/scholar?hl=zh-TW&as_sdt=0%2C5&q=Integrated+Wind+Turbine+Design%E2%80%9D+Component+Reliability+Ranking+with+Respect+to+WT+Concept+and+External+Environmental+Conditions+Deliverable+WP7.3.3&btnG (accessed on 17 October 2018).
- Fischer, K.; Besnard, F.; Bertling, L. Reliability-Centered Maintenance for Wind Turbines Based on Statistical Analysis and Practical Experience. IEEE Trans. Energy Convers. 2012, 27, 184–195. [Google Scholar] [CrossRef]
- Tavner, P. Offshore Wind Turbines: Reliability, Availability and Maintenance; IET Digital Library: London, UK, 2012. [Google Scholar]
- Wilson, G.; McMillan, D. Assessing Wind Farm Reliability Using Weather Dependent Failure Rates. J. Phys. Conf. Ser. 2014, 524. [Google Scholar] [CrossRef]
- Staffell, I.; Green, R. How Does Wind Farm Performance Decline with Age? Renew. Energy 2014, 66, 775–786. [Google Scholar] [CrossRef]
- Pérez, P.; María, J.; Márquez, F.P.G.; Tobias, A.; Papaelias, M. Wind Turbine Reliability Analysis. Renew. Sustain. Energy Rev. 2013, 23, 463–472. [Google Scholar] [CrossRef]
- Reder, M.; Yürüşen, N.Y.; Melero, J.J. Data-Driven Learning Framework for Associating Weather Conditions and Wind Turbine Failures. Reliabil. Eng. Syst. Saf. 2018, 169, 554–569. [Google Scholar] [CrossRef]
- Slimacek, V.; Lindqvist, B.H. Reliability of Wind Turbines Modeled by a Poisson Process with Covariates, Unobserved Heterogeneity and Seasonality. Wind Energy 2016, 19, 1991–2002. [Google Scholar] [CrossRef]
- Mazidi, P.; Tjernberg, B.L.; Bobi, M.A.S. Wind Turbine Prognostics and Maintenance Management Based on a Hybrid Approach of Neural Networks and a Proportional Hazards Model. Proceed. Ins. Mech. Engineers Part O J. Risk Reliabil. 2017, 231, 121–129. [Google Scholar] [CrossRef]
- Carlos, S.; Sánchez, A.; Martorell, S.; Marton, I. Onshore Wind Farms Maintenance Optimization Using a Stochastic Model. Math. Comput. Model. 2011, 57, 1884–1890. [Google Scholar] [CrossRef]
- Andrawus, J. Maintenance Optimisation for Wind Turbines. Ph.D. Thesis, The Robert Gordon University, Aberdeen, UK, 2008. [Google Scholar]
- Kerres, B.; Fischer, K.; Madlener, R. Economic Evaluation of Maintenance Strategies for Wind Turbines: A Stochastic Analysis. Inst. Eng. Technol. 2014, 9, 766–774. [Google Scholar] [CrossRef]
- Christodoulou, S.E. Water Network Assessment and Reliability Analysis by Use of Survival Analysis. Water Resour. Manag. 2011, 25, 1229–1238. [Google Scholar] [CrossRef]
- IEA WIND TASK 33. Reliability Data Standardization of Data Collection for Wind Turbine Reliability and Operations & Maintenance Analyses: Initiatives Concerning Reliability Data (2nd Release). 2013. Available online: https://community.ieawind.org/HigherLogic/System/DownloadDocumentFile.ashx?DocumentFileKey=7b6fdbfe-9b58-addf-0bc6-78c2d3f4aa5d&forceDialog=0 (accessed on 10 May 2018).
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Aalen, O.O. Nonparametric inference for a family of counting processes. Ann. Stat. 1978, 6, 701–726. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. The Logrank Test. BMJ 2004, 328. [Google Scholar] [CrossRef] [PubMed]
- IBM Corp. IBM SPSS Statistics for Windows; Version 25.0, Released 2017; IBM Corp: Armonk, NY, USA, 2017; Available online: http://www-01.ibm.com/support/docview.wss?uid=swg21476197 (accessed on 12 May 2018).
- Peel, M.C.; Finlayson, B.L.; Mcmahon, T.A. Updated World Map of the Koppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. Discuss. 2007, 4, 439–473. [Google Scholar] [CrossRef]
- Global Wind Atlas. Available online: https://globalwindatlas.info/ (accessed on 26 June 2018).
- Ribrant, J.; Bertling, L.M. Survey of Failures in Wind Power Systems with Focus on Swedish Wind Power Plants during 1997-2005. IEEE Trans. Energy Conver. 2007, 22, 167–173. [Google Scholar] [CrossRef]
- Miller, C.R. Illustrated Guide to the National Electrical Code; Delmar Publishers: Albany, NY, USA, 1999; Available online: https://catalog.hathitrust.org/Record/004044318 (accessed on 26 June 2018).
- Patrick, D.R. Electricity and Electronics Fundamentals, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]

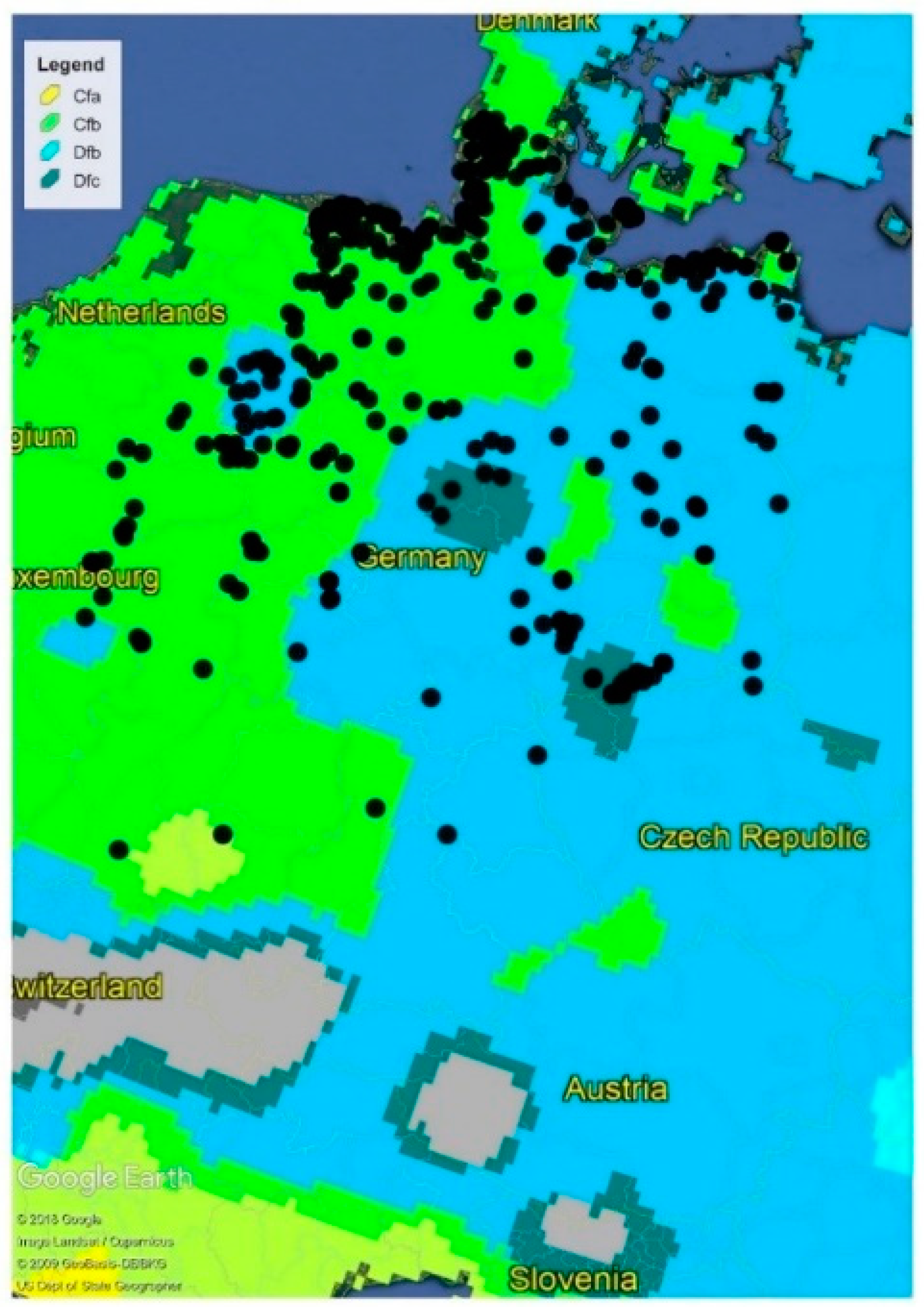


| Geographical and Environmental Factors | Operational Factors |
|---|---|
| 1. Koppen–Geiger Climatic Regions: Cfb, Dfb, Dfc | 5. Turbine age (years): 0–3, 4–14 |
| 2. Elevational location: High land (>100 m), Low land (≤100 m) | 6. Turbine type: Geared-drive, Direct-drive |
| 3. Distance to coast: Coastal (0–20 km), Inland (>20 km) | 7. Number of previous failures (NOPF) Varies |
| 4. Mean annual wind speed (MAWS)High (>6.25 m/s), Low (≤6.25 m/s) | 8. Scheduled maintenance history: Yes, No |
| 1st | 2nd | 3rd | Description | Criteria * |
|---|---|---|---|---|
| C | Temperate | Thot ≥ 10 & 0 < Tcold < 18 | ||
| s | - Dry Summer | Psdry < 40 & Psdry < Pwwet/3 | ||
| w | - Dry Winter | Pwdry < Pswet/10 | ||
| f | - Without dry season | Not (Cs) or (Cw) | ||
| a | - Hot Summer | Thot ≥ 22 | ||
| b | - Warm Summer | Not (a) & Tmon10 ≥ 4 | ||
| c | - Cold Summer | Not (a or b) & 1 ≤ Tmon10 < 4 | ||
| D | Cold | Thot ≥ 10 & Tcold ≤ 0 | ||
| s | - Dry Summer | Psdry < 40 & Psdry < Pwwet/3 | ||
| w | - Dry Winter | Pwdry < Pswet/10 | ||
| f | - Without dry season | Not (Ds) or (Dw) | ||
| a | - Hot Summer | Thot ≥ 22 | ||
| b | - Warm Summer | Not (a) & Tmon10 ≥ 4 | ||
| c | - Cold Summer | Not (a, b or d) | ||
| d | - Very Cold Winter | Not (a or b) & Tcold < −38 |
| Turbine Model | Time to Failure (days) | Status | Design Type | Climatic Regions | Turbine Age (years) | Distance to Coast | Elevational Location | MAWS |
|---|---|---|---|---|---|---|---|---|
| Model A | 675 | Failed | Geared | Cfb | 0–3 | Coastal | Low | High |
| Model A | 2978 | Censored | Geared | Cfb | 0–3 | Coastal | Low | High |
| Model A | 1572 | Failed | Geared | Cfb | 0–3 | Inland | Low | Low |
| Model B | 3849 | Censored | Direct | Dfb | 0–3 | Coastal | Low | Low |
| Characteristics | Wind Turbine System Study | Electrical Subsystem Study | Component Study | |||||
|---|---|---|---|---|---|---|---|---|
| Fuses | Switches | |||||||
| Turbine type | Geared | Direct | Geared | Direct | Geared | Direct | Geared | Direct |
| Number of participants | 1477 | 3334 | 269 | 704 | 47 | 123 | 157 | 126 |
| Factors | Groups | Test Statistics | |
|---|---|---|---|
| Chi-Square | Sig. | ||
| Design type | Direct vs. Geared | 53.01 | 0.000 |
| Scheduled maintenance history | No vs. Yes | 991.01 | 0.000 |
| Factors | B | SE | Wald | Df | Sig. | Exp (B) | 95.0% CI for Exp (B) | |
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| Design type | 0.22 | 0.035 | 39.3 | 1 | 0.000 | 1.25 | 1.16 | 1.34 |
| Scheduled (Y/N) | 1.02 | 0.033 | 935.2 | 1 | 0.000 | 2.77 | 2.59 | 2.95 |
| Factors | Groups | Test Statistics | |
|---|---|---|---|
| Chi-Square | Sig. | ||
| Design type | Direct vs. Geared | 22.77 | 0.000 |
| Scheduled maintenance history | No vs. Yes | 351.76 | 0.000 |
| Factors | B | SE | Wald | df | Sig. | Exp (B) | 95.0% CI for Exp (B) | |
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| Design type | 0.35 | 0.080 | 18.99 | 1 | 0.000 | 1.42 | 1.21 | 1.66 |
| Scheduled (Y/N) | 1.34 | 0.075 | 319.29 | 1 | 0.000 | 3.81 | 3.30 | 4.42 |
| Elevational location | 0.06 | 0.077 | 0.68 | 1 | 0.408 | 1.07 | 0.916 | 1.24 |
| Distance to coast | 0.04 | 0.087 | 0.20 | 1 | 0.652 | 1.04 | 0.88 | 1.23 |
| Factors | B | SE | Wald | Df | Sig. | Exp (B) | 95.0% CI for Exp (B) | |
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| Design type | 1.13 | 0.381 | 8.73 | 1 | 0.003 | 3.09 | 1.46 | 6.52 |
| Turbine age | −0.95 | 0.329 | 8.35 | 1 | 0.004 | 0.39 | 0.203 | 0.74 |
| Factors | B | SE | Wald | df | Sig. | Exp (B) | 95.0% CI for Exp (B) | |
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| Design type | −1.08 | 0.167 | 41.48 | 1 | 0.000 | 0.34 | 0.25 | 0.47 |
| Distance to coast | −0.50 | 0.177 | 8.04 | 1 | 0.005 | 0.61 | 0.43 | 0.86 |
| MAWS | −0.43 | 0.178 | 5.89 | 1 | 0.015 | 0.65 | 0.46 | 0.92 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozturk, S.; Fthenakis, V.; Faulstich, S. Assessing the Factors Impacting on the Reliability of Wind Turbines via Survival Analysis—A Case Study. Energies 2018, 11, 3034. https://doi.org/10.3390/en11113034
Ozturk S, Fthenakis V, Faulstich S. Assessing the Factors Impacting on the Reliability of Wind Turbines via Survival Analysis—A Case Study. Energies. 2018; 11(11):3034. https://doi.org/10.3390/en11113034
Chicago/Turabian StyleOzturk, Samet, Vasilis Fthenakis, and Stefan Faulstich. 2018. "Assessing the Factors Impacting on the Reliability of Wind Turbines via Survival Analysis—A Case Study" Energies 11, no. 11: 3034. https://doi.org/10.3390/en11113034
APA StyleOzturk, S., Fthenakis, V., & Faulstich, S. (2018). Assessing the Factors Impacting on the Reliability of Wind Turbines via Survival Analysis—A Case Study. Energies, 11(11), 3034. https://doi.org/10.3390/en11113034






