Stochastic Small Signal Stability of a Power System with Uncertainties

Abstract

The ever-increasing penetration of wind power generation and plug-in electric vehicles introduces stochastic continuous disturbances to the power system. This paper proposes an analytical approach to analyze the influence of stochastic continuous disturbances on power system small signal stability. The noise-to-state stability (NSS) and NSS Lyapunov function (NSS-LF) are adopted for stability analysis with respect to the magnitude of uncertainties in a power system. The power system is modeled as a set of stochastic differential equations (SDEs). The supremum of the norm of the covariance is employed to characterize the influence of magnitudes of uncertainties on the power system. Then the relationship between the magnitudes of stochastic variations and probabilistic stability is explicitly identified by NSS. The proposed method can assess the stochastic stability of the power system by checking some algebraic expressions. Hence, it has high computation efficiency compared with the well-established Monte Carlo based method. Besides, since the magnitudes of the stochastic variations are integrated into the definition of the stochastic stability, the proposed method provides theoretical explanations for the impacts of uncertainties.

1. Introduction

The environmental pollution resulting from fossil fuels is posing a great challenge for human society. To address this problem, wind farms and plug-in electric vehicles (PEVs) are increasingly employed and integrated into the power system as a result of their green characteristics. However, the randomness associated with wind power outputs and power demands of PEVs could have significantly negative impacts on the secure, stable, and economic operation of the power system concerned, especially in the scenarios with high-level penetrations. As a result, the stochastic stability analysis of a power system with uncertainties has attracted much attention in the academic as well as industrial communities. Given this background, power system stochastic small signal stability is investigated in this work.

Up to now, much effort has been dedicated to power system stability analysis with uncertainties, and some methods have been proposed. Generally, there are two main categories; i.e., probabilistic small-signal stability [1,2] and probabilistic transient stability [3,4,5]. The index for identifying stochastic stability is related to involved random factors through the algebraic relationship. By assuming that random factors follow certain probability distributions, the probability density function (PDF) of the index can be derived by the well-established Monte Carlo simulation. On the other hand, power system stabilizers (PSSs) are applied for enhancing stochastic small-signal stability via eigenvalue sensitivity analyses [6]. Furthermore, the adaptive control based strategies [7,8], frequency-domain approach [9], and particle swarm optimization-based methods [10] are adopted to enhance power system stability with stochastic disturbances. In [11], uncertainties are characterized by a compact set, then robust optimization is carried out for the worst-case scenario, or the random factors are measured in real time in the context of the adaptive control. However, these approaches rely on a deterministic modeling of the power system, and this means that the electromechanical transient of the power system is still governed by ordinary differential equations, and hence, the stochastic nature of the system dynamic process is neglected. Besides, the PDF is obtained by the Monte Carlo simulation, and the curse of computing is involved.

To capture the stochastic nature, the stochastic differential equation (SDE) theory [12,13] is employed to model a power system and investigate the system stability. In [14], a general stochastic modeling approach for a power system is described based on SDE. In [15], system transient stability is assessed by the trajectories obtained from stochastic calculus. In [16], the evolution of the PDF of power system state variables is solved by the Fokker–Planck equation for examining the impacts of random load disturbances on the system stability. In [17], the singular perturbation theory is employed for accurate stability assessment with variable wind power outputs taken into account. In [18], mean-value stability and mean-square stability are utilized to assess the stochastic small-signal stability in a power system. The stochastic counterpart of the direct method using energy functions for power system stability analysis has also been investigated. The direct method is a common analytical approach for deterministic transient stability assessment [19,20,21]. In [20], it is pointed out that limited scalability and conservativeness limit the applicability of the direct method, and the energy function represents a specific form of the Lyapunov function. The Lyapunov function approach is proposed to mitigate the drawbacks of the classical energy method [20]. In [22], the structure-preserved model is employed for power system stochastic transient stability using a stochastic energy function. However, these existing publications compute the stability probability of the power system through the Monte Carlo simulation approach, and heavy computation burden is involved especially for large-scale power systems. In light of the quasi-Hamiltonian form, the stochastic energy function is utilized to analyze power system transient stability [23] and dynamic performance [24], but this method needs to solve a partial differential equation (PDE) for attaining the stability probability and hence involves a very hard solving procedure. In addition, in the mentioned methods, the impacts of uncertainties are only investigated through numerical simulations, and these methods fail to explicitly consider the magnitude of uncertainties in the stability index. Moreover, based on our knowledge, few publications have focused on power system small signal stability analysis using the SDE theory. Even though the work [18] focuses on this topic, the method in [18] cannot provide the information regarding the stability probability.

There is another body of publications relevant to this work. For example, in [25], unit commitment is used to enhance the capability of accommodating a high penetration level of wind power outputs, and the maximum penetration level is determined by taking the probabilistic transient stability and frequency security into account. In [26], the impacts of various wind power penetration levels in a power system are investigated by evaluating the eigenvalue sensitivity with respect to generator inertia. However, these approaches are based on the deterministic model, and uncertain factors are not taken into account.

The noise-to-state stability (NSS) is first proposed for the problem of stochastic disturbance attenuation [27]. This approach makes the system states bounded by a monotone function of the norm of the disturbance magnitude. Besides, this notion can deal with the case where disturbances do not vanish at the origin of the state space. These characteristics are suitable for analyzing the stability of a power system with uncertainties. NSS is related to the concept of the input-to-state stability [28,29,30]. Local input-to-state stability has been applied for voltage stability analysis of an isolated power system [31].

Given the above stated background, this paper proposes an analytical method for stochastic small signal stability analysis of a power system with respect to the magnitudes of uncertainties. The power system is considered as a set of SDEs. Then the norm of covariance is utilized to quantify the impacts of the magnitudes of stochastic variations. Next, the stochastic stability index of the power system is given with respect to this supremum through NSS. NSS-LF is next employed to deduce the algebraic conditions for stochastic small signal stability of the power system. The proposed method has three advantages:

(1)

First, the probability of the state deviations falling within an interval is provided in an analytical way, so it is easier than the existing methods by solving a partial differential equation;

(2)

Secondly, only some algebraic conditions need to be examined for identifying stochastic stability and this can be carried out efficiently compared with the Monte Carlo based approaches for practical applications;

(3)

Thirdly, since the proposed system stability index explicitly takes the uncertainty magnitudes into consideration, the dynamic process of the system states with uncertainties can be theoretically explained.

The organization of this paper is as follows: Section 2 describes necessary notions of the NSS and stochastic Lyapunov function. Section 3 is devoted to the application of the NSS-LF for stochastic small signal stability analysis. Section 4 presents the simulation results to demonstrate the analytical results. Conclusions are given in Section 5.

2. Mathematical Background

An operating power system is continually subject to uncertainties. A class of typical stochastic variations involves a sequence of switching events (e.g., a device is disconnected, and then reconnected after a while). These switching events usually lead to the changes in the power network topology during the fault-on stage, and hence the power system suffers an immediate state change. In this case, power system transient stability is identified by comparing the system energy at the fault clearing time with the critical potential energy. Another class of stochastic variations is generation and/or load level fluctuation, which generally cause slight changes of the system state but may also lead to the small signal stability problem. This work focuses on power system small signal stability with respect to various degrees of uncertainty magnitudes. To formulate this problem, some stochastic analysis tools are given first below.

A nonlinear stochastic dynamic procedure of a power system can be expressed as follows:

$$dx=f(x)dt+g(x)\mathsf{\Sigma }(t)dW$$

(1)

where x(t) $\in$ Rⁿ is the state vector; W(t) $\in$ R^r denotes the stochastic continuous variations, and its elements are independent standard Wiener processes; Σ $\in$ R^r×r is a non-negative-definite matrix, and its elements denote the variation magnitudes. Assume that the vector field f(x): Rⁿ→Rⁿ and matrix function g(x): Rⁿ→R^n×r are both locally Lipschitz continuous.

Unlike the mean stability [18], the probability stability is employed for the stochastic small signal stability analysis.

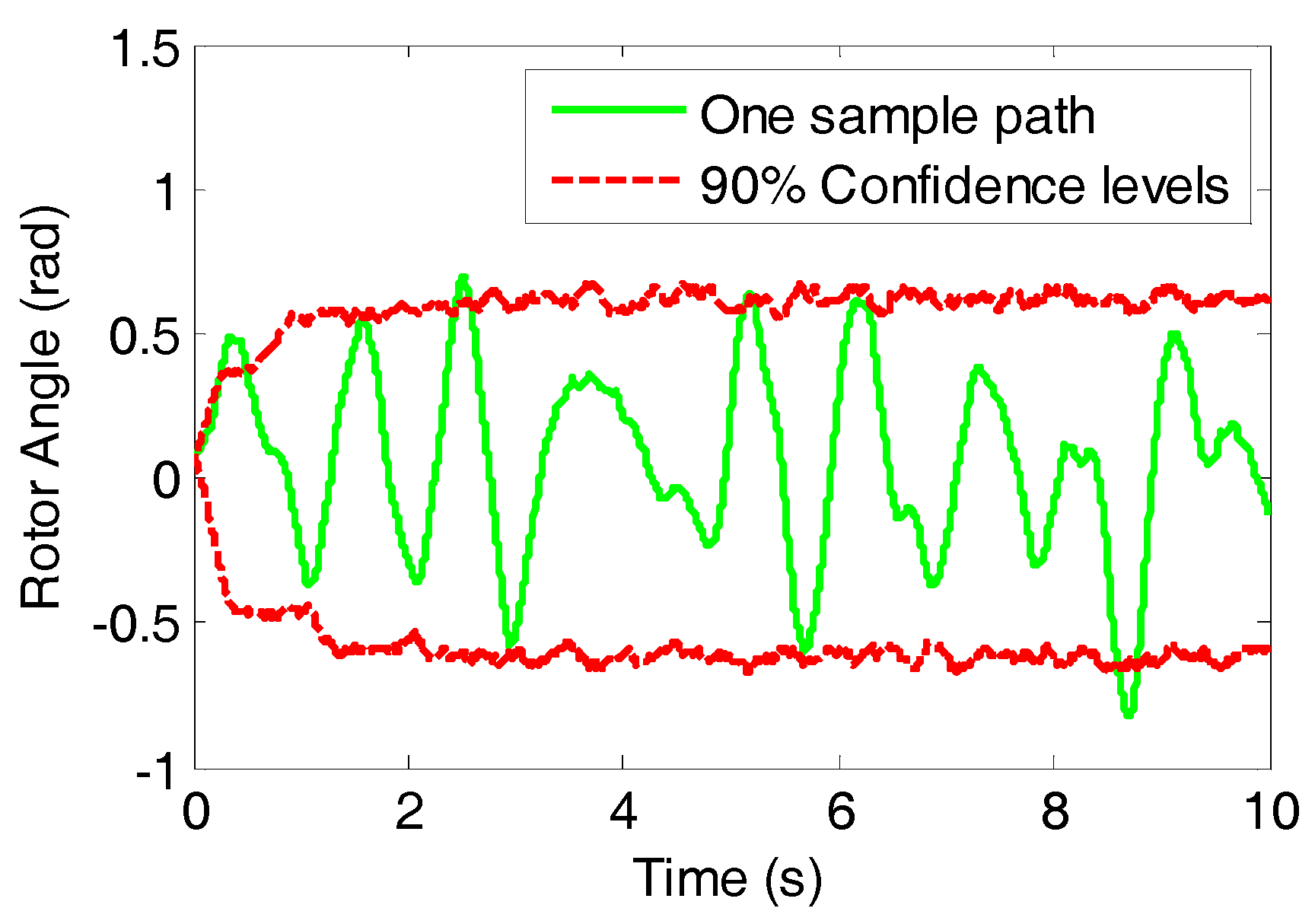
Definition 1.

[32,33]The equilibrium point x = x*$\in$Rⁿ of the system (1) is locally stable in probability if, for every ε > 0 and δ > 0, there exists a number r > 0 such that ||x₀ − x^*|| < r implies

$$\mathrm{P}\left\{\right|\left|x\right(t,x_0)-x^{\ast }||<\delta \}\ge 1-\epsilon ,\mathrm{for}\mathrm{any}t>0\mathrm{and}x\in R^n-\{x^{\ast }\}$$

(2)

where x(t,x₀) is a solution of the system (1) starting from x₀ at t = 0.

This definition means that, given a fixed value of ε, the system with the initial state x₀ is stable if the event ||x(t) − x*|| ≤ δ happens with a probability larger than 1 − ε. Note that the larger the parameter ε is, the smaller the stability probability will be. So ε indicates the risk level.

In the literature, the traditional probabilistic stability index is extensively used for power system stochastic stability analysis, see [3,4,5,6,14,15,16]. The existing methods require carrying out Monte Carlo simulation or solving a PDE. Thus, the use of this formulation of the probability stability is limited due to heavy computation burden. Besides, the magnitudes of the stochastic power fluctuations are not explicitly considered in the probabilistic stability index and only investigated by numerical simulations. In [22,25,26], it is pointed out that the uncertainty magnitudes can affect the system stochastic stability. To theoretically investigate the system probabilistic stability with the consideration of uncertainty magnitudes, an additional term needs to be incorporated into the probabilistic stability index.

To overcome the abovementioned drawbacks, the NSS based probabilistic stability index is proposed in this paper. The probabilistic stability index in this paper is formulated through the class $\mathcal{K}$ function [28]. This formulation facilitates the probabilistic stability analysis of a power system without the use of Monte Carlo simulation or solving a PDE. Moreover, it is convenient for the incorporation of uncertainty magnitudes into the index. The definition of the NSS based probabilistic stability index is given as follows.

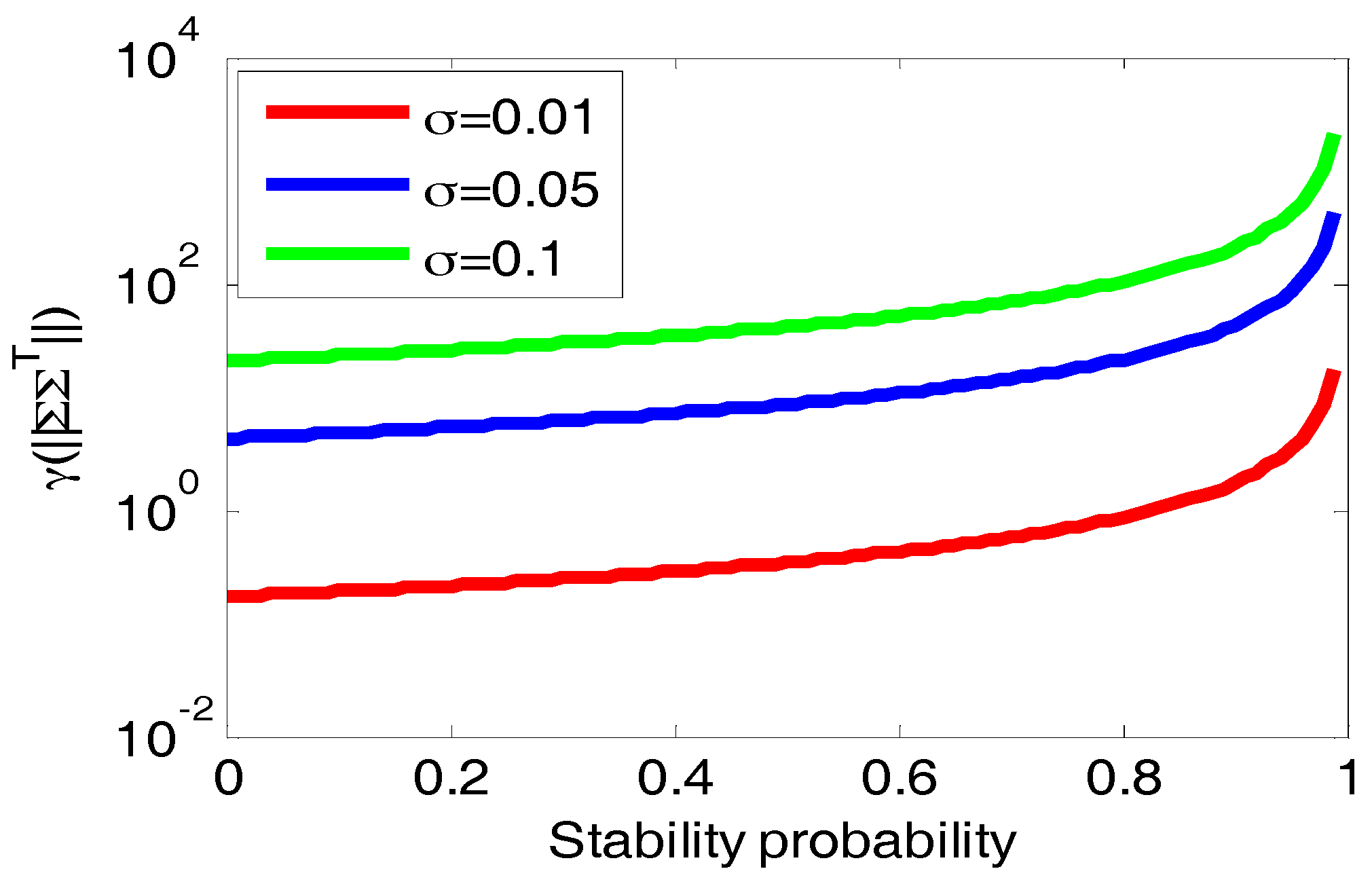
Definition 2.

[27] The equilibrium point x* of the nonlinear stochastic system (1) is called locally noise-to-state stable (NSS) if, for any ε > 0, there exist β$\in$$\mathcal{K}\mathcal{L}$and γ$\in$${\mathcal{K}}_{\infty }$such that

P{||x(t) − x*|| ≤ β(|x₀|,t) + γ(||Σ(t)Σ(t)^T||)} ≥ 1 − ε

(3)

for any x₀$\in$Ω,Σ$\in$U^r×r, and t ≥ 0.

In comparison with Definition 1, the term β(||x₀||,t) in (3) corresponds to the quantity δ (2), which represents the impact of the initial state on the system stability. The additional term γ(||ΣΣ^T||) in (3) quantifies the impact of the uncertainty magnitude. Since the parameter Σ in the stochastic model (1) denotes the uncertainty magnitude, it is natural to consider how this magnitude affects the probabilistic stability of the power system. The Expression (3) means that the system is probabilistically stable if and only if ||x(t) − x*|| is not larger than the sum of these two terms with a probability P ≥ 1 − ε. It is obvious that the impacts of stochastic continuous variations are explicitly taken into account in the stability index.

Note that both β(||x₀||,t) and γ(||ΣΣ^T||) in (3) need to be identified to reach the conclusion regarding the system probabilistic stability. For power system small signal stability, β(||x₀||,t) is related to the eigenvalues of the system matrix. When all the eigenvalues are located within the left-half complex plane, the term β(||x₀||,t) will decay to zero. Then the probabilistic stability of the power system is identified, and ||x(t) − x*|| is bounded above by the terms γ(||ΣΣ^T||). This means that, after a small disturbance occurs, when t→∞, the state deviations of the system will fall within a range [−γ(||ΣΣ^T||), γ(||ΣΣ^T||).] with a probability 1 − ε. This agrees with the conclusions in [18]. Unlike the mean stability index in [18], the NSS based probabilistic stability index can provide the probability information regarding the system stability.

Based on the above discussions, the proposed analytical method for power system stochastic small signal stability analysis can be presented as follows:

Theorem 1.

(NSS based Probabilistic Stability) For a stochastic system (1), if the following conditions are satisfied: (1) the stochastic system (1) is locally NSS; (2) β(||x₀||,t)→0 as t→∞, then the system is stable in probability and P{||x(t) − x*|| ≤ γ(||ΣΣ^T||)} ≥ 1 − ε.

The formal proof of this theorem is provided in the Appendix A.

NSS-LF is a useful tool to verify condition (1) in Theorem 1. It is defined as follows:

Definition 3.

[27] Suppose there exists a proper function V: Rⁿ → R₊, such that class$\mathcal{K}$functions α₁, α₂, α₃, and α₄ satisfy

$${\alpha }_1(|\left|x\right||)\le V(x)\le {\alpha }_2(|\left|x\right||)$$

(4)

and for all Σ$\in$U^r×r

$$\begin{array}{ll}\mathcal{L}V(x,\mathsf{\Sigma })& \triangleq \frac{\partial V}{\partial x}f(x)+\frac{1}{2}Tr\{{(g\mathsf{\Sigma })}^T\frac{{\partial }^{2}V}{\partial x^2}g\mathsf{\Sigma }\}\hfill \\ & \le -{\alpha }_3(|x|)+{\alpha }_4(|\mathsf{\Sigma }{\mathsf{\Sigma }}^T|)\hfill \end{array}$$

(5)

Then, V(x) is called a NSS-LF.

Theorem 2.

[27] If a nonlinear stochastic system admits a NSS-LF, then the system is locally NSS.

Note that the NSS-LF is given for nonlinear systems. It can also be applied to linear systems for small signal stability analysis such as linearized power systems. When the term α₄(||ΣΣ^T||) is sufficiently small, the inequality $\mathcal{L}V$≤ −α₃(||x||) + α₄(||ΣΣ^T||) in Definition 3 reduces to $\mathcal{L}V$≤ −α₃(||x||) which implies $\mathcal{L}V\le 0$. In this case, the function V(x) is the stochastic Lyapunov function (sLF) as in [22]. In this sense, the NSS-LF is a generalization of the sLF. Hence, NSS-LF is adopted to identify the probabilistic stability of power systems in this work.

3. Noise-to-State Stability Based Probabilistic Stability Analysis

In this section, the idea for NSS based probabilistic stability assessment is presented. First, the supremum of the norm of the covariance of power stochastic variations is given for characterizing the impacts of uncertainty magnitudes. Then, the NSS-LF is employed to implement the NSS based probabilistic stability assessment. Finally, the proposed algorithm is applied to a typical power system.

3.1. The Stochastic Model of a Power System

A renewable energy system (RES), such as wind power generation and solar power generation, can be integrated to a power system concerned. To study the impacts of the stochastic variations from a RES on the system stability, the RES can be introduced into the power balance equation. By transformations in [34], these stochastic continuous variations can be manifested through the dynamic model of a power system. Then the approaches for the stochastic stability problem of a power system can be derived considering generation and/or load level fluctuation.

In this work, the proposed method aims at analyzing power system stability with the stochastic continuous variations of generation, so the power system is modeled as a set of SDEs. Synchronous generators are modeled using the traditional swing equation model. Loads are assumed to be constant impedances. When the losses in the transmission network are ignored, the load nodes can be eliminated by transformations, this leads to a reduced network with only generator nodes contained. The stochastic model of a power system can be expressed as follows [16,23]:

$$\{\begin{array}{l}\mathrm{d}{\delta }_i={\omega }_N{\omega }_{i}dt\\ H_i\mathrm{d}{\omega }_i=(P_{mi}-{\displaystyle \sum _{j=1,j\ne i}^n{E}_i{E}_j{B}_{ij}\sin ({\delta }_i-{\delta }_j)}-D_i{\omega }_i)dt+{\mathsf{\Sigma }}_i(t)d{W}_i\\ y_i=c_1{\delta }_i+c_2{\omega }_i\end{array}(i=1,2,\dots ,n)$$

(6)

Here Σ_i(t)dW_i(t) represents stochastic continuous variations; W_i(t) represents independent standard Wiener processes; Σ_i represents uncertainty magnitudes; δ_i, ω_i, H_i, P_mi, E_i, and D_i are the rotor angle, rotor speed deviation, inertia coefficient, mechanical power, internal voltage magnitude and damping coefficient of the ith generator, respectively; B_ij is the element in the ith row and jth column of Kron-reduced susceptance matrix; ω_N is the synchronous machine speed. The quantity y_i is the output. c₁ and c₂ are the weighted coefficients of state variables. e.g., if we want to examine the stability of the angle, c₁ can be set to 1 and c₂ can be set to 0. This input-output formulation is a standard paradigm in robust control theory [35] and has been adopted in power systems in [31,36].

As in [18,22], the terms Σ_i(t)dW_i(t) are added to the rotor motion equations of synchronous generators. By doing this, it can be used to represent the stochastic variations generated from generation and/or load.

The stochastic continuous variation is usually modeled as a stochastic process. Naturally, the covariance of the stochastic process is considered as the degree of the impact. To see this point, it is helpful to note that in (6) Σ(t)dW satisfies the following equations:

$$E(\mathsf{\Sigma }(t)dW)=0$$

(7)

$$\begin{array}{ll}\hfill D(\mathsf{\Sigma }(t)dW)& =E(\mathsf{\Sigma }(t)dW{(\mathsf{\Sigma }(t)dW)}^T)\hfill \\ & =\mathsf{\Sigma }(t)\mathsf{\Sigma }{(t)}^{T}dt\hfill \end{array}$$

(8)

since dW~N (0, dt). Here, E(∙) is the mean value function, and D(∙) is the infinitesimal covariance function.

As in (3), the system probabilistic stability index requires the computation of the term γ(||Σ(t)Σ(t)^T||). Based on the above analysis, Σ(t)Σ(t)^T is the covariance. According to [27], the impact of the magnitudes of uncertainties is quantified as the norm of the covariance in that the stochastic continuous variation may be unbounded.

Both the Wiener process and the supremum of the norm of the covariance are plotted in Figure 1. It can be seen that Σ(t)dW is a time-dependent stochastic process which is used in the numerical integration for the SDE model, as in [22,23]. For the model of sup||Σ(t)Σ(t)^T||, it only gives an upper bound of the uncertainty magnitude and has the potential for the analytical method of the probabilistic stability analysis. Thus, the latter is adopted in this paper.

3.2. Stochastic Small Signal Stability Analysis

In this paper, Σ is assumed to be independent of time [16,22,23]. To apply the proposed method in Section 2 for the stochastic small signal stability, the linearization of the stochastic nonlinear system (6) at a steady state operating point yields to:

$$d\Delta x=A\Delta xdt+\mathsf{\Sigma }dW$$

(9)

where A $\in$ R^n×n and Σ $\in$ R^n×n. Δx denotes the state deviation from the steady state point.

Since the two conditions in Theorem 1 need to be satisfied, they are separately illustrated in the remaining part of this subsection.

For the condition (1) in Theorem 1, the existence of the NSS-LF ensures that the system is NSS based on the Theorem 2. Hence, the NSS-LF is proposed to construct the function γ.

Theorem 3.

The term γ can be obtained by the following expression:

$$\gamma (\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )=\sqrt{{\alpha }_1^{-1}\left(\frac{c^{-1}{\alpha }_4(\underset{0\le s\le t}{\sup }\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )}{\epsilon }\right)}$$

(10)

if the system (9) admits a NSS-LF.

The proof is given in the Appendix A.

To evaluate the condition (2) in Theorem 1, the following linear matrix inequality (LMI) is proposed

$$A^{T}P+PA\le -cP(\mathrm{for}c>0)$$

(11)

Here, P is a positive definite and symmetric matrix. The superscript T denotes the transpose operator. c is a scalar.

Theorem 4.

If the inequality (11) holds, then the probability of the state deviation for the system (9) satisfies:

$$P\left\{\Vert \Delta x\Vert \le \sqrt{{\alpha }_1^{-1}\left(\frac{c^{-1}{\alpha }_4(\underset{0\le s\le t}{\sup }\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )}{\epsilon }\right)}\right\}\ge 1-\epsilon$$

(12)

The proof is provided in Appendix A.

The feasibility of (11) can be guaranteed by solving the following semi-definite programming (SDP) problem:

$$\underset{P}{\max }c$$

(13)

$$\mathrm{subject}\mathrm{to}P>0$$

(14)

$$A^{T}P+PA+cP<0$$

(15)

where superscript T denotes the transpose operator. P is a symmetric matrix and P = P^T.

Here the optimization is carried over the matrix P. The constraint (14) ensures that P is a positive definite matrix. The constraint (15) guarantees that the NSS-LF exists. Whenever the value c is positive, the NSS-LF for the system (9) can be constructed by P (see Appendix A).

3.3. Application of Noise-to-State Stability Based Probabilistic Stability Analysis

To qualitatively illustrate the application of the proposed approach, a stochastic single-machine infinite-bus (sSMIB) power system is considered in this subsection. The sSMIB system comprises of a classical SMIB system with the integration of stochastic power fluctuations; i.e., active power outputs from a wind power plant (WPP) and/or load fluctuation, as shown in Figure 2.

Assume that the system operates in the steady-state state with the initial values of δ* and ω*. When a small disturbance occurs, the system model (6) is linearized around the equilibrium point, and rewritten as the form in (9) with

$$\Delta x=\left[\begin{array}{c}\Delta \delta \\ \Delta \omega \end{array}\right],A=\left[\begin{array}{cc}0& {\omega }_N\\ -\cos {\delta }^{\ast }& -\overline{D}\end{array}\right],\mathsf{\Sigma }=\left[\begin{array}{cc}0& 0\\ 0& \sigma \end{array}\right].$$

Based on Section 3.2, P can be obtained by solving the linear matrix inequality (LMI) (11). Then the Lyapunov function can be selected as V(x) = x^TPx. Suppose the matrix P is [a d; d b], then α₄ can be chosen as b such that

$$\frac{1}{2}\mathrm{Tr}({\mathsf{\Sigma }}^T\frac{{\partial }^{2}V}{\partial x^2}\mathsf{\Sigma })=b{\sigma }^2\le {\alpha }_4(\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )$$

(16)

Let α₁ and α₂ be the minimum eigenvalue and the maximum eigenvalue of P, respectively. Then (12) holds for the system (9) and the proposed probabilistic stability index (3) is identified.

To examine the probabilistic stability of the rotor angle, we can choose c₁ = 1 and c₂ = 0 in (6) and then attain

$$\Vert \Delta \delta \Vert =\Vert [10]\Delta x\Vert \le \Vert [10]\Vert \Vert \Delta x\Vert =\Vert \Delta x\Vert$$

(17)

It follows that

$$P\left\{\Vert \Delta \delta \Vert \le \sqrt{{\alpha }_1^{-1}\left(\frac{c^{-1}{\alpha }_4(\underset{0\le s\le t}{\sup }\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )}{\epsilon }\right)}\right\}\ge 1-\epsilon$$

(18)

By similar procedures, the following expression can be derived:

$$P\left\{\Vert \Delta \omega \Vert \le \sqrt{{\alpha }_1^{-1}\left(\frac{c^{-1}{\alpha }_4(\underset{0\le s\le t}{\sup }\Vert \mathsf{\Sigma }{\mathsf{\Sigma }}^T\Vert )}{\epsilon }\right)}\right\}\ge 1-\epsilon$$

(19)

3.4. Algorithm of Noise-to-State Stability Based Probabilistic Stability Analysis

The flowchart of the proposed NSS based approach is depicted in Figure 3.

Step 1: Set the values of Σ, ε, and c. A smaller value ε amounts to a more reliable result from the proposed method.

Step 2: Choose the NSS-LF V(x).

Step 3: Select the class $\mathcal{K}$ functions α₁, α₂, α₃ and α₄ based on the method presented in Appendix A. As shown in Section 3.2, the selection principle is to satisfy the conditions in Theorem 1.

Step 4: Compute the value of the function γ(||ΣΣ^T||).

Step 5: Set the weighted coefficient to obtain the stability probability of the power system state.

4. Case Studies

In this section, two case studies are employed to demonstrate the proposed NSS based approach. The first case study is to verify the proposed method on the sSMIB system as shown in Section 3.3. The analytical results are obtained from the approach proposed in Section 3.2 and compared with numerical results based on the Monte Carlo simulation. The second case study is performed on the 145-bus test system to demonstrate the effectiveness of the proposed approach to analyzing the large scale power system.

4.1. A Stochastic Single-Machine Infinite-Bus System

Consider the sSMIB system depicted in Figure 2. In this case study, analytical results obtained from the proposed approach are compared with numerical results from the Monte Carlo simulation. The parameters of synchronous generators are drawn from [37]. The Stochastic continuous variation of power fluctuations is represented as the Gauss white noise with the uncertainty magnitudes σ = 0.01 at Generator 1. The risk level ε is set to 0.1.

Applying (9) to the system gives A = [0, 377; −0.1082, −1.4286] and Σ = [0, 0; 0, σ]. Let the Lyapunov function V = x^TPx, then the scalar c and the matrix P can be solved by the SDP problem (13), which leads to c = 1 and P = [1.1931, 10.1412; 10.1412, 4117.8].

On the other hand, we can choose α₄ = 4117.8σ² so that the Inequality (5) holds. Since the eigenvalues of P are 1.2 and 4117.8, α₁ and α₂ are chosen as α₁ = 1.2(x₁² + x₂²) and α₂ = 4117.8(x₁² + x₂²), respectively. Then the Inequality (4) is satisfied. Hence, from Theorem 2, the system is NSS. Now the stochastic small signal stability can be identified by the proposed method.

Clearly, β(||x₀||,t)→0 as t→∞ since c is larger than zero and α₁ and α₂ is nonnegative. Only the bound level of the state deviation in (3) needs to be computed. Substituting the value of the parameter into (10), it leads to γ(||ΣΣ^T||) = 1.8524. From (18), the interval of the rotor angle deviation that the corresponding stability probability are shown in

Table 1. Theoretical results with SMIB. SMIB: single-machine infinite-bus.

State Variables	Estimated Interval	Stability Probability
|δ|	≤1.8524	≥0.9
|δ|	≤1.3099	≥0.8

. It indicates that the range of the interval decreases with the decrease of the stability probability 1 − ε.

To further elucidate the relationship between the interval bounding the state deviations and the stability probability, γ(||ΣΣ^T||) is plotted as a function of the stability probability 1 − ε in light of (10), as shown in Figure 4. Note that y-axis is scaled by logarithm in order to show it more clearly.

From Figure 4, the value of γ(||ΣΣ^T||) increases with the increase of the uncertainty magnitude σ when the stability probability is fixed. In parallel, the increase of ε results in the decrease of γ(||ΣΣ^T||). This is because, based on (10), the range of the interval is proportional to the uncertainty magnitude, while it is inversely proportional to the risk level ε.

To verify the above theoretical results, 90% confidence interval is constructed to characterize the upper and lower bounds of the systems state deviations based on the Monte Carlo simulation [38], which is summarized in Figure 5. More specifically, the sample paths of the system states are generated by the Euler-Maruyama (EM) method. Then the lower 90% confidence level can be obtained by taking the 5% percentile of the trajectories. The upper 90% confidence level can be obtained by taking the 95% percentile of the trajectories. Figure 6 shows the numerical results obtained from 1000 samples.

From Figure 6, one sample path (the green line) of the rotor angle deviation is bounded by the confidence levels (the red dashes) with a probability 0.9. Thus, the system satisfies the proposed probabilistic stability index. This confirms the theoretical result, which concludes that the probability of the rotor angle deviation bounded is larger than 0.9. Figure 6 also implies that the rotor angle deviation can exceed these bounds with a finite probability.

It can also be seen from Figure 6 that numerical results indicate the upper and lower bounds of the interval are about $\pm$0.5 (the red dashes), respectively. It is less than the bound level of 1.8524 obtained from the proposed approach.

This risk is measured by the value of ε in (3). A similar observation can be made for the rotor angle speed deviation in Figure 7.

4.2. The 145-Bus Test System

In this subsection, a large-scale power system is employed to illustrate the scalability of the proposed approach. The test system composes of 50 machines and 145 buses. Generators are modeled as the classical second-order model. All the generators and network data can be found in [39]. Stochastic continuous variations are represented as Gauss white noises with the uncertainty magnitudes of σ₁ = 0.01, σ₂ = 0.03, and σ₃ = 0.05 at Generator 1, Generator 6, and Generator 37, respectively.

A small disturbance is applied to the system at t = 0 s. The state space model (9) is derived by linearizing the system at a stationary operating point. The matrix P can be obtained by solving the semi-definite program problem (13). Using the proposed method, it can be verified that the system satisfies the probabilistic stability index (3) with γ(||ΣΣ^T||) = 3.5174. Thus, from (17) the probability of the rotor angle deviation satisfies P{||x(t)|| ≤ 3.5174} ≥ 0.9, and the theoretical results are given in

Table 2. Theoretical Results with the 145-Bus Test System.

State variables of G1, G6, and G37	Estimated Interval	Stability Probability
|δ|	≤3.5174	≥0.9
|δ|	≤2.4871	≥0.8
|δ|	≤2.0307	≥0.7

for different risk levels ε.

Numerical results based on the Monte Carlo simulation with 1000 samples are given in Figure 8.

One sample path (the green line) of the corresponding generator is plotted in Figure 8, which is bounded in the upper and lower bounds (the red dashes). The stability probability of bounding the system states by these two levels is 90%. There is also a possibility that a sample path is unbounded by the upper and lower levels. The maximum value of the upper level is about 0.6, while the minimum value of the lower level is about −0.1. Note that the theoretical values of the bounds are $\pm$3.5174 for ε = 0.1. Clearly, the interval obtained from the Monte Carlo simulation is contained in the interval derived from the proposed approach.

The above discussions also imply the existence of some conservativeness, since the bound level of the interval derived from the proposed approach is larger than that from numerical simulations. From (10), one possible solution for this problem is to make a tradeoff between the acceptable level of the risk ε and the accuracy of the estimated bound levels based on Figure 4. On the other hand, the Expression (10) shows that the theoretical value of the bound decreases with the increase of c and α₁, which leads to the reduction of the conservativeness.

To study the computation efficiency, the computation time of the proposed method is compared with that of the Monte Carlo simulation. The results, attained in the New England test system and the 145-bus test system, are provided in

Table 3. Computational Time Comparisons.

Test System	Proposed Method	Monte Carlo Simulation
New England test system	0.019	99.92
145-bus test system	0.022	195.47

. The observation can be made that the proposed method has significantly higher computation efficiency than the Monte Carlo simulation. This is because the Monte Carlo simulation requires a large number of simulation times to yield the reliable results regarding the probabilistic stability analysis. But in the proposed method, the probabilistic stability can be judged by checking the algebraic Expression (10) only once with basic matrix manipulations. This feature makes it very attracting in practical applications.

5. Conclusions

In this paper, an analytical approach based on the noise-to-state stability is proposed for the stochastic small signal stability analysis of the power system in the SDE framework. The probability stability of a power system is attained in an analytical way, and hence superior to the existing methods of solving a partial differential equation set. Besides, since only algebraic conditions need to be checked for attaining the conclusion, the proposed method is much faster than the Monte Carlo based approach for practical applications. To be specific, the main contributions of this paper are summarized as:

(a)

The NSS based probabilistic stability index is proposed for the stochastic stability analysis of a power system;

(b)

The impact of power stochastic variation magnitudes is explicitly presented in the proposed NSS based probabilistic stability index;

(c)

The NSS based probabilistic stability analysis for the power system is obtained by using the NSS-LF;

(d)

The algorithm for the stability probability computation is given for power system small signal stability analysis;

(e)

The algebraic relation between the magnitude of uncertainty and the probabilistic stability of the system responses is found.

Note that the system response can be estimated within a range by the PDF. From the case studies, it can be seen that the estimated range from the proposed method is larger than the 90% confidence interval from the EM method. A large interval means a large fluctuation range of the system response in the stead sate. In this sense, the proposed method implies the existence of some conservativeness. The Expression (10) shows that the choice of the Lyapunov function has some impact on the computation of the estimated interval. Hence, the future research will focus on finding better estimates of the interval through the Lyapunov function.