1. Introduction
Power grids are among the most complex man-made systems. The increasing penetration of fluctuating and only partially-predictable Renewable Energies Sources as well as new connections of distributed energy resources (DER) have even more increased the complexity of grid management for grid operators, while actually consisting in an opportunity to schedule resources more flexibly. In this context, grid operators will have a more and more important role in operating the grid optimally, planning and re-dispatching distributed resources more frequently, applying demand side management techniques, collaborating closely both at the market level and with each other. According to these preambles, it is reasonable to assume more frequent power flow calculations, made by grid operators, possibly coordinated, to assess voltage profiles, to manage congestions and to achieve best utilization of resources [
1].
At the same time, the electricity sector is becoming an ever more liberalized and competitive market, where parties act strategically to maximize their profits and hence struggle to share sensible information. This poses on one hand the necessity of sharing more information among grid operators to coordinate grid operation, on the other, keeping confidentiality of information for the sake of competitive, strategical and political reasons.
This work presents the development of a new distributed power flow (DPF) trial-tool, thereby testing its performances and providing a case-study in the context of TSO–TSO coordination at cross-borders. The same approach could be exploited in the future also to foster the TSO–DSO (distribution system operator) operations, as discussed in
Section 5.1. Regarding the current and expected growing interaction between TSO and DSO, see for instance [
2,
3,
4].
In order to carry out the distributed algorithm, a suitable mathematical approach has been adopted. Traditionally power flows are solved by means of exact-Newton (EN) methods, in order to maximize computational efficiency [
5]. EN solvers are based on a nonlinear iteration step that approximate the problem to a linear one. The arising Jacobian linear system is then solved by means of a direct linear solver (e.g., lower-upper (
) matrix factorization). Direct solvers are robust, solve exactly a linear system and ensure fast computational time for the majority of cases that can be faced in practice. However, such methods are not well suited to parallelization. On the other hand, inexact Newton (IN) methods [
6,
7,
8] are based on an inner iterative linear procedure. Such solvers are notoriously less robust than direct methods due to the outer-inner iterative procedure that they have to carry out. However, in the context of power flow equations, reference [
9] has already shown good robustness properties in the range of grid operations of interest for Newton–Krylov methods. Newton–Krylov methods are an example of IN Methods.
The DPF tool proposed in this work is indeed based on an IN method, the Newton–Krylov–Schwarz (NKS). The NKS has good convergence properties and provide the solution through a minimal amount of linear iterations as the Newton–Krylov showed in [
9]. The main role of the Schwarz preconditioner is to carry out the parallellism, hence allowing the remote-coordinated solution of power flow equations. It’s worth keeping in mind that the minimization of linear iterations is of fundamental importance to minimize the amount of communication messages among workstations and thus keep the overall simulation time near standard-local power flow simulations. This is the second main role of Schwarz preconditioner. By sharing a small amount of nodes among entities involved in the computation, namely called overlapping nodes (more detailed description in
Section 3.2), the convergence is greatly accelerated. It is crucial to underline that only a small amount of overlapping nodes is sufficient to decrease the number of linear iterations by a great amount. Reference [
10] provides a rigorous proof that shows the exponential dependence between the number of overlapping variables and iteration count.
The idea of choosing NKS to carry out the DPF is definitely based on achieving data-locality sacrificing the least possible computational efficiency. The mathematical methodology of
Section 3 and the implementation methodology of
Section 4 explains how the data-locality is achieved. The implementation is done using portable, extensible toolkit for scientific computation (PETSc) [
11,
12], a powerful parallel library for solving complex mathematical problems, so that the power flow computations can be done on remote computer clusters (more information about PETSc can be found in
Appendix A). In
Section 5, a study case is presented. Firstly, a policy review on TSO–TSO common interaction in the EU is done; then, the test case used is presented. The test case represents a portion of the European grid topology taken from the MATPOWER (Ithaca, NY, USA) libraries [
13,
14], namely the case9241pegase.m [
15,
16].
Section 6 presents the results obtained, showing that computational efficiency can be just slightly traded to achieve the remote simulation. Eventually, conclusions are drawn and presented in
Section 7.
2. Power Flow
In this work, we use the standard formulation of the power flow problem (further details can be found, for example, in [
17]), based on the standard bus classification. The PQ (P and Q for active and reactive power, respectively) buses act as loads on the grid. They mainly withdraw power from a given bus. The PV (P for active power and V for voltage magnitude) buses are the generating buses. They mainly inject power into the grid. The slack bus acts as both a reference for the calculation of voltage angles and magnitudes as well as act as a balance for losses. These losses are known only after the solution of the power flow (and cannot be determined before the load flow computation). We will consider a network made of
N buses, with one single Slack bus. The power flow problem is the problem of finding the power flows over the grid that grid operators solve to get a steady-state assessment of the grid, hence to plan and operate the grid efficiently and safely. Given the topology, a model for each component in the grid (i.e., transformers, phase-shifters, loads, bus, generators and branches), the demand and production for electricity and the voltage magnitudes at PV buses, the power flow problem consists of the determination of the voltage magnitude and phase at PQ buses and of the voltage phase for the PV buses. (In this work, we use the MATPOWER modelling of components. Our DPF solver actually takes as input the MATPOWER case format (
mpc). Demand and production profiles are known as a result of the hourly clearing of an electricity market. Once the power flow problem is solved, power losses, currents flows and power flows can be consequently determined easily). The power flow problem thus consists of the determination of
unknowns for the PQ buses and
G unknowns for PV buses, resulting in a total number of unknowns of
. An equal number of equations that do not introduce further unknowns must be defined to solve the power flow problem. These equations are namely the active and reactive power balances for PQ buses and reactive power balance for PV buses.
Below, we will make the above formal under mathematical terms. For the generic bus
p, the power flow equations take the following (nodal) form:
where
,
are the nodal voltage magnitude and voltage angles, respectively,
, the
,
are the net injections (or withdrawals) of active power and reactive power,
are the nodal conductance and susceptance with respect to the generic bus
p.
and
values are obtained following to the definition of the nodal admittance matrix
Y (of dimensions
), which, in turn, is constructed from modelling of components in the grid. Let us remind readers that:
Let us now introduce the vector of unknowns
as:
and the active and reactive power mismatch functions
relative to the bus
p as:
where the terms:
contain the unknowns and will be computed terms over the iteration process, as it will be shown further below. Rather, the
and
are pre-defined known values. In other terms, the problem sets as: find the values of
that make
and
equal to
and
, respectively, that make:
thus, the solution of Equation (
8) is a problem of finding the zero-vector of the nonlinear function:
with respect to
.
Solution of Equation (
9) can be only carried out iteratively. In Power Flow context, the most common approach is based on Newton–Raphson’s method (NR). Newton’s method approximates the nonlinear problem to a linear problem, from the generic iteration
k to
according to:
which means that, at each step
, the solution vector is the zero vector of the local approximation function
. Notice that application of the gradient operator to a vector yields a matrix. In tensor algebra, scalars, vectors and matrices are interpreted as tensors of order zero, one and two, respectively. Under this nomenclature, say that
t is the order of the tensor
T, then the gradient operator applied to
T gives a tensor
of order
. Thus, we define:
as the Jacobian matrix (namely, the matrix of the partial derivatives) and:
as the correction vector on solution. From Equation (
10), we thus define the nonlinear step update as:
where, as initial guesses on
and
we take the regular
flat start, which means that all voltage magnitudes are set at 1 per-unit and all voltage angles are set to zero.
Since NR is only locally convergent, the nonlinear iteration is usually modified to increase robustness according to:
where
parameters are chosen so as to minimize the norm:
to ensure a descent direction for the norm of
at each iteration. This modification takes the name of a
line-search method.
Summarily, our IN method solves the power flow problem through the following two steps:
- Step 1:
solve (approximately)
- Step 2:
update
IN methods differentiate depending upon the linear solver used in the first step. In the next section, this aspect will be discussed in detail.
3. Linear Solvers
The arising Jacobian’s linear system can be either solved through direct techniques (i.e., in one single step) or through an inner linear iteration procedure. Given a linear system
, direct methods factorize
A (e.g.,
matrix factorization) to get the linear system into an equivalent-eased form. On the other hand, iterative linear solvers attempt to find a solution through a sequence of repeated approximations. In this work, an iterative method is used to specifically accommodate the parallelism, hence the data-locality for grid operators. This is practically carried out by coupling a Krylov accelerator with a domain decomposition technique, which works as a preconditioner. This latter aspect will be analyzed further on. The most of iterative procedures are based on a linear fixed point iteration scheme, namely:
where
f is a linear function giving the convergence properties of the succession and
l stands for the number of linear iterations.
In this work, we make use of an IN method based on a Krylov Subspace Projection method (KSP) that we briefly discuss in the next subsection.
3.1. Krylov Subspace Methods
Krylov Subspace Methods are considered among the most accepted techniques for solving large sparse linear systems in a broad range of subjects [
18]. Given a full rank matrix
A of order
n, representing the coefficient matrix of the linear system, the idea of KSP is to look for solution into a projected space
out of
, where
denotes the space spanned by the columns of
A. The KSP subspace is built starting from the initial residual
, involving
A-matrix multiplications:
where
the dimension of
. Notice that
is of actual dimension
m only in the case the vectors above are linear independent. KSP searches for an approximate solution
of
into the affine space
in the form:
The correction vector
has
m unknown components, hence the same amount of constraining equations must be imposed. This is done through the Petrov–Galerkin (PG) condition:
where
is another subspace of dimension
m related to
. The choice of
distinguishes the projection process. Two main classes of KSP derive from that: when
, the projection is orthogonal, namely the KSP orthogonal; otherwise, it is oblique.
The PG condition not only gives a set of constrains; it practically sets the norm minimization of the error for orthogonal projection processes and the residual minimization for oblique processes, thus giving convergence in least iterations. This is why KSP methods are also known as accelerators.
Let us shortly derive an expression for the correction vector
. Since
, given a basis for
, we can write:
where
is the matrix representation of the KSP basis in Equation (
17) and
a vector of
m components. The imposition of PG condition actually makes the
m components of
, a set of optimal parameters for the minimization of the error (orthogonal projections) or of the residual (oblique projections). A euristic interpretation of this is that
sets the
direction of the update and
the
length of the update. Since the error/residual is minimized (set to zero) along each independent direction, a KSP based on
would converge, to the exact solution (round-off errors aside) exactly in
n projection steps.
In practice, the projection process of a KSP method involves dimensions much lower than n. This is for two reasons: (1) the projection process is increasingly computationally expensive as the dimension of scales up; and (2) an approximate solution is sufficient. KSP does not build the whole subspace at the beginning, but rather starts ortho-normalizing each new with respect to the previous. When m increases too much, the projection process is restarted taking as . This flexible feature of KSP greatly decreases the possibilities for the iterative procedure to fail.
The literature offers a broad range of KSP methods, showing drawbacks and advantages depending on the mathematical problem at issue. In the context of IN methods for AC power flow problems, the Generalized Minimal RESidual method (GMRES, [
19]) already has shown good robustness and least iteration count [
9,
20]. These justify the use of GMRES for this work. Summarily, GMRES calculates the solution through two subsequent steps:
where
minimizes the residual at projection step
m over the Krylov Subspace of dimension
m. The calculation of
vector requires the solution of a least-squares problem of dimension
, hence computations are much less expensive than the initial ones. However, GMRES can be used standalone, and its preconditioned version can even perform better. In the following subsection, preconditioning is introduced, the core underlying idea that allows for carrying out the DPF.
3.2. Preconditioned-Generalized Minimal RESidual Method
Preconditioning is a broad used technique that can have different aims, depending upon application. In the literature, preconditioned-Krylov have been used to improve the robustness and provide a fast-time solution for huge problems [
21,
22]. In this work, the main aim of preconditioning is to accomodate the parallel solution of the power flow equations. At the same time, the overlapping variables related to adjacent sub-networks ease the remote solution by decreasing the number of linear iterations. Various formulations of preconditioning are proposed in the literature. In this work, we use the left-preconditioning formulation, based on:
This system is equivalent to the original one and thus yields the same solution. This leads to an important result in the power flow context: the distributed solution will be exactly the same as in a global power flow simulation, which means the same as solving locally one single network.
The preconditioned-GMRES iteration proceeds with the straightforward application of the GMRES algorithm to the modified system of Equation (
22) by solving Equation (
21) and eventually updating the solution according to:
In the next section, we introduce the specific preconditioner applied in this work.
3.3. Domain Decomposition
Domain decomposition methods (DDMs) are known as divide-and-conquer techniques. The idea is to split the initial problems into many sub-problems, which are much easier to solve. DDMs can be either used directly (as standalone techniques) or as preconditioners, for solution of linear systems. In this work, the overlapping additive-Schwarz method (ASM) (for a detailed mathematical description of ASM, see, for instance, [
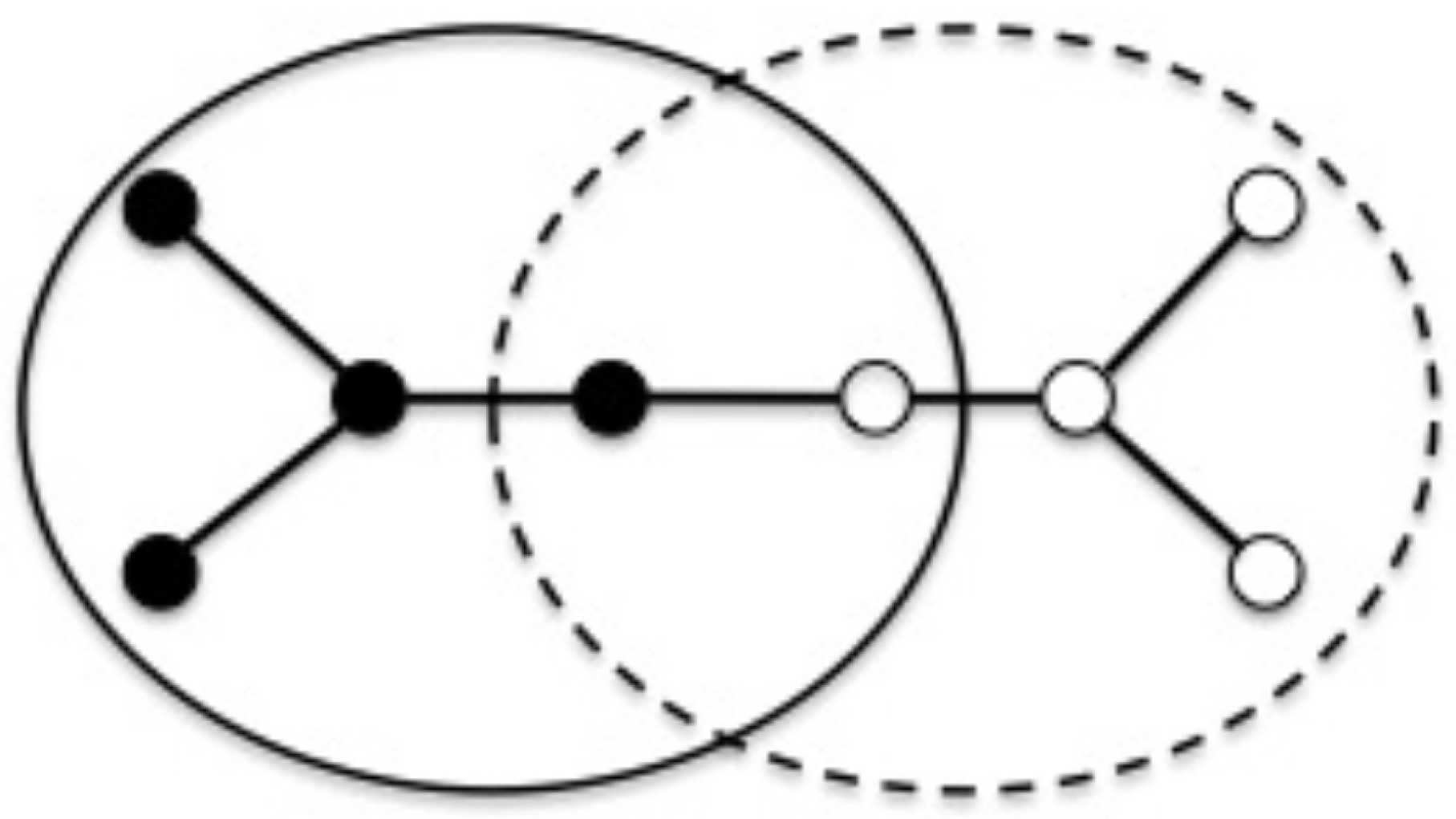
23]), a DDM technique, is used to decompose the network into separate zones, which only share some nodes with each other. The idea is showed in
Figure 1 for a simple two-zones network with two overlapping buses.
What mathematically ASM does is to divide into blocks the coefficient matrix of the linear system and let those blocks overlap through a small number of elements, which are those that practically are related to overlapping buses in the network. Each block is related to a zone in the network. This is formalized into:
where
and
are respectively the prolongation and restriction operators and
S the total number of blocks. The
and
operators extract/put the
t block of
A into the consistent dimension. Each block is then assigned to a processor and solved as a separated linear system. Sub-solvers can be defined at will for sub-problems. In this work, a direct solver based on
factorization is used. As to the shared unknowns, each block solves them giving out a different solution. The update for these unknowns is relaxed and mediated among the solution provided by neighboring blocks, leading to fast convergence at interface [
10].
3.4. Newton–Krylov–Schwarz
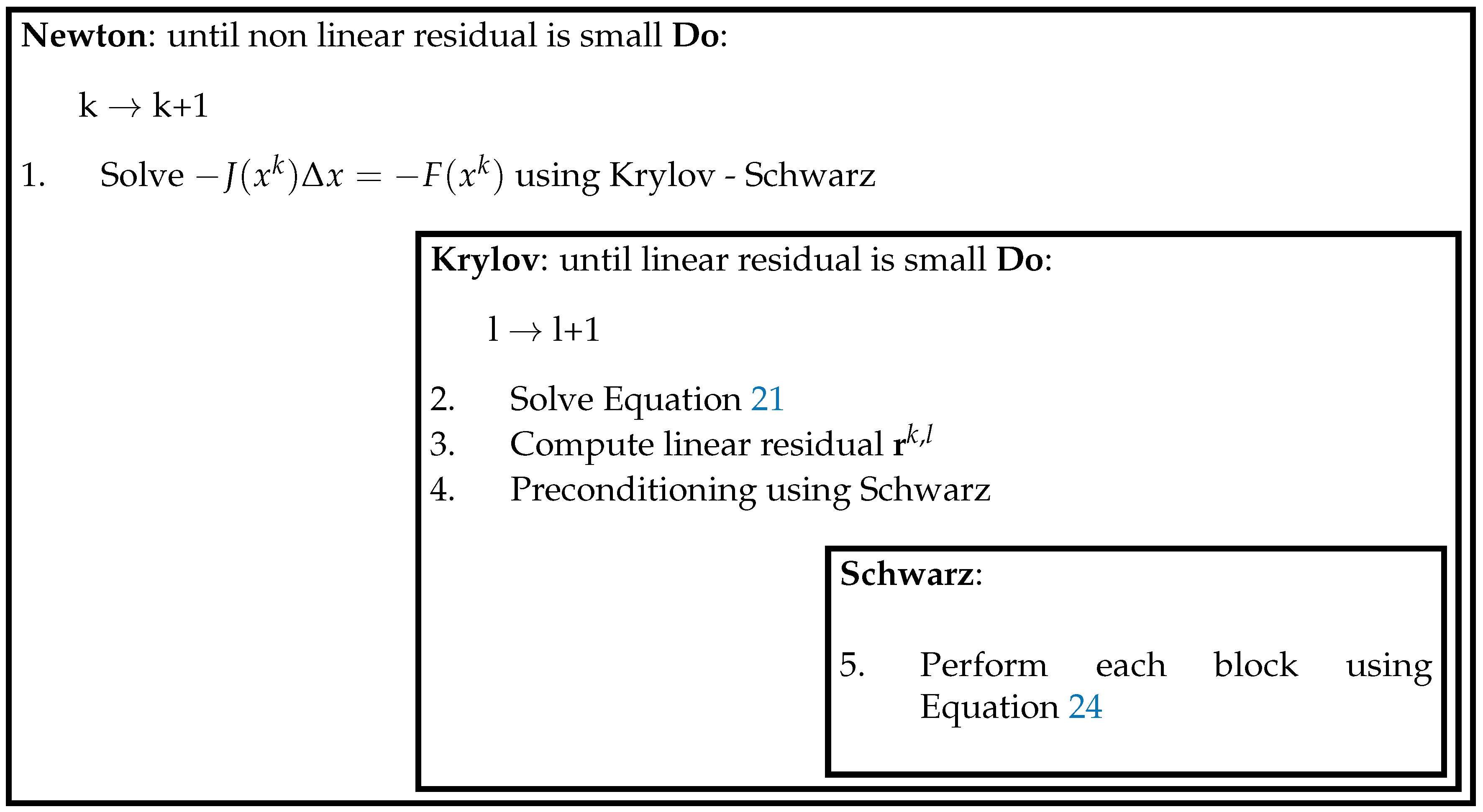
The action of the NKS algorithm for a parallel solution of the power flow problem practically combines different techniques together. This can be outlined as follows in
Figure 2.
The Newton method allows for getting the nonlinear problem into a sequence of linear ones through Equation (
14). Line-search fosters the minimization of nonlinear iterations.
An inner iterative procedure is then started by means of GMRES preconditioned by ASM. The Krylov solver works as an accelerator for the iterative solution of the Jacobian’s linear problem, giving the least number of linear iterations to solve the problem.
Schwarz preconditioning both reduces the amount of linear iterations by letting the sub-zones to overlap and allows for the network decomposition into sub-zones itself. For each sub-zone, there is a sub-linear problem that is solved directly by means of factorization. Interfacing nodes are shared, meaning that the related equations are solved by all the zones sharing them.
Therefore, the Krylov–Schwarz linear solver manages the convergence at neighboring zones. The procedure runs until convergence is reached, according to a given tolerance.
The way the algorithm works suggest the possibility to carry out distributed calculations on different workstations, which is part of the scope of this work. According to ASM, messages about computed variables at interface must be exchanged between workstations. Hence, overall time of computation will be both affected by message communications and computations, which also means that both software and hardware architectures are fundamental to get practically implementable results. In the next sections, the implementation methodology for the DPF calculation is presented.
4. Distributed Power Flow
The parallel execution of code must be supported by proper hardware. Parallel computing simulations are carried out on shared-memory systems to minimize the communication times related to message passing of information among processors. This is fundamental in parallel computing, since it is all about minimization of overall computational time. On the other hand, distributed computing does not focus on speeding-up computations; it is rather used out of necessity to perform calculations in different geographical locations, keep confidentiality of information, to provide fault-tolerance, and others. In these kinds of applications, the machines are physically separated, meaning that the architecture is distributed-memory based. In this work, a distributed computation of power flow guaranteeing complete confidentiality of information is desired, while keeping an acceptable overall time of simulation.
In this section, a description of the parallel implementation, of the hardware, of the software tools, of assumptions and test cases used to carry out distributed computing of power flow equations are presented.
4.1. Parallel Implementation Using Message Passing
The NKS algorithm is schematically represented in
Figure 2. This algorithm can be formulated as a sequence of vector and matrix-vector operations. Vector operations include inner products and updates. Matrix-vector operations include the matrix-vector multiplication. Vectors and matrices are distributed across the various processors involved in the computation. Each processor has a unique identifier referred to as rank. A form of message passing between the processors is thus required to perform computations. We distinguish between local and global communications. Local communications involve only a only a few processors across an interface separating subnetworks. Global communications involve all processors involved in the computation. Global communication are required to execute the aforementioned vector operations. In computing for instance the inner product of two vectors, each processor computes the inner product of the subvectors that it owns. All non-rank-0 processors subsequently send their result to the rank-0 processor. This rank-0 processor finally computes the final answer. The size of the message in this example is equal to the size of a double precision data type. The number of messages depends on factors such as the algorithmic variant of the NKS method and the number of iterations required in outer, intermediate and inner-most loop. Local communications are required to compute for instance the matrix-vector products. Before the actual computations take place, data between neighboring processors needs to be exchanged. The size of the message in this example is equal to the size a double precision data type times the number of nodes that two processors share. The number of local communication is again a function of algorithmic variant and number of iterations.
4.2. Software—PETSc
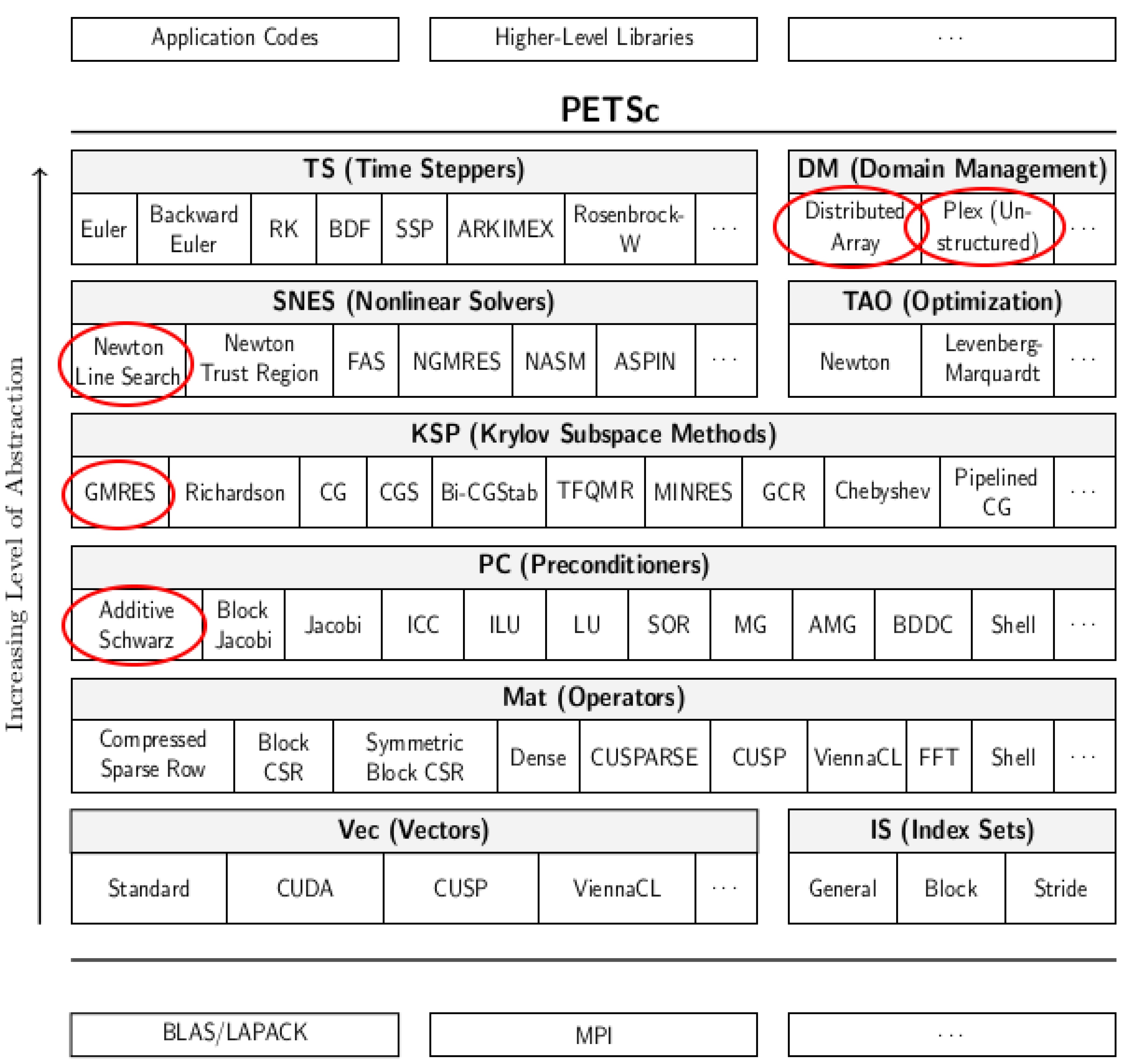
PETSc (see
Appendix A for more details) is a collection of a variety of numerical libraries for solving efficiently complex mathematical problems. The hierarchy is shown in
Figure 3, which highlight in red the PETSc objects used for the distributed calculation. For the context of this work,
PETSc has been selected for mainly three reasons: (1) The PETSc libraries are implemented to work in parallel and manage inter-process communication on their own through the underlying message passing interface (MPI) protocol [
24]; (2) PETSc offers an implementation of the NKS as well as an already implemented code for solving AC power flow equations named
power.c. If the
power.c program is called sequentially (i.e., by typing from terminal
./power), by default,
power makes use of the nonlinear solver class SNES to carry out the nonlinear line-search Newton iteration (see
Section 2) for solution of Equation (
9). The power.c code must be first compiled to produce the executable
power. This can be done by simply typing into its containing directory
make power. Then, KSP and PC objects are called by SNES to solve the Jacobian’s linear system. If the user wants to use a different linear and nonlinear solvers, he can just specify them at run-time (this includes the NKS solver). Parallel run of
power.c can be done by means of MPI command
mpiexec. (To execute the parallel run the user must type in the folder containing the
power executable:
mpiexec <np> ./power where
np is the number of processes the user desires to use.) (3) PETSc offers specific sub-classes to handle structured and unstructured grid (in our context, electricity grids) for modelling and managing the topology and the physics for large-scale networks (an application example can be found in [
25]). In this work, these are the DMPlex and DMNetwork sub-classes, built on top of DM class, to manage electricity grids actually used by
power.c. These abstractions provide several routines and features for network system composition and decomposition. In
power.c, the decomposition is managed by the function DMNetworkDistribute and it follows an e.g., partitioning among processors. The nodes and all the attached components are then split according to the e.g., ownership.
Since this work aims at keeping confidentiality of information for entities involved in the computation, a proper graph partitioning method must be employed to decompose the network according to grid operators ownership. There are six different partitioners that allow the user to decompose the problem in the most suitable way for his own application [
26,
27]; by default,
PETSc decomposes the grid in such a way that all the processors own approximately the same number of elements, hence not respecting the ownership of grid operators. Our application code (
dpower.c to reflect the improved distributed attitude of the code) uses
power.c as a template and has thus been developed to use a shell partitioner, meaning making the partition of network as desired and following topological criteria that reflect the ownership of zones of grid operators.
4.3. Hardware—Cluster Computing
To test out the distributed model, a simple cluster of two machines is employed. The two machines are physically separated (so they are not memory-shared machines) and actually make up a simple distributed computing cluster. Generally speaking, the overall performance of a distributed computing environment is mostly set by communication time among workstations. The technical hardware specifications used for the simulation are below.
The first workstation (machine1) is an 8-node 32 GB RAM machine, each node being an Intel Xeon E3-1275 3.50 Ghz (Santa Clara, CA, USA) running on an Ubuntu 17.10 64-bit GNU/Linux distribution and mounting a network card of 1 Gbit/s. The second workstation (machine2) is a 4-node 4 GB RAM machine, each node being an Intel Core i3-3110M 2,4 Ghz, running on a GNU/Linux Mint 18.3 64-bit distribution and mounting a network card of 100 Mbit/s. Notice that different GNU/Linux distributions have been used on purpose to guarantee portability of the model. Moreover, a quite low-performing network card is used on machine2 to purposely act as a bottleneck, to consider a not extremely high-performance environment. This is because, in reality, grid operators would likely coordinate through a lower performance wide area network (WAN).
The distributed computing simulation is tested under three different network configurations, all running on two processors: (a) a reference case, where distributed computation is done on 2-nodes on the same machine (the master); (b) run on 1-processor on master and on 1-processor client through a mid-latency wireless local area network (WLAN) managed by a switch (108 Mbit/s of ideal maximimum data transfer); and (c) the same as (b), but this time workstations are connected at the switch through a 100 Mbit/s cable. These different network configurations aim at simulating real conditions for DPF computing, hence understanding the practical feasibility. Notice that, only in case (c), the actual transfer rate is almost that of the cable capacity (i.e., 100 Mbit/s). To get the actual transfer rate in case (b), we checked the Linux Network Manager, which showed: 72 Mbit/s for the master machine and 54 Mbit/s for the client machine as transfer rate, so that the client acts as a bottleneck for the system setting the actual transfer rate to 54 Mbit/s.
Latency influence of communications on the overall times can be seen by comparing (a) with (b) and (c) (
Table 1). The codes are compiled using the MPICH2 compiler
mpicc, where MPICH2 is a portable open-source wide-used MPI implementation by Argonne National Laboratory. The configuration of machines cluster have been done through GNU bash built-in commands of UNIX systems. First, the
mpiuser profiles on both machines have been configured. Then, connection between machines is configured through
ssh (Secure Shell) command capabilities. The standard
ssh configuration is used, so that message passing actually take place through underlying
tcp (Transfer Control Protocol). In order to control the stability of transfer rate (i.e., to control the network traffic), each simulation is repeated up to 10 times, excluding simulation times that prove to be much slower (hence clearly affected by network traffic) and eventually taking the average of the left-over values.
Although the cluster computing setup is simple, it allows for demonstrating the feasibility of the model as well as to test out the influence of message passing communications between machines on the overall simulation time.
5. Case Study
This section presents a case study used to validate the DPF model. Firstly, a short review for the current national cross-border flow management is presented; then, the DPF solver is inserted into the corresponding context. Finally, the test case for validation is presented.
5.1. Policy Motivation
In the specific context of European electricity grid, the harmonization of markets with grid operation is the matter of concern for the next generation power grids. In order to cooperate fruitfully and allow power flows from one network to the other following market rules, grid operators need to interact closely. Although this would result in a better resource management both at transmission and distribution level across Europe, grid operators still struggle for sharing detailed information (particularly in real-time data or short-term trends correlated to the electricity market). For this reason, collaboration is still hindered.
At a high-voltage transmission level, the wholesale national markets define different market zones (in a few cases, like Italy or Sweden, Finland, Denmark, Norway, countries are split into multiple market zones). In order to allow exchanges between markets, some market coupling criteria are employed to link the markets and allow electricity to flow from one zone to the other. Wholesalers buy together with energy the right to transmit that energy using cross-border interconnection capacity (through so-called “implicit auctions”) to actually import (or export) electricity from/to another market zone. Cross-border capacity is first calculated by grid operators and then implicitly (or sometimes explicitly) auctioned in the power market (or, in case of explicit allocation, through a separate capacity allocation market). In this context, the aim is to allocate in the market the greatest possible cross-border capacity while ensuring a safe grid operation. There are two main methodologies currently applied in Europe for cross-border capacity calculation and subsequent implicit allocation in the day ahead markets (DAMs): (1) the available transfer capacity (ATC) methodology; and (2) the Flow-Based (FB) methodology, with the second being more complex but giving a better estimation on available capacity. These methods are hence used to define a “physical flow domain”, that is then integrated in the DAM coupling clearing so that the outcome of the market respect the physical constraints given at the borders. A quick overview on ATC and FB methodologies can be found in [
28].
It is straightforward to think that better ex-ante capacity estimations allow for releasing more capacity, thus a better economic arrangement [
29] and ultimately a truly integrated and a more efficient European power market. A distributed calculation of power flow equations aim at providing full-confidentiality of input-output data for entities involved in the computation, while ensuring that feasible simulation times may find its application in the European framework. In this way, entities may include detailed input information (load forecast, generating units, critical network elements (CNEs) modelling, short-term market trends, bounds correlated with maintenance activities, etc.) and actually carry out a coordinated capacity calculation, obtaining an exact forecast on interfacing flows from the computation.
It is worthwhile to stress that the DPF model could also be applied to foster TSO–DSO cooperation. At distribution level, the current integration of RES generation is changing the way the grid is operated. The distribution grid is turning from a passive fit-and-forget approach to an active grid. At the same time, distributed resources (such as storage and flexible loads) are showing up as a possibility to manage the grid more efficiently. All this is changing the role of DSOs to actively manage the distribution grid. In this context, we expect the need of more frequent power flow calculations and a closer cooperation among operators, yet keeping them unbundled on functional roles. The specific application of DPF in this context could be thought as follows. Regular power flow simulations made by TSOs do not include distribution grid nodes. At the same time, TSOs do not have access to all the information at distribution level (nor will they reasonably have it in the future, for unbundling of grid operator set by policy) while actually owning assets at the distribution level. In this context, a DPF computation, where TSO and DSOs respectively input their detailed data and confidentially, receives computed complex voltages and exact power flows over owned branches. Considering both HV and MV buses of a rather large national European grid (e.g., Italy), the solution of a power flow problem would lead to hundreds of thousands of buses. This is a complexity that conventional direct methods barely address, which is well addressed by Newton–Krylov methods instead, as it has been shown in [
9]. In this paper, a TSO–TSO case study is investigated; future activities will be focused on TSO–DSOs scenarios’ formulation and analysis.
5.2. Test Case
The case study is structured imagining that two grid operators have to perform a coordinated power flow simulation over their managed network. The test case will serve both as a framework to test the feasibility of the DPF model in terms of remote simulation times, according to grid operators’ needs, and to assess the influence of the overlap in speeding up the overall simulation time.
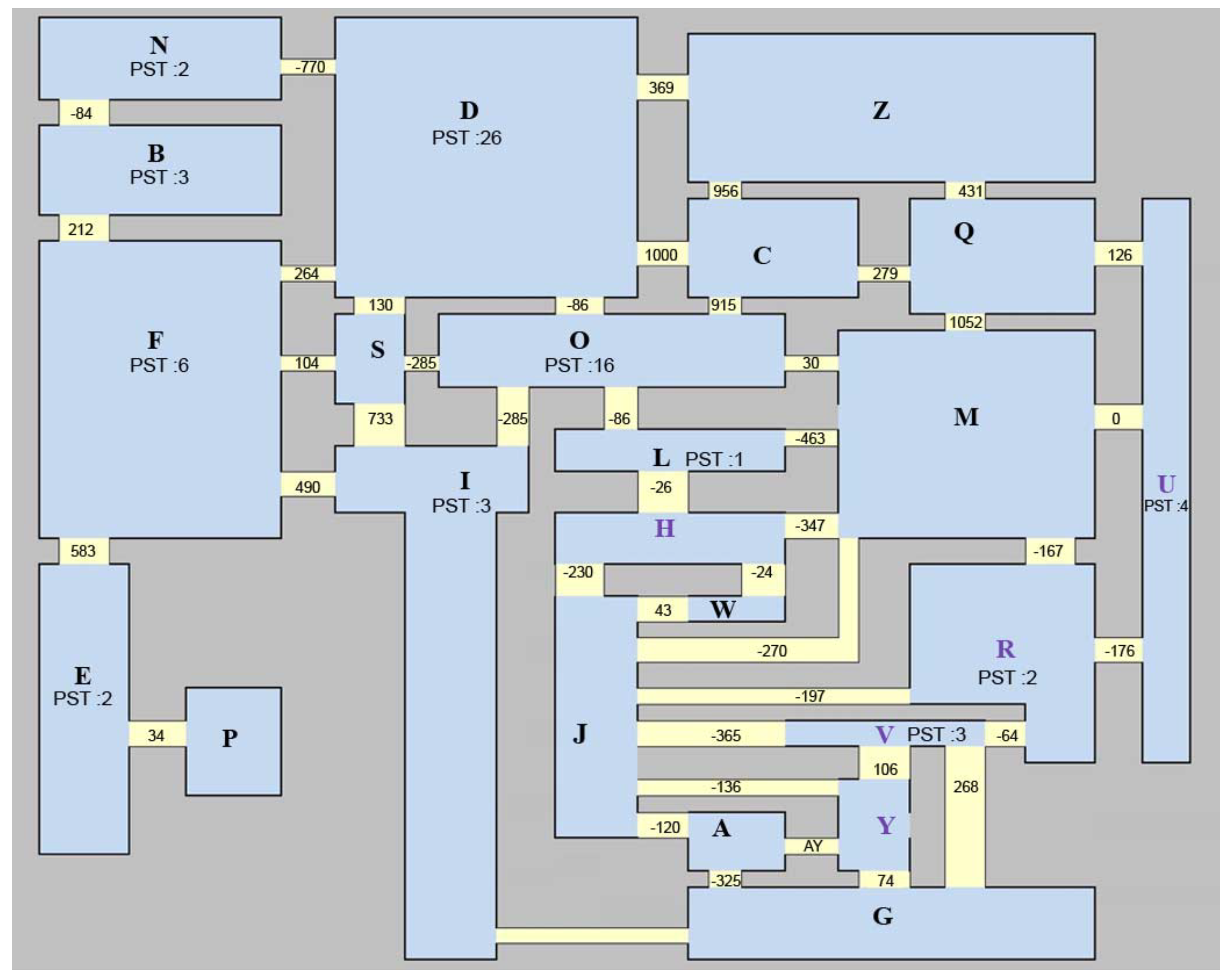
To test out the model, we created a new
MATPOWER case out of
case9241pegase.m (see
Figure 4), where this latter is a case that can be found in the
MATPOWER libraries. Such case models the high voltage EU Transmission Network of 24 state members detailing 9241 buses, 1445 generators, 16049 branches and 1319 transformers. There are nine voltage levels: 750, 400, 380, 330, 220, 154, 150, 120, 110 kV.
The
case9241pegase.m case is divided into zones, each zone representing a national transmission grid. Our test case is built up by extracting two zones from the
case9241pegase.m, namely the Zone 4 and Zone 5 (which correspond to Zones D and E in
Figure 4). In order to avoid confusion, Zone 4 will be simply called Zone 1 and Zone 5 will be called Zone 2.
Notice that zone 1 has 682 buses, 1172 branches and 169 generators. Zone 2 is characterized by 1354 buses, 1992 branches and 260 generators. The two zones are connected by a single branch.
6. Numerical Results
According to
Section 4.3, three scenarios are simulated. The
shell partitioner splits the network according to zone 1 and 2 ownership. Results in terms of simulation time are reported in
Table 1 (
s represents the number of overlapping variables). Notice that each simulation has been repeated up to 10 times and eventually averaged (see
Section 4.3) to control the impact of network traffic.
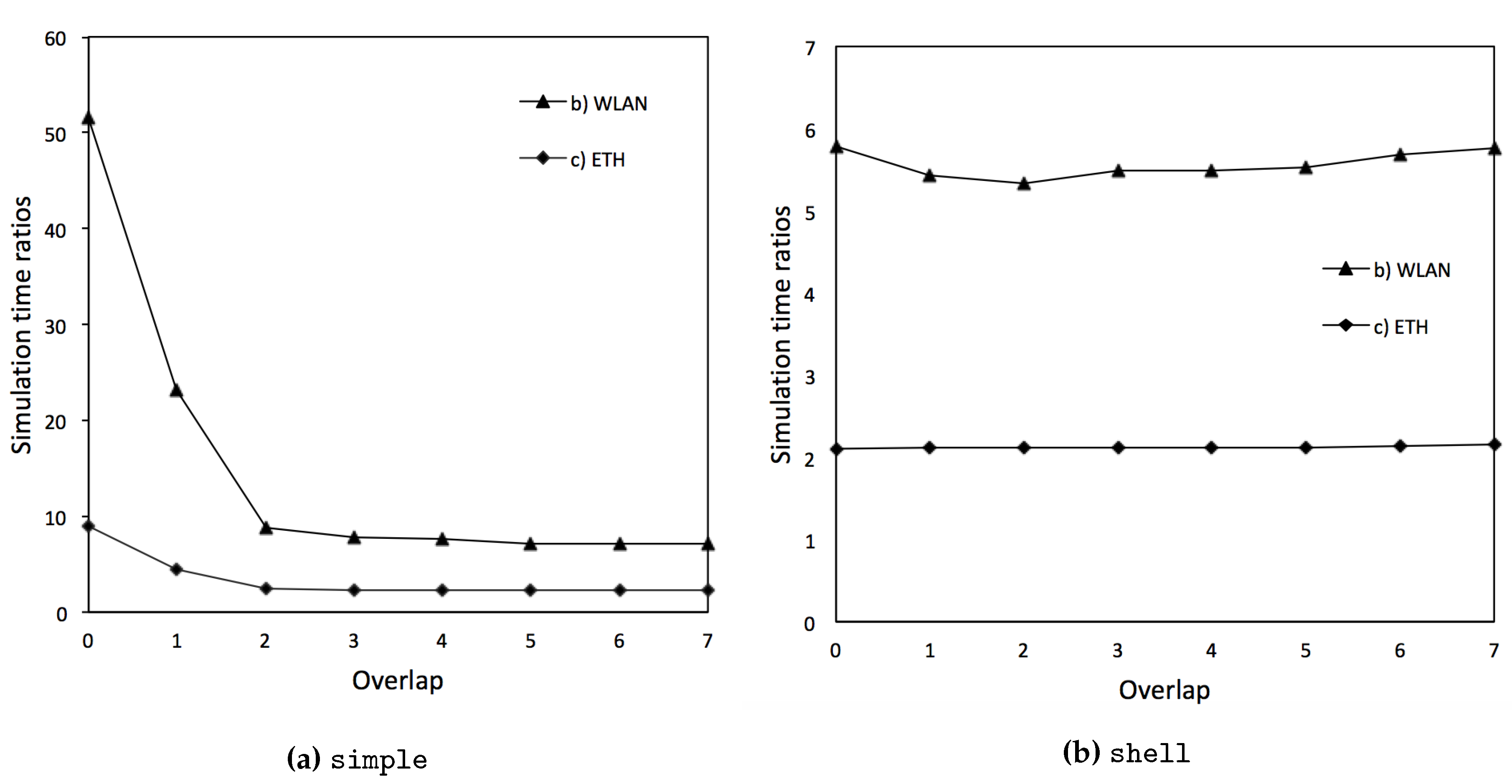
The results show that increasing the number of overlapping variables over 2 does not lead to a decreasing simulation time. This is due to the topology of the case taken into account. In fact, Zone 1 and Zone 2 are connected through one branch, which means that there are only two off-diagonal block elements in the Jacobian matrix. Setting the overlap to 2 includes all the off-diagonal elements into blocks, thus solving the linear problem in the least number of iterations. In other terms, increasing the overlap cannot decrease the number of iterations and hence the simulation time.
On the other hand, the performance gain would be greater if the number of off-diagonal elements was higher. This fact can be seen in the case of simple partitioner. In this case, the network is not split through the connection branch, but somewhere else. With this partition, the amount of off-block diagonal elements increases, as the branches connecting the zones are increased.
Increasing overlap values leads to a decreasing number of linear iterations, but, at the same time, it increases the message passing of information between processors during the single linear iteration. Basically, higher overlap value effort for message passing becomes greater than the advantages due to a decreasing number of linear iterations. The optimal overlap value should take into account both aspects as shown in
Table 2.
In
Figure 5, the above performances are represented into two distinct charts in terms of simulation time ratios. The time-ratio values are obtained dividing the simulation times of (b) and (c) by simulation time of (a) (best scenario, i.e., local simulations) in order to get a comparison between local times and distributed simulation times.
The latency introduced due to communications through inter-connection between workstations proves to be as reasonable (same order of magnitude). In reality, grid operators would rather communicate through a WAN or a cloud rather than a WLAN or Ethernet cable. This could certainly cause delays in the simulation. However, this is not expected to be a relevant issue. First, we adopted rather conservative WLAN speeds on purpose; second, fast WAN interconnection can nowadays reach even 1 GBit/s; third, the main scope here is to keep data confidentiality for parties involved in the computation, so that the overall delay is offset by the possibility of achieve confidentiality.
In any case, a test case based on WAN interconnection will be investigated in future works to further assess the possibility for reality applications of the model, hopefully simulating more than two operators taking part in the simulation.