Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids
Abstract
1. Introduction
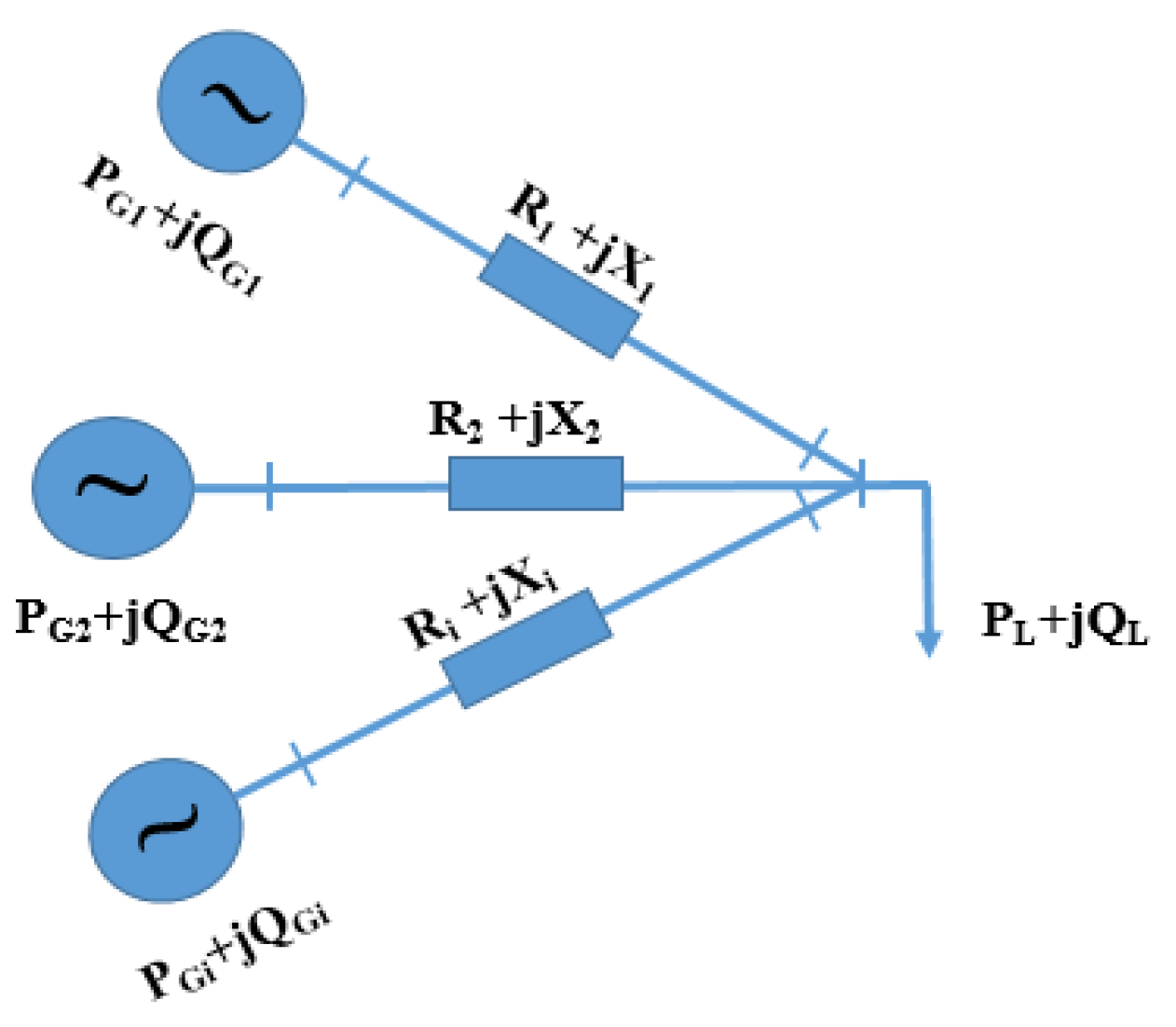
2. Driven Primary Regulation for Minimum Power Losses Operation
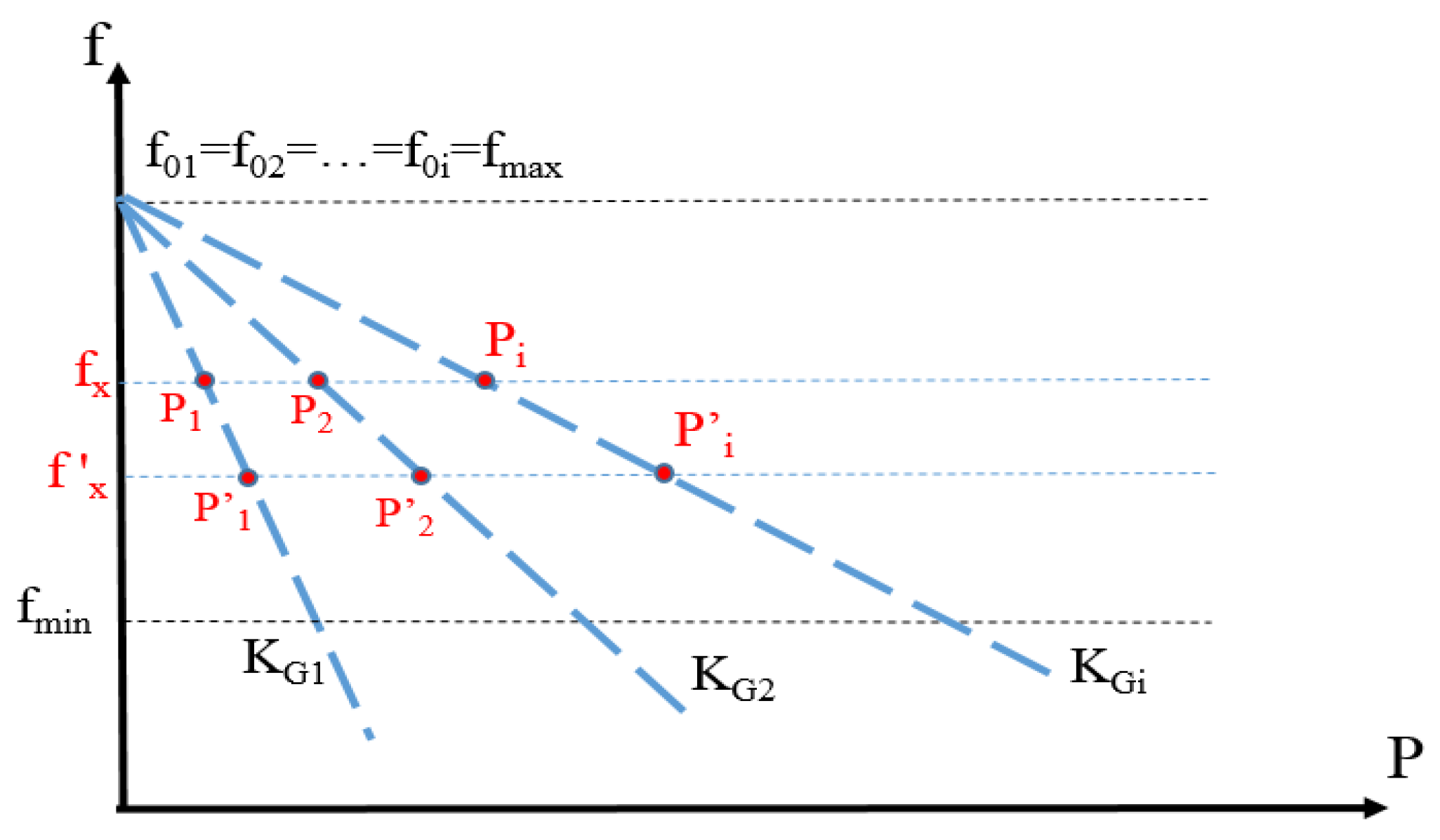
2.1. Conventional Droop Control Method
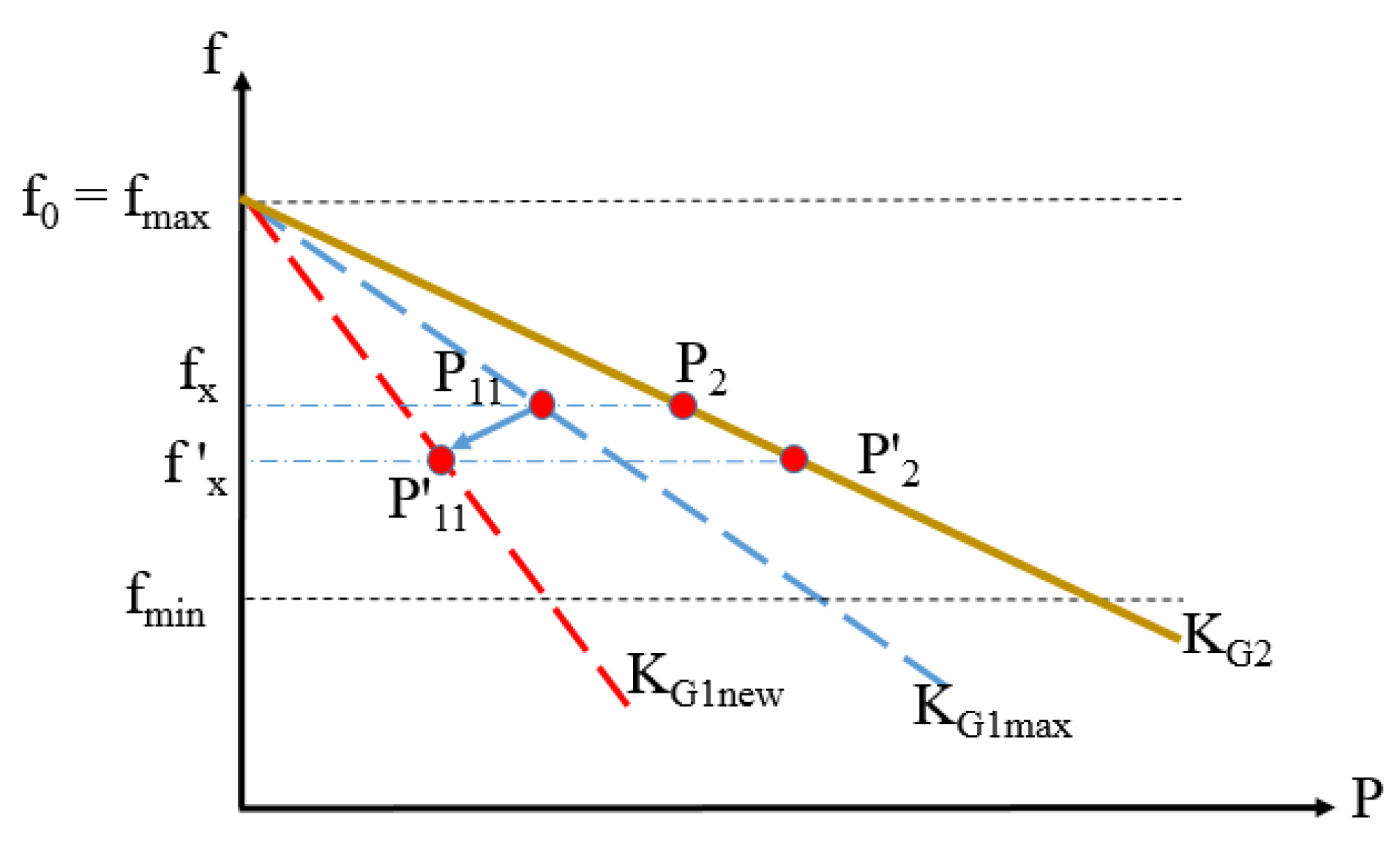
2.2. Proposed Driven Primary Regulation Method
- The amplitude and displacement of the voltage phasors at the P–Q buses.
- The amplitude and displacement of the voltage phasors at all the P–V buses except the reference bus (Qi depends on Vi by (2));
- The voltage amplitude at the reference bus;
- The frequency of the system in the range [fmin, fmax].
2.3. Glow-worm Swarm Optimization Algorithm
- Step 1: Start.
- Step 2: Collect input data regarding the microgrid (including real power and reactive power of generators, bus voltages, features of the lines, droop parameters, etc.).
- Step 3: Initialize a population of glow-worms randomly. Every glow-worm is a potential solution of optimization problem.
- Step 4: Generate luciferin lo, local decision range ro at time t = 0.
- Step 5: The objective function is calculated by running the OPF for each solution and is stored in vector J(x).
- Step 6: Update the value of luciferin li(t + 1) using (11):where ρ is the luciferin decay constant (0 < ρ < 1) and γ is the enhancement constant (0 < γ < 1).
- Step 7: Find the neighborhood agents having stronger luciferin in the local decision range.
- Step 8: Update the probability of glow–worm i moving to neighbor j in the t iteration denoted by pij(t):where Ni(t) is the set of neighborhood of glow-worm i at the t-th iteration.
- Step 9: Update the location of glow-worms as following:where s is the step-size.
- Step 10: Update the local decision range :
- Step 11: Iterate the step from 5 to 10 until reach the maximum iterations number.
- Step 12: Show the results.
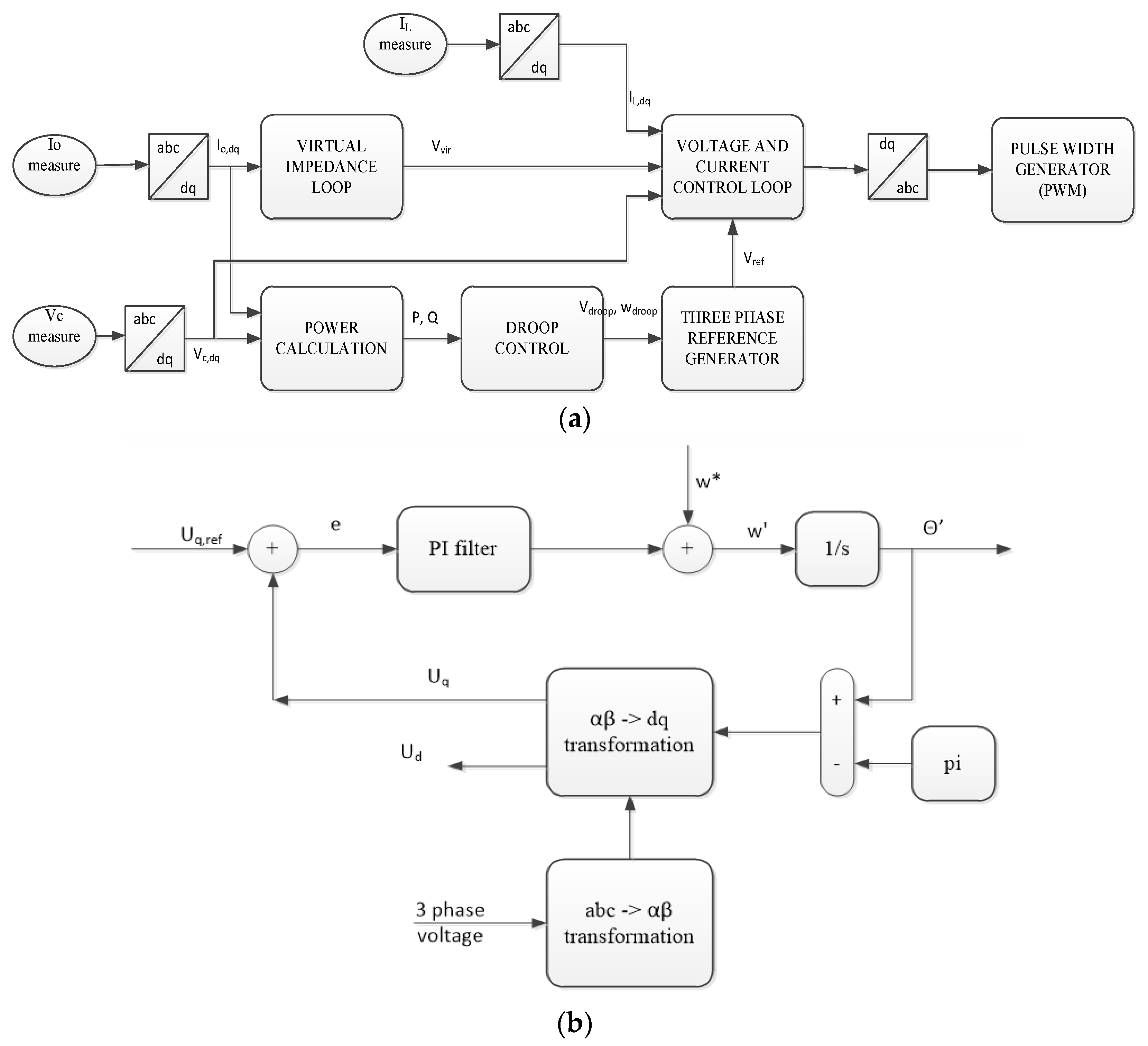
2.4. Simulation of the Droop Control Loop
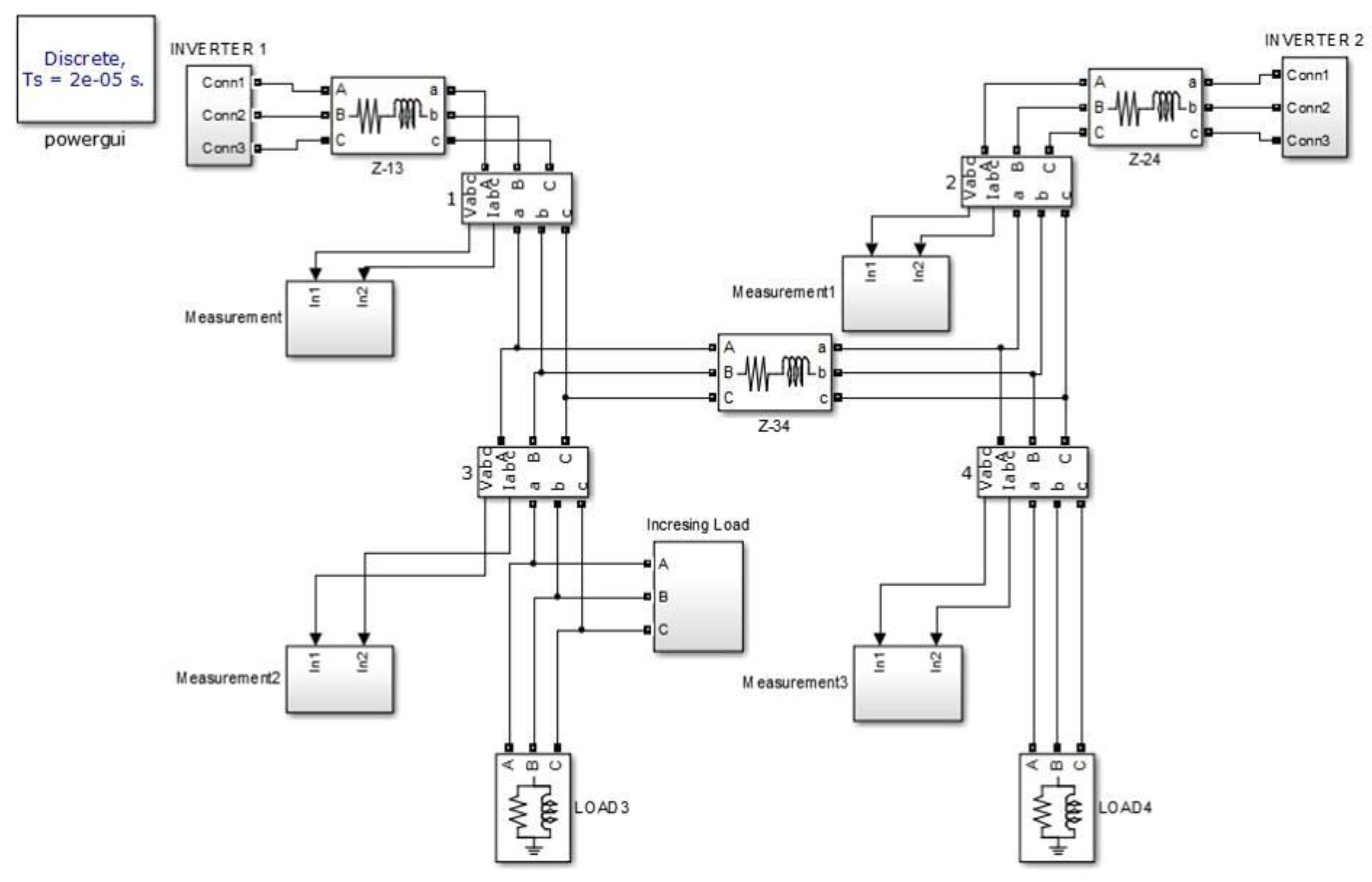
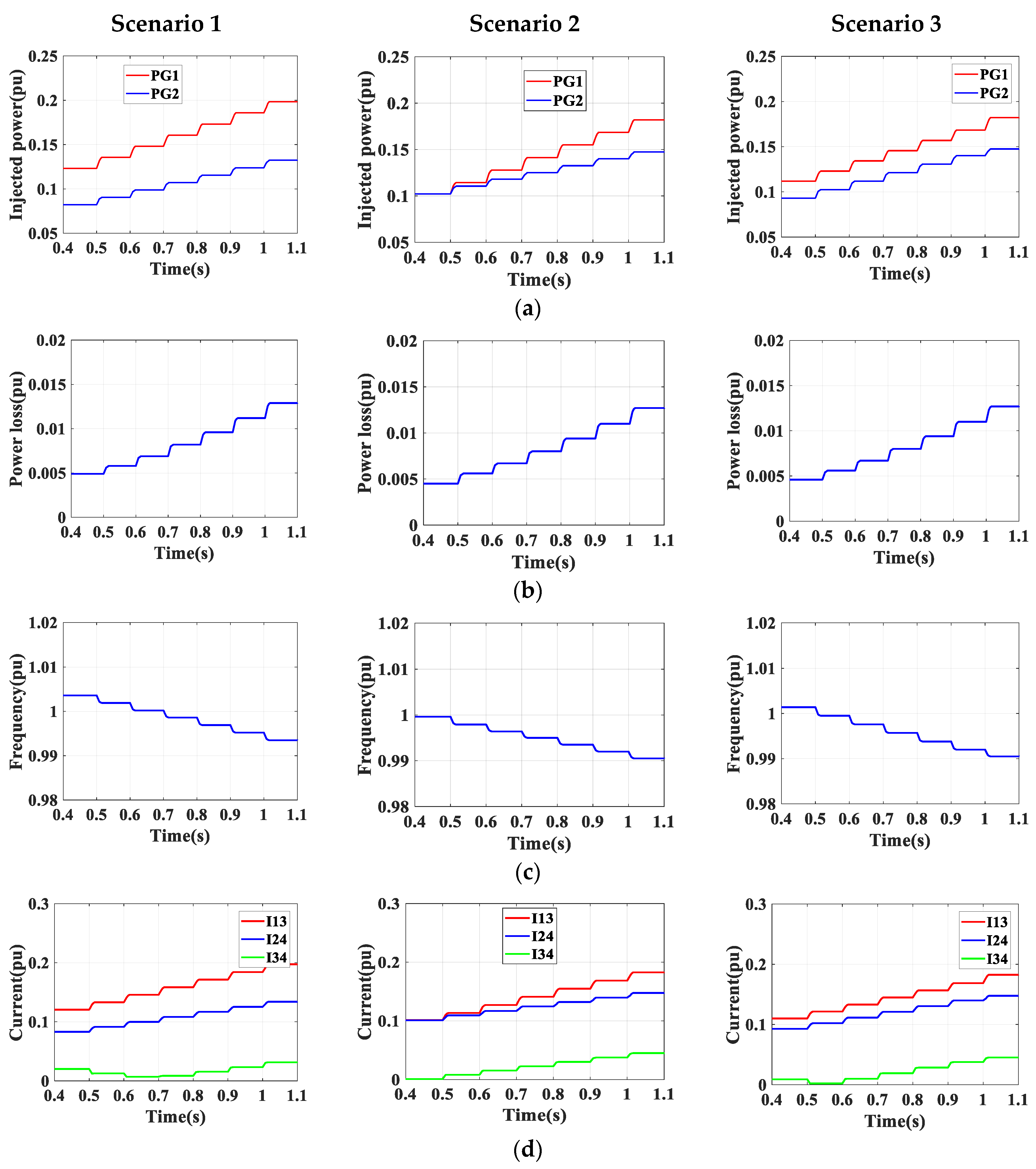
3. Case Study
- Scenario 1, implementing the conventional droop control method
- Scenario 2, implementing the proposed optimized control method with KG1 selected optimally in the range [5–7.5]
- Scenario 3, implementing the proposed optimized control method with KG1 selected optimally in the range [6–7.5]
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclature
| DG | Distributed generator | δi | Phase angles of the voltages at bus i |
| OPF | Optimal Power Flow | θij | Phase angle of Yij |
| GSO | Glow-worm Swarm Optimization | nbr | Number of branches connected to bus i |
| OF | Objective Function | P0i | Real power of the load in the operating point |
| ICT | Information and Communications Technology | Q0i | Reactive power of the load in the operating point |
| ACO | Ant Colony Optimization | α | Real power exponents |
| PSO | Particle Swarm Optimization | β | Reactive power exponents |
| PWM | Pulse Width Modulator | Yij | Admittance of the ij branch |
| PLL | Phase-Locked Loop | Kpf | Coefficient, ranging from 0 to 3.0 |
| PI | Proportional Integral | Kqf | Coefficient ranging from −2.0 to 0 |
| PGi | Real power generated of the i-th generator | ∆P | Real power deviation |
| QGi | Reactive power generated of the i-th generator | x(t) | Location of glow-worms in the search space at iteration t |
| KGi | Frequency droop coefficient of the i-th generator | l(t) | Value of luciferin at iteration t |
| Kdi | Voltage droop coefficient of the i-th generator | ρ | Luciferin decay constant |
| fx,i | Frequency at the i-th generator | γ | Enhancement constant |
| Vi | Output voltage at the i-th generator | Ni(t) | Set of neighborhood of glow-worm i at the t-th iteration |
| f0i | Frequency of the i-th generator at no load | s | Step-size |
| V0i | Voltage of the i-th generator at no load | rdi | Local decision range |
| KGmaxi | Maximum value of frequency droop coefficient of the i-th generator | KP | Proportional gain constant |
| PGmaxi | Rated power of i-th generator | fsw | The switching frequency of the PWM |
| nG | Number of generators in microgrid | Ti | Integral time constant |
| nd | Number of load buses | σ | Symmetrical distance |
| PLi | Real power demand of the i-th load | fc | Crossover frequency |
| Ibranchi | Current flowing in the i-th branch of the microgrid | Lv(s) | LC filter transfer function |
| Imaxbranchi | Ampacity of the i-th branch of the microgrid | Pv(s) | PI controller transfer function |
| nbranch | Number of transmission branches in the microgrid | GC,CL(s) | Inner current control transfer function |
| fmax | Frequency upper limit | Cf | Filter parameters |
| fmin | Frequency lower limit | Lf, Rf | Filter parameters |
| Pi | Injected power at bus i | Tf | System time constant |
| Ploss | Power losses of the microgrid | Gv(s)OL | Open loop transfer function |
| nbus | Number of buses of the microgrid | Gv(s)CL | Close loop transfer function |
| Vi | Voltages at buses i | ∆f | Frequency deviation |
References
- Hirase, Y.; Sugimoto, K.; Sakimoto, K.; Ise, T. Analysis of Resonance in Microgrids and Effects of System Frequency Stabilization Using a Virtual Synchronous Generator. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1287–1298. [Google Scholar] [CrossRef]
- Karavas, C.; Kyriakarakos, G.; Arvanitis, K.G.; Papadakis, G. A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 2015, 103, 166–179. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and Analysis of Renewable Energy and Battery Systems in Residential Microgrids. IEEE Trans. Smart Grid 2016, 7, 1204–1213. [Google Scholar] [CrossRef]
- Han, H.; Hou, X.; Yang, J.; Wu, J.; Su, M.; Guerrero, J.M. Review of Power Sharing Control Strategies for Islanding Operation of AC Microgrids. IEEE Trans. Smart Grid 2016, 7, 200–215. [Google Scholar] [CrossRef]
- Chandorkar, M.C.; Divan, D.M.; Adapa, R. Control of parallel connected inverters in stand-alone AC supply systems. In Proceedings of the Conference Record of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991. [Google Scholar]
- Andrade, E.T.; Ribeiro, P.E.M.J.; Pinto, J.O.P.; Chen, C.L.; Lai, J.S.; Kees, N. A novel power calculation method for droop-control microgrid systems. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012. [Google Scholar]
- Klem, A.; Nehrir, M.H.; Dehghanpour, K. Frequency stabilization of an islanded microgrid using droop control and demand response. In Proceedings of the 2016 North American Power Symposium (NAPS), Denver, CO, USA, 18–20 September 2016. [Google Scholar]
- Ramezani, M.; Li, S. Voltage and frequency control of islanded microgrid based on combined direct current vector control and droop control. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Villa, A.; Belloni, F.; Chiumeo, R.; Gandolfi, C. Conventional and reverse droop control in islanded microgrid: Simulation and experimental test. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016. [Google Scholar]
- Hou, X.; Sun, Y.; Yuan, W.; Han, H.; Zhong, C.; Guerrero, M.J. Conventional P-ω/Q-V Droop Control in Highly Resistive Line of Low-Voltage Converter-Based AC Microgrid. Energies 2016, 9, 943. [Google Scholar] [CrossRef]
- Mariani, V.; Vasca, F.; Vásquez, J.C.; Guerrero, J.M. Model Order Reductions for Stability Analysis of Islanded Microgrids With Droop Control. IEEE Trans. Ind. Electron. 2015, 62, 4344–4354. [Google Scholar] [CrossRef]
- Brabandere, K.D.; Bolsens, B.; Keybus, J.V.d.; Woyte, A.; Driesen, J.; Belmans, R. A Voltage and Frequency Droop Control Method for Parallel Inverters. IEEE Trans. Power Electron. 2007, 22, 1107–1115. [Google Scholar] [CrossRef]
- Moazami Goodarzi, H.; Kazemi, H.M. A Novel Optimal Control Method for Islanded Microgrids Based on Droop Control Using the ICA-GA Algorithm. Energies 2017, 10, 485. [Google Scholar] [CrossRef]
- Elrayyah, A.; Cingoz, F.; Sozer, Y. Construction of Nonlinear Droop Relations to Optimize Islanded Microgrid Operation. IEEE Trans. Ind. Appl. 2015, 51, 3404–3413. [Google Scholar] [CrossRef]
- Sinha, M.; Dhople, S.; Johnson, B.; Ainsworth, N.; Dörfler, F. Nonlinear supersets to droop control. In Proceedings of the 2015 IEEE 16th Workshop on Control and Modeling for Power Electronics (COMPEL), Vancouver, BC, Canada, 12–15 July 2015. [Google Scholar]
- Ashabani, S.M.; Mohamed, Y.A.R.I. General Interface for Power Management of Micro-Grids Using Nonlinear Cooperative Droop Control. IEEE Trans. Power Syst. 2013, 28, 2929–2941. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, W.; Wang, G.; Wenjun, W.; Wang, D.; Li, Z. Study of control strategy of DG based on nonlinear droop characteristic. In Proceedings of the 2012 China International Conference on Electricity Distribution, Shanghai, China, 10–14 September 2012. [Google Scholar]
- Krismanto, A.U.; Mithulananthan, N.; Lomi, A. Dynamic droop control in microgrid for stability enhancement considering RES variation. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017. [Google Scholar]
- Hernandez-Aramburo, C.A.; Green, T.C.; Mugniot, N. Fuel consumption minimization of a microgrid. IEEE Trans. Ind. Appl. 2005, 41, 673–681. [Google Scholar] [CrossRef]
- Carniato, L.A.; Godoy, R.B.; Pinto, J.O.P.; Canesin, C.A.; Ribeiro, P.E.M.J. Dynamic adaptation of droop control curves for microgrid connected inverters with variable input power. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013. [Google Scholar]
- Arani, M.F.M.; Mohamed, Y.A.I. Dynamic Droop Control for Wind Turbines Participating in Primary Frequency Regulation in Microgrids. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Sanseverino, E.R.; Favuzza, S.; Silvestre, M.L.; Tran, Q.; Zizzo, G.; Pham, N.T.; Kieu, T.T.H. Improved primary regulation for minimum energy losses in islanded microgrids. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017. [Google Scholar]
- Sanseverino, E.R.; Nguyen, N.Q.; Silvestre, M.L.D.; Zizzo, G.; Bosio, F.d.; Tran, Q.T.T. Frequency constrained optimal power flow based on glow-worm swarm optimization in islanded microgrids. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015. [Google Scholar]
- Buckspan, A.; Aho, J.; Fleming, P.; Jeong, Y.; Pao, L. Combining droop curve concepts with control systems for wind turbine active power control. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012. [Google Scholar]
- Krpan, M.; Kuzle, I. Inertial and primary frequency response model of variable-speed wind turbines. J. Eng. 2017, 2017, 844–848. [Google Scholar] [CrossRef]
- Quang, N.N.; Sanseverino, E.R.; Silvestre, M.L.D.; Madonia, A.; Li, C.; Guerrero, J.M. Optimal power flow based on glow worm-swarm optimization for three-phase islanded microgrids. In Proceedings of the 2014 AEIT Annual Conference—From Research to Industry: The Need for a More Effective Technology Transfer (AEIT), Trieste, Italy, 18–19 September 2014. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Bibliography on load models for power flow and dynamic performance simulation. IEEE Trans. Power Syst. 1995, 10, 523–538. [CrossRef]
- Patel, M.J.; Patel, M.V.; Sorathiya, J. Real Power Loss Allocation Based on Circulating Current between Generators. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 232–239. [Google Scholar]
- Zhang, D.; Wang, F.F.; Burgos, R.; Boroyevich, D. Common-Mode Circulating Current Control of Paralleled Interleaved Three-Phase Two-Level Voltage-Source Converters With Discontinuous Space-Vector Modulation. IEEE Trans. Power Electron. 2011, 26, 3925–3935. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Zhao, W. A Novel Stability Improvement Strategy for a Multi-Inverter System in a Weak Grid Utilizing Dual-Mode Control. Energies 2018, 11, 2144. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Power management of an isolated hybrid AC/DC micro-grid with fuzzy control of battery banks. IET Renew. Power Gener. 2015, 9, 484–493. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.d.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Karegowda, A.G.; Prasad, M. A Survey of Applications of Glowworm Swarm Optimization Algorithm. In Proceedings of the International Conference on Computing and information Technology 2013 (IC2IT), Bangkok, Thailand, 9–10 May 2013. [Google Scholar]
- Krishnanand, D.G.; Kaipa, N. Glowworm Swarm Optimization: Theory, Algorithms, and Applications, 1st ed.; Springer: Norfolk, VA, USA, 2017; ISBN 978-331-951-594-6. [Google Scholar]
- Sheikh, A.; Youssef, T.; Mohammed, O. AC Microgrid Control Using Adaptive Synchronous Reference Frame PLL. In Proceedings of the 2017 Ninth Annual IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 29–31 March 2017. [Google Scholar]
- Barbosa, A.L.S.; Barros, P.R.; Acioli, G. Identification and PI controller redesign in symmetrical optimum based design. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014. [Google Scholar]
- Bajracharya, C.; Molinas, M.; Suul, J.A.; Undeland, T.M. Understanding of tuning techniques of converter controllers for VSC-HVDC. In Proceedings of the Nordic Workshop on Power and Industrial Electronics Conference, Helsinki, Finland, 9–11 June 2008. [Google Scholar]
- IEEE Power and Eenergy Society, Analytic Methods for Power Systems Committee Distribution System Analysis Subcommittee Test Feeder Working Group. Available online: http://sites.ieee.org/pes-testfeeders/resources/ (accessed on 1 January 2018).



| Droop Control Methods | Conventional Droop Control | Non-Linear Droop Control | Dynamic Droop Control | Proposed Droop Control |
|---|---|---|---|---|
| References | [9,10,11] | [5,12,13,14,15,16,17] | [18,19,20,21] | |
| Simple | ✓ | - | - | ✓ |
| Easy to implement | ✓ | - | - | ✓ |
| Quick response | ✓ | - | - | ✓ |
| No communication signals between the inverters | ✓ | - | - | ✓ |
| Improved power sharing | - | ✓ | ✓ | ✓ |
| Improved stability | - | ✓ | ✓ | ✓ |
| Branch | R (pu) | X (pu) | R/X | Imaxbranch (pu) |
|---|---|---|---|---|
| 1–3 | 0.22229917 | 0.02873961 | 7.7 | 0.5396 |
| 2–4 | 0.22229917 | 0.02873961 | 7.7 | 0.5396 |
| 3–4 | 0.22229917 | 0.02873961 | 7.7 | 0.5396 |
| Scenario | Initial Load | Scenario 1 | Scenario 2 | Scenario 3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PL3 | PL4 | KG1 | PG1 | Ploss | f | KG1 | PG1 | Ploss | f | KG1 | PG1 | Ploss | f | |
| 1 | 0.1 | 0.1 | 7.5 | 0.1233 | 0.0049 | 1.0036 | 5.01 | 0.1022 | 0.0045 | 0.9996 | 6.01 | 0.1118 | 0.0046 | 1.0014 |
| 2 | 0.12 | 0.1 | 7.5 | 0.1357 | 0.0058 | 1.0019 | 5.18 | 0.1144 | 0.0055 | 0.9979 | 6.00 | 0.123 | 0.0056 | 0.9995 |
| 3 | 0.14 | 0.1 | 7.5 | 0.1482 | 0.0069 | 1.0002 | 5.42 | 0.1279 | 0.0066 | 0.9964 | 6.00 | 0.1343 | 0.0067 | 0.9976 |
| 4 | 0.16 | 0.1 | 7.5 | 0.1607 | 0.0082 | 0.9986 | 5.66 | 0.1414 | 0.0079 | 0.995 | 5.99 | 0.1456 | 0.0080 | 0.9957 |
| 5 | 0.18 | 0.1 | 7.5 | 0.1732 | 0.0096 | 0.9969 | 5.85 | 0.1550 | 0.0093 | 0.9935 | 5.99 | 0.1569 | 0.0094 | 0.9938 |
| 6 | 0.2 | 0.1 | 7.5 | 0.1858 | 0.0112 | 0.9952 | 6.02 | 0.1686 | 0.0110 | 0.992 | 6.02 | 0.1685 | 0.0110 | 0.992 |
| 7 | 0.22 | 0.1 | 7.5 | 0.1985 | 0.0129 | 0.9935 | 6.17 | 0.1821 | 0.0127 | 0.9905 | 6.17 | 0.1821 | 0.0127 | 0.9905 |
| 8 | 0.24 | 0.1 | 7.5 | 0.2112 | 0.0147 | 0.9918 | 6.32 | 0.1958 | 0.0146 | 0.989 | 6.32 | 0.1958 | 0.0146 | 0.989 |
| 9 | 0.26 | 0.1 | 7.5 | 0.2239 | 0.0168 | 0.9901 | 6.44 | 0.2094 | 0.0167 | 0.9875 | 6.44 | 0.2094 | 0.0167 | 0.9875 |
| 10 | 0.28 | 0.1 | 7.5 | 0.2368 | 0.019 | 0.9884 | 6.54 | 0.2231 | 0.0189 | 0.9859 | 6.55 | 0.2232 | 0.0189 | 0.9859 |
| 11 | 0.3 | 0.1 | 7.5 | 0.2496 | 0.0214 | 0.9867 | 6.65 | 0.2369 | 0.0213 | 0.9844 | 6.65 | 0.2369 | 0.0213 | 0.9844 |
| 12 | 0.32 | 0.1 | 7.5 | 0.2626 | 0.0239 | 0.985 | 6.74 | 0.2507 | 0.0238 | 0.9828 | 6.74 | 0.2506 | 0.0238 | 0.9828 |
| 13 | 0.34 | 0.1 | 7.5 | 0.2755 | 0.0266 | 0.9833 | 6.82 | 0.2645 | 0.0265 | 0.9812 | 6.82 | 0.2645 | 0.0265 | 0.9812 |
| 14 | 0.36 | 0.1 | 7.5 | 0.2886 | 0.0295 | 0.9815 | 7.01 | 0.2805 | 0.0295 | 0.98 | 7.01 | 0.2803 | 0.0295 | 0.98 |
| 15 | 0.37 | 0.1 | 7.5 | 0.2952 | 0.0311 | 0.9806 | 7.29 | 0.2918 | 0.0311 | 0.98 | 7.29 | 0.2918 | 0.0311 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
T.T Tran, Q.; Luisa Di Silvestre, M.; Riva Sanseverino, E.; Zizzo, G.; Pham, T.N. Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies 2018, 11, 2890. https://doi.org/10.3390/en11112890
T.T Tran Q, Luisa Di Silvestre M, Riva Sanseverino E, Zizzo G, Pham TN. Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies. 2018; 11(11):2890. https://doi.org/10.3390/en11112890
Chicago/Turabian StyleT.T Tran, Quynh, Maria Luisa Di Silvestre, Eleonora Riva Sanseverino, Gaetano Zizzo, and Thanh Nam Pham. 2018. "Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids" Energies 11, no. 11: 2890. https://doi.org/10.3390/en11112890
APA StyleT.T Tran, Q., Luisa Di Silvestre, M., Riva Sanseverino, E., Zizzo, G., & Pham, T. N. (2018). Driven Primary Regulation for Minimum Power Losses Operation in Islanded Microgrids. Energies, 11(11), 2890. https://doi.org/10.3390/en11112890








