1. Introduction
Efficient energy management is crucial for the performance [
1], in terms of power consumption and security, of hybrid electric vehicles (HEVs) and electric vehicles (EVs). As the most popular form of energy storage, the lithium-ion battery needs a high-performing energy management system to extend its life [
2,
3]. A battery management system (BMS) is used to provide accurate battery information and ensure reliable operation. The key function of the BMS is to monitor the online battery package statement, especially the state of charge (SOC) [
4], which is the most critical element for the charge-discharge strategy and battery safety. Unfortunately, the state of charge is an indirectly measured variable and can only be estimated through relative quantities, such as battery voltage, current, temperature, etc. [
5,
6].
Several methods have been proposed for estimating SOC. The first method is the Coulomb counting method, which measures the current constantly and counts the Coulomb charge/discharge in order to estimate SOC [
7,
8]. This method is simple and easy to implement but it is sensitive to an initial value and accumulation errors. The second method is the open-circuit voltage (OCV) method, which measures the voltage of a lithium-ion battery after a long rest time [
9,
10], which is not suitable for HEVs or EVs. In order to overcome the defects of these methods, the extended Kalman filter (EKF) has been proposed as an optimum adaptive algorithm for SOC. However, this method depends strongly on the accuracy of a model parameter that is not consistent [
11]. For instance, the battery internal resistance, as a significant parameter of the battery model, varies according to different SOC, temperature and state of health (SOH).
In order to obtain the online parameter of a lithium-ion cell, such as the internal resistance of the battery, some researchers have proposed electrochemical impedance spectroscopy (EIS) to study the impedance of the battery [
12], which is incompatible with the constraints of EV or HEV applications. Others have improved existing battery models and algorithms to estimate the online internal resistance [
13]. However, this approach inevitably increases the complexity and uncertainty of SOC estimation.
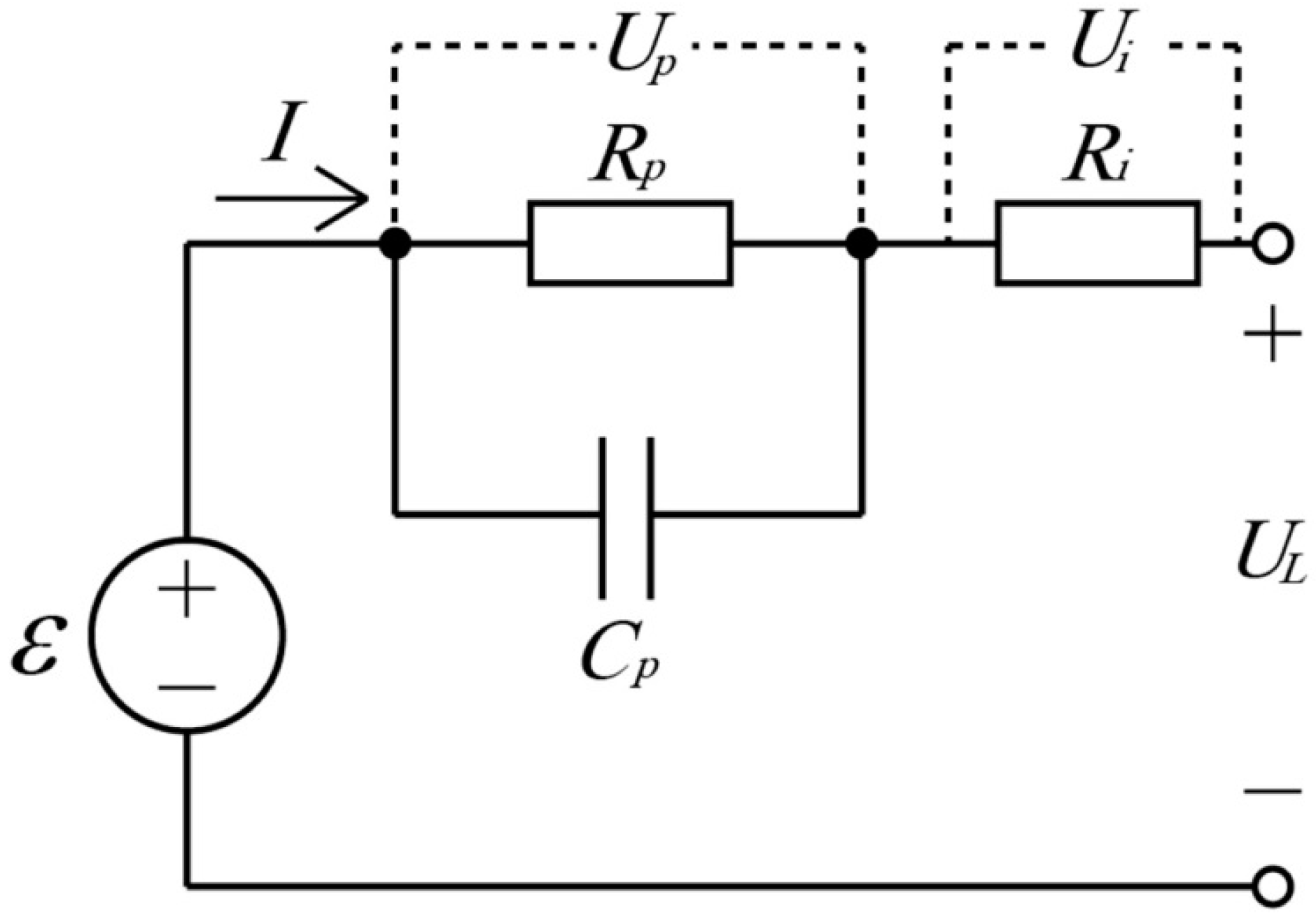
In this paper, we present an effort to use the online measurement of internal resistance to estimate battery SOC that employs the traditional extended Kalman filter. This work is useful for studying the effect of internal resistance on SOC evaluation. Firstly, based on an equivalent circuit model (ECM), the internal resistance of a lithium-ion battery is measured by a device that can generate a controllable direct current short-pulse (DCSP) current source. Then, this real-time internal resistance is used as parameter of EKF algorithms to estimate the battery SOC. Finally, the improvement to the SOC evaluation error that comes from using online internal resistance is demonstrated by comparing this with the simple EKF operation error.
3. Internal Resistance Characterization
First,
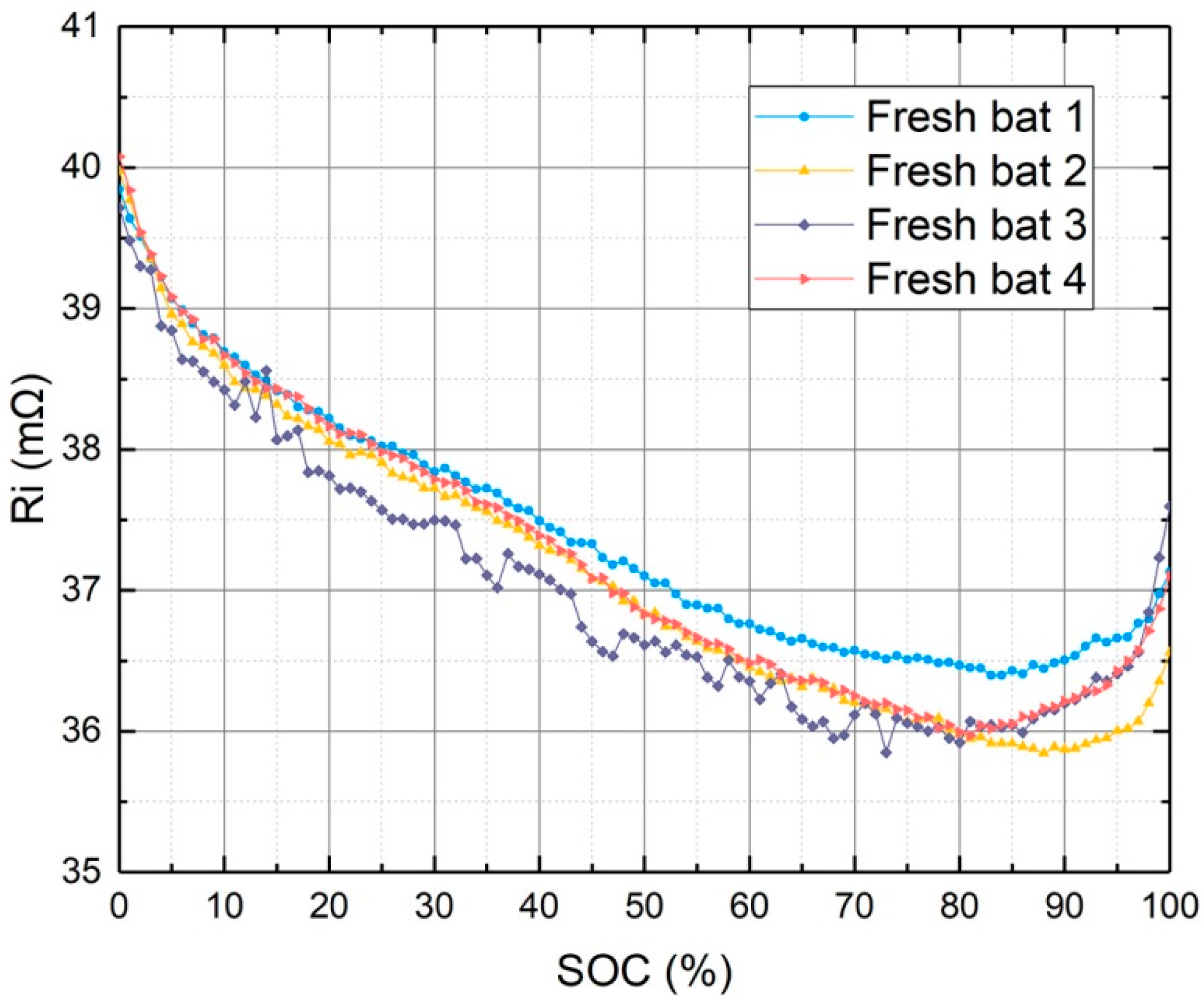
Figure 4 shows the relationship curves between internal resistance and SOC. The experiment samples were four new 18650 batteries operating at room temperature. The experimental results showed that the internal resistance of the battery varied with the battery’s SOC. Internal resistance was at maximum value when the battery capacity was empty. However, the minimum value of the internal resistance was not noticeable at the time of SOC 100%, but at a point between 80% and 90% of SOC. This phenomenon is consistent with the internal resistance characteristics of the hybrid pulse power characterization test [
15] and the real part of the impedance detection characteristics by EIS [
7]. In addition, the experimental results showed that the difference between the individual cells can be distinguished by internal resistance even if these lithium-ion batteries are fabricated with the same structures and materials. Since the internal resistance is an important parameter in the battery model, this individual difference can eventually be reflected in efforts to estimate the battery’s SOC.
Second, the internal resistance of the battery at different temperatures was studied.
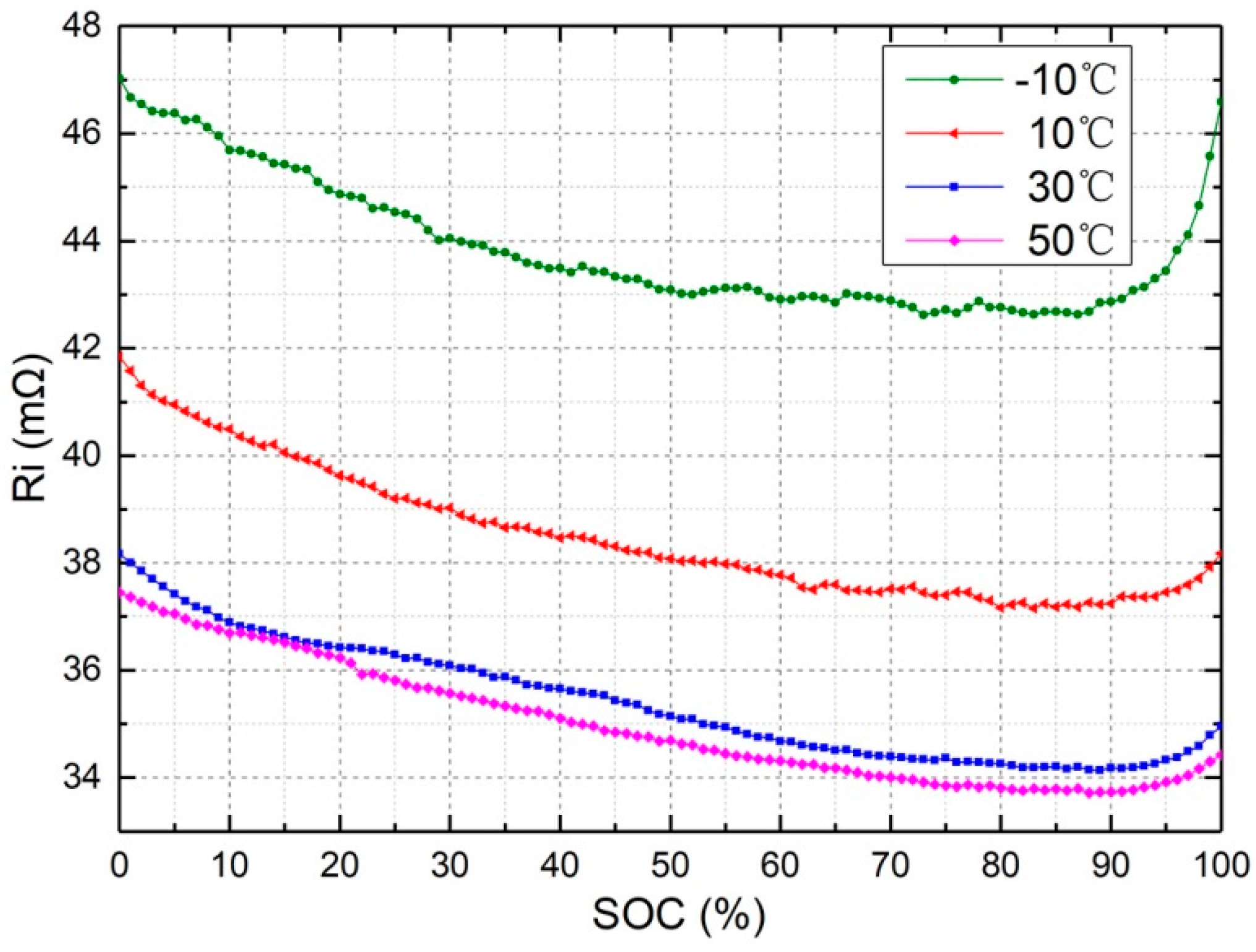
Figure 5 shows the relationship curves between internal resistance and SOC. The experiment sample was the same brand new battery used at different temperatures. In the experiment, data were collected at −10 °C, 10 °C, 30 °C and 50 °C. The data curves show that the temperature has a greater effect on the internal resistance than that from SOC only. At low temperature, such as −10 °C, the value of internal resistance of the battery increased significantly. Therefore, for accurate SOC evaluation, temperature must be considered a factor, and this can be partially characterized by changes in real-time internal resistance.
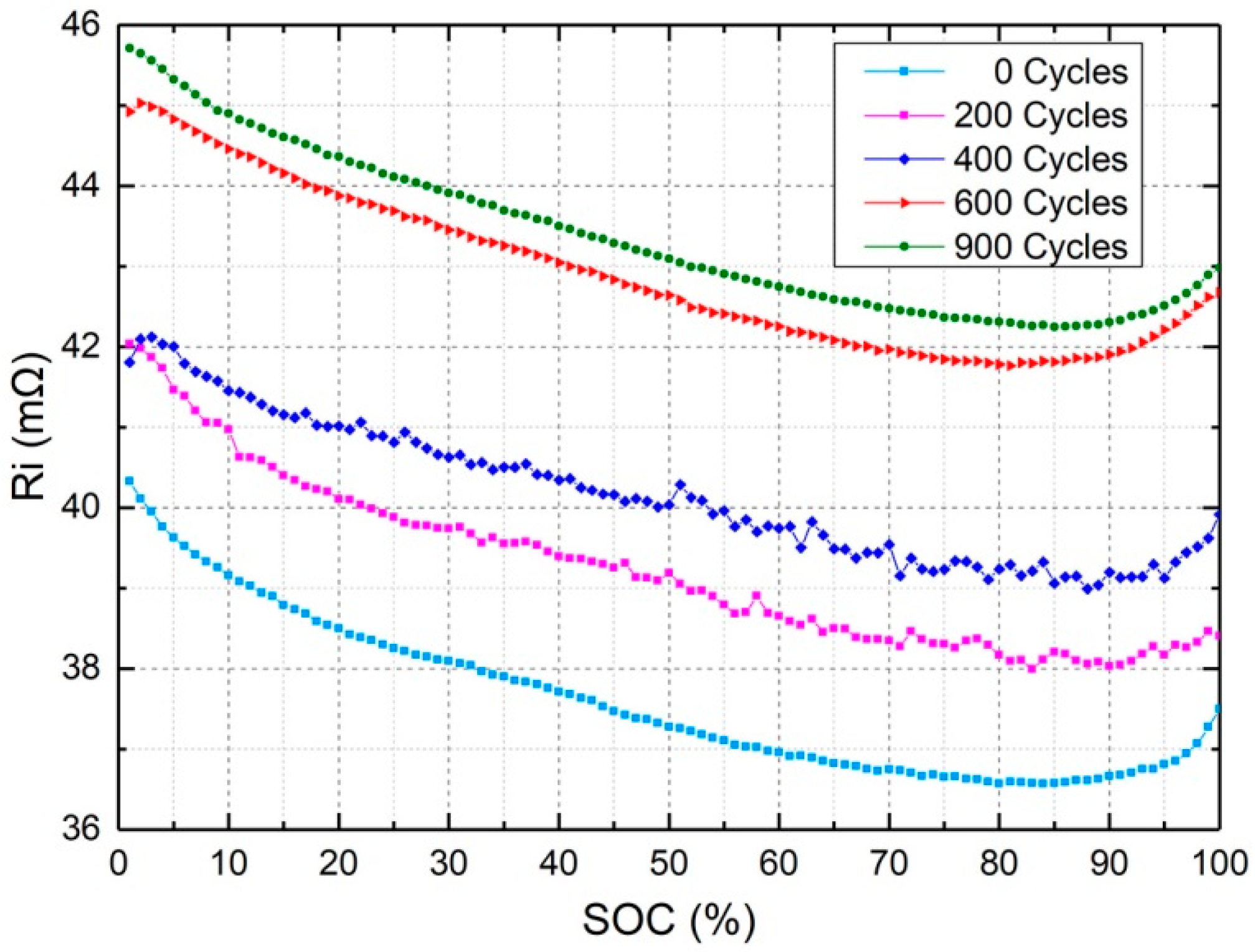
Finally, this research studied the change in internal resistance caused by the aging of the battery. In the experiment, eight 18650 lithium-ion battery samples were studied through a charging and discharging cycle. Each cycle includes a 1600 mA charging process and a 3200 mA discharging process. A cycle includes the process of charging the battery to 100% of SOC and discharging it to 0% of SOC. In order to determine the experimental data range, in this study battery voltage of 4.2V UL within 0.1 A charge current was defined as battery 100% SOC; and battery voltage of 2.5 V UL was defined as battery 0% SOC. As can be seen in
Figure 6, the average internal resistance of the sample batteries increased with the number of cycles. In other words, at a selected SOC point, the battery internal resistance increases as the battery ages. In addition, this change occurred at almost every SOC point. This result provides an experimental basis for studying the SOC and SOH of the battery through real-time internal resistance.
4. EKF with Internal Resistance Measurement
The Kalman filter is a state observer that is randomly adjusted based on the correction gain. As a recursive algorithm, the Kalman filter is suitable for real-time linear applications. In order to apply the Kalman filter to a non-linear system, such as lithium-ion battery SOC estimation, an extended Kalman filter [
16,
17] linearizes the non-linear system equations by using Taylor series expansion and partial derivatives. Since the second-order Taylor series will greatly increase the computational complexity of the algorithm, first order Taylor expansion is widely used. The EKF equations are illustrated in
Table 1.
However, due to the estimation error caused by the linearization process, EKF cannot handle highly non-linear systems. In order to improve the accuracy of EKF estimation, some researchers have proposed absorbing battery non-linear factors, such as the hysteresis effect, the relaxation effect and the temperature effect, through the modified SOC-OCV relationship [
7,
18]. However, this process ignores variations in battery internal resistance, which is a significant parameter of the model. Some other scholars are aware of the importance of internal resistance in the evaluation of battery status parameters and measure the cell internal resistance using various techniques. For instance, the hybrid pulse power characterization (HPPC) technique and the direct current internal resistance (DCIR) technique are widely used to measure battery resistance [
19,
20,
21]. However, these techniques tend to measure the battery's lumped resistance rather than the pure internal resistance because of the unavoidable hysteresis effect in the measurement. In addition, due to a series of complex trigger conditions, these techniques are not suitable for EV and HEV online measurement applications.
This work has studied the consequence of battery internal resistance on the estimation of SOC by EKF. In order to highlight the impact of real-time internal resistance, the study used the simplest EKF equations in which all parameters in the battery model are constrained as fresh battery parameters, which is given in
Table 2. As a result, the value of matrix
and
in
Table 1 remains unchanged in this study.
In EKF equations, system inputs are
and
; system output is SOC.
is the state variable, which contains the voltage of the capacitance and battery SOC. Matrix
and matrix
are system matrices and input control matrices, respectively.
is the sampling interval.
is the rated capacity.
is the observation matrix that contains the internal resistance.
In this study, was the experimental value rather than the function value of battery SOC.
Therefore, the real-time internal resistance simplified observation matrix was:
5. Simulation and Experimental Results
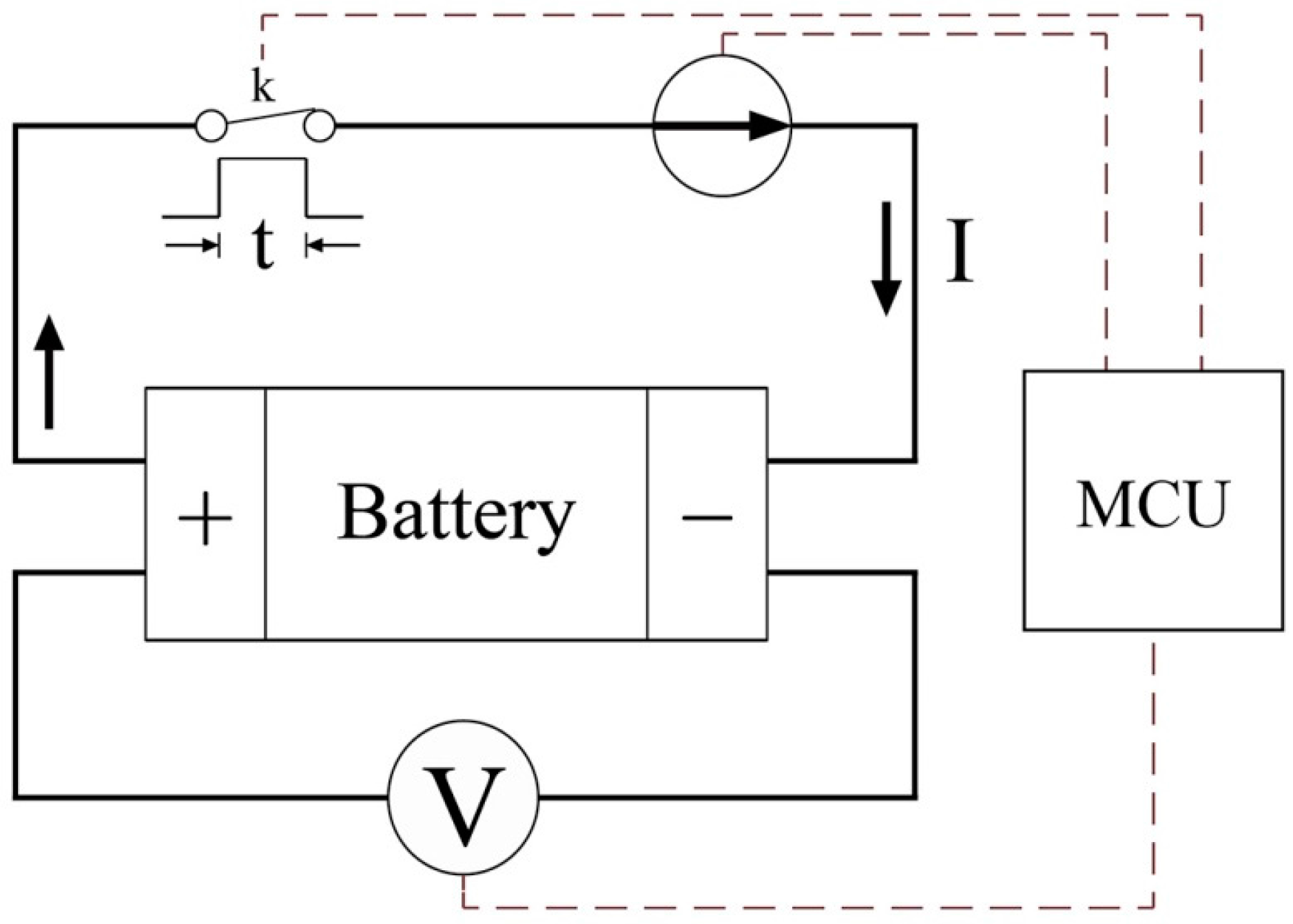
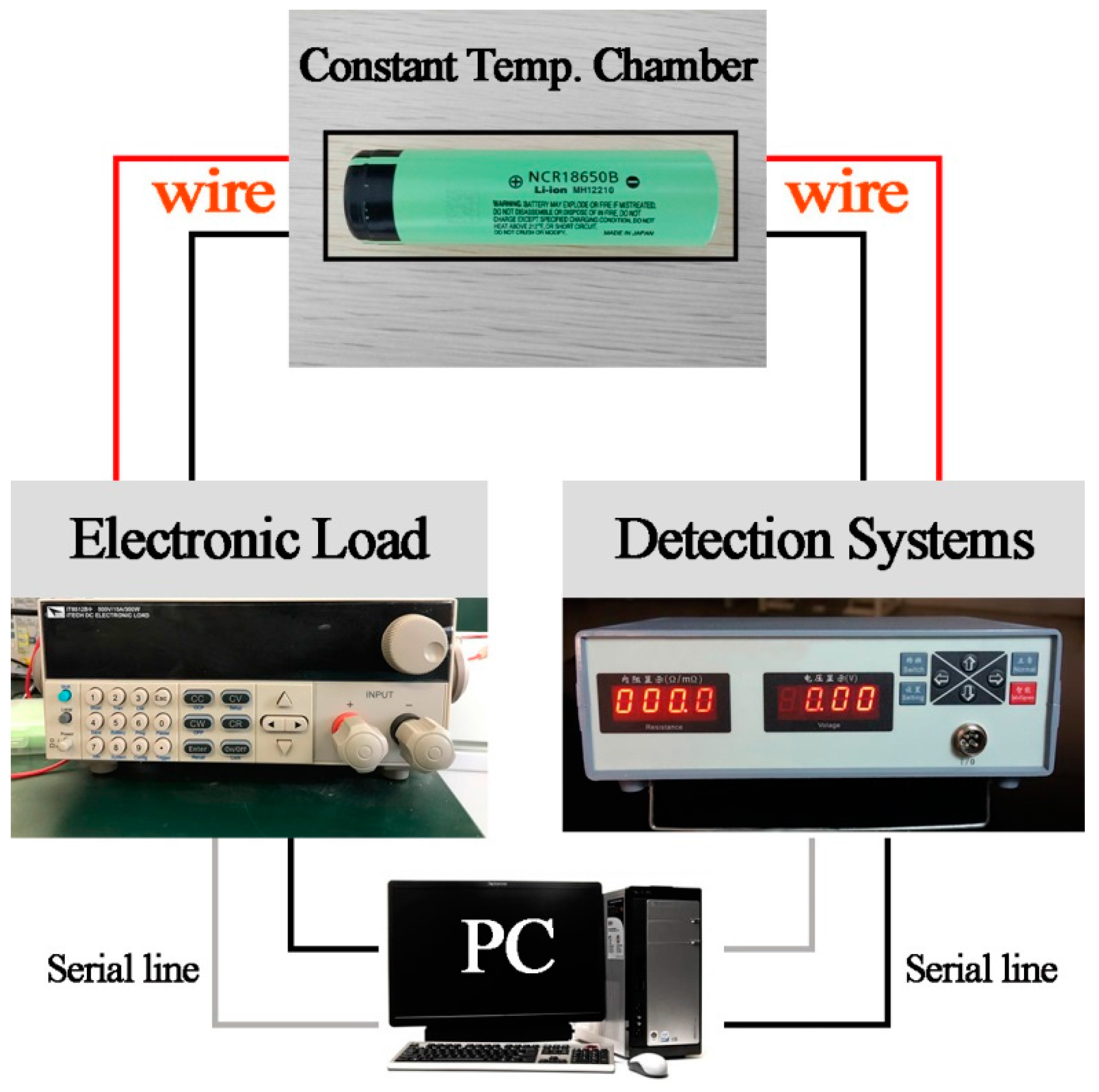
In order to observe the effect of real-time internal resistance on SOC estimation under the EKF algorithm, a simulation and an experiment were performed. The experiment equipment included a constant temperature chamber, internal resistance testing equipment, a power supply, an electronic load, and a computer, as shown in
Figure 7. The experimental data was collected and maintained by the equipment and computer. At the same time, these data were used as input data for the simulation system. In this study, the simulation tool used was Matlab 2016b.
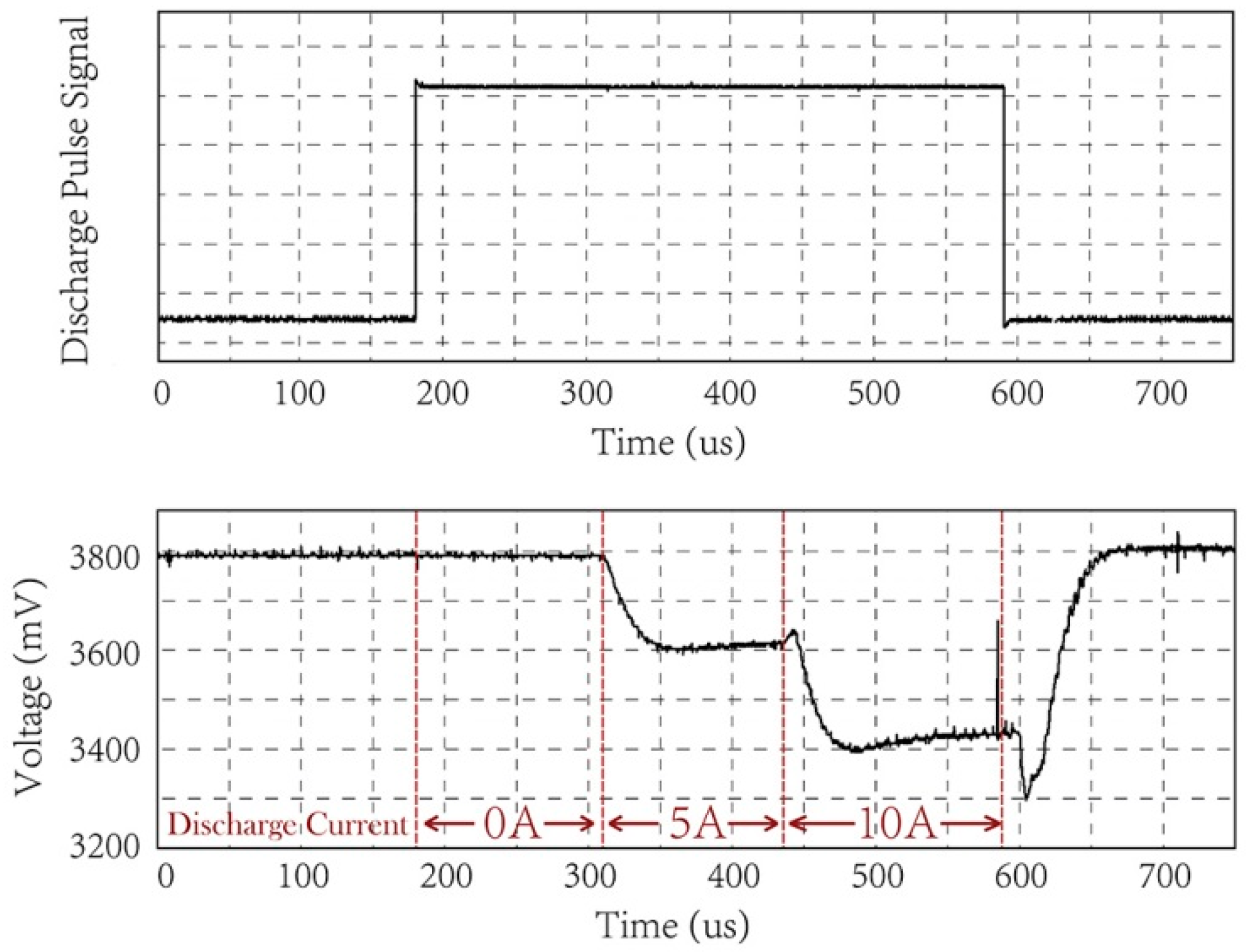
The lithium-ion batteries used in the experiment were type 18650 with the capacity of 3200 mAh. Here, the electronic load was used to keep a constant current discharge at 1600 mA. The internal resistance of the battery was continuously sampled during the whole discharge process by the internal resistance testing equipment. The internal resistance sampling interval was every 2 s. Considering that the actual discharge pulse width did not exceed 250 us in each detection period (
Figure 3), SOC variation due to the detection discharge pulse could largely be ignored.
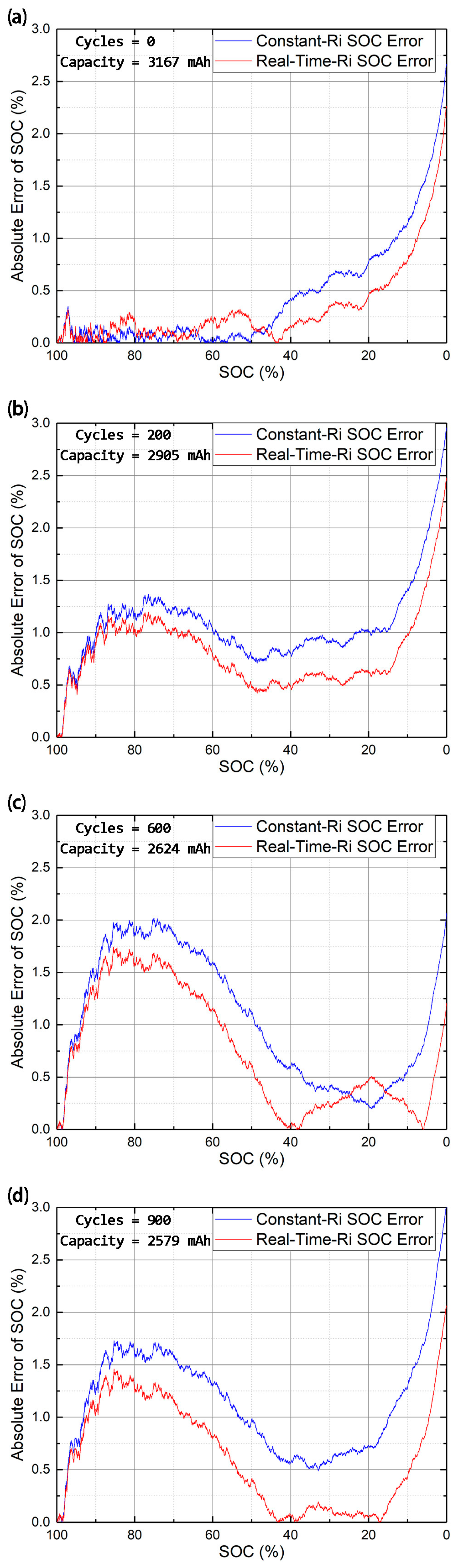
Here, the effect of SOC estimation by internal resistance changes induced by aging was studied at room temperatures. The internal resistances of batteries of different ages were used as a parameter of battery model for the EKF evaluation. In the experiment, the battery samples with different aging degree were obtained by repeated constant current-constant voltage (CC-CV) charge and discharge cycles. As mentioned earlier, each cycle contained a 3200 mA discharge and a 1600 mA charge process. The battery SOC, in completing each cycle, was varied from 100% to 0%, and then back to 100%. Here, the study focused on the battery with 0 cycles, 200 cycles, 600 cycles and 900 cycles respectively. In the experiment, we found that the battery capacity declined significantly with the increase in the number of cycles. In this case, the battery capacity was not only the most effective indicator of battery SOH, but also the reference for a modified SOC-OCV curve [
18].
With reference to the modified SOC-OCV relationship,
Figure 8 shows the SOC estimation error with different EKF evaluations. These two evaluations used exactly the same SOC-OCV curve and battery model parameters, except for internal resistance. The first one used the new battery internal resistance
Ri (in
Table 2) at 25 °C while the other was the real-time battery internal resistance measured during discharge. It can be seen from
Figure 8 that the SOC estimation with real-time internal resistance yielded a better evaluation result than the fixed internal resistance, although the absolute error of SOC varied during the whole estimation process. Since the real-time internal resistance is more accurate than the preset fixed internal resistance, the value of this alternative in terms of improved accuracy is self-evident.
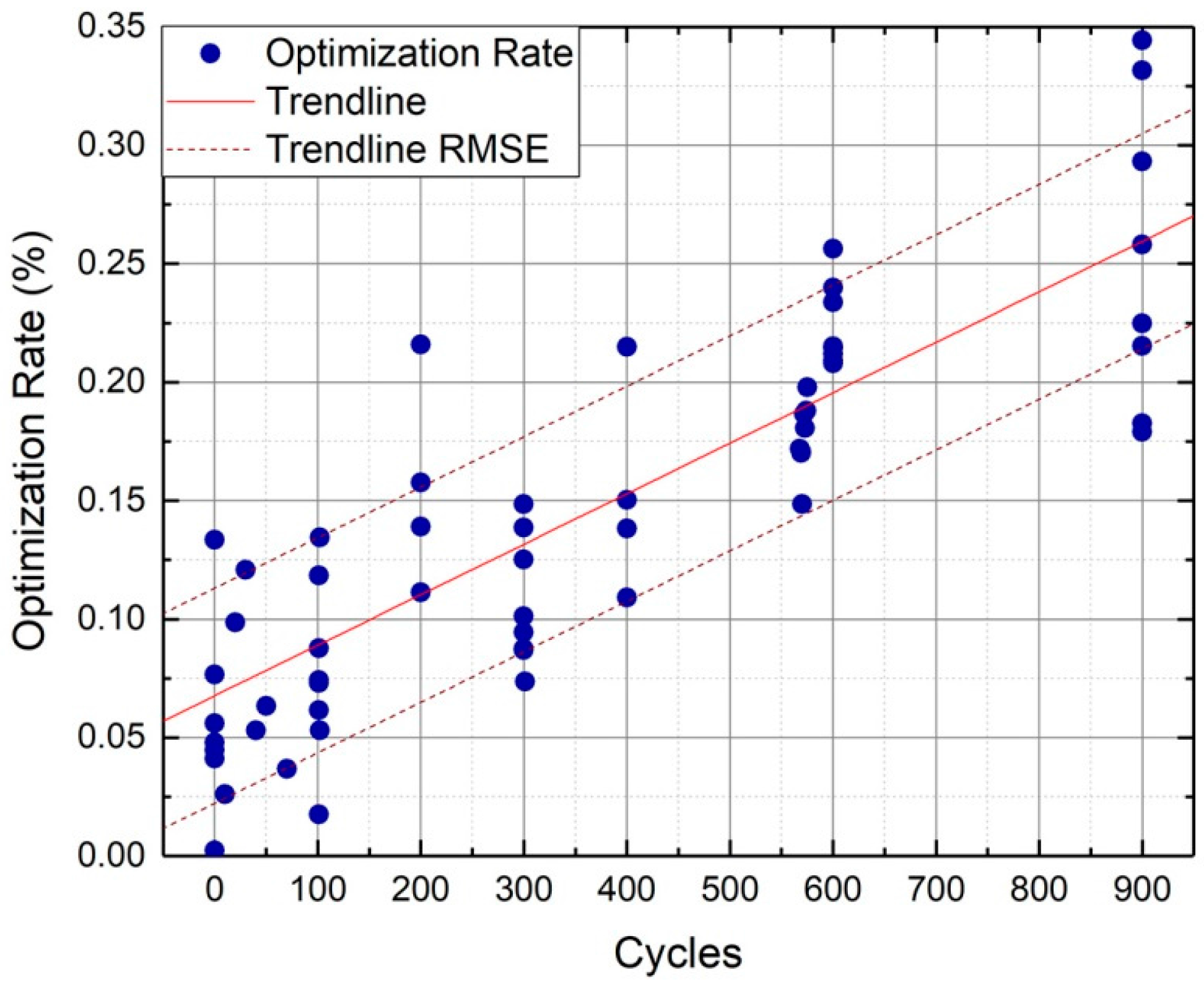
In order to further quantify the improvement of real-time resistance to SOC evaluation, we compared the error rates of the two types of internal resistance under the same experimental conditions.
Figure 9 shows this improvement with battery samples of various ages. The experimental results showed that the optimization rate of SOC estimation increases with the number of battery cycles. In addition, this degree of optimization increased linearly with the degree of battery aging. The SOC optimization strategy can be included in battery cycles by integrating the following from the trendline of
Figure 9.
Considering the entire battery life in
Figure 9, the SOC estimation with EKF can yield more than 15% average optimization with real-time resistance measurement.
Based on the above experimental and simulation results, it can be seen that real-time internal resistance is helpful in improving SOC accuracy using EKF algorithms. This improvement will become more obvious as the battery ages. Previous research [
7,
18] has shown that the change in the OCV-SOC relationship due to battery capacity variation may be the most significant factor for estimating SOC with EKF. For example, SOC evaluation results can be improved significantly by the effectively modified SOC-OCV relationship [
7]. However, as a measurable physical quantity, the effect of internal resistance on battery SOC evaluation optimization is obvious in this work. In addition, as a constructive parameter, real-time internal resistance can also be easily used for battery SOC estimation using the EKF algorithm. Moreover, compared with other impedance monitoring methods, the DCSP internal resistance detection method in this work can be achieved at very low cost and with high accuracy in hybrid electric vehicles and electric vehicles.
6. Conclusions
In this paper we have studied the real-time internal resistance of the lithium-ion battery during high-speed pulsed discharge. This measurement system can observe changes in internal resistance caused by either external temperature or internal aging. Thanks to this online internal resistance, individual battery SOC differences can be distinguished. In addition, real-time internal resistance can improve SOC estimation with the EKF algorithm. The advantage of real-time internal resistance can not only simplify the process in a particular algorithm operation, but can also optimize the accuracy of SOC estimation under the same conditions.
The experimental results also show that deviation of an aging battery’s SOC evaluation may be improved through real-time internal resistance methods. This correction cannot be achieved by the modified SOC-OCV curve using capacity correction only.