Abstract
This paper proposes an economic dispatch strategy for the electricity system with one generation company, multiple utility companies and multiple consumers, which participate in demand response to keep the electricity real-time balance. In the wholesale markets, multiple utility companies will commonly select a reliable agent to negotiate with the generation company on the wholesale price. It is challengeable to find a wholesale price to run the electricity market fairly and effectively. In this study, we use the multiple utility companies’ profits to denote the utility function of the agent and formulate the interaction between the agent and the generation company as a bargaining problem, where the wholesale price was enforced in the bargaining outcome. Then, the Raiffa–Kalai–Smorodinsky bargaining solution (RBS) was utilized to achieve the fair and optimal outcome. In the retail markets, the unfavorable disturbances exist in the power management and price when the consumers participate in the demand response to keep the electricity real-time balance, which motivates us to further consider the dynamic power management algorithm with the additive disturbances, and then obtain the optimal power consumption and optimal retail price. Based on the consumers’ utility maximization, we establish a price regulation model with price feedback in the electricity retail markets, and then use the iterative algorithm to solve the optimal retail price and the consumer’s optimal power consumption. Hence, the input-to-state stability condition with additive electricity measurement disturbance and price disturbance is given. Numerical results demonstrate the effectiveness of the economic dispatch strategy.
1. Introduction
Smart grid is an intelligent power system that integrates advanced control, communications, demand response, storage, and sensing technologies into the power grid. A smart metering system is crucial in order to provide management capabilities and obtain metering data with additional information [1]. Additionally, demand forecasting as a forecast technology plays an important role in the smart grid and the energy generation process [2]. In the smart grid, demand-side management (DSM) is an effective technology to keep the energy real-time balance in the deregulated electricity market. It is widely accepted that demand response can transform the traditional power grid into a more reliably and economically operated smart grid [3,4,5,6]. An overview for various types of DSM is given in [7]. Demand response can motivate consumers to shift their loads from on-peak to off-peak periods. To reduce the peak load of a smart distribution network feeder, a self-decision method for load management is proposed in [8]. In general, the demand response programs include two categories: incentive-based programs and price-based programs [9]. The incentive-based programs include the direct load control, the emergency demand response, and the ancillary services market. For the price-based program, there are two types of consumers: pricing-taking (PT) consumers [10] and price-anticipating (PA) consumers [11,12,13]. The utility companies can adjust the power consumption of customers by pricing strategy, such as time of use (TOU), critical peak pricing (CPP), and real-time pricing (RTP) that can match the supply with demand [14,15,16]. Generally, the regulation service is defined by the North American Electric Reliability Council (NERC) as the provision of generation and load response capability, which responds to automatic control signals issued by the system operator updated every four seconds [17].
Recently, different pricing-based demand response programs were developed based on game theory and kinds of optimization methods. For example, the authors analyzed the cooperation between the small-scale electricity suppliers (SESs) and end-users (EUs) based on the coalitional game in [18,19,20]. Solving potential games with dynamical constraint, and improving the Pareto efficiency with punishment mechanism were developed in [21,22]. The Stackelberg game was developed to formulate the energy trading between the consumers and multiple utility companies who aim to maximize their own profits from the energy exchange between the plug-in electric vehicles (PEVs) and the smart grid [23,24,25]. The authors in [26,27] developed a load curtailment strategy and analyzed the energy consumption control in the smart grid based on the noncooperative game and aggregate game theory. The dual decomposition method was developed to achieve the social welfare maximization by optimizing the individual utilities of the consumers [28,29,30]. Distributed power control algorithms with a linear pricing function and a nonlinear pricing function were developed to achieve the balance between supply and demand for demand response [31,32]. The authors use the Nash bargaining theory to study the financial bilateral contract negotiation process between a generation company and a load-serving entity in a wholesale electric power market [33]. Nash bargaining was developed in the demand response and microgrid to derive the optimal solutions for the load reduction and maximize the social welfare [34,35]. To minimize the emission by optimizing the total power generation, an economic dispatch algorithm for congestion management in power system is proposed in [36]. In [37], the author proposed a novel unsymmetrical faults analysis method for microgrid distribution systems. This method can achieve the advantages of reducing computation time, increasing convergence robustness and improving accuracy for unsymmetrical faults analysis. The computation time of the algorithm is important to the power system; thus, we take into account the computation time of the proposed algorithm in the paper. To achieve a fast and stable response for real power control, a dynamic operation and control strategy for a microgrid hybrid power system under different load conditions with disturbances was proposed in [38]. In [39], the authors proposed a novel intelligent damping controller (NIDC) for the static synchronous compensator (STATCOM) to reduce the power fluctuations, voltage support and damping in a hybrid power multi-system. To mitigate the voltage imbalance and deviation, the authors in [40] developed a modified bird-mating optimization approach to enhance the phase-connection adjustment of distribution transformers, and ensure a satisfactory supplying power. The differences between our work and the above work are shown in Table 1.

Table 1.
Differences of the proposed work with the literature.
On the whole, the above work didn’t consider the unfavorable disturbances on the power system when the consumers participate in the demand response to keep the energy real-time balance. Moreover, the wholesale price bargaining between the the utility company and generation company is neglected. Therefore, a systematic study with an effective approach is important to match supply with demand; thereby, it motivates the study in this paper.
In this paper, based on the consumers’ utility maximization, we establish a price regulation model with price feedback in the electricity retail markets, and use the iterative algorithm to solve the optimal retail price and the consumer’s optimal power consumption. Then, we formulate the wholesale price negotiation problem by the bargaining framework between the multiple utility companies and the generation company. The utility companies and generation company negotiate the wholesale price to maximize their revenues. We prove that the interaction between the utility companies and generation company is a bargaining problem. Furthermore, the input-to-state stability condition with additive electricity measurement disturbance and price disturbance is given. We have three contributions in this work:
- We formulate a wholesale price negotiation problem between the multiple utility companies and the generation company. Then, we prove that the wholesale price negotiation is a bargaining problem and the Raiffa–Kalai–Smorodinsky bargaining solution (RBS) was utilized to achieve the optimal solution.
- We establish a price regulation model with price feedback in the electricity retail markets based on the consumers’ utility maximization and the negotiated wholesale price.
- The iterative algorithm is used to search for the optimal retail price and the power consumption. Moreover, we prove that the power management system is input-to-state stability under additive electricity measurement disturbance and price disturbance.
The rest of the paper is organized as follows. Some preliminaries are given in Section 2. In Section 3, the electricity market model is established and the problem is formulated. In Section 4, the wholesale price negotiation between the generation company and multiple utility companies is developed; then, the Raiffa–Kalai–Smorodinsky bargaining solution (RBS) is utilized to achieve the optimal outcome. In Section 5, the power management system with additive disturbances is developed. The input-to-state stability of the power management system is proved. System implementation is described in Section 6. Numerical results are given in Section 7, and conclusions are summarised in Section 8.
2. Definition and Preliminaries
This section presents the definition of the bargaining problem, and the RBS (please refer to [41,42] for more details).
Definition 1.
(Bargaining problem). Let be the set of players and T denote the set of feasible payoffs, which is a closed and convex set on . , where denotes the minimum payoff player i. Then, is a n-person bargaining problem, and is the bargaining outcome.
Definition 2.
where is player i’s utility function, which is denoted as:
where is the minimum payoff of player i and is the maximum payoff of player j. This bargaining solution indicates that one player takes into account both its own minimum payoff and others’ maximum payoffs.
(RBS) If the mapping satisfies the following axioms:
- Independence: ;
- Feasibility: ;
- Pareto Optimality: is Pareto optimal;
- Linear Axiom: For any linear transformation function ϕ, ;
- Symmetry: If T is invariant under all exchanges to consumers, then for all , ;
- Monotonicity: For any where , if and , then, , then, the bargaining solution can be expressed as:
3. System Model and Problem Formulation
We consider an electricity system composed of one generation company, one agent, multiple utility companies, and consumers, as shown in Figure 1.
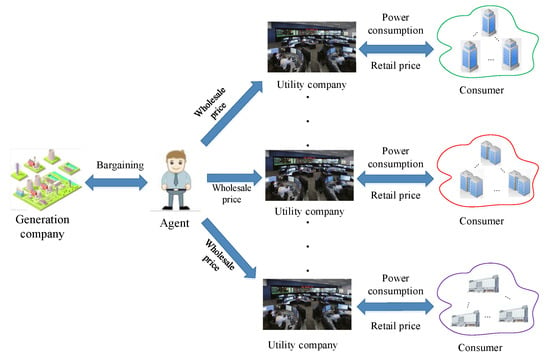
Figure 1.
An electricity market.
The agent negotiates with the generation company on wholesale price instead of the multiple utility companies. Additionally, the operation cycle of the power system is divided into several time slots. In each time slot, the utility company decides the electricity price and announces it to the consumers. Then, the consumers manage their power consumption according to the announced price. We employ the utility functions to characterize the profits of the customers, where denotes the utility of consumer i, and is the power consumption of the consumer i. Thus, the maximization of the social welfare can be formulated as the following optimization problem:
where w is the wholesale price, and Q denotes the total power supply of the utility companies. The constraint indicates that the total power consumption should match with the power supply. The optimization problem is a convex optimization problem and can be solved by the following primal-dual algorithm:
and:
where and z are the control gain, p is the price of the utility company, and denotes the set of power consumption of all the customers.
4. Bargaining Model and Solution
The agent representing the multiple utility companies negotiates with the generation company on the wholesale price w, and then announces the wholesale price to each utility company to maximize the efficiency of the electricity market. It can be formulated as a bargaining problem between the agent and the generation company according to Definition 1. The agent’s utility function can be regarded as the total utility function of the utility companies, which is denoted as:
denotes the power supply of the utility company j. The profit of the generation company can be denoted as:
where , is the cost of the generation.
Next, we prove that the negotiation between the agent and generation company is a bargaining problem. The set of feasible profit is defined as:
where is the minimum wholesale price and is the maximum wholesale price.
It is easy to see that the set T is a closed subset of from the profit functions of the utility company and generation company, i.e., Equations (7) and (8). Assume any two elements and :
and:
Next, we construct the weighted summation of the two elements, i.e.,
where . Comparing Equations (10) and (12), we define:
It can be proved that and ; then, we have:
Meanwhile, it can be proved that and ; then, we have:
Therefore, we can conclude that T is closed and convex on , and the negotiation between the agent and the generation company is a bargaining problem. The cooperative strategy based on RBS can be denoted as:
where
and:
Next, we can obtain the globally optimal solution:
where is the abscissa axis of symmetry.
5. Power Management System with Additive Disturbances
In reality, the utility company set the optimal retail price according to Equation (6) based on the wholesale price, and the consumers determine the optimal power consumption according to Equation (5). It is dependent on the two-way communications between the utility company and the customers. It is necessary to study the impact of disturbances on the power management system because of the errors in the power measurements and the price. As shown in Figure 2, and denote the additive disturbances on the price and the total power consumption, respectively. Then, the power management algorithm with disturbances is denoted as:
and:
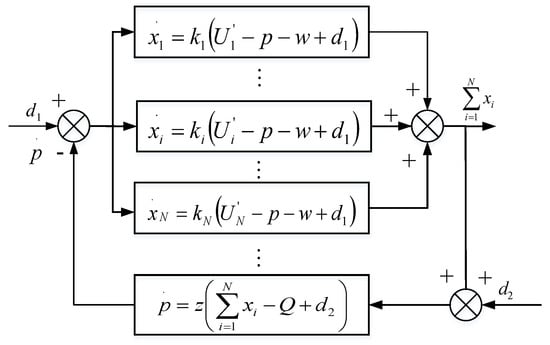
Figure 2.
Power management system with additive disturbances.
Next, we study the input-to-state stability of the power management system with additive disturbances and denote as p for short. Before the proof, we first give the following lemma:
Lemma 1.
(input-to-state Stability [43]) Support that satisfies
where denotes the upper Dini derivative, α is a positive constant, and . Then,
Then, we obtain the following theorem:
Theorem 1.
The power management algorithm is input-to-state stable when the utility function satisfies , yields
where ,
- ,
- ,
- , z is a positive constant,
- ,
- ,
- ,
- ,
- ,
- ,
- .
6. System Implementation
The system implementation is shown in Figure 3, and the process is shown as below.
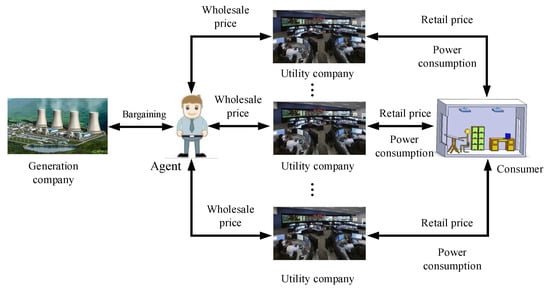
Figure 3.
System implementation.
Generation company: the generation company produces the electric energy and then sells it to the utility companies at a wholesale price to maximize its profits.
Agent: the agent represents the multiple utility companies and then bargains the wholesale price with the generation company to maximize the efficiency of the electricity market.
Utility company: the utility company receives the wholesale price announced by the agent and then sets the optimal retail price. Furthermore, the optimal retail price is sent to the consumers through the bidirectional communication link.
Consumer: the consumers accept the optimal retail price sent by the utility company through the smart meters and then determine the optimal power consumption to maximize their utilities. Then, the consumers send the optimal power consumption to the utility company.
7. Numerical Results
In this section, we consider a smart power system consisting of one generation company (GC), one agent and multiple utility companies (UC). Moreover, each utility company services for several consumers. The utility company decides the electricity price and announces it to the consumers. Then, the consumers manage their power consumption according to the announced price. We employ the utility functions to characterize the profits of consumers. A quadratic utility function with decreasing marginal benefit is defined as:
where is the power consumption of consumer , denotes the willingness to increase the power consumption, and denotes the maximum demand of consumer i. The power management algorithm with disturbance is denoted as:
and:
The discrete-time power management algorithm with disturbance is denoted as:
The flowchart of the pricing regulation strategy is given in Figure 4.
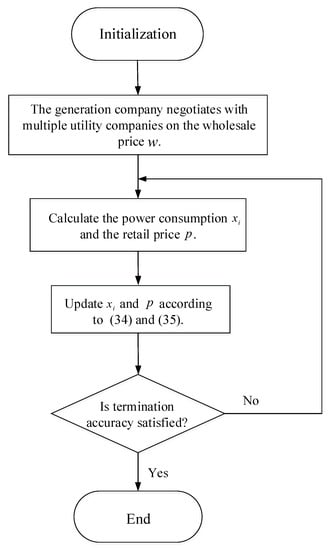
Figure 4.
The flowchart of the pricing regulation algorithm.
Assuming that the wholesale price is set in , the generation and agent negotiate on the wholesale price based on Equation (19), and the RBS solution is . Moreover, the influence of the maximum wholesale price and minimum wholesale price on the RBS solution are shown in Figure 5, where is changed from 2 to 8 when is fixed (green bar) and is changed from 2 to 8 when is fixed (red bar). For convenience, we select 1000 consumers from one utility company. Each consumer’s willingness parameter is randomly selected from [22,28], and the power supply Q is varying from 5 kW to 12 kW. Figure 6 shows the convergence of 1000 consumer’s power consumption bounded by 4.456 kWh and 5.379 kWh. Next, we focus on studying the disturbance impact on the system; for convenience, we select three consumers from the 1000 consumers to analyze the disturbance influence on the system. The parameters of the system are given in Table 2. The changes of the power consumption and the retail price versus the iterations of the algorithm are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, respectively. In the simulations, we mainly focus on the influence of the communication disturbances and on the power control algorithm. We take three different parameter values in Table 3, where and follow normal distribution. From Figure 7 and Figure 9, we observe that the fluctuations of the power consumption will increase with the variance of . Furthermore, it is shown that the fluctuations of the retail price will increase greatly with the variance of from Figure 8 and Figure 12. In general, the power system has a good robustness for the additive disturbances, and the errors can be bounded by 1%, 2% and 6% under Case I, Case II and Case III, respectively. From the simulation results, we can observe that the power control algorithm has a fast convergence speed. In the first 100 iterations, the fluctuations are large, and the convergence rate slows down after 100 iterations. The optimal consumption and optimal retail price are given in Table 4. The proposed algorithm can calculate the optimal power consumption and retail price with short time as shown in Table 5, which was conducted in MATLAB R2010b (MathWorks, Natick, MA, USA) with a 3.60 GHz CPU and 4.0 GB of RAM.
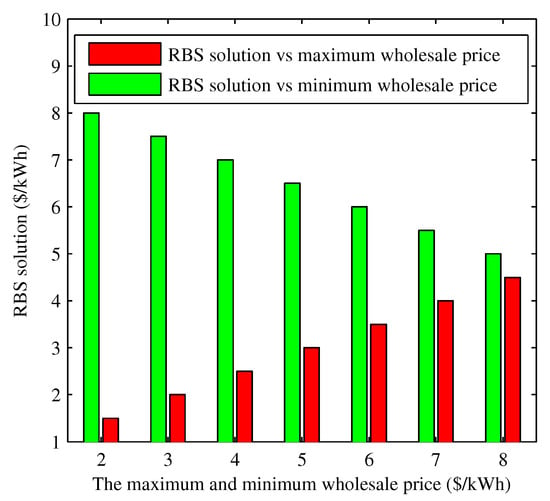
Figure 5.
The Raiffa–Kalai–Smorodinsky bargaining solution (RBS) versus maximum wholesale price and minimum wholesale price.
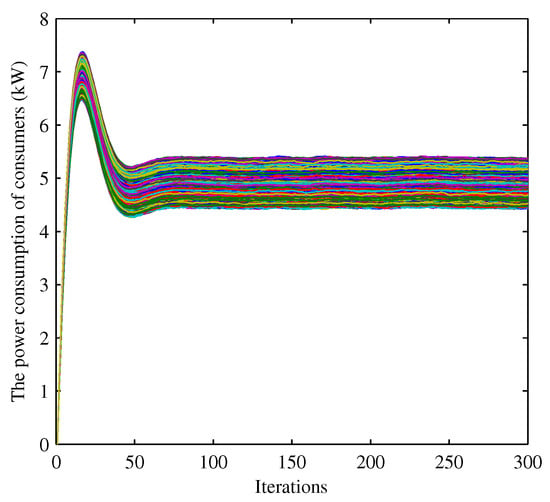
Figure 6.
Convergence of 1000 consumers’ power consumption.

Table 2.
Parameter settings of the system.
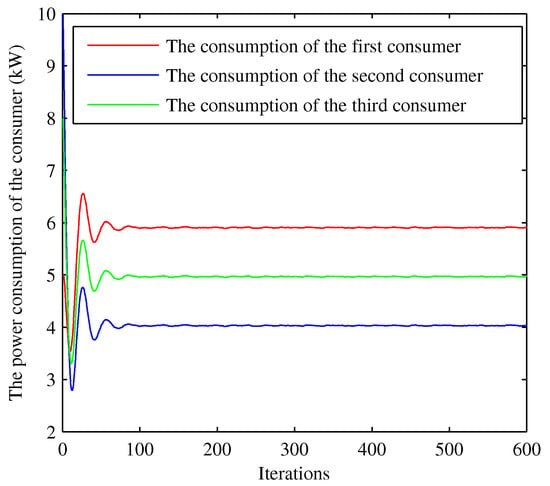
Figure 7.
Convergence of the power consumption under case I.
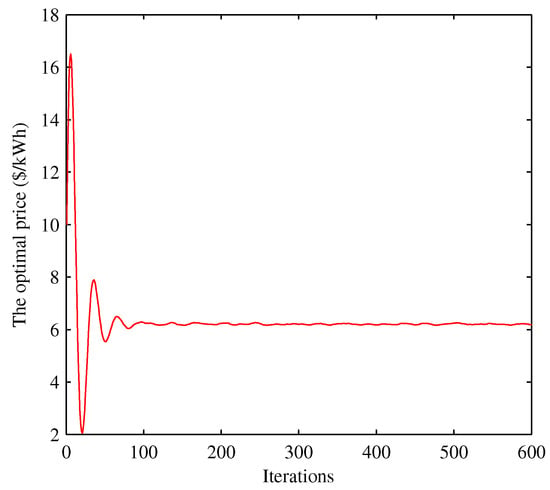
Figure 8.
Convergence of the retail price under case I.
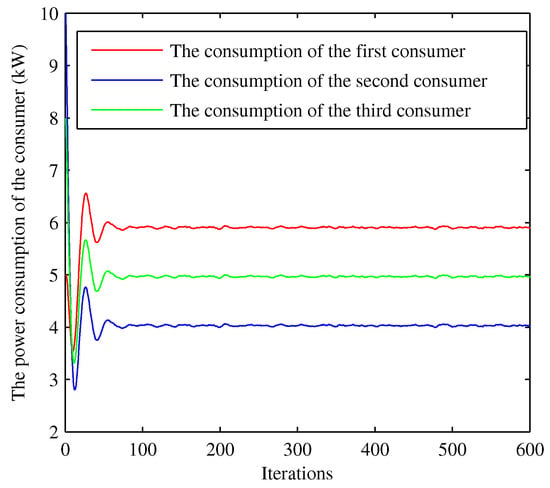
Figure 9.
Convergence of the power consumption under case II.
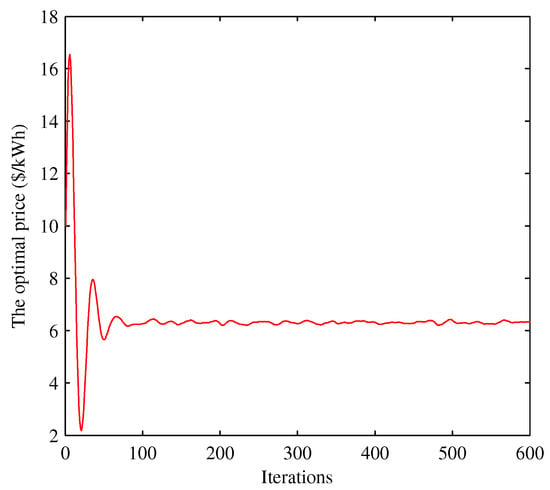
Figure 10.
Convergence of the retail price under case II.
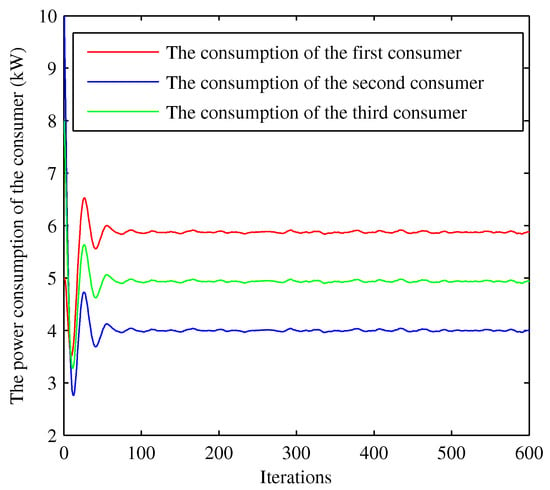
Figure 11.
Convergence of the power consumption under case III.
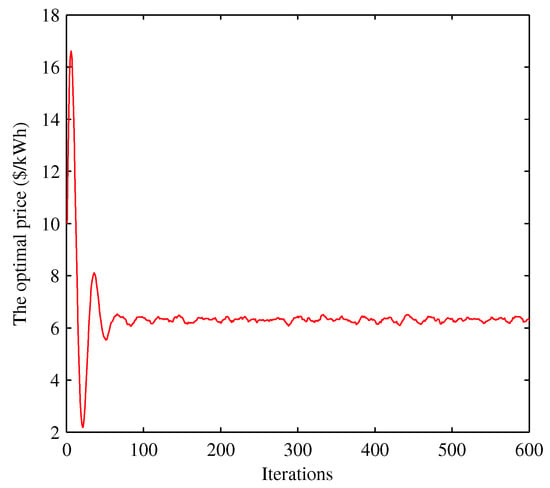
Figure 12.
Convergence of the retail price under case III.

Table 3.
Disturbance parameter settings.

Table 4.
The optimal power consumption and the retail price.

Table 5.
The computation time of the pricing regulation algorithm.
8. Conclusions
In this paper, we propose an economic dispatch strategy for the electricity system. We formulate a wholesale price negotiation problem between the generation company and multiple utility companies. Then, we prove that the negotiation problem between the generation company and multiple utility companies is a bargaining problem. Next, the RBS is utilized to achieve the optimal bargaining outcome. In the simulation, we find that the RBS solution is increasing with the maximum wholesale price when the minimum wholesale price is fixed. Meanwhile, when the maximum wholesale price is fixed, the RBS solution is decreasing with the minimum wholesale price. Moreover, based on the consumers’ utility maximization and the negotiated wholesale price, we establish a utility function model of utility company with price feedback in the electricity retail markets, and then use the iterative algorithm to obtain the optimal retail price and the optimal power consumption. Additionally, we prove that the algorithm is input-to-state stable and give the input-to-state stability condition under the additive power measurement disturbance and price disturbance. In this work, the proposed algorithm can converge to the optimal value within 100 steps, and the errors can be bounded by 1%, 2% and 6% under Case I, Case II and Case III, respectively. In the future, an interesting topic is to consider the incomplete information game between the utility company and the consumers. The consumers determine the optimal power consumption and the utility company sets the optimal retail price to maximize their own profits, respectively. Then, the Markov game and robust game are promising methods to deal with this problem.
Acknowledgments
This research was supported in part by the National Key Research and Development Program of China under Grant 2016YFB0901900, in part by the National Natural Science Foundation of China under Grants 61573303 and 61503324, in part by the Natural Science Foundation of Hebei Province under Grants F2016203438, E2017203284, E2016203092, and F2017203084, in part by the Project Funded by China Postdoctoral Science Foundation under Grants 2015M570233 and 2016M601282, in part by the Project Funded by Hebei Education Department under Grant BJ2016052, in part by the Technology Foundation for Selected Overseas Chinese Scholar under Grant C2015003052, and in part by the Project Funded by the Key Laboratory of System Control and Information Processing of Ministry of Education under Grant Scip201604.
Author Contributions
Kai Ma wrote the paper and performed the experiments; Congshan Wang conceived and designed the experiments; Jie Yang contributed the idea; Qiuxia Yang analyzed the data; Yazhou Yuan contributed analysis tools.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| p | The retail price of utility company. |
| w | The wholesale price charged by the generation company to the utility company. |
| The maximum wholesale price. | |
| The minimum wholesale price. | |
| The cost of the generation. | |
| The power consumption of consumer i. | |
| The utility function of consumer i. | |
| Q | The total power supply of the utility companies. |
| The power supply of utility company j. | |
| K | The diagonal matrix composed of . |
| k, z | The control gains of system. |
| N | The number of the consumers. |
| M | The number of the utility companies. |
| The additive disturbance on the price. | |
| The additive disturbance on the total power consumption. | |
| The maximum disturbance in the disturbance set . | |
| The maximum value in . | |
| The positive coefficient. | |
| The minimum value in . | |
| The maximum value in . | |
| The positive coefficient. | |
| The positive constant. | |
| The estimated value of the power consumption. | |
| The estimated value of the price. | |
| The consumer’s willingness. | |
| a | The coefficient of consumer’s willingness. |
| The upper Dini derivative. | |
| The iterative step size of the power consumption. | |
| b | The iterative step size of the price. |
| The weighted coefficient. | |
| T | The set of feasible payoff. |
| Feasible payoffs in T. | |
| Feasible payoffs in T. | |
| , , | The wholesale price. |
| The optimal bargaining solution of player i. | |
| The minimum payoff player i. | |
| The maximum payoff player i. | |
| The Pareto optimum. | |
| The n-dimensional real number set. | |
| The linear transformation function. | |
| The player i’s utility function. | |
| RBS | Raiffa–Kalai–Smorodinsky bargaining solution. |
| DSM | Demand-side management. |
| UC | Utility company. |
| GC | Generation company. |
| PT | Pricing-taking. |
| PA | Price-anticipating. |
| TOU | Time of use. |
| CPP | Critical peak pricing. |
| RTP | Real-time pricing. |
| NERC | North American Electric Reliability Council. |
| SECs | Small-scale electricity suppliers. |
| EUs | End users. |
| PEVs | Plug-in electric vehicles. |
| NIDC | Novel intelligent damping controller. |
| STATCOM | Static synchronous compensator. |
References
- Hernández, L.; Uribe-Pérez, N.; Vega, D.D.L.; Angulo, I. State of the Art and Trends Review of Smart Metering in Electricity Grids. Appl. Sci. 2016, 6, 68. [Google Scholar]
- Hernández, L.; Baladron, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J.; Massana, J. A Survey on Electric Power Demand Forecasting: Future Trends in Smart Grids, Microgrids and Smart Buildings. IEEE Commun. Surv. Tutor. 2014, 16, 1460–1495. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S. Dependable Demand Response Management in the Smart Grid: A Stackelberg Game Approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]
- Jung, S.; Kim, D. Pareto-Efficient Capacity Planning for Residential Photovoltaic Generation and Energy Storage with Demand-Side Load Management. Energies 2017, 10, 426. [Google Scholar] [CrossRef]
- Liu, R.S. An Algorithmic Game Approach for Demand Side Management in Smart Grid with Distributed Renewable Power Generation and Storage. Energies 2016, 9, 654. [Google Scholar] [CrossRef]
- Samadi, P.; Mohsenian-Rad, H.; Schober, R.; Wong, V.W.S. Advanced Demand Side Management for the Future Smart Grid Using Mechanism Design. IEEE Trans. Smart Grid 2012, 3, 1170–1180. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inf. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Amini, M.H.; Nabi, B.; Haghifam, M.R. Load management using multi-agent systems in smart distribution network. In Proceedings of the Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Yang, J.; Zhang, G.; Ma, K. A nonlinear control method for price-based demand response program in smart grid. Int. J. Electr. Power Energy Syst. 2016, 74, 322–328. [Google Scholar] [CrossRef]
- Gatsis, N.; Giannakis, G.B. Residential load control: Distributed scheduling and convergence with lost AMI messages. IEEE Trans. Smart Grid 2012, 3, 770–786. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.S.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous Demand-Side Management Based on Game-Theoretic Energy Consumption Scheduling for the Future Smart Grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chen, J.; Asr, N.; Chow, M.Y. Residential Energy Consumption Scheduling: A Coupled-Constraint Game Approach. IEEE Trans. Smart Grid 2014, 5, 1340–1350. [Google Scholar] [CrossRef]
- Cao, W.; Yang, B.; Chen, C.; Guan, X. PHEV Charging Strategy With Asymmetric Information Based On Contract Design. IFAC Proc. Vol. 2013, 46, 520–525. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Jeong, M.G.; Moon, S.I.; Hwang, P.I. Indirect Load Control for Energy Storage Systems Using Incentive Pricing under Time-of-Use Tariff. Energies 2016, 9, 558. [Google Scholar] [CrossRef]
- Park, S.C.; Jin, Y.G.; Yong, T.Y. Designing a Profit-Maximizing Critical Peak Pricing Scheme Considering the Payback Phenomenon. Energies 2015, 8, 11363–11379. [Google Scholar] [CrossRef]
- Chown, G.A.; Coetzee, M.G. Implementation of regulation as an ancillary service in Eskom and the use of Eskom internal web for this service. IEEE Trans. Power Syst. 2000, 15, 1132–1136. [Google Scholar] [CrossRef]
- Lee, W.; Xiang, L.; Schober, R.; Wong, V.W.S. Direct Electricity Trading in Smart Grid: A Coalitional Game Analysis. IEEE J. Sel. Areas Commun. 2014, 32, 1398–1411. [Google Scholar] [CrossRef]
- Ni, J.; Ai, Q. Economic power transaction using coalitional game strategy in micro-grids. IET Gener. Transm. Distrib. 2016, 10, 10–18. [Google Scholar] [CrossRef]
- Fan, W.; Liu, N.; Zhang, J.; Lei, J. Online Air-Conditioning Energy Management under Coalitional Game Framework in Smart Community. Energies 2016, 9, 689. [Google Scholar] [CrossRef]
- Ma, K.; Hu, G.; Spanos, C.J. A Cooperative Demand Response Scheme Using Punishment Mechanism and Application to Industrial Refrigerated Warehouses. IEEE Trans. Ind. Inf. 2015, 11, 1520–1531. [Google Scholar] [CrossRef]
- Ye, M.; Hu, G. Solving Potential Games With Dynamical Constraint. IEEE Trans. Cybern. 2016, 46, 1156–1164. [Google Scholar] [CrossRef] [PubMed]
- Tushar, W.; Saad, W.; Poor, H.V.; Smith, D.B. Economics of Electric Vehicle Charging: A Game Theoretic Approach. IEEE Trans. Smart Grid 2012, 3, 1767–1778. [Google Scholar] [CrossRef]
- Chen, L.; Li, N.; Jiang, L.; Low, S.H. Optimal demand response: Problem formulation and deterministic case. In Control and Optimization Methods for Electric Smart Grids; Springer: New York, NY, USA, 2012; pp. 63–85. [Google Scholar]
- Bu, S.; Yu, F.R. A Game-Theoretical Scheme in the Smart Grid With Demand-Side Management: Towards a Smart Cyber-Physical Power Infrastructure. IEEE Trans. Emerg. Top. Comput. 2013, 1, 22–32. [Google Scholar] [CrossRef]
- Ma, K.; Hu, G.; Spanos, J.C. Distributed energy consumption control via real-time pricing feedback in smart grid. IEEE Trans. Control Syst. Technol. 2014, 22, 1907–1914. [Google Scholar]
- Ye, M.; Hu, G. Game Design and Analysis for Price-Based Demand Response: An Aggregate Game Approach. IEEE Trans. Cybern. 2017, 47, 720–730. [Google Scholar] [CrossRef] [PubMed]
- Samadi, P.; Mohsenian-Rad, A.; Schober, R.; Wong, V.W.; Jatskevich, J. Optimal real-time pricing algorithm based on utility maximization for smart grid. In Proceedings of the 1st IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 415–420. [Google Scholar]
- Li, N.; Chen, L.; Low, S.H. Optimal demand response based on utility maximization in power networks. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Voronin, S.; Partanen, J. Price Forecasting in the Day-Ahead Energy Market by an Iterative Method with Separate Normal Price and Price Spike Frameworks. Energies 2013, 6, 5897–5920. [Google Scholar] [CrossRef]
- Fan, Z. A Distributed Demand Response Algorithm and Its Application to PHEV Charging in Smart Grids. IEEE Trans. Smart Grid 2012, 3, 1280–1290. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, G.; Ma, K. Matching supply with demand: A power control and real time pricing approach. Int. J. Electr. Power Energy Syst. 2014, 61, 111–117. [Google Scholar] [CrossRef]
- Yu, N.; Tesfatsion, L.; Liu, C.C. Financial Bilateral Contract Negotiation in Wholesale Electricity Markets Using Nash Bargaining Theory. IEEE Trans. Power Syst. 2012, 27, 251–267. [Google Scholar] [CrossRef]
- Guo, Y.; Li, H.; Pan, M. Colocation Data Center Demand Response using Nash Bargaining Theory. IEEE Trans. Smart Grid 2017, PP, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Cooperative Planning of Renewable Generations for Interconnected Microgrids. IEEE Trans. Smart Grid 2016, 7, 2486–2496. [Google Scholar] [CrossRef]
- Boroojeni, K.G.; Amini, M.H.; Iyengar, S.S.; Rahmani, M.; Pardalos, P.M. An economic dispatch algorithm for congestion management of smart power networks. Energy Syst. 2016, 8, 643–667. [Google Scholar] [CrossRef]
- Ou, T.C. A novel unsymmetrical faults analysis for microgrid distribution systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1017–1024. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Ou, T.C.; Lu, K.H.; Huang, C.J. Improvement of Transient Stability in a Hybrid Power Multi-System Using a Designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Ou, T.C.; Su, W.F.; Liu, X.Z.; Huang, S.J.; Tai, T.Y. A Modified Bird-Mating Optimization with Hill-Climbing for Connection Decisions of Transformers. Energies 2016, 9, 671. [Google Scholar] [CrossRef]
- Nash, J.F., Jr. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Aruoba, S.B.; Rocheteau, G.; Waller, C. Bargaining and the value of money. J. Monet. Econ. 2005, 54, 2636–2655. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control Syst. Technol. 2013, 21, 67–78. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).