Optimal Scheduling for Electric Vehicle Charging under Variable Maximum Charging Power
Abstract
:1. Introduction
- We consider the aggregator’s EV charging-scheduling problem under the assumption of variable maximum charging power.
- We propose mathematical formulations for two different charging schemes: non-preemptive and preemptive charging.
- We also introduce an adaptation of the proposed formulation as a way of preventing frequent interruptions in the charging process.
- Our numerical simulations compare the different charging schemes and demonstrate that preemptive charging with limited interruptions is an attractive alternative in terms of both cost and practicality.
- We also show that our formulation is computationally efficient in solving practical, large-scale charging-scheduling problems.
2. Scenario Description
2.1. Aggregator Settings
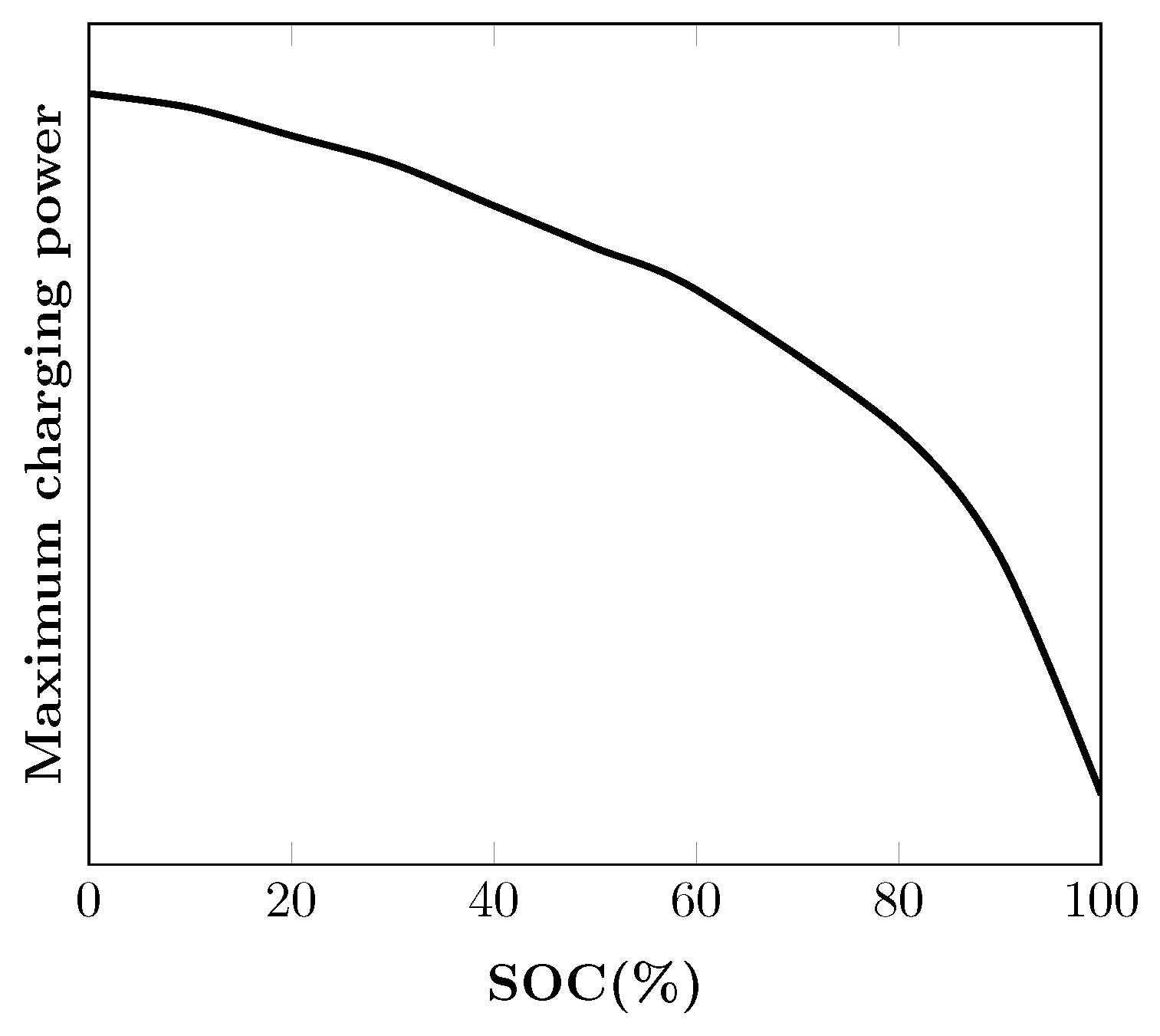
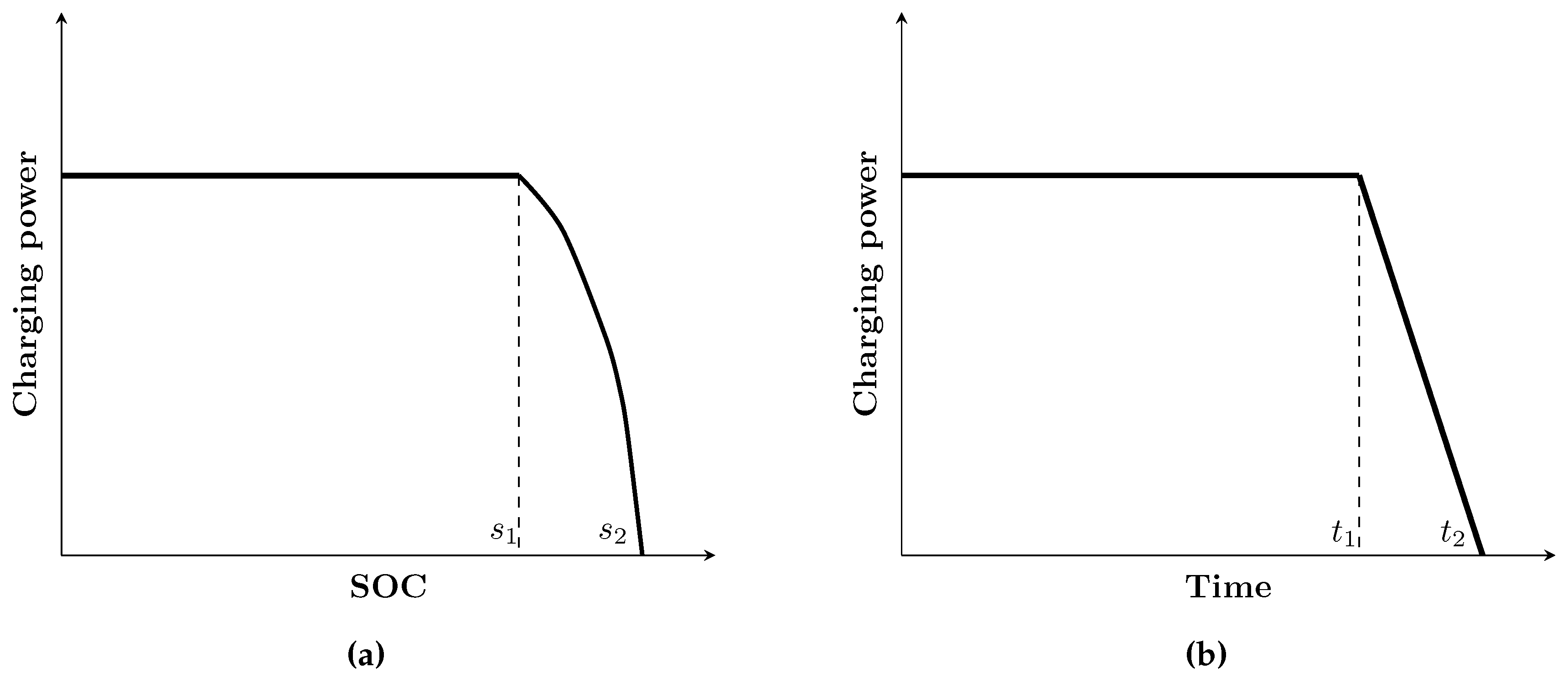
2.2. Variable Maximum Charging Power
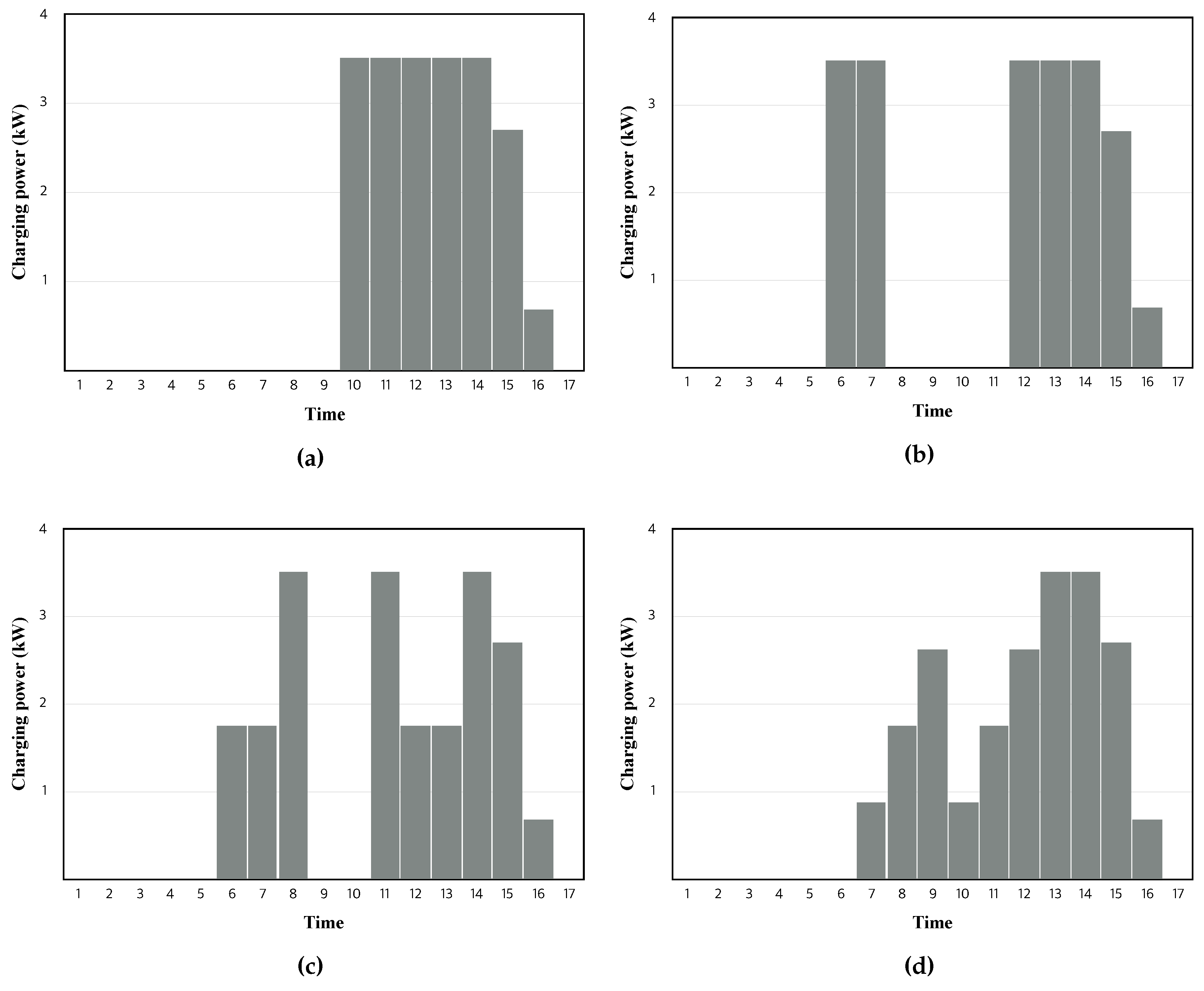
2.3. Charging Schemes
3. Problem Formulation
3.1. Non-Preemptive Charging
3.2. Preemptive Charging
- Charging transition : EV v with SOC level k at the outset of time t is charged during time t,
- Idle transition : EV v with SOC level k at the outset of time t is not charged during time t.
3.3. Controlling Frequency of Interruption
4. Numerical Simulations
4.1. Simulation Settings
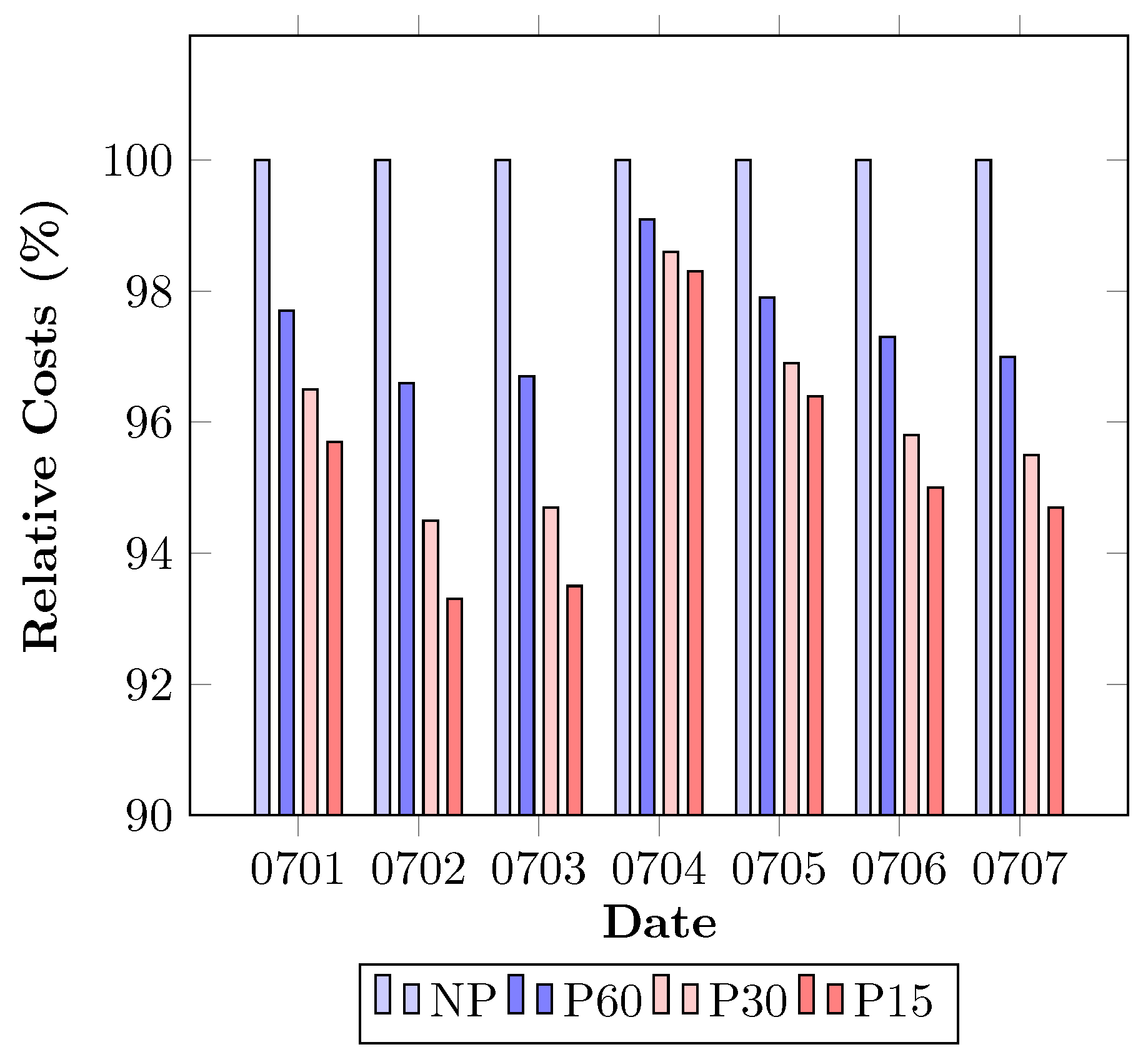
4.2. Results and Discussion
- NP: Non-preemptive charging,
- P60: Preemptive charging with = 60 min,
- P30: Preemptive charging with = 30 min,
- P15: Preemptive charging with = 15 min.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Sortomme, E.; Hindi, M.M.; MacPherson, S.J.; Venkata, S. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses. IEEE Trans. Smart Grid 2011, 2, 198–205. [Google Scholar] [CrossRef]
- Clement, K.; Haesen, E.; Driesen, J. Coordinated charging of multiple plug-in hybrid electric vehicles in residential distribution grids. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–7. [Google Scholar]
- Bessa, R.J.; Matos, M.A. The role of an aggregator agent for EV in the electricity market. In Proceedings of the 7th Mediterranean Conference and Exhibition on Power Generation, Transmission, Distribution and Energy Conversion (MedPower 2010), Agia Napa, Cyprus, 7–10 November 2010; pp. 1–9. [Google Scholar]
- Momber, I.; Wogrin, S.; San Román, T.G. Retail pricing: A bilevel program for PEV aggregator decisions using indirect load control. IEEE Trans. Power Syst. 2016, 31, 464–473. [Google Scholar] [CrossRef]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Cao, Y.; Tang, S.; Li, C.; Zhang, P.; Tan, Y.; Zhang, Z.; Li, J. An optimized EV charging model considering TOU price and SOC curve. IEEE Trans. Smart Grid 2012, 3, 388–393. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Resource scheduling under uncertainty in a smart grid with renewables and plug-in vehicles. IEEE Syst. J. 2012, 6, 103–109. [Google Scholar] [CrossRef]
- Korolko, N.; Sahinoglu, Z. Robust Optimization of EV charging schedules in unregulated rlectricity markets. IEEE Trans. Smart Grid 2017, 8, 149–157. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, L.; Ouyang, M.; Wang, H.; Lu, L.; Li, J.; Li, Z. Optimal decentralized valley-filling charging strategy for electric vehicles. Energy Convers. Manag. 2014, 78, 537–550. [Google Scholar] [CrossRef]
- Wu, D.; Aliprantis, D.C.; Ying, L. Load scheduling and dispatch for aggregators of plug-in electric vehicles. IEEE Trans. Smart Grid 2012, 3, 368–376. [Google Scholar] [CrossRef]
- Vayá, M.G.; Andersson, G. Optimal bidding strategy of a plug-in electric vehicle aggregator in day-ahead electricity markets under uncertainty. IEEE Trans. Power Syst. 2015, 30, 2375–2385. [Google Scholar] [CrossRef]
- You, P.; Yang, Z.; Chow, M.Y.; Sun, Y. Optimal Cooperative Charging Strategy for a Smart Charging Station of Electric Vehicles. IEEE Trans. Power Syst. 2016, 31, 2946–2956. [Google Scholar] [CrossRef]
- Jin, C.; Tang, J.; Ghosh, P. Optimizing electric vehicle charging with energy storage in the electricity market. IEEE Trans. Smart Grid 2013, 4, 311–320. [Google Scholar] [CrossRef]
- Rivera, J.; Goebel, C.; Jacobsen, H.A. Distributed convex optimization for electric vehicle aggregators. IEEE Trans. Smart Grid 2017, 4, 1852–1863. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S.H. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 28, 940–951. [Google Scholar] [CrossRef]
- de Hoog, J.; Alpcan, T.; Brazil, M.; Thomas, D.A.; Mareels, I. Optimal charging of electric vehicles taking distribution network constraints into account. IEEE Trans. Power Syst. 2015, 30, 365–375. [Google Scholar] [CrossRef]
- Han, S.; Han, S.; Sezaki, K. Development of an optimal vehicle-to-grid aggregator for frequency regulation. IEEE Trans. Smart Grid 2010, 1, 65–72. [Google Scholar]
- Gan, L.; Topcu, U.; Low, S.H. Stochastic distributed protocol for electric vehicle charging with discrete charging rate. In Proceedings of the Name of the Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Binetti, G.; Davoudi, A.; Naso, D.; Turchiano, B.; Lewis, F.L. Scalable real-time electric vehicles charging with discrete charging rates. IEEE Trans. Smart Grid 2015, 6, 2211–2220. [Google Scholar] [CrossRef]
- Beaude, O.; Lasaulce, S.; Hennebel, M.; Mohand-Kaci, I. Reducing the Impact of EV Charging Operations on the Distribution Network. IEEE Trans. Smart Grid 2016, 7, 2666–2679. [Google Scholar] [CrossRef]
- Sun, B.; Huang, Z.; Tan, X.; Tsang, D.H. Optimal Scheduling for Electric Vehicle Charging with Discrete Charging Levels in Distribution Grid. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Rotering, N.; Ilic, M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets. IEEE Trans. Power Syst. 2011, 26, 1021–1029. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, F. Scheduling for charging plug-in hybrid electric vehicles. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 2495–2501. [Google Scholar]
- Huang, Q.; Jia, Q.S.; Qiu, Z.; Guan, X.; Deconinck, G. Matching EV charging load with uncertain wind: A simulation-based policy improvement approach. IEEE Trans. Smart Grid 2015, 6, 1425–1433. [Google Scholar] [CrossRef]
- Xu, Y.; Pan, F.; Tong, L. Dynamic Scheduling for Charging Electric Vehicles: A Priority Rule. IEEE Trans. Autom. Control 2016, 61, 4094–4099. [Google Scholar] [CrossRef]
- Vayá, M.G.; Andersson, G.; Boyd, S. Decentralized control of plug-in electric vehicles under driving uncertainty. In Proceedings of the Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Istanbul, Turkey, 12–15 Octomber 2014; pp. 1–6. [Google Scholar]
- Sortomme, E.; El-Sharkawi, M.A. Optimal combined bidding of vehicle-to-grid ancillary services. IEEE Trans. Smart Grid 2012, 3, 70–79. [Google Scholar] [CrossRef]
- Yao, W.; Zhao, J.; Wen, F.; Xue, Y.; Ledwich, G. A hierarchical decomposition approach for coordinated dispatch of plug-in electric vehicles. IEEE Trans. Power Syst. 2013, 28, 2768–2778. [Google Scholar] [CrossRef]
- Talebizadeh, E.; Rashidinejad, M.; Abdollahi, A. Evaluation of plug-in electric vehicles impact on cost-based unit commitment. J. Power Sources 2014, 248, 545–552. [Google Scholar] [CrossRef]
- Valentine, K.; Temple, W.G.; Zhang, K.M. Intelligent electric vehicle charging: Rethinking the valley-fill. J. Power Sources 2011, 196, 10717–10726. [Google Scholar] [CrossRef]
- Ma, Z.; Callaway, D.S.; Hiskens, I.A. Decentralized charging control of large populations of plug-in electric vehicles. IEEE Trans. Control Syst. Technol. 2013, 21, 67–78. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Vandael, S.; Boucké, N.; Holvoet, T.; De Craemer, K.; Deconinck, G. Decentralized coordination of plug-in hybrid vehicles for imbalance reduction in a smart grid. In Proceedings of the Name of the 10th International Conference on Autonomous Agents and Multiagent Systems, Taipei, Taiwan, 2–6 May 2011; pp. 803–810. [Google Scholar]
- Mukherjee, J.C.; Gupta, A. A review of charge scheduling of electric vehicles in smart grid. IEEE Syst. J. 2015, 9, 1541–1553. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Foley, A. Computational scheduling methods for integrating plug-in electric vehicles with power systems: A review. Renew. Sustain. Energy Rev. 2015, 51, 396–416. [Google Scholar] [CrossRef]
- Zhang, P.; Qian, K.; Zhou, C.; Stewart, B.G.; Hepburn, D.M. A methodology for optimization of power systems demand due to electric vehicle charging load. IEEE Trans. Power Syst. 2012, 27, 1628–1636. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows: Theory, Algorithms, and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993; ISBN 0-13-027765-7. [Google Scholar]
- PJM. PJM Power Market, 2016. Available online: http://www.pjm.com (accessed on 30 October 2016).
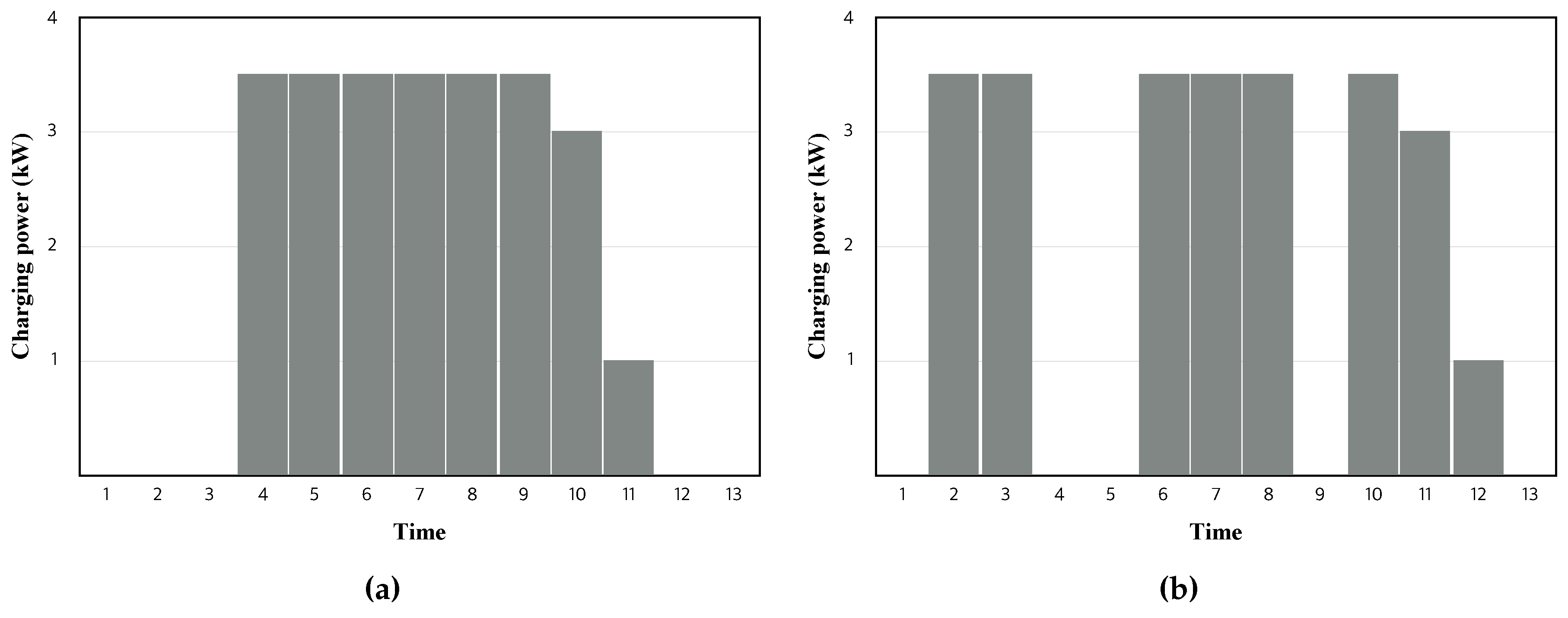

| Parameter | PCP-E | PCP | |||||
|---|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | ||
| 500 | 600 | 1.1 | 0.8 | 1.5 | 4.2 | 1.9 | 19.4 |
| 750 | 0.9 | 0.8 | 1.3 | 33.4 | 1.6 | 300* | |
| 900 | 0.9 | 0.8 | 1.0 | 2.0 | 1.0 | 2.5 | |
| 1000 | 1200 | 2.2 | 1.9 | 3.6 | 11.9 | 5.5 | 58.0 |
| 1500 | 2.0 | 1.8 | 3.5 | 5.8 | 2.9 | 11.5 | |
| 1800 | 2.0 | 1.9 | 2.1 | 5.3 | 3.6 | 8.6 | |
| 1500 | 1800 | 3.4 | 3.3 | 3.5 | 9.3 | 7.5 | 13.2 |
| 2250 | 2.9 | 2.8 | 3.0 | 8.1 | 6.5 | 10.0 | |
| 2700 | 3.1 | 2.9 | 3.3 | 7.7 | 7.0 | 9.4 | |
| 2000 | 2400 | 4.8 | 4.6 | 5.0 | 14.1 | 7.6 | 27.1 |
| 3000 | 4.0 | 3.8 | 4.2 | 21.5 | 4.5 | 122.5 | |
| 3600 | 4.2 | 3.9 | 4.5 | 10.4 | 4.6 | 23.1 | |
| 2500 | 3000 | 8.4 | 6.7 | 10.0 | 16.6 | 7.5 | 22.6 |
| 3750 | 5.4 | 5.2 | 5.6 | 11.8 | 6.0 | 17.1 | |
| 4500 | 5.9 | 5.3 | 7.1 | 15.5 | 8.0 | 24.1 | |
| 3000 | 3600 | 11.7 | 8.4 | 15.1 | 24.1 | 8.4 | 28.9 |
| 4500 | 6.9 | 6.6 | 7.4 | 19.2 | 7.2 | 49.8 | |
| 5400 | 7.6 | 6.7 | 8.4 | 17.6 | 7.3 | 24.8 | |
| Parameter | Non-Preemptive | Preemptive | Difference(%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | avg | min | max | ||
| 500 | 600 | 232 | 144 | 287 | 226 | 140 | 275 | 2.63 | 0.76 | 4.06 |
| 750 | 212 | 130 | 254 | 208 | 127 | 248 | 1.95 | 1.00 | 2.55 | |
| 900 | 206 | 124 | 244 | 203 | 121 | 239 | 1.49 | 0.85 | 2.40 | |
| 1000 | 1200 | 476 | 293 | 593 | 458 | 284 | 557 | 3.58 | 0.89 | 6.15 |
| 1500 | 429 | 264 | 511 | 420 | 258 | 499 | 1.93 | 0.94 | 2.53 | |
| 1800 | 416 | 251 | 493 | 409 | 244 | 480 | 1.86 | 1.09 | 2.85 | |
| 1500 | 1800 | 696 | 430 | 858 | 676 | 420 | 818 | 2.72 | 0.65 | 4.66 |
| 2250 | 629 | 388 | 747 | 620 | 381 | 733 | 1.55 | 0.75 | 2.00 | |
| 2700 | 612 | 371 | 721 | 603 | 362 | 705 | 1.51 | 0.83 | 2.36 | |
| 2000 | 2400 | 934 | 576 | 1159 | 899 | 557 | 1088 | 3.72 | 0.96 | 6.17 |
| 3000 | 840 | 517 | 998 | 824 | 505 | 976 | 1.89 | 0.94 | 2.48 | |
| 3600 | 816 | 492 | 961 | 803 | 479 | 938 | 1.60 | 0.92 | 2.59 | |
| 2500 | 3000 | 1174 | 723 | 1456 | 1132 | 701 | 1371 | 3.47 | 0.87 | 5.82 |
| 3750 | 1058 | 651 | 1258 | 1038 | 637 | 1229 | 1.89 | 0.90 | 2.45 | |
| 4500 | 1026 | 619 | 1210 | 1008 | 603 | 1179 | 1.75 | 0.99 | 2.62 | |
| 3000 | 3600 | 1404 | 866 | 1740 | 1358 | 842 | 1645 | 3.22 | 0.80 | 5.48 |
| 4500 | 1266 | 780 | 1504 | 1244 | 764 | 1474 | 1.70 | 0.82 | 2.26 | |
| 5400 | 1229 | 743 | 1450 | 1208 | 724 | 1414 | 1.66 | 0.97 | 2.52 | |
| Preemptive | Non-Preemptive | |||
|---|---|---|---|---|
| x = 0 | x = 0.5 | x = 1 | ||
| # Interruptions (average) | 0.76 | 0.52 | 0.49 | 0 |
| Total costs (average) | 19,629.2 | 19,631.9 | 19,637.5 | 20,113.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Park, J.; Lee, K. Optimal Scheduling for Electric Vehicle Charging under Variable Maximum Charging Power. Energies 2017, 10, 933. https://doi.org/10.3390/en10070933
Han J, Park J, Lee K. Optimal Scheduling for Electric Vehicle Charging under Variable Maximum Charging Power. Energies. 2017; 10(7):933. https://doi.org/10.3390/en10070933
Chicago/Turabian StyleHan, Jinil, Jongyoon Park, and Kyungsik Lee. 2017. "Optimal Scheduling for Electric Vehicle Charging under Variable Maximum Charging Power" Energies 10, no. 7: 933. https://doi.org/10.3390/en10070933
APA StyleHan, J., Park, J., & Lee, K. (2017). Optimal Scheduling for Electric Vehicle Charging under Variable Maximum Charging Power. Energies, 10(7), 933. https://doi.org/10.3390/en10070933




