1. Introduction
Electric vehicles (EVs) and wind energy provide economic and environmental benefits, which demonstrate their large-scale interconnection possibilities at distribution grid level. EVs and wind power have capability to help reduce the emissions and depletion of fossil fuel. Despite the benefits, integration of EVs and wind generators (WGs) in the power network also causes adverse impacts because of the increased load from EV charging and intermittency of wind power [
1,
2]. The placement and number of EV loads and WGs impact the voltage profile in the distribution network. Similarly, studies have shown that uncoordinated charging of EVs leads increased peak demand, which impacts the overall reliability of the grid [
3,
4]. Also, the presence of EVs can cause increased power losses and power quality issues including harmonic distortions in the distribution grids.
Past studies focus on optimal planning and dispatch of WGs, optimal EV scheduling, impact of EV loads in distribution grids, and combined impact of EVs and WGs to the distribution grid operations. A Genetic Algorithm (GA) based approach is used in [
5] to determine the location and size of the distributed generators (DGs) with feeder loss minimization as the objective. In [
6], a multi-objective programming and decision theory based approach is used to solve voltage quality and total harmonic distortion (THD) issues with the help of DGs. Similar studies are carried out in [
7,
8,
9], where Particle Swarm Optimization (PSO) is used for optimal siting and sizing of DGs with objectives to reduce THDs and to improve voltage profiles in the grid.
Uncoordinated charging of a large number of EVs impacts the overall residential load curve, increases power losses, causes overloading of lines, and also increases harmonics in the power grid due to non-linearity. Two EV charging schemes are considered in [
10] to analyze such adverse impacts. In the uncoordinated random charging scenario, maximum node voltage deviation and poor power quality are observed. However, power losses and voltage THDs are found much less in the case of coordinated charging of EVs. In [
10], it is demonstrated that when the EV penetration is low, THDs are not significant and the scenario is not concerning to the utilities. Similar conclusion is made in [
11] that low EV penetration may not cause significant impact on THDs. Harmonics in EV currents cause abnormal operation including increased power losses, temperature rise, premature insulation and windings failure of transformers, etc. [
12]; this can cause adverse impacts on reliability, security, and efficiency of the power grid. Previous studies carried out in [
10,
12,
13,
14] find the impact on harmonics due to the integration of EVs; however, these studies do not consider WGs in the network which has potentials to reduce THDs if operated in coordination with the EVs. In [
15], EVs and WGs are considered to demonstrate their impacts on voltage THDs but without considering the possible coordinated operations of EVs and WGs to reduce THDs. Uncoordinated charging of EVs in a system with significant WGs can lead to significant harmonic distortions that may exceed IEEE prescribed limits [
16].
Power-electronic interfacing based devices used in the EV chargers and WG system cause harmonic currents. The current drawn by EVs contains significant 5th , 7th , 11th , and 13th harmonic components [
17,
18]. The harmonic profiles of WGs show significant 2nd to 8th, 11th, and 13th harmonic currents [
19]. It is interesting to note that WGs and EVs have some common harmonic profiles. Therefore, when EVs are connected to the grid, the harmonic pollution EVs impart onto the grid can be reduced to some extent by the amount of wind power injecting into the grid and vice versa. In this context, this work studies the impact of EVs on harmonic distortions and careful utilization of wind power to minimize the distortions in distribution feeders.
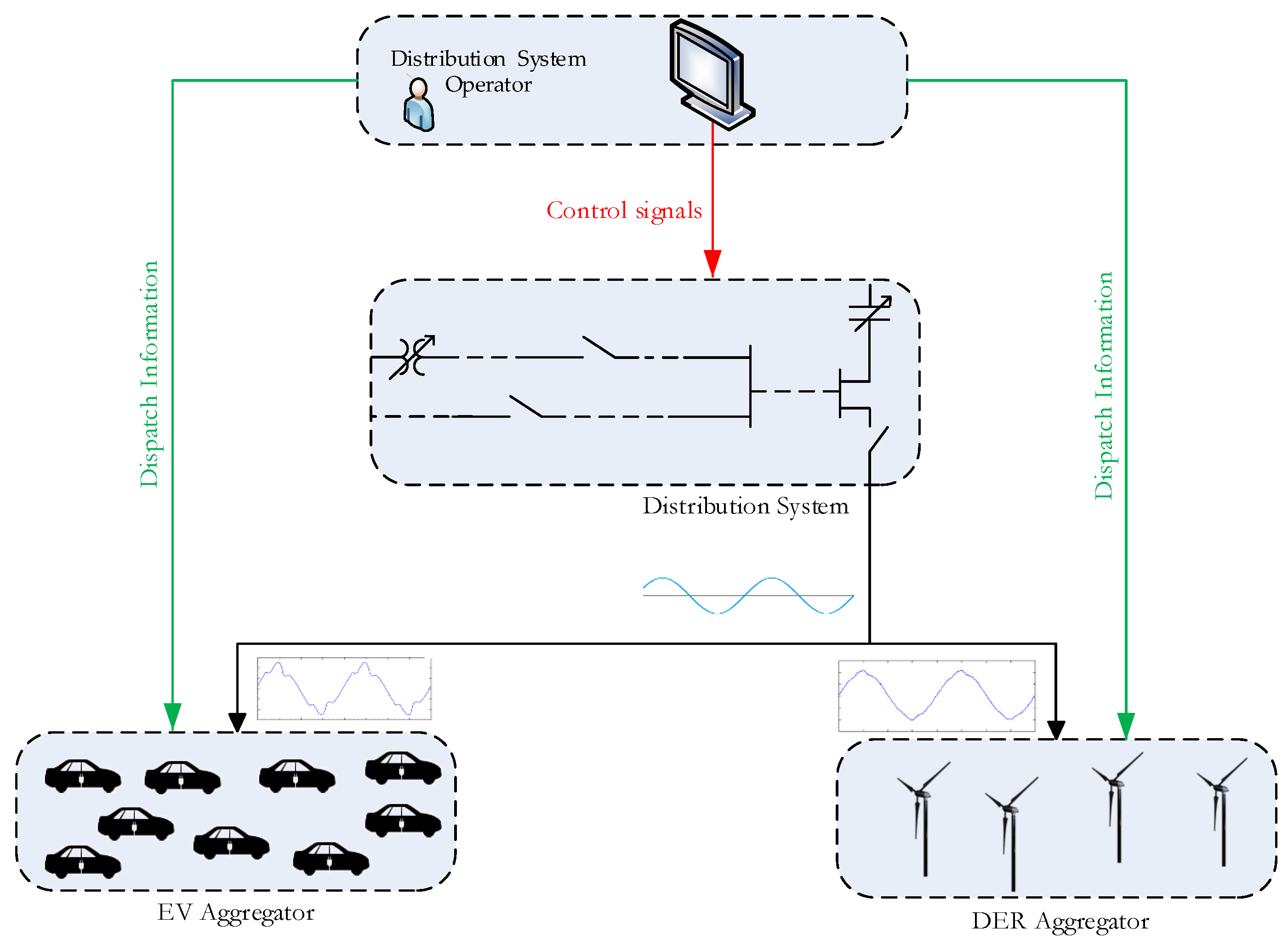
Figure 1 shows a high-level conceptual diagram that demonstrates the distorted currents withdrawn by EVs can be compensated by controlling WG output power. The distribution system operator can send dispatch signals to wind farm and EV aggregators to achieve this objective. The distribution system operator requires harmonic analysis tools and optimal harmonic power flow type models to reduce the harmonic pollution by controlling EV charging and WG output. In this context, this paper contributes on the following:
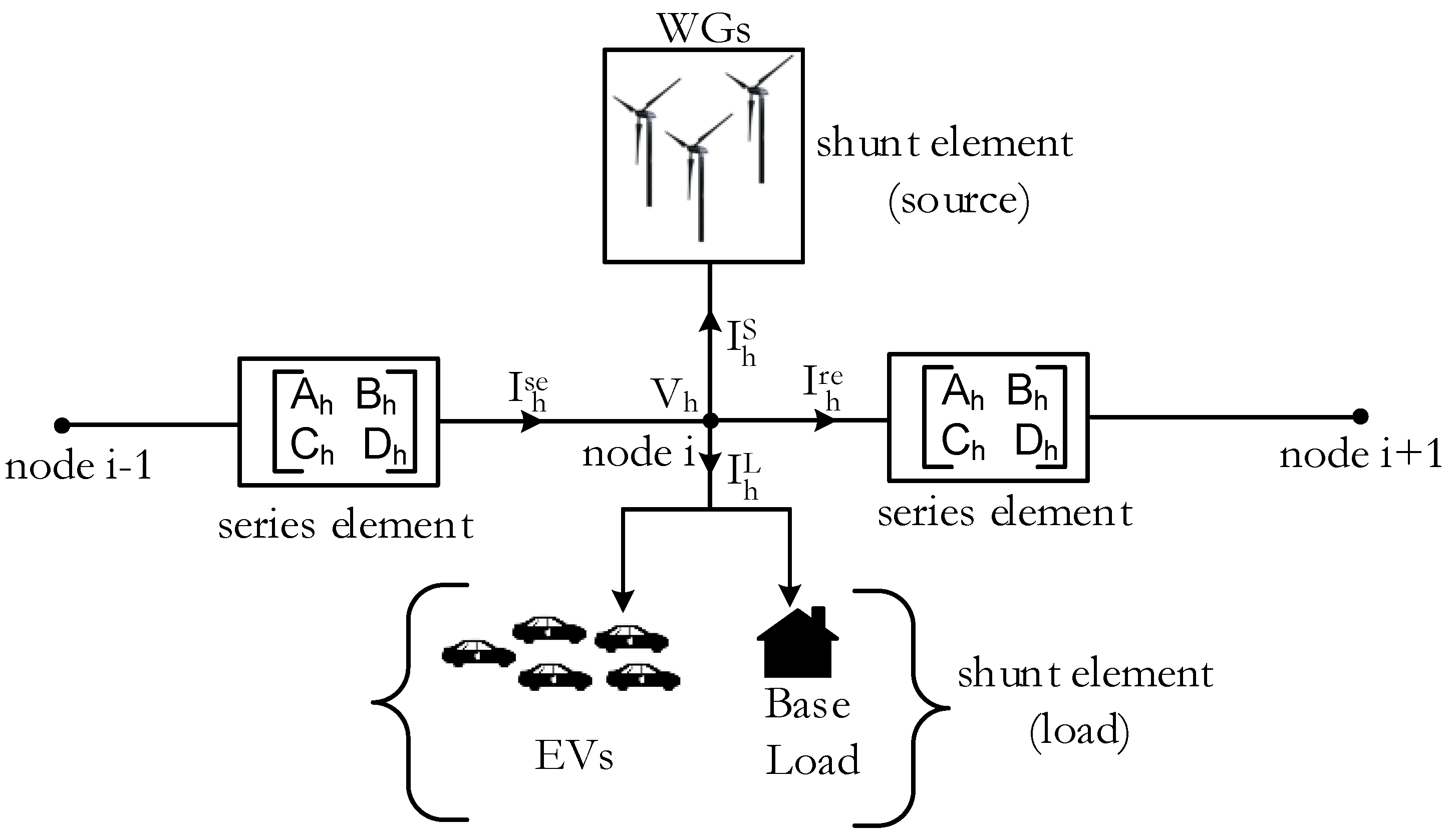
To develop a three-phase unbalanced distribution system model required for harmonic power flow (HPF) studies. The model is used to study the impact of EVs on voltage and current THDs in distribution system with varying degree of penetration. The same model is used to demonstrate that careful dispatch of WGs can help to reduce the harmonic distortions caused by the EVs.
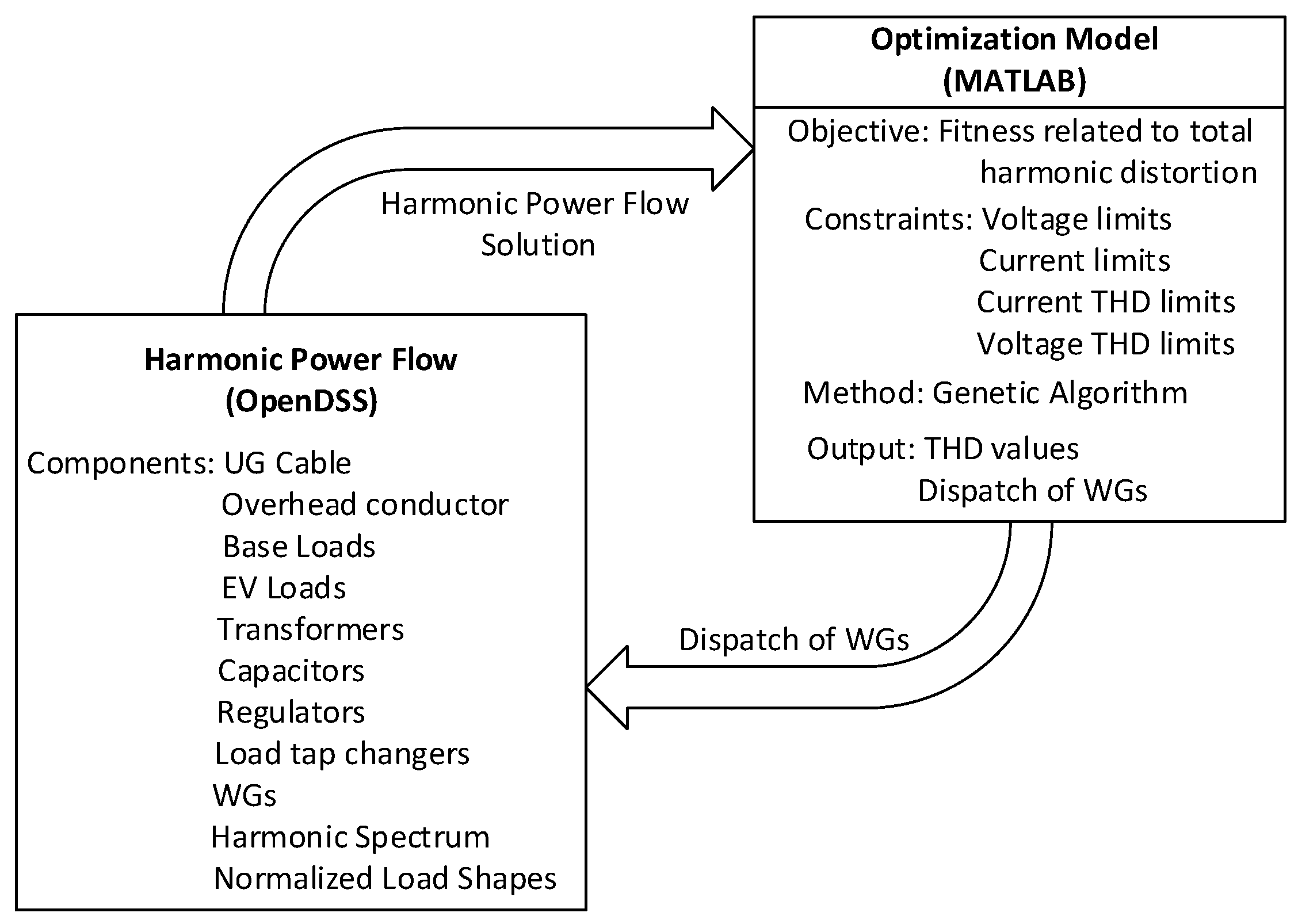
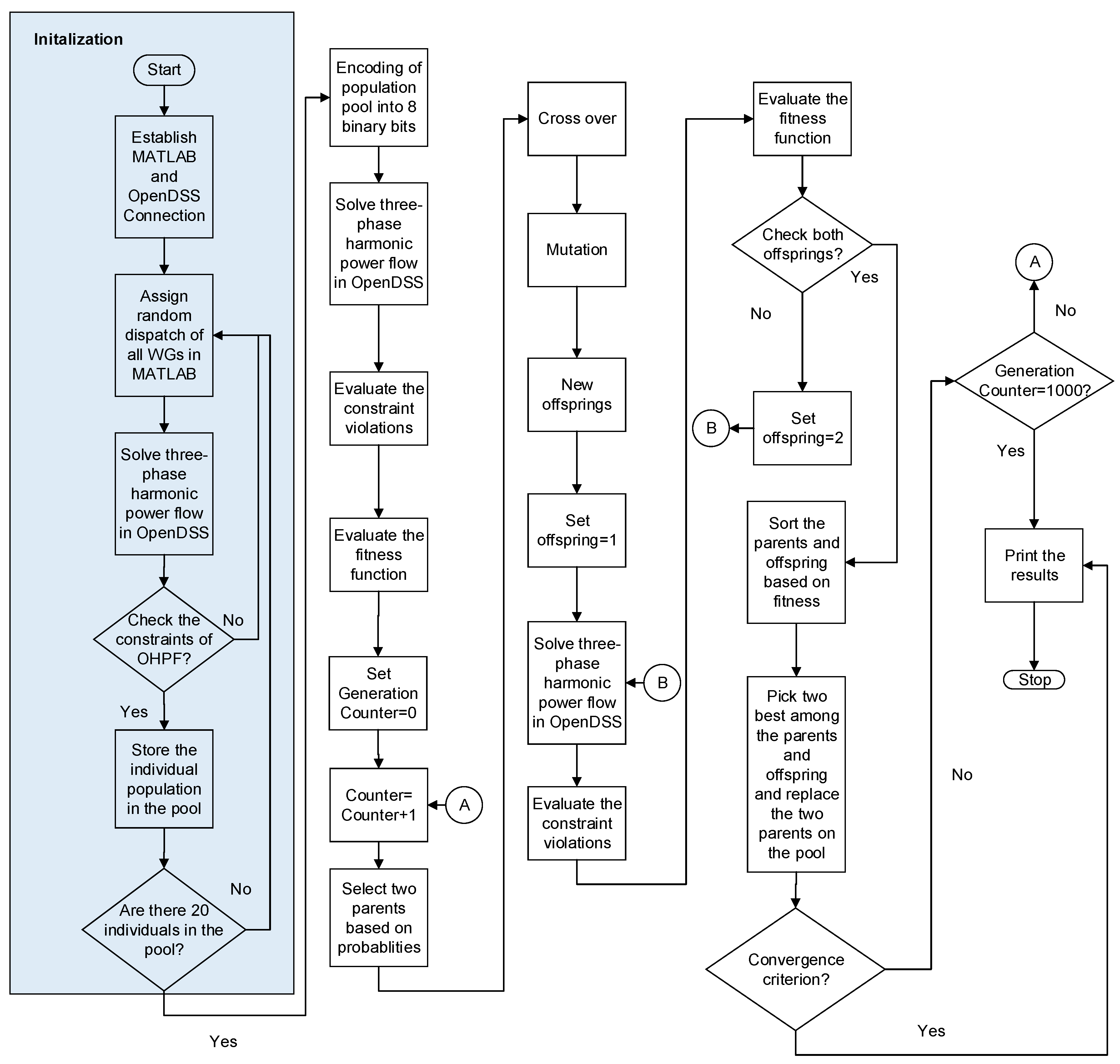
To develop optimal harmonic power flow (OHPF) model that utilizes previous HPF model as constraints and WGs as decision variables, and solution method based on GA. The model is then used to find optimal dispatch WGs that will reduce the voltage or current THDs in the distribution circuit with varying penetration level of the EVs.
The rest of the paper is organized as follows:
Section 2 describes the HPF and and OHPF models.
Section 3 presents the solution approach.
Section 4 discusses impact of low and high EV penetration on IEEE 34-node distribution test feeder. The results of the OHPF is presented in the
Section 5. A summary of the presented work is discussed in
Section 6.
4. Impact of EV Penetration on THD
To demonstrate the impact of EV on THD, IEEE 34-node test feeder is considered. Level-2 charging infrastructure is assumed with a socket rating of 8.8 kW. The number of EVs is calculated based on the 30% residential load mix in the aggregated load profile (base load), the average residential monthly energy of 1500 kWh and average hourly electricity load of 2.0833 kW [
2]. EV current harmonic profiles are obtained from [
17,
18] and are listed in
Table 1. Wind generator current harmonic profiles are obtained from [
19], which are listed in
Table 2.
First, an uncoordinated EV-WG system is studied with low EV penetration, i.e., 30%. In the
Case-1, only base loads and the EV loads are considered. The system loads of the IEEE 34-node test feeder are used as base load at the fundamental frequency, i.e., 60 Hz. EVs are modeled as non-linear loads with no reactive power. For the
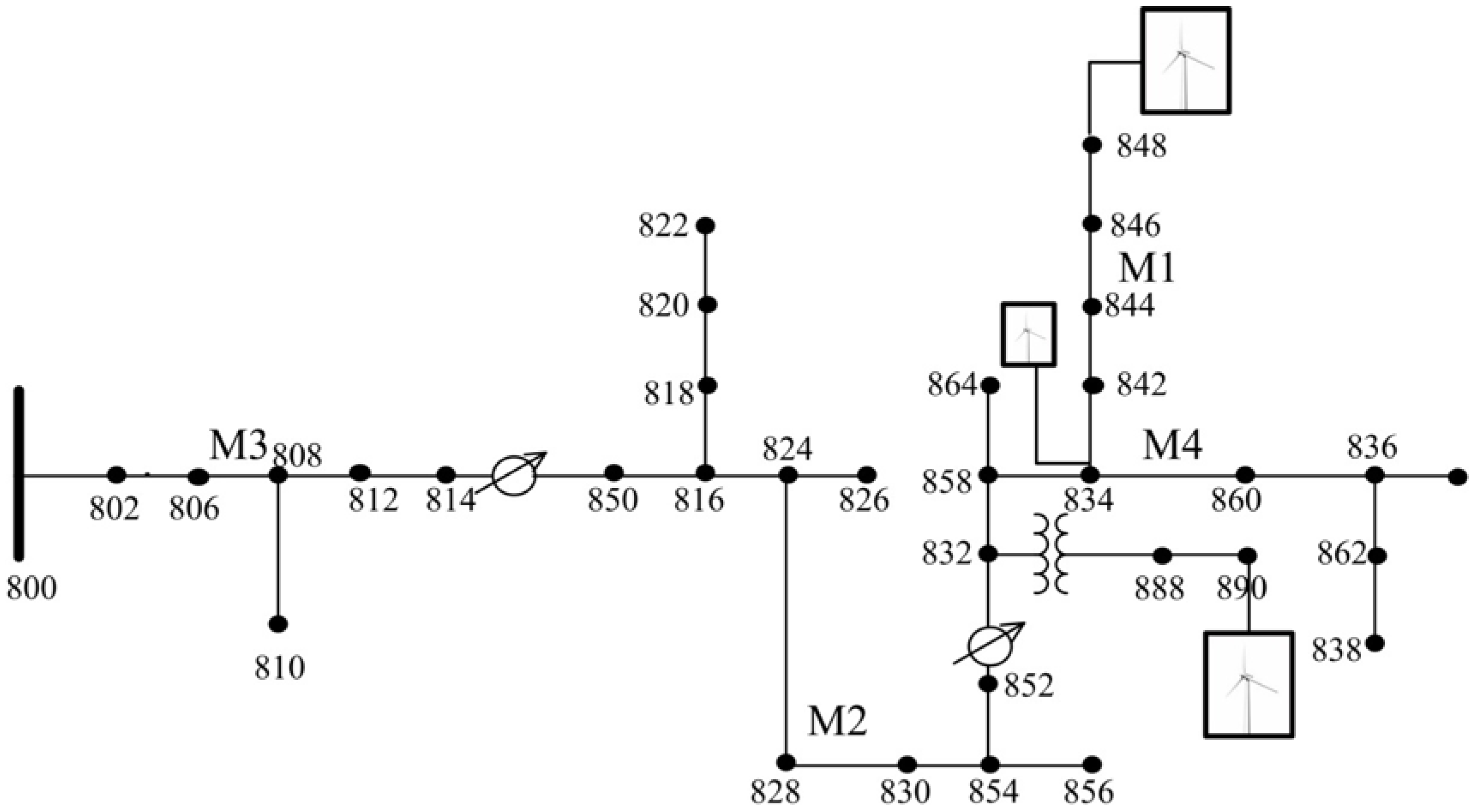
Case-2, one WG of 2 MW is added at node 848 as shown in
Figure 5. For the
Case-3, two more WGs of 2 MW are added at node 834 and node 890.
Table 3 lists voltage THDs obtained (for selective feeder sections) from the three case studies with low EV penetration. It can be seen that THD values are subsequently low, i.e., less than 5% and are under the limits prescribed by the IEEE [
16]. This implies that the lower EV penetration does not make significant impact on the voltage THDs. On the other hand, current THD values (see
Table 4) are higher in feeder sections away from the substation node. With the addition of WGs, the voltage THDs are reduced at some of the feeder nodes (e.g., THD of
at line 844–846). This is an interesting observation that the WGs can help reduce the harmonic distortions caused by the EV charging. Similarly, with the introduction of WGs, the current THD values are also significantly reduced in the range of 1.5–4.5%.
Three more case studies are carried out with large EV penetration, i.e., 100%.
Case-4 considers no WG, while
Case-5 and
Case-6 include 1 and 3 WGs, respectively. For 100% EV penetration, it is expected that the EV load will inject more harmonics into the system. Therefore, the current THDs are increased as high as 50% (see
Table 5), which is a clear indication that harmonics distortion gets worse with increased EV penetration. The voltage THDs are reached around 9.7% (see
Table 6). With the introduction of WGs, the current THDs are reduced below 8%, while the voltage THDs are reduced below 7%.
It can be inferred from the aforementioned case studies that the inclusion of WGs certainly helps to reduce the voltage/current THD values caused by the EVs. However, the positioning and sizing of the WGs make differences in the THD profile of the system. So, it would be more acceptable if the process is more systematic to bring down the THD values. To do it in a more acceptable and systematic way, in the next Section a GA based approach is used to reduce voltage and current THD in a system with EV penetration and WGs.
5. Reduction of Voltage and Current THDs
In this section, GA-based approach is used to optimally reduce the THDs by coordinated dispatch of EVs and WGs. Case studies with two EV penetration levels are discussed (low penetration of 30%, and high penetration of 100%). WGs are assumed to be connected at all nodes in the 34-node distribution feeder.
Case 7 considers 30% EV penetration and solves for optimal dispatch of WGs. The resulting voltage THDs are shown in
Table 7, and the corresponding optimal dispatch of WGs are shown in
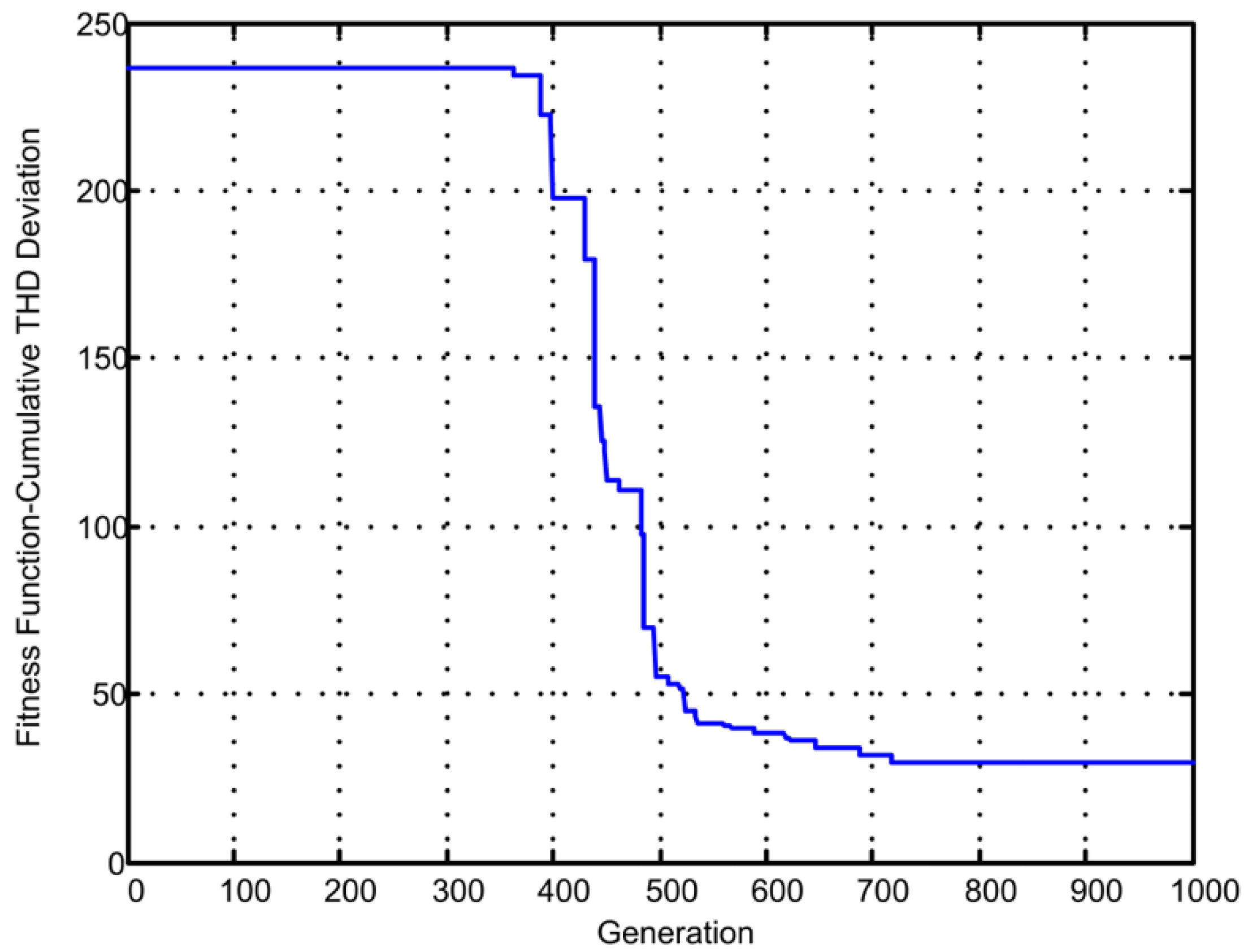
Table 8. In
Figure 6, the characteristics of the GA fitness function over the iteration is shown. The case studies demonstrate that the coordinated optimal dispatch of EVs and WGs significantly reduces the harmonics. The voltage THDs are below 3%.
Case 8 considers 100% EV penetration and solves for optimal dispatch of WGs. The resulting voltage THDs are shown in
Table 9, and the corresponding optimal dispatch of WGs are shown in
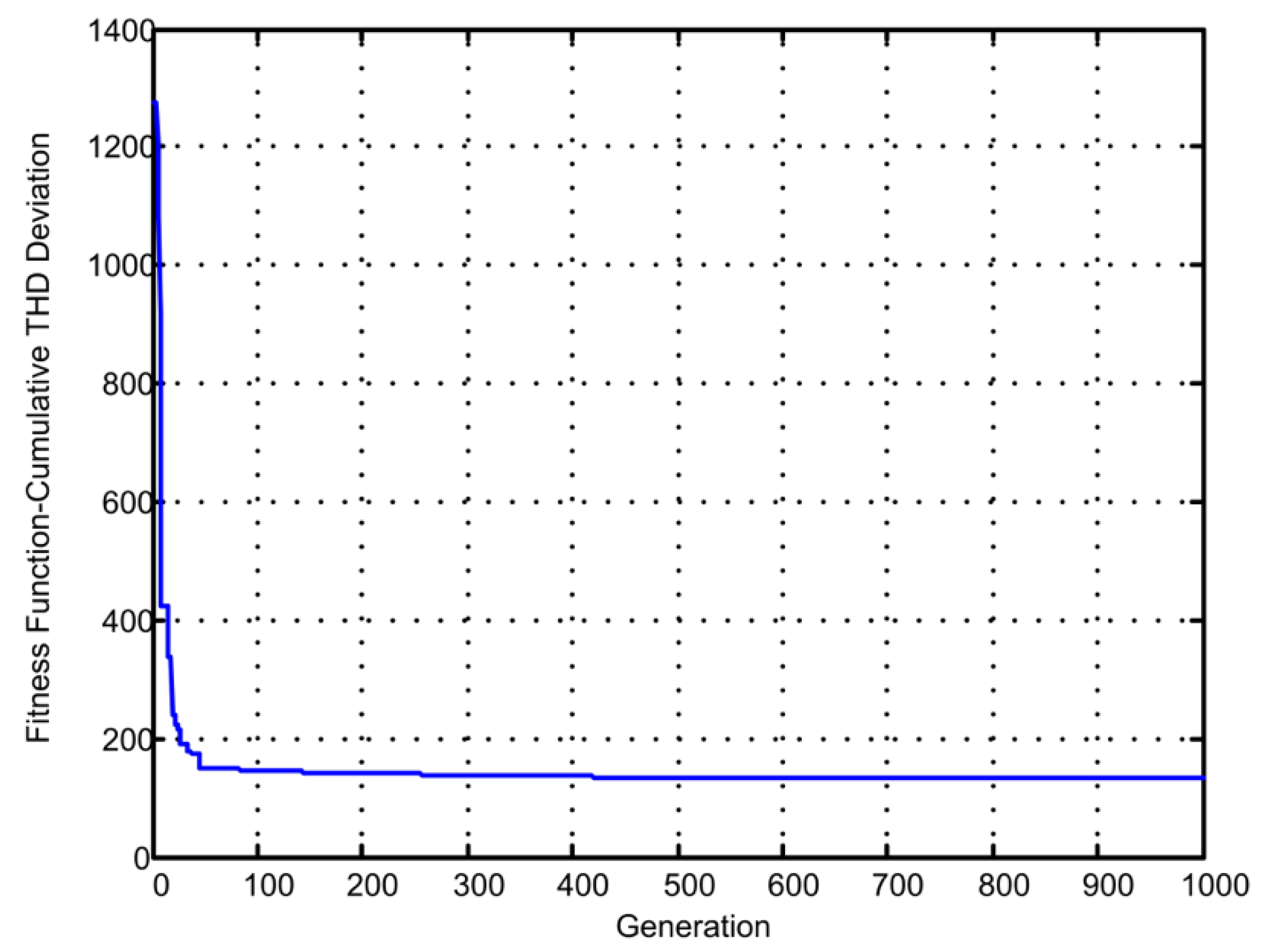
Table 10. In
Figure 7, the characteristics of the GA fitness function over the iteration is shown. The voltage THDs are obtained below 5%.
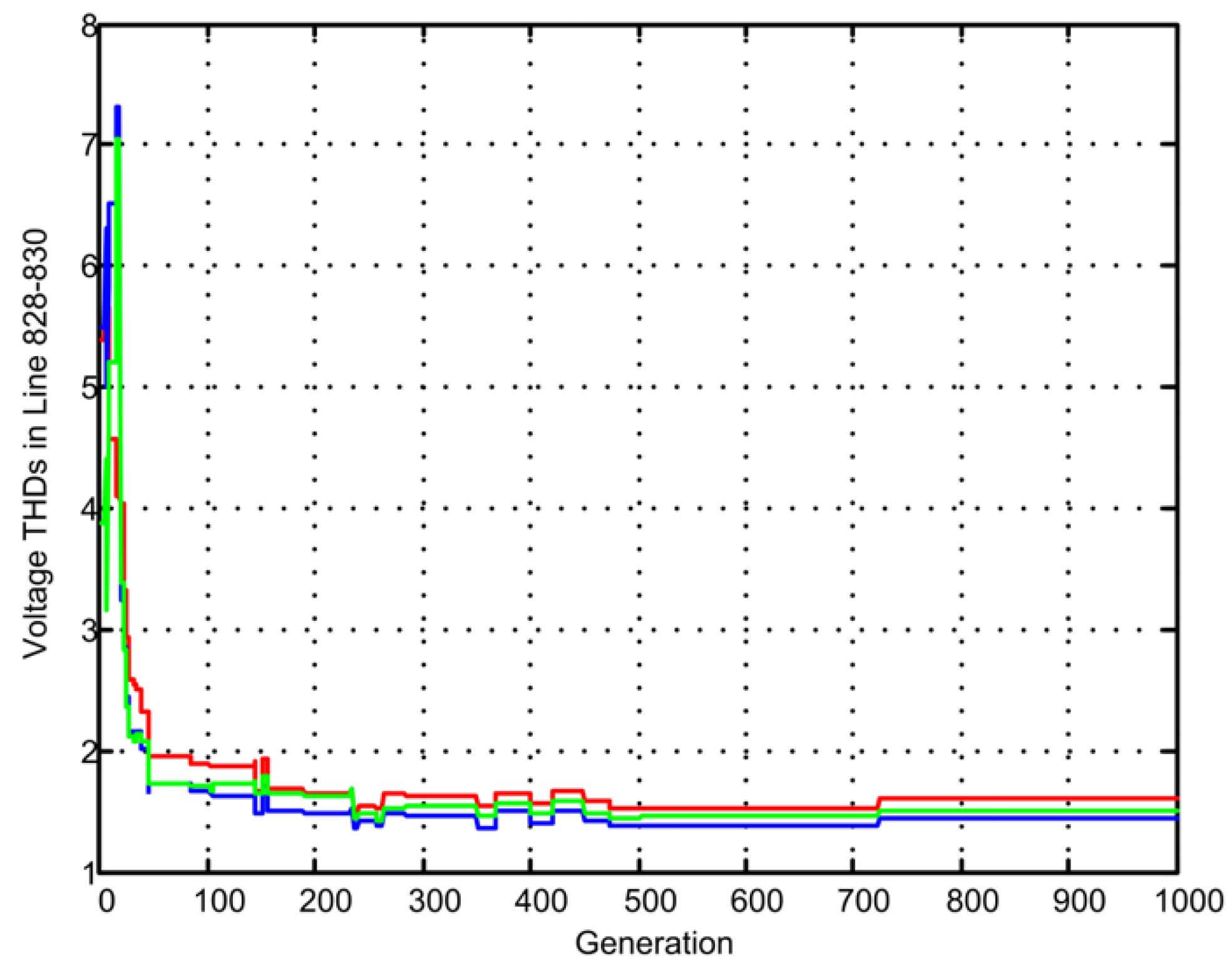
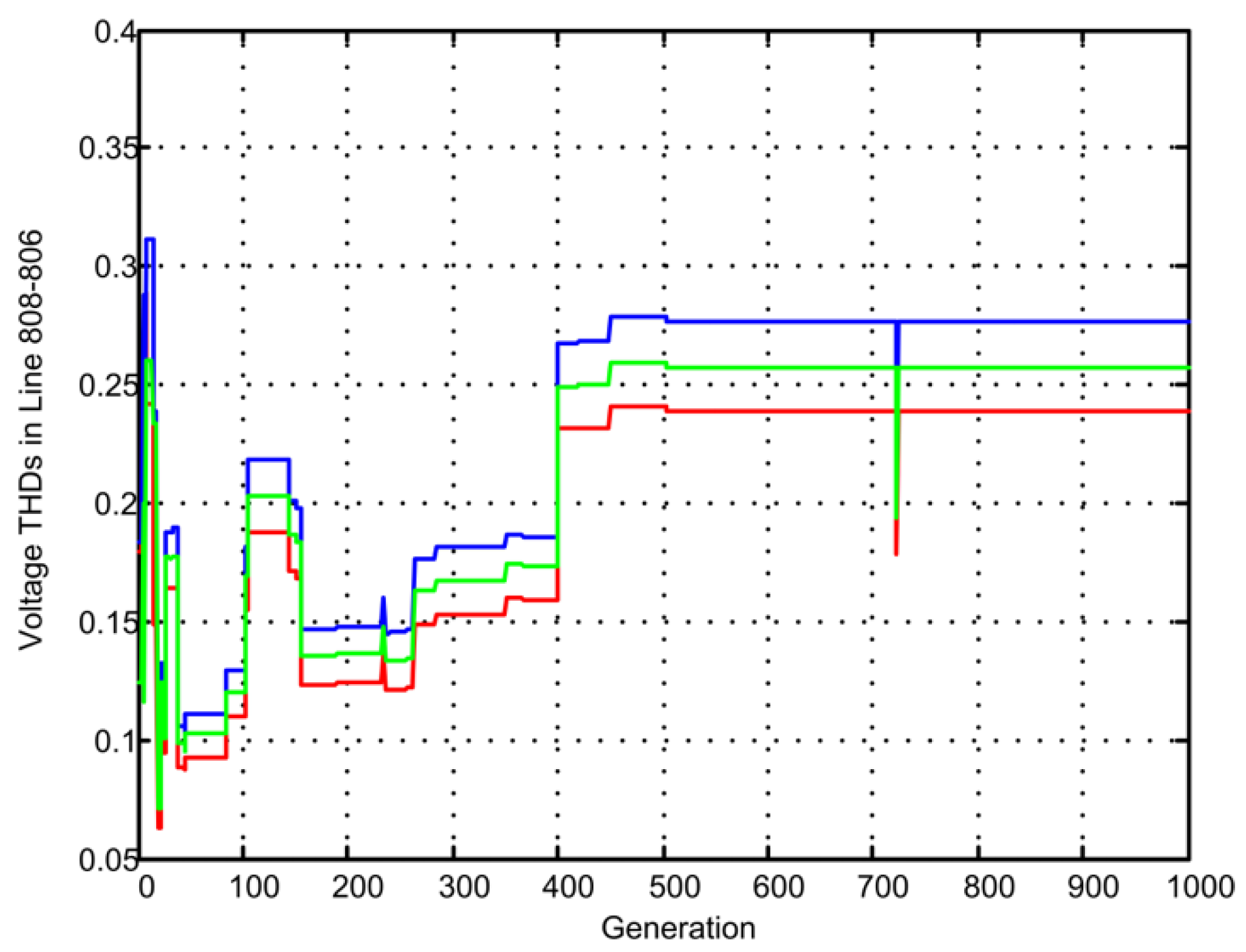
Figure 8 and
Figure 9 show the voltage THDs on two selective feeder branches. It is interesting to observe that THDs on individual feeder section could increase over the GA iterations given that the fitness function is the cumulative THDs over all the feeder sections. However; the individual THDs are well below 5%, which are the constraints included in the OHPF model.
The harmonic reduction observed in the coordinated optimal dispatch is significant as the voltage THDs reductions for high EV penetration are below 5% (compared to 10% in uncoordinated cases). Similarly, the current harmonic THDs are significantly reduced to 5% compared to 50% in uncoordinated cases. The GA algorithms took nearly one hour to run for each of the case studies in a Windows machine with 6 GB memory and 2.80 GHz processor. The optimality tolerance was set at ; however, the solution might have converged locally as the GA method alone does not guarantee global optimal solutions.
6. Conclusions
In this paper, a harmonic decoupled power flow model is developed to study the impact of EVs and WGs on the current and voltage THDs. Simulations carried out in the IEEE 34-node test feeder demonstrate that low EV penetration is not a concern for voltage THDs, as the THDs are below 5%, which are within the limits prescribed by the IEEE. However, low EV penetration is shown to have significant impacts on current THDs. Also, high penetration of EVs are shown to have adverse impacts on both current and voltage THDs. With the integration of WGs in the test feeder consisting of EV loads, it is demonstrated that WGs can help to reduce THDs at some nodes in the feeder, while it causes increased THDs at other nodes. This demonstrated that WGs have the capability to reduce the THDs caused by the EVs. However, the appropriate dispatch of WGs is to be determined in order to achieve the benefits of WGs to reduce THDs. Thus, this paper also presented a GA based method to find optimal dispatch of WGs in the IEEE 34-node test feeder to reduce the voltage and current THDs at each node and phase of the test feeder below the IEEE limits.